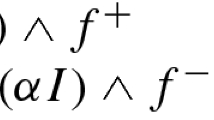On special elements and pseudocomplementation in lattices with antitone involutions

Abstract

The so-called basic algebras correspond in a natural way to lattices with antitone involutions and hence generalize both MV-algebras and orthomodular lattices. The paper deals with several types of special elements of basic algebras and with pseudocomplemented basic algebras.

1 Introduction

The previous papers on the so-called basic algebras, or lattices with antitone involutions, often dealt only with particular cases when the antitone involutions had certain additional properties, which led either to algebras similar to MV-algebras [see Botur and Halaš (2008), Botur and Kühr (2014) and Krňávek and Kühr (2011)] or to lattice effect algebras [see Chajda and Kühr (2013a) and Kühr et al. (2015)]. Recently, we realized that some results on such special algebras are actually related to the properties of certain elements rather than to the properties of the algebras as such, or have to do with the fact that these algebras (lattices) are sometimes pseudocomplemented. In the present paper, we collect several observations of this kind.

The exact definitions are given in Sect. 2, but to give a flavour of the structures and results in question, the situation is as follows. Suppose that $(A,\vee ,\wedge ,0,1)$ is a bounded lattice and every principal filter [a, 1] is equipped with an antitone involution $f_a$. For instance, in algebras of logic such as MV-algebras, $f_a$ could be the restriction of implication $\rightarrow$ to the pairs (x, a) with $x\ge a$, i.e. $f_a(x)=x\rightarrow a$ for $x\ge a$. If we define $\lnot x=f_0(x)$ and $x\oplus y=f_y(\lnot x\vee y)$ for all $x,y\in A$, the algebra $(A,\oplus ,\lnot ,0,1)$ is lattice-ordered, with $x\le y$ iff $\lnot x\oplus y=1$, and $f_a(x)=\lnot x\oplus a$ for all $a\in A$ and $x\ge a$. These algebras are called basic algebras [see Chajda et al. (2009a)].

Already in Chajda et al. (2009a), special attention was paid to the set $\mathcal {S}(A)$ of sharp elements of the algebra $(A,\oplus ,\lnot ,0,1)$, where an element $a\in A$ is sharp if $\lnot a$ is its complement in the lattice; the terminology is borrowed from effect algebras. There is not much to say about $\mathcal {S}(A)$ in general, though $\mathcal {S}(A)$ has a nice structure in some particular cases. For instance, in lattice effect algebras, $\mathcal {S}(A)$ forms an orthomodular lattice [see Jenča and Riečanová (1999)], and in basic algebras satisfying the identity $x\le x\oplus y$, it is a Boolean algebra [see Botur and Kühr (2014)]. The key property of sharp elements in basic algebras satisfying the latter identity is that $a\in \mathcal {S}(A)$ iff $a\oplus x=a\vee x$ for every $x\in A$. Hence, in Sect. 3, given an arbitrary basic algebra $(A,\oplus ,\lnot ,0,1)$, we focus on the set $\mathcal {B}(A)$ of those elements $a\in A$ which have this property. It turns out that $\mathcal {B}(A)$ forms a Boolean subalgebra, and we therefore refer to the elements of $\mathcal {B}(A)$ as Boolean. We prove that the Boolean elements correspond to certain congruences of the “i-lattice” $(A,\vee ,\wedge ,\lnot ,0,1)$. We also prove that every Boolean element is a neutral element of the underlying lattice, which gives rise to a few observations on distributive, standard and neutral elements.

In Sect. 4, we discuss two variants of Boolean elements, and as a corollary we obtain a simple characterization of central elements in basic algebras and in particular in lattice effect algebras. In Sect. 5, we study basic algebras with pseudocomplementation, i.e. algebras $(A,\oplus ,\lnot ,{^*},0,1)$, where $(A,\oplus ,\lnot ,0,1)$ is a basic algebra and ${^*}$ is pseudocomplementation on its underlying lattice. We describe the subdirectly irreducible basic algebras with pseudocomplementation satisfying the condition that the elements $a^*$ are central. This allows us to (re)prove that any finite basic algebra satisfying the identity¹ $x\oplus (y\wedge z)=(x\oplus y)\wedge (x\oplus z)$ is an MV-algebra [see Krňávek and Kühr (2011)].

2 Preliminaries

2.1 Basic algebras

We first recall some relevant facts about lattices with antitone involution(s)² and basic algebras [see Chajda et al. (2009a)].

A lattice with an antitone involution is an algebra $(A,{\vee },{\wedge },f,0,1)$ where $(A,{\vee },{\wedge }, 0,1)$ is a bounded lattice and f is an antitone involution on it, i.e. for all $x,y{\in } A$, one has:

$$\begin{aligned} x\le y \quad \text {iff}\quad f(y)\le f(x), \quad \text {and}\quad f(f(x))=x. \end{aligned}$$

In the literature, e.g. in Kalman (1958), these structures are sometimes called “i-lattices”. By a lattice with antitone involutions we mean a structure $(A,\vee ,\wedge ,(f_a)_{a\in A},0,1)$ where $(A,\vee ,\wedge ,0,1)$ is a bounded lattice and $(f_a)_{a\in A}$ is a collection of antitone involutions on the principal filters [a, 1], $a\in A$. In other words, for every $a\in A$, $([a,1],\vee ,\wedge ,f_a,a,1)$ is a lattice with an antitone involution.

Let $(A,\vee ,\wedge ,(f_a)_{a\in A},0,1)$ be a lattice with antitone involutions. With intent to generalize MV-algebras, we define “negation” and “addition” by

$$\begin{aligned} \lnot x=f_0(x) \quad \text {and}\quad x\oplus y=f_y(\lnot x\vee y), \end{aligned}$$

(2.1)

for all $x,y\in A$. The lattice operations can be expressed by

$$\begin{aligned} x\vee y{=}\lnot (\lnot x{\oplus } y)\oplus y \quad \text {and}\quad x\wedge y{=}\lnot (\lnot x\vee \lnot y), \end{aligned}$$

(2.2)

for all $x,y\in A$, and for every $a\in A$, the antitone involution $f_a$ on [a, 1] is given by

$$\begin{aligned} f_a(x)=\lnot x\oplus a, \end{aligned}$$

(2.3)

for $x\ge a$. The algebra $(A,\oplus ,\lnot ,0,1)$ obtained by (2.1) is the basic algebra associated with the lattice with antitone involutions $(A,\vee ,\wedge ,(f_a)_{a\in A},0,1)$; it satisfies the following identities:

$$\begin{aligned}&x\oplus 0=x, \end{aligned}$$

(2.4)

$$\begin{aligned}&\lnot \lnot x=x, \end{aligned}$$

(2.5)

$$\begin{aligned}&\lnot (\lnot x\oplus y)\oplus y=\lnot (\lnot y\oplus x)\oplus x, \end{aligned}$$

(2.6)

$$\begin{aligned}&\lnot (\lnot (\lnot (x\oplus y)\oplus y)\oplus z)\oplus (x\oplus z)=1. \end{aligned}$$

(2.7)

Axiomatically, a basic algebra is an algebra $(A,\oplus ,\lnot ,0,1)$ of type (2, 1, 0, 0) which satisfies identities (2.4)–(2.7). The definition of Chajda et al. (2009a) also contained the superfluous identities $x\oplus 1=1=1\oplus x$.

For any basic algebra $(A,\oplus ,\lnot ,0,1)$, (2.2) defines a bounded lattice (with bounds 0 and 1 and with induced order $x{\le } y$ iff $\lnot x\oplus y=1$), and for every $a{\!\in } A$, (2.3) defines an antitone involution $f_a$ on the principal filter [a, 1]. Thus, $(A,\vee ,\wedge ,(f_a)_{a\in A},0,1)$ is a lattice with antitone involutions. It is straightforward to show that the basic algebra associated with $(A,\vee ,\wedge ,(f_a)_{a\in A},0,1)$ via (2.1) is precisely the algebra $(A,\oplus ,\lnot ,0,1)$. Therefore, basic algebras are equivalent to lattices with antitone involutions, and when we want to make an ordered structure into a basic algebra, if possible, it suffices to show that it is a bounded lattice and that there are antitone involutions on the principal filters. For technical details, see Chajda et al. (2009a) or Chajda and Emanovský (2004).

In Chajda et al. (2009a), the motivation was to find a reasonable common generalization of orthomodular lattices and MV-algebras in the signature of MV-algebras; hence, orthomodular lattices and MV-algebras are our first examples of basic algebras (or lattices with antitone involutions). For completeness, we recall the definitions, though we assume some familiarity with the elements of orthomodular lattices and/or MV-algebras.

An orthomodular lattice is a lattice with an antitone involution $(A,\vee ,\wedge ,{^\perp },0,1)$ which satisfies the orthomodular law $x\le y$ $\Rightarrow$ $x\vee (x^\perp \wedge y)=y$. For every $a\in A$, $a^\perp$ is a complement of a. The standard reference is Kalmbach (1983). In any orthomodular lattice, the maps $f_a:x\mapsto x^\perp \vee a$ are antitone involutions on the principal filters [a, 1], and hence, if we put $\lnot x=f_0(x)=x^\perp$ and $x\oplus y=f_y(\lnot x\vee y)=(x^\perp \vee y)^\perp \vee y=(x\wedge y^\perp )\vee y$, then $(A,\vee ,\wedge ,{^\perp },0,1)$ can be regarded as $(A,\oplus ,\lnot ,0,1)$. Basic algebras corresponding to orthomodular lattices in this way can be axiomatized by the quasi-identity

$$\begin{aligned} x\le y \quad \Rightarrow \quad y\oplus x=y, \end{aligned}$$

(2.8)

which is a translation of the orthomodular law and which can obviously be replaced with the identity $x\oplus (x\wedge y)=x$. In particular, basic algebras corresponding to Boolean algebras can be axiomatized by this (quasi-)identity together with commutativity $x\oplus y=y\oplus x$, or simply by

$$\begin{aligned} x\oplus y=x\vee y. \end{aligned}$$

(2.9)

However, this does not mean that $(A,\vee ,\wedge ,\lnot ,0,1)$ is an orthomodular lattice or a Boolean algebra if and only if the basic algebra $(A,\oplus ,\lnot ,0,1)$ satisfies (2.8) or (2.9), respectively.

As a matter of fact, MV-algebras coincide with associative basic algebras, but the usual definition is this: An MV-algebra is an algebra $(A,\oplus ,\lnot ,0,1)$ of type (2, 1, 0, 0) such that $(A,\oplus ,0)$ is a commutative monoid satisfying identities (2.5), (2.6), $x\oplus 1=1$ and $\lnot 0=1$. We refer the reader to Cignoli et al. (2000). For any MV-algebra, rules (2.2) and (2.3) define a distributive lattice with antitone involutions, and basic algebras corresponding to these lattices with antitone involutions are exactly MV-algebras. Interestingly, an associative basic algebra is automatically commutative, hence an MV-algebra, but commutativity does not imply associativity; there exist infinite commutative basic algebras distinct from MV-algebras [cf. Krňávek and Kühr (2016) and Botur and Halaš (2008)].

Another important example of basic algebras is lattice effect algebras, including both MV-algebras and orthomodular lattices. An effect algebra is a structure $(A,+,0,1)$, where $+$ is a partial binary operation and 0, 1 distinguished constants, satisfying the following conditions:

• (i) $x+y=y+x$ if one side is defined;

• (ii) $x+(y+z)=(x+y)+z$ if one side is defined;

• (iii) for every $x\in A$ there exists a unique $x'\in A$ such that $x'+x=1$;

• (iv) $x+1$ is defined only if $x=0$.

Effect algebras were introduced in Foulis and Bennett (1994) and are equivalent to D-posets which were introduced in Kôpka and Chovanec (1994). For more information, we refer the reader to Dvurečenskij and Pulmannová (2000). A lattice effect algebra is an effect algebra $(A,+,0,1)$, which is a (bounded) lattice with respect to the natural order defined as follows:

$$\begin{aligned} x\le y \quad \text {iff}\quad y=z+x \text { for some } z\in A. \end{aligned}$$

For any $a\in A$, the map $f_a:x\mapsto x'+a$ is an antitone involution on [a, 1], whence $(A,+,0,1)$ can be made into a basic algebra by letting $\lnot x=f_0(x)=x'$ and $x\oplus y=f_y(\lnot x\vee y)=(x'\vee y)'+y=(x\wedge y')+y$. The basic algebra so obtained satisfies the quasi-identity³

$$\begin{aligned} x\oplus y\le \lnot z\quad \Rightarrow \quad (x\oplus y)\oplus z=x\oplus (y\oplus z). \end{aligned}$$

(2.10)

On the other hand, if a basic algebra $(A,\oplus ,\lnot ,0,1)$ satisfies (2.10), then the structure $(A,+,0,1)$, where $x+y$ is defined and is equal to $x\oplus y$ iff $x\le \lnot y$, is a lattice effect algebra in which $x'=\lnot x$, and the basic algebra associated with it is exactly $(A,\oplus ,\lnot ,0,1)$. Therefore, lattice effect algebras are equivalent to basic algebras satisfying (2.10). The quasi-identity (2.10) can be replaced with an identity; it suffices to write $\lnot (x\oplus y)\wedge z$ in place of z.

Relative to (the variety of basic algebras equivalent to) lattice effect algebras, MV-algebras are characterized by $x\oplus y=y\oplus x$, and orthomodular lattices by $x\oplus x=x$ (or alternatively, by $x\wedge \lnot x=0$). The smallest variety containing both the variety of MV-algebras and the variety of (basic algebras equivalent to) orthomodular lattices was recently axiomatized in Kühr et al. (2015).

We close this paragraph with a few notes on arithmetic of basic algebras. Recalling (2.1) and using the fact that the $f_a$’s are antitone involutions, we have

$$\begin{aligned} (x\wedge y)\oplus z&=f_z(\lnot (x\wedge y)\vee z)=f_z(\lnot x\vee \lnot y\vee z)\\&=f_z(\lnot x\vee z)\wedge f_z(\lnot y\vee z)\\&=(x\oplus z)\wedge (y\oplus z). \end{aligned}$$

Thus, all basic algebras satisfy the identity

$$\begin{aligned} (x\wedge y)\oplus z=(x\oplus z)\wedge (y\oplus z), \end{aligned}$$

(2.11)

and consequently, the addition $\oplus$ is isotone in the first argument, i.e. $x\le y$ implies $x\oplus z\le y\oplus z$. We will also frequently use the equivalence

$$\begin{aligned} \lnot x\le y\oplus z \quad \text {iff}\quad \lnot y\le x\oplus z, \end{aligned}$$

(2.12)

which easily follows from isotonicity in the first argument and (2.2). However, the “mirror image” of (2.11), i.e. the identity

$$\begin{aligned} x\oplus (y\wedge z)=(x\oplus y)\wedge (x\oplus z), \end{aligned}$$

(2.13)

does not hold in general and $\oplus$ is not isotone in the second argument.⁴ Basic algebras satisfying (2.13), and even those satisfying the weaker identity $x\le x\oplus y$, have some notable properties. For instance, they are distributive as lattices, and in the finite case, they are just finite MV-algebras [see Krňávek and Kühr (2011), Botur et al. (2014) and Botur and Kühr (2014)].

In basic algebras, it is sometimes more convenient to work with certain antitone involutions, say $g_a$, on principal ideals [0, a] instead of the antitone involutions $f_a$ on principal filters [a, 1]. Here, for any $a\in A$, the antitone involution $g_a$ in question is the composite map $f_0\circ f_{\lnot a}\circ f_0$, i.e.

$$\begin{aligned} g_a(x)=\lnot (x\oplus \lnot a) \end{aligned}$$

(2.14)

for $x\le a$. It is obvious that the basic algebra $(A,\oplus ,\lnot ,0,1)$ is determined by its underlying lattice and the collection $(g_a)_{a\in A}$ of antitone involutions on the principal ideals. Indeed, $\lnot x=g_1(x)$ and $x\oplus y=\lnot g_{\lnot y}(x\wedge \lnot y)$ for all $x,y\in A$.

2.2 Special elements

Since basic algebras include orthomodular lattices, it follows that basic algebras satisfy no special lattice identities. We therefore focus on special elements of basic algebras as lattices, i.e. distributive, standard and neutral elements. First, we recall from Grätzer (2011), Sect. III.2 that an element a of a lattice $(A,\vee ,\wedge )$ is

• (i) distributive if $a\vee (x\wedge y)=(a\vee x)\wedge (a\vee y)$ for all $x,y\in A$;

• (ii) standard if $(a\vee x)\wedge y=(a\wedge y)\vee (x\wedge y)$ for all $x,y\in A$;

• (iii) neutral if $(a\vee x)\wedge (a\vee y)\wedge (x\vee y)=(a\wedge x)\vee (a\wedge y)\vee (x\wedge y)$ for all $x,y\in A$.

Dually distributive and dually standard elements are defined dually. The sets of distributive, dually distributive, standard, dually standard and neutral elements of the lattice $(A,\vee ,\wedge )$ are denoted, respectively, by $\mathrm {Distr}(A)$, $\mathrm {Distr}^{\partial }(A)$, $\mathrm {Stand}(A)$, $\mathrm {Stand}^{\partial }(A)$ and $\mathrm {Neutr}(A)$. The following is worth recalling. For any $a\in A$:

• (i) $a\in \mathrm {Distr}(A)$ iff the relation

  $$\begin{aligned} \varvec{\alpha }_a=\{(x,y)\in A^2:x\vee a=y\vee a\} \end{aligned}$$

  is a congruence of the lattice $(A,\vee ,\wedge )$;

• (ii) $a\in \mathrm {Stand}(A)$ iff the relation

  $$\begin{aligned}&\widetilde{\varvec{\alpha }_a}=\{(x,y)\in A^2 :x\vee y=(x\wedge y)\vee a_1\\&\quad \text { for some } a_1\le a\} \end{aligned}$$

  is a congruence of the lattice $(A,\vee ,\wedge )$, in which case $a\in \mathrm {Distr}(A)$ and $\widetilde{\varvec{\alpha }_a}=\varvec{\alpha }_a$;

• (iii) $a\in \mathrm {Neutr}(A)$ iff $a\in \mathrm {Distr}(A) \cap \mathrm {Distr}^{\partial }(A)$, and for all $x,y\in A$, whenever $x\vee a=y\vee a$ and $x\wedge a=y\wedge a$, then $x=y$.

As the next lemma shows, distributive and standard elements of basic algebras can be easily characterized in the language of basic algebras. The lemma is a strengthening of the fact [see Krňávek and Kühr (2011), Lemma 2.13] that a basic algebra is distributive if and only if it satisfies the identity

$$\begin{aligned} (x\vee y)\oplus z=(x\oplus z)\vee (y\oplus z). \end{aligned}$$

Lemma 2.1

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. For every $a\in A$, we have:

• (i) $a\in \mathrm {Distr}(A)$ iff $\lnot a\in \mathrm {Distr}^{\partial }(A)$ iff for all $x,y\in A$,

  $$\begin{aligned} (x\vee y)\oplus a=(x\oplus a)\vee (y\oplus a)\text {;} \end{aligned}$$

• (ii) $a\in \mathrm {Stand}(A)$ iff $\lnot a\in \mathrm {Stand}^{\partial }(A)$ iff for all $x,y\in A$,

  $$\begin{aligned} (x\vee a)\oplus y=(x\oplus y)\vee (a\oplus y)\text {.} \end{aligned}$$

Proof

First, it is evident that $a\in A$ is distributive or standard if and only if $\lnot a$ is dually distributive or dually standard, respectively.

If $a\in \mathrm {Distr}(A)$, then by the definition of the addition $\oplus$, and since $f_a$ is an antitone involution on [a, 1], we have

$$\begin{aligned} (x\vee y)\oplus a&= f_a (\lnot (x\vee y)\vee a)\\&=f_a ((\lnot x\wedge \lnot y)\vee a)\\&=f_a ((\lnot x\vee a)\wedge (\lnot y\vee a))\\&=f_a (\lnot x\vee a)\vee f_a (\lnot y\vee a)\\&=(x\oplus a)\vee (y\oplus a) \end{aligned}$$

for any $x,y\in A$. Conversely, suppose that $a\in A$ satisfies the equality for all $x,y\in A$. Then almost the same calculation shows that $a\in \mathrm {Distr}(A)$. Indeed, for any $x,y\in A$ we have

$$\begin{aligned} f_a ((x\wedge y)\vee a)&= (\lnot x\vee \lnot y)\oplus a\\&=(\lnot x\oplus a)\vee (\lnot y\oplus a)\\&=f_a (x\vee a) \vee f_a (y\vee a)\\&=f_a ((x\vee a)\wedge (y\vee a)), \end{aligned}$$

whence $(x\wedge y)\vee a=(x\vee a)\wedge (y\vee a)$. This proves (i).

The proof of (ii) is analogous. $\square$

Of course, it is possible to give a similar characterization of neutral elements, but we find it opaque in comparison with the usual definition.

3 Boolean elements

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. An element $a\in A$ is central if there is an isomorphism $h:A\rightarrow A_1\times A_2$ of $(A,\oplus ,\lnot ,0,1)$ onto the direct product of some basic algebras $(A_1,\oplus ,\lnot ,0,1)$ and $(A_2,\oplus ,\lnot ,0,1)$ such that $a=h^{-1}(0,1)$ or $a=h^{-1}(1,0)$. The central elements obviously correspond to the factor congruences. Specifically, $a\in A$ is central if and only if the equivalence relation

$$\begin{aligned} \varvec{\alpha }_a=\{(x,y)\in A^2:x\vee a=y\vee a\}, \end{aligned}$$

or equivalently, the equivalence relation

$$\begin{aligned} \varvec{\beta }_a=\{(x,y)\in A^2:x\wedge a=y\wedge a\}, \end{aligned}$$

is a factor congruence of the basic algebra $(A,\oplus ,\lnot ,0,1)$. It comes as no surprise that the set $\mathcal {C}(A)$ of the central elements forms a Boolean subalgebra of $(A,\oplus ,\lnot ,0,1)$. Here, by a Boolean subalgebra we mean a subalgebra which satisfies identity (2.9); in other words, the subalgebra is a Boolean algebra in its own right.⁵

Further, an element $a\in A$ is sharp if $\lnot a$ is its complement in the underlying lattice (i.e. if $a\vee \lnot a=1$, which is the same as $a\wedge \lnot a=0$). It is not hard to show that being sharp is equivalent to $a\oplus a=a$. In lattice effect algebras, the set $\mathcal {S}(A)$ of the sharp elements forms an orthomodular subalgebra of $(A,\oplus ,\lnot ,0,1)$, in the sense that it is a subalgebra which satisfies quasi-identity (2.8).⁶

In basic algebras satisfying identity (2.13), we even have $\mathcal {S}(A)=\mathcal {C}(A)$, but in general, $\mathcal {S}(A)$ is neither a subalgebra nor a sublattice.

Therefore, it might be of some interest to find a Boolean subalgebra between $\mathcal {C}(A)$ and $\mathcal {S}(A)$. To this end, given an arbitrary basic algebra $(A,\oplus ,\lnot ,0,1)$, we define an element $a\in A$ to be Boolean if

$$\begin{aligned} a\oplus x=a\vee x \quad \text {for\;all } \;x\in A, \end{aligned}$$

and we let $\mathcal {B}(A)$ denote the set of Boolean elements of the algebra $(A,\oplus ,\lnot ,0,1)$. It is easy to see that $a\in \mathcal {B}(A)$ iff $\lnot a\in \mathcal {B}(A)$. Indeed, if $a\in \mathcal {B}(A)$, then $\lnot a\vee x=\lnot (a\oplus x)\oplus x=\lnot (a\vee x)\oplus x=(\lnot a\wedge \lnot x)\oplus x=\lnot a\oplus x$ for any $x\in A$, thus $\lnot a\in \mathcal {B}(A)$.

We have

$$\begin{aligned} \mathcal {C}(A)\subseteq \mathcal {B}(A)\subseteq \mathcal {S}(A), \end{aligned}$$

with strict inclusions in general. Our first goal is to prove that $\mathcal {B}(A)$ forms a Boolean subalgebra. We also prove that Boolean elements are closely related to the so-called weak congruences of basic algebras, where, by Chajda and Kühr (2013b), a weak congruence of a basic algebra is an equivalence relation $\varvec{\theta }$ with the property that

$$\begin{aligned} (x,y)\in \varvec{\theta }\text { implies } (\lnot x,\lnot y)\in \varvec{\theta }\text { and } (x\oplus z,y\oplus z)\in \varvec{\theta }. \end{aligned}$$

Recalling (2.2), it is clear that any weak congruence is a lattice congruence (compatible with $\lnot$), but the converse fails to be true in general. Thus, weak congruences of $(A,\oplus ,\lnot ,0,1)$ are a special case of congruences of $(A,\vee ,\wedge ,\lnot ,0,1)$.

Lemma 3.1

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. The following are equivalent for any $a\in A$:

• (i) $a\in \mathcal {B}(A)$;

• (ii) $a\vee (x\oplus y)=(a\vee x)\oplus y$ for all $x,y\in A$;

• (iii) $a\in \mathcal {S}(A)$ and $a\oplus (x\oplus y)=(a\oplus x)\oplus y$ for all $x,y\in A$;

• (iv) $\varvec{\alpha }_a$ is a weak congruence of $(A,\oplus ,\lnot ,0,1)$.

Proof

In doing calculations, we will repeatedly use equivalence (2.12).

(i) implies (ii). Let $a\in \mathcal {B}(A)$. We have

$$\begin{aligned} a\vee (x\oplus y) = a\vee y\vee (x\oplus y) = (a\oplus y)\vee (x\oplus y) \le (a\vee x)\oplus y \end{aligned}$$

(3.1)

for all $x,y\in A$. Since $\lnot a\le \lnot a\vee x=\lnot (a\oplus x)\oplus x$ and $a\in \mathcal {S}(A)$, by (3.1) we have $1=a\vee \lnot a\le a\vee (\lnot (a\oplus x)\oplus x)\le (a\vee \lnot (a\oplus x))\oplus x$, hence $(a\vee \lnot (a\oplus x))\oplus x=1$ and so

$$\begin{aligned} \lnot x\le a\vee \lnot (a\oplus x) \end{aligned}$$

(3.2)

for every $x\in A$. But then, again by (3.1), for all $x,y\in A$ we have

$$\begin{aligned}&\lnot x \le a\vee [\lnot (a\oplus x)\vee y] = a\vee [\lnot ((a\oplus x)\oplus y)\oplus y]\\&\quad \le [a\vee \lnot ((a\oplus x)\oplus y)]\oplus y, \end{aligned}$$

whence $\lnot z\le x\oplus y$ by (2.12), where $z=a\vee \lnot ((a\oplus x)\oplus y)=a\oplus \lnot ((a\oplus x)\oplus y)$. Then

$$\begin{aligned} (a\oplus x)\oplus y \le a\vee \lnot z \le a\vee (x\oplus y), \end{aligned}$$

where the first inequality follows from (3.2). We have proved that $a\vee (x\oplus y)=a\oplus (x\oplus y)=(a\oplus x)\oplus y=(a\vee x)\oplus y$ for all $x,y\in A$.

(ii) implies (iii). Clearly, by substituting 0 for x we get $a\vee y=a\oplus y$, for every $y\in A$. Hence $a\in \mathcal {B}(A)$ and by what we have proved above we conclude that $a\oplus (x\oplus y)=(a\oplus x)\oplus y$ for all $x,y\in A$.

(iii) implies (i). For any $x\in A$, we have $a\oplus (\lnot a\oplus x)=(a\oplus \lnot a)\oplus x=1$, so $\lnot a\le \lnot a\oplus x$, which is equivalent to $a\le a\oplus x$ by (2.12). Then, for any $x\in A$, $a\le a\oplus \lnot (\lnot a\oplus x)$, whence

$$\begin{aligned}&a\oplus x\le (a\oplus \lnot (\lnot a\oplus x))\oplus x\nonumber \\&\quad =a\oplus (\lnot (\lnot a\oplus x)\oplus x)=a\oplus (a\vee x). \end{aligned}$$

By (2.12) this entails $\lnot a\le \lnot (a\oplus x)\oplus (a\vee x)$. We also have $a\le \lnot (a\oplus x)\oplus (a\vee x)$ and $a\in \mathcal {S}(A)$, and thus, $\lnot (a\oplus x)\oplus (a\vee x)=1$, i.e. $a\oplus x\le a\vee x$. Since $a\le a\oplus x$, we see that $a\oplus x=a\vee x$ and so $a\in \mathcal {B}(A)$.

Now, we prove that (i) implies (iv). Let $a\in \mathcal {B}(A)$ and suppose that $(x,y)\in \varvec{\alpha }_a$ for some $x,y\in A$. Then $x\le a\vee x=a\vee y=a\oplus y$ yields $\lnot a\le \lnot x\oplus y$ by (2.12), whence $1=a\oplus (\lnot x\oplus y)=(a\oplus \lnot x)\oplus y$, which means that $\lnot y\le a\oplus \lnot x=a\vee \lnot x$, and so $a\vee \lnot y\le a\vee \lnot x$. The inequality $a\vee \lnot x\le a\vee \lnot y$ is obtained by interchanging x and y, thus $a\vee \lnot x=a\vee \lnot y$, proving $(\lnot x,\lnot y)\in \varvec{\alpha }_a$. Moreover, for every $z\in A$ we have $a\vee (x\oplus z)=(a\vee x)\oplus z=(a\vee y)\oplus z=a\vee (y\oplus z)$, i.e. $(x\oplus z,y\oplus z)\in \varvec{\alpha }_a$.

(iv) implies (i). Let $\varvec{\alpha }_a$ be a weak congruence. It is obvious that $(a,0)\in \varvec{\alpha }_a$, whence $\lnot (\lnot a\oplus x) \equiv _{\varvec{\alpha }_a} \lnot (\lnot 0\oplus x) = 0 \equiv _{\varvec{\alpha }_a} a$ for every $x\in A$. This means that $a\vee \lnot (\lnot a\oplus x)=a$, i.e. $\lnot a\le \lnot a\oplus x$ and, equivalently, $a\le a\oplus x$. But $(a,0)\in \varvec{\alpha }_a$ also yields $(a\oplus x,x)\in \varvec{\alpha }_a$, i.e. $a\oplus x=a\vee (a\oplus x)=a\vee x$. Hence $a\in \mathcal {B}(A)$. $\square$

Theorem 3.2

In any basic algebra $(A,\oplus ,\lnot ,0,1)$, the set of Boolean elements $\mathcal {B}(A)$ forms a Boolean subalgebra.

Proof

Let $a,b\in \mathcal {B}(A)$ and $x\in A$. By Lemma 3.1, we have $(a\oplus b)\oplus x=a\oplus (b\oplus x)=a\vee b\vee x=(a\oplus b)\vee x$, thus $a\oplus b=a\vee b\in \mathcal {B}(A)$. We already know that $a\in \mathcal {B}(A)$ iff $\lnot a\in \mathcal {B}(A)$, and thus, $\mathcal {B}(A)$ is a subalgebra. For any $a,b,c\in \mathcal {B}(A)$, since $a\wedge b\in \mathcal {B}(A)$, and recalling identity (2.11) we have $(a\wedge b)\vee c=(a\wedge b)\oplus c=(a\oplus c)\wedge (b\oplus c)=(a\vee c)\wedge (b\vee c)$. Hence, $\mathcal {B}(A)$ forms a Boolean algebra. $\square$

The Boolean subalgebra $\mathcal {B}(A)$ is generally larger than $\mathcal {C}(A)$, but it need not be the largest Boolean subalgebra of $(A,\oplus ,\lnot ,0,1)$. It can happen that $\mathcal {S}(A)$ is a Boolean subalgebra and $\mathcal {B}(A) \subsetneqq \mathcal {S}(A)$. For example, it suffices to take a Boolean algebra (with at least eight elements) and “perturb” the antitone involutions⁷ in some filters [a, 1] with $a\ne 0$; then $\mathcal {B}(A)\subsetneqq A=\mathcal {S}(A)$.

Lemma 3.3

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. If $a\in \mathcal {B}(A)$, then $\varvec{\beta }_a=\varvec{\alpha }_{\lnot a}$ is a weak congruence of $(A,\oplus ,\lnot ,0,1)$ with the property that

$$\begin{aligned} \varvec{\alpha }_a \cap \varvec{\beta }_a = \Delta _A \quad \text {and}\quad \varvec{\alpha }_a \circ \varvec{\beta }_a = \nabla _A. \end{aligned}$$

Moreover, $a\in \mathrm {Neutr}(A)$. Thus $\mathcal {B}(A) \subseteq \mathrm {Neutr}(A)$.

Proof

We have already seen that $a\in \mathcal {B}(A)$ iff $\lnot a\in \mathcal {B}(A)$. Hence, $\varvec{\alpha }_{\lnot a}$ is a weak congruence. Consequently, we have $(x,y)\in \varvec{\alpha }_{\lnot a}$ iff $(\lnot x,\lnot y)\in \varvec{\alpha }_{\lnot a}$ iff $\lnot a\vee \lnot x=\lnot a\vee \lnot y$ iff $a\wedge x=a\wedge y$ iff $(x,y)\in \varvec{\beta }_a$. Thus, $\varvec{\alpha }_{\lnot a}=\varvec{\beta }_a$.

Suppose that $(x,y)\in \varvec{\alpha }_a \cap \varvec{\beta }_a$, i.e. $a\vee x=a\vee y$ and $\lnot a\vee x=\lnot a\vee y$. Then, $x\le a\vee y=a\oplus y$ implies $\lnot a\le \lnot x\oplus y$, and at the same time $x\le \lnot a\vee y=\lnot a\oplus y$ implies $a\le \lnot x\oplus y$. Since $a\in \mathcal {S}(A)$, we have $\lnot x\oplus y=1$, so $x\le y$. By interchanging x and y, we get $y\le x$, and so $x=y$. Thus, $\varvec{\alpha }_a \cap \varvec{\beta }_a=\Delta _A$.

Now, since both $\varvec{\alpha }_a$ and $\varvec{\beta }_a$ are lattice congruences, the element a is both distributive and dually distributive. Since $\varvec{\alpha }_a \cap \varvec{\beta }_a=\Delta _A$ (i.e. $a\vee x=a\vee y$ and $a\wedge x=a\wedge y$ imply $x=y$), it follows that a is neutral.

There remains to prove that $\varvec{\alpha }_a \circ \varvec{\beta }_a = \nabla _A$. Let $x,y\in A$ be arbitrary elements and put $z=(x\vee a)\wedge (y\vee \lnot a)$. Since a as well as $\lnot a$ is a neutral element, it is straightforward to verify that $a\vee z=a\vee x$ and $a\wedge z=a\wedge y$, i.e. $(x,z)\in \varvec{\alpha }_a$ and $(z,y)\in \varvec{\beta }_a$. $\square$

Remark

Since $\mathcal {B}(A)\subseteq \mathrm {Neutr}(A)$, in Lemma 3.1 (iv) we could replace $\varvec{\alpha }_a$ with

$$\begin{aligned}&\widetilde{\varvec{\alpha }_a}=\{(x,y)\in A^2:x\vee y=(x\wedge y)\vee a_1 \\&\quad \text { for some } a_1\le a\}. \end{aligned}$$

Indeed, if $a\in \mathcal {B}(A)$, then $a\in \mathrm {Stand}(A)$, and so $\varvec{\alpha }_a=\widetilde{\varvec{\alpha }_a}$ is a weak congruence of $(A,\oplus ,\lnot ,0,1)$. Conversely, if $\widetilde{\varvec{\alpha }_a}$ is a weak congruence of the basic algebra, then $a\in \mathrm {Stand}(A)$ because any weak congruence is a lattice congruence, and in this case we have $\varvec{\alpha }_a=\widetilde{\varvec{\alpha }_a}$. Thus, $\varvec{\alpha }_a$ is a weak congruence of $(A,\oplus ,\lnot ,0,1)$, which yields $a\in \mathcal {B}(A)$.

The map $a\mapsto \varvec{\alpha }_a$ is a one-to-one correspondence between Boolean elements and certain weak congruences (“factor” weak congruences):

Lemma 3.4

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. Let $\varvec{\varphi }$ be a weak congruence such that $\varvec{\varphi }\cap \varvec{\psi }=\Delta _A$ and $\varvec{\varphi }\circ \varvec{\psi }=\nabla _A$ for some weak congruence $\varvec{\psi }$. Then the only element $a\in A$ such that $(0,a)\in \varvec{\varphi }$ and $(a,1)\in \varvec{\psi }$ is a Boolean element, and we have $\varvec{\varphi }=\varvec{\alpha }_a$ and $\varvec{\psi }=\varvec{\beta }_a$.

Proof

Clearly, there exists a unique $a\in A$ such that $(0,a)\in \varvec{\varphi }$ and $(a,1)\in \varvec{\psi }$. Then, for any $x\in A$ we have $a\oplus x \equiv _{\varvec{\varphi }} x \equiv _{\varvec{\varphi }} a\vee x$ and $a\oplus x \equiv _{\varvec{\psi }} 1 \equiv _{\varvec{\psi }} a\vee x$, which entails $a\oplus x=a\vee x$ as $\varvec{\varphi }\cap \varvec{\psi }=\Delta _A$. Thus, $a\in \mathcal {B}(A)$.

If $(x,y)\in \varvec{\alpha }_a$, then $x \equiv _{\varvec{\varphi }} a\vee x=a\vee y \equiv _{\varvec{\varphi }} y$. Thus, $\varvec{\alpha }_a\subseteq \varvec{\varphi }$. Conversely, we have $x \equiv _{\varvec{\varphi }} a\vee x \equiv _{\varvec{\psi }} 1$ and $y \equiv _{\varvec{\varphi }} a\vee y \equiv _{\varvec{\psi }} 1$, and hence, $(x,y)\in \varvec{\varphi }$ implies $a\vee x=a\vee y$, i.e. $(x,y)\in \varvec{\alpha }_a$. Thus, $\varvec{\varphi }\subseteq \varvec{\alpha }_a$, proving $\varvec{\alpha }_a=\varvec{\varphi }$. Similarly, $\varvec{\beta }_a=\varvec{\psi }$. $\square$

In the remainder of this section, given a basic algebra $(A,\oplus ,\lnot ,0,1)$ and a non-empty subset $X\subseteq A$ we use (X] to denote the order ideal (of the underlying lattice of the algebra) generated by the set X, i.e. $(X] = \{a\in A:a\le x \text { for some } x\in X\}$.

Lemma 3.5

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. For every $a\in A{\setminus }\{0\}$ there exists a maximal ideal M of the Boolean subalgebra $\mathcal {B}(A)$ such that $a\notin (M]$. Consequently,

$$\begin{aligned} \bigcap \{(M]:M \text { is\; a\; maximal \; ideal \;of}\; \mathcal {B}(A)\} = \{0\}. \end{aligned}$$

Proof

Let $\mathfrak {M}$ be the set of all ideals I of $\mathcal {B}(A)$ with $a\notin (I]$. Since $a\ne 0$, it is obvious that $\{0\}\in \mathfrak {M}$ and so, by Zorn’s lemma, $\mathfrak {M}$ ordered by set inclusion has a maximal element, M say. Suppose to the contrary that M is not a maximal ideal of $\mathcal {B}(A)$, i.e. there exists $b\in \mathcal {B}(A)$ such that $b,\lnot b\notin M$. Let J and K be the ideals of $\mathcal {B}(A)$ generated by $M\cup \{b\}$ and $M\cup \{\lnot b\}$, respectively. It is easily seen that $J\cap K=M$. Since M is contained properly in both J and K, it follows that $J,K\notin \mathfrak {M}$ and $a\in (J]\cap (K]=(J\cap K]=(M]$, which contradicts the choice of M. Therefore, M is a maximal ideal of $\mathcal {B}(A)$ and $a\notin (M]$.

The statement about the intersection of the order ideals (M] where M ranges over the maximal ideals of $\mathcal {B}(A)$ is a straightforward corollary. $\square$

By Lemma 3.1, we know that for any $a\in \mathcal {B}(A)$, the relation $\varvec{\alpha }_a$ is a weak congruence of the basic algebra $(A,\oplus ,\lnot ,0,1)$. Moreover, we have

$$\begin{aligned} (x,y)\in \varvec{\alpha }_a \quad \text {iff}\quad d(x,y) \le a, \end{aligned}$$

where

$$\begin{aligned} d(x,y)=\lnot (\lnot x\oplus y) \vee \lnot (\lnot y\oplus x). \end{aligned}$$

Indeed, it suffices to observe that $x\vee a\le y\vee a$ iff $x\le y\vee a=a\oplus y$ iff $\lnot a\le \lnot x\oplus y$ iff $\lnot (\lnot x\oplus y)\le a$. It easily follows that when we are given an ideal I of $\mathcal {B}(A)$, then the relation

$$\begin{aligned} \varvec{\alpha }_I=\bigcup \{\varvec{\alpha }_a:a\in I\} \end{aligned}$$

is a weak congruence of $(A,\oplus ,\lnot ,0,1)$, too, and

$$\begin{aligned} (x,y)\in \varvec{\alpha }_I \quad \text {iff}\quad d(x,y) \in (I]. \end{aligned}$$

Theorem 3.6

For any basic algebra $(A,\oplus ,\lnot ,0,1)$,

$$\begin{aligned} \bigcap \{\varvec{\alpha }_M:M \text { is a maximal ideal of } \mathcal {B}(A)\} = \Delta _A. \end{aligned}$$

The lattice with antitone involution $(A,\vee ,\wedge ,\lnot ,0,1)$ is a subdirect product of the quotient lattices with antitone involution $(A,\vee ,\wedge ,\lnot ,0,1)/\varvec{\alpha }_M$ where M ranges over the maximal ideals of $\mathcal {B}(A)$.

Proof

If $(x,y)\in \varvec{\alpha }_M$ for all maximal ideals M of $\mathcal {B}(A)$, then $d(x,y)\in (M]$ for all maximal ideals M of $\mathcal {B}(A)$. Thus, $d(x,y)=0$ by the previous lemma, which means that $x=y$. In other words, the intersection of the $\varvec{\alpha }_M$’s is $\Delta _A$. Since each $\varvec{\alpha }_M$ is a congruence of $(A,\vee ,\wedge ,\lnot ,0,1)$, we conclude that $(A,\vee ,\wedge ,\lnot ,0,1)$ is a subdirect product of the quotient algebras $(A,\vee ,\wedge ,\lnot ,0,1)/\varvec{\alpha }_M$. $\square$

4 Two variants of Boolean elements

We have seen that $a\in A$ is a Boolean element if and only if the equivalence relation $\varvec{\alpha }_a$ is a weak congruence of $(A,\oplus ,\lnot ,0,1)$. This raises the question under which conditions $\varvec{\alpha }_a$ is a congruence of the basic algebra $(A,\oplus ,\lnot ,0,1)$ in the stronger version, or of the lattice with antitone involution $(A,\vee ,\wedge ,\lnot ,0,1)$ in the weaker version.

First, it turns out that $\varvec{\alpha }_a$ is a congruence of the basic algebra, roughly speaking, when the conditions (ii) and (iii) of Lemma 3.1 are replaced by their “mirror images”. Such elements a are “strongly Boolean”.

Lemma 4.1

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. The following are equivalent for any $a\in A$:

• (i) $x\oplus (y\vee a)=(x\oplus y)\vee a$ for all $x,y\in A$;

• (ii) $a\in \mathcal {S}(A)$ and $x\oplus (y\oplus a)=(x\oplus y)\oplus a$ for all $x,y\in A$;

• (iii) $\varvec{\alpha }_a$ is a congruence of $(A,\oplus ,\lnot ,0,1)$.

If $a\in A$ satisfies these conditions, then $a\in \mathcal {B}(A)$.

Proof

(i) implies (ii). By substituting 0 for y, we obtain $x\oplus a=x\vee a$. Hence, $a\in \mathcal {S}(A)$ and $x\oplus (y\oplus a)=x\oplus (y\vee a)=(x\oplus y)\vee a=(x\oplus y)\oplus a$ for all $x,y\in A$.

(ii) implies (i). Since $x\oplus a\le (x\vee a)\oplus a$, we have

$$\begin{aligned}{}[\lnot (x\oplus a)\oplus (x\vee a)]\oplus a{=}\lnot (x\oplus a)\oplus ((x\vee a)\oplus a)=1, \end{aligned}$$

so $\lnot a\le \lnot (x\oplus a)\oplus (x\vee a)$. At the same time, $a\le \lnot (x\oplus a)\oplus (x\vee a)$. Since $a\in \mathcal {S}(A)$, it follows that $\lnot (x\oplus a)\oplus (x\vee a)=1$, i.e. $x\oplus a\le x\vee a$ for every $x\in A$. Conversely, $\lnot x\oplus (x\oplus a)=(\lnot x\oplus x)\oplus a=1\oplus a=1$, i.e. $x\le x\oplus a$, whence we conclude that $x\vee a=x\oplus a$. Thus, $x\oplus (y\vee a)=x\oplus (y\oplus a)=(x\oplus y)\oplus a=(x\oplus y)\vee a$ for all $x,y\in A$.

Now, we are able to prove that a is a Boolean element whenever it satisfies the equivalent conditions (i) and (ii). We have $1=\lnot a\oplus (x\oplus a)=(\lnot a\oplus x)\oplus a$, so $\lnot a\le \lnot a\oplus x$, which is the same as $a\le a\oplus x$. We have seen above that $x\vee a=x\oplus a$, and hence, $x\oplus a=x\vee a\le a\oplus x$. On the other hand,

$$\begin{aligned}&\lnot (a\oplus x)\oplus (x\oplus a)=(\lnot (a\oplus x)\oplus x)\oplus a\\&\quad =(\lnot a\vee x)\oplus a=1, \end{aligned}$$

thus $a\oplus x\le x\oplus a$ and $x\oplus a=x\vee a=a\oplus x$, proving that $a\in \mathcal {B}(A)$.

(i) implies (iii). If $(x,y)\in \varvec{\alpha }_a$, then $(z\oplus x)\vee a=z\oplus (x\vee a)=z\oplus (y\vee a)=(z\oplus y)\vee a$, i.e. $(z\oplus x,z\oplus y)\in \varvec{\alpha }_a$. Moreover, we know that $a\in \mathcal {B}(A)$ and so, by Lemma 3.1, $\varvec{\alpha }_a$ is a weak congruence of $(A,\oplus ,\lnot ,0,1)$. Therefore, $\varvec{\alpha }_a$ is a congruence of $(A,\oplus ,\lnot ,0,1)$.

(iii) implies (i). We have $(y,y\vee a)\in \varvec{\alpha }_a$, whence $(x\oplus y,x\oplus (y\vee a))\in \varvec{\alpha }_a$. So $(x\oplus y)\vee a=(x\oplus (y\vee a))\vee a=x\oplus (y\vee a)$. $\square$

Remark

As in Lemma 3.1, we could replace $\varvec{\alpha }_a$ with $\widetilde{\varvec{\alpha }_a}$ because $\widetilde{\varvec{\alpha }_a}$ is a lattice congruence if and only if $a\in \mathrm {Stand}(A)$, in which case $\widetilde{\varvec{\alpha }_a}$ coincides with $\varvec{\alpha }_a$.

Lemma 4.1 together with Lemma 3.3 allows us to describe the central elements of basic algebras; our characterization below is more concise than the one given in Chajda and Kolařík (2009).

Corollary 4.2

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. The following are equivalent for any $a\in A$:

• (i) $a\in \mathcal {C}(A)$;

• (ii) $x\oplus (y\vee z)=(x\oplus y)\vee z$ for all $x,y\in A$ and $z\in \{a,\lnot a\}$;

• (iii) $a\in \mathcal {S}(A)$ and $x\oplus (y\oplus z)=(x\oplus y)\oplus z$ for all $x,y\in A$ and $z\in \{a,\lnot a\}$;

• (iv) $\varvec{\alpha }_a$ and $\varvec{\alpha }_{\lnot a}$ are congruences of $(A,\oplus ,\lnot ,0,1)$.

The next lemma answers the question of when the relation $\varvec{\alpha }_a$ is a congruence of the “i-lattice” $(A,\vee ,\wedge ,\lnot ,0,1)$. The weaker version of Boolean elements mentioned at the beginning of the section is the sharp distributive elements.

Lemma 4.3

Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra. For any $a\in A$, we have:

• (i) $a\in \mathcal {S}(A) \cap \mathrm {Distr}(A)$ iff $\varvec{\alpha }_a$ is a congruence of the lattice with antitone involution $(A,\vee ,\wedge ,\lnot ,0,1)$, in which case $(x,y)\in \varvec{\alpha }_a$ iff $x\oplus a=y\oplus a$;

• (ii) $a\in \mathcal {S}(A) \cap \mathrm {Stand}(A)$ iff $\widetilde{\varvec{\alpha }_a}$ is a congruence of $(A,\vee ,\wedge ,\lnot ,0,1)$;

• (iii) $a\in \mathcal {S}(A)\cap \mathrm {Neutr}(A)$ iff $\varvec{\alpha }_a$ and $\varvec{\beta }_a$ are congruences of $(A,\vee ,\wedge ,\lnot ,0,1)$ such that $\varvec{\alpha }_a\cap \varvec{\beta }_a=\Delta _A$.

Proof

(i) Let $a\in \mathcal {S}(A) \cap \mathrm {Distr}(A)$. Clearly, the relation $\varvec{\alpha }_a$ is a lattice congruence. If $(x,y)\in \varvec{\alpha }_a$, i.e. $x\vee a=y\vee a$, then

$$\begin{aligned} \lnot x\vee a&= (\lnot x\vee a)\wedge (\lnot a\vee a)=(\lnot x\wedge \lnot a)\vee a\\&=\lnot (x\vee a)\vee a=\lnot (y\vee a)\vee a\\&=(\lnot y\wedge \lnot a)\vee a=(\lnot y\vee a)\wedge (\lnot a\vee a)\\&=\lnot y\vee a \end{aligned}$$

since the element a is distributive. Thus $(\lnot x,\lnot y)\in \varvec{\alpha }_a$. Conversely, if $\varvec{\alpha }_a$ is a congruence of $(A,\vee ,\wedge ,\lnot ,0,1)$, then a is a distributive element and $(0,a)\in \varvec{\alpha }_a$ implies $(1,\lnot a)\in \varvec{\alpha }_a$, so $1=\lnot a\vee a$, whence $a\in \mathcal {S}(A)$.

Now, if $a\in \mathcal {S}(A) \cap \mathrm {Distr}(A)$, then $(x,y)\in \varvec{\alpha }_a$ yields $x\oplus a=(x\vee a)\oplus a=(y\vee a)\oplus a=y\oplus a$, and on the other hand, $x\oplus a=y\oplus a$ yields $\lnot x\vee a=\lnot (x\oplus a)\oplus a=\lnot (y\oplus a)\oplus a=\lnot y\vee a$, i.e. $(\lnot x,\lnot y)\in \varvec{\alpha }_a$, which is equivalent to $(x,y)\in \varvec{\alpha }_a$.

(ii) Suppose that $a\in \mathcal {S}(A) \cap \mathrm {Stand}(A)$. Then $\widetilde{\varvec{\alpha }_a}$ is a lattice congruence and it coincides with $\varvec{\alpha }_a$, which is a congruence of $(A,\vee ,\wedge ,\lnot ,0,1)$ in the light of (i). Conversely, let $\widetilde{\varvec{\alpha }_a}$ be a congruence of $(A,\vee ,\wedge ,\lnot ,0,1)$. Then a is a standard element and $(0,a)\in \widetilde{\varvec{\alpha }_a}$ implies $(1,\lnot a)\in \widetilde{\varvec{\alpha }_a}$, so $1=\lnot a\vee a_1$ for some $a_1\le a$, whence $\lnot a\vee a=1$. Thus $a\in \mathcal {S}(A)$.

(iii) Let $a\in \mathcal {S}(A)\cap \mathrm {Neutr}(A)$. Then $a\in \mathcal {S}(A)\cap \mathrm {Distr}^{\partial }(A)$, so that, by duality, item (i) entails that $\varvec{\beta }_a$ is a congruence of $(A,\vee ,\wedge ,\lnot ,0,1)$. An alternative argument: $a\in \mathcal {S}(A)\cap \mathrm {Distr}^{\partial }(A)$ is equivalent to $\lnot a\in \mathcal {S}(A)\cap \mathrm {Distr}(A)$, and hence, $\varvec{\alpha }_a$ and $\varvec{\alpha }_{\lnot a}$ are congruences of $(A,\vee ,\wedge ,\lnot ,0,1)$ by (i), and we have $(x,y)\in \varvec{\alpha }_{\lnot a}$ iff $(\lnot x,\lnot y)\in \varvec{\alpha }_{\lnot a}$ iff $\lnot x\vee \lnot a=\lnot y\vee \lnot a$ iff $x\wedge a=y\wedge a$ iff $(x,y)\in \varvec{\beta }_a$. Thus, $\varvec{\alpha }_{\lnot a}=\varvec{\beta }_a$. Neutrality of a implies $\varvec{\alpha }_a\cap \varvec{\beta }_a=\Delta _A$.

Conversely, if $\varvec{\alpha }_a$ and $\varvec{\beta }_a$ are congruences of $(A,\vee ,\wedge ,\lnot ,0,1)$ such that $\varvec{\alpha }_a\cap \varvec{\beta }_a=\Delta _A$, then the element a is neutral, and it is also sharp by (i). $\square$

In contrast to $\mathcal {B}(A)$, $\mathcal {S}(A)\cap \mathrm {Neutr}(A)$ is a subalgebra of $(A,\vee ,\wedge ,\lnot ,0,1)$ (which is a Boolean algebra in its own right) but not of $(A,\oplus ,\lnot ,0,1)$ in general, and $\mathcal {S}(A)\cap \mathrm {Distr}(A)$, $\mathcal {S}(A)\cap \mathrm {Stand}(A)$ and the set of “strongly Boolean elements” satisfying the equivalent conditions of Lemma 4.1 do not form subalgebras of $(A,\vee ,\wedge ,\lnot ,0,1)$ or $(A,\oplus ,\lnot ,0,1)$.

In lattice effect algebras, all these sets coincide with the centre $\mathcal {C}(A)$:

Theorem 4.4

If $(A,\oplus ,\lnot ,0,1)$ is a basic algebra satisfying (2.10), then

$$\begin{aligned} \mathcal {C}(A) =\mathcal {B}(A)&=\mathcal {S}(A)\cap \mathrm {Distr}(A)=\mathcal {S}(A)\cap \mathrm {Distr}^{\partial }(A)\\&=\mathcal {S}(A)\cap \mathrm {Stand}(A)=\mathcal {S}(A)\cap \mathrm {Stand}^{\partial }(A)\\&=\mathcal {S}(A)\cap \mathrm {Neutr}(A). \end{aligned}$$

To prove the theorem, we need to recall the concept of compatible elements. Let $(A,\oplus ,\lnot ,0,1)$ be a basic algebra satisfying (2.10). Two elements $x,y\in A$ are compatible (in the corresponding lattice effect algebra, in symbols $x\leftrightarrow y$) if there exist $x_1,y_1,z\in A$ such that $x=x_1+z$, $y=y_1+z$ and $x_1+y_1+z$ is defined. In the language of basic algebras, we have

$$\begin{aligned} x\leftrightarrow y \quad \text {iff}\quad x\oplus y=y\oplus x \quad \text {iff}\quad x\le x\oplus y; \end{aligned}$$

see Chajda et al. (2009a) and Kühr et al. (2015). We will use the following facts, see e.g. Riečanová (1997, 1999) or Dvurečenskij and Pulmannová (2000):

• (i) if $x,y\in A$ are comparable, then $x\leftrightarrow y$;

• (ii) $x\leftrightarrow y$ iff $x\leftrightarrow \lnot y$;

• (iii) if $x\leftrightarrow y$ and $x\wedge y=0$, then $x\vee y=x+y=x\oplus y$;

• (iv) $a\in \mathcal {C}(A)$ iff $a\in \mathcal {S}(A)$ and $a\leftrightarrow x$ for every $x\in A$.

Proof of Theorem 4.4

In the light of Lemma 3.3, we have

$$\begin{aligned}&\mathcal {C}(A)\subseteq \mathcal {B}(A)\subseteq \mathcal {S}(A)\cap \mathrm {Neutr}(A)\\&\quad \subseteq \mathcal {S}(A)\cap \mathrm {Stand}(A)\subseteq \mathcal {S}(A)\cap \mathrm {Distr}(A). \end{aligned}$$

If $a\in \mathcal {B}(A)$, then $a\le a\oplus x$, i.e. $a\leftrightarrow x$ for every $x\in A$. Hence $\mathcal {B}(A)=\mathcal {C}(A)$ by (iv), and it remains to prove that $\mathcal {S}(A)\cap \mathrm {Distr}(A)\subseteq \mathcal {B}(A)$.

Suppose that $a\in \mathcal {S}(A)\cap \mathrm {Distr}(A)$. Then $(\lnot a\wedge x)\vee a=x\vee a$ for any $x\in A$. Since $(\lnot a\wedge x)\wedge a=0$ and $a\leftrightarrow \lnot a\wedge x$ (as $\lnot a\ge \lnot a\wedge x$), it follows that $x\vee a=(\lnot a\wedge x)\vee a=(\lnot a\wedge x)+a=(\lnot a\wedge x)\oplus a=x\oplus a$. But this yields $x\le x\oplus a$, so $x\leftrightarrow a$ for every $x\in A$, which proves that $a\in \mathcal {C}(A)$, by the above item (iv). $\square$

5 Basic algebras with pseudocomplementation

In this section, we deal with the case that the underlying lattice is pseudocomplemented and, in fact, also dually pseudocomplemented. We first recall [see, e.g. Balbes and Dwinger (1975) or Grätzer (2011)] that a double p-algebra is an algebra $(A,\vee ,\wedge ,{^*},{^+},0,1)$ where $(A,\vee ,\wedge ,0,1)$ is a bounded lattice and, for every $a\in A$, $a^*$ is the pseudocomplement of a (i.e. $x\le a^*$ iff $x\wedge a=0$) and $a^+$ is the dual pseudocomplement of a (i.e. $x\ge a^+$ iff $x\vee a=1$). A double p-algebra is called a double Stone algebra if it is distributive as a lattice and satisfies the identities

$$\begin{aligned} x^{**}\vee x^*=1 \quad \text {and}\quad x^{++}\wedge x^+=0. \end{aligned}$$

(5.1)

For any double p-algebra $(A,\vee ,\wedge ,{^*},{^+},0,1)$, the skeletons

$$\begin{aligned} A^*=\{a^* :a\in A\} \quad \text {and}\quad A^+=\{a^+ :a\in A\} \end{aligned}$$

form Boolean algebras $(A^*,\sqcup ,\wedge ,{^*},0,1)$ and $(A^+,\vee ,\sqcap ,{^+},0,1)$ with $x\sqcup y=(x\vee y)^{**}$ and $x\sqcap y=(x\wedge y)^{++}$, respectively. The two skeletons coincide in double Stone algebras.

Now, we define a basic algebra with pseudocomplementation as a basic algebra the underlying lattice of which is pseudocomplemented, with pseudocomplementation considered to be a unary operation. More precisely, by a basic algebra with pseudocomplementation we mean an algebra $(A,\oplus ,\lnot ,{^*},0,1)$ such that $(A,\oplus ,\lnot ,0,1)$ is a basic algebra and, for every $a\in A$, $a^*$ is the pseudocomplement of a in the underlying lattice of the algebra $(A,\oplus ,\lnot ,0,1)$. It is easily seen that for every $a\in A$,

$$\begin{aligned} a^+=\lnot (\lnot a)^* \end{aligned}$$

is the dual pseudocomplement of a. (Indeed, $x\ge \lnot (\lnot a)^*$ iff $\lnot x\le (\lnot a)^*$ iff $\lnot (x\vee a)=\lnot x\wedge \lnot a=0$ iff $x\vee a=1$.) Therefore, $(A,\vee ,\wedge ,{^*},{^+},0,1)$ is a double p-algebra and so, in a sense, we could regard basic algebras with pseudocomplementation as double p-algebras with antitone involutions.

It is worth observing that (since $\lnot x^*=(\lnot x)^+$ and $\lnot x^+=(\lnot x)^*$, and $x\in \mathcal {S}(A)$ iff $\lnot x\in \mathcal {S}(A)$):

• (i) $a\in A^*$ implies $\lnot a\in A^+$, and $a\in A^+$ implies $\lnot a\in A^*$;

• (ii) $A^*\subseteq \mathcal {S}(A)$ iff $A^+\subseteq \mathcal {S}(A)$;

• (iii) $\mathcal {S}(A)\subseteq A^*$ iff $\mathcal {S}(A)\subseteq A^+$.

Theorem 5.1

The class of basic algebras with pseudocomplementation is a variety which can be axiomatized by identities (2.4)–(2.7) together with the identities

$$\begin{aligned} 0^*=1,\quad 1^*=0 \quad \text {and}\quad x\wedge (x\wedge y)^*=x\wedge y^*. \end{aligned}$$

Proof

It is known and easy to prove that the above identities characterize pseudocomplementation in meet semilattices with 0 [see Grätzer (2011), Exercise I.6.27]. To be more accurate, the language used there does not include the constant 1 and the axiomatization contains the identities $x\wedge 0^*=x$ and $0^{**}=0$, which can evidently be replaced with the identity $1^*=0$. $\square$

Lemma 5.2

Let $(A,\oplus ,\lnot ,{^*},0,1)$ be a basic algebra with pseudocomplementation.

• (i) If $a\in \mathcal {S}(A)$, then $a^+ \le \lnot a\le a^*$.

• (ii) If $a\in \mathcal {S}(A)\cap \mathrm {Distr}(A)$, then $a=(\lnot a)^*$ and $\lnot a=a^+$. Dually, if $a\in \mathcal {S}(A) \cap \mathrm {Distr}^{\partial }(A)$, then $a=(\lnot a)^+$ and $\lnot a=a^*$. Hence, $\mathcal {S}(A) \cap \mathrm {Distr}(A) \subseteq A^*$ and $\mathcal {S}(A) \cap \mathrm {Distr}^{\partial }(A) \subseteq A^+$.

• (iii) If $a\in \mathcal {S}(A)\cap \mathrm {Distr}(A)\cap \mathrm {Distr}^{\partial }(A)$, then $\lnot a=a^*=a^+$.

Proof

(i) It is plain that $a\wedge \lnot a=0$ implies $\lnot a\le a^*$, and $a\vee \lnot a=1$ implies $\lnot a\ge a^+$.

(ii) Let $a\in \mathcal {S}(A) \cap \mathrm {Distr}(A)$. Then $a=a\vee (\lnot a \wedge (\lnot a)^*)=a \vee (\lnot a)^*$, so $a\ge (\lnot a)^*$. At the same time, $a\wedge \lnot a=0$ implies $a\le (\lnot a)^*$, and hence, $a=(\lnot a)^*\in A^*$. Now, if $a\in \mathcal {S}(A)\cap \mathrm {Distr}^{\partial }(A)$, then $\lnot a\in \mathcal {S}(A)\cap \mathrm {Distr}(A)$ and by what we have just shown we have $\lnot a=(\lnot \lnot a)^*=a^*$, whence $a=\lnot a^*=(\lnot a)^+\in A^+$.

(iii) This is a direct consequence of (ii). $\square$

Note that Lemmas 3.3 and 5.2 entail $\mathcal {B}(A)\subseteq \mathcal {S}(A)\cap \mathrm {Neutr}(A)\subseteq A^*\cap A^+$ with $\lnot a=a^*=a^+$ for all $a\in \mathcal {B}(A)$.

Lemma 5.3

Let $(A,\oplus ,\lnot ,{^*},0,1)$ be a basic algebra with pseudocomplementation. Then, the underlying lattice is modular if and only if it is distributive, in which case $\mathcal {S}(A)\subseteq A^* \cap A^+$ and $\lnot a=a^*=a^+$ for every $a\in \mathcal {S}(A)$.

Proof

Suppose to the contrary that the lattice is modular but not distributive, i.e. it contains the following sublattice (the so-called diamond):

Since the map $g_i:x\mapsto \lnot (x\oplus \lnot i)$ defined by (2.14) is an antitone involution on [0, i], there is a copy of the diamond at the bottom of A, and so we may safely assume that $o=0$. We then have $a,b\le c^*$ because $a\wedge c=b\wedge c=0$. Thus, $c\le i=a\vee b\le c^*$, whence $c=c\wedge c^*=0$, a contradiction. Therefore, the lattice is distributive and by Lemma 5.2 (ii) and (iii) we conclude that $\mathcal {S}(A)\subseteq A^* \cap A^+$ and $\lnot x=x^*=x^+$ for every $x\in \mathcal {S}(A)$. $\square$

We have just seen that in distributive basic algebras with pseudocomplementation we have $\mathcal {S}(A)\subseteq A^* \cap A^+$ with $\lnot a=a^*=a^+$ for all $a\in \mathcal {S}(A)$. Another class where this holds true is the class of lattice effect algebras with pseudocomplementation [i.e. basic algebras with pseudocomplementation satisfying quasi-identity (2.10)]. This was essentially proved in Riečanová (2009). Indeed, if $(A,\oplus ,\lnot ,{^*},0,1)$ is a basic algebra with pseudocomplementation satisfying (2.10), then by Riečanová (2009), Theorem 3.4, $\lnot a=a^*$ for every $a\in \mathcal {S}(A)$, whence $a=\lnot a^*=(\lnot a)^+\in A^+$. Since $a\in \mathcal {S}(A)$ iff $\lnot a\in \mathcal {S}(A)$, we get $a=(\lnot a)^*\in A^*$ and $\lnot a=a^+$.

However, the next simple example shows that in general, when $(A,\oplus ,\lnot ,{^*},0,1)$ is neither distributive nor satisfies (2.10), then $\mathcal {S}(A)$ need not be a subset of $A^*\cap A^+$.

Example 5.4

Let $(A,\oplus ,\lnot ,{^*},0,1)$ be the basic algebra with pseudocomplementation with the following underlying lattice (the so-called benzene):

The linearly ordered intervals bear unique antitone involutions; thus, $\oplus$ is determined by the lattice and $\lnot$. The basic algebra $(A,\oplus ,\lnot ,0,1)$ is neither distributive nor satisfies (2.10) because, e.g. $a\oplus b=\lnot a$ but $(a\oplus b)\oplus a=\lnot a\oplus a=1$ and $a\oplus (b\oplus a)=a\oplus \lnot b=\lnot b$. We have $\mathcal {S}(A)=A$, $A^*=\{0,\lnot a,\lnot b,1\}$ and $A^+=\{0,a,b,1\}$, and hence, $\mathcal {S}(A)\nsubseteq A^*\cap A^+$.

Lemma 5.5

Let $(A,\oplus ,\lnot ,{^*},0,1)$ be a basic algebra with pseudocomplementation such that $A^*\subseteq \mathcal {S}(A)$. Then $(A,\oplus ,\lnot ,{^*},0,1)$, or the double p-algebra $(A,\vee ,\wedge ,{^*},{^+},0,1)$, satisfies identities (5.1).

Proof

For any $x\in A$, since $x^*\in A^*\subseteq \mathcal {S}(A)$, we have $x^*\vee \lnot x^*=1$ and $x^*\wedge \lnot x^*=0$, whence $\lnot x^*\le x^{**}$, and so $1=x^*\vee \lnot x^*\le x^*\vee x^{**}$. Thus, $x^*\vee x^{**}=1$. The dual identity is satisfied because $x^{++}\wedge x^+ = \lnot (\lnot x)^{**}\wedge \lnot (\lnot x)^*=\lnot ((\lnot x)^{**}\vee (\lnot x)^*)=\lnot 1=0$. $\square$

Note that the condition $A^*\subseteq \mathcal {S}(A)$ can be captured by the identity $x^*\oplus x^*=x^*$.

Lemma 5.6

Let $(A,\oplus ,\lnot ,{^*},0,1)$ be a basic algebra with pseudocomplementation satisfying identity (2.13). Then

$$\begin{aligned} \mathcal {C}(A)=\mathcal {B}(A)=\mathcal {S}(A)=A^*=A^+. \end{aligned}$$

Consequently, the double p-algebra $(A,\vee ,\wedge ,{^*},{^+},0,1)$ is a double Stone algebra.

Proof

Owing to (2.13), the underlying lattice of the algebra is distributive [see Krňávek and Kühr (2011), Lemma 2.11 or Botur and Kühr (2014), Lemma 4.2] and $\mathcal {C}(A)=\mathcal {S}(A)$ [see Krňávek and Kühr (2015), Lemma 2], whence we have $\mathcal {C}(A)=\mathcal {B}(A)=\mathcal {S}(A)\subseteq A^*\cap A^+$ by Lemma 5.3.

Let $a\in A^*$. Using identities (2.11) and (2.13) we get $0=(a\wedge a^*)\oplus (a\wedge a^*)=(a\oplus a)\wedge (a\oplus a^*)\wedge (a^*\oplus a)\wedge (a^*\oplus a^*)\ge (a\oplus a)\wedge a^*$, so $(a\oplus a)\wedge a^*=0$, whence $a\oplus a\le a^{**}=a$. Thus $a\oplus a=a$, which means that $a\in \mathcal {S}(A)$.

We have proved that $A^*=\mathcal {S}(A)$, and hence, by the remarks (ii) and (iii) before Theorem 5.1, also $A^+=\mathcal {S}(A)$. By Lemma 5.5, $(A,\oplus ,\lnot ,{^*},0,1)$ satisfies identities (5.1), whence $(A,\vee ,\wedge ,{^*},{^+},0,1)$ is a double Stone algebra. $\square$

In what follows, we focus on basic algebras with pseudocomplementation satisfying the condition $\mathcal {C}(A)=A^*$, which is the same as $\mathcal {C}(A)=A^+$. By Corollary 4.2 we have:

Lemma 5.7

A basic algebra with pseudocomplementation $(A,\oplus ,\lnot ,{^*},0,1)$ satisfies the condition $\mathcal {C}(A)=A^*$ if and only if it satisfies the identities

$$\begin{aligned}&x\oplus (y\vee z^*)=(x\oplus y)\vee z^* \nonumber \\&\quad \text {and}\quad x\oplus (y\vee \lnot z^*)=(x\oplus y)\vee \lnot z^*. \end{aligned}$$

(5.2)

Lemma 5.8

Let $(A,\oplus ,\lnot ,{^*},0,1)$ be an arbitrary basic algebra with pseudocomplementation. If $a\in \mathcal {C}(A)$, then $\varvec{\alpha }_a$ as well as $\varvec{\beta }_a=\varvec{\alpha }_{\lnot a}$ is a factor congruence of $(A,\oplus ,\lnot ,{^*},0,1)$.

Proof

Let $a\in \mathcal {C}(A)$. By Lemma 5.2 (iii), we have $\lnot a=a^*$. By Lemma 3.3, we know that $\varvec{\beta }_a=\varvec{\alpha }_{\lnot a}$, $\varvec{\alpha }_a\cap \varvec{\beta }_a=\Delta _A$ and $\varvec{\alpha }_a\circ \varvec{\beta }_a=\nabla _A$. Clearly, $\varvec{\alpha }_a=\varvec{\beta }_{\lnot a}$. If $(x,y)\in \varvec{\alpha }_a$, then $x^*\wedge \lnot a=x^*\wedge a^*=(x\vee a)^*=(y\vee a)^*=y^*\wedge a^*=y^*\wedge \lnot a$, and so $(x^*,y^*)\in \varvec{\beta }_{\lnot a}=\varvec{\alpha }_a$. $\square$

Now, we can describe subdirectly irreducible members of the variety of basic algebras with pseudocomplementation satisfying the condition $\mathcal {C}(A)=A^*$:

Theorem 5.9

Let $(A,\oplus ,\lnot ,{^*},0,1)$ be a basic algebra with pseudocomplementation such that $\mathcal {C}(A)=A^*$. The following statements are equivalent:

• (i) $(A,\oplus ,\lnot ,{^*},0,1)$ is a subdirectly irreducible algebra;

• (ii) the underlying lattice is a chain;

• (iii) $(A,\oplus ,\lnot ,{^*},0,1)$ is a simple algebra.

Proof

(i) implies (ii). Suppose that $a,b\in A$ are two incomparable elements. Since the map $g_{i}$ defined by (2.14) is an antitone involution on [0, i] where $i=a\vee b$, by eventually replacing a, b with $g_{i}(a),g_{i}(b)$, we may assume that $a\wedge b=0$. Then $a\le b^*$ and $a^*\ge b^{**}$, whence $a^*\vee b^*\ge b^{**}\vee b^*=1$ because $(A,\oplus ,\lnot ,{^*},0,1)$ satisfies identities (5.1) by Lemma 5.5. Thus $a^* \vee b^*=1$.

Let $\varvec{\varphi }=\varvec{\beta }_{a^*}$ and $\varvec{\psi }=\varvec{\beta }_{b^*}$. Since $a^*,b^*\in A^*=\mathcal {C}(A)$, the relations $\varvec{\varphi },\varvec{\psi }$ are congruences of $(A,\oplus ,\lnot ,{^*},0,1)$. We have $\varvec{\varphi }\ne \Delta _A\ne \varvec{\psi }$ as otherwise $a^*=1$ or $b^*=1$ which would contradict $a\ne 0\ne b$. Moreover, if $(x,y)\in \varvec{\varphi }\cap \varvec{\psi }$, then $x=x\wedge (a^*\vee b^*)=(x\wedge a^*)\vee (x\wedge b^*)=(y\wedge a^*)\vee (y\wedge b^*)=y\wedge (a^*\vee b^*)=y$. Thus, $\varvec{\varphi }\cap \varvec{\psi }=\Delta _A$, so the algebra is not subdirectly irreducible.

(ii) implies (iii). Let $\varvec{\theta }\ne \Delta _A$ be a congruence of $(A,\oplus ,\lnot ,{^*},0,1)$. Let $(x,y)\in \varvec{\theta }$ with $x\ne y$, say $x>y$. Then $\lnot x\oplus y\ne 1$ and $0\ne \lnot (\lnot x\oplus y) \equiv _{\varvec{\theta }} \lnot (\lnot y\oplus y)=\lnot 1=0$ which yields $0=(\lnot (\lnot x\oplus y))^*\equiv _{\varvec{\theta }} 0^*=1$. This shows that $\varvec{\theta }=\nabla _A$. Thus, the algebra is simple.

(iii) implies (i). This is trivial. $\square$

The following result follows from Krňávek and Kühr (2011), Theorem 4.4 as well as from Botur and Kühr (2014), Theorem 4.7, where it was proved that finite basic algebras satisfying certain identities⁸ weaker than (2.13) are automatically MV-algebras. Our present proof is much shorter.

Corollary 5.10

Every finite basic algebra which satisfies identity (2.13) is an MV-algebra.

Proof

Let $(A,\oplus ,\lnot ,0,1)$ be a finite basic algebra satisfying (2.13). We know that it is distributive [see the introduction, also see Krňávek and Kühr (2011), Lemma 2.11 or Botur and Kühr (2014), Lemma 4.2]. Then for every $a\in A$, $a^*=\bigvee \{x\in A:x\wedge a=0\}$ is the pseudocomplement of a, thus $(A,\oplus ,\lnot ,{^*},0,1)$ is a basic algebra with pseudocomplementation. By Lemma , we have $\mathcal {C}(A)=A^*$, and hence, by Theorem , $(A,\oplus ,\lnot ,{^*},0,1)$ is a subdirect product of linearly ordered algebras $(A_t,\oplus ,\lnot ,{^*},0,1)$. But these algebras are finite, and since the only finite linearly ordered basic algebras are MV-algebras, each $(A_t,\oplus ,\lnot ,0,1)$ is an MV-algebra and it follows that $(A,\oplus ,\lnot ,0,1)$ is an MV-algebra. $\square$

The only lattice effect algebras with pseudocomplementation satisfying the condition $\mathcal {C}(A)=A^*$ are MV-algebras:

Corollary 5.11

Let $(A,\oplus ,\lnot ,{^*},0,1)$ be a basic algebra with pseudocomplementation satisfying identity (2.10). Then $\mathcal {C}(A)=A^*$ if and only if $(A,\oplus ,\lnot ,0,1)$ is an MV-algebra.

Proof

If $(A,\oplus ,\lnot ,0,1)$ is an MV-algebra, then it satisfies (2.13) and hence $\mathcal {C}(A)=A^*$ by Lemma . Conversely, suppose that $\mathcal {C}(A)=A^*$. Since this condition is equivalent to identities (5.2), the algebra $(A,\oplus ,\lnot ,{^*},0,1)$ is a subdirect product of linearly ordered effect algebras with pseudocomplementation, by Theorem . But linearly ordered effect algebras are a fortiori MV-algebras, whence we may conclude that $(A,\oplus ,\lnot ,0,1)$ is an MV-algebra. $\square$

Corollary 5.12

The variety of basic algebras with pseudocomplementation satisfying identities (5.2) is a discriminator variety.

Proof

It is easy to check that the term

$$\begin{aligned} t(x,y,z)=(d(x,y)^* \vee x) \wedge (d(x,y)^{**} \vee z), \end{aligned}$$

where $d(x,y)=\lnot (\lnot x\oplus y)\vee \lnot (\lnot y\oplus x)$, is a discriminator term for the variety. Indeed, if $(A,\oplus ,\lnot ,{^*},0,1)$ is a subdirectly irreducible basic algebra with pseudocomplementation satisfying (5.2), then it is linearly ordered, and hence, for all $a,b,c\in A$ we have $d(a,a)^*=1$ and $d(a,b)^*=0$ when $a\ne b$, whence $t(a,a,c)=c$ and $t(a,b,c)=a$ when $a\ne b$. $\square$