Solving a nonhomogeneous linear system of interval differential equations

Abstract

In most application problems, the exact values of the input parameters are unknown, but the intervals in which these values lie can be determined. In such problems, the dynamics of the system are described by an interval-valued differential equation. In this study, we present a new approach to nonhomogeneous systems of interval differential equations. We consider linear differential equations with real coefficients, but with interval initial values and forcing terms that are sets of real functions. For each forcing term, we assume these real functions to be linearly distributed between two given real functions. We seek solutions not as a vector of interval-valued functions, as usual, but as a set of real vector functions. We develop a method to find the solution and establish an existence and uniqueness theorem. We explain our approach and solution method through an illustrative example. Further, we demonstrate the advantages of the proposed approach over the differential inclusion approach and the generalized differentiability approach.

1 Introduction

1.1 Applications where interval-valued differential equations arise

The vast majority of real-world problems in fields such as engineering mechanics, material science, and thermal analysis contain varying degrees of uncertainty (Blackwell and Beck 2010). This uncertainty can be caused by environmental factors, measurement errors, or lack of information. Depending on the type of uncertainty, the relevant mathematical models can be stochastic, fuzzy, or interval-valued. In some problems, it may be necessary to model some variables as intervals and others as fuzzy numbers. For example, Wang et al. (2015) considered some parameters to be intervals and some to be fuzzy numbers in the fuzzy interval perturbation method, which they proposed to solve the uncertain heat conduction problem. For uncertainties determined by expert opinion, the authors used fuzzy variables but, for uncertainties of deterministic nature that change within certain limits, they used interval variables.

In cases where we know that the values of the (uncertain) input variable are uniformly distributed within a certain interval, it is natural to use the methods of interval-valued analysis. In these cases, the dynamic behavior of the system is described by an interval-valued differential equation. Interval-valued differential equations are a particular case of set-valued differential equations.

Set-valued differential equations are also involved in the investigation of fuzzy differential equations (Lakshmikantham et al. 2003) and ordinary differential inclusions.

Set differential equations are encountered as well when studying the classical optimal control problems (which do not contain uncertainty). An optimal control problem, the equation of motion of which is given by an ordinary differential equation, can be transformed into a differential inclusion problem, and the methods of set differential equations can then be applied to solve the resulting problem (Blagodatskikh and Filippov 1986; Komleva et al. 2008; Plotnikova 2005).

1.2 Related work

The first studies on set-valued analysis were reported in Aubin and Frankowska (1990), Lakshmikantham et al. (2006), and Moore (1966). To date, a number of significant studies have examined interval (in particular) and set (in general) differential equations (see Bede and Stefanini 2009; Boese 1994; Dabbous 2012; Hoa 2015; Hoa et al. 2014; Lakshmikantham and Sun 1991; Lupulescu 2013; Pan 2015; Phu et al. 2014; Quang et al. 2016; Sivasundaram and Sun 1992; Stefanini 2010; Stefanini and Bede 2009; Azzam-Laouir and Boukrouk 2015; Galanis et al. 2005; Komleva et al. 2008; Malinowski 2012b, 2015; Plotnikov and Skripnik 2014).

Bede and Stefanini (2009) proposed a numerical method for interval differential equations with generalized Hukuhara differentiability. Hoa (2015) obtained the existence and uniqueness results of solutions for the initial value problem to interval-valued second-order differential equations under generalized H-differentiability. Lupulescu (2013) studied the differentiability and the integrability for the interval-valued functions on timescales. Pan (2015) investigated the Euler rule and Simpson rule for the interval-valued differential and integral equations. Sivasundaram and Sun (1992) applied the interval analysis to impulsive differential equations. Azzam-Laouir and Boukrouk (2015) proved the existence and uniqueness of a solution for a second-order set-valued differential equation with three-point boundary conditions. Komleva et al. (2008) considered a special space of convex compact sets and introduced the notions of derivative and integral for a set-valued mapping that differ from the previous ones. They also proved theorems on the existence and uniqueness for the differential equations with set-valued right-hand side satisfying the Carathéodory conditions. Malinowski (2012b) introduced the notion of a second type Hukuhara derivative and considered delay set-valued differential equations.

The main difference in the above-mentioned studies lies in the derivatives they use. The point is that there is no commonly accepted concept of the set derivative, in contrast to the real calculus.

Various concepts of set derivative [such as the Huygens derivative (Bridgland 1970), $\pi$-derivative (Banks and Jacobs 1970), Markov-derivative (Markov 1979), and T-derivative (Plotnikov 2000)] have been proposed and used to investigate differential equations (Chalco-Cano and Román-Flores 2011).

Most researchers use the Hukuhara derivative (Hukuhara 1967). The Hukuhara derivative has significant importance in solving set-valued differential equations, but over time, it has been observed that this derivative remains inadequate in addressing certain real-world problems. This derivative is only suitable for solutions in which the uncertainty increases with time. To eliminate this deficiency, Stefanini and Bede (2009) introduced a second concept of the Hukuhara derivative. This second type is suitable for describing decreasing uncertainties (Malinowski 2012a, b, 2015; Pan 2015). The next extension of the Hukuhara derivative was the generalized derivative (Amrahov et al. 2016; Bede and Gal 2005; Plotnikov and Skripnik 2014; Stefanini and Bede 2009), which allows alternating uncertainties to be modeled (Bede and Stefanini 2009; Hoa 2015; Lupulescu 2013; Phu et al. 2014; Plotnikov and Skripnik 2014; Skripnik 2012). A further extension of the Hukuhara derivative was proposed by Stefanini (2010). He extended the Hukuhara difference to the concept of a generalized Hukuhara difference and (based on this new difference) introduced a new concept of the generalized derivative. This concept is employed for solving differential equations by Chalco-Cano et al. (2013), Stefanini (2010), and Tao and Zhang (2016).

1.3 Shortcomings of the existing methods

The above-mentioned studies are mainly based on two approaches: the differential inclusions approach and the set-valued derivative approach. In the first approach, a set-valued differential equation is interpreted as a differential inclusion problem (Hüllermeier 1997). This is a powerful tool for theoretical investigations, but there is no concept of the derivative behind this approach. Consequently, we cannot define an antiderivative (integral) operation. Therefore, regarding set-valued differential equations, developing an effective solution method based on differential inclusions is a difficult task.

Most of the studies cited in Sect. 1.2 use the second approach. Concerning this approach, our viewpoint is as follows. To solve set-valued differential equations, we have to develop a set-valued calculus (similar to the real calculus). For this, we must first define basic arithmetic operations on sets. The Minkowski sum is used for the addition of two sets of vectors, but a difficulty arises immediately when we define subtraction. This is because the Minkowski difference is not the opposite operation to the Minkowski sum. This difficulty is resolved by using the Hukuhara difference. However, using the Hukuhara difference causes a drawback since it is not defined for every two sets. That is, for the Hukuhara difference $A-B$ to exist, A must be at least wider than B (provided that $A\ne B$). The generalized Hukuhara difference, suggested recently by Stefanini (2010), is defined for every two sets, but is not the opposite operation to the Minkowski sum. In summary, the present set-valued operations do not reflect the properties of the arithmetic operations on real numbers. Consequently, any attempt to create a set-valued calculus, which would be similar to the real calculus, fails. Another difficulty with the set derivatives is that, in general, the uniqueness of the solution does not hold.

1.4 Motivation and the proposed approach

In this paper, our motivation is to overcome the above-mentioned difficulties. Our starting point is that the set-valued functions are not the only tool for modeling uncertainties that change with time. We interpret a function with interval uncertainty as a set (in other words, as a bunch) of real functions. The proposed approach can be considered as a further development of the approach employed by Gasilov et al. (2014a, b, 2015) for fuzzy differential equations. The proposed approach becomes useful from different perspectives. First, it avoids the difficulties of set-valued derivatives. Second, the solution exists and is unique under the proposed approach.

1.5 Structure of the paper

The remainder of this paper is organized as follows. In Sect. 2, we introduce the concept of a convex bunch generated by two real functions, which play a crucial role in our solution method. Section 3 contains a description of the system of interval differential equations of interest, an introduction to the concept of a solution, and a description of the solution method. In Sect. 4, we solve a practical example that illustrates the proposed method. The advantages of the proposed method over existing methods are discussed in Sect. 5.

2 Convex bunch generated by two functions

First, we describe a representation for intervals. This representation is used intensively throughout the paper. Consider an interval $A=\left[ a,\ b \right]$. Set $c=\frac{a+b}{2}$ and $\delta =\frac{b-a}{2}$. Then, $A=c+ \left[ -\delta ,\ \delta \right]$. Here, c is the central point of interval A. Hereinafter, we interpret $\left[ -\delta ,\ \delta \right]$ as the uncertainty of A. Then, $\delta$ can be considered as the radius of uncertainty. To summarize, each interval $A=\left[ a,\ b\right]$ can be represented as $A=c+A_{un}$ (central point + symmetric uncertainty), where $A_{un}=\left[ -\delta ,\ \delta \right]$.

In this paper, we consider interval differential equations with forcing terms involving uncertainties. The forcing terms are interpreted as a bunch of real functions, rather than as interval-valued functions.

First, we define the main concept of our approach.

Definition 1

(Bunch of functions). A set

$$\begin{aligned} F=\left\{ y_{\alpha }(\cdot )\ \left| \ \alpha \in \varLambda \right. \right\} \end{aligned}$$

(where $y_{\alpha }$ is a real function, and $\varLambda$ is a set of indices) is called a bunch of functions. The set

$$\begin{aligned} F(t)=\left\{ y_{\alpha }(t)\ \left| \ y_{\alpha }\in F\right. \right\} \end{aligned}$$

is called the value of the bunch F at the point t.

In fact, a bunch is a set of real functions. Usually, these functions are assumed to be related to each other. F(t) is the set, consisting of the values of all functions (from the bunch F) at t.

Definition 2

(Convex bunch). Let $f_{a}(\cdot )$ and $f_{b}(\cdot )$ be given continuous functions on an interval I. The set (of functions), determined by the formula

$$\begin{aligned} F=\left\{ y(\cdot )\ \left| \ y=\alpha f_{a}+(1-\alpha )f_{b},\ \ \alpha \in \left[ 0,1\right] \right. \right\} \end{aligned}$$

is called a convex bunch generated by the functions $f_{a}$ and $f_{b}$, and is denoted as $F=\left\langle f_{a},f_{b}\right\rangle$.

Geometrically, a convex bunch is a set of curves that is linearly distributed between the graphs of $f_{a}$ and $f_{b}$.

Let us introduce $f_{c}=\frac{f_{a}+f_{b}}{2}$ (the central function) and $\delta _{F}=\frac{f_{b}-f_{a}}{2}$ (the function that expresses the radius of uncertainty). It can easily be checked that $\alpha f_{a}+(1-\alpha )f_{b}=\frac{f_{a}+f_{b}}{2}+\alpha \left( -\frac{f_{b}-f_{a}}{2}\right) +(1-\alpha )\frac{f_{b}-f_{a}}{2}=f_{c}+\alpha \left( -\delta _{F}\right) +(1-\alpha )\delta _{F}$. From here, we can conclude that each convex bunch $F=\left\langle f_{a},\ f_{b}\right\rangle$ can be represented as $F=f_{c}+F_{un}$ (central function + uncertainty), where $F_{un}=\left\langle -\delta _{F},\ \delta _{F}\right\rangle$.

Remark 1

Note that a bunch $\left\langle -f,\ f\right\rangle$ consists of functions $k\,f$, where $k=1-2\alpha \in \left[ -1,\ 1\right]$, (i.e., multiples of the function f).

Example 1

In Fig. 1, we depict the convex bunch $F=\left\langle f_{a},\ f_{b}\right\rangle$, where $f_{a}(t)=3t-t^{2}-3$ (the bottom curve); $f_{b}(t)=e^{-t}$ (the upper curve).

Functions that correspond to $\alpha =\frac{1}{6}$, $\frac{2}{6}$, $\frac{3}{6}$, $\frac{4}{6}$, and $\frac{5}{6}$ are represented by (from up to bottom) dashed–dotted, dotted, dashed, dotted, and dashed–dotted curves, respectively.

Fig. 1

A linear bunch $F=\left\langle f_{a},\ f_{b}\right\rangle$ consists of real functions, linearly distributed between the graphs of two given functions, $f_{a}$ and $f_{b}$. The dashed line represents the central function $f_{c}$

According to Definition 1, for the value of the bunch $F=\left\langle f_{a},\ f_{b}\right\rangle$ at a point t, we have:

$$\begin{aligned} F(t)=\left[ \min \left\{ f_{a}(t),\ f_{b}(t)\right\} ,\ \ \max \left\{ f_{a}(t),\ f_{b}(t)\right\} \right] \end{aligned}$$

Note that the value F(t) is an interval.

3 System of interval differential equations

In this section, we describe the problem of interest, our concept of a solution, and a solution method.

For simplicity, we consider the two-dimensional case. We will investigate the following system of linear differential equations:

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right] =\left[ \begin{array}{ll} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] +\left[ \begin{array}{l} F \\ G \end{array} \right] \end{aligned}$$

(1)

with the initial values

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right] =\left[ \begin{array}{l} A \\ B \end{array} \right] , \end{aligned}$$

(2)

where $a_{11}$, $a_{12}$, $a_{21}$, $a_{22}$ are given real numbers; $A= \left[ a_{1},\ a_{2}\right]$ and $B=\left[ b_{1},\ b_{2}\right]$ are given intervals; $F=\left\langle f_{a},\ f_{b}\right\rangle$ and $G=\left\langle g_{a},\ g_{b}\right\rangle$ are given convex bunches of functions.

The initial value problem (IVP) (1)–(2) can be interpreted in different ways. Usually, x and y are considered to be independent interval-valued functions, and the derivative to be an interval derivative (for example, the generalized derivative).

Our approach is essentially different. We interpret the interval IVP (1)–(2) as a family of classical IVPs, where such a classical IVP is obtained by taking an element from each of four sets: $u(\cdot )$ from F, $v(\cdot )$ from G, c from A, and d from B. Namely, we consider the family of classical IVPs

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right]= & {} \left[ \begin{array}{ll} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] +\left[ \begin{array}{l} u(t) \\ v(t) \end{array} \right] \end{aligned}$$

(3)

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right]= & {} \left[ \begin{array}{l} c \\ d \end{array} \right] , \end{aligned}$$

(4)

where $u(\cdot )\in F$ and $v(\cdot )\in G$ are real functions; $c\in A$ and $d\in B$ are real numbers.

Let us explain our concept of a solution.

Definition 3

(Solution). Consider the interval IVP (1)–(2). We interpret this problem as the family of classical IVPs (3)–(4), where $u(\cdot )\in F$, $v(\cdot )\in G$, $c\in A$, and $d\in B$. Each IVP (3)–(4) has a unique solution, say $(x_{uvcd}(\cdot ),\ y_{uvcd}(\cdot ))$. The set (bunch) of all such real vector functions $(x_{uvcd}(\cdot ),\ y_{uvcd}(\cdot ))$ is defined to be the solution X of the interval IVP (1)–(2).

The above definition determines the solution X formally, but the main issue is to find X(t), the value of X at a given time t. By definition, X is a bunch of real vector functions. At t, each vector function has a value that can be interpreted as a point in the coordinate space. Hence, X(t) is the set of these points, i.e., it is a region. Thus, our task is to determine the region X(t) geometrically and calculate it effectively.

We now describe the solution method. First, we represent all interval values as the sum of the central value and the interval uncertainty:

$$\begin{aligned} \left. \begin{array}{l} A\equiv \left[ a_{1},\ a_{2}\right] =a_{c}+A_{un};\ \ a_{c}=\frac{a_{1}+a_{2} }{2}; \\ \ \ A_{un}=\left[ -\delta _{A},\ \delta _{A}\right] ;\ \ \delta _{A}=\frac{ a_{2}-a_{1}}{2} \\ B\equiv \left[ b_{1},\ b_{2}\right] =b_{c}+B_{un};\ \ b_{c}=\frac{b_{1}+b_{2} }{2}; \\ \ \ B_{un}=\left[ -\delta _{B},\ \delta _{B}\right] ;\ \ \delta _{B}=\frac{ b_{2}-b_{1}}{2} \\ F\equiv \left\langle f_{a},\ f_{b}\right\rangle =f_{c}+F_{un};\ \ f_{c}= \frac{f_{a}+f_{b}}{2}; \\ \ \ F_{un}=\left\langle -\delta _{F},\ \delta _{F}\right\rangle ;\ \ \delta _{F}=\frac{f_{b}-f_{a}}{2} \\ G\equiv \left\langle g_{a},\ g_{b}\right\rangle =g_{c}+G_{un};\ \ g_{c}= \frac{g_{a}+g_{b}}{2}; \\ \ \ G_{un}=\left\langle -\delta _{G},\ \delta _{G}\right\rangle ;\ \ \delta _{G}=\frac{g_{b}-g_{a}}{2} \end{array} \right. \end{aligned}$$

(5)

The IVP (1)–(2) is a linear problem. Hence, we can employ the superposition principle to find the solution. Namely, we can split the given problem (1)–(2) into the following three subproblems.

1) The first subproblem is the nonhomogeneous problem with the central values (we will call this the central problem and its solution the central solution):

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right]= & {} \left[ \begin{array}{ll} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] +\left[ \begin{array}{l} f_{c} \\ g_{c} \end{array} \right] \end{aligned}$$

(6)

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right]= & {} \left[ \begin{array}{l} a_{c} \\ b_{c} \end{array} \right] \end{aligned}$$

(7)

The solution $\mathbf {x}_{c}=\left( x_{c}(t),\ y_{c}(t)\right)$ of this classical IVP is a vector function. It is unique and can be calculated using well-known methods.

2) The second subproblem, which gives the uncertainty $X_{unIV}$ of the solution resulting from the initial values, is the homogeneous problem

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right]= & {} \left[ \begin{array}{ll} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] \end{aligned}$$

(8)

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right]= & {} \left[ \begin{array}{l} A_{un} \\ B_{un} \end{array} \right] \end{aligned}$$

(9)

Let us describe how to calculate $X_{unIV}(t)$, the value of this uncertainty at a given time t.

The solution of the corresponding classical problem

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf {x}^{\prime }=\mathbf {Ax} \\ \mathbf {x}(0)=\mathbf {u} \end{array} \right. \end{aligned}$$

(10)

is $\mathbf {x}(t)=e^{\mathbf {A\,}t}\ \mathbf {u}$, where $\mathbf {A}=\left[ \begin{array}{ll} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right]$ is the matrix of the system. This fact can be interpreted as the point $\mathbf {x}(t)$ being the image of the initial point $\mathbf {u}$ under the linear transformation $\mathbf {x}=L(\mathbf {v})=e^{\mathbf {A\,}t}\ \mathbf {v}$.

The initial values of the problem (8)–(9) constitute the rectangle $A_{un}\times B_{un}$ in the coordinate plane. Then, $X_{unIV}(t)$ is the image of this rectangle under the linear transformation L:

$$\begin{aligned} X_{unIV}(t)= & {} e^{\mathbf {A\,}t}\ \left[ \begin{array}{l} A_{un} \\ B_{un} \end{array} \right] \\= & {} \left\{ e^{\mathbf {A\,}t}\ \mathbf {u}\ \left| \ \mathbf {u}=\left[ \begin{array}{l} a \\ b \end{array} \right] ,\ a\in A_{un},\ b\in B_{un}\right. \right\} \end{aligned}$$

As the image of a parallelogram (or rectangle, in particular) under a linear transformation is another parallelogram, at each time t, the value $X_{unIV}(t)$ of the solution forms a parallelogram (Gasilov et al. 2011).

Remark 2

An alternative way of calculating $X_{unIV}$ is as follows. According to Definition 3, we consider the problem (8)–(9) as a family of classical problems (10), where $\mathbf {u}=\left[ \begin{array}{l} a \\ b \end{array} \right]$ with$\ a\in A_{un}$ and $b\in B_{un}$. Set $\alpha =a/\delta _{A}$ and $\beta =b/\delta _{B}$. Then, $\alpha \in \left[ -1,1\right]$ and $\beta \in \left[ -1,1\right]$. Represent $\mathbf {u}=\left[ \begin{array}{l} a \\ b \end{array} \right] =\alpha \left[ \begin{array}{l} \delta _{A} \\ 0 \end{array} \right] +\beta \left[ \begin{array}{l} 0 \\ \delta _{B} \end{array} \right] =\alpha \mathbf {u}_{1}+\beta \mathbf {u}_{2}$. For $\mathbf {u=u}_{1}= \left[ \begin{array}{l} \delta _{A} \\ 0 \end{array} \right]$ and $\mathbf {u=u}_{2}=\left[ \begin{array}{l} 0 \\ \delta _{B} \end{array} \right]$, let the solutions of (10) be $\mathbf {x}_{1}$ and $\mathbf {x}_{2}$, respectively. Then, the solution of (10) for $\mathbf {u}=\left[ \begin{array}{l} a \\ b \end{array} \right]$ is $\mathbf {x}=\alpha \,\mathbf {x}_{1}+\beta \,\mathbf {x}_{2}$. The set of these vector functions $\mathbf {x}$ constitutes the solution of (8)–(9). Consequently,

$$\begin{aligned} X_{unIV}(t)=\left\{ \mathbf {v}\ \left| \ \mathbf {v}=\alpha \,\mathbf {x} _{1}(t)+\beta \,\mathbf {x}_{2}(t);\ \ \alpha ,\ \beta \in \left[ -1,1\right] \right. \right\} \end{aligned}$$

3) The third subproblem, which determines the uncertainty $X_{unF}$ of the solution resulting from the forcing terms, is the nonhomogeneous problem

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right]= & {} \left[ \begin{array}{ll} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] +\left[ \begin{array}{l} \left\langle -\delta _{F},\ \delta _{F}\right\rangle \\ \left\langle -\delta _{G},\ \delta _{G}\right\rangle \end{array} \right] \end{aligned}$$

(11)

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right]= & {} \left[ \begin{array}{l} 0 \\ 0 \end{array} \right] \end{aligned}$$

(12)

Let us describe our solution method for (11)–(12). By Definition 3, we interpret problem (11)–(12) as a set of classical problems. According to Remark 1, the bunch $\left\langle -\delta _{F},\ \delta _{F}\right\rangle$ consists of functions of the form $r\,\delta _{F}$, ($-1\le r\le 1$). Analogously, the bunch $\left\langle -\delta _{G},\ \delta _{G}\right\rangle$ consists of functions of the form $s\,\delta _{G}$, ($-1\le s\le 1$). Consequently, we consider problem (11)–(12) as a set of classical problems such as

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right]= & {} \left[ \begin{array}{ll} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] +\left[ \begin{array}{l} r\,\delta _{F} \\ s\,\delta _{G} \end{array} \right] \end{aligned}$$

(13)

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right]= & {} \left[ \begin{array}{l} 0 \\ 0 \end{array} \right] , \end{aligned}$$

(14)

where $-1\le r\le 1$ and $-1\le s\le 1$. The solution $(x(\cdot ),y(\cdot ))$ of (13)–(14) is a member of the solution set. The bunch of all vector functions $(x(\cdot ),y(\cdot ))$ constitutes the solution of (11)–(12), $X_{unF}$. To express this solution in an effective manner, we apply the following procedure.

Each of problems (13)–(14) is of the form

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf {x}^{\prime }=\mathbf {Ax}+\mathbf {f} \\ \mathbf {x}(0)=\mathbf {0} \end{array} \right. \end{aligned}$$

(15)

We solve this problem for two particular cases of $\mathbf {f}$. For $\mathbf { f=f}_{1}=\left[ \begin{array}{l} \delta _{F} \\ 0 \end{array} \right]$ and $\mathbf {f=f}_{2}=\left[ \begin{array}{l} 0 \\ \delta _{G} \end{array} \right]$, let the solutions of (15) be $\mathbf {x}_{3}$ and $\mathbf {x}_{4}$, respectively. Then, the solution of (15) for $\mathbf {f=}\left[ \begin{array}{l} r\,\delta _{F} \\ s\,\delta _{G} \end{array} \right]$ is $\mathbf {x}=r\,\mathbf {x}_{3}+s\,\mathbf {x}_{4}$. The set (bunch) of all vector functions such as $\mathbf {x}$ gives the solution $X_{unF}$ of (11)–(12). Therefore, $X_{unF}(t)$, the value of the solution at time t, is determined by the following formula:

$$\begin{aligned} X_{unF}(t)=\left\{ \mathbf {v}\ \left| \ \mathbf {v}=r\,\mathbf {x} _{3}(t)+s\,\mathbf {x}_{4}(t);\ \ r,\ s\in \left[ -1,1\right] \right. \right\} \end{aligned}$$

In the coordinate plane, this value forms a parallelogram.

The Minkowski sum of uncertainties from the initial values $X_{unIV}(t)$ and from the forcing terms $X_{unF}(t)$, which are parallelograms in the coordinate plane, gives the total uncertainty $X_{un}(t)$. The Minkowski sum of two parallelograms is a polygon (rectangle, parallelogram, hexagon, or octagon). Furthermore, this polygon is convex and symmetric about its center. Therefore, in the coordinate plane, the value of the total uncertainty $X_{un}(t)$ forms a convex, centrally symmetric polygon.

If we add the total uncertainty $X_{un}$ to the central solution $\mathbf {x} _{c}$, we obtain the solution to the given problem (1)–(2).

According to the above arguments, all three subproblems have unique solutions. Thus, we have proved the following theorem.

Theorem 1

In the sense of Definition 3, the solution of the interval IVP (1)–(2) exists and is unique.

Summarizing the above steps, we can suggest a solution algorithm.

3.1 Solution algorithm

Let the interval IVP (1)–(2) be given.

• 1. Represent each interval value as the sum of the central value and the interval uncertainty, as in (5).

• 2. Solve IVP (6)–(7) and find the central solution $\mathbf {x}_{c}=\left( x_{c}(t),\ y_{c}(t)\right)$.

• 3. Solve (10) for $\mathbf {u}=\mathbf {u}_{1}=\left[ \begin{array}{l} \delta _{A} \\ 0 \end{array} \right]$ and $\mathbf {u}=\mathbf {u}_{2}=\left[ \begin{array}{l} 0 \\ \delta _{B} \end{array} \right]$. Let the solutions be $\mathbf {x}_{1}$ and $\mathbf {x}_{2}$, respectively. Then, the uncertainty resulting from the initial values is the bunch

  $$\begin{aligned} X_{unIV}=\left\{ \alpha \,\mathbf {x}_{1}+\beta \,\mathbf {x}_{2}\ \left| \ \alpha \in \left[ -1,1\right] ,\quad \beta \in \left[ -1,1\right] \right. \right\} \end{aligned}$$

  (16)

• 4. Solve (15) for $\mathbf {f=f}_{1}=\left[ \begin{array}{l} \delta _{F} \\ 0 \end{array} \right]$ and $\mathbf {f=f}_{2}=\left[ \begin{array}{l} 0 \\ \delta _{G} \end{array} \right]$. Let the solutions be $\mathbf {x}_{3}$ and $\mathbf {x}_{4}$, respectively. Then, the uncertainty resulting from the forcing terms is the bunch

  $$\begin{aligned} X_{unF}=\left\{ r\,\mathbf {x}_{3}+s\,\mathbf {x}_{4}\ \left| \ r\in \left[ -1,1\right] ,\ s\in \left[ -1,1\right] \right. \right\} \end{aligned}$$

  (17)

• 5. The solution to the given problem (1)–(2) is the Minkowski sum

  $$\begin{aligned} X=\left\{ \mathbf {x}_{c}\right\} +X_{unIV}+X_{unF} \end{aligned}$$

Remark 3

Note that, we only need to solve five classical IVPs in order to determine the solution to the given interval IVP (to calculate $\mathbf {x}_{c}$, $\mathbf {x}_{1}$, $\mathbf {x}_{2}$, $\mathbf {x} _{3}$, and $\mathbf {x}_{4}$).

4 Example

We now clarify the proposed solution method using an example.

Example 2

Let us consider the system of differential equations

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right] =\left[ \begin{array}{ll} 3 &{}\quad -1 \\ 4 &{}\quad -2 \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] +\left[ \begin{array}{l} F \\ G \end{array} \right] \end{aligned}$$

(18)

with the initial values

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right] =\left[ \begin{array}{l} A \\ B \end{array} \right] =\left[ \begin{array}{l} \left[ 14.75,\ 15.25\right] \\ \left[ 5,\ \ \ 7\right] \end{array} \right] , \end{aligned}$$

(19)

where

$$\begin{aligned} F= & {} \left\langle f_{a},\ f_{b}\right\rangle \\= & {} \left\langle 5t^{2}-15t-25-1.5e^{-t},\ 5t^{2}-15t-25+1.5e^{-t}\right\rangle \\ G= & {} \left\langle g_{a},\ g_{b}\right\rangle =\left\langle 10t^{2}-10t-40.6,\ 10t^{2}-10t-39.4\right\rangle \end{aligned}$$

Using the central values, we represent

$$\begin{aligned}&A =\left[ 14.75,\ 15.25\right] =a_{c}+A_{un}=15+\left[ -0.25,\ 0.25\right] \\&B = \left[ 5,\ 7\right] =b_{c}+B_{un}= 6 + \left[ -1,\ 1\right] \\&F =f_{c}+F_{un};\ \ f_{c}=5t^{2}-15t-25; \\&F_{un} =\left\langle -\delta _{F},\ \delta _{F}\right\rangle =\left\langle -1.5e^{-t},\ 1.5e^{-t}\right\rangle \\&G =g_{c}+G_{un};\ \ g_{c}=10t^{2}-10t-40;\ \ \\&G_{un} =\left\langle -\delta _{G},\ \delta _{G}\right\rangle =\left\langle -0.6,\ 0.6\right\rangle \end{aligned}$$

First, let us explain once again our concept of a solution on the basis of the example under consideration.

Assume we have taken an element from each of the intervals and bunches involved in the formulation of the problem. For instance, let $u(t)=5t^{2}-15t-25+0.3e^{-t}\in F$, $v(t)=10t^{2}-10t-40-0.4\in G$, $c=15-0.125=14.875\in A$, and $d=6+0.75=6.75\in B$. We solve (3)–(4) and find the solution $(x_{uvcd}(\cdot ),\ y_{uvcd}(\cdot ))$:

$$\begin{aligned} \left\{ \begin{array}{l} x_{uvcd}(t)= 5(t+2)-0.2+(0.625-0.1t)e^{-t}+4.45e^{2t} \\ y_{uvcd}(t)= 5t^{2} -0.6+(2.900-0.4t)e^{-t}+4.45e^{2t} \end{array} \right. \end{aligned}$$

Then, we say that the vector function $(x_{uvcd}(\cdot ),y_{uvcd}(\cdot ))$ is a member of the solution set. The set (bunch) of all such vector functions is defined as the solution X of (18)–(19).

Now, we apply the proposed solution method step by step. We split the given problem (18)–(19) into the following three subproblems.

1) First, we solve the central nonhomogeneous problem

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right]= & {} \left[ \begin{array}{ll} 3 &{}\quad -1 \\ 4 &{}\quad -2 \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] +\left[ \begin{array}{l} f_{c} \\ g_{c} \end{array} \right] \end{aligned}$$

(20)

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right]= & {} \left[ \begin{array}{l} 15 \\ 6 \end{array} \right] \end{aligned}$$

(21)

The solution (see Fig. 2) is

$$\begin{aligned} \left[ \begin{array}{l} x_{c}(t) \\ y_{c}(t) \end{array} \right] =\left[ \begin{array}{l} 5(t+2)+\frac{1}{3}e^{-t}+\frac{14}{3}e^{2t} \\ \ \ \ 5t^{2}\ \ \ +\frac{4}{3}e^{-t}+\frac{14}{3}e^{2t} \end{array} \right] \end{aligned}$$

Fig. 2

Central solution

2) Second, to find the uncertainty of the solution resulting from the initial values, we solve the homogeneous problem

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right]= & {} \left[ \begin{array}{ll} 3 &{}\quad -1 \\ 4 &{}\quad -2 \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] \end{aligned}$$

(22)

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right]= & {} \left[ \begin{array}{l} \left[ -0.25, 0.25\right] \\ \left[ -1, 1\right] \end{array} \right] \end{aligned}$$

(23)

To do this, we solve (10) for two particular cases of $\mathbf {u}$.

For $\mathbf {u=u}_{1}=\left[ \begin{array}{l} \delta _{A} \\ 0 \end{array} \right] =\left[ \begin{array}{l} 0.25 \\ 0 \end{array} \right]$, we have

$$\begin{aligned} \mathbf {x}_{1}=\left[ \begin{array}{l} x_{1}(t) \\ y_{1}(t) \end{array} \right] =\left[ \begin{array}{l} \left( 4e^{2t}-e^{-t}\right) /12 \\ \left( e^{2t}-e^{-t}\right) /3 \end{array} \right] \end{aligned}$$

For $\mathbf {u=u}_{2}=\left[ \begin{array}{l} 0 \\ \delta _{B} \end{array} \right] =\left[ \begin{array}{l} 0 \\ 1 \end{array} \right]$, we obtain

$$\begin{aligned} \mathbf {x}_{2}=\left[ \begin{array}{l} x_{2}(t) \\ y_{2}(t) \end{array} \right] =\left[ \begin{array}{l} \left( e^{-t}-e^{2t}\right) /3 \\ \left( 4e^{-t}-e^{2t}\right) /3 \end{array} \right] \end{aligned}$$

The solution of (22)–(23) is determined by formula (16) and is represented in Fig. 3. Note again that the uncertainty of the solution resulting from the initial values is a parallelogram at each time t.

Fig. 3

Uncertainty of the solution as a result of the initial values at $t=0$, $t=0.25$, and $t=0.5$ (from left to right)

3) Third, to find the uncertainty of the solution resulting from the forcing terms, we solve the nonhomogeneous problem

$$\begin{aligned} \left[ \begin{array}{l} x^{\prime } \\ y^{\prime } \end{array} \right]= & {} \left[ \begin{array}{ll} 3 &{}\quad -1 \\ 4 &{}\quad -2 \end{array} \right] \left[ \begin{array}{l} x \\ y \end{array} \right] +\left[ \begin{array}{l} \left\langle -\delta _{F},\ \delta _{F}\right\rangle \\ \left\langle -\delta _{G},\ \delta _{G}\right\rangle \end{array} \right] \end{aligned}$$

(24)

$$\begin{aligned} \left[ \begin{array}{l} x(0) \\ y(0) \end{array} \right]= & {} \left[ \begin{array}{l} 0 \\ 0 \end{array} \right] \end{aligned}$$

(25)

For this, we solve (15) for two particular cases of $\mathbf {f}$.

For $\mathbf {f=f}_{1}=\left[ \begin{array}{l} \delta _{F} \\ 0 \end{array} \right] =\left[ \begin{array}{l} 1.5e^{-t} \\ 0 \end{array} \right]$, we have

$$\begin{aligned} \mathbf {x}_{3}=\left[ \begin{array}{l} x_{3}(t) \\ y_{3}(t) \end{array} \right] =\left[ \begin{array}{l} \left( -(3t+4)e^{-t}+4e^{2t}\right) /6 \\ \left( -(12t+4)e^{-t}+4e^{2t}\right) /6 \end{array} \right] \end{aligned}$$

For $\mathbf {f=f}_{2}=\left[ \begin{array}{l} 0 \\ \delta _{G} \end{array} \right] =\left[ \begin{array}{l} 0 \\ 0.6 \end{array} \right]$, we have

$$\begin{aligned} \mathbf {x}_{4}=\left[ \begin{array}{l} x_{4}(t) \\ y_{4}(t) \end{array} \right] =\left[ \begin{array}{l} \left( 3-2e^{-t}-e^{2t}\right) /10 \\ \left( 9-8e^{-t}-e^{2t}\right) /10 \end{array} \right] \end{aligned}$$

Thus, the solution $X_{unF}$ of (24)–(25) is determined by formula (17). At each time t, the value $X_{unF}(t)$ forms a parallelogram in the coordinate plane. We represent $X_{unF}$, the uncertainty of the solution resulting from the forcing terms, in Fig. 4.

Fig. 4

Uncertainty of the solution as a result of the forcing terms at $t=0$, $t=0.25$, and $t=0.5$ (from left to right)

The Minkowski sum of the uncertainties from the initial values and from the forcing terms (i.e., the sum of two parallelograms) gives the total uncertainty. This is represented in Fig. 5.

Fig. 5

Total uncertainty of the solution at $t=0$, $t=0.25$, and $t=0.5$ (from left to right)

We add the total uncertainty to the central solution to obtain the solution to the given problem (18)–(19) (see Fig. 6).

Fig. 6

Values of the solution at $t=0$, $t=0.25$, and $t=0.5$ (from left to right)

5 Comparison with existing methods

5.1 Comparison with the method of differential inclusions

In this subsection, we demonstrate the difference between the proposed method and the method of differential inclusions with the help of a numerical example. For simplicity, we consider the one-dimensional case.

Example 3

Let us consider the IVP

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }=F \\ x(0)=0 \end{array} \right. , \end{aligned}$$

(26)

where

$$\begin{aligned} F=\left\langle f_{a},\ f_{b}\right\rangle =\left\langle -\sin t,\ \sin t\right\rangle \end{aligned}$$

(27)

First, we solve IVP (26) using our method. For this, we consider the corresponding classical IVP

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }(t)=f(t) \\ x(0)=0 \end{array} \right. \end{aligned}$$

For $f=f_{b}=\sin t$, the solution is found to be

$$\begin{aligned} x_{b}(t)=1-\cos t \end{aligned}$$

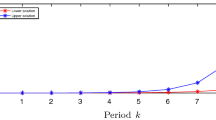
Hence, the solution of IVP (26) given by our method is the convex bunch

$$\begin{aligned} x=\left\langle -x_{b},\ x_{b}\right\rangle =\left\langle -(1-\cos t),\ 1-\cos t\right\rangle \end{aligned}$$

(28)

(see Fig. 7, dashed lines).

Fig. 7

Boundaries of the solutions obtained by the proposed approach (dashed lines) and by the differential inclusions approach (continues lines)

Now, we solve (26) using the method of differential inclusions. We must solve

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }(t)\in \left[ -\left| \sin t\right| ,\ \left| \sin t\right| \right] \\ x(0)=0 \end{array} \right. \end{aligned}$$

(29)

To find the boundaries of the solution, we solve the IVP

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }(t)=\left| \sin t\right| \\ x(0)=0 \end{array} \right. \end{aligned}$$

(30)

It can be checked that the solution of (30) is

$$\begin{aligned} \overline{x}(t)=2k+1-(-1)^{k}\cos t, \ \ \ t\in \left[ k\pi ,\ (k+1)\pi \right] , \end{aligned}$$

(31)

where $k=0$, 1, 2, 3, $\ldots$. Therefore, the solution of (26) given by the method of differential inclusions is the interval-valued function

$$\begin{aligned} x(t)=\left[ -\overline{x}(t),\ \overline{x}(t)\right] \end{aligned}$$

(32)

(see Fig. 7, continues lines).

Remark 4

What conclusion can be drawn from the above calculations? The initial value of the given differential equation (26) is zero, and the right-hand side is periodic. Thus, it is natural to expect the solution to be periodic too. However, the solution given by the method of differential inclusions is not periodic, as it expands with time. In contrast, our method gives a periodic solution, in accordance with expectations.

To summarize, we can conclude the following. Although the idea of our approach is close to that of differential inclusions, there is a class of problems for which our method provides more adequate solutions.

5.2 Comparison with generalized derivative

In this subsection, we compare our method with the method of the generalized derivative. For this purpose, we use Example 2. For clarity, we consider subproblem (22)–(23), where only the initial values are intervals. The solution of (22)–(23) given by our method is depicted in Fig. 3.

Below, we solve (22)–(23) using the generalized derivative. We consider x(t) and y(t) to be intervals. To emphasize that they are sets, we rename them X(t) and Y(t), respectively. Therefore, we must solve the following interval IVP:

$$\begin{aligned} \left. \begin{array}{l} X^{\prime }(t)=3X(t)-Y(t) \\ Y^{\prime }(t)=4X(t)-2Y(t) \\ X(0)=\left[ -0.25, 0.25\right] \\ Y(0)=\left[ -1, 1\right] \end{array} \right. \end{aligned}$$

(33)

Let the solution of (33) be $X(t)=\left[ \underline{x}(t),\ \overline{x}(t)\right]$ and $Y(t)=\left[ \underline{y}(t),\ \overline{y}(t) \right]$. As the initial values are symmetric with respect to 0, the solution is also symmetric. Then, $X(t)=\left[ -u(t),\ u(t)\right]$ and $Y(t)=\left[ -z(t),\ z(t)\right]$, where $u(t)=\overline{x}(t)$ and $z(t)= \overline{y}(t)$.

To follow the calculations below, note that $-Y(t)\equiv (-1)Y(t)= \left[ -z(t),\ -\left( -z(t)\right) \right] =\left[ -z(t),\ z(t)\right]$ and $(-2)Y(t)=\left[ -2z(t),\ 2z(t)\right]$.

The interval-valued function X(t) can have two generalized derivatives (of type 1 or 2). The same is true for Y(t). Therefore, to solve (33), we have to examine four cases.

First, we examine the case where X(t) and Y(t) both have generalized derivatives of type 1. We call this the (1, 1)-derivative case. In this case, $X^{\prime }(t)=\left[ -u^{\prime }(t),\ u^{\prime }(t)\right]$ and $Y^{\prime }(t)=\left[ -z^{\prime }(t),\ z^{\prime }(t)\right]$. From (33), for u and z, we have the following IVP:

$$\begin{aligned}&u^{\prime } =3u+z \\&z^{\prime } =4u+2z \\&u(0) =0.25 \\&z(0) =1 \end{aligned}$$

Therefore,

$$\begin{aligned} u\left( t\right)= & {} 0.397853e^{\frac{5+\sqrt{17}}{2}t}-0.147853e^{\frac{5- \sqrt{17}}{2}t} \\ z\left( t\right)= & {} 0.621268e^{\frac{5+\sqrt{17}}{2}t}+0.378732e^{\frac{5- \sqrt{17}}{2}t} \end{aligned}$$

It can be seen (see Fig. 8) that $X(t)=\left[ -u(t),\ u(t) \right]$ and $Y(t)=\left[ -z(t),\ z(t)\right]$ determine a valid solution for (33) on the entire interval $\left[ 0,\ \infty \right)$.

Fig. 8

(1, 1)-solution for IVP (33)

Second, we consider the case where X(t) and Y(t) have generalized derivatives of types 1 and 2, respectively. In this (1, 2)-derivative case, $X^{\prime }(t)=\left[ -u^{\prime }(t),\ u^{\prime }(t)\right]$ and $Y^{\prime }(t)=\left[ z^{\prime }(t),\ -z^{\prime }(t)\right]$. Then, from ( 33), we have:

$$\begin{aligned}&u^{\prime } =3u+z \\&z^{\prime } =-4u-2z \\&u(0) =0.25 \\&z(0) =1 \end{aligned}$$

Hence,

$$\begin{aligned} u\left( t\right)= & {} \frac{2}{3}e^{2t}-\frac{5}{12}e^{-t} \\ z\left( t\right)= & {} \frac{5}{3}e^{-t}-\frac{2}{3}e^{2t} \end{aligned}$$

The solution $\left( X(t),\ Y(t)\right)$ is depicted in Fig. 9. Let us focus on $X(t)=\left[ -z(t),\ z(t) \right]$. Since $z^{\prime }\left( t\right) =-\left( \frac{5}{3}e^{-t}+ \frac{4}{3}e^{2t}\right)<-\frac{4}{3}e^{2t}<-1$ (for $t>0$), the upper solution (z(t)) decreases at speed more than 1. In contrary, the lower solution ($-z(t)$) increases at speed more than 1. Therefore, the upper and lower solutions intersect at some point $t=t_{*}$. (For $t>t_{*}$, the values of $z\left( t\right)$ become negative and, consequently, $X(t)= \left[ -z(t),\ z(t)\right]$ becomes an improper interval). Consequently, the (1, 2)-solution $\left( X(t),\ Y(t)\right)$ is valid only on $\left[ 0,\ t_{*}\right] \approx \left[ 0,\ 0.305431\right]$.

Fig. 9

(1, 2)-solution for IVP ( 33)

In the case of the (2, 1)-derivative, where $X^{\prime }(t)=\left[ u^{\prime }(t),\ -u^{\prime }(t)\right]$ and $Y^{\prime }(t)=\left[ -z^{\prime }(t),\ z^{\prime }(t)\right]$, we have:

$$\begin{aligned}&u^{\prime } =-3u-z \\&z^{\prime } =4u+2z \\&u(0) =0.25 \\&z(0) =1 \end{aligned}$$

From this, we obtain:

$$\begin{aligned} u\left( t\right)= & {} \frac{2}{3}e^{-2t}-\frac{5}{12}e^{t} \\ z\left( t\right)= & {} \frac{5}{3}e^{t}-\frac{2}{3}e^{-2t} \end{aligned}$$

The solution $\left( X(t),\ Y(t)\right)$ (see Fig. 10) is valid on $\left[ 0,\ t_{*}\right] \approx \left[ 0,\ 0.156668\right]$.

Fig. 10

(2, 1)-solution for IVP ( 33)

In the case of the (2, 2)-derivative, where $X^{\prime }(t)=\left[ u^{\prime }(t),\ -u^{\prime }(t)\right]$ and $Y^{\prime }(t)=\left[ z^{\prime }(t),\ -z^{\prime }(t)\right]$, from (33), we have:

$$\begin{aligned} u^{\prime }= & {} -3u-z \\ z^{\prime }= & {} -4u-2z \\ u(0)= & {} 0.25 \\ z(0)= & {} 1 \end{aligned}$$

Therefore,

$$\begin{aligned} u\left( t\right)= & {} 0.397853e^{-\frac{5+\sqrt{17}}{2}t}-0.147853e^{-\frac{5- \sqrt{17}}{2}t} \\ z\left( t\right)= & {} 0.621268e^{-\frac{5+\sqrt{17}}{2}t}+0.378732e^{-\frac{5- \sqrt{17}}{2}t} \end{aligned}$$

The solution $\left( X(t),\ Y(t)\right)$ (see Fig. 11) is valid on $\left[ 0,\ t_{*}\right] \approx \left[ 0,\ 0.240077\right]$.

Fig. 11

(2, 2)-solution for IVP ( 33)

Fig. 12

Values of (1, 1)-solution for IVP ( 33) at $t = 0, t = 0.25$, and $t = 0.5$ (from left to right)

Remark 5

Let us comment on the results of the above calculations.

• 1) On the interval $\left[ 0,\ t_{*}\right] \approx \left[ 0,\ 0.156668 \right]$, there are four solutions under generalized derivative. In the n-dimensional case, the number of solutions may be up to $2^{n}$. How can we build a final solution from these $2^{n}$ solutions? This question has not been answered in the existing literature.

• 2) The (1, 1)-solution is the only one that is valid on the entire time interval $\left[ 0, \infty \right)$. Consequently, it is the only one that can be compared with our solution. In the coordinate plane, the value of the (1, 1)-solution at $t=0.5$ forms the rectangle $R=X(0.5)\times Y(0.5)=\left[ -u(0.5),\ u(0.5) \right] \times \left[ -z(0.5),\ z(0.5)\right] \approx \left[ -3.70861,\ 3.70861\right] \times \left[ -6.55022,\ 6.55022\right]$ (see Fig. 12). The value of the solution obtained by our method is in the form of a parallelogram (see Fig. 3). This parallelogram P is much smaller than the rectangle R and is completely contained within R. Consequently, our method evaluates the uncertainty more precisely.

• 3) The generalized derivative only allows the uncertainty at time t to be evaluated as a rectangle (see Fig. 12). In contrast, our method provides a wider range of evaluations (rectangles, parallelograms, hexagons, and octagons) (see Figs. 3, 4, 5).

The above comparison of the proposed method with the generalized derivative and differential inclusions techniques can be summarized as follows.

• 1) The proposed method allows the uncertainty to be evaluated more meticulously than with the other methods.

• 2) Under the proposed approach, the solution exists and is unique.

• 3) The proposed method is easy to implement. The set-valued solution is calculated on the basis of the knowledge of the real calculus.

  Therefore, the proposed method is more effective for the class of systems of differential equations.