Modified multiple search cooperative foraging strategy for improved artificial bee colony optimization with robustness analysis

Abstract

Considering that extending the concept of bees partitioning into subgroups of foragers to the onlooker phase of the cooperative learning artificial bee colony (CLABC) strategy is not only feasible from algorithmic viewpoint but might reflect real behavioral foraging characteristics of bee swarms, this paper studies whether the performance of CLABC can be enhanced by developing a new model for the proposed cooperative foraging scheme. Relying on this idea, we design a modified cooperative learning artificial bee colony algorithm, referred to as mCLABC. The design procedure is built upon the definition of a partitioning scheme of onlookers allowing the generation of subgroups of foragers that might evolve differently by using specific solution search rules. In order to improve the involving of local and global search at both employed and onlooker levels, the multiple search mechanism is further tuned and scheduled according to a random selection strategy defined on the evolving parameters. Moreover, a detailed performance and robustness study of the proposed algorithm dealing with the analysis of the impact of different structural and parametric settings is conducted on benchmark optimization problems. Superior convergence performance, better solution quality, and strong robustness are the main features of the proposed strategy in comparison with recent ABC variants and advanced methods.

1 Introduction

During past decades, population-based search algorithms have shown great success in solving different kinds of optimization problems. Evolutionary and swarm intelligence methods are common population-based algorithms which have received particular interest in recent years. Extensive efforts are still being made on basic population-based algorithms such as differential evolution (DE) (Storn and Price 1997), evolutionary programming (EP) (Fogel 1995), particle swarm optimization (PSO) (Kennedy and Eberhart 1995), ant colony optimization (ACO) (Dorigo and Stutzle 2004), artificial bee colony optimization (ABC) (Karaboga 2005), in an attempt to improve their essential computational features such as convergence performance and robustness with regard to exploration and exploitation abilities.

The ABC optimization concept relies on a stochastic search mechanism that mimics the natural behavioral foraging process of honeybees as being initially introduced by Karaboga (2005). The ABC model has shown considerable improvements over existing classical and advanced optimization strategies (Karaboga and Akay 2009). It requires only three control parameters to be tuned, i.e., the population size (number of food sources), the exploration parameter called “limit,” and the maximum number of generations. In general, it has been proven that ABC achieves efficient global search and, hence, can be seen as a global optimizer. So far, ABC has gained substantial interest with an increasing number of applications to various scientific and engineering problems, such as clustering problems (Karaboga and Ozturk 2011), economic dispatch problem (Secui 2015), training neural networks (Karaboga and Ozturk 2009), vehicle routing problem (Szeto et al. 2015), image processing (Banharnsakun et al. 2011), scheduling problems (Taheri et al. 2013), wireless sensor network (Okdem et al. 2011), optimal filter design (Bose et al. 2014), optimal power flow problem (Yuan et al. 2015; Jadhav and Bamane 2016), fuzzy systems design (Habbi et al. 2015), truss structure design (Sonmez 2011), stock price prediction (Hsieh et al. 2011) and other problems (Saffari et al. 2016; Habbi et al. 2015; Habbi and Boudouaoui 2014; Aydoğdu et al. 2016; Habbi 2012; Liang and Lee 2015; Sun et al. 2013). However, like any other population-based techniques, ABC has its own shortcomings: the ABC model has good exploration ability, but its exploitation level needs further improvement, which represents a challenging issue for ABC convergence and performance.

The basic ABC model was subjected to many enhancements aiming to increase its computational performance and robustness. To this end, different modified and hybridized ABC-based algorithms have been developed in order to achieve good balance between exploration and exploitation. Let us mention for instance the work by Zhu and Kwong (2010) where a global-best-guided ABC variant is proposed. Akay and Karaboga (2012) designed a modified ABC algorithm by controlling the frequency of perturbation and introducing the ratio of the variance operator. Gao et al. (2014) developed new search equations to adjust exploration and exploitation capability of the ABC algorithm. Xiang et al. (2014) hybridized DE and ABC with a new search strategy inspired from gbest-guided ABC to enhance the convergence rate of traditional ABC. Kiran and Findik (2014) developed a simple version of the basic ABC algorithm by using direction information regarding the solutions to improve the convergence characteristics of the basic algorithm. Li and Yang (2016), inspired by the biological study of natural honeybees, presented a new ABC variant which imitates a memory mechanism to the artificial bees to memorize their previous successful experiences of foraging behavior. Babaoglu (2015) proposed a distribution-based solution update rule for the basic ABC algorithm, which uses the mean and standard deviation of selected two food sources to obtain a new candidate solution. Alatas (2010) proposed a chaotic ABC algorithm, in which many chaotic maps for parameters adapted from the standard ABC algorithm were introduced to improve its convergence performance. Biswas et al. (2014) presented migratory multi-swarm ABC where subpopulations of swarms employ different search strategies. Harfouchi and Habbi (2016) developed a novel multiple search ABC variant with cooperative learning paradigm. Wang et al. (2014) proposed an integration of update rules for ABC algorithm and analyzed the performance of the proposed method on solving numerical functions. Li et al. (2012) proposed an improved ABC algorithm with the abilities of prediction and selection by introducing an inertia weight and two acceleration coefficients.

Following up ABC improvement efforts, we presented in Harfouchi and Habbi (2016) a novel variant of ABC model relying on the concept of cooperative foraging learning among bee swarms as highlighted above. In the proposed ABC variant, referred to as CLABC (Cooperative learning artificial bee colony) algorithm, a structural modification of the employed phase is introduced. Employed bees are partitioned into subgroups of foragers which evolve differently with multiple search mechanism. The onlookers are not subjected to this modified behavioral structure and thus are supposed to operate into a unique group as defined in the basic ABC model. From behavioral analysis viewpoint, extending the general concept of foragers partitioning to cover onlookers is not only feasible but might reflect natural features of bee swarms. Relying on this idea, the present paper addresses the problem of designing a modified framework of the CLABC algorithm by introducing structural modifications to better characterize the involving of subgroups of employed and onlooker bees in the foraging process. The proposed optimization strategy also performs with multiple search mechanism that allows mutual and simultaneous exchange of information among the foraging subgroups. Moreover, a detailed performance and robustness study of the proposed ABC variant dealing with the analysis of the impact of different parameter and structural settings is conducted on benchmark and complex optimization problems.

The remaining of this paper is organized as follows. Section 2 introduces the basics of ABC optimization method. The modified cooperative learning artificial bee colony (mCLABC) strategy is described in Sect. 3. To assess its performance, experiments on benchmark numerical and composition test functions are presented in Sect. 4. In Sect. 5, a detailed robustness study is conducted with respect to a number of structural and parameter settings of the proposed method. Finally, conclusions and remarks are given in Sect. 6.

Fig. 1

Pseudo-code of the basic ABC algorithm

2 Basics of artificial bee colony optimization

As to simulate the foraging behavior of honeybees, the ABC model employs three types of foragers that are categorized into employed bees, onlooker bees and scouts (Karaboga 2005). With regard to natural foraging process of bees, three operational phases are distinguished through which multi-tasks are rigorously performed for profitable search. From behavioral viewpoint, an employed bee searches around the current food source to find a new source position with better nectar amount. If the nectar amount of the discovered position is higher than that of the previous one, the bee saves the new position in her memory and forgets the old one. Each employed bee is associated with a food source which means the number of employed bees is same as the number of food sources. After all employed bees complete their search, they share the gathered information about foraging with onlooker bees which are waiting in the hive. An onlooker bee chooses a food source according to a probabilistic greedy selection mechanism. Therefore, food sources with better profitability will get higher probability to be selected by the onlookers. Similarly, each onlooker bee produces a modification on the position in her memory and checks the nectar amount of the generated candidate source. If a position cannot be improved further through a predetermined limit tolerance called “limit”, then that food source is assumed to be abandoned. The corresponding employed bee becomes then a scout. The abandoned position will be replaced with a new food source found by the scout.

From algorithmic viewpoint, the first step of the ABC optimization process consists in generating randomly a population of SN solutions (food source positions) in the admissible search domain by using the following equation:

$$\begin{aligned} x_i^j =x_{\min }^j +rand(0,1)(x_{\max }^j -x_{\min }^j ) \end{aligned}$$

(1)

where $i=1,2,...,\mathrm{SN}, j=1,2,...,D$ and D is the number of optimization parameters; $x_{\min }^j$ and $x_{\max }^j$ are the lower and upper bounds of the dimension j, respectively.

After the initialization step, the population of food sources is subjected to repeated cycles of three-phase search process of employed bees, onlooker bees, and scout bees. Employed bees use the following search equation to generate new candidate solutions $v_i$ from the old ones $x_i$ (Karaboga and Basturk 2008):

$$\begin{aligned} v_i^j =x_i^j +\phi _i^j (x_i^j -x_k^j ) \end{aligned}$$

(2)

where $i=1,2,...,\mathrm{SN}, j\in \{{1,2,...,D}\}$ and $k\in \{ {1,2,...,\mathrm{SN}}\}$ are indexes selected randomly, and k different from i. $\phi _i^j$ is a uniform random number in $[-1,1]$. Greedy selection between the old and the updated food source position is performed by the employed bee based on fitness value evaluation. This valuable information about the position and the quality of the food sources is shared with the onlooker bees.

Unlike the employed bee, an onlooker bee chooses a food source with a probability that depends on its nectar amount and is calculated as follows:

$$\begin{aligned} p_i =\frac{\mathrm{fit}_i }{\sum _{n=1}^{\mathrm{SN}} {\mathrm{fit}{ }_n} } \end{aligned}$$

(3)

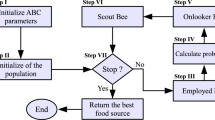
where $\mathrm{fit}_i$ indicates the fitness value of the solution i. After having chosen a food source, an onlooker bee determines a new candidate solution by using Eq. (2), and then greedy selection is applied between the new solution and the old one. If a solution cannot be further improved by means of a predefined limit value, it is considered as exhausted and is abandoned. In this case, a new position is randomly determined by a scout bee by using Eq. (1). The three-phase procedure of the basic ABC optimization model is summarized in Fig. 1.

3 The modified cooperative learning strategy for improved ABC optimization

Search equations in population-based algorithms are key operators based on which solution updating is performed. Obviously, the search mechanism guides the optimization process to optimal or near-optimal solutions in a predefined or randomly chosen direction by updating rules. Evaluating the computational performance of a population-based algorithm might be done in accordance with two important features which are the exploration and the exploitation abilities. The exploration process is related to the ability of carrying out independent search for optimal solution finding, whereas the exploitation process is related to the ability of integrating existing knowledge to improve solutions (Akay and Karaboga 2012). For the sake of efficiency, search equations have to be designed so that exploration and exploitation are adequately balanced. As mentioned above, the basic ABC model uses the search rule defined by Eq. (2) which is suitable for global search. However, ABC might be slow to converge and easily get trapped in local solutions, which is a challenging issue for many population-based search algorithms. To deal with this common drawback, one actual and active research trend in ABC optimization consists in the design of well-established search strategies. The literature reports a number of tentative works on this particular subject (Gao et al. 2012, 2013a; Zhu and Kwong 2010; Gao and Liu 2011; Gao et al. 2014).

With the aim to further improve the performance of ABC optimization, a modified cooperative learning strategy is investigated in the present study. To implement the proposed cooperative concept, structural modifications are introduced into the original CLABC described in Harfouchi and Habbi (2016). The design procedure is built upon the definition of a partitioning scheme of onlookers allowing the generation of subgroups of foragers that might evolve differently by using specific search equations. The updating rules describing the multi-search mechanism have also been adjusted together with some parameter settings. Unlike the original CLABC, the transformed cooperative learning framework which is referred to as mCLABC (modified cooperative learning ABC) involves local and global search rules at both employed and onlooker levels. This might of course impact positively the exploration and the exploitation capabilities of the designed model. Based on this scheme, a random cooperative foraging learning strategy is built upon the combination of a set of local and global search equations through which separate subgroups of foragers evolve simultaneously at both employed or onlooker stages. More precisely, the idea relies on modeling the foraging behavior of swarm honeybees according to the following behavioral concept: “In a bee swarm, employed and onlooker bees could be divided into subgroups of foragers. The subgroups of employed foragers or onlooker might perform food search independently, engage at each level specific search tools differently and also might exchange information about the foraging process mutually”.

Modeling such a behavioral concept needs first a search mechanism to be defined for each foraging subgroup. A multiple search mechanism is then adopted which consists in a set of global and local search equations that allow mutual and simultaneous exchange of foraging information between the subgroups of a given bees category. The solution updating equations are defined as follows:

$$\begin{aligned} v_i^j= & {} x_i^j +\phi _i^j (x_i^j -x_k^j )\nonumber \\&i=1,2,...,\mathrm{SN},\,i\ne k,\,j\in \left\{ {1,2,...,D} \right\} \end{aligned}$$

(4)

$$\begin{aligned} v_i^j= & {} x_k^j +\phi _i^j (x_k^j -x_{k1}^j )\nonumber \\&i=1,2,...,\mathrm{SN},\,i\ne k\ne k_1 ,\,j\in \left\{ {1,2,...,D} \right\} \end{aligned}$$

(5)

$$\begin{aligned} v_i^j= & {} x_k^j +\phi _i^j (x_{k1}^j -x_{k2}^j )\nonumber \\&i=1,2,...,\mathrm{SN},i\ne k\ne k_1 \ne k_2 ,\nonumber \\&j\in \left\{ {1,2,...,D} \right\} \end{aligned}$$

(6)

$$\begin{aligned} v_i^j= & {} x_{\mathrm{best}}^j +\varphi _i^j (x_i^j -x_{\mathrm{mean}}^j )+\phi _i^j (x_k^j -x_{k1}^j ) \nonumber \\&i=1,2,...,\mathrm{SN},\,i\ne k\ne k_1 ,\,j\in \left\{ {1,2,...,D} \right\} \end{aligned}$$

(7)

$$\begin{aligned} v_i^j= & {} x_{\mathrm{best}}^j +\phi _i^j (x_k^j -x_{k1}^j )\nonumber \\&i=1,2,...,\mathrm{SN},\,i\ne k\ne k_1 ,\,j\in \left\{ {1,2,...,D} \right\} \end{aligned}$$

(8)

$$\begin{aligned} v_i^j= & {} x_i^j +\varphi _i^j (x_i^j -x_{\mathrm{mean}}^j )+\phi _i^j (x_k^j -x_{k1}^j )\nonumber \\&i=1,2,...,\mathrm{SN},\,i\ne k\ne k_1 ,\,j\in \left\{ {1,2,...,D} \right\} \end{aligned}$$

(9)

where $\phi _i^j \in [{-1,1} ], \varphi _i^j \in [{0,1}]$ are random numbers generated for each dimension at each processing time. $x_k^j , x_{k1}^j$ and $x_{k2}^j$ are the jth dimensions of solutions selected randomly from the populations of bee subgroups (subpopulations), $k, k_1$ and $k_2$ are not equal to each other and to $i, x_{\mathrm{best}}^j$ denotes the jth dimension of the best solution obtained by the subpopulations so far, and $x_{\mathrm{mean}}^j$ is the average solution corresponding to the jth dimension for all solutions in the subpopulations.

Fig. 2

The algorithmic framework of the proposed mCLABC algorithm

Here, Eqs. (4)–(6) are suitable for global search and Eqs. (7)–(9) for local search. To incorporate the multiple search mechanism described by Eqs. (4)–(9) into the framework of ABC model, the employed and onlooker foragers are first categorized into a predefined number of subgroups. Subpopulations of potential solutions are then generated iteratively at both employed and onlooker phases. The formed subgroups of employed and onlooker bees will have to evolve differently during the foraging process by engaging specific search strategies which are not similar to those defined for the other subgroups. According to design, the search Eqs. (4) and (5) will be called by the first group of employed and onlooker bees to generate new candidate solutions. Only one of those two search equations is used to update the solution with regard to a specified probability which depends on the current iteration and the maximum number of cycles as defined in Mohamed (2015). The nonlinear decreasing probability rule introduced in Mohamed (2015) has been determined empirically to enhance the global exploration capability of the evolutionary strategy. Following this reasoning and based on several experiments, we adopted a different form of probability rule for our design which is given by the increasing nonlinear form $\gamma =\left( {iter/MCN} \right) ^{1/2}$. Based on this definition, we can for instance define the following selective updating rule for a given subgroup of foragers:

$$\begin{aligned}&\textit{if}\left( {\textit{random}\le \gamma } \right) \textit{then} \nonumber \\&v_i^j =x_i^j +\phi _i^j (x_i^j -x_k^j )\nonumber \\&\text {else} \nonumber \\&v_i^j =x_k^j +\phi _i^j (x_k^j -x_{k1}^j )\nonumber \\&\text {end} \end{aligned}$$

(10)

where iter is the current generation number and MCN is the maximum number of cycles. Obviously, it is clear that, from Eq. (10), the probability of using one of the two search rules is a function of the iteration number. The nonlinear form of the probability is determined empirically with regard to search process convergence rate which is guided by the above probabilistic strategy. Based on the same definition of probability given above, the random search Eq. (6) and the gbest-guided Eq. (7) are used for the second subgroup of employed and onlooker bees. Similarly, the third subgroup employs Eqs. (8) and (9) to update candidate solutions. Here, search Eq. (8) performs solution updating in a random direction guided by the gbest solution found so far, while search Eq. (9) is mean-oriented. On the other hand, a strategy to select the number of evolving optimization parameters is incorporated in the modified algorithmic framework of mCLABC at both employed and onlooker levels. For this purpose, employed bees are managed to start by changing one random dimension. Then, when the number of iterations reaches $\textit{iter}=\frac{1}{5}{\mathrm{MCN}}$, the algorithm will have to optimize randomly one or all parameters simultaneously. While reaching the end of the optimization process, i.e., between $\textit{iter}=\frac{4}{5}{\mathrm{MCN}}$ and $\textit{iter}={\mathrm{MCN}}$, the employed bees will update all parameters of the solution. Subsequently, after completion of the employed bee phase and based on greedy selection, the subgroups of onlookers start to update one random parameter of the solution. Then, when $\textit{iter}=\frac{1}{5}{\mathrm{MCN}}$, the onlooker bees will have to change randomly one or all parameters until $\textit{iter}={\mathrm{MCN}}$. In this way, we attempt to mimic the natural behavior of honeybees which might look highly selective when concerned with the alteration of the features of a given food source. In the absence of tight characterization of such a behavioral foraging concept, we adopted a random selection strategy. Figure 2 describes the general framework of the modified CLABC algorithm. The pseudo-codes describing the foraging process of the associated employed and onlooker subgroups are given in Figs. 3 and 4, respectively.

Fig. 3

Pseudo-code of the employed subgroup foraging process

Fig. 4

Pseudo-code of the onlooker subgroup foraging process

The proposed multi-search strategy is designed with the possibility to apply all updating rules at any level of the search process. The mechanism is set to ensure more global search in the beginning of the process to increase exploration, and more local search through generations to increase exploitation. Regarding probability definition, search Eqs. (5), (6), and (9) will have higher possibility to be called in the beginning of the optimization process which might ensure diversity. Then, all global Eqs. (4), (5), and (6) and local Eqs. (7), (8), and (9) will be used randomly to intensify the search. Accordingly, both global exploration and local exploitation are balanced at this level. Afterward, and depending on $\gamma$ values, all search strategies might be employed, but again Eqs. (4), (7) and (8) will have higher probability to be involved which might increase exploitation ability and convergence performance and preserve exploration capability. This strategy of being involved of solutions updating rules in mCLABC algorithm is described in Fig. 5.

4 Numerical experiments and results

4.1 Experiments on benchmark numerical functions

To demonstrate the computational performance of the proposed mCLABC algorithm, a set of 22 benchmark functions with dimensions $D=15, 30, 50, 60, 100$ and 200 are used. The test functions are listed in Table 1. They are categorized into the low-, middle- and high-dimensional functions. For instance, the high-dimensional functions are the functions F1–F20 with $D=60$ and the functions F21 and F22 with $D=200$. For all experiments, the maximum number of function evaluations (FEs) is used as termination condition. FEs is taken as 50,000, 100,000, and 200,000 for the low-, middle-, and high-dimensional functions, respectively. Colony size is chosen as CS $=40$. The limit value is set to limit $= D*\mathrm{SN}$, where D is the dimensionality of the problem and SN is the number of food sources.

Fig. 5

Rate of being selected of the search equations in mCLABC algorithm

The compared results are taken directly from their corresponding literature, and thus setting parameters of mCLABC are set same as the compared methods. The best results obtained over running times are marked in bold.

4.1.1 Comparison of mCLABC with the basic ABC and CLABC

The proposed mCLABC model is first compared with the basic ABC algorithm and the original CLABC algorithm. The results are shown in Tables 2, 3 and 4 in terms of means and standard deviations of the solutions obtained over 30 independent runs. Figure 6 depicts the convergence curves of ABC, CLABC, and mCLABC on some representative test functions. The resulting plots show that mCLABC performs differently and better in the most of cases and achieves faster convergence than ABC and CLABC especially on middle- and high-dimensional test functions. Significant conclusions on the performance of different algorithms can be drawn from the results summarized in Tables 2, 3 and 4.

Table 1 Benchmark numerical functions: U unimodal, M multimodal, S separable, N non-separable

Table 2 Comparison of mCLABC, CLABC, and ABC on solving 15-dimensional functions F1–F20 and 50-dimensional functions F21–F22

Table 3 Comparison of mCLABC, CLABC, and ABC on solving 30-dimensional functions F1–F20 and 100-dimensional functions F21–F22

Table 4 Comparison of mCLABC, CLABC, and ABC on solving 60-dimensional functions F1–F20 and 200-dimensional functions F21–F22

Indeed, as given in Table 2, the mCLABC and CLABC operate clearly better than ABC. However, CLABC outperforms mCLABC on the low-dimensional unimodal functions F1, F2, F3, F5, F9, and F10, while the mCLABC algorithms shows superiority over CLABC on most of low-dimensional multimodal functions F14, F15, F18, F19, F20, and F22 which are rather complex numerical functions.

From Table 3, it can be seen that mCLABC has significantly improve the optimization results in the majority of middle-dimensional unimodal and multimodal test functions. The CLABC results outperform the mCLABC on only three test functions F4, F5, and F14 with a slight improved difference for F15.

Moreover, Table 4 shows that the proposed mCLABC exhibits a remarkable high performance in solving different kinds of high-dimensional separable, non-separable, unimodal, and multimodal numerical functions. It is worth noting that both ABC and CLABC fail to overpass the proposed mCLABC in any of those test functions except the F15 test case where the CLABC improved slightly the function mean values.

According to the above analysis and results, it can be concluded that the structural modifications introduced into the CLABC framework contributed to the improvement of the cooperative learning ABC optimization strategy and, at the same time, showed visible superiority in solving middle- and high-dimensional problems.

4.1.2 Comparison of mCLABC with ABC variants

In this numerical experiment, mCLABC is compared to five variants of the ABC algorithm, namely ABC based on modified search strategy (CABC) (Gao et al. 2013a), global-best ABC (ABCbest) (Gao et al. 2012), global-best-guided ABC based on orthogonal learning strategy (OGABC) (Gao et al. 2013a), ABC with multiple search strategies (MuABC) (Gao et al. 2015), and ABC with variable search strategy (ABCVSS) (Kiran et al. 2015). The compared results are taken directly from Kiran et al. (2015) and Gao et al. (2015). The comparative study is summarized in Table 5 for low-dimensional functions, in Table 6 for middle-dimensional functions and in Table 7 for high-dimensional functions. The results are recorded over 30 independent runs.

Based on the results presented in Table 5, it can be seen that the mCLABC and the compared ABC variants have given same mean function values for F7, F11, F12, F16, F20, and F21. However, mCLABC improves visibly well the results obtained by the ABC variants on the unimodal functions F1, F2, F3, F4, F5, and F6. For the rest of test functions, mCLABC has better performance than at least three compared algorithms.

For middle-dimensional functions of Table 6, mCLABC shows better results on solving F1, F2, F4, F5, F10 and F15. Same performance with ABC variants is therefore obtained for F7, F11, and F21. For the rest of functions, the mCLABC has equal or better performance than at least three algorithms.

From Table 7, the compared results of mCLABC and ABC variants demonstrate again the superiority of mCLABC on solving the most of high-dimensional test functions. Better or slightly improved functions means values are therefore produced by the ABC variants on only five test cases. In addition, it is important to note that the optimal solution for the multimodal function F20 has only been reached by the proposed mCLABC.

Summarizing the above statements, it can be found that mCLABC performed very well on the unimodal functions for low-, middle-, and high-dimensional problems. For the multimodal functions, MuABC and ABCVSS showed better results in solving low-dimensional problems, while mCLABC outperforms the other algorithms for the middle and high-dimensional problems.

Fig. 6

Convergence curves of basic ABC, CLABC, and mCLABC for selected numerical test functions

Table 5 Comparison of mCLABC and ABCs variants on solving 15-dimensional functions F1–F20 and 50-dimensional functions F21–F22

Table 6 Comparison of mCLABC and ABCs variants on solving 30-dimensional functions F1–F20 and 100-dimensional functions F21–F22

Table 7 Comparison of mCLABC and ABCs variants on solving 60-dimensional functions F1–F20 and 200-dimensional functions F21–F22

Table 8 Convergence speed and successful rate comparisons of ABCs on solving 15-dimensional functions F1–F20 and 50-dimensional functions F21–F22

Table 9 Convergence speed and successful rate comparisons of ABCs on solving 30-dimensional functions F1–F20 and 100-dimensional functions F21–F22

Table 10 Convergence speed and successful rate comparisons of ABCs on solving 60-dimensional functions F1–F20 and 200-dimensional functions F21–F22

4.1.3 Comparison of mCLABC and ABC variants by means of statistical tests

In order to assess the convergence and stability of the proposed mCLABC algorithm, experiments involving statistical tests of mCLABC and ABC variants are conducted on numerical functions optimization problems. The results are reported in Tables 8, 9, and 10 in terms of average number of fitness evaluations (AVEN) and the ratio of the number of successful runs (SR). More precisely, AVEN refers to the average number of the fitness evaluations exhausted when an algorithm reaches the threshold defined as “accept”, and SR refers to the ratio of the number of successful runs over the total number of runs. Boldface indicates the best results among those obtained by mCLABC and three other compared algorithms, namely CABC, ABCbest, and MuABC. The results of the compared algorithms are taken directly from Gao et al. (2015). As can be seen from Tables 8, 9, and 10, the proposed method shows a comparatively better convergence behavior than CABC and ABCbest on all cases. The mCLABC can achieve the 100% success rate on all test functions except the Griewank function (F13) with 15 dimensions, it is competitive to the recent introduced multiple search MuABC algorithm which has 100% success rate on all the cases except the Quartic function (F9) with 60 dimensions; however, in order to get the full success rate, MuABC needed more FEs (AVEN) than mCLABC in the most of test cases. The statistical tests results motivate clearly the robustness of the proposed mCLABC method.

4.2 Experiments on CEC 2005 and CEC 2013 composition functions

Now, to further assess the effectiveness of the proposed mCLABC approach, experiments on CEC functions are conducted in this section. For this purpose, composition functions of CEC2005-type (Suganthan et al. 2005) and CEC2013-type (Liang et al. 2013) are used. For each type, unimodal and multimodal composition functions including basic functions, expanded functions, and hybrid functions are considered.

Table 11 Experimental results of ABC variants, QBPSO, and mCLABC on 10-dimensional CEC 2005 test functions

For CEC 2005 test case, the population size is chosen as 40, the maximum number of evaluations is set to 320,000, and the parameter limit is 1000. All functions are tested with dimensionality of 10 and run for 30 times. The optimization results of mCLABC, and the compared ones obtained by binary version ABC based on genetic operators (GB-ABC) (Ozturk et al. 2015), quantum inspired binary PSO (QBPSO) (Chung et al. 2011) and binary version of the ABC (DisABC) (Kashan et al. 2012) are presented in Table 11. From this table, it is easy to notice that mCLABC shows the best performance among the compared algorithms on four unimodal complex composition functions f1, f2, f4, and f5. Here, only the mCLABC can obtain a global optimal solution for f1 and a near-global optimal solution for f4 and f5. For the multimodal functions f6–f17, mCLABC is much better than DisABC, QBPSO, and GB-ABC on f6, f7, f9, and f11–f17 test functions. The mCLABC was able to reach the optimum for two multimodal functions f9 and f15. Besides, as far as we know, there is no algorithm that was able to find global or near-global optimal solution for any of the composition test functions f1–f17 with the same performance as the proposed mCLABC does.

Besides, mCLABC is compared with recent differential evolution (DE) algorithms on solving CEC 2005 optimization problems. Table 12 shows the obtained results for 30-dimensional composition functions processed over 300,000 evaluations (FEs) with population size set to 60, a parameter limit value of 900 and run for 25 times independently. The comparative study is conducted with reference to the experiments and settings reported in Wang et al. (2014), where the results of some other powerful DEs are provided. More precisely, the performance of mCLABC is compared with DE algorithm based on self-adaptive parameter control (jDE) (Brest et al. 2006), self-adaptive DE (SaDE) (Qin et al. 2009), composite DE (CoDE) (Wang et al. 2011), and DE based on covariance matrix learning and bimodal distribution parameter setting (CoBiDE) (Wang et al. 2014). As can be noticed, comparable results were achieved on most of the CEC 2005 functions with visible improvements on multimodal composition functions. The proposed mCLABC found better results than the compared DE variants on optimizing the basic multimodal functions f6–f12, the expanded multimodal functions f13–f14 and the hybrid composition functions f15, f18–f20, f22, and f25. Our strategy performed same or better than jDE in 20 tests, SaDE in 19 tests, CoDE in 15 tests, and CoBiDE in 16 tests. Moreover, mCLABC outperforms or is same as the adaptive differential evolution with optional external archive algorithm, named JADE (Wang et al. 2014), in 18 test cases. The results of JADE are not included in Table 12 for the sake of brevity only. Additionally, among all optimization results of JADE, jDE, SaDE, CoDE, and CoBiDE, a noticeable achievement of the proposed mCLABC giving an average value of 9.04e−08 and a standard deviation value of 2.55e−07 of the multimodal f6 error values was obtained over 25 independent runs. For this particular test case, the recent DE variant referred to as CoBiDE algorithm (Wang et al. 2014) showed a mean value of 4.13e−02 and a standard deviation of 9.21e−02. On the other hand, similar performance to at least one compared new DE algorithm on five test functions is reached by using the modified cooperative learning ABC algorithm.

For CEC 2013 test case, the proposed algorithm is compared to four ABC variants and two DE variants, i.e., ABC with Powell’s local search (PABC) (Gao et al. 2013b), modified ABC (MABC) (Akay and Karaboga 2012), compact ABC (comABC) (Dao et al. 2014), enhanced compact ABC (EcABC) (Banitalebi et al. 2015), persistent compact DE (cDE) (Mininno et al. 2011), and memetic compact DE (McDE) (Neri and Mininno 2010) by considering 28 composition functions with $D=50$, 100. In the experiments, we use the same parameter settings as those of the compared methods reported in Banitalebi et al. (2015). The number of FEs is set to $5000*D$. All the results are obtained from 50 independent runs. The experimental results are provided in Tables 13 and 14. As can be seen from Table 13 ($D=50$) and Table 14 ($D=100$), the proposed mCLABC was able to get better solutions than the other compared algorithms on 21 test functions with $D=50$ and 23 test functions with $D=100$. Specifically, the performance of mCLABC is clearly the best among the six algorithms for the unimodal functions f1–f5. The mCLABC outperforms all the compared algorithms on solving f1, f3, and f5, while EcABC shows better results on only f2 and f4. In addition, it can be seen that only mCLABC can find the near-optimum of f1 and f5 with dimensionality of 100. Moreover, comparison results on the set of multimodal composition functions f6–f20 show us that the EcABC performs better for f16 and f6 (with $D=50$), while MABC and McDE are the best for f15 with $D=50$ and $D=100$, respectively. For the rest of the compared multimodal test functions, mCLABC is visibly superior. Besides, with regard to composition functions f21–f28, PABC outperforms mCLABC for functions f21 and f22 with $D=50$, and EcABC looks better than mCLABC for only f27 with $D=100$. However, the performance of mCLABC is same or better than the compared algorithms for the rest of composition functions.

Based on the above comparisons, the superiority of mCLABC on solving complex CEC high-dimensional problems is then clearly justified. In fact, reaching global or near-global optimums of some composition test functions by the proposed method is a great finding.

Table 12 Experimental results of DEs and mCLABC on 30-dimensional CEC 2005 test functions

Table 13 Performance of mCLABC on 50-dimensional CEC 2013 test functions

5 Study of the robustness of the proposed optimization strategy

The demonstrated performance of the proposed mCLABC strategy is achieved on the basis of the optimization process as described by the algorithmic structure, which is given in Fig. 2. Obviously, some settings need to be set in a convenient way for satisfactory results. The adequacy of the settings might result from the study of the robustness and performance of the mCLABC model with respect to a number of design parameters, in particular, the number of subgroups of employed and onlooker foragers, the multi-search strategy, and the mechanism of selecting the number of food features to be altered by the foragers simultaneously at each processing time.

To complete the study, we investigated the effects of all of these design parameters by conducting a number of experiments on five benchmark numerical functions selected as F1, F10, F11, F13 and F15 from Table 1. For this purpose, the test functions are set with dimension 30 and the maximum number of FEs is chosen as 100,000. The experiments are repeated 30 times.

5.1 Subgroups partitioning effect

The proposed mCLABC strategy employs three subgroups of foragers at both employed and onlooker phases. For analysis purpose, five test cases introducing different structural modifications on the original mCLABC are considered. For clarity, the test case denoted as mCLABC (EBS, OBS) stands for mCLABC strategy with EBS employed subgroups and OBS onlooker subgroups. In the first test case, employed bees are categorized into three subgroups while the onlookers are kept in one group. The second test operates with one group of employed and three subgroups of onlookers. The remaining test cases use equal number of subgroups (2, 4 or 6) of both employed and onlooker bees. The search strategies of the compared variants are chosen same as the original mCLABC.

The results are listed in Table 15 where it appears clearly that the mCLABC is better than mCLABC(3,1) and mCLABC(6,6) for the multimodal functions F11 and F13, respectively, and again performs in the same way as mCLABC(1,3), mCLABC(2,2) and mCLABC(4,4) for those two multimodal functions (F11 and F13). Also, mCLABC(6,6) outperforms mCLABC on F10 and F15, but easily traps into local optimum when solving the multimodal function F13. Overall, it should be noticed that increasing the number of equal employed and onlooker partitions from 3 to 6 will not have significant improvement on the results.

Table 14 Performance of mCLABC on 100-dimensional CEC 2013 test functions

Table 15 Performance analysis of mCLABC by means of foragers subgroups partitioning

Table 16 Performance analysis of mCLABC by means of food features alteration strategy

Table 17 Performance analysis of mCLABC by means of search updating rule strategy

5.2 Food features alteration effect

During foraging process, employed or onlooker bees modify the features of the food source being exploited. Thus, the number of altered features at a given processing time might affect considerably the process of food sources exploitation. This in turn might influence the quality of the results. To analyze this aspect, four food features alteration strategies are tested. The first strategy labeled as “Single” adopts an updating mechanism that alters one random parameter only for all processing times. The second referred to as “Full” modifies all dimensions of a food source simultaneously. The strategy “Random” selects randomly the number of simultaneous evolving parameters in the range [1, D], while the strategy “Combined” combines the mechanisms of the above strategies according to the following rule: employed bees are managed to start by changing one random dimension. Then, when the number of iterations reaches $iter={MCN}/5$, the algorithm will have to select randomly the number of parameters to be optimized from [1, D]. While reaching the end of the optimization process, i.e., between $iter=\frac{4}{5}MCN$ and $iter=MCN$, the employed bees will update all parameters of the solution. Subsequently, after completion of the employed bee phase, the three subgroups of onlookers will start to update one random parameter of the solution. Then, when $iter={MCN}/5$, the onlooker bees will have to select randomly the number of parameters to be optimized from [1, D]. The search strategies in those test cases are same as mCLABC.

The results are compared in Table 16. As can be seen, mCLABC that alters all parameters simultaneously (full) is unable to outperform the original mCLABC on any test function. The mCLABC with “Single” strategy and mCLABC with “Random” strategy show slightly improved or same results as the mCLABC on only one test function. The mCLABC with combined strategy overpasses the mCLABC on F1 and F15, while the mCLABC is better on F10, F11, and F13, and finds the global optimal solution for F11 and F13.

This analysis proves that the process used in mCLABC to select the number of food features to be altered simultaneously at each iteration provides better results. The strategy to select the number of parameters to be optimized by processing time operates as a scheduling mechanism that contributes to the enhancement of the overall mCLABC performance.

5.3 Search strategy effect

The effect of solution updating rules on the mCLABC algorithm is now investigated through three different variants using multiple search strategies labeled as SS1 (search strategy 1), SS2 (search strategy 2) and SS3 (search strategy 3). The SS1 uses three global search equations, i.e., Eqs. (4), (5) and (6) for employed subgroups 1, 2 and 3, respectively, while onlooker foragers subgroups 1, 2 and 3 employ the local search equations Eqs. (7), (8), and (9), respectively. The search mechanism will call the whole solution updating rules at each iteration. Similarly, according to the search mechanism defined in SS2, a search equation from the set described above could be called more than one time in a given processing time or even could not be used at all. For SS3, the Eqs. (4), (7) and (8) are used by the employed subgroups 1, 2 and 3, respectively and the Eqs. (5), (6) and (9) by the onlooker subgroups 1, 2 and 3, respectively. The strategy of selecting the evolving parameters in those test cases is same as mCLABC. The results are shown in Table 17.

According to the obtained results, it can be concluded that whether SS1, SS2 or SS3 is used, the mCLABC algorithm shows superiority on functions F1 and F10. On the other hand, mCLABC and mCLABC with SS1 were able to determine the global optimum of functions F11 and F13. The proposed mCLABC gives generally better results on all test functions except for the case F15 where the solutions are slightly different.

From this thorough analysis and based on the results shown in Tables 15, 16 and 17, it is important to notice that the design parameters of the cooperative learning ABC optimization strategy influence differently the quality of the obtained solutions. Although the original mCLABC shows superiority in the most of test cases, the analysis of the impact of structural and parameter settings being introduced through different tests demonstrate the robustness and the merits of the proposed optimization strategy.

6 Conclusion

Aiming to further improve the performance of ABC optimization, a modified cooperative foraging learning strategy based on multiple solution search rules is developed in the present study. The original scheme of generating subgroups of employed foragers adopted in the CLABC framework is extended to the onlooker phase with modified structural and parametric settings. Since the feasibility of the approach can be fully motivated upon natural behavioral principles of bee swarms, it was of major importance for us to consider its integration to the algorithmic structure of the original CLABC algorithm with making all necessary tunings and modifications so that higher computational performance and robustness can be achieved. The modified cooperative foraging strategy, referred to as mCLABC, involves local and global search rules through which separate subgroups of foragers evolve differently and simultaneously at both employed or onlooker stages with allowing mutual exchange of information about the foraging process. To assess the extent of improvement, the proposed mCLABC algorithm is compared to ABC and CLABC algorithms, and to other recent ABCs variants on solving numerical and composition functions optimization problems. From different simulations, it can be concluded that the mCLABC improved considerably well the quality of the solutions and the convergence performance in the most of numerical experiments. Moreover, the superiority of the proposed mCLABC algorithm on solving complex CEC high-dimensional problems was visibly justified, where reaching global or near-global optimums of some composition test functions represents a great finding. To complete the study, a robustness analysis is conducted in order to evaluate the impact of different parametric and structural settings on the performance of the proposed strategy, namely the partitioning scheme of foragers, the search strategy and the food sources alteration mechanism. Future works will be devoted to the parallelization of the proposed algorithm with application to intelligent systems design.