Axiomatic approaches to rough approximation operators via ideal on a complete completely distributive lattice

Abstract

In 2014, Zhou and Hu (Inf Sci 269:378–387, 2014) introduced a kind of rough sets on a complete completely distributive lattice (short for CCD lattice), which can be seen as a unified framework for the study of rough sets based on ordinary binary relations, rough fuzzy sets and interval-valued rough fuzzy sets. Han et al. (Soft Comput 20:1853–1861, 2016) introduced a new pair of rough approximation operators via ideal on a CCD lattice in 2016, which is more general and accurate than Zhou and Hu’s. In this paper, we further investigate its properties, and then the axiomatic approaches are studied. Through some of our axioms, the rough approximations via ideal on a complete atomic Boolean lattice can be viewed as special cases of rough approximation operators via ideal on a CCD lattice if the ideal is well given.

1 Introduction

As a mathematical tool to deal with inaccuracy and nondeterminacy in data analysis, rough set theory was introduced by Pawlak (1982). It has been triumphantly applied to intelligent systems, machine learning, inductive reasoning, pattern recognition and many other fields (see Pawlak 1991; Pawlak and Skowron 2007a, b, c). The core tool of Pawlak rough set model is the equivalence relation; however, in the practice, this is not always satisfied. To break through this obstacle, some scholars extended Pawlak rough set into many interesting and meaningful models; for example, equivalence relations were replaced by tolerance relations in Skowron and Stepaniuk (1996), similarity relations in Vanderpooten (1997), binary relations in Liu and Zhu (2008), Yao (1998b) and so on. On the other hand, various fuzzy generalizations of rough approximations have been proposed in Dubois and Prade (1990), Nanda (1992), Qin and Pei (2005) and Wu et al. (2003), where the fuzzy rough set was acquired by replacing the crisp relations with fuzzy relations and crisp subsets with fuzzy sets. As generalizations, rough sets defined with a mapping were introduced by Järvinen (2002) and Tantawy and Mustafa (2013). In addition, there is another direction for promoting the Pawlak rough set model. It is well known that the crisp power set of a universe is an atomic Boolean lattice, thus a complete completely distributive lattice (short for CCD lattice), where all the single point sets are atoms and equivalence classes are the elements of this power set in the Pawlak’s rough sets, and the fuzzy power set of a universe is also a CCD lattice. This leads authors to take a CCD lattice as the universe to construct rough set models, which brings different kinds of generalizations of rough set models into a unified framework. In fact, Chen et al. (2006) have introduced rough approximations based on covers of a CCD lattice; later on, the topological properties and structure of these rough sets were investigated in Gao et al. (2009). Qin et al. (2013) studied approximation operators on a CCD lattice based on neighborhoods in terms of a cover, and the connections among the operators were studied. By using a binary relation on a CCD lattice, Zhou and Hu (2014) defined one type of rough sets, which was a generalization of rough sets based on a binary relation (Yao 1998a, b), rough fuzzy sets (Dubois and Prade 1990), rough sets on Boolean lattices (Qi and Liu 2005) and interval-valued rough fuzzy sets (Gong et al. 2008). As we know, the ideal plays an important role in making some foregone and related concepts of the universe together, through which the imprecise concept can be approximately gained. Based on the above work, Han et al. (2016) improved the rough approximation operators in Zhou and Hu (2014) by means of an ideal on a CCD lattice and obtained new rough approximation operators on a CCD lattice; moreover, they concluded that Zhou and Hu’s (2014) approximations, Yao’s (1996) approximations, Pawlak’s (1982) approximations and Dubois’s (1990) approximations are all their special cases. It is shown that the accuracy measure of the approximations via ideal is better than Zhou and Hu’s (2014).

By making a general survey of the approaches for the research of approximation operators, the axiomatic approach is important for the conceptual understanding of the rough set theory. Many authors explored and refined the axiomatic approaches in the development of rough set theory and fuzzy rough set theory (see Liu 2013; Lin and Liu 1994; Mi and Zhang 2004; Wu and Zhang 2004; Wu et al. 2016), where Lin and Liu (1994) adopted six axioms on two abstract operators acting on the power set in the framework of topological spaces. Mi and Zhang (2004) and Wu and Zhang (2004) considered axioms for approximation operators in the context of fuzzy sets. Liu (2013) proved that each axiomatic system of upper approximations of rough sets and fuzzy rough sets without any restriction on the cardinality of the universal set can be replaced by only one axiom. And Wu et al. (2016) investigated the axiomatic characterizations of (S, T)-fuzzy rough approximation operators, where S and T are triangular conorm and triangular norm on [0, 1], respectively. Following the work in Zhou and Hu (2014), the authors also discussed the axiomatic approaches of rough approximation operators on a CCD lattice (Zhou and Hu 2016), which are the generalization of the axiomatic approaches of rough sets, rough fuzzy sets and fuzzy rough sets.

For the new pair of rough approximation operators via ideal on a CCD lattice (Han et al. 2016), this paper addresses the study for the axiomatic approaches of these operators. With the help of the Galois connection, we overcome the difficulty that there is no duality between lower and upper rough approximation operators via ideal on a CCD lattice successfully. Simultaneously, some small loopholes in Zhou and Hu (2014, 2016) are rectified, with which the readers can reduce some confusion.

The rest of this paper is organized as follows. In Sect. 2, we show some basic definitions and results to be used in the paper. In Sect. 3, some new properties of the rough approximation operators via ideal on a CCD lattice are investigated, and then the axiomatic characterizations of upper rough approximation operators are obtained. In Sect. 4, we study the axiomatic approaches of rough approximation operators via ideal on a CCD lattice with the assistance of the Galois connection. Conclusions and future work are given in Sect. 5.

2 Preliminaries

At the beginning, we review some definitions and previous results which will be used in the subsequent parts of this text.

2.1 Lattice theory

A complete completely distributive lattice (abb. CCD lattice) $(L,\vee ,\wedge , 0, 1)$ is a complete lattice which satisfies the completely distributivity laws: for any $a_{ij}\in L$,

$$\begin{aligned} \bigvee \limits _{i\in \tau }\left( \bigwedge \limits _{j\in J_i}a_{ij}\right) =\bigwedge \limits _{f\in \prod _{i\in \tau } J_i}\left( \bigvee \limits _{i\in \tau }a_{if(i)}\right) ,\\ \bigwedge \limits _{i\in \tau }\left( \bigvee \limits _{j\in J_i}a_{ij}\right) =\bigvee \limits _{f\in \prod _{i\in \tau }J_i}\left( \bigwedge \limits _{i\in \tau }a_{if(i)}\right) , \end{aligned}$$

where $\tau$ and $J_i$ are non-empty index sets, and $f\in \prod _{i\in \tau }J_i$ means that f is a mapping $f: \tau \rightarrow \cup _{i\in \tau } J_i$ such that $f(i) \in J_i$ for every $i \in \tau$. Throughout this paper, we denote by L a CCD lattice unless otherwise stated.

In a lattice L, whether the element 0 (in case L has a zero) is join irreducible or not, there is a bit of difference about the introduction in Gierz et al. (2003) and Wang (1992), we keep pace with Zhou and Hu’s (2014). A nonzero element e is called join irreducible if for any $a, b \in L$, $e \le a \vee b$ implies $e \le a$ or $e \le b$. The set of all join-irreducible elements of a CCD lattice L is denoted by M(L). In a CCD lattice L, for any nonzero element a, $a=\bigvee \{e\in M(L):e\le a\}$, moreover, denote $u_a=\{e\in M(L):e\le a \ \text {and}\ \forall e'\in M(L), e'\le a \Longrightarrow e\not \le e'\}$, then $a=\bigvee u_a$.

An element c in a complete lattice L is called completely join irreducible if for any $S\subseteq L$, $c \le \bigvee S$ implies that there exists $s\in S$ such that $c\le s$ (see Raney 1952).

Example 1

We give the following examples about CCD lattices, join-irreducible elements and completely join-irreducible elements, the related details can be found in Draškovičová (1974), Järvinen and Radeleczki (2011), Järvinen et al. (2009) and Raney (1952).

• 1. $L=([0, 1],\vee ,\wedge , 0, 1)$ is a CCD lattice and $M(L)=L-\{0\}$. However, one can easily verify that every element in M(L) is not a completely join-irreducible element, since every element $x\in L$ is the join of the set of $y\in L$ such that $y\le x$.

• 2. A complete Brouwerian, dually Brouwerian lattice and weakly atomic lattice is a CCD lattice, and every element of L is a join of completely join-irreducible elements.

• 3. Let L be a lattice. Then, the following are equivalent:

  • (a) L is isomorphic to a complete ring of sets.

  • (b) L is algebraic, distributive and every element is a join of completely join-irreducible elements.

• 4. $\mathscr {RS}=\{(X^\blacktriangledown , X^\blacktriangle ): X\subseteq U\}$ determined by a quasiorder R is a CCD lattice isomorphic to a complete ring of sets, and its completely join-irreducible elements are members of $\{ (\emptyset , \{x\}^\blacktriangle ): |R(x)| \ge 2\}\cup \{(\{x\}^\vartriangle ,\{x\}^{\vartriangle \blacktriangle }): x\in U\}$, for more details see Järvinen et al. (2009).

Definition 1

(Chen et al. 2006) Let L be a CCD lattice and $C \subseteq L\backslash \{0\}$ so as to $\bigvee \limits _{a\in C}a = 1$. Then, C is called a partition of L if for every $a, b \in C, a \ne b$ implying $a \wedge b = 0$.

Definition 2

(Gierz et al. 1980) Let L be a complete lattice and $x, y \in L$. We say that x is wedge-below y, in symbols, $x\lhd y$, iff for any $D \subseteq L, y \le \vee D$ always implies that $x \le d$ for some $d \in D$.

Obviously, in a complete lattice L, if $a\in L$ is a completely join-irreducible element, then for any $b\in L, b\le a$ implies $b\lhd a$.

Proposition 1

(Gierz et al. 1980) Let L be a complete lattice and $x, y, u, v \in L$. Then

• 1. $x \lhd y \Longrightarrow x \le y$.

• 2. $u \le x \lhd y \le v \Longrightarrow u \lhd v$.

• 3. $x\ne 0 \Longrightarrow 0\lhd x$.

Theorem 1

(Gierz et al. 1980) A complete lattice L is a CCD lattice iff $a = \bigvee \{x \in L: x \lhd a\}$ for each $a \in L$.

Proposition 2

(Wang 1988) Let L be a CCD lattice. Then, for any $a,b\in L$, $a\lhd b\Longrightarrow \exists c\in L\ s.t.\ a\lhd c\lhd b$. Specially, for any $S\subseteq L$, $a\lhd \bigvee S\Longrightarrow \exists s\in S\ s.t.\ a\lhd s$.

Remark 1

Let L be a CCD lattice. Then

• 1. for any $a\ne 0$, there exists $z\in M(L)$ such that $z\lhd a$.

Proof

For any $a\ne 0$, there exists $b\in L$ and $b\ne 0$ such that $b\lhd a$ by Theorem 1. Then, it follows from the properties of M(L) that there exists $z\in M(L)$ such that $z\le b$, which means $z\lhd a$ by Proposition 1. $\square$

• 2. $a\le b$ if and only if for any $z\in M(L), z\lhd a$ implies $z\le b$.

Proof

($\Longrightarrow$) It holds by Proposition 1.

($\Longleftarrow$) Assuming that for any $z\in M(L), z\lhd a$ implies $z\le b$. Then, for any $x\in L, x\lhd a$, since $x=\bigvee \{y\in M(L):y\le x\}$, we claim that $x\le b$. Because for any $y\in M(L), y\le x$ implies $y\lhd a$ by Proposition 1, which means $y\le b$ by the assumption, it follows from Theorem 1 that $a\le b$ holds. $\square$

2.2 Rough approximation operators on a CCD lattice

We recall the binary relation on a CCD lattice, which is introduced in Zhou and Hu (2014, 2016).

A binary relation R on a CCD lattice L is a subset of $M(L)\times M(L)$. For any $x, y \in M(L)$, if $(x, y) \in R$, we say that y is R-related to x, denoted by xRy. Moreover, $R^c$ denotes the inverse relation of R, i.e., $x R^c y \Longleftrightarrow y R x$, $\forall x, y \in M (L)$. Given $x \in M(L)$, we note $xR = \{y \in M(L) : xRy\}$, $r_x = \bigvee xR$ and $Rx = \{y \in M(L) : yRx\}$, $r_x^* = \bigvee Rx$, respectively. For any $x,y,z\in M(L)$, we say that R is reflexive iff xRx, R is symmetric iff $xRy\Longrightarrow yRx$, R is transitive iff $xRy, yRz \Longrightarrow xRz$ and R is an equivalence relation iff R is reflexive, symmetric and transitive.

In this text, R is a tolerance iff R is reflexive and symmetric, R is a quasiorder iff R is reflexive and transitive.

Theorem 2

(Zhou and Hu 2014) Let R be an equivalence relation on a CCD lattice L. Then, the following assertions are equivalent:

• 1. $\{r_x\}_{x\in M(L)}$ is a partition of L.

• 2. For every $x, y\in M(L), y \le x \Longrightarrow xRy$.

The assertion (2) in Theorem 2 implies that R is reflexive, which is denoted as (C1). R is called an ordered equivalence relation iff R is symmetric, transitive and satisfies the condition (C1).

When considering Theorem 2, we find that the authors maybe confuse the concepts of join-irreducible elements and completely join-irreducible elements in the proof of $(2)\Longrightarrow (1)$, a more rigorous proof is given in the following in order to avoid causing difficulties for the readers.

Proof of

$(2)\Longrightarrow (1)$ On the one hand, R is reflexive, which implies $\bigvee _{x\in M(L)}r_x\ge \bigvee _{x\in M(L)}x=1$ by the properties of M(L). On the other hand, for any $r_x, r_y \in \{r_x\}_{x\in M(L)}$, if $r_x \wedge r_y \ne 0$, then there is $z\in M(L)$ such that $z\lhd r_x\wedge r_y$ by (1) in Remark 1. $z\lhd r_x$ implies that there exists $z'\in M(L)$ such that $xRz'$ and $z\le z'$ by Propositions 2 and 1, i.e., $xRz'$ and $zRz'$. Then, we get xRz because R is symmetric and transitive. Analogously, yRz holds. Hence, $z\in xR \cap yR\ne \emptyset$, which means $r_x =r_y$.

One can give the proper proofs of Eq. (L3), (LH4) and (LH5) in Zhou and Hu (2014) and Lemma 1 in Zhou and Hu (2016) likewise.

Definition 3

(Zhou and Hu 2014) Let R be a binary relation on a CCD lattice L. Two mappings $\underline{R}, \overline{R} : L \longrightarrow L$, called lower and upper rough approximation operators, respectively, are defined as follows, for each $a \in L$,

• $\underline{R}(a) = \bigvee \{x \in M(L) : r_x \le a\}$,

• $\overline{R}(a) = \bigvee \{x \in M(L) : \exists y\in xR,y\le a\}$.

$\underline{R}(a)$ is called a lower rough approximation of a, $\overline{R}(a)$ is called an upper rough approximation of a.

2.3 Rough approximations via ideal on a CCD lattice

Han et al. (2016) investigated the rough approximations based on a binary relation via ideal on a CCD lattice, we present a review.

Definition 4

(Davey and Priestley 2002) Let L be a lattice. A non-empty subset I of L is called an ideal if

• 1. $a,b\in I$ implies $a\vee b\in I$.

• 2. $a\in L, b\in I$ and $a\le b$ imply $a\in I$.

Definition 5

(Han et al. 2016) Let R be a binary relation on L and I an ideal of L. Define lower and upper approximation operators, $\underline{R}_I , \overline{R}_I: L \longrightarrow L$, respectively. For each $a \in L$,

• 1. $\underline{R}_I(a) = a\wedge \bigvee \{x : x \in M(L),\vee (xR \cap L\backslash {\downarrow }a)\in I \}$.

• 2. $\overline{R}_I(a) = a\vee \bigvee \{x : x\in M(L),\vee (xR\cap {\downarrow } a)\not \in I\}$.

The elements $\underline{R}_I(a)$ and $\overline{R}_I(a)$ are called the lower and the upper approximations of a via ideal I with respect to R, respectively. For convenience, we denote $R_*(a)=\bigvee \{x : x \in M(L),\vee (xR \cap L\backslash {\downarrow }a)\in I \}$, $R^*(a)=\bigvee \{x : x\in M(L),\vee (xR\cap {\downarrow } a)\not \in I\}$.

Remark 2

(Han et al. 2016) Let R be a reflexive binary relation on L and I the least ideal $\{0\}$ of L. Then, for each $a \in L$, $\underline{R}_I (a) = \underline{R}(a), \ \overline{R}_I (a) = \overline{R}(a)$.

Lemma 1

(Han et al. 2016) Let I be an ideal of L. Then, $\mathscr {I}={\downarrow }\{{\downarrow }m\cap M(L): m \in I \}$ is an ideal on $\mathscr {P}(M(L))$.

Theorem 3

(Han et al. 2016) Let R be a binary relation on L and I an ideal of L. Then, for each $a \in L$,

• 1. $R_*(a)=\bigvee \{x : x \in M(L), xR \cap L\backslash {\downarrow } a \in \mathscr {I}\}$.

• 2. $R^*(a) = \bigvee \{ x : x \in M(L), xR\cap {\downarrow } a \not \in \mathscr {I}\}$.

Proposition 3

(Han et al. 2016) Let R be a binary relation on L and I an ideal of L. Then, for every $a, b \in L$,

• 1. $\underline{R}_I(a) \le a \le \overline{R}_I(a)$.

• 2. $\underline{R}_I(1) = 1, \overline{R}_I (0) = 0$.

• 3. if $a \le b$, then $\underline{R}_I(a) \le \underline{R}_I(b), \ \overline{R}_I (a) \le \overline{R}_I(b)$.

• 4. $\underline{R}_I (a \wedge b) \le \underline{R}_I (a) \wedge \underline{R}_I (b)$, moreover, if R is a transitive relation satisfying (C1), then $\underline{R}_I(a\wedge b)=\underline{R}_I(a)\wedge \underline{R}_I(b)$ and $\underline{R}_I(\wedge A)=\bigwedge \{\underline{R}_I(a): a\in A\}$.

• 5. $\overline{R}_I (a \vee b) = \overline{R}_I (a) \vee \overline{R}_I (b)$.

• 6. if R is transitive, then $\underline{R}_I\underline{R}_I(a)=\underline{R}_I(a)$.

• 7. if R is an ordered equivalence relation, then $\overline{R}_I\overline{R}_I(a)=\overline{R}_I(a)$.

Theorem 4

(Han et al. 2016) Let I be an ideal of L. If R is a reflexive binary relation on L, then for each $a \in L$,

$$\begin{aligned} \underline{R}(a) \le \underline{R}_I (a)\le a \le \overline{R}_I (a) \le \overline{R}(a). \end{aligned}$$

3 Axioms of upper rough approximation operators via ideal on a CCD lattice

Zhou and Hu (2016) studied the axiomatic approaches of rough approximation operators on a CCD lattice. In this section, we investigate the axiomatic approaches of upper rough approximation operators via ideal on a CCD lattice, which are appropriate for the case that the ideal is a special ideal $\{0\}$, i.e., they fit Zhou and Hu’s rough approximation operators. For the convenience of readers, we point out a small mistake in Zhou and Hu (2016), the authors recalled the condition (C1) improperly, they consider it as $x\le y\Longrightarrow xRy$ in Lemma 2 and Theorem 7; unfortunately, they are not typing errors after our careful verification.

Remark 3

If I is not only an ideal but also a complete sublattice of L, we call it a complete sublattice ideal (for short) of L in the rest of this paper.

Theorem 5

Let R be a binary relation on L and I a complete sublattice ideal of L. Then, for each $a \in L$, $A\subseteq L$,

• 1. $R_*(a)=\bigvee \{x : x \in M(L), xR \cap L\backslash {\downarrow } a \subseteq I\}$.

• 2. $R^*(a) = \bigvee \{x: x \in M(L), \exists y\in xR, y\le a, but\ y\not \in I\}$

  $\ \ \ \ \ \ \ \ \ \ =\bigvee \{r_y^* : y\in M(L), y\in {\downarrow } a\backslash I\}$.

• 3. $\overline{R}_I(\vee A) =\bigvee \{\overline{R}_I(a): a\in A\}$.

Proof

• 1. It is sufficient to prove that for every $a\in L$, $x \in M(L)$, $\vee (xR \cap L\backslash {\downarrow }a)\in I\Longleftrightarrow xR \cap L\backslash {\downarrow } a \subseteq I$.

($\Longrightarrow$):

Assuming that $\vee (xR \cap L\backslash {\downarrow }a)\in I\$, then for any $y\in xR\cap L\backslash {\downarrow }a$, $y\le \vee (xR \cap L\backslash {\downarrow }a)\in I$ implies $y\in I$ by the properties of the ideal I, i.e., $xR \cap L\backslash {\downarrow }a\subseteq I$.

($\Longleftarrow$):

It is directly obtained by the condition that I is a complete sublattice of L.

• 2. For every $a\in L$, $x \in M(L)$, the proof of “$\vee (xR\cap {\downarrow } a)\not \in I\Longleftrightarrow \exists y\in xR, y\le a, but\ y\not \in I$” is similar to (1). Furthermore, we have

  $$\begin{aligned} R^*(a)= & {} \bigvee \{x: x \in M(L), \exists y\in xR, y\le a, but\ y\not \in I\}\\= & {} \bigvee \{r_y^* : y\in M(L), y\le a,\ but\ y\not \in I\}\\= & {} \bigvee \{r_y^* : y\in M(L), y\in {\downarrow } a\backslash I\}. \end{aligned}$$

• 3. For any $A\subseteq L$, by (3) in Proposition 3, we only need to prove $\overline{R}_I(\vee A) \le \bigvee \{\overline{R}_I(a): a\in A\}$. Obviously,

  • $\overline{R}_I(\vee A)=\vee A\vee R^*(\vee A)$,

  • $\bigvee \{\overline{R}_I(a): a\in A\}=\bigvee \{a\vee R^*(a): a\in A\}=\vee A\vee \bigvee \{R^*(a): a\in A\}$.

  We claim that $R^*(\vee A)\le \bigvee \{R^*(a): a\in A\}$.

  In fact, for any $x\in M(L)$, let $\vee (xR\cap {\downarrow } \vee A)\not \in I$. Then, $\vee (xR\cap {\downarrow } \vee A)\le \vee xR \wedge \bigvee {\downarrow }\vee A =\vee xR \wedge \vee A =\bigvee \{\vee xR \wedge a:a\in A\}$ implies $\bigvee \{\vee xR \wedge a:a\in A\}\not \in I$. Moreover, I is a complete sublattice, which implies that $\vee xR \wedge a\not \in I$ for some $a\in A$, i.e., $R^*(\vee A)\le \bigvee \{R^*(a): a\in A\}$. $\square$

Remark 4

Let R be a transitive relation on L and satisfies condition (C1). Then, for every $x , y \in M ( L ), x\le y$ implies $r_x \le r_y$, specially, if R is an ordered equivalence relation, then it also implies $r_x^* \le r_y^*$, which is denoted as (C3).

Proof

Suppose R is a transitive relation on L satisfying condition (C1). Then, for every $x , y \in M ( L ), x\le y\Longrightarrow yRx\Longrightarrow xR\subseteq yR\Longrightarrow r_x \le r_y$. In the case of ordered equivalence relation, $x\le y\Longrightarrow yRx\Longrightarrow xRy\Longrightarrow Rx\subseteq Ry\Longrightarrow r_x^* \le r_y^*, \ \forall x , y \in M ( L )$. $\square$

Lemma 2

Let R be a binary relation satisfying (C3) on L and I a complete sublattice ideal of L. Then, for any $x\in M(L)$,

$$\begin{aligned} \overline{R}_I(x)= \left\{ \begin{array}{lll}x, &{}\quad x\in I,\\ x \vee r_x^*, &{}\quad x\not \in I.\end{array}\right. \end{aligned}$$

Proof

Denote $S=\{r_y^* : \exists y\in M(L), y\le x,\ but\ y\not \in I\}$. According to (2) in Theorem 5, we have

• 1. If $x\in I$, then $y\in I$ for any $y\le x$, i.e., $S=\emptyset$. Thus, $\overline{R}_I(x)=x$.

• 2. If $x\not \in I$, first, $r_x^*\in S$ implies $x\vee r_x^*\le \overline{R}_I(x)$, second, $r_y^*\le r_x^*$ if $y\le x$ by (C3), which implies $\overline{R}_I(x) \le x\vee r_x^*$. Thus, $\overline{R}_I(x) = x\vee r_x^*$. $\Box$

Now, with the help of Lemma 2, we discuss the upper rough approximation operators via ideal on a CCD lattice.

Theorem 6

Let I be a complete sublattice ideal of L and f a mapping on L. Then, there exists a binary relation $R'$ satisfying (C3) on L, such that $f = \overline{R'}_I$ if and only if f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ) , \ \forall a_i\in L$.

• 3. for any $x\in M(L)$,

  $$\begin{aligned} f(x)\left\{ \begin{array}{lll}=x, &{}\quad x\in I,\\ \ge x, &{}\quad x\not \in I.\end{array}\right. \end{aligned}$$

Proof

($\Longrightarrow$) If $f = \overline{R'}_I$, condition (1) holds by (2) in Proposition 3 and condition (2) holds by (3) in Theorem 5. Moreover, since $R'$ satisfies condition (C3), it follows from Lemma 2 that condition (3) holds.

($\Longleftarrow$) Define a binary relation R on L as: $xR'y \Longleftrightarrow x\in u_{f(y)}$. Since $r_x^*= \bigvee \{ y\in M(L ): yR'x \}=\bigvee u_{f(x)}= f(x)$, from (C3), Lemma 2 and condition (3), we obtain that for any $x\in M(L)$, if $x\in I$, then $\overline{R'}_I(x)=x=f(x)$ and $\overline{R'}_I(x)=x \vee r_x^*=x \vee f(x)=f(x)$ if $x\not \in I$, which means $\overline{R'}_I(x)=f(x), \ \forall x\in M(L)$.

Then, for any $a \in L$, if $a = 0$, it is straightforward that $f(0) = 0 = \overline{R'}_I (0)$. If $a \ne 0$, we have $\overline{R'}_I(a)=\overline{R'}_I (\bigvee \{ x_i \in M(L ): x_i\le a \} )=\bigvee \{ \overline{R'}_I(x_i ): x_i\le a, x_i\in M(L) \} =\bigvee \{ f(x_i ): x_i\le a, x_i\in M(L ) \} = f(\bigvee \{ x_i\in M(L ): x_i\le a \} )=f(a)$. $\square$

Theorem 7

Let I be a complete sublattice ideal of L and f a mapping on L. Then, there exists a reflexive relation R satisfying (C3) on L, such that $f = \overline{R}_I$ if and only if f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ) , \ \forall a_i\in L$.

• 3. for any $x\in M(L)$,

  $$\begin{aligned} f(x)\left\{ \begin{array}{lll}=x, &{}\quad x\in I,\\ \ge x, &{}\quad x\not \in I.\end{array}\right. \end{aligned}$$

Proof

We only state ($\Longleftarrow$) here, define a binary relation R on L as: $xRy \Longleftrightarrow x\le f(y)$, $\forall x, y \in M(L)$. Apparently, R is reflexive by condition (3) and $r_x^*= \bigvee \{ y\in M(L ): yRx \}= \bigvee \{ y\in M(L ): y\le f(x) \}= f(x)$. Then, $f = \overline{R}_I$ can be obtained similarly. $\square$

Remark 5

If L is a complete atomic Boolean lattice, then $R'=R$, where $R'$ and R are binary relations defined in the proofs of Theorem 6 and 7, respectively.

Example 2

By using an ideal on B, Tantawy and Mustafa (2013) introduced two pairs of rough approximations on a complete atomic Boolean lattice B.

(1) Let $\varphi : A(B) \longrightarrow B$ be an any mapping, where A(B) is the set of atoms of B. For each $a \in B$, the lower and upper approximations of a via ideal I with respect to $\varphi$ are defined as:

• $a^{\nabla I} = a\wedge \bigvee \{y : y \in A (B), \varphi (y) \wedge a' \in I, a \ne 0\}$.

• $a^{\vartriangle I} = a \vee \bigvee \{y : y \in A (B), \varphi (y) \wedge a \not \in I, a \ne 1\}$.

(2) Let $\langle \varphi \rangle$ be a mapping induced from $\varphi$ as $\langle \varphi \rangle (x) = \bigwedge _{x\le \varphi (y)} \varphi (y)$, for all $x \in A (B)$. For each $a \in B$, the lower and upper approximations of a via ideal I with respect to $\langle \varphi \rangle$ are defined as:

• $a^{\vee I} = a\wedge \bigvee \{y : y \in A (B), \langle \varphi \rangle (x) \wedge a' \in I, a \ne 0\}$.

• $a^{\wedge I} = a\vee \bigvee \{y : y \in A (B), \langle \varphi \rangle (x) \wedge a \not \in I, a \ne 1\}$.

where $^{\vartriangle I}$ satisfies the following properties:

• (a) (Proposition 3.1 in Tantawy and Mustafa 2013) $0^{\vartriangle I} = 0$.

• (b) (Proposition 3.3 in Tantawy and Mustafa 2013) if every element in I is completely join irreducible, then $\bigvee S^{\vartriangle I}=(\bigvee S)^{\vartriangle I}$ for any $S\subseteq B$.

• (c) for any $x\in A (B)$, if $x\in I$, then $x^{\vartriangle I} =x$.

Proof of (c)

Denote $H= \{y : y \in A (B), \varphi (y) \wedge x \not \in I, x \ne 1\}$. If $x\in I$, then $\varphi (y) \wedge x \in I$ because $\varphi (y) \wedge x\le x$ for any $y\in A (B)$, i.e., $H=\emptyset$, thus, $x^{\vartriangle I} =x$.

Thus, let I be a complete sublattice ideal of a complete atomic Boolean lattice B. If every element in I is completely join irreducible, since the mapping $^{\vartriangle I}$ on B satisfies the condition in Theorem 7 and any complete atomic Boolean lattice is a CCD lattice, it follows from Theorem 7 that there exists a reflexive relation R on B, defined as $xRy\Longleftrightarrow x\le \varphi (y),\ \forall x,y\in A(B)$, such that $^{\vartriangle I} = \overline{R}_I$. Similarly, let I be a complete sublattice ideal of a complete atomic Boolean lattice B. If every element in I is completely join irreducible, then there exists a reflexive relation R on B, defined as $xRy\Longleftrightarrow x\le \langle \varphi \rangle (y),\ \forall x,y\in A(B)$, such that $^{\wedge I} = \overline{R}_I$.

The example above shows that if the ideal I is a complete sublattice ideal and every element in I is completely join irreducible, then Tantawy and Mustafa’s rough approximations can be seen as rough approximation operators based on a reflexive relation via ideal on a CCD lattice.

Remark 6

In Theorem 7, if we set $I=\{0\}$, then it coincides with Theorem 5 in Zhou and Hu (2016).

Theorem 8

Let I be a complete sublattice ideal of L and f a mapping on L. If f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ) , \ \forall a_i\in L$.

• 3. for any $x\in M(L)$,

  $$\begin{aligned}f(x)\left\{ \begin{array}{lll}=x, &{}\quad x\in I,\\ \ge x, &{}\quad x\not \in I.\end{array}\right. \end{aligned}$$

• 4. for any $x\in M(L)$, $f(x)\ge \vee \{y\in M(L):x\le f(y)\}$.

then there exists a tolerance R on L, such that $f = \overline{R}_I$.

Proof

Define a binary relation R on L as Theorem 7. It is immediate to get $f = \overline{R}_I$ from the proof of Theorem 7. We only prove the symmetry of R, for any $x\in M(L)$, condition (4) implies $f(x)\ge \vee \{y:x\le f(y)\}=\vee \{y:xRy\}=r_x$, then $xRy\Longrightarrow y\le r_x\le f(x)\Longrightarrow yRx,\ \forall x,y\in M(L)$. $\square$

The condition of Theorem 8 is sufficient but not necessary, and we consider the following example.

Fig. 1

The lattice L

Table 1 The tolerance R in Example 3

Example 3

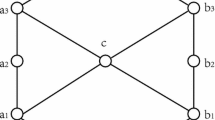
Let $L=\{0,a_1,a_2,a_3,b_1,b_2,b_3,c,1\}$ be a CCD lattice depicted in Fig. 1, where $M(L)=\{a_1,a_2,b_1,b_2\}$. Define a tolerance R on L as Table 1. Then $a_1R=\{a_1,b_2\}$, $a_2R=\{a_2,b_2\}$, $b_1R=\{b_1\}$, $b_2R=\{a_1,a_2,b_2\}$, $r_{a_1}=r_{a_1}^*=b_3$, $r_{a_2}=r_{a_2}^*=1$, $r_{b_1}=r_{b_1}^*=b_1$ and $r_{b_2}=r_{b_2}^*=1$, it is trivial that R satisfies (C3).

Let $I=\{0,a_1,b_1,c\}$. We have $\overline{R}_I(a_1) = a_1$ and $\overline{R}_I(b_1) = b_1$ by Lemma 2. Moreover,

$$\begin{aligned} \overline{R}_I(a_2)= & {} a_2\vee \bigvee \{x : x\in M(L),\exists y\in xR, y\le a_2, but\ y\not \in I\}\\= & {} a_2\vee (a_2\vee b_2)=1,\\ \overline{R}_I(b_2)= & {} b_2\vee \bigvee \{x : x\in M(L),\exists y\in xR, y\le b_2, but\ y\not \in I\}\\= & {} b_2\vee (a_1\vee a_2\vee b_2)=1. \end{aligned}$$

Thus,

$$\begin{aligned} \overline{R}_I(a_1)= & {} a_1 \not \ge 1=a_1\vee a_2\vee b_2\\= & {} \vee \{y\in M(L):a_1\le \overline{R}_I(y) \}. \end{aligned}$$

Corollary 1

Let f be a mapping on L. If f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ), \ \forall a_i\in L$.

• 3. for any $x\in M(L)$, $f(x)\ge x$.

• 4. for any $x\in M(L)$, $f(x)\ge \vee \{y\in M(L):x\le f(y)\}$.

then there exists a tolerance R on L, such that $f = \overline{R}$.

Theorem 9

Let I be a complete sublattice ideal of L and f a mapping on L. If f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ) , \ \forall a_i\in L$.

• 3. for any $x\in M(L)$, $f(x)=x$.

then there exists a quasiorder R on L, such that $f = \overline{R}_I$.

Proof

Define a binary relation R on L as Theorem 7. We only illustrate that R is transitive, assume that $x,y,z\in M(L)$, xRy and yRz, then $x\le f(y), y\le f(z)$, it follows from condition (3) that $x\le f(y)=y\le f(z)$, thus, $z\le f(x)$, i.e., xRz. $\square$

The following example indicates that the inverse of Theorem 9 does not always hold.

Example 4

Let L be the same CCD lattice and I the same complete sublattice ideal of L as in Example 3, respectively. Define a quasiorder R on L as Table 2. Then, $a_1R=\{a_1,b_1,b_2\}$, $a_2R=\{a_2\}$, $b_1R=\{b_1,b_2\}$, $b_2R=\{b_2\}$. Thus,

$$\begin{aligned} \overline{R}_I(b_2)= & {} b_2\vee \bigvee \{x : x\in M(L),\exists y\in xR, \\&y\le b_2, but\ y\not \in I\}\nonumber \\= & {} b_2\vee (a_1\vee b_1\vee b_2)=b_3\ne b_2. \end{aligned}$$

Table 2 The quasiorder R in Example 4

Corollary 2

Let f be a mapping on L. If f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ) , \ \forall a_i\in L$.

• 3. for any $x\in M(L)$, $f(x)=x$.

then there exists a quasiorder R on L, such that $f = \overline{R}$.

Theorem 10

Let I be a complete sublattice ideal of L and f a mapping on L. If f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ) ,\ \forall a_i\in L$.

• 3. for any $x\in M(L)$,

  $$\begin{aligned}f(x)\left\{ \begin{array}{lll}=x, &{}\quad x\in I,\\ \ge x, &{}\quad x\not \in I.\end{array}\right. \end{aligned}$$

• 4. for any $a\in L$, $f(a)=f(f(a))$.

then there exists a quasiorder R on L, such that $f = \overline{R}_I$.

Proof

Define a binary relation R on L as Theorem 7. The transitivity of R is examined here. Suppose $x,y,z\in M(L)$, xRy and yRz. It follows from conditions (4) and (2) that $r_y^*= f(y)=f(f(y))=f(r_y^*)=f(\bigvee \{p:pRy\})=\bigvee \{f(p):pRy\}=\bigvee \{r_p^*:pRy\}$, then xRy implies $r_x^*\in \{r_p^*:pRy\}$, i.e., $r_x^*\le r_y^*$, similarly, $r_y^*\le r_z^*$, thus, $x\le r_x^*\le r_y^*\le r_z^*=f(z)$, i.e., xRz. $\square$

Example 5

Continue with Example 2, we note that $^{\vartriangle I}$ also possesses the property:

• (d) (Lemma 3.2 in Tantawy and Mustafa 2013) if $\varphi$ is a closed mapping, then $a^{\vartriangle I\vartriangle I} =a^{\vartriangle I}$ for any $a\in B$.

Thus, let I be a complete sublattice ideal of a complete atomic Boolean lattice B, $\varphi : A(B) \longrightarrow B$ a closed mapping on B. If every element in I is completely join irreducible, it follows from Theorem 10 that there exists a quasiorder R on B, defined as $xRy\Longleftrightarrow x\le \varphi (y),\ \forall x,y\in A(B)$, such that $^{\vartriangle I} = \overline{R}_I$. Similarly, let I be a complete sublattice ideal of a complete atomic Boolean lattice B, $\varphi : A(B) \longrightarrow B$ a closed mapping on B. If every element in I is completely join irreducible, then there exists a quasiorder R on B, defined as $xRy\Longleftrightarrow x\le \langle \varphi \rangle (y),\ \forall x,y\in A(B)$, such that $^{\wedge I} = \overline{R}_I$.

The example above indicates that Tantawy and Mustafa’s rough approximations can be taken for rough approximation operators based on a quasiorder via ideal on a CCD lattice if $\varphi$ is a closed mapping, the ideal I is a complete sublattice ideal, and every element in I is completely join irreducible.

The following example demonstrates that the condition in Theorem 10 is non-necessity.

Example 6

Let L be a CCD lattice defined as shown in Fig. 2, where $M(L)=\{a,b,d,e,f,l,p\}$. Define a quasiorder on L in Table 3. Then $aR=\{a\}, \ bR=\{b\}$, $dR=\{d,e\},\ eR=\{e\},\ fR=\{e,f\}$, $lR=\{b,l\}$, $pR=\{p\}$.

Let $I=\{0,a\}$. We get,

$$\begin{aligned} \overline{R}_I(e)= & {} e\vee \bigvee \{x : x\in M(L),\exists y\in xR, y\le e, but\ y\not \in I\}\nonumber \\= & {} e\vee (d\vee e\vee f)=m,\\ \overline{R}_I\overline{R}_I(e)= & {} \overline{R}_I(m)\nonumber \\= & {} m\vee \bigvee \{x : x\in M(L),\exists y\in xR, y\le m, but\ y\not \in I\}\nonumber \\= & {} m\vee (b\vee d\vee e\vee f\vee l)=n\ne m.\nonumber \end{aligned}$$

Fig. 2

The lattice L

Table 3 The quasiorder R in Example 6

Corollary 3

Let f be a mapping on L. If f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ) ,\ \forall a_i\in L$.

• 3. for any $x\in M(L)$, $f(x)\ge x$.

• 4. for any $a\in L$, $f(a)=f(f(a))$.

then there exists a quasiorder R on L, such that $f = \overline{R}$.

Theorem 11

Let I be a complete sublattice ideal of L and f a mapping on L. If f satisfies

• 1. $f(0) = 0$.

• 2. $f(\bigvee \limits _{i\in \tau } a_i ) =\bigvee \limits _{i\in \tau } f(a_i ) , \ \forall a_i\in L$.

• 3. for any $x\in M(L)$,

  $$\begin{aligned}f(x)\left\{ \begin{array}{lll}=x, &{}x\in I,\\ \ge x, &{}x\not \in I.\end{array}\right. \end{aligned}$$

• 4. for any $x,y\in M(L)$, $f(x)\ne f(y)\Longrightarrow f(x)\wedge f(y)=0$.

then there exists an ordered equivalence relation R on L, such that $f = \overline{R}_I$.

Proof

Define a binary relation R on L as Theorem 7. We need to illustrate that R is symmetric, transitive and satisfies (C1). For any $x,y\in M(L)$, $xRy\Longrightarrow x\le f(y)\Longrightarrow x\wedge f(y)\ne 0$, then $x\wedge f(y) \le f(x)\wedge f(y)\ne 0$, thus, $f(x)=f(y)$ by (4), it follows from (3) that $y\le f(y)=f(x)$, i.e., xRy. Suppose $x,y,z\in M(L)$, xRy and yRz. Then, by the proof above, $x\le f(x)=f(y)=f(z)$, i.e., xRz. Condition (3) and the symmetry of R imply that $y\le x\le f(x)\Longleftrightarrow yRx\Longleftrightarrow xRy$, i.e., R satisfies (C1). $\square$

Remark 7

When we pick $I=\{0\}$ in Theorem 11, the condition in Theorem 11 is necessary and sufficient for the existence of an ordered equivalence relation (see Theorem 8 in Zhou and Hu 2016). However, it does not hold for the general ideal. The following example indicates this view.

Example 7

Let L be the same CCD lattice as in Example 3. We consider the ordered equivalence relation $R=1_{M(L)\times M(L)}$, i.e., $xRy, \ \forall x,y\in M(L)$. Then, $a_1R=a_2R=b_1R=b_2R=M(L)$, thus, $\overline{R}_I(a_1)=a_1\ne 1=\overline{R}_I(a_2)$. But,

$$\begin{aligned} \overline{R}_I(a_1)\wedge \overline{R}_I(a_2)=a_1\wedge 1=a_1\ne 0.\end{aligned}$$

4 Axioms of rough approximation operators via ideal on a CCD lattice in terms of Galois connection

The following concepts and results of Galois connection are reviewed in order to further explore the axiomatic approaches of rough approximation operators via ideal on a CCD lattice, for more details, see Gierz et al. (2003). We claim that the condition (2) of Theorem 10, 12 and 13 in Zhou and Hu (2016) is erroneous, because the formulas $g(s)\ge t\Longleftrightarrow s\ge f(t)$ and $g(s)\le t\Longleftrightarrow s\le f(t)$ are not equivalence in the theory of Galois connection.

Definition 6

(Gierz et al. 2003) For posets P and Q, a pair (g, f) of maps $g:P\longrightarrow Q$ and $f:Q\longrightarrow P$ is called a Galois connection between P and Q iff for all $p\in P$ and $q\in Q$,

$$\begin{aligned}g(p)\ge q \Longleftrightarrow p\ge f(q).\end{aligned}$$

Theorem 12

(Gierz et al. 2003) Let $g:P\longrightarrow Q$ and $f:Q\longrightarrow P$ be two order preserving functions between posets P and Q. Then, for any $p\in P, q\in Q$, the following conditions are equivalent:

• 1. $g(p)\ge q \Longleftrightarrow p\ge f(q)$.

• 2. $p\ge f(g(p)),\ g(f(p))\ge q$.

Moreover, these conditions imply

• 3. $f\circ g\circ f=f$ and $g\circ f\circ g=g$.

• 4. The map g is a meet preserving function and f is a join preserving function.

Theorem 13

(Gierz et al. 2003) In a Galois connection (g, f), each of g and f uniquely determines the other via the formulae

• 1. $g(p) = \bigvee \{q : p\ge f(q)\} , \ \ \forall p \in P$.

• 2. $f(q) = \bigwedge \{p : g(p)\ge q\} , \ \ \forall q \in Q$.

Remark 8

According to Pawlak (1982) and Yao (1998a), when L is a power set of a universe X, the symmetry of R implies the following property: for any $a\in L$, $a \le \underline{R}\overline{R}(a)$ and $\overline{R}\underline{R}(a)\le a$, which imply that $a \le \underline{R^c}\overline{R}(a)$ and $\overline{R}\underline{R^c}(a)\le a$ if R is an ordinary binary relation, i.e., $(\underline{R^c},\overline{R})$ forms a Galois connection on $\mathscr {P}(X)$. For these two formulas, Zhou and Hu (2014) illustrated that $\overline{R}\underline{R^c}(a)\le a$ does not hold for the general CCD lattice L by a counterexample, of course, it does not hold for rough approximation operators via ideal on a CCD lattice either. Let I be an ideal of L. The following example states that $a \le \underline{R^c}_I\overline{R}_I(a)$ is not always true for rough approximation operators via ideal on a CCD lattice.

Example 8

Let L be the same CCD lattice as in Example 6. Define a binary relation R on L as Table 4. Then, $aR=\{a\}, \ bR=\{b\}$, $dR=\{d,e\},\ eR=\{e\},\ fR=\{f\}$, $lR=\{b,d, l\}$, $pR=\{p\}$ and $Ra=\{a\}, \ Rb=\{b,l\}$, $Rd=\{d,l\},\ Re=\{d,e\},\ Rf=\{f\}$, $Rl=\{l\}$, $Rp=\{p\}$.

We consider $I=\{0,a,b, c\}$, then

$$\begin{aligned} \overline{R}_I(g)= & {} g\vee \bigvee \{x : x\in M(L),\exists y\in xR, y\le g, but\ y\not \in I\}\\= & {} g\vee (d\vee e)=i,\\ \underline{R^c}_I\overline{R}_I(g)= & {} \underline{R^c}_I(i)=i\wedge \bigvee \{x:x\in M(L), Rx\cap L\backslash {\downarrow }i\subseteq I\}\\= & {} i\wedge (a\vee e)=e\not \ge g. \end{aligned}$$

Table 4 The binary relation R in Example 8

Now, we present when $(\underline{R^c}_I,\overline{R}_I)$ is a Galois connection on a CCD L.

Remark 9

Denote (I1): $xR y\Longrightarrow x\le y, \ \forall x,y\in M(L)$. Then, if R is a transitive relation satisfying (C1) and (I1) on L, it is easy to verify that R is an ordered equivalence relation.

Proposition 4

Let R be a binary relation satisfying (I1) on L and I an ideal of L. Then, for every $a \in L$,

• 1. $a\le \underline{R^c}_I\overline{R}_I(a)$.

• 2. if I is a complete sublattice of L, then $\overline{R}_I\underline{R^c}_I(a ) \le a, \forall a \in L$.

Proof

(1) $\underline{R^c}_I\overline{R}_I(a)=\overline{R}_I(a)\wedge \bigvee \{x : x \in M(L), Rx \cap L\backslash {\downarrow } \overline{R}_I(a)\in \mathscr {I}\}$. Denote $S=\{x : x \in M(L), Rx \cap L\backslash {\downarrow } \overline{R}_I(a)\in \mathscr {I}\}$. For any $z\in M(L), z\lhd a$, we claim that $z\le \overline{R}_I(a)\wedge \bigvee S$.

In fact, it is direct that $z\le a\le \overline{R}_I(a)$ by (1) in Proposition 1 and (1) in Proposition 3. According to (I1), we have $r_z^*\le z$, which implies $r_z^*\le \overline{R}_I(a)$, it is equivalent to $Rz\subseteq {\downarrow }\overline{R}_I(a)$, thus, $Rz \cap L\backslash {\downarrow } \overline{R}_I(a)=\emptyset \in \mathscr {I}$, i.e., $z\in S$. Therefore, $z\le \underline{R^c}_I\overline{R}_I(a)$, i.e., $a\le \underline{R^c}_I\overline{R}_I(a)$.

(2) $\overline{R}_I\underline{R^c}_I(a)=\underline{R^c}_I(a )\vee \bigvee \{r_y ^*: y\in M(L), y\in {\downarrow } \underline{R^c}_I(a)\backslash I\}$. Denote $T=\{r_y^* : y\in M(L), y\in {\downarrow } \underline{R^c}_I(a)\backslash I\}$. We only need to prove $\bigvee T\le a$ by (1) in Proposition 3. It follows from Proposition 2 that for any $z\in M(L), z\lhd \bigvee T$, there exists $y\in M(L)$, $y\in {\downarrow } \underline{R^c}_I(a)\backslash I$ such that $z\lhd r_y^*$, thus there exists $p\in Ry$ such that $z\le p$, $p\in Ry$ implies $p\le y$ by (I1), moreover, $y\le \underline{R}^c_I(a)\le a$, Thus, $z\le p\le y\le a$. This completes the proof. $\square$

Theorem 14

Let R be a binary relation satisfying (I1) on L and I a complete sublattice ideal of L. Then, $(\underline{R^c}_I, \overline{R}_I)$ is a Galois connection.

Proof

It follows from Proposition 4 and Theorem 12. $\square$

Corollary 4

Let R be a binary relation satisfying (I1) on L and I a complete sublattice ideal of L. Then, for any $a, b\in L, A\subseteq L$, we have

• 1. $\underline{R^c}_I(a\wedge b)=\underline{R^c}_I(a)\wedge \underline{R^c}_I(b)$ and $\underline{R^c}_I(\wedge A)=\bigwedge \{\underline{R^c}_I(a): a\in A\}$.

• 2. if R is transitive, then $\overline{R}_I\overline{R}_I(a)=\overline{R}_I(a)$.

• 3. $\underline{R^c}_I\overline{R}_I\underline{R^c}_I(a)=\underline{R}_I(a)$.

• 4. $\overline{R}_I\underline{R^c}_I\overline{R}_I(a) = \overline{R^c}_I(a)$.

Proof

(1) holds by Theorem 14 and (3) in Theorem 5.

(2) R is transitive implies that $R^c$ is transitive, thus, $\underline{R^c}_I\underline{R^c}_I(a)=\underline{R^c}_I(a)$ by (6) in Proposition 3. According to Theorem 13 and 14, we have

$$\begin{aligned} \overline{R}_I\overline{R}_I(a)= & {} \bigwedge \{b:\underline{R^c}_I(b)\ge \overline{R}_I(a)\}=\bigwedge \{b:\underline{R^c}_I\underline{R^c}_I(b)\\\ge & {} a\}\\= & {} \bigwedge \{b:\underline{R^c}_I(b)\ge a\}=\overline{R}_I(a). \end{aligned}$$

(3) and (4) hold by Theorem 12 and 14. $\square$

Theorem 15

Let I be a complete sublattice ideal of L and (g, f) a Galois connection on L. Then, there exists a quasiorder R satisfying (C3) and (I1) on L, such that $g = \underline{R^c}_I$ and $f = \overline{R}_I$ if and only if f satisfies

• 1. $f(0) = 0$.

• 2. for any $x\in M(L)$, $f(x)=x$.

Proof

($\Longrightarrow$) We only need to prove (2), it follows from (C3) that for any $x\in M(L)$,

$$\begin{aligned}\overline{R}_I(x)= \left\{ \begin{array}{lll}x, &{}\quad x\in I,\\ x \vee r_x^*, &{}\quad x\not \in I.\end{array}\right. \end{aligned}$$

(I1) implies $x\ge r_x^*$, thus, $\overline{R}_I(x)=x$.

($\Longleftarrow$) (g, f) a Galois connection on L, which implies that f is a join preserving function by Theorem 12. From Theorem 9, there exists a quasiorder R such that $f = \overline{R}_I$, and (C3) holds by the property of f. Furthermore, condition (2) implies $xRy\Longleftrightarrow x\le f(y)=y$, which means that R satisfies (I1). Then $(\underline{R^c}_I,\overline{R}_I)$ is a Galois connection by Theorem 14, thus $g = \underline{R^c}_I$. $\square$

Theorem 16

Let I be a complete sublattice ideal of L and (g, f) a Galois connection on L. Then, there exists an ordered equivalence relation R satisfying (I1) on L, such that $g = \underline{R^c}_I$ and $f = \overline{R}_I$ if and only if f satisfies

• 1. $f(0) = 0$.

• 2. for any $x\in M(L)$, $f(x)=x$.

• 3. for any $x,y\in M(L)$, $f(x)\ne f(y)\Longrightarrow f(x)\wedge f(y)=0$.

Proof

($\Longrightarrow$) Since R is an ordered equivalence relation, it follows from Remark 4 that R satisfies (C3), then (2) holds by the proof of Theorem 15. We state (3) here, R is reflexive, symmetric and satisfies (I1), which implies that for any $x\in M(L)$, $x= r_x^*=r_x$. Thus, $\overline{R}_I(x)=x=r_x$. It follows from Theorem 2 that $\{r_x\}_{x\in M(L)}$ is a partition of L, i.e., $\overline{R}_I(x)\ne \overline{R}_I(y)\Longrightarrow \overline{R}_I(x)\wedge \overline{R}_I(y)=0$.

($\Longleftarrow$) Combining with Theorem 11, it can be proved by a similar way to the proof of Theorem 15. $\square$

5 Conclusions and future work

In this paper, we have studied the axiomatic approaches to relation-based rough approximation operators via ideal on a CCD lattice. This work may be taken for the extension of Zhou and Hu (2016) and may also be considered as the completeness of Han et al. (2016). We believe that the axiomatic approaches we offer here will help us to gain much more insights into the mathematical structures of rough approximation operators.

The recent research has shown that rough set theory and formal concept analysis provide complementary data modeling techniques for information retrieval and knowledge representation (Li et al. 2013). In Yao (2004), by combining these two theories, the author obtained a better understanding of knowledge embedded in data. Guo et al. (2014) applied rough set theory to formal concept analysis and then got a representation of algebraic domains.

Zhou and Hu (2014) also discussed generalized rough approximation operators defined on two CCD lattices $(X,\vee ,\wedge ,0,1)$ and $(Y,\vee ,\wedge ,\bot ,\top )$ based on a binary relation $R\subseteq M(X)\times M(Y)$. Yao et al. (2016) presented a concept of lattice-theoretic contexts $(G,P,\mathbb {I})$ for G, P being complete lattices and $\mathbb {I}$ a Galois ideal of G and P, which is a common generalization of classical formal concept analysis. Furthermore, when the lattices G, P are completely distributive, a reduction of the relation $\mathbb {I}$ in the lattice-theoretic context $(G,P,\mathbb {I})$ was obtained.

In the future, we will investigate the relation between rough set theory and formal concept analysis from the following aspects:

• 1. For Zhou and Hu’s rough sets defined on two CCD lattices $(X,\vee ,\wedge ,0,1)$ and $(Y,\vee ,\wedge ,\bot ,\top )$ with a binary relation $R\subseteq M(X)\times M(Y)$, we can consider the corresponding lattice-theoretic context $(X,Y,\mathbb {I}_R)$, where $\mathbb {I}_R$ is the generated Galois ideal of R (the smallest Galois ideal of X and Y contains R). Then, there comes a natural question that: What is the relation between the generalized rough approximation operators defined on the two CCD lattices $(X,\vee ,\wedge ,0,1)$ and $(Y,\vee ,\wedge ,\bot ,\top )$ based on a binary relation $R\subseteq M(X)\times M(Y)$ and concept lattices of related CCD lattice-theoretic contexts $(X,Y,\mathbb {I}_R)$?

• 2. In a CCD lattice-theoretic context $(G,P,\mathbb {I})$, if we put $R_\mathbb {I}=\mathbb {I}\mid _{M(G)\times M(P)}$ (or equivalently $R_\mathbb {I}=\mathbb {I}\cap ({M(G)\times M(P)})$). Then we can research related rough approximation operators defined on two CCD lattices G and M with respect to $R_\mathbb {I}$. Hence, a second question arises: What is the connection between the concept lattices of CCD lattice-theoretic contexts $(X,Y,\mathbb {I})$ and corresponding generalized rough approximation operators defined on the two CCD lattices G and P with $R_\mathbb {I}$?

• 3. Due to the nice features of ideal, we will further study lattice-theoretic contexts via an ordinary ideal.