A new portfolio selection model with interval-typed random variables and the empirical analysis

Abstract

This paper proposes a new portfolio selection model, where the goal is to maximize the expected portfolio return and meanwhile minimize the risks of all the assets. The average return of every asset is considered as an interval number, and the risk of every asset is treated by probabilistic measure. An algorithm for solving the portfolio selection problem is given. Then a Pareto-maximal solution could be obtained under order relations between interval numbers. Finally, the empirical analysis is presented to show the feasibility and robustness of the model.

1 Introduction

In recent years, the model of portfolio selection has been a hot topic and the algorithm has attracted great attention in financial area. One of the critical research problems is how to find the best option from all the feasible alternatives for investors around the world. In order to solve the problem, Markowitz (1952) initiated a mean-variance portfolio optimization model, where the risk was measured by the portfolio variance and the rate of return was assumed to reach a special level. Thereafter, many portfolio selection models (Abdelaziz et al. 2007; Corazza and Favaretto 2007; Markowitz 1959) have been established, and there have several different ways to characterize the risk of assets such as semi-variance risk measure (Markowitz 1959), the mean absolute deviation risk measure (Konno 1990; Konno and Yamazaki 1991) and the value-at-risk (abbreviated as VAR) (Basak and Shapiro 2001; Chen 2011; Chen and Tang 2005; Goh et al. 2012). However, VAR measure disregards the loss beyond VAR and lacks the features of subadditivity and convexity (Artzner et al. 1999), and moreover, the portfolio selection model with a VAR measure is computationally difficult (Cui et al. 2013). Then mean-CVaR portfolio selection models (Yao et al. 2013) are established by utilizing conditional value-at-risk to measure risk. Considering a given time periods, a portfolio selection model (Teo and Yang 2001) by minimizing the average of maximum individual risks has been presented. A minimax-type model (Deng et al. 2005) is given by maximizing the worst possible expected ratios of returns on portfolio. Recently, risk management strategies via minimax portfolio optimization (Polak et al. 2010) have been established, where the risk measure was considered as the worst-case return in portfolio.

Owing to the incomplete information provided by financial market and human subjective judgments, the uncertain rates of return of assets are often difficult to present exactly. Therefore, researchers introduce interval numbers (Moore et al. 2009), fuzzy sets and random variables to analyze and describe the rates of returns respectively. Several portfolio selection models associated with fuzzy set theory, possibility theory and probability theory have been developed (Florentin et al. 2015; Inuiguchi and Ramik 2000; Lai et al. 2002; Liu and Liu 2003; Liu 2001; Liu and Liu 2005; Sun et al. 2015). An interval semi-absolute deviation model (Lai et al. 2002) with interval coefficients in both the objective functions and the constraints is established, which is then transformed to a linear programming via two order relations between intervals.

From fuzzy set theory viewpoint, fuzzy mean-semi-variance models for fuzzy portfolio selection have been proposed (Huang 2008a). If the security returns are assumed to be random but the expected returns of the securities are fuzzy, different random fuzzy mean-variance models have been established (Huang 2007, 2008b). When considering each security return as belonging to a certain class of fuzzy variables but the exact fuzzy variable could not be given, two credibility-based minimax mean-variance models for a fuzzy portfolio selection problem have been presented (Huang 2011). Considering the rates of returns on securities as LR-fuzzy numbers, Vercher et al. (2007) propose two fuzzy portfolio selection models by minimizing fuzzy downside risk constrained by a given expected return and present a generalized mean absolute semi-deviation by utilizing interval-valued probabilistic and possibilistic means. Hasuike et al. (2009) study random fuzzy portfolio selection problems by introducing a fuzzy goal considering decision makers’ intentions with a target profit and the probability, which could be transformed into nonlinear programming problems in the basis of both stochastic and fuzzy programming approaches. Their efficient solution algorithms are also investigated and approve to be more effective compared with Vercher et al. model by numerical examples. At the same time, in possibility framework, Ma et al. (2009) establish fuzzy value-at-risk (VaR) and fuzzy conditional value-at-risk (CVaR) models based on credibility measure and investigate a chaos genetic algorithm based on fuzzy simulation. To cope with subjectivity of investors in the real market, Hasuike and Ishii (2009) establish a new portfolio selection model with future returns stated as type-2 fuzzy sets, which is transformed into a type-1 fuzzy programming model involving interval numbers by introducing possibility measure. The possibility measure involves that the total return could be more than the target profit level. Utilizing the hybrid solution method based on the interval programming problem and the standard linear programming approach, Hasuike and Ishii provide an effective solution superior to Vercher et al. model’s optimal portfolio solution in Tokyo Stock Exchange data.

Recently, a portfolio selection method with a probabilistic risk measure is provided (Sun et al. 2015), where a bi-criteria optimization model is constructed as maximizing the expected portfolio return and minimizing the maximum individual risk of the assets. In the literature related to the given time periods of recorded returns of all the assets, the fluctuation of the data may be changed frequently due to some influences such as time and external environment. Obviously, such influences are too complicated to be described properly. As we know, the expected return of portfolio has a close connection with the chosen historical time periods. Therefore, a new minimax portfolio selection model in this paper is established by introducing interval numbers to deal with and record the average rates data of returns of all the assets and describing the distribution of the returns as interval-typed random variables, where the motivation is to maximize the expected portfolio return and minimize the maximum risk of all the assets based on the probability measure. The model allows for investors with different degree of risk tolerance. Particularly, the returns of all the assets are assumed to follow normal distribution. The algorithm is presented comprehensively in this paper. And moreover, the model is feasible for extra additional assets.

The remainder of the paper is arranged as follows. Basic definitions and properties are presented in Sect. 2. Section 3 establishes a new model for portfolio selection based on interval numbers and interval-typed random variables, where the risk is measured by probability of a random event that satisfies the risk tolerance of the investor. Then an algorithm to the model is developed and an analytical solution could be given under the order relation between intervals. The feasibility and robustness of the model is shown by the empirical analysis in Sect. 4. Finally, Sect. 5 gives the conclusions.

2 Preliminaries

The basic concepts and properties of interval numbers are given in this section.

Definition 1

(Lai et al. 2002) An interval number is a set defined as follows:

$$\begin{aligned} \tilde{a}=\{x|a_{l}\le x\le a_{u}, x\in R\}, \end{aligned}$$

where R is the set of all the real number, $a_{l}\in R$ represents the lower bound and $a_{u}\in R$ represents the upper bound of an interval number $\tilde{a}$, respectively.

An interval number $\tilde{a}$ is usually denoted as $[a_{l},a_{u}]$. That is $\tilde{a}=[a_{l},a_{u}]$. If $a_{l}=a_{u}$, then an interval number $\tilde{a}$ degenerates an exact real number. Obviously, an interval number $\tilde{a}$ could be regarded as a trapezoid fuzzy number whose membership degree takes value 1 over the interval $[a_{l},a_{u}]$ and 0 anywhere else. Let $\tilde{a}=[a_{l},a_{u}],\tilde{b}=[b_{l},b_{u}]$ be two interval numbers. Then $\tilde{a}=\tilde{b}$ if and only if $a_{l}=b_{l}$ and $a_{u}=b_{u}$.

Let $L=\{[a_{l},a_{u}]|a_{l}\in R, a_{u}\in R,a_{l}\le x\le a_{u}\}$ denote the family of all the interval numbers.

Definition 2

Let $\tilde{a}=[a_{l},a_{u}],\tilde{b}=[b_{l},b_{u}]$ be two interval numbers. Then the operations on interval numbers used in this paper are as follows:

$$\begin{aligned} \tilde{a}+\tilde{b}= & {} [a_{l}+b_{l},a_{u}+b_{u}], \\ \tilde{a}-\tilde{b}= & {} [a_{l}-b_{u},a_{u}-b_{l}], \end{aligned}$$

$\tilde{a}\cdot \tilde{b}=[min\{a_{l}\cdot b_{l},a_{l}\cdot b_{u},a_{u}\cdot b_{l},a_{u}\cdot b_{u}\},max\{a_{l}\cdot b_{l},a_{l}\cdot b_{u},a_{u}\cdot b_{l},a_{u}\cdot b_{u}\}]$

Let $\le$ represent the classical inequality relation between real numbers. Then the order relations between interval numbers are given as follows.

Definition 3

(Lai et al. 2002) Let $\tilde{a}=[a_{l},a_{u}],\tilde{b}=[b_{l},b_{u}]$ be two interval numbers. Then two order relations $\preceq _{1}$ and $\preceq _{2}$ between $\tilde{a}$ and $\tilde{b}$ are defined as,

• (i) $\tilde{a}\preceq _{1}\tilde{b}$ if and only if $a_{l}\le b_{l}$ and $\frac{a_{l}+a_{u}}{2}\le \frac{b_{l}+b_{u}}{2}$;

• (ii) $\tilde{a}\prec _{1}\tilde{b}$ if and only if $\tilde{a}\preceq _{1}\tilde{b}$ and $\tilde{a}\ne \tilde{b}$;

• (iii) $\tilde{a}\preceq _{2}\tilde{b}$ if and only if $a_{u}\le b_{u}$ and $\frac{a_{l}+a_{u}}{2}\le \frac{b_{l}+b_{u}}{2}$;

• (iv) $\tilde{a}\prec _{2}\tilde{b}$ if and only if $\tilde{a}\preceq _{2}\tilde{b}$ and $\tilde{a}\ne \tilde{b}$.

Definition 4

(Li 2005) Let $\preceq$ be a binary relation on a nonempty set P. Then $(P, \preceq )$ is called a partial ordered set (abbreviated as poset) if the following conditions hold:

• (1) reflexivity: $\forall x \in P, x\preceq x$ ;

• (2) symmetry: $\forall x, y \in P$, both $x\preceq y$ and $y\preceq x$ imply that $x=y$;

• (3) transitivity: $\forall x, y, z \in P$, both $x\preceq y$ and $y\preceq z$ imply that $x\preceq z$.

If for any element $x, y \in P, x\preceq y$ or $y\preceq x$, then we say that $(P, \preceq )$ is a totally ordered set.

Property 1

Let L be the family of all the interval numbers. Then both $(L, \preceq _{1})$ and $(L, \preceq _{2})$ are posets.

Proof

$L\ne \phi , \preceq _{1}$ is a partial order on L. In fact,

• (1) $\preceq _{1}$ is reflexive. For any element $\tilde{a}\in L, \tilde{a}\preceq _{1}\tilde{a}$ ;

• (2) $\preceq _{1}$ is symmetric. For any element $\tilde{a}=[a_{l},a_{u}],\tilde{b}=[b_{l},b_{u}],\tilde{a}, \tilde{b}\in L$, If $\tilde{a}\preceq _{1}\tilde{b}$ and $\tilde{b}\preceq _{1}\tilde{a}$, then

  $$\begin{aligned}&a_{l}\le b_{l}, \frac{a_{l}+a_{u}}{2}\le \frac{b_{l}+b_{u}}{2} \\&b_{l}\le a_{l}, \frac{b_{l}+b_{u}}{2}\le \frac{a_{l}+a_{u}}{2} \end{aligned}$$

  So $a_{l}=b_{l}, a_{u}=b_{u}$. Therefore $\tilde{a}=\tilde{b}$.

• (3) $\preceq _{1}$ is transitive. For any element $\tilde{a}, \tilde{b}, \tilde{c}\in L$, $\tilde{a}=[a_{l},a_{u}],\tilde{b}=[b_{l},b_{u}],\tilde{c}=[c_{l},c_{u}]$, if $\tilde{a}\preceq _{1}\tilde{b}$ and $\tilde{b}\preceq _{1}\tilde{c}$, then

  $$\begin{aligned} a_{l}\le b_{l}\le c_{l}, \frac{a_{l}+a_{u}}{2}\le \frac{b_{l}+b_{u}}{2}\le \frac{c_{l}+c_{u}}{2} \end{aligned}$$

  So $\tilde{a}\preceq _{1}\tilde{c}$.

It is concluded that $(L, \preceq _{1})$ is a poset from the above.

Similarly, it is easily concluded that $(L, \preceq _{2})$ is also a poset by Definitions 3 and 4.

3 A new portfolio selection model and the algorithm

Suppose an investor aims to allocate his wealth into n risky assets. The period time T represents the time length of the investment. The interval number $\tilde{r}_{i}$ is the average return of asset $i, i\in \{1,2,\ldots , n\}$. $x=(x_{1}, x_{2}, \ldots , x_{n})$ is an investment strategy of the investor, where $x_{i}\in [0,1]$ represents the proportion of the total amount invested in asset $i, i\in \{1,2,\ldots , n\}$ and $\sum \nolimits _{i=1}^{n}x_{i}=1$. $r_{it}\in R$ is the historical return of asset i at time $t, i\in \{1,2,\ldots , n\}, t\in \{1,2,\ldots , T\}$.

In this paper, $T, r_{it}$ can be given in advance. Let $r_{ih}$ be the historical mean return tendency of the return of asset i. Then $\tilde{r}_{i}$ is obtained in the following way.

$$\begin{aligned} \tilde{r}_{i}= & {} [r_{il}, r_{iu}] \end{aligned}$$

(3.1)

$$\begin{aligned} r_{il}= & {} \min \left\{ \frac{1}{T}\sum \limits _{t=1}^\mathrm{T}r_{it},r_{ih}\right\} \end{aligned}$$

(3.2)

$$\begin{aligned} r_{iu}= & {} \max \left\{ \frac{1}{T}\sum \limits _{t=1}^\mathrm{T}r_{it},r_{ih}\right\} \end{aligned}$$

(3.3)

The return of asset i is assumed to follow normal distribution. To exactly describe the return of asset i, we introduce interval-typed random variables $\lceil \xi _{il}, \xi _{iu}\rceil$, where $\xi _{il}$ follows normal distribution with mean $r_{il}$ and standard deviation $\sigma _{il}$ and $\xi _{iu}$ follows normal distribution with mean $r_{iu}$ and standard deviation $\sigma _{iu}, i\in \{1,2,\ldots , n\}$.

The definition of interval-typed random variable is given specifically as follows.

Definition 5

A variable $\tilde{\xi }=\lceil \xi _{l}, \xi _{u}\rceil$ is said to be an interval-typed random variable if both the variables $\xi _{l}$ and $\xi _{u}$ are random variables, and the mathematical expectation of $\xi _{l}$ is no more than that of $\xi _{u}$.

In particular, if $\xi _{l}$ follows normal distribution with mean $r_{l}$ and standard deviation $\sigma _{l}$, abbreviated as $\xi _{l}\sim N(r_{l}, \sigma _{l}^{2})$, $\xi _{u}$ follows normal distribution with mean $r_{u}$ and standard deviation $\sigma _{u}$, abbreviated as $\xi _{u}\sim N(r_{u}, \sigma _{u}^{2})$, $r_{l}=r_{u}$ and $\sigma _{l}=\sigma _{u}$, then an interval-typed random variable $\lceil \xi _{l}, \xi _{u}\rceil$ degenerates a typical variable with normal distribution.

Definition 6

Let $\tilde{\xi }=\lceil \xi _{l}, \xi _{u}\rceil$ and $\tilde{\eta }=\lceil \eta _{l}, \eta _{u}\rceil$ be two interval-typed random variables. Then the operations on interval-typed random variables are defined as follows:

• (1) $\tilde{\xi }+\tilde{\eta }=\lceil \xi _{l}+\eta _{l},\xi _{u}+\eta _{u}\rceil$,

• (2) if $k\in R$ and $k\ge 0$, then $k\tilde{\xi }=\lceil k\xi _{l}, k\xi _{u}\rceil$; if $k< 0$, then $k\tilde{\xi }=\lceil k\xi _{u},k\xi _{l}\rceil$.

Clearly, Definition 6 is well defined by Definition 5 and probability theory.

Property 2

Let $\tilde{\xi }_{i}=\lceil \xi _{il}, \xi _{iu}\rceil$ be an interval-typed random variable, $\xi _{il}\sim N(\mu _{il}, \sigma _{il}^{2}), \xi _{iu}\sim N(\mu _{iu}, \sigma _{iu}^{2}), i=1,2,\ldots , n$, the variables $\xi _{1l},\xi _{2l},\ldots ,\xi _{nl}$ are mutually independent, and the variables $\xi _{1u},\xi _{2u},\ldots ,\xi _{nu}$ are mutually independent. Then

$$\begin{aligned} \tilde{\xi }=k_{1}\tilde{\xi }_{1}+k_{2}\tilde{\xi }_{2}+\cdots +k_{n}\tilde{\xi }_{n}=\lceil \tilde{\xi }_{l},\tilde{\xi }_{u}\rceil \end{aligned}$$

is an interval-typed random variable, where

$$\begin{aligned}&\tilde{\xi }_{l}\sim N\left( \sum \limits _{i=1}^{n}k_{i}\mu _{il},\sum \limits _{i=1}^{n}k_{i}^{2}\sigma _{il}^{2}\right) , \\&\tilde{\xi }_{u}\sim N\left( \sum \limits _{i=1}^{n}k_{i}\mu _{iu},\sum \limits _{i=1}^{n}k_{i}^{2}\sigma _{iu}^{2}\right) , \end{aligned}$$

$k_{i}\ge 0,i=1, 2, \ldots , n$.

Proof

Suppose $\tilde{\xi }=\lceil \xi _{l}, \xi _{u}\rceil$. Then the following results hold by Definition 6:

$$\begin{aligned} \xi _{l}= & {} k_{1}\xi _{1l}+k_{2}\xi _{2l}+\cdots +k_{n}\xi _{nl},\\ \xi _{u}= & {} k_{1}\xi _{1u}+k_{2}\xi _{2u}+\cdots +k_{n}\xi _{nu}. \end{aligned}$$

Since $\xi _{1l},\xi _{2l},\ldots ,\xi _{nl}$ are mutually independent variables, $\xi _{1u},\xi _{2u}, \ldots ,\xi _{nu}$ are mutually independent variables, and $k_{i}\ge 0,i=1, 2, \ldots , n.$ It is followed by probabilistic theory that, $\xi _{l}\sim N(\mu _{l}, \sigma _{l}^{2}), \xi _{u}\sim N(\mu _{u}, \sigma _{u}^{2}),$ where

$$\begin{aligned} \mu _{l}= & {} k_{1}\mu _{1l}+k_{2}\mu _{2l}+\cdots +k_{n}\mu _{nl},\\ \sigma _{l}^{2}= & {} k_{1}^{2}\sigma _{1l}^{2}+k_{2}^{2}\sigma _{2l}^{2}+\cdots +k_{n}^{2}\sigma _{nl}^{2},\\ \mu _{u}= & {} k_{1}\mu _{1u}+k_{2}\mu _{2u}+\cdots +k_{n}\mu _{nu},\\ \sigma _{u}^{2}= & {} k_{1}^{2}\sigma _{1u}^{2}+k_{2}^{2}\sigma _{2u}^{2}+\cdots +k_{n}^{2}\sigma _{nu}^{2}. \end{aligned}$$

Moreover, $\mu _{l}\le \mu _{u}$. So the proof is completed by Definition 5.

Assuming that the investor with a conservative and pessimistic mind allows to sustain a certain degree of risk aversion, we introduce a probabilistic risk measure function defined as follows:

$$\begin{aligned} f(x_{i})=\frac{Pr\{|\xi _{il}x_{i}-r_{il}x_{i}|\le \theta \varepsilon _{1}\}+Pr\{|\xi _{iu}x_{i}-r_{iu}x_{i}|\le \theta \varepsilon _{2}\}}{2}\nonumber \\ \end{aligned}$$

(3.4)

where $\theta$ is a constant to adjust the risk level and the parameters $\varepsilon _{1}$ and $\varepsilon _{2}$ denote the average risks of the entire portfolio, which could be computed by the following formula.

$$\begin{aligned} \varepsilon _{1}=\frac{1}{n}\sum \limits _{i=1}^{n}\sigma _{il}, \varepsilon _{2}=\frac{1}{n}\sum \limits _{i=1}^{n}\sigma _{iu}. \end{aligned}$$

(3.5)

The value $f(x_{i})$ in equation (3.4) obviously belongs to the interval [0, 1]. Moreover, the more $f(x_{i})$ approximates to 1, the less the individual risk of asset i. Hence the expression $\min _{1\le i\le n}f(x_{i})$ represents the risk of the portfolio $x=(x_{1},x_{2},\ldots ,x_{n})$.

Assume that the investor seeks to maximize the expected portfolio return and minimize the portfolio risk. Then the model of portfolio selection could be established as follows:

$$\begin{aligned}&(P1) \ \ \ \ \ \ \ \max \left\{ \min _{1\le i\le n} f(x_{i}),\ \sum \limits _{i=1}^{n}g(x_{i})\right\} \\&\quad \hbox {s.t.}\\&\qquad \left\{ \begin{array}{l} g(x_{i})=\lambda r_{il}x_{i}+(1-\lambda )\frac{r_{il}+r_{iu}}{2}x_{i}, \\ f(x_{i})=\frac{Pr\{|\xi _{il}x_{i}-r_{il}x_{i}|\le \theta \varepsilon _{1}\}+Pr\{|\xi _{iu}x_{i}-r_{iu}x_{i}|\le \theta \varepsilon _{2}\}}{2}, \\ \sum \limits _{i=1}^{n}x_{i}=1, \\ 0\le x_{i}\le 1, i=1,2,\ldots , n. \end{array}\right. \end{aligned}$$

where $\lambda$ is a constant between 0 and 1, i.e., $0\le \lambda \le 1$, $[r_{il},r_{iu}]$ is average return of asset i from Equations (3.2) and (3.3), and $g(x_{i})$ represents the expected return of the $i\hbox {th}$ asset. Particularly, a pessimistic and conservative investor tends to select the parameter $\lambda =1$. The expression $\sum \nolimits _{i=1}^{n}g(x_{i})$ expresses the expected return of the portfolio $x=(x_{1},x_{2},\ldots , x_{n}), x_{i}\ge 0 (i=1,2,\ldots , n)$ shows that short selling of the $i\hbox {th}$ risky asset is not allowed.

Definition 7

A solution $x^{*}=(x_{1}^{*}, x_{2}^{*}, \ldots , x_{n}^{*})$ is said to be a Pareto-maximal solution for the model (P1) if there does not exist a solution $\hat{x}=(\hat{x}_{1}, \hat{x}_{2}, \ldots , \hat{x}_{n})$ such that

$$\begin{aligned} \min _{1\le i\le n} f(x_{i}^{*})\le \min _{1\le i\le n} f(\hat{x}_{i}) \end{aligned}$$

and

$$\begin{aligned} \sum \limits _{i=1}^{n}g(x_{i}^{*})\le \sum \limits _{i=1}^{n}g(\hat{x}_{i}), \end{aligned}$$

for which at least one of the inequalities holds strictly.

The model (P1) could be solved in the following way.

Step 1. (P1) is transformed equivalently to the model (P2):

$$\begin{aligned}&(P2) \ \ \ \ \ \ \ \max \left\{ y, \sum \limits _{i=1}^{n}g(x_{i})\right\} \\&\quad \hbox {s.t.} \\&\qquad \left\{ \begin{array}{l} y\le f(x_{i}), \\ g(x_{i})=\lambda r_{il}x_{i}+(1-\lambda )\frac{r_{il}+r_{iu}}{2}x_{i}, \\ \sum \limits _{i=1}^{n}x_{i}=1, \\ 0\le x_{i}\le 1, i=1,2,\ldots , n. \end{array}\right. \end{aligned}$$

where y is a positive constant between 0 and 1, representing a probabilistic level of risk measure. $y\le f(x_{i})$ is the ith probabilistic constraint.

Step 2. Let $F(z)= \int _0^z \frac{1}{\sqrt{2\pi }}e^{-\frac{t^{2}}{2}}\hbox {d}t =\phi (z)-0.5, z\in [0,+\infty ),$ where $\phi (z)=\int _{-\infty }^z \frac{1}{\sqrt{2\pi }}e^{-\frac{t^{2}}{2}}\hbox {d}t$.

Since the interval-typed random variable $\lceil \xi _{il}, \xi _{iu}\rceil$ of asset i follows normal distribution, $\xi _{ij}$ follows normal distribution with mean $r_{ij}$ and standard deviation $\sigma _{ij}, j\in \{l,u\}$.

Thus, $\xi _{ij}-r_{ij}$ is also normally distributed with mean 0 and standard deviation $\sigma _{ij}, i\in \{1,2,\ldots , n\}, j\in \{l,u\}$.

$$\begin{aligned} f(x_{i})= & {} \frac{Pr\{|\xi _{il}x_{i}-r_{il}x_{i}|\le \theta \varepsilon _{1}\}+Pr\{|\xi _{iu}x_{i}-r_{iu}x_{i}|\le \theta \varepsilon _{2}\}}{2}\\= & {} \frac{Pr\left\{ |\xi _{il}-r_{il}|\le \frac{\theta \varepsilon _{1}}{x_{i}}\right\} +Pr\{|\xi _{iu}-r_{iu}|\le \frac{\theta \varepsilon _{1}}{x_{i}}}{2}\\= & {} \int _0^\frac{\theta \varepsilon _{1}}{x_{i}} \frac{1}{\sqrt{2\pi }\sigma _{il}}e^{-\frac{t^{2}}{2\sigma _{il}^{2}}}\hbox {d}t+\int _0^\frac{\theta \varepsilon _{2}}{x_{i}} \frac{1}{\sqrt{2\pi }\sigma _{iu}}e^{-\frac{t^{2}}{2\sigma _{iu}^{2}}}\hbox {d}t\\= & {} \int _0^\frac{\theta \varepsilon _{1}}{x_{i}\sigma _{il}} \frac{1}{\sqrt{2\pi }}e^{-\frac{q^{2}}{2}}\hbox {d}q+\int _0^\frac{\theta \varepsilon _{2}}{x_{i}\sigma _{iu}} \frac{1}{\sqrt{2\pi }}e^{-\frac{q^{2}}{2}}\hbox {d}q\\= & {} F\left( \frac{\theta \varepsilon _{1}}{x_{i}\sigma _{il}}\right) +F\left( \frac{\theta \varepsilon _{2}}{x_{i}\sigma _{iu}}\right) \\= & {} \phi \left( \frac{\theta \varepsilon _{1}}{x_{i}\sigma _{il}}\right) +\phi \left( \frac{\theta \varepsilon _{2}}{x_{i}\sigma _{iu}}\right) -1 \end{aligned}$$

Clearly, $f(x_{i})$ is a monotonically decreasing function with respect to $x_{i}$.

For the model (P2), it is shown that during the process of maximizing the objective function, the value of y is to be pushed to reach

$$\begin{aligned} \min _{1\le i\le n}f(x_{i}). \end{aligned}$$

If y is chosen to be an arbitrary but fixed real number between 0 and 1, then an upper bound $U_{i}$ for $x_{i}$ could be obtained by utilizing the monotonic property of $f(x_{i})$. Define

$$\begin{aligned} U_{i}=min\{1,\hat{x}_{i}\} \end{aligned}$$

where $\hat{x}_{i}=f^{-1}(y),\ i=1,2,\ldots , n$.

Therefore, for a fixed value of $y\in [0,1]$, the model (P2) is equivalent to the linear programming model (P3) stated as follows:

$$\begin{aligned}&(P3) \ \ \ \ \ \ \ max\ \varphi (x)= \sum \limits _{i=1}^{n}\left[ \lambda r_{il}x_{i}+(1-\lambda )\frac{r_{il}+r_{iu}}{2}x_{i}\right] \\&\qquad \hbox {s.t.} \\&\qquad \qquad \left\{ \begin{array}{l} \sum \limits _{i=1}^{n}x_{i}=1, \\ 0\le x_{i}\le U_{i} , i=1,2,\ldots , n. \end{array}\right. \end{aligned}$$

Step 3. The model (P3) is solved by the simplex algorithm and computed by using MATLAB software on PC.

Specially, if the set of all the risky assets’ average return

$$\begin{aligned} P=\{\tilde{r}_{i}|\tilde{r}_{i}=[r_{il}, r_{iu}]\in L, i=1,2,\ldots , n\} \end{aligned}$$

is a totally ordered poset on the binary relation $\preceq _{1}$, then an analytical solution of model (P3) could be obtained.

Theorem 1

Let $(P,\preceq _{1})$ be a totally ordered set, where P is a set of all the risky assets’ average return. Moreover, $\widetilde{r}_{n}\preceq _{1}\widetilde{r}_{n-1}\preceq _{1}\cdots \preceq _{1}\widetilde{r}_{2}\preceq _{1}\widetilde{r}_{1}$. Then there exists an integer $k\le n$ such that $x^{*}=(x_{1}^{*}, x_{2}^{*}, \ldots , x_{n}^{*})$ is a Pareto-maximal solution of model (P3), where $\sum \nolimits _{i=1}^{k-1}U_{i}< 1$, $\sum \nolimits _{i=1}^{k}U_{i}\ge 1$, and

$$\begin{aligned} x_{i}^{*}=\left\{ \begin{array}{l@{\quad }l} U_{i}, &{}i=1,2,\ldots , k-1 \\ 1-\sum \nolimits _{i=1}^{k-1}U_{i}, &{}i=k \\ 0, &{}i>k \end{array}\right. \end{aligned}$$

Proof

Recall that $U_{i}=min\{1,\hat{x}_{i}\}\le 1, U_{i}$ is the upper bound of $x_{i}$, $i=1,2,\ldots , n$. Therefore, the following inequality holds by the constraint of model (P3):

$$\begin{aligned} \sum \limits _{i=1}^{n}U_{i}\ge 1. \end{aligned}$$

So there exists an integer $k, 1\le k\le n$, such that

$$\begin{aligned} \sum \limits _{i=1}^{k-1}U_{i}< 1,\ \sum \limits _{i=1}^{k}U_{i}\ge 1. \end{aligned}$$

For the linear programming model (P3), $\hat{x}=(\hat{x}_{1}, \hat{x}_{2},\, \ldots , \hat{x}_{n})$ is a Pareto-maximal solution if and only if there exists $C\in R$, $V=(v_{1}, v_{2},\ldots ,v_{n})\in R^{n}$ and $\omega =(\omega _{1}, \omega _{2},\ldots ,\omega _{n})\in R^{n}$, such that

Let $C^{*}=\lambda r_{kl}+(1-\lambda )\frac{r_{kl}+r_{ku}}{2}$,

$v_{i}^{*}=\left\{ \begin{array}{l@{\quad }l} 0, &{}i=1,2,\ldots , k \\ C^{*}-\lambda r_{il}-(1-\lambda )\frac{r_{il}+r_{iu}}{2}, &{}i>k \end{array}\right.$

and

$\omega _{i}^{*}=\left\{ \begin{array}{l@{\quad }l} \lambda r_{il}+(1-\lambda )\frac{r_{il}+r_{iu}}{2}-C^{*}, &{}i=1,2,\ldots , k-1 \\ 0, &{}i>k-1 \end{array}\right.$.

Then it is easily derived by simple calculation that $x^{*}=(x_{1}^{*}, x_{2}^{*}, \ldots , x_{n}^{*})$ is a Pareto-maximal solution of the linear programming model (P3).

4 The empirical analysis

To validate the method proposed in portfolio selection, this section considers the following three data sets.

4.1 The latest historical data set on the website

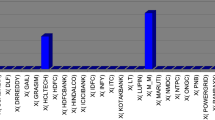
The historical data of the eight assets shown in Table 1 are collected from September 27, 2012, to August 31, 2015, which are downloaded from the Web site http://quote.ea-stmoney.com. One month is remarked as a basic time period to obtain the historical returns over 36 months. The data are shown in Table 2 and shown in Fig. 1.

Table 1 Names of eight stocks

Table 2 Historical returns of the eight stocks $(\%)$

Owing to incomplete information and inaccurate date obtained by statistics and expert acknowledgement, interval numbers are used to describe the average returns of all the assets, and interval-typed random variables are used to characteristic the returns’ feature of all the assets. The historical mean return tendency of the returns of every asset is determined by adopting the latest 12-month returns of every given asset. Therefore, the intervals of the average returns of all the assets are shown in Table 3. The return distribution of every asset $\xi _{i}$ shown in Table 4 is characterized by interval-typed random variable $\lceil \xi _{il},\xi _{iu}\rceil ,$ $\xi _{il}\sim N(\mu _{il},\sigma _{il}^{2})$, $\xi _{iu}\sim N(\mu _{iu},\sigma _{iu}^{2}),$ $i=1,2,\ldots ,8$.

For example, the return distribution of the first asset is characterized as an interval-typed random variable $\xi _{1}=\lceil \xi _{1l},\xi _{1u}\rceil$, where $\xi _{1l}\sim N(0.3554, 0.2748)$ represents $\xi _{1l}$ follows normal distribution with mean 0.3554 and variance 0.2748, and $\xi _{1u}\sim N(0.9457,0.3004)$ represents $\xi _{1u}$ follows normal distribution with mean 0.9457 and variance 0.3004. The return distribution of the stock 1 is shown in Fig. 2.

The model (P1) is solved by MATLAB software and the algorithm. When the parameters $\theta ,\lambda$ and y are given such as $\theta =1$, $\lambda =0.5$ and $y\in [0,1]$, the portfolio selection of model (P3) is shown in Table 5. And the expected return for portfolio selection corresponding to the parameter $y\in [0,1]$ is plotted in Fig. 3. It is shown that the more $y\in [0,1]$ the less the expected return. That is to say, the expected return of portfolio selection is decreasing whenever the probability of random event that every asset deviated from the average return of the asset is increasing.

Let the period time T be 36 months. When the historical mean return tendency of the returns of every asset is determined by adopting the latest 8-month returns of every given asset instead of 12-month returns, the portfolio selection solutions are shown in Table 6. When the historical mean return tendency of the returns of every asset is determined by adopting the latest 16-month returns of every given asset instead of 12-month returns, the portfolio selection solutions are shown in Table 7.

Fig. 1

Returns figure of eight stocks

Table 3 Intervals of the average returns

Table 4 Returns distribution of eight assets

Fig. 2

Returns figure of stock 1

Table 5 Portfolio solutions of eight assets

Let us introduce the following formula to express the relative error between two solution vectors:

$\forall (x_{1}, x_{2}, \ldots , x_{n}), \forall (z_{1}, z_{2}, \ldots , z_{n}),\sum \nolimits _{i=1}^{n}x_{i}=\sum \nolimits _{i=1}^{n}z_{i}=1, x_{i}\ge 0, z_{i}\ge 0, i=1,2,\ldots , n$.

$E_{y}=\max (\{\frac{|x_{i}-z_{i}|}{x_{i}}|i=1, 2, \ldots , n, x_{i}\ne 0\}\cup \{\frac{|x_{i}-z_{i}|}{z_{i}}| i=1, 2, \ldots , n, z_{i}\ne 0\})$.

The distance between the two solution vectors is given as follows:

$$\begin{aligned} d=\sqrt{\sum \limits _{i=1}^{n}(x_{i}-z_{i})^{2}}. \end{aligned}$$

In Table 8, the second column is the relative error between the optimal solutions when the historical mean return tendency of the returns of every asset was determined by adopting the latest 12- and 8-month returns of all the assets, and the third column is the relative error between the optimal solutions when the historical mean return tendency of the returns of every asset was determined by adopting the latest 12- and 16-month returns of all the assets. Table 8 shows that when y is given from 0.70 to 1, all the relative errors between the corresponding optimal solutions are no more than 0.0473.

Fig. 3

Expected returns with given probability level of risk measure

Table 6 Portfolio solutions of eight assets

Table 7 Portfolio solutions of eight assets

Table 9 shows the distance among the optimal solutions when $y\in [0, 1]$ is given, where the first column is the value of y, the second column $d_{1}$ is the distance between the optimal solutions derived from Tables 5 and 6, the third column $d_{2}$ is the distance between the optimal solutions derived from Tables 5 and 7, and the fourth column $d_{3}$ is the distance between the optimal solutions derived from Tables 6 and 7. Moreover, when y is given from 0.7 to 1, the biggest distance among all the corresponding solutions is 0.0424. The numbers in Table 9 show that when the value in the first column increases gradually, the value in the other columns becomes smaller. It tells us that the smaller the risk, the better the stability of the expected return of portfolio selection.

Therefore, Tables 8 and 9 show that the model in this paper is feasible and robust.

Table 8 Relative errors

Table 9 Distance among the optimal solutions

Next we compare our proposed model with the previous models including Hasuike et al. model (2009) based on random fuzzy variable returns, Hasuike and Ishii model (2009) with the optimistic satisfaction and Vercher et al. model (2007). These problems are formulated as the following form.

Hasuike et al. model (2009) is given as follows:

$$\begin{aligned}&\qquad \quad \quad \qquad \qquad \max \ \ h \nonumber \\&\hbox {s.t.} \nonumber \\&\left\{ \begin{array}{ll} \sum \nolimits _{j=1}^{n}[m_{j}+R^{*}(h)\alpha _{j}]x_{j}-K_{g_{p}^{-1}(h)}\psi (x_{i},x_{j})\ge g_{F}^{-1}(h) &{} \\ \psi (x_{i},x_{j})=\sqrt{\sum \nolimits _{j=1}^{n}\sum \nolimits _{i=1}^{n}\sigma _{ij}x_{i}x_{j}} &{} \\ \sum \nolimits _{j=1}^{n}x_{j}=1 , 0\le x_{j}\le p_{j}, j=1,2,\ldots , n. \end{array}\right. \end{aligned}$$

(4.1)

where each fuzzy goal is as follows:

$\mu _{G}(f)=\left\{ \begin{array}{l@{\quad }l} 1, &{} f_{2}\le f \\ g_{F}(f)=\frac{f-f_{1}}{f_{2}-f_{1}}, &{} f_{1}\le f\le f_{2} \\ 0, &{} f\le f_{1} \end{array}\right.$

and

$\mu _{G}(p)=\left\{ \begin{array}{l@{\quad }l} 1, &{} q_{2}\le p \\ g_{P}(p)=\frac{p-q_{1}}{q_{2}-q_{1}}, &{} q_{1}\le p\le q_{2} \\ 0, &{} p\le q_{1} \end{array}\right.$.

Hasuike and Ishii model (2009) is as follows:

$$\begin{aligned}&\qquad \quad \quad \qquad \qquad max\ \ h \nonumber \\&\hbox {s.t.} \nonumber \\&\left\{ \begin{array}{ll} \frac{\sum \nolimits _{j=1}^{n}\bar{r}_{j}x_{j}+L^{*}(h)\sum \nolimits _{j=1}^{n}\underline{\alpha }_{j}x_{j}-\overline{f}}{\frac{1}{2}\left[ L^{*}(h) \left( \sum \nolimits _{j=1}^{n} \left( \overline{\alpha }_{j}-\underline{\alpha }_{j}\right) x_{j}\right) +\left( \overline{f}-\underline{f}\right) \right] }\ge \beta &{} \\ \sum \nolimits _{j=1}^{n}x_{j}=1 , 0\le x_{j}\le p_{j}, j=1,2,\ldots , n. \end{array}\right. \end{aligned}$$

(4.2)

Vercher et al. model (2007) is stated as follows:

$$\begin{aligned}&\qquad \qquad \hbox {Min} \sum \limits _{j=1}^{n}\left[ b_{j}-a_{j}+\frac{1}{3}(\alpha _{j}+\beta _{j})\right] x_{j} \nonumber \\&\hbox {s.t.} \nonumber \\&\left\{ \begin{array}{ll} \sum \nolimits _{j=1}^{n}\frac{1}{2}\left[ a_{j}+b_{j}+\frac{1}{3}(\beta _{j}-\alpha _{j})\right] x_{j}\ge \rho &{} \\ \sum \nolimits _{j=1}^{n}x_{j}=1, 0\le x_{j}\le p_{j}, j=1,2,\ldots ,n. \end{array}\right. \end{aligned}$$

(4.3)

Let us reconsider eight securities shown in Table 2. In the models above, the asset allocation rate to each security is denoted as $x_{j}$, and its upper value $p_{j}$ is assumed to be 0.2,0.4 and 0.5, respectively, $j\in \{1,2,\ldots ,8\}$. $f_{1}=0.57$, $f_{2}=0.686$, $q_{1}=0.7$ and $q_{2}=0.8$. The target value of optimistic satisfaction index $\beta$ is given as $\beta =1$. $[\underline{f},\bar{f}]=[0.4, 0.5]$. The minimum expected return parameter $\rho$ is set as $\rho =0.5$, parameters of trapezoidal fuzzy number $(a_{j},b_{j},\alpha _{j},\beta _{j})$ based on study (Vercher et al. 2007) are shown in Table 10, and interval numbers for $[\underline{\alpha }_{j},\bar{\alpha }_{j}]$ are given as the following form based on Tables 10 and 11:

$$\begin{aligned}{}[\underline{\alpha }_{j},\bar{\alpha }_{j}]=[\min \{SD^{2},b_{j}-a_{j}\}/5,\max \{SD^{2},b_{j}-a_{j}\}/5]. \end{aligned}$$

where sample mean values and standard deviations (abbreviated as SD), shown in Table 11, are based on historical data from September 27, 2012, to August 31, 2015.

Table 10 Parameters based on the historical data

Table 11 Sample data from eight assets

Table 12 Optimal solutions of four models $(p_{j}=0.2,y=0.999)$

Table 13 Optimal solutions of four models $(p_{j}=0.4,y=0.85)$

From the optimal portfolios, Tables 12, 13 and 14 show that the optimal solution for our model chooses higher return securities such as assets 2 and 5 than the others. Hence, it is similar to the optimal solutions of Hasuike and Ishii model (2009) and Hasuike et al. model (2009). It is also shown that the optimal portfolio of our model could be influenced by the probabilistic risk measure level $y\in [0,1]$ while those of the other three models have heavily depended on limited upper value of the corresponding budgeting to each asset. This means that the pessimistic or optimistic attitude of an investor has played an important role in the optimal portfolios of these models. In Table 12, an investor with a pessimistic and conservative opinion allows to sustain degree of portfolio risk aversion as 0.999 or set upper value of the budgeting to each asset as 0.2 in advance, hence the diversification for all the four models. However, in Table 14, the investor with a comparative optimistic and nonconservative mind, who chooses the degree of portfolio risk aversion as 0.75 or assume upper value of the budgeting to each asset to be 0.5 in advance, would obtain centralized portfolios of all the four models.

Table 14 Optimal solutions of four models $(p_{j}=0.5,y=0.75)$

Table 15 Total return with respect to each models

From Table 15, total return of our model is the biggest among the four portfolio models whenever the parameters $p_{j}$ and y are given, where the total returns are computed according to the average return of each asset and the optimal portfolio. This is because our model considers not only minimizing the portfolio risk but also maximizing the expected portfolio return. However, total return of Vercher et al. model is the smallest among the four portfolio models since Vercher et al. model aims to minimize the downside risk of the investment, and total returns of both Hasuike and Ishii model (2009) and Hasuike et al. model (2009) are nearly equal to that of our model owing to the maximization goal of the total profits. Consequently, it is found that our proposed model could be applied to other various cases in practical investments, especially the case that the investor pursues for both the maximum of the total expected return and the minimum of the degree of risk aversion.

4.2 Tokyo Stock Exchange data

Let us consider another numerical example based on the data of securities (Hasuike and Ishii 2009) on the Tokyo Stock Exchange in this subsection. Table 16 presents mean values and standard deviations of sample data between 1995 and 2004. We compare our proposed model with the previous models for portfolio selection problems, including Hasuike et al. model (2009) with random fuzzy variable returns, Hasuike and Ishii model (2009) based on the optimistic satisfaction and Vercher et al. model (2007).

Table 16 Sample data from Tokyo Stock Exchange

In the models shown in Equations (4.1)–(4.3), the asset allocation rate to each security is denoted as $x_{j}$, and its upper value $p_{j}$ is assumed to be $p_{j}=0.2$, $j\in \{1,2,\ldots ,10\}$. $f_{1}=0.03$, $f_{2}=0.06$, $q_{1}=0.7$ and $q_{2}=0.8$. The target value of optimistic satisfaction index $\beta$ is given as $\beta =1$. $[\underline{f},\bar{f}]=[0.04, 0.08]$. The minimum expected return parameter $\rho$ is set as $\rho =0.06$, parameters of trapezoidal fuzzy number $(a_{j},b_{j},\alpha _{j},\beta _{j})$ and interval numbers for $[\underline{\alpha }_{j},\bar{\alpha }_{j}]$ are given as the same as the data from the reference (Hasuike and Ishii 2009).

Since the constraint inequalities,

$$\begin{aligned} 0\le x_{i}\le p_{i}, \quad i\in \{1,2,\ldots ,10\}, \end{aligned}$$

have been required for Eqs. (4.1)–(4.3), where $p_{i}$ is the limited upper value of each budgeting to the i’th stock, our model (P3) also considers adding the constraint inequalities. Hence, the model (P3) is then transformed to the following form:

$$\begin{aligned} \max \ \ \varphi (x)=\sum \limits _{j=1}^{10}\left[ \lambda r_{il}x_{i}+(1-\lambda )\frac{r_{il}+r_{iu}}{2}x_{i}\right] \end{aligned}$$

      s.t.

$$\begin{aligned} \left\{ \begin{array}{l} \sum _{i=1}^{10}x_{i}=1, \\ 0\le x_{i}\le \min \{p_{i}, U_{i}\}, i=1,2,\ldots , n. \end{array}\right. \end{aligned}$$

where $U_{i}=\min \{1,\hat{x}_{i}\}$ and $\hat{x}_{i}=f^{-1}(y)$.

Suppose the returns of stocks are interval-typed random variable, $\tilde{\xi }_{i}=\lceil \xi _{il}, \xi _{iu}\rceil$, and $\xi _{il}\sim N(r_{il},\sigma _{il}^{2})$, $\xi _{iu}\sim N(r_{iu},\sigma _{iu}^{2}), i\in \{1,2,\ldots , 10\}$.

To compute conveniently, $r_{il}$ and $\sigma _{il}$ are considered as the same as the mean and standard deviation of the $i\hbox {th}$ stock, and $r_{il}=r_{iu},\sigma _{il}=\sigma _{iu},i\in \{1,2,\ldots , 10\}$. Therefore, utilizing these data and setting the probabilistic level y as 0.7, we obtain the optimal portfolio strategies of four models shown in Table 17.

Table 17 Optimal solutions of four models

Table 17 shows that all the optimal strategies of the four models select higher sample mean securities than the others. Moreover, the optimal portfolio strategy of our model is the same as Hasuike and Ishii model’s result, and the major ratios in our optimal portfolio strategy are basically consistent with Hasuike et al. model’s result. In our model, the algorithm allows for different degree of investors’ risk aversion. If investors give their risk tolerance probability, then the parameters which represent the risk level are provided and thus an optimal portfolio strategy of our model would be obtained easily by the linear programming method. However, the analytical solution approach for type-2 fuzzy return based on possibility measure and interval programming, proposed by Hasuike and Ishii model (2009), heavily depends on the choice of the parameters involving the membership function characterization of future returns, interval values for spreads and the target profit. It may spend more time gaining an optimal portfolio of this model if the parameters are unsuitably set.

4.3 Shanghai Stock Exchange data

In order to more clearly show the feasibility of our proposed model, we consider the third numerical example based on the Shanghai Stock Exchange data (Ma et al. 2009). Let us discuss 20 stocks shown in Table 18, whose data originate from the average of historical rates of returns, the historical mean return tendency of returns and experts valuation of investment corporations.

Table 18 Expected rates of returns

Our proposed model regards the return of every stock concerning to the data set as interval-typed random variable. Let the return of stock i be stated as $\tilde{\xi }=\lceil \xi _{il},\xi _{iu}\rceil$, where $\xi _{il}\sim N(r_{il},\sigma _{il}^{2})$, $\xi _{iu}\sim N(r_{iu},\sigma _{iu}^{2}), i\in \{1,2,\ldots ,20\}$. Based on Table 18, $r_{il}$ and $r_{iu}$ from Eqs. (3.1–3.3) could be considered as the left spread and the right spread of the expected rates of stock i’s return, respectively. The standard deviation of stock i could be computed by the following formula:

$$\begin{aligned} \sigma _{il}=\sigma _{iu}=\sqrt{\frac{(r_{il}-r_{ic})^{2}+(r_{iu}-r_{ic})^{2}}{2-1}}, \end{aligned}$$

(4.4)

where $r_{ic}$ is the center spread of the expected rates of the $i\hbox {th}$ stock return. For example, based on Table 18, $[r_{8l},r_{8u}]=[0.0048,0.0160]$, $\sigma _{8l}=\sigma _{8u}=0.0080$. It follows that the return distributions of all the stock are given in Table 19.

Table 19 Returns distribution of 20 assets

Table 20 Optimal solution based on our model

Table 21 Optimal solution based on FVaR

Table 22 Optimal solution based on FCVaR

Then, let $\lambda =0.5,\theta =1$ in our model (P1), $\varepsilon _{1}=\varepsilon _{2}=\frac{1}{20}\sum \nolimits _{i=1}^{20}\sigma _{il}=0.0262$. By utilizing our proposed algorithm, the optimal portfolio strategy could be attainable and is shown in Table 20.

Ma et al. (2009) study two portfolio optimization models based on FVaR and FCVaR measure, respectively, propose a chaos genetic algorithm and present the optimal portfolio strategy of 20 stocks selected from Shanghai Stock Exchange in Tables 21 and 22.

The model (Ma et al. 2009) for minimizing FVaR is given by

$$\begin{aligned}&\min \ \ FVaR_{\beta }(x) \\&\quad \hbox {s.t.} \left\{ \begin{array}{l} x^\mathrm{T}m\ge \sigma , \\ l\le x\le u,\\ \sum \nolimits _{i=1}^{n}x_{i}=1, \\ x\ge 0. \end{array}\right. \end{aligned}$$

And the model for minimizing FCVaR is given by

$$\begin{aligned}&\min \ \ FCVaR_{\beta }(x) \\&\quad \hbox {s.t.} \left\{ \begin{array}{l} x^\mathrm{T}m\ge \sigma , \\ l\le x\le u, \\ \sum \nolimits _{i=1}^{n}x_{i}=1, \\ x\ge 0. \end{array}\right. \end{aligned}$$

where $\beta \in (0,1)$ is prescribed confidence level, $l=(l_{1},\ldots ,l_{n})^\mathrm{T}$ and $u=(u_{1},\ldots ,u_{n})^\mathrm{T}$ are given lower and upper bounds on the portfolios, $\sigma$ is the minimum expected by the investor and let $\sigma =0.0020$, $m=(m_{1},\ldots , m_{n})^\mathrm{T}, m_{i}$ represents the expected return of the $i\hbox {th}$ risk stock, $i=1,\ldots , n$.

Table 23 Optimal solutions of four models $(p_{j}=0.2,y=0.90)$

Table 20 shows that the optimal portfolio solutions are robust when our model is applied to the portfolio selection problem in Shanghai Stock Exchange. From the results in Tables 20, 21 and 22, our model approves to be the larger total return than Ma et al. model (2009). Furthermore, when the confidence level equals to our given probabilistic constraint level, all the larger optimal selection ratios tendencies such as 15th and 19th stocks are consistent accordingly. Compared to the chaos genetic algorithm, our algorithm may be more convenient. Therefore, our proposed model could be appropriate and useful.

Table 24 Optimal solutions of four models $(p_{j}=0.3,y=0.80)$

Table 25 Total return of each optimal solution

Considering the models (4.1–4.3), an investor with a conservative and pessimistic mind would set the parameters’ value as follows: The corresponding upper rate value to each security, $p_{j}$, is assumed to be 0.2 and 0.3, respectively. $f_{1}=0.0292$, $f_{2}=0.0325$, $q_{1}=0.8$ and $q_{2}=0.9$. The target value of optimistic satisfaction index $\beta$ is given as $\beta =1$. The average of historical rates of return to the $j\hbox {th}$ security, $\overline{r}_{j}$, is given by the corresponding center of the $j\hbox {th}$ security’s expected return rate shown in Table 18. $[\underline{f},\bar{f}]=[0.0292, 0.0325]$. The minimum expected return parameter $\rho$ is set as $\rho =0.03$; parameters of trapezoidal fuzzy number $(a_{j},b_{j},\alpha _{j},\beta _{j})$ are determined by the following form: Both $a_{j}$ and $b_{j}$ are equal to the center of the $j\hbox {th}$ security’s expected return rate in Table 18, $\alpha _{j}$ equals the center of the $j\hbox {th}$ security’s expected return rate minus the corresponding left spread of the $j\hbox {th}$ security’s expected return rate in Table 18 and $\beta _{j}$ equals the right spread of the $j\hbox {th}$ security’s expected return rate minus the corresponding center of the $j\hbox {th}$ security’s expected return rate in Table 18. In fact the above trapezoidal fuzzy numbers have become triangular fuzzy numbers. Interval numbers for $[\underline{\alpha }_{j},\bar{\alpha }_{j}]$ are given as the following form:

$$\begin{aligned}&[\underline{\alpha }_{j},\bar{\alpha }_{j}]=\left[ \min \left\{ \hbox {SD}_{j}^{2},b_{j}-a_{j}\right\} \Big /5, \right. \\&\quad \left. \max \left\{ \hbox {SD}_{j}^{2},b_{j}-a_{j}\right\} \Big /5\right] , \end{aligned}$$

where standard deviations (abbreviated as SD) are obtained from Eq. (4.4) and

$\hbox {SD}_{j}=\sigma _{jl}=\sigma _{ju}$, $j=1,\ldots ,20$.

Table 23 shows that the optimal portfolio of four models prefer to choose higher center values of the historical return rates of securities such as the 11th, 15th and 19th securities than the others. Moreover, for a very conservative investor with upper value of the corresponding budgeting $p_{j}$ to each asset given by 0.2 or associated with the degree of a probabilistic risk aversion given by 0.90, the total return of our model shown in Table 25 is the highest among the four models even if the Hasuike and Ishii model, Vercher et al. model and Hasuike et al. model select more diversification portfolio in Table 23 because of the requirement of parameter $p_{j}$.

For a comparative conservative investor with parameter values $p_{j}=0.3$ or $y=0.80$, Table 24 shows that the optimal strategy of our model is similar to those of both Hasuike and Ishii model and Hasuike et al. model, whose total returns are approximately equal to that of our model in Table 25. However, the total returns of Vercher et al. model are lower than those of the other three models since Vercher et al. model mainly considers minimizing the expected downside risk of the investment.

5 Conclusion

A new model for portfolio selection associated with interval numbers and interval-typed random variables is established in this paper, where the probabilistic risk measure is flexible for investors with different risk tolerance. The algorithm for the model has been provided. An analytical solution is given when the average returns of the assets satisfy the order relations between intervals. So inclusion of additional assets is easily implemented by utilizing our model. Then, comparing the proposed model with other previous models through illustrated examples, we have found that it could be available and feasible for our model to apply to more flexibly cases and our algorithm could be simpler and easier to operate. Furthermore, compared with different time periods of the historical mean return tendency originated from the first data set, the optimal solutions present a strong stability. So the model in this paper is robust and effective in the application of portfolio selection.