Root system growth biomimicry for global optimization models and emergent behaviors

Abstract

Terrestrial plants have evolved remarkable adaptability that enables them to sense environmental stimuli and use this information as a basis for governing their growth orientation and root system development. In this paper, we explain the foraging behaviors of plant root and develop simulation models based on the principles of adaptation processes that view root growing as optimization. This provides us with new methods for global optimization. Accordingly a novel bioinspired optimizer, namely the root system growth algorithm (RSGA), is proposed, which adopts the root foraging, memory and communication and auxin-regulated mechanism of the root system. Then RSGA is benchmarked against several state-of-the-art reference algorithms on a suit of CEC2014 functions. Experimental results show that RSGA can obtain satisfactory performances on several benchmarks in terms of accuracy, robustness and convergence speed. Moreover, a comprehensive simulation is conducted to investigate the explicit adaptability of root system in RSGA. That is, in order to be able to climb noisy gradients in nutrients in soil, the foraging behaviors of root system are social and cooperative that is analogous to animal foraging behaviors.

1 Introduction

The success of a species in evolution mainly depends on its foraging strategy, namely the ability to effectively search for resources, such as food and water, in a given environment. Accordingly, natural selection optimizes the foraging strategies, since species that have poor foraging performance do not survive. As a result, when we observed within the natural world, different species develop a variety of foraging strategies depending on their physiological characteristics, the environment and the resources available to them. In each of these foraging processes, the foraging individual or group make optimal decisions so as to search for and obtain nutrients in a way that maximizes the ratio E/T (where E is the energy obtained and T is the time spent foraging) or maximizes the long-term average rate of energy intake (Pyke 1984; Catania 2012).

Logically, such optimal foraging principles have led scientists in the field of optimization theory to exploit the analogy between searching a given problem space for an optimal solution and the natural search process of foraging for food (El-Abd 2012). In recent years a considerable amount of natural foraging strategies has inspired natural computing paradigms in optimization area, prominent examples being ant colony system (ACS) (Socha and Dorigo 2008; Twomey et al. 2010), particle swarm optimization (PSO) (Shi and Eberhart 1998; Kennedy and Mendes 2002) and artificial bee colony algorithm (ABC) (Akay and Karaboga 2012). Accordingly, these state-of-the-art bioinspired paradigms have been widely investigated and developed (Valdez et al. 2011; David et al. 2013; Alexandru-Ciprian et al. 2013; Savio et al. 2014). For instances, a novel hybrid approach to PSO, namely FPSO + FGA (Valdez et al. 2011), utilizes fuzzy logic to integrate the advantages of both PSO and GA algorithms. A new GSA variant is developed by incorporating the fuzzy control systems with a reduced parametric sensitivity (David et al. 2013). A successful multi-objective variant based on NSGA-II and based on artificial neural networks (ANNs) is designed (Alexandru-Ciprian et al. 2013), which can effectively reduce computational load in the multi-objective optimization process. In these optimization models, communication strategies are also applied for cooperatively foraging in groups of animals.

Although foraging behavior is typically considered as a feature of animals, this definition does not exclude the responses of other organisms, including plants (McNickle et al. 2009). However, Because of their specific lifestyle, the areas where plants can access to forage for resources are confined to those which can be explored by growth (Kroon and Mommer 2006). This is the major difference between plant growth and animal foraging. Obviously, efficient searching of the soil for the nutrients and water is principal to the survival of each plant species in the earth. Therefore, plant roots have evolved the ability to both sense myriad factors in their local environment and use this information to drive changes in growth direction and root system development (Falik et al. 2005; Gilroy and Masson 2008).

Plant root growth is marked by a diversity of adaptation to continuous changes in environment, including increased lateral branching, root biomass, root length and uptake capacity. Particularly, all these developmental events require correct auxin transport and signaling (Karban 2008). Plants also adjust root demography and the length per unit mass of roots in response to heterogeneity (McNickle et al. 2009). Many studies have implied that plants are optima foragers, but there is little experimental evidence built on this assumption and only a handful of studies that explicitly develop optimality models for plant foraging (Kembel and Cahill 2005; Kembel et al. 2008).

The objective of this paper is to present a new optimization algorithm based on principles from plant root growth and foraging behaviors, which will be called the root system growth algorithm (RSGA). We utilize the optimal foraging theory perspective in formulating our RSGA model for global numerical optimization. The proposed algorithm is presented by modeling of the root foraging, memory and communication and auxin-regulated mechanisms of the root system. In the proposed algorithm emulating the distributed optimization process represented by the activity of plant root growth, several efficient ways to search for space optimization problems are proposed. The local search and global search using root branching and elongation (tropism) both controlled by auxin concentration during the foraging process are implemented. The random walk of lateral roots and root tip death mechanisms are also developed to keep the diversity and efficiency of the algorithm.

We examined the proposed algorithm in the shifted and rotated benchmarks. The empirical results obtained from implementing the proposed algorithm with the benchmark functions indicated that the speed of convergence and the quality of solutions are better than the CMA-ES, PSO, ABC and GA algorithms in terms of accuracy, robustness and convergence speed. Moreover, in order to illustrate the inherent adaptive mechanism in the proposed model of root system growing, the root tropic growth, auxin-controlled population dynamic and root system structure formulation are simulated based on RSGA model in this paper. The simulation results capture some important aspects of the dynamics of root growth that some plant biologists believe takes place in nature.

The rest of this paper is organized as follows. Section 2 presents the basic aspects and the characteristics of the root foraging behavior, including root growth responds to nutrition gradient, root memory and communication and auxin-regulated root system development. In Sect. 3, we introduce the proposed RSGA. Section 4 presents the empirical results on several benchmark functions and further analyze the evolution dynamics of the RSGA model. Then RSGA is applied to solve the TSP in Sect. 5. The last section includes conclusions and future work.

2 Root foraging behaviors

2.1 Root growth responds to nutrition gradient in soil

In keeping with their functions as the main nutrients foraging organ of plant, roots are highly sensitive to the availability of essential resources in the soil. Indeed, plant roots from different species are able to sense multiple environmental nutrition gradients and exert different responses by adjusting their growth direction to promote exploration of nutrition-rich areas. This directional growth response is called tropism (Rubio et al. 2002). Plant roots display different tropisms, namely gravitropism, phototropism, hydrotropism, thermotropism, electrotropism, magnetotropism and chemotropism, in response to the gradient of environmental gravity, light, water (moisture gradient), touch (mechanical stimuli), temperature, electric fields, magnetic fields and chemicals, respectively (Rubio et al. 2002; Eapen et al. 2005; Leitner et al. 2010). Among these important tropisms and movements, gravitropism and hydrotropism are regarded as the major influences in the directional growth of roots.

In order to maximize the resource acquisition from soil, the root system of plants has evolved a self-adaptive growing ability to control primary root growth and lateral root branching dynamically. That is, the primary roots from different species usually show the same orthogravitropism (i.e., growing down to exploration), while the lateral roots always take on the diagravitropism or plagiotropism (i.e., growing sideways to exploitation) (Dupuy et al. 2010).

2.2 Root memory and communication

Compared with animal foraging, plant behaviors have been considered simpler due to its specific lifestyle (Banks et al. 2009; Bradbury and Vehrencamp 1998). However, recent studies of microorganisms have revealed that past experience also greatly influences plant growth by means of conditioning (Karban 2008; Karban et al. 2000, 2006). Although they lack central nervous systems, plants still display memory and communication behaviors via specific growth approaches. For example, plants alter their behaviors depending on their memory, namely previous experiences or the experiences of their parents. In nature, the growth of a clover branch depends upon its current neighbors and also upon the neighbors that it encountered over the past year (Banks et al. 2009). Plants communicate with other plants, herbivores and mutualists (Heil et al. 2001; Heil 2004; Hodge 2009). Plant competitors in the soil with uniform nutrient distribution exhibit obvious reduction in root system breadth and spatial segregation, while plant competitors in the soil with heterogeneous nutrient distribution reduce their root growth modestly, indicating that plants integrate information about both neighbor and resource distribution in determining their root foraging behaviors.

2.3 Auxin-regulated root system development

The different stages of root development are mainly controlled and regulated by correct auxin transport and signaling (Leyser 2006). In particular, auxin plays a major role in lateral root initiation and development. For example, auxin local accumulation in Arabidopsis root pericycle cells adjacent to xylem vessels triggers lateral root initiation by re-specifying these cells into lateral root founder cells (Dubrovsky et al. 2008). Furthermore, it also influences the growth and organization of lateral root primordia and emergence from the parent root (Laskowski et al. 2006). Additionally, overexpression of the DFL1/GH3-6 or the IAMT1 genes, which encode enzymes modulating free IAA levels, results in a reduction in lateral root formation (Qin et al. 2005).

Fig. 1

The plant root foraging behavior

Root branching is a significant growth behavior, which flexibly adjusts the overall surface of the root system.

Accordingly, plants have evolved efficient auxin-based regulation mechanism. Auxin transport into the regions where lateral root initiates also seems crucial for the regulation of root branching, including when and where to start lateral root formation, and during which the development of primordia can be arrested for a certain time (Hodge et al. 2009).

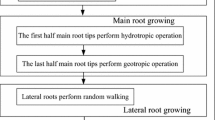
Then we model the foraging behaviors of a plant root system (Fig. 1) by making the following assumptions:

• 1. Root tips move throughout the soil through the main root growth and branching, lateral root random walk and root tip death. For each root tip, the branching and death are governed by its auxin concentration state.

• 2. The growth of a main root tip is a sequence of straight-line trajectories joined by instantaneous turns.

• 3. When a main root grows, its choice of a new direction is governed by two major tropisms, namely hydrotropism and gravitropism.

• 4. When a main root branches lateral root tips, the branching number is governed by the current root system scale and the angle between lateral and main root tips is governed by a probability distribution.

• 5. When there is a lateral root random walk, the angle between two successive trajectories and root elongation length are both governed by different probability distributions.

• 6. All root tips with less auxin values will die and will be simply eliminated from the root group.

These assumptions yield an optimization model that can be described by the algorithm presented in Sect. 3.

3 Root system growth for optimization (RSGO)

Based on the principles of root foraging behaviors described in Sect. 2, a novel optimization model and its algorithm, namely the root system growth model for optimization (RSGO) and root system growth algorithm (RSGA), are developed in this section in detail.

3.1 Auxin concentration

Assume that the primary objective is to search the minimum of f(x), $x\in {R}^{D}$. f(x) can be viewed as the nutrient distribution in soil. That is, $f(x)>0$, $f(x)=0$, $f(x)<0$ represent the presence of nutrients, a neutral medium and the presence of noxious substances, respectively.

In RSGO, plant root system is made up of a collection of root tips, which is defined as:

$$\begin{aligned} \mathrm{PRS}=\left\{ {r_i^t \big |i=1,2,\ldots , S^{t};t=1,2,\ldots , T} \right\} \end{aligned}$$

(1)

where

$$\begin{aligned} r_i^t=\left\langle {x_i^t, f_i^t, nt_i^t, an_i^t, \phi _i^t } \right\rangle \end{aligned}$$

(2)

is a single root tip; $\hbox {S}^{\mathrm{t}}$ is the root tips’ number at time t; T is the final time of the root system growing process; $r_i^t$ has its own position $x_i^t$, fitness $f_i^t$, nutrient $nt_i^t$ and the auxin $an_i^t$ which depends on $f_i^t$ and $nt_i^t$ that control this root tip to elongate, branch or die at time t. If it is foraging, the root tip moves with an orientation $\phi _i^t$ as an angle formed by the root axis.

At the initial stage $t=0$, a population of $S^{0}$ root tips are initialized randomly in the D-dimensional space. The position and heading angle of the $i\hbox {th}$ root tip are represented as $x_i=(x_{i1}, x_{i2}, \ldots x_{iD} )$ and $\phi _i=(\phi _{i1}, \phi _{i2}, \ldots \phi _{i(D-1)} )$, respectively, where $x_{id} \in [l_d, \,u_d ],{\begin{array}{l} {d\in [1,\, D]}\end{array} }$, $l_{d}$, $u_{d}$ are the lower and upper bounds for the $d\hbox {th}$ dimension, respectively. In each growth step t, the root tip i will grow to absorb nutrient and its nutrient $nt_i^t$ can be updated by:

$$\begin{aligned} nt_i^{t+1}=\left\{ {{\begin{array}{ll} {nt_i^t +1}&{} \quad {\mathrm{if}\, f_i^{t+1} <f_i^t }\\ {nt_i^t -1}&{} \quad \mathrm{else}\end{array} }} \right. \end{aligned}$$

(3)

In initialization phase, nutrients of all root tips are zero. During the development of root system, if the position of the new root tip is better than the last one, this root tip will absorb nutrient from the soil and the nutrient is added by one. Otherwise, the root tip’s nutrient is reduced by one.

Then the auxin concentration $an_i^t$, combining the health and energy information of the $i\hbox {th}$ root tip, is calculated by the following equations:

$$\begin{aligned}&\mathrm{health}_i^{t}=\frac{f_i^t -f_\mathrm{worst}^t }{f_\mathrm{best}^t -f_\mathrm{worst}^t } \end{aligned}$$

(4)

$$\begin{aligned}&\mathrm{energy}_i ^{t}=\frac{nt_i^t -nt_\mathrm{worst}^t }{nt_\mathrm{best}^t -nt_\mathrm{worst}^t } \end{aligned}$$

(5)

$$\begin{aligned}&\alpha t_i^t=\omega \frac{\mathrm{health}_i ^{t}}{\sum \nolimits _{j=1}^{S^{t}} {\mathrm{health}_j^{t}} }\nonumber \\&\qquad \quad +\;(1-\omega )\frac{\mathrm{energy}_i ^{t}}{\sum \nolimits _{j=1}^{S^{t}} {\mathrm{energy}_j^{t}} }, \omega \subset [0,1] \end{aligned}$$

(6)

where $f_\mathrm{worst}^t {\big /} f_\mathrm{best}^t$ and $nt_\mathrm{worst}^t {\big /} nt_\mathrm{best}^t$ are the current worst/best fitness and nutrient of the whole root system at time t, and $\omega$ is a uniform random quantity varying from 0 to 1.

In each cycle of roots growth process, all root taps are sorted by auxin concentration values defined above. That is, the strong root tips prefer to be chosen as main roots for branching. The number of main roots is calculated as:

$$\begin{aligned} S_m^t=S^{t}\times Sr \end{aligned}$$

(7)

where $S_m^t$ is the number of selected main root, $S^{t}$ is the size of root population, and Sr is the selection probability. The rest $S_l^{t}=\hbox {S}^{\mathrm{t}}-S_m^t$ root tips are selected as lateral roots. In our research, the Sr can be empirically pre-set to 0.5.

3.2 Root branching

Then a threshold Tbranch is used to determine whether it performs branching via comparing with the auxin concentration value of each main root:

$$\begin{aligned} \left\{ {{\begin{array}{ll} {\mathrm{branching}}&{}\quad {\mathrm{if}\,\alpha t_i^t >\mathrm{Tbranch}}\\ {\mathrm{nobranching}}&{}\quad \mathrm{other}\;\mathrm{else}\\ \end{array} }} \right. \end{aligned}$$

(8)

Note that the Tbranch can be empirically set to 5 in our research. If $r_i^t$ is selected as main root and its auxin concentration is enough to conduct branching, the branching number $w_{i}$ of $r_i^t$ is determined by:

$$\begin{aligned} S_i^t=\left\lceil {R_1 \alpha t_i^{t}(S_{\max } -S_{\min } )+S_{\min } } \right\rceil \end{aligned}$$

(9)

where $S_{\max }$ and $S_{\min }$ are defined as the maximum and minimum of the new growing tips, respectively, and $R_{1}$ is a random distribution coefficient. Based on growth direction of $r_i^t$ as reference angle, the searching space of its all branches is divided into $S_{\max }$ subzones; the angle of new growing tips (i.e., the new root branches of $r_i^t$) is randomly falling within one of these subzones. Then these new branching tips will grow as the following equations:

The fitness f is the sum of the result of applying the following function to consecutive groups of three components each:

$$\begin{aligned} \phi _{j}^{t+1}= & {} \phi _{i}^{t}+\lambda _{j}\phi _{{\max }}/S_{{\max }} \end{aligned}$$

(10)

$$\begin{aligned} x_j^{t+1}= & {} x_i^t +R_2 l_{\max } H\left( \phi _j^{t+1}\right) \end{aligned}$$

(11)

where $j\subseteq \left[ S_{\min }, S_i^t\right]$ is the root branch index of root tip $r_i^t, \lambda _{j} \subseteq [1, S_{\max }]$, is the selecting subzone number of the root branch $x_j^{t+1}, \phi _{\max }$, is the maximum growing turning angle, which is limited to $\pi$, $R_{2}$ is random value between 0 and 1, $l_{\max }$ is the maximum of root elongation length, and $H\left( \phi _j^{t+1} \right) =\left( h_{j1}^{t+1}, h_{j2}^{t+1}, \ldots , h_{jD}^{t+1} \right) \in R^{D}$ is a polar to Cartesian coordinates transform function, which can be calculated as:

$$\begin{aligned} \begin{aligned} h_{j1}^{t+1}&=\prod _{p=1}^{D-1} {\cos \left( \phi _{jp}^{t+1} \right) }\\ h_{jk}^{t+1}&=\sin \left( \phi _{j(k-1)}^{t+1} \right) \prod _{p=j}^{D-1} {\cos \left( \phi _{jp}^{t+1} \right) }\\ h_{jD}^{t+1}&=\sin \left( \phi _{j(D-1)}^{t+1} \right) \end{aligned} \end{aligned}$$

(12)

3.3 Tropisms

As described in Sect. 2, the spatial development of root system is significantly influenced by various tropisms. In RSGO, two major tropisms, namely hydrotropism and gravitropism, are considered and modeled. Firstly, the effect of gravitropism depends on the communication mechanism in root system. That is, a half of main roots will grow toward the best position with most moisture among the root system, given by:

$$\begin{aligned} x_i^{t+1}=x_i^t +R_3 \left( x_\mathrm{best}^t -x_i^t\right) \end{aligned}$$

(13)

where $i\subseteq [1, S_{m}^{t}/2]$, $R_{{ 3}}$ is random value in the range (0, 1), and $x_\mathrm{best}^t$ is the best position in the root tip group.

Considering the hydrotropism gravitropism depends on the root memory, the rest of main roots will grow along their original directions as:

$$\begin{aligned} x_i^{t+1}=x_i^t +R_4 l_{\max } H\left( \phi _i^t \right) \quad { if}\,x_i^t >x_i^{t-1} \end{aligned}$$

(14)

where $i\subseteq [S_{m}^{t}/2, S_{m}^{t}], l_{\max }$, is the maximum of root elongation length, $R_{{ 4}}$ is a normally distributed random number with mean 0 and standard deviation 1; $H\left( \phi _i^t \right)$ is a D-dimensional growth direction of the main root i; $\phi _i^{t}=\left( \phi _{i1}^{t,}\phi _{i2} ^{t}, \ldots , \phi _{i(D-1)}^{t}\right) \in R^{D-1}$ is a D-1-dimensional growth angle, given by:

$$\begin{aligned} r_i^{t+1}=r_i^{t}+R_5 *\omega _{\max _{,}} 0<\omega _{\max } <\pi \end{aligned}$$

(15)

where $R_5 \in R^{D-1}$ is a uniformly distributed random sequence in the range (0, 1); $\omega _{\max }$ is the maximum of growing angle, which is limited to $\pi$.

Fig. 2

The flowchart of RSGA

Table 1 Pseudo-code of RSGA

3.4 Random walk of lateral roots

During each foraging bout, all the lateral root tips will perform random walk, which are thought to be the most efficient foraging strategy for randomly distributed nutrition (Banks et al. 2009). At the $t\mathrm{th}$ iteration, each lateral root tip generates a random head angle and a random elongation length, given by:

$$\begin{aligned} \phi _i^{t+1}= & {} \phi _i^t +R_5 \phi _{\max } \end{aligned}$$

(16)

$$\begin{aligned} x_i^{t+1}= & {} x_i^t +R_6 \phi _{\max } H\left( \phi _i^{t+1} \right) \end{aligned}$$

(17)

where $i\subseteq [0, S_{l}^{t}]$, $R_{{ 5}}$ and $R_{{ 6}}$ are random values in the range $(0, 1), \phi _{\max }$ is the maximum growing turning angle, and $l_{\max }$ is the maximum of root elongation length.

3.5 Root tip death

Lower auxin concentration represents that a root tip did not get as many nutrients during its lifetime of foraging and hence is not as active and thus unlikely to continue to grow. Then in each cycle of roots growth process, all root tips with auxin values less than zero die and will be simply eliminated from the root group.

3.6 RSGA

Accordingly, based on above definitions, the RSGA instantiated from RSGO can be given, and the flowchart and pseudo-code of the RSGA are presented in Fig. 2 and Table 1, respectively. The corresponding variables of RSGA are summarized in Table 2.

Table 2 Parameters of the RSGA

4 Test and simulation

4.1 Test functions

4.1.1 Test benchmarks

Instead of the easy benchmarks, a set of 15 shifted and rotated benchmarks from CEC 2014 test beds $(f_{{ 1}} \sim f_{{ 15}})$ on real parameter optimization are employed (Ma et al. 2015; Liang et al. 2013; Karaboga and Basturk 2007). The dimensions, initialization ranges, global optimum of each function are listed in Table 3.

Table 3 Parameters of test functions (x* is the optimal solution; f(x*) is the best values of function; $O_{i}$ is the shifted global optimum defined in “shift_data_x.txt,” which is randomly distributed in $[-100,100]^{\mathrm{D}}$)

Table 4 The parameter settings for RSGA

4.1.2 Traveling salesman problem (TSP)

TSP can be abstracted as a task to find the shortest closed tour that visits each city exactly once (Noon 1988). Concretely, a traveling salesman is required to travel through n cities for sale promotion and arrive at the destination city that is same to the beginning point, and the distance between any two notes (represented by city i and city j) is $d_{ij}(i, j=1, 2{\ldots } n)$. Let $G=(N, V)$, where N donates a set of n cities or nodes, V donates a set of arcs, and $V=d_{ij}$ donates the distance or cost matrix D ( which can be either symmetric or asymmetric) associated with each arc $(i, j)\in V$. The initial motivation of TSP is to search for a shortest closed tour visiting each of the $n={\vert }N{\vert }$ nodes of G exactly once. In particular, in the symmetric TSP case, the distance $d_{ij}$ between any city i and city j is independent of the direction of traversing the arcs, that is, $d_{ij}=d_{ji}$ for every pair of cities.

Objective functions:

$$\begin{aligned} Z=\min \sum _i \sum _j {d_{ij} x_{ij}} \end{aligned}$$

(18)

S.T.

$$\begin{aligned} x_{ij}= & {} \left\{ {\begin{array}{ll} 1,&{} \quad {\mathrm{if}\;\mathrm{the}\;\mathrm{arc} (i,j) \mathrm{is}\;\mathrm{in}\;\mathrm{the}\;\mathrm{tour}},\\ 0,&{} \quad \mathrm{otherwise},\\ \end{array}} \right. \end{aligned}$$

(19)

$$\begin{aligned} \sum _{i=1}^n&{x_{ij}=1,\quad j=1,2, \ldots , n}, \end{aligned}$$

(20)

$$\begin{aligned} \sum _{j=1}^n&{x_{ij}=1,\quad i=1,2, \ldots , n}, \end{aligned}$$

(21)

where Eq. (18) gives the total cost to be minimized, and Eqs. (19–21) are constraints’ condition. Constraint Eq. (20) ensures that each position is occupied by only one city, while constraint Eq. (21) guarantees that each city is assigned to one exact position.

4.2 Parameter settings

In this experiment, four successful algorithms are employed for comparison with RSGA, namely PSO (Shi and Eberhart 1998; Kennedy 2007), ABC (Karaboga and Basturk 2007), CMA-ES (Kämpf and Robinson 2009) and GA (Sumathi et al. 2008). The number of function evaluations (FEs) is used as a measure criterion. All algorithms are terminated after 100,000 FEs. The parameter settings for the proposed RSGA are summarized in Table 4. The parameter configurations of other tested algorithms are all based on the suggestions in the corresponding references. Details are given as follows:

• PSO Settings: This traditional PSO is the standard one (i.e., the global version with inertia weight). The parameters are given as following (Shi and Eberhart 1998): c1 = c2 = 2.0, $\omega$ starts at 0.9 and ends at 0.4.

• ABC Settings: The canonical ABC follows the same parameter settings given in Karaboga and Basturk (2007): SN = 50, Limit = 200.

• CMA-ES Settings: For CMA-ES, we take $\upsigma _{F} = 0.2$, $\lambda =10$, $\mu =5$, which is the standard set for these three parameters. The rest parameters setting follows the default values recommended in Kämpf and Robinson (2009).

• GA Settings: The parameters setting of the standard GA can be given as follows (Sumathi et al. 2008): stochastic uniform sampling technique is the chosen selection method, single-point crossover is used and its rate is 0.95, and mutation rate is 0.1.

Figure 3 shows the scheme procedure of all involved algorithms to generate solutions for selected test problems. Each bioinspired algorithm including the proposed RSGA is implemented, respectively, and repeatedly evolving on each test function for 30 runs (all algorithms are terminated after 100,000 function evaluations). Then the comparative results among the five algorithms are shown in the next subsection.

Fig. 3

The scheme procedure for all algorithms tested on test functions

4.3 Experimental results

4.3.1 Computation results on benchmarks

In this section, we compare the performance of RSGA, CMA-ES, PSO, GA and ABC on the test suite with D = 30 and 100, respectively. Tables 5 and 6 present the average and standard deviation values in 30 runs of the above five algorithms for all benchmark functions with D = 30 and 100, respectively. Here all algorithms are terminated after 100,000 function evaluations in each run and the best results among the five algorithms are shown in bold.

From Table 5, it can be observed that RSGA obtains best solutions on $f_{3}$, $f_{8}$, $f_{9}$, $f_{ 11}$, $f_{12}$ and $f_{14}$, six of all fifteen benchmarks. PSO also achieves satisfactory results, performing best on $f_{4}$, $f_{5}$, $f_{13}$ and $f_{15}$, while CMA-ES obtains best performances on 6 functions, $f_{1}$, $f_{2}$, $f_{4}$, $f_{6}$ and $f_{ 10}$. For majority of test functions, RSGA and CMA-ES exhibit almost the same performance. Compared to ABC and GA, RSGA obtains significantly better results on all test functions except for $f_{5}$ and $f_{7}$.

Table 5 Performances of all algorithms on 30-dimensional test functions

It should be noted that although some algorithms generated good results on relatively low-dimensional $(\hbox {D }\le 30)$ benchmark problems, they do not perform satisfactorily for some large-scale problems (Wang and Ni 2008). Therefore, in order to assess the high-dimensional optimization performance of RSGA, the test benchmarks are extended to 100 dimensions and used in our experimental studies as high-dimensional benchmark functions. The results (D = 100) are presented in Table 6.

Table 6 Performances of all algorithms on 100-dimensional test functions

When the dimension increases to 100, RSGA maintains powerful performance, while others deteriorate obviously. PSO and CMA-ES also obtain satisfactory results on some functions. For example, PSO can perform best $f_{4, }f_{10}, f_{12}$ and $f_{14}$.However, RSGA outperforms the other algorithms on most of test benchmarks, all functions except for $f_{4},\, f_{5},\, f_{10},\, f_{12}$ and $f_{14}$. In particular, for shifted and rotated functions $f_{6}$, $f_{7}$ and $f_{15}$, only RSGA performs well on all of them, while other algorithms fall into local minima.

From the distinct difference between D = 20 and 100 results, we can clearly see that most evolutionary and swarm intelligence algorithms only work well on low-dimensional problems, while as dimensionality increases, the proposed foraging-based algorithm, RSGA, shows its persistence and generates better performances. This achieved improvement of RSGA is due to the dynamical exploration and exploitation balance ability of the introduced main and lateral root foraging strategies.

In order to measure the efficiency of algorithm on high-dimensional problems, Fig. 4 gives the average convergence results of 100D benchmarks with 30 runs. Owing to its dynamically control to root tip’s branching and death by auxin concentration, it can be observed that RSGA is able to evolve in a very efficient manner. In particular, for high-dimensional problems, convergence rates of RSGA are strikingly higher than those of other algorithms. RSGA also demonstrates reasonable robustness by its consistent performances in all 30 runs. That is, across all of the randomly initialized runs on each benchmark function, RSGA is always given out similar evolution speed and converged to the same point or a small region, whereas for ABC, PSO and GA, they sometimes had diverse behaviors that resulted from the random initialization.

4.3.2 Computation results on TSP

In this section, simulation experiments are conducted in TSP with an instance of eil51 from TSPLIB (the coordinate locations of nodes in this problem are given in Fig. 5). Meanwhile, comparison of performance between RSGA and GA algorithm in solving TSP is carried out (Turkington et al. 1991). The parameters of GA follow those of Sect. 4.2. The maximum iterations can be set to 4000. Each experiment the simulation runs 30 times, and the experimental results in terms of average length, best length, worst length, consuming time and the convergence counts obtained by RSGA and GA are given in Table 7. The optimal solution obtained by RSGA is (31-28-3-36-35-20-29-21-50-9-49-38-11-5-15-45-33-39-10-30-34-16-2-22-1-32-27-51-46-12-47-18-4-17-37-44-42-19-40-41-13-25-14-24-43-7-23-6-48-8-26), and the length of the shortest tour is 441.62. The panoramas of the shortest tour by RSGA and GA are given in Figs. 6, and 7, respectively. Besides, the convergence performance comparison between RSGA and GA is also shown in Fig. 8.

Table 7 demonstrates that our proposed RSGA is effective in solving the 51-cities TSP problem. In particular, RSGA exhibits significant superiority to the compared algorithm in terms of accuracies of best solution, average solution and worst solution. As can be seen from Table 2 and Fig. 8, the computation efficiency (i.e., consuming time) and convergence performance are better than GA. In other words, RSGA searches out optimal solution quickly in a relatively smaller consuming cost, with performance better than GA. However, we must also realize the shortest path obtained by our proposed algorithm (432.11) is still slightly worse than the optimal solution of eil51 (426), and there is great potential to improve the applications of RSGA.

Fig. 4

The median convergence results on each test functions. a–o correspond to 100-dimensional $f_{1}-f_{15}$, respectively

In addition, our proposed RSGA is compared with some existing results in the literature. The compared algorithms involve GA and ACO (Administrator 2015) on Berlin52, EiI76 and A280. GA and ACO are both efficient in handling these instances of the TSP where the search space is complex and no prior mathematical analysis is given. Table 8 gives the experimental results. The three algorithms show satisfactory performance over the TSP instances. The GA and ACO perform excellently on the small-size and medium-size instances. The RSGA obtains better results in large-size instances regarding error rate, and time computation, with the help of local search technique based on root growth behaviors, and it ensures finding better solutions than other two algorithms.

4.4 The simulation of root growth behaviors

In this section, the root growth behaviors and social foraging of RSGA are simulated, which shows a connection between social foraging strategies developed over millennia within the natural world and distributed nongradient optimization algorithms design for global search over noise space. Specifically, simulations at three different scales are carried out and compared to observations on real plant species. At the individual level, only one tip is initialized as main root and grows virtually in order to examine its tropism that response to environmental constraints. Then the population-level simulation is performed that focuses on the dynamic of the auxin regulation underlying root tip branching and death. Finally, a number of emerging characteristics concerning root architecture formation can be observed through the simulation on the developmental processes of the root system in RSGA model.

4.4.1 Root tropic growth: tropism

Plant roots have evolved the most important property that their foraging is social in order to be able to climb nutrient gradients in soil. The directional growth of plant roots relative to the direction of environmental stimuli is a tropism. Among the important tropisms, gravitropism is considered to exert a major influence in the directional growth of roots. That is, main roots usually grow down (i.e., orthogravitropism), and lateral roots always grow sideways (i.e., diagravitropism). The other important root tropism is hydrotropism, which is the ability to sense environmental moisture gradient for governing root growth orientation. Both gravitropism and hydrotropism have been relatively well studied.

Fig. 5

The coordinate locations of nodes in eil51

Table 7 Comparison results of RSGA and GA

Fig. 6

The optimal solution obtained by RSGA for eil51

Fig. 7

The optimal solution obtained by GA for eil51

Fig. 8

The convergence comparison between RSGA and GA on eil51

Table 8 Overview of simulation results

Fig. 9

Simulation on 2-dimensional Sphere considering: a gravitropism; b hydrotropism; c hydrotropism and gravitropism

Fig. 10

Simulation on 2-dimensional Griewank considering:: a gravitropism; b hydrotropism; c hydrotropism and gravitropism

Different from previous root growth models, we focus on social and optimal foraging ability of root system and use them as the basis for implementing gravitropism and hydrotropism. As described in Sect. 3.2, an easy way to implement gravitropism is to calculate all root tips’ fitness and pick out the best one that leads to a dominant movement of the root tip group toward the best position with most moisture, while the hydrotropism is implemented as that each root tip in RSGA is able to find and climb the environmental nutrient gradient.

We simulated the directional root growth behaviors, namely the hydrotropism and gravitropism of RSGA model, on 2D Sphere and Griewank’s landscapes, respectively (as shown in Figs. 9, 10). In both cases, the simulations were carried out on three independent scenarios, namely the hydrotropic response without gravitational force, the gravitational force without hydrotropic response and both tropic responses exist. In each simulation, only one tip is initialized at ($-3, -3$) as main root (represented as the red lines in the figures), which is the unique one that can branch lateral roots (represented as the green lines in the figures) in its whole life cycle. The growth trajectories, which only consider hydrotropic response in RSGA model, in 2D Sphere and Griewank’s landscapes are shown in Figs. 9a and 10a, respectively. From Figs. 9a, 10a, we can observe that underlying hydrotropic rule in RSGA, the root tips climb the moisture gradients through increasing the number of branches and elongation of roots. It can be obviously observed that the hydrotropic rule in RSGA is a typical local search strategy that is well documented by empirical studies in both plants and animals: when there are multiple types of a resource with different costs and benefits, organisms are expected to select among these resources in a way that maximizes benefits and minimizes costs.

Fig. 11

The spatial and temporal branching process based on RSGA on Rosenbrock’s environment

Fig. 12

The population size evolution process on Rosenbrock’s environment

Fig. 13

Auxin concentration distribution on Sphere

From the growth trajectories in Figs. 9b and 10b, we can observe that the root tips move throughout both the unimodal and multimodal landscapes (defined by Sphere and Griewank, respectively) through the gravitational force in RSGA model. That is, the gravitational force designed in RSGA is the global search strategy that makes each tip a social forager to maximize the performance of the root system as a whole, rather than their own individual performance.

Figures 9c and 10c illustrate the root growth trajectories under the influence of both tropisms. As we can see, in this simulation, gravitropism interferes with hydrotropism, which provides an understanding of how roots sense multiple environmental cues and exhibit different tropic responses. That is, the hydrotropic rule in RSGA encourages exploitation ability, while the gravitational force designed in RSGA improves exploration ability.

This shared and divergent mechanism that mediating the two tropisms is important because it permits the root system to refine its foraging behavior adaptively. At the beginning of the simulation, the root tips start exploring the search space. In that manner, the main root does not waste much time before finding the promising region that contains the global optimum, because the gravitational force designed in RSGA improves exploration ability. On the other hand, by the hydrotropic rule in RSGA, the main root slows down near the optimum and increases the number of branches in order to pursue the more and more precise solutions.

Fig. 14

Auxin concentration distribution on Rosenbrock

Fig. 15

Root system architecture formulation by interacting with the environment defined by: a 2-dimensional Rosenbrock; b 2-dimensional Rastrigin; c 3-dimensional Rosenbrock; d 3-dimensional Rastrigin

4.4.2 Auxin-controlled population dynamic

This section focuses on the dynamic of the auxin regulation underlying root tip branching and death in RSGA model. In this experiment, the population size of RSGA is adjusted dynamically during the optimization, and this phenomenon can be monitored through our simulation experiment as shown in Fig. 11. Figure 11 shows the spatial and temporal branching process based on RSGA on Rosenbrock’s environment. The corresponding population size evolution process of the root tips along with the generations is shown in Fig. 12. The population size variation of root tips as shown in Figs. 11 and 12 can be divided into three phases, namely branch, decay and death, which are consistent with the life cycle of all types of plant roots in nature.

The underlying auxin regulation mechanism is simulated in Figs. 13, 14, which illustrates the dynamic of auxin concentration in each root tips along the root growth process. From these cases, we can observe that if the root tips enter the areas near the local or global optima, these root tips generate higher auxin level to multiplying the number of roots; while entering in the plateaus areas, these root tips cease to branch and could decay when their auxin level reaches zero. That is, from a plant resource allocation view, if root systems exhibit plasticity in producing new roots in favorable soil zones, they should also be able to shed these roots when resource uptake is no longer efficient.

4.4.3 Root system structure formulation

Modeling of root architecture is helpful in linking knowledge gained at the level of the individual root to that of the entire root system. Conceptually, root system architecture can be modeled in different ways, depending on the goals, actual knowledge and parameterization of the different processes available. Here, the root system is represented by the developmental processes of the root system. This results in a three-dimensional set of connected branching points, representing the roots and their tips, each characterized by properties such as age, root type, angle, length and foraging ability that defined in RSGA model.

We simulated the root–soil interactions and the dynamics of rhizosphere in RSGA model, on 2-dimensional/3-dimensional Rosenbrock’s and Rastrigin’s landscapes, respectively (as shown in Fig. 15). From the simulation results, we can observe that root system architecture is flexible and can alter as a result of prevailing soil conditions. This flexibility arises due to the modular structure of roots which enables root deployment in zones or patches rich in moisture or nutrients. Although the relationship between root foraging precision and scale remains elusive, it can be clearly observed that the root systems allocated more of their new root growth into the nutrient-rich zones, while less of their new root growth into the nutrient-poor zones in all simulation cases.

5 Conclusions

In this paper, we adopt the optimal foraging theory perspective in formulating our simulation model for root foraging behaviors. The optimal root foraging behaviors and root growth controlling by auxin are combined in our model. Next, the proposed model is instantiated as an optimization algorithm called RSGA that emulates the distributed optimization process represented by the activity of plant root growth.

The proposed optimization method can be classified as natural computing paradigms for global optimization. While the previously proposed GA, PSO and ABC can solve similar optimization problems, their structure and operation are quite different. To illustrate their difference, we validate the models on several widely used benchmark functions and briefly discuss the principle of a number of emerging characteristics, namely the root tropic growth, auxin-controlled population dynamic and root system structure formulation, which are valid for both model and plant root system. Finally, the RSGA is applied to solve TSP.

Based on this comprehensive analysis of RSGA performance, there may be benefits over existing optimization methods, and we believe RSGA has a great potential of being applied to a variety of complex real-world problems. Indeed, there is ongoing research that is studying this now.