1 Introduction

Uncertainty in the data degrades the process of analyzing the data leading to uncertain conclusions (Gantayat et al. 2014). Classical rough set theory (RST) proposed by Pawlak (1982) made a great success in processing and analyzing complete information systems characterized by uncertainty (Qin et al. 2015). Reduct (Jensen et al. 2014; Jiang and Yu 2015) is the most important issue of RST which eliminates unnecessary attributes and creates a minimal sufficient subset of attributes for decision table. Approximation accuracy measure (Dai and Xu 2012) that measures the imprecision of approximation space is employed as heuristics measure to guide the reduct process. Consequently, for a minimal feasible subset of features, the approximation accuracy should be maximal. RST uses the lower and upper approximations that are defined using the indiscernibility relation to define the approximation space. The indiscernibility relation is considered equivalent relation because it is reflexive, symmetric, and transitive. However, the indiscernibility relation is a rigid relation (Huang et al. 2014) because it is based on the assumption that all object’s values for every attribute are known. This assumption contrasts with several real-valued information systems situations where the information may be incomplete (DU and ZI 2014). This limits the applicability of RST in real-world applications where some of the attribute values are unknown. For RST to deal with incomplete information systems (IIS), two strategies are proposed. The first one is an indirect method that transforms the IIS into a complete one according to some rules such as probability statistical methods; this is called data preparation (Wang 2001; Grzymala-Busse and Hu 2005). However, this may cause loss in the original information leading to uncertain conclusions. The second one is a direct method that extends the basic concepts of RST under IIS by relaxing the requirement of indiscernibility relation of reflexivity, symmetry and transitivity (Kryszkiewicz 1998, 1999; Stefanowski and Tsoukiàs 1999, 2001; Skowron and Stepaniuk 1996; Wang 2002; Wang et al. 2008; Leung and Li 2003; Cheng et al. 2007; Yin and XiuyiJia 2006; Yang 2009; Yang and Yang 2012; Nguyen et al. 2013; Grzymala-Busse and Wang 1997; Liu and Shao 2014; Huang and Li 2014).

The unknown values were categorized by Grzymała-Busse (2004) as follows:

  1. 1.

    The unknown values are “lost ?”, this unknown value means that it is an absent value and cannot be compared with any other values in the domain of the corresponding attribute.

  2. 2.

    The unknown values are “don’t care *,” this unknown value means that it is a missing value and can be compared with any other values in the domain of the corresponding attribute.

In recent years, many researchers extended RST model by replacing the indiscernibility relation by another non-equivalent relation to process IIS directly. For example, Kryszkiewicz (1998, (1999) proposed the tolerance relation that is reflexive and symmetric but not necessarily transitive to deal with “*” values. In this relation, objects that have no values in common are considered indistinguishable. For example, with two objects \(X = \{1,*,3,*\}\) and \(Y = \{*,2,*,4\}\) then according to the tolerance relation, object X is considered indistinguishable from object Y and will be gathered in the same tolerance class. Obviously, this is unreasonable case which limits the applicability of the tolerance relation. Stefanowski and Tsoukiàs (1999, (2001) investigated the similarity relation of Skowron and Stepaniuk (1996) to be reflexive and transitive but not necessarily symmetric to deal with “?” values. This relation separates two objects that are very similar to each other but with little loss in the information. At the same time, objects in the same similarity class are not necessarily similar to each other and may belong to different target classes. This excludes some objects from the lower approximation of the target set. For example, with four objects \(X = \{a,?,c,d,?,d_1\}\), \(Y = \{?,s,c,d,?,d_1\}\), \(Z = \{a,b,c,d,e,d_2\}\) and \(W = \{a,s,c,d,f,d_1\}\) then according to the non-symmetric similarity relation \(R^{-1}(X) = \{X,Z,W\}\). Obviously, object Y is not included in the same similarity class of object X in spite of the fact two attribute values are perceived as common, at the same time objects X, Z and W belong to the same similarity class in spite of the fact that objects Z and W are not similar, this lead to \(R^{-1}(X) \not \subseteq d_1\) which prevents objects X and Z from being included in the lower approximation of \(d_1\). This decreases the cardinality of the lower approximation leading to unpromising results with respect to approximation accuracy. Wang et al. (2008) recognized that the tolerance relation requirement is too weak as it regards two objects with no common values as indistinguishable, also, the requirement of the NS-RSM is too strict as it separates two objects that are very similar to each other but with little loss in the information. This makes the process too extreme. Consequently, Wang proposed the limited tolerance relation that tries to relax the requirements of both tolerance relation and NS-RSM. Limited tolerance relation is reflexive and symmetric but not necessarily transitive. However, limited tolerance relation has not differentiated the two types of unknown attribute values. Leung and Li (2003) proposed the maximal consistent block relation that is reflexive and symmetric but not necessarily transitive to deal with “*” values. Maximal consistent block relation describes the maximal collection of indistinguishable objects in the tolerance classes (Cheng et al. 2007). This relation achieves better approximation accuracy than that provided by tolerance relation, but it inherits the limitation of the tolerance relation where objects that have no values in common are considered indistinguishable. Yin and XiuyiJia (2006) proposed the constrained dis-symmetrical similarity relation that is reflexive and transitive but not necessarily symmetric to deal with “?” values. This relation extends the non-symmetrical similarity relation based on the limited tolerance relation. In this relation, two objects are considered to be similar due to high loss in the information of one of the two objects. For example, with two objects \(A = \{3,2,1,0,d_1\}\) and \(B = \{?,2,?,?,d_2\}\) then according to dis-symmetrical similarity relation, object A is considered similar to object B which prevents object A from being included in the lower approximation of \(d_1\) in spite of the fact it contains no “?” values. Yang (2009), Yang and Yang (2012) proposed the difference relation that is not necessarily reflexive, symmetric and transitive to deal with “?” values. The requirement of the difference relation is too strict as it separates two objects that are very dissimilar but with a slight bit of similarity. For example, with two objects \(S = \{?,?,3,4,5\}\) and \(D = \{?,6,7,8,5\}\) then according to the difference relation, object S is not considered dissimilar to object D because value 5 is common in both objects. This may not allow the difference relation to approximate the target set whenever all tuples are similar to each other, even so, with partial similarity. Nguyen et al. (2013) proposed a parametric relation that extends the non-symmetric similarity relation by computing the probability of matching for each attribute. This relation is reflexive and symmetric but not necessarily transitive. This relation needs in advance threshold (\(\alpha \)) to control the tolerance degree.

Słowiński et al. (2014) reported that up till now, NS-RSM is the only RST extension that correctly characterizes the target set as it computes the lower/upper approximations using two different relations. This is because of the fact that NS-RSM does not partition the data, instead it uses the similarity classes, but objects in the same similarity class are not necessarily similar to each other which leads to unpromising results with respect to approximation accuracy. Consequently, the aim of this paper is to enhance the capability of NS-RSM to provide promising results with respect to approximation accuracy which can be further used to provide promising results with respect to reduct. In this paper, we propose the maximal limited similarity-based rough set model (MLS-RSM) that is a modified version of NS-RSM able to provide promising approximation accuracy under IIS with “?” values. MLS-RSM finds the maximal limited consistent blocks of similar objects for each similarity class in NS-RSM. Maximal limited consistent blocks describes the maximal collection of indistinguishable objects that are limited tolerance to each other in the similarity classes. This ensures that objects in the same block are similar to each other leading to accurate computation to be done for the lower approximation. Furthermore, approximation accuracy comparisons have been conducted among NS-RSM and MLS-RSM. The results demonstrate that MLS-RSM model outperforms NS-RSM model.

The rest of this paper is organized as follows. Section 2 introduces some preliminaries on basic concepts and rough set theory. Some related RST extensions under IIS are reviewed in Sect. 3. In Sect. 4, we propose the maximal limited similarity-based rough set model (MLS-RSM) model. In Sect. 5, approximation accuracy comparisons among NS-RSM and MLS-RSM have been conducted. Section 6 concludes the paper.

2 Preliminaries

2.1 Basic concepts

For the convenience of discussion, some basic notions and relevant concepts are introduced at first.

Definition 1

An information system is a quadruple IS = \((U,\mathrm{AT},V,f)\), where, U is a non-empty finite set of objects; AT is a non-empty finite set of features; V is the union of attribute domains, \(V = \bigcup _{a \in A} V_\mathrm{a}\), where, \(V_\mathrm{a}\) is the value set of attribute a; \(f: U \times \mathrm{AT} \rightarrow V\) is the information function that assigns a particular value of the object attributes.

If there exist \(x \in U\) such that \(f_a(x)\) equals to an unknown value where \(a \in \mathrm{AT}\), then the information system is said to be incomplete information system (IIS).

2.2 Rough set theory

The classical RST uses the indiscernibility relation that is given by \(E(A) = \{(x,y)\in U^2: \forall a \in A, f_a(x) = f_a(y)\}\), where \(A \subseteq \) AT. The equivalence classes are given by \([x]_E = \{y \in U: xEy\}\). The lower/upper approximations of a set X under RST are given respectively by, \(\underline{\mathrm{Apr}}(X) = \bigcup \{[x]_E: [x]_E \subseteq X\}\), \(\overline{\mathrm{Apr}}(X) = \bigcup \{[x]_E: [x]_E \bigcap X \ne \phi \}\). The pair (\(\underline{\mathrm{Apr}}(X),\overline{\mathrm{Apr}}(X)\)) is called the approximation space. The positive, negative and the boundary regions are defined respectively by, \(\mathrm{POS}(X) = \underline{\mathrm{Apr}}(X)\), \(\mathrm{NEG}(X) = U - \overline{\mathrm{Apr}}(X)\), \(\mathrm{BND}(X) = \overline{\mathrm{Apr}}(X) - \underline{\mathrm{Apr}}(X)\).

2.3 Approximation accuracy measure

Approximation and reduction are two key issues in RST. The approximation refers to approximately describe a subset of the universe with respect to a given set of features. While the reduction is the process of finding a minimal subset of features that preserve the discriminatory power as the whole features using the approximation concept. Consequently, the finer the approximation, the finer the reduction. The approximation accuracy measure \(\tau \) (Dai and Xu 2012) is uncertainty measure that measures the imprecision of rough approximation. This measure reflects RST ability to find the minimal subset of features that preserve the discriminatory power as the whole features. The form of approximation accuracy is given by

$$\begin{aligned} \tau = \frac{|\underline{\mathrm{Apr}}(X)|}{|\overline{\mathrm{Apr}}(X)|} \end{aligned}$$
(1)

where \(|\cdot |\) denotes cardinality. Clearly, the greater the approximation accuracy, the greater the characterizing power of the available features. Consequently, for a minimal subset of features, the approximation accuracy should be maximal.

3 Some RST extensions under IIS

In this section, we review some related RST extensions under IIS with their issues.

3.1 Non-symmetric similarity relatio-based rough set model (NS-RSM)

Stefanowski and Tsoukiàs (1999, (2001) redefined the similarity relation of Skowron and Stepaniuk (1996) to deal with the “?” values as Definition 2.

Definition 2

Given IIS in which \(A \subseteq \) AT, the non-symmetric similarity relation is given by

$$\begin{aligned} \forall _{x,y} S(x,y) \Longleftrightarrow \forall _{a\in A} f_a(x) \ne ? , f_a(x) = f_a(y) \end{aligned}$$
(2)

For each object, two similarity classes are defined as follows:

$$\begin{aligned}&R(x) =\{y \in U : S(y,x)\} \end{aligned}$$
(3)
$$\begin{aligned}&R^{-1}(x) = \{y \in U :S(x,y)\} \end{aligned}$$
(4)

where, R(x) represents the set of objects similar to x and \(R^{-1}(x)\) represents the set of objects to which x is similar.

The lower/upper approximations of set X under NS-RSM are given respectively as follows:

$$\begin{aligned}&\underline{R}^{-1}_A(X) = \{x \in U : R^{-1}(x) \subseteq X\} \end{aligned}$$
(5)
$$\begin{aligned}&\overline{R}_A(X) = \bigcup \{R(x) : x \in X\} \end{aligned}$$
(6)

Słowiński et al. (2014) stated that the discrimination task between objects using indiscernibility relation is difficult due to the imprecision of data describing the objects. This situation is considered perfectly using non-symmetric similarity relation.

In the following we will illustrate NS-RSM with a small IIS shown in Table 1.

Table 1 Small illustrative example
Full size table

Example 1

Consider the IIS presented in Table 1, where \(U =\{x_1,x_2,..., x_{13}\}\), \(A = \{a_1,a_2,a_3,a_4\}\) with 25 % lost (“?”) values and d is the decision attribute that determines a partition on the universe such that \(U/d = \{d_1,d_2\} = \{\{x\in U:f_d(x) = 1\},\{x\in U:f_d(x) = 2\}\}\).

Thus,

$$\begin{aligned} \begin{array}{ll} R^{-1}(x_1) = \{x_1,x_9,x_{12}\}&{} R(x_1) = \{x_1,x_{11}\}\\ R^{-1}(x_2) = \{x_2,x_3,x_6,x_8\}&{} R(x_2) = \{x_2\}\\ R^{-1}(x_3) = \{x_3\}&{} R(x_3) = \{x_2,x_{3}\}\\ R^{-1}(x_4) = \{x_4,x_5,x_{12}\}&{} R(x_4) = \{x_4,x_5\}\\ R^{-1}(x_5) = \{x_4,x_5,x_{12}\}&{} R(x_5) = \{x_4,x_5\}\\ R^{-1}(x_6) = \{x_6\}&{} R(x_6) = \{x_2,x_6\}\\ R^{-1}(x_7) = \{x_7,x_9,x_{13}\}&{}R(x_7) = \{x_7\}\\ R^{-1}(x_8) = \{x_8\}&{} R(x_8) = \{x_2,x_8\}\\ R^{-1}(x_9) = \{x_9\}&{} R(x_9) = \{x_1,x_7,x_{9},x_{11}\}\\ R^{-1}(x_{10}) = \{x_{10}\}&{}R(x_{10}) = \{x_{10}\} \\ R^{-1}(x_{11}) = \{x_1,x_9,x_{11},x_{12},x_{13}\}&{} R(x_{11}) = \{x_{11}\}\\ R^{-1}(x_{12}) = \{x_{12}\}&{}R(x_{12}) = \{x_1,x_4,x_5,x_{11},x_{12}\} \\ R^{-1}(x_{13}) = \{x_{13}\}&{}R(x_{13}) = \{x_7,x_{11},x_{13}\} \\ \end{array} \end{aligned}$$

Obviously, NS-RSM separates objects that are very similar to each other but with little loss in the information, for example, in \(R^{-1}(x_3)\) object \(x_2\) is not considered similar to object \(x_3\) in spite of the fact three of their attribute values are common. At the same time, objects are included in the same similarity class in spite of the fact they are not similar to each other. For example, in \(R^{-1}(x_1) = \{x_1,x_9,x_{12}\}\) object \(x_{9}\) and object \(x_{12}\) are not similar, this leads to \(R^{-1}(x_1)\not \subseteq d_1\) which prevents object \(x_1\) from being included in the lower approximation of \(d_1\). In \(R^{-1}(x_2) = \{x_2,x_3,x_6,x_8\}\) objects \(x_{3}\), \(x_{6}\) and \(x_8\) are not similar, this leads to \(R^{-1}(x_2)\not \subseteq d_1\) which prevents object \(x_2\) from being included in the lower approximation of \(d_1\). This shrinks the lower approximation leading to unpromising results with respect to approximation accuracy.

The lower/upper approximations are as follows:

$$\begin{aligned} \underline{R}^{-1}_A(d_{1})&= \{x_6,x_{10},x_{12}\}\\ \overline{R}_A(d_{1})&= \{x_1,x_2,x_4,x_5,x_6,x_7,x_{10},x_{11},x_{12}\}\\ \underline{R}^{-1}_A(d_{2})&= \{x_3,x_8,x_{9},x_{13}\}\\ \overline{R}_A(d_{2})&= \{x_1,x_2,x_3,x_4,x_5,x_7,x_8,x_9,x_{11},x_{13}\} \end{aligned}$$

Consequently, \(\tau (d_1) = \frac{3}{9} = \frac{1}{3}\) and \(\tau (d_2) = \frac{4}{10} = \frac{2}{5}\).

3.2 Limited tolerance relation

Wang et al. (2008) recognized that the requirement of NS-RSM is too strict as it separates two objects that are very similar to each other but with little loss in the information. This makes the process too extreme. Consequently, Wang proposed the limited tolerance relation that tries to relax the requirements of NS-RSM as Definition 3.

Definition 3

Given IIS in which \(A \subseteq \) AT, the limited tolerance relation is given by

$$\begin{aligned} \begin{aligned} \forall _{x,y\in U\times U}( \mathrm{LT}_A(x,y) \Longleftrightarrow&\forall _{a \in A}(f_a(x) = f_a(y) = {\text {unknown}}) \\&\vee ((P_A(x)\bigcap P_A(y) \ne \phi )\\&\wedge \forall _{a \in A}(f_a(x) \ne {\text {unknown}} \\&\wedge f_a(y) \ne {\text {unknown}}) \\&\rightarrow (f_a(x) = f_a(y)))) \end{aligned} \end{aligned}$$
(7)

where \(P_A(x) = \{a \in A : f_a(x)\,is\, known\ value\}\) and the unknown values can be interpreted as * or ? values.

The limited tolerance classes of x is denoted by \(I_{A}(x)\) where

$$\begin{aligned} I_{A}(x) = \{y:y \in U \wedge \mathrm{LT}_A(x,y)\} \end{aligned}$$
(8)

The lower and upper approximations of set X under limited tolerance relation are given, respectively, as follows:

$$\begin{aligned} \underline{I}_A(X)= & {} \{x :x\in U \wedge I_{A}(x) \subseteq X\} \end{aligned}$$
(9)
$$\begin{aligned} \overline{I}_A(X)= & {} \{x:x \in U \wedge I_{A}(x) \bigcap X \ne \phi \} \end{aligned}$$
(10)

Continue with Example 1. we illustrate Definition 3.

Thus,

$$\begin{aligned} \begin{array}{ll} I_A(x_1) = \{x_1, x_4,x_5,x_7,x_9,\\ \qquad \qquad \qquad x_{11},x_{12}\} &{}I_A(x_8) = \{x_2,x_8\} \\ I_A(x_2) = \{x_2,x_3,x_6,x_8\}&{} I_A(x_9) = \{x_1,x_7,x_9,x_{11}\} \\ I_A(x_3) = \{x_2,x_3\} &{} I_A(x_{10}) = \{x_{10}\} \\ I_A(x_4) = \{x_1,x_4,x_5,x_{11},x_{12}\} &{} I_A(x_{11}) = \{x_1,x_4,x_5,x_7,x_9,\\ {} &{}\qquad \qquad \qquad x_{11}, x_{12},x_{13}\} \\ I_A(x_5) = \{x_1,x_4,x_5,x_{11},x_{12}\} &{} I_A(x_{12}) = \{x_1,x_4,x_5,x_{11},x_{12}\} \\ I_A(x_6) = \{x_2,x_6\} &{} I_A(x_{13}) = \{x_7,x_{11},x_{13}\} \\ I_A(x_7) = \{x_1,x_7,x_9,x_{11},x_{13}\} \\ \end{array} \end{aligned}$$

Obviously, limited tolerance relation relaxed the requirement of NS-RSM, for example in \(\mathrm{LT}_A(x_3) = \{x_2,x_3\}\), object \(x_2\) is considered indistinguishable from object \(x_3\) which is not the case in \(R^{-1}(x_3)\). However, limited tolerance relation failed to relax the requirement of gathering non-similar objects in the same limited tolerance class, for example, in \(I_A(x_2)\) = \(\{x_2,x_3,x_6,x_8\}\) objects \(x_3\), \(x_6\) and \(x_8\) are not similar to each other.

The lower/upper approximations are as follows:

$$\begin{aligned} \underline{I}_A(d_1)&= \{x_2,x_6,x_{10}\},\\ \overline{I}_A(d_1)&= U,\\ \underline{I}_A(d_2)&= \phi ,\\ \overline{I}_A(d_2)&= U - {x_{10}.} \end{aligned}$$

4 Maximal limited similarity-based rough set model (MLS-RSM)

As we discussed in Sect. 3.1, objects in the same similarity classes are not necessarily similar to each other and may belong to different target classes which increase uncertainty in the data. This excludes some objects from the lower approximation of the target set in spite of the fact they could be classified in the lower approximation leading to unpromising results with respect to approximation accuracy. In order to overcome this problem, we propose the maximal limited similarity-based rough set model (MLS-RSM) which finds the maximal limited consistent blocks of similar objects for each similarity class \((R(x),R^{-1}(x))\). Maximal limited consistent blocks describe the maximal collection of indistinguishable objects that are limited tolerance to each other in similarity classes. This reduces the uncertainty from the data allowing accurate computation to be done for the lower approximation leading to promising results with respect to approximation accuracy.

Similar to NS-RSM, for each object, two similarity classes are defined as Definitions 4 and 5, respectively.

Definition 4

Given IIS and R(x) be set of objects similar to x in which \(A\subseteq \) AT and \(X\subseteq R(x)\), we say that X is limited consistent block of objects similar to x with respect to A if \((x,y) \in S(y,x)\) and \(\forall y,z \in X, (y,z) \in \mathrm{LT}_A(y,z)\). We say that X is maximal limited consistent block of objects similar to x if there does not exist \(Y\subseteq R(x)\) where \(X \subset Y\) and Y is limited consistent with respect to A. We denote the maximal limited consistent blocks of all R(x) as \(\zeta _{R_A}^{\mathrm{{LT}}}\) and the maximal limited consistent blocks of objects similar to x with respect to A as \(\zeta _{R_A(x)}^{\mathrm{{LT}}}\).

Definition 5

Given IIS and \(R^{-1}(x)\) be set of objects to which x is similar in which \(A\subseteq \) AT and \(X\subseteq R^{-1}(x)\), we say that X is limited consistent block of objects to which x is similar with respect to A if \((x,y) \in S(x,y)\) and \(\forall y,z \in X, (y,z) \in \mathrm{LT}_A(y,z)\). We say that X is maximal limited consistent block of objects to which x is similar if there does not exist \(Y\subseteq R^{-1}(x)\) where \(X \subset Y\) and Y is limited consistent with respect to A. We denote the maximal limited consistent blocks of all \(R^{-1}\) as \(\zeta _{R_A^{-1}}^{\mathrm{LT}}\) and the maximal limited consistent blocks of objects to which x is similar with respect to A as \(\zeta _{R_A^{-1}(x)}^{\mathrm{LT}}\).

These relations (\(\zeta _{R_A}^{\mathrm{LT}}\) and \(\zeta _{R_A^{-1}}^{\mathrm{LT}}\)) are reflexive but not necessarily transitive and symmetric.

The lower/upper approximations of set X under MLS-RSM are given respectively as follows:

$$\begin{aligned} \underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(X)= & {} \bigcup \left\{ Y \in \zeta _{R^{-1}}^{\mathrm{LT}}(A) : Y \subseteq X\right\} \end{aligned}$$
(11)
$$\begin{aligned} \overline{\zeta _{R_{A}}^{\mathrm{LT}}}(X)= & {} \bigcup \left\{ Z \in \zeta _{R(x)}^{\mathrm{LT}}(A): x \in X \right\} \end{aligned}$$
(12)

Similar to the classical RST, the positive, negative and the boundary regions under MLS-RSM are given, respectively, as follows:

$$\begin{aligned} \mathrm{POS}(X)&= \underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(X), \end{aligned}$$
(13)
$$\begin{aligned} \mathrm{NEG}(X)&= U - \overline{\zeta _{R_{A}}^{\mathrm{LT}}}(X),\end{aligned}$$
(14)
$$\begin{aligned} \mathrm{BND}(X)&= \overline{\zeta _{R_{A}}^{\mathrm{LT}}}(X) - \underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(X). \end{aligned}$$
(15)

4.1 Properties of MLS-RSM

Property 1

Any similarity class \(R^{-1}(x)\) of attributes subset A can be represented as the union of maximal limited consistent blocks included in it. In other words,

$$\begin{aligned} R^{-1}(x)= & {} \bigcup \left\{ Y\in \zeta _{R_A^{-1}}^{\mathrm{LT}}:Y\subseteq R^{-1}(x)\right\} \\= & {} \bigcup \left\{ Y\in \zeta _{R_A^{-1}(x)}^{\mathrm{LT}}\right\} . \end{aligned}$$

Proof

Suppose that \(R^{-1}(x_1) = \{x_1,x_2,x_3\}\), then one of the following is true with respect to MLS-RSM model.

  1. 1.

    \(\zeta _{R_A^{-1}(x)}^{\mathrm{LT}} = \{Y_1 = \{x_1,x_2,x_3\}\}\)

  2. 2.

    \(\zeta _{R_A^{-1}(x)}^{\mathrm{LT}} = \{Y_1 = \{x_1,x_2\},Y_2 = \{x_1,x_3\}\}\)

Obviously, for both cases it is clear that \(R^{-1}(x_1)\) is the union of the blocks \(Y_s\) found in \(\zeta _{R_A^{-1}(x)}^{\mathrm{LT}}\), consequently, we can say that the similarity class \(R^{-1}(x_1)\) is the union of the blocks Y found in \(\zeta _{R_A^{-1}(x)}^{\mathrm{LT}}\).

For instance, continue with example 1, we have \(\zeta _{R_A^{-1}(x_1)}^{\mathrm{LT}} = \{Y_1 = \{x_1,x_{9}\}, Y_2 = \{x_1,x_{12}\}\}\) and \(\bigcup \{Y_1,Y_2\} = \{x_1,x_{9},x_{12}\} = R^{-1}(x_1)\). \(\square \)

Property 2

Any similarity class R(x) of attributes subset A can be represented as the union of maximal limited consistent blocks included in it. In other words,

$$\begin{aligned} R(x) = \bigcup \left\{ Z\in \zeta _{R_A}^{\mathrm{LT}}:Z\subseteq R(x)\right\} = \bigcup \left\{ Z\in \zeta _{R_A(x)}^{\mathrm{LT}}\right\} . \end{aligned}$$

Proof

please refer to the proof of Property 1. \(\square \)

Property 3

Given IIS in which \(A,B\subseteq \) AT and \(X\subseteq U\), then

  1. 1.

    \(\underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(X)\subseteq X\subseteq \overline{\zeta _{R_{A}}^{\mathrm{LT}}}(X)\).

  2. 2.

    If \(A\subseteq B \implies \overline{\zeta _{R_{B}}^{\mathrm{LT}}}(X) \subseteq \overline{\zeta _{R_{A}}^{LT}}(X)\). But \(\underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(X)\subseteq \underline{\zeta _{R_B^{-1}}^{\mathrm{LT}}}(X)\) does not hold.

Theorem 1

Given IIS, the lower approximation of \(X \subseteq U\) obtained using MLS-RSM model is a refinement of the one obtained using NS-RSM.

Proof

We have to clarify that the lower approximation of NS-RSM obtained using Eq. (5) is subset of lower approximation of MLS-RSM obtained using Eq. (11).

Suppose that \(x \in \,\underline{R}^{-1}_A(X)\) obtained using Eq. (5), then \(R^{-1}(x) \subseteq X\) holds. By property 1, \(R^{-1}(x) = \bigcup \{Y\in \zeta _{R_A^{-1}}^{\mathrm{LT}}:Y\subseteq R^{-1}(x)\} = \bigcup \{Y\in \zeta _{R_A^{-1}(x)}^{\mathrm{LT}}\}\). Then there exist \(Y\in \zeta _{R_A^{-1}(x)}^{\mathrm{LT}}\) that contain x where \(Y\subseteq X\). Therefore, \(x\in \,\underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(X)\) obtained using Eq. (11). This means that \(\forall x\in \) \(\underline{R}^{-1}_A(X)\), \(x\in \) \(\underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(X)\). The inverse is not necessarily true. Consequently, the lower approximation of X obtained using MLS-RSM is at least equal to the lower approximation of X obtained using NS-RSM. \(\square \)

Theorem 2

Given IIS, the upper approximation of \(X \subseteq U\) obtained using MLS-RSM relation is equal to the one obtained using NS-RSM.

Table 2 Data sets description
Full size table
Table 3 Approximation space comparison
Full size table

Proof

The upper approximation of NS-RSM is given by \(\overline{R}_A(X) = \bigcup \{R(x) : x \in X\}\). From property 2, \(R(x) = \bigcup \{Z\in \zeta _{R_A}^{\mathrm{LT}}:Z\subseteq R(x)\} = \bigcup \{Z\in \zeta _{R_A(x)}^{\mathrm{LT}}\}\) for any \(x\in U\). So, \(\overline{R}_A(X) = \bigcup \{\bigcup \{Z\in \zeta _{R_A(x)}^{\mathrm{LT}}\}:x\in X\} = \bigcup \{Z\in \zeta _{R_A(x)}^{\mathrm{LT}}:x\in X\} =\) \(\overline{\zeta _{R_{A}}^{\mathrm{LT}}}(X) =\) upper approximation of MLS-RSM. \(\square \)

We know that, in RST, approximation accuracy for a given target set \(X \subseteq U\) is defined as the cardinality of the lower approximation of X divided by the cardinality of the upper approximation of X.

Theorem 1 means that a better approximation accuracy for a given target set \(X \subseteq U\) can be obtained using MLS-RSM than NS-RSM. The following example is an illustration

Continue with Example 1. we illustrate Definitions 4 and 5.

Thus,

$$\begin{aligned} \begin{array}{ll} \zeta _{R_A(x_1)}^{\mathrm{LT}} = \{Z_1 = \{x_1,x_{11}\}\} &{} \\ \zeta _{R_A^{-1}(x_1)}^{\mathrm{LT}} = \{Y_1 = \{x_1,x_{9}\}, \\ \quad Y_2 = \{x_1,x_{12}\}\} \\ \zeta _{R_A(x_2)}^{\mathrm{LT}} = \{Z_2 = \{x_2\}\} &{} \\ \zeta _{R_A^{-1}(x_2)}^{\mathrm{LT}} = \{Y_3 = \{x_2,x_3\},\\ \quad Y_4 = \{x_2,x_6\}, &{} Y_5 = \{x_2,x_8\}\} \\ \zeta _{R_A(x_3)}^{\mathrm{LT}} = \{Z_3 = \{x_2,x_3\}\} &{} \zeta _{R_A^{-1}(x_3)}^{\mathrm{LT}} = \{Y_6 = \{x_3\}\} \\ \zeta _{R_A(x_4)}^{\mathrm{LT}} = \{Z_4 = \{x_4,x_5\}\} &{} \zeta _{R_A^{-1}(x_4)}^{\mathrm{LT}} = \{Y_7 = \{x_4,x_5\,x_{12}\}\} \\ \zeta _{R_A(x_5)}^{\mathrm{LT}} = \{Z_4 = \{x_4,x_5\}\} &{} \zeta _{R_A^{-1}(x_5)}^{\mathrm{LT}} = \{Y_7 = \{x_4,x_5,x_{12}\}\} \\ \zeta _{R_A(x_6)}^{\mathrm{LT}} = \{Z_5 = \{x_2,x_6\}\} &{} \zeta _{R_A^{-1}(x_6)}^{\mathrm{LT}} = \{Y_8 = \{x_6\}\} \\ \zeta _{R_A(x_7)}^{\mathrm{LT}} = \{Z_6 = \{x_7\}\} &{} \zeta _{R_A^{-1}(x_7)}^{\mathrm{LT}} = \{Y_9 = \{x_7,x_{9}\},\\ &{}\quad Y_{10} = \{x_7,x_{13}\}\} \\ \zeta _{R_A(x_8)}^{\mathrm{LT}} = \{Z_7 = \{x_2,x_8\}\} &{} \zeta _{R_A^{-1}(x_8)}^{\mathrm{LT}} = \{Y_{11} =\{x_8\}\} \\ \zeta _{R_A(x_9)}^{\mathrm{LT}} = \{Z_8 = \{x_1,x_7,x_9,x_{11}\}\} &{} \zeta _{R_A^{-1}(x_9)}^{\mathrm{LT}} = \{Y_{12} = \{x_9\}\} \\ \zeta _{R_A(x_{10})}^{\mathrm{LT}} = \{Z_9 = \{x_{10}\}\} &{} \zeta _{R_A^{-1}(x_{10})}^{\mathrm{LT}} = \{Y_{13} = \{x_{10}\}\} \\ \zeta _{R_A(x_{11})}^{\mathrm{LT}} = \{Z_{10} = \{x_{11}\}\} &{} \\ \zeta _{R_A^{-1}(x_{11})}^{\mathrm{LT}} = \{Y_{14} = \{x_1,x_{9},x_{11}\}, &{} Y_{15} = \{x_1,x_{11},x_{12}\},\\ &{}\quad Y_{16} = \{x_{11},x_{13}\}\} \\ \zeta _{R_A(x_{12})}^{\mathrm{LT}} = \{Z_{11} = \{x_1,x_4,x_5,\\ \quad x_{11},x_{12}\}\} &{} \zeta _{R_A^{-1}(x_{12})}^{\mathrm{LT}} = \{Y_{17} = \{x_{12}\}\} \\ \zeta _{R_A(x_{13})}^{\mathrm{LT}} = \{Z_{12} = \{x_7,x_{11},x_{13}\}\} &{} \zeta _{R_A^{-1}(x_{13})}^{\mathrm{LT}} = \{Y_{18} = \{x_{13}\}\} \\ \end{array} \end{aligned}$$

Consequently, \(\zeta _{R_A}^{\mathrm{LT}} = \{Z_1 = \{x_1,x_{11}\},Z_2 = \{x_2\},Z_3 = \{x_2,x_3\},Z_4 = \{x_4,x_5\},Z_5 = \{x_2,x_6\},Z_6 = \{x_7\},Z_7 = \{x_2,x_8\},Z_8 = \{x_1,x_7,x_9,x_{11}\},Z_9 = \{x_{10}\},Z_{10} = \{x_{11}\},Z_{11} = \{x_1,x_4,x_5,x_{11},x_{12}\},Z_{12} = \{x_7,x_{11},x_{13}\}\}\) and \(\zeta _{R_A^{-1}}^{\mathrm{LT}}= \{Y_1 = \{x_1,x_{9}\}, Y_2 = \{x_1,x_{12}\},Y_3 = \{x_2,x_3\}, Y_4 = \{x_2,x_6\}, Y_5 = \{x_2,x_8\},Y_6 = \{x_3\},Y_7 = \{x_4,x_5,x_{12}\},Y_8 = \{x_6\}, Y_9 = \{x_7,x_{9}\},Y_{10} = \{x_7,x_{13}\},Y_{11} =\{x_8\},Y_{12} = \{x_9\},Y_{13} = \{x_{10}\},Y_{14} = \{x_1,x_{9},x_{11}\}, Y_{15} = \{x_1,x_{11},x_{12}\},Y_{16} = \{x_{11},x_{13}\}, Y_{17} = \{x_{12}\},Y_{18} = \{x_{13}\}\}\).

Noting \(\zeta _{R_A^{-1}(x_1)}^{\mathrm{LT}} = \{Y_1 = \{x_1,x_{9}\}, Y_2 = \{x_1,x_{12}\}\}\) object \(x_{9}\) and object \(x_{12}\) are not included in the same block as NS-RSM does. This leads to \(Y_2 \subseteq d_1\) which allows object \(x_1\) to be included in the lower approximation of \(d_1\). In \(\zeta _{R_A^{-1}(x_2)}^{\mathrm{LT}} = \{Y_3 = \{x_2,x_3\}, Y_4 = \{x_2,x_6\}, Y_5 = \{x_2,x_8\}\}\) objects \(x_{3}\), \(x_{6}\) and \(x_8\) are not in the same block. This leads to \(Y_4 \subseteq d_1\) which allows object \(x_2\) to be included in the lower approximation of \(d_1\).

In \(\zeta _{R_A^{-1}(x_{11})}^{\mathrm{LT}} = \{Y_{14} = \{x_1,x_{9},x_{11}\}, Y_{15} = \{x_1,x_{11},x_{12}\},Y_{16} = \{x_{11},x_{13}\}\}\) objects \(x_{1}\), \(x_{12}\) and \(x_{13}\) are not included in the same block. This leads to \(Y_{16} \subseteq d_2\) which allows object \(x_{11}\) to be included in the lower approximation of \(d_2\).

The lower/upper approximations are as follows:

$$\begin{aligned} \underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(d_{1})&= \{x_1,x_2,x_6,x_{10},x_{12}\} \\ \overline{\zeta _{R_{A}}^{\mathrm{LT}}}(d_{1})&= \{x_1,x_2,x_4,x_5,x_6,x_7,x_{10},x_{11},x_{12}\} \\ \underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(d_{2})&= \{x_3,x_8,x_9,x_{11},x_{13}\} \\ \overline{\zeta _{R_{A}}^{\mathrm{LT}}}(d_{2})&= \{x_1,x_2,x_3,x_4,x_5,x_7,x_8,x_9,x_{11},x_{13}\} \end{aligned}$$

Consequently, \(\tau (d_1) = \frac{5}{9}\) and \(\tau (d_2) = \frac{5}{10} = \frac{1}{2}\). The results are more informative than NS-RSM model. This is because MLS-RSM finds the maximal limited consistent blocks of indiscernible objects and now objects in the same block are similar to each other.

It is worth noting that \(\underline{R}^{-1}_A(d_{1}) \subseteq \underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(d_{1})\), \(\underline{R}^{-1}_A(d_{2}) \subseteq \underline{\zeta _{R_A^{-1}}^{\mathrm{LT}}}(d_{2})\), \(\overline{\zeta _{R_{A}}^{\mathrm{LT}}}(d_{1}) = \overline{R}_A(d_{1})\) and \(\overline{\zeta _{R_{A}}^{\mathrm{LT}}}(d_{2}) = \overline{R}_A(d_{2})\) which verifies the validity of MLS-RSM.

5 Experimental evaluation

5.1 Experimental setup

The proposed approach (MLS-RSM) and the related one (NS-RSM) are implemented using MATLAB R12a on PC with windows 8, Intel(R) Core(TM) i7 CPU 2.4 GHZ and 6GB memory, to verify the validity of MLS-RSM. Our experiments employ three publicly accessible data sets; mammographic (Team 2015), hepatitis and congress (UCI 2015). The datasets are outlined in Table 2. The objective of the experiment is to compare the approximation space located by MLS-RSM and NS-RSM.

5.2 Approximation space comparison

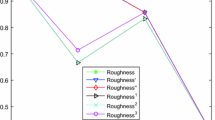
We obtain the numbers of objects in the lower and upper approximations and the approximation accuracy in terms of MLS-RSM and NS-RSM as Table 3.

By Table 3, it is easy to note that using MLS-RSM, the number of objects in the lower approximations of MLS-RSM model is equal or greater than those in NS-RSM lower approximations. The number of objects in the upper approximations of MLS-RSM model is equal to those in NS-RSM upper approximation. This shrinks the boundary region leading to promising approximation accuracy which verifies the validity of MLS-RSM model.

Consequently, we can say that MLS-RSM model can approximate the target set more accurately than NS-RSM in IIS with “?” values. This is a perfect indicator that MLS model can improve the feature subset selection technique in IIS with “?” values.

6 Conclusion

Uncertainty in the data degrades the process of analyzing the data. Non-symmetric similarity relation-based rough set model (NS-RSM) is viewed as a mathematical tool to deal with uncertainty in incomplete information systems with “?” values. Unfortunately, NS-RSM results in unpromising approximation space when addressing inconsistent data sets that have lots of boundary objects. This is because objects in the same similarity classes are not necessarily similar to each other and may belong to different target classes. To enhance NS-RSM capability, we introduce the maximal limited similarity relation-based rough set model (MLS-RSM) which describes the maximal collection of indistinguishable objects that are limited tolerance to each other in similarity classes. This allows accurate computation to be done for the approximation space.Theoretical analysis shows that MLS-RSM can approximate the target set more efficiently and more accurately than NS-RSM. The experimental results show that MLS-RSM can deal with the analysis of imprecise and uncertain information in IIS. In the future work, MLS-RSM can be used to improve the reduct issue.