Multi-objective multi-robot deployment in a dynamic environment

Abstract

Finding a distribution of a group of robots in an environment is known as Deployment problem, which is one of the challenges in multi-robot systems. In real applications, the environment may change over time and thus deployment must be repeated periodically in order to redistribute the robots. In this paper, we propose a multi-objective optimization method to deploy/redeploy robots in the environment by considering two objectives for the deployment. One objective represents a good estimation of final positions, where the robots will be located, while the second objective is finding the shortest path from the robots initial location to these positions. Thus, our problem is modeled as a multi-objective optimization problem, which is approached with a multi-objective optimization evolutionary algorithm. To deal with the deployment problem, a discrete setup of locational optimization framework and Voronoi partitioning technique are employed. Simulation results on real application testify the performance of our proposed method in comparison with other methods.

1 Introduction

A multi-robot system is a collection of robots, collaborating together to fulfill the global goal. Every robot is a physical agent equipped with processors and sensors to be able to perform independent operation and individual autonomous behaviors. Numerous applications of multi-robot systems can be found, such as environmental surveillance and monitoring (Chaimowicz et al. 2005), search and rescue (Bhattacharya et al. 2013b), risky material removal, and so on. In such applications, robots need to be distributed in the environment in order to perform the entire task. In this way, multi-robot deployment represents one of the challenges in locational-based robot distribution (Cortes et al. 2004). Among different topics, covering an area is an important objective in deployment problem. In this problem, the environment is partitioned into regions and each robot of the team should be responsible for covering the events happening inside its assigned region. To measure the performance of any specific solution, a deployment function represents the quality of the robots distribution over the field. Such a function might be defined based on the distance of robots to the points in the environment, which must be minimized. Therefore, the deployment problem can be translated to a minimization problem.

In this paper, we address the deployment problem in a dynamic environment, where the size or location of the region that should be covered by the robots might change, and thus the robots must be redistributed over time. This dynamic behavior is very common but unpredictable in our real life application, since the entities in the environment move, i.e., peoples or vehicles in a city. Therefore, in contrast to studies in the state of the art that applied gradient descent techniques, for instance Cortes et al. (2004), Pimenta et al. (2008), Bhattacharya et al. (2013c), etc., which are local search-based methods and may stuck in local minimum, in this paper we develop a global search platform to deploy and redeploy the robots time by time. Thus, two objectives are taken into account: (i) minimizing the deployment function; and (ii) minimizing the path from initial to final position in the redeployment process.

For better understanding and also testing our approach, two scenarios are presented in this paper: One considers an indoor non-convex environment with the presence of obstacles, and another one is a convex map in outdoor environment. In the second scenario, which is related to rescue services application, the entire task is conveying first aid to victims that must be distributed among the robots. In our algorithm, the Voronoi tessellation technique partitions the environment among the robots. Generally, the Voronoi diagram is one of the useful methods in partitioning environments, and thus in robotics it has received a great deal of attention, see Bhattacharya et al. (2013c), Yun and Rus (2013), Tzes and Stergiopoulos (2010), Stergiopoulos and Tzes (2011).

Similar to other works in the literature about the deployment problem, we also define a density function that shows the priority of regions in the map, computed based on the distribution of a crowd¹ in the environment. As the distribution of the crowd and correspondingly the density function change during time, robots will be redeployed through our algorithm periodically. In a different way, we develop an ellipse-based technique to define a multi-modal density function given by fitted ellipses over the crowd. Therefore, not only the locational distribution is considered but also the crowd number is taken into account.

In order to have a global search in the problem space, a well-known multi-objective optimization evolutionary algorithm (MOEA) is applied to minimize the two objectives. Unlike other heuristic methods in deployment, our approach provides a set of compromise solutions and thus the user has the opportunity to select one of them based on his/her desired criterion. The priority of objectives is considered during the evolutionary process by using a modified version of NSGA-II proposed in Friedrich et al. (2013); and also during the decision-making stage with the method ELECTRE I (Roy 1968) at the end.

It is worthwhile to remark that dynamic obstacles, robots localization and networking are not considered in the present paper; therefore, only a high level planning is addressed.

The paper is organized as follows. Next section reviews the literature about the robot deployment problem and multi-objective optimization methods. In Sect. 3, the formulations for the deployment problem and p-median are explained. The proposed methods in the deployment problem are discussed in Sect. 4. For better understanding two case studies are described in Sect. 5. Section 6 indicates the simulation results and comparisons, and finally Sect. 7 is dedicated to the conclusion and future works.

2 Related work

In this section, some studies on deployment problem and related subjects such as path planning and coverage are reviewed at first. Secondly, a short discussion about multi-objective optimization problems is presented.

One category of multi-robot deployment control schemes is based on artificial potential or force fields. Parker (2002) developed a low-level control, which is described in terms of attractive and repulsive force fields. The author tried to deploy a group of homogeneous robots into an uncluttered environment to observe multiple moving targets. very large scale robots (VLSR) with hundreds, even thousands of mobile robots, are considered by Reif and Wang (1999) in their study. They used social potential field method for computing the control law for deploying each individual robot given by artificial force imposed by other robots and other components of the system. In another work by Poduri and Sukhatme (2004), the authors presented a deployment algorithm for mobile sensor networks by using repulsive and attractive forces to control the interaction between vertices of the network. Moreover, Ji and Egerstedt (2007) used graph-based nonlinear feedback control laws in a group of mobile agents to make the graph stay connected for all times.

A second category is based on common coverage control approach through the definition of feedback control laws defined with respect to the centroids of Voronoi regions. Cortes et al. (2004) presented a distributed approach for optimally deploying a team of robots in a domain based on the Lloyd algorithm (Lloyd 1982). Each robot follows a control law, which is a gradient descent algorithm that minimizes the functional encoding the quality of the deployment. Different variations of their work have been proposed, including Pimenta et al. (2008), Bhattacharya et al. (2013a), Yun and Rus (2013) and Alitappeh and Pimenta (2016), in which robots in non-convex environment were taken into account. They used geodesic distance metric to address non-convex region instead of Euclidean distance. Other extensions were done in Bhattacharya et al. (2013b) and Nowzari and Cortés (2012), where the authors address general Riemannian manifolds with boundaries, and self-triggered coverage algorithms, respectively.

These studies were established relying on gradient descent methods to minimize the deployment function; therefore, they may get stuck in a local minimum. In contrast to these studies, in our work we define a new model of this problem, such that the solution is found by running a MOEA, thus providing some probability of escaping local minima. Furthermore, our proposed method considers the initial position of the robots in order to find the shortest path in redeployment. To the best of our knowledge, this issue has not been considered yet in the literature.

In our problem, the second objective (minimizing the distance from the initial to the final position) can be considered as a path planning problem. Thus, we are going to review and compare some of the articles in multi-objective path planning problem. Among such previous approaches, usually two objectives, namely safety and length, are of importance (Davoodi et al. 2013; Huang 2013; Wanga et al. 2015; Hidalgo-Paniagua et al. 2015; Jeddisaravi et al. 2016) etc. More specifically, Davoodi et al. (2013) defined the length and clearance of the path as two main objectives in a discrete space. They used genetic algorithm and NSGA-II to solve the optimization problem, and in a later work, they consider smoothness of the path and energy consumption, see Davoodi et al. (2015). Considering the same objectives (namely safety, length and smoothness), Hidalgo-Paniagua et al. (2015) proposed a multi-objective firefly algorithm (MO-FA) that works based on the flashing behavior of fireflies to solve the path planning problem. In another study, the NSGA-II algorithm has been applied to address the same objectives by Ahmed and Deb (2013). Similar objectives (shortest collision-free paths) were considered by Wanga et al. (2015), and a hybrid of genetic algorithm and particle swarm optimization (GA-PSO) algorithm is proposed to solve the welding robot path planning problem. Zhang et al. (2012) also presented a multi-objective path planning algorithm based on particle swarm optimization for robot navigation. They consider two common objectives to search for a path for a single robot: risk degree of the path (or safety) and the length of the path. A new multi-objective evolutionary algorithm (RankMOEA) is also developed by Ortiza et al. (2013), who consider the length and safety of the path as objectives. In Ioannidisa et al. (2011), the problem of finding a collision-free path is solved by a method based on Cellular Automaton technique.

In path planning problems, the final position is usually known, whereas in our problem the objective is to find undefined positions where the robots will be deployed. Additionally, in our paper we employ a multi-robot system to solve the deployment problem, which consists of dividing the region among the robots, and path planning for them simultaneously.

As we mentioned before, in our problem one of the challenges is how to balance the workload among robots or partition the environment into regions and assign a robot to each of the regions. Obviously, this challenge does not exist in the single robot path planning problem. Hence, we reviewed some of the related works regarding the p-median problem.

According to the environment, the state of the art in deployment problem is divided into continuous and discrete setups. Some of the mentioned works deal with continuous workspace for instance (Cortes et al. 2004; Pimenta et al. 2008). On the other hand, some applications in the real world have a discrete nature, and thus, the discrete version of the Lloyd algorithm (DLA) was provided to solve them by Holder et al. (2007). In this way, one of the useful preprocessing techniques is modeling the workspace as a form of graph (Alitappeh and Pimenta 2016), and then the problem becomes one of graph partitionings, which has been extensively studied (Fjallstrom 1998; Reese 2006). In the graph representation, the deployment problem can be interpreted as a p-median problem, in which a limited number of facilities will be assigned to customers. Solving this problem is useful in many public applications, such as determining bus stations, health centers and so on over a city or country. A large amount of algorithms can be found in the literature, e.g., see works proposed by Resende and Werneck (2004), Senne et al. (2005), Fleszar and Hindi (2008), Landa-Torres et al. (2012), Brimberg and Drezner (2013), Yaghini et al. (2013). Among these works, metaheuristic-based algorithms have been intensively investigated. For instance, Yaghini et al. (2013) proposed a cutting-plane neighborhood structure combined with tabu search, while Fleszar and Hindi (2008) used a variable neighborhood search heuristic method to solve the capacitated p-median problem (CPMP). Resende and Werneck (2004) achieved a better running time and solution quality, by applying a multi-start hybrid heuristic that combines elements of several traditional metaheuristics to find near-optimal solutions, and in a recent work, Landa-Torres et al. (2012) presented grouping heuristic-based approaches, which are called Grouping Genetic Algorithm (GGA) and Grouping Harmony Search (GHS). To overcome continuous p-median problem in Brimberg and Drezner (2013), the authors improved the local search and used simulated annealing and tabu search to find the solution. Senne et al. (2005) applied a branching rule and the tree search on a binary integer programming model of the uncapacited p-median problem.

For the purpose of application in robotics, Gabriely and Rimon (2001) presented a centralized coverage algorithm in a discrete environment, and applied Spanning Tree Covering (STC) on the corresponding grid cell in order to partition the graph and direct the robots to cover the environment. Senthilkumar and Bharadwaj (2012) built multiple spanning trees corresponding to multiple robots simultaneously using the depth first search (DFS) technique and named as the Simultaneous Multiple Spanning Trees Construction (S-MSTC) algorithm. In fact this work extends their previous method, such that in the extended S-MSTC (ES-MSTC), ant-type robots were used to cover the terrain leaving marks on the terrain by solving the challenge of finding k spanning trees for k robots simultaneously. Durham and Carli (2012) considered a discrete partitioning and coverage optimization algorithm for robots with short-range Gossip communication. Authors in Bhattacharya et al. (2013a); Alitappeh and Pimenta (2016); Yun and Rus (2013) represented a discrete non-convex environment by a graph. With the same platform Alitappeh and Pimenta (2016) added safety to robot motion in deployment problem. Yun and Rus (2013) proposed a distributed algorithm for coverage using Voronoi tessellation. They prove that the proposed controller guarantees convergence to the locally optimal configuration.

Similar to these cited papers, in the proposed technique a graph representation discretizes the environment into cells. We model the multi-objective problem as a mixed linear integer programming with two objectives: finding the best position in the environment to deploy the robots on them (similar to the p-median problem) and minimizing the length of robots paths from the initial to the end position. Later Dijkstra algorithm is applied on the given graph to define the Voronoi regions of each robot. In the implementation a multi-source Dijkstra reduces the computational complexity and memory usage, which is achievable by starting the wavefront from robots’ current position and ending when it collides with the neighbor regions.

Finally, multi-objective optimization algorithms are explained briefly. Nevertheless, a good survey of principles is available in Marler and Arora (2004). The main challenge in multi-objective optimization is finding an estimate of the Pareto set or finding the solution that maximizes satisfaction for the decision-maker. The Pareto-optimal set contains those solutions in which any improvement in one objective degrades the value of at least one other objective. Moreover, in Multi-objective Evolutionary Algorithm (MOEA) the challenge is assessing fitness to solutions that are vector valued in the multi-objective context. There are several methods to address this problem. One of standard approach is an extension of the Genetic Algorithm, which was proposed by Deb et al. (2002) and is called Non-dominated Sorting Genetic Algorithm (NSGA-II). There are other works in King and Rughooputh (2003); Zitzler et al. (2002), Knowles and Corne (1999), which are suggested to the reader to get more details. Along the variety of algorithms, we engaged a MOEA algorithm similar to NSGA-II because of its high capability in globally searching for the set of solutions. Among extensions of NSGA-II, we applied a version that incorporates weights of objectives during the evolution (Friedrich et al. 2013). Furthermore, the Elimination and Choice Translating Reality (ELECTRE I) is employed as decision-making method to find the best solution in the Pareto set (Roy 1968). This technique provides a partial ordering of solutions based on declared preferences of each objective.

After running the algorithm, the robots will be deployed on their corresponding positions and will respond to events occurring in their allocated region. In our case studies, robots are supposed to give different kinds of service to humans, which is explained in detail in Sect. 5. However, there are other works about service robots in Xue and Liu (2010), Budiharto et al. (2011), Veloso et al. (2012), Ma et al. (2015), which have proposed different kinds of service that should be done by the robots.

Statement of Contributions:

Comparing to traditional search and optimization methods, such as calculus-based and enumerative strategies, the evolutionary algorithms are robust and global; hence, as our first extension, we propose a new MOEA platform to address the multi-robot deployment problem. Since the environment is dynamic and robots need to be redeployed periodically, in our problem definition, in addition to the quality of the deployment, we consider the initial location of robots as the secondary objective, which has not been addressed in deployment/redeployment problem yet. This objective can be vital in a given application where the transportation of the source of deployment, which can be a robot, car, facilities, etc., has a very high cost. Therefore, a shorter distance from the initial position to the new deploying location is preferred.

As MOEA is applied to solve our multi-objective Mixed Integer Linear Programming (MILP) problem the result will be a set of solutions instead of a single one, thus an expert can choose one of the alternatives based on preferences about the problem. Those preferences are considered in both the evolutionary process and also when selecting the final solution over the estimate of the Pareto front.

Another contribution of our work is the way of defining the density function, such that the concentration ellipse method is applied to find an ellipse centered on the mean point of the crowd. By using this technique a realistic representation of the distribution of the crowd is achieved, also modeling a multi-modal density function is straightforward based on different clusters of crowds, in which the number and locational information of the crowd is taken into account.

Finally, to investigate the performance of our proposed platform, we simulate and compare our method with other methods.

3 Preliminary definitions

In this section, we explain the basic concept of deployment and p-median problems.

3.1 Deployment problem formulation

Given a team of n robots that are distributed in the bounded environment, $\varOmega \subset \mathbb {R}^2$. The configuration of robots can be represented by $P = \{{p}_1,\ldots , {p}_n\}$, where $p_j \in \mathbb {R}^2$. Also, $V=\{v_1,\cdots ,v_n\}$ is the Voronoi regions that represent a partitioning of the environment given by:

$$\begin{aligned} v_j = \{{q} \in \varOmega |d({q},{p}_j) \le d({q},{p}_i), \forall j \ne i\}. \end{aligned}$$

(1)

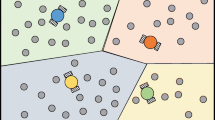
An example of environment with four robots is depicted in Fig. 1a. The main objective of deploying a team of robots is that each robot j be responsible for covering a region $v_j$. By covering region $v_j$, we mean that the robot must be responsible to service all the events occurring inside its dedicated region. The performance of this process can be measured by using a deployment function proposed originally by Cortes et al. (2004) as follows:

$$\begin{aligned} {\mathcal {H}}(P, V) = \sum _{j=1}^{n}{\mathcal {H}}({p}_j,v_j)= \sum _{j = 1}^{n} \int _{q \in v_j} d({q},{p}_j)\phi ({q})d{q}.\nonumber \\ \end{aligned}$$

(2)

Fig. 1

Partitioning an environment and the density function. a A group of robots with corresponding Voronoi region. b Gaussian distribution function centered at the point $\mathbf {q}_c = [0.5, 0.5]^T$

The density function $\phi$ indicates the priority of points in the environment, such that regions with higher value have more priority to be covered ($\phi : \varOmega \rightarrow \mathbb {R}^+$). Figure 1b shows an example of a density function in a 2D environment for which high coverage is required in the central area, while no coverage is required at the boundary. $d(q,p_j)$ gives the distance between a point q and the robot configuration, $p_j$. Different metrics can be used to compute the distance between any two points in the map. In Fig. 2a, comparison between Euclidean and geodesic distance in the non-convex environment is shown. While the Euclidean distance between p and q is shorter and suitable for a convex map, the geodesic distance is more realistic and addresses non-convex environment (dash line).

Fig. 2

Euclidean and geodesic (dash line) distance in non-convex environment

According to the explanation above, the problem of deployment is then translated to a minimization problem of the function in Eq. (2). While this section explained the definition of a continuous deployment setup, a discrete definition is discussed next.

3.2 p-median problem

If we consider that the input map is discretized into cells and represented by a graph, the deployment problem can be viewed as a p-median problem. In the p-median problem, the objective is to find the location of n facilities (or medians) relative to a set of users or customers, in which the sum of the shortest demanded distance from customers to facilities is minimized. This problem is classified as NP-hard problem; therefore, many heuristic methods have been proposed to solve it. The mathematical model of this problem can be defined as follows:

Consider a set of possible locations for facilities $W=\{1,\cdots ,n\}$, and a set of customers $U=\{1, \cdots ,m\}$. d is a distance function, in which d(i, j) indicates the shortest distance from customer i to facility j ($i \in U$ and $j \in J$), where J is a subset of W. Thus, the objective is to minimize the following function:

$$\begin{aligned} F= ~~ \sum _{i \in U~} \min \limits _{j \in J} ~d(i,j), \end{aligned}$$

(3)

where $J \subseteq W$ and $|J|=p$.

An example of this problem with seven customers and two facilities is shown in Fig. 3.

Fig. 3

A solution of p-median problem with two facilities and seven customers

The deployment problem that is addressed in this paper, works in a discrete setup, so that m points (vertices or customers) will be assigned to n robots (representing the facilities).

4 Multi-robot deployment

In our proposed method, we construct the graph G from the input map by applying discretization technique; thereafter, all the computation is done upon this graph. In this section, we discuss about graph representation, computing Voronoi Diagram (VD), dynamic environment, objective functions and also the proposed algorithm.

Fig. 4

A descritized map represented by a graph and it corresponding VD. a Result of growing a circular robot on a map to compute $\mathcal Q_\mathrm{free}$ (white region). b Discretized map and corresponding grid graph with small filled square inside cells as vertices and lines are edges. c Voronoi diagram corresponding to three robots placed at three highlighted cells

4.1 Graph-based tessellation in non-convex environments

For representing the map in a discrete way, we use an occupancy grid approach. But before discretization, we compute free configuration space ($\mathcal Q_\mathrm{free}$) of the input map. This is done by growing the obstacles by the size of the robot. Figure 4a points to the result of growing a circular robot by a specific radius around the obstacles. Also in Fig. 4b, the result of dividing $\mathcal Q_\mathrm{free}$ into cells is shown. It is apparent from Fig. 4b that cells are considered as obstacles if they are occupied partially with obstacles (unmarked). In contrast, the cells are called free cells if they are completely free of obstacles (marked by green squares at the center).

We define a discretization rate ($\alpha$) that can be set based on the size of robots. In this way, if we consider a map with size $M \times N$ ($N,M=2k,~k \in \mathbb {N}$), after discretization the number of cells (in row and column) will be:

$$\begin{aligned} \left( \frac{M}{\alpha }, \frac{N}{\alpha } \right) . \end{aligned}$$

Based on this uniform square tiling of 2-dimensional configuration space, we will generate a grid graph and perform efficient graph search algorithms to compute the Voronoi Diagram. Let a weighted graph given by $G = \{ \mathcal {V}(G), \mathcal {E}(G), \mathcal {C}(G) \}$ that is constructed with vertices ($\mathcal {V}$), edges ($\mathcal {E}: \mathcal {V}\times \mathcal {V} \rightarrow \mathbb {R}^+$) and weights ($\mathcal {C}: \mathcal {V} \rightarrow \mathbb {R}^+$). Vertices can be shown also in the form of a set $\mathcal {V}=\{1,\cdots , m\}$, where $m=\frac{M}{\alpha }.\frac{N}{\alpha }$ is the number of vertices that is obtained by converting the 2D discretized map matrix into a single row matrix with m vertices.

This is evident in Fig. 4b, where vertices of the graph are placed in every accessible discretized cell, and edges are established between neighboring vertices based on Moor-neighborhood (8-connectivity). The cost of each edge is computed by relying on the metric induced by the configuration space, typically the Euclidean length of the edges.

In order to locate robots in this discretized map, we assume that the robots can move over the centers of cells (or corresponding nodes on the graph), and thus the distance between robots and other cells (nodes) can be computed simply by searching on the graph.

4.2 Computing Voronoi diagram on the graph

Since computing the Voronoi diagram is one of the important steps in our framework, we explain the details of this technique here.

In order to compute the Voronoi diagram on the graph G, one technique has recently been presented by Bhattacharya et al. (2013a). The strategy is based on the Dijkstra algorithm with multiple sources (Cormen et al. 2009) and (Dijkstra 1959), in which multiple wavefront start from multiple sources (vertices that can pose the location of the robots) and propagate until colliding with the neighborhood wavefront. This region indicates the boundaries of two neighboring VDs. Figure 4c presents the result of computing VD for three robots positioned at three arbitrary configurations.

In this study, we develop a parallel implementation of Multi-Source Shortest Path (MSSP). In Fig. 5, we show some of the iterations starting the wavefront from the initial positions of the vertices (robots). In each iteration, a new level is added to the prior one and it stops on the Voronoi boundary, where wavefronts collide. As it is explained in Klein (2005), this implementation reduces the time complexity and the required space.

Fig. 5

Running parallel wavefront algorithm. Robots are represented as circles. a 1st iteration, b 2nd iteration, c 4th iteration, d Final result

After computing VD and partitioning the graph G, a given subgraph, $g_i$ is induced as follows:

$$\begin{aligned} g_i= \{ \mathcal {V}(g_i), \mathcal {E}(g_i), \mathcal {C}(g_i) \}, \end{aligned}$$

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {V}(g_i)\subseteq \mathcal {V}(G)\\ \mathcal {E}(g_i) \subseteq \mathcal {E}(G),\,1 \le i \le m ,\\ \mathcal {V}(g_i) \bigcap \mathcal {V}(g_j)=\emptyset , i \ne j\\ \mathcal {E}(g_i) \bigcap \mathcal {E}(g_j)=\emptyset , i \ne j, \end{array}\right. } \end{aligned}$$

where n is the number of sources or, in this case, robots.

It should be noticed that applying Dijkstra algorithm upon our grid graph representation enables our solution to be applied on both convex and non-convex environments. This is achieved due to its ability to compute the shortest distance between two arbitrary points based on the geodesic metric instead of the Euclidean one, although in convex environments both metrics lead to the same result.

4.3 Objective functions

As we mentioned, in our problem the robots are located at some nodes at the beginning, but after running our algorithm they must be deployed to new configurations. Thus minimizing the deployment function and minimizing the path from the initial to the deploying position are considered as our main objectives. The multi-objective problem considered in this paper can be formulated as the following binary integer programming problem, which is similar to the p-median problem (Lim et al. 2009).

Let $P=\{p_1,\cdots ,p_n\}$ be the location of a team of robots, where $p_j$ indicates the position of robot j (or the index of the vertex that robot j is located at). The map is represented by G with m vertices. Moreover, d(i, j) denotes the shortest distance from vertex i to j in the graph G, and X is an m by n matrix (m is the number of vertices and n is the number of robots), where X(i, j) is a binary variable to determine whether vertex i is associated with a robot with vertex j or not, which is given by:

$$\begin{aligned} X(i,j)= {\left\{ \begin{array}{ll} \quad 1 \qquad \text {if vertex} \,\,\, i \,\,\, \text {is associated to vertex} \,\,\, j \\ \quad 0 \qquad \text {otherwise}, \end{array}\right. } \end{aligned}$$

Therefore, the formulation can be defined as:

$$\begin{aligned} (1) \quad \min F_1= & {} \sum _{i = 1}^{m} \sum _{j = 1}^{n} d(i,j).\phi (i) X(i,j)\nonumber \\ (2) \quad \min F_2= & {} \sum _{k \in \tau } \sum _{j = 1}^{n} d(k,j)X(k,j) \end{aligned}$$

(4)

subject to the following constraints:

$$\begin{aligned} {\left\{ \begin{array}{ll} ~a) ~\sum _{j = 1}^{n} X(i,j)=1, { for} i=1, \ldots , m, \\ ~b) ~\sum _{j= 1}^{n} X(j,j)=n \\ ~c) ~X(j,j) \ge X(i,j), ~~ i=1, \ldots , m, ~~j=1,\ldots ,n,~ i \ne j, \\ ~d) ~X(i,j) \in \{ 0,1\} \end{array}\right. } \end{aligned}$$

(5)

In the first objective, $F_1$, constraints (a) force each vertex of the graph to be assigned to exactly one vertex and constraint (b) specifies the total number of centroids, which is equal to the number of robots, n. Constraints (c) limit the vertices to be associated with only centroids.

It should be noticed that in this equation the distance d(i, j) is weighted by $\phi$ such that when $\phi$ has higher value, the corresponding d(i, j) becomes more important. Thus those weighted d(i, j) should be minimized since the first objective is considered as a minimization problem.

In the second objective, $F_2$, $\tau$ is the set of initial positions of the robots. And d(k, j) represents the shortest distance from the initial position of a robot, $p_k$, to the deploying position, $p_j$. As we mentioned, in our algorithm, the shortest distance between two points (vertices) and its corresponding path is computed by Dijkstra algorithm for computing $F_1$ (an example of the shortest path found by Dijkstra is shown in Fig. 6); hence, no more computation is needed to compute $F_2$. In fact, by minimizing the second objective robots try to be close to their initial (or last) locations. The inherent conflict between these two objectives is explained in the next subsection.

Fig. 6

Shortest path between two points (vertices) $p_i$ and $p_k$ is computed by Dijkstra algorithm.

4.4 Robots in dynamic workspace

The environment is dynamic in the sense that the working space changes over the time. In a specific application, if, for example, we define the density function based on the spatial distribution of the crowd (people), they might move in our dynamic environment, hence changing the density function.

Regarding to this dynamic behavior, we can figure out the conflict between two defined objectives as follows. Whenever the distribution of the crowd changes significantly, we start the redeployment process. If the crowd stays close to the robots current positions, they do not need to change much their positions and the two objectives are not conflicting. However, when the distribution of the crowd changes in a way far from the robots current positions, the objectives become conflicting and we need to repeat redeployment process.

Figure 7 encompasses the possible states that the robots can take in our system: servicing, deployment or redeployment and rest. For instance in servicing state robot responses to a call from a customer; deployment or redeployment happens in two conditions: (i) periodically in each $\Delta t$, see Fig. 7a; (ii) change detected in the crowd distribution, as the system senses the crowd distribution changing more than a specific threshold, see Fig. 7b.

Whenever a robot needs any kind of service (such as charging or stop working), it will enter to the rest state. It is important to remark that this state machine can be generalized to deployment of any kind of service robot.

Fig. 7

The state machine that contains different states of a robot in our proposed framework. a Redeployment based on time event. b Redeployment based on change in the distribution of crowd

Fig. 8

The flowchart of the proposed deployment algorithm

4.5 Algorithm design

In order to solve the multi-objective problem, a similar method to NSGA-II is chosen because of its popularity and its ability to find a good spread of solutions and fairly good convergence toward the true Pareto-optimal front compared to other methods. In general, the entire process to achieve the solution is shown in the flowchart of Fig. 8. In the following, we describe the algorithm with more detail.

The configurations of a robot in final deploying position, $p_i$, is given by the position of the cells on the map or its corresponding vertex index in the graph. Hence, the chromosome contains a set of points, $P^* = \{p_1,~.~ .~. ~, p_n\}$, where n is the robot number (see Fig. 9).

Fig. 9

Representation of candidate solutions

Also we define another set $\hat{P}_{init}=\{\hat{p}_1,~.~.~.~ , \hat{p}_n\}$ as initial positions of the robots in the environment that will not be changed during each run of the algorithm. Each element in this set has its corresponding pair in $P^*$. Algorithm 1 shows all the steps in the MOEA. This algorithm repeats whenever a new deployment is needed. Two different conditions for calling this algorithm are explained in Sect. 4.4.

As this algorithm is well known, we just show how in line 3 and we evaluate each individual in Algorithm 2 and also our genetic operators.

In Algorithm 2, to compute the Voronoi region in line 2, the Multi-Source Shortest Path technique, based on Dijkstra algorithm, explained in Sect. 4.2, is applied.

After computing Voronoi region, first objective is obtained in line 3. Later the shortest path between the previous and the new position of the robot is calculated in line 4. Finally, in line 5 the second objective is assigned to the corresponding chromosome.

For creating the new generation, two different types of mutation operators are applied. In the first type, after selecting one of the individuals randomly, all the genes will be changed by new random values. This operator plays the role of global exploration over the problem space. In addition, second operator performs a local search by changing one of the genes in a random selected parent. Indeed, a single gene will be selected, and then we add a small disturbance that might change the position, $p_i$ within range (r) around it. An example of this operator is depicted in Fig. 10.

Fig. 10

Mutation operator changes the deploying position (square) with range r. a Selected parent, b created children

After running algorithm 1, a non-dominated set will be obtained, and then through this set of results, the final answer will be selected via multi-criteria decision-making technique (Figueira et al. 2005). The Elimination and Choice Translating Reality (ELECTRE I) (Roy 1968) is employed since the decision-maker can define a preference of each objective in this method; after comparing all pairs of alternatives, ELECTRE I provides a partial ordering of solutions based on the declared preferences.

4.6 Density function

Since in this work the distribution of the robots is based on the density of the crowd in the environment, we obtain the density function $\phi$, based on a concentration ellipse method proposed by Belta and Kumar (2004). After clustering the distributed crowd in the workspace to specific number of clusters, which can be determined based on the size (area) of workspace and the capacity of crowd in the field, a fitted ellipse to each cluster about the mean of the cluster is found. For this ellipse, a Gaussian function is defined:

$$\begin{aligned} f(x,y)=\exp \left\{ -\left( \frac{(x - x_0)^2}{{2a_0}^2} + \frac{(y - y_0)^2}{{2b_0}^2} \right) \right\} , \end{aligned}$$

(6)

where $a_0$, $b_0$ are equal to the semiaxis (or spreads of the blob), and $x_0$ and $y_0$ are set to the center of the ellipse (see Fig. 11).

Fig. 11

An ellipse centered on $(x_0,y_0)$ with semiaxis ($a_0,b_0$), rotated by $\theta$ degree

Such an example of crowd clustering, finding the fitted ellipse and obtaining a density function is depicted in Fig. 12. In this example, the distributed crowd is divided into three clusters by applying k-means clustering algorithm (Hartigan and Wong 1979). Later in Fig. 12b, three ellipses are found, such that they enclose the points in each cluster, and a multi-modal density function is obtained on the union of these three ellipses (c, d). It is worth to mention that the number of crowd in each cluster affects the peak of the corresponding cluster relatively. Therefore, based on Eq. (6) the Gaussian function of the $i^{th}$ cluster can be modeled as follows:

$$\begin{aligned} \hat{f}_i=\epsilon + \alpha f(x,y), \end{aligned}$$

(7)

In Eq. (7), $\epsilon$ is defined as a small bias value to avoid $\hat{f}$ returns zeros ($\hat{f}_i\ne 0$), $\alpha$ is a coefficient representative of the crowd number in a cluster. A cluster more crowded has a bigger $\alpha$, accordingly a bigger peak in its density function.

Fig. 12

Example of applying concentration ellipse method on a sample crowd. a A distribution of crowd, b corresponding clustering and fitted ellipse, c 2D Gaussian function correspondingly, d 3D representation of Gaussian function

In order to find the ellipse over the crowd, let $q_i=[x_i,y_i] \in \mathbb R^2$ represents the position of individual i, and thus the mean and covariance of N samples are given by Eqs. (8, 9):

$$\begin{aligned}&\mu =\frac{1}{N} \sum _{i=1}^N{q_i},\end{aligned}$$

(8)

$$\begin{aligned}&\Sigma =\frac{1}{N-1} \sum _{i=1}^N{(q_i-\mu )(q_i-\mu )^T}. \end{aligned}$$

(9)

The position of individuals (q) according to the fitted ellipse in a cluster is given by:

$$\begin{aligned} \hat{q}= [\hat{x}_i,\hat{y}_i]=R^T(q_i-\mu ) , i=1,2, ~. ~.~ .~N, \end{aligned}$$

such that R is the rotation matrix [Eq. (10)] and $\theta$ indicates the rotation of the ellipse in the workspace (see Fig. 11):

$$\begin{aligned} R= \left[ \begin{array}{cc} \hbox {Cos}(\theta ) &{} -\hbox {Sin}(\theta ) \\ \hbox {Sin}(\theta ) &{} \hbox {Cos}(\theta ) \end{array}\right] . \end{aligned}$$

(10)

The semiaxes of the ellipse can be obtained by

$$\begin{aligned} l_1=\frac{1}{N-1} \sum _1^N{\hat{x}_i}^2, \quad \quad \quad \quad l_2=\frac{1}{N-1} \sum _1^N{\hat{y}_i}^2. \end{aligned}$$

(11)

According to Eqs. (8) and (9), the ellipse in terms of contours of probability p for normally distribution crowd in workspace can be explained as:

$$\begin{aligned} (x-\mu )^T \Sigma ^{-1} (x-\mu )=c, ~~ c=-2\ln (1-p). \end{aligned}$$

(12)

Given the above explanation, we can induce an abstraction $a=(R,\mu ,l_1,l_2,\alpha )$, which indicates that p percentage of normally distributed $\alpha$ crowd in workspace lies inside an ellipse centered at $\mu$, with semiaxes $\sqrt{cl_1}$, $\sqrt{cl_2}$, rotated by R. The rotation matrix, $R \in SO(2)$, is defined around $\theta \in (-\pi /2,\pi /2)$ as follows:

$$\begin{aligned} \theta =\frac{1}{2}\tan ^{-1}\left( \sum _{i=1}^N(q_i-\mu )E_1(q_i-\mu )^T,\sum _{i=1}^N(q_i-\mu )^TE_2(q_i-\mu )\right) ,\nonumber \\ \end{aligned}$$

(13)

where

$$\begin{aligned} E_1= \left[ \begin{array}{l@{\quad }l} 0 &{} 1\\ 1 &{} 0 \end{array}\right] , \qquad \qquad E_2= \left[ \begin{array}{l@{\quad }l} 1 &{} 0\\ 0 &{} -1 \end{array}\right] . \end{aligned}$$

A comprehensive explanation can be found in Belta and Kumar (2004). Finally, a map function $c:\bigcup a_k \rightarrow \phi$, (k is number of ellipses) creates a density function $\phi$ based on the abstraction a of multi-ellipse representing the distribution of the crowd in the environment.

4.7 Complexity

In order to compute the total complexity of our algorithm, it is considered in two main parts: the complexity of MOEA and the operation of constructing Voronoi tessellation. The complexity of a standard implementation of NSGA-II is equal to $O (GMN^2)$, where G is the number of iterations and M and N are the number of objectives and population size, respectively. However, in Jensen (2003) and Liu and Zeng (2010), the authors decreased this complexity to ${O} (GN \log ^{M-1}N)$ and ${O} (kN+\log {N})$, where k is the number of non-dominated front. Hence, a logarithmic computational cost can be considered for executing NSGA-II. Moreover, the complexity of creating Voronoi tessellation, which is done by using Dijkstra algorithm and heap structure, is given by: $O( |\mathcal {V}| \log {|\mathcal {V}|})$.

5 Case study

As we explained in the introduction, we defined two different scenarios for indoor and outdoor environments. We consider an office-like environment with the presence of obstacles and a very large obstacle-free beach area (ocean) which are explained in the continuation.

5.1 Office-like environment

Such an office-like building contains obstacles (walls), rooms and persons (employees or applicants). In this map, a group of service robots will service to people who are working in this building. In this way, robots can perform different tasks, i.e., delivering/transferring documents between rooms, guiding applicants, cleaning, etc. Fig. 13 shows the given map. In order to have the location and distribution of the applicants, we assume an internal camera-based system that produces their locational information.

Fig. 13

Office-like environment

5.2 Lifeguard robot in beach

Second scenario is associated with a group of lifeguard robots in an outdoor environment (beach). In this application, robots must be responsible to give aid to victims in minimum time. Hence, robots must get positions somewhere in the arena in order to be accessible through the whole environment in the minimum distance. Indeed a group of robots play a role of life security on a beach, such that many people are swimming inside an ocean close to a beach, while robots are surveilling the environment (swimming region) to help victims on demand. As the given area is very large a group of robots are distributed over the environment and service the events in their assigned region. Thus, by solving deployment problem in this scenario we can guarantee that the robots can access to victims in minimum time, which is vital when a victim is drowning or in danger. It should be noticed that the number and positions of swimmers are varying in time; therefore, robots must be redeployed periodically. Indeed, we deem each swimmer has a sensor to send his/her current position to the main system, and after updating locational information of swimmers in each $\Delta t$, redeployment might be triggered. Such an environment is shown in Fig. 14.

Fig. 14

A beach (ocean) area

In this area, the density function shows the crowd of swimmers; therefore, the density function for a region with more swimmers has a higher value.

6 Simulation result

Experiments are done in the two defined scenarios, and solutions were found using MATLAB on a computer with processor Intel (R) Core (TM) i7-3520M 2.90 GHz with 6 GB RAM.

6.1 First scenario

In the fist scenario, six robots are going to find the best configuration to be deployed in an office. As it is explained in Sect. 4.1, the map is discretized into cells, in which the center of cells (highlighted by small points) indicates the vertices of graph in Fig. 15a. In Fig. 15b a single modal density function that will be used in this simulation is presented.

Fig. 15

Office-like map, and its corresponding density function. a Descretized map (Highlighted points are the center of cells). b Density function (3D view)

The reported parameters in Fig. 16 are used for this simulation.

Fig. 16

Parameters in the first scenario

In order to have a more realistic problem, we did not centralize all robots in the same position. So robots are divided into 3 groups, and each group contains 2 robots. They start moving from 3 different corners of the map.

We also compute the estimation of the Pareto front, for this scenario, based on the idea of Monte Carlo algorithm to validate that our results are very close to the estimated Pareto front. To obtain that, we simulate random population for 100 times. Later non-dominated sorting algorithm finds the estimation of the Pareto front, see Fig. 17a.

Fig. 17

An estimation of the Pareto front and the non-dominated set obtained by proposed solution. a The result of applying Monte Carlo algorithm to obtain an estimation of the Pareto front. b The result of proposed solution. The square shows the selected solution by ELECTRE I ($F_1=0.26,~ F_2=0.43$)

After running the algorithm for 200 iterations, an estimation of the Pareto front is obtained. In Fig. 17b, we present the set of solutions that are distributed along the Pareto front. Because of the overlaps between solutions, just eight solutions are visible in this figure. The same situation has happened in Figs. 21 and 26. Afterward, by applying the decision-making tool, ELECTRE I, it finds the best solution regarding to the weights of the objectives. The selected solution is highlighted by a black square in this figure. Since the weights of both objectives are equal (0.5), a balanced solution on both objectives is selected.

The corresponding representation of the selected solution is depicted in Fig. 18a, in which the input map is partitioned into 6 regions (with different colors) and each of the robots is responsible for its associated region. Also, robots have converged to the peak of the density function at the center of map. The trajectory of the robots from the initial configuration (circles) to the deploying configuration (squares) is also shown. In order to compare the selected solution with other solutions in the non-dominated set, another solution with higher $F_2$ is illustrated in Fig. 18b. It is obvious that the length of the explored path (with bigger value in $F_2$) by robots is longer than the one for the selected solution by ELECTRE I.

Fig. 18

Result of deployment on office-like map. a Selected solution by ELECTRE I ($F_1=0.26,~ F_2=0.43$). b Another solution in the Pareto front with higher $F_2$ ($F_1=0.18 ,~ F_2=0.76$)

Fig. 19

Beach map with distribution of swimmers in ocean. a Discretized map (gray is land and white is the ocean). b People distribution and clustering. c Corresponding density of the crowd. d 3D view

6.2 Second scenario

In this scenario, we consider an outdoor map with more complex density function. The discretized map and its corresponding multi-modal density function are depicted in Fig. 19a, b. In this scenario, although the map is convex, according to our technique described in Sects. 4.1 and 4.2, the geodesic distance metric is applied to compute the shortest path and Voronoi diagram. Therefore, since there is no obstacles in the outdoor convex scenario, the computed geodesic distance became equal to the Euclidean distance.

It should be noticed that the input map is converted to a grayscale image and comprises two regions: land (gray region) and water (white region). In this realistic map, we are going to show not only deployment of the robots inside the ocean, but also their redeployment based on changes in the crowd distribution in the time unit. The initial distribution of swimmers in the ocean, corresponding clusters, fitted ellipses and the density function are shown in Fig. 19b–d. The maximum number of clusters for this map is considered equal to 5. This parameter can be defined regarding to the area of the map and relative capacity of crowd. The video of the whole process of deployment and redeployment is available at https://youtu.be/QNbovdZfH7s.

The parameters that have been applied in this simulation are reported in Fig. 20.

Fig. 20

Applied parameters in the second scenario

Fig. 21

An estimation of the Pareto front and the non-dominated set with the selected solution. a The result of applying Monte Carlo algorithm to obtain an estimation of the Pareto front in the second scenario (100 times random simulation). b The square shows the selected solution by ELECTRE I ($F_1=0.37 ~,~ F_2=0.29$) obtained by the proposed method

Fig. 22

Explored paths by the robots. Circles show the initial configurations. More robots are deployed about the peaks. Representation of the selected solution with $F_1=0.37 ~,~ F_2=0.29$

Similar to the previous test, we find and estimation of the Pareto set in Fig. 21a. After solving the problem, the approximated Pareto set, the selected solution by ELECTRE I and the robots trajectories are illustrated in Figs. 21b and 22, accordingly. It can be understood through these figures that the whole environment is covered by robots, and the number of robots deployed about the peak of the density function is more. For example, in the right side of the map, as the crowd (swimmers) is bigger than other regions, more robots are deployed there.

6.3 Comparison with standard NSGA-II

Generally, from the figures shown so far, in both scenarios more robots were deployed around the peaks of the density function, which are our desired regions.

As we mentioned in Sect. 4.5 in the NSGA-II, we applied a new mutation operator instead of using crossover. In order to investigate the efficiency of this operator, we also simulate both scenarios by using standard NSGA-II. This standard version uses a mutation (similar to ours) and 2 points crossover operator. Apart from the crossover rate, which is 0.85, all other parameters are equal to the values in Figs. 16, 20. Also the number of runs for both our modified NSGA-II$^*$ and the standard NSGA-II is equal to 100. As a result, Table 1 contains the mean and standard deviation of both objectives in two defined scenarios, for both algorithms. It can be understood that our modified NSGA-II works better than the standard one. A remarkable effect of our new mutation operator is keeping diversity during iterations and better exploration. In contrast crossover could not save diversity since it is biased by the initial population. This is clear from the standard deviation in the table. In NSGA-II$^*$ (our method), the values of standard deviation in the selected solution indicate the successful convergence in the last generations with diversity. In contrast to the first scenario, in ocean case study because of its convexity, the last population has converged with less difference in the standard deviation.

Table 1 Comparison between NSGAII-$^*$: our modified version, and NSGAII: the standard one

Fig. 23

Non-dominated set obtained by standard NSGA-II in 200 iterations. a Pareto front of applying standard NSGA-II in office-like scenario. b Pareto front of applying standard NSGA-II in beach scenario

The estimates of the Pareto front for both scenarios obtained by a typical run of the standard NSGA-II are shown in Fig. 23. While the statistical performance of both methods is contrasted in Table 1, this snapshot of one of the runs gives an idea of this difference. Compare these with the corresponding estimates achieved by our modified NSGA-II$^*$, see Figs. 17b and 21b. Our method could find not only a better solution, but also a better distribution of the non-dominated solutions over the Pareto front.

The dominated hypervolume (or S-metric) is a commonly accepted quality measure for comparing approximations of Pareto fronts generated by multi-objective optimizers. The area comprised by the approximated front and a reference (dominated) point, in our case the point (1, 1) in the objective space, can be used to indicate both convergence and distribution of solutions. The bigger this value, the better the approximation generated by the multi-objective method. By having the hypervolume value for the outcomes of 100 runs, we take the sample mean and standard deviation. Table 2 shows the results obtained by our method NSGA-II$^*$ and the standard NSGA-II. As can be seen, our method provides higher values for this metric, showing that the approximations of the Pareto front obtained by NSGA-II$^*$ are indeed better.

Table 2 Comparison between NSGA-II-$^*$: our modified version, and NSGA-II: the standard one, in terms of the hypervolume values

6.4 Comparison with gradient descent-based method

Since the multi-robot deployment problem is considered as an NP-hard problem, cited local search methods offer acceptable solutions in many cases, by minimizing the function in Eq. (2). But because of the nature of gradient descent-based approaches, they may stuck in local minimum specially in a complicated non-convex environment. In this simulation, we are trying to compare our global search multi-objective approach (we call it “method 1” here) with one of the most common gradient descent-based techniques from the literature (called “method 2”). We applied a similar discrete controller proposed by Bhattacharya et al. (2013b) and Alitappeh and Pimenta (2016) to solve the problem in the first scenario. It should be mentioned that in this simulation we intended to compare the ability of these methods in finding a better solution in deployment, thus in contrast to previous simulation we assume a static environment (without changing in density function).

We selected the non-convex office-like map from our first scenario (Sect. 6.1). In both methods, the first step is discretizing the map into cells, and hence the input map is divided into $80\times 120$cells (discretization rate is 5). We employed six robots starting from the same initial positions in both methods. Figure 24 includes all the applied parameters in this simulation.

Fig. 24

Applied parameters in this simulation

By decreasing the discretization rate and cell size consequently, robots will have more precise movement in the environment. Since the main objective in method 2 is minimizing the deployment function ($F_1$), we give more priority to this objective with $w_1=0.9$ and the weight of $F_2$ is set to $w_2=0.1$. To make a fair comparison, we set the maximum iteration number to 70 in both methods.

Fig. 25

Density function (3D view) centered at most top right of the map

The center of density function is defined at the most top right of the map, which indicates that this region has more priority to be covered. If we consider this scenario as an office, this means more applicants need to be serviced in that area (see Fig. 25).

After executing the algorithms, results are depicted in Figs. 26 and 27. In Fig. 26a, the Pareto front of method 1 and the selected solution by ELECTRE is shown. Moreover, by computing the second objective in method 2, it is shown that our method could find a better Pareto and even dominate the solution of method 2. In another comparison, we show in Fig. 26b, how the values of $F_1$ and $F_2$ evolve over iterations in both methods (in method 1 the mean of objectives in each iteration are shown). It should be noticed that in method 2, since the robots started from the initial location and get closer to the final location iteratively, $F_1$ and $F_2$ started form the worse (max) or best (min) values. For instance, the value of $F_2$ (total traversed path by robots) starts from 0 and increases linearly with time. While we set a higher priority for the first objective, in method 1, $F_2$ gets worse over the evolution. But it reached to a better value than method 2.

Fig. 26

Comparison between proposed method (M1) and method 1 (M2). a Final solution in objective space. (M1:Method 1 and M2:Method 2). b Evolution of objective functions over iterations

Finally, for the sake of clarity we illustrate robots behavior in this simulation in Fig. 27. Robots started from the same depots, in (a), robots directed toward the peak of density function, and move over the straight shortest path to the final deployment position. In contrast, in (b), method 2 made some redundant motion (even sometimes backward), which increases the traversed path by robots. Corresponding Voronoi region for each robot is highlighted with different color.

Fig. 27

Final deployment of six robots. a Voronoi region for each robot and the trajectory (start to end) in proposed method. b Voronoi region and robots’ trajectory of method 2

7 Conclusion

In this work, we address the multi-robot deployment/redeployment problem in non-convex environments. In our application, we assumed that the robots must run the deployment algorithm periodically, since the distribution of the crowd (or density function) in the area varies with time. Differently from previous works, we consider a multi-objective setup in a mixed integer linear programming and MOEA was applied to solve this optimization problem. The first objective is about minimizing the cost function of deployment problem that shows accessibility of robots in the field. The second objective includes the length of the path between robots initial positions and final deploying configuration. Finally, for selecting one of the solutions on the estimated Pareto front, we applied ELECTRE I as a decision-making technique.

We also employed an ellipse technique to find an ellipse centered about the mean of the crowd, and thus the density function is defined by using this ellipse as its main level curve.

In simulation results, we validated the performance of the proposed algorithm in two different maps. Moreover, we show that not only the quality of deploying a team of robots is important, but also the path that the robots must traverse in order to get to these locations. In future work, this technique can be extended to consider other objectives in different applications in robotics.