Abstract
Restarting automata have been introduced as a formal model for the linguistic technique of analysis by reduction, which can be used to check the correctness of natural language sentences. In order to study quantitative aspects of restarting automata, we introduce the concept of a weighted restarting automaton. Such an automaton is given through a pair \((M,\omega )\), where M is a restarting automaton on some input alphabet \(\Sigma \), and \(\omega \) is a weight function that assigns an element of a given semiring S to each transition of M. Thus, \((M,\omega )\) defines a function \(f_\omega ^M:\Sigma ^*\rightarrow S\) that associates an element of S to each input word over \(\Sigma \). By looking at different semirings S and different weight functions \(\omega \), various quantitative aspects of the behavior of M can be expressed through these functions. We are interested in the syntactic and semantic properties of these functions, e.g., their growth rates and the closure properties under various operations.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Analysis by reduction as described by Straňáková (2000) is a linguistic technique used to verify the syntactic correctness of sentences of a natural language through sequences of local simplifications. During the process of simplifying a given sentence, each step preserves the correctness or incorrectness of the sentence. After a finite number of steps, either a correct simple sentence is obtained, or an error is detected. In addition, by this process the structure of the given sentence can be analyzed and information on dependencies and independencies between certain parts of the sentence can be derived.
The restarting automaton was presented by Jančar et al. (1995) as a formal model of analysis by reduction. Such an automaton consists of a finite-state control and a flexible tape with end markers, on which a read/write window of a fixed positive size operates. Based on the state and the window content, the automaton may perform a move-right step, which shifts the window one position to the right and changes the state. It may also execute a rewrite step, which replaces the content of the window by a word that is strictly shorter, places the window immediately to the right of the newly written word, and changes the state. Finally, it may perform a restart step, which moves the window back to the left end of the tape and resets the automaton to its initial state, or it may make an accept step. Observe that a rewrite step shortens the content of the tape, and it is assumed that the length of the tape is shortened accordingly. In addition, it is required that before a restart operation can be executed, exactly one rewrite must have taken place, that is, the automaton can be seen as working in cycles, where each cycle begins with the window at the left end of the tape and the finite-state control being in the initial state, then some move-right steps are executed, then a single rewrite step is performed, then again some move-right steps may be executed, and finally the cycle is completed by a restart step. Thus, a computation consists of a finite sequence of cycles that is followed by a tail computation, which consists of a number of move-right steps, possibly a single rewrite step, and which is completed by an accept step or ends by reaching a configuration for which no further step is defined. In the latter case we say that the current computation halts without acceptance.
Many different types and variants of restarting automata have been introduced and studied since 1995 (see, e.g., Jančar et al. 1997, 1998, 1999). In particular, many well-known classes of formal languages, like the regular languages REG, the deterministic context-free languages DCFL, the context-free languages CFL, the Church–Rosser languages CRL, and the growing context-sensitive languages GCSL have been characterized by various types of restarting automata. A recent overview on restarting automata is given by Otto (2006).
Just as finite automata, also restarting automata accept or reject their inputs. Therefore, such an automaton can be seen as computing a Boolean function. Weighted automata were introduced by Schützenberger (1961). In these automata each transition gets a quantitative value from some semiring S as a weight. These weights can model the cost involved when executing a transition such as the needed resources or time, or the probability or reliability of its successful execution. By forming the product of all weights along a computation, a weight can be assigned to that computation, and by forming the sum of all weights of all accepting computations for a given input, an element of S is associated with that input. For example, by using appropriate weights, we can determine the number of ways that a word can be accepted by a finite automaton. Weighted automata and their properties are described in detail in the recent handbook by Droste et al. (2009).
After their introduction, weighted automata have been applied in many areas like natural-language processing, speech recognition, optimization of energy consumption, and probabilistic systems. Also many applications of them can be found in digital image compression and model checking. Due to these applications, many different variants of weighted automata have been invented and studied (see, e.g., Chatterjee et al 2009; Bollig et al 2010; Droste and Meinecke 2011; Droste and Götze 2013). Following this development, we introduce weighted restarting automata in order to study quantitative aspects of computations of restarting automata.
A weighted restarting automaton is given by a pair \((M,\omega )\), where M is a restarting automaton on some input alphabet \(\Sigma \), and \(\omega \) is a weight function that assigns a weight from some semiring S to each transition of M. As outlined above, \((M,\omega )\) defines a value \(f_\omega ^M(w)\) from S for each input word \(w\in \Sigma ^*\). Thus, \((M,\omega )\) defines a function \(f_\omega ^{M}:\Sigma ^*\rightarrow S\). If the semiring S is linearly ordered, then we can abstract this function to a function from \(\mathbb {N}\) into S by taking \(\hat{f}_\omega ^M(n) = \max \{\,f_\omega ^M(w)\mid w\in \Sigma ^*,\,|w|=n\,\}\), where |w| denotes the length of the word w.
By looking at different semirings S and different weight functions \(\omega \), various quantitative aspects of the behavior of M can be expressed through these functions. For example, by taking S to be the semiring of natural numbers with addition and multiplication, we can count the number of accepting computations for each input, or by using the tropical semiring, we can determine the minimal number of cycles in an accepting computation for each input. Further, if S is the semiring of formal languages over a finite alphabet \(\Delta \), then \(f_\omega ^M\) is a transformation from \(\Sigma ^*\) into the languages over \(\Delta \). In fact, it is easily seen that the transformations computed by the restarting transducers introduced by Hundeshagen and Otto (2012) occur as a special case.
Which functions \(f: \Sigma ^{*} \rightarrow S\) or \(\hat{f}: \mathbb {N}\rightarrow S\) can be realized in this way? We are interested in the syntactic and semantic properties of these functions, e.g., their growth rates and the closure properties under various operations. It is easily seen that the recognizable functions \(S_{\mathrm {REC}}\langle \langle \Sigma ^*\rangle \rangle \) occur as special cases. Here we will prove that, for the semiring \((\mathbb {N},+,\cdot ,0,1)\) of natural numbers with addition and multiplication, the functions of the form \(\hat{f}:\mathbb {N}\rightarrow \mathbb {N}\) are bounded from above by \(2^{O(n^2)}\). Exactly which functions obeying this bound can be realized by weighted restarting automata over \(\mathbb {N}\)? Ideally we would like to derive characterizations of these functions in terms of other machines or syntactic properties.
This paper is structured as follows. In the next section we recall some notions on monoids and semirings in short, and we introduce the basic notions and results on restarting automata. Then we define the weighted restarting automata and the functions defined by them in detail, illustrating these definitions by examples. Finally, Sect. 4 presents our result on the upper bound for the functions of the form \(\hat{f}:\mathbb {N}\rightarrow S\) mentioned above, and it contains the results that the classes of functions of the form \(f_\omega ^{M}:\Sigma ^*\rightarrow S\) are closed under pointwise addition, scalar multiplication, and Cauchy product, if the restarting automata M considered can use auxiliary symbols. The paper closes with a short summary and some problems for future work.
2 Preliminaries
Here we restate some definitions that we will use below.
2.1 Monoids and semirings
First we recall the notions of monoid and semiring and present some examples of semirings.
Definition 1
A monoid \(M=(M,\circ ,i_M)\) is a non-empty set M with a binary operation \(\circ :M\times M\rightarrow M\) and an element \(i_M\in M\) such that
-
\(\circ \) is associative, that is, \((a\circ b)\circ c = a\circ (b\circ c)\) for all \(a,b,c\in M\), and
-
\(i_M\) is a neutral element for \(\circ \), that is, \(i_M\circ a = a\circ i_M = a\) for all \(a\in M\).
The monoid M is called commutative if \(a\circ b = b\circ a\) holds for all \(a,b\in M\). It is called ordered if there exists a partial order \(\le \) on M that is compatible with the operation \(\circ \), that is, if \(a\le b\), then \((a\circ c)\le (b\circ c)\) and \((c\circ a)\le (c\circ b)\) for all \(a,b,c\in M\). Finally, it is called linearly ordered if it is ordered with respect to a linear order.
Let \(\mathbb {N}\) denote the set of all non-negative integers, let \(\mathbb {Z}\) be the set of all integers, let \(\mathbb {Q}\) be the set of all rational numbers, and let \(\mathbb {R}\) be the set of all real numbers. Obviously, \((\mathbb {N},+,0)\) and \((\mathbb {N},\cdot ,1)\) are commutative monoids that are linearly ordered, while the commutative monoids \((\mathbb {Z},\cdot ,1)\), \((\mathbb {Q},\cdot ,1)\), and \((\mathbb {R},\cdot ,1)\) are not ordered with respect to the standard order relation \(\le \), as in general, \(a\le b\) does not imply \(a\cdot c\le b\cdot c\). Further, let \(\mathbb {N}^\infty = \mathbb {N}\cup \{\infty \}\) and \(\overline{\mathbb {N}} = \mathbb {N}\cup \{-\infty ,\infty \}\). Then \((\mathbb {N}^\infty ,\min ,\infty )\) and \((\overline{\mathbb {N}},\max ,-\infty )\) are commutative monoids that are linearly ordered.
If \(\Sigma \) is a finite alphabet, then, for each \(n\ge 0\), \(\Sigma ^n\) is the set of all words of length n over \(\Sigma \). Further, \(\Sigma ^+\) denotes the set of all non-empty words over \(\Sigma \) and \(\Sigma ^* = \Sigma ^+\cup \{\lambda \}\), where \(\lambda \) denotes the empty word, which is the only word of length 0. The operation of concatenation \(\cdot :\Sigma ^*\times \Sigma ^*\rightarrow \Sigma ^*\) is defined by taking \(u\cdot v = uv\) for all words \(u,v\in \Sigma ^*\). Then \((\Sigma ^*,\cdot ,\lambda )\) is a monoid, the free monoid generated by \(\Sigma \). It is not commutative unless \(|\Sigma |=1\) holds. It is linearly ordered with respect to the length-lexicographical ordering (see, e.g., Book and Otto 1993).
Finally, for any set S, we use \(\mathbb {P}(S)\) to denote the power set of S, and \(\mathbb {P}_\mathrm{fin}(S)\) to denote the set of all finite subsets of S. Then \((\mathbb {P}(S),\cup ,\emptyset )\), \((\mathbb {P}(S),\cap ,S)\), and \((\mathbb {P}_\mathrm{fin}(S),\cup ,\emptyset )\) are commutative monoids for any set S, and \((\mathbb {P}(\Sigma ^*),\cdot ,\{\lambda \})\) and \((\mathbb {P}_\mathrm{fin}(\Sigma ^*),\cdot ,\{\lambda \})\) are monoids, where \(U\cdot V = \{\,u\cdot v\mid u\in U, v\in V\,\}\) denotes the extension of the concatenation operation from words to languages. These monoids are ordered with respect to the inclusion relation, which, however, is not a linear order.
Definition 2
A semiring \(S=(S,+,\cdot ,0,1)\) is a non-empty set S together with two binary operations \(+:S\times S\rightarrow S\) and \(\cdot : S\times S\rightarrow S\) and two elements \(0,1\in S\) such that the following conditions are satisfied:
-
1.
\((S,+,0)\) is a commutative monoid,
-
2.
\((S,\cdot ,1)\) is a monoid,
-
3.
the distributive laws
$$\begin{aligned}&(a+b)\cdot c = (a\cdot c) + (b\cdot c) \text{ and } \\&c\cdot (a+b) = (c\cdot a)+(c\cdot b) \end{aligned}$$hold for all \(a,b,c\in S\), and
-
4.
\(0\cdot a = a\cdot 0 = 0\) holds for all \(a\in S\).
The semiring S is called commutative if \((S,\cdot ,1)\) is a commutative monoid. It is (linearly) ordered with respect to an order \(\le \), if \((S,+,0)\) is a (linearly) ordered monoid with respect to \(\le \) and if multiplication by elements \(s\ge 0\) preserves the order, that is, if \(s\ge 0\) and \(a\le b\), then \((s\cdot a)\le (s\cdot b)\) and \((a\cdot s)\le (b\cdot s)\).
Obviously, \((\mathbb {N},+,\cdot ,0,1)\) and \((\mathbb {R},+,\cdot ,0,1)\) as well as \((\mathbb {B},\vee ,\wedge ,0,1)\), where \(\mathbb {B}=\{0,1\}\), are commutative semirings that are linearly ordered with respect to the standard order. \((\mathbb {N}^\infty ,\min ,+,\infty ,0)\) is the tropical or min-plus semiring and \((\overline{\mathbb {N}},\max ,+,-\infty ,0)\) is the arctic or max-plus semiring, which are also commutative and linearly ordered under the standard order. Further,
are semirings that are not commutative unless \(|\Sigma |=1\), and the same holds for
where \(\text{ REG }(\Sigma )\) and \(\text{ CFL }(\Sigma )\) denote the classes of regular and context-free languages over \(\Sigma \). These semirings are ordered with respect to the inclusion relation. More information on and further examples of semirings can be found in Golan (1999) or Hebisch and Weinert (1998).
We complete this subsection by restating the notions of weighted automaton and recognizable function in short.
Definition 3
Let \(S=(S,+,\cdot ,0,1)\) be a semiring, and let \(\Sigma \) be a finite alphabet. A weighted automaton is given through a four-tuple \(A=(Q,\mathrm {in},\omega ,\mathrm {out})\), where
-
Q is a finite set of states,
-
\(\mathrm {in}:Q\rightarrow S\) assigns an entrance weight to each state,
-
\(\mathrm {out}: Q\rightarrow S\) assigns an exit weight to each state,
-
and \(\omega : Q\times \Sigma \times Q\rightarrow S\) assigns a weight to each possible transition.
A path in A is any sequence
where \(q_0,q_1,\ldots ,q_n\in Q\) and \(a_1,a_2,\ldots ,a_n\in \Sigma \), and the word \(a_1a_2\ldots a_n\in \Sigma ^*\) is called its label. The run weight of P is the product
where \(\mathrm {rweight}((q_0))=1\) is taken, and the weight of P is
Finally, let \({\mathrm {Path}}(w)\) denote the set of all paths in A that have label w. Then the behavior of A is the function \(||A||:\Sigma ^*\rightarrow S\) that is defined by
for all \(w\in \Sigma ^*\). The set of recognizable functions over S and \(\Sigma \) is the set \(S_{\mathrm {REC}}\langle \langle \Sigma ^*\rangle \rangle \) of all functions that are the behavior of some weighted automaton over S.
For more information on these notions see, e.g., Droste and Kuich (2009).
2.2 Restarting automata
As described above a restarting automaton is a nondeterministic machine model that has a finite-state control and a read/write window that works on a flexible tape that is delimited by end markers.
Formally, a restarting automaton, an RRWW-automaton for short, is a one-tape machine that is described by an 8-tuple  , where Q is a finite set of states, \(\Sigma \) is a finite input alphabet, \(\Gamma \) is a finite tape alphabet containing \(\Sigma \), the symbols
, where Q is a finite set of states, \(\Sigma \) is a finite input alphabet, \(\Gamma \) is a finite tape alphabet containing \(\Sigma \), the symbols  serve as markers for the left and right border of the work space, respectively, \(q_0\in Q\) is the initial state, \(k\in \mathbb {N}_+\) is the size of the read/write window, and
serve as markers for the left and right border of the work space, respectively, \(q_0\in Q\) is the initial state, \(k\in \mathbb {N}_+\) is the size of the read/write window, and

is the transition relation. Here \({\mathcal {PC}}^{(k)}\) is the set of possible contents of the read/write window of M, where


and
The relation \(\delta \) describes four different types of transition steps:
-
(1)
A move-right step has the form \((q,u,q',\mathsf{MVR})\), where \(q,q'\in Q\) and \(u\in {\mathcal {PC}}^{(k)}\),
 . If M is in state q and sees the string u in its read/write window, then this move-right step causes M to shift the read/write window one position to the right and to enter state \(q'\). However, if the content u of the read/write window is only the symbol $, then no move-right step is possible.
. If M is in state q and sees the string u in its read/write window, then this move-right step causes M to shift the read/write window one position to the right and to enter state \(q'\). However, if the content u of the read/write window is only the symbol $, then no move-right step is possible. -
(2)
A rewrite step has the form \((q,u,q',v)\), where \(q,q'\in Q\), \(u\in {\mathcal {PC}}^{(k)}\),
 , and \(v\in {\mathcal {PC}}^{\le (k-1)}\) such that \(|v| < |u|\). It causes M to replace the content u of the read/write window by the string v, and to enter state \(q'\). Further, the read/write window is placed immediately to the right of the string v. However, some additional restrictions apply in that the border markers
, and \(v\in {\mathcal {PC}}^{\le (k-1)}\) such that \(|v| < |u|\). It causes M to replace the content u of the read/write window by the string v, and to enter state \(q'\). Further, the read/write window is placed immediately to the right of the string v. However, some additional restrictions apply in that the border markers  and $ must not disappear from the tape nor that new occurrences of these markers are created. Further, the read/write window must not move across the right border marker $, that is, if the string u ends in $, then so does the string v, and after performing the rewrite operation, the read/write window is placed on the $-symbol.
and $ must not disappear from the tape nor that new occurrences of these markers are created. Further, the read/write window must not move across the right border marker $, that is, if the string u ends in $, then so does the string v, and after performing the rewrite operation, the read/write window is placed on the $-symbol. -
(3)
A restart step has the form \((q,u,{\text{ Restart }})\), where \(q\in Q\) and \(u\in {\mathcal {PC}}^{(k)}\). It causes M to move its read/write window to the left end of the tape, so that the first symbol it contains is the left border marker
 , and to reenter the initial state \(q_0\).
, and to reenter the initial state \(q_0\). -
(4)
An accept step has the form \((q,u,{\text{ Accept }})\), where \(q\in Q\) and \(u\in {\mathcal {PC}}^{(k)}\). It causes M to halt and accept.
For some \(q\in Q\) and \(u\in {\mathcal {PC}}^{(k)}\), if there is no operation op such that \((q,u,{op})\in \delta \), then M necessarily halts in a corresponding situation, and we say that M rejects in this case. Further, the letters in \(\Gamma {\backslash } \Sigma \) are called auxiliary symbols.
A configuration of M is a string \(\alpha q\beta \), where \(q\in Q\), and either \(\alpha =\lambda \) and  or
or  and
and  ; here \(q\in Q\) represents the current state, \(\alpha \beta \) is the current content of the tape, and it is understood that the read/write window contains the first k symbols of \(\beta \) or all of \(\beta \) when \(|\beta |\le k\). A restarting configuration is of the form
; here \(q\in Q\) represents the current state, \(\alpha \beta \) is the current content of the tape, and it is understood that the read/write window contains the first k symbols of \(\beta \) or all of \(\beta \) when \(|\beta |\le k\). A restarting configuration is of the form  , where \(w\in \Gamma ^*\); if \(w\in \Sigma ^*\), then
, where \(w\in \Gamma ^*\); if \(w\in \Sigma ^*\), then  is an initial configuration. Thus, initial configurations are a particular type of restarting configurations. Further, we use \(\text{ Accept }\) to denote the accepting configurations, which are those configurations that M reaches by executing an accept instruction. A configuration of the form \(\alpha q \beta \) such that \(\delta \) does not contain any triple of the form \((q,\beta _1,op)\), where \(\beta _1\) is the current content of the read/write window, is a rejecting configuration. A halting configuration is either an accepting or a rejecting configuration. By \(\vdash _M\) we denote the single-step computation relation that M induces on the set of configurations, and its reflexive and transitive closure \(\vdash _M^*\) is the computation relation of M.
is an initial configuration. Thus, initial configurations are a particular type of restarting configurations. Further, we use \(\text{ Accept }\) to denote the accepting configurations, which are those configurations that M reaches by executing an accept instruction. A configuration of the form \(\alpha q \beta \) such that \(\delta \) does not contain any triple of the form \((q,\beta _1,op)\), where \(\beta _1\) is the current content of the read/write window, is a rejecting configuration. A halting configuration is either an accepting or a rejecting configuration. By \(\vdash _M\) we denote the single-step computation relation that M induces on the set of configurations, and its reflexive and transitive closure \(\vdash _M^*\) is the computation relation of M.
In general, the automaton M is nondeterministic, that is, there can be two or more instructions for the same pair (q, u), and thus, there can be more than one computation for an input word. If this is not the case, the automaton is deterministic. We use the prefix det- to denote deterministic classes of restarting automata.
We observe that any finite computation of a restarting automaton M consists of certain phases. A phase, called a cycle, starts in a restarting configuration, the head moves along the tape performing move-right operations and a rewrite operation until a restart operation is performed and thus, a new restarting configuration is reached. If no further restart operation is performed, any finite computation necessarily finishes in a halting configuration—such a phase is called a tail. We require that M performs exactly one rewrite operation during any cycle—thus each new phase starts on a shorter word than the previous one. During a tail at most one rewrite operation may be executed. By \(\vdash ^c_M\) we denote the execution of a complete cycle, and \(\vdash ^{c^*}_M\) is the reflexive transitive closure of this relation. It can be seen as the rewrite relation that is realized by M on the set of restarting configurations.
An input \(w\in \Sigma ^*\) is accepted by M, if there exists a computation of M which starts with the initial configuration  , and which finally ends with executing an accept instruction. The language L(M) accepted by M is the set that consists of all input strings that are accepted by M.
, and which finally ends with executing an accept instruction. The language L(M) accepted by M is the set that consists of all input strings that are accepted by M.
In the following, we introduce some restricted types of restarting automata. A restarting automaton is called an RWW-automaton if it makes a restart immediately after performing a rewrite operation. In particular, this means that it cannot perform a rewrite step during the tail of a computation. An RRWW-automaton is called an RRW-automaton if its tape alphabet \(\Gamma \) coincides with its input alphabet \(\Sigma \), that is, if no auxiliary symbols are available. It is an RR-automaton if it is an RRW-automaton such that, for each rewrite transition \((q,u,q',v)\in \delta \), v is a scattered subword of u. Analogously, we obtain the RW-automaton and the R-automaton from the RWW-automaton.
For a type X of restarting automata, let \({\mathcal L}(X)\) denote the class of languages that are accepted by the restarting automata of type X. As shown by Niemann and Otto (2000),
where CRL denotes the class of Church–Rosser languages introduced by McNaughton et al. (1988), and that
where GCSL denotes the class of growing context-sensitive languages introduced by Dahlhaus and Warmuth (1986). Jurdziński et al. (2004) proved that the language classes \({\mathcal L}(\text{ RWW })\) and \({\mathcal L}(\text{ RRWW })\) are closed under union, concatenation, and reversal, but not under projection, and that
In passing we remark that it is still open whether or not the latter inclusion above is proper. Next we present a simple example of a restarting automaton.
Example 1
Let  be the RR-automaton that is defined by taking \(Q:=\{q_0,q_c,q_d,q_e\}\), \(\Gamma :=\Sigma :=\{a,b,c,d\}\), and \(k:=3\), where \(\delta \) contains the following transitions:
be the RR-automaton that is defined by taking \(Q:=\{q_0,q_c,q_d,q_e\}\), \(\Gamma :=\Sigma :=\{a,b,c,d\}\), and \(k:=3\), where \(\delta \) contains the following transitions:

For example, \(M_1\) can execute the following computations on the input aabbc, where we write \(\vdash \) for \(\vdash _{M_1}\):

The configuration  does not admit any transition step anymore, that is, \(M_1\) halts without accepting. However, from the configuration
does not admit any transition step anymore, that is, \(M_1\) halts without accepting. However, from the configuration  , \(M_1\) can continue as follows:
, \(M_1\) can continue as follows:

Accordingly, \(M_1\) accepts on input aabbc. It is easily seen that the language \(L(M_1)\) that is accepted by \(M_1\) is
3 Definitions and examples
A restarting automaton M is a language accepting device: Given a word \(w\in \Sigma ^*\) as input, it either accepts or rejects. But in case of acceptance, one may be interested in the number of accepting computations of M on input w, or one may be interested in the least number of steps (or cycles) in such an accepting computation.
For answering such quantitative questions in the setting of finite automata, the notion of weighted finite automaton was introduced by Schützenberger (1961) (see also, e.g., Droste and Kuich 2009). Such an automaton consists of a finite automaton A and a weight function \(\omega \) that associates elements of a semiring S to the transitions of A. Following the same fundamental idea, we define the notion of weighted restarting automaton.
Definition 4
-
(a)
Let
 be a restarting automaton. A weight function \(\omega \) from M into a semiring \(S=(S,+,\cdot ,0,1)\) is a function \(\omega :\delta \rightarrow S\), that is, \(\omega \) assigns an element of S as a weight to each tuple \((q,u,op)\in \delta \).
be a restarting automaton. A weight function \(\omega \) from M into a semiring \(S=(S,+,\cdot ,0,1)\) is a function \(\omega :\delta \rightarrow S\), that is, \(\omega \) assigns an element of S as a weight to each tuple \((q,u,op)\in \delta \). -
(b)
A weighted restarting automaton of type X, a wX-automaton for short, is a pair \((M,\omega )\), where M is a restarting automaton of type X, and \(\omega \) is a weight function from M into a semiring S.
-
(c)
Let \((M,\omega )\) be a weighted restarting automaton, where \(\omega \) is a weight function from M into the semiring \(S=(S,+,\cdot ,0,1)\). If \(c_1\) and \(c_2\) are configurations of M such that \(c_1\vdash _M c_2\) holds, then there exists a transition \((q,u,{op})\in \delta \) such that \(c_2\) is obtained from \(c_1\) by applying this transition. By \(t(c_1,c_2)\) we denote this transition, and accordingly, \(\omega (t(c_1,c_2))\) is the weight that is associated with this computational step of M. If \(C=(c_0\vdash _M c_1 \vdash _M c_2 \vdash _M \dots \vdash _M c_{n-1} \vdash _M c_n)\) is a computation of M, then \(\omega (C)\in S\) denotes the product
$$\begin{aligned}&\omega (t(c_0,c_1)) \cdot \omega (t(c_1,c_2)) \cdot \ldots \cdot \omega (t(c_{n-1},c_n)), \end{aligned}$$which is the weight of this computation. Finally, for each input word \(w\in \Sigma ^*\), let \(C_M(w)\) be the set of all accepting computations of M on input w. Then
$$\begin{aligned}&f^M_\omega (w) := \left( \sum _{C\in C_M(w)} \omega (C)\right) \in S \end{aligned}$$is the element of S that is associated to w by \((M,\omega )\), that is, \(f^M_\omega \) is a function from \(\Sigma ^*\) into S.
Observe that each computation C of M is of finite length, and so \(\omega (C)\) is defined as a finite product in S. Further, for each \(w\in \Sigma ^*\), the set \(C_M(w)\) of accepting computations of M on input w is also finite, which implies that \(f^M_\omega (w)\) is obtained as a finite sum in S. These observations imply that indeed \(f^M_\omega \) is a well-defined function from \(\Sigma ^*\) into S. If \(w\not \in L(M)\), then \(C_M(w)\) is empty, which means that \(f^M_\omega (w)=0\) holds.
For a type X of restarting automata, we are interested in the class of functions that are induced by wX-automata. Accordingly, we introduce the following notion.
Definition 5
For a type X of restarting automata, a finite alphabet \(\Sigma \), and a semiring S, let \(\mathbb {F}(\mathsf{X},\Sigma ,S)\) denote the set of all functions of the form \(f^M_\omega :\Sigma ^*\rightarrow S\), where M is a restarting automaton of type X with input alphabet \(\Sigma \), and \(\omega \) is a weight function from M into the semiring S.
We continue with some examples that are obtained from the RR-automaton \(M_1\) of Example 1 by combining it with different weight functions.
Example 2
Let  be the RR-automaton from Example 1 that accepts the language \(L(M_1) = L_1 =\{\,a^nb^nc,a^nb^{2n}d \mid n\ge 0\,\}\).
be the RR-automaton from Example 1 that accepts the language \(L(M_1) = L_1 =\{\,a^nb^nc,a^nb^{2n}d \mid n\ge 0\,\}\).
-
(a)
Let \(\mathbb {B}=(\mathbb {B},\vee ,\wedge ,0,1)\) be the Boolean semiring, and let \(\omega _1\) be the weight function that assigns weight 1 to each transition of \(M_1\). Then \(\omega _1(C)=1\) for each computation of \(M_1\), and
$$\begin{aligned} f^{M_1}_{\omega _1}(w) = \left\{ \begin{array}{ll} 1, &{} \quad \text{ for } w\in L_1\\ 0, &{} \quad \text{ for } w\not \in L_1 \end{array}\right\} , \end{aligned}$$that is, \(f^{M_1}_{\omega _1}:\Sigma ^*\rightarrow \mathbb {B}\) is simply the characteristic function of the language \(L_1\).
-
(b)
Let \(\mathbb {N}^\infty =(\mathbb {N}^\infty ,\min ,+,\infty ,0)\) be the tropical semiring, and let \(\omega _2\) be the weight function that assigns weight 1 to each restart transition of \(M_1\), and that assigns weight 0 to all other transitions of \(M_1\). Then \(\omega _2(C)= {|C|_\mathrm{rs}}\) for each computation C of \(M_1\), where \(|C|_\mathrm{rs}\) denotes the number of restart steps in C. Although \(M_1\) is nondeterministic (see its rewrite transitions), it has only a single accepting computation C(w) for each word \(w\in L_1\). Accordingly,
$$\begin{aligned} f^{M_1}_{\omega _2}(w) = \left\{ \begin{array}{ll} {|C(w)|_\mathrm{rs}}, &{} \quad \text{ for } w\in L_1\\ \infty , &{} \quad \text{ for } w\not \in L_1 \end{array}\right\} . \end{aligned}$$ -
(c)
Let \((\mathbb {P}_\mathrm{fin}(\Delta ^*),\cup ,\cdot ,\emptyset ,\{\lambda \})\) be the semiring of finite languages over the finite alphabet \(\Delta =\{c,d\}\), and let \(\omega _3\) be the weight function that assigns the set \(\{c\}\) to the transitions
 and
and  , that assigns the set \(\{dd\}\) to
, that assigns the set \(\{dd\}\) to  , and that assigns the set \(\{\lambda \}\) to all other transitions. It can now be checked easily that, for all \(n\ge 0\), $$\begin{aligned} f^{M_1}_{\omega _3}(a^nb^nc) = \{c^n\} \end{aligned}$$
, and that assigns the set \(\{\lambda \}\) to all other transitions. It can now be checked easily that, for all \(n\ge 0\), $$\begin{aligned} f^{M_1}_{\omega _3}(a^nb^nc) = \{c^n\} \end{aligned}$$and
$$\begin{aligned} f^{M_1}_{\omega _3}(a^nb^{2n}d) = \{d^{2n}\}, \end{aligned}$$and that \(f^{M_1}_{\omega _3}(w) = \emptyset \) for all \(w\not \in L_1\). Hence, using weight functions of this form, the restarting transducers of Hundeshagen (2013) can be simulated.
-
(d)
Let \(\overline{\mathbb {N}} = (\overline{\mathbb {N}},\max ,+,-\infty ,0)\) be the arctic semiring. Let \(\omega _4\) be the weight function that assigns weight 2 to the transitions \((q_0,abc,q_e,c)\) and \((q_0,abb,q_c,b)\), weight 3 to \((q_0,abb,q_d,\lambda )\), and weight 0 to all other transitions. Then \(\omega _4(C)\) is the number of symbols that are deleted in the course of the computation C, and accordingly,
$$\begin{aligned} f^{M_1}_{\omega _4}(w) = \left\{ \begin{array}{ll} 2n, &{} \quad \text{ for } w=a^nb^nc,\\ 3n, &{} \quad \text{ for } w=a^nb^{2n}d,\\ -\infty , &{} \quad \text{ for } w\not \in L_1. \end{array}\right. \end{aligned}$$
We continue with an example of a nondeterministic RWW-automaton.
Example 3
Let \(L_2:=\{\,w_1w_1^Rw_2w_2^R\dots w_nw_n^R\mid n\ge 1, w_i\in \{a,b\}^+, |w_i|\equiv 0 \mod 2, i=1,\dots ,n\,\}\), and let  be the RWW-automaton that is defined by taking
be the RWW-automaton that is defined by taking
-
\(Q:=\{q_0,q_r\}\), \(\Sigma :=\{a,b\}\), \(k:=4\),
-
\(\Gamma := \{a,b,\#\}\cup \{\,[c,d]\mid c,d\in \Sigma \,\}\),
-
and by defining the transition relation \(\delta \) as follows, where \(c,d,e,f,g,h,x\in \Sigma \):

For example, \(M_2\) can execute the following computation:

In fact, it can be shown that \(L(M_2)=L_2\) holds, and that on input \(w\in \Sigma ^+\), \(M_2\) has an accepting computation for each factorization of w of the form \(w=w_1w_1^Rw_2w_2^R\dots w_nw_n^R\) such that \(w_i\in \Sigma ^+\) and \(|w_i|\equiv 0 \mod 2\) for all \(i=1,\dots ,n\).
-
(a)
Let \(\mathbb {N}^\infty =(\mathbb {N}^\infty ,\min ,+,\infty ,0)\) be the tropical semiring, and let \(\omega _1\) be the weight function that assigns weight 1 to each transition of the groups (3) and (9) of \(M_2\), and that assigns weight 0 to all other transitions of \(M_2\). Then, for each computation C of \(M_2\), \(\omega _1(C)\) is the number of times the symbol # is introduced during C, and hence, if C is an accepting computation on input w, then this is the number n of factors \(w_iw_i^R\) in the factorization of w that is guessed in the course of this computation. Accordingly, \(f^{M_2}_{\omega _1}(w)=\)
$$\begin{aligned} \left\{ \begin{array}{ll} \text{ minimal } \text{ number } \text{ of } \text{ factors } \text{ of } w, &{} \quad \text{ for } w\in L_2\\ \infty , &{} \quad \text{ for } w\not \in L_2 \end{array}\right\} . \end{aligned}$$ -
(b)
Let \((\mathbb {P}_\mathrm{fin}(\Gamma ^*),\cup ,\cdot ,\emptyset ,\{\lambda \})\) be the semiring of finite languages over the finite alphabet \(\Gamma =\{a,b,\#\}\), and let \(\omega _2\) be a weight function that assigns the set \(\{cd\}\) to the transitions of group (1), \(\{ef\}\) to the transitions of group (2), and \(\{gh\}\) to the transitions of group (8), that assigns the set \(\{\#\}\) to the transitions of the groups (3) and (9), and that assigns the set \(\{\lambda \}\) to all other transitions. It can now be checked that \(\omega _2(C)=\{aaba\#ab\#\}\) for the computation C on input \(w=aabaabaaabba\) presented above. It follows that
$$\begin{aligned} f^{M_2}_{\omega _2}(w) = \left\{ \,w_1\#\dots \#w_n\#\mid w=w_1w_1^R\dots w_nw_n^R\,\right\} , \end{aligned}$$that is, \(f^{M_2}_{\omega _2}(w)\) is the set of possible factorizations that witness that w belongs to \(L_2\).
Examples 2 and 3 clearly show that weighted restarting automata can be used to express interesting quantitative aspects of computations and of languages of restarting automata. We close this section with the following inclusion relation.
Proposition 1
For each semiring S, each alphabet \(\Sigma \), and each type of restarting automaton X,
If S is a commutative semiring that is zero-sum free, then this inclusion is proper.
Proof
Let \(A=(Q,{\mathrm {in}},\omega ,{\mathrm {out}})\) be a weighted automaton with input alphabet \(\Sigma \) over the semiring S. To prove the statement above, it suffices to construct a weighted R-automaton  and a weight function \(\omega '\) such that \(||A||(w) = f^{M}_{\omega '}(w)\) holds for all \(w\in \Sigma ^*\). We define the weighted R-automaton \((M,\omega ')\) by taking
and a weight function \(\omega '\) such that \(||A||(w) = f^{M}_{\omega '}(w)\) holds for all \(w\in \Sigma ^*\). We define the weighted R-automaton \((M,\omega ')\) by taking
-
\(Q':=Q\cup \{q_0\}\), where \(q_0\) is a new state,
-
and by defining \(\delta \) and \(\omega '\) as follows, where \(p,q\in Q\) and \(a\in \Sigma \):

Then, for all \(w\in \Sigma ^*\), the paths in A with label w are in one-to-one correspondence to the accepting computations of M on input w. From the definition of the weight function \(\omega '\) and the fact that each accepting computation of M begins with a transition of type \(t_{q_0,p}\) and ends with a transition of type \(t_{q,\$}\), it now follows immediately that \(||A||(w) = f^{M}_{\omega '}(w)\) holds.
Now let \(S=(S,+,\cdot ,0,1)\) be a commutative semiring that is zero-sum free, that is, \(s+t\not =0\) for all \(s,t\in S{\backslash }\{0\}\). Then the support \(\{\,w\in \Sigma ^*\mid ||A||(w)\not =0\,\}\) of each recognizable series \(||A||\in S_{\mathrm {REC}}\langle \langle \Sigma ^*\rangle \rangle \) is a regular language by Kirsten (2009) (see also Kirsten 2011). As already R-automata accept non-regular languages (see, e.g., Otto 2006), it is clear that in this case the inclusion \(S_{\mathrm {REC}}\langle \langle \Sigma ^*\rangle \rangle \subseteq {\mathbb {F}}(\mathsf{X},\Sigma ,S)\) is strict. \(\square \)
4 Results
In this section, we present our results on the properties of the functions that are induced by weighted restarting automata.
4.1 Growth rates
In a linearly ordered semiring S (see Sect. 2.1), the maximum and the minimum of a finite subset T of S can be defined.
Definition 6
If \(S=(S,+,\cdot ,0,1)\) is a semiring that is ordered with respect to a linear order \(\le \), then
and
for each finite non-empty subset T of S.
Definition 7
Let \(S=(S,+,\cdot ,0,1)\) be a linearly ordered semiring, let M be a restarting automaton of type X with input alphabet \(\Sigma \), and let \(\omega \) be a weight function that maps the transitions of M into S. As \(\Sigma ^n\) is finite for all \(n\ge 0\), we can extend the function \(f^M_\omega :\Sigma ^*\rightarrow S\) to a function \(\hat{f}^M_\omega :\mathbb {N}\rightarrow S\) as follows:
By \(\hat{\mathbb {F}}(\mathsf{X},\Sigma ,S)\) we denote the set of all functions of the form \(\hat{f}^M_\omega :\mathbb {N}\rightarrow S\), where M is a restarting automaton of type X with input alphabet \(\Sigma \).
In the following, we provide an upper bound for a large subclass of functions in \(\hat{\mathbb {F}}(\mathsf{X},\Sigma ,S)\). For \(s\in S\) and \(k\in \mathbb {N}\), we use the notation \(s^k\) to denote the k-fold product \(s\cdot s\cdot \ldots \cdot s\). In addition, \(k\cdot s\) is used to denote the k-fold sum \(s+s+\cdots +s\).
Theorem 1
Let \(S=(S,+,\cdot ,0,1)\) be a semiring that is ordered with respect to a linear order \(\le \), let M be a restarting automaton, and let \(\omega \) be a weight function that maps the transitions of M into the subset \(S_+ = \{\,s\in S\mid s\ge 0\,\}\) of S. Further, let \(s_M = \max (\{\,\omega (t) \mid t \text{ is } \text{ a } \text{ transition } \text{ of } M \,\}\cup \{1\})\). Then there exist constants \(c_1,c_2\in \mathbb {N}\) such that, for all \(n\ge 1\), \(\hat{f}^M_\omega (n) \le c_1^{n^2}\cdot s_M^{c_2\cdot n^2}\) holds.
Proof
In order to derive the intended upper bound for the function \(\hat{f}^M_\omega :\mathbb {N}\rightarrow S\), we have to answer the following two questions:
-
(1)
What is the maximal length of a computation of M on an input of length n? For \(n\ge 0\), let
$$\begin{aligned} \hat{l}_M(n) = \max \{\, |C| \mid C\in C_M(w), w \in \Sigma ^{n}\,\}, \end{aligned}$$where |C| denotes the number of steps in the computation C, that is, its length, and \(C_M(w)\) is the set of accepting computations of M on input w.
-
(2)
What is the maximal number of accepting computations of M for any input of length n? For \(n\ge 0\), let
$$\begin{aligned} \hat{r}_M(n) = \max \{\, |C_M(w)| \mid w \in \Sigma ^{n}\, \}, \end{aligned}$$where \(|C_M(w)|\) denotes the cardinality of the set \(C_M(w)\).
Then we obviously have
for all \(n\ge 1\). Hence, it suffices to derive upper bounds for the numbers \(\hat{l}_M(n)\) and \(\hat{r}_M(n)\).
First, we consider the former number. For an integer \(n\ge 1\), let \({\mathrm {mcl}}_M(n)\) denote the maximal number of steps in any cycle of M on any input of length at most n. From the definition of the restarting automaton it follows that \({\mathrm {mcl}}_M(n) \le n+2\), as a cycle of M that begins with a tape inscription of the form  , where \(|w|=n\), contains exactly one rewrite operation, one restart operation, and up to at most n move-right steps. Analogously, a tail computation that begins with the above tape inscription consists of at most \(n+2\) steps, where an accept step may replace the restart step. Further, the rewrite operation that M executes within a cycle shortens the length of the tape inscription, and so, each new cycle starts on a shorter word than the previous one. Hence, for any input w of length at most n, the length of any computation of M on input w is bounded from above by the number
, where \(|w|=n\), contains exactly one rewrite operation, one restart operation, and up to at most n move-right steps. Analogously, a tail computation that begins with the above tape inscription consists of at most \(n+2\) steps, where an accept step may replace the restart step. Further, the rewrite operation that M executes within a cycle shortens the length of the tape inscription, and so, each new cycle starts on a shorter word than the previous one. Hence, for any input w of length at most n, the length of any computation of M on input w is bounded from above by the number
that is, we see that \(\hat{l}_M(n) \le 5\cdot n^2\) holds for all \(n \ge 1\).
Now, we turn to the number \(\hat{r}_M(n)\). Let \(d_M\) denote the maximal number of instructions of the form (q, u, op) of M for any state q of M and any possible window content u. Then any configuration of M has at most \(d_M\) many immediate successor configurations. Hence, it follows that
for all \(n\ge 1\). Thus, we obtain that
for all \(n\ge 1\), that is, the statement in the theorem holds with the constants \(c_1=d_M^5\) and \(c_2=5\). \(\square \)
Our next result shows that the upper bound given in the theorem above is actually sharp.
Theorem 2
Let \(S=(S,+,\cdot ,0,1)\) be a linearly ordered semiring, let \(s\in S\) such that \(s\ge 0\), let \(\Sigma \) be a finite alphabet, and let \(c_1,c_2\in \mathbb {N}_+\). Then there exist a det-R-automaton M with input alphabet \(\Sigma \) and a weight function \(\omega \) for M such that
holds for all \(n\ge 0\).
Proof
We define a det-R-automaton  , where \(Q:=\{q_0,q_1,q_r\}\) and \(\delta \) contains the following transitions:
, where \(Q:=\{q_0,q_1,q_r\}\) and \(\delta \) contains the following transitions:

For example, M executes the following computation given \(w=aabb\) as input, where \(a,b\in \Sigma \):

As M is deterministic, it only has a single computation for each input. Actually, it is easily seen that \(L(M)=\Sigma ^*\), and that, for each word \(w\in \Sigma ^n\), the accepting computation of M on input w consists of n cycles. For a tape inscription x of length \(k>0\), the cycle starting from the restarting configuration  consists of k move-right steps, a single rewrite step that deletes the last symbol of x, and a restart step, that is, it has length \(k+2\). As the tail computation consists of a single accept step, we see that
consists of k move-right steps, a single rewrite step that deletes the last symbol of x, and a restart step, that is, it has length \(k+2\). As the tail computation consists of a single accept step, we see that
for each computation C of M on any input of length n, that is, \(\hat{l}_M(n)=\frac{1}{2}(n^2+5n+2)\) in the notation of the proof of the previous theorem.
Now we define the weight function \(\omega \) by taking
for each transition t of M. It follows that
for each word \(w\in \Sigma ^n\), which implies that
for all \(n\ge 0\). \(\square \)
In the remaining part of this section, we restrict our attention to the semiring \(\mathbb {N}=(\mathbb {N},+,\cdot ,0,1)\) with the standard order, and we present some families of functions from \(\mathbb {N}\) into that semiring that are contained in the class of growth functions \(\hat{\mathbb {F}}(\text{ RWW },\{a\},\mathbb {N})\).
Theorem 3
For all constants \(c_1,c_2\in \mathbb {N}_+\), there exist a det-R-automaton M with input alphabet \(\Sigma =\{a\}\) and a weight function \(\omega \) such that \(\hat{f}^M_\omega (n)= c_1\cdot c_2^n\) holds for all \(n\ge 0\).
Proof
We define a det-R-automaton  , where \(Q:=\{q_0,q_r\}\) and \(\delta \) contains the following transitions:
, where \(Q:=\{q_0,q_r\}\) and \(\delta \) contains the following transitions:

Then it is easily seen that \(L(M)=\Sigma ^*\). Each cycle of any computation of M consists of exactly two steps, that is, a rewrite and a restart step, the tail computation for the tape inscription  consists of two steps, that is, a move-right step and an accept step, and the tail computation for the tape inscription
consists of two steps, that is, a move-right step and an accept step, and the tail computation for the tape inscription  consists of a single accept step. Thus, it follows that \(\hat{l}_{M}(n) = 2n\) for all \(n\ge 1\), and \(\hat{l}_M(0) = 1\).
consists of a single accept step. Thus, it follows that \(\hat{l}_{M}(n) = 2n\) for all \(n\ge 1\), and \(\hat{l}_M(0) = 1\).
Let \(c_1,c_2\in \mathbb {N}_+\), and let \(\omega \) be the weight function that assigns weight \(c_1\) to the two accept transitions, that assigns weight \(c_2\) to all rewrite and move-right transitions, and that assigns weight 1 to all restart transitions. For \(n\ge 1\), the computation of M on input \(a^n\) contains \(n-1\) rewrite steps, \(n-1\) restart steps, a single move-right step, and a single accept step, and hence, we see that \(f^M_\omega (a^n) = c_1\cdot c_2^n\) for \(n\ge 1\), and \(f^M_\omega (a^0) = f^M_\omega (\lambda ) = c_1 = c_1\cdot c_2^0\). \(\square \)
Theorem 4
For all constants \(c,k\in \mathbb {N}_+\), there exist a det-RWW-automaton M with input alphabet \(\Sigma =\{a\}\) and a weight function \(\omega \) such that
Proof
Let  be the det-RWW-automaton that is defined by taking \(Q:=\{q_0, q_r\}\) and \(\Gamma :=\{a,b,A\}\), and by defining \(\delta \) as follows, where
be the det-RWW-automaton that is defined by taking \(Q:=\{q_0, q_r\}\) and \(\Gamma :=\{a,b,A\}\), and by defining \(\delta \) as follows, where  :
:

For example, M can execute the following computation given \(w=aaaa\) as input:

It is easily seen that \(L(M) = \{\,a^{2^n}\mid n\ge 0\,\}.\)
Now let \(c,k\in \mathbb {N}_+\). We define the weight function \(\omega \) by assigning weight \(2^k\) to transitions (8), (10), and (12), by assigning weight c to transitions (14), (15), and (16), and by assigning weight 1 to all other transitions. Given \(a^{2^m}\) as input, M first executes \(2^{m-1}\) cycles, in which \(a^{2^m}\) is rewritten into \(b^{2^{m-1}}\). In the first of these cycles, rewrite transition (8) is used, while in the other cycles, rewrite transition (7) is used. Thus, this part of the computation has weight \(2^k\). Next the tape inscription \(b^{2^{m-1}}\) is rewritten into \(A^{2^{m-2}}\) within \(2^{m-2}\) cycles, where in the first cycle rewrite transition (10) is used, while in the other cycles, rewrite transition (9) is used. Thus, also this part of the computation has weight \(2^k\). Finally, the tape inscription \(A^{2^{m-2}}\) is rewritten into \(b^{2^{m-3}}\) within \(2^{m-3}\) cycles, where in the first cycle rewrite transition (12) is used, while in the other cycles, rewrite transition (11) is used. Thus, also this part of the computation has weight \(2^k\). The latter two types of sequences of cycles alternate until tape inscription b or A is reached, which is then accepted by using transition (15) or (16). It follows that, if \(n=2^m\) for some \(m\ge 0\), then
and \(f^M_\omega (a^n) = 0\), if n is not a power of 2. \(\square \)
Exploiting nondeterminism, we can generalize the above result as follows.
Theorem 5
For each polynomial P(x) over \(\mathbb {N}\), there exist an RWW-automaton M with input alphabet \(\Sigma =\{a\}\) and a weight function \(\omega \) such that
Proof
Let P(x) be a polynomial over \(\mathbb {N}\), that is,
where \(r\ge 0\), \(c_1,k_1,c_2,k_2,\ldots ,c_r,k_r\ge 1\), and \(d\ge 0\).
For the proof we use an RWW-automaton M that essentially consists of \(r+1\) copies of the RWW-automaton from the proof of the previous theorem. Accordingly, we define  by taking \(Q:=\{q_0,q_r\}\) and \(\Gamma := \{\,a,b_i,A_{i}\mid i=1,\ldots ,r+1\, \}\), and by defining \(\delta \) as follows:
by taking \(Q:=\{q_0,q_r\}\) and \(\Gamma := \{\,a,b_i,A_{i}\mid i=1,\ldots ,r+1\, \}\), and by defining \(\delta \) as follows:

Then \(L(M)=\{\,a^{2^n}\mid n\ge 0\,\}\), and it is easily seen that, for each \(n\ge 1\), M has \(r+1\) accepting computations on input \(a^{2^n}\), one for each choice of auxiliary symbols \(b_i\) and \(A_i\) (\(1\le i\le r+1\)) that are used in the course of the computation (see instructions (4.i)).
Now we define a weight function \(\omega \) as follows, where t denotes an instruction of \(\delta \) according to the above definition:
As in the proof of Theorem 4, it now follows that the computation of M on input \(a^{2^m}\) (\(m\ge 1\)) that uses the auxiliary symbols \(b_i\) and \(A_i\) for some \(i\in \{1,\ldots ,r\}\) has weight \(c_i\cdot \left( 2^{k_i}\right) ^{m}\). Further, the corresponding computation that uses the auxiliary symbols \(b_{r+1}\) and \(A_{r+1}\) has weight d. Accordingly, it follows that, if \(n=2^m\) for some \(m\ge 1\), then
Further, we have \(f^M_\omega (a) = P(1)\), and \(f^M_\omega (a^n)=0\), if n is not a power of two. This completes the proof of Theorem 5. \(\square \)
By combining the RWW-automaton from the proof of the last theorem with the det-R-automaton from the proof of Theorem 3, it can be shown that weighted restarting automata can also represent functions that can be expressed as a sum of a polynomial and exponential functions. Thus, we see that the class of functions \(\hat{\mathbb {F}}({\text{ RWW }},\{a\},(\mathbb {N},+,\cdot ,0,1))\) is quite rich.
4.2 Closure Properties
Jurdziński et al. (2004) proved that the language classes \({\mathcal L}(\text{ RWW })\) and \({\mathcal L}(\text{ RRWW })\) are closed under the operations of union and concatenation. Here we extend these results to weighted RWW- and RRWW-automata by showing that the classes of functions \({\mathbb {F}}(\mathsf{RWW},\Sigma ,S)\) and \({\mathbb {F}}(\mathsf{RRWW},\Sigma ,S)\) are closed under the operations of addition, scalar multiplication, and Cauchy product, that is, if \(f,g:\Sigma ^*\rightarrow S\) belong to \({\mathbb {F}}(\mathsf{RWW},\Sigma ,S)\) (or \({\mathbb {F}}(\mathsf{RRWW},\Sigma ,S)\)), then also the functions \((f+g)\), \((s\cdot f)\) (for \(s\in S\)), and \((f\cdot g):\Sigma ^*\rightarrow S\) belong to this class of functions, where, for all \(w\in \Sigma ^*\),
and
Hence, if \(M_1\) and \(M_2\) are two restarting automata of type RWW (or RRWW) with input alphabet \(\Sigma \), and if \(\omega _1\) and \(\omega _2\) are weight functions for \(M_1\) and \(M_2\), respectively, then there exist restarting automata of the same type as \(M_1\) and \(M_2\), say \(M_+,M_s\), and \(M_c\), and weight functions \(\omega _+,\omega _s\), and \(\omega _c\) such that \(f^{M_+}_{\omega _+} = f + g\), \(f^{M_s}_{\omega _s} = s\cdot f\), and \(f^{M_c}_{\omega _c} = f\cdot g\). We begin with the operation of addition.
Theorem 6
For all alphabets \(\Sigma \) and semirings S, the classes of functions \(\mathbb {F}(\text{ RWW },\Sigma ,S)\) and \(\mathbb {F}(\text{ RRWW },\Sigma ,S)\) are closed under the operation of addition.
Proof
Let \(S=(S,+,\cdot ,0,1)\) be a semiring, let \(\Sigma \) be a finite alphabet, let  and
and  be RWW-automata with input alphabet \(\Sigma \), and let \(\omega _1\) and \(\omega _2\) be weight functions that map the transitions of \(M_1\) and of \(M_2\) to S. In order to prove that \(\mathbb {F}({\text{ RWW }},\Sigma ,S)\) is closed under the operation of addition, we construct an RWW-automaton \(M_+\) with input alphabet \(\Sigma \) and a weight function \(\omega _+\) such that
be RWW-automata with input alphabet \(\Sigma \), and let \(\omega _1\) and \(\omega _2\) be weight functions that map the transitions of \(M_1\) and of \(M_2\) to S. In order to prove that \(\mathbb {F}({\text{ RWW }},\Sigma ,S)\) is closed under the operation of addition, we construct an RWW-automaton \(M_+\) with input alphabet \(\Sigma \) and a weight function \(\omega _+\) such that
holds for all \(w\in \Sigma ^*\).
On input \(w\in \Sigma ^*\), the automaton \(M_+\) will have the option to either simulate a computation of \(M_1\) or a computation of \(M_2\) on input w. However, as \(M_+\) is reset to its initial state by each restart operation, it will not be able to store its choice within its finite-state control. Therefore, it has to store this information on the tape in such a way that it can read this information right after performing a restart step. Accordingly, \(M_+\) will store it in the first field to the right of the left sentinel  . Unfortunately, this causes another problem, as each rewrite step must be strictly length-reducing. The solution consists in rewriting the prefix
. Unfortunately, this causes another problem, as each rewrite step must be strictly length-reducing. The solution consists in rewriting the prefix  of length three of the tape content
of length three of the tape content  by
by  , where \([a_1,a_2,i]\) is a new symbol that encodes the input symbols \(a_1\) and \(a_2\) and the information (\(i=1\) or \(i=2\)) about the automaton that \(M_+\) has chosen to simulate.
, where \([a_1,a_2,i]\) is a new symbol that encodes the input symbols \(a_1\) and \(a_2\) and the information (\(i=1\) or \(i=2\)) about the automaton that \(M_+\) has chosen to simulate.
This solves the problem above, but it causes still another technical problem. In some later transition, the automaton \(M_1\) (or \(M_2\)) being simulated may just delete the symbol \(a_1\) or \(a_2\) without changing any other symbol, which means that \(M_+\) would have to replace the symbol \([a_1,a_2,i]\) by some symbol encoding the remaining symbol \(a_2\) (or \(a_1\)) together with the indicator i, that is, this rewrite step of \(M_+\) would not be length-reducing. To overcome this problem, \(M_+\) will combine the pair \((a_2,i)\) (or \((a_1,i)\)) with the next symbol, say x, into the new symbol \([a_2,x,i]\) (or \([a_1,x,i]\)), which means that \(M_+\) needs a read/write window that is larger than those of \(M_1\) and \(M_2\). Thus, we see that in order to realize the above idea, the construction of \(M_+\) is quite involved. We now present the details of this construction. Together with \(M_+\), we also describe the weight function \(\omega _+\).
Let  be the RWW-automaton that is defined as follows:
be the RWW-automaton that is defined as follows:
-
\(\begin{array}{llll} Q &{} := &{} \{q_0, q_r\} \cup \{\,q^{(1)} \mid q \in Q_1\,\} \cup \{\,q^{(2)} \mid q \in Q_2\,\}\\ &{} &{} \cup \, \{\,q_{\mathrm {MVR}}^{(i)}, q_a^{(i)}, q_{a'}^{(i)}, q_{0'}^{(i)}, q_{0''}^{(i)} \mid i = 1,2\, \}, \end{array}\)
-
\(\begin{array}{llll} \Gamma &{} := &{} \Gamma _1 \cup \Gamma _2\\ &{} &{} \cup \, \{\,[a_1,a_2,1],[a_1,1],[1] \mid a_1, a_2 \in \Gamma _1\,\}\\ &{} &{} \cup \, \{\,[a_1,a_2,2],[a_1,2],[2] \mid a_1, a_2 \in \Gamma _2\,\}, \end{array}\)
-
\(k := \max \{k_1, k_2 \} + 1\), and
-
the transition relation \(\delta \) and the weight function \(\omega _+\) are as described below.
We now present the definition of \(\delta \) step by step. Here we only consider the case that \(k_1,k_2\ge 3\), which means that \(k\ge 4\), as it is easily seen how to simulate an automaton with window size 1 or 2 by an automaton with window size 3. For example, each transition of the form \(t:(q,u,q',\text{ MVR })\) of \(M_i\), where \(u \in \Gamma \), can be replaced by the set of transitions  , where all these transitions are assigned the weight \(\omega _i(t)\), and analogously for the other types of transitions and for \(|u|=2\).
, where all these transitions are assigned the weight \(\omega _i(t)\), and analogously for the other types of transitions and for \(|u|=2\).
-
1.
First we define some transitions that enable \(M_+\) to deal with those inputs \(w\in \Sigma ^*\) that satisfy the condition \(|w|\le k-2\) by introducing, for all \(w\in \Sigma ^{\le k-2}\), the following transition, if \(w\in L(M_1)\cup L(M_2)\):
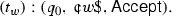
In addition, we define \(\omega _+(t_w) = f^{M_1}_{\omega _1}(w)+f^{M_2}_{\omega _2}(w)\). Then it is immediate that, for all input words w of length at most \(k-2\), \(f^{M_+}_{\omega _+}(w) = f^{M_1}_{\omega _1}(w)+f^{M_2}_{\omega _2}(w)\) holds.
-
2.
Next we define those transitions that allow \(M_+\) to process restarting configurations of the form
 , where \(z\in \Gamma ^+{\backslash }\Sigma ^*\) is of length at most \(k-2\), that is, the complete tape content
, where \(z\in \Gamma ^+{\backslash }\Sigma ^*\) is of length at most \(k-2\), that is, the complete tape content  is contained in the window of \(M_+\). By our strategy described above, the first letter \(z_1\) of z encodes the choice of which automaton \(M_+\) currently simulates, that is, \(z_1\in \Gamma {\backslash }(\Gamma _1\cup \Gamma _2)\). Accordingly, \(z_1=[a_1,a_2,i]\) (or \(z_1=[a_1,i]\) or \(z_1=[i]\)) for some \(a_1,a_2\in \Gamma _i\) and some \(i\in \{1,2\}\). Then \(M_+\) has an accepting transition
is contained in the window of \(M_+\). By our strategy described above, the first letter \(z_1\) of z encodes the choice of which automaton \(M_+\) currently simulates, that is, \(z_1\in \Gamma {\backslash }(\Gamma _1\cup \Gamma _2)\). Accordingly, \(z_1=[a_1,a_2,i]\) (or \(z_1=[a_1,i]\) or \(z_1=[i]\)) for some \(a_1,a_2\in \Gamma _i\) and some \(i\in \{1,2\}\). Then \(M_+\) has an accepting transition 
with weight \(\omega _+(t_z) = s_i\), where \(s_i\in S\) is the sum of the weights of all accepting computations of \(M_i\) that start from the restarting configuration
 (respectively,
(respectively,  or
or  ), where \(z=z_1z'\). During its simulation of \(M_1\) or \(M_2\), whenever \(M_+\) reaches a restarting configuration
), where \(z=z_1z'\). During its simulation of \(M_1\) or \(M_2\), whenever \(M_+\) reaches a restarting configuration  such that \(|z|\le k-2\), then the corresponding transition \(t_z\) is used, which ends the current computation. Hence, in what follows we only need to consider the case that the length of the tape content exceeds the size k of the window of \(M_+\).
such that \(|z|\le k-2\), then the corresponding transition \(t_z\) is used, which ends the current computation. Hence, in what follows we only need to consider the case that the length of the tape content exceeds the size k of the window of \(M_+\). -
3.
Now we define those transitions that allow \(M_+\) to make and fix the choice between simulating \(M_1\) or \(M_2\) on a given input word that is of length at least \(k-1\ge 3\):

where \(a_1,a_2\in \Sigma \), \(i\in \{1,2\}\), and \(x\in \Sigma ^{k-3}\). Further, we take \(\omega _+(t_{(a_1,a_2,i)}) = \omega _+(t_r) = 1\) for all \(a_1,a_2\in \Sigma \) and \(i\in \{1,2\}\).
-
4.
Here we define those transitions that allow \(M_+\) to simulate move-right steps of \(M_1\) and \(M_2\), where we must distinguish between several cases.
-
(4.1)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form

for some \(q_l\in Q_i\), \(a_1,a_2\in \Gamma _i\), and \(u\in \Gamma _i^*\) satisfying
 , then \(\delta \) contains the following transitions for all admissible choices of
, then \(\delta \) contains the following transitions for all admissible choices of  :
: 
For these transitions the weight function \(\omega _+\) is defined by taking
$$\begin{aligned}&\omega _+(\hat{t}_1) = \omega _+(\hat{t}_2) = \omega _+(\hat{t_4}) = \omega _i(t) \end{aligned}$$and \(\omega _+(\hat{t}_3) = 1\). Then \(\omega _+(\hat{t}_3) \cdot \omega _+(\hat{t}_4) = \omega _i(t)\), which corresponds to the fact that together \(\hat{t}_3\) and \(\hat{t}_4\) simulate the effect of t on a tape content of the form
 .
. -
(4.2)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form
$$\begin{aligned}&t : (q_m, a_1a_2u,q_l,\text{ MVR }) \end{aligned}$$for some \(q_m, q_l \in Q_i\), \(a_1,a_2 \in \Gamma _i\), and \(u \in \Gamma _i^*\) satisfying \(|a_1a_2u| = k_i\), then \(\delta \) contains the following transitions for all admissible choices of
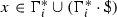 : $$\begin{aligned}&\begin{array}{rl} \hat{t}_1: &{} (q_m^{(i)}, a_1a_2ux,q_l^{(i)},\text{ MVR }), \\ \hat{t}_2: &{} (q_m^{(i)}, [a_1,i]a_2ux,q_l^{(i)},\text{ MVR }), \\ \end{array} \end{aligned}$$
: $$\begin{aligned}&\begin{array}{rl} \hat{t}_1: &{} (q_m^{(i)}, a_1a_2ux,q_l^{(i)},\text{ MVR }), \\ \hat{t}_2: &{} (q_m^{(i)}, [a_1,i]a_2ux,q_l^{(i)},\text{ MVR }), \\ \end{array} \end{aligned}$$and we take \(\omega _+(\hat{t}_1) = \omega _+(\hat{t}_2) = \omega _i(t)\).
In order to simulate the transition t correctly on a tape content of the form  , we need to combine this transition with those transitions that \(M_i\) can perform in the configuration
, we need to combine this transition with those transitions that \(M_i\) can perform in the configuration  . Based on the latter transitions, we have various options:
. Based on the latter transitions, we have various options:
-
(a)
If \(\delta _i\) contains a transition of the form
$$\begin{aligned} t'_1: (q_l, a_2ua,q_{l'},\text{ MVR }) \end{aligned}$$for some \(q_{l'} \in Q_i\), \(a \in \Gamma _i\), and \(u \in \Gamma _i^*\) satisfying \(|a_2ua| = k_i\), then \(\delta \) contains the following additional transitions for all admissible choices of
 : $$\begin{aligned} \hat{t}'_1: (q_m^{(i)}, [a_1,a_2,i]uax,q_{l'}^{(i)},\text{ MVR }), \end{aligned}$$
: $$\begin{aligned} \hat{t}'_1: (q_m^{(i)}, [a_1,a_2,i]uax,q_{l'}^{(i)},\text{ MVR }), \end{aligned}$$where \(\omega _+(\hat{t}'_1) = \omega _i(t)\cdot \omega _i(t'_1)\), as \(\hat{t}'_1\) simulates the sequence of transitions \((t,t'_1)\) of \(M_i\).
-
(b)
If \(\delta _i\) contains a transition of the form
$$\begin{aligned} t'_2: (q_l, a_2ua,q_{l'}, v) \end{aligned}$$for some \(q_{l'} \in Q_i\), \(a \in \Gamma _i\), \(u, v \in \Gamma _i^*\) such that \(|a_2ua| = k_i\) and \(|v| < k_i\), then \(\delta \) contains the following additional transitions for all admissible choices of
 : $$\begin{aligned} \hat{t}'_2: (q_m^{(i)}, [a_1,a_2,i]uax,q_{l'}^{(i)},v'x), \end{aligned}$$
: $$\begin{aligned} \hat{t}'_2: (q_m^{(i)}, [a_1,a_2,i]uax,q_{l'}^{(i)},v'x), \end{aligned}$$where
$$\begin{aligned} v'= \left\{ \begin{array}{ll} \,[a_1,i]v, &{}\quad \text{ if } |v| < |ua|,\\ \,[a_1,a_3,i]\tilde{v}, &{}\quad \text{ if } |v|=|ua| \text{ and } v = a_3\tilde{v}. \end{array} \right. \end{aligned}$$Further, we take \(\omega _+(\hat{t}'_2) = \omega _i(t)\cdot \omega _i(t'_2)\), as \(\hat{t}'_2\) simulates the sequence of transitions \((t,t'_2)\).
-
(c)
If \(\delta _i\) contains a transition of the form
$$\begin{aligned} t'_3:\ (q_l, a_2ua,\text{ Accept }) \end{aligned}$$for some \(a \in \Gamma _i\) and \(u \in \Gamma _i^*\) satisfying \(|a_2ua|=k_i\), then \(\delta \) contains the following additional transitions for all admissible words
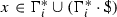 : $$\begin{aligned} \hat{t}'_3: (q_m^{(i)}, [a_1,a_2,i]uax,\text{ Accept }), \end{aligned}$$
: $$\begin{aligned} \hat{t}'_3: (q_m^{(i)}, [a_1,a_2,i]uax,\text{ Accept }), \end{aligned}$$and the weight function \(\omega _+\) is extended by taking \(\omega _+(\hat{t}'_3) = \omega _i(t) \cdot \omega _i(t'_3).\)
-
(4.3)
The case that \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form

for some \(q_m, q_l \in Q_i\), \(a_1,a_2 \in \Gamma _i\), and \(u \in \Gamma _i^*\) satisfying
 is dealt with in the same way as (4.2). However, observe that here we do not need to consider the case of a symbol of the form \([a_1,a_2,i]\), as by our construction such a symbol can only occur immediately to the right of the left sentinel
is dealt with in the same way as (4.2). However, observe that here we do not need to consider the case of a symbol of the form \([a_1,a_2,i]\), as by our construction such a symbol can only occur immediately to the right of the left sentinel  , and \(k> k_i\).
, and \(k> k_i\). -
5.
Here we present those transitions that allow \(M_+\) to simulate rewrite steps of \(M_1\) and \(M_2\). Again we must distinguish between several cases.
-
(5.1)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form

for some \(q_l\in Q_i\), \(a_1,a_2\in \Gamma _i\), and \(u,v\in \Gamma _i^*\) satisfying
 and \(|v|\le |u|+1\), then \(\delta \) contains the following transitions for all admissible choices of
and \(|v|\le |u|+1\), then \(\delta \) contains the following transitions for all admissible choices of  :
: 
Further, \(\omega _+(\hat{t}_1) = \omega _+(\hat{t}_2) = \omega _+(\hat{t}_3) = \omega _i(t)\) is chosen.
-
(5.2)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form
$$\begin{aligned} t : (q_m, a_1a_2u,q_l,v), \end{aligned}$$where \(q_m, q_l \in Q_i\), \(a_1, a_2 \in \Gamma _i\), \(u,v \in \Gamma _i^*\) satisfying \(|a_1a_2u|=k_i\) and \(|v|\le |u|+1\), then \(\delta \) contains the following transitions for all admissible choices of
 : $$\begin{aligned} \begin{array}{l} \hat{t}_1 : (q_m^{(i)},[a_1,a_2,i]ux,q_l^{(i)},\alpha x), \text{ where }\\ \alpha = \left\{ \begin{array}{ll} \,[i]v, \qquad \qquad \qquad \text{ if } |v|<|u|,\\ \,[a_3,i]\tilde{v},\qquad \qquad \text{ if } |v|=|u|,\, v=a_3\tilde{v},\\ \,[a_3,a_4,i]\tilde{v},\qquad \text{ if } |v|=|u|+1,\, v=a_3a_4\tilde{v}, \end{array} \right. \\ \hat{t}_2 : (q_m^{(i)},[a_1,i]a_2ux,q_l^{(i)},\alpha x), \text{ where }\\ \alpha = \left\{ \begin{array}{ll} \,[i]v,\qquad \qquad \text{ if } |v|\le |u|,\\ \,[a_3,i]\tilde{v}, \qquad \text{ if } |v|=|u|+1,\, v=a_3\tilde{v}, \end{array} \right. \\ \hat{t}_3 : (q_m^{(i)},a_1a_2ux,q_l^{(i)},vx).\\ \end{array} \end{aligned}$$
: $$\begin{aligned} \begin{array}{l} \hat{t}_1 : (q_m^{(i)},[a_1,a_2,i]ux,q_l^{(i)},\alpha x), \text{ where }\\ \alpha = \left\{ \begin{array}{ll} \,[i]v, \qquad \qquad \qquad \text{ if } |v|<|u|,\\ \,[a_3,i]\tilde{v},\qquad \qquad \text{ if } |v|=|u|,\, v=a_3\tilde{v},\\ \,[a_3,a_4,i]\tilde{v},\qquad \text{ if } |v|=|u|+1,\, v=a_3a_4\tilde{v}, \end{array} \right. \\ \hat{t}_2 : (q_m^{(i)},[a_1,i]a_2ux,q_l^{(i)},\alpha x), \text{ where }\\ \alpha = \left\{ \begin{array}{ll} \,[i]v,\qquad \qquad \text{ if } |v|\le |u|,\\ \,[a_3,i]\tilde{v}, \qquad \text{ if } |v|=|u|+1,\, v=a_3\tilde{v}, \end{array} \right. \\ \hat{t}_3 : (q_m^{(i)},a_1a_2ux,q_l^{(i)},vx).\\ \end{array} \end{aligned}$$Further, we take
$$\begin{aligned} \omega _+(\hat{t}_1) = \omega _+(\hat{t}_2) = \omega _+(\hat{t}_3) = \omega _i(t). \end{aligned}$$ -
(5.3)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form

where \(q_m,q_l\in Q_i\), \(a_1,a_2\in \Gamma _i\), \(v\in \Gamma _i^{\le 1}\), then \(\delta \) contains the following transitions:

where we take \(\omega _+(\hat{t}_3) = \omega _i(t).\) Observe that by our assumption (see the remark at the end of Case 2 above) we do not need to consider the cases that \(M_+\) must simulate transition t on a tape content of the form
 or
or  . Analogously, a transition
. Analogously, a transition  of \(M_i\) just yields the transition
of \(M_i\) just yields the transition  for \(M_+\) with weight \(\omega _+(\hat{t}_3)=\omega _i(t)\).
for \(M_+\) with weight \(\omega _+(\hat{t}_3)=\omega _i(t)\). -
6.
Now we consider the restart transitions. For RWW-automata, each rewrite operation is immediately followed by a restart step. Hence, if a state q of \(M_i\) (\(i\in \{1,2\}\)) is entered through a rewrite step, then in state q, \(M_i\) must restart immediately, that is, \(\delta _i\) contains the transitions
$$\begin{aligned}&t_u : (q,u,\text{ Restart }) \end{aligned}$$for each possible window content u. Accordingly, \(\delta \) contains the following transitions for all admissible words
 : $$\begin{aligned}&\hat{t}_{u,x} : (q^{(i)},ux,\text{ Restart }), \end{aligned}$$
: $$\begin{aligned}&\hat{t}_{u,x} : (q^{(i)},ux,\text{ Restart }), \end{aligned}$$and \(\omega _+(\hat{t}_{u,x}) = \omega _i(t_u)\). Recall that a restart operation is only performed after a rewrite step has been executed, which means that at this point the read/write window of \(M_+\) does not contain any symbol from \(\Gamma {\backslash }(\Gamma _1\cup \Gamma _2)\).
-
7.
Finally, we consider the accept transitions of \(M_1\) and \(M_2\), where we distinguish between two cases.
-
(7.1)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form

for some \(a_1, a_2 \in \Gamma _i\) and \(u\in \Gamma _i^*\) such that
 , then \(\delta \) contains the following transitions for all admissible words
, then \(\delta \) contains the following transitions for all admissible words 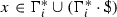 :
: 
and \(\omega _+(\hat{t}_1) = \omega _+(\hat{t}_2) = \omega _+(\hat{t}_3) = \omega _i(t)\).
-
(7.2)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form
$$\begin{aligned} t : (q_m, a_1a_2u,\text{ Accept }) \end{aligned}$$for some \(q_m\in Q_i\), \(a_1, a_2 \in \Gamma _i\), and \(u\in \Gamma _i^*\) such that \(|a_1a_2u| = k_i\), then \(\delta \) contains the following transitions for all admissible choices of
 : $$\begin{aligned} \begin{array}{ll} \hat{t}_1 : &{} (q_m^{(i)}, [a_1,a_2,i]ux,\text{ Accept }),\\ \hat{t}_2 : &{} (q_m^{(i)},[a_1,i]a_2ux,\text{ Accept }),\\ \hat{t}_3 : &{} (q_m^{(i)}, a_1a_2ux,\text{ Accept }),\\ \end{array} \end{aligned}$$
: $$\begin{aligned} \begin{array}{ll} \hat{t}_1 : &{} (q_m^{(i)}, [a_1,a_2,i]ux,\text{ Accept }),\\ \hat{t}_2 : &{} (q_m^{(i)},[a_1,i]a_2ux,\text{ Accept }),\\ \hat{t}_3 : &{} (q_m^{(i)}, a_1a_2ux,\text{ Accept }),\\ \end{array} \end{aligned}$$and \(\omega _+(\hat{t}_1) = \omega _+(\hat{t}_2) = \omega _+(\hat{t}_3) = \omega _i(t)\). This completes the proof for the case that \(M_1\) and \(M_2\) are RWW-automata.
Finally, we turn to the case that \(M_1\) and \(M_2\) are RRWW-automata. First, in order to simplify the discussion, we observe that we can assume without loss of generality that \(M_1\) and \(M_2\) only perform restart operations at the right end of their tapes, that is, when the read/write window only contains the right sentinel $. This is easily achieved by replacing every other restart transition by a move-right step (with the same weight as the corresponding restart step), which enters a special state \(q_{\mathrm {mv}}\), and in state \(q_{\mathrm {mv}}\), the RRWW-automaton moves all the way to the right end of its tape and performs a restart step on the $-symbol, where all these additional transitions have weight 1.
-
8.
Under this assumption we now describe the construction of \(M_+\) from \(M_1\) and \(M_2\). The transitions of \(M_+\) for making the choice between simulating \(M_1\) or \(M_2\) and the transitions for simulating move-right and accept steps of \(M_1\) and \(M_2\) are defined as for RWW-automata (see above). Because of the above assumption on the restart operations, these are also easily simulated by \(M_+\). Hence, it remains to deal with the rewrite transitions of \(M_1\) and \(M_2\), where we have to solve the following technical difficulty: Whenever \(M_i\) (\(i\in \{1,2\}\)) applies a rewrite operation \((q_m,u,q_l,v)\) to a configuration of the form
 , then the configuration
, then the configuration  is obtained. As the size k of the read/write window of \(M_+\) is strictly larger than that of the read/write window of \(M_i\), the above operation is simulated by rewrite operations of the form \((q_m^{(i)},ux,q_{l'}^{(i)},vx)\) for all admissible words \(x\in \Gamma _i^+\). This, however, means that, from the configuration
is obtained. As the size k of the read/write window of \(M_+\) is strictly larger than that of the read/write window of \(M_i\), the above operation is simulated by rewrite operations of the form \((q_m^{(i)},ux,q_{l'}^{(i)},vx)\) for all admissible words \(x\in \Gamma _i^+\). This, however, means that, from the configuration  , the configuration
, the configuration  is obtained in a single step, that is, the window of \(M_+\) skips across the prefix x of \(w_2\) of length \(k-k_i\), while the window of \(M_i\) must be shifted across x by applying |x| many move-right steps. Unfortunately, we cannot simply define the weights of the above transitions of \(M_+\) as the product of the weights of the rewrite transition of \(M_i\) and the corresponding move-right transitions of \(M_i\), as the latter will in general also depend on the next \(k_i-1\) symbols following the factor x. To overcome this problem, we proceed as follows. For \(i=1,2\), let \(Q_i^{\mathrm {rw}}\) denote the set of states of \(M_i\) that are reached through a rewrite step. Further, for \(q\in Q_i^{\mathrm {rw}}\), \(x\in \Gamma _i^{k-k_i}\), and
is obtained in a single step, that is, the window of \(M_+\) skips across the prefix x of \(w_2\) of length \(k-k_i\), while the window of \(M_i\) must be shifted across x by applying |x| many move-right steps. Unfortunately, we cannot simply define the weights of the above transitions of \(M_+\) as the product of the weights of the rewrite transition of \(M_i\) and the corresponding move-right transitions of \(M_i\), as the latter will in general also depend on the next \(k_i-1\) symbols following the factor x. To overcome this problem, we proceed as follows. For \(i=1,2\), let \(Q_i^{\mathrm {rw}}\) denote the set of states of \(M_i\) that are reached through a rewrite step. Further, for \(q\in Q_i^{\mathrm {rw}}\), \(x\in \Gamma _i^{k-k_i}\), and  , let \(C_{i}(q,x,y)\) be the set of computations of \(M_i\) that consist of |x| move-right steps that take a configuration of the form
, let \(C_{i}(q,x,y)\) be the set of computations of \(M_i\) that consist of |x| move-right steps that take a configuration of the form  into a configuration of the form
into a configuration of the form  for some state \(q'\in Q_i\). We introduce the following additional states for \(M_+\):
for some state \(q'\in Q_i\). We introduce the following additional states for \(M_+\): 
Now we can proceed by replacing the rewrite transitions introduced in Case 5 above as follows, where again we distinguish between several cases.
-
(8.1)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form

for some \(q_l\in Q_i^{\mathrm {rw}}\), \(a_1,a_2\in \Gamma _i\), and \(u,v\in \Gamma _i^*\) satisfying
 and \(|v|\le |u|+1\), then \(\delta \) contains the following transitions for all admissible choices of
and \(|v|\le |u|+1\), then \(\delta \) contains the following transitions for all admissible choices of  ,
,  , and \(C\in C_{i}(q_l,x,y)\):
, and \(C\in C_{i}(q_l,x,y)\): 
Further, \(\omega _+(\hat{t}_{j,x,y,C}) = \omega _i(t)\), \(j=1,2,3\).
-
(8.2)
If \(\delta _i\) (\(i\in \{1,2\}\)) contains a transition of the form
$$\begin{aligned} t : (q_m, a_1a_2u,q_l,v), \end{aligned}$$where \(q_m\in Q_i\), \(q_l \in Q_i^{\mathrm {rw}}\), \(a_1, a_2 \in \Gamma _i\), \(u,v \in \Gamma _i^*\) satisfying \(|a_1a_2u|=k_i\) and \(|v|\le |u|+1\), then \(\delta \) contains the following transitions for all admissible choices of
 ,
,  , and \(C\in C_{i}(q_l,x,y)\): $$\begin{aligned} \begin{array}{l} \hat{t}_{1,x,y,C} : (q_m^{(i)},[a_1,a_2,i]ux,q_{l,x,y,C}^{(i)},\alpha x), \text{ where }\\ \alpha = \left\{ \begin{array}{ll} \,[i]v, &{} \text{ if } |v|<|u|,\\ \,[a_3,i]\tilde{v}, &{}\text{ if } |v|=|u|,\, v=a_3\tilde{v},\\ \,[a_3,a_4,i]\tilde{v}, &{}\text{ if } |v|=|u|+1,\, v=a_3a_4\tilde{v}, \end{array} \right. \\ \hat{t}_{2,x,y,C} : (q_m^{(i)},[a_1,i]a_2ux,q_{l,x,y,C}^{(i)},\alpha x), \text{ where }\\ \alpha = \left\{ \begin{array}{ll} \,[i]v, &{} \text{ if } |v|\le |u|,\\ \,[a_3,i]\tilde{v}, &{}\text{ if } |v|=|u|+1,\, v=a_3\tilde{v}, \end{array} \right. \\ \hat{t}_{3,x,y,C} : (q_m^{(i)},a_1a_2ux,q_{l,x,y,C}^{(i)},vx). \end{array} \end{aligned}$$
, and \(C\in C_{i}(q_l,x,y)\): $$\begin{aligned} \begin{array}{l} \hat{t}_{1,x,y,C} : (q_m^{(i)},[a_1,a_2,i]ux,q_{l,x,y,C}^{(i)},\alpha x), \text{ where }\\ \alpha = \left\{ \begin{array}{ll} \,[i]v, &{} \text{ if } |v|<|u|,\\ \,[a_3,i]\tilde{v}, &{}\text{ if } |v|=|u|,\, v=a_3\tilde{v},\\ \,[a_3,a_4,i]\tilde{v}, &{}\text{ if } |v|=|u|+1,\, v=a_3a_4\tilde{v}, \end{array} \right. \\ \hat{t}_{2,x,y,C} : (q_m^{(i)},[a_1,i]a_2ux,q_{l,x,y,C}^{(i)},\alpha x), \text{ where }\\ \alpha = \left\{ \begin{array}{ll} \,[i]v, &{} \text{ if } |v|\le |u|,\\ \,[a_3,i]\tilde{v}, &{}\text{ if } |v|=|u|+1,\, v=a_3\tilde{v}, \end{array} \right. \\ \hat{t}_{3,x,y,C} : (q_m^{(i)},a_1a_2ux,q_{l,x,y,C}^{(i)},vx). \end{array} \end{aligned}$$Further, we take \(\omega _+(\hat{t}_{j,x,y,C}) = \omega _i(t)\) for all \(j=1,2,3\).
-
(8.3)
For each state \(q_{l,x,y,C}^{(i)}\in Q_{\mathrm {rw}}\), we have to add some transitions to \(\delta \). From the definition above we see that C is a computation of \(M_i\) that takes a configuration of the form
 to the configuration
to the configuration  for some \(q'\in Q_i\). For \(b\in \Gamma _i\), let $$\begin{aligned}&t_{q',yb}: (q',yb,q_j,\text{ MVR }) \end{aligned}$$
for some \(q'\in Q_i\). For \(b\in \Gamma _i\), let $$\begin{aligned}&t_{q',yb}: (q',yb,q_j,\text{ MVR }) \end{aligned}$$be a transition of \(M_i\) that is applicable to a configuration of the form
 . Then we add the transition $$\begin{aligned}&\hat{t}_{l,x,y,C,b,z}: (q_{l,x,y,C}^{(i)},ybz,q_j^{(i)},\text{ MVR }) \end{aligned}$$
. Then we add the transition $$\begin{aligned}&\hat{t}_{l,x,y,C,b,z}: (q_{l,x,y,C}^{(i)},ybz,q_j^{(i)},\text{ MVR }) \end{aligned}$$to \(M_+\) for all admissible choices of
 . Further, we take $$\begin{aligned}&\omega _+(\hat{t}_{l,x,y,C,b,z}) = \omega _i(C)+\omega _i(t_{q',yb}), \end{aligned}$$
. Further, we take $$\begin{aligned}&\omega _+(\hat{t}_{l,x,y,C,b,z}) = \omega _i(C)+\omega _i(t_{q',yb}), \end{aligned}$$where \(\omega _i(C)\) is the weight associated to the computation C of \(M_i\).
Finally, if \(M_i\) contains the transition

then we add the transitions

to \(M_+\), where we take

This completes the proof also for the case that \(M_1\) and \(M_2\) are RRWW-automata. \(\square \)
While the proof above is technically quite involved, the next result is rather obvious.
Theorem 7
For all alphabets \(\Sigma \), all commutative semirings S, and all types X of restarting automata, the class of functions \({\mathbb {F}}(\mathsf{X},\Sigma ,S)\) is closed under the operation of scalar multiplication.
Proof
Let S be a semiring, let M be a restarting automaton of some type X with input alphabet \(\Sigma \), and let \(\omega \) be a weight function for M. For each input \(w\in \Sigma ^*\), we have
where \(C_M(w)\) is the set of all accepting computations of M on input w, and \(\omega (C)\) is the product of the weight of all transitions that are used in the accepting computation C.
For \(s\in S\), we define a new weight function \(\omega _s\) as follows:
As each computation \(C\in C_M(w)\) uses exactly one accept transition, and as S is commutative, we see that \(\omega _s(C) \!=\! s\cdot \omega (C)\), which implies that \(f^M_{\omega _s}(w) \!=\! s\cdot f^M_\omega (w)\) holds. \(\square \)
For RWW- and RRWW-automata, Theorem 7 also extends to semirings that are not commutative. This can be shown using the technique from the proof of Theorem 6. From this observation and from Theorem 6 we see that the sets of functions \({\mathbb {F}}({\text{ RWW }},\Sigma ,S)\) and \({\mathbb {F}}({\text{ RRWW }},\Sigma ,S)\) are semi-modules over S (see, e.g., Salomaa and Soittola 1978). Finally, we derive the following additional closure property.
Theorem 8
For all alphabets \(\Sigma \) and all semirings S, \({\mathbb {F}}({\text{ RWW }},\Sigma ,S)\) and \({\mathbb {F}}({\text{ RRWW }},\Sigma ,S)\) are closed under the operation of Cauchy product.
Proof
Let \(S=(S,+,\cdot ,0,1)\) be a semiring, let \(\Sigma \) be a finite alphabet, let  and
and  be RWW- or RRWW-automata with input alphabet \(\Sigma \), and let \(\omega _1\) and \(\omega _2\) be weight functions that map the transitions of \(M_1\) and of \(M_2\) to S. In order to prove that \({\mathbb {F}}({\text{ RWW }},\Sigma ,S)\) is closed under the operation of Cauchy product, we construct an RWW- or RRWW-automaton \(M_c\) with input alphabet \(\Sigma \) and a weight function \(\omega _c\) such that
be RWW- or RRWW-automata with input alphabet \(\Sigma \), and let \(\omega _1\) and \(\omega _2\) be weight functions that map the transitions of \(M_1\) and of \(M_2\) to S. In order to prove that \({\mathbb {F}}({\text{ RWW }},\Sigma ,S)\) is closed under the operation of Cauchy product, we construct an RWW- or RRWW-automaton \(M_c\) with input alphabet \(\Sigma \) and a weight function \(\omega _c\) such that
holds for all \(w\in \Sigma ^*\). To simplify this construction we can assume that \(M_1\) and \(M_2\) perform accept transitions only on the right sentinel $, which is easily achieved by using special states and additional move-right steps.
On input \(w\in \Sigma ^*\), the automaton \(M_c\) first guesses a factorization \(w=u\cdot v\) of w. This will be done in the first cycle by replacing the last symbol a of the prefix u and the first symbol b of the suffix v by an auxiliary symbol of the form [a, b]. For choosing the factorization \(w=\lambda \cdot w\) or \(w=w\cdot \lambda \), the first two symbols \(a_1\) and \(a_2\) or the last two symbols \(b_1\) and \(b_2\) of w are replaced by the auxiliary symbol  or
or  , respectively. As \(M_c\) restarts in its initial state after performing this rewrite step, it will not remember that it has already chosen a factorization of w; however, if at a later point in the computation, \(M_c\) realizes that two (or more) factorizations have been chosen, then the corresponding computation halts immediately without accepting.
, respectively. As \(M_c\) restarts in its initial state after performing this rewrite step, it will not remember that it has already chosen a factorization of w; however, if at a later point in the computation, \(M_c\) realizes that two (or more) factorizations have been chosen, then the corresponding computation halts immediately without accepting.
After having guessed a factorization \(w=u\cdot v\), \(M_c\) simulates a computation of \(M_1\) on the prefix u, where the special symbol of the form [a, b] serves as the right end marker. If this computation of \(M_1\) is accepting, then \(M_c\) replaces the special symbol [a, b] by a new symbol of the form \([+,b]\), it deletes all letters to the left of this symbol in subsequent cycles, and then it simulates a computation of \(M_2\) on the suffix v. Finally, \(M_c\) accepts if this computation of \(M_2\) is also accepting.
As in the proof of Theorem 6 we need auxiliary symbols and additional transitions for \(M_c\) to enable it to perform the above simulations, as the special symbols of the form [a, b], \([+,b]\),  , or
, or  must be dealt with appropriately. However, this can be realized using essentially the same techniques.
must be dealt with appropriately. However, this can be realized using essentially the same techniques.
It follows that, for each factorization \(w=u\cdot v\), for each accepting computation of \(M_1\) on input u, and for each accepting computation of \(M_2\) on input v, the automaton \(M_c\) has exactly one accepting computation. By assigning weight 1 to all the transitions that are used in the guessing phase and to all transitions that are used in the phase between the simulation of \(M_1\) and the simulation of \(M_2\), by assigning weight \(\omega _1(t_1)\) to all transitions of \(M_c\) that correspond to a transition \(t_1\) of \(M_1\), and by assigning weight \(\omega _2(t_2)\) to all transitions of \(M_c\) that correspond to a transition \(t_2\) of \(M_2\), it can be shown that indeed the equality
holds for all input words \(w\in \Sigma ^*\). \(\square \)
5 Conclusion
We have introduced the weighted restarting automaton in order to express and study quantitative aspects of restarting automata and their computations. For each semiring S, each input alphabet \(\Sigma \), and each type X of restarting automaton, the class of functions \({\mathbb {F}}(\mathsf{X},\Sigma ,S)\) extends the class \(S_{\mathrm {REC}}\langle \langle \Sigma ^*\rangle \rangle \) of recognizable functions over S and \(\Sigma \), and for RWW- and RRWW-automata, the corresponding class of functions is a semi-module over S that is additionally closed under the operation of Cauchy product. Further, for the special case of \(S=(\mathbb {N},+,\cdot ,0,1)\), we have also studied the extended functions of the form \(\hat{f}^M_\omega :\mathbb {N}\rightarrow S\), establishing an upper bound for their growth. In addition, we have seen that all polynomials and finite sums of polynomials and exponential functions can be realized by RWW-automata.
It remains open whether the classes \({\mathbb {F}}(\mathsf{X},\Sigma ,S)\) are closed under addition and/or Cauchy product also for those types of restarting automata that cannot use auxiliary symbols. Further, for all types of restarting automata, it remains to characterize the classes of functions \({\mathbb {F}}(\mathsf{X},\Sigma ,S)\) and \(\hat{\mathbb {F}}(\mathsf{X},\Sigma ,S)\) in a syntactic manner.
References
Bollig B, Gastin P, Monmege B, Zeitoun M (2010) Pebble weighted automata and transitive closure logics. In: Abramsky S, Gavoille C, Kirchner C, Meyer auf der Heide F, Spirakis PG (eds) ICALP 2010, Part II, Lecture notes in computer science, Springer, Heidelberg, vol 6199, pp 587–598
Book RV, Otto F (1993) String-rewriting systems. Texts and monographs in computer science. Springer, New York
Chatterjee K, Doyen L, Henzinger TA (2009) Probabilistic weighted automata. In: Bravetti M, Zavattaro G (eds) CONCUR 2009, Proc., Lecture Notes in Computer Science, vol 5710, Springer, Heidelberg, pp 244–258
Dahlhaus E, Warmuth MK (1986) Membership for growing context-sensitive grammars is polynomial. J Comput Syst Sci 33:456–472
Droste M, Götze D (2013) The support of nested weighted automata. In: Bensch S, Drewes F, Freund R, Otto F (eds) NCMA 2013, Proc., Oesterreichische Computer Gesellschaft, Wien, books@ocg.at, Band 294, pp 101–116
Droste M, Kuich W (2009) Semirings and formal power series. In: Droste M, Kuich W, Vogler H (eds) Handbook of weighted automata, monographs in theoretical computer science. Springer, Heidelberg, pp 3–28
Droste M, Meinecke I (2011) Weighted automata and regular expressions over valuation monoids. Int J Found Comput Sci 22:1829–1844
Droste M, Kuich W, Vogler H (2009) Handbook of weighted automata. Monographs in theoretical computer science. Springer, Heidelberg
Golan JS (1999) Semirings and their applications. Kluwer Academic Publishers, Dordrecht
Hebisch U, Weinert HJ (1998) Semirings: algebraic theory and applications in computer science. World Scientific, Singapore
Hundeshagen N (2013) Relations and transductions realized by restarting automata. Doctoral thesis, Universität Kassel
Hundeshagen N, Otto F (2012) Characterizing the rational functions by restarting transducers. In: Dediu AH, Martín-Vide C (eds) LATA 2012, Proc., Lecture notes in computer science, vol 7183. Springer, Heidelberg, pp 325–336
Jančar P, Mráz F, Plátek M, Vogel J (1995) Restarting automata. In: Reichel H (ed) FCT, Lecture notes in computer science, vol 965. Springer, Heidelberg, pp 283–292
Jančar P, Mráz F, Plátek M, Vogel J (1997) On restarting automata with rewriting. In: Pǎun G, Salomaa A (eds) New trends in formal languages, Lecture notes in computer science, vol 1218. Springer, Heidelberg, pp 119–136
Jančar P, Mráz F, Plátek M, Vogel J (1998) Different types of monotonicity for restarting automata. In: Arvind V, Ramanujam S (eds) Foundations of software technology and theoretical computer science, Lecture notes in computer science, vol 1530. Springer, Heidelberg, pp 343–354
Jančar P, Mráz F, Plátek M, Vogel J (1999) On monotonic automata with a restart operation. J Autom Lang Comb 4(4):287–311
Jurdziński T, Loryś K, Niemann G, Otto F (2004) Some results on RWW- and RRWW-automata and their relation to the class of growing context-sensitive languages. J Autom Lang Comb 9(4):407–437
Kirsten D (2009) The support of a recognizable series over a zero-sum free, commutative semiring is recognizable. In: Diekert V, Nowotka D (eds) DLT 2009, Lecture Notes in Computer Science, vol 5583. Springer, Heidelberg, pp 326–333
Kirsten D (2011) The support of a recognizable series over a zero-sum free, commutative semiring is recognizable. Acta Cybern 20:211–221
McNaughton R, Narendran P, Otto F (1988) Church–Rosser Thue systems and formal languages. J ACM 35(2):324–344
Niemann G, Otto F (2000) Restarting automata, Church–Rosser languages, and representations of r.e. languages. In: Rozenberg G, Thomas W (eds) Developments in Language Theory—Foundations, Applications, and Perspectives, DLT 1999, Proc., World Scientific, Singapore, pp 103–114
Otto F (2006) Restarting automata. In: Ésik Z, Martín-Vide C, Mitrana V (eds) Recent advances in formal languages and applications, studies in computational intelligence, vol 25. Springer, Heidelberg, pp 269–303
Salomaa A, Soittola M (1978) Automata-theoretic aspects of formal power series. Texts and monographs in computer science. Springer, New York
Schützenberger MP (1961) On the definition of a family of automata. Inform Control 4(2–3):245–270
Straňáková M (2000) Selected types of pg-ambiguity: processing based on analysis by reduction. In: Sojka P, Kopeček I, Pala K (eds) Text, speech and dialogue, Lecture notes in computer science, vol 1902. Springer, Heidelberg, pp 139–144
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they do not have any conflict of interest.
Additional information
Communicated by M. Droste, Z. Esik and K. Larsen.
Rights and permissions
About this article
Cite this article
Otto, F., Wang, Q. Weighted restarting automata. Soft Comput 22, 1067–1083 (2018). https://doi.org/10.1007/s00500-016-2164-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-016-2164-4





 . If M is in state q and sees the string u in its read/write window, then this move-right step causes M to shift the read/write window one position to the right and to enter state
. If M is in state q and sees the string u in its read/write window, then this move-right step causes M to shift the read/write window one position to the right and to enter state  , and
, and  and $ must not disappear from the tape nor that new occurrences of these markers are created. Further, the read/write window must not move across the right border marker $, that is, if the string u ends in $, then so does the string v, and after performing the rewrite operation, the read/write window is placed on the $-symbol.
and $ must not disappear from the tape nor that new occurrences of these markers are created. Further, the read/write window must not move across the right border marker $, that is, if the string u ends in $, then so does the string v, and after performing the rewrite operation, the read/write window is placed on the $-symbol. , and to reenter the initial state
, and to reenter the initial state  be a restarting automaton. A weight function
be a restarting automaton. A weight function  and
and  , that assigns the set
, that assigns the set  , and that assigns the set
, and that assigns the set 

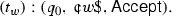
 , where
, where  is contained in the window of
is contained in the window of 
 (respectively,
(respectively,  or
or  ), where
), where  such that
such that 

 , then
, then  :
: 
 .
.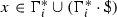 :
:  :
:  :
: 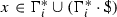 :
: 
 is dealt with in the same way as (4.2). However, observe that here we do not need to consider the case of a symbol of the form
is dealt with in the same way as (4.2). However, observe that here we do not need to consider the case of a symbol of the form  , and
, and 
 and
and  :
: 
 :
: 

 or
or  . Analogously, a transition
. Analogously, a transition  of
of  for
for  :
: 
 , then
, then 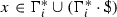 :
: 
 :
:  , then the configuration
, then the configuration  is obtained. As the size k of the read/write window of
is obtained. As the size k of the read/write window of  , the configuration
, the configuration  is obtained in a single step, that is, the window of
is obtained in a single step, that is, the window of  , let
, let  into a configuration of the form
into a configuration of the form  for some state
for some state 

 and
and  ,
,  , and
, and 
 ,
,  , and
, and  to the configuration
to the configuration  for some
for some  . Then we add the transition
. Then we add the transition  . Further, we take
. Further, we take