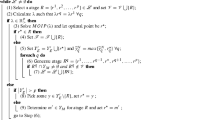1 Introduction

In the solution set of an multi-objective optimization problem (MOP), some points are very important, such as ideal points, knee points, and nadir points. It is easy to obtain an ideal point by optimizing every single objective separately. Around a knee point (Branke et al. 2004), a small improvement of any objective leads to a large degeneration of other objectives. Knee points are interesting to decision makers if they do not know their preferences. A nadir point is derived from the extreme points in a non-dominated solution set, which describes the range of the non-dominated solution set indirectly. Therefore, nadir points play an important role in MOPs, especially in many-objective optimization problems.

Many-objective optimization problems (MaOPs) are a type of MOPs with more than three objectives (Khare et al. 2003). One of the challenges in this research area is that the non-dominated solution set becomes too large to handle effectively as the dimension of the objective space increases. Recently, many new MOEAs have been designed for MaOPs. For example, NSGA-III (Deb and Jain 2014) uses a set of reference points to maintain diversity; Two_Arch2 (Wang et al. 2015) tackles convergence and diversity in separate archives; MOEA/D-DU (Yuan et al. 2015b) tries to introduce NSGA-III’s diversity maintenance scheme into MOEA/D; and \(\theta \)-dominance (Yuan et al. 2015a) introduces a new dominance relation that can provide more selection pressure for MaOPs, inspired by penalty-based boundary intersection (PBI).

Usually, decision makers do not need the entire solution set. They only need the solutions in their interested regions. In such situations, preference-based many-objective optimization (Thiele et al. 2009) can be used to obtain those solutions. However, it is not easy to obtain a comprehensive view of the preferences of decision makers (Fan and Liu 2010; Hsu and Wang 2011; Dai et al. 2013; He et al. 2015) without knowing the range of the non-dominated solution set before running preference-based multi-objective evolutionary algorithms (MOEAs). Nadir points can provide more accurate information about preferences for decision makers (Branke et al. 2008; Deb and Kumar 2007). Nadir points can also be used for normalizing objectives and portfolio problems (Amiri et al. 2010).

Approaches to obtain nadir points can be classified into two categories, namely non-evolutionary and evolutionary approaches:

Non-evolutionary approaches The pay-off table (Benayoun et al. 1971) is the earliest nadir point estimation method. All the objective values of the optimal solutions for every single objective are listed on the pay-off table. Then, the worst objectives from the table are obtained to construct a nadir point. The pay-off table is easy to construct but does not guarantee to obtain the true nadir points (Szczepanski and Wierzbicki 2003; Klamroth and Miettinen 2008; Deb et al. 2006). Several improvements to the pay-off table were proposed (Dessouky et al. 1986; Korhonen et al. 1997). For example, the method proposed in (Ehrgott and Tenfelde-Podehl 2003) decomposes an m-objective optimization problem into \(C_m^2\) 2-objective optimization problems. However, it is impractical for MaOPs because of its high computational cost. There are some other nadir point estimation methods based on reference directions (Korhonen et al. 1997) and points (Metev and Vassilev 2003) in nadir regions. However, these methods still cannot obtain the true nadir points.

Evolutionary approaches According to (Deb and Miettinen 2009), the existing nadir point estimation approaches based on evolutionary approaches can be classified into three types—‘Surface-to-Nadir’, ‘Edge-to-Nadir’, and ‘Extreme-point-to-Nadir’. Popular MOEAs such as NSGA-II (Deb et al. 2002a), MOEA/D-IR (Li et al. 2015), MOEA-DLA (Chen et al. 2015), MOEA/DVA (Ma et al. 2015) and MOEA/D-ACO (Ke et al. 2013) can obtain extreme points from the entire Pareto front (PF) to construct a nadir point. All the MOEAs mentioned above follow the ‘Surface-to-Nadir’ approach. ‘Surface-to-Nadir’ approaches cannot be applied to MaOPs because of their unsatisfactory performance on MaOPs (Praditwong and Yao 2007). One of the ‘Edge-to-Nadir’ approaches (Szczepanski and Wierzbicki 2003) decomposes the original problem into \(C_m^2\) 2-objective subproblems to build a nadir point from the obtained solutions of those subproblems, which leads to \(C_m^2\) edges. As the method in (Szczepanski and Wierzbicki 2003) only considers two objectives at a time, it does not guarantee to obtain the true nadir points in all cases. The ‘Extreme-point-to-Nadir’ approach focuses on extreme points rather than the entire solution set or edges to build nadir points, such as Worst Crowded NSGA-II (Deb et al. 2006) and Extremized Crowded NSGA-II (Deb et al. 2006). Since nadir point estimation can be seen as a special preference problem of MOPs (Thiele et al. 2009), the task of nadir point estimation was treated as solving a preference problem in nadir regions in (Amiri et al. 2010). Also, NSGA-III views nadir point estimation as a preference problem by employing m reference points near m extreme points (Deb and Jain 2014). However, these reference points are based on some strong assumptions, which may not hold for different PF structures.

‘Extreme-point-to-Nadir’ approaches are shown to be the most effective methods to obtain nadir points so far (Deb et al. 2010). Only extreme points are needed for the extraction of a nadir point. That is the reason why the existing approaches focus on extreme points. Based on the frame of ‘Extreme-point-to-Nadir’ approaches, some local search strategies (Deb et al. 2010, 2009; Bechikh et al. 2010; Miettinen et al. 2010) are applied to further improve their performance, but extra computational expenses are added inevitably. For example, a reference-point-based bi-level local search approach with scalarizing functions is adopted in (Deb et al. 2010), and a bi-level optimization method is needed to suit the characteristics of the specific problem. Therefore, a hybrid approach can improve performance for nadir point estimation on specific problems rather than general problems.

However, focusing on extreme points too much causes poor diversity in the population during search. The population is easily trapped into local optima. Therefore, poor extreme points may be obtained in the population with poor diversity. The performance of the existing approaches such as Worst Crowded and Extremized Crowded NSGA-II (Deb et al. 2006) on MaOPs has been shown less than satisfactory. In order to improve their performance, we propose a novel ‘Extreme-point-to-Nadir’ based estimation method (non-hybrid approach, the local search strategies in (Deb et al. 2010, 2009; Bechikh et al. 2010; Miettinen et al. 2010) can be employed to improve its performance), named emphasized critical regions based nadir point estimation (ECRNPE). Its main idea is to employ the emphasized critical regions strategy (ECR) to add more diversity in the population to obtain extreme points more effectively. The proposed method can be easily incorporated into a wide range of MOEAs to obtain nadir points by replacing their diversity maintenance methods with ECR. The detailed contributions of our paper are summarized.

Emphasized critical regions strategy In nadir point estimation approaches, only focusing on extreme points during the search does not help the convergence towards extreme points. Meanwhile, it is unnecessary either to keep the entire PF for nadir point estimation, which increases the computational cost significantly. In order to find the trade-off between these two extreme cases, ECR is employed in this paper. Critical regions are the regions of the best objective values, which approximate the outline of a PF. Nadir regions are in critical regions. A PF can be simply expressed by critical regions. Therefore, the individuals near extreme points as well as critical regions are emphasized by ECR.

Individual number assignment in critical regions ECR selects the individuals in different critical regions independently. Thus, it is very important to assign a number of individuals in different regions for diversity maintenance and balanced computational cost. The number of individuals in each critical region is assigned self-adaptively in ECR.

Self-adaptive \(\varepsilon \) -clearing strategy The \(\varepsilon \)-clearing strategy (Ben Said et al. 2010) has been widely used for diversity maintenance. For nadir point estimation, the approach in (Amiri et al. 2010) adopts the \(\varepsilon \)-clearing strategy, where a pre-defined parameter \(\varepsilon \) is required. However, \(\varepsilon \) is sensitive to the distribution of the population. Therefore, a fixed \(\varepsilon \) might not help accurate nadir point estimation. In this paper, a self-adaptive \(\varepsilon \)-clearing strategy is proposed, which adjusts the parameter \(\varepsilon \) according to the distribution of the current population.

The rest of this paper is organized as follows: Problem definitions are introduced in Sect. 2. Section 3 gives the details of ECRNPE. Section 4 describes the simulation experiment to analyze the behavior of ECRNPE. The Sect. 5 presents the concluding remarks.

2 Problem definitions

2.1 Multi-objective and many-objective optimization

An MOP (Miettinen 1999) with m objectives can be described by

$$\begin{aligned} \begin{array}{c} \hbox {Minimize} \ \mathbf{{F(x)}} = (f_1 (\mathbf{{x}}),f_2 (\mathbf{{x}}),\ldots f_m (\mathbf{{x}}))^T {}\\ \hbox {Subject}\ \hbox {to} \ \mathbf{{x}} \in X, \end{array} \end{aligned}$$
(1)

where \(X \subset \mathbb {R}^n\) is the feasible space, \(\mathbf{{x}} = \{ x_1,x_2,\ldots ,x_n \} ^T\) is the decision variable vector, and \(\mathbf{{F(x)}}\) is the objective vector. The final result of an MOP is a set of non-dominated solutions (or Pareto optima). The set of all Pareto optimal objective values is called the Pareto front (PF). An MaOP (Khare et al. 2003; Hughes 2005) is an MOP with more than 3 objectives. For MaOPs, it is hard to select good solutions by the Pareto dominance relation, because most solutions cannot be dominated by others (Ishibuchi et al. 2008). The PFs of MaOPs are hard to be described by a limited number of solutions, which makes MaOPs very challenging (Praditwong and Yao 2007; Purshouse and Fleming 2003).

2.2 Important points for MOPs

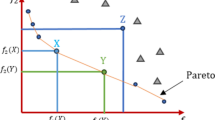
As illustrated in Fig. 1, there exist several important points which can be used to characterize the solution set of an MOP.

Fig. 1
figure 1

Illustration of important points for MOPs

Full size image

An ideal point is constructed by all the optimal objective values as shown in Eq. (2), where m is the number of objectives. An ideal point describes the ideal situation of an MOP. Ideal points cannot be achieved as solutions, because the objectives of MOPs are usually in conflict with each other (Deb et al. 2010).

$$\begin{aligned} z^\mathrm{ideal} = (\min (f_1 ),\ldots ,\min (f_i ),\ldots ,\min (f_m )),1 \le i \le m \end{aligned}$$
(2)

A worst point is constructed by all the worst objective values in the feasible area as shown in Eq. (3). It describes the worst situation to an MOP (Deb et al. 2010).

$$\begin{aligned} z^\mathrm{worst} = (\max (f_1 ),\ldots ,\max (f_i ),\ldots ,\max (f_m )),1 \le i \le m\nonumber \\ \end{aligned}$$
(3)

A nadir point is constructed by all the worst objective values on the PF as shown in Eq. (4). It describes the range of the PF (Deb et al. 2010).

$$\begin{aligned} \begin{array}{c} z^\mathrm{nadir} = (\max (f_1 ),\ldots ,\max (f_i ),\ldots ,\max (f_m )), \\ f_i \in PF,1 \le i \le m \\ \end{array} \end{aligned}$$
(4)

There are m extreme points for an MOP with m objectives. The definition of the ith extreme point is given in Eq. (5). Obtaining these m extreme points is equivalent to obtaining a nadir point. The extraction method of a nadir point from extreme points is given in Sect. 3.3.4.

$$\begin{aligned} \begin{array}{c} z_i^\mathrm{extreme} = (f_1 (\mathbf{{x}}),\ldots ,f_i (\mathbf{{x}}),\ldots f_m (\mathbf{{x}})), \\ \mathbf{{x}} = \arg \min (f_i), \\ f_i \in PF,1 \le i \le m \\ \end{array} \end{aligned}$$
(5)

3 Nadir point estimation based on emphasized critical regions

3.1 Critical region

The critical region of an MOP is defined as the region on the PF with the best value of one objective. Theoretically, there are m critical regions for an MOP with m objectives. The critical regions can be seen as the boundaries of the solution set in the objective space. Taking the 3-objective optimization problem in Fig. 2 as an example, points A, B, and C are extreme points, and edges BC, CA, and AB representing the best objective values of \(f_3\), \(f_2\), \(f_1\), respectively, are from critical regions. The dimension of the critical region depends on the structure of the PF.

Fig. 2
figure 2

Illustration of critical regions

Full size image

3.2 Main idea of ECRNPE

ECR is a diversity maintenance method for nadir point estimation. As shown in Fig. 3, the selection of conventional MOEAs aims at convergence and diversity. By simply replacing their diversity maintenance methods with ECR, any conventional MOEAs can be used to estimate nadir points. By adding nadir point extraction at the end of ECR, it becomes ECRNPE, a method to obtain nadir points. In other words, ECRNPE is used (instead of common diversity maintenance methods) in every generation of MOEAs to obtain nadir points.

Fig. 3
figure 3

Embed ECR in conventional MOEAs

Full size image

As a nadir point is extracted from extreme points, searching extreme points is essential to nadir point estimation approaches. Extreme points are a small part of the entire PF. Only focusing on extreme points during search does not help the convergence towards extreme points. Therefore, the main idea of ECR is to maintain diversity in both the areas near extreme points and critical regions. In ECR, the individuals near extreme points and critical regions are ranked higher for selection. As shown in Fig. 4, ECR has three main parts, i.e., the individual number assignment, the critical region emphasizing strategy, and the self-adaptive \(\varepsilon \)-clearing strategy. Every objective has a critical region, in which the individuals have the best value of this objective. ECR first assigns the number of the individuals which should be maintained in those different critical regions. Then, it is repeated for m times to select a fixed number of individuals by the critical region emphasizing strategy and the \(\varepsilon \)-clearing strategy. The outputs from ECR will be the selected individuals, which are then used for the final step of ECRNPE (nadir point extraction). The details of ECRNPE are explained in the following sections.

Fig. 4
figure 4

Flow-chart of ECRNPE

Full size image

3.3 Proposed approach

3.3.1 Individual number assignment to critical regions

According to the definition in Sect. 3.1, an MOP with m objectives and N solutions in its population has m extreme points and m critical regions. ECR selects the individuals in different critical regions separately. It is necessary to assign the same number of individuals in m critical regions to balance the computational cost of the later individual selection. The number of the maintained individuals in each region is \(n_1\) (\(\left\lfloor {{N / m}} \right\rfloor \)). Because of the round-off operation in \(n_1\), the remaining \(n_2\) (\(N-mn_1\)) individuals are randomly selected from different regions. As \(n_2\) is very small in comparison to the population size N, those \(n_2\) individuals have very little influence on the uniformity of the assignment. The uniformity of different critical regions will be shown through the PF results in Sect. 4.3.2.

3.3.2 Emphasized critical regions strategy

The emphasized critical regions strategy is the first step of individual selection in the critical region of one objective, which essentially ranks the unselected individuals in the population. It first assigns the highest rank to extreme points. Then, it assigns ranks to the remaining individuals according to their distances to critical regions. Taking a minimization objective \(f_i\) as an example, the individual with the worst \(f_i\) which can be seen as an extreme point in the current population is ranked as “1”; the remaining individuals are ranked by sorting the values of objective \(f_i\) in an ascending order. By applying this emphasized critical regions strategy, the individuals close to extreme points and critical regions are emphasized with higher ranks.

As shown in Fig. 4, the emphasized critical regions strategy and the \(\varepsilon \)-clearing strategy work together in m iterations to select the individuals close to the critical region of objective \(f_i\) (\(i=1,\ldots ,m\)). After each iteration, \(n_1\) individuals are selected. They will not be considered in the later iterations for other critical regions. An individual with better values on both objectives \(f_i\) and \(f_j\) will be selected for either objective. Therefore, the order of the individual selection of different regions has no influence on the final selected individuals. In this paper, ECR uses the sequential order from \(f_1\) to \(f_m\).

3.3.3 Self-adaptive \(\varepsilon \)-clearing strategy

In order to avoid selecting similar individuals, ECR applies the \(\varepsilon \)-clearing strategy (Ben Said et al. 2010) to eliminate similar individuals from the sorted population obtained from the emphasized critical regions strategy. The pseudo-code of the selection is shown in Algorithm 1:

figure a

The \(\varepsilon \)-clearing strategy is an effective technique to maintain diversity (Amiri et al. 2010; Ben Said et al. 2010). In previous studies, parameter \(\varepsilon \) was fixed. However, it is very difficult to choose an optimal parameter \(\varepsilon \) in advance. Furthermore, a fixed \(\varepsilon \) may not be suitable for different distributions of individuals in a population in the process of optimization. Therefore, we propose a self-adaptive \(\varepsilon \)-clearing strategy. Parameter \(\varepsilon \) is self-adaptive according to the distribution in the current population and calculated by Eq. (6), in which \(n_1\) is the number of the maintained individuals in one critical region, \(f_i\) is the ith objective value in the current population.

$$\begin{aligned} \varepsilon = {{\sqrt{\sum \nolimits _{i = 1}^m {\left( \max (f_i )-\min (f_i )\right) ^2}}}/ {n_1 }} \end{aligned}$$
(6)

3.3.4 Extraction of the nadir point

As the individuals obtained are approximate extreme points, the last step of ECR is to extract the nadir point from the population. The details are described in Algorithm 2.

figure b

3.3.5 Discussion

ECR appears to divide a population into m sub-populations as in an island model (Branke et al. 2000). Island model is well known for its separate sub-populations, which independently optimize and occasionally interact each other. In fact, ECR is not the case, only the selected individuals are divided into m parts for those m different selections to different regions. Neither the population nor the final selected population is divided. As we know, the interaction between different sub-populations is the main characteristic of an island model. Different from the island model, ECR does not apply such interactions as crossover among multiple populations.

4 Simulation experiments

As ECR can be embedded in any MOEA, we embed ECR in both Pareto-based MOEAs [NSGA-II (Deb et al. 2002a) and Two-Archive Algorithm (TwoArch) (Praditwong and Yao 2006)] and non-Pareto-based MOEAs (IBEA Zitzler and Künzli 2004) in our experiments to evaluate ECR’s effectiveness in finding nadir points. Through the experiments below, the performance of ECR is analyzed from different aspects.

4.1 Metric, test problems, and parameters

As the nadir point is not a solution to an MOP, most metrics cannot be used in our experiments, such as Hypervolume (Zitzler and Thiele 1999; Jiang et al. 2014). Error metric E (Deb et al. 2002b) has been used for evaluating the accuracy of obtaining nadir points, which describes the distance from the estimated nadir point to the true nadir point. The formula is shown in Eq. (7), where \(z^\mathrm{ideal}\) and \(z^\mathrm{nadir}\) stand for the true ideal point and nadir point, and z is the estimated nadir point. It is clear that E is a normalized distance. The scales of different objectives have no influence on E.

$$\begin{aligned} E = \sqrt{\sum \nolimits _{i = 1}^m {\left( {{\left( z_i^\mathrm{nadir} -z_i \right) } / {\left( z_i^\mathrm{nadir} -z_i^\mathrm{ideal} \right) }}\right) ^2 }} \end{aligned}$$
(7)

Recently, many benchmark MOPs were proposed (Ishibuchi et al. 2014), such as the ZDT problems (Zitzler et al. 2000), the DTLZ problems (Deb et al. 2002b), the WFG problems (Huband et al. 2006), and some other problems (Szczepanski and Wierzbicki 2003; Klamroth and Miettinen 2008). The DTLZ and WFG problems are selected as the test problems in this paper because they can be extended to MaOPs and their nadir points are known as listed in Table 1. We use the same parameter setting as that used in (Deb et al. 2002a) [SBX crossover (\(\eta =15\)) and polynomial mutation (\(\eta =15\))]. All the experiments were repeated independently for 29 times. The population size is set to 100 for the problems with 2–10 objectives, and 200 for the problems with more than 10 objectives.

Table 1 True ideal and nadir points of the DTLZ and WFG problems
Full size table

4.2 Experiments on self-adaptive \(\varepsilon \)-clearing strategy

The self-adaptive \(\varepsilon \)-clearing strategy is one of our main contributions in this paper. In the following experiment, we compare ECR NSGA-IIs with and without the self-adaptive \(\varepsilon \)-clearing strategy on DTLZ2 with 10 objectives. Both algorithms repeated for 29 independent times with a population of 100 individuals and for 1000 generations. The metric E is employed to evaluate the performance of these two algorithms. The boxplot of E of the final result is shown in Fig. 5. According to Fig. 5, the ECR NSGA-II without the self-adaptive \(\varepsilon \)-clearing strategy cannot obtain the true nadir point within 1000 generations, while the ECR NSGA-II with the self-adaptive \(\varepsilon \)-clearing strategy can. As the \(\varepsilon \)-clearing strategy eliminates similar individuals, more individuals in critical regions can be maintained for better diversity. Thus, the self-adaptive \(\varepsilon \)-clearing strategy improves the convergence to the true nadir point.

Fig. 5
figure 5

Boxplot of E for ECR NSGA-IIs with and without the self-adaptive \(\varepsilon \)-clearing strategy on DTLZ2 with 10 objectives. Obviously, the ECR NSGA-II with the self-adaptive \(\varepsilon \)-clearing strategy found the true nadir point while the ECR NSGA-II without the self-adaptive \(\varepsilon \)-clearing strategy did not find the true nadir point

Full size image
Fig. 6
figure 6

Function evaluations with a variable number of objectives on the DTLZ problems within limited computational time

Full size image
Fig. 7
figure 7

Final populations of all the runs of ECR NSGA-II, Extremized Crowded NSGA-II, and Original NSGA-II on the 3-objective DTLZ problems

Full size image

4.3 Experimental study on computational time and scalability

4.3.1 Comparative experiments

ECR NSGA-II, Extremized Crowded NSGA-II (Deb et al. 2006), NSGA-II, ECR TwoArch, TwoArch, ECR IBEA, and IBEA are included in our comparisons in this section. We test the DTLZ problems with 2–20 objectives. Because of the different difficulties of different problems, the true nadir points of the DTLZ1 with 2–15 objectives, the DTLZ2 with 2–20 objectives, the DTLZ3 with 2–10 objectives, and the DTLZ4 with 2–20 objectives can be obtained within a limited computational cost. Normally, these approaches run for a fixed number of generations. In order to fairly evaluate the convergence speed to nadir points, the stopping criterion is changed to \(E<0.01\), which indicates very close approximation to the true nadir points. Under this criterion, an algorithm with the smallest number of function evaluations has the highest speed. The metric E is calculated in every generation. If \(E<0.01\), the algorithm stops. It is worth noting that the true nadir point is only used for calculating E. The true nadir point has no influence on the behaviors of the compared algorithms. It is only used for performance evaluation. The parameter settings were given in Sect. 4.1. The numbers of function evaluations of the seven algorithms under the same stopping criterion (\(E<0.01\)) are listed in Fig. 6.

It is clear that the Original NSGA-II had difficulties in converging to the true nadir point when the number of objectives increases. With the increasing number of objectives, the required function evaluations of the Original NSGA-II increase more significantly in comparison with the other two NSGA-IIs. Extremized Crowded NSGA-II performs better than ECR NSGA-II on problems with a smaller number of objectives. With more than 7 objectives for DTLZ1, 6 objectives for DTLZ2, and 10 objectives for DTLZ4, ECR NSGA-II uses fewer function evaluations than Extremized Crowded NSGA-II. For DTLZ3 with 2 to 10 objectives, Extremized Crowded NSGA-II uses fewer function evaluations than ECR NSGA-II. As DTLZ3 is hard to converge to its true PF, we speculate that the diversity in the critical regions cannot improve convergence.

For TwoArch, we can find that ECR improves the nadir point estimation performance of the Original TwoArch on most of the DTLZ problems. When the number of objectives increases, the Original TwoArch does not obtain the true nadir point, while ECR TwoArch performs well on these problems. Since the Original TwoArch is specifically designed for MaOPs, both algorithms perform unsatisfacorily on the 2-objective problems. For DTLZ4, we find that the required number of function evaluations of ECR TwoArch does not increase with the number of objectives. Especially, the number of function evaluations for the DTLZ4 with 7 objectives is the smallest. DTLZ4 is the easiest problem to obtain the solutions near its extreme points among all of the DTLZ problems. Furthermore, there are only three kinds of solutions (the non-dominated solutions with domination, the non-dominated solutions without domination, and the dominated solutions) in the Original TwoArch, which increases the convergence speed on DTLZ4. However, this characteristic of the Original TwoArch leads to varied performance on the same problem in different runs. That is the reason why the curve of DTLZ4 becomes such irregular.

For IBEA, we find that ECR can improve its nadir point estimation ability significantly. For DTLZ1, DTLZ3, and DTLZ4, the Original IBEA did not obtain any points close to extreme points. Even for DTLZ3 with two objectives, the Original IBEA does not obtain the nadir point within the limited computational time. After adding ECR, IBEA improves the performance of nadir point estimation on MaOPs.

Comparing the above results from different algorithms, we find that the results of ECR IBEA are not better than that of ECR NSGA-II. Theoretically, IBEA is an excellent MOEA on MaOPs. We expect that it should perform better than NSGA-II, especially in terms of convergence. However, because IBEA has almost no diversity maintenance mechanisms, extreme points are harder to be maintained in IBEA than in NSGA-II, which might explain the worse results from ECR IBEA (its maximum number of objectives is much smaller than 20). Similarly, comparing the results of IBEA to those of TwoArch, we find that the results of ECR IBEA are not better than those of ECR TwoArch, either. However, it is worth noting that the performance of estimating nadir points is not the same thing as the performance for solving the MOP itself.

4.3.2 Discussion

In order to analyze the mechanism of ECR, we show the final populations of ECR NSGA-II, Extremized Crowded NSGA-II, and Original NSGA-II on the DTLZ problems with 3 objectives in Fig. 7. According to Fig. 7, the final population of the Original NSGA-II is distributed on the entire PF, that from Extremized Crowded NSGA-II is distributed in the regions of extreme points, and that from ECR NSGA-II is distributed in the critical regions most uniformly as expected in Sect. 3.3.1.

The results show different behaviors caused by different diversity maintenance strategies on different problems. The solutions of Original NSGA-II are distributed on the entire PF. Original NSGA-II are not suitable for the nadir point estimation of MaOPs. Extremized Crowded NSGA-II improves the above disadvantages by concentrating on extreme points. In order to maintain the diversity of the current population, Extremized Crowded NSGA-II maintains some individuals in critical regions. It can solve some MOPs with 15–20 objectives. However, its diversity is unsatisfactory. The individuals are distributed in some areas non-uniformly. To overcome this weakness, ECR NSGA-II applies the self-adaptive \(\varepsilon \)-clearing strategy to delete similar individuals for better diversity. Larger diversity in critical regions helps to improve convergence to the true nadir point. ECR NSGA-II performs better than Extremized Crowded NSGA-II on most MaOPs.

However, the individuals in the critical regions of DTLZ3 cannot be maintained as well as we expected, which was shown in Fig. 7. The critical regions of DTLZ3 sre hard to obtain. In ECR, we only keep the individuals of critical regions, which is of insufficient diversity for DTLZ3. Because we cannot obtain the expected individuals, the behavior of ECR NSGA-II on DTLZ3 was less satisfactory.

4.3.3 Scalability and extension

We find that ECR NSGA-II can solve DTLZ2 with 20 objectives easily. DTLZ2 with 25–35 objectives are chosen to test the scalability of ECR. In our experiments, the stopping criterion is set as \(E<0.01\). All the experiments are repeated with 29 independent runs. The number of objectives increases until ECR is not able to find satisfactory nadir points. The results in Table 2 show that ECR can find the nadir points for MOPs with 25–35 objectives within a reasonable number of function evaluations.

Table 2 Number of function evaluations of ECR NSGA-II (the stopping criterion is \(E<0.01\)) on DTLZ2
Full size table

DTLZ2 has no local optima, which might be the reason why the scalability of proposed method can be up to 35 objectives. Fairly, we take another group of experiments to analyze the sensitivity from local optima by a series of modified DTLZ1 problems with 5 objectives. \(g(\mathbf{x _M})=100[\left| {\mathbf{x _M}} \right| + \sum \nolimits _{{x_i} \in \mathbf{x _M}}{({{({x_i}-0.5)}^2}-\cos (\alpha \pi ({x_i}-0.5)))}]\) in DTLZ1 controls the local optima, and \(\alpha \) controls the frequency of local optima. In the following experiment, we run ECR NSGA-II (the stopping criterion is set as \(E<0.01\)) on DTLZ1 with \(\alpha \) from 0 to 20 (no local optima to large amount of local optima). From the result in Table 3, we find that the amount of local optima weakly affects the performance of our method.

Table 3 Number of function evaluations of ECR NSGA-II (the stopping criterion is \(E<0.01\)) on DTLZ1 with \(\alpha \) from 0 to 20
Full size table
Table 4 Number of function evaluations of ECR NSGA-II, Extremized Crowded NSGA-II, and NSGA-III (the stopping criterion is \(E<0.01\)) on the new DTLZ2 problem
Full size table

The existing test problems all have special PFs, on which a single Pareto optimal solution has the best values of all objectives. NSGA-III (Deb and Jain 2014) is based on such a strong assumption to assign reference points, which is the reason why it can perform well on nadir point estimation. However, the PFs of MOPs may have very different structures in practice. In order to thoroughly evaluate the performance of our method, we use a modified DTLZ2 by changing its PF structure as shown in Fig. 8. The modified DTLZ2 is given in Eq. (8). Thus, only one single Pareto optimal solution has the best objective value of a single objective on the PF of the new DTLZ2. Its true nadir point is (1,1,...,1).

$$\begin{aligned} \begin{array}{l} f_1 (\mathbf x ) = (1 + g(\mathbf x _M ))(1 - \cos (x_1 \pi /2)\cdots \cos (x_{m - 1} \pi /2)) \\ f_2 (\mathbf x ) = (1 + g(\mathbf x _M ))(1 - \cos (x_1 \pi /2)\cdots \sin (x_{m - 1} \pi /2)) \\ \vdots \\ f_m (\mathbf x ) = (1 + g(\mathbf x _M ))(1 - \sin (x_1 \pi /2)) \\ \mathbf x _M=\{x_i |i = m,\ldots n\},n>m\\ 0 \le x_i \le 1(i = 1,2,\ldots n) \\ \hbox {where}\ \ g(\mathbf x _M ) = \sum \nolimits _{x_i \in \mathbf x _M } {(x_i - 0.5)^2 } \end{array} \end{aligned}$$
(8)
Fig. 8
figure 8

PF of the modified DTLZ2 with 3 objectives

Full size image

ECR NSGA-II, Extremized Crowded NSGA-II and NSGA-III are selected for the comparison. The constraint \(g(\mathbf x )\) of the new DTLZ2 has 10 dimensions, which is the same as the original DTLZ2 problem. The stopping criterion is \(E<0.01\). Other parameters are shown in Sect. 4.1.

From Table 4, we find that ECR NSGA-II performed better than Extremized Crowded NSGA-II on this modified DTLZ2. Comparing to the results in Sect. 4.3, the nadir point of the modified DTLZ2 is harder to obtain than that of the original DTLZ2. Extremized Crowded NSGA-II cannot obtain the nadir point of the new DTLZ2 with more than 4 objectives. ECR NSGA-II cannot work well on the new DTLZ2 with more than 7 objectives. Such results show that the structure of PF influences significantly the behaviors of different nadir point estimation methods. Additionally, NSGA-III fails to solve the modified DTLZ2 with more than 2 objectives, because it assumes the extreme point as (1,0,...,0) rather than the true situation (0,1,...,1).

4.4 Experimental study on accuracy

From the results in Sect. 4.3, we now understand the general performance of these compared algorithms. However, the true nadir point is usually unknown in practice. Involving the true nadir point is only a method to evaluate the performance of different algorithms. We carry on the comparison of their accuracy in this section. The stopping criterion of the experiments is set as a fixed number of function evaluations.

A comparative experiment between ECR NSGA-II, Extremized Crowded NSGA-II, ECR TwoArch, and ECR IBEA on the WFG problems with 10 objectives for 900000 function evaluations is conducted. The metric E is calculated in every generation to show the results. The experiment runs for 29 independent times, and the average and standard deviation values of the metric E are given in Table 5. The results are analyzed by Kruskal–Wallis test with Tukey test (Derrac et al. 2011) in Table 6.

Table 5 E values of ECR NSGA-II, Extremized Crowded NSGA-II, ECR TwoArch, and ECR IBEA (the stopping criterion is 900000 function evaluations) on the WFG problems with 10 objectives
Full size table

From the results on the E values and the nonparametric statistical test, TwoArch and IBEA are not suitable for estimating nadir points even after embedding ECR. The reason is that both algorithms do not have strategies to keep extreme points. NSGA-II has advantages in this aspect. Therefore, the E values of ECR NSGA-II and Extremized Crowded NSGA-II are much better than that of ECR TwoArch and ECR IBEA on all WFG problems.

Table 6 p vales of Kruskal–Wallis test with Tukey test on the results in Table 5, where A–D stands for ECR NSGA-II, Extremized Crowded NSGA-II, ECR TwoArch, and ECR IBEA
Full size table

The nadir points of the WFG problems are harder to be obtained than that of the DTLZ problems, especially WFG1, WFG3, WFG5, WFG6, WFG8, and WFG9. Although ECR NSGA-II performs better than Extremized Crowded NSGA-II on WFG1, WFG6, and WFG8, the advantages are not as significant as that on the DTLZ problems. The performance of ECR NSGA-II and Extremized Crowded NSGA-II are similar in the remaining WFG problems.

Figure 9 is the average E values of ECR NSGA-II, Extremized Crowded NSGA-II, ECR TwoArch, and ECR IBEA on WFG1 with 10 objectives in 29 independent runs. TwoArch and IBEA embedded with ECR are not suitable to estimate nadir points of the WFG problems. NSGA-II has significant advantages on nadir point estimation. As ECR keeps solutions in the critical regions, the diversity of ECR NSGA-II is better than Extremized Crowded NSGA-II. That is the reason why ECR NSGA-II has a faster convergence speed to the true nadir point than Extremized Crowded NSGA-II.

Fig. 9
figure 9

The evolution of the average E values of ECR NSGA-II, Extremized Crowded NSGA-II, ECR TwoArch, and ECR IBEA on WFG1 with 10 objectives in 29 independent runs

Full size image

5 Concluding remarks

Nadir point estimation based on emphasized critical regions is proposed in this paper, which can estimate nadir points of MaOPs with better performance than the other existing methods. It has been shown that the proposed method is capable of estimating the nadir point for the DTLZ2 with up to 35 objectives. In this paper, three major contributions have been made, as follows:

5.1 Emphasized critical regions

ECR emphasizes not only extreme points but also critical regions, which increases the diversity of the current population. For a MaOP, the objective space is large, and it is hard to select individuals only by the Pareto dominance relation. Therefore, the emphasized critical regions strategy is important for improving both diversity and convergence. Although the diversity in critical regions seems to be useless for finding nadir points directly, it improves the convergence to extreme points, from which better estimation of nadir points can be obtained.

5.2 Individual number assignment to critical regions

In ECR, the computational cost is assigned uniformly among all critical regions. Individual number assignment in critical regions in ECR maintains the balance of searching different critical regions.

5.3 Self-adaptive \(\varepsilon \)-clearing strategy

In ECR, the \(\varepsilon \)-clearing strategy is adopted self-adaptively, which deletes similar individuals to enhance the diversity of the population. Parameter \(\varepsilon \) can be set automatically according to the distribution of the current population.

Although ECR achieves good performance on the MaOPs tested here, there is room for improvement. For example, it has been found that our ECR method cannot solve the MOPs with more than 35 objectives; the performance on the WFG problems is less than satisfactory. Our future work includes: 1) Some local search strategies such as (Deb et al. 2010) could be added to ECR. 2) More studies should focus on the impact of the structures of PFs on the performance of ECR.