Abstract
Using recent characterisations of topologies of spaces of vector fields for general regularity classes—e.g., Lipschitz, finitely differentiable, smooth, and real analytic—characterisations are provided of geometric control systems that utilise these topologies. These characterisations can be expressed as joint regularity properties of the system as a function of state and control. It is shown that the common characterisations of control systems in terms of their joint dependence on state and control are, in fact, representations of the fact that the natural mapping from the control set to the space of vector fields is continuous. The classes of control systems defined are new, even in the smooth category. However, in the real analytic category, the class of systems defined is new and deep. What are called “real analytic control systems” in this article incorporate the real analytic topology in a way that has hitherto been unexplored. Using this structure, it is proved, for example, that the trajectories of a real analytic control system corresponding to a fixed open-loop control depend on initial condition in a real analytic manner. It is also proved that control-affine systems always have the appropriate joint dependence on state and control. This shows, for example, that the trajectories of a control-affine system corresponding to a fixed open-loop control depend on initial condition in the manner prescribed by the regularity of the vector fields.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In nonlinear control theory, one considers systems of the form
where
 is a curve taking values in a control set
is a curve taking values in a control set
 and
and
 is the corresponding trajectory, taking values in a differentiable manifold
is the corresponding trajectory, taking values in a differentiable manifold
 . In this paper, we are concerned with two related questions: (1) what is the most natural structure to assume for the control set
\(\mathscr {C}\)? and (2) what is the proper way to account for regular dependence of the system on state? Before we carefully answer these questions, in this introduction, we develop their control theoretic backdrop, as they do arise quite naturally, but are presently not answered in any sort of general or systematic manner.
. In this paper, we are concerned with two related questions: (1) what is the most natural structure to assume for the control set
\(\mathscr {C}\)? and (2) what is the proper way to account for regular dependence of the system on state? Before we carefully answer these questions, in this introduction, we develop their control theoretic backdrop, as they do arise quite naturally, but are presently not answered in any sort of general or systematic manner.
1.1 Structures for control sets
Let us first consider the matter of what structure one should assume for the control set. The control set is often taken to be a subset of some Euclidean space \({\mathbb {R}}^m\); this is especially meaningful for control-affine systems, where
for vector fields \(f_0,f_1,\dots ,f_m\). However, there are certainly instances where one requires the control to take values in something more general than a finite-dimensional Euclidean space. This is pointed out by Sontag [59, Definition 2.6.1] as being useful in allowing finite control sets, for example. Moreover, in this definition of Sontag, the time dependence for nonautonomous systems is supposed to come through the dependence of the dynamics on another parameter, again metric space-valued (the space \(\mathscr {S}\) in Sontag’s definition), to allow for a sufficiently general theory of linearisation. The theory of Sussmann [63] on the coordinate-free Maximum Principle is developed in the context of controls taking values in a Fréchet space. The idea here is that the system vector fields themselves are the controls, and prescribing an open-loop control is then a prescription of a time-varying vector field. (This idea is also the genesis of the chronological calculus of Agrachev and Gamkrelidze [2]; see also [3].) In the “bundle” view of control systems, first espoused by Brockett [12] and Willems [69] and then developed in subsequent work [4, 13, 19, 41], control sets are banished, at least in their usual sense, and then thinking of the controls as being vector fields becomes quite natural. Finally, although it may be true in practice that controls quite often take values in some subset of Euclidean space, it seems unnatural to include all of the structure of Euclidean space for a control set, and then never use it. For example, is the vector space structure of Euclidean space useful, especially for control sets that are compact? is the particular nature of the topology for Euclidean space useful? is it necessary that controls take values in a space where derivatives can be defined? If one looks at the development of the theory, one sees that all of this structure is, in fact, superfluous and, like anything that is superfluous, serves only to ultimately obfuscate the essential elements of the theory. This is, in fact, well understood by many researchers in control theory, and the supposition that the control set be some sort of metric space (typically separable, sometimes compact) is a common one; its appearance in the book of Sontag [59] is just one of the many places where such a development can be found. In this work, we will in fact consider control sets that are general topological spaces. This certainly, then, subsumes all existing assumptions on control sets. Moreover, the fact that we can develop a coherent theory with this degree of generality suggests that this generality is actually quite natural, and that additional assumptions are superfluous.
1.2 Lipschitz, finitely differentiable, and smooth control systems
Next let us turn to the development of regularity of control systems. Before we begin with specifics, let us point out that the primary issue one must confront here is that one must develop joint conditions on state and control; it is not sufficient to simply say that the regularity of a control system is the regularity of the dependence on state, for each fixed control value (this would be separate regularity). The reason for this is that, in existence and uniqueness theorems for ordinary differential equations, there are joint conditions required on state and time, e.g., the time dependence should be locally integrable, and bounded by a locally integrable function locally uniformly in state, e.g., [15, Theorem 2.2.1]. Since time enters a control system by way of the control, the way in which one ensures the correct joint conditions on time and state is to specify appropriate joint conditions on control and state. We shall see this issue of joint regularity conditions come up repeatedly in our ensuing discussion. One way to view the contribution of the paper is that it provides a unified way of specifying these joint conditions across a broad range of regularity conditions. Moreover, in cases that are understood in the literature, our joint conditions agree with the commonly accepted ones. But they also apply in cases that are not understood in the existing literature. We also mention here that in [35] the problem of joint conditions for time and state are studied. In the present work, these are translated into joint conditions on control and state, but these translations are by no means immediate or a priori clear.
Let us do this by first considering the very weakest sort of regularity one might consider for a control system of the form (1). This would be that regularity required to give a theory for existence and uniqueness of solutions, as well as continuous dependence on initial conditions. The idea here is that one demands this sort of theory upon substitution of any open-loop control. This idea is quite common in the literature, and is developed nicely in [11, §3.2] and [59, Appendix C.2]. The most natural minimal condition one can impose is that the function F in (1) be locally Lipschitz in the state variable x, and that the local Lipschitz constant be locally bounded as a function of control. We point out that this is a joint condition on state and control. Moreover, this sort of condition abounds in the control theory literature, as for example in [11, Page 38] and [59, Page 43]Footnote 1 (although here Lipschitz is replaced by the slightly stronger condition of being
\(\text {C}^1\)). This natural and commonly made assumption is exactly that giving rise to the class of system we would call a “ -control system” in our general Definition 13. This assertion is proved as Proposition 3.
-control system” in our general Definition 13. This assertion is proved as Proposition 3.
Let us ramp up the regularity requirements of our system beyond those required for mere existence, uniqueness, and continuous dependence. In any control theory requiring linearisation, as for example the Maximum Principle of optimal control, one needs, of course, enough regularity to differentiate. However, it is not enough to simply append to the condition of the preceding paragraph the additional condition that the state dependence be \(\text {C}^1\) for each fixed control value. Indeed, what one needs is a condition that ensures that trajectories depend continuously differentiably on initial condition. This will happen when the function F is differentiable and the derivatives are continuous as functions of both state and control. Again, we point out that this is a joint condition on state and control. The fact that this is actually the right condition to ensure continuously differentiable dependence on initial conditions is not always proved, but proofs can be found in [59, §2.8, §2.9] and [49, §12]. We also point out here that this condition comes out naturally in our development, and is exactly that giving rise to what we call a “\(\text {C}^1\)-control system” in Definition 13. That this is so is proved in Proposition 3.
It is not difficult now to see the direction in which this is heading. For more differentiable dependence of trajectories on initial conditions, such as are required for higher-order necessary conditions in optimal control theory [40] or for higher-order controllability [6, 37], one wants dependence on initial conditions to be of class
\(\text {C}^m\) for some
 . Beyond the case
\(m=1\) discussed above, this sort of regularity is almost never discussed carefully in the control theory literature. One place where it is discussed carefully is in [64]. Here, it is pointed out that the proper condition, a natural extension of the case
\(m=1\), is that the function F in (1) be m-times differentiable in state, with the first m derivatives being continuous as functions of state and control. Again, these are joint conditions. Moreover, they are also the conditions for what we refer to as a “\(\text {C}^m\)-control system” in Definition 13, a fact that is proved in Proposition 3.
. Beyond the case
\(m=1\) discussed above, this sort of regularity is almost never discussed carefully in the control theory literature. One place where it is discussed carefully is in [64]. Here, it is pointed out that the proper condition, a natural extension of the case
\(m=1\), is that the function F in (1) be m-times differentiable in state, with the first m derivatives being continuous as functions of state and control. Again, these are joint conditions. Moreover, they are also the conditions for what we refer to as a “\(\text {C}^m\)-control system” in Definition 13, a fact that is proved in Proposition 3.
Of course, in the geometric theory of control, it is assumed that systems are at least smooth, and often real analytic. The manner in which smoothness is dealt with, analogously to how finite differentiability is dealt with above, is quite natural, and is considered in [64]. Indeed, the definition we give of a “\(\text {C}^\infty \)-control system” in Definition 13 is, by Proposition 2, precisely the condition that the function F in (1) possess all derivatives with respect to state, and that the dependence of each of the derivatives on state and control be continuous.
1.3 What is a real analytic control system?
The importance of real analyticity in geometric control theory is well understood, given its importance in the Frobenius Theorem for distributions [47], the theory of accessibility [65], and the Orbit Theorem [60]. Additional virtues of real analyticity in control theory are extolled in [61, 62]. It is then natural to ask, “What is a real analytic control system?” Beyond control-affine systems, there is in the existing literature no understanding of the answer to this question. Moreover, it is difficult to see how the conditions developed above for Lipschitz, finitely differentiable, and smooth systems can be usefully adapted to real analytic systems. For example, Sussmann [64], having properly made definitions in all of these other cases, gives a completely orthogonal characterisation of what he wishes to be a real analytic control system; the definition given is simply not related to the other notions in any way at all. This is not intended as a criticism of this work, but more as an illustration that the question we are asking in this section, while natural, is not so easy to answer.
What we do here is provide a definition of what is meant by “real analytic control system,” and our definition is a natural adaptation of the notions in the preceding section in the Lipschitz, finitely differentiable, and smooth cases. What is different in the real analytic case is that there is no pithy one line description of the required condition, like there is in the other cases. Indeed, the analogue of Propositions 2 and 3 in the real analytic case is Proposition 5, which is somewhat more complicated to state. However, the basic fact is this: the three results, Propositions 2, 3, and 5, are reformulations of the requirement that the map
 is continuous in a suitable topology; it is just that the topology in the real analytic case is more complicated.
is continuous in a suitable topology; it is just that the topology in the real analytic case is more complicated.
Given that our unifying framework relies in an essential way on topologies for spaces of vector fields, and that this topology appears to be quite difficult in the real analytic case, one may balk and consider other approaches for defining what is meant by a real analytic control system. Let us examine some of these possible approaches.
One might declare that one is only interested in control-affine systems, where F is given by (2). Then one can just say that the vector fields \(f_0,f_1,\dots ,f_m\) are real analytic and be done with it. This is true, and this is what is always done. But let us point out a few facts. First of all, a control-affine system is real analytic in this simple sense if and only if it is a \(\text {C}^\omega \)-control system as per our general Definition 13; see Sect. 5.3. Thus our very general definition reduces to the simple one for control-affine systems (in fact, this is true for all sorts of regularity, not just real analyticity). Thus there is nothing gained (except simplicity) by the simple definition. However, there is something lost. For example, part of our approach is to develop classes of control systems with the property that, upon substitution of an open-loop control, they give rise to time-varying vector fields whose flows depend on initial condition in a manner compatible with the system regularity; this is the content of Corollaries 1 and 2. This applies, for example, to real analytic control-affine systems, and the real analytic dependence of real analytic systems, even control-affine systems, on initial conditions is a result that is not present in the existing literature. Thus, even for control-affine systems, our approach gives new and deep results.
Another way of dealing with the definition of real analyticity might be to take the control set to be an open subset of \({\mathbb {R}}^m\), and ask that the function F in (1) be real analytic as a function of control and state. Indeed, this can be done for all sorts of regularity, and is done, for example, in [42, Page 31] and [8, Page 37] in the \(C^1\) case, in [18] in the smooth setting, and in [58] in the real analytic setting. Control theoretically, this is not a good approach, since many interesting attributes of control systems are lost when the control set is open in this way. For example, in optimal control theory, one may loose the existence of optimal arcs. One might relax this openness requirement by asking that, while the control set not be an open subset of \({\mathbb {R}}^m\), the function F be the restriction to the control set of a mapping defined on an open set. This, for example, is certainly tacit when dealing with control-affine systems with non-open control sets. However, outside the control-affine setting, this approach has the form of a desperate kludge, and certainly we know of nowhere in the literature where this is done.
To summarise: the constructions in this paper give a very general definition of what is meant by “real analytic control system,” and the definition is “correct” in that (1) it adapts the existing definitions for Lipschitz, finitely differentiable, and smooth control systems, and (2) it has nontrivial attributes such as giving rise to open-loop systems whose flows depend in a real analytic manner on initial condition. That is to say, it is both natural and useful.
1.4 A summary of our approach
With the preceding paragraphs setting the stage for our approach, in this section we give a brief summary of this approach, touching a little more carefully on some points of the discussion above. Based on Sect. 1.1, we consider the control set to be a topological space \(\mathscr {C}\). As per (1), we then have the mapping

that describes the dynamics of the system. We shall denote the regularity of the system by
\(\nu \). In the paper, we consider
 (finitely differentiable),
(finitely differentiable),
 for
for
 (finitely differentiable with Lipschitz top derivative), \(\nu =\infty \) (smooth), \(\nu =\omega \) (real analytic), and \(\nu =\text {hol}\) (holomorphic). As is made clear in Sect. 1.2, one needs to prescribe joint conditions on x and u to ensure that, if one substitutes a sufficiently nice control
(finitely differentiable with Lipschitz top derivative), \(\nu =\infty \) (smooth), \(\nu =\omega \) (real analytic), and \(\nu =\text {hol}\) (holomorphic). As is made clear in Sect. 1.2, one needs to prescribe joint conditions on x and u to ensure that, if one substitutes a sufficiently nice control  , the resulting differential equation has an existence and uniqueness theory, as well as
\(\text {C}^\nu \)-dependence on initial conditions. The crucial observation in the paper is that there is an alternative way of prescribing these joint conditions. To describe this alternative characterisation, let us denote
\(F^u(x)=F(x,u)\) for
\(u\in \mathscr {C}\); thus
\(F^u\) is a
\(\text {C}^\nu \)-vector field. In this paper, we describe the appropriate joint regularity conditions by phrasing them in terms of continuity of the map
, the resulting differential equation has an existence and uniqueness theory, as well as
\(\text {C}^\nu \)-dependence on initial conditions. The crucial observation in the paper is that there is an alternative way of prescribing these joint conditions. To describe this alternative characterisation, let us denote
\(F^u(x)=F(x,u)\) for
\(u\in \mathscr {C}\); thus
\(F^u\) is a
\(\text {C}^\nu \)-vector field. In this paper, we describe the appropriate joint regularity conditions by phrasing them in terms of continuity of the map
 . Of course, continuity of this map requires topologies for both
\(\mathscr {C}\) and the set of vector fields. Therefore, a crucial ingredient in this approach is the prescription of appropriate topologies for spaces of vector fields. Such topologies are well known in the smooth and finitely differentiable categories [3, 31, 46]. Recent work of Jafarpour and Lewis [35] has provided, for the first time, a useable characterisation of the natural topology for the space of real analytic vector fields. Our definition of a “
\(\text {C}^\nu \)-control system” is simply one for which the mapping
. Of course, continuity of this map requires topologies for both
\(\mathscr {C}\) and the set of vector fields. Therefore, a crucial ingredient in this approach is the prescription of appropriate topologies for spaces of vector fields. Such topologies are well known in the smooth and finitely differentiable categories [3, 31, 46]. Recent work of Jafarpour and Lewis [35] has provided, for the first time, a useable characterisation of the natural topology for the space of real analytic vector fields. Our definition of a “
\(\text {C}^\nu \)-control system” is simply one for which the mapping
 is continuous. The main results in the paper are then the following.
is continuous. The main results in the paper are then the following.
-
1.
In Propositions 2, 3, and 5 we provide concrete characterisations of our topological characterisation of \(\text {C}^\nu \)-control systems. As we shall see, and as we have discussed above, in the Lipschitz, finitely differentiable, and smooth cases, these concrete characterisations are the ones that are more or less well-known in the literature. The extension to the real analytic case is novel and substantial, however.
-
2.
We prove in Corollaries 1 and 2 the result that, upon substitution of an open-loop control, the resulting time-varying vector field has a flow depending on initial conditions in a \(\text {C}^\nu \) manner. These results rely on the development of [35] on the role of regularity in the theory of time-varying vector fields. The results are classical when
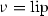 , and are understood to be true (and occasionally proved) when
\(\nu =m\) or
, and are understood to be true (and occasionally proved) when
\(\nu =m\) or
 . When \(\nu =\infty \) this result is often assumed, but we are not aware of a complete proof before that published in [35, Theorem 6.6]. The proof uses classical techniques. However, the real analytic theory is only given for the first time in [35, Theorem 6.26], and the proof uses methods developed in this work on the real analytic topology. Note that our adaptation of the results of Jafarpour and Lewis [35] to control systems is not simply immediate.
. When \(\nu =\infty \) this result is often assumed, but we are not aware of a complete proof before that published in [35, Theorem 6.6]. The proof uses classical techniques. However, the real analytic theory is only given for the first time in [35, Theorem 6.26], and the proof uses methods developed in this work on the real analytic topology. Note that our adaptation of the results of Jafarpour and Lewis [35] to control systems is not simply immediate. -
3.
Our characterisation of real analytic control systems is shown to coincide with the naïve “substitute the complex variable z for the real variable x” notion of real analyticity, at least when the control set is locally compact. This is gratifying, since the conditions that determine a “\(\text {C}^{\text {hol}}\)-control system” are comparatively simple (see Proposition 4) compared to those that determine a “ \(\text {C}^\omega \)-control system” (see Proposition 5). This result is proved in Theorem 3, and here we see that ideas regarding locally convex spaces feature prominently and in nontrivial ways, e.g., we show in Example 1 that lack of local compactness of the control set may cause the conclusion to be false.
In closing this section, let us say a few words about the role in our theory of the theory of locally convex spaces. First of all, while it is true that the theory of locally convex spaces is not a part of the standard body of material learnt in control theory, it is not completely unknown to the community. Some examples of where it plays a role are the following.
-
1.
The chronological calculus developed by Agrachev and Gamkrelidze [2], and which forms the foundation of the presentation in [3], uses the theory in an essential way. Indeed, the ideas in [35] have chronological calculus as their starting point (but not their ending point). The adaptation of these ideas to control systems, as laid out in this paper, is entirely new, however, e.g., it is not a branch of chronological calculus or the extension of this in [35].
-
2.
Even if one sticks to the perceived-to-be-easier world of Banach spaces, weak topologies for Banach spaces are locally convex. In control theory, this fact features prominently in optimal control, where weak compactness is often used to prove the existence of optimal arcs [27, §8.1].
-
3.
In the theory of distributions of Schwartz [56], locally convex topologies play an essential role; indeed, the theory of distributions motivated much of the development of the theory of locally convex spaces. In control theory, the theory of distributions comes up in many places, e.g., in the basic theory of systems [28] and in the theory of weak solutions in the control of partial differential equations [44, 66].
Thus, while the theory of locally convex spaces may not be a part of the standard corpus of control theory, possibly it could be, and we believe that the formulation of control systems here is a compelling argument for this to be the case.
1.5 Outline of the paper
In Sect. 2, following [35], we review the topologies for the spaces of Lipschitz, finitely differentiable, smooth, holomorphic, and real analytic vector fields. (While we are not, per se, interested in holomorphic control systems, the treatment of real analytic systems is often made easier by considerations of holomorphic systems.) The presentation we give of these topologies is intended to be of the “user friendly” variety. That is to say, we simply present the seminorms we use to describe these topologies. A reader wishing to understand the topologies and their properties is encouraged to refer to [35]. However, even a functional understanding of these topologies will require an understanding of locally convex topologies, and for this we refer to [52] as a gentle introduction and [17, 29, 33, 36, 55] as more advanced treatments (which are certainly needed to understand the material in [35]).
One of the nice features of our characterisations of control systems is that, upon substitution of an open-loop control, the resulting initial value problem has solutions depending on initial conditions in a manner consistent with the regularity of the system dependence on state. In Sect. 3 we review the material from [35] regarding vector fields with measurable time dependence required to prove these results.
A control system, in a certain precise sense, is a parameterised family of vector fields, the parameter being control. In Sect. 4 we discuss vector fields parameterised by a parameter in a topological space. In particular, we are interested when the parameterised vector field depends continuously on control, where the topology on the space of vector fields is one of the topologies from Sect. 2. We characterise this continuous dependence by pointwise conditions on state and control. The characterisation in the real analytic case is novel, given that we are using the novel characterisation of the real analytic topology of [35]. We also characterise the real analytic case using holomorphic extensions, as this will likely be the easiest thing to do in practice.
Finally, in Sect. 5 we apply the results up to this point in the paper to control systems. We provide definitions of such systems, and show that, as mentioned above, the corresponding initial value problems have regular dependence on initial conditions. In Sect. 5.3 we illustrate our definitions in a few special cases. As part of this, we show that control-affine systems always have the continuous dependence on control as prescribed in Sect. 4.
1.6 Notation
Let us review the notation we shall use in the paper. There is a lot of machinery used, even with the fairly abbreviated treatment of the topologies for spaces of vector fields. We shall try to give as precise references as possible in the text to facilitate the reader acquiring the necessary background, if needed.
We shall use the slightly unconventional, but perfectly rational, notation of writing \(A\subseteq B\) to denote set inclusion, and when we write \(A\subset B\) we mean that \(A\subseteq B\) and \(A\not =B\). By \({\text {id}}_A\) we denote the identity map on a set A. For a product  of sets,
of sets,  is the projection onto the jth component. For a subset \(A\subseteq X\), we denote by \(\chi _{A}\) the characteristic function of A, i.e.,
is the projection onto the jth component. For a subset \(A\subseteq X\), we denote by \(\chi _{A}\) the characteristic function of A, i.e.,
By  we denote the symmetric group on k symbols. By \({\mathbb {Z}}\) we denote the set of integers, with \({\mathbb {Z}}_{\ge 0}\) denoting the set of nonnegative integers and \({\mathbb {Z}}_{>0}\) denoting the set of positive integers. We denote by \({\mathbb {R}}\) and \({\mathbb {C}}\) the sets of real and complex numbers. By \({\mathbb {R}}_{\ge 0}\) we denote the set of nonnegative real numbers and by \({\mathbb {R}}_{>0}\) the set of positive real numbers.
we denote the symmetric group on k symbols. By \({\mathbb {Z}}\) we denote the set of integers, with \({\mathbb {Z}}_{\ge 0}\) denoting the set of nonnegative integers and \({\mathbb {Z}}_{>0}\) denoting the set of positive integers. We denote by \({\mathbb {R}}\) and \({\mathbb {C}}\) the sets of real and complex numbers. By \({\mathbb {R}}_{\ge 0}\) we denote the set of nonnegative real numbers and by \({\mathbb {R}}_{>0}\) the set of positive real numbers.
Elements of \({\mathbb {F}}^n\), \({\mathbb {F}}\in \{{\mathbb {R}},{\mathbb {C}}\}\), are typically denoted with a bold font, e.g., “\({x}\).”
We shall use constructions from algebra and multilinear algebra, referring to [34], [9, Chapter III], and [10, §IV.5]. If  is a field (for us, typically
is a field (for us, typically  ) and if
) and if  is an
is an  -vector space, we denote by
-vector space, we denote by  the algebraic dual. The k-fold tensor product of
the algebraic dual. The k-fold tensor product of  with itself is denoted by
with itself is denoted by  . Thus, if
. Thus, if  is finite-dimensional, we identify
is finite-dimensional, we identify  with the k-multilinear
with the k-multilinear  -valued functions on
-valued functions on  by
by
By  we denote the symmetric tensor algebra of degree k, which we identify with the symmetric k-multilinear
we denote the symmetric tensor algebra of degree k, which we identify with the symmetric k-multilinear  -valued functions on
-valued functions on  , or polynomial functions of homogeneous degree k on
, or polynomial functions of homogeneous degree k on  .
.
For a topological space \(\mathscr {X}\) and \(A\subseteq \mathscr {X}\), \(\mathrm{int}(A)\) denotes the interior of A and \(\mathrm{cl}(A)\) denotes the closure of A. Neighbourhoods will always be open sets.
By \(\lambda \) we denote Lebesgue measure. If \(I\subseteq {\mathbb {R}}\) is an interval and if \(A\subseteq {\mathbb {R}}\), by \(\text {L}^1(I;A)\) we denote the set of Lebesgue integrable A-valued functions on I. By \({\text {L}}_{\mathrm{loc}}^1(I;A)\) we denote the A-valued locally integrable functions on I, i.e., those functions whose restrictions to compact subintervals are integrable. In like manner, we denote by \(\text {L}^\infty (I;A)\) and \({\text {L}}_{\mathrm{loc}}^\infty (I;A)\) the essentially bounded A-valued functions and the locally essentially bounded A-valued functions, respectively.
For an interval I and a topological space \(\mathscr {X}\), a curve \(\gamma :I\rightarrow \mathscr {X}\) is measurable if \(\gamma ^{-1}(\mathscr {B})\) is Lebesgue measurable for every Borel set  . By \(\text {L}^\infty (I;\mathscr {X})\) we denote the measurable curves
. By \(\text {L}^\infty (I;\mathscr {X})\) we denote the measurable curves  for which there exists a compact set \(K\subseteq \mathscr {X}\) with
for which there exists a compact set \(K\subseteq \mathscr {X}\) with
i.e., \(\text {L}^\infty (I;\mathscr {X})\) is the set of essentially bounded curves. By  we denote the locally essentially bounded curves, meaning those measurable curves whose restrictions to compact subintervals are essentially bounded.
we denote the locally essentially bounded curves, meaning those measurable curves whose restrictions to compact subintervals are essentially bounded.
Our differential geometric conventions mostly follow [1]. Whenever we write “manifold,” we mean “second-countable Hausdorff manifold.” This implies, in particular, that manifolds are assumed to be metrisable [1, Corollary 5.5.13]. If we use the letter “n” without mentioning what it is, it is the dimension of the connected component of the manifold  with which we are working at that time. The tangent bundle of a manifold
with which we are working at that time. The tangent bundle of a manifold  is denoted by
is denoted by  and the cotangent bundle by
and the cotangent bundle by  . If \(I\subseteq {\mathbb {R}}\) is an interval and if
. If \(I\subseteq {\mathbb {R}}\) is an interval and if  is a curve that is differentiable at \(t\in I\), we denote the tangent vector field to the curve at t by \(\xi '(t)\).
is a curve that is differentiable at \(t\in I\), we denote the tangent vector field to the curve at t by \(\xi '(t)\).
If  is a vector bundle, we denote the fibre over
is a vector bundle, we denote the fibre over  by
by  and we sometimes denote by \(0_x\) the zero vector in \(E_x\). If
and we sometimes denote by \(0_x\) the zero vector in \(E_x\). If  is a submanifold, we denote by
is a submanifold, we denote by  the restriction of
the restriction of  to
to  which we regard as a vector bundle over
which we regard as a vector bundle over  . If \({\mathbb {G}}\) is a fibre metric on
. If \({\mathbb {G}}\) is a fibre metric on  , i.e., a smooth assignment of an inner product to each of the fibres of
, i.e., a smooth assignment of an inner product to each of the fibres of  , then \(||\cdot ||_{{\mathbb {G}}}\) denotes the norm associated with the inner product on fibres.
, then \(||\cdot ||_{{\mathbb {G}}}\) denotes the norm associated with the inner product on fibres.
We will work in both the smooth and real analytic categories, with occasional forays into the holomorphic category. We will also work with finitely differentiable objects, i.e., objects of class \(\text {C}^r\) for \(r\in {\mathbb {Z}}_{\ge 0}\). (We will also work with Lipschitz objects, but will develop the notation for these in the text.) A good reference for basic real analytic analysis is [39], but we will need ideas going beyond those from this text, or any other text. Relatively recent work of e.g., [23, 24, 67] has shed a great deal of light on real analytic analysis, and we shall take advantage of this work. An analytic manifold or mapping will be said to be of class
\({\varvec{\text {C}}}^\omega \). Let \(r\in {\mathbb {Z}}_{\ge 0}\cup \{\infty ,\omega \}\). The set of sections of a vector bundle  of class \(\text {C}^r\) is denoted by
of class \(\text {C}^r\) is denoted by  . Thus, in particular,
. Thus, in particular,  denotes the set of vector fields of class \(\text {C}^r\). We shall think of
denotes the set of vector fields of class \(\text {C}^r\). We shall think of  as a \({\mathbb {R}}\)-vector space with the natural pointwise addition and scalar multiplication operations.
as a \({\mathbb {R}}\)-vector space with the natural pointwise addition and scalar multiplication operations.
We also work with holomorphic, i.e., complex analytic, manifolds and associated geometric constructions; real analytic geometry, at some level, seems to unavoidably rely on holomorphic geometry. A nice overview of holomorphic geometry, and some of its connections to real analytic geometry, is given in the book [14]. There are many specialised texts on the subject of holomorphic geometry, including [20, 26, 30, 32]. For our purposes, we shall just say the following things. By  we denote the holomorphic tangent bundle of
we denote the holomorphic tangent bundle of  . This is the object which, in complex differential geometry, is commonly denoted by
. This is the object which, in complex differential geometry, is commonly denoted by  . By
. By  we denote the space of holomorphic sections of an holomorphic vector bundle
we denote the space of holomorphic sections of an holomorphic vector bundle  . We shall use both the natural \({\mathbb {C}}\)- and, by restriction, \({\mathbb {R}}\)-vector space structures for
. We shall use both the natural \({\mathbb {C}}\)- and, by restriction, \({\mathbb {R}}\)-vector space structures for  .
.
We shall make use of locally convex topological vector spaces, and refer to [17, 29, 33, 36, 52, 55] for details. In the proof of Theorem 3 we shall make use of the contemporary research literature on locally convex spaces, and will indicate this when required. We shall denote by  the set of continuous linear maps from a locally convex space
the set of continuous linear maps from a locally convex space  to a locally convex space
to a locally convex space  . We will break with the usual language one sees in the theory of locally convex spaces and call what are commonly called “inductive” limits, instead “direct” limits, in keeping with the rest of category theory. (The notion of a direct limit only occurs in the proof of Theorem 3, so readers not interested in understanding this proof can forgo the rather difficult notion of direct limit topologies.)
. We will break with the usual language one sees in the theory of locally convex spaces and call what are commonly called “inductive” limits, instead “direct” limits, in keeping with the rest of category theory. (The notion of a direct limit only occurs in the proof of Theorem 3, so readers not interested in understanding this proof can forgo the rather difficult notion of direct limit topologies.)
2 Topologies for spaces of vector fields
In this section, we review the definitions of the topologies we use for spaces of Lipschitz, finitely differentiable, smooth, holomorphic, and real analytic vector fields. We will not work explicitly with holomorphic systems, but it is often easiest to describe real analytic attributes in terms of holomorphic extensions, particularly in practice, where one simply “replaces x with z.”
While our interest in this paper is solely in vector fields, it is notationally simpler, and mathematically no more complicated, to work instead with general vector bundles much of the time. Thus, throughout this section we shall consider a vector bundle  that is either smooth, real analytic, or holomorphic, depending on our needs. A reader may, if they wish, have in mind the tangent bundle at all times.
that is either smooth, real analytic, or holomorphic, depending on our needs. A reader may, if they wish, have in mind the tangent bundle at all times.
We comment that all topologies we define are locally convex topologies, of which the normed topologies are a special case. That is, the topologies are defined using seminorms, not norms. Moreover, few of the topologies we define, and none of the interesting ones, are normable. So a reader who is not familiar with locally convex topologies will have to do some reading; we recommend [52] as a nice introduction.
For a reader looking for the “punchline” of this section, we comment that the principle constructions that we carry forward are the seminorms defined in Eqs. (4), (5), (6), (7), and (8). Except for the last of these, the seminorms for the real analytic topology, these seminorms are easy to understand, essentially being some form of “sup-norm” for derivatives on compact sets. The complexity of the real analytic seminorms seems unavoidable, although sometimes one can reduce to the holomorphic case, as in Theorem 3.
2.1 Fibre norms for jet bundles
The classes of sections we consider are all characterised by their derivatives in some manner. The appropriate device for considering derivatives of sections is the theory of jet bundles, for which we refer to [54] and [38, §12]. By  we denote the vector bundle of m-jets of sections of
we denote the vector bundle of m-jets of sections of  , with
, with  denoting the projection. If \(\xi \) is a smooth section of
denoting the projection. If \(\xi \) is a smooth section of  , we denote by \(j_m\xi \) the corresponding smooth section of
, we denote by \(j_m\xi \) the corresponding smooth section of  . The reader would do well to remember that, in local coordinates, points in
. The reader would do well to remember that, in local coordinates, points in  simply represent a section and its first m derivatives. To arrive at a formulation that is independent of coordinates, we perform some complicated decompositions with these derivatives using connections. However, the basically simple idea that an m-jet is comprised of the first m derivatives should not be lost.
simply represent a section and its first m derivatives. To arrive at a formulation that is independent of coordinates, we perform some complicated decompositions with these derivatives using connections. However, the basically simple idea that an m-jet is comprised of the first m derivatives should not be lost.
In a local trivialisation of  , one has the local representatives of the derivatives of sections, order-by-order. Such an order-by-order decomposition of derivatives is not possible globally, however. Nonetheless, following [35, §2.1], we shall mimic this order-by-order decomposition globally using a linear connection \(\nabla ^0\) on
, one has the local representatives of the derivatives of sections, order-by-order. Such an order-by-order decomposition of derivatives is not possible globally, however. Nonetheless, following [35, §2.1], we shall mimic this order-by-order decomposition globally using a linear connection \(\nabla ^0\) on  and an affine connection \(\nabla \) on
and an affine connection \(\nabla \) on  . First note that \(\nabla \) defines a connection on
. First note that \(\nabla \) defines a connection on  by duality. Also, \(\nabla \) and \(\nabla ^0\) together define a connection \(\nabla ^m\) on
by duality. Also, \(\nabla \) and \(\nabla ^0\) together define a connection \(\nabla ^m\) on  by asking that the Leibniz Rule be satisfied for tensor product. Then, for a smooth section \(\xi \) of
by asking that the Leibniz Rule be satisfied for tensor product. Then, for a smooth section \(\xi \) of  , we denote
, we denote
which is a smooth section of  . By convention we take \(\nabla ^{(-1)}\xi =\xi \).
. By convention we take \(\nabla ^{(-1)}\xi =\xi \).
We then have a map

which can be verified to be an isomorphism of vector bundles [35, Lemma 2.1]. Here  is defined by
is defined by

Now we note that inner products on the components of a tensor product induce in a natural way inner products on the tensor product [35, Lemma 2.3]. Thus, if we suppose that we have a fibre metric \({\mathbb {G}}_0\) on  and a Riemannian metric \({\mathbb {G}}\) on
and a Riemannian metric \({\mathbb {G}}\) on  , there is induced a natural fibre metric \({\mathbb {G}}_m\) on
, there is induced a natural fibre metric \({\mathbb {G}}_m\) on  for each \(m\in {\mathbb {Z}}_{\ge 0}\). We then define a fibre metric \(\overline{{\mathbb {G}}}_m\) on
for each \(m\in {\mathbb {Z}}_{\ge 0}\). We then define a fibre metric \(\overline{{\mathbb {G}}}_m\) on  by
by

(The factorials are required to make things work out with the real analytic topology.) The corresponding fibre norm we denote by \(||\cdot ||_{\overline{{\mathbb {G}}}_m}\).
2.2 Seminorms for spaces of smooth vector fields
Let  be a smooth vector bundle. Using the fibre norms from the preceding section, it is a straightforward matter to define appropriate seminorms that define the locally convex topology for
be a smooth vector bundle. Using the fibre norms from the preceding section, it is a straightforward matter to define appropriate seminorms that define the locally convex topology for  . For
. For  compact and for \(m\in {\mathbb {Z}}_{\ge 0}^m\), define a seminorm \(p_{K,m}^\infty \) on
compact and for \(m\in {\mathbb {Z}}_{\ge 0}^m\), define a seminorm \(p_{K,m}^\infty \) on  by
by
The family of seminorms \(p_{K,m}^\infty \),  compact, \(m\in {\mathbb {Z}}_{\ge 0}\), defines a locally convex topology, called the \(\varvec{\text {C}}^\infty \)
-topology.Footnote 2 One can see, looking at these seminorms, that the topology is just that of uniform convergence of all derivatives on compact sets. This topology has the following properties:
compact, \(m\in {\mathbb {Z}}_{\ge 0}\), defines a locally convex topology, called the \(\varvec{\text {C}}^\infty \)
-topology.Footnote 2 One can see, looking at these seminorms, that the topology is just that of uniform convergence of all derivatives on compact sets. This topology has the following properties:
-
1.
it is Hausdorff, metrisable, and complete, i.e., it is a Fréchet topology;
-
2.
it is separable;
-
3.
it is characterised by the sequences converging to zero, which are the sequences \((\xi _j)_{j\in {\mathbb {Z}}_{>0}}\) such that, for each
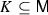 and \(m\in {\mathbb {Z}}_{\ge 0}\), the sequence \((j_m\xi _j|K)_{j\in {\mathbb {Z}}_{>0}}\) converges uniformly to zero.
and \(m\in {\mathbb {Z}}_{\ge 0}\), the sequence \((j_m\xi _j|K)_{j\in {\mathbb {Z}}_{>0}}\) converges uniformly to zero.
In this paper we shall not make reference to other properties of the \(\text {C}^\infty \)-topology, but we mention that there are other properties that play an important role in the results in Sect. 3. For these details, and for references where the above properties are proved, we refer to [35, §3.2].
2.3 Seminorms for spaces of finitely differentiable vector fields
We again take  to be a smooth vector bundle, and we fix \(m\in {\mathbb {Z}}_{\ge 0}\). For the space
to be a smooth vector bundle, and we fix \(m\in {\mathbb {Z}}_{\ge 0}\). For the space  of m-times continuously differentiable sections, we define seminorms \(p_K^m\),
of m-times continuously differentiable sections, we define seminorms \(p_K^m\),  compact, for
compact, for  by
by
The locally convex topology defined by the family of seminorms \(p_K^m\),  compact, we call the \(\varvec{\text {C}}^m\)
-topology. Analogously to our interpretation above of the seminorms in the smooth case, the seminorms clearly define the topology of uniform convergence of the first m derivatives on compact sets. The \(\text {C}^m\)-topology has the following properties:
compact, we call the \(\varvec{\text {C}}^m\)
-topology. Analogously to our interpretation above of the seminorms in the smooth case, the seminorms clearly define the topology of uniform convergence of the first m derivatives on compact sets. The \(\text {C}^m\)-topology has the following properties:
-
1.
it is Hausdorff, metrisable, and complete, i.e., it is a Fréchet topology;
-
2.
it is separable;
-
3.
it is characterised by the sequences converging to zero, which are the sequences \((\xi _j)_{j\in {\mathbb {Z}}_{>0}}\) such that, for each
 , the sequence \((j_m\xi _j|K)_{j\in {\mathbb {Z}}_{>0}}\) converges uniformly to zero;
, the sequence \((j_m\xi _j|K)_{j\in {\mathbb {Z}}_{>0}}\) converges uniformly to zero; -
4.
if
 is compact, then
is compact, then  is a norm that gives the \(\text {C}^m\)-topology.
is a norm that gives the \(\text {C}^m\)-topology.
As with the \(\text {C}^\infty \)-topology, we refer to [35, §3.4] for details.
2.4 Seminorms for spaces of Lipschitz vector fields
In this section, we again work with a smooth vector bundle  . In defining the fibre metrics from Sect. 2.1, for the Lipschitz topologies the affine connection \(\nabla \) is required to be the Levi–Civita connection for the Riemannian metric \({\mathbb {G}}\) and the linear connection \(\nabla ^0\) is required to be \({\mathbb {G}}_0\)-orthogonal. While Lipschitz vector fields are often used, spaces of Lipschitz vector fields are not. Nonetheless, one may define seminorms for spaces of Lipschitz vector fields rather analogous to those defined above in the smooth and finitely differentiable cases. Let \(m\in {\mathbb {Z}}_{\ge 0}\). By
. In defining the fibre metrics from Sect. 2.1, for the Lipschitz topologies the affine connection \(\nabla \) is required to be the Levi–Civita connection for the Riemannian metric \({\mathbb {G}}\) and the linear connection \(\nabla ^0\) is required to be \({\mathbb {G}}_0\)-orthogonal. While Lipschitz vector fields are often used, spaces of Lipschitz vector fields are not. Nonetheless, one may define seminorms for spaces of Lipschitz vector fields rather analogous to those defined above in the smooth and finitely differentiable cases. Let \(m\in {\mathbb {Z}}_{\ge 0}\). By  we denote the space of sections of
we denote the space of sections of  that are m-times continuously differentiable and whose m-jet is locally Lipschitz. (One can think of this in coordinates, but Jafarpour and Lewis [35] provide geometric definitions, if the reader is interested.) If a section \(\xi \) is of class
that are m-times continuously differentiable and whose m-jet is locally Lipschitz. (One can think of this in coordinates, but Jafarpour and Lewis [35] provide geometric definitions, if the reader is interested.) If a section \(\xi \) is of class  , then, by Rademacher’s Theorem [25, Theorem 3.1.6], its \((m+1)\)st derivative exists almost everywhere. Thus, we define
, then, by Rademacher’s Theorem [25, Theorem 3.1.6], its \((m+1)\)st derivative exists almost everywhere. Thus, we define
which is the local sectional dilatation of \(\xi \). Here \(\nabla ^{[m]}\) is the connection in  defined by the decomposition (3). Let
defined by the decomposition (3). Let  be compact and define
be compact and define
for  . We can then define a seminorm
. We can then define a seminorm  on
on  by
by

The family of seminorms  defines a locally convex topology for
defines a locally convex topology for  , which we call that
, which we call that  -topology. One sees that the seminorms ensure that our topology possesses the attribute of uniform convergence of the first m derivatives on compact sets, as well as uniform control over the local Lipschitz constant of the top derivative. The topology has the following attributes:
-topology. One sees that the seminorms ensure that our topology possesses the attribute of uniform convergence of the first m derivatives on compact sets, as well as uniform control over the local Lipschitz constant of the top derivative. The topology has the following attributes:
-
1.
it is Hausdorff, metrisable, and complete, i.e., it is a Fréchet topology;
-
2.
it is separable;
-
3.
it is characterised by the sequences converging to zero, which are the sequences \((\xi _j)_{j\in {\mathbb {Z}}_{>0}}\) such that, for each
 , the sequence \((j_m\xi _j|K)_{j\in {\mathbb {Z}}_{>0}}\) converges uniformly to zero in both seminorms \(\lambda _K^m\) and \(p_K^m\);
, the sequence \((j_m\xi _j|K)_{j\in {\mathbb {Z}}_{>0}}\) converges uniformly to zero in both seminorms \(\lambda _K^m\) and \(p_K^m\); -
4.
if
 is compact, then
is compact, then  is a norm that gives the
is a norm that gives the  -topology.
-topology.
We refer to [35, §3.5] for details.
2.5 Seminorms for spaces of holomorphic vector fields
Now we consider a holomorphic vector bundle  and denote by
and denote by  the space of holomorphic sections of
the space of holomorphic sections of  . We let \({\mathbb {G}}\) be an Hermitian metric on the vector bundle and denote by \(||\cdot ||_{{\mathbb {G}}}\) the associated fibre norm. For
. We let \({\mathbb {G}}\) be an Hermitian metric on the vector bundle and denote by \(||\cdot ||_{{\mathbb {G}}}\) the associated fibre norm. For  compact, denote by \(p_K^\text {hol}\) the seminorm
compact, denote by \(p_K^\text {hol}\) the seminorm
on  . The family of seminorms \(p_K^\text {hol}\),
. The family of seminorms \(p_K^\text {hol}\),  compact, define a locally convex topology for
compact, define a locally convex topology for  that we call the \(\varvec{\text {C}^\mathbf{hol }}\)
-topology. The seminorms defines a very simple topology, that of uniform convergence on compact sets. It is the miracle of the Cauchy estimates (a global version of which we state as Proposition 1 below) that ensures that this is adequate to ensure a topology consistent with the holomorphic nature of the sections. This topology has the following properties:
that we call the \(\varvec{\text {C}^\mathbf{hol }}\)
-topology. The seminorms defines a very simple topology, that of uniform convergence on compact sets. It is the miracle of the Cauchy estimates (a global version of which we state as Proposition 1 below) that ensures that this is adequate to ensure a topology consistent with the holomorphic nature of the sections. This topology has the following properties:
-
1.
it is Hausdorff, metrisable, and complete, i.e., it is a Fréchet topology;
-
2.
it is separable;
-
3.
it is characterised by the sequences converging to zero, which are the sequences \((\xi _j)_{j\in {\mathbb {Z}}_{>0}}\) such that, for each \(K\subseteq \mathsf {M}\), the sequence \((\xi _j|K)_{j\in {\mathbb {Z}}_{>0}}\) converges uniformly to zero;
-
4.
if
 is compact, then
is compact, then  is a norm that gives the \(\text {C}^\text {hol}\)-topology.
is a norm that gives the \(\text {C}^\text {hol}\)-topology.
We refer to [35, §4.2] and the references therein for details about the \(\text {C}^\text {hol}\)-topology.
We shall also require a result related to the classical Cauchy estimates from complex analysis. To state the result, denote by

the subspace of bounded sections. This is a normed space with the norm

We then have the following result.
Proposition 1
(Cauchy estimates for vector bundles) Let  be an holomorphic vector bundle, let \(K\subseteq \mathsf {M}\) be compact, and let \(\mathscr {U}\) be a relatively compact neighbourhood of K. Then there exist \(C,r\in {\mathbb {R}}_{>0}\) such that
be an holomorphic vector bundle, let \(K\subseteq \mathsf {M}\) be compact, and let \(\mathscr {U}\) be a relatively compact neighbourhood of K. Then there exist \(C,r\in {\mathbb {R}}_{>0}\) such that

for every \(m\in {\mathbb {Z}}_{\ge 0}\) and  .
.
Proof
We refer to [35, Proposition 4.2]. \(\square \)
2.6 Seminorms for spaces of real analytic vector fields
The topologies described above for spaces of smooth, finitely differentiable, Lipschitz, and holomorphic sections of a vector bundle are quite simple to understand in terms of their converging sequences. The topology one considers for real analytic sections does not have this attribute. There is a bit of a history to the characterisation of real analytic topologies, and we refer to [35, Chapter 5] for four equivalent characterisations of the real analytic topology for the space of real analytic sections of a vector bundle. Here we will give the most elementary of these definitions to state, although it is probably not the most practical definition. In practice, it is probably best to somehow complexify and use the holomorphic topology; we give an instance of this in Theorem 3 below.
In this section, we let  be a real analytic vector bundle and let
be a real analytic vector bundle and let  be the space of real analytic sections. One can show that there exist a real analytic linear connection \(\nabla ^0\) on
be the space of real analytic sections. One can show that there exist a real analytic linear connection \(\nabla ^0\) on  , a real analytic affine connection \(\nabla \) on
, a real analytic affine connection \(\nabla \) on  , a real analytic fibre metric on
, a real analytic fibre metric on  , and a real analytic Riemannian metric on
, and a real analytic Riemannian metric on  [35, Lemma 2.4]. Thus we can define real analytic fibre metrics \(\overline{{\mathbb {G}}}_m\) on the jet bundles
[35, Lemma 2.4]. Thus we can define real analytic fibre metrics \(\overline{{\mathbb {G}}}_m\) on the jet bundles  as in Sect. 2.1.
as in Sect. 2.1.
To define seminorms for  , let \(\text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\) denote the space of sequences in \({\mathbb {R}}_{>0}\), indexed by \({\mathbb {Z}}_{\ge 0}\), and converging to zero. We shall denote a typical element of \(\text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\) by \(\mathbf {a}=(a_j)_{j\in {\mathbb {Z}}_{\ge 0}}\). Now, for
, let \(\text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\) denote the space of sequences in \({\mathbb {R}}_{>0}\), indexed by \({\mathbb {Z}}_{\ge 0}\), and converging to zero. We shall denote a typical element of \(\text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\) by \(\mathbf {a}=(a_j)_{j\in {\mathbb {Z}}_{\ge 0}}\). Now, for  and \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), we define a seminorm \(p_{K,\mathbf {a}}^\omega \) for
and \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), we define a seminorm \(p_{K,\mathbf {a}}^\omega \) for  by
by
Unlike the seminorms for all of our regularity classes above, there is no “short form” for describing these seminorms in the real analytic case. The reason for this is that, while all real analytic functions can be extended to holomorphic functions, the size of the domain on which this extension is valid depends on the function. This dependence of the domain of extension on the function is the genesis of the complicated nature of the above seminorms or the real analytic topology. This notwithstanding, the family of seminorms \(p_{K,\mathbf {a}}^\omega \), \(K\subseteq \mathsf {M}\) compact, \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), defines a locally convex topology on  that we call the \(\varvec{\text {C}}^\omega \)
-topology. This topology has the following attributes:
that we call the \(\varvec{\text {C}}^\omega \)
-topology. This topology has the following attributes:
-
1.
it is Hausdorff and complete;
-
2.
it is not metrisable (and so it not a Fréchet topology);
-
3.
it is separable.
We shall generally avoid dealing with the rather complicated structure of this topology, and shall be able to do what we need by just working with the seminorms. However, in the proof of the quite useful Theorem 3, we shall make reference to some of the more complicated characterisations of the \(\text {C}^\omega \)-topology; we will make the appropriate references required in the course of that proof.
2.7 Summary and notation
In the real case, the degrees of regularity are ordered according to
and in the complex case the ordering is the same, of course, but with an extra \(\text {C}^\text {hol}\) on the right. Sometimes it will be convenient to write  for \(\nu \in \{{\mathbb {Z}}_{\ge 0},\infty ,\omega \}\), and in doing this we adopt the obvious convention that
for \(\nu \in \{{\mathbb {Z}}_{\ge 0},\infty ,\omega \}\), and in doing this we adopt the obvious convention that  and \(\omega +\text {lip}=\omega \).
and \(\omega +\text {lip}=\omega \).
Where possible, we will state definitions and results for all regularity classes at once. To do this, we will let \(m\in {\mathbb {Z}}_{\ge 0}\) and  , and consider the regularity classes \(\nu \in \{m+m',\infty ,\omega \}\). In such cases we shall require that the underlying manifold be of class “\(\text {C}^r\), \(r\in \{\infty ,\omega \}\), as required.” This has the obvious meaning, namely that we consider class \(\text {C}^\omega \) if \(\nu =\omega \) and class \(\text {C}^\infty \) otherwise. Proofs will typically break into the four cases \(\nu =\infty \), \(\nu =m\),
, and consider the regularity classes \(\nu \in \{m+m',\infty ,\omega \}\). In such cases we shall require that the underlying manifold be of class “\(\text {C}^r\), \(r\in \{\infty ,\omega \}\), as required.” This has the obvious meaning, namely that we consider class \(\text {C}^\omega \) if \(\nu =\omega \) and class \(\text {C}^\infty \) otherwise. Proofs will typically break into the four cases \(\nu =\infty \), \(\nu =m\),  , and \(\nu =\omega \). In some cases there is a structural similarity in the way arguments are carried out; so we will sometimes do all cases at once. In doing this, we will, for
, and \(\nu =\omega \). In some cases there is a structural similarity in the way arguments are carried out; so we will sometimes do all cases at once. In doing this, we will, for  be compact, for \(k\in {\mathbb {Z}}_{\ge 0}\), and for \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), denote
be compact, for \(k\in {\mathbb {Z}}_{\ge 0}\), and for \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), denote
The convenience and brevity more than make up for the slight loss of preciseness in this approach.
3 Time-varying vector fields
One of the principle contributions of this paper is that, for the control systems we define in Sect. 5, if we substitute an open-loop control \(\mu =\mu _*\) into a system
to obtain a time-varying dynamical system
then the flow of this dynamical system depends on initial condition in a manner consistent with the regularity of F. We shall do this in Sect. 5 by showing that the time-varying vector field  falls into a class of vector fields having the appropriate regular dependence on initial condition. The body of work which characterises these classes of vector fields is, in and of itself, quite nontrivial, and we refer to [35, Chapter 6] for details. Here we present the relevant definitions, and state the results from [35] that we shall require.
falls into a class of vector fields having the appropriate regular dependence on initial condition. The body of work which characterises these classes of vector fields is, in and of itself, quite nontrivial, and we refer to [35, Chapter 6] for details. Here we present the relevant definitions, and state the results from [35] that we shall require.
The first four subsections below are, thus, dedicated to definitions, while the final subsection is dedicated to a summary of the required results. As in the preceding section, we give our definitions for sections of vector bundles rather than vector fields, since this is simpler notationally, and costs nothing in terms of complication.
The reader will see that in all cases except the real analytic case, the conditions we give for time-varying vector fields have a “theme” in their definition, and this theme is deduced from the seminorms defining the topology for the respective degrees of regularity. The basic idea here can be summarised as follows. For the finitely differentiable case, one asks that the first finitely many derivatives are integrally bounded, locally uniformly in state. The Lipschitz case is similar, but one also requires that the local Lipschitz constant be integrally bounded, locally uniformly in state. For the smooth case, one simply requires that what holds in the finitely differentiable case holds for all derivatives. The real analytic case is not so easy to interpret. This, however, is not really a crippling deficiency of the theory, because in Theorem 1 we see that in all degrees of regularity, our definitions amount to the local integrability of a naturally defined map into the topological space of vector fields. This explains the importance of our locally convex topologies for time-varying vector fields.
3.1 Smooth time-varying vector fields
We will work with a smooth vector bundle  with a linear connection \(\nabla ^0\) on
with a linear connection \(\nabla ^0\) on  , an affine connection \(\nabla \) on
, an affine connection \(\nabla \) on  , a fibre metric \({\mathbb {G}}_0\) on
, a fibre metric \({\mathbb {G}}_0\) on  , and a Riemannian metric \({\mathbb {G}}\) on
, and a Riemannian metric \({\mathbb {G}}\) on  . This defines the fibre norms \(||\cdot ||_{\overline{{\mathbb {G}}}_m}\) on
. This defines the fibre norms \(||\cdot ||_{\overline{{\mathbb {G}}}_m}\) on  and seminorms \(p^\infty _{K,m}\),
and seminorms \(p^\infty _{K,m}\),  compact, \(m\in {\mathbb {Z}}_{\ge 0}\), on
compact, \(m\in {\mathbb {Z}}_{\ge 0}\), on  as in Sect. 2.2.
as in Sect. 2.2.
Definition 1
(Smooth Carathéodory section) Let  be a smooth vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section of class
\({\varvec{\text {C}}}^\infty \) of
be a smooth vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section of class
\({\varvec{\text {C}}}^\infty \) of  is a map
is a map  with the following properties:
with the following properties:
-
(i)
 for each
for each  ;
; -
(ii)
for each \(t\in {\mathbb {T}}\), the map
 defined by \(\xi _t(x)=\xi (t,x)\) is of class \(\text {C}^\infty \);
defined by \(\xi _t(x)=\xi (t,x)\) is of class \(\text {C}^\infty \); -
(iii)
for each
 , the map
, the map  defined by \(\xi ^x(t)=\xi (t,x)\) is Lebesgue measurable.
defined by \(\xi ^x(t)=\xi (t,x)\) is Lebesgue measurable.
We shall call \({\mathbb {T}}\) the time-domain for the section. By  we denote the set of Carathéodory sections of class \(\text {C}^\infty \) of
we denote the set of Carathéodory sections of class \(\text {C}^\infty \) of  .\(\circ \)
.\(\circ \)
Note that the curve  is in the finite-dimensional vector space
is in the finite-dimensional vector space  , and so Lebesgue measurability of this is unambiguously defined, e.g., by choosing a basis and asking for Lebesgue measurability of the components with respect to this basis.
, and so Lebesgue measurability of this is unambiguously defined, e.g., by choosing a basis and asking for Lebesgue measurability of the components with respect to this basis.
Now we put some conditions on the time dependence of the derivatives of the section.
Definition 2
(Locally integrally
\(\text {C}^\infty \)-bounded and locally essentially
\(\text {C}^\infty \)-bounded sections) Let  be a smooth vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section
be a smooth vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section  of class \(\text {C}^\infty \) is
of class \(\text {C}^\infty \) is
-
(i)
locally integrally \({\varvec{\text {C}}}^\infty \)-bounded if, for every compact set
 and every \(m\in {\mathbb {Z}}_{\ge 0}\), there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K, \end{aligned}$$
and every \(m\in {\mathbb {Z}}_{\ge 0}\), there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K, \end{aligned}$$and is
-
(ii)
locally essentially \(\varvec{\text {C}}^\infty \)-bounded if, for every compact set
 and every \(m\in {\mathbb {Z}}_{\ge 0}\), there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K. \end{aligned}$$
and every \(m\in {\mathbb {Z}}_{\ge 0}\), there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K. \end{aligned}$$
The set of locally integrally \(\text {C}^\infty \)-bounded sections of  with time-domain \({\mathbb {T}}\) is denoted by
with time-domain \({\mathbb {T}}\) is denoted by  and the set of locally essentially \(\text {C}^\infty \)-bounded sections of
and the set of locally essentially \(\text {C}^\infty \)-bounded sections of  with time-domain \({\mathbb {T}}\) is denoted by
with time-domain \({\mathbb {T}}\) is denoted by  . \(\circ \)
. \(\circ \)
3.2 Finitely differentiable and Lipschitz time-varying vector fields
In this section, so as to be consistent with our definition of Lipschitz norms in Sect. 2.4, we suppose that the affine connection \(\nabla \) on  is the Levi–Civita connection for the Riemannian metric \({\mathbb {G}}\) and that the vector bundle connection \(\nabla ^0\) in
is the Levi–Civita connection for the Riemannian metric \({\mathbb {G}}\) and that the vector bundle connection \(\nabla ^0\) in  is \({\mathbb {G}}_0\)-orthogonal.
is \({\mathbb {G}}_0\)-orthogonal.
Definition 3
(Finitely differentiable or Lipschitz Carathéodory section) Let  be a smooth vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. Let \(m\in {\mathbb {Z}}_{\ge 0}\) and let
be a smooth vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. Let \(m\in {\mathbb {Z}}_{\ge 0}\) and let  . A Carathéodory section of class \(\varvec{\text {C}}^{m+m'}\) of
. A Carathéodory section of class \(\varvec{\text {C}}^{m+m'}\) of  is a map
is a map  with the following properties:
with the following properties:
-
(i)
 for each
for each  ;
; -
(ii)
for each \(t\in {\mathbb {T}}\), the map
 defined by \(\xi _t(x)=\xi (t,x)\) is of class \(\text {C}^{m+m'}\);
defined by \(\xi _t(x)=\xi (t,x)\) is of class \(\text {C}^{m+m'}\); -
(iii)
for each
 , the map
, the map  defined by \(\xi ^x(t)=\xi (t,x)\) is Lebesgue measurable.
defined by \(\xi ^x(t)=\xi (t,x)\) is Lebesgue measurable.
We shall call \({\mathbb {T}}\) the time-domain for the section. By  we denote the set of Carathéodory sections of class \(\text {C}^{m+m'}\) of
we denote the set of Carathéodory sections of class \(\text {C}^{m+m'}\) of  . \(\circ \)
. \(\circ \)
Now we put some conditions on the time dependence of the derivatives of the section.
Definition 4
(Locally integrally
\(\text {C}^{m+m'}\)-bounded and locally essentially
\(\text {C}^{m+m'}\)-bounded sections) Let  be a smooth vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. Let \(m\in {\mathbb {Z}}_{\ge 0}\) and let
be a smooth vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. Let \(m\in {\mathbb {Z}}_{\ge 0}\) and let  . A Carathéodory section
. A Carathéodory section  of class \(\text {C}^{m+m'}\) is
of class \(\text {C}^{m+m'}\) is
-
(i)
locally integrally \(\varvec{\text {C}}^{m+m'}\)-bounded if:
-
(a)
\(m'=0\): for every compact set
 , there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K; \end{aligned}$$
, there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K; \end{aligned}$$ -
(b)
 : for every compact set
: for every compact set  , there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} \text {dil}\,j_m\xi _t(x),||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K, \end{aligned}$$
, there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} \text {dil}\,j_m\xi _t(x),||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K, \end{aligned}$$
and is
-
(a)
-
(ii)
locally essentially \(\varvec{{\text {C}}^{m+m'}}\)-bounded if:
-
(a)
\(m'=0\): for every compact set
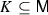 , there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K; \end{aligned}$$
, there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K; \end{aligned}$$ -
(b)
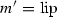 : for every compact set
: for every compact set  , there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} \text {dil}\,j_m\xi _t(x),||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K. \end{aligned}$$
, there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} \text {dil}\,j_m\xi _t(x),||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K. \end{aligned}$$
-
(a)
The set of locally integrally \(\text {C}^{m+m'}\)-bounded sections of  with time-domain \({\mathbb {T}}\) is denoted by
with time-domain \({\mathbb {T}}\) is denoted by  and the set of locally essentially \(\text {C}^{m+m'}\)-bounded sections of
and the set of locally essentially \(\text {C}^{m+m'}\)-bounded sections of  with time-domain \({\mathbb {T}}\) is denoted by
with time-domain \({\mathbb {T}}\) is denoted by  . \(\circ \)
. \(\circ \)
3.3 Holomorphic time-varying vector fields
We will consider an holomorphic vector bundle  with an Hermitian fibre metric \({\mathbb {G}}\). This defines the seminorms \(p^{\text {hol}}_K\),
with an Hermitian fibre metric \({\mathbb {G}}\). This defines the seminorms \(p^{\text {hol}}_K\),  compact, describing the \(\text {C}^{\text {hol}}\)-topology for
compact, describing the \(\text {C}^{\text {hol}}\)-topology for  as in Sect. 2.5.
as in Sect. 2.5.
Let us get started with the definitions.
Definition 5
(Holomorphic Carathéodory section) Let  be an holomorphic vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section of class
\(\varvec{\text {C}^{\text {hol}}}\) of
be an holomorphic vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section of class
\(\varvec{\text {C}^{\text {hol}}}\) of  is a map
is a map  with the following properties:
with the following properties:
-
(i)
 for each
for each  ;
; -
(ii)
for each \(t\in {\mathbb {T}}\), the map
 defined by \(\xi _t(z)\) is of class \(\text {C}^{\text {hol}}\);
defined by \(\xi _t(z)\) is of class \(\text {C}^{\text {hol}}\); -
(iii)
for each
 , the map
, the map  defined by \(\xi ^z(t)=\xi (t,z)\) is Lebesgue measurable.
defined by \(\xi ^z(t)=\xi (t,z)\) is Lebesgue measurable.
We shall call \({\mathbb {T}}\) the time-domain for the section. By  we denote the set of Carathéodory sections of class \(\text {C}^{\text {hol}}\) of
we denote the set of Carathéodory sections of class \(\text {C}^{\text {hol}}\) of  . \(\circ \)
. \(\circ \)
The associated notions for time-dependent sections compatible with the \(\text {C}^{\text {hol}}\)-topology are as follows.
Definition 6
(Locally integrally
\(\text {C}^{\text {hol}}\)-bounded and locally essentially
\(\text {C}^{\text {hol}}\)-bounded sections) Let  be an holomorphic vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section
be an holomorphic vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section  of class \(\text {C}^{\text {hol}}\) is
of class \(\text {C}^{\text {hol}}\) is
-
(i)
locally integrally \(\varvec{\text {C}^{\text {hol}}}{\varvec{-bounded}}\) if, for every compact set
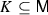 , there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||\xi (t,z)||_{{\mathbb {G}}}\le g(t),\qquad (t,z)\in {\mathbb {T}}\times K \end{aligned}$$
, there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||\xi (t,z)||_{{\mathbb {G}}}\le g(t),\qquad (t,z)\in {\mathbb {T}}\times K \end{aligned}$$and is
-
(ii)
locally essentially \(\varvec{\text {C}^{\text {hol}}}\) -bounded if, for every compact set
 , there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||\xi (t,z)||_{{\mathbb {G}}}\le g(t),\qquad (t,z)\in {\mathbb {T}}\times K. \end{aligned}$$
, there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} ||\xi (t,z)||_{{\mathbb {G}}}\le g(t),\qquad (t,z)\in {\mathbb {T}}\times K. \end{aligned}$$
The set of locally integrally \(\text {C}^{\text {hol}}\)-bounded sections of  with time-domain \({\mathbb {T}}\) is denoted by
with time-domain \({\mathbb {T}}\) is denoted by  and the set of locally essentially \(\text {C}^{\text {hol}}\)-bounded sections of
and the set of locally essentially \(\text {C}^{\text {hol}}\)-bounded sections of  with time-domain \({\mathbb {T}}\) is denoted by
with time-domain \({\mathbb {T}}\) is denoted by  . \(\circ \)
. \(\circ \)
3.4 Real analytic time-varying vector fields
We will consider a real analytic vector bundle  with \(\nabla ^0\) a real analytic linear connection on
with \(\nabla ^0\) a real analytic linear connection on  , \(\nabla \) a real analytic affine connection on
, \(\nabla \) a real analytic affine connection on  , \({\mathbb {G}}_0\) a real analytic fibre metric on
, \({\mathbb {G}}_0\) a real analytic fibre metric on  , and \({\mathbb {G}}\) a real analytic Riemannian metric on
, and \({\mathbb {G}}\) a real analytic Riemannian metric on  . This defines the seminorms \(p^\omega _{K,\mathbf {a}}\),
. This defines the seminorms \(p^\omega _{K,\mathbf {a}}\),  compact, \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), describing the \(\text {C}^\omega \)-topology as in Sect. 2.6.
compact, \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), describing the \(\text {C}^\omega \)-topology as in Sect. 2.6.
Definition 7
(Real analytic Carathéodory section) Let  be a real analytic vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section of class
\(\varvec{\text {C}}^\omega \) of
be a real analytic vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section of class
\(\varvec{\text {C}}^\omega \) of  is a map
is a map  with the following properties:
with the following properties:
-
(i)
 for each
for each 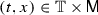 ;
; -
(ii)
for each \(t\in {\mathbb {T}}\), the map
 defined by \(\xi _t(x)\) is of class \(\text {C}^\omega \);
defined by \(\xi _t(x)\) is of class \(\text {C}^\omega \); -
(iii)
for each \(x\in \mathsf {M}\), the map
 defined by \(\xi ^x(t)=\xi (t,x)\) is Lebesgue measurable.
defined by \(\xi ^x(t)=\xi (t,x)\) is Lebesgue measurable.
We shall call \({\mathbb {T}}\) the time-domain for the section. By  we denote the set of Carathéodory sections of class \(\text {C}^\omega \) of
we denote the set of Carathéodory sections of class \(\text {C}^\omega \) of  . \(\circ \)
. \(\circ \)
Now we turn to placing restrictions on the time dependence to allow us to do useful things.
Definition 8
(Locally integrally
\(\text {C}^\omega \)-bounded and locally essentially
\(\text {C}^\omega \)-bounded sections) Let  be a real analytic vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section
be a real analytic vector bundle and let \({\mathbb {T}}\subseteq {\mathbb {R}}\) be an interval. A Carathéodory section  of class \(\text {C}^\omega \) is
of class \(\text {C}^\omega \) is
-
(i)
locally integrally \(\varvec{\text {C}^\omega }\)-bounded if, for every compact set
 and every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} a_0a_1\cdots a_m||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K,\ m\in {\mathbb {Z}}_{\ge 0}, \end{aligned}$$
and every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), there exists \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} a_0a_1\cdots a_m||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t),\qquad (t,x)\in {\mathbb {T}}\times K,\ m\in {\mathbb {Z}}_{\ge 0}, \end{aligned}$$and is
-
(ii)
locally essentially \(\varvec{{\text {C}}^\omega }\)-bounded if, for every compact set
 and every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} a_0a_1\cdots a_m||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t), \qquad (t,x)\in {\mathbb {T}}\times K,\ m\in {\mathbb {Z}}_{\ge 0}. \end{aligned}$$
and every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), there exists \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\) such that $$\begin{aligned} a_0a_1\cdots a_m||j_m\xi _t(x)||_{\overline{{\mathbb {G}}}_m}\le g(t), \qquad (t,x)\in {\mathbb {T}}\times K,\ m\in {\mathbb {Z}}_{\ge 0}. \end{aligned}$$
The set of locally integrally \(\text {C}^\omega \)-bounded sections of  with time-domain \({\mathbb {T}}\) is denoted by
with time-domain \({\mathbb {T}}\) is denoted by  and the set of locally essentially \(\text {C}^\omega \)-bounded sections of
and the set of locally essentially \(\text {C}^\omega \)-bounded sections of  with time-domain \({\mathbb {T}}\) is denoted by
with time-domain \({\mathbb {T}}\) is denoted by  . \(\circ \)
. \(\circ \)
3.5 Topological characterisations and regularity of flows
In this section, we shall state two results, one giving topological characterisations of the preceding definitions and one giving regular dependence of flows on initial conditions. We shall state the results in such a way that all regularity cases are dealt with at once, recalling our notation from Sect. 2.7. Both of these results are important. The first is important because it shows that the myriad definitions from the first four subsections above are unified by the use of the locally convex topologies; the four definitions are really just one definition, and what varies is the topology. The second result is important because it gives us a clue that our characterisations of time-varying vector fields are “correct,” because they have this property of giving rise to flows with the appropriate regularity.
The topological characterisations we give associated with the above definitions have to do with measurability, integrability, and boundedness of the curve  in the space of sections. In general, these notions require some care in their formulation for arbitrary locally convex topological vector spaces. However, the locally convex spaces we consider here are highly structured, and so many of the generally inequivalent definitions for measurability and integrability agree for our spaces.
in the space of sections. In general, these notions require some care in their formulation for arbitrary locally convex topological vector spaces. However, the locally convex spaces we consider here are highly structured, and so many of the generally inequivalent definitions for measurability and integrability agree for our spaces.
Let us give the definitions for measurability, integrability, and boundedness we shall use for an arbitrary locally convex space  .
.
-
1.
A curve
 is measurable if the preimage of every Borel set is Lebesgue measurable.
is measurable if the preimage of every Borel set is Lebesgue measurable. -
2.
The notion of integral we use is known as the Bochner integral. It permits a construction highly reminiscent of that of the Lebesgue integral. This is well understood for Banach spaces [22] and is often mentioned in an offhand manner as being “the same” for locally convex spaces, e.g., [55, page 96]. A detailed textbook treatment does not appear to exist, but fortunately this has been worked out in the note of [5], to which we shall refer for details as needed. One has a notion of simple functions, meaning functions that are finite linear combinations, with coefficients in
 , of characteristic functions of measurable sets. The integral of a simple function \(\sigma =\sum _{j=1}^kv_j\chi _{A_j}\) is $$\begin{aligned} \int _{{\mathbb {T}}}\sigma \,{ \text {d}}\mu =\sum _{j=1}^k\mu (A_j)v_j, \end{aligned}$$
, of characteristic functions of measurable sets. The integral of a simple function \(\sigma =\sum _{j=1}^kv_j\chi _{A_j}\) is $$\begin{aligned} \int _{{\mathbb {T}}}\sigma \,{ \text {d}}\mu =\sum _{j=1}^k\mu (A_j)v_j, \end{aligned}$$in the usual manner. A measurable curve \(\gamma \) is Bochner approximable if it can be approximated with respect to any continuous seminorm by a net of simple functions. A Bochner approximable function \(\gamma \) is Bochner integrable if there is a net of simple functions approximating \(\gamma \) whose integrals converge in
 to a unique value, which is called the integral of \(\gamma \). If
to a unique value, which is called the integral of \(\gamma \). If  is separable and complete, as will be the case for us in this paper, then a measurable curve
is separable and complete, as will be the case for us in this paper, then a measurable curve  is Bochner integrable if and only if
is Bochner integrable if and only if 
for every continuous seminorm p on
 [5, Theorems 3.2 and 3.3]. The curve \(\gamma \) is locally Bochner integrable if \(\gamma |{\mathbb {T}}'\) is Bochner integrable for every compact subinterval \({\mathbb {T}}'\subseteq {\mathbb {T}}\). If
[5, Theorems 3.2 and 3.3]. The curve \(\gamma \) is locally Bochner integrable if \(\gamma |{\mathbb {T}}'\) is Bochner integrable for every compact subinterval \({\mathbb {T}}'\subseteq {\mathbb {T}}\). If  , by
, by  we denote the A-valued Bochner integrable mappings and by
we denote the A-valued Bochner integrable mappings and by  we denote the A-valued locally Bochner integrable mappings.
we denote the A-valued locally Bochner integrable mappings. -
3.
A subset
 is von Neumann
bounded if
is von Neumann
bounded if  is bounded for every continuous seminorm p for
is bounded for every continuous seminorm p for  . The curve
. The curve  is essentially von Neumann
bounded if there exists a bounded set
is essentially von Neumann
bounded if there exists a bounded set  such that
such that 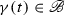 for almost every
for almost every  , and is locally essentially von Neumann bounded if \(\gamma |{\mathbb {T}}'\) is essentially von Neumann bounded for every compact subinterval \({\mathbb {T}}'\subseteq {\mathbb {T}}\). We note that, if
, and is locally essentially von Neumann bounded if \(\gamma |{\mathbb {T}}'\) is essentially von Neumann bounded for every compact subinterval \({\mathbb {T}}'\subseteq {\mathbb {T}}\). We note that, if  is a normed vector space, then von Neumann bounded is the same as norm bounded.Footnote 3
is a normed vector space, then von Neumann bounded is the same as norm bounded.Footnote 3
With these definitions, we now have the following result.
Theorem 1
(Topological characterisations of time-varying vector fields) Let  and
and  , let
, let  , and let
, and let  , as required. For a
, as required. For a  -vector bundle and for a map
-vector bundle and for a map  satisfying
satisfying  for each
for each  , the following two statements are equivalent:
, the following two statements are equivalent:
-
(i)
 ;
; -
(ii)
the map
 is measurable,
is measurable,
the following two statements are equivalent:
-
(i)
 ;
; -
(ii)
the map
 is measurable and locally Bochner integrable,
is measurable and locally Bochner integrable,
and the following two statements are equivalent:
-
(i)
 ;
; -
(ii)
the map
 is measurable and locally essentially von Neumann bounded.
is measurable and locally essentially von Neumann bounded.
Proof
We refer to Theorems 6.3, 6.9, and 6.21 of [35]. \(\square \)
Next we state our result concerning regularity of flows of time-varying vector fields. In the statement of the result, we use the notation

In the following result, we do not provide the comprehensive list of properties of the flow, but only those required to make sense of its regularity with respect to initial conditions.
Theorem 2
(Flows of time-varying vector fields) Let  , let
, let  , and let
, and let  , as required. Let
, as required. Let  be a
be a  -manifold, let
-manifold, let  be an interval, and let
be an interval, and let  . Then there exist a subset
. Then there exist a subset  and a map
and a map  with the following properties for each
with the following properties for each  :
:
-
(i)
the set
$$\begin{aligned} {\mathbb {T}}_X(t_0,x_0)=\{t\in {\mathbb {T}}\;|(t,t_0,x_0)\in D_X\} \end{aligned}$$is an interval;
-
(ii)
there exists an absolutely continuous curve
 satisfying $$\begin{aligned} \xi '(t)=X(t,\xi (t)),\quad \xi (t_0)=x_0, \end{aligned}$$
satisfying $$\begin{aligned} \xi '(t)=X(t,\xi (t)),\quad \xi (t_0)=x_0, \end{aligned}$$for almost all
 if and only if
if and only if 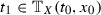 ;
; -
(iii)
 for almost all
for almost all  ;
; -
(iv)
for each
 for which
for which  , there exists a neighbourhood
, there exists a neighbourhood  of \(x_0\) such that the mapping
of \(x_0\) such that the mapping 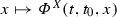 is defined and of class \(\text {C}^\nu \) on
is defined and of class \(\text {C}^\nu \) on  .
.
Proof
We refer to Theorems 6.6, 6.11, and 6.26 of [35]. \(\square \)
4 Parameterised vector fields
One can think of a control system as a family of vector fields parameterised by control. It is the exact nature of this dependence on the parameter that we discuss in this section. Specifically, we give pointwise characterisations that are equivalent to continuity of the natural map from the parameter space into the space of sections, using the topologies from Sect. 2.
As we have been doing thus far, we shall consider sections of general vector bundles rather than vector fields to simplify the notation.
Our closing remarks at the beginning of Sect. 3 apply equally here; so let us repeat them. In our definition of parameterised sections, there is a “theme” consistent throughout, and very much related to the seminorms for that degree of regularity, and hence very much related to the topology. For example, in the finitely differentiable case, a parameterised section should have the property that the finitely many derivatives in state (we never differentiable with respect to the control variable, and indeed one should not do this in control theory) are continuous as functions of state and control. In the Lipschitz case, the same idea holds, but as well one requires that the dilatation have an appropriate continuity property in state and control. As always, the real analytic case is more difficult to understand. However, just as for time-varying vector fields, this is not problematic since, as is shown in Propositions 2, 3, 4, and 5, all of these conditions are equivalent to the continuity of a naturally defined map from the control set into the space of vector fields. Again, there is a single definition that describes what is meant by a parameterised vector field, and what varies with regularity class is the topology. It is this that explains the importance in our development of locally convex topologies in describing control systems, just as Theorem 1 does for time-varying vector fields.
4.1 The smooth case
We begin by discussing parameter dependent smooth sections. Throughout this section we will work with a smooth vector bundle  with a linear connection
with a linear connection  on
on  , an affine connection \(\nabla \) on
, an affine connection \(\nabla \) on  , a fibre metric \({\mathbb {G}}_0\) on
, a fibre metric \({\mathbb {G}}_0\) on  , and a Riemannian metric \({\mathbb {G}}\) on
, and a Riemannian metric \({\mathbb {G}}\) on  . These define the fibre metrics \(||\cdot ||_{\overline{{\mathbb {G}}}_m}\) and the seminorms \(p^\infty _{K,m}\),
. These define the fibre metrics \(||\cdot ||_{\overline{{\mathbb {G}}}_m}\) and the seminorms \(p^\infty _{K,m}\),  compact, \(m\in {\mathbb {Z}}_{\ge 0}\), on
compact, \(m\in {\mathbb {Z}}_{\ge 0}\), on  as in Sects. 2.1 and 2.2.
as in Sects. 2.1 and 2.2.
Definition 9
(Sections of parameterised class
\(\text {C}^\infty \)) Let  be a smooth vector bundle and let \(\mathscr {P}\) be a topological space. A map
be a smooth vector bundle and let \(\mathscr {P}\) be a topological space. A map  such that
such that  for every
for every 
-
(i)
is a separately parameterised section of class \(\varvec{{\text {C}}^\infty }\) if
-
(a)
for each
 , the map
, the map  defined by \(\xi _x(p)=\xi (x,p)\) is continuous and
defined by \(\xi _x(p)=\xi (x,p)\) is continuous and -
(b)
for each
 , the map
, the map  defined by \(\xi ^p(x)=\xi (x,p)\) is of class \(\text {C}^\infty \),
defined by \(\xi ^p(x)=\xi (x,p)\) is of class \(\text {C}^\infty \),
and
-
(a)
-
(ii)
is a jointly parameterised section of class \({\varvec{\text {C}}^\infty }\) if it is a separately parameterised section of class \(\text {C}^\infty \) and if the map
 is continuous for every \(m\in {\mathbb {Z}}_{\ge 0}\).
is continuous for every \(m\in {\mathbb {Z}}_{\ge 0}\).
By  we denote the set of separately parameterised sections of
we denote the set of separately parameterised sections of  of class \(\text {C}^\infty \) and by
of class \(\text {C}^\infty \) and by  we denote the set of jointly parameterised sections of
we denote the set of jointly parameterised sections of  of class \(\text {C}^\infty \). \(\circ \)
of class \(\text {C}^\infty \). \(\circ \)
It is possible to give purely topological characterisations of this class of sections.
Proposition 2
(Characterisation of jointly parameterised sections of class \(\text {C}^\infty \)) Let  be a smooth vector bundle, let \(\mathscr {P}\) be a topological space, and let
be a smooth vector bundle, let \(\mathscr {P}\) be a topological space, and let  satisfy
satisfy  for every
for every  . Then
. Then  if and only if the map
if and only if the map  is continuous, where
is continuous, where  has the \(\text {C}^\infty \)-topology.
has the \(\text {C}^\infty \)-topology.
Proof
Given  , we let
, we let  be the map \(\xi _m(x,p)=j_m\xi ^p(x)\). We also denote by
be the map \(\xi _m(x,p)=j_m\xi ^p(x)\). We also denote by  the map given by \(\sigma _\xi (p)=\xi ^p\).
the map given by \(\sigma _\xi (p)=\xi ^p\).
First suppose that \(\xi _m\) is continuous for every \(m\in {\mathbb {Z}}_{\ge 0}\). Let  be compact, let \(m\in {\mathbb {Z}}_{\ge 0}\), let \(\varepsilon \in {\mathbb {R}}_{>0}\), and let
be compact, let \(m\in {\mathbb {Z}}_{\ge 0}\), let \(\varepsilon \in {\mathbb {R}}_{>0}\), and let  . Let \(x\in K\) and let \(\mathscr {W}_x\) be a neighbourhood of \(\xi _m(x,p_0)\) in
. Let \(x\in K\) and let \(\mathscr {W}_x\) be a neighbourhood of \(\xi _m(x,p_0)\) in  for which
for which

By continuity of \(\xi _m\), there exist a neighbourhood  of x and a neighbourhood
of x and a neighbourhood  of \(p_0\) such that
of \(p_0\) such that  . Now let \(x_1,\dots ,x_k\in K\) be such that
. Now let \(x_1,\dots ,x_k\in K\) be such that  and let
and let  . Then, if \(p\in \mathscr {O}\) and \(x\in K\), we have
. Then, if \(p\in \mathscr {O}\) and \(x\in K\), we have  for some \(j\in \{1,\dots ,k\}\). Thus
for some \(j\in \{1,\dots ,k\}\). Thus  . Thus
. Thus
Therefore, taking supremums over \(x\in K\), \(p^\infty _{K,m}(\sigma _\xi (p)-\sigma _\xi (p_0))\le \varepsilon \). As this can be done for every compact  and every \(m\in {\mathbb {Z}}_{\ge 0}\), we conclude that \(\sigma _\xi \) is continuous.
and every \(m\in {\mathbb {Z}}_{\ge 0}\), we conclude that \(\sigma _\xi \) is continuous.
Next suppose that \(\sigma _\xi \) is continuous and let \(m\in {\mathbb {Z}}_{\ge 0}\). Let  and let
and let  be a neighbourhood of \(\xi _m(x_0,p_0)\). Let
be a neighbourhood of \(\xi _m(x_0,p_0)\). Let  be a relatively compact neighbourhood of \(x_0\) and let \(\varepsilon \in {\mathbb {R}}_{>0}\) be such that
be a relatively compact neighbourhood of \(x_0\) and let \(\varepsilon \in {\mathbb {R}}_{>0}\) be such that

where  is the projection. By continuity of \(\sigma _\xi \), let \(\mathscr {O}\subseteq \mathscr {P}\) be a neighbourhood of \(p_0\) such that \(p^\infty _{\mathrm{cl}(\mathscr {U}),m}(\sigma _\xi (p)-\sigma _\xi (p_0))<\varepsilon \) for \(p\in \mathscr {O}\). Therefore,
is the projection. By continuity of \(\sigma _\xi \), let \(\mathscr {O}\subseteq \mathscr {P}\) be a neighbourhood of \(p_0\) such that \(p^\infty _{\mathrm{cl}(\mathscr {U}),m}(\sigma _\xi (p)-\sigma _\xi (p_0))<\varepsilon \) for \(p\in \mathscr {O}\). Therefore,
Therefore, if \((x,p)\in \mathscr {U}\times \mathscr {O}\), then \(\pi _m(\xi _m(x,p))=x\in \mathscr {U}\) and so \(\xi _m(x,p)\in \mathscr {W}\), showing that \(\xi _m\) is continuous at \((x_0,p_0)\). \(\square \)
4.2 The finitely differentiable or Lipschitz case
The preceding development in the smooth case is easily extended to the finitely differentiable and Lipschitz cases, and we quickly give the results and definitions here. In this section, when considering the Lipschitz case, we assume that \(\nabla \) is the Levi–Civita connection associated to \({\mathbb {G}}\) and we assume that \(\nabla ^0\) is \({\mathbb {G}}_0\)-orthogonal.
Definition 10
(Sections of parameterised class
\(\text {C}^{m+m'}\)) Let  be a smooth vector bundle and let
be a smooth vector bundle and let  be a topological space. A map
be a topological space. A map  such that
such that  for every
for every 
-
(i)
is a separately parameterised section of class \(\varvec{{\text {C}}^{m+m'}}\) if
-
(a)
for each
 , the map
, the map  defined by \(\xi _x(p)=\xi (x,p)\) is continuous and
defined by \(\xi _x(p)=\xi (x,p)\) is continuous and -
(b)
for each
 , the map
, the map  defined by \(\xi ^p(x)=\xi (x,p)\) is of class \(\text {C}^{m+m'}\),
defined by \(\xi ^p(x)=\xi (x,p)\) is of class \(\text {C}^{m+m'}\),
and
-
(a)
-
(ii)
is a jointly parameterised section of class \(\varvec{{\text {C}}^{m+m'}}\) if it is a separately parameterised section of class \(\text {C}^{m+m'}\) and
-
(i)
\(m'=0\): the map
 is continuous;
is continuous; -
(ii)
 : the map
: the map  is continuous and, for each
is continuous and, for each  and each \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood
and each \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood  of \(x_0\) and a neighbourhood
of \(x_0\) and a neighbourhood  of \(p_0\) such that
of \(p_0\) such that 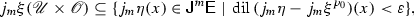
where, of course, \(j_m\xi (x,p)=j_m\xi ^p(x)\).
-
(i)
By  we denote the set of separately parameterised sections of
we denote the set of separately parameterised sections of  of class \(\text {C}^{m+m'}\) and by
of class \(\text {C}^{m+m'}\) and by  we denote the set of jointly parameterised sections of
we denote the set of jointly parameterised sections of  of class \(\text {C}^{m+m'}\). \(\circ \)
of class \(\text {C}^{m+m'}\). \(\circ \)
Let us give the purely topological characterisation of this class of sections.
Proposition 3
(Characterisation of jointly parameterised sections of class \(\text {C}^{m+m'}\)) Let  be a smooth vector bundle, let
be a smooth vector bundle, let  be a topological space, and let
be a topological space, and let  satisfy \(\xi (x,p)\in \mathsf {E}_x\) for every
satisfy \(\xi (x,p)\in \mathsf {E}_x\) for every  . Then
. Then  if and only if the map
if and only if the map  is continuous, where
is continuous, where  has the \(\text {C}^{m+m'}\)-topology.
has the \(\text {C}^{m+m'}\)-topology.
Proof
We will prove the result only in the case that \(m=0\) and  , as the general case follows by combining this case with the computations from the proof of Proposition 2. We denote \(\sigma _\xi (p)=\xi (x,p)\).
, as the general case follows by combining this case with the computations from the proof of Proposition 2. We denote \(\sigma _\xi (p)=\xi (x,p)\).
Suppose that  is continuous and that, for every
is continuous and that, for every  and for every \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood
and for every \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood  of \(x_0\) and a neighbourhood
of \(x_0\) and a neighbourhood  of \(p_0\) such that, if \((x,p)\in \mathscr {U}\times \mathscr {O}\), then \(\text {dil}\,(\xi ^p-\xi ^{p_0})(x)<\varepsilon \). Let
of \(p_0\) such that, if \((x,p)\in \mathscr {U}\times \mathscr {O}\), then \(\text {dil}\,(\xi ^p-\xi ^{p_0})(x)<\varepsilon \). Let  be compact, let \(\varepsilon \in {\mathbb {R}}_{>0}\), and let
be compact, let \(\varepsilon \in {\mathbb {R}}_{>0}\), and let  . Let \(x\in K\). By hypothesis, there exist a neighbourhood
. Let \(x\in K\). By hypothesis, there exist a neighbourhood  of x and a neighbourhood
of x and a neighbourhood  of \(p_0\) such that
of \(p_0\) such that

Now let \(x_1,\dots ,x_k\in K\) be such that \(K\subseteq \cup _{j=1}^k\mathscr {U}_{x_j}\) and let \(\mathscr {O}=\cap _{j=1}^k\mathscr {O}_{x_j}\). Then, if \(p\in \mathscr {O}\) and \(x\in K\), we have \(x\in \mathscr {U}_{x_j}\) for some \(j\in \{1,\dots ,k\}\). Thus
Therefore, taking supremums over \(x\in K\), we have \(\lambda _K(\sigma _\xi (p)-\sigma _\xi (p_0))\le \varepsilon \). By choosing \(\mathscr {O}\) to be possibly smaller, the argument of Proposition 2 ensures that \(p_K^0(\sigma _\xi (p)-\sigma _\xi (p_0))\le \varepsilon \), and so  for \(p\in \mathscr {O}\). As this can be done for every compact
for \(p\in \mathscr {O}\). As this can be done for every compact  , we conclude that \(\sigma _\xi \) is continuous.
, we conclude that \(\sigma _\xi \) is continuous.
Next suppose that \(\sigma _\xi \) is continuous, let  , and let \(\varepsilon \in {\mathbb {R}}_{>0}\). Let \(\mathscr {U}\) be a relatively compact neighbourhood of \(x_0\). Since \(\sigma _\xi \) is continuous, let \(\mathscr {O}\) be a neighbourhood of \(p_0\) such that
, and let \(\varepsilon \in {\mathbb {R}}_{>0}\). Let \(\mathscr {U}\) be a relatively compact neighbourhood of \(x_0\). Since \(\sigma _\xi \) is continuous, let \(\mathscr {O}\) be a neighbourhood of \(p_0\) such that
Thus, for every \((x,p)\in \mathscr {U}\times \mathscr {O}\), \(\text {dil}\,(\xi ^p-\xi ^{p_0})(x)<\varepsilon \). Following the argument of Proposition 2 one also shows that \(\xi \) is continuous at \((x_0,p_0)\), which shows that  . \(\square \)
. \(\square \)
4.3 The holomorphic case
As with time-varying vector fields, we are not really interested, per se, in holomorphic control systems, and in fact we will not even define the notion. However, it is possible, and possibly sometimes easier, to verify that a control system satisfies our rather technical criterion of being a “real analytic control system” by verifying that it possesses an holomorphic extension. Thus, in this section, we present the required holomorphic definitions. We will consider an holomorphic vector bundle  with an Hermitian fibre metric \({\mathbb {G}}\). This defines the seminorms \(p^{\text {hol}}_K\),
with an Hermitian fibre metric \({\mathbb {G}}\). This defines the seminorms \(p^{\text {hol}}_K\),  compact, describing the \(\text {C}^{\text {hol}}\)-topology for
compact, describing the \(\text {C}^{\text {hol}}\)-topology for  as in Sect. 2.5.
as in Sect. 2.5.
Definition 11
(Sections of parameterised class
\(\text {C}^{\text {hol}}\)) Let  be an holomorphic vector bundle and let
be an holomorphic vector bundle and let  be a topological space. A map
be a topological space. A map  such that \(\xi (z,p)\in \mathsf {E}_z\) for every
such that \(\xi (z,p)\in \mathsf {E}_z\) for every 
-
(i)
is a separately parameterised section of class \(\varvec{\text {C}^{\text {hol}}}\) if
-
(a)
for each
 , the map
, the map  defined by \(\xi _z(p)=\xi (z,p)\) is continuous and
defined by \(\xi _z(p)=\xi (z,p)\) is continuous and -
(b)
for each
 , the map
, the map  defined by \(\xi ^p(z)=\xi (z,p)\) is of class \(\text {C}^\text {hol}\),
defined by \(\xi ^p(z)=\xi (z,p)\) is of class \(\text {C}^\text {hol}\),
and
-
(a)
-
(ii)
is a jointly parameterised section of class \(\varvec{\text {C}^{\text {hol}}}\) if it is a separately parameterised section of class \(\text {C}^{\text {hol}}\) and if the map
 is continuous.
is continuous.
By  we denote the set of separately parameterised sections of
we denote the set of separately parameterised sections of  of class \(\text {C}^{\text {hol}}\) and by
of class \(\text {C}^{\text {hol}}\) and by  we denote the set of jointly parameterised sections of
we denote the set of jointly parameterised sections of  of class \(\text {C}^{\text {hol}}\). \(\circ \)
of class \(\text {C}^{\text {hol}}\). \(\circ \)
As in the smooth case, it is possible to give purely topological characterisations of these classes of sections.
Proposition 4
(Characterisation of jointly parameterised sections of class \(\text {C}^{\text {hol}}\)) Let  be an holomorphic vector bundle, let
be an holomorphic vector bundle, let  be a topological space, and let
be a topological space, and let  satisfy
satisfy  for every
for every  . Then
. Then  if and only if the map
if and only if the map  is continuous, where
is continuous, where  has the \(\text {C}^{\text {hol}}\)-topology.
has the \(\text {C}^{\text {hol}}\)-topology.
Proof
We define  by \(\sigma _\xi (p)=\xi ^p\).
by \(\sigma _\xi (p)=\xi ^p\).
First suppose that \(\xi \) is continuous. Let  be compact, let \(\varepsilon \in {\mathbb {R}}_{>0}\), and let
be compact, let \(\varepsilon \in {\mathbb {R}}_{>0}\), and let  . Let \(z\in K\) and let \(\mathscr {W}_z\subseteq \mathsf {E}\) be a neighbourhood of \(\xi (z,p_0)\) for which
. Let \(z\in K\) and let \(\mathscr {W}_z\subseteq \mathsf {E}\) be a neighbourhood of \(\xi (z,p_0)\) for which

By continuity of \(\xi \), there exist a neighbourhood  of z and a neighbourhood
of z and a neighbourhood  of \(p_0\) such that \(\xi (\mathscr {U}_z\times \mathscr {O}_z)\subseteq \mathscr {W}_z\). Now let \(z_1,\dots ,z_k\in K\) be such that \(K\subseteq \cup _{j=1}^k\mathscr {U}_{z_j}\) and let \(\mathscr {O}=\cap _{j=1}^k\mathscr {O}_{z_j}\). Then, if \(p\in \mathscr {O}\) and \(z\in K\), we have \(z\in \mathscr {U}_{z_j}\) for some \(j\in \{1,\dots ,k\}\). Thus \(\xi (z,p)\in \mathscr {W}_{z_j}\). Thus \(||\xi (z,p)-\xi (z,p_0)||_{\overline{{\mathbb {G}}}}<\varepsilon \). Therefore, taking supremums over \(z\in K\), \(p^{\text {hol}}_K(\sigma _\xi (p)-\sigma _\xi (p_0))\le \varepsilon \). As this can be done for every compact
of \(p_0\) such that \(\xi (\mathscr {U}_z\times \mathscr {O}_z)\subseteq \mathscr {W}_z\). Now let \(z_1,\dots ,z_k\in K\) be such that \(K\subseteq \cup _{j=1}^k\mathscr {U}_{z_j}\) and let \(\mathscr {O}=\cap _{j=1}^k\mathscr {O}_{z_j}\). Then, if \(p\in \mathscr {O}\) and \(z\in K\), we have \(z\in \mathscr {U}_{z_j}\) for some \(j\in \{1,\dots ,k\}\). Thus \(\xi (z,p)\in \mathscr {W}_{z_j}\). Thus \(||\xi (z,p)-\xi (z,p_0)||_{\overline{{\mathbb {G}}}}<\varepsilon \). Therefore, taking supremums over \(z\in K\), \(p^{\text {hol}}_K(\sigma _\xi (p)-\sigma _\xi (p_0))\le \varepsilon \). As this can be done for every compact  , we conclude that \(\sigma _\xi \) is continuous.
, we conclude that \(\sigma _\xi \) is continuous.
Next suppose that \(\sigma _\xi \) is continuous. Let  and let
and let  be a neighbourhood of \(\xi (z_0,p_0)\). Let
be a neighbourhood of \(\xi (z_0,p_0)\). Let  be a relatively compact neighbourhood of \(z_0\) and let \(\varepsilon \in {\mathbb {R}}_{>0}\) be such that
be a relatively compact neighbourhood of \(z_0\) and let \(\varepsilon \in {\mathbb {R}}_{>0}\) be such that

By continuity of \(\sigma _\xi \), let  be a neighbourhood of \(p_0\) such that \(p^{\text {hol}}_{\mathrm{cl}(\mathscr {U})}(\sigma _\xi (p)-\sigma _\xi (p_0))<\varepsilon \) for \(p\in \mathscr {O}\). Therefore,
be a neighbourhood of \(p_0\) such that \(p^{\text {hol}}_{\mathrm{cl}(\mathscr {U})}(\sigma _\xi (p)-\sigma _\xi (p_0))<\varepsilon \) for \(p\in \mathscr {O}\). Therefore,
Therefore, if \((z,p)\in \mathscr {U}\times \mathscr {O}\), we have \(\xi (z,p)\in \mathscr {W}\), showing that \(\xi \) is continuous at \((z_0,p_0)\). \(\square \)
4.4 The real analytic case
Now we repeat the procedure above for real analytic sections. We thus will consider a real analytic vector bundle  with \(\nabla ^0\) a real analytic linear connection on
with \(\nabla ^0\) a real analytic linear connection on  , \(\nabla \) a real analytic affine connection on
, \(\nabla \) a real analytic affine connection on  , \({\mathbb {G}}_0\) a real analytic fibre metric on
, \({\mathbb {G}}_0\) a real analytic fibre metric on  , and \({\mathbb {G}}\) a real analytic Riemannian metric on
, and \({\mathbb {G}}\) a real analytic Riemannian metric on  . This defines the seminorms \(p^\omega _{K,\mathbf {a}}\),
. This defines the seminorms \(p^\omega _{K,\mathbf {a}}\),  compact, \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), describing the \(\text {C}^\omega \)-topology as in Sect. 2.6.
compact, \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), describing the \(\text {C}^\omega \)-topology as in Sect. 2.6.
Definition 12
(Sections of parameterised class
\(\text {C}^\omega \)) Let  be a real analytic vector bundle and let
be a real analytic vector bundle and let  be a topological space. A map
be a topological space. A map  such that
such that  for every
for every 
-
(i)
is a separately parameterised section of class \(\varvec{{\text {C}}^\omega }\) if
-
(a)
for each
 , the map
, the map  defined by \(\xi _x(p)=\xi (x,p)\) is continuous and
defined by \(\xi _x(p)=\xi (x,p)\) is continuous and -
(b)
for each
 , the map
, the map  defined by \(\xi ^p(x)=\xi (x,p)\) is of class \(\text {C}^\omega \),
defined by \(\xi ^p(x)=\xi (x,p)\) is of class \(\text {C}^\omega \),
and
-
(a)
-
(ii)
is a jointly parameterised section of class \(\varvec{{\text {C}}^\omega }\) if it is a separately parameterised section of class \(\text {C}^\infty \) and if, for each
 , for each \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0},{\mathbb {R}}_{>0})\), and for each \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood
, for each \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0},{\mathbb {R}}_{>0})\), and for each \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood  of \(x_0\) and a neighbourhood
of \(x_0\) and a neighbourhood  of \(p_0\) such that
of \(p_0\) such that 
for every \(m\in {\mathbb {Z}}_{\ge 0}\), where, of course, \(j_m\xi (x,p)=j_m\xi ^p(x)\).
By  we denote the set of separately parameterised sections of
we denote the set of separately parameterised sections of  of class \(\text {C}^\omega \) and by
of class \(\text {C}^\omega \) and by  we denote the set of jointly parameterised sections of
we denote the set of jointly parameterised sections of  of class \(\text {C}^\omega \). \(\circ \)
of class \(\text {C}^\omega \). \(\circ \)
Remark 1
(Jointly parameterised sections of class \(\text {C}^\omega \)) The condition that  can be restated like this: for each
can be restated like this: for each  , for each \(m\in {\mathbb {Z}}_{\ge 0}\), and for each \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood
, for each \(m\in {\mathbb {Z}}_{\ge 0}\), and for each \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood  of \(x_0\) and a neighbourhood
of \(x_0\) and a neighbourhood  of \(p_0\) such that
of \(p_0\) such that

that this is so is, more or less, the idea of the proof of Proposition 2. Phrased this way, one sees clearly the grammatical similarity between the smooth and real analytic definitions. Indeed, the grammatical transformation from the smooth to the real analytic definition is, put a factor of \(a_0a_1\cdots a_m\) before the norm, precede the condition with “for every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\)”, and move the “for every \(m\in {\mathbb {Z}}_{\ge 0}\)” from before the condition to after. This was also seen in the definitions of locally integrally bounded and locally essentially bounded sections in Sect. 3. Indeed, the grammatical similarity is often encountered when using our locally convex topologies, and contributes to the unification of the analysis of the varying degrees of regularity. \(\circ \)
The following result records topological characterisations of jointly parameterised sections in the real analytic case.
Proposition 5
(Characterisation of jointly parameterised sections of class \(\text {C}^\omega \)) Let  be a real analytic vector bundle, let
be a real analytic vector bundle, let  be a topological space, and let
be a topological space, and let  satisfy
satisfy  for every
for every  . Then
. Then  if and only if the map
if and only if the map  is continuous, where
is continuous, where  has the \(\text {C}^\omega \)-topology.
has the \(\text {C}^\omega \)-topology.
Proof
For \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\) and \(m\in {\mathbb {Z}}_{\ge 0}\), given  satisfying
satisfying  , we let
, we let  be the map
be the map
We also denote by  the map given by \(\sigma _\xi (p)=\xi ^p\).
the map given by \(\sigma _\xi (p)=\xi ^p\).
Suppose that, for every  , for every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and for every \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood
, for every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and for every \(\varepsilon \in {\mathbb {R}}_{>0}\), there exist a neighbourhood  of \(x_0\) and a neighbourhood
of \(x_0\) and a neighbourhood  of \(p_0\) such that, if \((x,p)\in \mathscr {U}\times \mathscr {O}\), then
of \(p_0\) such that, if \((x,p)\in \mathscr {U}\times \mathscr {O}\), then
Let  be compact, let \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), let \(\varepsilon \in {\mathbb {R}}_{>0}\), and let
be compact, let \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), let \(\varepsilon \in {\mathbb {R}}_{>0}\), and let  . Let \(x\in K\). By hypothesis, there exist a neighbourhood
. Let \(x\in K\). By hypothesis, there exist a neighbourhood  of x and a neighbourhood
of x and a neighbourhood  of \(p_0\) such that
of \(p_0\) such that

for each \(m\in {\mathbb {Z}}_{\ge 0}\). Now let \(x_1,\dots ,x_k\in K\) be such that \(K\subseteq \cup _{j=1}^k\mathscr {U}_{x_j}\) and let \(\mathscr {O}=\cap _{j=1}^k\mathscr {O}_{x_j}\). Then, if \(p\in \mathscr {O}\) and \(x\in K\), we have \(x\in \mathscr {U}_{x_j}\) for some \(j\in \{1,\dots ,k\}\). Thus
Therefore, taking supremums over \(x\in K\) and \(m\in {\mathbb {Z}}_{\ge 0}\), we have \(p^\omega _{K,\mathbf {a}}(\sigma _\xi (p)-\sigma _\xi (p_0))\le \varepsilon \). As this can be done for every compact  and every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), we conclude that \(\sigma _\xi \) is continuous.
and every \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), we conclude that \(\sigma _\xi \) is continuous.
Next suppose that \(\sigma _\xi \) is continuous, let  , let \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and let \(\varepsilon \in {\mathbb {R}}_{>0}\). Let \(\mathscr {U}\) be a relatively compact neighbourhood of \(x_0\). Since \(\sigma _\xi \) is continuous, let \(\mathscr {O}\) be a neighbourhood of \(p_0\) such that
, let \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and let \(\varepsilon \in {\mathbb {R}}_{>0}\). Let \(\mathscr {U}\) be a relatively compact neighbourhood of \(x_0\). Since \(\sigma _\xi \) is continuous, let \(\mathscr {O}\) be a neighbourhood of \(p_0\) such that
Thus, for every \((x,p)\in \mathscr {U}\times \mathscr {O}\),
which shows that  . \(\square \)
. \(\square \)
One can wonder about the relationship between sections of jointly parameterised class \(\text {C}^\omega \) and sections that are real restrictions of sections of jointly parameterised class \(\text {C}^{\text {hol}}\). We address this with a result and an example. First the result. The result here is a nontrivial one, and is the only place in this paper where we call upon the deeper properties of the real analytic topology. A reader wishing to comprehend all of the details of the proof will probably need to consult [35, Chapter 5]. Despite the complicated nature of the theorem statement—necessary due to the fact that the domain of an holomorphic extension will depend on the system—it really just says (1) that the restriction of an holomorphic control system is a real analytic control system and (2) that a real analytic control system extends to an holomorphic one when the control set is locally compact.
Theorem 3
(Jointly parameterised real analytic sections as restrictions of jointly parameterised holomorphic sections) Let  be a real analytic vector bundle with complexificationFootnote 4
be a real analytic vector bundle with complexificationFootnote 4
 and let
and let  be a topological space. For a map
be a topological space. For a map  satisfying
satisfying  for all
for all  , the following statements hold:
, the following statements hold:
-
(i)
if
 and if
and if  is locally compact and Hausdorff, then, for each
is locally compact and Hausdorff, then, for each  , there exist a neighbourhood
, there exist a neighbourhood  of \(x_0\), a neighbourhood
of \(x_0\), a neighbourhood 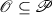 of \(p_0\), and
of \(p_0\), and  such that \(\xi (x,p)=\overline{\xi }(x,p)\) for all
such that \(\xi (x,p)=\overline{\xi }(x,p)\) for all  ;
; -
(ii)
if there exists a section
 such that \(\xi (x,p)=\overline{\xi }(x,p)\) for every
such that \(\xi (x,p)=\overline{\xi }(x,p)\) for every  , then
, then  .
.
Proof
(i) Let  and let \(\mathscr {O}\) be a relatively compact neighbourhood of \(p_0\), this being possible since
and let \(\mathscr {O}\) be a relatively compact neighbourhood of \(p_0\), this being possible since  is locally compact. Let
is locally compact. Let  , let \(\mathscr {U}\) be a relatively compact neighbourhood of \(x_0\), and let \((\overline{\mathscr {U}}_j)_{j\in {\mathbb {Z}}_{>0}}\) be a sequence of neighbourhoods of \(\mathrm{cl}(\mathscr {U})\) in
, let \(\mathscr {U}\) be a relatively compact neighbourhood of \(x_0\), and let \((\overline{\mathscr {U}}_j)_{j\in {\mathbb {Z}}_{>0}}\) be a sequence of neighbourhoods of \(\mathrm{cl}(\mathscr {U})\) in  with the properties that \(\mathrm{cl}(\overline{\mathscr {U}}_j)\subseteq \overline{\mathscr {U}}_{j+1}\) and that \(\cap _{j\in {\mathbb {Z}}_{>0}}\overline{\mathscr {U}}_j=\mathrm{cl}(\mathscr {U})\). Let
with the properties that \(\mathrm{cl}(\overline{\mathscr {U}}_j)\subseteq \overline{\mathscr {U}}_{j+1}\) and that \(\cap _{j\in {\mathbb {Z}}_{>0}}\overline{\mathscr {U}}_j=\mathrm{cl}(\mathscr {U})\). Let  be the set of germs of those holomorphic sections of
be the set of germs of those holomorphic sections of  about \(\mathrm{cl}(\mathscr {O})\) that, when restricted to
about \(\mathrm{cl}(\mathscr {O})\) that, when restricted to  , are real. We recall from [35, §5.2.1] that
, are real. We recall from [35, §5.2.1] that  is the direct limit of the directed system
is the direct limit of the directed system  . For
. For  for some \(j\in {\mathbb {Z}}_{>0}\), let \([\overline{\xi }]_{\mathrm{cl}(\mathscr {U})}\) be the germ of \(\overline{\xi }\). We note that
for some \(j\in {\mathbb {Z}}_{>0}\), let \([\overline{\xi }]_{\mathrm{cl}(\mathscr {U})}\) be the germ of \(\overline{\xi }\). We note that

and

with  denoting the completed injective tensor product; see [36, Chapter 16] for the injective tensor product for locally convex spaces and [21, Theorem 1.1.10] for the preceding isomorphisms for Banach spaces (the constructions apply more or less verbatim to locally convex spaces [7, Proposition 5.4]). Note that since
denoting the completed injective tensor product; see [36, Chapter 16] for the injective tensor product for locally convex spaces and [21, Theorem 1.1.10] for the preceding isomorphisms for Banach spaces (the constructions apply more or less verbatim to locally convex spaces [7, Proposition 5.4]). Note that since  and
and  , \(j\in {\mathbb {Z}}_{>0}\), are nuclear, the injective tensor product can be swapped with the projective tensor product in the above constructions [48, Proposition 5.4.2].
, \(j\in {\mathbb {Z}}_{>0}\), are nuclear, the injective tensor product can be swapped with the projective tensor product in the above constructions [48, Proposition 5.4.2].
We claim that, with these identifications,  is the direct limit of the directed system
is the direct limit of the directed system  with the associated mappings
with the associated mappings  ,
,  , where
, where

We, moreover, claim that the direct limit topology is boundedly retractive, meaning that bounded sets in the direct limit are contained in and bounded in a single component of the directed system and, moreover, the topology on the bounded set induced by the component is the same as that induced by the direct limit.
Results of this sort have been the subject of research in the area of locally convex topologies, with the aim being to deduce conditions on the structure of the spaces comprising the directed system, and on the corresponding mappings (for us, the inclusion mappings and their tensor products with the identity on \(\text {C}^0(\mathrm{cl}(\mathscr {O});{\mathbb {R}})\)), that ensure that direct limits commute with tensor product, and that the associated direct limit topology is boundedly retractive. We shall make principal use of the results given in [45]. To state the arguments with at least a little context, let us reproduce two conditions used by Mangino.
Condition (M) of Retakh [51] Let  be a directed system of locally convex spaces with strict direct limit
be a directed system of locally convex spaces with strict direct limit  . The direct limit topology of
. The direct limit topology of  satisfies condition (M) if there exists a sequence
satisfies condition (M) if there exists a sequence  for which
for which
-
1.
\(\mathscr {O}_j\) is a balanced convex neighbourhood of
 ,
, -
2.
\(\mathscr {O}_j\subseteq \mathscr {O}_{j+1}\) for each \(j\in {\mathbb {Z}}_{>0}\), and
-
3.
for every \(j\in {\mathbb {Z}}_{>0}\), there exists \(k\ge j\) such that the topology induced on \(\mathscr {O}_j\) by its inclusion in
 and its inclusion in
and its inclusion in  agree. \(\circ \)
agree. \(\circ \)
Condition (MO) of Mangino [45] Let  be a directed system of metrisable locally convex spaces with strict direct limit
be a directed system of metrisable locally convex spaces with strict direct limit  . Let
. Let  be the inclusion for \(k\ge j\) and let
be the inclusion for \(k\ge j\) and let  be the induced map into the direct limit.
be the induced map into the direct limit.
Suppose that, for each \(j\in {\mathbb {Z}}_{>0}\), we have a sequence \((p_{j,l})_{l\in {\mathbb {Z}}_{>0}}\) of seminorms defining the topology of  such that \(p_{j,l_1}\ge p_{j,l_2}\) if \(l_1\ge l_2\). Let
such that \(p_{j,l_1}\ge p_{j,l_2}\) if \(l_1\ge l_2\). Let

and denote by \({\hat{p}}_{j,l}\) the norm on  induced by \(p_{j,l}\) [55, page 97]. Let
induced by \(p_{j,l}\) [55, page 97]. Let  be the canonical projection. Let
be the canonical projection. Let  be the completion of
be the completion of  . The family
. The family  is called a projective spectrum for
is called a projective spectrum for  . Denote
. Denote

The direct limit topology of  satisfies condition (MO) if there exists a sequence \((\mathscr {O}_j)_{j\in {\mathbb {Z}}_{>0}}\) and if, for every \(j\in {\mathbb {Z}}_{>0}\), there exists a projective spectrum
satisfies condition (MO) if there exists a sequence \((\mathscr {O}_j)_{j\in {\mathbb {Z}}_{>0}}\) and if, for every \(j\in {\mathbb {Z}}_{>0}\), there exists a projective spectrum  for
for  for which
for which
-
1.
\(\mathscr {O}_j\) is a balanced convex neighbourhood of
 ,
, -
2.
\(\mathscr {O}_j\subseteq \mathscr {O}_{j+1}\) for each \(j\in {\mathbb {Z}}_{>0}\), and
-
3.
for every \(j\in {\mathbb {Z}}_{>0}\), there exists \(k\ge j\) such that, for every \(l\in {\mathbb {Z}}_{>0}\), there exists
 satisfying
satisfying 
the closure on the right being taken in the norm topology of
 . \(\circ \)
. \(\circ \)
With these concepts, we have the following statements. We let  be a directed system of metrisable locally convex spaces with strict direct limit
be a directed system of metrisable locally convex spaces with strict direct limit  .
.
-
1.
If the direct limit topology on
 satisfies condition (MO), then, for any Banach space
satisfies condition (MO), then, for any Banach space  ,
,  (\(\otimes _\pi \) is the uncompleted projective tensor product) is the direct limit of the directed system
(\(\otimes _\pi \) is the uncompleted projective tensor product) is the direct limit of the directed system  , and the direct limit topology on
, and the direct limit topology on  satisfies condition (M) [45, Theorem 1.3].
satisfies condition (M) [45, Theorem 1.3]. -
2.
If the inclusion of
 in
in  is nuclear and if the direct limit topology on
is nuclear and if the direct limit topology on  is regular, then the direct limit topology on
is regular, then the direct limit topology on  satisfies condition (MO) [45, Theorem 1.3].
satisfies condition (MO) [45, Theorem 1.3]. -
3.
If the direct limit topology on
 satisfies condition (M), then this direct limit topology is boundedly retractive [68].
satisfies condition (M), then this direct limit topology is boundedly retractive [68].
Using these arguments we make the following conclusions.
-
4.
The direct limit topology on
 satisfies condition (MO) (by virtue of assertion 2 above and by the properties of the direct limit topology enunciated in [35, §5.3], specifically that the direct limit is a regular direct limit of nuclear Fréchet spaces).
satisfies condition (MO) (by virtue of assertion 2 above and by the properties of the direct limit topology enunciated in [35, §5.3], specifically that the direct limit is a regular direct limit of nuclear Fréchet spaces). -
5.
The space
 is the direct limit of the directed sequence
is the direct limit of the directed sequence  (by virtue of assertion 1 above).
(by virtue of assertion 1 above). -
6.
The direct limit topology on
 satisfies condition (M) (by virtue of assertion 1 above).
satisfies condition (M) (by virtue of assertion 1 above). -
7.
The direct limit topology on
 is boundedly retractive (by virtue of assertion 3 above).
is boundedly retractive (by virtue of assertion 3 above).
We shall also need the following lemma.
Lemma 1
Let  be compact. If
be compact. If  then there exists a sequence \(([\overline{\xi }_k]_K)_{k\in {\mathbb {Z}}_{>0}}\) in
then there exists a sequence \(([\overline{\xi }_k]_K)_{k\in {\mathbb {Z}}_{>0}}\) in  converging to \([\overline{\xi }]_K\) in the topology of
converging to \([\overline{\xi }]_K\) in the topology of  .
.
Proof
Since  is the completion of
is the completion of  , there exists a net
\(([\overline{\xi }_i]_K)_{i\in I}\) converging to \([\overline{\xi }]\), so the conclusion here is that we can actually find a converging sequence. This can be proved, however, using the argument from the proof of [21, Theorem 1.1.10] (see top of page 15 of that reference)\(\circ \)
, there exists a net
\(([\overline{\xi }_i]_K)_{i\in I}\) converging to \([\overline{\xi }]\), so the conclusion here is that we can actually find a converging sequence. This can be proved, however, using the argument from the proof of [21, Theorem 1.1.10] (see top of page 15 of that reference)\(\circ \)
The remainder of the proof is straightforward. Since  , the map
, the map

is an element of  by Theorem 1. Therefore, if \([\overline{\xi }]_{\mathrm{cl}(\mathscr {U})}\) is the image of \(\xi \) under the natural mapping from
by Theorem 1. Therefore, if \([\overline{\xi }]_{\mathrm{cl}(\mathscr {U})}\) is the image of \(\xi \) under the natural mapping from  to
to  , the map
, the map

is an element of  . Therefore, by the preceding lemma, there exists a sequence
. Therefore, by the preceding lemma, there exists a sequence  in
in  that converges to
that converges to  . By our conclusion 5 above, the topology in which this convergence takes place is the completion of the direct limit topology associated to the directed system
. By our conclusion 5 above, the topology in which this convergence takes place is the completion of the direct limit topology associated to the directed system  . The sequence \(([\overline{\xi }_k]_{\mathrm{cl}(\mathscr {U})})_{k\in {\mathbb {Z}}_{>0}}\) is a Cauchy sequence and so bounded. The direct limit topology on
. The sequence \(([\overline{\xi }_k]_{\mathrm{cl}(\mathscr {U})})_{k\in {\mathbb {Z}}_{>0}}\) is a Cauchy sequence and so bounded. The direct limit topology on  is boundedly retractive by our conclusion 7 above. Thus, in particular, it is regular, and so there exists \(j\in {\mathbb {Z}}_{>0}\) such that the sections \((\overline{\xi }_k)_{k\in {\mathbb {Z}}_{>0}}\) can be holomorphically extended to \(\overline{\mathscr {U}}_j\). Bounded retractivity additionally implies that j can be chosen so that the sequence \((\overline{\xi }_k)_{k\in {\mathbb {Z}}_{>0}}\) is a Cauchy sequence in
is boundedly retractive by our conclusion 7 above. Thus, in particular, it is regular, and so there exists \(j\in {\mathbb {Z}}_{>0}\) such that the sections \((\overline{\xi }_k)_{k\in {\mathbb {Z}}_{>0}}\) can be holomorphically extended to \(\overline{\mathscr {U}}_j\). Bounded retractivity additionally implies that j can be chosen so that the sequence \((\overline{\xi }_k)_{k\in {\mathbb {Z}}_{>0}}\) is a Cauchy sequence in  and so converges to a limit \(\overline{\eta }\) satisfying
and so converges to a limit \(\overline{\eta }\) satisfying  . Thus \(\overline{\xi }\) can be holomorphically extended to \(\overline{\mathscr {U}}_j\). This completes this part of the proof.
. Thus \(\overline{\xi }\) can be holomorphically extended to \(\overline{\mathscr {U}}_j\). This completes this part of the proof.
(ii) Let  , let \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and let \(\varepsilon \in {\mathbb {R}}_{>0}\). Let
, let \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and let \(\varepsilon \in {\mathbb {R}}_{>0}\). Let  be a relatively compact neighbourhood of \(x_0\) and let \(\overline{\mathscr {U}}\) be a relatively compact neighbourhood of \(\mathrm{cl}(\mathscr {U})\). By Proposition 1, there exist \(C,r\in {\mathbb {R}}_{>0}\) such that
be a relatively compact neighbourhood of \(x_0\) and let \(\overline{\mathscr {U}}\) be a relatively compact neighbourhood of \(\mathrm{cl}(\mathscr {U})\). By Proposition 1, there exist \(C,r\in {\mathbb {R}}_{>0}\) such that
for all \(m\in {\mathbb {Z}}_{\ge 0}\) and  . Now let \(N\in {\mathbb {Z}}_{\ge 0}\) be such that \(a_{N+1}<r\) and let \(\mathscr {O}\) be a neighbourhood of \(p_0\) such that
. Now let \(N\in {\mathbb {Z}}_{\ge 0}\) be such that \(a_{N+1}<r\) and let \(\mathscr {O}\) be a neighbourhood of \(p_0\) such that
for \((z,p)\in \overline{\mathscr {U}}\times \mathscr {O}\). Then, if \(m\in \{0,1,\dots ,N\}\), we have
for \((x,p)\in \mathscr {U}\times \mathscr {O}\). If \(m>N\) we also have
for \((x,p)\in \mathscr {U}\times \mathscr {O}\), as desired. \(\square \)
The next example shows that the assumption of local compactness cannot be generally relaxed.
Example 1
(Jointly parameterised real analytic sections are not always restrictions of jointly parameterised holomorphic sections) Let  , let
, let  , and define
, and define  by \(f(x,g)=g(x)\). Since
by \(f(x,g)=g(x)\). Since  is the identity map, we conclude from Proposition 5 that
is the identity map, we conclude from Proposition 5 that  . Let \(x_0\in {\mathbb {R}}\). We claim that, for any neighbourhood \(\overline{\mathscr {U}}\) of \(x_0\) in \({\mathbb {C}}\) and any neighbourhood \(\mathscr {O}\) of
. Let \(x_0\in {\mathbb {R}}\). We claim that, for any neighbourhood \(\overline{\mathscr {U}}\) of \(x_0\) in \({\mathbb {C}}\) and any neighbourhood \(\mathscr {O}\) of  , there exists \(g\in \mathscr {O}\) such that g, and therefore \(f^g\), does not have an holomorphic extension to \(\overline{\mathscr {U}}\). To see this, let \(\sigma \in {\mathbb {R}}_{>0}\) be such that the closed disk
, there exists \(g\in \mathscr {O}\) such that g, and therefore \(f^g\), does not have an holomorphic extension to \(\overline{\mathscr {U}}\). To see this, let \(\sigma \in {\mathbb {R}}_{>0}\) be such that the closed disk  of radius \(\sigma \) centred at \(x_0\) in \({\mathbb {C}}\) is contained in \(\overline{\mathscr {U}}\). Let \(K_1,\dots ,K_r\subseteq {\mathbb {R}}\) be compact, let \(\mathbf {a}_1,\dots ,\mathbf {a}_r\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and let \(\varepsilon _1,\dots ,\varepsilon _r\in {\mathbb {R}}_{>0}\) be such that
of radius \(\sigma \) centred at \(x_0\) in \({\mathbb {C}}\) is contained in \(\overline{\mathscr {U}}\). Let \(K_1,\dots ,K_r\subseteq {\mathbb {R}}\) be compact, let \(\mathbf {a}_1,\dots ,\mathbf {a}_r\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and let \(\varepsilon _1,\dots ,\varepsilon _r\in {\mathbb {R}}_{>0}\) be such that
Now define
with \(\alpha \in {\mathbb {R}}_{>0}\) chosen sufficiently small that \(p_{K_j,\mathbf {a}_j}(g)<\varepsilon _j\), \(j\in \{1,\dots ,r\}\), and note that \(g\in \mathscr {O}\) does not have an holomorphic extension to \(\overline{\mathscr {U}}\). Indeed, suppose that such an holomorphic extension \(\overline{g}\) exists. Then \(\overline{g}(z)\) must be equal to \(\frac{\alpha \sigma ^2}{\sigma ^2+(z-x_0)^2}\) for z in the open disk  by uniqueness of holomorphic extensions [14, Lemma 5.40]. But this immediately prohibits \(\overline{g}\) from being holomorphic on any neighbourhood of the closed disk
by uniqueness of holomorphic extensions [14, Lemma 5.40]. But this immediately prohibits \(\overline{g}\) from being holomorphic on any neighbourhood of the closed disk  , giving our claim. \(\circ \)
, giving our claim. \(\circ \)
4.5 Mixing regularity hypotheses
It is possible to consider parameterised sections with mixed regularity hypotheses. Indeed, the conditions of Definitions 9, 10, and 12 are joint on state and parameter. Thus we may consider the following situation. Let \(m\in {\mathbb {Z}}_{\ge 0}\),  , \(r\in {\mathbb {Z}}_{\ge 0}\cup \{\infty ,\omega \}\), and
, \(r\in {\mathbb {Z}}_{\ge 0}\cup \{\infty ,\omega \}\), and  . If \(r+r'\ge m+m'\) (with the obvious convention that
. If \(r+r'\ge m+m'\) (with the obvious convention that  and
and  ), we may then consider a parameterised section in
), we may then consider a parameterised section in

As with time-varying vector fields, there is nothing wrong with this—indeed this is often done—as long as one remembers what is true and what is not in the case when \(r+r'>m+m'\).
5 Control systems
In this section, we introduce classes of control systems that integrate the properties of the locally convex topologies from Sect. 2, noting that, of course, control systems are merely parameterised vector fields as in Sect. 4. We show that, for the classes of control systems we introduce, the regularity of the initial value problem one obtains upon substitution of a control matches the regularity of the system in a satisfying manner. As we have been doing all along so far, we consider the finitely differentiable, Lipschitz, smooth, and real analytic cases. We see that the manner in which we have characterised the topologies for spaces of vector fields allows for a unified way of treating control systems, across all sorts of regularity, in our framework, cf. the notation of Sect. 2.7. Indeed, much of the hard work in the paper has already been done, and now we need only collect together the equipment, assign names to things, and make some now fairly obvious (but deep) conclusions. The new results here are Propositions 6 and 7 and their Corollaries 1 and 2. As can be seen, these results are quite easy applications of the results of Jafarpour and Lewis [35] summarised in Sect. 3 and of the new results in Sect. 4. It is interesting to contrast this with the detailed technical arguments used in [11, 59] to prove results of substantially less generality and power. Thus, while the background required to understand the results of Sects. 3 and 4 is certainly nontrivial, once one has it at hand many other facets of the theory become routine.
5.1 Control systems with locally essentially bounded controls
With the notions of parameterised sections from the preceding section, we readily define what we mean by a control system.
Definition 13
(Control system) Let \(m\in {\mathbb {Z}}_{\ge 0}\) and  , let \(\nu \in \{m+m',\infty ,\omega \}\), and let \(r\in \{\infty ,\omega \}\), as required. A \(\varvec{\text {C}}^\nu \)-control system is a triple
, let \(\nu \in \{m+m',\infty ,\omega \}\), and let \(r\in \{\infty ,\omega \}\), as required. A \(\varvec{\text {C}}^\nu \)-control system is a triple  , where
, where
-
(i)
 is a \(\text {C}^r\)-manifold whose elements are called states,
is a \(\text {C}^r\)-manifold whose elements are called states, -
(ii)
\(\mathscr {C}\) is a topological space called the control set, and
-
(iii)
 . \(\circ \)
. \(\circ \)
The governing equations for a control system are
for suitable functions  and
and  . To ensure that these equations make sense, the differential equation should be shown to have the properties needed for existence and uniqueness of solutions, as well as appropriate dependence on initial conditions. We do this by allowing the controls for the system to be as general as reasonable.
. To ensure that these equations make sense, the differential equation should be shown to have the properties needed for existence and uniqueness of solutions, as well as appropriate dependence on initial conditions. We do this by allowing the controls for the system to be as general as reasonable.
Proposition 6
(Property of control system when the control is specified) Let \(m\in {\mathbb {Z}}_{\ge 0}\) and  , let \(\nu \in \{m+m',\infty ,\omega \}\), and let \(r\in \{\infty ,\omega \}\), as required. Let
, let \(\nu \in \{m+m',\infty ,\omega \}\), and let \(r\in \{\infty ,\omega \}\), as required. Let  be a \(\text {C}^\nu \)-control system. If \(\mu \in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};\mathscr {C})\) then
be a \(\text {C}^\nu \)-control system. If \(\mu \in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};\mathscr {C})\) then  , where
, where  is defined by \(F^\mu (t,x)=F(x,\mu (t))\).
is defined by \(F^\mu (t,x)=F(x,\mu (t))\).
Proof
Let us define  by \({\hat{F}}^\mu (t)=F^\mu _t\). By Propositions 2, 3, and 5, the mapping
by \({\hat{F}}^\mu (t)=F^\mu _t\). By Propositions 2, 3, and 5, the mapping  is continuous. Since \({\hat{F}}^\mu \) is thus the composition of the measurable function \(\mu \) and the continuous mapping
is continuous. Since \({\hat{F}}^\mu \) is thus the composition of the measurable function \(\mu \) and the continuous mapping  , it follows that \({\hat{F}}^\mu \) is measurable. It follows from Theorem 1 that \(F^\mu \) is a Carathéodory vector field of class \(\text {C}^\nu \).
, it follows that \({\hat{F}}^\mu \) is measurable. It follows from Theorem 1 that \(F^\mu \) is a Carathéodory vector field of class \(\text {C}^\nu \).
Let \({\mathbb {T}}'\subseteq {\mathbb {T}}\) be compact. Since \(\mu \) is locally essentially bounded, there exists a compact set \(K\subseteq \mathscr {C}\) such that
Since the mapping  is continuous,
is continuous,
is contained in a compact subset of  , i.e., \(F^\mu \) is locally essentially bounded. \(\square \)
, i.e., \(F^\mu \) is locally essentially bounded. \(\square \)
This then gives the following result, characterising the nature of flows associated with open-loop control systems.
Corollary 1
(Regularity of flows of open-loop control systems) Let \(m\in {\mathbb {Z}}_{\ge 0}\), let \(\nu \in \{m,\infty ,\omega \}\), and let \(r\in \{\infty ,\omega \}\), as required. Let  be a
be a  -control system and let \(\mu \in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};\mathscr {C})\), with
-control system and let \(\mu \in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};\mathscr {C})\), with  defined by \(F^\mu (t,x)=F(x,\mu (t))\). Then there exist a subset
defined by \(F^\mu (t,x)=F(x,\mu (t))\). Then there exist a subset  and a map
and a map  with the following properties for each
with the following properties for each  :
:
-
(i)
the set
$$\begin{aligned} {\mathbb {T}}_{\varSigma ,\mu }(t_0,x_0)=\{t\in {\mathbb {T}}\;|(t,t_0,x_0)\in D_{\varSigma ,\mu }\} \end{aligned}$$is an interval;
-
(ii)
there exists an absolutely continuous curve
 satisfying $$\begin{aligned} \xi '(t)=X(t,\xi (t)),\quad \xi (t_0)=x_0, \end{aligned}$$
satisfying $$\begin{aligned} \xi '(t)=X(t,\xi (t)),\quad \xi (t_0)=x_0, \end{aligned}$$for almost all \(t\in |t_0,t_1|\) if and only if \(t_1\in {\mathbb {T}}_{\varSigma ,\mu }(t_0,x_0)\);
-
(iii)
 for almost all
for almost all 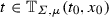 ;
; -
(iv)
for each \(t\in {\mathbb {T}}\) for which \((t,t_0,x_0)\in D_{\varSigma ,\mu }\), there exists a neighbourhood \(\mathscr {U}\) of \(x_0\) such that the mapping
 is defined and of class \(\text {C}^\nu \) on \(\mathscr {U}\).
is defined and of class \(\text {C}^\nu \) on \(\mathscr {U}\).
Proof
This follows from Proposition 6 and Theorem 2. \(\square \)
5.2 Control systems with locally integrable controls
In this section, we specialise the discussion from the preceding section in one direction, while generalising it in another. To be precise, we now consider the case where our control set \(\mathscr {C}\) is a subset of a locally convex topological vector space, and the system structure is such that the notion of integrability is preserved (in a way that will be made clear in Proposition 7 below).
Definition 14
(Sublinear control system) Let \(m\in {\mathbb {Z}}_{\ge 0}\) and \(m'\in \{0,\text {lip}\}\), let \(\nu \in \{m+m',\infty ,\omega \}\), and let \(r\in \{\infty ,\omega \}\), as required. A \(\varvec{\text {C}}^\nu \)-sublinear control system is a triple  , where
, where
-
(i)
 is a \(\text {C}^r\)-manifold whose elements are called states,
is a \(\text {C}^r\)-manifold whose elements are called states, -
(ii)
\(\mathscr {C}\) is a subset of a locally convex topological vector space
 ,
,  being called the control set, and
being called the control set, and -
(iii)
F has the following property: for every continuous seminorm p for
 , there exists a continuous seminorm q for
, there exists a continuous seminorm q for  such that $$\begin{aligned} p(F^{u_1}-F^{u_2})\le q(u_1-u_2),\qquad u_1,u_2\in \mathscr {C}.\qquad \qquad \qquad \qquad \qquad \circ \end{aligned}$$
such that $$\begin{aligned} p(F^{u_1}-F^{u_2})\le q(u_1-u_2),\qquad u_1,u_2\in \mathscr {C}.\qquad \qquad \qquad \qquad \qquad \circ \end{aligned}$$
Note that, by Propositions 2, 3, and 5, the sublinearity condition (iii) implies that a \(\text {C}^\nu \)-sublinear control system is a \(\text {C}^\nu \)-control system.
One may want to regard the generalisation from the case where the control set is a subset of \({\mathbb {R}}^k\) to being a subset of a locally convex topological vector space to be mere fancy generalisation, but this is, actually, far from being the case. Indeed, this observation is the foundation for a general, control parameterisation-independent formulation for control theory [43]. We shall see an illustration of this in our list of examples below.
We also have a version of Proposition 6 for sublinear control systems.
Proposition 7
(Property of sublinear control system when the control is specified) Let \(m\in {\mathbb {Z}}_{\ge 0}\) and \(m'\in \{0,\text {lip}\}\), let \(\nu \in \{m+m',\infty ,\omega \}\), and let \(r\in \{\infty ,\omega \}\), as required. Let  be a \(\text {C}^\nu \)-sublinear control system for which \(\mathscr {C}\) is a subset of a locally convex topological vector space
be a \(\text {C}^\nu \)-sublinear control system for which \(\mathscr {C}\) is a subset of a locally convex topological vector space  . If \(\mu \in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};\mathscr {C})\), then
. If \(\mu \in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};\mathscr {C})\), then  , where
, where  is defined by \(F^\mu (t,x)=F(x,\mu (t))\).
is defined by \(F^\mu (t,x)=F(x,\mu (t))\).
Proof
The proof that \(F^\mu \) is a Carathéodory vector field of class \(\text {C}^\nu \) goes exactly as in Proposition 6.
To prove that  , let
, let  be compact, let \(k\in {\mathbb {Z}}_{\ge 0}\), let \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and denote
be compact, let \(k\in {\mathbb {Z}}_{\ge 0}\), let \(\mathbf {a}\in \text {c}_0({\mathbb {Z}}_{\ge 0};{\mathbb {R}}_{>0})\), and denote

Define  by \(g(t)=p_K(F^\mu _t)\). We claim that \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\). From the first part of the proof of Proposition 6,
by \(g(t)=p_K(F^\mu _t)\). We claim that \(g\in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};{\mathbb {R}}_{\ge 0})\). From the first part of the proof of Proposition 6,  is measurable for every
is measurable for every  . By Theorem 1, it follows that
. By Theorem 1, it follows that  is measurable. Since \(p_K\) is a continuous function on
is measurable. Since \(p_K\) is a continuous function on  , it follows that
, it follows that  is measurable, as claimed. We claim that \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\). Note that
is measurable, as claimed. We claim that \(g\in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};{\mathbb {R}}_{\ge 0})\). Note that  is a continuous seminorm on
is a continuous seminorm on  . By hypothesis, there exists a continuous seminorm q for the locally convex topology for
. By hypothesis, there exists a continuous seminorm q for the locally convex topology for  such that
such that
for every \(u_1,u_2\in \mathscr {C}\). Therefore, if \({\mathbb {T}}'\subseteq {\mathbb {T}}\) is compact and if \(u_0\in \mathscr {C}\), we also have
the last inequality by the characterisation of Bochner integrability from [5, Theorems 3.2 and 3.3]. Thus g is locally integrable. It follows from Theorem 1 that  , as desired. \(\square \)
, as desired. \(\square \)
One also has the associated result regarding the regularity of flows of open-loop systems in this case.
Corollary 2
(Regularity of flows of open-loop sublinear control systems) Let \(m\in {\mathbb {Z}}_{\ge 0}\), let \(\nu \in \{m,\infty ,\omega \}\), and let \(r\in \{\infty ,\omega \}\), as required. Let  be a
be a  -sublinear control system and let \(\mu \in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};\mathscr {C})\), with
-sublinear control system and let \(\mu \in {\text {L}}_{\mathrm{loc}}^1({\mathbb {T}};\mathscr {C})\), with  defined by \(F^\mu (t,x)=F(x,\mu (t))\). Then there exist a subset
defined by \(F^\mu (t,x)=F(x,\mu (t))\). Then there exist a subset  and a map
and a map  with the following properties for each
with the following properties for each  :
:
-
(i)
the set
$$\begin{aligned} {\mathbb {T}}_{\varSigma ,\mu }(t_0,x_0)=\{t\in {\mathbb {T}}\;|(t,t_0,x_0)\in D_{\varSigma ,\mu }\} \end{aligned}$$is an interval;
-
(ii)
there exists an absolutely continuous curve
 satisfying $$\begin{aligned} \xi '(t)=X(t,\xi (t)),\quad \xi (t_0)=x_0, \end{aligned}$$
satisfying $$\begin{aligned} \xi '(t)=X(t,\xi (t)),\quad \xi (t_0)=x_0, \end{aligned}$$for almost all \(t\in |t_0,t_1|\) if and only if \(t_1\in {\mathbb {T}}_{\varSigma ,\mu }(t_0,x_0)\);
-
(iii)
 for almost all
for almost all  ;
; -
(iv)
for each \(t\in {\mathbb {T}}\) for which \((t,t_0,x_0)\in D_{\varSigma ,\mu }\), there exists a neighbourhood \(\mathscr {U}\) of \(x_0\) such that the mapping
 is defined and of class \(\text {C}^\nu \) on \(\mathscr {U}\).
is defined and of class \(\text {C}^\nu \) on \(\mathscr {U}\).
Proof
This follows from Proposition 7 and Theorem 2. \(\square \)
5.3 Examples
As mentioned in the introduction of the paper, one of the ideas of the paper is to produce a definition of a control system with a prescribed regularity that (1) agrees with any “standard” existing definitions and (2) extends these definitions to new cases, primarily a definition of what we mean by a “real analytic control system.” In this section we give some illustrations of how our definitions work in practice, and as well give some important special cases of systems that satisfy our definition of “control system.”
Throughout this section, we let \(m\in {\mathbb {Z}}_{\ge 0}\) and \(m'\in \{0,\text {lip}\}\), and let \(\nu \in \{m+m',\infty ,\omega \}\). Throughout,  is a manifold of class \(\text {C}^r\) for \(r\in \{\infty ,\omega \}\), as required.
is a manifold of class \(\text {C}^r\) for \(r\in \{\infty ,\omega \}\), as required.
Control-linear and control-affine systems
We first illustrate how control-affine systems, whose drift and control vector fields are of class \(\text {C}^\nu \), are \(\text {C}^\nu \)-control systems, indeed \(\text {C}^\nu \)-sublinear control systems.
To do this, we actually first work with more generality. Let  be a locally convex topological vector space and let
be a locally convex topological vector space and let  . We suppose that we have a continuous linear map
. We suppose that we have a continuous linear map  and we correspondingly define
and we correspondingly define  by \(F_\varLambda (x,u)=\varLambda (u)(x)\). Continuity of \(\varLambda \) immediately gives that the control system
by \(F_\varLambda (x,u)=\varLambda (u)(x)\). Continuity of \(\varLambda \) immediately gives that the control system  is sublinear, and we shall call a system such as this a \(\varvec{\text {C}}^\nu \)-control-linear system.
is sublinear, and we shall call a system such as this a \(\varvec{\text {C}}^\nu \)-control-linear system.
Note that we can regard a control-affine system as a control-linear system as follows. For a control-affine system with control set \(\mathscr {C}\subseteq {\mathbb {R}}^k\) and with
we let  and take
and take
Clearly we have \(F(x,{u})=F_\varLambda (x,(1,{u}))\) for every \({u}\in \mathscr {C}\). Since linear maps from finite-dimensional locally convex spaces are continuous [33, Proposition 2.10.2], we conclude that control-affine systems are control-linear systems. Thus they are also control systems as per Definition 13.
Since control-affine systems are sublinear systems, for these systems it makes sense to talk about controls that are locally integrable and not just locally essentially bounded, and this is typically what one does for control-affine systems.
Systems where control does not appear linearly
While many applications in control theory have the structure of control-affine systems, it is nonetheless true that non-affine systems arise. In this section we consider a general framework where control enters “multiplicatively.” This would include, for example, systems for which control enters through expressions like f(x)g(u), but would not include control entering through expressions like \(\sin (f(x)g(u))\), for a function f of state x and a function g of control u.
To model this multiplicative dependence on control, we consider the control set to be a general topological space \(\mathscr {C}\). We denote by  the space of continuous \({\mathbb {R}}\)-valued functions on \(\mathscr {C}\), equipped with the pointwise convergence topology. This is a locally convex space defined by the family of seminorms \(p_u\), \(u\in \mathscr {C}\), given by \(p_u(f)=|f(u)|\). Let
the space of continuous \({\mathbb {R}}\)-valued functions on \(\mathscr {C}\), equipped with the pointwise convergence topology. This is a locally convex space defined by the family of seminorms \(p_u\), \(u\in \mathscr {C}\), given by \(p_u(f)=|f(u)|\). Let  , with
, with  denoting the not completed injective tensor product, i.e., the tensor product with the injective tensor product topology [36, Chapter 16]. Given
denoting the not completed injective tensor product, i.e., the tensor product with the injective tensor product topology [36, Chapter 16]. Given  , we define a linear map
, we define a linear map

by asking that  , and then extending by linearity. We then define
, and then extending by linearity. We then define

We claim that  is a \(\text {C}^\nu \)-control system. One can imagine doing this by directly verifying the conditions of Definitions 9, 10, and 12, possibly using Theorem 3 in the real analytic case. However, according to Propositions 2, 3, and 5, we shall verify this by showing that the map
is a \(\text {C}^\nu \)-control system. One can imagine doing this by directly verifying the conditions of Definitions 9, 10, and 12, possibly using Theorem 3 in the real analytic case. However, according to Propositions 2, 3, and 5, we shall verify this by showing that the map

is continuous. Proceeding in this way has two benefits: (1) it allows us to treat all regularity classes at once; (2) it provides an effective demonstration of how the theory of locally convex spaces can be used in our setting to answer basic questions.
To prove the continuity of \({\hat{F}}\), first, for \(u\in \mathscr {C}\), denote by  the evaluation map \(\mathrm{ev}_u(f)=f(u)\). Note that
the evaluation map \(\mathrm{ev}_u(f)=f(u)\). Note that  , the latter space being the continuous dual. On
, the latter space being the continuous dual. On  we make use of the weak topology, i.e., the locally convex topology defined by the family of seminorms \(p_f\),
we make use of the weak topology, i.e., the locally convex topology defined by the family of seminorms \(p_f\),  given by
given by  . Now define
. Now define

We claim that \(\mathrm{ev}\) is continuous. Indeed, because a locally convex topology is the initial topology defined by a family of seminorms prescribing the topology, to show this we need to only show that  is continuous for every
is continuous for every  . Since
. Since  , the continuity of \(\mathrm{ev}\) simply follows from the continuity of f. Now we note that we have an inclusion
, the continuity of \(\mathrm{ev}\) simply follows from the continuity of f. Now we note that we have an inclusion

defined by the requirement that \(X\otimes f(\alpha )=\alpha (f)X\), cf. [53, Equation (3.4)]. Therefore, we can think of \(F^\otimes \) as being a continuous linear map from  into
into  . Now we merely note that
. Now we merely note that

from which we conclude that  , and so \({\hat{F}}\) is continuous, being a composition of continuous maps.
, and so \({\hat{F}}\) is continuous, being a composition of continuous maps.
The preceding development can be extended from simple multiplicative dependence by considering \(F^\otimes \) to be in the completion  , but we shall not pursue this here.
, but we shall not pursue this here.
Control systems with discrete control sets
Discrete control sets are common in control theory, as they represent situations where control actions are only selectable from a finite set of possibilities. We consider this in a general setting by considering a control set \(\mathscr {C}\) equipped with the discrete topology. In this topology, every subset of \(\mathscr {C}\) is open, and so the map  is always continuous. Thus, when dealing with a discrete control set \(\mathscr {C}\) in this sense, every mapping
is always continuous. Thus, when dealing with a discrete control set \(\mathscr {C}\) in this sense, every mapping  for which
for which  is a \(\text {C}^\nu \)-control system.
is a \(\text {C}^\nu \)-control system.
Let us now consider what trajectories look like in this case. Note that, if \(\mathscr {C}\) has the discrete topology, its compact subsets are exactly the finite subsets. Therefore, for an interval \({\mathbb {T}}\subseteq {\mathbb {R}}\),
Now let \(\mu \in {\text {L}}_{\mathrm{loc}}^\infty ({\mathbb {T}};\mathscr {C})\) and consider the time varying vector field

Define  by \({\hat{F}}^\mu (t)(x)=F^\mu (t,x)\). Then we see that \({\hat{F}}^\mu \) is exactly characterised by the fact that, for every \({\mathbb {T}}'\subseteq {\mathbb {T}}\), \({\hat{F}}^\mu |{\mathbb {T}}'\) is a simple function, in the sense of measure theory, i.e., \({\hat{F}}^\mu |{\mathbb {T}}\) is a finite linear combination, with coefficients in
by \({\hat{F}}^\mu (t)(x)=F^\mu (t,x)\). Then we see that \({\hat{F}}^\mu \) is exactly characterised by the fact that, for every \({\mathbb {T}}'\subseteq {\mathbb {T}}\), \({\hat{F}}^\mu |{\mathbb {T}}'\) is a simple function, in the sense of measure theory, i.e., \({\hat{F}}^\mu |{\mathbb {T}}\) is a finite linear combination, with coefficients in  , of characteristic functions of measurable sets. In summary, trajectories for \(\text {C}^\nu \)-control systems with a discrete control set are integral curves of time-varying vector fields that are locally simple functions of time.
, of characteristic functions of measurable sets. In summary, trajectories for \(\text {C}^\nu \)-control systems with a discrete control set are integral curves of time-varying vector fields that are locally simple functions of time.
Control systems prescribed by families of vector fields
The notion of a control system being prescribed by a family of vector fields is common. Our framework of locally convex topologies allows an important extension of how such control systems are normally treated. Indeed, for “family of vector fields” models for control systems, one typically considers trajectories that are concatenations of integral curves of the system vector fields. This translates into controls being piecewise constant. In our framework, this class of controls can be broadened.
We let  be an arbitrary family of vector fields on a \(\text {C}^r\)-manifold \(\mathsf {M}\). We then define a \(\text {C}^\nu \)-control system \(\varSigma _{{\mathscr {F}}}=(\mathsf {M},F_{{\mathscr {F}}},{\mathscr {F}})\) with control set \({\mathscr {F}}\) (equipped with the relative topology) and with
be an arbitrary family of vector fields on a \(\text {C}^r\)-manifold \(\mathsf {M}\). We then define a \(\text {C}^\nu \)-control system \(\varSigma _{{\mathscr {F}}}=(\mathsf {M},F_{{\mathscr {F}}},{\mathscr {F}})\) with control set \({\mathscr {F}}\) (equipped with the relative topology) and with
In this case, the induced map from the control set \({\mathscr {F}}\) to  is simply the inclusion map, which is certainly continuous; thus \(\varSigma _{{\mathscr {F}}}\) is indeed a \(\text {C}^\nu \)-control system. Indeed, it is an example of a control-linear system, as discussed above. Thus, for systems such as this, one can work with controls that are locally integrable, with this meaning locally Bochner integrable in this case.
is simply the inclusion map, which is certainly continuous; thus \(\varSigma _{{\mathscr {F}}}\) is indeed a \(\text {C}^\nu \)-control system. Indeed, it is an example of a control-linear system, as discussed above. Thus, for systems such as this, one can work with controls that are locally integrable, with this meaning locally Bochner integrable in this case.
This rather abstract approach to a control system is used elegantly in optimal control theory by Sussmann [63], and is also part of the approach to control theory in [43].
Systems defined by “control bundles”
The work of Brockett [12] and Willems [69] introduces the notion of a control system as being prescribed by a bundle over the state manifold. Let us be clear about this. We have a fibre bundle
 that prescribes the space where controls take values. Precisely, a control is a mapping
that prescribes the space where controls take values. Precisely, a control is a mapping  . (The matter of what is the appropriate regularity, e.g., measurability, boundedness, integrability, of this control is one of the difficulties of this control bundle formulation.) The dynamics are prescribed by a \(\text {C}^\nu \)-bundle mapping
. (The matter of what is the appropriate regularity, e.g., measurability, boundedness, integrability, of this control is one of the difficulties of this control bundle formulation.) The dynamics are prescribed by a \(\text {C}^\nu \)-bundle mapping  over \({\text {id}}_{\mathsf {M}}\):
over \({\text {id}}_{\mathsf {M}}\):

Thus, a trajectory associated with a control  is a curve
is a curve  satisfying
satisfying  and \(\xi '(t)=F(\mu (t))\). This is encapsulated by the following commutative diagram:
and \(\xi '(t)=F(\mu (t))\). This is encapsulated by the following commutative diagram:

It is possible to include this formulation in our notion of a control system as follows. Let us denote by  the set of \(\text {C}^\nu \)-sections of
the set of \(\text {C}^\nu \)-sections of  . (Here we run into a possible problem, since we may have
. (Here we run into a possible problem, since we may have  . This can be overcome by working with local sections.) We then denote by
. This can be overcome by working with local sections.) We then denote by

the set of \(\text {C}^\nu \)-vector fields arising, through F, from \(\text {C}^\nu \)-sections of  . This then allows us to work with the family of \(\text {C}^\nu \)-vector fields
. This then allows us to work with the family of \(\text {C}^\nu \)-vector fields
 ,
and so define a control system as in our preceding example. With this formulation, the matter of regularity of controls becomes unambiguous: we can work with locally (Bochner) integrable controls.
,
and so define a control system as in our preceding example. With this formulation, the matter of regularity of controls becomes unambiguous: we can work with locally (Bochner) integrable controls.
Notes
The condition on page 35 of this text is not sufficient to ensure uniqueness of trajectories.
This is actually not a very good name. A better name, and the name used by Jafarpour and Lewis [35], would be the “smooth compact-open topology.” However, we wish to keep things simple here, and also use notation that is common between regularity classes.
There is a potential confusion about “boundedness” in this paper. In Sect. 1.6 we have defined a notion of “essentially bounded” that is different, in general, from the notion of “essentially von Neumann bounded” that we use here. We will not quite encroach on areas where this confusion causes problems, but it is something to bear in mind. Jafarpour and Lewis [35] are a little more careful about this, explicitly making use of “bornologies.”
Such complexifications exist, as shown in [35, §5.1.1].
References
Abraham R, Marsden JE, Ratiu TS (1988) Manifolds, tensor analysis, and applications, 2nd edn. Applied Mathematical Sciences, vol 75. Springer, New York
Agrachev AA, Gamkrelidze RV (1978) The exponential representation of flows and the chronological calculus. Math USSR Sbornik 107(4):467–532
Agrachev AA, Sachkov Y (2004) Control theory from the geometric viewpoint. Encyclopedia of Mathematical Sciences, vol 87. Springer, New York
Barbero-Liñán M, Muñoz-Lecanda MC (2009) Geometric approach to Pontryagin’s maximum principle. Acta Appl Math 108(2):429–485
Beckmann R, Deitmar A (2011) Strong vector valued integrals. arXiv:1102.1246v1 [math.FA]
Bianchini RM, Stefani G (1993) Controllability along a trajectory: a variational approach. SIAM J Control Optim 31(4):900–927
Bierstedt KD (2007) Introduction to topological tensor products. Course notes, Mathematical Institute, University of Paderborn. http://tinyurl.com/mo64rdk
Bonnard B, Chyba M (2003) Singular trajectories and their role in control theory. Mathematics and Applications, vol 40. Springer, New York
Bourbaki N (1989) Algebra I. Elements of mathematics. Springer, New York
Bourbaki N (1990) Algebra II. Elements of mathematics. Springer, New York
Bressan A, Piccoli B (2007) Introduction to the mathematical theory of control. Applied Mathematics, vol 2. American Institute of Mathematical Sciences, Wilmington
Brockett RW (1977) Control theory and analytical mechanics. In: Martin C, Hermann R (eds) Geometric control theory. Math Sci Press, Brookline, pp 1–48
Bus JCP (1984) The Lagrange multiplier rule on manifolds and optimal control of nonlinear systems. SIAM J Control Optim 22(5):740–757
Cieliebak K, Eliashberg Y (2012) From Stein to Weinstein and back: symplectic geometry of affine complex manifolds. American Mathematical Society Colloquium Publications, vol 59. American Mathematical Society, Providence
Coddington EE, Levinson N (1955) Theory of ordinary differential equations. McGraw-Hill, New York. New edition: [16]
Coddington EE, Levinson N (1984) Theory of ordinary differential equations, 8th edn. Robert E. Krieger Publishing Company, Huntington. First edition: [15]
Conway JB (1985) A course in functional analysis, 2nd edn. Graduate Texts in Mathematics, vol 96. Springer, New York
Coron JM (1994) Linearized control systems and applications to smooth stablization. SIAM J Control Optim 32(2):358–386
Delgado-Téllez M, Ibort A (2003) A panorama of geometric optimal control theory. Extracta Math 18(2):129–151
Demailly JP (2012) Complex analytic and differential geometry. Unpublished manuscript made publicly available . http://www-fourier.ujf-grenoble.fr/~demailly/manuscripts/agbook
Diestel J, Fourie JH, Swart J (2008) The metric theory of tensor products: Grothendieck’s Résumé Revisited. American Mathematical Society, Providence
Diestel J, Uhl Jr, JJ (1977) Vector measures. American Mathematical Society Mathematical Surveys and Monographs, vol 15. American Mathematical Society, Providence
Domański P (2010) Notes on real analytic functions and classical operators. In: Blasco O, Bonet J, Calabuig J, Jornet D (eds) Proceedings of the third winter school in complex analysis and operator theory, Contemporary Mathematics, vol 561. American Mathematical Society, Providence, pp 3–47
Domański P, Vogt D (2000) The space of real-analytic functions has no basis. Polska Akademia Nauk. Instytut Matematyczny. Studia Math 142(2):187–200
Federer H (1996) Geometric measure theory. Classics in mathematics. Springer, New York. Reprint of 1969 edition
Fritzsche K, Grauert H (2002) From holomorphic functions to complex manifolds. Graduate Texts in Mathematics, vol 213. Springer, New York
Gamkrelidze RV (1978) Principles of optimal control theory. Mathematical Concepts and Methods in Science and Engineering, vol 7. Plenum Press, New York
Gasquet C, Witomski P (1999) Fourier analysis and applications. Texts in Applied Mathematics, vol 30. Springer, New York. Translated from the French by Robert Ryan
Groethendieck A (1973) Topological vector spaces. Notes on Mathematics and its Applications. Gordon & Breach Science Publishers, New York
Gunning RC, Rossi H (1965) Analytic functions of several complex variables. American Mathematical Society, Providence. 2009 reprint by AMS
Hirsch MW (1976) Differential topology. Graduate Texts in Mathematics, vol 33. Springer, New York
Hörmander L (1973) An introduction to complex analysis in several variables, 2nd edn. North-Holland, Amsterdam
Horváth J (1966) topological vector spaces and distributions, vol I. Addison Wesley, Reading
Hungerford TW (1980) Algebra. Graduate Texts in Mathematics, vol 73. Springer, New York
Jafarpour S, Lewis AD (2014) Time-varying vector fields and their flows. Springer Briefs in Mathematics. Springer, New York
Jarchow H (1981) Locally convex spaces. Mathematical textbooks. Teubner, Leipzig
Kawski M (1990) High-order small-time local controllability. Nonlinear Controllability and Optimal Control, Monographs and Textbooks in Pure and Applied Mathematics, vol 133. Dekker Marcel Dekker, New York, pp 431–467
Kolář I, Michor PW, Slovák J (1993) Natural operations in differential geometry. Springer, New York
Krantz SG, Parks HR (2002) A primer of real analytic functions. Birkhäuser Advanced Texts, 2nd edn. Birkhäuser, Boston
Krener AJ (1977) The higher order maximum principle and its applications to singular extremals. SIAM J Control Optim 15(2):256–293
Langerock B (2003) Geometric aspects of the maximum principle and lifts over a bundle map. Acta Appl Math 77(1):71–104
Lee EB, Markus L (1967) Foundations of optimal control theory. Wiley, New York
Lewis AD (2014) Tautological control systems. Springer Briefs in Electrical and Computer Engineering—Control, Automation and Robotics. Springer, New York
Lions JL (1971) Optimal control of systems governed by partial differential equations. Grundlehren der Mathematischen Wissenschaften, vol 170. Springer, New York
Mangino EM (1997) (LF)-spaces and tensor products. Math Nachr 185:149–162
Michor PW (1980) Manifolds of differentiable mappings. Shiva Mathematics Series, vol 3. Shiva Publishing Limited, Orpington (1980)
Nagano T (1966) Linear differential systems with singularities and an application to transitive Lie algebras. J Math Soc Japan 18:398–404
Nagano T (1966) Linear differential systems with singularities and an application to transitive Lie algebras. J Math Soc Japan 18:398–404
Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, Mishchenko EF (1961) Matematicheskaya teoriya optimal’ nykh protsessov. Gosudarstvennoe izdatelstvo fiziko-matematicheskoi literatury, Moscow. Reprint of translation: [50]
Nagano T (1966) Linear differential systems with singularities and an application to transitive Lie algebras. J Math Soc Japan 18:398–404
Retakh VS (1970) The subspaces of a countable inductive limit. Soviet Mathematics. Doklady. A translation of the mathematics section of. Doklady Akademii Nauk SSSR 11:1384–1386
Rudin W (1991) Functional analysis, 2nd edn. International Series in Pure and Applied Mathematics. McGraw-Hill, New York
Ryan RA (2002) Introduction to tensor products of Banach spaces. Springer Monographs in Mathematics. Springer, New York
Saunders DJ (1989) The geometry of jet bundles. London Mathematical Society Lecture Note Series, vol 142. Cambridge University Press, New York
Schaefer HH, Wolff MP (1999) Topological vector spaces, 2nd edn. Graduate Texts in Mathematics, vol 3. Springer, New York
Schwartz L (1950–1951) Théorie des distributions. Publications de l’Institut de Mathématique de l’Université de Strasbourg. Hermann, Paris. Reprint: [57]
Schwartz L (1997) Théorie des distributions. Publications de l’Institut de Mathématique de l’Université de Strasbourg. Hermann, Paris. Original: [56]
Sontag ED (1992) Universal nonsingular controls. Syst Control Lett 19(3):221–224
Sontag ED (1998) Mathematical control theory: deterministic finite dimensional systems, 2nd edn. Texts in Applied Mathematics, vol 6. Springer, New York
Sussmann HJ (1973) Orbits of families of vector fields and integrability of distributions. Trans Am Math Soc 180:171–188
Sussmann HJ (1983) Lie brackets, real analyticity and geometric control. In: Differential geometric control theory, Progress in Mathematics, vol 27. Birkhäuser, Boston
Sussmann HJ (1990) Why real analyticity is important in control theory. Perspectives in Control Theory (Sielpia), Progress in Systems and Control Theory, vol 2. Birkhäuser, Boston, pp 315–340
Sussmann HJ (1997) An introduction to the coordinate-free maximum principle. In: Jakubczyk B, Respondek W (eds) Geometry of feedback and optimal control. Dekker Marcel Dekker, New York, pp 463–557
Sussmann HJ (1998) Some optimal control applications of real-analytic stratifications and desingularization. Singularities Symposium-Łojasiewicz 70, Banach Center Publications, vol 44. Polish Academy of Sciences, Institute for Mathematics, Warsaw, pp 211–232
Sussmann HJ, Jurdjevic V (1972) Controllability of nonlinear systems. J Differ Equ 12:95–116
Tröltzsch F (2010) Optimal control of partial differential equations. Graduate Studies in Mathematics, vol 112. American Mathematical Society, Providence
Vogt D (2013) A fundamental system of seminorms for \(A(K)\) (2013). arXiv:1309.6292v1 [math.FA]
Wengenroth J (1995) Retractive (LF)-spaces. Ph.D. thesis, Universität Trier, Trier
Willems JC (1979) System theoretic models for the analysis of physical systems. Ricerche di Automatica 10(2):71–106
Acknowledgements
The second author was a Visiting Professor in the Department of Mathematics at University of Hawaii, Manoa, when the paper was written, and would like to acknowledge the hospitality of the department, particularly that of Monique Chyba and George Wilkens. The second author would also like to thank his departmental colleague Mike Roth for numerous useful conversations over the years. While conversations with Mike did not lead directly to results in this paper, Mike’s willingness to chat about complex geometry and to answer ill-informed questions was always appreciated, and ultimately very helpful.
Author information
Authors and Affiliations
Corresponding author
Additional information
Research supported in part by a grant from the Natural Sciences and Engineering Research Council of Canada.
Rights and permissions
About this article
Cite this article
Jafarpour, S., Lewis, A.D. Locally convex topologies and control theory. Math. Control Signals Syst. 28, 29 (2016). https://doi.org/10.1007/s00498-016-0179-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00498-016-0179-0



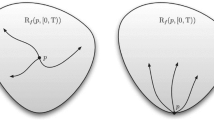
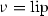 , and are understood to be true (and occasionally proved) when
, and are understood to be true (and occasionally proved) when
 . When
. When  and
and  , the sequence
, the sequence  is compact, then
is compact, then  is a norm that gives the
is a norm that gives the  , the sequence
, the sequence  is compact, then
is compact, then  is a norm that gives the
is a norm that gives the  -topology.
-topology. is compact, then
is compact, then  is a norm that gives the
is a norm that gives the  for each
for each  ;
; defined by
defined by  , the map
, the map  defined by
defined by  and every
and every  and every
and every  for each
for each  ;
; defined by
defined by  , the map
, the map  defined by
defined by  , there exists
, there exists  : for every compact set
: for every compact set  , there exists
, there exists  , there exists
, there exists 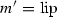 : for every compact set
: for every compact set  , there exists
, there exists  for each
for each  ;
; defined by
defined by  , the map
, the map  defined by
defined by 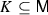 , there exists
, there exists  , there exists
, there exists  for each
for each 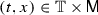 ;
; defined by
defined by  defined by
defined by  and every
and every  and every
and every  is measurable if the preimage of every Borel set is Lebesgue measurable.
is measurable if the preimage of every Borel set is Lebesgue measurable. , of characteristic functions of measurable sets. The integral of a simple function
, of characteristic functions of measurable sets. The integral of a simple function  to a unique value, which is called the integral of
to a unique value, which is called the integral of  is separable and complete, as will be the case for us in this paper, then a measurable curve
is separable and complete, as will be the case for us in this paper, then a measurable curve  is Bochner integrable if and only if
is Bochner integrable if and only if 
 [
[ , by
, by  we denote the A-valued Bochner integrable mappings and by
we denote the A-valued Bochner integrable mappings and by  we denote the A-valued locally Bochner integrable mappings.
we denote the A-valued locally Bochner integrable mappings. is von Neumann
bounded if
is von Neumann
bounded if  is bounded for every continuous seminorm p for
is bounded for every continuous seminorm p for  . The curve
. The curve  is essentially von Neumann
bounded if there exists a bounded set
is essentially von Neumann
bounded if there exists a bounded set  such that
such that 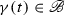 for almost every
for almost every  , and is locally essentially von Neumann bounded if
, and is locally essentially von Neumann bounded if  is a normed vector space, then von Neumann bounded is the same as norm bounded.
is a normed vector space, then von Neumann bounded is the same as norm bounded. ;
; is measurable,
is measurable, ;
; is measurable and locally Bochner integrable,
is measurable and locally Bochner integrable, ;
; is measurable and locally essentially von Neumann bounded.
is measurable and locally essentially von Neumann bounded. satisfying
satisfying  if and only if
if and only if 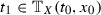 ;
; for almost all
for almost all  ;
; for which
for which  , there exists a neighbourhood
, there exists a neighbourhood  of
of 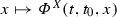 is defined and of class
is defined and of class  .
. , the map
, the map  defined by
defined by  , the map
, the map  defined by
defined by  is continuous for every
is continuous for every  , the map
, the map  defined by
defined by  , the map
, the map  defined by
defined by  is continuous;
is continuous; : the map
: the map  is continuous and, for each
is continuous and, for each  and each
and each  of
of  of
of 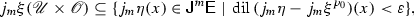
 , the map
, the map  defined by
defined by  , the map
, the map  defined by
defined by  is continuous.
is continuous. , the map
, the map  defined by
defined by  , the map
, the map  defined by
defined by  , for each
, for each  of
of 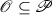 of
of 
 and if
and if  is locally compact and Hausdorff, then, for each
is locally compact and Hausdorff, then, for each  , there exist a neighbourhood
, there exist a neighbourhood  of
of 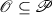 of
of  such that
such that  ;
; such that
such that  , then
, then  .
. ,
, and its inclusion in
and its inclusion in  agree.
agree.  ,
, satisfying
satisfying 
 .
.  satisfies condition (MO), then, for any Banach space
satisfies condition (MO), then, for any Banach space  ,
,  (
( , and the direct limit topology on
, and the direct limit topology on  satisfies condition (M) [
satisfies condition (M) [ in
in  is nuclear and if the direct limit topology on
is nuclear and if the direct limit topology on  is regular, then the direct limit topology on
is regular, then the direct limit topology on  satisfies condition (MO) [
satisfies condition (MO) [ satisfies condition (M), then this direct limit topology is boundedly retractive [
satisfies condition (M), then this direct limit topology is boundedly retractive [ satisfies condition (MO) (by virtue of assertion 2 above and by the properties of the direct limit topology enunciated in [
satisfies condition (MO) (by virtue of assertion 2 above and by the properties of the direct limit topology enunciated in [ is the direct limit of the directed sequence
is the direct limit of the directed sequence  (by virtue of assertion 1 above).
(by virtue of assertion 1 above). satisfies condition (M) (by virtue of assertion 1 above).
satisfies condition (M) (by virtue of assertion 1 above). is boundedly retractive (by virtue of assertion 3 above).
is boundedly retractive (by virtue of assertion 3 above). is a
is a  .
.  satisfying
satisfying  for almost all
for almost all 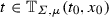 ;
; is defined and of class
is defined and of class  is a
is a  ,
,  being called the control set, and
being called the control set, and , there exists a continuous seminorm q for
, there exists a continuous seminorm q for  such that
such that  satisfying
satisfying  for almost all
for almost all  ;
; is defined and of class
is defined and of class