Joint identification of contaminant source and dispersion coefficients based on multi-observed reconstruction and ensemble Kalman filtering

Abstract

Accurate and efficient identification of pollution sources is a key process that assists in the treatment of water pollution incidents. The ensemble Kalman filter (EnKF) has been proven to be an effective approach for identifying pollution source parameters (e.g., source location, release time, and mass released). In this paper, a method involving multiple observations of reconstruction (MOR) is proposed for reconstructing multidimensional state vectors for assimilation based on pollutant concentration monitoring techniques. The newly reconstructed state variables have dimensionless characteristics that decouple the source mass from the parameter group to be identified before assimilation is performed. This approach can mitigate the interference of assimilation caused by nonmain source parameters. As a result, the pollution sources and material dispersion coefficients can be simultaneously identified at limited observation sites. Then, a set of synthetic numerical examples with 7 scenarios is assembled to investigate and compare the unique characteristics of the derived state variables during assimilation. A laboratory experiment for unknown parameter identification based on monitoring the chemical oxygen demand (COD) concentration is carried out in an annular flume to verify the applicability of the method in real events. The results show that the EnKF combined with the MOR method based on the decoupling pattern performs well in identifying pollution sources and dispersion coefficients simultaneously. The method can still perform excellently in identifying parameters in practice when some data in the observation sequences are lost, with relative errors of pollution source parameters being controlled within 4%. The relative errors of the identified transverse and longitudinal dispersion coefficients are 39% and 12%, respectively. Overall, by evaluating the original data, reconstructing the dataset, and combining it with the EnKF method, it is proven that the MOR–EnKF method is an effective measure for identifying high-dimensional unknown parameter groups.

1 Introduction

Source identification during water pollution accidents is an important part of surface water environmental management (Cheng and Jia 2010; Jerez et al. 2021; Gong et al. 2023). The identification of water contaminant sources is an inverse problem (Maryam et al. 2022). Specifically, based on existing monitoring conditions and information, reverse optimization is performed to identify the unknown parameters of contaminant sources. In general, for sudden water pollution accidents, the unknown parameters of contaminant sources are the source location, release time, and total mass released (Yang et al. 2016; Ghane et al. 2016). In reality, water pollution accidents are generally contingent and urgent; thus, quickly and accurately identifying the parameters of pollution sources is crucial for understanding the causes of pollution accidents and determining subsequent measures for pollution treatment.

Regarding the inverse problem, many optimization methods have been developed to solve this problem (Michalak and Kitanidis 2004; Barati Moghaddam et al. 2021; Gómez-Hernández and Xu 2022). In the past, unknown parameters were identified by optimizing the objective function according to the relationships between the observation variables and the simulation variables. For example, Neupauer et al. (2000) inverted the release history of groundwater pollution sources in one-dimensional scenarios based on Tikhonov regularization (TR) and minimum relative entropy (MRE). The TR method was determined to be more robust when the magnitudes of the data measurement errors are unknown. Alapati and Kabala (2000) adopted the nonlinear least squares method to identify the release history of a groundwater contaminant plume from the currently measured spatial distribution. However, the method was found to be extremely sensitive to the observation noise and pollutant dissipation degree and only suitable for catastrophic pollution release events. Michalak and Kitanidis (2004) adopted the inverse model to recover the historical contaminant distribution based on combining the geostatistical method with the adjoint state method, which might improve the efficiency of solving underdetermined problems. However, observation data with sufficient quantity and quality are needed. Li et al. (2016) inverted the convection–dispersion governing equation based on the spatiotemporal radial basis function collocation method and adopted the least squares method to solve the overdetermined system of equations. The contaminant source parameters were identified by optimizing the constructed target cost function. However, global spatial observation data were needed for calculations. The parameter search mode was simple and only suitable for solving constant current problems. These studies were mainly based on analytical solutions of fluid dynamics and pollution diffusion, resulting in many limitations in their application. Moreover, these scholars relied heavily on large amounts of unbiased or less biased observation data to recover the release history of the pollution source or plume. However, in practice, it is quite difficult to obtain these observation data. Moreover, the recovery of the release history cannot comprehensively describe the pollution source, and some source information needs to be assumed.

Some scholars have combined intelligence algorithms when solving these inverse problems. For instance, Zhang et al. (2016) combined Gaussian process (GP) and Markov chain Monte Carlo (MCMC) methods to construct an adaptive surrogate model for identifying groundwater pollution sources based on location and time-varying strength. In their numerical case, the porosity and longitudinal and transverse dispersion coefficients were assumed. Pan et al. (2021a) proposed a simulation optimization method based on the Bayesian regularization deep neural network surrogate model, in which Bayesian regularization was applied to the training of a neural network to solve the overfitting problem. This method could identify the location and release intensity parameters of two pollution sources and the hydraulic conductivity values of two zones. Pan et al. (2021b) developed a hybrid heuristic algorithm that combined the local search capabilities of particle swarm optimization (PSO) with the global search capabilities of differential evolution Markov chain (DEMC) method to prevent local optimization in parameter identification. Secci et al. (2022) developed a data-driven model based on an artificial neural network (ANN) to solve forwards and backwards mass transport problems in a system with strong nonlinearity, which has a low computational burden and little uncertainty in identifying the release history of pollution. In these studies, the information on the pollution sources to be identified was not confined to the release history, and additional parameters that could describe the sources were recognized. However, the prior ranges of unknown variables were narrow, and the methods were highly dependent on dense observation points and high-quality data.

In addition to the two methods mentioned above, probabilistic methods have received additional attention, and they have been further developed by researchers worldwide in recent years (Hendricks Franssen and Kinzelbach 2009; Zhang et al. 2015; Gómez-Hernández and Xu 2022). The ensemble Kalman filter (EnKF) algorithm, which was originally proposed by Evensen (2003) and has been widely used to solve parameter assimilation problems in various fields, such as meteorology, oceanography, hydrology, environmental ecology, petroleum engineering, and navigation technology (Gao et al. 2022; Shah et al. 2020; Zhou et al. 2011; Li et al. 2012; Chen et al. 2023; Nejadi et al. 2015; Xu and Guo 2022), has been proven to be highly effective for parameter assimilation. Due to the high assimilation efficiency, the convenience of embedding the EnKF algorithm into prediction models, the comprehensive consideration of model prediction error and observation error, and the uncertainty of parameters to be assimilated, this algorithm has become one of the most popular methods for solving the inverse problem (Chen et al. 2018; Xu and Gómez-Hernández 2015; Li et al. 2012). For the inverse problem of pollution source identification, some scholars have applied the EnKF algorithm to solve this problem and have made some progress. Xu and Gómez-Hernández (2016) successfully applied the normal score EnKF (NS-EnKF) to identify contaminant source locations, release times and release concentrations and evaluated the uncertainty of identification. On this basis, Xu and Gómez-Hernández (2018) proposed the restart NS-EnKF to simultaneously identify contaminant sources and spatially variable hydraulic conductivity in aquifers by assimilating pressure head and concentration data from observation wells and compared the results of three different scenarios. However, since the mass transport parameters, the external sources and sinks, and the initial and boundary conditions in the system are difficult to determine precisely and because the number of observation sites might not be sufficient in practice, this approach is difficult to apply widely. Zhang and Huang (2017) proposed a fully sequential inverse estimation method for reconstructing the temporal release of river pollution accidents. This method was based on the one-dimensional advection‒dispersion model combined with the augmented EnKF method. Compared with the Tikhonov method, this method could reduce the relative errors of the total release estimation by approximately 12.4% on average. However, in this research, the location of the source was assumed. Wang et al. (2019) combined the EnKF and backwards position probability (BLP) to identify the river contaminant source. This method could support online identification and reduce the influences of observation conditions. However, since the method was only applicable to simple one-dimensional conditions, it could not be used to solve source identification problems under complex hydraulic conditions. Jing et al. (2023) introduced the relationship coefficient as the object assimilated in the EnKF to identify contaminant source information. The performance of the proposed method was compared with that of the traditional EnKF in terms of different observation errors, observation site quantities, ensemble realizations and model grid sizes. This method was proven to be a highly effective and robust method for estimating pollution sources. In their studies, the dispersion coefficients were assumed, but in practice, these parameters could not be determined in advance. The miscalculated coefficients were bound to cause great deviations in simulations of the spatial distributions of pollutants and in estimates of the pollution source information (Liang et al. 2010; Kong et al. 2013). Thus, it is crucial to provide a reasonable estimation of dispersion coefficients simultaneously while identifying pollution source information. Similar to other research methods, the assimilation effect of the EnKF algorithm depends heavily on the quantity and location of observation points. However, it is very difficult to ensure sufficient observation points in reality since monitoring sensors may be unreliable due to various factors, including weather and humans (Shang et al. 2023; Wen et al. 2024). When such a situation is encountered, considering the uncertainty of the model and parameters (Dai et al. 2024), insufficient observation data may lead to great deviations in the assimilation results from the true values.

The purpose of this paper is to avoid the problems mentioned above and make full use of limited observation data to simultaneously identify unknown pollution source parameters (i.e., source location, release time, and mass released) and hydraulic parameters (i.e., transverse and longitudinal coefficients) as accurately as possible, which is highly valuable and significant. A new method is proposed to exploit the maximum amount of information from limited observation data. We introduce dataset reconstruction technology and decoupling methods, which increase the efficiency and accuracy of the EnKF method for solving traceability problems.

The paper is organized as follows. In Section 2, the mass transport model used for prediction is introduced, in addition to a combination of the EnKF and MOR methods. In Section 3, a synthetic example for analysis and a laboratory experiment carried out in an annular flume for application are described. Then, the performance and verification of EnKF–MOR method for identifying the source information and a discussion of the results are presented in Section 4. In Section 5, some conclusions are provided.

2 Methodology

2.1 Two-dimensional convection dispersion model

A plane two-dimensional model can be used to calculate fluid dynamics and material transport/dispersion to ensure calculation efficiency. The substance is assumed to be completely dissolved in water. The lack of conservation of pollution, which may be caused by pollutant decomposition, chemical and biological transformations or a combination of these processes, is neglected when the transmission time is short and when the substance is alone in the system. Then, the depth-averaged two-dimensional convection–dispersion governing equation is as follows (Chen and Wang 2013):

$$\frac{\partial HC}{\partial t}+\frac{\partial HuC}{\partial x}+\frac{\partial HvC}{\partial y}=\frac{\partial }{\partial x}\left(H{D}_{xx}\frac{\partial C}{\partial x}+H{D}_{xy}\frac{\partial C}{\partial y}\right)+\frac{\partial }{\partial y}\left(H{D}_{yx}\frac{\partial C}{\partial x}+H{D}_{yy}\frac{\partial C}{\partial y}\right)$$

(1)

where H is the water depth, and if the water depth is constant, H can be removed from Eq. (1); t is the time; C is the depth-average solute concentration; u and v are the velocity components in the x and y directions (Cartesian coordinate system), respectively; and ${D}_{xx}$, ${D}_{xy}$, ${D}_{yx}$, and ${D}_{yy}$ are the components of the 2-D dispersion coefficient tensor of depth-averaged mixing, in which the principal direction coincides with the flow direction. Through tensor rotation, the mixing coefficients can be calculated by Preston (1985):

$${D}_{xx}={D}_{L}{cos}^{2}\left(\theta \right)+{D}_{T}{sin}^{2}\left(\theta \right)$$

(2a)

$${D}_{xy}={D}_{yx}={(D}_{L}-{D}_{T})cos\left(\theta \right)\text{s}\text{i}\text{n}(\theta )$$

(2b)

$${D}_{yy}={D}_{L}{sin}^{2}\left(\theta \right)+{D}_{T}{cos}^{2}\left(\theta \right)$$

(2c)

where $\theta$ is the angle of the flow direction to the x-axis and ${D}_{L}$ and ${D}_{T}$ are the dispersion coefficients along the longitudinal and transverse directions, respectively, which are related to the velocity (Elder 1959).

The values of u and v in Eq. (1), which denote the flow field, are calculated by the Elcirc model (Zhang et al. 2004). The values of concentration C in Eq. (1) are calculated by a high-accuracy finite volume method, which is based on an alternating operator splitting technique. The operator splitting technique is used to separate advective and diffusive transport into two stages based on a physical definition, and appropriate numerical methods have been proposed to solve this problem (Valocchi and Malmstead 1992; Rubio et al. 2008; Liang et al. 2010; Kong et al. 2013). To provide the concentration fields of the synthetic example and flume experiment in Sect. 3, the method from Kong et al. (2013) is adopted to solve the advection diffusion equation, in which the initial global concentrations are all 0 and the diffusion flux at the boundary is 0.

2.2 Traditional EnKF for source identification

There are two kinds of variables involved in the EnKF algorithm: system parameters and system states. When the EnKF algorithm is used to identify pollution sources, system parameters are usually identified. The system state refers to the observed variables. In contrast to the forwards assimilation problem, in traceability assimilation, only the pollution source information is updated, while the state variables (i.e., concentration) do not need to be updated (Xu and Gómez-Hernández 2018). The steps of the traditional EnKF algorithm for source identification are as follows:

• (1) The ensemble of the system parameter group to be identified is constructed. An ensemble of N_r realizations of the parameter group that contains X, Y, T, M D_L, and D_T to be identified is generated.

  $$S={[X,Y,T,M,{D}_{L},{D}_{T}]}^{T}$$

  (3)

• (2) The state variables are predicted. The vector of the parameter group updated at time step t-1 is substituted into the convection dispersion model to calculate the concentrated state at time step t. Then, the concentration prediction is given by the following equation:

  $${C}_{t}^{s}={\Delta }\left({C}_{0},{S}_{t-1}\right)$$

  (4)

  where ${\Delta }$ is the convection dispersion operator; ${C}_{0}$ is the initial distribution of contaminant concentration; and ${C}_{t}^{s}$ is the vector of forecasted concentration at observation sites.

• (3) The system parameters are updated. The unknown parameters are identified by assimilating the observed concentrations, given by the following expression:

  $${S}_{t}^{a}={S}_{t}^{f}+{K}_{t}({C}_{t}^{ob}-{C}_{t}^{s}+{e}_{t})$$

  (5)

  where superscripts a and f are the parameters after updating and before updating, respectively; $e$ is the observation error vector, which is ignored and set to 0 (Jing et al. 2023); and K is the Kalman gain matrix:

  $${K}_{t}={P}_{S,C}{({P}_{C,C}+{r}_{t})}^{-1}$$

  (6)

  where ${P}_{S,C}$ is the cross-covariance matrix between the source parameters and the state variable; ${P}_{C,C}$ is the autocovariance of the state variable; and ${r}_{t}$ is the covariance matrix of the error vector $e$. ${P}_{S,C}$ and ${P}_{C,C}$ are as follows:

  $$P_{S,C}=\frac1{N_r-1}\sum\nolimits_{i=1}^{N_r}\left\{\left(S_t^f(i)-\overline{S_t^f\left(i\right)}\right)\left(C_t^s\left(i\right)-\overline{C_t^s\left(i\right)}\right)^T\right\}$$

  (7)
  $$P_{C,C}=\frac1{N_r-1}\sum\nolimits_{i=1}^{N_r}\left\{\left(C_t^s(i)-\overline{C_t^s\left(i\right)}\right)\left(C_t^s\left(i\right)-\overline{C_t^s\left(i\right)}\right)^T\right\}$$

  (8)

Finally, the calculation steps 2 and 3 are repeated until the assimilation process is complete. There are two finishing criteria. One criterion is the difference in the ensemble means at two adjacent assimilation steps. The critical value of the difference is set to 10% of the mean of the previous step. The condition is met if the difference is less than the critical value. The other criterion is the variances in the ensembles of parameters. When the sum of the variances in ensembles decreases to 1e-5, the centralizations of the ensembles of all the parameters are high. When both criteria are met, the assimilation process is finished.

To address the ensemble collapse during assimilation (Bauser et al. 2018; Chen et al. 2021), we consider the covariance damping in the calculation of the EnKF (Hendricks Franssen and Kinzelbach 2008) and add a damping factor ${\upalpha }$ with the range (0,1) in the assimilation step of the updating process:

$${S}_{t}^{a}={S}_{t}^{f}+\alpha {K}_{t}({C}_{t}^{ob}-{C}_{t}^{s}+{e}_{t})$$

(9)

2.3 Multiple observations of reconstruction (MOR) method

In the traditional source identification algorithm, only the values of the observed variables at the t observation step are used in the t assimilation step. Considering the continuity of the propagation after the contaminants are released, it is obvious that the observation data at steps 0 ~ t-1 are available for updating the simulated state variables at assimilation step t. Jing et al. (2023) proposed introducing the concept of the relationship coefficient into the EnKF to identify the group of source parameters by replacing concentrations with the relationship coefficient of contaminant concentrations as the observation variables for assimilation. This method considers the temporal process of contaminant concentration in every assimilation step, which increases the stability of source identification.

In this paper, in addition to the contaminant source parameters, the dispersion coefficients in the convection-dispersion model need to be identified, i.e., the D_L and D_T in Eq. (2). When the dimension of the parameter group to be identified is increased (e.g., the dispersion coefficients need to be identified simultaneously in the present paper), the calculation efficiency and accuracy are greatly reduced. To efficiently and precisely identify unknown parameters with insufficient and incomplete observation data, additional hidden information must be obtained from limited observation sequences; thus, a new method based on multiple observations of reconstruction (MOR) of raw data is established. Multiple variables are derived from the temporal process of contaminant concentrations to replace the observed concentration as the state variables to be assimilated. Moreover, the decoupling mode is used in assimilation to reduce the dimensionality of the unknown parameter group. Normally, information about the contaminant released, such as the release location, release time and mass, is considered necessary for describing a pollution source. The relative concentration is designed to reconstruct dimensionless variables that have nothing to do with the mass released. Thus, the mass released can be separated from the unknown source parameter group.

A specific feature of the new variables is that their values have no direct relationship to the contaminant source mass. The reconstructed variables are the relationship coefficient (RC), the relative deviation of the relative concentration (RDRC) and the mean relative concentration (MRC). The RDRC and MRC are designed based on the relative concentration, which can be described by the following formula:

$${C}_{i}^{{\prime }}=\frac{{C}_{i}}{\sqrt{\frac{{{C}_{1}}^{2}+{{C}_{2}}^{2}{{+C}_{3}}^{2}+\cdots {{C}_{t}}^{2}}{t}}}$$

(10)

where subscript i is the time step; ${C}_{i}^{{\prime }}$ is the relative concentration at time step i; and ${C}_{t}$ is the observed concentration at time step t.

The three reconstructed variables are expressed as the following equations:

$$R_t=\frac{\sum_{i=1}^t(C_i^{ob}-\overline{C^{ob,t}})(C_i^s-\overline{C^{s,t}})}{\sqrt{\sum_{i=1}^t{(C_i^{ob}-\overline{C^{ob,t}})}^2}\sqrt{\sum_{i=1}^t{(C_i^s-\overline{C^{s,t}})}^2}}$$

(11a)

$${V}_{t}={\sum }_{i=1}^{t}{\left(\frac{{C}_{i}^{{\prime }ob}-{C}_{i}^{{\prime }s}}{{C}_{i}^{{\prime }ob}}\right)}^{2}$$

(11b)

$${A}_{t}=\frac{1}{n}{\sum }_{i=1}^{t}{C}_{i}^{{\prime }}$$

(11c)

where C is the contaminant concentration; superscripts s and ob are the simulated and observed concentrations, respectively; superscript ${\prime }$ is the relative concentration; ${C}_{i}^{ob}$ is the observed concentration at step i; $\overline{{C}^{ob,t}}$ is the mean value of the observed concentration from steps 1 to t; ${C}_{i}^{s}$ is the simulated concentration at step i; $\overline{{C}^{s,t}}$ is the mean value of the simulated concentration from steps 1 to t; ${C}_{i}^{{\prime }ob}$ and ${C}_{i}^{{\prime }s}$ are the relative concentrations observed and simulated at step i, respectively; ${R}_{t}$ is the relationship coefficient; ${V}_{t}$ is the relative variance of relative concentrations; and ${A}_{t}$ is the mean value of relative concentrations.

The three reconstructed variables are all dimensionless and not related to the mass released from the pollution source. Another common feature of these reconstructed variables is that the values of three variables at step t are related to the concentration sequences from observation steps 1 to t. ${R}_{t}$ represents the overall fit of the observed and simulated concentration trends. The closer the value of ${R}_{t}$ is to 1.0, the more similar the overall trends of the observed and simulated results. This variable is useful for obtaining a relatively appropriate combination of all parameters. ${V}_{t}$ represents the fit of the relative concentration observed and simulated at every step. Compared with ${R}_{t}$, ${V}_{t}$ reflects the role of every relative concentration equally regardless of the size of the relative concentration. The closer the value of ${V}_{t}$ is to 0, the smaller the deviation of relative concentrations observed and simulated from step 1 to t. ${A}_{t}$ is a simple representation of the state of the relative concentration process from step 1 to t. This parameter is not as detailed as ${V}_{t}$ and ${R}_{t}$, which describe the fit of the concentration process observed and simulated. ${A}_{t}$ can be considered a supplementary description, and it is important when the observation error is unstable and uncontrollable at each step. The effects of ${V}_{t}$ and ${A}_{t}$ result in increasingly meticulous optimization of all parameters, especially the dispersion coefficients.

By reconstructing the multiple variables mentioned above, there are only 5 unknown parameters to be identified in total, i.e., the source location (X, Y), the source release time (T), and the dispersion coefficients (D_L, D_T).

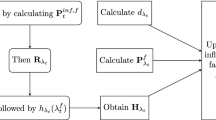
2.4 EnKF combined with the MOR method for source identification

Based on the MOR method, the calculation steps of the modified EnKF algorithm are as follows:

• (1) The ensemble of the parameter group decoupled from M is constructed.

  $$S={[X,Y,T,{D}_{L},{D}_{T}]}^{T}$$

  (12)

• (2) A prediction is made.

  $${\varphi }_{t}^{s}=\psi \left({C}_{0},{S}_{t-1}\right)$$

  (13)

  where $\psi$ is the composition operator, which can be written as ${\Gamma }\cdot {\Delta }$; ${\Delta }$ is the convection dispersion operator; ${\Gamma }$ is the derived variable transformation operator; and ${\varphi }_{t}^{s}$ is the vector of derived variables, which can be written as ${\varphi }_{t}={[{R}_{t},{V}_{t},{A}_{t}]}^{T}$. In contrast to ${C}_{t}^{s}$ in Eq. (4), ${\varphi }_{t}$ is related to the concentration process from time step 0 to t, which is calculated by substituting the parameters updated at time step t–1 into the convection dispersion model.

• (3) The equation is updated.

  $${S}_{t}^{a}={S}_{t}^{f}+{K}_{t}({\varphi }_{t}^{ob}-{\varphi }_{t}^{s}+{e}_{t})$$

  (14)

  where $e$ is the derived observation error vector, which is set to 0. K is rewritten as follows:

  $${K}_{t}={P}_{S,\varphi }{({P}_{\varphi ,\varphi }+{r}_{t})}^{-1}$$

  (15)

  where ${P}_{S,\varphi }$ is the cross-covariance matrix between the source parameters and the derived variables; ${P}_{\varphi ,\varphi }$ is the autocovariance of the derived variables; and ${r}_{t}$ is the covariance matrix of the error vector $e$. ${P}_{S,\varphi }$ and ${P}_{\varphi ,\varphi }$ are rewritten as follows:

  $$P_{S,\varphi}=\frac1{N_r-1}\sum\nolimits_{i=1}^{N_r}\left\{\left(S_t^f(i)-\overline{S_t^f(i)}\right){\;\left(\varphi_t^s(i)-\overline{\varphi_t^s(i)}\right)}^T\right\}$$

  (16)
  $$P_{\varphi,\varphi}=\frac1{N_r-1}\sum\nolimits_{i=1}^{N_r}\left\{\left(\varphi_t^s(i)-\overline{\varphi_t^s(i)}\right){\;\left(\varphi_t^s(i)-\overline{\varphi_t^s(i)}\right)}^T\right\}$$

  (17)

The last step of the modified EnKF is as follows, and it is rewritten as Eq. (9):

$${S}_{t}^{a}={S}_{t}^{f}+\alpha {K}_{t}({\varphi }_{t}^{ob}-{\varphi }_{t}^{s}+{e}_{t})$$

(18)

3 Synthetic example and flume experiment

Two investigations are considered in this paper. One investigation is a synthetic numerical example to test the rationality and feasibility of the method proposed above and to compare the effects of different derived observation variables on assimilation. The other investigation is an annular flume experiment in the laboratory to test the reliability of the method in practical applications.

3.1 Synthetic numerical example

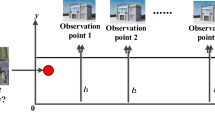
A single point source identification example is performed in which a certain amount of pollutant is released from the source at a certain time, and the unknown parameter group containing the source parameters and hydrological parameters needs to be identified. The numerical example is carried out in a two-dimensional square area of 500 m×500 m. In this system, a constant flow field is provided in advance, and all domain boundaries are open boundaries. Both the initial concentrations and diffusion fluxes of the boundaries are 0 (Jin et al. 2010). Pollutants are released at the source site and are ultimately transported from the domain through boundaries. No other pollutant enters this area. The initial concentration of released pollutants is calculated based on the pollutant mass and grid volume corresponding to the release location at the mesh. The mass of the outflow occurs through boundary meshes and is no longer related to the system. The known hydrological parameters are listed in Table 1. The three observation sites are arranged in the region with coordinates of (290, 260) m, (300, 255) m, and (330, 270) m. The locations of the observation sites and the pollutant release sites are shown in Fig. 1.

Table 1 Values of known hydrological parameters

Fig. 1

Spatial distributions of the pollution sources and observation points

3.2 Laboratory flume experiment

To verify the reliability of the method proposed for practical applications, a laboratory flume experiment for contaminant source identification is performed in the Hydraulics Laboratory at Hohai University. The water flow in the annular flume can be regulated online by the control system. By adjusting the inlet flow rate and the outlet gate angle, the water flow regime can be adjusted until our requirements are met. After performing multiple regulations, the water flow regime in the flume gradually stabilizes to a constant value. In this experiment, the inlet flow rate is 11 L/s, and the water depth is 0.295 m when the flow regime is steady. The flume has a constant width of 1 m. Therefore, the velocity is 0.037 m/s, which is identical to the result measured by the current meter. We dump the contaminant into the inlet of the annular flume instantaneously after the water flow regime stabilizes, and two monitoring points are arranged upstream of the outlet to monitor the concentration process. Considering the maturity of the monitoring technology and the decreased level of harm in the experimental process, we select chemical oxygen demand (COD) as the contaminant monitoring index. COD is a comprehensive indicator. In the flume, there is a stable background concentration of COD due to some organic pollutants. We consider this indicator and provide an initial concentration field in the model. Potassium hydrogen phthalate is a conventional COD reference substance (Andre et al. 2017; Kolb et al. 2017). The increase in COD is attributed to the release of potassium hydrogen phthalate, which is the real pollutant in this study. The transformational relationship between potassium hydrogen phthalate and COD is simple because 1500 mg/L of COD solution can be prepared from 1.2754 g of potassium hydrogen phthalate mixed in 1000 mL of pure water. Therefore, we can determine the concentration of potassium hydrogen phthalate by directly measuring the COD. In this study, 51 g of potassium hydrogen phthalate, which is used as a pollution source, is dissolved in water, and all the solution is released. Due to the narrow width of the flume, we choose a small digital COD sensor to reduce the impact of COD monitoring equipment on the characteristics of the water flow. The UV–COD sensor is placed in the centre of the cross section, and the vertical position of the sensor light source is 15 cm from the bottom of the flume, as shown in Fig. 2. The observation interval of the sensor is 5 s. The size of the annular flume and the spatial distributions of the contaminant release points and monitoring points are shown in Fig. 3.

Fig. 2

Image of the UV–COD sensor fixed in the flume for collecting COD concentration data

Fig. 3

Picture of the annular flume in the laboratory and the locations where pollutants are pumped into and observed

4 Results and discussion

4.1 Synthetic numerical example

In this example, the real values and the initial ranges of the unknown parameter groups to be identified, including X, Y, T, D_L, and D_T, are listed in Table 2. The observation sequence of pollutant concentrations (from t = 130 s to t = 430 s) are shown in Fig. 4. To represent the observation errors of the anti-interference performance, random errors of 0–10% are added to the observation data. The observation interval is 1 s, which is equal to the interval of the assimilation step.

Table 2 Real values and initial ranges of the parameters to be identified

Fig. 4

Time-series concentration data at the observation sites (with 0–10% random error)

The example consists of 7 scenarios to compare the effects of different reconstructed observations on assimilation for the purpose of identifying parameters, as detailed in Table 3. These 7 scenarios are all the same, except for the different derivatives involved in assimilation. The space of parameter realizations is set to 200, and the initial ensembles of the parameter group in the 7 scenarios are all consistent to eliminate the influence of the initial sampling on the assimilation results. The observed time-series concentration data need to be converted to ${R}_{t}$, ${V}_{t}$ and ${A}_{t}$ at each assimilation step, and the initial assimilation also needs to be based on the data sequences. Therefore, the 150th observation step (i.e., t = 280 s) is set as the initial assimilation step in this example.

Table 3 Comparison scenarios used in the example

Jing et al. (2023) compared the effect of parameter recognition by assimilating the correlation coefficient based on the observation sequence and by assimilating the absolute observed concentration; the scholars confirmed the superiority of the former process. When the parameter group to be identified contains only pollution source parameters (no hydrological parameters), the EnKF method, which is based on directly assimilating the observed concentration, has a very poor effect on source parameter identification. In the present paper, two hydrological parameters (D_L, D_T) are added to the parameter group for identification. It was more difficult to identify the parameter group by the traditional EnKF method proposed in Jing et al. (2023) than by the method proposed herein; therefore, the scenario of assimilating the traditional state variable (the observed concentrations) does not need to be considered in the synthetic comparison. For the 7 scenarios of the synthetic numerical example, the contaminant source parameters and hydrological parameters are identified by assimilating different derived observation variables. The boxplots clearly indicate the changes in the parameter group ensembles in each scenario, and we use these plots to compare the results and analyse the influences of the derived variables on assimilation. The assimilation step of each scenario starts from the 150th observation step and ends with the 230th observation step.

Figures 5, 6 and 7 show the changes in the parameter group ensembles of scenarios V1, V2, and V3 in the assimilation process, respectively. The top and bottom of the blue boxes in the boxplot represent the upper and lower quartiles of the ensembles, respectively, while the red horizontal line represents the median value of the ensembles. By comparing the results of V1, V2 and V3, we find that the identification performance of ${A}_{t}$ is better than those of ${R}_{t}$ and ${V}_{t}$ in terms of a single derived observation variable during assimilation. Although the identification results of V3 are highly accurate, the ensembles of parameters are still prone to collapse even if the damping coefficient is added in the assimilation process. This phenomenon may be related to the characteristics of the derived variable. By taking the mean values of the parameter ensembles of V1, V2 and V3 at the 230th observation step as the inputs of the convection–dispersion model, the relative concentration series of the three observation sites during the observation period are calculated, as shown in Fig. 13. The results show that the relative concentration process of V2 exhibits the largest deviation from the observation. There is a time phase difference at the peak between V2 and the observation, although the overall trends are similar. The relative concentration of V1 is the second highest behind that of V2. Similar to scenario V2, there is still a time-phase difference at the peak between the relative concentration and the observation of V1. Moreover, the concentrations during the increasing concentration stage at the three observation sites are generally higher than the overall observed values. Undoubtedly, the results of scenario V3 are closest to the observation process, but due to the identification error of the transverse dispersion coefficient D_T, the concentration values at observation sites 1 and 2 are significantly lower than those observed during the increasing concentration stage. Therefore, if the parameter ensembles after assimilation is complete are used to predict the concentration characteristics at a point far downstream from the pollution source, then the deviation between the predicted concentration and the actual concentration will be more obvious, thereby interfering with the pollution treatment that we select.

Fig. 5

Changes in the ensemble realizations of the parameter group to be identified from the 150th observation time step to the 230th observation time step in scenario V1

Fig. 6

Changes in the ensemble realizations of the parameter group to be identified from the 150th observation time step to the 230th observation time step in scenario V2

Fig. 7

Changes in the ensemble realizations of the parameter group to be identified from the 150th observation time step to the 230th observation time step in scenario V3

Given the unsatisfactory results of parameter identification when only a single derived variable is involved in assimilation, we utilize two derived observation variables for assimilation to strengthen the constraints on the assimilation process and evaluate the identification effect. Figures 8, 9 and 10 show the identification results of the parameter groups in scenarios V4, V5 and V6, respectively. Overall, the identification results in these three scenarios are better than those in scenarios with a single derived observation variable involved in assimilation (i.e., V1, V2, and V3). Comparing V4, V5 and V6 in terms of the mean values of the parameter ensembles, the assimilation effect of V4 is the poorest, that of V6 is moderate, and that of V5 is the best. Among these scenarios, the identification of parameter T of V5 is more accurate than that of V6, but the D_T of V5 is slightly less accurate than that of V6. Compared with scenario V3, in which the ensembles of the parameter group are prone to premature collapse during assimilation, the conditions of premature collapse of the ensembles in scenarios V5 and V6 are improved after involving other variables in assimilation. Based on Fig. 13, in scenario V4 with low-precision identification, the simulated relative concentration at observation point 3 fits well with the observation, while the simulated series at observation points 1 and 2 both deviate from the observed series, which is similar to the results in scenario V5. Notably, although the results in V5 are slightly better than those in V6 in terms of the accuracy of identifying parameters, the simulated series of V6 are more consistent with the observed series at the three observation sites. Thus, can both be achieved? While the identification of parameters is ensured to be accurate, the simulated relative concentration series are closer to the observed series. In fact, this requirement can be satisfied if the identification accuracy of the transverse dispersion coefficient D_T is improved on the results of V5.

Fig. 8

Changes in the ensemble realizations of the parameter group to be identified from the 150th observation time step to the 230th observation time step in scenario V4

Fig. 9

Changes in the ensemble realizations of the parameter group to be identified from the 150th observation time step to the 230th observation time step in scenario V5

Fig. 10

Changes in the ensemble realizations of the parameter group to be identified from the 150th observation time step to the 230th observation time step in scenario V6

Considering that the accuracies of identifying parameter groups and subsequently simulating concentration series in cases involving the assimilation of two derived state variables are generally better than those involving the assimilation of a single derived state variable, we test the parameter identification performance by simultaneously assimilating three derived variables (i.e., scenario V7). Figure 11 shows the changes in the ensembles of the parameter group in V7. The mean values of the ensembles of the parameter group to be identified are very close to the true values. At the 230th observation time step, the relative error of the transverse dispersion coefficient D_T is slightly larger than that of the other parameters, and the change in the ensemble of this parameter is slower than that of the other parameters. This phenomenon may result from the system itself changing its D_T. This parameter has little influence on the values of the state variables involved in assimilation. Compared with the results of V5, the identification accuracy of the parameter D_T is improved in V7. The identification accuracy of the parameter T in V7 is more accurate than that in V6. According to the results in Fig. 13, the simulated relative concentration series of V6 and V7 coincide with the observed concentration series at the three observation points. Therefore, the effects of identifying parameters involving two derived state variables in assimilation are similar to those involving three derived state variables. To further explore the differences between the two scenarios, we perform a separate comparison between V6 and V7. We select the 50th observation step as the initial assimilation step for the two scenarios, and the other conditions are the same as before. The changes in the ensembles of V6 and V7 are presented in Figs. 15 and 16, respectively. When the concentration sequence of the initial calculation step is shortened, the assimilation of parameters is affected to a certain extent. In the new V6, the identification of the pollution source location Y and the transverse dispersion coefficient D_T largely deviate from the real values compared with those in the previous V6. In contrast, the results of identifying parameters in the new V7 are even more accurate than those in the previous V7, especially for the parameter D_T. However, the stabilities of ensembles in the assimilation process are poorer than those in the previous V7, and there is a large fluctuation in the mean values of ensembles in assimilation. This fluctuation is related to the length of the concentration sequence involved in assimilation. This comparison between V6 and V7 shows that the accuracy and stability of identifying the parameter group are improved when the three derived state variables are involved in assimilation simultaneously.

Fig. 11

Changes in the ensemble realizations of the parameter group to be identified from the 150th observation time step to the 230th observation time step in scenario V7

Figure 12 shows the changes in the derived state variables involved in the three observation points and the calculation steps in scenarios V1–V7. It is evident that when ${R}_{t}$ is involved in assimilation, there is a bias in the results of parameter identification (e.g., V1 and V4). However, the final assimilated values of ${R}_{t}$ are very close to the real value of 1.0, indicating that satisfactory results of parameter identification cannot be obtained only through assimilating the derived variable ${R}_{t}$. The same is true for ${V}_{t}$ and ${A}_{t}$, but the result of identifying parameters by assimilating ${A}_{t}$ is slightly better than that by assimilating ${R}_{t}$ or ${V}_{t}$. In the latter cases, the identification process cannot accurately determine the transverse dispersion coefficient. Based on the results shown in Figs. 12 and 13, the characteristics of these three derived state variables are analysed. The derivation of ${R}_{t}$ is based on assimilating the overall trend of the concentration sequences at the observation points. Even if there is a phase deviation between the simulated concentration sequence and the observed sequence, the value of ${R}_{t}$ might still be very close to 1. This value contributes to the identification of the overall combination of parameter groups in assimilation, but it cannot accurately identify all parameters. Only when the number of observation points is increased, the number of identification parameters is reduced, or the system is increasingly nonlinear (such as unsteady flow) may the effect of parameter identification be improved. The derivation of ${A}_{t}$ is based on consideration of the overall assimilation of the relative concentration sequence. Compared with ${R}_{t}$, ${A}_{t}$ can more accurately capture the characteristics of the entry and departure of the contaminant plume. Specifically, the changes in the contaminant concentration values at the observation points from absence to existence and from existence to absence are observed. Although the derived variable can play the role of the anchoring dispersion coefficient to a certain extent, when the assimilation deviation of the state variable is small, the corresponding simulated concentration sequence may greatly deviate from the observation sequence. This phenomenon is well reflected in V3 in Fig. 13. Like ${R}_{t}$ and ${A}_{t}$, ${V}_{t}$ carries out overall assimilation for the relative concentration sequence; compared with ${A}_{t}$, it is more focused on the deviation of each concentration value in the concentration sequence. Regardless of the concentration magnitude, all concentrations are considered equally, which can compensate for the problems existing in the assimilation of ${A}_{t}$ to some extent. However, when there is an error in the observed concentration sequence, only assimilating this derived state variable can easily cause distortion in the identification of the parameter group. As shown in the middle row of Fig. 12, a comparison of the assimilation results of the scenarios involving ${V}_{t}$ indicates that there is a significant gap between the identification results of assimilating the derived variable in scenario V2 and the combined derived variables determined in other scenarios. Therefore, it is obvious that when assimilating these derivatives alone, it is impossible to avoid their own shortcomings, but these derivatives contribute to parameter identification during the assimilation process. In the present paper, the three derived variables are used for combined assimilation. This combination can compensate for the deficiencies of other derivatives while taking advantage of the characteristics of each; thus, the assimilation process tends to be relatively stable, and the identification accuracy of each parameter increases, as shown in Figs. 14 and 15.

Fig. 12

Changes in the values of the derived variables in scenarios V1–V7 from the 150th observation time step to the 230th observation time step

Fig. 13

Relative concentration sequences of scenarios V1–V7 simulated by the parameters identified at the 230th observation time step

Fig. 14

Changes in the ensemble realizations of the parameter group to be identified from the 150th observation time step to the 230th observation time step in scenario V6

Fig. 15

Changes in the ensemble realizations of the parameter group to be identified from the 50th observation time step to the 230th observation time step in scenario V7

In general, this experiment proves that the assimilation of multidimensional derived observation variables proposed in this paper has high stability and accuracy in identifying pollution source parameters, and it can contribute to the identification of unknown hydrological parameters; in particular, the identification of dispersion coefficients in the mainstream direction is relatively reliable.

4.2 Laboratory flume experiment

Based on the comparison results of the above synthetic numerical example, we combine the assimilation of derived observation variables with the simultaneous identification of the source and hydrological parameters in the flume experiment and test the performance of this method in practice. In this example, except for the advection diffusion model, which always follows the principle of conservation of mass, the mass in the flume experiment is always conserved. The increase in COD in the flume is attributed to potassium hydrogen phthalate. The stable chemical characteristics of the flume make it a very suitable reference material for analysis. In the flume experiment, the time of the first observation record is 12 min after pollutant release. The continuous observation time is 9 min. Therefore, the duration of this experiment is very short, at only 21 min. The degradation rate of COD is assumed to be 0.18 d⁻¹ (Huang et al. 2017). Even if potassium hydrogen phthalate is degraded in this experiment, the mass loss can be ignored during this period.

The parameter group to be identified includes two parts: contaminant source parameters and dispersion coefficients. The real values and initial ranges of the parameters to be identified are listed in Table 4 (for the coordinates, refer to Fig. 17). The contaminant release time is set to t = 540 s since the first record of the contaminant in the observation sequence occurs 9 min after the contaminant is removed. The time difference between the real contaminant release time and the first observation in the observed concentration sequence is 540 s. The temporal processes of concentration observation at the two observation points are shown in Fig. 16.

Fig. 16

Time-series concentration data at the observation sites

Table 4 Real values and initial ranges of the parameter groups to be identified

The pollution source parameters in this experiment are the pollution source locations X and Y and the release time T. However, unlike in the previous synthetic example, the parameter Y does not need to be analysed. Considering that the flume is equal in width and that the width is much smaller than the length of the flume, the impact of the dumping causes the pollutants to quickly and uniformly disperse in the transverse direction when transported in the flume. Therefore, the pollution source parameter Y has a negligible influence on the concentrations at the observation points. For the hydrological dispersion coefficients D_L and D_T related to the flow rate, if the water flow is not uniform or constant, the hydrological dispersion coefficients in different areas are not the same. In this annular flume, the water flow in the long straight section on each side of the flume can be considered uniform and constant, and the length of the bending section is short. Therefore, the dispersion coefficients D_L and D_T are considered constants. The reference values of D_L and D_T are 0.005 and 0.002, respectively, in Eq. (2) according to a calibration. The real values and initial ranges of the parameters to be identified for this experimental example are listed in Table 4. The number of realizations is set to 30.

The initial assimilation step is set at the 85th observation step in the observation sequence. Figure 17 clearly shows the distributions of the source location ensembles at observation steps 85, 90, 100, and 110. Although only 30 simulations are contained in the ensemble, the efficiency and accuracy of identifying the pollution source location are still very high. After the 5th assimilation step, the distribution of the realizations of the source position is concentrated near the true location. At the 25th assimilation step, all ensemble realizations of the source location are very close to the position where the pollutants are input. The changes in the mean and variance of the pollution source (X_S, T_S) and the dispersion coefficients (D_L, D_T) in the assimilation process are shown in Fig. 18. The ensembles of the pollution source location Xs and the release time Ts are roughly stable when assimilation is carried out to the 100th observation step. Furthermore, the means of the ensembles are close to the true value, and the variances are very close to 0. However, the assimilation of the dispersion coefficients is not stable because the ensemble variances decrease gradually during this process. The mean values of the ensemble fluctuate greatly. Moreover, the variance of the ensemble of D_T is much greater than that of D_L, indicating that the range of the ensemble of D_T is large and that the values of the realizations are not yet centralized. According to the anisotropy of pollution dispersion, the value of the longitudinal dispersion coefficient D_L should be greater than that of the transverse dispersion coefficient D_T. However, as shown in Fig. 18, the mean value of the ensemble of D_L at the 110th observation step is almost equal to that of D_T, demonstrating that the identified transverse dispersion coefficients exhibit certain deviations. This issue is reflected to some extent in Fig. 19. The relative concentration sequence simulated by the identified parameter group has a high overall fitting degree; specifically, the trend of the sequence and the peak time are consistent with the observations. However, due to the large deviation of the identified transverse dispersion coefficient, there are certain differences in the increase in the COD concentration sequence at observation point 1 and the decrease in the sequence at observation point 2 compared with the observations. The peak value of the observation is larger than that of the simulation, indicating that the fitting degree of the concentration sequence is not very high. The reasons for the differences in parameter identification in this example may have arisen due to the following three reasons. First, the material convection–dispersion model we adopted is based on the depth-integrated theory. The vertical-averaged effect may not be achieved in a short period after pouring the pollutant. The vertical positions of the monitoring sensors affect the concentration sequences of the observation points. Second, due to the small width of the flume, soluble pollutants easily mix in the transverse direction during transport, which allows for the identification of the transverse position of the pollution source and the distortion of the transverse dispersion coefficient. Third, when using a plastic bucket to remove pollutants, it is impossible to ensure that all pollutants enter the flume at the same coordinates simultaneously and that the actual pollution source is a pollution plume near the ideal source location. These characteristics affect the simulation of contaminant concentrations.

Fig. 17

Distribution of ensemble realizations of the source at the 85th, 90th, 100th, and 110th observation time steps

Fig. 18

Changes in the mean and variance values of the parameter ensembles to be identified via assimilation

Fig. 19

Comparison of relative concentration sequences simulated and observed at the two observation sites (the simulated sequences are calculated by the parameters identified)

Furthermore, an extra comparative test is used to verify the performance of the method in this paper (V7) and the method proposed in Jing et al. 2023 (V1) to identify parameters synthetically for incomplete observation sequences. The observation data from the 41st to 80th time steps of the two observation points, as shown in Fig. 19, are removed artificially to construct the scenario with data loss, and the remaining data sequences are used as incomplete assimilation data. In the test, the initial calculation step is set as the 81st observation time step.

From Fig. 20, the results of the MOR method recommended by this paper are obviously better than those of the correlation coefficient assimilation method proposed by Jing et al. (2023). Although the recognition accuracy of the D_L parameter is not ideal, that of the other parameters is satisfactory in scenario V7. Combined with the results of Fig. 18, the recognition of dispersion coefficients seems to be influenced more than the pollution source according to the observation data. According to the prediction results of the relative concentration in Fig. 21, although the recognition accuracies of parameters in V1 are poor, the predicted trends for the relative concentration sequences of the two observation points are similar to those of the observation sequences, and the correlation coefficients at these two observation points reach 0.91 and 0.95. This finding indicates that with few observation points, it is very difficult to identify the parameter group accurately without effective reconstruction of the original observation data because the optimal combined solution is not unique when only the correlation coefficient is involved in assimilation. The MOR method presented in this paper can solve this problem when there are few and incomplete observation data for identifying high-dimensional parameter groups. Notably, in certain cases, the analytical solution of pollutant transport (Liang et al. 2010; Liao et al. 2021) can be integrated with the MOR method to replace the complex difference calculation for Eq. (1), which can greatly improve the efficiency of source identification and treat pollution from sources relatively early.

Fig. 20

Changes in the mean and variance values of the parameter ensembles to be identified via assimilation by V1 and V7

Fig. 21

Comparison of relative concentration sequences simulated by V1 and V7 and the observed incomplete consequences at the two observation sites (the simulated sequences are calculated by the parameters identified)

5 Conclusions

In this paper, the MOR method based on assimilating multidimensional variables derived from observations is proposed to identify pollution sources and hydrological parameters simultaneously. This method is an extension of the ensemble Kalman filter algorithm, which adopts the variables reconstructed from the observation data as the state variables to participate in assimilation instead of the original observation data. The following conclusions can be drawn from the results:

• (1) Due to the characteristics of the reconstructed observation variables, the pollution mass released can be effectively decoupled from the parameter group to be identified, which reduces the dimension of the unknown parameter group and improves the efficiency and stability of assimilation. This method can be used to comprehensively identify pollution sources and 2D dispersion coefficients.

• (2) The reliability and accuracy of the method in identifying parameters are confirmed by a numerical synthesis example including 7 comparison scenarios, and the characteristics of these derived variables are analysed and evaluated. The multidimensional state variables involved in assimilation can compensate for the pseudoidentification of the single state variable in the unknown parameter group. Specifically, the error of the assimilated state is already small, but the parameter group in this system still deviates greatly from the real values. Therefore, the multidimensional variables derived from observations in assimilation can balance the defects of each derivative and improve the performance of the algorithm.

• (3) Based on the results of the numerical synthesis example, a laboratory experiment is performed to identify parameters that use COD as the pollutant by monitoring these characteristics in an annular flume. Through the data observed at the two observation sites, it is successfully proven that the method can be fully applied to simultaneously identify the pollution source and dispersion coefficients in real-world scenarios, even when there are uncontrollable deviations in the experiment. Notably, a test is designed to verify the performance of this method for identifying parameters when the observation sequences are incomplete. This finding proves that this method can still work excellently despite partial data loss.

In the present paper, the flow patterns of the two examples applied by this method are constant, and the nonlinearity levels of the two systems are not high. These phenomena increase the difficulty of parameter identification to a certain extent. In future studies, we will continue to develop the EnKF method by integrating other methods (e.g., artificial neural networks and differential evolution) to further improve the accuracy of identification and increase the number of assimilation applications.