1 Introduction

Natural channel flow may be laminar, turbulent, or mixed depending on the flow and channel characteristics. For flow characterization, velocity distribution studies play an essential role in open channel hydrodynamics and aid the determination of several important quantities, such as flow rate, bridge pier scouring, channel bed erosion, and sediment concentration (Singh 2016). The laminar flow is easily characterized; however, in a natural scenario, the turbulent flow predominates, which tends the velocity to vary in multiple directions. Numerous techniques are discussed in the literature for quantifying the open channel flow’s velocity distribution, including the renowned classical laws (Power and Logarithmic laws) or the probabilistic methods based on the famous Information entropy (Shannon 1948). Briefing the classical laws, they were initially devised to study smooth pipe flows (Blasius 1913). Later, the classical laws advanced to examine open-channel hydraulics (Vanoni 1941; Rouse 1959; Sarma et al. 1983) but only apply to the wide-open channel flows in which the velocity increases monotonically in the vertical direction toward the free surface owing to the absence of the secondary currents.

Additionally, the researchers presented many theoretical single equation models to study the open channel flows. Guo (1998) presented the Modified log wake (MLW) law that contained a correction factor for the free-surface boundary. Later, Yang et al. (2004) carried the analysis of the RANS equations and proposed the dip-modified log (DML) law. Based on the modifications in the DML law, Absi (2011) introduced the full dip-modified log wake (fDMLW) law. Further, due to the inherited complex numerical calculation associated with Absi’s law, the Total dip-modified log wake (TDMLW) law was developed (Kundu and Ghoshal 2012). However, the traditional laws assumed the velocity as a deterministic flow feature without any element of uncertainty and have restricted precision because of the straightforward applicability as they fail to accurately estimate the velocity close to the boundary regions subjected to the turbulence effects. Summing up, the classical laws catered well to the one-dimensional flow situations.

However, the naturally occurring turbulent flows need a thorough study of the flow hydrodynamics as the presence of the secondary currents increases the flow complexity (through the momentum transport), which tends the maximum value of velocity to happen below the free-surface. This was termed as the dip phenomenon, which has intrigued academics for a long time (Stearns 1883). This way, the velocity distribution varies in vertical and horizontal (transverse) directions, i.e., two-dimensionally. The information about the exact dip-position in natural flows is critical as it characterizes the velocity profile shapes (Chen and Chiu 2004; Bonakdari and Moazamnia 2015; Kundu 2017; Termini and Moramarco 2018). Hence, the natural flows were studied by applying the probability-based methods involving the use of the Information entropy concept, which facilitates the creation of an effective approach for studying the complicated two-dimensional flow behaviors in addition to the one-dimensional analysis (Termini and Moramarco 2017, 2020; Mirauda et al. 2018). Henceforth, the entropy concept acted as a basis and link between the deterministic and probabilistic worlds. The entropy concept's fundamental is quantifying the system's disorder or uncertainty. Extensive research has been conducted for a long time employing experimental or deterministic approaches to investigate the open channel flow (Singh et al. 1986; Singh 1997, 2010, 2011). In contrast, the velocity profile characterization based on the entropy concept is limited to a few entropy types (such as Shannon, Tsallis, Renyi, and Fractional entropies), leaving much room for expansion. Using Kapur entropy, this paper examines the open channel flow velocity distribution.

At first, Chiu (1988) introduced the idea of entropy application to water resources by assuming the velocity as a random variable due to the inherited uncertainties alongside formulating a new \(\upxi\)-\(\upeta\) coordinate system comprising of the orthogonal curvilinear curves simulating the velocity isovels and developed entropy-based 2-D velocity distribution equation (Chiu and Lin 1983; Chiu and Chiou 1986; Chiu and Murray 1992). Further, the connection between the conventional x–y system and \(\upxi\)-\(\upeta\) coordinate system was established (Chiu 1987, 1989; Chiu and Tung 2002). A new entropy parameter (M) to characterize the velocity distribution was introduced (Chiu 1989) that was able to link the maximum and mean velocities facilitating direct flow discharge computation (Chiu and Said 1995). Advancing the research, the energy and momentum coefficients were revisited in terms of entropy parameter M (Chiu 1991). Recently, the Shannon entropy approach has been successfully employed to establish a link between the free surface velocity and cross-sectional mean velocity and thereby quantifying the discharge quickly (Moramarco et al. 2017; Fulton et al. 2020; Bahmanpouri et al. 2022a, b). In line, the subsequent development was the employment of the non-extensive Tsallis entropy (Tsallis 1988), and thereby the velocity and sediment distribution equations were derived (Luo and Singh 2011; Singh and Luo 2011; Cui and Singh 2014; Singh 2016). A new dimensionless entropy parameter G was also defined in Tsallis’ case to fulfill the same purpose. In order to reduce the parameter estimation related to Chiu’s curvilinear coordinate system, a new cumulative distribution function (CDF) was developed and experimented with the Shannon entropy to derive the 2-D velocity model (Marini et al. 2011). The same was also employed for deriving the Tsallis entropy-based velocity model (Cui and Singh 2013).

Further, the Renyi entropy (Renyi 1961) was explored to study open channel hydrodynamics, and the relations like one- and two-dimensional velocity distribution, suspended sediment, and shear stress distribution models were derived (Kumbhakar and Ghoshal 2016, 2017; Ghoshal et al. 2018, 2019; Khozani and Bonakdari 2018). Similarly, the dimensionless entropy parameter R was defined in Renyi’s case. Interestingly, the Renyi entropy model provided better results than the earlier Shannon and Tsallis entropy-based models. Further advancing the application of the entropy concept, fractional entropy (Wang 2003) was recently employed to examine the open channel flow (Ahamed and Kundu 2022), which thoroughly considered the dip phenomenon in contrast to all the previous velocity models. However, the fractional entropy-based model rendered improved results compared to others but ended up in a complex and tedious two different velocity distribution equations applicable to the two zones separated by the location of the maximum velocity below the water surface. Secondly, the main drawback is the extensive calculations of several parameters to characterize the whole flow depth completely. Table 1 summarizes the above-discussed entropy-based velocity equations for the different entropies.

Table 1 Expressions of the considered Entropy-based velocity distributions
Full size table

In literature, many distinct entropy types and the generalized forms of the earlier versions exist, and a brief review is reported in Singh (2019). Among them, the Kapur entropy (Kapur 1986) of the fourth kind is being utilized in the present study to examine the open channel flow hydrodynamics. Similar to Tsallis and Renyi entropy, Kapur entropy also hosts an additional parameter (entropy index, \(\mathrm{\alpha }\)) whose value influences the probability distribution type. To date, the Kapur entropy’s potential remains unexplored in the water resources domain though it has demonstrated decent results in image multi-threshold segmentation (Kapur et al. 1985; Manic et al. 2016; Zhao et al. 2021). To further clarify, this study applies Kapur entropy to the water resources field for the first time and further derives the Kapur entropy-based model for characterizing the open channel flow. Finally, the velocity model is validated based on the laboratory and field velocity observations and compared with the four existing entropy-based models.

2 Theoretical framework

The fundamental nature of the methodology for the entropy theory-based derivation of the velocity distribution in the open channel flows remains the same as employed in the existing velocity models. The main difference arises in entropy type and, thereby, forthcoming results. The framework for the proposed derivation is as follows: (1) Kapur entropy definition, (2) specifying the required constraints, (3) POME-based entropy maximization, (4) derive velocity probability distribution and Lagrange multipliers, (5) velocity CDF hypothesis, (6) derivation of the desired velocity distribution and involved parameters. The said procedure is discussed in detail and implemented in the later sections.

2.1 Kapur (4th order) entropy

Kapur defined several families of entropy measures with and without parameter involvement (Kapur 1986). Kapur’s entropy (\({H}_{\alpha }\)) of the fourth kind, having one parameter and applicable to the complete probability law, is used in the present study.

$${H}_{\alpha }\left({p}_{1},{p}_{2},{p}_{3}\dots {p}_{n}\right)=1-{\left(\sum_{i=1}^{n}{p}_{i}^{\alpha }\right)}^{\frac{1}{\alpha -1}}$$
(1)

where \(\alpha\) is Kapur entropy index (subjected to the \(\alpha >0\)); n is the total number of outcomes that the random variable can have; \({p}_{i}\)’s are the probability values associated with the random variable for each \(i=1, 2, 3\dots , n\). Considering the cross-sectional time-averaged velocity (u) as a random variable, Eq. (1) can be written in a continuous manner given by Eq. (2).

$${H}_{\alpha }\left(u\right)=1-{\left({\int }_{0}^{{u}_{max}}{\left[f\left(u\right)\right]}^{\alpha }du\right)}^{\frac{1}{\alpha -1}}$$
(2)

where \(f\left(u\right)\) is the probability density function (PDF) of the random variable (u). The velocity is bounded, having the lower value as zero and the upper value as the maximum velocity (\({u}_{max}\)), which may be at the water's surface or some depth below.

2.2 Specification of constraints

The meaningful outcome of the entropy concept through utilizing the principle of maximum entropy (POME) is based on fulfilling the particular constraints for which the information on flow characteristics must be gathered via observations. In natural channels, the flow must adhere to mass, momentum, and energy conservation rules, which can be utilized to design specific constraints.

$${C}_{1}\to {\int }_{0}^{{u}_{max}}f\left(u\right)du=1$$
(3)
$${C}_{2}\to {\int }_{0}^{{u}_{max}}uf\left(u\right)du={u}_{mean}$$
(4)
$${C}_{3}\to {\int }_{0}^{{u}_{max}}{u}^{2}f\left(u\right)du={\beta u}_{mean}^{2}$$
(5)
$${C}_{4}\to {\int }_{0}^{{u}_{max}}{u}^{3}f\left(u\right)du={\gamma u}_{mean}^{3}$$
(6)

where \(\beta\) and \(\gamma\) are the momentum and energy distribution coefficients, respectively. Here, the constraint (\({C}_{2}\)) for the PDF of velocity, \(f\left(u\right)\) is defined with \({u}_{mean}\) as the mean value of \(u,\) which equals the \(Q/A\) (Q is the flow rate in m3/s, and A is the channel cross-sectional area in m2). The constraint (\({C}_{2}\)) ensures the uniform distribution (mass conservation) of the random variable (\(u\)), i.e., the equality (\({u}_{mean}=Q/A\)) holds. Constraints \({C}_{3}\) and \({C}_{4}\) involving the \(\beta\) and \(\gamma\) are excluded in the present study due to their minimal effect. Mass conservation is adequate for obtaining the velocity distribution, as demonstrated by Barbé et al. (1991). Hence, only the first two constraints, i.e., the total probability law (\({C}_{1}\)) and conservation of mass constraint (\({C}_{2}\)) are applied to entropy maximization in this study.

2.3 Entropy maximization

Theoretically, the maximum entropy value can be obtained if the uniform probability distribution exists within the bounds and, due to constraints, uniformity is frequently not possible. However, entropy maximization creates a way to approach uniformity maximally while fulfilling the requirements laid in the form of constraints. Hence, to achieve the required velocity probability density function with the least amount of bias, the considered \({H}_{\alpha }\left(u\right)\) (Eq. 2) is maximized subjected to the constraints (Eqs. 3, 4) in agreement with the maximum entropy principle (Jaynes 1957). The required \(f\left(u\right)\) is obtained by utilizing the Lagrange multipliers method, and the Lagrangian function (\(\mathcal{L}\)) is constructed as follows.

$$\mathcal{L}=1-{\left({\int }_{0}^{{u}_{max}}{\left[f\left(u\right)\right]}^{\alpha }du\right)}^{\frac{1}{\alpha -1}}-{\lambda }_{o}\left\{{\int }_{0}^{{u}_{max}}f\left(u\right)du-1\right\}+{\lambda }_{1}\left\{{\int }_{0}^{{u}_{max}}uf\left(u\right)du-{u}_{mean}\right\}$$
(7)

Equation (7) can be expressed without the integration sign as follows.

$$\mathcal{L}=1-{\left({f}^{\alpha }\left(u\right)\right)}^{1/\alpha -1}+{\lambda }_{o}f\left(u\right)+{\lambda }_{1}uf\left(u\right)$$
(8)

where \({\lambda }_{o}\) and \({\lambda }_{1}\) are the Lagrange’s multipliers to be evaluated using the respective constraints (Eqs. 3, 4). Further, the Calculus of variation’s Euler–Lagrange formula was used to determine the desired \(f\left(u\right)\) having the least bias, i.e., it maximizes entropy subject to predefined constraints. In this procedure, the \(f\left(u\right)\) is considered to be dependent on the independent variable \(\left(u\right)\) and the Euler–Lagrange formula is restructured as follows.

$$\frac{\partial \mathcal{L}}{\partial f}-\frac{d}{du}\left(\frac{\partial \mathcal{L}}{{\partial f}^{^{\prime}}}\right)=0$$
(9)

Evident from the Eq. (8), the \(\mathcal{L}\) is independent of the derivative \(\left({f}^{^{\prime}}\right)\). Hence, the Eq. (9) becomes,

$$\frac{\partial \mathcal{L}}{\partial f}=0$$
(10)

Solution of the Eq. (10) results in,

$${-\left(\frac{\alpha }{\alpha -1}\right)\left(f\right)}^{\frac{1}{\alpha -1}}+{\lambda }_{o}+{\lambda }_{1}u=0$$
(11)

2.4 Probability distribution and Lagrange multipliers

Addressing the main objective of the study, the least-biased velocity PDF, \(f\left(u\right)\) is derived by employing the POME, which resulted in an exponential-type relation. The derived \(f\left(u\right)\) in terms of the \({\lambda }_{o}\) and \({\lambda }_{1}\) represents the velocity probability distribution satisfying the predefined constraints.

$$f\left(u\right)={\left[\frac{\alpha -1}{\alpha }\left({\lambda }_{o}+{\lambda }_{1}u\right)\right]}^{\alpha -1}$$
(12)

Now, the derived \(f\left(u\right)\) along with the constraints (Eqs. 3, 4), was utilized to solve for the Lagrange multipliers. Solving for the \({\lambda }_{o}\) and \({\lambda }_{1}\) starts with the substitution of the Eq. (12) into the Eqs. (3) and (4), and integrating both equations within the defined limits results in two implicit relations given by the Eqs. (13) and (14), respectively.

$${\alpha \lambda }_{1}{\left(\frac{\alpha }{\alpha -1}\right)}^{\alpha -1}={\left({\lambda }_{o}+{\lambda }_{1}{u}_{max}\right)}^{\alpha }-{\left({\lambda }_{o}\right)}^{\alpha }$$
(13)
$$\frac{1}{{\lambda }_{1}^{2}\left(\alpha \right)\left(\alpha +1\right)}\left\{{\left({\lambda }_{o}+{\lambda }_{1}{u}_{max}\right)}^{\alpha }\cdot \left({\alpha \lambda }_{1}{u}_{max}-{\lambda }_{o}\right)+{\left({\lambda }_{o}\right)}^{\alpha +1}\right\}={u}_{mean}$$
(14)

The solution of the resulting non-linear system renders the expressions of the \({\lambda }_{o}\) and \({\lambda }_{1}\) given the values of the \({u}_{mean}\), \({u}_{max}\) and parameter \(\alpha\).

2.5 Influence of parameter (\(\boldsymbol{\alpha }\)) on PDF and velocity profile

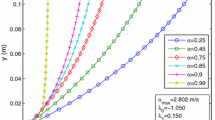
Evident from the Eq. (12), the Kapur entropy-based velocity PDF depends on the Kapur entropy index \(\left(\alpha \right)\). The PDF dependence for different \(\alpha\) values is shown in Fig. 1. Run 25 of the experimental velocity data measured in a rectangular laboratory flume having dimensions as 30.9 cm (width), 45 cm (depth), and 7.5 m (length) (Singh 2019, personal communication) with flow details given in Table 2, was used to determine the Lagrange multipliers.

Fig. 1
figure 1

Variation of the Kapur entropy-based velocity PDF (Eq. 12) for different entropy index \(\left(\alpha \right)\) values for the Run 25 for clear water flow (Singh 2019)

Full size image
Table 2 Flow Characteristics of considered velocity datasets
Full size table

Figure 1 demonstrates the usual trend, i.e., for the given velocity data, the velocity PDF rises with increasing velocity. Initially, the velocity gradient is comparatively lower for the higher \(\alpha\) values whereas, the situation is vice versa as the velocity increases gradually. Further, to narrow down the value of \(\alpha\), the field and experimental velocity data were utilized. Two field datasets, namely, P. Nuovo gauging station (June 3, 1997 flood event) of Tiber River (Luo and Singh 2011) and Iran (Run 1) River data (Luo 2009). Also, run 25 of the experimental velocity dataset (Singh 2019, personal communication) was considered. The relevant flow characteristics of the selected datasets are listed in Table 2. From Fig. 4, it can be inferred that the derived velocity distribution depicts the usual monotonic increasing behavior of the velocity with depth being measured from the channel bed. Further, the velocity distribution can be seen as sensitive to the changes in \(\alpha\) values. Figure 2 (Tiber River data Luo and Singh 2011) and Fig. 4 (Singh 2019, personal communication) are based on the velocity observations, which demonstrates the dip-phenomena whereas, the Fig. 3 (Iran Run 1 Luo 2009) was based on the velocity data from a wide channel cross-section. Further, to fix a single value of the entropy index for the whole study, the Mean, \(\mu (E)\) and Standard deviation, \(\sigma (E)\) of error (E) between the predicted and observed velocity data corresponding to different \(\alpha\) values was performed (Table 3). It is evident from the Table 3 that the \(\alpha =10\) gave the lowest mean and standard deviation values for all three figures in comparison to the other \(\alpha\) values. As a result, the α value of 10 is adopted to generalize the entropy index for all types of flow data throughout the present study.

Fig. 2
figure 2

Vertical velocity profile for different entropy index \(\left(\alpha \right)\) values, using the velocity observations taken at the P. Nuovo gauging station of Tiber River. Flood event selected—June 3, 1997 (Luo and Singh 2011)

Full size image
Fig. 3
figure 3

Vertical velocity profile for different entropy index \(\left(\alpha \right)\) values, using the Iran (Run 1) River data (Luo 2009)

Full size image
Table 3 Mean, \(\mu (E)\) and Standard deviation, \(\sigma (E)\) of error (E) for predicting velocity distribution corresponding to different \(\alpha\) values
Full size table
Fig. 4
figure 4

Vertical velocity profile for different entropy index \(\left(\alpha \right)\) values, using the experimental (Run 25) velocity data (Singh 2019)

Full size image

3 2-D velocity distribution

The Kapur entropy-based velocity distribution can be generated using the entropy theory discussed in the preceding section. A prerequisite for obtaining the desired velocity distribution is formulating the hypothesis on the velocity cumulative distribution function (CDF).

3.1 Spatial variation and cumulative density function (CDF) of velocity

In a narrow open channel, the notable change of longitudinal velocity can be observed in both directions, i.e., vertical (y) and horizontal (z). Along with other variables, the effect of the channel walls causes the isovels (lines of equal velocity) to curve upwards toward the water's surface. Secondly, the maximum velocity happens at some depth below the free surface because of the dip phenomenon (Fig. 5), leading to the many-to-one mapping of depth (y) and velocity. Figure 5 shows a typical rectangular cross-section showing the dip-phenomena. In order to conveniently model the velocity distribution and get the one-to-one mapping of velocity with involved coordinates, it is advantageous to translate the Cartesian (y–z) coordinate system (Fig. 5) into another suitable system. Here, the ξ–η coordinate system is employed, and the whole idea of the coordinate system transformation can be traced to the circular pipe studies where the cylindrical coordinate system was used instead of the cartesian system. In the ξ–η system, the ξ coordinate curves represent the isovels, whereas the η coordinate curves are their corresponding orthogonal trajectories. Detailed insights about the ξ–η coordinate system can be found in Chiu and Chiou (1986), Chiu and Lin (1983), which includes the derivation of the relation between the ξ coordinate curves and the cartesian coordinates (Eq. 15) that efficiently correlates the isovel characteristics.

$$\upxi =\frac{y}{D+h}exp\left(1-\frac{y}{D+h}\right)$$
(15)

where, y varies from 0 (channel bed) to D (free-surface), and the y-axis is located at the middle of the channel cross-section (as shown in Fig. 5) or appropriately chosen to contain the maximum velocity point. h denotes the location of the maximum velocity from the free-surface. Hence, it takes on values from \(-D\) to \(+\infty\). For the \(h>0\), it is merely a coefficient without any physical significance that influences the pattern of maximum velocity isovels. However, if \(h<0\), its magnitude denotes the actual location of the maximum velocity below the free-surface termed as a dip of the maximum velocity. Further, the hypothesis on the Cumulative Density Function, \(F\left(u\right)\) of velocity can be given by Eq. (16),

$$F\left(u\right)={\int }_{0}^{{u}_{max}}f\left(u\right)du=\frac{\xi -{\xi }_{0}}{{\xi }_{max}-{\xi }_{o}}$$
(16)

where \({\upxi }_{\mathrm{o}}\) and \({\upxi }_{max}\) are the least and maximal values of the Eq. (15) representing the zero velocity isovel (i.e., boundary line) and maximum velocity, respectively. The velocity PDF can be obtained by differentiating Eq. (16) as,

Fig. 5
figure 5

Schematic diagram of rectangular cross-section, with origin (0,0) at the middle of the channel cross-section

Full size image
$$f\left(u\right)=\frac{dF\left(u\right)}{du}=\frac{dF\left(u\right)}{d\upxi }\frac{d\upxi }{du}=\frac{1}{{\upxi }_{max}-{\upxi }_{o}}\frac{d\upxi }{du}$$
(17)

3.2 Derivation of velocity distribution equations

Finally, the Kapur entropy-based velocity distribution can be obtained by combining the Eqs. (12) and (17) and integrating the result within the limits of \(u\) (\(0\) to \(u\)) and \(\upxi\) (\({\upxi }_{o}\) to \(\upxi\)).

$$u=\frac{1}{{\lambda }_{1}}\left\{-{\lambda }_{o}+{\left[{\left({\lambda }_{o}\right)}^{\alpha }+\frac{{\alpha }^{\alpha }{\cdot \lambda }_{1}}{{\left(\alpha -1\right)}^{\alpha -1}}\cdot \frac{\xi -{\xi }_{0}}{{\xi }_{max}-{\xi }_{o}}\right]}^{1/\alpha}\right\}$$
(18)

The CDF or the ratio involving the \(\xi\), \({\xi }_{0}\) and \({\xi }_{max}\) can be evaluated for the \(h\le 0\) (Eq. 19), as \(h>0\) does not hold any physical meaning. For any vertical, the \({\xi }_{o}\) will be zero as it represents the zero velocity isovel and \({\xi }_{max}\) will occur at \(y=D+h\).

$$\frac{\xi -{\xi }_{0}}{{\xi }_{max}-{\xi }_{o}}=\frac{y}{D+h}exp\left(1-\frac{y}{D+h}\right)$$
(19)

Eventually, the desired velocity distribution in the parametric form is given by Eq. (20) and these parameters (such as \({\lambda }_{o}, {\lambda }_{1}, \alpha , h, D\)) are needed to be evaluated for the precise analysis. As discussed in Sect. 2.5, the \(\alpha =10\) is fixed for the present analysis.

$$u=\frac{1}{{\lambda }_{1}}\left\{-{\lambda }_{o}+{\left[{\left({\lambda }_{o}\right)}^{\alpha }+\frac{{\alpha }^{\alpha }{\cdot \lambda }_{1}}{{\left(\alpha -1\right)}^{\alpha -1}}\cdot \frac{y}{D+h}exp\left(1-\frac{y}{D+h}\right)\right]}^{1/\alpha}\right\}$$
(20)

3.3 Entropy parameter (B)

The nonlinear system constituting (Eqs. 13, 14), when solved programmatically using Matlab, furnishes the values of Lagrange’s multipliers (\({\lambda }_{o}\) and \({\lambda }_{1}\)). Avoiding the complicated nonlinear system solution and making the calculations simpler and straightforward. Similar to the other entropy-based velocity distributions such as Shannon entropy (Chiu 1988), Tsallis entropy (Cui and Singh 2013), and Renyi entropy (Kumbhakar and Ghoshal 2016), a new dimensionless entropy parameter B was introduced. Evident from the Eq. (21), parameter B links both the Lagrangian multipliers. Hence, it acts as an index for characterizing and comparing diverse velocity distribution patterns.

$$B=1+\frac{{\lambda }_{1}}{{\lambda }_{o}}{u}_{max}$$
(21)

The earlier studies related to the entropy-based velocity distributions have demonstrated that their respective entropy parameters tend to remain constant in the purview of the flow and channel characteristics within a particular river reach (Chiu et al. 2005), which was later substantiated theoretically (Moramarco and Singh 2010) and experimentally (Singh 2019; Singh and Khosa 2022a, b). Inferences regarding the variation of parameter B with the flow and channel characteristics can be examined as a separate study.

3.4 Mean and Maximum velocity ratio, \(\phi \left(B\right)\)

In hydrological studies especially involving the use of flow rates, the mean velocity is an essential component, and it cannot be calculated directly from the raw data. Additionally, the mean velocity is a prerequisite for the mass, momentum, and energy transfer calculations in natural flows. The relation or the ratio of the mean and maximum velocity is not a novel approach as its roots can be traced to the Chiu (1988), which deals with Shannon entropy-based distribution, and the relation in terms of Shannon entropy parameter M is given as,

$$\frac{{u}_{mean}}{{u}_{max}}=\frac{{e}^{M}}{{e}^{M}-1}-\frac{1}{M}$$
(22)

Similarly, Tsallis and Renyi entropy-based velocity distributions have their respective relationship given by Eqs. (23) and (24), respectively.

$$\frac{{u}_{mean}}{{u}_{max}}=\frac{G+12}{24}$$
(23)
$$\frac{{u}_{mean}}{{u}_{max}}=\frac{{\alpha }^{*}}{1-{\alpha }^{*}}\frac{{\left(1-{R}^{\frac{{\alpha }^{*}}{1-{\alpha }^{*}}}\right)}^{-1}}{{\left(\mathrm{R}-1\right)}^{\frac{{\alpha }^{*}}{1-{\alpha }^{*}}}}\left\{\frac{{\alpha }^{*}-1}{2{\alpha }^{*}-1}\left[{\left(\frac{1}{R-1}\right)}^{\frac{2{\alpha }^{*}-1}{{\alpha }^{*}-1}}-{\left(\frac{R}{R-1}\right)}^{\frac{2{\alpha }^{*}-1}{{\alpha }^{*}-1}}\right]+\frac{{\alpha }^{*}-1}{{\alpha }^{*}}\frac{R}{1-\mathrm{R}}\left[{\left(\frac{1}{R-1}\right)}^{\frac{{\alpha }^{*}}{{\alpha }^{*}-1}}-{\left(\frac{R}{R-1}\right)}^{\frac{{\alpha }^{*}}{{\alpha }^{*}-1}}\right]\right\}$$
(24)

where G and R are the entropy parameters involved in Tsallis and Renyi entropy-based velocity distributions, respectively. However, to avoid confusion, the parameter \(\alpha\) as involved in the Kumbhakar and Ghoshal (2016) is replaced here as \({\alpha }^{*}\) and its value ranges in the interval (\(\mathrm{0,1}\)). Interestingly, the lengthy-expression (Eq. 24) was modified and shortened to a new expression given by Eq. (25) (Singh and Khosa 2022c). The modified relation retained the same accuracy as the original work, as confirmed in Fig. 6.

Fig. 6
figure 6

Renyi entropy parameter (R) values based on the original (Eq. 24) and modified (Eq. 25) equation

Full size image
$$\frac{{u}_{mean}}{{u}_{max}}=\frac{R}{R-1}\left[1+\frac{{\alpha }^{*}}{2{\alpha }^{*}-1}\frac{\left({1-R}^{\left(\frac{2{\alpha }^{*}-1}{{\alpha }^{*}-1}\right)}\right)}{\left({R}^{\left(\frac{2{\alpha }^{*}-1}{{\alpha }^{*}-1}\right)}-R\right)}\right]$$
(25)

Similarly, the use of parameter B into Eqs. (13, 14), furnishes a simple expression for the \(\phi \left(B\right)\) in terms of B and \(\alpha\) only (Eq. 26). Here, the \(\phi \left(B\right)\) is equal to the ratio of the time-averaged mean velocity (umean) and the maximum velocity (umax).

$$\phi \left(B\right)=\frac{{u}_{mean}}{{u}_{max}}=\frac{{B}^{\alpha }}{{B}^{\alpha }-1}\left[1+\frac{\left({1-B}^{\alpha +1}\right)}{\left(\alpha +1\right){B}^{\alpha }\left(B-1\right)}\right]$$
(26)

The numerical value of the entropy parameter (B) can be evaluated using the historical datasets comprised of \({u}_{mean}\) and \({u}_{max}\) available for a particular open channel’s cross-section. Based on the Eq. (26), the theoretical range of B was evaluated mathematically as \(\left(1,\infty \right)\). However, in accordance with the field and experimental data, its interval will be reduced as the highest velocity value exceeds the mean velocity by 25–50% only. Moreover, owing to the surmised constant behavior of the new entropy parameter (B), the mean and maximum velocity ratio holds significant importance in the context of the entropy theory as it will furnish the mean velocity directly for the established historical velocity data.

3.5 Velocity distribution

Finally, with the application of the parameter B along with the Eq. (13), the simpler and straightforward version of the Eq. (20), i.e., the desired Kapur entropy-based velocity distribution can be obtained as,

$$u=\frac{{u}_{max}}{B-1}\left\{-1+{\left[1+\left({B}^{\alpha }-1\right)\cdot F(u)\right]}^{1/\alpha}\right\}$$
(27)
$$F\left(u\right)=\left\{\begin{array}{c}\frac{y}{D}; h\ge 0\\ \frac{\mathrm{y}}{D-h}exp\left(1-\frac{\mathrm{y}}{D-h}\right); h<0\end{array}\right.$$
(28)

Equation (27) involves only a single parameter (B) that can be obtained by several methods, such as from the historical datasets of mean and maximum velocity; or using the solution of the non-linear system of equations (Eqs. 13, 14). The other parameter (\(\alpha\)) appearing in the resulted equation was fixed for the present study as discussed earlier. Equation (28) gives the required CDF, and the desired expression can be utilized depending on the maximum velocity dip.

3.6 Measure of error

The error analysis was conducted to comment on the accuracy of the derived velocity model using the observed velocity data. Additionally, a comparative analysis with the other entropy-based velocity distributions was performed. The evaluation of relative inaccuracy between the predicted and observed value was computed as,

$${\text{Absolute}}\;{\text{error}} = E = \frac{{\left| {u_{o} - u_{p} } \right|}}{{u_{o} }}$$
(29)

where the \({u}_{o}\) and \({u}_{p}\) is the observed and predicted velocity values at a particular point in the considered velocity profile, respectively. Additionally, the mean \((\mu (E)\)) and standard deviation \((\sigma \left(E\right))\) of the absolute error are computed in the later section.

3.7 Validation of proposed velocity distribution

The validation of the proposed model was done using the velocity data having different flow characteristics. The field observations consist of the following velocity datasets measured at: (1) Mersch and Torre Accio cross-section of Alzette River (Mirauda et al. 2018); (2) transect A6 (Amazon River) for three verticals situated at a distance of 0.2B, 0.5B and 0.8B (B = channel width) from the left bank (Bahmanpouri et al. 2022a); (3) P. Nuovo (Nov. 1996 flood event) and P. Felcino (Nov. 1996 flood event) gauging station (Tiber River) (Luo and Singh 2011). The flow characteristics of the selected datasets are listed in Table 2. For the transect A6 and the gauging sections of Tiber river, the three different verticals were selected to demonstrate the potential of the proposed velocity model for the whole cross-section instead of the y-axis (centre-line).

Figures 7, 8, 9, 10 and 11 illustrates the predicted velocity profiles for the selected velocity datasets. The statistical analysis for the proposed model validation is reported in Table 4. With the low mean and standard deviation values, the proposed model depicted a good accuracy for the centreline verticals as well as the verticals located near the boundary regions for the different flow conditions under consideration, i.e., the new model was able to predict velocity with decent accuracy throughout the channel cross-section.

Fig. 7
figure 7

Proposed model validation for the velocity observations at the Mersch cross-section of Alzette River for Q = 44.3 m3/s (Mirauda et al. 2018)

Full size image
Fig. 8
figure 8

Proposed model validation for the velocity observations at the Torre Accio cross-section of Alzette River for Q = 197.9 m3/s (Mirauda et al. 2018)

Full size image
Fig. 9
figure 9

Proposed model validation using the velocity observations of the transect A6 (Amazon River) for three verticals situated at a distance of 0.2B, 0.5B and 0.8B (B = channel width) from the left bank (Bahmanpouri et al. 2022a)

Full size image
Fig. 10
figure 10

Proposed model validation using the velocity observations taken along three verticals (z =  − 20.8 m, 0 m, 16.64 m) at the P. Nuovo gauging station of Tiber River. Flood event selected—Nov. 1996 (Luo and Singh 2011)

Full size image
Fig. 11
figure 11

Proposed model validation using the velocity observations taken along three verticals (z =  − 14.66 m, 0 m, 7.34 m) at the P. Felcino gauging station of Tiber River. Flood event selected—Nov. 1996 (Luo and Singh 2011)

Full size image
Table 4 Statistical analysis for the proposed model validation based on the error (Eq. 29)
Full size table

3.8 Comparative analysis

For the comparative study, the proposed model is assessed against the existing four different entropy-based models using the different sets of field and experimentally observed data at the centre-line vertical (middle of the channel cross-section). The field observations considered was Run 2 (Iran River) for a clear water flow in a wide section of the river (Luo 2009), whereas the experimental observations consist of two datasets: (1) Run 1 velocity data (clear water flow) of experiments conducted on a recirculating laboratory flume having dimensions as 30 cm width, 40 cm depth, and 20 m length (Xingkui and Ning 1989); (2) Run 29 (medium-sized sediment particles having diameter 0.21 mm) of experiments conducted on a laboratory recirculating flume having narrow channel width of 35 mm and 15 m long (Coleman 1981). More relevant details regarding the selected datasets are listed in Table 2. Both the experimental dataset under consideration exhibits the dip phenomena. Apart from the proposed model, the other entropy-based distributions considered for comparison are listed in Table 1.

Figures 12, 13, and 14 report the results of the comparative analysis for different velocity datasets. In totality, the proposed model performed well for both clear water (Figs. 12 and 13) and sediment-loaded (Fig. 14) flows. Figure 12 is based on the field data from Run 2 (Iran River), and it can be clearly seen that the proposed model matches the observed data with good accuracy for the entire channel depth. Similar inferences can be drawn from the other two figures as Figs. 13 and 14 are based on the experimental data and present better accuracy than other models. It can be noted that the present model reported accurate results for the sediment-loaded flow subjected to higher turbulence (Fig. 14). Additionally, the model precisely predicted the maximum velocity location below the water surface. The previous models struggle to match the observed velocity in the portion near the channel bed, whereas the proposed model fits the lower region (near the channel bed) with higher correctness. Moreover, the statistical analysis (Table 5) of the comparative study results also supported the above claims regarding the proposed model and confirmed the usage of the proposed model for both the experimental and field velocity observations. From Table 5, it can be inferred that the present model resulted in lower mean values (of absolute error, E) for all the cases under consideration, whereas the standard deviation was also lower or comparable with the other entropy-based models.

Fig. 12
figure 12

Proposed model comparison with existing four entropy-based velocity distribution equations using the observed field data from Run 2 Iran River (Luo 2009)

Full size image
Fig. 13
figure 13

Proposed model comparison with existing four entropy-based velocity distribution equations using the observed data from Run 1 for clear water flow (Xingkui and Ning 1989)

Full size image
Fig. 14
figure 14

Proposed model comparison with existing four entropy-based velocity distribution equations using the observed data from Run 29 for medium-sized sediment particles having diameter 0.21 mm (Coleman 1981)

Full size image
Table 5 Statistical analysis for the comparative study of different entropy-based models for velocity calculations based on the error (Eq. 29)
Full size table

4 Conclusions

Several conclusions can be drawn from the preceding research work. Using Kapur entropy, the 2-D velocity distribution for the hypothesized CDF is determined in the present research, and the new model was validated using field and experimental observations. The proposed model is dependent on a non-negative entropic index (\(\alpha\)). Hence, the statistical analysis for the different \(\alpha\) values was performed, which resulted in the \(\alpha\) = 10 as the best suitable value and was fixed throughout the present study. A new entropy parameter (B) is defined for simplifying and eliminating the non-linear relations of Lagrange multipliers from the present model. Further, parameter B can be evaluated using the values of maximum and mean velocity and surmised constant for a particular channel section, as done in the earlier studies. Also, the known values of parameter B facilitate the direct estimation of the mean velocity for a particular open channel cross-section, thereby simplifying the discharge calculations. The comparative analysis with the existing four entropy-based models gave an advantage to the present model for both field and experimental observations and supported the application of the present model to the flows such as clear water or sediment-loaded flows. The statistical analysis is also done to get the quantitative notion of the present model’s performance, and it provided improved accuracy compared to the other models supported by the low mean and standard deviation values.