Land use structure optimization based on uncertainty fractional joint probabilistic chance constraint programming

Abstract

An uncertainty fractional joint probability chance constraint programming is developed to process land use structure optimization under uncertainty. The model integrate uncertainty programming into fractional programming, and the uncertainty programming include interval programming, fuzzy programming, stochastic programming and joint probability chance constraint programming. The results of the study are a series of land use policies in multiple scenarios with interval and deterministic numbers. The advantage of the model include it can (1) effectively integrate the two objectives of economic benefit maximization and pollution minimization by the fractional programming; (2) effectively process the uncertainty by the corresponding uncertainty programming; (3) reflect the impact of uncertainty on system benefit, pollutant discharge, and land use structure policy; and (4) develop a series of possible scenarios and corresponding feasible plans. The results of the study can help planners or decision makers develop flexible land use policy to address the multi-objective problems of maximum, minimum, and uncertainty. The proposed method is universal and can be extended to other cases.

1 Introduction

Land use structure optimization arranges the different types of land resources in the area rationally depending on the characteristic of the land resources and the land suitability evaluation to achieve certain ecological or economic objectives (Emanuela et al. 2018; Gao et al. 2010). The land use structure optimization not only can improve the efficiency of land use but also can maintain the ecological balance to achieve the sustainable use of land resources (Chibilev et al. 2016; Sadeghi et al. 2009). Mathematic method plays an increasingly high role in land use optimization, and the recent methods of land use structure optimization include linear programming (Wang et al. 2010a, b), multi-objective programming (Yang et al. 2013), system dynamic modeling (Domptail and Nuppenau 2010), cellular automata (Yang et al. 2012), and genetic algorithm (Wang et al. 2010a, b).

Most land use structure optimization models are certainty models; however, uncertainty is rooted in nature and human society and always considerably impacts the decision-making process and the decision (Gu et al. 2016b; Lu et al. 2014). Ignoring the uncertainty will cause deviation in the decision-making process and reduction in decision rationality (Gu et al. 2016a; Ma et al. 2019).

Uncertainty in land use structure optimization can be classified into two categories, namely, external and internal (Li et al. 2014). The reason for the former is that the objective of land use optimization is a complex system and the components of the system relate with one another closely (MuñozRojas et al. 2009). Furthermore, the features of the components are changeable; the system structure changes when the features change. For example, the system of land use optimization includes three closely related components, namely, natural environment, social economy, and land use; the features of population, such as migration, will change, and the variation in population will lead to changes in the human–land coordinate relationship (Li et al. 2014). Inner uncertainty stems from two reasons. The first is that the different planners have different decision-making notions and abilities of processing information, and the ability of processing information will influence the final scheme (Wu and Shao 2005). The other reason derives from the interest group that can influence the planning scheme, and variation arises in the joint force formed by the game decisions of multiple interest groups (Li et al. 2014). In addition, variation occurs in the benefit target of the same planner. Therefore, identifying and processing the uncertainty considerably impact the rationality of land use planning and the achievement of planning objective (Luo et al. 2019; Wang and Wang 2012; Zhou et al. 2015).

Although most studies on land use structure optimization are under certainty conditions, few correlational studies remain under uncertainty. The principle of these studies are establishing uncertainty optimization model based on identifying the character of uncertainty. Linear uncertainty mathematic programming and nonlinear mathematic programming are the two main method, and linear uncertainty programming are used more frequently (Ren et al. 2019). According to the mathematical form, uncertainty can be classified into three categories, namely, interval, fuzzy, and stochastic sets (Gu et al. 2018); the corresponding linear optimization methods are interval planning, fuzzy planning, and stochastic planning. In practical problems, when more than one type of uncertainty exists, the uncertainty methods can be integrated to solve the problem depending on the uncertainty types (Gu et al. 2013).

In the studies of land use structure optimization, optimal linear interval programming has been developed for land use management for surface source water protection under uncertainty (Liu et al. 2009). Fuzzy flexible programming also has been introduced to handle fuzzy coefficients in the objective function and constraint (Arlene 1995). However, in case of uncertainty in the interval form in addition to the fuzzy sets, the Fuzzy flexible programming cannot represent the interval number effectively. Furthermore, the hybrid inexact programming, which is developed by integrating the interval linear programming into fuzzy programming, is established to solve the interval uncertainty and fuzzy uncertainty in land use problem (Zhou 2015). When the uncertainty is in the form of interval and stochastic sets, the interval probabilistic programming that is integrated with interval programming and stochastic programming is developed to process the uncertainty. Lu et al. (2015) integrated the GIS model with interval probability to develop the integrated GIS based interval-probabilistic model for land-use planning management under uncertainty.

The optimization model always includes constraints, and probability violations exist in constraints. Thus, chance constraint programming (CCP) is introduced into uncertainty optimization to develop uncertainty CCP programming for solving the aforementioned problem. Zhou (2015) integrated interval programming, fuzzy programming, and CCP to develop an interval fuzzy CCP model for processing sustainable urban land use planning and land use policy analysis. In other complicated scenarios, uncertainty exists in the two sides of the constraint in the optimization programming. In such circumstances, the interval chance constraint is introduced into planning to solve the problem. Ou et al. (2017) developed the interval chance-constrained fuzzy modeling approach to address the problem of integration of environmental planning and land use planning in watershed scale. Liu et al. (2007) developed the ICCIP model for land use management of lake areas in urban fringes.

Although studies have been conducted on the uncertainty in land use planning, most of them focus on single-objective programming model. The objective of such model is mostly economic maximum. The environmental and resource factors are considered as constraints. Few studies have been performed on multi-objective model that focuses on the economy and the environment. Li and Ma (2017) used multi-objective uncertainty model to support land use planning. The objectives of the developed model are all the maximum objectives. Few studies have also been done on multi-objective model that includes maximum and minimum objectives for land use optimization, such as the model combining the maximum objective (such as land economy benefit of land use) and minimum objective (such as soil erosion or pollution). The possible problem of setting subjective weight in the non-Pareto optimization should also be avoided. Fractional programming can effectively solve multi-objective planning with maximum and minimum objectives and can avoid the subjective weight setting (Chadha and Chadha 2007; Lai et al. 2008). The uncertainty of fractional programming can be processed by integrating corresponding uncertainty programming (Ren et al. 2013).

Although there are studies about uncertainty multiple objective land use structure optimization (Li and Ma 2017), there are seldom studies about uncertainty land use structure optimization with maximum and minimum multiple objective and non subjective weight setting method. And although there are studies about constraint violation in land use structure (Zhou 2015; Ou et al. 2017), there are seldom researches for solving multiple constraints violation in land use planning. Solving above problems could help establishing uncertainty land use structure optimization model with maximum and minimum objectives and multiple constraint violation.

Therefore, the objective of the study is to develop a land use structure optimization model based on fractional uncertainty programming. The model aims to (1) identify the uncertainty that influences regional land use optimization; (2) take the objectives as the benefit maximum of the total land use and the pollution minimum of the area; (3) fully consider various constraints, such as the constraints of total invest, population, water resource, and land area; and (4) establish a fractional uncertainty optimization model to offer sustainable and flexible land use structure mode. The model can also help planners and decision-makers understand the relationship among land use structure planning, economy, environment, and society. Xiangjiang New District, Hunan Province is used as the research background.

2 Study area

Xiangjiang New District was founded in 2014, and it is located in Changsha City, Hunan Province. The district is located in a transition zone from hill to plain with complex topography. The climate of the district is of a humid subtropical monsoon climate, and the district has abundant water resources with a well-developed river system. The animal resources and vegetable resources of the area are very rich.

The total area of the district is 120,447.47 ha. The land use types in the district can be classified into 12 categories according to the “land use structural adjustment,” namely, basic farmland, garden plot, forest land, grassland, agro-land, urban land, rural residential land, industrial land, transportation and water conservancy land, other construction land, water area, and nature protected area. The study area and the land use master planning for Xiangjiang New District are in Fig. 1. The areas of all land use types of Xiangjiang New District in 2016 are shown in Table 1.

Fig. 1

The study area and the land use master planning for Xiangjiang New district (2016–2020)

Table 1 The table of land use scale and structure

The development objectives of the district are detailed below. In 2020, the district should be constructed as having (1) areas of harmonious development between the economy and environment, (2) high technology industry clusters, (3) areas that coordinate urban and rural development, and (4) ecological and livable districts. For the achievement of strategic objectives, the economic benefit and ecology should all be considered equally; thus, continuing the traditional land use types in which the main objective is economic development is not suitable. Therefore, optimizing the land use structure that can pay equal attention to economic development and ecological protection is meaningful.

The land regulation for each type of land is listed in “Land Use Master Planning for Xiangjiang New District, Hunan Province (2016–2020)”, and the regulation is also listed in Table 1.

3 Methodology

The uncertainty fractional joint probability CCP is developed to pay equal attention to economic development and environmental protection. The procedure of the model is as follows: (1) building a certainty model for land use structure optimization, (2) analyzing the uncertainty that will influence the model, and (3) integrating the certainty model with the corresponding uncertainty programming to establish the land use optimization model under uncertainty.

3.1 Building a certainty model for land use structure optimization

On the basis of the land regulation of “Planning” and the present situation of the study area, the uncertainty fractional joint probability CCP model is developed.

The objectives of the model are economic maximization and nitrogen discharge minimization. The model involves constraints of investment, water resources, population, labor, total area of land use, area regulation of each type of land use, and green space ratio.

3.1.1 Objective function

Economic maximization: maximizing the total economic benefit for all the types of land.

$$maxf\left( x \right) = \mathop \sum \limits_{i = 1}^{n = 12} \left[ {\left( {UB_{i} - UC_{i} } \right) \cdot x_{i} } \right]\quad i = 1,2, \ldots 12$$

(1)

$UB_{i}$ the benefit of the unit area of the $i{\text{-}}th$ land use; $UC_{i}$the cost of the unit area of the $i{\text{-}}th$ land use; $x_{i}$ the $i{\text{-}}th$ type of land use.

1	Basic farmland	2	Garden plot
3	Woodland	4	Pasture
5	Other agriculture land	6	Urban land
7	Rural residential	8	Industry and mining
9	Transportation and water conservancy	10	Other construction land
11	Water	12	Natural reserve

Environmental influence minimization: minimizing the nitrogen discharge of each type of land use.

$${\text{m}}inf\left( x \right) = \mathop \sum \limits_{i = 1}^{n = 12} \left( {TN_{i} \cdot x_{i} } \right)\quad i = 1,2, \ldots 12$$

(2)

$TN_{i}$ nitrogen discharge of $i{\text{-}}th$ type of land use.

The two objectives include objective maximization and minimization. Thus, fractional programming is utilized to integrate the two objectives, and the integrated model is

$${\text{m}}axf\left( x \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{n = 12} \left[ {\left( {UB_{i} - UC_{i} } \right) \cdot x_{i} } \right]}}{{\mathop \sum \nolimits_{i = 1}^{n = 12} \left( {TN_{i} \cdot x_{i} } \right)}}\quad i = 1,2, \ldots 12$$

(3)

The model is a fractional programming model, and the model maximization must maximize the numerator and minimize the denominator.

Constraints:

The total investment cannot exceed the governmental budget.

$$\mathop \sum \limits_{i = 1}^{n = 12} \left( {UI_{i} \cdot x_{i} } \right) \le TI\quad i = 1,2, \ldots 12$$

(4)

$UI_{i}$ the invest for ${\text{i-th}}$ type of land use; $TI$ the total governmental invest.

The total amounts of water consumption cannot exceed the amount of regionally available water resources.

$$\mathop \sum \limits_{i = 1}^{n = 12} \left( {UWC_{i} \cdot x_{i} } \right) \le AWC\quad i = 1,2, \ldots 12$$

(5)

$UWC_{i}$ the water requirement for the $i{\text{-}}th$ type of land use; $AWC$ the water resources of the study area.

The amount of AWC of the study is 660 × 10⁸ m³.

The population cannot exceed the total population of the study area.

$$\mathop \sum \limits_{i = 1}^{n = 12} \left( {UP_{i} \cdot x_{i} } \right) \le TP\quad i = 1,2, \ldots 12$$

(6)

$UP_{i}$ the population in unit area of the $i{\text{-}}th$ type of land use; $TP$ the total population of the study area.

The amount of labor cannot exceed the total amount of available labor in the study area.

$$\mathop \sum \limits_{i = 1}^{n = 12} \left( {UL_{i} \cdot x_{i} } \right) \le AL\quad i = 1,2, \ldots 12$$

(7)

$UL_{i}$ the amount of labor for the $i{\text{-}}th$ type of land use; $AL$ the amount of labor in the study area.

The total area of the land use cannot exceed the amount of available area in the study area.

$$\mathop \sum \limits_{i = 1}^{n = 12} x_{i} \le AA\quad i = 1,2, \ldots 12$$

(8)

$AA$ the amount of available area in the study area, and the values are set based on the planning index of “2020 planning”

The area of each type of land use should be no less than the minimum area of land use for “planning.”

$$x_{i} \ge MA_{i} \quad i = 1,2, \ldots 12$$

(9)

$MA_{i}$ the minimum area of the $i{\text{-}}th$ type of land use of the “planning”

The green space ratio of the study area should be no less than the minimum requirement of the green-spaced ratio.

$${{\left( {x_{2} + x_{3} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{2} + x_{3} } \right)} {\mathop \sum \limits_{i = 1}^{n = 12} \left( {x_{i} } \right) \ge MFCR\quad i = 1,2, \ldots 12}}} \right. \kern-0pt} {\mathop \sum \limits_{i = 1}^{n = 12} \left( {x_{i} } \right) \ge MFCR\quad i = 1,2, \ldots 12}}$$

(10)

$MFCR$ the minimum requirement of the green spaced ratio, and according to the <Land Use Master Planning for Xiangjiang New District>, the MFCR is 0.34.

3.2 Analyzing the uncertainty that will influence the model

Uncertainty is inherent in nature and human society. Thus, uncertainty is inevitable in the land use structure optimization. The uncertainty that influences the land use structure optimization can be classified into two categories: the environmental and society economy factors.

The environment factor includes total nitrogen $TN$ discharge. TN discharge is not a constant value owing to the uncertainty of heterogeneity of soil, rainfall and runoff, and thus, the TN discharge is also an uncertainty number. Due to the difference in soil erosion amount, terrain factor, vegetation coverage factor and so on, the $TN$ discharge has been shown to follow stochastic normal distribution (Li 2010), and the distribution interval of the TN discharge are listed in Table 1.

The society economic uncertainties include $UB_{i}$, $UC_{i}$, $TI$, $UWC_{i}$, $UP_{i}$, $TP$, and $UL_{i}$. $AL$, $UB_{i}$, and $UC_{i}$ are economic factors and can be characterized as a fuzzy set. This situation is due to that economic factors such as cost and benefit will fluctuate in certain intervals in the future, and the boundary of the interval is difficult to identify because of its fuzzy feature. The fuzzy distribution interval of $UB$ and $UC$ are listed in Table 1. The distribution form of $TI$ $UWC$ $TP$ $AL$ are interval distribution, and the distribution intervals are listed in Table 2.

Table 2 The interval distribution of UC (10⁴ CNY/ha), UB (10⁴ CNY/ha), TN (kg/ha), UWC (10⁴ m³/ha), UL (person/ha), UP (person/ha) for the 12 types of land use

3.2.1 Violation probability

Joint probabilities exist in the violation probability of the constraints, and violation probability exists in the constraints of labor amount and minimum agriculture land area.

With regard to violation probability of labor amount constraint, the number of people in a large city always exceeds the number that is calculated by the industry prediction or population prediction model owing to the effect of population gathering in the city. Furthermore, the scale can barely be restricted in an accurate value, and the violation probability can be used to reflect the possible population scope. To reflect the different degree of violation, the violation probability is assigned as [0.7, 0.8, 0.9].

For violation probability of a basic minimum area of agricultural land, a minimum basic area of agricultural land exists in each district that is delimited by agricultural safety red line. The part of basic minimum area of agricultural land can be allocated to other districts to ensure the achievement of economic and environmental objectives given that Xiangjiang New District has been planned as a high-technology industry cluster and an ecological and livable district. To reflect the different violation degrees for basic agriculture land area, the violation probability is assigned as [0.7, 0.8, 0.9], and the Labor amount and minimum agriculture area in different violation probabilities scenarios are listed in Table 3.

Table 3 Labor amount and minimum agriculture area in different violation probabilities scenarios

Given that different degrees of violation probabilities occur for the labor amount and the minimum agricultural land area, the combination of the two violation probabilities will generate different combinations, and the different combinations represent the different types of joint probability. Furthermore, the different joint probabilities can reflect different scenarios of probability violation.

3.3 Uncertainty fractional joint probabilistic chance constraint programming

3.3.1 Fractional programming

Formally, a linear fractional programming is defined as the problem of maximizing/minimizing a ratio of affine function over a polyhedron, and it could be written as (Lata and Mittal 1976; Singh and Hanson 1991)

$$\begin{aligned} & maxmize\frac{{c^{T} x + \alpha }}{{d^{T} x + \beta }} \\ & {\text{Subject to}}\quad Ax \le b \\ \end{aligned}$$

(11)

where x represents the vector of variables to be determined, $c,d \in R^{n}$ are vectors of (know) coefficients, $\alpha ,\beta \in R$ are constants, $A \in R^{m \times n}$ is a (know) matrix of coefficients, $b \in R^{m}$ are vectors of (know) coefficients, T denotes the transpose.

The general uncertainty fractional model could be expressed as

$$\begin{aligned} & Maxf^{ \pm } = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {C_{i}^{ \pm } x_{i}^{ \pm } + \alpha^{ \pm } } \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {d_{i}^{ \pm } x_{i}^{ \pm } + \beta^{ \pm } } \right)}} \\ & \mathop \sum \limits_{i = 1}^{n} A_{ij}^{ \pm } x_{i}^{ \pm } \le B_{j}^{ \pm } \quad i = 1,2 \ldots n;\quad j = 1,2 \ldots m \\ & x_{i}^{ \pm } \ge 0\quad i = 1,2 \ldots n \\ \end{aligned}$$

(12)

where $A_{ij}^{ \pm } , B_{j}^{ \pm } , C_{i}^{ \pm } , x_{i}^{ \pm }$ are the uncertainties, and the uncertainties could be interval numbers or stochastic numbers. In the uncertainty model above, the two types of uncertainties are all in the interval number form with the deterministic and closed boundary, in which the stochastic number could be transformed into the interval number by its probability distribution, and the ‘−’ represents the lower bound, and the ‘+’ represents the upper bound.

Besides interval number and stochastic number, another type of uncertainty number is fuzzy number. In the case of the three types of uncertainties appear in the objective function or in the constraints, the uncertainty optimization programming could be expressed as (Jain et al. 2011; Mehlawat and Kumar 2012)

$$Maxf^{ \pm } = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left\{ {\left( {C_{i}^{ \pm } + \tilde{C}_{i}^{{\prime }} } \right) \cdot x_{i}^{ \pm } + \alpha^{ \pm } } \right\}}}{{\mathop \sum \nolimits_{i = 1}^{n} \left\{ {\left( {d_{i}^{ \pm } + \tilde{d}_{i}^{{\prime }} } \right) \cdot x_{i}^{ \pm } + \beta^{ \pm } } \right\}}}$$

(13)

Subject to

$$\begin{aligned} & \mathop \sum \limits_{i = 1}^{n} A_{ij}^{ \pm } x_{i}^{ \pm } \le B_{j}^{ \pm } \quad i = 1,2 \ldots n;\quad j = 1,2 \ldots m \\ & \mathop \sum \limits_{i = 1}^{n} \tilde{A}_{ig}^{{\prime }} x_{i}^{ \pm } \le B_{g}^{ \pm } \quad i = 1,2 \ldots n;\quad g = 1,2 \ldots m \\ & x_{i}^{ \pm } \ge 0\quad i = 1,2 \ldots n \\ \end{aligned}$$

wherein $\tilde{A}_{ig}^{{\prime }}$ and $\tilde{C}_{i}^{{\prime }}$ are the fuzzy numbers, and $\tilde{A}_{ig}^{{\prime }}$ and $\tilde{C}_{i}^{{\prime }}$ could be triangle fuzzy numbers or trapezoidal fuzzy numbers. If ${\tilde{\text{A}}}_{\text{ig}}^{{\prime }}$ and ${\tilde{\text{C}}}_{\text{i}}^{{\prime }}$ are trapezoidal, the fuzzy numbers could be expressed as ${\tilde{\text{A}}}_{\text{ig}}^{{\prime }} = \left( {{\text{A}}_{\text{ig}}^{ - } , {\text{A}}_{{{\text{ig}}1}} , {\text{A}}_{{{\text{ig}}2}} , {\text{A}}_{\text{ig}}^{ + } } \right)$ and ${\tilde{\text{C}}}_{\text{i}}^{{\prime }} = \left( {{\text{C}}_{\text{i}}^{ - } , {\text{C}}_{{{\text{i}}1}} , {\text{C}}_{{{\text{i}}2}} , {\text{C}}_{\text{i}}^{ + } } \right)$.

The $\upalpha{\text{ - cut}}$ method could be used to represent the distribution interval of fuzzy number. The distribution interval of fuzzy numbers $\tilde{A}_{ig}^{{\prime }}$ and $\tilde{C}_{i}^{{\prime }}$ could be represented as $\left[ {\left( {1 - \alpha } \right) \cdot A_{ig}^{ - } + \alpha \cdot A_{ig1} , \left( {1 - \alpha } \right) \cdot A_{ig}^{ + } + \alpha \cdot A_{ig2} } \right]$ and $\left[ {\left( {1 - \alpha } \right) \cdot C_{i}^{ - } + \alpha \cdot C_{i1} , \left( {1 - \alpha } \right) \cdot C_{i}^{ + } + \alpha \cdot C_{i2} } \right]$. Wherein α is the membership.

The uncertainties of fractional programming could be processed by integrating the uncertainty number in programming. However, dynamic and varying interaction would exist between the uncertainties, and this feature which is reflected in the equation is the random distribution in the right hand side of the constraint, then it would cause the constraint be violated. In this circumstance, CCP could be used to deal with the randomness in constraint (Gupta 2009). The principle of CCP include (1) Setting a series of probabilities $P_{i} \left( {P_{i} \in \left[ {0, 1} \right]} \right)$. (2) Defining constraint equation which ensuring the probability is no less than of $\left( {1 - P_{i} } \right)$. On the premise of satisfying the conditions above, the equation could be expressed as (Charnes and Cooper 1983; Guo et al. 2014)

$$P_{i} \left[ {\left\{ {t |A_{i} \left( t \right) \cdot x \le B_{i} \left( t \right)} \right\}} \right] \ge 1 - P_{i} ,\quad A\left( t \right) \in A\left( t \right), \quad i = 1,2 \ldots n$$

(14)

where $A_{i} \left( t \right)$ is deterministic number, and $B_{i} \left( t \right)$ is stochastic number.

The constraint above is always in a nonlinear form, and it could be converted to linear programming (Guo et al. 2014). The transformed expression is $A_{i} \left( t \right) \cdot x \le \widetilde{{B_{i} \left( t \right)}}^{P}$, $A_{i} \left( t \right) \in A\left( t \right)$, $i = 1,2 \ldots n$ where $\widetilde{{B_{i} \left( t \right)}}^{P} = \left\{ {B_{i} \left( t \right)^{{P_{i} }} |i = 1,2 \ldots n} \right\}$

When there are more than one CCP exist in an uncertainty programming, the joint probability would exist in violation probabilities.

The expression of the developed uncertainty fractional joint probabilistic chance constraint programming is

$$Maxf^{ \pm } = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left\{ {\left( {C_{i}^{ \pm } + \tilde{C}_{i}^{'} } \right) \cdot x_{i}^{ \pm } + \alpha^{ \pm } } \right\}}}{{\mathop \sum \nolimits_{i = 1}^{n} \left\{ {\left( {d_{i}^{ \pm } + \tilde{d}_{i}^{'} } \right) \cdot x_{i}^{ \pm } + \beta^{ \pm } } \right\}}}$$

(15)

subject to

$$\begin{aligned} & \mathop \sum \limits_{i = 1}^{n} A_{ij}^{ \pm } \cdot x_{i}^{ \pm } \le B_{j}^{ \pm } ,\quad i = 1,2 \ldots n,\quad j = 1,2 \ldots m \\ & \mathop \sum \limits_{i = 1}^{n} \tilde{A}_{ig}^{{\prime }} \cdot x_{i}^{ \pm } \le B_{g}^{ \pm } , \quad i = 1,2 \ldots n;\quad g = 1,2 \ldots m \\ & Pr\left[ {\mathop \sum \limits_{i = 1}^{n} A_{ij}^{ \pm } \cdot x_{i}^{ \pm } \le B_{j}^{ \pm } } \right] \ge Q_{g} ,\quad i = 1,2 \ldots n,\quad j = 1,2 \ldots m \\ & Pr\left[ {\mathop \sum \limits_{i = 1}^{n} \tilde{A}_{ig}^{{\prime }} \cdot x_{i}^{ \pm } \le B_{g}^{ \pm } } \right] \ge Q_{g} ,\quad i = 1,2 \ldots n,\quad j = 1,2 \ldots m \\ & x_{i}^{ \pm } \ge 0,\quad i = 1,2 \ldots n \\ \end{aligned}$$

where $Q_{g}$ are tolerance measures,and $0 \le Q_{g} \le 1$.

The interactive algorithm could be used to solve the uncertainty programming, its principle is dividing the programming into two sub-models of $f^{ + }$ and $f^{ - }$ with two-stage method, the method is (1) establishing the sub-model $f^{ - }$ which minimize the objective function, (2) establishing the sub-model $f^{ + }$ which maximize the objective function according to the result of the sub-model $f^{ - }$ (Maqsood et al. 2005).

3.4 Uncertainty fractional joint probabilistic chance constraint programming for land use structure optimization

Integrating the certainty land use structure optimization model with the uncertainty fractional joint probabilistic chance constraint programming, and the developed model is as follows.

Objective function:

Economic maximization and environmental influence minimization

$$maxf\left( x \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{n = 12} \left[ {\left( {UB_{i}^{ \pm } - UC_{i}^{ \pm } } \right) \cdot x_{i}^{ \pm } } \right]}}{{\mathop \sum \nolimits_{i = 1}^{n = 12} \left( {TN_{i}^{ \pm } \cdot x_{i}^{ \pm } } \right)}}\quad i = 1,2, \ldots 12$$

(16)

Constraint:

The total investment cannot exceed the governmental budget under uncertainty.

$$\mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{n}} = 12}} \left( {{\text{UI}}_{\text{i}}^{ \pm } \cdot {\text{x}}_{\text{i}}^{ \pm } } \right) \le {\text{TI}}^{ \pm } \quad {\text{i}} = 1,2, \ldots 12$$

(17)

The total amounts of water consumption cannot exceed the amount of regionally available water resources under uncertainty.

$$\mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{n}} = 12}} \left( {{\text{UWC}}_{\text{i}}^{ \pm } \cdot {\text{x}}_{\text{i}}^{ \pm } } \right) \le {\text{AWC}}^{ \pm } \quad {\text{i}} = 1,2, \ldots 12$$

(18)

The population cannot exceed the total population of the study area under uncertainty.

$$\mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{n}} = 12}} \left( {{\text{UP}}_{\text{i}}^{ \pm } \cdot {\text{x}}_{\text{i}}^{ \pm } } \right) \le {\text{TP}}^{ \pm } \quad {\text{i}} = 1,2, \ldots 12$$

(19)

The amount of labor cannot exceed the total amount of available labor in the study area under uncertainty.

$$Pr\left[ {\mathop \sum \limits_{i = 1}^{12} \left( {UL_{i}^{ \pm } \cdot x_{i}^{ \pm } } \right) \le AL^{ \pm } } \right] \ge Q_{g} \quad i = 1,2, \ldots 12$$

(20)

The total area of the land use cannot exceed the amount of available area in the study area under uncertainty.

$$\mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{n}} = 12}} {\text{x}}_{\text{i}}^{ \pm } \le {\text{AA}}^{ \pm } \quad {\text{i}} = 1,2, \ldots 12$$

(21)

The area of each type of land use should be no less than the minimum area of land use for “planning” under uncertainty.

$${\text{x}}_{\text{i}}^{ \pm } \ge {\text{MA}}_{\text{i}}^{ \pm } \quad {\text{i}} = 1,2, \ldots 12$$

(22)

The area of basic agriculture land use should be no less than the minimum basic agricultural land use area for “planning” under uncertainty.

$$Pr\left[ {x_{1}^{ \pm } \ge MA_{1}^{ \pm } } \right] \ge Q_{g}$$

(23)

The green space ratio of the study area should be no less than the minimum requirement of the green-spaced ratio.

$${{\left( {x_{2} + x_{3} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{2} + x_{3} } \right)} {\mathop \sum \limits_{i = 1}^{n = 12} \left( {x_{i}^{ \pm } } \right) \ge MFCR\quad i = 1,2, \ldots 12}}} \right. \kern-0pt} {\mathop \sum \limits_{i = 1}^{n = 12} \left( {x_{i}^{ \pm } } \right) \ge MFCR\quad i = 1,2, \ldots 12}}$$

(24)

The framework of the methodology is listed in Fig. 2.

Fig. 2

The framework of the methodology

4 Results and discussion

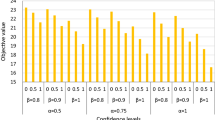
The results of the study are a series of land use structure planning schemes and the corresponding economic benefits and pollution discharges. Furthermore, the results are composed of fixed and interval numbers (Table 4).

Table 4 The total benefit (CNY), total TN discharge (kg), ratio of benefit to pollution and land use structure planning schemes in different scenarios

The study results shows the interval of system benefit and land use distribution scheme as well as total TN discharge. Table 4 shows the results in different P scenarios. The variables of UB+, UC−, TN−, UP−, UL− and UWC− lead to upper bound of system benefit and the ratio of economic benefit to pollution discharge as well as lower bound of TN discharge, while the variables of UB−, UC+, TN+, UP+, UL+ and UWC+ lead to lower bound of system benefit and ratio of economic benefit to pollution discharge as well as upper bound of TN discharge, and they are two extreme. Taking P11 scenario as example, the economic benefit, TN discharge and the ratio of economic benefit to pollution discharge in P11+ are 121,077,116.6 CNY, 2,757,750.51 kg and 43.90, while in P11− are 79,743,734.4, 3,924,675.39 and 20.32 separately, it is obviously that the values of benefit and ratio of economic benefit to pollution in P11+ scenario are much larger than the values in P11− scenario, while the value of TN discharge in P11+ scenario is much lower than the value in P11− scenario. Except for economic index and pollution index, the areas of wood land, pasture, urban land and industry and mining land are also different, and the area of four land are 40,600.77, 103.98, 33,693.29 and 579.86 separately in P11+ scenario, while the four land are 35,079.08, 6058.18, 33,408.81 and 431.81 separately in P11− scenario.

• 1. Comparison between optimization results and planning index in objective year 2020

  Comparing the optimization results with the planning index in 2020 of “Land use master planning for Xiangjiang new district (2016–2020)”. The area of farmland in optimization results are lower than the area of the farmland in “planning 2020” in all scenarios. The area of woodland and industry and mining land are lower than the same types of land in planning 2020 in many scenarios.

  The results show that the area of the land with high ecological benefit (woodland) and high economic benefit (industry and mining land) are higher than the area of the same land in planing year 2020, and the land with high pollution and low economic benefit (agriculture land) is lower than the area of the same land in the planning year 2020.

  The constraint boundary value of the constraint function is set based on planning index of “Land use planning for Xiangjiang new district (2016–2020)”. The upper boundary of the construction land constraint value and other land (water and natural reserve land) are set based on the planning index in 2020 year. One of the aims of the study is identify the differences between optimization results and the planning index in target year within the framework of the “planning”.

• 2. Relationship between uncertainty and P and system

  When the land use planning model is integrated with uncertainty, fluctuation for the total benefit, pollution discharge, and land use policy due to the uncertainty influence will occur.

  The joint probability P represents the violation probability for the quantity of the available labor and the minimum agriculture area, and it also represents the system risk. P is closely related to the benefit, pollution discharge, and land use policy. The increase in P indicates a slack land use policy and high pollution. In the study of single objective optimization with the objective of benefit maximization, the system benefit increases as P increases. By contrast, in the multi-objective fractional programming, the system benefit and pollution discharge will not increase with the increase in P. For example, the total benefits of P1+, P2+ and P3+ are 121,077,116.6, 121,071,036.7 and 121,066,650.4 separately, and the benefits show a declining trend, whereas the benefits of P11−, P12− and P13− are 79,743,734.4, 80,520,858.1 and 80,520,858.1 separately, and the benefits do not increase with P. The TN discharge of P1+, P2+ and P3+ are 2,757,750.51, 2,750,752.30 and 2,745,706.74 separately, and it also shows a declining trend, however the TN discharge of P1−, P2− and P3− show no trend.

  The reason is that, in single-objective programming, the benefits increase with the increment in the areas of highly beneficial land (such as business land use and industrial land use). In general, these types of land cause high pollution; when the policy is slack, areas with pollution can be supplied abundantly.

  In fractional programming, the policy is slack with the increase in P. Thus, the land use scheme should have optimal values to either maximize the benefit or minimize the pollution for maximizing the objectives.

• 3. Relationship among uncertainty, economy, and pollution

  The economic benefit and pollution discharge are in the interval form because the distribution interval of uncertainty in the model directly influences the values of the system benefit and the pollution discharge; the effects on the results will be overlaid together. The interval number of the study represents the maximum boundary of the uncertainty influence on the system.

  In terms of P1, P2, and P3, which represent the area of minimum agricultural land, no progressive increase or decrease for economic benefit and pollution discharge occurs. The reason is that the research objective of the study is fractional, and the objective is to maximize the ratio of economic benefit to pollution discharge. In terms of P1, P2, and P3, the upper and lower boundaries of F increase gradually. The upper boundary of ratio of P1, P2 and P3 are 43.9, 44.01 and 44.09 separately, and the inter number of lower boundary are [20.32, 20.44], [20.44, 20.49] and [20.43, 20.53].

  In terms of the joint probabilities in which i represents agriculture land (exp: $P_{i1}$, $P_{i2}$, $P_{i3}$), the upper bound of the economic benefit and the pollution discharge remain the same in scenarios $P_{ij}$ in which i represents agricultural land. The reason is that, in the upper boundary, the constraint values of the constraint programming can satisfy the maximum demand. In terms of the lower bounds of benefit and pollution discharge, in each scenario of $P_{i}$, the values of scenarios $P_{i2}$ and $P_{i3}$ are the same and the two values are different from the values of scenario $P_{i1}$. The reason is that the constraint values of the violation probability $P_{i2}$ and $P_{i3}$ have satisfied the maximum demand for the area of land use and economy. Thus, the values of scenario $P_{i2}$ are the same as the value of scenario $P_{i3}$, whereas the constraint values of $P_{i}$ still cannot achieve the maximum demand of the constraint. Therefore, $P_{i1}$ is different from $P_{i2}$ and $P_{i3}$.

• 4. Relationship of uncertainty between land use types

  • 1. The results of the land use planning are the combination of interval and single values, such as the results of P11 scenario. The interval sets are caused by the labor amount uncertainty and the other uncertainty factors, and the area of a type of land in the lower bound scenario will be less than the area in the upper bound scenario. The reasons for this result include the labor amount constraint in the lower bound scenario and the choice of the upper boundaries of the labor amount per unit area. For example, in P11, the interval distribution of the forest land area, urban land area, and industrial land area are [35,079.08, 40,600.77], [33,408.81, 33,693.29], and [431.81, 579.86], respectively. The results show that the numbers of low bound scenarios are all lower than the numbers of upper bound scenarios. However, the value of the grassplot area is [6058.18, 103.98], and the results show that the area of lower bound scenario is higher than the area of upper bound scenario. The reason is that all of the land needs to be in use. The restriction of labor amount and labor for unit area of grassplot is lower than that of the labor for unit area of forest and other types of land. Thus, the amount of grassplot land area in the lower bound scenario is higher than the number in the upper bound scenario.

    In other scenarios of land use planning, the amounts of labor in the scenarios of upper and lower levels are the same. This situation leads to the same land use type and same area for all the types of land use. In P12 and P13, the amount of labor in all the scenarios of lower and higher bounds can satisfy the need of labor for all the types of land. Thus, the land use plans in the two scenarios are the same.

    In the other scenarios, the regularities of distribution are the same as P.

  • 2. The areas of agricultural land in the upper scenario are 20,217.48 ha (P1), 19,799.54 ha (P2), and 19,498.18 ha (P3). The values show a decreasing tendency, and the values are the results of the violation probability of the area of agricultural land.

• 5. Relationship between the constraint value and the influence of P

  The values that are associated with P are the minimum agricultural area and the labor amount. The initialization of the two values influences the land use policy, the system benefit, and the pollution discharge. When the labor amount is larger than a threshold value, the variation in P will not affect the land use policy because the amount of labor can satisfy the labor demand for all the industries in each scenario.

• 6. All the uncertainty factors would influence the optimization system. In the study, the factors which influence land use distribution scheme are mainly the human uncertainty which include constraint violation of workforce and basic farmland area, and also include the TN discharge of different types of land use. The natural uncertainty in the study is AWC(available water resources), because the amount of AWC in the study area is much higher than the water requirement, thus the natural uncertainty do not influence the system. If the budget and water resources are inadequate, the UC and UWC would also influence the scheme.

• 7. The dependency of the selected variables is not checked in the study, that is because the there are very likely the interplay between the variables. However the fractional programming is converted in linear programming when calculating the model, then it could avoid the concavity in the function.

• 8. The interval numbers of the results represent the maximum scale of the uncertainty influence. Therefore, all the possible uncertainty results will be in the intervals.

• 9. The developed model of the study can process the multi-objective fractional programming under uncertainty and has the following advantages:

  • 1. The economic factor and environmental factor can be considered equally in the model, and sustainable land use structure planning can be structured.

  • 2. The model can reflect the different types of uncertainties, and the results of the model are in the form of interval number to express the scale of the uncertainty influence.

• 10. The objectives function of the model are only economic benefit maximization and TN charge minimization, and it lead to some types of land use with high ecological value are not increase in planning. However, if the ecological benefit maximization is increased as one of the objective functions, it mean each type of unit land should be calculated in certain amount of ecological benefit, then the land use with high ecological value, such as pasture and natural reserve land, would be increased, and this question refers to multiple fractional programming, and we would study it in future.

• 11. The land use structure planning under uncertainty will become increasingly important in the future. Owing to uncertainties in nature and society, the land use structure optimization will gradually transfer from the certainty planning to more flexible planning and management, and this situation will represent one of the tendencies for land use planning.

5 Conclusion

• 1. The uncertainty fractional joint probabilistic CCP model is developed for land use structure planning. The model integrates fractional programming with interval programming, fuzzy programming, stochastic programming, and CCP. The model can process the fractional programming and the uncertainty in the form of interval, fuzzy, and stochastic numbers. Furthermore, the model can process the problem of probability violation.

• 2. Few fractional models are used in land use structure planning. The developed model of the study is used in land use planning in Xiangjiang New District, Changsha, Hunan. The model can consider the objectives of economy and environment in land use structure planning and can identify and process the possible uncertainty in the form of interval, fuzzy, and stochastic numbers. Furthermore, the approach can reflect the joint probability of labor amount and minimum agricultural area. The results of the study are in the form of combination of deterministic and interval numbers.

• 3. The developed method is a flexible model for planners. The method can help planners provide flexible planning to address the uncertainty and variation depending on the possible scenarios.

• 4. The interval of the result is the maximum scale of the uncertainty impact, and the possible results of the uncertainty are all in the interval in practical terms.

• 5. With the increase in P, the system risk also increases. These increases are accompanied by the increase in objective function value but no progressive increase in economy and pollution discharge.

• 6. Our method has universality and can be extended to the other studies of land use planning.

• 7. The method of the study cannot solve the problems of multiple fractional objectives and the land distribution between districts and sub-districts. These problems need further research.

Appendix

$UB_{i}$ :

the benefit of the unit area of the $i{\text{-}}th$ land use

$x_{i}$ :

the $i{\text{-}}th$ type of land use

$TN_{i}$ :

nitrogen discharge of $i{\text{-}}th$ type of land use

$UI_{i}$ :

the invest for ${\text{i-th}}$ type of land use

$TI$ :

the total governmental invest

$UWC_{i}$ :

the water requirement for the $i{\text{-}}th$ type of land use

$AWC$ :

the water resources of the study area

$UP_{i}$ :

the population in unit area of the $i{\text{-}}th$ type of land use

$TP$ :

the total population of the study area

$UL_{i}$ :

the amount of labor for the $i{\text{-}}th$ type of land use

$AL$ :

the amount of labor in the study area

$AA$ :

the amount of available area in the study area

$MA_{i}$ :

the minimum area of the $i{\text{-}}th$ type of land use of the “planning”

$MFCR$ :

the minimum requirement of the green spaced ratio