Global and local diagnostic analytics for a geostatistical model based on a new approach to quantile regression

Abstract

Data with spatial dependence are often modeled by geoestatistical tools. In spatial regression, the mean response is described using explanatory variables with georeferenced data. This modeling frequently considers Gaussianity assuming the response follows a symmetric distribution. However, when this assumption is not satisfied, it is useful to suppose distributions with the same asymmetric behavior of the data. This is the case of the Birnbaum–Saunders (BS) distribution, which has been considered in different areas and particularly in environmental sciences due to its theoretical arguments. We propose a geostatistical model based on a new approach to quantile regression considering the BS distribution. Global and local diagnostic analytics are derived for this model. The estimation of model parameters and its local influence are conducted by the maximum likelihood method. Global influence is based on the Cook distance and it is compared to local influence, in both cases to detect influential observations, whose detection and removal can modify the conclusions of a study. We illustrate the proposed methodology applying it to environmental data, which shows this situation changing the conclusions after removing potentially influential observations. A comparison with Gaussian spatial regression is conducted.

1 Introduction

The Birnbaum–Saunders (BS) distribution constantly arises in the applied statistical literature. In the last decades, it has been shown to be versatile and efficient in several fields of science, being widely studied, due to its theoretical justification, its good properties and its close relation with the Gaussian or normal model. The BS distribution is unimodal, with asymmetry to the right and support defined on the positive real numbers, in addition to being indexed by two parameters that control its shape and scale. The BS distribution has its origins in physics and engineering, being it derived to model a fatigue phenomenon related to crack development in metallic objects; see Leiva (2019). Recently, Budsaba et al. (2020) suggested a physical model of this phenomenon which shows exactly how Birnbaum and Saunders (1969) derived their distribution to fit the model of a crack development. However, at the present, the BS distribution has gained increasing popularity in diverse areas including business (Leiva et al. 2014, 2016b; Saulo et al. 2019; Sánchez et al. 2020a), industry (Huerta et al. 2019; Leiva et al. 2019), and medicine (Lemonte et al. 2015; Leao et al. 2018a, b), among other areas. Nevertheless, outside the material fatigue phenomenon where the BS distribution was originated, the field where it has been widely applied is air pollution (Ferreira et al. 2012; Saulo et al. 2013; Marchant et al. 2018, 2019; Cavieres et al. 2020) and natural phenomena (Garcia-Papani et al. 2018a, b; Martinez et al. 2019; Carrasco et al. 2020), that is, in environmental sciences. The reason for this increasing applicability of the BS distribution in environmental sciences is because Leiva et al. (2015) proposed a chemical-physical model which shows how the derivation of Birnbaum and Saunders (1969) can be adapted to fit environmental data. These applications have been conducted by an interdisciplinary, international group of researchers. Note also that the study of methodological and theoretical issues of the BS distribution has received growing interest and a considerable amount of work is available; see Leiva and Saunders (2015), Leiva (2016), Aykroyd et al. (2018), Balakrishnan and Kundu (2019), Dasilva et al. (2020) and references therein, which summarize most of the works to the date.

Standard regression models describe the mean response given values of the explanatory variables. Nevertheless, if the response has an asymmetrical distribution, the mean is not a suitable centrality measure to summarize the data. Quantile regression was proposed by Koenker and Bassett (1978), extending the median regression to the ordinary quantiles by using the regression context. We propose to model the median or other quantiles of the BS distribution by regression. Considering a spatial component in the modeling may improve the accuracy of an estimator of the mean (or median); see Diggle and Ribeiro (2007). A first idea of spatial quantile regression was suggested by Kostov (2009). Trzpiot (2013) derived a spatial regression model using the quantile function; see McMillen (2013) for some variants of spatial quantile regressions. Garcia-Papani et al. (2017, 2018a, b) introduced BS spatial models for the mean, which need multivariate BS distributions; see, for example, Kundu (2015), Lemonte et al. (2015), Sánchez et al. (2015), Marchant et al. (2016a, b) and Garcia-Papani et al. (2017, 2018a, b). BS quantile regression was introduced by Sánchez et al. (2020a) and spatial BS quantile regression by Sánchez et al. (2020b), but to the best of our knowledge, global and local influence diagnostics for the spatial BS quantile regression do not have been formulated to the date.

Diagnostic analytics plays a relevant role in statistical modeling, which can be divided into global and local influence techniques. The Cook distance and residuals are well-known and often used as measures of global influence for detecting the model adequacy; see Krzanowski (1998) and Leiva et al. (2016a). However, the local influence technique is currently very popular, which allows us to evaluate the local effect of perturbations on the estimates of parameters and then to detect potentially influential cases in different models; see, for example, Diaz-Garcia et al. (2003), Santana et al. (2011), Garcia-Papani et al. (2017), Tapia et al. (2019a, b), and Liu et al. (2020). Detection and removal of potentially influential cases can modify the conclusions of a study.

This research has as objective to derive a geostatistical model based on Birnbaum–Saunders quantile regression and its global and local influence diagnostics. We use a new quantile parameterization to generate the model, which permits us to consider a similar framework to generalized linear models, providing wide flexibility. A comparison with Gaussian spatial regression is performed, but with other natural competing models, as gamma, lognormal or Weibull, it is not possible because such models based on our new parameterization are not available in the literature.

In Sect. 2, we present the original parameterization of the multivariate BS distribution and a new parameterization of it to model quantiles. Section 3 proposes the model and provides estimation of its parameters based on the maximum likelihood (ML) method. Then, in Sect. 4, we derive global influence measures based on the Cook distance for detecting influential potentially observations. Section 5 introduces the local influence technique for the new model including two schemes of perturbation. Next, we illustrate the proposed methodology in Sect. 6 considering an example related to environmental data. Some conclusions and future works are given in Sect.  7. All the numerical calculations were carried out with the aid of the R software; see R-Team (2018). Mathematical details of our results are provided in the Appendix.

2 The BS distribution and a new parameterization

2.1 The BS distribution

A random variable T given by the stochastic represention

$$\begin{aligned} T=T(Z; \alpha , \sigma )=\sigma \left( \alpha Z/2+\sqrt{\left( \alpha Z/{2}\right) ^2+1}\right) ^2, \end{aligned}$$

(1)

where $Z \sim \text {N}(0,1)$, follows a BS distribution of shape ($\alpha >0$) and scale ($\sigma >0$) parameters. We use the notation $T \sim \text {BS}(\alpha , \sigma )$ to indicate it.                                                          

Let the random vector ${\varvec{V}}= (V_1,\ldots ,V_n)^{\top } \in {\mathbb {R}}^n$ follow an n-variate normal distribution, which we denote as ${\varvec{V}}\sim \text {N}_n({\varvec{\mu }}, {\varvec{\Gamma }})$, where ${\varvec{\mu }}= (\mu _i) \in {\mathbb {R}}^n$ is a mean vector and ${\varvec{\Gamma }}= (\rho _{jk}) \in {\mathbb {R}}^{n \times n}$ is a variance-covariance matrix, with $\text {rank}({\varvec{\Gamma }})=n$. If ${\varvec{\mu }}= {\varvec{0}}_{n \times 1}$, that is, the null vector with ${\varvec{0}}_{n \times 1}$ being an $n \times 1$ vector of zeros, we use the notation $\phi _n$ and $\Phi _n$ for the n-variate normal density and distribution function, respectively. Then, ${\varvec{T}}=(T_1,\ldots , T_n)^{\top } \in {\mathbb {R}}_{+}^n$ is an $n \times 1$ random vector with n-variate BS distribution of parameters ${\varvec{\alpha }}=(\alpha _1,\ldots ,\alpha _n)^{\top } \in {\mathbb {R}}_{+}^n$, ${\varvec{\sigma }}=(\sigma _1,\ldots ,\sigma _n)^{\top } \in {\mathbb {R}}_{+}^n$, and ${\varvec{\Gamma }}\in {\mathbb {R}}^{n \times n}$, if $T_i=T(V_i; \alpha _i, \sigma _i)$, for $i=1,\ldots,n$, where the  T function, with V instead of Z, is given in (1) and ${\varvec{V}}=(V_1,\ldots ,V_n)^{\top } \in {\mathbb {R}}^{n} \sim \text {N}_n({\varvec{0}}_{n \times 1}, {\varvec{\Gamma }})$. Note from (1) that $Z \sim \text {N}(0,1)$ and then ${\varvec{\Gamma }}\in {\mathbb {R}}^{n \times n}$ has its diagonal elements equal to one. Hence, the variance-covariance matrix ${\varvec{\Gamma }}$ is also the correlation matrix of ${\varvec{V}}$, but not of ${\varvec{T}}$, although for simplicity we denote the n-variate BS distribution as ${\varvec{T}}\sim \text {BS}_n({\varvec{\alpha }}, {\varvec{\sigma }}, {\varvec{\Gamma }})$. The variance-covariance matrix of ${\varvec{T}}$ is expressed as

$$\begin{aligned} \text {Var}({\varvec{T}})= \dfrac{1}{16} {\varvec{\Omega }}\odot \left( {\varvec{\Gamma }}\odot {\varvec{\Gamma }}\odot {{\varvec{\Xi }}} + 4 {{\varvec{\Upsilon }}} \right) , \end{aligned}$$

(2)

where ${\varvec{\Omega }}=(\omega _{ij})$, ${{\varvec{\Xi }}}=(\xi _{ij})$ and ${{\varvec{\Upsilon }}} = (\upsilon _{ij})$ have elements $\omega _{ij}=\alpha _{i}^{2} \alpha _j^{2} \sigma _{i} \sigma _j$, $\xi _{ij}=\alpha _i \alpha _j$ and $\upsilon _{ij}=I(\alpha _i, \alpha _j, \rho _{ij})$, respectively, for $i, j=1,\ldots ,n$, and $\odot$ is the Hadamard product; see details in Marchant et al. (2016a) and Sánchez et al. (2020b). Thus, the density and distribution function of ${\varvec{T}}$ are, respectively, given by

$$\begin{aligned} &f_{{\varvec{T}}}({\varvec{t}}; {\varvec{\alpha }}, {\varvec{\sigma }}, {\varvec{\Gamma }}) = \phi _n({\varvec{A}}; {\varvec{\Gamma }}) \,a({\varvec{t}}; {\varvec{\alpha }}, {\varvec{\sigma }}),\\ &F_{{\varvec{T}}}({\varvec{t}}; {\varvec{\alpha }}, {\varvec{\sigma }}, {\varvec{\Gamma }}) = \Phi _n({\varvec{A}}; {\varvec{\Gamma }}), \, {\varvec{t}}= (t_1,\ldots ,t_n) \in {\mathbb {R}}_{+}^n, \end{aligned}$$

where ${\varvec{A}}= {\varvec{A}}({\varvec{t}}; {\varvec{\alpha }}, {\varvec{\sigma }})=(A_1,\ldots ,A_n)^{\top },\,$ with

$$A_j = ({1}/{\alpha _j}) (\sqrt{t_j/\sigma _j}-\sqrt{\sigma _j/{t_j}}),$$

and $a({\varvec{t}}; {\varvec{\alpha }}, {\varvec{\sigma }}) = \prod _{j=1}^n a(t_j; \alpha _j, \sigma _j),$ with

$$a(t_j; \alpha _j, \sigma _j) = ({1}/({2\alpha _j \sigma _j}))( \sqrt{{\sigma _j}/{t_j}} + \sqrt{(\sigma _j/t_j)^{3}}).$$

2.2 A new quantile parameterization of the BS distribution

Let ${\varvec{T}}=(T_1,\ldots ,T_n) \sim \text {BS}_n({\varvec{\alpha }}, {\varvec{\sigma }}, {\varvec{\Gamma }})$ and $q \in (0,1)$ be a fixed value. Then, we have a new parameterization of the n-variate BS distribution by the transformation expressed as $({\varvec{\alpha }}, {\varvec{\sigma }}, {\varvec{\Gamma }}) \mapsto ({\varvec{\alpha }}, {\varvec{Q}}, {\varvec{\Gamma }})$, where $Q_i$ and $\sigma _i$ are related by

$$\begin{aligned} Q_i=\frac{\sigma _i}{4} \gamma _{\alpha }^2,\end{aligned}$$

(3)

with $\gamma _{\alpha }= \alpha _i z_q + (\alpha _i^2 z_q^2+4)^{1/2}$, for the marginal distribution of $T_i$, $Q_i$ being the q-th quantile of the $\text {BS}(\alpha _i, \sigma _i)$ distribution (Sánchez et al. 2020a), for all $i=1,\ldots,n$, and $z_q$ being the q-th quantile of the standard normal distribution. This new parameterization of the n-variate BS distribution is denoted by ${\varvec{T}}\sim \text {BS}_n({\varvec{\alpha }}, {\varvec{Q}}, {\varvec{\Gamma }})$, with density and distribution function given, respectively, by

$$\begin{aligned} &f_{{\varvec{T}}}({\varvec{t}}; {\varvec{\alpha }}, {\varvec{Q}}, {\varvec{\Gamma }}) = \phi _n({\tilde{{\varvec{A}}}}; {\varvec{\Gamma }}) \,{\tilde{a}}({\varvec{t}}; {\varvec{\alpha }}, {\varvec{Q}}), \nonumber \\ &F_{{\varvec{T}}}({\varvec{t}}; {\varvec{\alpha }}, {\varvec{Q}}, {\varvec{\Gamma }}) = \Phi _n({\tilde{{\varvec{A}}}}; {\varvec{\Gamma }}), \quad {\varvec{t}}= (t_1,\ldots ,t_n) \in {\mathbb {R}}_{+}^n, \end{aligned}$$

(4)

where ${\tilde{{\varvec{A}}}}=(\tilde{A_1},\ldots ,\tilde{A_n})^{\top }$,  with

$$\begin{aligned} \tilde{A_j}& = \frac{1}{\alpha _j \gamma _{\alpha _j}}\sqrt{\frac{4Q_j}{t_j}}\left( \frac{t_j \gamma _{\alpha _j}^2}{4Q_j}-1\right) , \\{\tilde{a}}({\varvec{t}}; {\varvec{\alpha }}, {\varvec{Q}})& = \prod _{j=1}^n \frac{1}{\alpha _j \gamma _{\alpha _j}\sqrt{4Q_j t_j}} \left( \frac{\gamma _{\alpha _j}^2}{2}+\frac{2Q_j}{t_j}\right) , \end{aligned}$$

and $\gamma _{\alpha _j}$ being defined in (3).

2.3 A shape analysis of the BS distribution parameterized by its quantiles

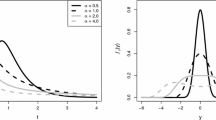
From Fig. 1, note that some shapes of the density expressed in (4) and their corresponding level curves are shown, for $n=2$, varying the parameters $\alpha$ (a)–(c) and Q ( d)–(f).

Fig. 1

Bivariate BS density plots for (a) $\alpha _i=0.3$, (b) $\alpha _i=0.7$, (c) $\alpha _i=1.3$, with $Q_i=1.0$, and (d) $Q_i=0.3$, (e) $Q_i=0.7$, (f) $Q_i=1.3$, with $\alpha _i=1.0$, for $i=1,2$ and $\rho =0.9$

3 Formulation and estimation of the geostatistical model

3.1 The BS spatial quantile regression model

To describe data dependent spatially, assume the stochastic process ${\varvec{T}}= \{T({\varvec{s}}); \, {\varvec{s}}\in {\varvec{D}}\}$ defined on ${\varvec{D}}\in {\mathbb {R}}^2$. We consider that ${\varvec{T}}$ is stationary and isotropic, and that for spatial locations in ${\varvec{s}}_i$, with $i=1,\ldots,n$, the quantile function of the process may be formulated as

$$\begin{aligned} Q(T({\varvec{s}}_i)) = Q_{i}({\varvec{\beta }}) = h^{-1}({\varvec{x}}_i^{\top } {\varvec{\beta }}), \quad i=1,\ldots,n, \end{aligned}$$

(5)

with h being a strictly monotone function of positive support and at least twice differentiable. Observe that ${\varvec{x}}_i^{\top }=(1, x_{i2}, \ldots , x_{ip})$ are the values of $p-1$ explanatory variables, with $x_{ij}=x_j({\varvec{s}}_i)$, for $j=1,\ldots,p-1$, that is, $x_{ij}$ is the value of the explanatory variable $X_j$ at ${\varvec{s}}_i$. Here, ${\varvec{\beta }}=(\beta _0, \beta _1, \ldots , \beta _{q})^{\top }$, for $q=p-1 < n$, corresponds to a vector of regression coefficients to be estimated. In addition,

$$\begin{aligned}&(T({\varvec{s}}_1),\ldots ,T({\varvec{s}}_n)) \sim \text {BS}_n(\alpha {\varvec{1}}_{n \times 1}, {\varvec{Q}}({\varvec{\beta }}), {\varvec{\Gamma }}), \, \alpha >0, \end{aligned}$$

(6)

Notice where $\alpha$ is a scalar shape parameter, ${\varvec{1}}_{n \times 1}$ is an $n \times 1$ vector of ones, ${\varvec{\Gamma }}$ is the $n \times n$ matrix defined in (4), and ${\varvec{Q}}({\varvec{\beta }})^{\top }=(Q_{1}({\varvec{\beta }}),\ldots , Q_{n}({\varvec{\beta }}))$, with $Q_{i}({\varvec{\beta }})$ given in (5), for $i=1,\ldots,n$. From (2), note that the variance-covariance matrix of the BS spatial quantile regression model can be written as

$$\begin{aligned} \text {Var}({\varvec{T}})=\frac{4\alpha ^{2}}{\gamma _{\alpha }^{4}}({\varvec{Q}}({\varvec{\beta }}) {\varvec{Q}}({\varvec{\beta }})^{\top }) \odot ( \alpha ^2 {\varvec{\Gamma }}\odot {\varvec{\Gamma }}+ 4 \, {{\varvec{\Upsilon }}}). \end{aligned}$$

(7)

Notice that the variance-covariance matrix of the BS spatial process stated in (7) depends on its quantile function.

3.2 Modeling spatial dependence

Suppose that the spatial dependence is established by means of the $n \times n$ spatial correlation matrix ${\varvec{\Gamma }}$, which is symmetric, non-singular and positive definite. The structure of this matrix is described by the Matérn model (Diggle and Ribeiro 2007) following an alternative parameterization proposed by Stein (1999). Thus, the elements of the matrix ${\varvec{\Gamma }}$ are given by

$$\begin{aligned} \rho _{ij}=\left\{ \begin{array}{l} 1,\quad i=j,\\ \frac{\varphi ^\delta }{2^{\delta -1}\Gamma (\delta )} h_{ij}^\delta K_\delta \left( h_{ij} \,\varphi \right) ,\quad i\ne j, \end{array} \right. \end{aligned}$$

(8)

where $\delta > 0$ is a shape parameter; $\Gamma$ is the usual gamma function; $h_{ij}$ is the Euclidean distance between the locations ${\varvec{s}}_i$ and ${\varvec{s}}_j$, that is, $h_{ij}=||{\varvec{s}}_i -{\varvec{s}}_j||$; $\varphi > 0$ is a parameter known as the inverse spatial dependence radius (Zhang and Wang 2010) and also related to a parameter named microergodic by Stein (1999); and $K_\delta$ is the modified Bessel function of the third kind of order $\delta$; see Gradshteyn and Ryzhik (2000). Note that the expression defined in (8) can be written in matrix form as

$$\begin{aligned} {\varvec{\Gamma }}= {\varvec{\Gamma }}(\varphi ) = {\varvec{I}}_n+ \dfrac{\varphi ^{\delta }}{2^{\delta -1} \Gamma (\delta )} \, {\varvec{J}} \odot {\varvec{H}}_{\delta } \odot {\varvec{K}}_{\delta }, \end{aligned}$$

(9)

where ${\varvec{I}}_n$ is the $n\times 1$ identity matrix; ${\varvec{J}}$ is a matrix with diagonal elements equal to zero and all other elements are ones; ${\varvec{H}}_{\delta }=(h_{ij}^{\delta })$ and ${\varvec{K}}_{\delta }=(K_{\delta }(\varphi \, h_{ij}))$. Table 1 provides some special members of the Matérn family.

Table 1 Special members of the Matérn correlation function

3.3 Estimation of model parameters

For the spatial model formulated in (5), as usual, we consider the shape parameter $\delta$ of the Matérn model to be a fixed value. Thus, the $(p+2)\times 1$ parameter vector of the BS spatial quantile regression model to be estimated is ${\varvec{\theta }}= ({\varvec{\beta }}^{\top }, \varphi ,\alpha )^{\top }$, where ${\varvec{\beta }}$ are the regression coefficients, $\varphi$ is the spatial correlation parameter, and $\alpha$ is the shape parameter of the BS distribution, which is assumed to be constant but unknown in the BS spatial process. Therefore, by using the observations ${\varvec{t}}= (t_1,\ldots ,t_n)$, the corresponding BS spatial quantile regression parameter can be estimated by the ML method with log-likelihood function for ${\varvec{\theta }}$ defined as

$$\begin{aligned} \ell ({\varvec{\theta }}) = -\frac{n}{2} \log (2\pi ) -\frac{1}{2} \log (|{\varvec{\Gamma }}|) - \frac{1}{2} {\tilde{{\varvec{A}}}}^{\top } {\varvec{\Gamma }}^{-1} {\tilde{{\varvec{A}}}} + \log ({\tilde{a}}), \end{aligned}$$

(10)

where ${\tilde{{\varvec{A}}}}={\tilde{{\varvec{A}}}}({\varvec{t}}; \alpha {\varvec{1}}_{n \times 1}, {\varvec{Q}})$ and ${\tilde{a}}={\tilde{a}}({\varvec{t}}; \alpha {\varvec{1}}_{n \times 1}, {\varvec{Q}})$, with ${\varvec{Q}}={\varvec{Q}}({\varvec{\beta }})$ given from (6), and ${\varvec{\Gamma }}= {\varvec{\Gamma }}(\varphi )$ given in (9). By taking the derivative of (10), with respect to ${\varvec{\theta }}$, allows us to obtain the $(p+2) \times 1$ score vector given by

$$\begin{aligned} {\dot{\ell }}({\varvec{\theta }})& = \left( \left( \dfrac{\partial \ell ({\varvec{\theta }})}{\partial {\varvec{\beta }}} \right) ^{\top }, \dfrac{\partial \ell ({\varvec{\theta }})}{\partial \varphi },\left( \dfrac{\partial \ell ({\varvec{\theta }})}{\partial \alpha } \right) ^{\top }\right) ^{\top } \\& = \left( {\dot{\ell }}_{\beta _1}, \ldots , {\dot{\ell }}_{\beta _p}, {\dot{\ell }}_{\varphi }, {\dot{\ell }}_{\alpha } \right) ^{\top }, \end{aligned}$$

where

$$\begin{aligned} {\dot{\ell }}_{\beta _j}& = -{\tilde{{\varvec{A}}}}^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial {\tilde{{\varvec{A}}}}}{\partial \beta _j} + \dfrac{\partial }{\partial \beta _j}(\log ({\tilde{a}})),\\ {\dot{\ell }}_{\varphi }& = -\dfrac{1}{2} \, \text {tr}\left( {\varvec{\Gamma }}^{-1} \dfrac{\partial \, {\varvec{\Gamma }}}{\partial \varphi }\right) +\dfrac{1}{2} {\tilde{{\varvec{A}}}}^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial \, {\varvec{\Gamma }}}{\partial \varphi } {\varvec{\Gamma }}^{-1} {\tilde{{\varvec{A}}}},\\ {\dot{\ell }}_{\alpha }& = -{\tilde{{\varvec{A}}}}^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial {\tilde{{\varvec{A}}}}}{\partial \alpha } + \dfrac{\partial }{\partial \alpha }(\log ({\tilde{a}})), \end{aligned}$$

with ${\partial {\tilde{{\varvec{A}}}}}/{\partial \beta _j} = ({\partial {\tilde{A}}_k}/{\partial \beta _j})$ and ${\partial {\tilde{{\varvec{A}}}}}/{\partial \alpha }=({\partial {\tilde{A}}_k}/{\partial \alpha })$, whose elements are expressed as

$$\begin{aligned} \dfrac{\partial {\tilde{A}}_k}{\partial \beta _j}& = -\dfrac{1}{\alpha \gamma _{\alpha } \sqrt{t_k Q_k}} \left( \dfrac{t_k \gamma _{\alpha }^2}{4Q_k}+1\right) \dfrac{1}{h^{\prime }(Q_k)} x_{kj},\\ \dfrac{\partial {\tilde{A}}_k}{\partial \alpha }& = \sqrt{\dfrac{4Q_k}{t_k}} \left( -\dfrac{1}{(\alpha \gamma _{\alpha })^2} (\gamma _{\alpha }+\alpha \gamma _{\alpha }^{\prime }) \left( \dfrac{t_k \gamma _{\alpha }^2}{4Q_k}-1 \right) + \dfrac{\gamma _{\alpha }^{\prime } t_k}{2 \alpha Q_k} \right) ,\\ \dfrac{\partial }{\partial \beta _j}(\log ({\tilde{a}}))& = \sum _{k=1}^n\, \left( -\dfrac{1}{2 Q_k} + \frac{4}{t_k \gamma _{\alpha }^2+4Q_k} \right) \frac{1}{h^{\prime }(Q_k)} x_{kj}, \\ \dfrac{\partial }{\partial \alpha }(\log ({\tilde{a}}))& = -\dfrac{n}{\alpha \gamma _{\alpha }}(\gamma _{\alpha }+\alpha \gamma _{\alpha }^{\prime })+\sum _{k=1}^n\,\dfrac{2 t_k \gamma _{\alpha } \gamma _{\alpha }^{\prime }}{t_k \gamma _{\alpha }^2+4Q_k}. \end{aligned}$$

In addition, ${\partial \, {\varvec{\Gamma }}}/{\partial \varphi }=(\partial \rho _{ij} / \partial \varphi )$, with elements defined as

$$\begin{aligned} \dfrac{\partial \rho _{ij}}{\partial \varphi }= \left\{ \begin{array}{ll} \dfrac{h_{ij}^{\delta }}{2^{\delta -1} \Gamma (\delta )} \left( \delta \varphi ^{\delta -1} K_{\delta }(\varphi \, h_{ij})+\varphi ^{\delta } K^{\prime }_{\delta }(\varphi \, h_{ij}) h_{ij} \right) ,&\quad i \ne j;\\ 0,&\quad i = j; \\ \end{array} \right. \end{aligned}$$

where $K^{\prime }_{\delta }(u)={\text {d} K_{\delta }(u)}/{\text {d}u}$. To estimate ${\varvec{\theta }}$, ${\dot{\ell }}({\varvec{\theta }})=\mathbf{0}_{(p+2)\times 1}$ must be solved. Note that this system does not have an analytical solution. Then, ${\widehat{{\varvec{\theta }}}}$ must be obtained with iterative procedures for non-linear systems; see Nocedal and Wright (1999) and Lange (2001).

4 Global influence diagnostics

4.1 Likelihood distance

A global influence technique of case-deletion is based on the likelihood distance (LD) and established as

$$\begin{aligned} \text {LD}_i({\varvec{\theta }}) = 2(\ell ({\widehat{{\varvec{\theta }}}})-\ell ({{\widehat{{\varvec{\theta }}}}_{(i)}})), \quad i=1,\ldots,n, \end{aligned}$$

(11)

where $\ell$ is the log-likelihood function, and ${\widehat{{\varvec{\theta }}}}, {\widehat{{\varvec{\theta }}}}_{(i)}$ are, respectively, the ML estimates of ${\varvec{\theta }}$ considering the full data set and the data set without case i; see Cook et al. (1988). The expression given in (11) measures the change in the LD with estimated parameters when case i is deleted and may be employed as global influence technique to assess the potential influence of this case.

4.2 Cook distance

The Cook distance (CD) is other global influence technique based on case deletion and an alternative to the measure defined in (11). This has been generalized to several non-normal models; see Desousa et al. (2018). The usual expression for the CD is given by

$$\begin{aligned} \text {CD}_{i}({\varvec{\theta }}) = ({\widehat{{\varvec{\theta }}}}-{\widehat{{\varvec{\theta }}}}_{(i)})^{\top } {\varvec{M}} ({\widehat{{\varvec{\theta }}}}-{\widehat{{\varvec{\theta }}}}_{(i)}), \quad i=1,\ldots,n, \end{aligned}$$

(12)

where ${\varvec{M}}$ is an appropriately chosen positive definite matrix, which can be, for example, the inverse of the asymptotic covariance matrix. Thus, a measure based on the CD established  in (12) is stated as

$$\begin{aligned} \text {CD}^{(1)}_{i}({\varvec{\theta }}) = ({\widehat{{\varvec{\theta }}}}-{\widehat{{\varvec{\theta }}}}_{(i)})^{\top } (-\ddot{\ell }_{(i)}({\widehat{{\varvec{\theta }}}})) ({\widehat{{\varvec{\theta }}}}-{\widehat{{\varvec{\theta }}}}_{(i)}), \quad i=1,\ldots,n, \end{aligned}$$

(13)

where

$$\begin{aligned}\ddot{\ell }_{(i)}({\varvec{\theta }}) = \dfrac{\partial \ell ^2_{(i)}({\varvec{\theta }})}{\partial {\varvec{\theta }}\partial {\varvec{\theta }}^{\top }},\end{aligned}$$

with $\ell _{(i)}$ being the log-likelihood function obtained after deleting case i. Note that

$$\begin{aligned} {\varvec{M}}=(-\ddot{\ell }_{(i)}({\widehat{{\varvec{\theta }}}})) \end{aligned}$$

defined in (12) is the inverse of $(-\ddot{\ell }_{(i)}({\widehat{{\varvec{\theta }}}}))^{-1}$, which is an estimate of the corresponding asymptotic covariance matrix. If n is too large, the computation of $\ddot{\ell }_{(i)}({\widehat{{\varvec{\theta }}}})$ may became hard and, in this case, $\ddot{\ell }({\widehat{{\varvec{\theta }}}})$ can be used instead of $\ddot{\ell }_{(i)}({\widehat{{\varvec{\theta }}}})$; see De Bastiani et al. (2018). Then, an alternative measure of global influence based on the CD expressed in (13) is given by

$$\begin{aligned} \text {CD}^{(2)}_{i}({\varvec{\theta }}) = ({\widehat{{\varvec{\theta }}}}-{\widehat{{\varvec{\theta }}}}_{(i)})^{\top } (-\ddot{\ell }({\widehat{{\varvec{\theta }}}})) ({\widehat{{\varvec{\theta }}}}-{\widehat{{\varvec{\theta }}}}_{(i)}), \quad i=1,\ldots,n. \end{aligned}$$

(14)

4.3 Generalized Cook distance

Other measure based on the CD defined in (14) uses the first order approximation ${\widehat{{\varvec{\theta }}}}-{\widehat{{\varvec{\theta }}}}_{(i)} \approx \ddot{\ell }_{(i)}^{-1}({\widehat{{\varvec{\theta }}}}) {\dot{\ell }}_{(i)}({\widehat{{\varvec{\theta }}}})$, which considers a Taylor expansion around ${\widehat{{\varvec{\theta }}}}$, until the second order term, and the one-step-late Newton-Raphson estimate. This third measure based on (14) is expressed as

$$\begin{aligned} \text {CD}^{(3)}_{i}({\varvec{\theta }}) = \big( {\dot{\ell }}_{(i)}({\widehat{{\varvec{\theta }}}})\big) ^{\top } \big( \ddot{\ell }_{(i)}({\widehat{{\varvec{\theta }}}})\big) ^{-1} \big( {\dot{\ell }}_{(i)} ({\widehat{{\varvec{\theta }}}})\big) ,\, i=1,\ldots,n, \end{aligned}$$

(15)

where

$$\begin{aligned} {\dot{\ell }}_{(i)}({\widehat{{\varvec{\theta }}}}) = \dfrac{\partial \ell _{(i)}({\varvec{\theta }})}{\partial {\varvec{\theta }}}. \end{aligned}$$

Other alternative measures based on the CD similar to (15) can be seen in Garcia-Papani et al. (2018b). In many cases, $\text {CD}_i({\varvec{\theta }})$ is preferred to $\text {LD}({\widehat{{\varvec{\theta }}}}_{(i)})$, because of its heavier computational burden. A large value of $\text {CD}_{(i)}({\varvec{\theta }})$ means that case i is potentially influential. A definition of what is large has been an unresolved aspect, but Cook et al. (1982) established this depends on each problem upon study.

5 Local influence diagnostics

5.1 Local influence distance based on normal curvature

The local influence technique examines the effect of small perturbations in the data and/or the model assumptions on the estimated parameters. Cook (1987) evaluated local influence considering

$$\begin{aligned} \text {LD}({\varvec{\theta }}_{{\varvec{\omega}}}) = 2 (\ell ({\widehat{{\varvec{\theta }}}})-\ell ({\widehat{{\varvec{\theta }}}}_{{\varvec{\omega}}})), \end{aligned}$$

(16)

with ${\widehat{{\varvec{\theta }}}}$ and ${\widehat{{\varvec{\theta }}}}_{{\varvec{\omega}}}$ being the ML estimates of ${\varvec{\theta }}$ in the proposed model and the model perturbed by ${\varvec{\omega}}$, respectively. Cook (1987) analyzed the normal curvature of the influence graph $\text {LD}({\varvec{\theta }}_{{\varvec{\omega}}})$ around the non-perturbation point ${\varvec{\omega}}_0$ in the direction of a unit vector ${\varvec{d}}$. Cook (1987) showed that this curvature based on (16) takes the form

$$\begin{aligned} C_{{\varvec{d}}}=2| {\varvec{d}}^{\top } {\varvec{B}}{\varvec{d}}|, \end{aligned}$$

where

$$\begin{aligned} {\varvec{B}}= -{\varvec{\Delta }}^{\top } \ddot{\ell }({\widehat{{\varvec{\theta }}}})^{-1} {\varvec{\Delta }}{,} \end{aligned}$$

(17)

with $\ddot{\ell }({\widehat{{\varvec{\theta }}}})$ being the Hessian matrix, evaluated at ${\varvec{\theta }}={\widehat{{\varvec{\theta }}}}$, and

$$\begin{aligned} {\varvec{\Delta }}= \dfrac{\partial ^2 \ell ({\varvec{\theta }}; {\varvec{\omega}})}{\partial \theta \partial {\varvec{\omega}}^{\top }} \end{aligned}$$

(18)

being the perturbation matrix, evaluated at ${\varvec{\theta }}= {\widehat{{\varvec{\theta }}}}$ and ${\varvec{w}}= {\varvec{w}}_0$. Specific details of the perturbation matrix defined in (18) are shown in the Appendix. Because the maximum normal curvature $C_{{\varvec{d}}_\text {max}}$ is reached at ${\varvec{d}}_\text {max}$, which is the eigenvector associated with the largest absolute eigenvalue of the matrix ${\varvec{B}}$, Cook (1987) stated that ${\varvec{d}}= {\varvec{d}}_\text {max}$ is an important direction to pay attention. Thus, the plot of the i-th element (in absolute value) of ${\varvec{d}}_\text {max}$ versus the index i can detect observations that are (in a local manner) potentially influential on ${\widehat{{\varvec{\theta }}}}$. The direction ${\varvec{d}}= {\varvec{e}}_i$, with ${\varvec{e}}_i$ being a basis vector of ${\mathbb {R}}^n$ whose i-th coordinate is one and the others are zero, corresponds to other relevant direction to analyze. For such a direction, the normal curvature is given by

$$\begin{aligned} C_i=2 \vert b_{ii} \vert , \quad i=1,\ldots,n, \end{aligned}$$

where $b_{ii}$ is the i-th element on the diagonal of the matrix ${\varvec{B}}$ indicated in (17). When considering case i, if

$$\begin{aligned} C_i > 2 \sum _{i=1}^n\, \dfrac{C_i}{n} = 2 {\bar{C}}, \quad i=1,\ldots,n, \end{aligned}$$

then this case is potentially influential; see Lesaffre and Verbeke (1998).

5.2 Local influence distance based on conformal curvature

In addition to the normal curvature of Cook (1987), other measures of local influence have been studied and employed. Poon and Poon (1999) defined the conformal curvature as

$$\begin{aligned} B_i = \dfrac{C_i}{\text {trace}({\varvec{B}})}, \quad i=1,\ldots,n, \end{aligned}$$

(19)

which demands a similar computational burden to $C_i$. The measure indicated in (19) is standard because it is invariant under conformal reparameterizations. Hence, it is not difficult to establish a cut-off point for it. According to Poon and Poon (1999), if for case i we obtain

$$\begin{aligned} B_i > 2 \sum _{i=1}^n\, \dfrac{B_i}{n} = 2{\bar{B}},\quad i=1,\ldots,n, \end{aligned}$$

where ${\bar{B}}$ is the arithmetic mean of the basic conformal curvatures, that is, of $B_1,\ldots ,B_n$, then case i is potentially influential. Another cut-off point implies to consider case i as potentially influential if

$$\begin{aligned} B_i > {\bar{B}}+2 \text {SD}(B), \quad {i} = 1,\ldots,n, \end{aligned}$$

where $\text {SD}(B)$ is the standard deviation (SD) of $B_1,\ldots ,B_n$.

5.3 Perturbation scheme in the response

We assume the perturbation

$$\begin{aligned} {\varvec{T}}_{{\varvec{\omega }}}({\varvec{s}})={\varvec{T}}({\varvec{s}})+{\varvec{A}}{\varvec{\omega}}, \end{aligned}$$

where ${\varvec{A}}$ is a symmetric, non-singular matrix and ${\varvec{\omega }}=(\omega _1,\ldots ,\omega _n) \in {\mathbb {R}}^n$ is a perturbation vector. It is clear that ${\varvec{\omega }}_0 = \mathbf{0}_{n \times 1}$ is the non-perturbation vector. In this scheme, the perturbed log-likelihood function is given by

$$\begin{aligned} \ell ({\varvec{\theta }}; {\varvec{\omega }}) = -\frac{n}{2} \log (2\pi ) -\frac{1}{2} \log (|{\varvec{\Gamma }}|) - \frac{1}{2} {\tilde{{\varvec{A}}}}_{{\varvec{\omega }}}^{\top } {\varvec{\Gamma }}^{-1} {\tilde{{\varvec{A}}}}_{{\varvec{\omega }}} + \log ({\tilde{a}}_{{\varvec{\omega }}}), \end{aligned}$$

(20)

where ${\tilde{{\varvec{A}}}}_{{\varvec{\omega }}}=({\tilde{A}}_1({\varvec{\omega }}),\ldots , {\tilde{A}}_n({\varvec{\omega }}))^{\top }$ and ${\tilde{a}}_{{\varvec{\omega }}}={\tilde{a}}({\varvec{t}}({\varvec{\omega }}); \alpha , {\varvec{Q}})$, with

$$\begin{aligned} {\tilde{A}}_k({\varvec{\omega }}) = A(t_k({\varvec{\omega }}); \alpha , Q_k), \quad k=1,\ldots,n. \end{aligned}$$

Zhu et al. (2007) established that the perturbation ${\varvec{\omega }}$ is appropriate if and only if ${\varvec{G}}({\varvec{\theta }}; {\varvec{\omega }}_0)= c {\varvec{I}}_n$, where $c>0$ and

$$\begin{aligned} {\varvec{G}}({\varvec{\theta }}; {\varvec{\omega }})=\text {E}( {\dot{\ell }}({\varvec{\theta }}; {\varvec{\omega }}) {\dot{\ell }}^{\top }({\varvec{\theta }}; {\varvec{\omega }}) ), \end{aligned}$$

with ${\dot{\ell }}({\varvec{\theta }}; {\varvec{\omega }})= \partial \ell ({\varvec{\theta }}; {\varvec{\omega }}) / \partial {\varvec{\omega }}$. Obtaining the matrix ${\varvec{G}}({\varvec{\theta }}; {\varvec{\omega }}_0)$ can be a very difficult. In this paper, we assume that the form of ${\varvec{A}}$ to obtain an appropriate perturbation ${\varvec{\omega }}$ is the same obtained in Garcia-Papani et al. (2018b), that is,

$$\begin{aligned} {\varvec{A}}= \left( \dfrac{\alpha }{4} {\varvec{\Gamma }}^{1/2} -\dfrac{1}{\alpha }{\varvec{\Gamma }}^{-1/2} \right) ^{-1}, \end{aligned}$$

(21)

where ${\varvec{\Gamma }}^{1/2}$ is the square root matrix of ${\varvec{\Gamma }}$, that is, ${\varvec{\Gamma }}^{1/2} {\varvec{\Gamma }}^{1/2} = {\varvec{\Gamma }}$. For details of computations for this square root matrix, see De Bastiani et al. (2015). Therefore, we assume that an appropriate perturbation scheme for the response is given by

$$\begin{aligned} {\varvec{T}}_{{\varvec{\omega }}}({\varvec{s}})={\varvec{T}}({\varvec{s}})+\left( \dfrac{\alpha }{4} {\varvec{\Gamma }}^{1/2} -\dfrac{1}{\alpha }{\varvec{\Gamma }}^{-1/2} \right) ^{-1} {\varvec{\omega }}{.} \end{aligned}$$

5.4 Perturbation in a continuous explanatory variable

Now, we perturb a continuous explanatory variable, labelled as $X_l$ namely, and the other explanatory variables are not perturbed. Thus, we have

$$\begin{aligned} {\varvec{x}}_{l,{\varvec{\omega}}}({\varvec{s}})={\varvec{x}}_l({\varvec{s}})+{\varvec{A}}{\varvec{\omega}}, \quad {\varvec{x}}_{j,{\varvec{\omega}}}({\varvec{s}})={\varvec{x}}_j({\varvec{s}}), \quad j \ne l, j=1,\ldots,q, \end{aligned}$$

where ${\varvec{\omega}}\in {\mathbb {R}}^n$ and ${\varvec{\omega}}_0={\varvec{0}}_{n \times 1}$. Hence, in this scheme, the perturbed log-likelihood function is given by

$$\begin{aligned} \ell ({\varvec{\theta }}; {\varvec{\omega }}) = -\frac{n}{2} \log (2\pi ) -\frac{1}{2} \log (|{\varvec{\Gamma }}|) - \frac{1}{2} {\tilde{{\varvec{A}}}}_{{\varvec{\omega }}}^{\top } {\varvec{\Gamma }}^{-1} {\tilde{{\varvec{A}}}}_{{\varvec{\omega }}} + \log ({\tilde{a}}_{{\varvec{\omega }}}), \end{aligned}$$

(22)

where ${\tilde{{\varvec{A}}}}_{{\varvec{\omega }}}=({\tilde{A}}_1({\varvec{\omega }}),\ldots , {\tilde{A}}_n({\varvec{\omega }}))^{\top }$ and ${\tilde{a}}_{{\varvec{\omega }}}={\tilde{a}}({\varvec{t}}; \alpha , {\varvec{Q}}({\varvec{\omega }}))$, with ${\tilde{A}}_k({\varvec{\omega }}) = A(t_k; \alpha , Q_k({\varvec{\omega }}))$, for $k=\overline{1,n}$. Once again, obtaining the matrix ${\varvec{A}}$ for an appropriate perturbation in $X_l$ can be a hard work. As in the case of the response perturbation with ${\varvec{A}}$ given in (21), we assume that the most appropriate explanatory variable perturbation may be expressed as

$$\begin{aligned} {\varvec{x}}_{t,{\varvec{\omega }}}({\varvec{s}}) = {\varvec{x}}_t({\varvec{s}}) + \left( \dfrac{\alpha }{4}{\varvec{\Gamma }}^{1/2}-\dfrac{1}{\alpha } {\varvec{\Gamma }}^{-1/2} \right) ^{-1} {\varvec{\omega }}. \end{aligned}$$

5.5 Other perturbations

In order to illustrate the methodology of perturbation associated with the local influence technique, we consider only perturbations in the response and in a continuous explanatory variable. However, other schemes of perturbation of the local influence technique can also be considered for the BS spatial quantile regression model derived in this investigation. These perturbation schemes may be proposed to assess changes in the cases (that is, case-weight perturbation), in the scalar parameters $\alpha$ or $\varphi$, as well as in the correlation matrix ${\varvec{\Gamma }}$. For instance, when perturbing the parameter $\alpha$, we must consider

$$\begin{aligned} \alpha _i = \dfrac{\alpha }{\omega _i}, \quad i= 1,\ldots,n, \end{aligned}$$

with $\omega _i>0$; see Sánchez et al. (2020a). Similarly for perturbing the parameter $\varphi$. For perturbing the correlation matrix ${\varvec{\Gamma }}$, see Marchant et al. (2016b).

6 Empirical illustrative example

6.1 The data set and exploratory analysis

The methodology presented in this paper is illustrated considering an environmental data set related to key nutrients in the soil. The data set belongs to $n=82$ locations of an area in Brazil, where levels of magnesium (Mg) and calcium (Ca) are measured. Mg affects the development of the root system, while Ca is analyzed as a competitor of Mg for absorption of nutrients. The response variable (T) is the content of Mg in the soil (in cmolc/dm3) and the explanatory variable (X) is the content of Ca in the soil (in cmolc/dm3).

Descriptive statistics for the vector of Mg values are summarized in Table 2. This summary shows the asymmetric behavior of the distribution of the response variable, which is also observed in the histogram of Fig. 2a, while the boxplot of the values of the response T allows us to observe two outliers, which are cases #12 and #47. A three-dimensional scatter plot of the response values is provided in Fig. 2b. The directional variogram of Fig. 2c indicates that there is no preferred direction, meaning an omni-directional semi-variogram is suitable. Hence, we can consider the associated stochastic process as isotropic.

Table 2 Descriptive statistics for Mg data (in cmolc/dm3)

Fig. 2

(a) Histogram with boxplot, (b) scatterplot, and (c) semi-variogram for the response variable of environmental data

6.2 Formulation, estimation of parameters, and comparison of models

We estimate the spatial dependence parameters assuming a variogram using the Matérn model with $\delta =0.5$. Suppose that

$$\begin{aligned} (T({\varvec{s}}_1),\ldots ,T({\varvec{s}}_n))=(T_1,\ldots ,T_n) \sim \text {BS}_n(\alpha {\varvec{1}}_{n \times 1}, {\varvec{Q}}({\varvec{\beta }}), {\varvec{\Gamma }}), \end{aligned}$$

considering three cases for the link function h defined in (5), that is, logarithm, square root and identity functions, which are expressed, for $i=1,\ldots,82$, as

$$\begin{aligned} \log (Q(T({\varvec{s}}_i)))&= {\varvec{x}}_i^{\top } {\varvec{\beta }}, \\ \sqrt{Q(T({\varvec{s}}_i))}&= {\varvec{x}}_i^{\top } {\varvec{\beta }}, \\ Q(T({\varvec{s}}_i))& = {\varvec{x}}_i^{\top } {\varvec{\beta }}, \end{aligned}$$

with ${\varvec{\beta }}=(\beta _0, \beta _1)^{\top }$ being the regression coefficient vector and ${\varvec{x}}_i^{\top }=(1, x_{i1})$ being the value of ${\varvec{X}}_i$.

In order to compare spatial regression models, we employ the Schwarz Bayesian information criterion (BIC) and corrected Akaike information criterion (CAIC) stated as

$$\begin{aligned} \text {BIC}& = d \log (n)-2\ell ({\widehat{{\varvec{\theta }}}}),\\ \text {CAIC}& = 2d -2 \ell ({\widehat{{\varvec{\theta }}}}) + \frac{2d^2+2d}{n-d-1}, \end{aligned}$$

where $d = p +2 = 4$ is the number of model parameters, $n =82$ is the dimension of the data set, and $\ell ({\widehat{{\varvec{\theta }}}})$ corresponds to the log-likelihood function for ${\varvec{\theta }}$ of the underlying model evaluated at ${\varvec{\theta }}= {\widehat{{\varvec{\theta }}}}$. BIC and CAIC use the log-likelihood function and penalize a model with more parameters. When a small quantity of information is obtained from a model in relation a specific data set, then large values for BIC and CAIC are obtained for this model, which indicates that the model is less adequate than other with smaller  BIC or CAIC. Then, the best model is that with the smallest value for the BIC or CAIC; see Ferreira et al. (2012). Table 3 reports the values of the log-likelihood function, CAIC and BIC for the model with link functions defined in (23). Also, we compare the models given in (23) with the Gaussian spatial regression model applied to the data set, which considers the description of the mean (or equivalently the median) with identity link function; see Table 3. Note that the BS model with square root link is the best one among the considered models  and therefore this should be used to describe the environmental data upon analysis. The ML estimates of the selected model parameters and their corresponding estimated asymptotic standard errors, estimated by using the robust covariance matrix method (Bhatti 2010) and indicated in parenthesis, are: $\begin{aligned} &{\widehat{\beta }}_0=0.382\,(0.0030), \quad {\widehat{\beta }}_1 =0.1884\,(0.0093),\nonumber\\ &{\widehat{\varphi }} =0.0045\,(0.0021), \quad {\widehat{\alpha }}=0.2323\,(0.0460),\nonumber\\ \end{aligned}$ and ${\widehat{\alpha }}=0.2323\,(0.0460)$. These standard errors are  small indicating all the parameters are estimated with good statistical precision and allow us to infer they must be part of the model. Therefore, the estimated model is ${\widehat{Q}}_i = (0.3821 + 0.1884 \, {x}_{i1})^2$, for $i=1,\ldots, 82$, while the scale-dependence matrix is estimated as ${\widehat{{\varvec{\Gamma }}}} = {\varvec{\Gamma }}({\widehat{\varphi }}),$ with ${\varvec{\Gamma }}(\varphi )$ being defined in (8) for $\delta =0.5$ and evaluated at ${{\widehat{\varphi }}}=0.0045$.

Table 3 Values of log-likelihood, CAIC and BIC for indicated models with environmental data

6.3 Spatial dependence, residuals analysis, and model fitting

Note that the parameter $\varphi$ is significant at 5% using the confidence interval-method, which means that exists spatial dependence.

The quantile versus quantile (QQ) plot of the residuals transformed by the Wilson-Hilferty approximation (Marchant et al. 2016b), after removing a location which was outside the bands, is displayed in Fig. 3a. An alternative method to evaluate the fit of the model is  to employ the randomized quantile residual defined by Dunn and Smyth (1996). Observe that most of the residuals are inside of the bands (at 1%). In addition, Fig. 3b shows a three-dimensional scatter plot of the estimated and observed values for the response. These two graphical plots permit us to detect a good fit of the BS spatial quantile regression model with square root link to the data. Thus, our model seems to be appropriate to describe the environmental data. However, if we use a heavy-tailed asymmetric distribution, such as the BS-Student-t model, we could obtain a better fitting, which implies further research this in line.

Fig. 3

(a) QQ plots for transformed residuals and (b) three-dimensional scatter plots of estimated versus observed response values with environmental data

6.4 Global and local influence diagnostic analytics

Figure 4 presents the potentially influential cases in the ML estimates of the parameter vector ${\varvec{\theta }}$ considering the CD as criterion of global influence. It is possible to see that cases #5, #31, #40 and #73 are potentially influential for the estimate of ${\varvec{\theta }}$ because their values of CD are outside of the cut-off point.

Fig. 4

Plots of the CD with environmental data

For local influence, we assume two types of scheme: (1) perturbation in the response; and (2) perturbation in the explanatory variable X. We consider three measures of local influence: (1) the absolute value of the components of ${\varvec{d}}_\text {max}$; (2) normal curvature in the direction of basis vectors ($C_i$); and (3) conformal curvature in the same direction ($B_i$). Figure 5 displays the local influence graphs corresponding to perturbations in the response and explanatory variable. Note that all cases detected in the global influence plots are not locally influential by the plots associated with ${\varvec{d}}_\text {max}$, $C_i$ and $B_i$ when the response or explanatory variable are perturbed. For the response, observe that three  cases (#17, #28 and #81) are detected as potentially influential points in two plots. For explanatory variable perturbation, we again detect the three earlier cases as potentially influential, but also cases #50 and #54; see plots (f) and (g). Note that no outliers are detected as potentially influential in plots of diagnostics, that is, in spatial statistics, an influential point is not necessarily an outlier and viceversa.

Fig. 5

Perturbation in the response for (a) ${\varvec{d}}_\text {max}$ , (b) $C_i$ and (c) $B_i$ and perturbation in the regressor for (d) ${\varvec{d}}_\text {max}$ ,  (e) $C_i$ and (f) $B_i$ with environmental data

We study the relative change (RC) when cases detected as potentially influential are removed, that is, cases #17, #28 and #81, which are the points detected for the most of the plots in Figs. 4 and 5. We consider removing individual cases and combinations of them. The impact of the potentially influential cases on the parameter estimates is evaluated by computing $\text {RC}_{\theta _{j(I_k)}}=| ({{\widehat{\theta }}_j - {\widehat{\theta }}_{j(I_k)}})/{{\widehat{\theta }}_j}| \times 100\%,$ where ${\widehat{\theta }}_{j(I_k)}$ is the ML estimate of $\theta _j$ after removing the subset $I_k$, for $j=1,\ldots ,4$ and $k=1,\ldots ,7$, with $\theta _1=\beta _0$, $\theta _2=\beta _1$, $\theta _3=\varphi$ and $\theta _4=\alpha$. The RCs in the parameter estimates obtained by considering the data with removed cases are presented in Table 4. In general, the RCs are larger for the parameters $\beta _0$ and $\beta _1$. Note that only when cases #17 and #81 are removed simultaneously the parameter $\varphi$ is not significant, and $\varphi$ and $\alpha$ presents the largest changes. In all other cases, each parameter is significant. When analyzing the p-values of the corresponding t-tests (see values in parentheses in Table 4), note that $\beta _0$, $\beta _1$ and $\varphi$ do not change their significance, but $\varphi$ changes. This indicates that the detection of potentially influential cases alters the conclusions of the study. Therefore, we conclude that removing the potentially influential cases can modify the spatial dependence and then our predictive model can be affected changing the conclusions of the study.

Table 4 RC in % of ML estimates for the indicated parameter and removed cases (and p-values in parentheses) with environmental data

7 Conclusions and future works

This paper reported the following findings:

• 1. A geostatistical model based on a new approach to quantile regression considering the multivariate Birnbaum–Saunders distribution was formulated and the maximum likelihood estimation of their parameters was performed.

• 2. Global and local influence diagnostic analytics were derived for this model based on the Cook and likelihood distances, respectively.

• 3. An illustration of the proposed methodology was considered using an example related to environmental data to show potential applications.

In summary, we developed a novel Birnbaum–Saunders spatial quantile regression model to describing data generated from a positive skew distribution. The principal characteristic of this spatial model is the description of a quantile for a response variable that follows the Birnbaum–Saunders distribution. The numerical evaluation reported the excellent performance of the new spatial model, indicating that the Birnbaum–Saunders distribution is a good modeling choice when dealing with data which have spatial dependence, positive support and follow a distribution skewed to the right. Therefore, our investigation may be a relevant addition to the tool-kit of engineers, applied statisticians, and data scientists.

Applications of the new Birnbaum–Saunders spatial quantile regression are of interest in household income data which must be georeferenced to model them spatially. Also, georeferenced criminal, epidemiological, political, socio-economic data, where an asymmetric behavior is detected for its distribution, could be described by this new model. Some open problems that arose from the present investigation to be studied in further works are the following:

• 1. A test for independence can be proposed considering $\text {H}_{0}\text{: } \rho _{ij}=0$ (or ${\varvec{\Gamma }}={\varvec{I}}_{n}$) based on the likelihood ratio test.

• 2. The hypothesis $\text {H}_{0}\text{: } \varphi =0$ versus $\text {H}_{1}\text{: } \varphi > 0$ can be contrasted using the likelihood ratio test.

• 3. The asymptotic behavior and performance of maximum likelihood estimators is also of interest, but applicability of asymptotic frameworks to spatial data is not an easy aspect; see Genton and Zhang (2012).

• 4. The Birnbaum–Saunders distribution is generated from the standard normal distribution and then its parameter estimation in spatial quantile regression can be affected by atypical cases. Thus, robust estimation to these cases, for example based on the Birnbaum–Saunders-t distribution, may be addressed to diminish their effects; see (Athayde et al. 2019).

• 5. Random effects may also be considered producing more sophisticated Birnbaum–Saunders spatial quantile regressions; see (Villegas et al. 2011).

• 6. Other perturbation schemes for local influence diagnostics can be conducted for Birnbaum–Saunders spatial quantile regression models.

Research on these and other issues are in progress and their findings will be reported in future articles.

Appendix: Perturbation matrices for the BS spatial model

For the model defined by (5) and its corresponding log-likelihood function given in (10), we have

$$\begin{aligned} \dfrac{\partial \ell ({\varvec{\theta }}; {\varvec{\omega }})}{\partial \omega _i} = -\tilde{{\varvec{A}}}_{{\varvec{\omega }}}^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \omega _i}+\dfrac{\partial }{\partial \omega _i} \left( \log (\tilde{a}_{{\varvec{\omega }}})\right) . \end{aligned}$$

The corresponding $(p+2) \times n$ perturbation matrix is given by $\displaystyle {\varvec{\Delta }}= ({\partial \ell ^2 ({\varvec{\theta }}; {\varvec{\omega }})}/{\partial \theta _j \omega _i})$, where $j={1,..., p+2}$ and $i={1,..., n}$, with $\theta _1=\beta _0, \ldots \theta _p=\beta _{p-1}$, $\theta _{p+1}=\varphi$ and $\theta _{p+2}=\alpha$. The elements of this matrix are given by

$$\begin{aligned} \dfrac{\partial \ell ^2({\varvec{\theta }}; {\varvec{\omega }})}{\partial \beta _j \, \partial \omega _i}= & {} - \left( \left( \dfrac{\partial \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \beta _j} \right) ^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \omega _i}+\tilde{{\varvec{A}}}_{{\varvec{\omega }}}^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial ^2 \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \omega _i \partial \beta _j}\right) \nonumber \\&+\dfrac{\partial }{\partial \beta _j} \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i}\right) , \nonumber \\ \dfrac{\partial \ell ^2({\varvec{\theta }}; {\varvec{\omega }})}{\partial \varphi \, \partial \omega _i}= & {} - \left( \left( \dfrac{\partial \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \varphi } \right) ^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \omega _i}+ \tilde{{\varvec{A}}}_{{\varvec{\omega }}}^{\top } \dfrac{\partial \, {\varvec{\Gamma }}^{-1}}{\partial \varphi } \dfrac{\partial \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \omega _i}\right. \nonumber \\&\left. +\tilde{{\varvec{A}}}_{{\varvec{\omega }}}^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial ^2 \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \omega _i \partial \varphi }\right) +\dfrac{\partial }{\partial \beta _j} \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i}\right) , \nonumber \\ \dfrac{\partial \ell ^2({\varvec{\theta }}; {\varvec{\omega }})}{\partial \alpha \, \partial \omega _i}= & {} - \left( \left( \dfrac{\partial \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \alpha } \right) ^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \omega _i}\right. \nonumber \\&\left. +\tilde{{\varvec{A}}}_{{\varvec{\omega }}}^{\top } {\varvec{\Gamma }}^{-1} \dfrac{\partial ^2 \tilde{{\varvec{A}}}_{{\varvec{\omega }}}}{\partial \omega _i \partial \alpha }\right) +\dfrac{\partial }{\partial \alpha } \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i}\right) . \end{aligned}$$

(23)

Perturbation in the response: In the case of perturbation in the response and based on its corresponding log-likelihood function given in (20), we have

$$\begin{aligned} \dfrac{\partial \tilde{A}_k({\varvec{\omega }})}{\partial \omega _i}= & {} a(t_k({\varvec{\omega }}); \alpha , Q_k) A_{ki}, \\ \dfrac{\partial \tilde{A}_k({\varvec{\omega }})}{\partial \beta _j}= & {} -\dfrac{1}{\alpha \gamma _{\alpha } \sqrt{t_k({\varvec{\omega }}) Q_k}}\nonumber \\&\left( \dfrac{t_k({\varvec{\omega }}) \gamma _{\alpha }^2}{4Q_k}+1\right) \dfrac{1}{h^{\prime }(Q_k)} x_{kj}, \\ \dfrac{\partial ^2 \tilde{A}_k({\varvec{\omega }})}{\partial \omega _i \partial \beta _j}= & {} \left( -\dfrac{\gamma _{\alpha }^2}{4Q_k}+\dfrac{1}{t_k({\varvec{\omega }})}\right) \nonumber \\&\dfrac{1}{2 \alpha \gamma _{\alpha } \sqrt{Q_k t_k({\varvec{\omega }})}} \dfrac{1}{h^{\prime }(Q_k)} x_{kj} A_{kj},\\ \dfrac{\partial }{\partial \beta _j} \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i}\right)= & {} -4 \sum _{k=1}^n\,\left( \dfrac{t_k({\varvec{\omega }}) \gamma _{\alpha }}{t_k^2({\varvec{\omega }}) \gamma _{\alpha }^2 + 4Q_k t_k({\varvec{\omega }})}\right) ^2\nonumber \\&\dfrac{1}{h^{\prime }(Q_k)} x_{kj} A_{kj},\\ \dfrac{\partial \tilde{A}_k({\varvec{\omega }})}{\partial \varphi }= & {} a(t_k({\varvec{\omega }}); \alpha , Q_k) \dfrac{\partial t_k({\varvec{\omega }})}{\partial \varphi },\\ \dfrac{\partial t_k({\varvec{\omega }})}{\partial \varphi }= & {} \left( k\text {-th row of } \dfrac{\partial {{\varvec{A}}}}{\partial \varphi }\right) {\varvec{\omega }}, \\ \dfrac{\partial {{\varvec{A}}}}{\partial \varphi }= & {} {{\varvec{A}}}\left( \dfrac{1}{\alpha } {\varvec{\Gamma }}^{-1/2} \dfrac{\partial \, {\varvec{\Gamma }}^{1/2}}{\partial \varphi } {\varvec{\Gamma }}^{-1/2} + \dfrac{\alpha }{4} \dfrac{\partial \, {\varvec{\Gamma }}^{1/2}}{\partial \varphi } \right) {{\varvec{A}}}, \\ \dfrac{\partial ^2 \tilde{A}_k({\varvec{\omega }})}{\partial \omega _i \partial \varphi }= & {} \dfrac{1}{\alpha \gamma _{\alpha } \sqrt{4Q_k}} \\&\left( -\dfrac{1}{2t_k^{3/2}({\varvec{\omega }})} \left( \dfrac{\gamma _{\alpha }^2}{2}+\dfrac{2Q_k}{t_k({\varvec{\omega }})}\right) -\dfrac{2Q_k}{t_k^{3/2}({\varvec{\omega }})}\right) \\&\times \dfrac{\partial t_k({\varvec{\omega }})}{\partial \varphi } A_{ki} + a(t_k({\varvec{\omega }}); \alpha , Q_k) \dfrac{\partial A_{ki}}{\partial \varphi },\\ \dfrac{\partial }{\partial \varphi } \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i}\right)= & {} \sum _{k=1}^n \, \left( \dfrac{1}{2t_k^2({\varvec{\omega }})} \dfrac{\partial t_k({\varvec{\omega }})}{\partial \varphi }\right. \\&\left. + \dfrac{4Q_k}{(t_k^2({\varvec{\omega }}) \gamma _{\alpha }^2+4Q_k t_k({\varvec{\omega }}))^2} \right. \\&\left. \left( 2t_k({\varvec{\omega }}) \dfrac{\partial t_k({\varvec{\omega }})}{\partial \varphi } \gamma _{\alpha }^2 + 2t_k^2({\varvec{\omega }}) \gamma _{\alpha } \gamma _{\alpha }^{\prime }\right. \right. \\&\left. \left. + 4Q_k \dfrac{\partial t_k({\varvec{\omega }})}{\partial \varphi }\right) \right) A_{ki} \\&+ \sum _{k=1}^n\, \left( -\dfrac{1}{2t_k({\varvec{\omega }})}-\dfrac{4Q_k}{t_k^2({\varvec{\omega }}) \gamma _{\alpha }^2 + 4Q_k t_k({\varvec{\omega }})} \right) \\&\dfrac{\partial A_{ki}}{\partial \varphi }, \\ \dfrac{\partial \tilde{A}_k({\varvec{\omega }})}{\partial \alpha }= & {} \dfrac{1}{\sqrt{4Q_k}} \left( -\dfrac{\gamma _{\alpha }+\alpha \gamma _{\alpha }^{\prime }}{\alpha ^2 \gamma _{\alpha }^2}\right. \\&\left. \left( \sqrt{t_k({\varvec{\omega }})} \gamma _{\alpha }^2-4Q_k t_k^{-1/2}({\varvec{\omega }})\right) \right. \\&\left. + \dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{1}{2 \sqrt{t_k({\varvec{\omega }})}} \dfrac{\partial t_k({\varvec{\omega }})}{\partial \alpha } \gamma _{\alpha }^2\right. \right. \\&\left. \left. + 2 \sqrt{t_k({\varvec{\omega }})} \gamma _{\alpha } \gamma _{\alpha }^{\prime } \right. \right. \\&\left. \left. + 2 Q_k t_k^{-3/2}({\varvec{\omega }}) \dfrac{\partial t_k({\varvec{\omega }})}{\partial \alpha } \right) \right) ,\\ \dfrac{\partial t_k({\varvec{\omega }})}{\partial \alpha }= & {} \left( k\text {-th row of } {{\varvec{A}}}\left( \dfrac{1}{\alpha ^2} {\varvec{\Gamma }}^{-1/2} + \dfrac{1}{4} {\varvec{\Gamma }}^{1/2} \right) {{\varvec{A}}}\right) {\varvec{\omega }}, \\ \dfrac{\partial ^2 \tilde{A}_k({\varvec{\omega }})}{\partial \omega _i \partial \alpha }= & {} \dfrac{1}{\sqrt{4Q_k}} \left( \left( -\dfrac{\gamma _{\alpha } + \alpha \gamma _{\alpha }^{\prime }}{\alpha \gamma _{\alpha }} \dfrac{1}{\sqrt{t_k({\varvec{\omega }})}}\right. \right. \\&\left. \left. -\dfrac{1}{2\alpha \gamma _{\alpha } t_k^{3/2}({\varvec{\omega }})} \dfrac{\partial t_k({\varvec{\omega }})}{\partial \alpha }\right) \right. \\&\left. \times \left( \dfrac{\gamma _{\alpha }^2}{2}+\dfrac{2Q_k}{t_k({\varvec{\omega }})}\right) +\dfrac{1}{\alpha \gamma _{\alpha }}\right. \\&\left. \left( \gamma _{\alpha } \gamma _{\alpha }^{\prime } - \dfrac{2Q_k}{t_k^2({\varvec{\omega }})} \dfrac{\partial t_k({\varvec{\omega }})}{\partial \alpha }\right) \right) A_{ki}\\&+ a(t_k({{\varvec{\omega }}}); \alpha , Q_k) \left( ki\text {-th\ element\ of } \dfrac{\partial {{\varvec{A}}}}{\partial \alpha }\right) ,\\ \dfrac{\partial }{\partial \alpha } \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i}\right)= & {} \sum _{k=1}^n\, \left( \dfrac{1}{2t_k^2({\varvec{\omega }})} \dfrac{\partial t_k({\varvec{\omega }})}{\partial \alpha }\right. \\&\left. +\dfrac{4Q_k}{(t_k^2({\varvec{\omega }}) \gamma _{\alpha }^2+4Q_k t_k({\varvec{\omega }}))^2} \right. \\&\left. \times \left( 2 t_k({\varvec{\omega }}) \dfrac{\partial t_k({\varvec{\omega }})}{\partial \alpha } \gamma _{\alpha }^2 + 2 \gamma _{\alpha } \gamma _{\alpha }^{\prime } t_k^2({\varvec{\omega }}) \right. \right. \\&\left. \left. + 4Q_k \dfrac{\partial t_k({\varvec{\omega }})}{\partial \alpha }\right) \right) A_{ki} \\&+ \sum _{k=1}^n\, \left( -\dfrac{1}{2t_k({\varvec{\omega }})}-\dfrac{4Q_k}{t_k^2({\varvec{\omega }}) \gamma _{\alpha }^2+4Q_k t_k({\varvec{\omega }})} \right) \\&\dfrac{\partial A_{ki}}{\partial \alpha }, \end{aligned}$$

where ${\partial \, {\varvec{\Gamma }}^{-1}}/{\partial \varphi } = -{\varvec{\Gamma }}^{-1}({\partial \, {\varvec{\Gamma }}}/{\partial \varphi }) {\varvec{\Gamma }}^{-1}$, ${\partial {{\varvec{A}}}}/{\partial \alpha } = {{\varvec{A}}}( ({1}/{\alpha ^2}) {\varvec{\Gamma }}^{-1/2}+({1}/{4}) {\varvec{\Gamma }}^{1/2}) {{\varvec{A}}}$ and $A_{ki}$ corresponds to the ki-th element of the matrix ${{\varvec{A}}}$. To calculate ${\partial \, {\varvec{\Gamma }}^{1/2}}/{\partial \varphi }$, see De Bastiani et al. (2015).

Perturbation in the explanatory variable: Based on the corresponding log-likelihood function given in (22), the elements defined in (23) have as components the expressions stated as

$$\begin{aligned} \dfrac{\partial \tilde{A}_k({\varvec{\omega }})}{\partial \omega _i}= & {} -\dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2} \\&\left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \beta _l A_{ki}, \\ \dfrac{\partial \tilde{A}_k({\varvec{\omega }})}{\partial \beta _j}= & {} -\dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2} \\&\left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} Z_{kj},\\ \dfrac{\partial ^2 \tilde{A}_k({\varvec{\omega }})}{\partial \omega _i \partial \beta _j}= & {} \dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2} \\&\left( \left( \dfrac{3 \gamma _{\alpha }^2}{8 Q_k^2({\varvec{\omega }})}+\dfrac{1}{2Q_k({\varvec{\omega }})}\right) \right. \\&\left. + \left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \dfrac{h^{\prime \prime } (Q_k({\varvec{\omega }}))}{(h^{\prime }(Q_k({\varvec{\omega }})))^2} \right) \\&\dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \beta _l A_{ki} Z_{kj},\\ \dfrac{\partial }{\partial \beta _j} \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i}\right)= & {} \sum _{k=1}^n\, \left( \left( \dfrac{1}{2 Q_k^2({\varvec{\omega }})}-\dfrac{16}{(t_k \gamma _{\alpha }^2 + 4Q_k({\varvec{\omega }}))^2} \right) \right. \\&\left.\times \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} + \left( \dfrac{1}{2Q_k({\varvec{\omega }})}-\dfrac{4}{t_k\gamma _{\alpha }^2+4Q_k({\varvec{\omega }})}\right) \right. \\&\left. \times \dfrac{h^{\prime \prime }(Q_k({\varvec{\omega }}))}{(h^{\prime }(Q_k({\varvec{\omega }})))^2} \right) \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \beta _l A_{ki} Z_{kj} \\&+ \sum _{k=1}^n\, \left( -\dfrac{1}{2 Q_k({\varvec{\omega }})}+\dfrac{4}{t_k \gamma _{\alpha }^2+4Q_k({\varvec{\omega }})}\right) \\&\dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} A_{ki} \rho _{jl},\\ \dfrac{\partial \tilde{A}_{k}({\varvec{\omega }})}{\partial \varphi }= & {} -\dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2} \left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \\&\dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \dfrac{\partial {{\varvec{A}}}_k}{\partial \varphi } {\varvec{\omega }},\\ \dfrac{\partial ^2 \tilde{A}_k({\varvec{\omega }})}{\partial \omega _i \partial \varphi }= & {} \beta _l \left( \dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2}\right. \\&\left. \left( \left( \dfrac{3 \gamma _{\alpha }^2}{8Q_k^2({\varvec{\omega }})}+\dfrac{1}{2Q_k({\varvec{\omega }})}\right) \right. \right. \\&\left. \left. \times \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} + \right. \right. \\&\left. \left. + \left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1 \right) \dfrac{h^{\prime \prime }(Q_k({\varvec{\omega }}))}{(h^{\prime }(Q_k({\varvec{\omega }})))^2} \right) \right. \\&\left. \times \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \dfrac{\partial Q_k({\varvec{\omega }})}{\partial \varphi } \dfrac{\partial {{\varvec{A}}}_k}{\partial \varphi } {\varvec{\omega }}A_{ki} \right. \\&\left. - \dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2} \left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \right. \\&\left. \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \dfrac{\partial A_{ki}}{\partial \varphi } \right) ,\\ \dfrac{\partial }{\partial \varphi } \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i} \right)= & {} \beta _l \sum _{k=1}^n\, \left( \left( \left( \dfrac{1}{2 Q_k^2({\varvec{\omega }})}-\dfrac{16}{(t_k \gamma _{\alpha }^2+4Q_k({\varvec{\omega }}))^2} \right) \right. \right. \\&\left. \left. \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \right. \right. \\&\left. \left. +\left( \dfrac{1}{2Q_k({\varvec{\omega }})}-\dfrac{4}{t_k \gamma _{\alpha }^2+4Q_k({\varvec{\omega }})} \right) \right. \right. \\&\left. \left. \dfrac{h^{\prime \prime }(Q_k({\varvec{\omega }}))}{(h^{\prime }(Q_k({\varvec{\omega }})))^2} \right) \right. \\&\left. \times \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \dfrac{\partial Q_k({\varvec{\omega }})}{\partial \varphi } A_{ki} \right. \\&+ \left. \left( -\dfrac{1}{2Q_k({\varvec{\omega }})}+\dfrac{4}{t_k \gamma _{\alpha }^2+4Q_k({\varvec{\omega }})}\right) \right. \\&\left. \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \dfrac{\partial A_{ki}}{\partial \varphi } \right) ,\\ \dfrac{\partial \tilde{A}_k({\varvec{\omega }})}{\partial \alpha }= & {} \dfrac{1}{\sqrt{4t_k}} \left( -\dfrac{\gamma _{\alpha }+\alpha \gamma _{\alpha }^{\prime }}{\alpha ^2 \gamma _{\alpha }^2} \left( \dfrac{t_k \gamma _{\alpha }^2 - 4Q_k({\varvec{\omega }})}{\sqrt{Q_k({\varvec{\omega }})}} \right) \right. \\&\left. +\dfrac{1}{\alpha \gamma _{\alpha } Q_k({\varvec{\omega }})} \left( \left( 2t_k \gamma _{\alpha } \gamma _{\alpha }^{\prime }-\frac{4\partial Q_k({\varvec{\omega }})}{\partial \alpha } \right) \sqrt{Q_k({\varvec{\omega }})}\right. \right. \\&\left. \left. -\frac{1}{2\sqrt{Q_k({\varvec{\omega }})}} \frac{\partial Q_k({\varvec{\omega }})}{\partial \alpha } (t_k \gamma _{\alpha }^2-4Q_k({\varvec{\omega }})) \right) \right) ,\\ \dfrac{\partial Q_k({\varvec{\omega }})}{\partial \alpha }= & {} \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \beta _l \dfrac{\partial {{\varvec{A}}}_k}{\partial \alpha } {\varvec{\omega }},\\ \dfrac{\partial ^2 \tilde{A}_k({\varvec{\omega }})}{\partial \omega _i \partial \alpha }= & {} -\beta _l \left( -\dfrac{\gamma _{\alpha }+\alpha \gamma _{\alpha }^{\prime }}{\alpha ^2 \gamma _{\alpha }^2} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})} \right) ^{1/2}\right. \\&\left. \times \left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} A_{ki} \right. \\&\left. + \dfrac{1}{\alpha \gamma _{\alpha }} \left( -\dfrac{1}{2} \left( \dfrac{Q_k({\varvec{\omega }})}{t_k}\right) ^{-3/2} \dfrac{1}{t_k} \dfrac{\partial Q_k({\varvec{\omega }})}{\partial \alpha }\right) \right. \\&\left. \times \left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} A_{ki} \right. \\&\left. + \dfrac{1}{\alpha \gamma _{\alpha }}\right. \\&\left. \times \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2} \left( \dfrac{8 \gamma _{\alpha } \gamma _{\alpha }^{\prime } Q_k({\varvec{\omega }}) - \frac{4\partial Q_k({\varvec{\omega }})}{\partial \alpha } \gamma _{\alpha }^2}{16 Q_k^2({\varvec{\omega }})}\right) \right. \\&\left. \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} A_{ki} \right. \\&\left. + \dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2} \left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \right. \\&\left. \times \left( -\dfrac{1}{(h^{\prime }(Q_k({\varvec{\omega }})))^2}\right) h^{\prime \prime }(Q_k({\varvec{\omega }})) \right. \\&\left. \dfrac{\partial Q_k({\varvec{\omega }})}{\partial \alpha } A_{ki} \right. \\&\left. + \dfrac{1}{\alpha \gamma _{\alpha }} \left( \dfrac{t_k}{Q_k({\varvec{\omega }})}\right) ^{1/2} \left( \dfrac{\gamma _{\alpha }^2}{4Q_k({\varvec{\omega }})}+1\right) \right. \\&\left. \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \dfrac{\partial A_{ki}}{\partial \alpha } \right) ,\\ \dfrac{\partial }{\partial \alpha } \left( \dfrac{\partial \log (\tilde{a}_{{\varvec{\omega }}})}{\partial \omega _i} \right)= & {} \beta _l \sum _{k=1}^n\, \left( \left( \dfrac{1}{2Q_k^2({\varvec{\omega }})} \dfrac{\partial Q_k({\varvec{\omega }})}{\partial \alpha } \right. \right. \\&\left. \left. - \dfrac{8t_k \gamma _{\alpha } \gamma _{\alpha }^{\prime }+4\frac{\partial Q_k({\varvec{\omega }})}{\partial \alpha }}{(t_k \gamma _{\alpha }^2+4 Q_k({\varvec{\omega }}))^2} \right) \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} A_{ki} \right. \\&\left. +\left( -\dfrac{1}{2Q_k({\varvec{\omega }})} + \dfrac{4}{t_k \gamma _{\alpha }^2+4Q_k({\varvec{\omega }})}\right) \right. \\&\left. \times \left( -\dfrac{h^{\prime \prime }(Q_k({\varvec{\omega }}))}{(h^{\prime }(Q_k({\varvec{\omega }})))^2}\right) \dfrac{\partial Q_k({\varvec{\omega }})}{\partial \alpha } A_{ki} \right. \\&\left. + \left( -\dfrac{1}{2Q_k({\varvec{\omega }})}+\dfrac{4}{t_k \gamma _{\alpha }^2+4Q_k({\varvec{\omega }})}\right) \right. \\&\left. \dfrac{1}{h^{\prime }(Q_k({\varvec{\omega }}))} \dfrac{\partial A_{ki}}{\partial \alpha } \right) , \end{aligned}$$

where $\rho _{jl}=1$, if $j=l$; $\rho _{jl}=0$, if $j\ne l$; $Z_{kj}=1$ for $j=1$; $Z_{kj}=X_{kl}({\varvec{\omega }})$, if $j=l$; $Z_{kj}=X_{kj}$, for $j\ne 1,l$; and ${{\varvec{A}}}_k$ corresponds to the k-th row of ${{\varvec{A}}}$.