1 Introduction

A differential equation relates a function with its derivatives (Newton 1736). The function and its derivatives represent a state variable and its rate of change, respectively. The differential equations have important application in science, engineering, economics and biology (Strang 2014; Vyshemirsky and Girolami 2007). Ordinary Differential Equations (ODEs) contain one or more functions of an independent variable and their derivatives, whereas Partial Differential Equations (PDEs) contain multivariate functions of independent variables and their partial derivatives.

In hydraulics and hydrology, differential equations are often used to represent conservation equations. The conventional method for estimating parameters of a differential equation is to minimize an error function [e.g. L1-Norm, L2-Norm or L-infinity-Norm of the error; though use of L2-Norm is more common (Kool et al. 1985)], where error is the difference between the observations and their estimates. The estimates are obtained from the forward solution (numerical or analytical) of the differential equation. This method of parameter estimation is referred to as inverse problem. There are many methods of error minimization (Rao 2009; Deb 2012), but gradient based methods are usually preferred (McLaughlin and Townley 1996; Simunek et al. 2005).

The conventional approach of parameter estimation requires initial and boundary conditions (which are not readily available and difficult to impose in forward solutions), and discretization of differential equations if the forward solution is obtained numerically. Further, the computational time of the conventional approach increases significantly with increase in the dimensionality of the state variable and the number of unknown parameters. If the initial and boundary conditions are not available, they are considered as parameters in the conventional approach, augmenting the parameter set, which further increases their computational burden. Moreover, sometimes the data may not be sufficient to estimate the augmented parameter set.

A number of studies have attempted to estimate the parameters without explicitly solving differential equations. These methods belong to the general class of collocation methods (Varah 1982; Poyton et al. 2006; Ramsay et al. 2007). The collocation methods for parameter estimation of differential equation require fitting of either a polynomial or a spline to the observations of the state variable, and adjusting the differential equation parameters such that the polynomial spline interpolated values of the state variable and its derivatives satisfy the differential equation relationship. Since the collocation methods do not solve the forward problem, the initial and boundary conditions are not required (Ramsay et al. 2007). The Gaussian process (GP) based methods, which also fall under the category of collocation method, have been developed and successfully applied to estimate the parameters of ODEs (Calderhead et al. 2008; Dondelinger et al. 2013; Wang and Barber 2014; Macdonald and Husmeier 2015). These methods require fitting a GP regression model to the observations of the state variable and estimating their derivatives using the property that derivative of a GP is also a GP, and finally adjusting the ODE parameters so that the GP derived derivatives satisfy the differential equations.

Calderhead et al. (2008) proposed the first GP based method for ODE parameter estimation and termed it gradient matching (GM) method. The GM method consists of two steps (1) fitting a GP regression model to the observed values of the state variable and evaluating the state variable and its derivatives using the fitted GP model, and (2) matching the estimates of the state derivative obtained from the GP model and obtained analytically from the given ODE relation by using the Product of Experts approach. A Product of Experts combines probability distributions of individual experts by taking their products (Mayraz and Hinton 2001; Hinton 2002). Thus in the GM method, there are two distributions for the state derivative, one from derivative of the fitted GP model and another from the ODE relation. Using these two distributions, the Product of Experts forms a new distribution. This new distribution is used to sample the parameters of the ODE.

The GM method lacks any feedback mechanism from the ODE back to the GP model. Dondelinger et al. (2013) proposed a sampling modification for the GM method, and termed their proposed method as Adaptive Gradient Method (AGM). In the AGM method, sampling of the GP regression model parameters and the ODE parameters are not done in two stages, rather these parameters are simultaneously sampled. The posterior distribution for the GP model and the ODE parameters are obtained by marginalizing over the state derivative and conditioning on the state variable. Sampling starts by initializing the GP parameters and then the ODE parameters are sampled using the Product of Experts. Next, fixing the ODE parameters to their estimated values, GP parameters are sampled using the Product of Experts. The sampling is repeated until the GP and the ODE parameters converge.

Wang and Barber (2014) proposed an alternate approach to AGM which they termed Gaussian process ordinary differential equation (GPODE). The GM and AGM methods were based on the idea that derivative of a GP is a GP, but the GPODE approach harnesses the fact that the state variable can be represented as a GP if the state derivative is a GP (in other words, the integral of a GP is also a GP). In the GPODE method, the posterior distribution of the unknown parameters is obtained by marginalizing over the state variable and conditioning on the state derivatives. Similar to the AGM method, the GPODE method also samples the GP and the ODE parameters simultaneously, rather than in two steps. A critical review of GPODE by Macdonald et al. (2015) points out an anomaly in the graphical representation of the method and its logical construct. Specifically, they demonstrated that GPODE suffers from intrinsic identifiability problem. Readers are referred to Macdonald et al. (2015) for further details.

The GP based gradient matching methods discussed above are applicable only to ODEs, where the state derivatives can be expressed as an explicit function of the state variable and the independent variables. However, for many ODEs, the state derivatives can not be expressed as an explicit function and it would not be possible to calculate the state derivative analytically as done in the GP based gradient matching methods (GM, AGM and GPODE have been demonstrated on the ODEs: Lotka–Volterra and Signal Transduction Cascade; wherein the gradients are explicit functions of state variables). Similarly for the PDEs, the partial derivatives of the state variable are not explicit functions and hence these GP based methods can not be applied to find PDE parameters. This study proposes Gaussian process for partial differential equation (GPPDE) method which addresses the above mentioned limitation.

Recently Raissi et al. (2017b) have proposed a GP based method for estimating the parameters of linear non-homogeneous PDEs. Their method is based on the ideas presented by Graepel (2003) and Särkkä (2011) to encode physics of a differential equation into the covariance function of the GP regression model. Raissi et al. (2017b) method assumes that the state variable and the forcing term in a differential equation are GPs. Since a linear operation on a GP results in another GP (Solak et al. 2003), the cross-covariance function of the state variable and the forcing term can be expressed in terms of the parameters of the differential equation. Thus, the parameters of the differential equation are turned into parameters of the GP which are estimated when fitting the GP regression model to the observations of the state variable and the forcing term. A limitation of this method is that it cannot be applied to nonlinear differential equations and to equations in which the forcing term is constant. Raissi et al. (2017a, 2018) used the same method for solving differential equations using noisy multi-fidelity data for linearized PDE. In addition, Cockayne et al. (2016) and Bilionis (2016) have also discussed the possibility of approximating the solutions of linear PDEs using GP.

In the context of Bayesian parameter estimation, GP regression model has been used as a surrogate to dynamical systems described by differential equations. In hydrology, Wang et al. (2014) proposed an Adaptive Surrogate Modeling based Optimization (ASMO) method that uses GP regression as a surrogate model and demonstrated its applicability by estimating parameters of Hartman Function and Sacramento Soil Moisture Accounting hydrological model. Gong and Duan (2017) proposed ASMO-Parameter Optimization and Distribution Estimation (ASMO-PODE) method as an improvement over ASMO method. The ASMO-PODE method uses an adaptive resampling strategy that significantly reduces the computation cost of estimating parameters. They demonstrated the effectiveness of ASMO-PODE by estimating parameters of a land surface model. Zhang et al. (2016) used GP regression to construct a locally accurate surrogate model and showed that it significantly reduces the computational cost for groundwater contaminant source identification problem.

The use of GP regression as a surrogate model in the above cited studies is different from the way it is used in the proposed GPPDE method. The surrogate models are trained on the forward simulations of the differential equations, and hence a method for forward solution is required. The surrogate GP models do not explicitly satisfy initial and boundary conditions, and it is not straight forward to account for measurement errors and mismatch between forward solution and GP regression in the parameter estimation. GPPDE, on the other hand, uses the gradient matching approach in which the estimates of the state variable and its derivatives are directly used to approximate parameters of the dynamical systems described by PDEs. It relies on the key observation that any linear transformation of a GP, such as differentiation and integration is still a GP. Since GP regression model in GPPDE is trained on observations, a forward solution of PDE is not required. The method can work even when initial and boundary conditions are not available, however, if these conditions are available, GPPDE can incorporate them. Further, if measurement errors are known they can be used in training the GP regression model.

To the best of our knowledge gradient matching methods for estimating parameters of PDE have never been used in water resources. The purpose of this paper is to propose a new GP based method for estimating parameters of both linear and non-linear PDEs and demonstrate its application. The application of the new GPPDE method is demonstrated on two PDEs (the groundwater diffusion and the Richards equations) using synthetic data. The diffusion equation is a parabolic PDE that describes the spatio-temporal variation of groundwater level in homogeneous aquifers. The Richards equation is a nonlinear parabolic PDE that describes the movement of water in unsaturated zone. Flow in unsaturated zone is one of the most complex flows in nature. The numerical solution of the Richards equation is computationally expensive, and a universally robust and accurate solution methodology is yet to be discovered (Farthing and Ogden 2017).

This paper is organized in six sections: the first section discusses differential equations and the conventional approach to estimate their parameters. The section also reviews the GP based parameter estimation methods for differential equations, presents their advantages over the conventional approach and discusses their limitations. The second section provides mathematical formulation of the proposed GPPDE method for estimating parameters of PDEs. The third section briefly explains the groundwater diffusion equation and the Richards equation. The fourth section describes the data used to demonstrate the GPPDE method. The fifth section presents and discusses the results from the GPPDE method. The sixth section summarizes and concludes the paper.

2 Mathematical formulation

The objective of the proposed GPPDE method is to estimate parameters of a PDE, given the observations of state variable. GP, like other regression methods, does not rely on physics but on the data to fit, which it tends to statistically fit the response surface. That’s why GPPDE method is able to estimate parameters of a PDE if the initial and boundary conditions are not available or available with measurement error. This section describes the mathematical formulation of the GPPDE method. In the following subsections, we will discuss the formulation and training of the GP regression model, provide expressions for its partial derivatives, explain the procedure for incorporating derivative information in the GP regression model, and present the methodology for estimating PDE parameters.

2.1 Gaussian process

Gaussian process (GP) is a kernel based non-parametric approach for supervised (regression and classification problem) and unsupervised (clustering problem) learning (Rasmussen and Williams 2006). In the field of geostatistics, GP was independently derived and termed as kriging (Krige 1951; Matheron 1963). In water resources, GP has been used as a regression model (Marrel et al. 2009; Sun et al. 2014; Holman et al. 2014; Zhang et al. 2016). A brief mathematical formulation of GP (using the properties of conditional Gaussian distribution) for a regression problem is provided below.

In this paper, the following notations are used. All vectors are column vectors and are represented by lower case bold letters. Matrices are represented by upper case bold letters. Italic letters represent scalars. Identity matrix is represented by \({\mathbf {I}}\).

GP assumes that the data points follow multivariate Gaussian distribution in which the covariance function is homogeneous and stationary, and depends only on the distance between the two points. A covariance function, also known as kernel, provides a measure of closeness between a training point \(({{\mathbf {x}}})\) and a test point \(({\mathbf {x'}})\), notationally given by \(k\left( {{{\mathbf {x}}},{\mathbf {x'}}} \right)\). In the present study, Gaussian covariance function is used, which is given by

$$\begin{aligned} k({{\mathbf {x}}},{\mathbf {x'}}) = {\sigma _s}^2\exp \left( {-\dfrac{1}{2}\sum _{j=1}^{m} \dfrac{{\left( {{x_j} - {x'_j}} \right) }^{2}}{l_j^2}} \right) ; \end{aligned}$$
(1)

where m is the dimension of the input space or the number of independent variables in \({\mathbf {x}}\), \(x_j \in {\mathbf {x}}\), \(l_j\) is the length scale for the jth independent variable \(x_j\), and \({\sigma _s}\) is the scale parameter of the covariance function. Together, they are referred as hyperparameters and are represented by \(\varvec{\phi }=[l_1, \ldots , l_m, \sigma _s]\). The Gaussian covariance function, also known as squared exponential covariance function, is infinitely differentiable and hence very smooth. It is probably the most widely used covariance function in GP regression models. The choice of covariance function depends on the physical process being modelled. Readers are referred to Chapter 4 of Rasmussen and Williams (2006) for a detailed discussion on other covariance functions and their properties.

For the formulation of GP, the conditional property of the Gaussian distribution is used, i.e., if two sets of random variables are jointly Gaussian, then the distribution of one set conditioned on the other set is also Gaussian (section 2.3 of Bishop (2006); Appendix A.3 of Rasmussen and Williams (2006)). Let the training dataset be given by,

\({\mathcal {D}} = \left\{ {\left( {{{{\mathbf {x}}}_i},{{{{\tilde{y}}}}_i}} \right) \mid i = 1, \ldots ,N;{{{\mathbf {x}}}_i} \in {{\mathbb {R}}^m};{{{{\tilde{y}}}}_i} \in {\mathbb {R}}} \right\} ,\) where, \({{{\mathbf {x}}}_i}\) is an input vector (independent variable) in m-dimensional space, \({\tilde{y}_i}\) is the corresponding observed value of the dependent variable and N is the number of observations. All training input vectors are arranged in \(N \times m\) training data matrix \(({{\mathbf {X}}})\) and the observations are collectively represented by \(N \times 1\) vector, \({{\tilde{{\mathbf {y}}}}}\). The observations have independent and identically distributed noise, which is assumed to be normally distributed with mean zero and standard deviation \(\sigma _y\)

$$\begin{aligned} {{{\tilde{y}}}_i} = {y_i} + {\mathcal {N}}\left( {0,\sigma _y^2} \right) \end{aligned}$$
(2)

where \({y_i}\) is the true value of the state variable at location \({{{\mathbf {x}}}_i}\) and all \(y_i\)’s are collected in vector \({\mathbf {y}}\). The vector of the state variable \({{\mathbf {y}}}\), follows a Gaussian distribution with mean \({m_y}\left( {{\mathbf {X}}} \right)\) and covariance matrix \({{\mathbf {K}}}\), represented as

$$\begin{aligned} {{\mathbf {y}}} \sim {{\mathcal {N}}}\left( {{m_y}\left( {{\mathbf {X}}} \right) ,{{\mathbf {K}}}} \right) \end{aligned}$$
(3)

where \({\mathbf {y}}\) is \(N \times 1\) vector, \({{\mathbf {K}}} = k\left( {{{\mathbf {X}}},{{\mathbf {X}}}} \right)\) is a \(N\times N\) positive definite covariance matrix and \(m_y \left( {\mathbf {X}} \right)\) is \(N{\times }1\) vector of the mean of GP at training data points \({\mathbf {X}}\) (also referred as a priori mean function). In most cases the a priori mean may not be available, but the GP model is powerful enough to capture trends in data even if the mean of GP is taken as zero or a constant value (Rasmussen and Williams 2006).

The GP model prediction \(\left( {{{{\mathbf {y}}}_*}} \right)\) at new test points \(({\mathbf {X}}_*)\) is given by

$$\begin{aligned} {{{\mathbf {y}}}_*} \sim {\mathcal {N}}\left( {{m_y}\left( {{{{\mathbf {X}}}_*}} \right) ,{{{\mathbf {K}}}_{**}}} \right) \end{aligned}$$
(4)

where \({{{\mathbf {K}}}_{**}} = k\left( {{{{\mathbf {X}}}_*},{{{\mathbf {X}}}_*}} \right)\) and \({{{\mathbf {X}}}_*}\) is the testing data matrix, in which, testing points are arranged in rows. The joint distribution of \({{\tilde{{\mathbf {y}}}}}\) and \({{{\mathbf {y}}}_*}\) is given by Eq. (5), in which, \({m_y}\left( {{\mathbf {X}}} \right)\) and \({m_y}\left( {{{{\mathbf {X}}}_*}} \right)\) are the vectors of mean values, evaluated for design matrix \({{\mathbf {X}}}\) and test matrix \({{{\mathbf {X}}}_*}\), respectively, and \({{{\mathbf {K}}}_*} = k\left( {{{\mathbf {X}}},{{{\mathbf {X}}}_*}} \right)\) (The elements of \({{\mathbf {K}}}_*, {k_{ij}}\) are covariance between the ith training point and the jth test point)

$$\begin{aligned} {\begin{bmatrix}{{\tilde{\mathbf {y}}}}\\{{{{\mathbf {y}}}_*}}\end{bmatrix}} \sim {\mathcal {N}}\left( { {\begin{bmatrix}{{m_y}\left( {{\mathbf {X}}} \right) }\\{{m_y}\left( {{{{\mathbf {X}}}_*}} \right) }\end{bmatrix}} , {\begin{bmatrix}{{{\mathbf {K}}} + \sigma _y^2{{\mathbf {I}}}}&{{{{\mathbf {K}}}_*}}\\{{{\mathbf {K}}}_*^{\mathrm{{T}}}}&{{{{\mathbf {K}}}_{**}}}\end{bmatrix}}} \right) . \end{aligned}$$
(5)

The predictive distribution \(p\left( {{{{\mathbf {y}}}_*}|{{{\mathbf {X}}}_*},\varvec{\phi }, \sigma _y, {{{\mathbf {X}}},{{\tilde{{\mathbf {y}}}}}}} \right)\), based on the conditional property of the Gaussian distribution, is given by

$$\begin{aligned} p\left( {{{{\mathbf {y}}}_*}|{{{\mathbf {X}}}_*},\varvec{\phi }, \sigma _y, {{{\mathbf {X}}},{{\tilde{{\mathbf {y}}}}}}} \right) = {\mathcal {N}}\left( {{{{\mathbf {y}}}_*}|{\varvec{\mu }},{\varvec{\Sigma }}} \right) \end{aligned}$$
(6)

where

$$\begin{aligned} {\varvec{\mu }}&= {\mathbb {E}}\left[ {{{{\mathbf {y}}}_*}|{{{\mathbf {X}}}_*},\varvec{\phi }, \sigma _y, {{{\mathbf {X}}},{{\tilde{{\mathbf {y}}}}}} } \right] \nonumber \\&= m_y\left( {{{{\mathbf {X}}}_*}} \right) + {{\mathbf {K}}}_*^{\mathrm{{T}}}{{\left( {{{\mathbf {K}}} + \sigma _y^2{{\mathbf {I}}}} \right) }^{ - 1}}\left( {{{\tilde{{\mathbf {y}}}}} - {m_y}\left( {{\mathbf {X}}} \right) } \right) \end{aligned}$$
(7a)
$$\begin{aligned} {\varvec{\Sigma }}&= {\mathrm{{cov}}}\left( {{{{\mathbf {y}}}_*}|{{{\mathbf {X}}}_*},\varvec{\phi } , \sigma _y, {{{\mathbf {X}}},{{\tilde{{\mathbf {y}}}}}} } \right) \nonumber \\&= {{{\mathbf {K}}}_{**}} - {{\mathbf {K}}}_*^{\mathrm{{T}}}{{\left( {{{\mathbf {K}}} + \sigma _y^2{{\mathbf {I}}}} \right) }^{ - 1}}{{{\mathbf {K}}}_*}+\sigma _y^2{{\mathbf {I}}} \end{aligned}$$
(7b)

2.2 Estimation of hyperparameters

Estimation of hyperparameters is still an open problem and there are many approaches for it (Rasmussen and Williams 2006). Generally, the nomenclature hyperparameter is used for the parameters of a covariance function, but in the present study, the noise \({\sigma _y}\) has also been considered as one of the hyperparameters. Collectively they are represented as, \(\Phi = \left[ {l_1,\ldots , l_m, {\sigma _s},{\sigma _y}} \right]\) and termed as hyperparameters of GP. In the present study, the approach of maximum marginal likelihood (Rasmussen and Williams 2006) is used for estimating the hyperparameters. A probabilistic graph for the GP regression model is given in Fig. 1a. The marginal likelihood function is obtained by marginalizing (integrating out) the state variable \({\mathbf {y}}\) from the joint distribution of \({{\tilde{{\mathbf {y}}}}}\) and \({{\mathbf {y}}}\), given the hyperparameters

$$\begin{aligned} \begin{aligned} p\left( {{{\tilde{{\mathbf {y}}}}}|{{\mathbf {X}}}, \varvec{\phi }, {\sigma _y}} \right)&= \int p\left( {{{\tilde{{\mathbf {y}}}}},{{\mathbf {y}}}|{{\mathbf {X}}}, \varvec{\phi }, {\sigma _y}} \right) d{{\mathbf {y}}}\\&=\int {p\left( {{{\tilde{{\mathbf {y}}}}}|{{\mathbf {y}}},{{\mathbf {X}}}}, \sigma _y \right) p\left( {{{\mathbf {y}}}|{{\mathbf {X}}},\varvec{\phi } } \right) } d{{\mathbf {y}}} \end{aligned} \end{aligned}$$
(8)

where the likelihood \(p\left( {{\tilde{\mathbf {y}}}|{{\mathbf {y}}},{{\mathbf {X}}}}, \sigma _y \right)\) in above equation using Eq. (2) is given by

$$\begin{aligned} p\left( {{{\tilde{{\mathbf {y}}}}}|{{\mathbf {y}}},{\mathbf {X}},{\sigma _y}} \right) &= {\mathcal {N}} \left( {{\tilde{\mathbf {y}}}|{{\mathbf {y}}},\sigma _y^2 {\mathbf {I}}} \right) \\& = \dfrac{1}{{{(2\pi )}^{N/2} {\sigma }_y^N}}\nonumber \exp \left\{ { - \dfrac{1}{{2\sigma _y^2}}{{\left( {{{\tilde{{\mathbf {y}}}}} - {{\mathbf {y}}}} \right) }^{\mathrm {T}}}\left( {{{\tilde{{\mathbf {y}}}}} - {{\mathbf {y}}}} \right) } \right\} \end{aligned}$$
(9)

and \(p\left( {{{\mathbf {y}}}|{{\mathbf {X}}},\varvec{\phi } } \right)\) is a GP and from Eq. (3) it is given by

$$\begin{aligned} p\left( {{{\mathbf {y}}}|{{\mathbf {X}}},\varvec{\phi } } \right) &= {\mathcal {N}}\left( {{{\mathbf {y}}}|{m_y}\left( {{\mathbf {X}}} \right) ,{{\mathbf {K}}}} \right) \\& = \frac{1}{{{{\left( {2\pi } \right) }^{N/2}}{{\left| {{\mathbf {K}}} \right| }^{1/2}}}}\nonumber \exp \left\{ { - \frac{1}{2}{{\left( {{{\mathbf {y}}} - {m_y}\left( {{\mathbf {X}}} \right) } \right) }^{\mathrm{{T}}}}{{{\mathbf {K}}}^{ - 1}}\left( {{{\mathbf {y}}} - {m_y}\left( {{\mathbf {X}}} \right) } \right) } \right\} . \end{aligned}$$
(10)

Combining Eqs. (8)–(10) and taking logarithm of \(p\left( {{{\tilde{{\mathbf {y}}}}}|{\mathbf {X}}, \varvec{\phi },\sigma _y } \right)\), gives

$$\begin{aligned} \log p\left( {{{\tilde{{\mathbf {y}}}}}|{{\mathbf {X}}},\Phi } \right) &= - \,\dfrac{1}{2}{\left( {{{\tilde{{\mathbf {y}}}}} - {m_y}\left( {{\mathbf {X}}} \right) } \right) ^{\mathrm{{T}}}}{{\mathbf {K}}}_y^{ - 1}\left( {{{\tilde{{\mathbf {y}}}}} - {m_y}\left( {{\mathbf {X}}} \right) } \right) \nonumber \\&\quad-\, \dfrac{1}{2}\log \left| {{{{\mathbf {K}}}_y}} \right| - \dfrac{N}{2}\log 2\pi \end{aligned}$$
(11)

where \({{{\mathbf {K}}}_y} = {{\mathbf {K}}} + \sigma _y^2{{\mathbf {I}}}\). The hyperparameters of GP, \(\Phi\), are estimated by maximizing the log marginal likelihood Eq. (11). Maximization using a gradient based approach requires the partial derivatives of Eq. (11) with respect to hyperparameters, which are given by

$$\begin{aligned}&\dfrac{\partial }{{\partial {\Phi _i}}}\log p({\tilde{\mathbf {y}}}|{{\mathbf {X}}},\Phi ) \nonumber \\&\quad = \dfrac{1}{2}{\left( {{{\tilde{{\mathbf {y}}}}} - {m_y}\left( {{\mathbf {X}}} \right) } \right) ^{\mathop {\mathrm{T}}\nolimits } }{{\mathbf {K}}}_y^{ - 1} \dfrac{{\partial {{{\mathbf {K}}}_y}}}{{\partial {\Phi _i}}}{{\mathbf {K}}}_y^{ - 1}\left( {{{\tilde{{\mathbf {y}}}}} - {m_y}\left( {{\mathbf {X}}} \right) } \right) \nonumber \\&\quad - \,\dfrac{1}{2}\mathrm{{tr}}\left( {{{\mathbf {K}}}_y^{ - 1}\dfrac{{\partial {{{\mathbf {K}}}_y}}}{{\partial {\Phi _i}}}} \right) ;i=1,2,\ldots ,m+2 \end{aligned}$$
(12)

The derivatives of \({{{\mathbf {K}}}_y}\) with respect to the hyperparameters \(l_i\), \({\sigma _s}\) and \({\sigma _y}\) are given in “Appendix 1” section. In this study, the log marginal likelihood function is maximized using Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm (Fletcher 2013; Nocedal and Wright 1999). The initial estimates of the length scales \((l_1, \dots, l_m)\) is taken as the standard deviations of the predictors \(({\mathbf {X}})\), and the initial values for the scale hyperparameter \((\sigma _s)\) and noise parameter \((\sigma _y)\) are taken as the standard deviation of the state variable (y) divided by \(\sqrt{2}\).

Fig. 1
figure 1

Probabilistic graphs for a GP, b ODE, c the gradient matching (GM) model as proposed by Calderhead et al. (2008), where, \(\gamma\) is variance of the state derivative and \(\varvec{\lambda }\) represents parameters of ODE, d proposed GPPDE model. The shaded nodes represent observations of the state variable, the non-shaded nodes represent random variables, the directed links represent dependencies and the undirected dashed link represent Product of Experts between the two variables connected by the link

Full size image

2.3 Derivatives of Gaussian process

The proposed GPPDE method requires derivatives of the state variable (fitted by a GP model) with respect to independent variables. Since derivative is a linear operator, the derivative of a GP is another GP (Solak et al. 2003). This section provides formulation of partial derivatives of GP at test points \(({\mathbf {X}}_{*})\).

The GP relation Eq. (7a) could be straightforwardly differentiated with respect to test input variable (see “Appendix 2” section). For a constant mean GP, the first order derivative is given by \(p({\dot{\mathbf {y}}^{\mathrm {GP}}}|{\mathbf {y}}, \Phi )=p({\dot{\mathbf {y}}^{\mathrm {GP}}}|m_y, \Phi )={\mathcal {N}}(\dot{\varvec{\mu }}, \dot{\varvec{\Sigma }}^{\mathrm {GP}})\)

$$\begin{aligned} {\dot{\varvec{\mu }}}&= \dfrac{\partial }{{\partial x_i^{_*}}}{\mathbb {E}}\left[ {{{{\mathbf {y}}}_*}|{{{\mathbf {X}}}_*},\varvec{\phi },\sigma _y, {{{\mathbf {X}}},{{\tilde{{\mathbf {y}}}}}}} \right] \nonumber \\&= {\dot{\mathbf {K}}}_*^{\mathop {\mathrm{T}}\nolimits } {\left( {{{\mathbf {K}}}\mathrm{{ + }}\sigma _{\mathrm{{y}}}^{\mathrm{{2}}}{{\mathbf {I}}}} \right) ^{ - 1}}\left( {{{\tilde{{\mathbf {y}}}}} - {m_y}\left( {{\mathbf {X}}} \right) } \right) \end{aligned}$$
(13a)
$$\begin{aligned} \dot{\varvec{\Sigma }}^{\mathrm {GP}}&= {\overset{\cdot ,\cdot }{{\mathbf {K}}}_{**}} - \dot{{\mathbf {K}}}_*^{\mathop {\mathrm{T}}\nolimits } {\left( {{{\mathbf {K}}}+\sigma _{\mathrm{{y}}}^{\mathrm{{2}}}{{\mathbf {I}}}} \right) ^{ - 1}}{{\dot{{\mathbf {K}}}}_*} \end{aligned}$$
(13b)

where \(\dot{\varvec{\Sigma }}^{\mathrm {GP}}\) is the covariance matrix of \({\dot{\mathbf {y}}}^{\mathrm {GP}}\) (Calderhead et al. 2008). Matrix \({{\dot{\mathbf {K}}}_*}\) is populated by mixed covariance function between the state variable and their first order partial derivatives, \({\mathop {\mathrm{cov}}} \left( {y,\dfrac{\partial }{{\partial {x}_{*_i}}}{y_*}} \right) = \dfrac{\partial }{{\partial {x}_{*_i}}}k\left( {{{\mathbf {x}}},{{{\mathbf {x}}}_*}} \right),\) also known as cross-covariance between the state variable and its derivative. The elements of matrix \({\overset{\cdot ,\cdot }{{\mathbf {K}}}_{**}}\) are mixed covariance function between partial derivatives \({\mathop {\mathrm{cov}}} \left( {\dfrac{\partial }{{\partial {x_i}}}y,\dfrac{\partial }{{\partial {x}_{*_j}}}{y_*}} \right) = \dfrac{\partial ^2 }{{\partial {x_i}\partial {x}_{*_j}}}k\left( {{{\mathbf {x}}},{{{\mathbf {x}}}_*}} \right)\), also known as auto covariance of the state derivative.

The second order derivative of GP is given by (see “Appendix 2”)

$$\begin{aligned} \ddot{{\mathbf {y}}}^{\mathrm {GP}}&= \dfrac{\partial ^2 }{{\partial x_i^{_*2}}}{\mathbb {E}}\left[ {{{{\mathbf {y}}}_*}|{{{\mathbf {X}}}_*},\varvec{\phi }, \sigma _y, {{{\mathbf {X}}},{{\tilde{{\mathbf {y}}}}}}} \right] \nonumber \\& = {\ddot{\mathbf {K}}}_*^{\mathop {\mathrm{T}}\nolimits } {\left( {{{\mathbf {K}}}\mathrm{{ + }}\sigma _{\mathrm{{y}}}^{\mathrm{{2}}}{{\mathbf {I}}}} \right) ^{ - 1}}\left( {{{\tilde{{\mathbf {y}}}}} - m_y\left( {{\mathbf {X}}} \right) } \right) \end{aligned}$$
(14)

where the matrix \({{{\ddot{\mathbf {K}}}}_*}\) is populated by mixed covariance function between the state variable and its second order partial derivative, \({\mathop {\mathrm{cov}}} \left( {y,\dfrac{\partial ^2 }{{\partial x_i^{_*2}}}{y^*}} \right) = \dfrac{\partial ^2}{{\partial x_i^{_*2}}}k\left( {{{\mathbf {x}}},{{{\mathbf {x}}}^*}} \right)\).

2.4 Incorporating derivatives information in GP

In some applications, along with the observations of the state variable, information about the derivatives of the state variable may also be available. To incorporate derivative information in the GP regression model, Eq. 3 can be changed to

$$\begin{aligned} \begin{pmatrix} {{\mathbf {y}}}_{N\times 1} \\ \dot{{\mathbf {y}}}_{M\times 1} \end{pmatrix} \sim {{\mathcal {N}}} \begin{pmatrix} \begin{bmatrix} m_y \\ m_{{\dot{y}}} \end{bmatrix}, \begin{bmatrix} {\mathbf {K}}_{N\times N} &{} \dot{{\mathbf {K}}}_{N\times M} \\ \dot{{\mathbf {K}}}^{\prime }_{M\times N} &{} \ddot{{\mathbf {K}}}_{M\times M} \end{bmatrix} \end{pmatrix} \end{aligned}$$
(15)

where \(\dot{{y}}=\dfrac{\partial y}{\partial x_j}\) is the derivation of the state variable with respect to the jth independent variable and M represents number of derivative observations. The a priori mean of the derivatives is represented by \(M\times 1\) vector \(m_{{\dot{y}}}\). The components of the covariance matrix are \({\dot{K}} = \begin{pmatrix} \dfrac{\partial k\left( \cdot \right) }{\partial x_j} \end{pmatrix} _{N \times M}\) and \({\ddot{K}} = \begin{pmatrix} \dfrac{\partial ^2 k\left( \cdot \right) }{\partial x_j \partial x_j^{\prime }} \end{pmatrix} _{M \times M}\).

To predict the state variable or its derivatives at a new test point \(({\mathbf {X}}_*)\), the conditional property of the Gaussian distribution as used in Eq. (5) can be applied to Eq. (15). The expressions for the predictive distributions are given in Solak et al. (2003) and Wu et al. (2017). The methodology presented above can be easily extended to incorporate higher order derivatives in the GP regression model.

2.5 PDE parameter estimation

Let the PDE be given by an implicit function \(f\left( {{x_1}, \ldots ,{x_m},y,\dfrac{{\partial y}}{{\partial {x_1}}}, \ldots ,\dfrac{{\partial y}}{{\partial {x_m}}},\dfrac{{{\partial ^2}y}}{{\partial {x_1}\partial {x_1}}}, \ldots ,\dfrac{{{\partial ^2}y}}{{\partial {x_1}\partial {x_m}}}, \ldots ,\varvec{\lambda }} \right) = 0\), where, y is the state variable, \({x_j}\ (j=1,\ldots m)\) are independent variables and \(\varvec{\lambda }\) is a set of PDE parameters. The GPPDE method uses a GP to model the observations of the state variable and estimate its derivatives involved in the PDE. The residual error in the PDE at an observed point is given by

$$\begin{aligned} \epsilon & =f\Bigg( {x_1}, \ldots ,{x_m},y^{\mathrm {GP}}, \nonumber \\ & \quad \quad \left( \dfrac{{\partial y}}{{\partial {x_1}}}, \left. \ldots \dfrac{{\partial y}}{{\partial {x_m}}},\dfrac{{{\partial ^2}y}}{{\partial {x_1}\partial {x_1}}}, \ldots ,\dfrac{{{\partial ^2}y}}{{\partial {x_1}\partial {x_m}}}, \ldots \right) \right| _{\mathrm{{GP}}} , \varvec{\lambda } \Bigg)\end{aligned}$$
(16)

where the notation \({ \left. {\Bigl ( \cdot \Bigr )} \right| _{\mathrm{{GP}}}}\), incorporates all the partial derivatives of the state variable, means that the arguments are evaluated using the GP relation given in Sect. 2.3. Figure 1 uses probabilistic graphs to represent a GP regression model, an ODE, the GM model of Calderhead et al. (2008) and the proposed GPPDE model.

The parameter set \(\varvec{\lambda }\) can be obtained by assuming a distribution for the residual errors and then applying either the method of maximum likelihood or the Bayesian estimation method using MCMC sampling. These methods not only provide a point estimate of \(\varvec{\lambda }\) but also an estimation interval. However, to keep the parameter estimation simple, we have obtained \(\varvec{\lambda }\) by minimizing the sum of square of residual error (SSRE), given as

$$\begin{aligned} SSRE &= {\varvec{\epsilon }^{\mathrm {T}}}{\varvec{\epsilon }} \\ &= \sum \limits _{\forall {\mathrm{{obs.}}}} f\bigg(\bigg( {x_1}, \ldots ,{x_m},y^{\mathrm {GP}}, \nonumber \\& \quad\quad {{\left. {\left( {\dfrac{{\partial y}}{{\partial {x_1}}}, \ldots ,\dfrac{{\partial y}}{{\partial {x_m}}},\dfrac{{{\partial ^2}y}}{{\partial {x_1}\partial {x_1}}}, \ldots ,\dfrac{{{\partial ^2}y}}{{\partial {x_1}\partial {x_m}}}},\ldots \right) } \right| }_{\mathrm{{GP}}}} ,\varvec{\lambda } \bigg) ^2 \bigg)\end{aligned}$$
(17)

where obs. denotes observations. The minimization is performed using Nelder–Mead simplex algorithm (Lagarias et al. 1998). The GP regression model provides standard error for the estimated state variables and its derivatives. This uncertainty information is propagated to SSRE by weighting each term in the Eq. (17), where weights are inversely proportional to the variance of the terms.

The confidence interval of the estimated parameters is obtained by Cram-rRao bound, which provides a lower bound on the variance of any unbiased estimator (Rao 2008). The confidence interval corresponding to estimated parameter set \(\hat{\varvec{\lambda }}\) is given by \(\hat{\varvec{\lambda }} \pm c\sqrt{\mathrm {diag}\left( I(\hat{\varvec{\lambda }})\right) }\), where \(I(\hat{\varvec{\lambda }})\) is the Fisher information matrix evaluated at estimated values of parameters \((\hat{\varvec{\lambda }})\) (in the present case it is taken as the Hessian matrix of SSRE) and c is z-critical value for a standard normal distribution. In the present study, 95% confidence interval has been estimated, for which the corresponding critical value is 1.96.

Since the GPPDE method does not solve the PDE (forward problem), the initial and boundary conditions are not required. However, if the initial and boundary conditions are available, exactly or with measurement errors, they could be easily incorporated in the GPPDE model. To impose Dirichlet boundary conditions, the values of the state variable at the boundaries are considered as observations with no measurement errors. In the GPPDE model, it is achieved by assigning a very small value to the noise term \((\sigma _y)\) for those boundary observations. If the measurement errors at the boundaries are known, the same can be assigned to \(\sigma _y\). Similarly, to impose Neumann boundary conditions, the values of the state derivatives at the boundaries are considered as observations and the methodology given in Sect. 2.4 is used to learn the GP model. The same approach can also be used to incorporate any combinations of Dirichlet and Neumann boundary conditions.

3 Application of GPPDE method

The proposed GPPDE method is applicable to PDEs and system of PDEs. In this study, we demonstrate its utility by applying it to one-dimensional groundwater diffusion equation and one-dimensional Richards equation. The mathematical representation of these equations is given in the following subsections.

3.1 Groundwater diffusion equation

The groundwater diffusion equation is a second order parabolic PDE that describes the spatio-temporal variation of groundwater level in homogeneous aquifers. It requires one initial and two boundary conditions for forward solution. One-dimensional form of the groundwater equation is given as

$$\begin{aligned} \dfrac{{\partial h}}{{\partial t}} = \lambda \dfrac{{{\partial ^2}h}}{{\partial {x^2}}} \end{aligned}$$
(18)

where h is the groundwater level or head (L; the state variable), t is time (T), x is distance from the origin of the coordinate axis (L) and \(\lambda\) is the parameter of the equation, known as aquifer diffusivity \(({\hbox {L}}^2\!\cdot\!{\hbox {T}}^{-1})\). The inverse problem is to find \(\lambda\) given observed values of head at different location and time. The GPPDE method estimates \(\lambda\) by minimizing the sum of the square of residual errors (SSRE), defined as

$$\begin{aligned} SSRE = {\varvec{\epsilon }^{\mathrm {T}}}{\varvec{\epsilon }}= \sum \limits _{\forall x} {{{\sum \limits _{\forall t} {\left( {{{\left. {\dfrac{{\partial h}}{{\partial t}}} \right| }_{\mathrm {GP}}} - \lambda {{\left. {\dfrac{{{\partial ^2}h}}{{\partial {x^2}}}} \right| }_{\mathrm {GP}}}} \right) } }^2}} \end{aligned}$$
(19)

where \({{\left. {\dfrac{{\partial h}}{{\partial t}}} \right| }_{\mathrm {GP}}}\) and \({{\left. {\dfrac{{{\partial ^2}h}}{{\partial {x^2}}}} \right| }_{\mathrm {GP}}}\) are obtained from a GP regression model fitted to observed head values.

3.2 Richards equation

The Richards equation is a nonlinear parabolic PDE that describes the movement of water in unsaturated zone (Richards 1931; Celia et al. 1990). Flow in unsaturated zone is one of the most complex flows in nature. One-dimensional form of the Richards equation is given by

$$\begin{aligned} \begin{aligned}\dfrac{{\partial \theta }}{{\partial t}}&= \dfrac{\partial }{{\partial z}}\left[ {k\dfrac{{\partial h}}{{\partial z}}} \right] + \dfrac{{\partial k}}{{\partial z}}\\&= \underbrace{\dfrac{{\partial k}}{{\partial z}}\dfrac{{\partial h}}{{\partial z}}}_{\mathrm{{Term 1}}} + \underbrace{k\dfrac{{{\partial ^2}h}}{{\partial {z^2}}}}_{\mathrm{{Term 2}}} + \underbrace{\dfrac{{\partial k}}{{\partial z}}}_{\mathrm{{Term 3}}}\end{aligned} \end{aligned}$$
(20)

where \(\theta\) is volumetric soil moisture \(({\hbox {L}}^{3}\!\cdot\!{\hbox {L}}^{-3}\); the state variable), t is time (T), z is vertical dimension (L; positive upward), k is hydraulic conductivity \(({\hbox {L} \!\cdot\! \hbox{T}}^{-1})\) and h is pressure head (L). The hydraulic conductivity (k) and the pressure head (h) can be related to the soil moisture by van Genuchten model (van Genuchten 1980), given by

$$\begin{aligned} k&= {k_s}{\Theta ^{1/2}}{\left[ {1 - {{\left( {1 - {\Theta ^{1/m}}} \right) }^m}} \right] ^2} \end{aligned}$$
(21a)
$$\begin{aligned} \Theta&= {\left\{ \begin{array}{ll} {\left[ {1 + {{\left| {\alpha h} \right| }^n}} \right] ^{ - m}} &{} h<0 \\ 1, &{} h \ge 0 \end{array}\right. } \end{aligned}$$
(21b)
$$\begin{aligned} \Theta&= \dfrac{{{\theta } - \theta _r}}{{{\theta _s} - {\theta _r}}} \end{aligned}$$
(21c)

where \({k_s}\) is saturated hydraulic conductivity, \(\Theta\) is relative saturation, and \({\theta _r}\) and \({\theta _s}\) are residual and saturated soil moisture content, respectively. The terms \(\alpha \,\,({\hbox {L}}^{-1})\), m and n represent model parameters where, m and n are related as \(n\left( {1 - m} \right) = 1\). The parameters \(\alpha\) and n are related to air-entry pressure head and pore-size distribution, respectively. Eq. (21a) is known as hydraulic conductivity function and Eq. (21b) is known as soil water retention function.

In the literature, field observations have been used to estimate soil hydraulic parameters using inverse solution of the Richards equation which requires initial and boundary conditions (Ritter et al. 2003; Simunek et al. 2005). Since, initial and boundary condition in real world are not easily available, the conventional approach becomes cumbersome (Farthing and Ogden 2017). The proposed GPPDE overcomes this limitation. In the GPPDE method, the estimation of parameters is done by minimizing SSRE, given by

$$\begin{aligned} SSRE&= {\varvec{\epsilon }^{\mathrm {T}}}{\varvec{\epsilon }}\nonumber \\&= \sum \limits _{\forall t's} {\sum \limits _{\forall z's} {{{\left[ {\left. \dfrac{{\partial \theta }}{{\partial t}}\right| _{\mathrm {GP}} - \left. \left( {\underbrace{\dfrac{{\partial k}}{{\partial z}}\dfrac{{\partial h}}{{\partial z}}}_{\mathrm{{Term 1}}} + \underbrace{k\dfrac{{{\partial ^2}h}}{{\partial {z^2}}}}_{\mathrm{{Term 2}}} + \underbrace{\dfrac{{\partial k}}{{\partial z}}}_{\mathrm{{Term 3}}}} \right) \right| _{\mathrm {GP}}} \right] }^2}} }. \end{aligned}$$
(22)

In the present work, we have estimated only \(\alpha\) and n, but the method can be easily extended to estimate any desired number of parameters. To apply GPPDE, the terms of \({\varvec{\epsilon }^{\mathrm {T}}}{\varvec{\epsilon }}\) should be expressed in the terms of the state variable \((\theta )\), independent variables (z and t) and derivatives of the state variable with respect to the independent variables \(\left( \dfrac{{\partial \theta }}{{\partial z}},\dfrac{{{\partial ^2}\theta }}{{\partial {z^2}}}\ {\mathrm {and}} \ \dfrac{{\partial \theta }}{{\partial t}}\right)\). This factorization of \({\varvec{\epsilon }^{\mathrm {T}}}{\varvec{\epsilon }}\) is provided in “Appendix 2” section.

We compared the GPPDE estimates of hydraulic parameters with that obtained from conventional approach by using HYDRUS-1D software (Simunek et al. 2005). The software first solves the forward problem and then estimates hydraulic parameters by minimizing the difference between the simulated and observed values. In the present paper z is discretized at 1 cm interval. For each iteration HYDRUS automatically adjusts the time step to achieve fast convergence and the time step varies in the range of 0.00024–0.024 h. The maximum number of iterations allowed for a given time step is set to 10 for forward solution of Richards equation using a modified Picard method. The maximum necessary absolute change in the value of the water content and pressure head between two successive iterations during a particular time step are set to 0.001 and 1 cm, respectively. Levenberg–Marquardt algorithm is used for minimization. If the observations have measurement error, HYDRUS-1D uses a weighted error function where weights are inversely proportional to the variance of the measurement error. However, unlike GPPDE, it cannot account for measurement error in initial or boundary conditions. Further minute details of implementation of HYDRUS model is available in the HYDRUS’ user manual.

4 Data used in the study

This section describes the data used for testing the GPPDE method on the diffusion equation and the Richards equation. Newly developed parameter estimation methods are usually first tested on synthetic data because the true parameters are known and sensitivity of these methods to measurement errors can be evaluated by introducing error of different levels. Hence, in this work we have tested the GPPDE method on synthetic data.

4.1 Data used for the groundwater diffusion equation

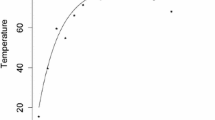
Reynolds (1987) reported the water level fluctuations for three sites in a glacial-outwash valley aquifer near Cortland, New York, USA. The data reported by Reynolds for Site-1 have been used in many studies to demonstrate the performance of parameter estimation methods in estimating aquifer diffusivity of the site (Srivastava 2006; Swamee and Singh 2003). In Reynolds’ study for Site-1, variation of water level in two different wells were observed, one close to a stream and other 152 m from the stream. Reynolds assumed that the water level in the well closer to the stream represents the water level of the stream. The data of water level fluctuations are provided in figures of the original study, which we extracted using WebPlotDigitizer software (Rohatgi 2011). The variation of water level of the wells are plotted in Fig. 2. The reported value of the aquifer diffusivity varies in range of 550–2200 \({\hbox {m}}^2\,\!\cdot\!\hbox {h}^{-1}\), depending on the assumptions and methodologies. The performance of GPPDE is evaluated for the following two cases.

4.1.1 Synthetic data

Synthetic data are generated by assuming observed water level of the stream for Site-1 as the left boundary condition and for the right boundary, it is assumed that there is no effect of variation in the stream water level on the groundwater level at \(x = 500\,{\hbox {m}}\), \(h\left( x=500 \,{\mathrm {m}}, t \right) = 0\, {\mathrm {m}}\). Initial condition is assumed as \(h\left( x, t = 0 \right) = 0\, {\mathrm {m}}\). To generate water level data, an implicit finite difference scheme was applied with \(\lambda = 1000\, {\mathrm {m}}^2\,\!\cdot\!{\mathrm {h}}^{-1}\). The synthetic data are plotted in Fig. 3a. The GPPDE method is demonstrated on the data generated for five intervals of x, \(\Delta x = [10, 25, 50, 75, 150]\, {\mathrm {m}}\) and for time \(t\in [0, 200]\) h. Simulations in the range \(x \in\) [1 150] m are used as observations for GPPDE analysis. For example, if \(\Delta x = 25\) m, simulations at \(x = [25, 50, 75, 100, 125, 150]\, {\mathrm {m}}\) are treated as observations for GPPDE parameter estimation.

4.1.2 Field data

For estimating aquifer diffusivity at the study site, the field observations made at the second well \((x = 152\) m) is considered as a response to fluctuations in the stream water level. For this analysis, we again made the assumption that the groundwater level at \(x = 500\) m is unaffected by the variations in the stream water level, i.e. \(h\left( x=500 \,{\mathrm {m}}, t \right) = 0\, {\mathrm {m}}\).

Fig. 2
figure 2

Observed water levels in two wells at Cortland, New York based on the data provided by Reynolds (1987). Dashed curve for well near the stream and the dotted curve for well 152 m from the stream

Full size image

4.2 Data used for the Richards equation

The applicability of GPPDE on the Richards equation is tested using synthetic data described in this subsection. Four cases with different combinations of boundary conditions are studied. Within these four cases, we also studied the effect of different number of observations and error levels on GPPDE parameter estimates.

The finite difference scheme for mixed-form of the Richards equation provided by Celia et al. (1990) is adopted to generate synthetic data. The synthetic data are generated with five hydraulic parameters \(\theta _r= 0.075\), \(\theta _s= 0.287\), \(\alpha =0.05\,{\hbox {cm}}^{-1}\), \(n = 2\), and \(k_s= 1.5\,{\hbox {cm}}\!\cdot\!{\hbox {h}}^{-1}\) with initial condition \(h\left( {z,t = 0} \right) = -\,65\, {\hbox {cm}}\), having boundary conditions as \(h\left( {z = 0,t} \right) = -\, 65\, {\hbox {cm}}\) at the bottom and \(h\left( {z = 60,t} \right) = - 20.7\, {\hbox {cm}}\) at the top. The above initial and boundary conditions are in terms of pressure head, which translates to volumetric water content as \(\theta \left( {z,t = 0} \right) = 0.137\), and \(\theta \left( {z = 0,t} \right) = 0.137\) and \(\theta \left( {z = 60,t} \right) = 0.222\), respectively, using the van Genuchten (1980) model. The soil moisture is estimated using the finite difference scheme at internal nodes with \(\Delta z = 1\,{\mathrm {cm}}\) and \(\Delta t= 1\, {\mathrm {h}}\) over the interval [0, 50] h.

Using the synthetic data described above, the following four cases are studied:

  1. 1.

    Case 1 (Top: Dirichlet and Bottom: Dirichlet): The boundary condition described in previous paragraph corresponds to Case-1. Figure 5a shows the 3-D plot of the synthetic data generated for this case.

  2. 2.

    Case 2 (Top: Dirichlet and Bottom: Free drainage): The top boundary in this case is as described in Case-1, and the bottom boundary is free drainage which is a Neumann boundary with \(\dfrac{\partial \theta }{\partial z} = 0\).

  3. 3.

    Case 3 (Top: Time Varying Dirichlet and Bottom: Dirichlet): The top boundary in this case represents diurnal variation of soil moisture at the soil surface which is obtained by superimposing the top boundary in Case-1 with a sinusoidal wave of amplitude 3 cm and periodicity of 24 h, mathematically \(h\left( {z = 60,t} \right) = -20.7+3\sin \left( \dfrac{2\pi t}{24}\right) \, {\mathrm {cm}}\), where \(t\in (0, 50]\,{\text {h}}\). The bottom boundary is fixed as in Case-1 \((h\left( {z = 0,t} \right) = - 65\, {\mathrm {cm}})\).

  4. 4.

    Case 4 (Top: Time Varying Dirichlet and Bottom: Free drainage): Time varying top boundary condition is adopted from Case-3 and a bottom Neumann condition is adopted from Case-2.

The boundary conditions for these four cases are summarized in Table 1. To study the performance of the GPPDE method for coarser data, the observations at five intervals of \(z\,\, (\Delta z = 1, 2, 3, 4, 5\) and 10 cm) are used. Next, to study the performance of GPPDE on noisy data, zero mean Gaussian noise of standard deviations 1, 2, 3, 4 and 5% of the soil moisture observation is added to the synthetic data.

Table 1 The boundary conditions used to demonstrate the application of GPPDE on the Richards equation
Full size table

5 Results and discussion

This section presents the results obtained from the proposed GPPDE method for the diffusion and the Richards equations. In the case of the Richards equation, the GPPDE parameter estimates are compared with the HYDRUS estimates.

Coefficient of determination \((R^2)\) and Root Mean Square Error (RMSE) are calculated by the following equations for evaluating the performance of GP regression, and parameter estimates by GPPDE and HYDRUS.

$$\begin{aligned} R^{2}&= 1-\dfrac{\sum \nolimits _{i=1}^{N}\left( {\tilde{y}}_{i} -{\hat{y}}_{i} \right) ^{2} }{\sum \nolimits _{i=1}^{N}\left( {\tilde{y}}_{i} -{\bar{y}}\right) ^{2} } \end{aligned}$$
(23)
$$\begin{aligned} {\mathrm {RMSE}}&= \sqrt{\dfrac{\sum \nolimits _{i=1}^{N}\left( {\tilde{y}}_{i} -{\hat{y}}_{i}\right) ^{2} }{N} } \end{aligned}$$
(24)

where \({\tilde{y}}_{i}\) are observations, \({\hat{y}}_{i}\) are predicted values, \({\bar{y}}\) is the mean of the observations, and N is the number of observations.

5.1 Groundwater diffusion equation

5.1.1 Synthetic data

The synthetic water level data used in this section are described in Sect. 4.1 and shown in Fig. 3a. The data with \(\Delta x = 1\, {\mathrm {m}}\) is used to train GP regression model and the hyperparameters of GP, \(\varPhi = [l_x, l_t, \sigma _s, \sigma _y]\) are estimated using the method explained in Sect. 2.2, where \(l_x\) and \(l_t\) are length scale parameters in spatial (x) and temporal (t) dimensions, respectively. The estimated values of the hyperparameters are \({\widehat{\varPhi }} = [130\,\mathrm{m}, 1.7\,\mathrm{h}, 0.875, 5.3{\hbox {E}}{-}04\,\mathrm{m}]\). The GPPDE method requires estimation of the state variable and its partial derivatives involved in the PDE. Using the obtained hyperparameters, the state variable (h) is calculated using Eq. (7a) and is plotted in Fig. 3b, which suggests a good fit. The state derivatives \(\left( {\dfrac{{\partial h}}{{\partial t}}\ {\mathrm {and}} \ \dfrac{{{\partial ^2}h}}{{\partial {x^2}}}} \right)\) are obtained from the methodology given in Sect. 2.3.

The PDE parameter \(\lambda\) is obtained by incorporating the estimates of the state variable and its derivative in SSRE Eq. 19, and then minimizing the SSRE function. For \(\Delta x = 10\, {\mathrm {m}}\), the GPPDE method estimates \({\hat{\lambda }} = 999.6 \pm 2.41\,{\hbox {m}}^2\!\cdot\!{\hbox {h}}^{-1}\) which is close to the true value of diffusivity (1000 \({\hbox {m}}^2\!\cdot\!{\hbox {h}}^{-1}\)), suggesting that the GPPDE method can successfully estimate the aquifer diffusivity \((\lambda )\).

To study the performance of the GPPDE method for coarse resolution data, the method is applied on sub-samples of the synthetic data, i.e. observations at intervals \(\Delta x = [25, 50,75,150]\, {\mathrm {m}}\) are used for learning the parameters. The estimates of \(\lambda\) for different number of observations along with their 95% confidence interval are given in Table 2. It is concluded from the table that with the decrease in number of observations, the uncertainty in the estimate of \(\lambda\) increases. The length scale parameters \((l_x\) and \(l_t)\) can be interpreted as characteristic length, which is the distance required in the input space (along a particular axis) for the function values to become uncorrelated (Rasmussen and Williams 2006). Thus, with decrease in the number of observations in the x-dimension, the \(l_x\) increases. It is observed that learning length-scale parameters from sparse data may sometimes result in an overly complicated function because of local minima in the marginal log likelihood function Eq. (11). This is a well known problem in GP models (Rasmussen and Williams 2006; Tripathi and Govindaraju 2007). We found in our experiments that if such a problem occurs, it can be easily detected by visualizing the fitted surface. Further, we realized that with some familiarity with the data, length scale parameters can be easily specified and the results are not sensitive to small changes in their values. The logarithm of SSRE for \(\Delta x = [10, 50, 150]\, {\mathrm {m}}\) versus \(\lambda\) is plotted in Fig. 4 (the logarithmic transformation of SSRE is chosen for better visualization). From the figure and the table, we realize that the GPPDE method can estimate \(\lambda\) with fewer observations, however it increases estimation uncertainty.

5.1.2 Field data

The GP model is trained with observations at \(x = [0, 152, 500]\, {\mathrm {m}}\). For \(x = 0\, {\mathrm {m}}\), the time series observations from the well closer to the stream is used; for \(x = 152\, {\mathrm {m}}\), the time series observations from the well away from the stream is used; and for \(x = 500\, {\mathrm {m}}\), it is assumed that the groundwater level is unaffected by any variations in the stream water level, \((h\left( x = 500\, {\mathrm {m}}, t \right) = 0\, {\mathrm {m}})\). The water level values at x equal to 0 and 500 m are treated as Dirichlet boundary conditions. The hyperparameters for the fitted GP model are \({\widehat{\varPhi }} = [330\,\mathrm{m}, 1.7\,\mathrm{h}, 0.610, 2.8{\hbox {E}}{-}03\,\mathrm{m}]\). The estimated aquifer diffusivity is \(\lambda = 564.8\pm 29.3\, {\mathrm {m}}^2\!\cdot\!{\mathrm {h}}^{-1}\), which is within the limits of reported values (550–2200 \({\mathrm {m}}^2\!\cdot\!{\mathrm {h}}^{-1})\) in the literature (Reynolds 1987; Swamee and Singh 2003; Srivastava 2006).

Fig. 3
figure 3

a Synthetically generated observations of groundwater level plotted at a resolution of 1 m, b mean of GP regression fit to the groundwater profile, trained using data with \(\Delta x= 10\, {\mathrm {m}}\)

Full size image
Table 2 The estimates of aquifer diffusivity, \(\lambda\), for different intervals of x, along with their 95% confidence interval
Full size table
Fig. 4
figure 4

The logarithmic transformed values of SSRE for different intervals of x as a function of aquifer diffusivity \((\lambda )\). The vertical black line represents the true value of \(\lambda\)

Full size image

5.2 Richards equation

The following subsections demonstrate the application of the GPPDE method to estimate soil hydraulic parameters and compare those estimates with HYDRUS-1D estimates. To evaluate the performance of the GPPDE method for coarse resolution data, the method is trained using observations at six intervals of \(z\,\,(\Delta z = [1, 2, 3, 4, 5, 10] \,{\mathrm {cm}})\), as described in Sect. 4.2. The estimated hyperparameters and the estimated soil hydraulic parameters of the Richards equation for the four cases (different boundary conditions) are presented in Table 3.

5.2.1 Parameter estimation

The first step in the GPPDE method is to fit a GP regression model to the soil moisture data and obtain the hyperparameters, \(\varPhi = [l_z, l_t, \sigma _s, \sigma _y]\) using the methodology given in Sect. 2.2, where \(l_z\) and \(l_t\) are length scale parameters of the covariance function in spatial (z) and temporal (t) dimensions, respectively. Next, the derivatives of the state variable \(\left( {\dfrac{{\partial \theta }}{{\partial t}},\dfrac{{\partial \theta }}{{\partial z}}\ {\mathrm {and}} \ \dfrac{{{\partial ^2}\theta }}{{\partial {z^2}}}} \right)\) are obtained using the methodology given in Sect. 2.3. As the final step, the estimates of the state variable and its partial derivatives (obtained from the GP modelling) are incorporated in SSRE Eq. (22) to estimate soil hydraulic parameters \(\varvec{\lambda }= [\alpha , n]\).

The synthetic soil moisture data generated using the Richards equation as described in Sect. 4.2 are plotted in Fig. 5a. This dataset consists of two Dirichlet boundaries and intermediate observations at 59 locations in the range \(z \in [1, 59]\, {\mathrm {cm}}\) with \(\Delta z = 1\, {\mathrm {cm}}\) and \(t \in [1, 50]\, {\mathrm {h}}\) with \(\Delta t = 1\, {\mathrm {h}}\). The GP regression model is forced to predict precise Dirichlet boundary conditions using the methodology presented in the last paragraph of Sect. 2.5. The curve obtained from the GP regression model for the learned hyperparameters \({\widehat{\varPhi }} = [5\,\mathrm{cm}, 3\,\mathrm{h}, 0.188, 9.3{\hbox {E}}{-}05]\) is plotted in Fig. 5b, which is very similar to the true data \((R^2 = 1, {\hbox {RMSE}} = 8.12{\hbox {E}}{-}05)\).

Fig. 5
figure 5

a 3-D plot of the synthetic soil moisture data for Case 1, b mean of GP regression fit to the soil moisture data

Full size image

The top row in Fig. 6a–c shows the variation of the estimated soil moisture with z, and its first and second order derivatives with respect to z at time \(t = 25\,{\hbox {h}}\). The bottom row of Fig. 6d, e shows the variation of the estimated soil moisture and its derivative with respect to t at height \(z = 30\,{\hbox {cm}}\). Like the state variable, the partial derivatives are also GP, which are smooth functions. Figure 6 shows that the GP estimates have fluctuations present near the boundaries, which increase for higher order derivatives. The standard errors of the fitted curves (shown as dashed lines) also increase near the boundaries. These fluctuations and increase in the standard error are reflections of higher uncertainty in the GP fitting near the boundaries.

Fig. 6
figure 6

GP regression fit to the synthetic soil moisture data for Case 1 and its partial derivatives. The first row shows the variations along the height (z) of soil column at \(t = 25\,{\hbox {h}}\)—a soil moisture observations and GP fit, b first derivative of \(\theta\) w.r.t. z, c) second derivative of \(\theta\) w.r.t. z. The second row shows the variations along the time (t) at \(z= 30\,{\hbox {cm}}\)—d soil moisture observations and GP fit, e derivative of \(\theta\) w.r.t. t. The vertical dashed lines represent the standard error of the fitted curves

Full size image

The estimated values of the hydraulic parameters are \(\hat{\varvec{\lambda }} = [0.049 \pm 0.001\,{\hbox {cm}}^{-1}, 2.008 \pm 0.008]\), which are very close to the true value \(\varvec{\lambda }_0 = [0.05\, {\mathrm {cm}}^{-1}, 2]\). Figure 8a shows the contours of the logarithmic transformed values of SSRE as a function of \(\alpha\) and n. Again, the logarithmic transformation is used to aid visualization. The contours are closely spaced near the vicinity of the true solution and their intervals are wider for the cases with sparser data. The estimate of parameters, \(\alpha\) and n, for Cases 2, 3 and 4 from GPPDE method are provided in Table 3. Like Case 1, the GPPDE model could reasonably estimate \(\varvec{\lambda }\) for these cases as well. The parameter uncertainties for both \(\alpha\) and n are higher for Cases 1 and 3, where bottom boundary condition imposes a fixed soil moisture (Dirichlet) compared to Cases 2 and 4, where bottom boundary condition is free drainage (Neumann). This could be attributed to the abrupt change in soil moisture near the bottom boundary for Dirichlet conditions (see Figs. 5, 7).

Fig. 7
figure 7

a 3-D plot of the synthetic soil moisture data for Case 2, b mean of GP regression fit to the soil moisture data

Full size image

5.2.2 Sparse observations

To study the performance of GPPDE for coarse resolution data, it is trained with data obtained at intervals, \(\Delta z = [1, 2, 3, 4, 5, 10]\, \mathrm{cm}\). Figure 6 compares the estimates of the state variable and its derivatives for different number of observations \((\Delta z = [1, 3, 5]\, {\mathrm {m}})\). With increase in \(\Delta z\) (decrease in number of observations), the standard error of the estimated state variable and its derivatives increase. The estimated values are however very close for different \(\Delta z\), except near the boundaries. These differences among the curves are relatively large for space derivatives that the time derivative because the number of observations have reduced in the space dimension.

The number of observational depths, the estimates of hyperparameters and estimated soil hydraulic parameters for different \(\Delta z\) and boundary conditions are shown in Table 3. The logarithm of SSRE as a function of \(\alpha\) and n for different z intervals are plotted in subfigures of Figs. 8 and 9 for Cases 1 and 2, respectively.

The training of GPPDE for different \(\Delta z\) showed that the time length scale hyperparameter \((l_t)\) do not change because the temporal resolution of data remains the same. The length scale \((l_z)\) increases with increase in \(\Delta z\), resulting in smoother curve for coarse resolution data. The contour plots of logarithmic SSRE (Fig. 8) show that even for the sparse data set, the true solution lies in the vicinity of the lowest contour. However, the differences between the true and the estimated values of the hydraulic parameters increase with decrease in number of observations (Table 3). The value of contours decreases with increase in \(\Delta z\) which happens due to smaller number of terms in SSRE estimates. Further, the contour intervals are wider for smaller number of observations, suggesting increased uncertainty in the estimated parameters (also see Table 3).

Fig. 8
figure 8

Contours of logarithm of SSRE for Case 1 for different intervals of z. The intersection of the horizontal and the vertical lines represents the true parameters

Full size image
Fig. 9
figure 9

Contours of logarithm of SSRE for Case 2 for different intervals of z. The intersection of the horizontal and the vertical lines represents the true parameters

Full size image

5.2.3 Measurement errors

Errors of five different levels are added to the soil moisture observations for investigating the performance of GPPDE method in the presence of noise. The additive errors are normally distributed noise with mean zero and standard deviation 1, 2, 3, 4 and 5% of the soil moisture observations. Figures 10 and 11 provide the estimates of the parameters \((\alpha\) and n) for Cases 1 and 2, respectively, obtained from 100 Monte Carlo simulations. As expected, higher error levels increase the variability in the estimated parameters. However, no significant systematic bias is evident in the estimated parameters with increased error levels. These figures do not plot HYDRUS estimates, because HYDRUS consistently estimated \(\alpha\) and n close to the true value for all the error levels.

Fig. 10
figure 10

Box plots for the estimates of \(\alpha\) and n corresponding to different levels of Gaussian noise for \(\Delta z = 5\, {\mathrm {cm}}\) and boundary conditions as specified for Case 1

Full size image
Fig. 11
figure 11

Box plots for the estimates of \(\alpha\) and n corresponding to different levels of Gaussian noise for \(\Delta z = 5\, {\mathrm {cm}}\) and boundary conditions as specified for Case 2

Full size image

5.2.4 Perturbed boundary conditions

In applications where boundary conditions are obtained from observations, the measurement errors may induce uncertainty in boundary conditions. To test the performance of GPPDE and HYDRUS under uncertain boundary conditions, the Dirichlet boundaries for Cases 1 and 2 are perturbed with zero mean Gaussian noise and standard deviations ranging from 1 to 5% of the true soil moisture value.

Figures 12 and 13 show the box plots of the estimated \(\alpha\) and n for GPPDE and HYDRUS (inverse modelling) for Cases 1 and 2, respectively. Since HYDRUS simulations were computationally expensive, results obtained from 60 Monte Carlo simulations are shown.

Fig. 12
figure 12

Figure compares the performance of GPPDE and HYDRUS under boundary conditions perturbed with zero mean Gaussian noise (standard deviation equal to 1, 2, 3, 4 and 5% of the boundary values) for Case 1. The estimates of \(\alpha\) and n obtained from 60 Monte Carlo simulations are shown as box plots. The parameters are obtained for the synthetic soil moisture data with \(\Delta z = 5 \, {\mathrm {cm}}\)

Full size image

For Case 1, HYDRUS marginally overestimates \(\alpha\) compared to GPPDE estimates, though it has relatively smaller variability. For n, the variability is smaller for GPPDE estimates at higher error levels. The results for Cases 2 are similar. Overall, the results suggest that GPPDE and HYDRUS estimates are only marginally different. However, GPPDE has significant advantages over HYDRUS in terms of computational time. For example, the computation time for one run of HYDRUS is \(5.787 \pm 0.004 \, {\mathrm {s}}\) (based on 100 simulations). Whereas for a MATLAB implementation of GPPDE on the same sample, the computational time for one run is \((5.002 \pm 0.065) \times 10^{-3} \, {\mathrm {s}}\).

Fig. 13
figure 13

Figure compares the performance of GPPDE and HYDRUS under boundary conditions perturbed with zero mean Gaussian noise (standard deviation equal to 1, 2, 3, 4 and 5% of the boundary values) for Case 2. The estimates of \(\alpha\) and n obtained from 60 Monte Carlo simulations are shown as box plots. The parameters are obtained for the synthetic soil moisture data with \(\Delta z = 5 \, {\mathrm {cm}}\)

Full size image
Table 3 Estimates of GP hyperparameters and soil hydraulic parameters obtained from the GPPDE method. The true values of \(\alpha\) and n are \(0.05\,{\hbox {cm}}^{-1}\) and \(n = 2\), respectively
Full size table

6 Summary and concluding remarks

A Gaussian process (GP) based method for estimating parameters of PDEs is proposed and termed as Gaussian process for Partial Differential Equation (GPPDE) method. Unlike the conventional method, the GPPDE method does not require setting-up of initial and boundary conditions explicitly, which is often difficult in real world applications. However, if the initial and boundary conditions are known (exactly or with measurement errors), they could be incorporated in the method.

The new GPPDE method is evaluated by applying it on the diffusion and the Richards equations. The results suggest that the GPPDE method can correctly estimate parameters of the diffusion equation for the synthetic data. It provided a reasonable estimate for the diffusivity of glacial-outwash valley aquifer, Cortland, New York. The GPPDE method has also estimated parameters of the Richards equation satisfactorily for all the four cases of different boundary conditions investigated in the study.

A comparison of the GPPDE and HYDRUS (a conventional inverse modelling approach) suggested that both the methods could reasonably estimate soil hydraulic parameters in the presence of Gaussian noise in the range 1–5%. However, GPPDE has significant advantages in terms of computational time. We found that for the same dataset and computer, GPPDE was three orders of magnitude faster than HYDRUS. However, to reliably estimate PDE parameters, GPPDE requires large dataset. Its performance, to a large extent, depends on the accuracy of the curve fitted to the observations of the state variable. Accuracy of GP regression fit is also limited by difficulty in selection of a suitable covariance function.

Several avenues should be explored to further refine the proposed GPPDE method for PDE parameter estimation. The GPPDE method can be formulated in the Bayesian framework that will provide credible intervals for the estimated values of the parameters. Also, methods should be developed to relate kernel length-scale parameters to the characteristic length-scales of the input dimensions based on the physics of the problem.

Comprehensively, the results suggest that the proposed method can be an effective alternate to the conventional PDE parameter estimation methods. It has advantages for large observational datasets in which the state variable has high dimensionality. Overall, the approach of interpreting numerical problems of differential equations as probabilistic inference problems, and solving them using machine learning methods like GP is an exciting new area of research. It has potential to provide novel methods for handling observational uncertainties, which are ubiquitous in water resources problems but often ignored when used with differential equations.