1 Introduction

Statistical modeling of water use is important for efficiently managing water utilities to meet demand and conserve resources (Lee et al. 2010; Donkor et al. 2014). Understanding the relationship of important environmental and demographic drivers with water use are critical for assessing and forecasting future demand. Quality household-level forecasts may be used to meet demand and to target high-demand and low-efficiency users for water conservation through, e.g. special pricing and rebate programs. Accurate high-resolution analyses and forecasts require the selection of important predictive features and the estimation of their possibly nonlinear effects from large, correlated data (Lee et al. 2015; Duerr et al. 2018). This paper motivated by the need of a fully Bayesian framework for model selection and analysis of urban water demand at fine spatial scale (e.g. household or census block level). However, our methodology is highly translational and is applicable to general environmental and geostatistical problems where variable selection and nonlinear associations between covariates and the response need to be identified.

A general model for the analysis of spatio-temporal data is

$$\begin{aligned} y_{i} = \eta (\varvec{x}_{i}) + \epsilon _{i}, \end{aligned}$$
(1)

where the response \(y_{i}\) at the space-time index i potentially depends on predictors \(\varvec{x}_i = (x_{1i},\ldots ,x_{Gi})\) and the errors \(\epsilon\) may be spatio-temporally structured or unstructured. An application of this model requires selecting a subset of significant predictors, choosing an appropriate form for \(\eta (\cdot )\), and estimating space-time dependence parameters associated with \(\varvec{\epsilon }\), possibly in computationally demanding settings. A formal statistical model selection framework that can address these challenges is needed to complement scientific expertise to inform about the inclusion and shape of covariate effects in future studies. The goal of this paper is therefore to develop a methodology to address variable selection in additive regression models with correlated errors in high-dimensional settings so that it can be applied to analyzing and forecasting urban water demand.

The generalized additive model (GAM; Hastie and Tibshirani 1986) is a useful extension of the generalized linear model (GLM) in which the linear predictor is modeled as a sum of smooth, unknown functions of covariates. GAMs may be fit by maximization of a penalized likelihood, where the penalty is placed on some measure of the “wiggliness” of the functions (Wood 2004). Bayesian GAMs may be fit using Markov Chain Monte Carlo (MCMC) methods (Crainiceanu et al. 2005; Wood 2016; Merrill et al. 2017) or by using fast approximations, e.g. the mean field variational Bayes (MFVB) approach, in which the full posterior distribution is approximated by a product of distributions (Wand and Ormerod 2011; Luts et al. 2014), or the integrated nested Laplace approximation (INLA) approach, which exploits a link between Gaussian random fields and Gaussian Markov random fields along with computationally efficient approximations of densities (Rue et al. 2009; Lindgren and Rue 2015). Extensions of the additive model for Gaussian data with correlated errors have been studied (see e.g. Opsomer et al. 2001; Francisco-Fernandez and Opsomer 2005; Bliznyuk et al. 2012). They showed that uncovering the true function \(\eta\) becomes difficult in the presence of correlated data, as the correlated observations can introduce additional “structure” not attributable to the mean trend which can lead to overfitting and poor trend estimates. Several methods are available to address correlated data; notably, the R package mgcv provides a generalized additive mixed model (GAMM) framework for estimating trends and correlation parameters in a semiparametric model with spatially and temporally correlated errors. The INLA method can also fit GAMs for spatio-temporal data by representing the spatio-temporal effect using stochastic partial differential equations (Lindgren et al. 2011; Blangiardo et al. 2013).

An important challenge facing additive modeling of correlated data is variable selection. Current research of variable selection in GAMs typically focuses on independent errors and addresses two problems: inclusion (whether a predictor belongs in the model) and linearity (whether assuming a linear form of the relationship between a predictor and the response is adequate). Partially linear models are extensions of the GAM that address linearity (Zhang et al. 2011). Inclusion was addressed by Ravikumar et al. (2009) by applying the group lasso penalty (Yuan and Lin 2006), in which the groups are the basis function representation of the functional form of the relationship with the response. Similarly, Lin et al. (2013) applied a lasso-type penalty to smoothing spline analysis-of-variance models for variable selection in quantile regression. Hypothesis testing methods have been proposed to address both inclusion and linearity (Wood 2006), and two methods for selection using penalized likelihoods can perform inclusion selection under certain types of correlation (Marra and Wood 2011). Until recently, variable selection in GAMs was limited to problems with a low to modest number of predictors G. Sparse selection of a high number of predictors has been accomplished using optimization of a penalized likelihood, in which the penalty controls the smoothness as well as the number of significant predictors (Lou et al. 2016; Chouldechova and Hastie 2017). A major issue with lasso-type methods is that the limiting distribution of the estimators is complicated, and therefore satisfactory standard errors cannot be easily obtained (Knight and Fu 2000; He and Huang 2016). Some recent work (Scheipl 2011; Banerjee and Ghosal 2014) has provided Bayesian methodology for variable selection in high-dimensional GAMs which does provide standard errors, but are limited by the assumption of independence of the errors. Duerr et al. (2018) showed that household water demand are spatio-temporally correlated with strong temporal autocorrelation; therefore there is a need to extend variable selection methods to the correlated data setting.

In this paper, we propose a fully Bayesian formulation of the semiparametric regression model defined in Eq. (1) that allows for simultaneous estimation, variable selection, and modeling of spatio-temporally correlated high-dimensional data. Our formulation is a hybrid of a Bayesian geoadditive model (e.g. Kamman and Wand 2003) and a modified version of the Bayesian group lasso with a spike-and-slab (BGL-SS) prior (Xu and Ghosh 2015), and is motivated by the need for variable selection and analysis of large spatio-temporally referenced urban water demand data. The proposed method allows selection for each predictor to iterate between null, linear, or nonlinear. Unlike the Bayesian group lasso, the point mass mixture in the BGL-SS prior produces exact zero coefficient estimates, yielding group variable selection. The proposed method offers three major advantages over existing methods for fitting and selecting GAMs: (i) relying on Bayesian machinery, it provides reliable uncertainty quantification as judged by posterior distributions and credible intervals for variables of interest, (ii) it can be implemented in the high-dimensional (“large p, small n”) setting, and (iii) it allows one to account for dependence in the errors. We fit the Bayesian model using a computationally efficient MCMC sampler.

The remainder of this article is organized as follows. In Sect. 2, we describe the urban water demand data from Tampa, FL. In Sect. 3, we describe the Bayesian additive regression model, variable selection extensions, and simultaneous model selection and parameter estimation, and use a simulation study to evaluate and compare the performance of the proposed method with existing methods. In Sect. 4, we present the results, and Sect. 5 contains further discussion. Full details on the Gibbs sampler used to fit this model, as well as additional simulation studies, are included in the supplementary material.

2 Data

The data consists of potable water billing records from Hillsborough, Pasco, and Pinellas counties in the Southwest Florida Water Management District (SWFWMD). Monthly billing records of water usage from approximately 1998 to 2010 were collected from Tampa Bay Water (TBW) customers (Boyer et al. 2014). Records were provided for over a million unique customers throughout the study region. Billing records included total (indoor and outdoor) water use by parcel for each customer. Only parcels used by single family residential customers were used in this study. For more information on data collection, see Boyer et al. (2014).

In addition, TBW provided addresses which were used to geolocate records for spatial analysis. The latitude and longitude of customer locations were projected to the Albers Conical Equal Area map projection to preserve distances for spatial correlation modeling, so that customer locations are referenced by easting and northing. Several exogenous environmental and demographic predictors were collected and merged by location and date with the billing records. In Florida, outdoor water use, such as irrigation, can account for almost \(75\%\) of total water use (Haley et al. 2007). Weather and irrigated area can influence the amount of irrigation and are therefore included in these analyses. Monthly average rainfall and evapotransporation (the total amount of water lost through evaporation and transpiration) were recorded via satellite throughout the Tampa Bay region and values were applied over a grid of 2 km by 2 km pixels and merged with parcel locations. These data were obtained from the USGS (2005, 2011) and SWFWMD. Available Water Holding Capacity (AWHC), the difference in the total amount of water that soil can hold and the amount of water at which plants can no longer extract water from the soil, was available by county and collected from the USDA Soil Data Mart (USDA, Natural Resources Conservation Service, U.S. Dept. of Agriculture 2013). Parcel-specific predictors were also included: land and building value in US dollars, the year the most recent structure was built, vegetated area within parcel (green space), and the area of heated structures on the parcel (Heat area), all collected from the Florida Department of Revenue. A summary of the exogenous features is shown in Table 1. All data was managed and analyzed in R (R Core Team 2017).

Table 1 Descriptions of potential predictors of water use in Tampa, FL
Full size table

A subset of the full data described above is used in this paper. The subset is chosen as follows: parcels may have been occupied by more than one unique customer during the study period, so all parcels with multiple unique customers were removed from the data before analysis to ensure that household-level effects are consistent. Furthermore, several records were incomplete, with some missing monthly billing records. Only parcels with complete monthly billing records for the full study period were included in this analysis. The final data set consists of over 130,000 observations (137 consecutive monthly water bills from 973 households). A map of locations used in this study is shown in Fig. 1. This subset was used in Duerr et al. (2018) for comparing forecasting and uncertainty quantification quality obtained from several different methods. Spatio-temporal correlation (particularly strong temporal autocorrelation) was identified in this study and was shown to be crucial in providing accuract forecasts; however, no formal variable selection was performed.

Fig. 1
figure 1

Locations of TBW customers used in this study, superimposed on a map of Tampa, FL

Full size image

3 Statistical model

This section provides a description of the proposed model. First, we introduce the spatio-temporal additive regression model, then propose priors that allow for partially linear selection and estimation of covariate effects. Finally, we describe estimation and prediction with the proposed model.

3.1 Additive model

The linear predictor has the form

$$\begin{aligned} \eta (\varvec{x}_i) = \beta _0 + \textstyle \sum _{g=1}^G f_g(x_{gi}), \end{aligned}$$
(2)

where the \(f_g\) are continuous functions. The functions \(f_1,\ldots ,f_G\) are represented using a linear combination of a sufficiently large set of basis functions:

$$\begin{aligned} f_g(x_g) = \beta _g x_g + \textstyle \sum _{k=1}^{K_g} u_{gk} \phi _{gk}(x_g), \end{aligned}$$
(3)

where \(\beta _g\) and \(\varvec{u}_g = (u_{g1}, \ldots , u_{g K_g})\) are the coefficients corresponding to the linear term and nonlinear basis functions \(\varvec{\phi }_{g} = (\phi _{g1}, \ldots , \phi _{g K_g})\), respectively. The spatio-temporal additive regression model assumes the response variable \(\varvec{y}\) follows a multivariate normal distribution: \(\varvec{y} \sim N(\varvec{\eta }, \sigma ^2 \varvec{\Omega })\), where \(\varvec{\Omega }\equiv \varvec{\Omega }(\varvec{\theta })\) is a \(n\times n\) space-time correlation matrix parameterized by \(\varvec{\theta }\) (Cressie and Wikle 2011; Banerjee et al. 2014).

The likelihood function is given by

$$\begin{aligned} L(\varvec{w},\varvec{\theta },\sigma ^2) = (2\pi \sigma ^2)^{-n/2}|\varvec{Q}|^{1/2}\exp \left\{ - \frac{1}{2\sigma ^2} \left( \varvec{y} - \varvec{\eta } \right) ^\intercal \varvec{Q}\left( \varvec{y} - \varvec{\eta }\right) \right\} , \end{aligned}$$

where \(\varvec{w} = (\beta _0,\varvec{w}_1^\intercal ,\ldots ,\varvec{w}_G^\intercal )^\intercal\), \(\varvec{w}_g = (\beta _g, \varvec{u}_g^\intercal )^\intercal\) and \(\varvec{Q} = \varvec{\Omega }^{-1}\). The intercept \(\beta _0\) is identifiable given that \(f_1,\ldots ,f_G\) follow some constraint, typically that they have mean zero. We represent the \(f_g\) using basis expansions of the form in Eq. (3), where \(u_{g1},\ldots ,u_{gK_g}\) are the coefficients for each of the \(K_g\) known basis functions \(\phi _{g1},\ldots ,\phi _{gK_g}\) for covariate \(x_g\). Basis functions can be constructed by selecting a set of knots \(\kappa _{g1}, \ldots , \kappa _{gK_g}\), e.g. a subset of values in the range of \(x_g\), over which smoothing is required (e.g. Ruppert et al. 2003) or using knot-free spline bases (e.g. Wood 2006). For this work, we also require that the span of \(\{\phi _{gk}(x)\}_{k = 1,\ldots ,K_g}\) is orthogonal to x to ensure that variable selection reliably differentiates between linear and non-linear effects.

Define the \(n \times G\) design matrix \(\varvec{X} = (\varvec{x}_1 \ldots \varvec{x}_G)\). We construct the \(n \times K_g\)-dimensional basis expansion matrices \(\varvec{Z}_1,\ldots ,\varvec{Z}_G\) with \((\varvec{Z}_g)_{ij} = \phi _{gj}(x_{gi})\), and rewrite the model in vector form as

$$\begin{aligned} \varvec{\eta }(\varvec{X}) = \beta _0 \varvec{1} + \textstyle \sum _{g=1}^G \varvec{C}_g \varvec{w}_g, \end{aligned}$$
(4)

where \(\varvec{C}_g = (\varvec{x}_g \varvec{Z}_g)\). Estimates for the coefficients \(\varvec{w} = (\beta _0, \varvec{w}_1^\intercal , \ldots , \varvec{w}_G^\intercal )^\intercal\) and the correlation parameters \(\varvec{\theta }\) are obtained in one of two ways: in the frequentist setting, by optimizing a penalized log likelihood,

$$\begin{aligned} \left( \widehat{\varvec{w}},\widehat{\varvec{\theta }},\widehat{\sigma }^2 \right) = {{\,\mathrm{arg\,min}\,}}_{\varvec{w},\varvec{\theta },\sigma ^2}\left\{ - \log L(\varvec{w},\varvec{\theta },\sigma ^2) + \sum _{g=1}^G \gamma _g\int f''_g(x)^2 dx \right\} , \end{aligned}$$

where the penalty parameter \(\gamma _g\) controls the smoothness of \(f_g\) and can be chosen by, e.g. cross-validation. The penalty functionals can be rewritten using a symmetric positive semidefinite penalty matrix \(\varvec{S}_g\) with \(\varvec{w}_g^\intercal \varvec{S}_g \varvec{w}_g = \int f''_g(x)^2 dx\) for each \(g=1,\ldots ,G\), where the penalty matrices \(\varvec{S}_1,\ldots ,\varvec{S}_G\) are known. Bayesian methods may be used by noting that the penalized likelihood is proportional to a posterior distribution in which the coefficients follow a normal prior with a singular precision matrix. Equivalently, a flat, improper uniform prior is placed on each linear coefficient \(\beta _1,\ldots ,\beta _G\), and the basis function coefficients \(\varvec{u}_g\) follow proper normal priors with precision matrices given by the submatrices \(\gamma _g\varvec{S}_g^*\) created by removing the row and column of \(\gamma _g\varvec{S}_g\) corresponding to the linear term. Furthermore, we reparameterize \(\varvec{Z}_g\varvec{u}_g = \varvec{Z}_g^*\varvec{u}_g^*\) where \(\varvec{Z}^*_g = \varvec{Z}_g {\varvec{S}_g^*}^{-1/2}\) and \(\varvec{u}_g^*\) follows a normal prior with precision matrix \(\gamma _g \varvec{I}_{K_g}\), a scalar multiple of the identity matrix of dimension \(K_g\) (for concise notation, these asterisks are dropped for the remainder of this paper). This reparameterization is useful for defining the variable selection priors in Eq. (5). For additional details see, e.g. Ruppert et al. (2003), Crainiceanu et al. (2005), Wood (2016).

3.2 Variable selection priors

The complete model space for regression models is often too large to exhaustively enumerate with a large number of predictors. In such a case, stochastic search algorithms are necessary to find appropriate parsimonious models. For this work we adopt spike-and-slab (SS) priors for variable selection in regression models (George and Mcculloch 1997; Piffady et al. 2013). To set notation, let Gamma(a, b) denote the Gamma distribution with shape a and rate b, \(\delta _0\) a point mass at zero, \(m_g = K_g + 1\) the size of the group of coefficients \(\varvec{w}_g\), and \(\sigma ^2\) the scale parameter for some covariance matrix \(\sigma ^2\varvec{\Omega }\) for the response data. The BGL-GAM prior is given by

$$\begin{aligned} \begin{aligned} \beta _g|\varvec{u}_g, \tau ^2_g, \sigma ^2, \pi _0&\sim (1-\pi _0)N\left( 0, \sigma ^2_\beta \right) + \pi _0 \delta _0(\beta _g), \quad g=1,\ldots ,G \\ \varvec{u}_g| \tau ^2_g, \sigma ^2, \pi _0&\sim (1-\pi _0)N\left( \varvec{0}, \sigma ^2 \tau ^2_g \varvec{I}_{K_g}\right) + \pi _0 \delta _0(\varvec{u}_g), \quad g=1,\ldots ,G \\ \tau ^2_g|\sigma ^2, \pi _0&\sim \text {Gamma}\left( \frac{K_g+1}{2}, \frac{\lambda ^2}{2} \right) , \quad g=1,\ldots ,G\\ \sigma ^2|\pi _0&\sim \text {Inverse Gamma}(\alpha , \xi ) \\ \pi _0&\sim \text {Beta}(a,b). \end{aligned} \end{aligned}$$
(5)

Sparsity is introduced via the zero mixture term with prior probability \(\pi _0\). Here, \(\pi _0\) is the prior probability that a group of coefficients is equal to zero. Under this formulation and conditional on \(\sigma ^2\) and the spike probability \(\pi _0 = 0\), the marginal prior distribution of \(\varvec{u}_g\) is given by \(\pi (\varvec{u}_g) \propto \exp \left( -\frac{\lambda }{\sigma } \Vert \varvec{u}_g\Vert _2 \right)\), which is the exponential of the frequentist group lasso penalty term (Raman et al. 2009; Kyung et al. 2010). This formulation encourages shrinkage of the nonlinear coefficients of each group, but posterior means and medians do not provide exact zero estimates in the absence of the spike at zero, as does optimization of the frequentist group lasso. The prior specification is completed by placing an uninformative normal prior distribution on the intercept parameter \(\beta _0\).

The linear and nonlinear coefficients have separate SS priors which allows variable selection to iterate between null (\(\beta _g = \varvec{u}_g = 0\)), linear (\(\beta _g \not = 0\), \(\varvec{u_g} = 0\)) and nonlinear (\(\varvec{u_g} \not = 0\)) functions. In the penalized splines setting, the prior variances \(\mathbf {\tau }^2 = (\tau ^2_1,\ldots ,\tau ^2_G)^\intercal\) replace the penalty parameters \(\gamma _1,\ldots ,\gamma _G\) and serve to penalize the wiggliness of the smooth functions. The linear coefficients \(\beta _g\) are conditionally independent of these variances to avoid “unfairly” penalizing linear terms, which could over-shrink functional estimates to zero.

3.3 Estimation and inference

To complete the model specification, priors are placed on correlation parameters \(\varvec{\theta }\). The full posterior distribution is then given by

$$\begin{aligned} \begin{aligned} p(\cdot |\varvec{y})&\propto (\sigma ^2)^{-\frac{n}{2}} |\varvec{Q}|^{1/2} \exp \left\{ -\frac{1}{2\sigma ^2} (\varvec{y} - \varvec{Cw})^\intercal \varvec{Q} (\varvec{y} - \varvec{Cw}) \right\} \\&\times \prod ^G_{g=1}\left\{ (1-\pi _0)(2\pi \sigma _\beta ^2)^{-\frac{1}{2}}\exp \left( \frac{-\beta _g^2}{2\sigma ^2_\beta } \right) \mathbb {I}(\beta _g \not = 0) + \pi _0\delta _0(\beta _g) \right\} \\&\times \prod ^G_{g=1}\left\{ (1-\pi _0)(2\pi \sigma ^2 \tau ^2_g)^{-\frac{m_g}{2}}\exp \left( \frac{-\Vert \varvec{u}_g\Vert ^2}{2\sigma ^2 \tau ^2_g} \right) \mathbb {I}(\varvec{u}_g \not = 0) + \pi _0\delta _0(\varvec{u}_g) \right\} \\&\times \prod ^G_{g=1}(\lambda ^2)^{\frac{m_g + 1}{2}}(\tau ^2_g)^{\frac{m_g + 1}{2}-1}\exp \left( -\frac{\lambda ^2}{2} \tau ^2_g \right) \\&\times (\sigma ^2)^{-\alpha -1}\exp \left( -\frac{\xi }{\sigma ^2} \right) \\&\times \pi _0^{a-1}(1-\pi _0)^{b-1} \\&\times \pi (\varvec{\theta }), \end{aligned} \end{aligned}$$
(6)

where \(\mathbb {I}(\cdot )\) is the indicator function. We use a Gibbs sampler to fit this model in which coefficients are sampled from their full conditional posterior distributions in blocks. The spike-and-slab priors for each \(\beta _g\) and \(\varvec{u}_g\) are conditionally conjugate, so that the draws from the conditional posterior distributions of \(\beta _g\) and \(\varvec{u}_g\) come from spike-and-slab normal distributions. The conditional posterior distributions for \(\varvec{\tau }^2\), \(\sigma ^2\) and \(\pi _0\) are also conjugate. The full conditional posterior distribution of \(\varvec{\theta }\) is typically not available in closed form, so a random walk Metropolis-Hastings (MH) step is used to sample \(\varvec{\theta }\). As in the original BGL-SS model, the estimates are sensitive to the choice of \(\lambda\) because it controls both selection and smoothness. Rather than fix \(\lambda\) at some known value, we update \(\lambda\) using the empirical method as in Xu and Ghosh (2015), in which \(\lambda\) is updated using an empirical estimate of its marginal expectation. When embedded in the Gibbs sampler, this is a Monte Carlo EM algorithm for \(\lambda\) (Casella 2001). For full details, see Sect. S1 of the supplementary material.

3.4 Model selection and prediction

The use of MCMC samples for estimation allows for several options for variable selection. Two notable options are the highest posterior probability model (HPPM) and the median thresholding model (MTM). The HPPM can be obtained by finding the model that appears most often in the posterior samples, and the MTM is the model obtained using the posterior median of the samples, which allows exact zero estimates for the linear and nonlinear coefficients (George and Mcculloch 1997; Johnstone and Silverman 2004). Xu and Ghosh (2015) showed that for the BGL-SS model under an orthogonal design matrix and without dependence in the errors, the MTM has variable selection consistency under some regularity conditions. Our simulations provide support for the MTM, so we use it for our analyses. Out-of-sample predictions are computed from the MCMC trajectory of model parameters using composition sampling (Bliznyuk et al. 2014; Banerjee et al. 2014). Details for obtaining predictions are given in Sect. S1 of the supplementary materials.

3.5 Performance on synthetic data

We now investigate the performance and operating characteristics of our method on low- and high-dimensional data sets of \(n=250\), 500, and 1000 spatio-temporally correlated observations, and make comparisons with other methods. Three additional simulation studies are provided in the Supplementary Materials, which investigate performance under independent errors, temporally correlated errors, and spatially correlated errors. The purpose of the simulation study is to show that, under data scenarios when other existing methods are applicable, our Bayesian method is competitive. (However, as we discussed earlier, our methodology applies to settings that existing methods cannot accommodate.) In the low-dimensional setting, we assess the performance of two methods proposed by Marra and Wood (2011) for three reasons: first, because their estimates are likelihood-based which facilitates a direct comparison with Bayesian estimates; second, because their methods can perform selection under some forms of spatial and temporal dependence; and third, because their methods are implemented in the widely used R package mgcv. The first method is a double penalty approach which penalizes both the smoothness and the magnitude of each smooth term. The second is a shrinkage approach in which the zero eigenvalues of the original penalty matrix are set to some small number \(\delta\), which allows the smoothing parameter to remove the term altogether. These two methods can not iterate selection between null, linear and nonlinear, but only select effects as being “on” or “off.” These two methods are also unable to handle high-dimensional (\(n < G\)) situations. The third method is spikeSlabGAM, a very flexible R library for Bayesian function selection in GAMs that does allow selection under high dimensionality but not under dependence (Scheipl 2011). This method can iterate between null, linear and nonlinear selection.

For the low-dimensional setting, we simulate twelve independent predictors for each data set. This avoids the high dimensionality problem and allows an average maximum basis expansion size of approximately 40 for each term. The predictors \(x_g\), \(g=1,\ldots ,G\), are drawn independently from a uniform distribution on [0, 1]. Six of the predictors are nuisance predictors and have no effect on the response variable, while the other six predictors are true predictors. The true functions of the six predictors are defined as in Marra and Wood (2011) and are listed here in Table 2 and illustrated in Figure S6 of the supplementary materials. We follow Marra and Wood (2011) and scale the functions to have range between zero and one. We consider the same three noise parameters, such that the approximate squared correlation coefficient between predicted and observed values is 0.4, 0.55, and 0.7, corresponding to “low”, “medium”, and “high” signal-to-noise ratios (SNR).

Table 2 True function definitions for the simulation study
Full size table

The data are simulated from temporal locations \(t = 1,2,\ldots ,10\) and n / 10 spatial locations drawn at random on the unit square for each sample size n, representing a spatial infill design with a fixed temporal extent as sample size increases. We use the separable exponential correlation function \(\exp (-r_S/\theta _S)\exp (-r_T/\theta _T)\) with spatial distance \(r_S\), temporal distance \(r_T\), and correlation parameters \(\varvec{\theta } = (\theta _S, \theta _T)\). In this setting, \(\varvec{\epsilon } \sim N(0,\sigma ^2\varvec{\Omega })\) with \(\varvec{\Omega }\) defined by the spatio-temporal correlation function. We use \(\theta _S = 0.1\) and \(\theta _T = -\log (0.75)\) to impose strong spatio-temporal correlations. Spatio-temporal dependence of this type is not supported by any of the three competing methods and are therefore not directly comparable. For these methods, we attempt to capture spatio-temporal variation of the data using tensor product smooths. The two methods of Marra and Wood (2011) use the tensor product of a bivariate spatial smooth with spatial dimension 25 and a univariate temporal smooth with dimension 10. The spikeSlabGAM method uses the trivariate tensor product of space and time, as described in Scheipl (2011) and implemented by default in the spikeSlabGAM package. The two penalized methods also explicitly account for lag-1 temporal autocorrelation within each location. Simulation results under three additional dependence structures (independent, temporal, and spatial) are reported in the Supplementary Materials.

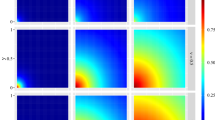
For 100 data sets in each setting, we compute the false positive rate (FPR), false negative rate (FNR) and the root mean squared error (RMSE) of the estimated and true functions of predictors for each method (for fair comparison, any estimated spatio-temporal trends using tensor products are excluded from the RMSEs). Specifically, the mean squared error (MSE) for the gth smooth function is computed as \(MSE_g = \int (f_g^*(x_g)-\widehat{f}_g(x_g))^2 dx_g \approx m^{-1}\sum\nolimits_{i=1}^m (f_g^*(z_{i})-\widehat{f}_g(z_{i}))^2,\) where \(\widehat{f}_g\) is the estimate of the true function \(f_g^*\) and \(z_1,\ldots ,z_m\) is a grid of values for \(x_g\). Under our Bayesian method, \(\widehat{f}_g\) is estimated pointwise as the Monte Carlo approximation to \(E_{\varvec{u}_g}(f_g(z))\) using MCMC samples of the basis function coefficients \(\varvec{u}_g\) under the median posterior probability model. The RMSE is subsequently obtained as \(\sqrt{\sum _g MSE_g}\). The FPR is defined as the proportion of null predictors selected, and the FNR is the proportion of non-null predictors that are excluded (Hastie et al. 2008). Models with lower FPR, FNR, and RMSE are preferred. For comparison with the mgcv methods in the low-dimensional setting, selected linear and nonlinear effects are both considered “on” by BGL-GAM and spikeSlabGAM. The RMSEs of recovered trends shown in Figure 2. As seen in this figure, the proposed Bayesian method is better able to recover the true mean functions in all scenarios. Average FPR and FNR for each method and scenario are shown in Table 3. The two Bayesian methods outperform the two shrinkage methods in both FNR and FPR. The proposed method has a slightly higher FPR than spikeSlabGAM in low sample sizes, but is the only method with FNR \(=0\) for every data set.

Fig. 2
figure 2

RMSE of estimated trends for the low dimensional setting

Full size image
Table 3 FNRs and FPRs for the low dimensional setting
Full size table

For the high-dimensional setting, we simulate 100 data sets similar to above but we instead include 100 predictors. The errors are correlated the same as in the low-dimensional setting. The performance of the two frequentist methods is not reported since the mgcv code throws errors when, after applying the basis expansion to each term, the design matrix has more columns than rows. To further explore false negatives from both Bayesian methods, we include several predictors that weakly influence the response so that estimated FNR is increased. The linear predictor is given by

$$\begin{aligned} \eta (\varvec{x}_i)&= \sum _{g=1}^{100} f_g(x_{gi}),&f_g(x_g) \text { defined in Table 1 for } g&= 1,\ldots ,6, \\ f_g(x_g)&= f_{g - 6}(x_g)/2&\text { for } g&= 7,\ldots ,12, \\ f_g(x_g)&= f_{g - 12}(x_g)/4&\text { for } g&= 13,\ldots ,18, \\ f_g(x_g)&= f_{g - 18}(x_g)/10&\text { for } g&= 19,\ldots ,24, \\ f_g(x_g)&= 0&\text { for } g&= 25,\ldots ,100. \end{aligned}$$

The RMSEs are shown in Figure 3. The proposed method is again better able to recover the true mean function in this setting. The FPR and FNR are shown in Table 4. Here we have split FPR and FNR by linear and nonlinear terms because the two Bayesian methods are able to perform selection on them separately. The linear FNR and FPR for both methods are comparable. The nonlinear FPR is again slightly higher for the proposed Bayesian method under low sample sizes. However, the proposed method consistently has a lower nonlinear FNR than spikeSlabGAM.

Fig. 3
figure 3

RMSE of estimated trends for the high dimensional setting

Full size image
Table 4 FNRs and FPRs for the high dimensional setting
Full size table

4 Results

The candidate models are all models with null, linear, or nonlinear functional relationships, and the base model contains only an intercept. Errors were assumed to follow the distance-based spatio-temporal correlation structure studied in Sect. 3.5. Since all timepoints at every spatial location were observed, we used computationally efficient Kronecker product formulas for inversion of the precision matrix (Harville 1997; Rakitsch et al. 2013). A large-scale temporal trend was included in the model to represent a trend common to all households to potentially capture average growth or decline in demand throughout the study period. Finally, the response variable was taken to be the natural log transform of the observed water use to remove skewness in the errors.

The estimate for the lag-1 temporal autocorrelation parameter was 0.89 with \(95\%\) credible interval (0.88, 0.90) indicating strong, significant temporal autocorrelation of the errors. This agrees well with the analysis in Duerr et al. (2018) that showed that strong temporal autocorrelation was a strong driver of water demand dynamics. The distance at which spatial correlations within the same month drop below 0.05, or the “effective distance,” was estimated to be 130 meters (100, 160). Of the 973 households in the study, 88 pairs were within 130 meters of each other, indicating a significant “neighborhood effect” that dissipates over longer distances.

Table 5 shows posterior probabilities for the associations of water demand with each predictor. Our proposed method selected six features as significant predictors, and five of those selected had significantly nonlinear relationships with the response. The median thresholding model and highest posterior probability model were identical. An important result of our method is the ability to differentiate between small-scale temporal patterns estimated through the precision matrix, and large-scale temporal changes represented by basis functions. Specifically, the method identified a significant nonlinear decrease in average water demand over the study period in the presence of strong month-to-month autocorrelation. This information could prove particularly useful for accurate inference and forecasting of urban water demand.

Table 5 Candidate covariates and linear and nonlinear posterior inclusion probabilities for the water demand model
Full size table

Figure 4 shows the estimated associations of the terms selected by the model. Demand generally decreased in a nonlinear way over the study period, possibly due to the adoption of efficient appliances. However, water demand increased on average for users with newer structures on parcels, possibly indicating that customers with newer structures may use water at a rate faster than efficient appliances conserve water. Evapotranspiration shows a nonlinear but generally increasing association with water demand, indicating that customers may be replacing water lost through evapotranspiration by irrigation. Similarly, demand increased on average with larger heated areas. Water demand decreased with increasing precipitation potentially because customers irrigated more when less rain had occured. The association between land value and water demand was significant and nonlinear, but is not readily interpretable.

Fig. 4
figure 4

Estimated smooth effects and \(95\%\) credible intervals for nonlinear terms

Full size image

Table 6 shows the five models with the highest estimated posterior probabilities. These five models account for \(99\%\) of the model posterior probability space. The majority of the uncertainty seems to be whether or not available water holding capacity is a significant predictor and whether or not the relationship between water demand and heat area is linear. For comparison, both methods from Marra and Wood (2011) select all predictors, and spikeSlabGAM selects all predictors except for available water holding capacity and precipitation.

Table 6 The five models with the highest posterior probability. T, P, ET, LV, YR, HA, and AW indicate the predictors time, precipitation, evapotranspiration, land value, year of most recent structure, heat area, and available water, respectively. s(x) indicates predictor x has a nonlinear relationship with water demand
Full size table

To quantify how well the competing models are able to make forecasts of water demand, we replicate the two scenarios from Duerr et al. (2018) by using the last 12 months of data as a validation set. The 1-month scenario makes forecasts one month in advance using all previous data, and metrics are averaged across each of the 12 left-out months. The 12-month scenario makes the forecasts for the full year. We compute the squared correlation between observations and forecasts (\(R^2\)) and the root mean squared prediction error (RMSPE) as validation metrics to measure forecast performance. Table 7 shows the validation results. The proposed method is able to make the best forecasts under both scenarios according to both metrics.

Table 7 Validation results for the case study
Full size table

5 Discussion

We have proposed a Bayesian methodology for simultaneous fitting and function selection in Gaussian partially linear additive regression models with general (e.g. spatio-temporal) dependence in the errors. The method was successfully used to select important environmental and demographic drivers of urban water demand in Tampa, FL, as well as simultaneously estimate linear and nonlinear associations of selected predictors, and detect a significant average decrease in water demand during the study period in the presence of strong month-to-month correlations. The model is sufficiently flexible to perform selection on any group of variables, such as an indicator matrix representation of a factor variable or a basis expansion matrix representing nonparametric components of the mean function. We have also developed an MCMC algorithm to fit the model and demonstrated our method with a simulation study.

A major advantage of our Bayesian approach is the ability to handle cases when \(n \ll p\), where p is the number of coefficients appearing in linear terms and basis expansions. The computational methods of Wood (2006) and Marra and Wood (2011) that are used in mgcv are limited to design matrices in which \(n > kG\), where k is the average basis expansion size. The proposed Bayesian method circumvents this limitation by sampling groups of coefficients separately in blocks. Therefore the limitation for the Bayesian method is \(n > \max _g (m_g)\), where \(m_g\) is the number of columns of the basis expansion of group g. The spikeSlabGAM method is also applicable under high dimensionality, but dependence in the errors is currently not implemented, which when ignored was shown in the simulation study to negatively affect trend estimates. Another advantage of the proposed method is the ability to provide reliable uncertainty quantification using the embedded Bayesian machinery. The asymptotic distributions of the parameters from lasso-type methods are complicated, and standard errors are typically obtained using bootstrapping. However, the MCMC samples from the Bayesian method come from the joint posterior distribution of the parameters and can be readily used for inference and prediction. Another important contribution of this work is filling a gap in the literature by addressing Bayesian variable selection of GAMs under general (e.g. spatial, temporal, spatio-temporal) dependence with a reliable and numerically stable algorithm for estimation and prediction.

Our hierarchical model is a major extension of that proposed and studied by Xu and Ghosh (2015), with three important differences. First, we incorporate the univariate functional smoothness penalty of Wood (2006) by using a linear mixed model formulation for GAMs and applying a linear transformation to the basis expansion matrices (equivalently, basis function coefficient reparameterization). This procedure is common in the literature as it sets the prior precision matrix of the coefficients to a diagonal matrix with the number of unique elements equal to the number of functional terms in the model, and allows for the use of an efficient Gibbs sampler (Ruppert et al. 2003; Crainiceanu et al. 2005; Gryparis et al. 2007; Wood 2016). Second, we adapt the BGL-SS prior to only shrink the coefficients corresponding to the “wiggly” part of the smooth function, and to perform selection of null, linear, and nonlinear terms. Third, we model dependence in the errors through the parametric precision matrix.

Our Bayesian framework relies on the assumption of multivariate normality for the responses, which is typical for “large” geostatistical applications (Sun et al. 2012) but may be viewed as overly restrictive for some applications if used directly. Possible skewness of the responses may often be mitigated with a Box-Cox family of transformations parameterized by a parameter \(\lambda _{BC}\) (or with another parametric transformation of the response). Our proposed Gibbs sampler can accommodate Box-Cox transformation of the response in two steps: (1) since, conditionally on the transformation parameter \(\lambda _{BC}\), the transformed response is multivariate normal, sampling of all other parameters can be achieved with our current sampler without change; (2) conditional on other parameters, one can sample \(\lambda _{BC}\) by a Metropolis-Hastings step.

Our sampler may be embedded in more complex sampling schemes by data augmentation. For example, proceeding as in Taylor-Rodriguez et al. (2017) for Bayesian site-occupancy models, one can use the Albert and Chib (1993) data augmentation strategy to use our sampler with minor modifications to handle probit regression (i.e., binary responses).

Although we use a separable form of the covariance function in simulations and case study, application of our methodology is not limited to this choice. Such structural assumptions are made to speed up the evaluation of the posterior densities (involving manipulations with the covariance matrix) and for efficient storage. For example, without the separability assumption, an unstructured covariance matrix for our case study would require over 40GB of memory (RAM) just for storage (\(n=10^5\), leading to roughly \(0.5 \cdot (10^5)^2\) entries thanks to the symmetry, each entry taking 8 bytes in double precision), and its direct factorization would be computationally infeasible on any workstation (and most high-performance computing clusters). Other computational strategies include inducing sparsity in the covariance matrix (covariance tapering) or precision matrix (Gaussian Markov Random Field approaches) to enable a sparse Cholesky factorization of \(\varvec{\Sigma }\) or its inverse \(\varvec{Q}\), respectively; or multiscale methods that rely on fixed-rank updates of a diagonal (or banded) matrix that make use of the Sherman-Woodbury-Morrison formula (Golub and Van Loan 2012) and low-rank updates to sparse Cholesky factorization. These broad classes of methods, discussed at length in Sun et al. (2012) and Heaton et al. (2018), may be employed for an alternative specification of the matrix \(\varvec{\Sigma }\) or \(\varvec{Q}\) without significant changes to other parts of our Gibbs sampler.

The code used for the simulation studies in this paper and the supplementary materials is available on GitHub at github.com/hrmerrill/SERR-2018-supp-code. At this time we do not have permission to release the water demand data.