Bayesian measurement error correction in structured additive distributional regression with an application to the analysis of sensor data on soil–plant variability

Abstract

The flexibility of the Bayesian approach to account for covariates with measurement error is combined with semiparametric regression models. We consider a class of continuous, discrete and mixed univariate response distributions with potentially all parameters depending on a structured additive predictor. Markov chain Monte Carlo enables a modular and numerically efficient implementation of Bayesian measurement error correction based on the imputation of unobserved error-free covariate values. We allow for very general measurement errors, including correlated replicates with heterogeneous variances. The proposal is first assessed by a simulation trial, then it is applied to the assessment of a soil–plant relationship crucial for implementing efficient agricultural management practices. Observations on multi-depth soil information and forage ground-cover for a seven hectares Alfalfa stand in South Italy were obtained using sensors with very refined spatial resolution. Estimating a functional relation between ground-cover and soil with these data involves addressing issues linked to the spatial and temporal misalignment and the large data size. We propose a preliminary spatial aggregation on a lattice covering the field and subsequent analysis by a structured additive distributional regression model, accounting for measurement error in the soil covariate. Results are interpreted and commented in connection to possible Alfalfa management strategies.

1 Introduction

Standard regression theory assumes that explanatory variables are deterministic or error-free. This assumption is quite unrealistic for many biological processes and replicated observations of covariates are often obtained to quantify the variability induced by the presence of measurement error (ME). Indeed, covariates measured with error are considered a serious danger for inferences drawn from regression models. The most well known effect of measurement error is the bias towards zero induced by additive i.i.d. measurement error. Under more general measurement error specifications (as considered in this paper), different types of misspecification errors are to be expected (Carroll et al. 2006; Loken and Gelman 2017). This is particularly true for semiparametric additive models, where the functional shape of the relation between responses and covariates is specified adaptively and therefore is also more prone to disturbances induced by ME. Recent papers advocate the hierarchical Bayesian modeling approach as a natural route for accommodating ME uncertainty in regression models. In particular, in the context of semiparametric additive models, Sarkar et al. (2014) provide a Bayesian model based on B-spline mixtures and Dirichlet process mixtures. These settings relax some assumptions about the ME model, such as normality and homoscedasticity of the underlying true covariate values. Muff et al. (2015) frame ME adjustments into Bayesian inference for latent Gaussian models with the integrated nested Laplace approximation (INLA). The INLA framework allows to incorporate various types of random effects into generalized linear mixed models, such as independent or conditional auto-regressive models to account for continuous or discrete spatial structures. Relatively few articles have explicitly addressed covariate ME in the context of spatial modeling. Arima et al. (2017) proposed a model for multivariate Bayesian small area estimation where small areas are not related through an explicit spatial relationship. A notable exception is given by the work of Huque et al. (2016) who assess the relationship between a covariate with ME and a spatially correlated outcome in a non-Bayesian semiparametric regression context. The authors assume that the true unobserved covariate can be modeled by a smooth function of the spatial coordinates.

In this paper we introduce a functional ME modeling approach allowing for replicated covariates with ME within structured additive distributional regression models (Klein et al. 2015a). In this modeling framework, each parameter of a class of potentially complex response distributions is modeled by an additive composition of different types of covariate effects, e.g. non-linear effects of continuous covariates, random effects, spatial effects or interaction effects. Structured additive distributional regression models are therefore in between the simplistic framework of exponential family mean regression and distribution-free approaches as quantile regression. In this context, we allow for a quite general measurement error specification including multiple replicates with heterogeneous dependence structure. Our proposal extends the model proposed by Kneib et al. (2010) that assumed independent replicates with constant variance. From a computational point of view, our implementation is based on the seminal work by Berry et al. (2002) for Gaussian scatterplot smoothing and Kneib et al. (2010) for general semiparametric exponential family and hazard regression models. We develop a flexible fully Bayesian ME correction procedure based on Markov chain Monte Carlo (MCMC) to generate observations from the joint posterior distribution of structured additive distributional regression models.

The main motivation of our investigation comes from a case study on the use of proximal soil and crop sensing technologies in agriculture. Agricultural fields are often characterized by a large spatial variability of soil properties, such as texture and structure, that are key parameters controlling water and nutrients availability for crop growth. Due to this variability, within-field yield variation can be expected (Basso et al. 2009). Over the last decades, increasing scientific and financial efforts have been devoted to the development of sensing technologies that allow low-cost, fast, non-destructive spatio-temporal monitoring of crop and soil properties. These technologies overcome the limitations of traditional surveys, such as poor data coverage and high labor/financial requirements (Guo et al. 2016). Among soil sensing technologies, soil electrical resistivity mapping plays a prominent role in the characterization of agricultural soils (Corwin et al. 2010). Soil electrical resistivity has long been used in soil science since it is correlated to several important soil parameters such as texture and structure. It is also sensitive to variation in the soil water content and salinity (Samouëlian et al. 2005). Resistivity is measured in Ohm per meter and can only assume positive values, commonly ranging from a few to several thousand, depending on the nature of the agricultural soil constituents. Among crop sensor data, the Normalized Difference Vegetation Index (NDVI) is a well-established proxy of crop biomass and ground cover. It is based on green leaf spectral reflectance and can range between $-1$ and $+1$. Negative values correspond to water bodies, values close to zero generally correspond to bare soils, positive values indicate increasing plant ground cover. Values close to 1 that indicate NDVI saturation, occurring with high plant biomass values. From the farmer’s perspective, a detailed knowledge of the relationship between soil parameters and crop performances in a given field can be used to discern soil-based constrains limiting the crop yield. Such knowledge helps delineating distinctive areas of the field in which specific management options (such as an appropriate irrigation schedule, fertilization plan) can be adopted to increase or stabilize the yield. Proximal sensor data are usually acquired at a very fine spatial resolution, covering several hectares in a day of work and yielding several thousands observations per hectare. Different sensors correspond to different spatial resolutions, while measurements taken at different dates with a given sensor frequently imply spatial misalignment between time points. Establishing a functional relationship between soil and plant sensor data involves addressing several issues linked to the spatial and temporal misalignment and to the large data size. In this work we tackle these issues analyzing the relationship between multi-depth high resolution soil information and data of forage ground-cover. The survey was undertaken in a seven hectares alfalfa (Medicago sativa L.) field in South Italy. Soil data were acquired only once, simultaneously investigating three consecutive depth layers by an on-the-go proximal sensing technology for the measurement of soil electrical resistivity. Ground-cover data were obtained at four sampling occasions with point locations changing over time through NDVI measurements collected by a multispectral radiometer, continuously towed across the field following a serpentine pattern. A non-linear relation between NDVI and soil electrical resistivity is estimated by additive distributional regression models with structured additive predictor and measurement error correction. While distributional regression allows to deal with the heterogeneity of the response scale at the four sampling occasions, the ME correction is motivated by observations of covariates being replicated along a depth gradient.

The paper is structured as follows: in Sect. 2, we introduce the Bayesian additive distributional regression model and the ME model specification. Section 3 reports details of the MCMC estimation algorithm and different tools for model choice and comparison. A simulation-based investigation of the model performance is contained in Sect. 4. Section 5 is dedicated to review some issues of the sampling design, describe the spatial aggregation method, report summary features of the data at hand, assess the model performance, interpret estimation results and comment on possible Alfalfa management strategies. The final Sect. 6 summarizes our main findings and includes comments on directions for future research.

2 Measurement error correction in distributional regression

The main motivation for our methodological proposal comes from the need to estimate the nonlinear dependence of ground-cover on soil information by a smooth function. Data features require to account for the heterogeneity in the position and scale of the response, the repeated measurements of the soil covariate and the residual variation of unobserved spatial features. A detailed discussion of the data collection and pre-processing is given in Sect. 5. There we address ground-cover differences in both location and scale by structured additive distributional regression models, in which two parameters of the response distribution are related to additive regression predictors (Klein et al. 2015a, and references therein). The estimate of the functional relationship between ground-cover and soil variables is obtained taking into account replicated covariate observations by a measurement error correction. In this section, the distributional regression model is set up, structured additive predictors and the ME correction are introduced with the relevant prior distributions.

2.1 Distributional regression

Our treatment of Bayesian measurement error correction is embedded into the general framework of structured additive distributional regression. Assume that independent observations $(y_i,{\varvec{\nu }}_i)\,i=1,\ldots ,n$ are available on the response $y_i$ and covariates ${\varvec{\nu }}_i$ and that the conditional distribution of the response belongs to a K-parametric family of distributions such that $y_i|{\varvec{\nu }}_i\sim {\mathcal {D}}({\varvec{\vartheta }}({\varvec{\nu }}_i))$. The K-dimensional parameter vector ${\varvec{\vartheta }}({\varvec{\nu }}_i) = (\vartheta _1({\varvec{\nu }}_i),\ldots ,\vartheta _K({\varvec{\nu }}_i))'$ is determined based on the covariate vector ${\varvec{\nu }}_i$. More specifically, we assume that each parameter is supplemented with a regression specification

$$\begin{aligned} \vartheta _k({\varvec{\nu }}_i) = h_k(\eta ^{\vartheta _k}({\varvec{\nu }}_i)) \end{aligned}$$

where $k=1,\ldots ,K$ and $h_k$ is a response function that ensures restrictions on the parameter space and $\eta ^{\vartheta _k}({\varvec{\nu }}_i)$ is a regression predictor. Unlike generalized additive models, structured additive regression models allow to put specific predictors on each of K parameters.

In our analyses, we will consider two cases where $y_i\sim {{\,\mathrm{N}\,}}(\mu ({\varvec{\nu }}_i), \sigma ^2({\varvec{\nu }}_i))$, i.e. the response is conditionally normal with covariate-dependent mean and variance and $y_i\sim {{\,\mathrm{Beta}\,}}(\mu ({\varvec{\nu }}_i), \sigma ^2({\varvec{\nu }}_i))$, i.e. conditionally beta distributed response with regression effects on location and scale. To ensure $\sigma ^2({\varvec{\nu }}_i)>0$ for the variance of the normal distribution, we use the logarithmic link function, i.e. $\sigma ^2({\varvec{\nu }}_i) = \exp (\eta ^{\sigma ^2}({\varvec{\nu }}_i))$ while for both parameters $\mu ({\varvec{\nu }}_i)$ and $\sigma ^2({\varvec{\nu }}_i)$ of the beta distribution we employ a logit link, since they are restricted to the unit interval (Ferrari and Cribari-Neto 2004).

2.2 Structured additive predictor

For each of the predictors, we assume an additive decomposition as

$$\begin{aligned} \eta ^{\vartheta _k}({\varvec{\nu }}_i) = \beta _0^{\vartheta _k} + f_1^{\vartheta _k}({\varvec{\nu }}_i) + \cdots + f_{J_k}^{\vartheta _k}({\varvec{\nu }}_i) \end{aligned}$$

(1)

i.e. each predictor consists of a total of $J_k$ potentially nonlinear effects $f_j^{\vartheta _k}({\varvec{\nu }}_i)$, $j=1,\ldots ,J_k$, and an additional overall intercept $\beta _0^{\vartheta _k}$. The nonlinear effects $f_j^{\vartheta _k}({\varvec{\nu }}_i)$ are a generic representation for a variety of different effect types (including nonlinear effects of continuous covariates, interaction surfaces, spatial effects, etc., see below for some more details on examples that are relevant in our application). Any of these effects can be approximated in terms of a linear combination of basis functions as

$$\begin{aligned} f({\varvec{\nu }}_i) = \sum _{l=1}^L\beta _lB_l({\varvec{\nu }}_i) = {\varvec{b}}_i'{\varvec{\beta }}\end{aligned}$$

where we dropped both the function index j and the parameter index $\vartheta _k$ for simplicity. $B_l({\varvec{\nu }}_i)$ denotes the different basis functions with basis coefficients $\beta _l$ and ${\varvec{b}}_i=(B_1({\varvec{\nu }}_i),\ldots ,B_L({\varvec{\nu }}_i))'$ and ${\varvec{\beta }}=(\beta _1,\ldots ,\beta _L)'$ denote the corresponding vectors of basis function evaluations and basis coefficients, respectively. Since in many cases the number of basis functions will be large, we assign informative multivariate Gaussian priors

$$\begin{aligned} p({\varvec{\beta }}|{\varvec{\theta }}) \propto \exp \left( -\frac{1}{2}{\varvec{\beta }}'{\varvec{K}}({\varvec{\theta }}){\varvec{\beta }}\right) \end{aligned}$$

(2)

to the basis coefficients to enforce properties such as smoothness or shrinkage. The specific properties are determined based on the prior precision matrix ${\varvec{K}}({\varvec{\theta }})$ which itself depends on further hyperparameters ${\varvec{\theta }}$.

To make things more concrete, we discuss some special cases that we will also use later in our application:

• Linear effects: for parametric, linear effects, the basis functions are only extracting certain covariate elements from the vector ${\varvec{\nu }}_i$ such that $B_l({\varvec{\nu }}_i) = \nu _{il}$. In case of no prior information, flat priors are obtained by ${\varvec{K}}({\varvec{\theta }})=\mathbf {0}$ which reduces the multivariate normal prior to a multivariate flat prior.

• Penalised splines for nonlinear effects f(x) of continuous covariates x: for nonlinear effects of continuous covariates, we follow the idea of Bayesian penalized splines (Brezger and Lang 2006) where B-spline basis functions are combined with a random walk prior on the regression coefficients. In this case, the prior precision matrix is of the form ${\varvec{K}}({\varvec{\theta }}) = \tau ^2{\varvec{D}}'{\varvec{D}}$ where $\tau ^2$ is a prior variance parameter and ${\varvec{D}}$ is a difference matrix. To obtain a data-driven amount of smoothness, we will assign an inverse gamma prior $\tau ^2\sim {{\,\mathrm{IG}\,}}(a,b)$ to $\tau ^2$ with $a=b=0.001$ as a default choice. Note that the number of basis functions chosen to approximate the nonlinear effect is of only minor importance as long as the number is chosen large enough. In typical applications, using 10 to 20 basis functions is sufficient (Eilers and Marx 1996).

• Tensor product splines for coordinate-based spatial effects $f(s_x, s_y)$: for modelling spatial surfaces based on coordinate information, we utilize tensor product penalized splines where each of the basis functions is constructed as $B_l(s_x,s_y) = B_{l,x}(s_x)B_{l,y}(s_y)$ with univariate B-spline bases $B_x(\cdot )$ and $B_y(\cdot )$. The penalty matrix is then given by

  $$\begin{aligned} {\varvec{K}}({\varvec{\theta }}) = \frac{1}{\tau ^2}\left[ \omega {\varvec{K}}_x \otimes {\varvec{I}}_{y} + (1-\omega ){\varvec{I}}_{x}\otimes {\varvec{K}}_y\right] \end{aligned}$$

  where ${\varvec{K}}_x$ is a random walk penalty matrix for a univariate spline in $s_x$, ${\varvec{K}}_y$ is a random walk penalty matrix for a univariate spline in $s_y$ and ${\varvec{I}}_x$ and ${\varvec{I}}_y$ are identity matrices of appropriate dimension. In this case, the prior precision matrix comprises two hyperparameters: $\tau ^2$ is again a prior variance parameter (and can therefore still be assumed to follow an inverse gamma distribution) while $\omega \in (0,1)$ is an anisotropy parameter that allows for varying amounts of smoothness along the x and y coordinates of the spatial effect. For the latter, we assume a discrete prior following the approach discussed in Kneib et al. (2017).

For some alternative model components comprise spatial effects based on regional data, random intercepts and random slopes or varying coefficient terms, see Fahrmeir et al. (2013, Ch.8)

2.3 Measurement error

In our application, we observe a continuous covariate with measurement error and model its potentially nonlinear effect f(x) by a penalized spline. We observe M replicates of the continuous covariate x contaminated with measurement error $u_i^{(m)}$

$$\begin{aligned} {\tilde{x}}_i^{(m)} = x_i + u_i^{(m)}, \quad m=1,\ldots ,M, \end{aligned}$$

(3)

For the measurement error, we consider a multivariate Gaussian model such that

$$\begin{aligned} {\varvec{u}}_i\sim {{\,\mathrm{N}\,}}_M(\mathbf {0}, {\varvec{\varSigma }}_{u,i}) \end{aligned}$$

where ${\varvec{u}}_i = (u_i^{(1)},\ldots ,u_i^{(M)})'$ and ${\varvec{\varSigma }}_{u,i}$ is the measurement error covariance matrix. Equation (3) is often referred to as classical measurement error model as opposed to the Berkson model assuming $x_i = {\tilde{x}}_i^{(m)} + u_i^{(m)}$ (see Carroll et al. 2006). Independent replicates with constant variance, i.e. $\varvec{\varSigma }_{u,i}=\sigma ^2_{u}{\mathbf {I}}_M$, were considered in Kneib et al. (2010) for a mean regression model specification. This assumption is here relaxed in the context of distributional regression, considering correlated replicates with potentially heterogeneous variances and covariances, leaving $\varvec{\varSigma }_{u,i}$ unstructured (as proposed and discussed in the seminal book of Fuller 1987). Of course, it would be conceptually straightforward to include priors on unknown parameters in ${\varvec{\varSigma }}_{u,i}$, but this would require a large number of replicates (M) to obtain reliable estimates. Following Buonaccorsi (2010), we obtain sample estimates of individual measurement error variances and covariances in ${\varvec{\varSigma }}_{u,i}$ and plug them into to the Bayesian model estimation algorithm.

The basic idea in Bayesian measurement error correction is to include the unknown, true covariate values $x_i$ as additional unknowns to be imputed by MCMC simulations along with estimating all other parameters in the model. This requires that we assign a prior distribution to $x_i$; we rely on the simplest version

$$\begin{aligned} x_i\sim {{\,\mathrm{N}\,}}(\mu _x, \tau _x^2) \end{aligned}$$

achieving flexibility by adding a further level in the prior hierarchy via

$$\begin{aligned} \mu _x\sim {{\,\mathrm{N}\,}}(0, \tau _\mu ^2), \qquad \tau _x^2\sim {{\,\mathrm{IG}\,}}(a_x, b_x). \end{aligned}$$

To obtain diffuse priors on these hyperparameters, we use $\tau _\mu ^2=1000^2$ and $a_x=b_x=0.001$ as default settings. This corresponds to the choice of being uninformative about the distribution of the true covariate. Of course, in case there would be better prior knowledge, it would be straightforward to extend the model to accommodate for more general and also non-Gaussian prior options.

3 Bayesian inference

All inferences rely on MCMC simulations implemented within the free, open source software BayesX (Belitz et al. 2015). As described in Lang et al. (2014), the software makes use of efficient storing schemes for large data sets and sparse matrix algorithms for sampling from multivariate Gaussian proposal distributions. In the following, we first describe the required sampling steps for the measurement error part and summarize inference for the remaining parameters along the scheme presented in Klein et al. (2015b) for structured additive distributional regression models without measurement error.

3.1 Measurement error correction

For the general case of distributional regression models, no closed form full conditional is available for the true covariate values $x_i$, then we rely on a Metropolis Hastings update. Proposals are generated based on a random walk

$$\begin{aligned} x_i^p = x_i^c + e_i, \qquad e_i\sim {{\,\mathrm{N}\,}}(0, g \cdot {{\,\mathrm{tr}\,}}({\varvec{\varSigma }}_{u,i})/M^2) \end{aligned}$$

(4)

where $x_i^p$ denotes the proposal, $x_i^c$ is the current value and the variance of the random walk is determined by the measurement error variability. More precisely, the variability is summarized by the trace of the covariance matrix ${\varvec{\varSigma }}_{u,i}$) divided by the squared number of replicates $M^2$ and multiplied with a user-defined scaling factor g that can be used to determine appropriate acceptance rates. The proposed value is then accepted with probability

$$\begin{aligned}&\alpha (x_i^p|x_i^c)\\&\quad = \min \left\{ 1,\frac{p(y_i|x_i^p)}{p(y_i|x_i^c)} \frac{\exp \left( -\frac{1}{2\tau _x^2}(x_i^p-\mu _x)^2\right) }{\exp \left( -\frac{1}{2\tau _x^2}(x_i^c-\mu _x)^2\right) } \frac{\exp \left( -\frac{1}{2}({\tilde{x}}_i-x_i^p\mathbf {1}_M)'{\varvec{\varSigma }}_{u,i}^{-1}({\tilde{x}}_i-x_i^p\mathbf {1}_M)\right) }{\exp \left( -\frac{1}{2}({\tilde{x}}_i-x_i^c\mathbf {1}_M)'{\varvec{\varSigma }}_{u,i}^{-1}({\tilde{x}}_i-x_i^c\mathbf {1}_M)\right) }\right\} \end{aligned}$$

where the first factor is the ratio of likelihood contributions for individual i given the proposed and current values of the covariate, the second factor is the ratio of the measurement error priors and the third factor is the ratio of the likelihoods from the measurement error model. The ratio of the proposal densities cancels as usual due to the symmetry of the Gaussian random walk proposal.

In contrast, the updates of the hyperparameters are standard due to the conjugacy between the Gaussian prior for the true covariate values and the hyperprior specifications. We therefore obtain

$$\begin{aligned} \mu _x|\cdot \sim {{\,\mathrm{N}\,}}\left( \frac{n{\bar{x}}\tau _\mu ^2}{n\tau _{\mu }^2 + \tau _x^2},\frac{\tau _x^2\tau _\mu ^2}{n\tau _{\mu }^2 + \tau _x^2}\right) \end{aligned}$$

and

$$\begin{aligned} \tau _x^2|\cdot \sim {{\,\mathrm{IG}\,}}\left( a_x + \frac{n}{2}, b_x + \frac{1}{2}\sum _{i=1}^n(x_i-\mu _x)^2\right) \end{aligned}$$

As mentioned before, priors could be assigned to incorporate uncertainty about elements of the covariance matrices ${\varvec{\varSigma }}_{u,i}$ of the measurement error model. However, reliable estimation of ${\varvec{\varSigma }}_{u,i}$ would typically require a large number of repeated measurements of the covariates. Therefore we will restrict our attention to the case of sample estimates of individual measurement error covariance matrices (Buonaccorsi 2010) obtained outside the model estimation framework and plugged in the Bayesian algorithm, as will be specified in Sect. 5.1.

3.2 Updating the structured addditive predictor

Updating the components of a structured additive predictor basically follows the same steps as in any distributional regression model (see Klein et al. 2015b; Kneib et al. 2017, for details). The vectors of regression coefficients corresponding to one of the functions in the predictor (1) follow the prior structure (2) and their full conditional distribution will in most cases not have a closed form. We therefore follow the idea of iteratively weighted least squares proposals as developed in Gamerman (1997) and Brezger and Lang (2006) and adapted to distributional regression in Klein et al. (2015b) where proposals are generated from multivariate normal distributions ${{\,\mathrm{N}\,}}({\varvec{\mu }},{\varvec{P}}^{-1})$ with mean and precision matrix given by

$$\begin{aligned} {\varvec{\mu }}=({\varvec{B}}'{\varvec{W}}{\varvec{B}}+ {\varvec{K}}({\varvec{\theta }}))^{-1}{\varvec{B}}'{\varvec{W}}({\tilde{y}}-{\tilde{\eta }}), \qquad {\varvec{P}}=({\varvec{B}}'{\varvec{W}}{\varvec{B}}+ {\varvec{K}}({\varvec{\theta }})) \end{aligned}$$

where ${\varvec{B}}$ is the design matrix for the coefficient vector of interest, ${\varvec{W}}$ is a matrix of working weights, ${\tilde{y}}$ is a vector of working observations (both of which are determined from a locally quadratic approximation of the log-full conditional) and ${\tilde{\eta }}$ is the partial predictor without the effect currently being updated. The working weights and working observations are specific to the chosen response distribution and to the parameters of this distribution.

One additional difficulty arises from the fact that the imputation of true covariate values in each iteration implies that the associated spline design matrix ${\varvec{B}}$ would have to be recomputed in each iteration, which would considerably slow down the MCMC algorithm. To avoid this, we utilize a binning approach (see Lang et al. 2014) where we assign each exact covariate value to a small interval. Using a large number of intervals allows us to control for potential rounding errors. On the positive side, the binning approach allows us to precompute the design matrix for all potential intervals. As a consequence, we only re-assign the observations based on an index vector in each iteration instead of recomputing the exact design matrix. Lang et al. (2014) found that the binning approach is not very sensitive with respect to the actual number of bins as long as this number is chosen sufficiently large relative to the total number of distinct covariate values observed in the data and the range of the covariate values. Usually a default of 50 to 100 bins ensures reasonable computing times along with sufficient approximation precision.

The hyperparameters in ${\varvec{\theta }}$ usually comprise a variance component $\tau ^2$ which we assume to follow an inverse gamma prior with parameters $a>0$ and $b>0$. The full conditional for $\tau ^2$ is then also inverse gamma, i.e.

$$\begin{aligned} \tau ^2|\cdot \sim {{\,\mathrm{IG}\,}}\left( a+\frac{{{\,\mathrm{rk}\,}}{({\varvec{K}}({\varvec{\theta }}))_{\tau ^2=1}}}{2}, b+\frac{1}{2}{\varvec{\beta }}'{\varvec{K}}({\varvec{\theta }})_{\tau ^2=1}{\varvec{\beta }}\right) \end{aligned}$$

where ${\varvec{K}}({\varvec{\theta }})_{\tau ^2=1}$ is the prior precision matrix from (2) with $\tau ^2$ set to one. The anisotropy parameter $\omega$ of the tensor product spline follows a discrete prior such that it can also straightforwardly be updated via sampling from the discrete full conditional.

3.3 Model evaluation

In what follows we refer to several model evaluation tools that consider the quality of estimation and the predictive ability in terms of probabilistic forecasts: the deviance information criterion (DIC, Spiegelhalter et al. 2002), the Watanabe–Akaike information criterion (WAIC, Watanabe 2010), proper scoring rules (Gneiting and Raftery 2007) as well as normalized quantile residuals (Dunn and Smyth 1996).

Measures of predictive accuracy are generally referred to as information criteria and are defined based on the deviance (the log predictive density of the data given a point estimate of the fitted model, multiplied by $-2$). Both DIC and WAIC adjust the log predictive density of the observed data by subtracting an approximate bias correction. However, while DIC conditions the log predictive density of the data on the posterior mean $\text{ E }({\varvec{\theta }}|{\varvec{y}})$ of all model parameters ${\varvec{\theta }}$ given the data ${\varvec{y}}$, WAIC averages it over the posterior distribution $p({\varvec{\theta }}|{\varvec{y}})$. Then, compared to DIC, WAIC has the desirable property of averaging over the whole posterior distribution rather than conditioning on a point estimate. This is especially relevant in a predictive Bayesian context, as WAIC evaluates the predictions that are actually being used for new data while DIC estimates the performance of the plug-in predictive density (Gelman et al. 2014).

As measures of the out-of-sample predictive accuracy we consider proper scoring rules based on based on R-fold cross validations. Namely, we use the logarithmic score $S(f_r,y_r)=\log (f_r(y_r))$, the spherical score $S(f_r,y_r)=f_r(y_r)/\Vert f_r(y_r)\Vert _2$ and the quadratic score $S(f_r,y_r)=2f_r(y_r)-\Vert f_r(y_r)\Vert _2^2$, with $\Vert f_r(y_r)\Vert _2^2=\int f_r(\omega )^2 d\omega$. Here $y_r$ is an element of the hold out sample and $f_r$ is the predictive distribution of $y_r$ obtained in the current cross-validation fold. The predictive ability of the models is then compared by the aggregated average score $S_R=(1/R) \sum _{r=1}^R S(f_r,y_r)$. Higher logarithmic, spherical and quadratic scores deliver better forecasts when comparing two competing models. With respect to the others, the logarithmic scoring rule is usually more susceptible to extreme observations that introduce large contributions in the log-likelihood (Klein et al. 2015a).

If F and $y_i$ are respectively the assumed cumulative distribution and a realization of a continuous random variable and ${\hat{\varvec{\vartheta }}}$ is an estimate of the distribution parameters, quantile residuals are given by ${{\hat{r}}}_i=\varPhi ^{-1}(u_i)$, where $\varPhi ^{-1}$ is the inverse cumulative distribution function of a standard normal distribution and $u_i=F(y_i|{\hat{\varvec{\vartheta }}}_i)$. If the estimated model is close to the true model, then quantile residuals approximately follow a standard normal distribution. Quantile residuals can be assessed graphically in terms of quantile-quantile-plots and can be an effective tool for deciding between different distributional options (Klein et al. 2013).

4 Simulation experiment

In this section, we present a simulation trial designed to show some advantages in the performance of the proposed approach with respect to two alternative specifications of the measurement error model. As a baseline, we consider Gaussian regression to describe the conditional distribution of the response, assuming that $y_{i}$’s follow a Gaussian law. Like in our case study, Beta regression is a useful tool to describe the conditional distribution of responses that take values in a pre-specified interval such as (0, 1). Thus, alternatively, we assume that $y_{i}$’s follow a Beta law. With both distributional assumptions, data are simulated from two scenarios corresponding to uncorrelated and correlated covariate repeated measurements. For the two distributional assumptions and the two scenarios, we compare three different measurement error model settings for structured additive distributional regression: (1) as a benchmark, we consider a model based on the “true” covariate values (i.e. those without measurement error), (2) a naive model that averages upon repeated measurements and ignores ME and (3) a model implementing the ME adjustment proposed in Sects. 2.3 and 3.1. Simulation and estimation model settings were defined after a careful and lengthy sensitivity analysis. For brevity, we don’t report these results, but they are available from the authors upon request. We expect that results produced by the proposed ME adjustment are closer to the benchmark than those obtained by the naive approach. Proper scoring rules are typically computationally inconvenient in simulation studies. As well, DIC and WAIC are conceptually unsuitable to compare models with and without measurement error, as the models are based on different data generating processes. Vidal and Iglesias (2008) perform the comparison by marginalizing over the unobserved true covariate, but this is computationally intractable in the distributional regression context. As a consequence, the measurement error model comparison is performed in terms of smooth effect estimates and RMSE. Notice that RMSE refers to the MSE between the estimated and the true smooth function and therefore it is not a predictive measure.

4.1 Simulation settings

For 100 simulations, $n=500$ samples of the “true” covariate $x_i\, (i=1,\ldots ,n)$ are generated from N(0, 5). Then 3 replicates with measurement error are obtained for each $x_i$ as $\tilde{{\mathbf {x}}}_i\thicksim N_3\left( x_i {\mathbf {1}}_3, \varSigma _{u,i}\right)$ with

$$\begin{aligned} \varSigma _{ui}=\sigma ^2_{u;i}\left( \begin{array}{ccc} 1 &{} c_u &{} c_u \\ c_u &{} 1 &{} c_u \\ c_u &{} c_u &{} 1\end{array}\right) \end{aligned}$$

(5)

We allow for ME heteroscedasticity setting $\sigma ^2_{u;i=1,\ldots ,n/2}=1$ and $\sigma ^2_{u;i=n/2+1,\ldots ,n}=2$ and we consider two alternative ME scenarios: Scenario 1 with uncorrelated replicates, i.e. $c_u=0$, and Scenario 2 where $c_u=0.8$.

For the Gaussian observation model, we simulate 500 values of the response with $y_{i}\sim \text{ N }(\mu _{i},\sigma _{i}^2)$, where $\mu _{i}=\sin (x_i)$ sets the nonlinear dependence with the covariate. To introduce response heteroscedasticity we divide the sample in two groups, each one with its own variance by means of a Bernoulli variable

$$\begin{aligned} \text{ Var }(y_i)=\sigma ^2_{i}=\left\{ \begin{array}{cc}0.3 &{} v_i = 1 \\ 0.5 &{} v_i = 0\end{array}\right. , \text{ with } v_i \sim \text{ Bernoulli }(0.5). \end{aligned}$$

We proceed in like vein for the Beta observation model and generate n samples from $\text{ Beta }(p_{i},q_{i})$ with $\mu _{i}=p_i/(p_i+q_i)$ and $\sigma ^2_i=1/(p_i+q_i+1)=\text{ Var }(y_i)/(\mu _i(1-\mu _i))$, where $\mu _{i}=\exp (\sin (x_i))/(1+\exp (\sin (x_i))$ and $\sigma ^2_i$ is specified as in the Gaussian case.

4.2 Model settings

For the estimation model, we consider Gaussian and Beta regression with the following settings. Assuming $y_i$’s are Gaussian with $\text{ N }(\mu _i,\sigma _i^2)$, model parameters are linked to regression predictors by the identity and the log link respectively: $\mu _i=\eta ^\mu (x_{i})$ and $\sigma ^2_i=\exp (\eta ^{\sigma ^2}(x_{i}))$. Alternatively, let $y_i$’s have Beta law $\text{ Beta }(p_{i},q_{i})$, then both model parameters $\mu _i$ and $\sigma ^2_i$ given in Sect. 4.1 are linked to respective regression predictors $\eta ^\mu (x_{i})$ and $\eta ^{\sigma ^2}(x_{i})$ by the logit link, such that $\mu _i=\exp (\eta ^\mu (x_{i}))/(1+\exp (\eta ^\mu (x_{i})))$ and $\sigma ^2_i=\exp (\eta ^{\sigma ^2}(x_{i}))/(1+\exp (\eta ^{\sigma ^2}(x_{i})))$.

Under both distributional assumptions, we consider the two predictors as simply given by $\eta ^\mu (x_{i})=\beta _0^\mu +f^{\mu }(x_{i})$ and $\eta ^{\sigma ^2}(x_{i})=\beta _0^{\sigma ^2}+\beta _1^{\sigma ^2}v_i$, with $f^{\mu }(\cdot )$ a penalized spline term and $v_i$ defined in Sect. 4.1.

For the measurement error, we consider the benchmark, naive and ME models defined at the beginning of Sect. 4. For the latter we specify $\varSigma _{u,i}$ as in Eq. 5, for the two ME scenarios. Finally, we set the scaling factor g in Eq. 4 to 1 in both distributional settings.

A different simulation setup was adopted in the two distributional settings: for Gaussian models we obtained 10,000 simulations with 5000 burnin and thinning by 5, while Beta models required longer runs of 50,000 iterations with 35,000 burnin and thinning by 15. In all cases, convergence was reached and checked by visual inspection of the trace plots and standard diagnostic tools.

Fig. 1

Average estimates of the smooth effect $f^{\mu }(x)$ (left) and width of 95% credibility intervals (right) obtained with 100 simulations of the three model settings and the two scenarios by the Gaussian distribution model

Fig. 2

Boxplots of RMSE’s of the Gaussian (left) and Beta (right) distribution models for 100 simulations of the three model settings and the two scenarios

Fig. 3

Average estimates of the smooth effect $f^{\mu }(x)$ (left) and width of 95% credibility intervals (right) obtained with 100 simulations of the three model settings and the two scenarios by the Beta distribution model

Fig. 4

Boxplots of variance estimates of the Gaussian (left) and Beta (right) distribution models for 100 simulations of the three model settings with scenario 1

4.3 Simulation results

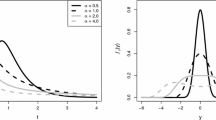
In Fig. 1 we show the averages and quantile ranges of smooth effect estimates obtained with 100 simulated samples for the three Gaussian model settings and the two scenarios. While the benchmark model setting obviously outperforms the other two, the ME correction provides a sharper fit with respect to the naive. In general, over-smoothing is only found with the naive model in the case of correlated measurement errors (Scenario 2). Notice that the naive model setting provides credible intervals as narrow as those obtained when the ME is not present (Fig. 1, right panel), thus underestimating the smooth effect variability in the presence of ME. Preference for the ME corrected model setting is also accorded by RMSE’s, as shown in Fig. 2. The Beta distribution model obtains very similar results, with even stronger evidence for underestimation of the smooth effect variability by the naive model in Fig. 3 (right). Estimates of response variances are summarized in Fig. 4 for Scenario 1 showing that, as expected, the ME correction provides a sharper fit with respect to the naive, with some evidence for overestimation of lower values. For the sake of brevity we don’t report the results obtained with Scenario 2 for which a very similar behavior is observed.

5 Analysis of sensor data on soil–plant variability

Alfalfa (Medicago sativa L.) plays a key role in forage production systems all over the world and increasing its competitiveness is one of the European Union’s agricultural priorities (Schreuder and de Visser 2014). Site-specific management strategies optimizing the use of crop inputs are a cost-effective way to increase crop profitability and stabilize yield (Singh 2017). To achieve this goal, precise management activities such as precision irrigation, variable-rate N targeting, etc. are required. Precision Agriculture (PA) strategies in deep root perennials like alfalfa require information on deep soil variability (Merrill et al. 2017). This is due to the high dependence of these crops on deep water reserves often influenced by soil resources such as texture and structure (Dardanelli et al. 1997; Saxton et al. 1986) that are correlated to soil electrical resistivity (ER) (Doolittle and Brevik 2014; Samouëlian et al. 2005; Banton et al. 1997; Tetegan et al. 2012; Besson et al. 2004). We focus on the relation between plant growth and soil features as measured by two sensors within a seven hectares Alfalfa stand in Palomonte, South Italy, with average elevation of 210 m a.s.l.. The optical sensor $\hbox {GreenSeeker}^{\text{ TM }}$ (NTech Industries Inc., Ukiah, California, USA) measures the normalized density vegetation index (NDVI), while Automatic Resistivity Profiling (ARP©, Geocarta, Paris, F) provides multi-depth readings of the soil electrical resistivity (ER). NDVI field measurements were taken at four time points in different seasons, while ER measurements were taken only once at three depth layers: 0.5 m, 1 m and 2 m. As shown in Table 1 and Fig. 5, NDVI point locations change with time and are not aligned with ER samples. Hence NDVI and ER samples are misaligned in both space and time. Other data issues include response space-time dependence with spatially dense data (big n problem, Lasinio et al. 2013) and repeated covariate measurements.

Table 1 Sampling time and number of sampled locations for NDVI and ER

Fig. 5

Maps of sampled NDVI, ER and grid point locations

5.1 Data pre-processing

Big n and spatial misalignment suggest to change the support of both NDVI and ER samples. The change of support problem (COSP, see Gelfand et al. 2010, and references therein) involves a change of the spatial scale that can be required for any of several reasons, such as predicting the process of interest at a new resolution or to fuse data coming from several sources and characterized by different spatial resolutions. Bayesian inference with COSP may be a computationally demanding task, as it usually involves stochastic integration of the continuous spatial process over the new support. For this reason, in case of highly complex models or huge data sets, some adjustments and model simplifications have been proposed to make MCMC sampling feasible (see Gelfand et al. 2010; Cameletti 2013). Although relatively efficient, these proposals don’t seem to fully adapt to our setting, mostly because of the need to overcome the linear paradigm. The most commonly used block average approach (see for example Banerjee et al. 2014; Cressie 2015) would become computationally infeasible with a semi-parametric definition of the relation between NDVI and ER.

Given the aim of this work and the data size, COSP is here addressed by a non-standard approach: spatial data were upscaled by aggregating samples to a 2574 cells square lattice overlaying the study area (validated in Rossi et al. 2015, 2018). Given the different number of sampled points corresponding to each sampling occasion (NDVI) and survey (ER), we used a proportional nearest neighbors neighborhood structure to compute the upscaled values. More precisely, 27 neighbors were just enough to obtain non-empty cells at all grid points with the least numerous NDVI series (at the $3^{{{rd}}}$ time point). We then modified this number proportionally to the samples sizes, obtaining 55, 59, and 65 neighbors respectively for NDVI at the 1st, 2nd and 4th time points and 35 neighbors for ER. At each grid point we calculated the neighbors’ means for both NDVI and ER, while neighbors’ variances and covariances between depth layers were obtained for ER. Summary measures of the scale and correlation of ER repeated measures at each of the 2574 grid points provide valuable information. Such a by-product of the upscaling of the original spatial data is used to obtain estimates of the elements of ${\varvec{\varSigma }}_{u,i}$ to be plugged into the model likelihood.

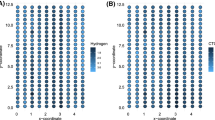
Exploratory analysis of the gridded data shows some interesting features that we use to drive the specification of the distributional regression model: ER does not show a strong systematic variation along depth (Fig. 6, left); the functional shape of the nonlinear relation between NDVI and ER is common to all NDVI sampling occasions and ER depth layers (Fig. 7); NDVI has much higher position and smaller variability at the second time point, when it approached saturation (Fig. 6, right). NDVI saturation commonly occurs at high aerial biomass levels. After September’s cut, the onset of autumn rains coupled with the mild average temperatures of the period favored alfalfa aerial biomass accumulation. As the canopy closes, NDVI values commonly increase to the point of reflectance saturation.

Fig. 6

ER distributions along depth (left) and NDVI distributions along time (right)

Fig. 7

Dependence of NDVI (vertical axis) on ER (horizontal axis) at different time points (rows) and depth layers (columns). XY plots of gridded data and lowess curves

5.2 Additive distributional regression models for location and scale

For available NDVI recordings, we consider Gaussian and Beta distributional regression models as those defined in Sect. 4.2. For $s=1,\ldots ,2574$ grid points and $t=1,\ldots ,4$ time points, the structured additive predictor of the location parameter $\eta ^\mu ({\varvec{\nu }}_{st})$ is determined as an additive combination of three linear and functional effects, such as a linear time effect, a spatial effect and a nonlinear effect of the continuous covariate ER:

$$\begin{aligned} \eta ^\mu ({\varvec{\nu }}_{st})=\beta _0^{\mu }+{\varvec{i}}'_t\varvec{\beta }_1^{\mu }+f_1^\mu (x_s)+f_2^\mu (lon_s,lat_s) \end{aligned}$$

(6)

where ${\varvec{i}}_t$ is a vector of time indicator variables with cornerpoint parametrization corresponding to the first sampling time, $x_s$ are latent replicate-free ER recordings specified as in Sects. 2.3 and 3.1, $f_1^\mu (x_s)$ is a nonlinear smooth function of $x_s$ and $f_2^\mu (lon_s, lat_s)$ is a bivariate nonlinear smooth function of geographical coordinates $lon_s$, $lat_s$. The spatial dependence is taken into account through a bivariate nonlinear smooth function of the coordinates, rather than by a latent Gaussian field with stationary spatial covariance function. The choice of a fine spatial modelling of the mean is due to the large number of data points after spatial aggregation over a square lattice. Considering a spatially correlated Gaussian field in this case would imply inversion of a large covariance matrix at each iteration of the MCMC algorithm, further increasing the computational complexity. As Fig. 6 (left) clearly shows, time has an effect on the variability (scale) of NDVI, while no analogous evidence is available concerning any other systematic variation of the NDVI scale. Then the linear predictor of the scale parameter $\eta ^{\sigma ^2}({\varvec{\nu }}_{st})$ is assumed to depend only on the effect of time, allowing heteroscedasticity of NDVI recordings:

$$\begin{aligned} \eta ^{\sigma ^2}({\varvec{\nu }}_{st})=\beta _0^{\sigma ^2}+{\varvec{i}}'_t\varvec{\beta }_1^{\sigma ^2} \end{aligned}$$

(7)

for $t=1,\ldots ,4$ time points where $\beta _0^{\sigma ^2}$ and $\varvec{\beta }_1^{\sigma ^2}$ represent the overall level of the predictor and the vector of seasonal effects on the transformed scale parameter. Fixed effects $\varvec{\beta }_1^{\mu }$ and $\varvec{\beta }_1^{\sigma ^2}$ in (6) and (7) respectively account for mean effects and heteroscedasticity of NDVI seasonal recordings.

Although the Beta model would be the correct model for NDVI (values range between 0 and 1, as the area does not comprise water bodies), it is much more computationally convenient to use the Gaussian model. Conjugacy allows to use Gibbs sampling to simulate from the full conditionals of the Gaussian model for the location parameter. The less computationally convenient Metropolis-Hastings algorithm is required to sample the posterior of the Gaussian model for the scale parameter and that of the Beta model for both parameters. As for the simulation experiment, 10,000 simulations with 5000 burnin and thinning by 5 were obtained for Gaussian models, while Beta models required longer runs of 50,000 iterations with 35,000 burnin and thinning by 15. In all cases, convergence was reached and checked by visual inspection of the trace plots and standard diagnostic tools. Fine tuning of hyperparameters lead us to 10 and 8 equidistant knots for each of the two components of the tensor product spatial smooth in the Gaussian and Beta case, respectively. All priors and hyperparameters were set as specified in Sects. 2 and 3. A sensitivity analysis was performed comparing 11 different prior settings for variance parameters of penalized spline and tensor product spline terms. The results (not shown for brevity, but available from the authors upon request) were generally quite stable and estimates never exceeded 95% credibility intervals obtained with the default prior setting.

The additive distributional regression model was compared to standard additive mean regression with the same mean predictor, applying the proposed measurement error correction to both models, under the Gaussian and Beta assumptions. By this comparison we show that adding a structured predictor for the scale parameter improves both the in-sample and out-of-sample predictive accuracy. In the following, M1 is an additive regression model with mean predictor as in (6), while M2 is an additive distributional regression model with the same mean predictor and scale predictor given by (7).

5.3 Results

Model comparison shows some interesting features of the proposed alternative model specifications. Concerning the distributional assumption, DIC, WAIC and the three proper scoring rules, calculated within $R=10$ cross validation folds, clearly favor the Beta models (Table 2), showing a better compliance with in-sample and out-of-sample predictive accuracy. As far as additive distributional regression is concerned, information criteria and scoring rules agree in assessing the proposed model (M2) as performing better than a simple additive mean regression (M1).

Table 2 Model fit statistics for Gaussian (G) and Beta (B) distribution additive mean (M1) and distributional (M2) regression models: deviance information criterion, Watanabe–Akaike information criterion, logarithmic score, spherical score and quadratic score

Quantile residuals of model M2 under the two distributional assumptions show a generally good behavior. A substantial reduction in scale is observed for the Beta case and only a slightly better compliance of the latter distributional shape with respect to the Gaussian (Fig. 8). When comparing the two distributional assumptions, it should be recalled that Gaussian models are by far much more convenient from the computational point of view.

Fig. 8

Quantile residuals for models M1 (left) and M2 (right) under the Gaussian (top panel) and Beta (bottom panel) assumptions: boxplots at different time points (left panel) and Normal q–q plots (right panel)

Values of the fixed time effects estimates of the mean (6) and variance (7) predictors and their 95% credibility intervals for the two models (Table 3) are expressed in the scale of the linear predictor and cannot be compared, due to different link functions being implied (back transformation to the response scale can be done for whole predictor, not for single additive effects). However, in both the Gaussian and Beta case the relative variation of fixed time effects estimates clearly reproduces the NDVI behavior in Fig. 6, left.

Table 3 Fixed time effects estimates of mean and variance predictors with 95% credibility intervals. To facilitate interpretation, estimates were transformed avoiding the cornerpoint parametrization

The effectiveness of the proposed approach for the data at hand was also checked by comparison of model estimates in Table 3 to those obtained with the same model without the measurement error correction, i.e. with the measurement error part specified as for the naive model in Sect. 4. As was previously shown in Sect. 4.3 with the results of the simulation experiment, neglecting the measurement error produces biased effects estimates with unduly low variability. Inspection of Table 4 shows that fixed effects estimates are constantly slightly smaller than those in Table 3 and that, as expected, credibility intervals are narrower than those obtained with the measurement error correction.

Table 4 Fixed time effects estimates of mean and variance predictors with 95% credibility intervals for the naive model without measurement error correction

Estimates of smooth effects of ER in Fig. 9 have common shapes for the two distributional assumptions. In both cases ER effects have quite small values if compared to those of the fixed time effects in Table 3. As a matter of fact, time is a predictable source of variation: canopy spectral properties reflect the crop phenology, growth and physiological status, and NDVI reflects the seasonal and year to year variation of the crop growth and development. Notice that the focus of the agronomic problem is analyzing the dependence of NDVI on ER, then the estimated time effect is rather to be considered as a confounder. Lack of the measurement error correction causes some overestimation of the higher values of the ER effect. Again, 95% credibility intervals (not reported, but available from the authors upon request) are much narrower than those obtained with the measurement error correction.

Fig. 9

Estimates of the smooth effect of ER $f_1^{\mu }(x_s)$ for models GM2 (left), and BM2 (right) with and without the measurement error correction (thin dotted lines are 95% credibility intervals for the models with the ME correction). GM2 effects are on the scale of the response (NDVI), while BM2 effects are estimated on the logit scale

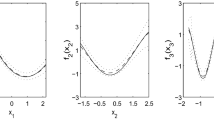
The inclusion of the nonlinear trend surface (Fig. 10, right), besides accounting for the spatial pattern and lack of independence between nearby observations, allows to separate the effect of ER from any other source of NDVI spatial variability, including erratic and deterministic components (such as slope and/or elevation). The estimated nonlinear effect of ER on NDVI (Fig. 10, left) shows a monotonically increasing relation up to approximately 10 Ohm m with a subsequent steep decline up to approximately 20 Ohm m. After dropping to lower values, the smooth function declines more slowly. Based on the resulting estimated smooth functions (Fig. 10, left), two ER cut-offs (at 10 and 20 Ohm m) are proposed that can be used to split the field into three areas characterized by a different monotonic soil–plant relationship (Rossi et al. 2018):

• Zone i: ER < 10Ohm m, where NDVI grows with ER and very low ER readings correspond to intermediate to high NDVI values;

• Zone ii: 10Ohm m < ER < 20 Ohm m, where ER is negatively related to NDVI and soil factors affecting ER act almost linearly and consistently on plant performance;

• Zone iii: ER > 20Ohm m, where despite the large variation in ER there is a limited NDVI-soil responsiveness and NDVI is constantly low.

Each zone conveys information on the shape and strength of the association between soil and crop variability, thus the proposed field zonation helps discerning areas characterized by different soil constraints. These information can be profitably used to improve the efficiency of destructive sampling strategies that are necessary to identify specific soil limiting factors in each zone. Management efforts are optimized by prioritizing interventions in areas characterized by a relatively high and time-persistent soil–plant responsiveness (e,g. areas where soil variability actually corresponds to yield variability) for which the ER map can itself be used as a prescription map.

Fig. 10

Estimates of the smooth effects ER $f_1^{\mu }(x_s)$ (left) and spatial coordinates $f_2^{\mu }(lon_s,lat_s)$ (right) for models GM2 (top), and BM2 (bottom). Notice that while GM2 effects are on the scale of the response (NDVI), BM2 effects are estimated on the logit scale. Vertical lines locate ER cut-offs corresponding to different monotonic soil–plant relationships

6 Concluding remarks and directions of future work

The work described in this paper was motivated by the analysis of a database characterized by some complex features: response space-time dependence with spatially dense data, data misalignment in both space and time and repeated covariate measurements. These data features were addressed by first changing the spatial support of the data. Subsequent analysis are based on our proposal of extending structured additive distributional regression models introducing replicated covariate measured with error. Within a fully Bayesian implementation, measurement error is dealt with in the context of the functional modeling approach, accounting for possibly heteroscedastic and correlated covariate replicates. In the paper we only allow for Gaussian and Beta distributed responses, but the proposed correction is implemented to accommodate for potentially any K-parametric family of response distributions. With a simulation experiment we show some advantages in the performance of the proposed ME correction with respect to two alternative less ambitious ME specifications. The proposed extension of the ME correction in Kneib et al. (2010) to structured additive regression models proves to be essential for the case study on soil–plant sensor data, where both mean and variability effects have to be modeled. Indeed in this case the proposed approach outperforms the simpler use of the ME correction with a mean regression model with the same (mean) predictor.

In the Bayesian framework, a straightforward extension would be the consideration of other types of (potentially non-normal) measurement error structures, as in Sarkar et al. (2014) under a structural ME approach. Given that a fully specified measurement error is given, this will only lead to a minor adaptation of the acceptance probability in our MCMC algorithm. A more demanding extension would be to include inference on the unknown parameters in the measurement error model, such as the covariance structure in our approach based on multivariate normal measurement error. Such parameters will typically be hard to identify empirically unless the number of replicates is very large. In the case of big spatial data, the computational burden induced by spatial correlation could be reduced integrating the ME correction with a low rank approach (see for instance Banerjee et al. 2014; Datta et al. 2016, and references therein). While in this paper we have considered measurement error in a covariate that enters the predictor of interest via a univariate penalized spline, other situations are also easily conceivable. One option would be to develop a Bayesian alternative to the simulation and extrapolation algorithm developed in Küchenhoff et al. (2006) to correct for misclassification in discrete covariates. Another route could be the consideration of measurement error in one or both covariates entering an interaction surface modeled as a bivariate tensor product spline.

In the Bayesian hierarchical framework it would be conceptually easy to address the dependence of ME-affected covariates on other auxiliary variables. In line with “exposure models” (Gustafson 2003), auxiliary variables could take the form of a spatial field, making the estimation algorithm computationally intensive (in our case study this would imply simulating 2574 points Gaussian fields for three replicates at each point at each MCMC iteration). A possible alternative solution would consider ME-affected covariates depending on a semiparametric function of the spatial coordinates, avoiding matrix inversions implied by GRF simulations.