1 Introduction

Glaciers lose mass through different processes such as melting, sublimation and calving. In particular, most of liquid water is lost by surface melting and runoff or surface melting, percolating inside the glacier and exit by the front and the base. Glacier discharge is defined as the rate of flow of meltwater through a vertical section perpendicular to the direction of the flow (Cogley et al. 2011). Modelling glacier discharge is a very important issue in climate and hydrology research (Jansson et al. 2003; La Frenierre et al. 2014). A review of the different approaches for glacier melt modelling can be found in Hock (2005). These models are usually classified in two main categories: energy balance models, which try to solve balance equations relating the gain and loss of ice in glacier systems (Ohmura 2001; Willis et al. 2002), and temperature index or degree-day models, which are essentially simple linear regression models relating the temperature and the glacier discharge (Gray and Prowse 1993; Hock 2003; Pellicciotti et al. 2005). Temperature-index models are often preferred for their simplicity and because the air temperature is usually easy available. However, the main drawback of these models is that they generally assume that the relation between temperature and glacier discharge is linear and constant along time, which is not realistic in practice.

Copulas have become a common tool to model nonlinear dependencies and nonstationarity. Although the copula concept appears by the late 50s, the computer development in the last decades has caused a fast growth of the number of scientific papers related with copulas, see Nelsen (2006) for an extensive review. The main advantage of copulas is that the marginal distributions can be defined separately from their dependence structure. Copulas have been widely used in many different fields such as a civil engineering, finance, medicine, etc. In particular, in climate and hydrology research, they have been considered for example to model the dependence between the temperature and rainfall (Scholzel and Friederichs 2008; Cong and Brady 2012), the relation between the intensity and duration of a rainfall (Cantet and Arnaud 2014), between the wind direction and rainfall (Carnicero et al. 2013), in characterization of droughts (Zhang et al. 2013), in the analysis of floods (Saad et al. 2014), in the behaviour of reconstructed watersheds (Nazemi and Elshorbagy 2012), spatial models (Kazianka and Pilz 2010), among others. See also Genest and Favre (2007) for an introduction to copulas in hydrology. In most of these works, copula models are static such that their parameters remain constant along time. Time-varying copulas have been widely used in finance (Patton 2012; Ausín and Lopes 2010) but their use is very limited in hydrological research.

GLACKMA (Glaciers, Cryokarst and Environment) association promotes scientific research in the polar regions, see http://www.glackma.es. Their researchers have been visiting both poles almost every year since 1985 with the goal of using the glaciers as natural warming sensors, (Hock et al. 2005; Bers et al. 2013). GLACKMA has implemented eight stations as Pilot Experimental Catchment areas at different latitudes and altitudes in glaciers of both hemispheres which are working continuously to register glacier discharge values. In this paper, we will concentrate on one of these stations located at the King George Island in the Antarctica, where there is available glacier discharge data from 2002. Temperature data are also obtained from the Russian Antarctic Base Bellingshausen, located at 4 km from the GLACKMA station on King George Island.

The main objective of this paper is to study the time-varying relationship between glacier discharge and temperature. We show that the dependence among these two variables is non constant and non linear through time. Therefore, we propose a time-varying seasonal copula model whose parameters follow a seasonal dynamic. The marginal distributions for the discharge and temperature are modelled using time-varying distribution models whose location, scale and shape parameters vary periodically on time. Bayesian inference and prediction is carried out such that it is possible to obtain credible Bayesian intervals for the missing data periods and credible predictive intervals for the glacier discharge value conditioned on the temperature at any given time point whose temperature is known.

This paper is organized as follows. Section 2 describes the study area in Antarctica where the GLACKMA experimental station is installed. A descriptive analysis of the available database is also provided. Section 3 introduces the proposed time-varying copula model where the rank correlations follow a seasonal dynamic and whose marginal distribution parameters also vary periodically along time. Section 4 explains how to undertake Bayesian inference and prediction based on MCMC methods and describes how to perform Bayesian model selection in this context based on DIC. The proposed methodology is applied in Sect. 5 for the GLACKMA database. Finally, Sect. 6 concludes with some discussion and extensions.

2 Study area and data description

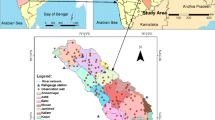
King George Island is the largest of the South Shetland Islands located at the tip of the Antarctic Peninsula. The glaciers of King George Island have suffered a retreat and loss of thickness in the recent decades associated with rising air temperatures (Rückamp et al. 2011; Osmanoglu et al. 2013). Collins Glacier, with around 1313 km2, covers most of the King George Island except the south-western end of the island, where the Fildes Peninsula is located. The study area is placed in this south west side of the icecap Collins, known as Smaller Dome or Bellingshausen Dome, see Fig. 1.

Fig. 1
figure 1

Left panel shows the location of King George Island in the Antarctica. Central panel shows the island, mostly covered by Collins glacier. Right panel zooms in the location of the CPE-KG-62°S station, indicated with a red arrow (Braun et al. 2002)

Full size image

More specifically, the GLACKMA measuring station, named as CPE-KG-62°S, is installed in a canyon near the Uruguayan Base Artigas (62°11 03S, 58°54 41W), where a stream bringing water runs from the unique lagoon which, after diverse proglacial routes, receives the flow from five springs redirecting the glacier discharge into the south side of the coast. These five springs drain water from a catchment area with a total surface of 2.92 km2, which comprises 1.31 km2 of glacier surface, 0.25 km2 of peripheral moraine and and 1.36 km2 of fluvial surface.

The GLACKMA monitoring station was installed in January of 2002 and consisted of a sounder with sensors for water temperature, conductivity and river level. After two years of hourly registrations, the hard meteorological conditions during the austral winter in 2003 caused a series of invalid records during the following austral summer. A new high-quality sounder was then set up which, although it only registers values from the river level, it is much more resistant under extreme conditions. The glacier discharge can be accurately estimated as an exponential function of the river level using a classical regression fit with \(R^2=0.99\), see Domínguez and Eraso (2007) for further details.

Therefore, the available discharge data for this project are from October 1st, 2002 to September, 30th 2012, with a missing hydrological year of records from December, 1st 2003 to June, 30th 2004. On the other hand, a complete time series of temperatures is obtained for the whole same period from the weather station of the Russian Antarctic Base Bellingshausen, located at 4 km from the CPE-KG-62°S station. Daily average values are obtained such that our database consists of a bivariate time series of 3653 observations from two main variables: the average daily glacier discharge, measured in m3/s·km2, and the average daily air temperature, measured in Celsius degrees (°C), during ten hydrological years, with 213 consecutive missing values for the discharge.

Figure 2 shows the boxplots of the average daily mean glacier discharge divided by 11-day groups for a smoother description. Note that there is a clear seasonality pattern. First, we observe that during the austral winter, which starts at the end of June, there is almost no glacier discharge. This produces a large amount of zero values which represent around the 57 % of the discharge observations. The period of positive discharge begins at the end of the austral spring, between November and December. During this initial discharge period, there are eventually some extreme values which are usually known as “spring events” or “burst” (Warburton et al. 1994), these are brief and violent episodes when the glacier brutally release a large amount of water. They are mostly originated when the bottom of full-of-water vertical wells are broken due to the increase in the temperatures.

Fig. 2
figure 2

Boxplots of the average daily glacier discharge from 2002 to 2012 divided in 11-day groups

Full size image

Figure 2 also shows that the maximum values for the median of the discharge are observed during the austral summer, from the end of December to the middle of March. The median discharge starts to decrease with the arrival of the autumn, at the end of March. However, we may also observe extreme values during this period, which are known as “aftershocks”(Warburton et al. 1994). These are kicks in the glacier drainage that may appear when the annual discharge wave seems to be over and are typically caused by the fluctuations in the temperature during this period.

Figure 3 shows the boxplots of the average daily temperatures divided again, for a smoother description, by 11-day groups (Whitfield et al. 2002). As before, we can observe a clear seasonality effect. Note that the average temperatures are above zero only during the austral summer, from the middle of December to the middle of March. Also during the summer period, we can observe less dispersion and more symmetry, in the temperature distribution, than in the rest of the year. On the contrary, temperatures start to decrease with the beginning of autumn and their dispersion increase such that they are almost always below zero during the austral winter, from the end of June to the end of September, when they present a strong left asymmetry. These plots has been obtained with the help of the R package seas (Toews et al. 2007).

Fig. 3
figure 3

Boxplots of the average daily temperature from 2002 to 2012 divided in 11-day groups

Full size image

Figures 2 and 3 also show that there is a clear relationship between temperature and glacier discharge. Also, we can observe that this dependence is not constant through time. During the austral winter, when the temperatures are very low, there is no glacier discharge. However, as commented before, the period of positive discharge starts in spring when the temperatures increase and during the austral summer, the median of the discharge reach their maximum values due to largest values for temperatures. Therefore, it is clear that there is also a seasonal dynamic in the dependence. Figure 4 shows the scatter plots for the temperature and the discharge separately for each season. We can observe that there is a strong dependence in summer that disappears in winter. We can also observe that this dependence is not linear. Figure 4 also shows the same scatter plots on copula scale. These are obtained using the empirical cdf evaluated at the observed temperatures and discharges for each season. Observe that the support of the copula function does not cover the whole unit square in some seasons due to the zero values observed in the glacier discharge.

Therefore, in the next section, we propose a model for a time-varying dependence which is not linear and shows a clear seasonal pattern. This is addressed by considering a dynamic joint distribution for the temperature and the glacier discharge whose dependence is measured in terms of a dynamic copula function whose Kendall’s tau coefficient moves periodically along time.

Fig. 4
figure 4

Scatter plots for the daily average temperature and discharge in each season on the upper row and the same scatter plots on copula scale on the bottom row

Full size image

3 Seasonal model

In this section, we present a general model to describe the joint seasonal dynamics for the temperature and the glacier discharge. Firstly, we define separately the marginal models for the temperature and the glacier discharge using time-varying periodic distributions. Then, we describe the seasonal dependence using a time-varying copula model whose parameters vary periodically along time.

3.1 Marginals

Firstly, we define a periodic time series model for the average daily temperature at each day t, which will be denoted by \(X_{t}\). In order to approximate its seasonal behavior, we assume that the distribution of \(X_{t}\) changes periodically through time with a location parameter, \(\mu _{t}\), given by:

$$\begin{aligned} \mu _{t}=a_{0\mu }+ {\displaystyle \sum \limits _{k=1}^{K_{1}}} a_{k\mu }\cos \left( \frac{2k\pi t}{c}-\psi _{k1}\right) , \end{aligned}$$
(1)

where \(c = 365.25\) is the annual periodic cycle. Observe that this is an approximation by a partial sum of a trigonometric Fourier series with \(K_1\) terms, where the fundamental frequency is \(2\pi /c\), the amplitude parameters are \({\varvec{a}}_\mu =(a_{0\mu },\ldots ,a_{K_1\mu })\), where \(a_{k\mu }\in {\mathbb{R}}\), and the phase angle parameters are \({\varvec{\psi}}_1=(\psi _{11},\ldots ,\psi _{K_11})\), where \(\psi _{k1}\in [0,\pi )\). Note that each angle phase, \(\psi _{k1}\), is only defined in the semi-unit circle \([0,\pi )\) since:

$$\begin{aligned} a_{k\mu }\cos \left( \frac{2k\pi t}{c}-\psi _{k1}\right) =-a_{k\mu }\cos \left( \frac{2k\pi t}{c}-\left( \psi _{k1}+\pi \right) \right) \end{aligned}$$

Figure 2 shows that not only the mean of temperature varies periodically along time, but also the variance and possibly, the shape of the distribution. Therefore, we assume similarly that the scale, \(\sigma _{t}\), and shape, \(\xi _{t}\), parameters of \(X_{t}\) vary periodically along time such that,

$$\begin{aligned} &\log \sigma _{t}=a_{0\sigma }+ {\displaystyle \sum \limits _{k=1}^{K_{1}}} a_{k\sigma }\cos \left( \frac{2k\pi t}{c}-\psi _{k1}\right) ,\\ &\xi _{t}=a_{0\xi }+ {\displaystyle \sum \limits _{k=1}^{K_{1}}} a_{k\xi }\cos \left( \frac{2k\pi t}{c}-\psi _{k1}\right) \nonumber , \end{aligned}$$
(2)

where \({\varvec{a}}_\sigma =(a_{0\sigma },\ldots ,a_{K_1\sigma })\) and \({\varvec{a}}_\xi =(a_{0\xi },\ldots ,a_{K_1\xi })\) are the amplitude parameters for the scale and shape, respectively, where \(a_{k\sigma }\in {\mathbb{R}}\) and \(a_{k\xi }\in {\mathbb{R}}\). And where \({\varvec{\psi }}_1\) is the same vector of phase parameters defined in (1) for the time-varying location. Note that it makes sense to assume that the phase vector is the same for the location, shape and scale, since we expect the same dynamics for the three parameters such that, for example, when the location increases, the scale and shape decreases. Note also that in (2), we have modelled the logarithm of the scale parameter, \(\sigma _t\), to avoid that it takes negative values. Therefore, the set of parameters for the temperature is given by \({\varvec{\vartheta }}_X=\left\{ {\varvec{a}}_\mu ,{\varvec{a}}_\sigma ,{\varvec{a}}_\xi ,{\varvec{\psi}}_1\right\}\) and the number of Fourier terms, \(K_1\).

Once we have defined the periodic pattern for the location, scale and shape parameters, it is necessary to specify a distribution model for the time-varying temperature, \(X_{t}\). For example, we may assume a skewed normal distribution, \(X_{t}\sim SN(\mu _{t},\sigma _{t},\xi _{t})\) (Azzalini 1985), whose density is given by,

$$\begin{aligned} f_{SN}\left( x_{t}\mid \mu _{t},\sigma _{t},\xi _{t}\right) =\,\frac{2}{\sigma _{t}}\phi \left( \frac{x_{t}-\mu _{t}}{\sigma _{t}}\right) \Phi \left( \xi _{t}\left( \frac{x_{t}-\mu _{t}}{\omega _{t}}\right) \right) , \end{aligned}$$
(3)

where \(\phi\) and \(\Phi\) denote the pdf and cdf of a standard Gaussian distribution. Note that when \(\xi _{t}=0\), we obtain the symmetric normal model, \(X_{t}\sim N(\mu _{t},\sigma _{t})\).

Alternatively, we can consider a generalized extreme value distribution model for the temperature, \(X_{t}\sim GEV(\mu _{t},\sigma _{t},\xi _{t})\) (Embrechts et al. 1997), whose density is given by,

$$\begin{aligned} f_{GEV}\left( x_{t}\mid \mu _{t},\sigma _{t},\xi _{t} \right) =\,&\frac{1}{\sigma }\left[ 1+\xi _{t}\left( \frac{x_{t}-\mu _{t}}{\sigma _{t}}\right) \right] ^{-\frac{1}{\xi _{t}}-1}\nonumber \\ &\times \exp \left\{ -\left[ 1+\xi _{t}\left( \frac{x_{t} -\mu _{t}}{\sigma _{t}}\right) \right] ^{-\frac{1}{\xi _{t}}}\right\} \end{aligned}$$
(4)

for \(x_{t}>\mu _{t}-\sigma _{t}/\xi _{t}\) when \(\xi _{t}>0\) and for \(x_{t}<\mu _{t}-\sigma _{t}/\xi _{t}\) when \(\xi _{t}<0\). This is a very flexible distribution which includes the Weibull or the Gumbel distribution as particular cases.

There are many other possibilities that could be considered to model the temperature distribution. In Sect. 4, we explain how to undertake model selection for the distribution model and for the number of Fourier terms from a Bayesian perspective.

Now, we define a periodic time series model for the average daily discharge at each day t, which will be denoted by \(Y_{t}\). As before, we approximate the seasonal dynamics for the location, \(\lambda _{t}\), and scale, \(\beta _{t}\), parameters of \(Y_{t}\) using partial sums of Fourier series:

$$\begin{aligned}&\log \lambda _{t}=a_{0\lambda }+ {\displaystyle \sum \limits _{k=1}^{K_{2}}} a_{k\lambda }\cos \left( \frac{2k\pi t}{c}-\psi _{k2}\right) ,\end{aligned}$$
(5)
$$\begin{aligned}&\log \beta _{t}=a_{0\beta }+ {\displaystyle \sum \limits _{k=1}^{K_{2}}} a_{k\beta }\cos \left( \frac{2k\pi t}{c}-\psi _{k2}\right) . \end{aligned}$$
(6)

where

$$\begin{aligned}&{\varvec{a}}_{\lambda }=(a_{0\lambda },\ldots ,a_{K_2\lambda }),\quad a_{k\lambda }\in {\mathbb{R}}, \\&{\varvec{a}}_{\beta }=(a_{0\beta },\ldots ,a_{K_2\beta }), \quad a_{k\beta }\in {\mathbb{R}}, \end{aligned}$$

are the amplitude parameters for the location and scale parameters and \({\varvec{\psi}}_{2}=(\psi _{12},\ldots ,\psi _{K_22})\), \(\psi _{k2}\in [0,\pi )\), is the vector of phase parameters. Thus, the vector of parameters for the glacier discharge is given by \({\varvec{\vartheta}} _{Y}=\left\{ \varvec{a}_{\lambda },\varvec{a} _{\beta },\varvec{\psi }_{2}\right\}\) and the number of Fourier terms, \(K_2\).

Clearly, we could also define a similar periodic dynamic for the shape parameter. However, for simplicity, we will only consider positive random variables with two parameters to model the glacier discharge. For example, we may assume a Log-Normal distribution for the glacier discharge whose density is given by,

$$\begin{aligned} f_{LN}\left( y_{t}\mid \lambda _{t},\beta _{t}\right) =\frac{1}{y_{t}\beta _{t}\sqrt{2\pi }}\exp \left\{ -\frac{\left( \log \left( y_{t}\right) -\lambda _{t}\right) ^{2}}{2\beta _{t}^{2}}\right\} . \end{aligned}$$
(7)

Altenatively, we could assume a Gamma distribution, \(Y_{t}\sim G\left( \alpha _{t},\beta _{t}\right) ,\) whose density is given by:

$$\begin{aligned} f_{G}\left( y_{t}\mid \alpha _{t},\beta _{t}\right) =\frac{\beta _{t} ^{\alpha _{t}}}{\Gamma \left( \alpha _{t}\right) }x_{t}^{\alpha _{t}-1} \exp \left\{ -\beta _{t}x_{t}\right\} , \end{aligned}$$
(8)

where the mean, \(\lambda _{t}=\alpha _{t}/\beta _{t}\) and scale parameter \(\beta _{t}\) are assumed to follow the seasonal dynamics given in (5) and (6), respectively. As commented before, model selection and parameter estimation will be addressed in Sect. 4.

3.2 Copula

As commented in the Introduction, the dependence between the temperature and the glacier discharge is not constant along time. There is a strong dependence between this two variables in the austral summer and there is almost no dependence in the austral winter. In order to describe this pattern, in this section we model the dependence between these two variables using a time-varying copula model. More specifically, we assume that the Kendall’s tau coefficient, \(\tau _{t}\), follows a seasonal dynamic described by a periodic function given by,

$$\begin{aligned} \tau _{t}=a_{0\tau }+ {\displaystyle \sum \limits _{k=1}^{K_{c}}} a_{k\tau }\cos \left( \frac{2k\pi t}{c}-\psi _{k\tau }\right) , \end{aligned}$$
(9)

where \(\varvec{a}_{\tau }=(a_{1\tau },\ldots ,a_{K_c\tau })\), \(a_{k\tau }\in {\mathbb{R}}^{+}\), are the amplitude parameters and \(\varvec{\psi }_{\tau }=(\psi _{1\tau },\ldots ,\psi _{K_c\tau })\), \(\psi _{k\tau }\in [0,2\pi )\), are the phase parameters of the time-varying tau rank correlation parameter. Now the angle phase, \(\psi _{k\tau }\), is defined in the unit circle \([0,2\pi )\) since:

$$\begin{aligned} a_{k\tau }\cos \left( \frac{2k\pi t}{c}-\psi _{k\tau }\right) =a_{k\tau }\cos \left( \frac{2k\pi t}{c}-\left( \psi _{k\tau }+2\pi \right) \right) , \end{aligned}$$

moreover, we put the restrictions \(a_{i\tau }\ge 0\) and \(a_{0\tau }=\sum a_{i\tau }\) to ensure that \(\tau\) is always in the interval [0, 1]. This makes sense since the dependence between the temperature and the discharge will never be negative. Thus, the vector of parameters for the copula is given by \(\varvec{\vartheta }_{C}=\left\{ \varvec{a}_{\tau },\varvec{\psi }_{\tau }\right\}\) and the number of Fourier terms, \(K_{c}.\)

Different copula models could be used. For example, we might consider that the dependence structure is defined by a time-varying Gumbel copula:

$$\begin{aligned} C_{G}\left( u_{t},v_{t}\mid \theta _{t}\right) =\exp&\left\{ -\left( \left( -\log u_{t}\right) ^{\theta _{t}}+ \left( -\log v_{t}\right) ^{\theta _{t} }\right) ^{-\frac{1}{\theta _{t}}}\right\} , \end{aligned}$$
(10)

where \(u_{t}=F_{X_{t}}(x_{t}\mid \vartheta _{X})\) and \(v_{t}=F_{Y_{t}}(y_{t} \mid \vartheta _{Y})\) are the marginal distribution functions for \(X_{t}\) and \(Y_{t}\), respectively, at time t, and where, \(\theta _{t}=\frac{1}{1-\tau _{t}},\) where the dynamics of \(\tau _{t}\) are specified in (9). One of the main advantages of the Gumbel copula is that it allows for right tail dependence (Embrechts et al. 2001). Similarly, we could consider many other parametric copula models with time-varying tau correlation, such as the Gaussian copula that do not allow for tail dependence:

$$\begin{aligned} C_{Ga}\left( u_{t},v_{t}\mid \theta _{t}\right) =&\int _{-\infty } ^{\Phi ^{-1}\left( u_{t}\right) }\int _{-\infty }^{\Phi ^{-1}\left( v_{t}\right) }\frac{1}{2\pi \left( 1-\theta _{t}^{2}\right) ^{1/2}}\nonumber \\ &\times\exp \left\{ -\frac{x^{2}-2\theta _{t}xy+y^{2}}{2\left( 1-\theta _{t} ^{2}\right) }\right\} dxdy, \end{aligned}$$
(11)

where \(\Phi ^{-1}\) denotes the inverse of the distribution function of the univariate standard normal distribution and where, \(\theta _{t}=\sin \left( \frac{\pi }{2}\tau _{t}\right)\).

Another alternative would be to assume a Student-t copula,

$$\begin{aligned} C_{St}\left( u_{t},v_{t}\mid \theta _{t},\upsilon \right) =&\int _{-\infty }^{t_{\upsilon }^{-1}\left( u_{t}\right) }\int _{-\infty }^{t_{\upsilon }^{-1}\left( v_{t}\right) }\frac{1}{2\pi \left( 1-\theta _{t}^{2}\right) ^{1/2}}\nonumber \\ &\times\left\{ 1+\frac{x^{2}-2\theta _{t}xy+y^{2}}{\upsilon \left( 1-\theta _{t}^{2}\right) }\right\} ^{-\frac{\upsilon +2}{2} }dxdy, \end{aligned}$$
(12)

where \(t_{\upsilon }^{-1}\) denotes the inverse of the distribution function of the univariate t distribution with \(\upsilon\) degrees of freedom and where, \(\theta _{t}=\sin \left( \frac{\pi }{2}\tau _{t}\right)\).

However, this copula model impose symmetric tail dependence, which does not seem realistic in this context, and would also require to estimate the degrees of freedom as an additional parameter.

Therefore, assuming that the number of terms in each Fourier sum is known, the joint density function for the temperature and the glacier discharge at time t will be given by,

$$\begin{aligned} f\left( x_{t},y_{t}\mid \varvec{\vartheta }_{X},\varvec{\vartheta } _{Y},\varvec{\vartheta }_{C}\right) =\,&f_{X_{t}}\left( x_{t}\mid \varvec{\vartheta }_{X}\right) \times f_{Y_{t}}\left( y_{t}\mid \varvec{\vartheta }_{Y}\right) \nonumber \\ & \times c\left( F_{X_{t}}\left( x_{t} |\varvec{\vartheta }_{X}\right) ,F_{Y_{t}}\left( y_{t} |\varvec{\vartheta }_{Y}\right) \mid \varvec{\vartheta }_{C} \right) , \end{aligned}$$
(13)

where \(f_{X_{t}}\) and \(f_{Y_{t}}\) represent the marginal density functions of the glacier discharge and the temperature, respectively, that can be specified for example using the distribution models given in (3) or (4) and (7) or (8), respectively, and where c represents the copula density function whose corresponding cumulative distribution function can be specified for example using (10), (11) or (12).

4 Inference, prediction and model selection

Consider now the observed data series,

$$\begin{aligned} \left({\mathbf{x}},{\mathbf{y}}\right) =\left\{ \left( x_{1},y_{1}\right) ,\ldots ,\left( x_{T},y_{T}\right) \right\} , \end{aligned}$$

which provides the daily temperature and discharge measurements during T days. Given these data, we would like to make inference on the model parameters, \(\varvec{\vartheta }=\left( \varvec{\vartheta } _{X},\varvec{\vartheta }_{Y},\varvec{\vartheta }_{C}\right).\) In this section, we first assume that the distribution models for the marginals and the copula are known. Also the number of terms in the Fourier approximations, \(K_1\), \(K_2\) and \(K_c\), are assumed to be known. Later, in Subsect. (4.1), we will explain how to perform Bayesian model selection to select both the distribution models and the number of Fourier terms.

If the data set were complete, the likelihood function would be just the product of the joint density functions, (13), for each \(t=1,\ldots ,T\). However, as commented in the data description, during the hydrological year 2003/2004, it was not possible to register measurements for the glacier discharge since the external data-logger suffered flaws due to the hard meteorological conditions during the winter months. These values will be treated as missing data. Further, there is a large amount of glacier discharge values that are recorded as zero. Considering that the glacier discharge is measured as a function of the level of the river, these zero values can be regarded as left-censored observations since they are actually smaller than a minimum value, \(y_{\min }\), below which it is not possible to register any discharge value. The glacier discharge values in these cases are so small that they can not be registered accurately.

Therefore, the likelihood function for the model parameters is given by,

$$\begin{aligned} l\left( \varvec{\vartheta }\mid {\mathbf{x}},{\mathbf{y}}\right) =&\prod \limits _{t:y_{t}>0}f\left( x_{t},y_{t}\mid \varvec{\vartheta }\right) \nonumber \\ &\times\prod \limits _{t:y_{t}=0}\Pr \left( Y_{t}<y_{\min }\mid x_{t} ,\varvec{\vartheta }\right) \cdot f\left( x_{t}\mid \varvec{\vartheta }_{X}\right) \cdot \nonumber \\ &\times\prod \limits _{t:y_{t}=na} { f\left( x_{t}\mid \varvec{\vartheta }_{X}\right) ,} \end{aligned}$$
(14)

where na represents a missing discharge value which is not available and where the conditional probability for the glacier discharge can be obtained as,

$$\begin{aligned} \Pr \left( Y_{t}<y_{\min }\mid x_{t},\varvec{\vartheta }\right) =C^{(1)}\left( F_{X_{t}}\left( x_{t}\mid \varvec{\vartheta }_{X}\right) ,F_{Y_{t}}\left( y_{\min }\mid \varvec{\vartheta }_{Y}\right) \mid \varvec{\vartheta }_{C} \right) , \end{aligned}$$

where \(C^{(1)}\) represents the partial derivative of the copula distribution function as described in e.g. Venter (2001),

$$\begin{aligned} C^{(1)}\left( u,v \mid \varvec{\vartheta }_{C} \right) =\frac{\partial C_{t}\left( u,v \mid \varvec{\vartheta }_{C} \right) }{\partial u}. \end{aligned}$$

Note that these correspond to the so-called h-functions defined in Aas et al. (2009).

For example, for the particular case of a Gumbel copula, it is obtained that,

$$\begin{aligned} C_{G}^{(1)}\left( u_{t},v_{t}\mid \theta _{t}\right) =&\,C_{G}\left( u_{t},v_{t} \mid \theta _{t}\right) \\ &\times\left[ \left( -\ln u_{t}\right) ^{\theta _{t} }+\left( -\ln v_{t}\right) ^{\theta _{t}}\right] ^{-1+\frac{1}{\theta _{t}}}\\ &\times\left( -\ln u_{t}\right) ^{\theta _{t}-1}\frac{1}{u_{t}}, \end{aligned}$$

where \(C_{G}(u_{t},v_{t}\mid \theta _{t})\) is the Gumbel copula distribution function given in (10). And for the Gaussian copula, the \(C^{(1)}\) function can be expressed as

$$\begin{aligned} C_{Ga}^{(1)}\left( u_{t},v_{t}\mid \theta _{t}\right) =\Phi \left( \Phi ^{-1}(v_{t})\mid \theta _t\cdot \Phi ^{-1}(u_{t}),1-\theta _t^2\right) , \end{aligned}$$

where \(\Phi (x\mid \mu ,\sigma ^2)\) denotes the Gaussian density function with mean \(\mu\) and variance \(\sigma ^2\), and \(\Phi (x)\) denotes the standard Gaussian density function.

In order to perform Bayesian inference, we must define prior distributions for the model parameters, \(\varvec{\vartheta }\). We impose proper but non informative prior distributions as follows. For each amplitude parameter, \(a_{kp}\), we assume a large variance Gaussian prior \(N(0,100^2)\), for \(k=0,\ldots ,K_j\), for \(j=1,2,c\) and for \(p=\mu ,\sigma ,\xi ,\lambda ,\beta ,\tau\). For each phase parameter, \(\psi _{kj}\), we assume a uniform semicircular variable in \([0,\pi )\), for \(k=0,\ldots ,K_j\) and for \(j=1,2\) and uniform circular variable in \([0,2\pi )\), for \(k=0,\ldots ,K_j\) and for \(j=c\).

Given these priors and the likelihood specified in (14), it is not straightforward to derive analytically the posterior distribution, \(f(\varvec{\vartheta }\mid {\mathbf{x}},{\mathbf{y}})\). Therefore, we use MCMC sampling strategies in order to obtain a sample from the joint posterior distribution of the parameters, which will allow us to develop Bayesian inference. We propose a Gibbs sampling scheme which is carried out by cycling repeatedly through draws of each parameter conditional on the remaining parameters (Tierney 1994). In particular, we use the Random Walk Metropolis Hastings (RWMH) algorithm for sampling from the conditional posterior distribution of the model parameters. We use a simple one-dimensional RWMH where each model parameter is updated separately using normal candidate distributions whose mean is given by the previous value of each parameter in the algorithm and whose variance can be calibrated to obtain good acceptance rates. The details of the proposed algorithm are explained in the Appendix.

Now, we are interested in estimating the predictive joint distribution of the temperature and discharge, \(f(x_t,y_t\mid {\mathbf{x}},{\mathbf{y}})\), at any time t. This can be done using Monte Carlo simulation based on the MCMC output. Consider a posterior sample of size M of the model parameters, \(\varvec{\vartheta }^{(i)}\), for \(i=1,\ldots ,M\). Then, the values of the time-varying parameters, \(\mu _{t}^{(i)},\sigma _{t}^{(i)},\xi _{t}^{(i)},\lambda _{t}^{(i)},\beta _{t}^{(i)}\) and \(\tau _{t}^{(i)}\), are known for each time t and we can simulate values from \(f(x_t,y_t\mid {\mathbf{x}},{\mathbf{y}})\) as follows.

For each \(t=1,\ldots ,T\) and \(i=1,\ldots ,M\).

  1. 1.

    Obtain the copula parameter \(\theta _{t}^{(i)}\) from \(\tau _{t}^{(i)}\)

  2. 2.

    Simulate a value from the copula: \(\left( u_{t}^{(i)},v_{t}^{(i)}\right) \mid \theta _{t}^{(i)}\)

  3. 3.

    Obtain the pair of values for the temperature and discharge:

$$\begin{aligned} x_{t}^{(i)}&=F_{X}^{-1}\left( u_{t} ^{(i)}\mid \mu _{t}^{(i)},\sigma _{t}^{(i)},\xi _{t}^{(i)}\right) ,\\ y_{t}^{(i)}&=F_{Y}^{-1}\left( v_{t}^{(i)}\mid \lambda _{t}^{(i)},\beta _{t}^{(i)} \right) . \end{aligned}$$

Given this sample of the joint posterior distribution, we can obtain a sample from the marginal predictive distribution of the temperature by just taking the values \(\{(x_{1}^{(i)},\ldots ,x_{T}^{(i)})\}_{i=1}^{M}\). The posterior predictive mean and 95 % credible predictive intervals can be approximated using the sample mean for each t and the corresponding 0.025 and 0.975 quantiles. Similarly, we can approximate the posterior predictive mean and predictive intervals for the glacier discharge.

Finally, we wish to estimate the conditional predictive distribution of the glacier discharge given a value for the temperature, \(f(y_t\mid X_t = x_t,{\mathbf{x}},{\mathbf{y}} )\), at any time t. As before, this can be done by Monte Carlo approximation given the MCMC output as follows.

For each \(t=1,\ldots ,T\) and \(i=1,\ldots ,M\),

  1. 1.

    Obtain \(u_{t}^{(i)}=F_X(x_{t}\mid \mu _{t}^{(i)},\sigma _{t}^{(i)},\xi _{t}^{(i)})\) from the distribution selected for the temperature,

  2. 2.

    Find \(v_{t}^{(i)}\) such that \(p=C^{(1)}( u_{t}^{(i)},v_{t}^{(i)}\mid \theta _{t}^{(i)})\) where \(p\sim U\left( 0,1\right)\)

  3. 3.

    Set \(y_{t}^{(i)}=F_{Y}^{-1}(v_{t}^{(i)}\mid \lambda _{t}^{(i)},\beta _{t}^{(i)})\)

Therefore, given a set of observed temperatures, \(\{x_{1},\ldots ,x_T\}\), we can obtain a sample of the conditional predictive distribution of the discharge for each time point, \(\{(y_{1}^{(i)},\ldots ,y_{T}^{(i)})\}_{i=1}^{M}\). Using this sample, we can estimate the posterior predictive mean and 95 % credible predictive intervals for the conditional discharge using the sample means and the 0.025 and 0.975 quantiles of the sample as before.

4.1 Model selection

In order to compare different models, we use de Deviance Information Criterion (DIC). Models with smaller DIC should be preferred to models with larger DIC (Spiegelhalter et al. 2002). This measure penalizes the effective number of parameters of the model. The DIC value is given by,

$$\begin{aligned} DIC=\,&-4E_{\varvec{\vartheta }}\left[ \log l\left( \varvec{\vartheta }\mid {\mathbf{x,y}}\right) \mid x,y\right] \nonumber \\&+\,2\log l\left( E_{\varvec{\vartheta }}\left[ \varvec{\vartheta }\mid {\mathbf{x,y}}\right] \mid {\mathbf{x,y}}\right) . \end{aligned}$$
(15)

where the log-likelihood of the model parameters, \(\varvec{\vartheta }=(\varvec{\vartheta }_X,\varvec{\vartheta }_Y,\varvec{\vartheta }_C)\), is given by:

$$\begin{aligned} \log l\left( \varvec{ \vartheta }\mid {\mathbf{x,y}}\right)=\,&\sum \limits _{t}\log \left( f_{X}(x_{t}\mid \varvec{\vartheta }_X)\right) \\&+\sum \limits _{t:y_{t}>0}\log \left( f_{Y}(y_{t}\mid \varvec{\vartheta }_Y)\right) \\&+\sum \limits _{t:y_{t}>0}\log \left( c(F_{X}(x_{t}\mid \varvec{\vartheta }_X ),F_{Y}(y_{t} \mid \varvec{\vartheta }_Y)\mid \varvec{\vartheta }_C)\right) \\&+\sum \limits _{t:y_{t}=0}\log \left( C^{1}(F_{X}(x_{t}\mid \varvec{\vartheta }_X),F_{Y}(y_{\min }\mid \varvec{\vartheta }_Y)\mid \varvec{\vartheta }_C)\right) , \end{aligned}$$

Given an MCMC sample of size M of the posterior distribution of the model parameters, \(\varvec{\vartheta }^{(i)}\), for \(i=1,\ldots ,M\), the DIC value, (15), can be approximated by,

$$\begin{aligned} DIC=&-\frac{4}{M}\sum \limits _{i=1}^{M}\log l\left( \varvec{ \vartheta }^{\left( m\right) }\mid x,y\right) \\&+\,2\log l\left( \frac{1}{M}\sum \limits _{i=1} ^{M}\vartheta ^{\left( m\right) }\mid x,y\right) , \end{aligned}$$

5 Results

In this section, we illustrate the proposed methodology with the real data provided by GLACKMA on the discharge and temperature measurements from October 1st, 2002 to September 30th, 2012. We have considered a large number of different models for the marginal and copula distributions that will be discussed later in Subsect. 5.1. Here, we present firstly the results for the preferred model according to the DIC criteria which consists of a GEV model, see (4), for the marginal distribution of the temperature with \(K_1=4\) Fourier components, a Gamma distribution, see (8), for the marginal distribution of the discharge with \(K_2=4\) Fourier components and Gumbel copula, see (10), with \(K_c=2\) Fourier components.

The proposed MCMC algorithm is run for 100,000 iterations, discarding the first 50,000 as burn-in iterations. The chains have converged and they have good mixing. Table 1 shows the mean, posterior deviation and 95 % credible intervals for the model parameters.

Table 1 Model parameters for the parameters of the GEV distribution for the temperature, the Gamma distribution for the discharge and the rank-tau for the copula. Each parameter is obtained as the mean of its MCMC. The posterior deviation is the number between parenthesis. The third column of each parameter are the credible intervals
Full size table

Figure 5 shows the observed discharge time series data, the posterior predictive means and 95 % credible intervals for the whole time period. Apparently the discharge is well modeled, for example the posterior means are very close to zero in those winter periods where no discharge is recorded and the length of the corresponding credible intervals are also very close to zero. On the contrary, during the summer periods, the posterior discharge means and credible intervals are far from zero. Also, we can observe that the proposed model captures the Spring events and aftershocks at the beginning and the end of each period, respectively. Finally, observe that the proposed method is also able to produce Bayesian estimates and credible intervals for the missing period during the hydrological year 2003/2004.

Figure 6 shows the observed temperature time series, the posterior predictive means and 95 % credible intervals for the whole time period. Observe that the model can capture the left-skewness and larger variability during the austral winter. In contrast, note that credible intervals are more symmetric and narrower during the summer periods.

Figure 7 shows the posterior mean and 95 % credible intervals of the Kendall’s tau together with the observed values for the temperature and discharge for the whole time period. This figure illustrates how the dependence varies over time, we can see that larger values of tau correspond to higher values of the temperature and discharge. Similarly, smaller values of tau correspond to lower temperatures and periods with no discharge.

Fig. 5
figure 5

Observed discharge data, posterior predictive means and 95 % credible intervals

Full size image
Fig. 6
figure 6

Observed temperature data, posterior predictive means and 95 % credible intervals

Full size image
Fig. 7
figure 7

Posterior mean of the Kendall’s tau and 95 % credible intervals together with the observed values of the temperature and discharge for each time point

Full size image

Now, we are interested in analyzing the influence of the temperature on the discharge. Observe that using our proposed approach, we can obtain estimations of the conditional predictive distribution of the discharge given any value of the temperature at any given time point. As an illustration, Fig. 8 shows the conditional density function of the discharge for one particular day of the austral summer (02/20/2006) given different values of the temperature. Note that, as expected, the larger is the temperature, the larger is the probability of observing large values for the glacier discharge.

Fig. 8
figure 8

Conditional predictive density of the discharge given different values of the temperature for one particular day in summer (02/20/2006)

Full size image

Using the same approach, Fig. 9 shows the Bayesian estimations of the missing discharge values conditioned on the observed values for the temperature during the hydrological year 2003/2004 when the data-logger did not record the data appropriately.

Fig. 9
figure 9

Predicted values for the missing discharge conditioned on the observed values for the temperature during the hydrological year 2003/2004. Dotted lines represent the 95 % credible intervals

Full size image

Finally, observe that our proposed methodology also enables future predictions of both the joint distribution of discharge and temperature and the conditional discharge distribution given the temperature values. In order to illustrate this, Fig. 10 shows the estimations of the predictive discharge distribution for the last hydrological year 2011/2012 given the information from previous years. These are compared with the true observed values during this year. Note that the predictive intervals always contain the true observed values. Figure 10 also shows the estimations of the conditional predictive discharge during this last year given the values for the temperature. Observe that this provides in general better estimations for the discharge, although there is one single day where the temperature was extremely high which leads a large estimation for discharge.

Fig. 10
figure 10

Observed data for the discharge, mean of the values of the predictive and 95 % credible intervals. Hydrological year 2011–2012

Full size image

5.1 Model selection

In this section, we illustrate how the model introduced before has been selected according to the DIC criteria. Firstly, we put the emphasis on selecting the number of Fourier terms for the time-varying parameters of the temperature, K 1, the discharge, K 2 and the copula, K c . Table 2 shows the DIC values for different choices of the number of Fourier terms assuming a Generalized Extreme Value for the temperature, a Gamma distribution for the discharge and a Gumbel copula for the dependence. Note that the minimum value corresponds to \(K_1=4\) terms for the temperature, \(K_2=4\) terms for the discharge and \(K_c=2\) terms for the time-varying \(\tau _t\) parameter of the copula.

Table 2 DIC values for different number of Fourier terms, \(K_{1}\), \(K_{2}\) and \(K_c\), assuming a GEV distribution for the temperature, a Gamma distribution for the discharge and Gumbel copula
Full size table

Similar tables have been obtained assuming different models for the marginal distributions of the temperature and the discharge and also for the copula. The number of selected Fourier terms is in general the same but the value of the DIC is larger in all cases. For example, the minimum DIC value assuming a Gaussian copula and the same marginal distribution models as before is DIC = 14,838. The same minimum DIC value is obtained for the t-copula since the estimated degrees of freedom is very large which implies that the obtained t-copula is very similar to the Gaussian copula. Finally, the DIC = 149,513 is obtained for the model with the Clayton copula. Note that these values are larger than the minimum value obtained in Table 2 with a Gumbel copula which is given by DIC = 14,825, indicating that the Gumbel model is preferred than the other considered copulas.

In order to illustrate the differences among copula models, Fig. 11 shows the conditional predictive density of the discharge given zero Celsius degree temperature for one particular day in summer using the different copula models. This figure shows that the Clayton copula is not appropriate for these data, as expected, since this copula has not right tail dependence and it only allows for left tail dependence. On the other side, the obtained estimated models with the Gaussian and t-copula are very similar to that obtained with the Gumbel copula. However, it can be observed that the tail of the conditional distribution is slightly heavier with the Gumbel copula.

Fig. 11
figure 11

Conditional predictive density of the discharge for the models built with different copulas, given zero degrees as the value of the temperature for all of them and for one particular day in summer (02/20/2006)

Full size image

6 Conclusion and extensions

In this paper, we have proposed a seasonal dynamic model to describe the joint distribution of the glacier discharge and air temperature where not only the marginal distributions are time varying but also, the relationship between these two variables is described by a time-varying copula. We have proposed a Bayesian procedure for inference on the model parameters and prediction of the joint discharge and temperature distribution. Our approach allows for the simultaneous estimation of the marginal and copula parameters, which is in contrast with the classical two-stage estimation procedures.

An improved model could include structural changes over the time such that not only the model parameters were time-varying, but also the marginal and copula models could vary along time. For example, we could consider for each different season the possibility of using a different copula model, Gumbel (10), Gaussian (11) or Student-t (12). Similarly, we could incorporate for different seasons the possibility of distinct marginal distribution models for the temperature and glacier discharge. This problem is currently under research.

The proposed procedure could be extended to a multivariate model by including more environmental variables like precipitation, humidity, solar radiation or atmospheric pressure. In this case, the use of multivariate copulas would be required. One possibility is the use of vine copulas that has been successfully applied for financial time series data (Aas et al. 2009). See also Czado (2010) for a survey of vine copulas.

The developed methodology could be also applied in other Pilot Experimental Watersheds installed by GLACKMA at different latitudes in both hemispheres, which could be compared with those obtained in this work.