A space-time formulation for time-dependent behaviors at small or finite strains

Abstract

A general formalism is proposed, based on the definition of a space-time potential, for developing space-time formulations adapted to nonlinear and time dependent behaviors. The focus is given to the case of standard generalized materials that are expressed from the knowledge of two potentials, a strain energy and a dissipation potential in a convex framework with the help of internal variables. Viscoplasticity with isotropic hardening and nonlinear finite viscoelasticity are investigated. Starting from the definition of an appropriate space-time potential, time discontinuous Galerkin forms are developed for use in the case of time singularities (in particular with regard to time integration of internal variables). Furthermore, NURBS approximation are used, such as to propose Space-Time Isogeometric Analysis models. Numerical examples allow to compare the obtained isogeometric space-time models with standard finite-element models (that are based on standard time integration procedures: radial return for viscoplasticity and backward euler for viscosity) and allow to illustrate the new possibilities offered with the proposed space-time formulations.

1 Introduction

Since the original work of [1, 2], space-time finite-element (FE) have been applied to different problematic and some advantages of these methods, compared to the standard paradigm of using finite difference for the time discretisation, have been put in evidence. Theses advantages can obviously be of different nature (theoretical, energetical, computational or related to the algorithmic setup of FE models) and they are related to the type of formulation and type of problem. Different approaches exist but the pioneer work of [3, 4] on a space-time discontinuous Galerkin formulation for elastodynamics is of particular importance because the authors have shown that these methods can be reliable and efficient to approach space and time discontinuous solutions for wave propagation problems. Furthermore, the proposed paradigm of time (or space and time) discontinuous formulation can be applied to other context than elastodynamics of solids. The computation of fluid flow is one example among others, e.g. [5,6,7] for 2D problems and [8, 9] for the first 3D problems with moving meshes. These works gave rise to many theoretical and numerical developments, see for instance [10,11,12,13,14,15,16,17,18] and references therein. For linear viscoelasticity a time continuous Galerkin formulation was proposed by [19, 20] and it was shown that space-time finite elements can offer new possibilities (space-time parallelization and space-time refinement) and better performance (with higher order space-time function at least for simple problems). To the best of our knowledge the case of nonlinear time dependent behaviors has not been investigated in the context of space-time methods excepted in [21] where a space-time approach is proposed for elasto-plasticity and gradient damage models but not explored from the numerical point of view. However, this numerical aspect is crucial to study the stability and the reliability of the proposed formulations. Furthermore, the formalism proposed in [21] raises certain theoretical questions related to causality, since the authors have used the Hamiltonian principle as a guidance to formulate space-time potential which is not adapted to non-conservative systems. Therefore, the main idea of this paper is to propose a generic way of developing space-time formulations adapted to this context and to evaluate the interest of using such methods both from a theoretical and a numerical point of view. As already mentioned we are particularly interested in time discontinuous formulations as time dependent behaviors can exhibit very sharp solutions in time (in the case of viscoplasticity for instance).

The isogeometric analysis (IGA), e.g. [22, 23], is a very interesting alternative to standard FE models (with Lagrange or Hermite polynomials). It offers the possibility to play with both the polynomial order of the functions and the continuity order. It can also simplify the management of the mesh in some situations (with the restriction that local refinement requires specific developments) and it has been shown from many numerical tests in the literature that less degree of freedom are required to get the same quality of the numerical solution compared to standard FE (using similar interpolation order). As a consequence of these interesting numerical properties, some authors have developed space-time IGA models (ST-IGA), e.g. [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. In a previous work, we get interested into elastodynamics problems with such methods, see [39]. We have proposed a continuous space-time formulation with specific stabilization terms that allowed us to investigate linear and nonlinear (incompressible) elasticity. Through comparisons between ST-FE and ST-IGA models we have shown that ST-IGA can achieve better numerical performances.

In most FE codes, in the case of time dependent behaviors formulated in the differential form (i.e. with internal variables), the set of evolution equations is resolved locally (at Gauss points). Therefore, there is at least two type of integration schemes for the time, one at the global level that treats the conservation equations of the problem and one at the local level for the evolution equations. The relevance of such an approach can be questioned especially if the system of equations exhibit a strong coupling with temporal sharp responses. There are some alternative proposals in the literature as for instance the LATIN method (e.g. [40]). Moreover, increasing the order (for the time discretisation) of one of the two schemes (local or global) does not ensure an optimal rate of convergence regarding the time. In this work we propose to consider the resolution of both type of equations simultaneously with the same time integration scheme. This paradigm leads to the fact that the internal variables should be treated at the same level than the primary variables (i.e. at nodes or control points) and therefore leads to multi-field formulations and larger global systems to be solved (with similar memory usage, since the internal variables must be be stored regardless the method used). In this paper, we compare the results obtained with ST-IGA models and standard FE models and we discuss the new possibilities offer by such methods but we do not explicitly address the question of the numerical performance. This should be done in a separate work with numerical examples for which we can explicitly measure the quality of the time dependent solutions.

As mentioned previously we propose a new route for constructing time discontinuous formulations within the context of ST-IGA methods. The main original feature of this work is the ability to obtain in a generic way this type of formulation especially for the time continuity terms. No supplementary numerical parameters are needed. We limit ourselves to the case of standard generalized materials (or bi-potential models) but this class of behavior is sufficiently large to study many different applications. In this paper we consider two examples: a small strain visco-plastic model with isotropic hardening and a finite-strain viscoelastic model (in a nearly incompressible context). Both cases are restricted to the quasi-static case but the proposed formulation can be extended to other situations (dynamics or with multi-physics coupling for instance).

The paper is organized as follows. In a first section we present the space-time formulation. In the second section, the case of a viscoplastic behavior is discussed. The nonlinear viscoelastic model is detailed in the third section. Finally, the last section is devoted to numerical examples for both material models.

2 Space-time formulations

2.1 Time and space weak forms for standard materials in quasi-static situation

We consider the case of time-dependent behaviors formulated as standard generalized materials (see [41]). The material behavior is therefore defined from the knowledge of two potentials: a strain energy, $\psi$, and a (pseudo-)potential of dissipation, $\varphi$. These potentials are defined from a set of thermodynamics variables which are all local in time and space (there exist a non-local version of standard generalized materials, see [42], that could be used in a similar way than the one proposed in this paper). The $i^{th}$ internal variable is here denoted $\alpha _i(\textbf{x},t)$, $\textbf{x}$ is the position of material point in the space domain $\Omega \in \mathbb {R}^d$, and $t\in [0,T]$.

For the sake of simplicity, in this section, we restrict ourselves to the small strain case and we assume isothermal and adiabatic states. Therefore the primary fields of interest are $\{\textbf{u},\alpha _i\}$. To establish a weak form of an equilibrium problem, we start from the definition of a potential and the main equations are obtained by studying the stationarity of the potential. This is similar to what were done in previous studies especially the so called incremental variational formulations, see for instance [43,44,45] among others. In these works, the authors proposed variational formulations which are based on an algorithmic assumption that the rate of the primary variables are constant over a time increment. However in the general case (for instance in dynamics or without any assumption in time), the establishment of a variational form for dissipative problems is only limited to very specific cases due to the irreversibility in time, see for instance [46, 47] and references therein for interesting discussions about possible variational formulations for these specific cases.

Here, we propose to consider the following space-time potential¹:

$$\begin{aligned} \begin{aligned} \Pi =&\int _\mathcal {Q}\left( \rho {\dot{\psi }}(\varvec{\varepsilon },\alpha _i)-\varphi (\dot{\alpha _i})\right) dQ + \int _\mathcal {Q}\dot{\textbf{u}}\textbf{f}dQ \\&+\int _{\mathcal {P}}\dot{\textbf{u}}\textbf{t}dP \end{aligned} \end{aligned}$$

(1)

where $\mathcal {Q}=\Omega \times [0,T]$ and $\mathcal {P}=\Gamma \times [0,T]$ are space-time domain and boundary. We define the Sobolev spaces $H^{l,k}(Q)=\lbrace u \in L^2(Q): \partial _x^\beta u \in L^2 (Q) \;\forall \; \beta \;\text {with}\; 0\le \vert \beta \vert \le l, \partial ^i_t \in L^2(Q), i=0,\ldots ,k\rbrace$ of functions defined in the space-time cylinder Q, where $L^2 (Q)$ denotes the space of square-integrable functions, $\beta =(\beta _1,\ldots ,\beta _d)$ is a multi-index with non-negative integers, $\vert \beta \vert =\beta _1+\ldots +\beta _d,\; \partial _x^\beta u:= \partial _{x_1}^{\beta _1} \partial _{x_2}^{\beta _2} \ldots \partial _{x_d}^{\beta _d} u\;\text {with}\;\partial _{x_i}^{\beta _i}\bullet =\partial ^{\beta _i}\bullet /\partial {x_i}^{\beta _i} \; \text {and} \; \partial ^i_t u:=\partial ^i u/\partial t^i$.

Lets study the stationarity conditions of the previous potential. One can easily obtain its first variation (assuming that the external forces do not depend on primary variables):

$$\begin{aligned} \delta \Pi =&\int _\mathcal {Q}\rho \frac{\partial {\dot{\psi }}}{\partial \varvec{\varepsilon }}:\delta \varvec{\varepsilon }dQ+ \int _\mathcal {Q}\delta {\dot{\textbf{u}}}\textbf{f}dQ+\int _{\mathcal {P}}\delta {\dot{\textbf{u}}}\textbf{t}dP\nonumber \\&+\sum _{i=1}^n\int _\mathcal {Q}\rho \frac{\partial {\dot{\psi }}}{\partial \alpha _i}\delta \alpha _i - \frac{\partial {\varphi }}{\partial \dot{\alpha _i}}\delta \dot{\alpha _i} dQ \end{aligned}$$

(2)

The primary variables $\{ \textbf{u},\alpha _i\}$ live in $\{\mathcal {H}^u,\mathcal {H}^\alpha \}$ and their variations are such that $\delta \textbf{u}\in \mathcal {H}^u_0$ and $\delta \alpha _i\in \mathcal {H}^\alpha _0$ where:

$$\begin{aligned} \mathcal {H}^u&=\{ \textbf{u} \in H^{1,1}(Q),\, \textbf{u}=g(t)\text { on } \Gamma _{u}\,, \nonumber \\ {}&\textbf{u}(x,t=0)= \textbf{u}_0(x)\} \nonumber \\ \mathcal {H}^\alpha&=\{ \alpha \in H^{0,1}(Q)\,, \alpha (x,t=0)= \alpha _0(x) \} \nonumber \\ \mathcal {H}^u_0&=\{ \textbf{u} \in H^{1,1}(Q),\, \textbf{u}=0\text { on } \Gamma _{u}\,, \nonumber \\&\textbf{u}(x,t=0)= 0,\textbf{u}(x,t=T)= 0\} \nonumber \\ \mathcal {H}^\alpha _0&=\{ \alpha \in H^{0,1}(Q)\,, \nonumber \\&\alpha (x,t=0)= 0,\alpha (x,t=T)= 0 \} \end{aligned}$$

(3)

It has to be noted here that compared to incremental variational theories we have made a supplementary hypothesis of regularity for the rate of the primary variables over time.

By using integrations by parts, one can obtain from Eq. (2):

$$\begin{aligned} \begin{aligned} \delta \Pi =&\int _\Omega \rho \left[ \frac{\partial \psi }{\partial \varvec{\varepsilon }}:\delta \varvec{\varepsilon }\right] _0^T d\Omega -\int _\mathcal {Q}\rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}:\varvec{\varepsilon }(\delta \dot{\textbf{u}}) +\\&\int _\mathcal {Q}\delta {\dot{\textbf{u}}}\textbf{f}dQ+\int _{\mathcal {P}}\delta {\dot{\textbf{u}}}\textbf{t}dP - \\&\sum _{i=1}^n \int _\Omega \rho \left[ \frac{\partial \psi }{\partial \alpha _i}\delta \alpha _i\right] _0^Td\Omega -\sum _{i=1}^n\int _\mathcal {Q}\rho \frac{\partial \psi }{\partial \alpha _i}\delta \dot{\alpha _i}dQ \\&- \sum _{i=1}^n\int _\mathcal {Q}\frac{\partial {\varphi }}{\partial \dot{\alpha _i}}\delta \dot{\alpha _i} dQ \end{aligned} \end{aligned}$$

(4)

The terms integrated over time are null due to homogeneous conditions on the time boundaries and we are left with the following conditions of stationarity:

$$\begin{aligned} \delta _{\textbf{u}} \Pi\equiv & {} \, \int _{\mathcal {Q}} \rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}:\delta {\dot{\varvec{\varepsilon }}}dQ -\int _\mathcal {Q}\delta \dot{\textbf{u}}\textbf{f}dQ \nonumber \\{} & {} -\int _{\mathcal {P}}\delta \dot{\textbf{u}}\textbf{t}dP=0 \end{aligned}$$

(5)

$$\begin{aligned} \delta _{{\alpha _i}} \Pi\equiv & {} \, \int _{\mathcal {Q}}\left( \rho \frac{\partial \psi }{\partial \alpha _i} + \frac{\partial \varphi }{\partial \dot{\alpha _i} } \right) \delta \dot{\alpha _i} dQ=0 \end{aligned}$$

(6)

The local form of the previous equations corresponds to the conservation of the linear momentum and to the normality rules, such that for $\textbf{x}\in \Omega$ and $t\in [0,T]$:

$$\begin{aligned} \text {div}\varvec{\sigma }= & {} \textbf{f} \end{aligned}$$

(7)

$$\begin{aligned} A_i= & {} \frac{\partial \varphi }{\partial \dot{\alpha _i} } \quad i\in [1,n] \end{aligned}$$

(8)

along with the Neumann boundary conditions:

$$\begin{aligned} \varvec{\sigma }\textbf{n}=\textbf{t} \quad \forall \textbf{x}\in \Gamma _{\varvec{\sigma }} \end{aligned}$$

(9)

where $\varvec{\sigma }=\rho \partial \psi /\partial \varvec{\varepsilon }$ is the stress and $A_i=-\rho \partial \psi /\partial \alpha _i$ is the $i^{th}$ thermodynamical force associated to the rate of the $i^{th}$ internal variable, $\dot{\alpha _i}$.

By using a partial Legendre transform, we can also slightly modify the potential defined at Eq. (1), so as to use the dual dissipation potential $\varphi ^\star (A_i)$ instead of the primal one, $\varphi (\dot{\alpha _i})$. One can for instance chose the following potential:

$$\begin{aligned} \Pi ^\star =&\int _\mathcal {Q}\left( \rho {\dot{\psi }}(\varvec{\varepsilon },\alpha _i)-A_i\dot{\alpha _i}+\varphi ^\star (A_i)\right) dQ \nonumber \\&+ \int _\mathcal {Q}\dot{\textbf{u}}\textbf{f}dQ+\int _{\mathcal {P}}\dot{\textbf{u}}\textbf{t}dP \end{aligned}$$

(10)

Without any particular difficulties, one can show that the conditions of stationarity associated to the previous dual potential are:

$$\begin{aligned} \delta _{\textbf{u}} \Pi ^\star\equiv & {} \, \int _{\mathcal {Q}} \varvec{\sigma }:\delta {\dot{\varvec{\varepsilon }}}dQ- \int _\mathcal {Q}\delta \dot{\textbf{u}}\textbf{f}dQ \nonumber \\{} & {} -\int _{\mathcal {P}}\delta \dot{\textbf{u}}\textbf{t}dP=0 \end{aligned}$$

(11)

$$\begin{aligned} \delta _{\alpha _i} \Pi ^\star\equiv & {} \, \int _{\mathcal {Q}}\left( A_i + \frac{\partial \psi }{\partial \alpha _i } \right) \delta \dot{\alpha _i} dQ=0 \end{aligned}$$

(12)

$$\begin{aligned} \delta _{A_i} \Pi ^\star\equiv & {} \, \int _{\mathcal {Q}}\left( \dot{\alpha _i} - \frac{\partial \varphi ^\star }{\partial A_i } \right) \delta A_i dQ=0 \end{aligned}$$

(13)

As previously, we recover the local form of the first momentum conservation and the dual normality rules. Equations (5)–(6) or (11)–(13) constitute a generic space-time primal or dual formulation adapted to quasi-static dissipative problems. These forms can be used to formulate space-time finite-elements.

2.2 Space-time finite-element (or IGA) discretisation: time continuous Galerkin form

We first consider the case of a time and space continuous discretisation that will allow us to introduce the various notations and operators needed for the development of space-time elements. Lets consider a finite discretisation, denoted $Q^h$, of the space-time cylinder Q with either finite elements (Lagrange approximation) or isogeometric analysis (NURBS approximation), $Q^h_e$ denotes the restriction of $Q^h$ to an element. The primary fields of interest are also approximated with the same functions (i.e. polynomials or NURBS), such as we can define on an element:

$$\begin{aligned} \textbf{u}^h_e(\textbf{x},t)=\textbf{N}_u(\textbf{x},t)\textbf{d}^u_e, \quad {\alpha _i^h}_e(\textbf{x},t)=\textbf{N}_\alpha (\textbf{x},t)\textbf{d}^\alpha _e \end{aligned}$$

(14)

where $\textbf{d}^u,\textbf{d}^\alpha$ are the global vectors containing the degree of freedom over the space-time domain and $\textbf{d}^u_e,\textbf{d}^\alpha _e$ the restriction of these vectors to an element. Therefore, the rate of the primary fields are simply defined from (we denote respectively, by $\textbf{B}^t$ the time, or by $\textbf{B}^x$ the space gradient operators, that contains the derivatives of the previous shape functions):

$$\begin{aligned} \dot{\textbf{u}}^h_e(\textbf{x},t)=\textbf{B}_u^t(\textbf{x},t)\textbf{d}^u_e, \quad \dot{\alpha _i}^h_e(\textbf{x},t)=\textbf{B}_\alpha ^t(\textbf{x},t)\textbf{d}^\alpha _e \end{aligned}$$

(15)

We also define the approximation of the strain and the strain rate as follows:

$$\begin{aligned} \varvec{\varepsilon }=\textbf{B}_u^{x}\textbf{d}^u_e, \quad {{\dot{\varvec{\varepsilon }}}}=\textbf{B}_u^{t,x}\textbf{d}^u_e \end{aligned}$$

(16)

It can be remarked that as we used the second derivatives of the space-time approximation functions, these functions should be at last of order 2 for the kinematic field.

Introducing approximated fields at Eq. (5) and (6), one can obtain the following weak form of the equilibrium and evolution laws:

$$\begin{aligned} \Pi ^h_{,d^u}&\equiv \mathcal {A}_e \left( \int _{\mathcal {Q}^h_e} {\textbf{B}_u^{t,x}}^T \left( \rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}\right) dQ \right. - \nonumber \\&\left. \int _{\mathcal {Q}^h_e}{\textbf{B}_u^t}^T\textbf{f}^h dQ-\int _{\mathcal {P}^h_e}{\textbf{B}_u^t}^T \textbf{t}^h dP \right) = \textbf{0} \end{aligned}$$

(17)

$$\begin{aligned} \Pi ^h_{,d^\alpha }&\equiv \mathcal {A}_e \left( \int _{\mathcal {Q}^h_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial \psi }{\partial \alpha _i}+\frac{\partial \varphi }{\partial \dot{\alpha _i}} \right) dQ \right) = \textbf{0} \end{aligned}$$

(18)

The system at Eqs. (17) and (18) is a nonlinear system that can be solved with a standard Newton scheme:

$$\begin{aligned} \left\{ \begin{array}{c} \textbf{d}^u \\ \textbf{d}^\alpha \end{array}\right\} \Leftarrow \left\{ \begin{array}{c} \textbf{d}^u \\ \textbf{d}^\alpha \end{array}\right\} - \left[ \begin{array}{cc} \Pi ^h_{,d^ud^u} &{} \Pi ^h_{,d^u d^\alpha } \\ \Pi ^h_{,d^\alpha d^u} &{} \Pi ^h_{,d^\alpha d^\alpha } \end{array}\right] ^{-1} \left\{ \begin{array}{c} \Pi ^h_{,d^u} \\ \Pi ^h_{,d^\alpha } \end{array}\right\} \end{aligned}$$

(19)

where:

$$\begin{aligned} \Pi ^h_{,d^u d^u}&= \mathcal {A}_e\int _{\mathcal {Q}^h_e} {\textbf{B}_u^{t,x}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \varvec{\varepsilon }^2}\right) {\textbf{B}_u^{x}} dQ \end{aligned}$$

(20)

$$\begin{aligned} \Pi ^h_{,d^u d^\alpha }&= \mathcal {A}_e \int _{\mathcal {Q}^h_e} {\textbf{B}_u^{t,x}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \varvec{\varepsilon }\partial \alpha _i}\right) {\textbf{N}_\alpha } dQ \end{aligned}$$

(21)

$$\begin{aligned} \Pi ^h_{,d^\alpha d^u}&= \mathcal {A}_e\int _{\mathcal {Q}^h_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \alpha _i\partial \varvec{\varepsilon }}\right) {\textbf{B}_u^{x}} dQ \end{aligned}$$

(22)

$$\begin{aligned} \Pi ^h_{,d^\alpha d^\alpha }&= \mathcal {A}_e\int _{\mathcal {Q}^h_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \alpha _i^2}\right) {\textbf{N}_\alpha } dQ + \end{aligned}$$

(23)

$$\begin{aligned}&\mathcal {A}_e\int _{\mathcal {Q}^h_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial ^2 \varphi }{\partial \dot{\alpha _i}^2}\right) {\textbf{B}_\alpha ^t} dQ \end{aligned}$$

(24)

The tangent operator of the Newton scheme is non-symmetric as a consequence of the time irreversibility. Similar developments can be made with the dual potential formulation presented previously.

2.3 Space-time finite-element (or IGA) discretisation: time-discontinuous Galerkin form

The previous space-time continuous form is not adapted for practical applications, especially when solutions are localized in space and time. An alternative solution is to define a time-discontinuous form.

Considering a partition of the time domain in N intervals, such that $t_1=0<t_2<..<t_n<t_{N+1}=T$. Taking a time interval $]t_n,t_{n+1}[$ one can define a space-time slab $\mathcal {Q}_n$ such that: $\mathcal {Q}_n=\Omega \times ]t_n,t_{n+1}[$ and $\mathcal {P}_n=\Gamma \times ]t_n,t_{n+1}[$. We assume that the fields are discontinuous over the time slabs, such that the temporal jumps are defined by

$$\begin{aligned} \begin{aligned}&[[\textbf{u}(\textbf{x},t_n)]]=\textbf{u}(\textbf{x},t_n^+)-\textbf{u}(\textbf{x},t_n^-), \\&[[\alpha _i((\textbf{x},t_n)]]=\alpha _i(\textbf{x},t_n^+)-\alpha _i(\textbf{x},t_n^-) \end{aligned} \end{aligned}$$

(25)

where $\textbf{u}(\textbf{x},t_n^+),\alpha _i(\textbf{x},t_n^+)$ denote values at time $t_n$ on $\mathcal {Q}_n$ and $\textbf{u}(\textbf{x},t_n^-),\alpha _i(\textbf{x},t_n^-)$ are values at the same time on $\mathcal {Q}_{n-1}$. The space-time discretisation $Q^h$ is defined from the union of the discretisation of each time slab: $Q^h=\cup _{n=1}^N Q^h_n$. We propose to consider here the following modified space-time potential:

$$\begin{aligned} \begin{aligned} \Pi _{DG}=&\sum _{n=1}^N\left( \int _{\mathcal {Q}_n} \left( \rho {\dot{\psi }}(\varvec{\varepsilon },\alpha _i)-\varphi (\dot{\alpha _i})\right) dQ \right. \\&+ \left. \int _{\mathcal {Q}_n}\dot{\textbf{u}}\textbf{f}dQ+\int _{\mathcal {P}_n}\dot{\textbf{u}}\textbf{t}dP \right) \\&+\sum _{n=2}^N \int _{\mathcal {B}_n} [[\rho \psi (\varvec{\varepsilon },\alpha _i)]]dB \\&+\int _{\mathcal {B}_1}\beta _u\frac{1}{2}(\textbf{u}(\textbf{x},t_1^+)-\textbf{u}_0(\textbf{x}))^2dB\\ {}&+\int _{\mathcal {B}_1}\beta _i\frac{1}{2}(\alpha _i(\textbf{x},t_1^+)-\alpha _0(\textbf{x}))^2 dB \end{aligned} \end{aligned}$$

(26)

where $\mathcal {B}_n$ stands for the space domain $\Omega$ at time $t_n^+$. It can be seen from the previous expression that we have chosen to distinguish the continuity terms that apply on the first time slab (to account of initial condition on the primary fields in a weak sense) and those who apply on the other time slabs (continuity of primary fields between each slabs in a weak and energetic sense). The parameters $\beta _u,\beta _i$ have been introduced for dimensioning purpose. For the sake of simplicity, we will take them to be equal to one (with appropriate dimension) in the following.

Taking the variation of $\Pi _{DG}$ and regrouping terms it can be seen that the solution can be determined iteratively time slab by time slab (the solution on a time slab depends only on the values of the previous time slab). More precisely, on $\mathcal {Q}_1$, we have:

$$\begin{aligned} \delta _{\textbf{u}} \Pi _{DG} \equiv&\, \int _{\mathcal {Q}_1} \rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}:\delta {\dot{\varvec{\varepsilon }}}dQ - \int _{\mathcal {Q}_1}\delta \dot{\textbf{u}}\textbf{f}dQ \nonumber \\&-\int _{\mathcal {P}_1}\delta \dot{\textbf{u}}\textbf{t}dP \nonumber \\&- \int _{\mathcal {B}_1} (\textbf{u}(\textbf{x},t_1^+)-\textbf{u}_0(\textbf{x})) \delta \textbf{u}^+ dB =0 \end{aligned}$$

(27)

$$\begin{aligned} \delta _{{\alpha _i}} \Pi _{DG} \equiv&\, \int _{\mathcal {Q}_1}\left( \rho \frac{\partial \psi }{\partial \alpha _i} + \frac{\partial \varphi }{\partial \dot{\alpha _i} } \right) \delta \dot{\alpha _i} dQ \nonumber \\&-\int _{\mathcal {B}_1} (\alpha _i(\textbf{x},t_1^+)-\alpha _0(\textbf{x})) \delta \alpha _i^+ dB =0 \end{aligned}$$

(28)

and on $\mathcal {Q}_n$ with $2\le n\le N$, we have:

$$\begin{aligned} \delta _{\textbf{u}} \Pi _{DG} \equiv&\, \int _{\mathcal {Q}_n} \rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}:\delta {\dot{\varvec{\varepsilon }}}dQ \nonumber \\&- \int _{\mathcal {Q}_n}\delta \dot{\textbf{u}}\textbf{f}dQ-\int _{\mathcal {P}_n}\delta \dot{\textbf{u}}\textbf{t}dP \nonumber \\&- \int _{\mathcal {B}_n} [[\rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}]]:\delta {\varvec{\varepsilon }^+} dB =0 \end{aligned}$$

(29)

$$\begin{aligned} \delta _{{\alpha _i}} \Pi _{DG} \equiv&\, \int _{\mathcal {Q}_n}\left( \rho \frac{\partial \psi }{\partial \alpha _i} + \frac{\partial \varphi }{\partial \dot{\alpha _i} } \right) \delta \dot{\alpha _i} dQ \nonumber \\&-\int _{\mathcal {B}_n} [[\rho \frac{\partial \psi }{\partial \alpha _i}]]:\delta {\alpha _i^+} dB =0 \end{aligned}$$

(30)

As mentioned previously, it can be seen that this formulation consists of imposing the continuity of the thermodynamical forces $\{\sigma ,A_i\}$ at the time interfaces for $n\ge 2$.

Each time slab $\mathcal {Q}_n$, is discretized with space-time elements and its discretisation is denoted by $\mathcal {Q}_n^h$ and ${\mathcal {Q}_n^h}_e$ for a restriction to the element e. For the sake of simplicity we assume that the space discretisation is the same on each time intervals. However, it is also possible to consider situations where a space-time slab is discretized (meshed) in time and space and eventually re-mesh (locally refine) during time slab iterations. One can therefore obtain a mix between the time continuous and discontinuous formulations (in each time slab one can have space-time continuous finite elements). The fields are approximated on a time slab as defined by Eqs. (14), (15), (16). For the first time slab we obtain

$$\begin{aligned} \Pi ^h_{DG,d^u} \equiv&\, \mathcal {A}_e\left( \int _{{\mathcal {Q}^h_1}_e} {\textbf{B}_u^{t,x}}^T \left( \rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}\right) dQ \right. \nonumber \\&\left. - \int _{{\mathcal {Q}^h_1}_e}{\textbf{B}_u^t}^T\textbf{f}^h dQ-\int _{{\mathcal {P}^h_1}_e}{\textbf{B}_u^t}^T \textbf{t}^h dP\right) \nonumber \\ {}&-\mathcal {A}_e\int _{{\mathcal {B}_1}_e}{\textbf{N}_u^+}^T(\textbf{u}^+-\textbf{u}_0)dB = \textbf{0} \end{aligned}$$

(31)

$$\begin{aligned} \Pi ^h_{DG,d^\alpha } \equiv&\, \mathcal {A}_e\left( \int _{{\mathcal {Q}^h_1}_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial \psi }{\partial \alpha _i}+\frac{\partial \varphi }{\partial \dot{\alpha _i}} \right) dQ\right. \nonumber \\&\left. -\int _{{\mathcal {B}_1}_e}{\textbf{N}_\alpha ^+}^T(\mathbf {\alpha }_i^+-\mathbf {\alpha }_0)dB \right) = \textbf{0} \end{aligned}$$

(32)

For the $n^{th}$ time slab (with $n\ge 2$), we have

$$\begin{aligned} \Pi ^h_{DG,d^u} \equiv&\, \mathcal {A}_e\left( \int _{{\mathcal {Q}^h_n}_e} {\textbf{B}_u^{t,x}}^T \left( \rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}\right) dQ \right. \nonumber \\&\left. - \int _{{\mathcal {Q}^h_n}_e}{\textbf{B}_u^t}^T\textbf{f}^h dQ-\int _{{\mathcal {P}^h_n}_e}{\textbf{B}_u^t}^T \textbf{t}^h dP\right) \nonumber \\ {}&-\mathcal {A}_e\int _{{\mathcal {B}_n}_e}{{\textbf{B}_u^x}^+}^T[[\varvec{\sigma }]]dB = \textbf{0} \end{aligned}$$

(33)

$$\begin{aligned} \Pi ^h_{DG,d^\alpha } \equiv&\, \mathcal {A}_e\left( \int _{{\mathcal {Q}^h_n}_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial \psi }{\partial \alpha _i}+\frac{\partial \varphi }{\partial \dot{\alpha _i}} \right) dQ \right. \nonumber \\&\left. -\int _{{\mathcal {B}_n}_e}{\textbf{N}_\alpha ^+}^T[[A_i]]dB \right) = \textbf{0} \end{aligned}$$

(34)

On each time slab, the non linear system of Eqs. (31)–(32) or (33)–(34) is solved with a Newton scheme. The tangent operator is similar to the one define in the previous section, for the nth time slab (with $n\ge 2$), we have

$$\begin{aligned} \Pi ^h_{DG,d^u d^u} =&\, \mathcal {A}_e\int _{{\mathcal {Q}^h_n}_e} {\textbf{B}_u^{t,x}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \varvec{\varepsilon }^2}\right) {\textbf{B}_u^{x}} dQ \nonumber \\&- \mathcal {A}_e\int _{{\mathcal {B}_n}_e} {{\textbf{B}_u^x}^+}^T \left( \rho \frac{\partial ^2 \psi }{\partial \varvec{\varepsilon }^2}\right) {{\textbf{B}_u^{x}}^+} dB \end{aligned}$$

(35)

$$\begin{aligned} \Pi ^h_{DG,d^u d^\alpha } =&\, \mathcal {A}_e \int _{{\mathcal {Q}^h_n}_e} {\textbf{B}_u^{t,x}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \varvec{\varepsilon }\partial \alpha _i}\right) {\textbf{N}_\alpha } dQ \nonumber \\&- \mathcal {A}_e\int _{{\mathcal {B}_n}_e} {{\textbf{B}_u^x}^+}^T \left( \rho \frac{\partial ^2 \psi }{\partial \varvec{\varepsilon }\partial \alpha _i}\right) {{\textbf{N}_\alpha }^+} dB\end{aligned}$$

(36)

$$\begin{aligned} \Pi ^h_{DG,d^\alpha d^u} =&\, \mathcal {A}_e\int _{{\mathcal {Q}^h_n}_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \alpha _i\partial \varvec{\varepsilon }}\right) {\textbf{B}_u^{x}} dQ \nonumber \\&- \mathcal {A}_e\int _{{\mathcal {B}_n}_e} {{\textbf{N}_\alpha }^+}^T \left( \rho \frac{\partial ^2 \psi }{\partial \alpha _i\partial \varvec{\varepsilon }}\right) {{\textbf{B}_u^x}^+} dB\end{aligned}$$

(37)

$$\begin{aligned} \Pi ^h_{DG,d^\alpha d^\alpha } =&\, \mathcal {A}_e\int _{{\mathcal {Q}^h_n}_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \alpha _i^2}\right) {\textbf{N}_\alpha } dQ \nonumber \\&+ \mathcal {A}_e\int _{{\mathcal {Q}^h_n}_e} {\textbf{B}_\alpha ^{t}}^T \left( \rho \frac{\partial ^2 \varphi }{\partial \dot{\alpha _i}^2}\right) {\textbf{B}_\alpha ^t} dQ \nonumber \\&- \mathcal {A}_e\int _{{\mathcal {B}_n}_e} {\textbf{N}_\alpha ^{+}}^T \left( \rho \frac{\partial ^2 \psi }{\partial \alpha _i^2}\right) {\textbf{N}_\alpha ^+} dB \end{aligned}$$

(38)

As mentioned previously, hybrid forms (continuous space-time element within a discontinuous formulation) may have an interest to develop parallel space-time resolutions within a discontinuous space time formulation. In this work we will not investigate such hybrid forms and we only consider cases where the time slab are meshed with only one element in time. The space time mesh can therefore be viewed as an extrusion in time of the spatial mesh.

3 Viscoplasticity with isotropic hardening

As a first example of application we consider the case of an isotropic viscoplastic behavior with isotropic hardening. The set of internal variables are the plastic strain and the hardening parameter $\alpha _i:=\{\varvec{\varepsilon }_p,p\}$. The Helmoltz energy and the pseudo-potential of dissipation are chosen as follows

$$\begin{aligned} \rho \psi (\varvec{\varepsilon },\varvec{\varepsilon }_p,p)=&\, \mu (\varvec{\varepsilon }-\varvec{\varepsilon }_p)^D:(\varvec{\varepsilon }-\varvec{\varepsilon }_p)^D\nonumber \\&+ \frac{k}{2} tr(\varvec{\varepsilon })^2 + k_m R(p) \end{aligned}$$

(39)

$$\begin{aligned} \varphi ^\star (\textbf{S},A_p)=&\,\frac{1}{2\eta }\left\langle \sqrt{\frac{3}{2}}||\textbf{S}|| +A_p - \sigma _0 \right\rangle ^2 \end{aligned}$$

(40)

where $\mu ,k,k_m,\eta ,\sigma _0$ are material parameters, $\textbf{S}$ and $A_p$ are the thermodynamical forces associated to $\varvec{\varepsilon }_p$ and p and $<.>$ are the Macaulay brackets. The isotropic hardening function, R(p), can be chosen from available potentials in the literature but for the sake of simplicity and without any particular limitations we consider in the following linear hardening, i.e $R(p)=1/2p^2$. Introducing these potentials into the mixed form defined at Eq. (10), one can obtain the following weak space-time form

$$\begin{aligned} \delta _{\textbf{u}} \Pi ^\star \equiv&\int _{\mathcal {Q}} \varvec{\sigma }:\delta {\dot{\varvec{\varepsilon }}}dQ- \int _\mathcal {Q}\delta \dot{\textbf{u}}\textbf{f}dQ \nonumber \\&-\int _{\mathcal {P}}\delta \dot{\textbf{u}}\textbf{t}dP=0 \end{aligned}$$

(41)

$$\begin{aligned} \delta _{\varvec{\varepsilon }_p} \Pi ^\star \equiv&\int _{\mathcal {Q}}\left( \textbf{S} - 2\mu (\varvec{\varepsilon }-\varvec{\varepsilon }_p)^D \right) :\delta \dot{\varvec{\varepsilon }_p} dQ=0 \end{aligned}$$

(42)

$$\begin{aligned} \delta _{p} \Pi ^\star \equiv&\int _{\mathcal {Q}}\left( A_p + k_m R'(p) \right) \delta {\dot{p}} dQ=0 \end{aligned}$$

(43)

$$\begin{aligned} \delta _{\textbf{S}} \Pi ^\star \equiv&\, \int _{\mathcal {Q}}\left( \dot{\varvec{\varepsilon }_p} - \Lambda \sqrt{\frac{3}{2}}\textbf{n} \right) : \delta \textbf{S} dQ=0 \end{aligned}$$

(44)

$$\begin{aligned} \delta _{A_p} \Pi ^\star \equiv&\, \int _{\mathcal {Q}}\left( {\dot{p}} - \Lambda \right) \delta A_p dQ=0 \end{aligned}$$

(45)

where $\Lambda =\frac{1}{\eta }\left\langle \sqrt{\frac{3}{2}}||\textbf{S}|| +A_p - \sigma _0 \right\rangle$ is the plastic multiplier, $\textbf{n}=\textbf{S}/||\textbf{S}||$ is the plastic flow direction, and $\varvec{\sigma }=2\mu (\varvec{\varepsilon }-\times \varvec{\varepsilon }_p)^D+k\text {tr}(\varvec{\varepsilon })\textbf{1}$ is the Cauchy stress.

The previous weak form can be discretized with space-time elements but rather to consider a five field form, we proposed here to consider the following reduced weak form:

$$\begin{aligned}&\int _{\mathcal {Q}} \varvec{\sigma }:\delta {\dot{\varvec{\varepsilon }}}dQ- \int _\mathcal {Q}\delta \dot{\textbf{u}}\textbf{f}dQ-\int _{\mathcal {P}}\delta \dot{\textbf{u}}\textbf{t}dP=0 \end{aligned}$$

(46)

$$\begin{aligned}&\int _{\mathcal {Q}}\left( \dot{\varvec{\varepsilon }_p} - \tilde{\Lambda } \sqrt{\frac{3}{2}}{\tilde{\textbf{n}}} \right) :(2\mu \delta \varvec{\varepsilon }_p) dQ=0 \end{aligned}$$

(47)

$$\begin{aligned}&\int _{\mathcal {Q}}\left( {\dot{p}} - \tilde{\Lambda } \right) k_m R'(p)\delta p dQ=0 \end{aligned}$$

(48)

We have implicitly assumed that the equalities $\textbf{S}=\varvec{\sigma }^D$ and $A_p=-k_m R'(p)$ hold and we use the following definition: $\tilde{\Lambda }=\frac{1}{\eta }\left\langle \sqrt{\frac{3}{2}}||\varvec{\sigma }^D|| -k_mR'(p) - \sigma _0 \right\rangle$ and ${\tilde{\textbf{n}}}=\varvec{\sigma }^D/||\varvec{\sigma }^D||$. The set of Eqs. (46)–(48) do not derive from conditions of stationarity but the Euler equations are the same than the one obtain from the system defined at Eqs. (41)–(45).

The deviatoric structure of the plastic strain field allows to determine one diagonal component of the tensor by the knowledge of the two other. For instance, in 2D, on a space-time element we have the following approximation

$$\begin{aligned} \begin{aligned} {\varvec{\varepsilon }_p}^h_e=\textbf{N}_{\varvec{\varepsilon }}(\textbf{x},t)\textbf{d}^{\varvec{\varepsilon }}_e, \quad {\varvec{\varepsilon }_p}^h_e=\left[ \begin{array}{c} {\varvec{\varepsilon }_p}_{11} \\ {\varvec{\varepsilon }_p}_{22} \\ {\varvec{\varepsilon }_p}_{12} \\ {\varvec{\varepsilon }_p}_{33}\end{array}\right] , \\ \textbf{N}_{\varvec{\varepsilon }}=\left[ \begin{array}{ccc} N(\textbf{x},t) &{} 0 &{} 0 \\ 0 &{} N(\textbf{x},t) &{} 0 \\ 0 &{} 0 &{} N(\textbf{x},t) \\ -N(\textbf{x},t) &{} -N(\textbf{x},t) &{} 0 \end{array}\right] \end{aligned} \end{aligned}$$

(49)

The derivation of the time continuous formulation defined at Eqs. (46)–(48) allows to define the following elemental tangent operator:

$$\begin{aligned} \textbf{K}^e=\left[ \begin{array}{ccc} \textbf{k}^e_{uu} &{} \textbf{k}^e_{u\varvec{\varepsilon }_p} &{} 0 \\ \textbf{k}^e_{\varvec{\varepsilon }_p u} &{} \textbf{k}^e_{\varvec{\varepsilon }_p \varvec{\varepsilon }_p} &{} \textbf{k}^e_{\varvec{\varepsilon }_p p} \\ \textbf{k}^e_{pu} &{} \textbf{k}^e_{p\varvec{\varepsilon }_p} &{} \textbf{k}^e_{pp} \end{array}\right] \end{aligned}$$

(50)

with

$$\begin{aligned}&\textbf{k}^e_{uu}=\int _{\mathcal {Q}_e^h} {\textbf{B}_u^{t,x}}^T \left( 2\mu \mathbb {P} + k \textbf{1}\otimes \textbf{1} \right) {\textbf{B}_u^{x}}dQ \end{aligned}$$

(51)

$$\begin{aligned}&\textbf{k}^e_{u{\varvec{\varepsilon }_p}}=\int _{\mathcal {Q}_e^h} {\textbf{B}_u^{t,x}}^T \left( - 2\mu \mathbb {P} \right) {\textbf{N}_{\varvec{\varepsilon }}} dQ \end{aligned}$$

(52)

$$\begin{aligned}&\textbf{k}^e_{{\varvec{\varepsilon }_p}u}= \int _{\mathcal {Q}_e^h} {\textbf{N}_{\varvec{\varepsilon }}}^T \left( 2\mu \left( -\frac{3}{2}H(f)\frac{\mu }{\eta } \textbf{n}\otimes \textbf{n} \right. \right. \nonumber \\&\qquad \qquad \left. \left. - \Lambda \sqrt{\frac{3}{2}}\frac{2\mu }{\Vert \varvec{\sigma }^D\Vert } ( \mathbb {I}-\textbf{n}\otimes \textbf{n})\right) :\mathbb {P}\right) {\textbf{B}_u^{x}} dQ \end{aligned}$$

(53)

$$\begin{aligned}&\textbf{k}^e_{{\varvec{\varepsilon }_p}{\varvec{\varepsilon }_p}} = \int _{\mathcal {Q}_e^h} {\textbf{N}_{\varvec{\varepsilon }}}^T \left( 2\mu \left( \frac{3}{2}H(f)\frac{\mu }{\eta } \textbf{n}\otimes \textbf{n} \right. \right. \nonumber \\&\qquad \qquad \left. \left. + \Lambda \sqrt{\frac{3}{2}}\frac{2\mu }{\Vert \varvec{\sigma }^D\Vert } ( \mathbb {I}-\textbf{n}\otimes \textbf{n})\right) :\mathbb {P}\right) {\textbf{B}_u^{x}} dQ \nonumber \\&\qquad \qquad + \int _{\mathcal {Q}_e^h} 2\mu {\textbf{N}_{\varvec{\varepsilon }}}^T \textbf{B}_{\varvec{\varepsilon }}^t dQ \end{aligned}$$

(54)

$$\begin{aligned}&\textbf{k}^e_{{\varvec{\varepsilon }_p}{p}}=\int _{\mathcal {Q}_e^h} {\textbf{N}_{\varvec{\varepsilon }}}^T \left( \frac{6\mu }{2}H(f)\frac{k_m}{\eta }R''(p) \textbf{n} \right) \textbf{N}_{p} dQ \end{aligned}$$

(55)

$$\begin{aligned}&\textbf{k}^e_{{p}{u}}= \int _{\mathcal {Q}_e^h} {\textbf{N}_{p}}^T \left( -H(f)k_m R'(p)\frac{2\mu }{\eta }\sqrt{\frac{3}{2}}\textbf{n}:\mathbb {P}\right) {\textbf{B}_u^{x}} dQ \end{aligned}$$

(56)

$$\begin{aligned}&\textbf{k}^e_{{p}{\varvec{\varepsilon }_p}}= \int _{\mathcal {Q}_e^h}{\textbf{N}_{p}}^T \left( H(f)k_m R'(p)\frac{2\mu }{\eta }\sqrt{\frac{3}{2}}\textbf{n}\right) {\textbf{N}_{\varvec{\varepsilon }_p}} dQ \end{aligned}$$

(57)

$$\begin{aligned}&\textbf{k}^e_{{p}{p}}= \int _{\mathcal {Q}_e^h}{\textbf{N}_{p}}^T\left( H(f)k_m R'(p)\sqrt{\frac{3}{2}}\frac{k_m}{\eta }R''(p)\right. \nonumber \\&\qquad \qquad \left. - \tilde{\Lambda } k_m R''(p) \right) \textbf{N}_{p} dQ + \int _{\mathcal {Q}_e^h} {\textbf{N}_{p}}^T\textbf{B}_{p}^t dQ \end{aligned}$$

(58)

where H() is the Heaviside function and $f=\sqrt{\frac{3}{2}}||\varvec{\sigma }^D|| -k_mR'(p) - \sigma _0$ is the yield function, $\mathbb {I}$ is the fourth order identity tensor and $\mathbb {P}=(\mathbb {I}-(1/3)\textbf{1}\otimes \textbf{1})$ is the deviatoric projector.

For the time discontinuous formulation we proceed as presented in the previous section. On the first time slab, $Q_1$, we have

$$\begin{aligned}&\int _{\mathcal {Q}_1} \varvec{\sigma }:\delta {\dot{\varvec{\varepsilon }}}dQ- \int _{\mathcal {Q}_1}\delta \mathbf {\dot{u}}\textbf{f}dQ-\int _{\mathcal {P}_1}\delta \dot{\textbf{u}}\textbf{t}dP \nonumber \\&\qquad - \int _{\mathcal {B}_1} (\textbf{u}(\textbf{x},t_1^+)-\textbf{u}_0(\textbf{x}))(2\mu \delta \textbf{u}^+ )dB =0 \end{aligned}$$

(59)

$$\begin{aligned}&\int _{\mathcal {Q}_1}\left( \dot{\varvec{\varepsilon }_p} - \tilde{\Lambda } \sqrt{\frac{3}{2}}{\tilde{\textbf{n}}} \right) :(2\mu \delta \varvec{\varepsilon }_p) dQ \nonumber \\&\qquad - \int _{\mathcal {B}_1} (\varvec{\varepsilon }_p(\textbf{x},t_1^+)-\varvec{\varepsilon }_{p_0}(\textbf{x})): ( 2\mu \delta \varvec{\varepsilon }_p^+) dB =0 \end{aligned}$$

(60)

$$\begin{aligned}&\int _{\mathcal {Q}_1}\left( {\dot{p}} - \tilde{\Lambda } \right) k_m R'(p)\delta p dQ \nonumber \\ {}&- \int _{\mathcal {B}_1} (p(\textbf{x},t_1^+)-p_0(\textbf{x})) ( k_m R'(p) \delta p^+) dB =0 \end{aligned}$$

(61)

where $\varvec{\varepsilon }_{p_0}$ and $p_0$ are values of the fields at $t=0$. For the $n^{th}$ time slab, we obtain

$$\begin{aligned}&\int _{\mathcal {Q}_n} \varvec{\sigma }:\delta {\dot{\varvec{\varepsilon }}}dQ- \int _{\mathcal {Q}_n}\delta \mathbf {\dot{u}}\textbf{f}dQ-\int _{\mathcal {P}_n}\delta \mathbf {\dot{u}}\textbf{t}dP \nonumber \\&\qquad - \int _{\mathcal {B}_n} [[\varvec{\sigma }]]:\delta \varvec{\varepsilon }^+dB =0 \end{aligned}$$

(62)

$$\begin{aligned}&\int _{\mathcal {Q}_n}\left( \dot{\varvec{\varepsilon }_p} - \tilde{\Lambda } \sqrt{\frac{3}{2}}{\tilde{\textbf{n}}}{} {\textbf {}} \right) :(2\mu \delta \varvec{\varepsilon }_p) dQ \nonumber \\&\qquad - \int _{\mathcal {B}_n} [[\textbf{S}]]:\delta \varvec{\varepsilon }_p^+ dB =0 \end{aligned}$$

(63)

$$\begin{aligned}&\int _{\mathcal {Q}_n}\left( {\dot{p}} - \tilde{\Lambda } \right) k_m R'(p)\delta p dQ- \int _{\mathcal {B}_n} [[A_p]] \delta p^+ dB =0 \end{aligned}$$

(64)

The tangent operator on each time slab is the same as the one presented previously complemented by the time continuity terms. It can be remarked that this formulation does not allows to consider the limit case $\eta =0$ which seems natural as a purely plastic (quasi-static) problem is only implicitly time dependent (due to the fact that the loads can depends on time).

4 Nearly incompressible nonlinear viscoelasticity (Zener model)

For this example, we extend the previous concepts to the finite strain case. The strain energy is defined from: the isochoric left Cauchy Green tensor, ${{\bar{\textbf{C}}}}$, the $i^{th}$ elastic isochoric left Cauchy-Green tensor, ${{\bar{\textbf{C}}_e}}$, and the hydrostatic pressure, q. To define isochoric tensors we used the so-called volumic/isochoric splitting of the deformation gradient, $\textbf{F}$:

$$\begin{aligned} \textbf{F}={{\bar{\textbf{F}}}}(J^{1/3}\textbf{1}) \end{aligned}$$

(65)

where $J=\det \textbf{F}$ is the volume variation.

The elastic intermediate configuration is obtained from the multiplicative split of the isochoric deformation gradient (e.g. [48, 49]):

$$\begin{aligned} {{\bar{\textbf{F}}}}={{\bar{\textbf{F}}_e}}{\bar{\textbf{F}}_v} \end{aligned}$$

(66)

The left Cauchy-Green tensors and the Green-Lagrange strain are defined such as:

$$\begin{aligned} {{\bar{\textbf{C}}}}= & {} {{\bar{\textbf{F}}}}^\text {T}{{\bar{\textbf{F}}}}\end{aligned}$$

(67)

$$\begin{aligned} {{\bar{\textbf{C}}_e}}= & {} {{\bar{\textbf{F}}_e}}^{\text {T}}{{\bar{\textbf{F}}_e}}\end{aligned}$$

(68)

$$\begin{aligned} \textbf{E}= & {} \frac{1}{2}(\textbf{C}-\textbf{I}) \end{aligned}$$

(69)

The strain energy is assumed to depend on ${{\bar{\textbf{C}}}},{{\bar{\textbf{C}}_e}}$ and q this last variable can be viewed as the hydrostatic pressure (for more details see [50]). The pseudo potential of dissipation is assumed to depend only on ${{{\dot{\bar{\textbf{C}}}_v}}}$.

For this application, the potential at Eq. (1) is slightly modified as follows:

$$\begin{aligned} \Pi =&\int _{\mathcal {Q}_0}\left( \rho _0 {\dot{\psi }}({{\bar{\textbf{C}}}},{{\bar{\textbf{C}}_e}},q)-\rho _0{\dot{\beta }}(q,J)-\varphi ({{{\dot{\bar{\textbf{C}}}_v}}})\right) dQ \nonumber \\&+ \int _{\mathcal {Q}_0}\dot{\textbf{u}}\textbf{f}dQ+\int _{\mathcal {P}_0}\dot{\textbf{u}}\textbf{t}dP \end{aligned}$$

(70)

where $\beta$ is a potential that relates q and J (in the present case it can be obtained from a partial Legendre transform of the Helmoltz free energy), $\mathcal {Q}_0=\Omega _0\times [0,T]$ where $\Omega _0$ is the initial space domain and $\mathcal {P}_0=\Gamma _0\times [0,T]$ where $\Gamma _0$ is the initial space boundary, $\textbf{f}$ and $\textbf{t}$ are assumed to be defined in terms of non deformed units in space, $\rho _0$ is the initial density. We assume that $\beta$ is defined from:

$$\begin{aligned} \beta (q,J)=q\frac{1-J}{\rho _0} \end{aligned}$$

(71)

After some calculus and using similar time integration by part as in the previous sections we obtain the following weak form of the Euler equations from the stationarity of the potential:

$$\begin{aligned} \delta _u\Pi =&\,\int _{\mathcal {Q}_0}\textbf{S}:\delta \dot{\textbf{E}} dQ-\int _{\mathcal {Q}_0}\textbf{f}\delta \dot{\textbf{u}}dQ-\int _{\mathcal {P}_0}\textbf{t}\delta \dot{\textbf{u}}dP \end{aligned}$$

(72)

$$\begin{aligned} \delta _q\Pi =&\,\int _{\mathcal {Q}_0}\rho _0\left( -\frac{\partial \psi }{\partial q}+\frac{\partial \beta }{\partial q}\right) \delta {\dot{q}} dQ \end{aligned}$$

(73)

$$\begin{aligned} \delta _{{{\bar{\textbf{C}}_v}}}\Pi =&\int _{\mathcal {Q}_0}\left( \rho _0 {\bar{\textbf{F}}_v}^{{-1}}{{\bar{\textbf{C}}_e}}\frac{\partial \psi }{\partial {{\bar{\textbf{C}}_e}}}{\bar{\textbf{F}}_v}^{\text {-T}} -\frac{\partial \varphi }{\partial {{{\dot{\bar{\textbf{C}}}_v}}}}\ \right) :\delta {{{\dot{\bar{\textbf{C}}}_v}}}dQ \end{aligned}$$

(74)

where, the second Piola-Kirchoff stress $\textbf{S}$ is defined as follows

$$\begin{aligned} \textbf{S}=2\rho _0 \left( \frac{\partial \psi }{\partial {{\bar{\textbf{C}}}}}+{\bar{\textbf{F}}_v}^{{-\text {T}}}\frac{\partial \psi }{\partial {{\bar{\textbf{C}}_e}}}{\bar{\textbf{F}}_v}^{{-1}}\right) :\mathbb {P}_{{\bar{\textbf{C}}}}+ \rho _0\frac{\partial \beta }{\partial J} J\textbf{C}^{-1} \end{aligned}$$

(75)

with ${\mathbb {P}}_{{{\bar{\textbf{C}}}}}$ a deviatoric projector for the Lagrangian configuration, defined as follows:

$$\begin{aligned} \mathbb {P}_{{\bar{\textbf{C}}}}=J^{-2/3}\left( \mathbb {I} - \frac{1}{3}\textbf{C} \otimes \textbf{C}^{-1} \right) \end{aligned}$$

(76)

Limiting ourselves to the case of isotropy, we adopt the following forms for the strain energy and the pseudo potential of dissipation:

$$\begin{aligned} \rho _0\psi ({{\bar{\textbf{C}}}},{{\bar{\textbf{C}}_e}},q)=&\,c_{10}(I_1({{\bar{\textbf{C}}}})-3)+c_{01}(I_2({{\bar{\textbf{C}}}})-3)\nonumber \\&+ \mu (I_1({{\bar{\textbf{C}}_e}}) -3) -k \left( \exp (\frac{q}{k})-1 \right) + q \end{aligned}$$

(77)

$$\begin{aligned} \varphi ({{{\dot{\bar{\textbf{C}}}_v}}})=&\, \frac{\eta }{2} {{{\dot{\bar{\textbf{C}}}_v}}}:{{{\dot{\bar{\textbf{C}}}_v}}}\end{aligned}$$

(78)

where $c_{10},\mu ,k,\eta$ are material parameters and $I_1,I_2$ are the two first strain invariants. As a consequence, the Euler equations (72)–(74) can be rewritten as:

$$\begin{aligned} \delta _u\Pi =&\,\int _{\mathcal {Q}_0}\varvec{\Pi }:\delta \dot{\textbf{F}} dQ-\int _{\mathcal {Q}_0}\textbf{f}\delta \dot{\textbf{u}}dQ-\int _{\mathcal {P}_0}\textbf{t}\delta \dot{\textbf{u}}dP \end{aligned}$$

(79)

$$\begin{aligned} \delta _q\Pi =&\,\int _{\mathcal {Q}_0}\left( \exp (\frac{q}{k})-J\right) \delta {\dot{q}} dQ \end{aligned}$$

(80)

$$\begin{aligned} \delta _{{{\bar{\textbf{C}}_v}}}\Pi =&\,\int _{\mathcal {Q}_0}\left( \mu {{\bar{\textbf{C}}_v}^{{-1}}}{{\bar{\textbf{C}}}}{{\bar{\textbf{C}}_v}^{{-1}}}-\eta {{{\dot{\bar{\textbf{C}}}_v}}}\right) :\delta {{{\dot{\bar{\textbf{C}}}_v}}}dQ \end{aligned}$$

(81)

The first Euler equation has been slightly modified compare to Eq. (72), we have here considered the first Piola-Kirchoff stress $\varvec{\Pi }$ instead of the second Piola-Kirchoff stress ($\varvec{\Pi }=\textbf{F}\textbf{S}$). This allows a more concise expression of the elemental approximation of the virtual strain rate $\delta \dot{\textbf{F}}$ rather than $\delta \dot{\textbf{E}}$. The first Piola-Kirchoff stress is in this case:

$$\begin{aligned}\begin{aligned} \varvec{\Pi }=&\,2 \left( c_{10}{{\bar{\textbf{F}}}}+c_{01}{{\bar{\textbf{F}}}}(I_1\textbf{1}-{{\bar{\textbf{C}}}}) +\mu {{\bar{\textbf{F}}}}{{\bar{\textbf{C}}_v}^{{-1}}}\right) :\mathbb {P}_{{\bar{\textbf{F}}}}-q J\textbf{F}^{-\text {T}} \end{aligned} \end{aligned}$$

where $\mathbb {P}_{{\bar{\textbf{F}}}}$ is

$$\begin{aligned} \mathbb {P}_{{\bar{\textbf{F}}}}=J^{-1/3}\left( \mathbb {I} - \frac{1}{3}\textbf{F}\otimes \textbf{F}^{-T} \right) \end{aligned}$$

(82)

As in the previous case of viscoplasticity, the space-time approximation of the $i^{th}$ viscous strain tensor, can be obtained from the knowledge of space-time shape functions. For the 2D case, we have adopted the following approximation (to simplify the definition of initial conditions we approximate ${{\bar{\textbf{C}}_v}}-\textbf{1}$ rather that ${{\bar{\textbf{C}}_v}}$ which is perfectly equivalent)

$$\begin{aligned} \begin{aligned}&{{{\bar{\textbf{C}}_{v_e}}^{h}}-\textbf{1}}=\textbf{N}_{{{\bar{\textbf{C}}_v}}}(\textbf{X},t)\textbf{d}^{{{\bar{\textbf{C}}_v}}}_e, \, {{{\bar{\textbf{C}}_{v_e}}^{h}}-\textbf{1}}=\left[ \begin{array}{c} {\bar{C}}_{v_{11}}-1 \\ {\bar{C}}_{v_{22}}-1 \\ {\bar{C}}_{v_{12}} \\ {\bar{C}}_{v_{33}}-1 \end{array}\right] , \\ {}&\textbf{N}_{{{\bar{\textbf{C}}_v}}}=\left[ \begin{array}{cccc} N(\textbf{x},t) &{} 0 &{} 0 &{} 0\\ 0 &{} N(\textbf{x},t) &{} 0 &{} 0\\ 0 &{} 0 &{} N(\textbf{x},t) &{} 0 \\ 0 &{} 0 &{} 0&{} N(\textbf{x},t) \end{array}\right] \end{aligned} \end{aligned}$$

(83)

From the previous approximation it can be deduced that:

$$\begin{aligned} \begin{aligned}&\delta {{\bar{\textbf{C}}_{v_e}}^{h}}=\textbf{N}_{{{\bar{\textbf{C}}_v}}}(\textbf{X},t)\delta \textbf{d}^{{{\bar{\textbf{C}}_v}}}_e, \quad {{{\dot{\bar{\textbf{C}}}_v}}}=\textbf{B}^t_{{\bar{\textbf{C}}_v}}\textbf{d}^{{{\bar{\textbf{C}}_v}}}_e, \\&\textbf{B}^t_{{{\bar{\textbf{C}}_v}}}=\left[ \begin{array}{cccc} \frac{\partial N(\textbf{x},t)}{\partial t} &{} 0 &{} 0 &{} 0\\ 0 &{} \frac{\partial N(\textbf{x},t)}{\partial t} &{} 0 &{} 0\\ 0 &{} 0 &{} \frac{\partial N(\textbf{x},t)}{\partial t} &{} 0 \\ 0 &{} 0 &{} 0&{} \frac{\partial N(\textbf{x},t)}{\partial t} \end{array}\right] \end{aligned} \end{aligned}$$

(84)

It can be seen that the chosen approximation does not take into account of the isobaric constraint. The condition $\det ({{\bar{\textbf{C}}_v}})=1$ is therefore not guaranty from a numerical point of view. We choose to slightly modify the strain energy at Eq. (77) by adding a perturbation term such that:

$$\begin{aligned} \rho _0\tilde{\psi }({{\bar{\textbf{C}}}},{{\bar{\textbf{C}}_e}},q)=\rho _0\psi ({{\bar{\textbf{C}}}},{{\bar{\textbf{C}}_e}},q)+\frac{\alpha }{2}(\det ({{\bar{\textbf{C}}_v}})-1)^2 \end{aligned}$$

(85)

where $\alpha$ is a perturbation parameter. As a consequence, Euler Eq. (81) is modified such that:

$$\begin{aligned} \begin{aligned} \delta _{{{\bar{\textbf{C}}_v}}}\Pi =&\,\int _{\mathcal {Q}_0}\left( \mu {{\bar{\textbf{C}}_v}^{{-1}}}{{\bar{\textbf{C}}}}{{\bar{\textbf{C}}_v}^{{-1}}}-\eta {{{\dot{\bar{\textbf{C}}}_v}}}\right) :\delta {{{\dot{\bar{\textbf{C}}}_v}}}dQ+ \\&\alpha \int _{\mathcal {Q}_0} (\det ({{\bar{\textbf{C}}_v}})-1)\det ({{\bar{\textbf{C}}_v}}){{\bar{\textbf{C}}_v}^{{-1}}}:\delta {{{\dot{\bar{\textbf{C}}}_v}}}dQ\end{aligned} \end{aligned}$$

(86)

The elemental tangent operator takes the following form with this formulation (for the sake of simplicity we consider here the case where $\alpha =0$):

$$\begin{aligned} \textbf{K}^e=\left[ \begin{array}{ccc} \textbf{k}^e_{uu} &{} \textbf{k}^e_{uq} &{} \textbf{k}^e_{u {{\bar{\textbf{C}}_v}}} \\ \textbf{k}^e_{qu} &{} \textbf{k}^e_{qq} &{} 0 \\ \textbf{k}^e_{{{\bar{\textbf{C}}_v}}u} &{} 0 &{} \textbf{k}^e_{{{\bar{\textbf{C}}_v}}{{\bar{\textbf{C}}_v}}} \end{array}\right] \end{aligned}$$

(87)

with

(88)

(89)

(90)

(91)

(92)

(93)

(94)

In the previous expressions we have used the following tensorial operators: $(\textbf{A}\otimes \textbf{B})_{ijkl}=A_{ij}B_{kl}$, $(\textbf{A}\obar \textbf{B})_{ijkl}=A_{ik}B_{jl}$ and .

It has to be noted that the operator $\textbf{B}_{u}^x$ is not identical to the one of the previous section on viscoplasticity. It corresponds here to the Lagrangian gradient operator of the displacement field, such that:

$$\begin{aligned} \nabla _\textbf{X}\textbf{u}_h= \textbf{B}_{u}^x \textbf{d}_e^u, \quad \text {and}\quad \nabla _\textbf{X}\dot{\textbf{u}}_h= \textbf{B}_{u}^{t,x} \textbf{d}_e^u \end{aligned}$$

(95)

For the time discontinuous formulation we apply the same principle as established at Sect. 2.3. On the first time slab, $Q_1$, we have (to obtain shorter expressions we consider here the case $\alpha =0$)

$$\begin{aligned}&\int _{\mathcal {Q}_1} \varvec{\Pi }:\delta {\dot{\textbf{F}}}dQ- \int _{\mathcal {Q}_1}\delta \dot{\textbf{u}}\textbf{f}dQ-\int _{\mathcal {P}_1}\delta \dot{\textbf{u}}\textbf{t}dP \nonumber \\&\qquad - \int _{\mathcal {B}_1} (\textbf{u}(\textbf{x},t_1^+)-\textbf{u}_0(\textbf{x}))k \delta \textbf{u}^+ dB =0 \end{aligned}$$

(96)

$$\begin{aligned}&\int _{\mathcal {Q}_1}\left( \exp ( \frac{q}{k})-J\right) \delta {\dot{q}} \nonumber \\&\qquad - \int _{\mathcal {B}_1}\frac{1}{k} (q(\textbf{x},t_1^+)-q_0(\textbf{x})) \delta q^+ dB =0 \end{aligned}$$

(97)

$$\begin{aligned}&\int _{\mathcal {Q}_1}\left( \mu {{\bar{\textbf{C}}_v}^{{-1}}}{{\bar{\textbf{C}}}}{{\bar{\textbf{C}}_v}^{{-1}}}-\eta {{{\dot{\bar{\textbf{C}}}_v}}}\right) :\delta {{{\dot{\bar{\textbf{C}}}_v}}}dQ \nonumber \\&\qquad - \int _{\mathcal {B}_1} \mu ({{\bar{\textbf{C}}_v}}(\textbf{x},t_1^+)-{\bar{\textbf{C}}_{v_0}}(\textbf{x})): \delta {\bar{\textbf{C}}_v}^{+}dB =0 \end{aligned}$$

(98)

where ${\bar{\textbf{C}}_{v_0}}$ and $q_0$ are values of the fields at $t=0$. For the $n^{th}$ time slab, we obtain

$$\begin{aligned}&\int _{\mathcal {Q}_n} \varvec{\Pi }:\delta {\dot{\textbf{F}}}dQ- \int _{\mathcal {Q}_n}\delta \dot{\textbf{u}}\textbf{f}dQ-\int _{\mathcal {P}_n}\delta \dot{\textbf{u}}\textbf{t}dP \nonumber \\&- \int _{\mathcal {B}_n} [[\varvec{\Pi }]]:\delta \textbf{F}^+dB =0 \end{aligned}$$

(99)

$$\begin{aligned}&\int _{\mathcal {Q}_n}\left( \exp ( \frac{q}{k})-J\right) \delta {\dot{q}} dQ \nonumber \\&- \int _{\mathcal {B}_n} [[\exp ( \frac{q}{k})]]\delta q^+ dB =0 \end{aligned}$$

(100)

$$\begin{aligned}&\int _{\mathcal {Q}_n}\left( \mu {{\bar{\textbf{C}}_v}^{{-1}}}{{\bar{\textbf{C}}}}{{\bar{\textbf{C}}_v}^{{-1}}}-\eta {{{\dot{\bar{\textbf{C}}}_v}}}\right) :\delta {{{\dot{\bar{\textbf{C}}}_v}}}dQ \nonumber \\&- \int _{\mathcal {B}_n} \frac{\mu }{2}[[{{\bar{\textbf{C}}_v}^{{-1}}}{{\bar{\textbf{C}}}}{{\bar{\textbf{C}}_v}^{{-1}}}]] :\delta {\bar{\textbf{C}}_v}^{+}dB =0 \end{aligned}$$

(101)

The tangent operator on each time slab is the same as the one presented previously complemented by the time continuity terms.

5 Numerical applications

5.1 Homogeneous extension in the case of viscoplasticity

We consider the case of a homogeneous monotonic tension test in plane strain. The initial conditions are $\textbf{u}_0(x)=\textbf{0}$, $\varvec{\varepsilon }_{p_0}(x)= \textbf{0}$, $p_0(x)=0$. We impose a displacement controlled tension on one side of a unit square with $\textbf{u}(t)=v\times t$ and $v=0.16\,$mm/s. The final time is $T=0.25\,$s. Symmetry boundary conditions applied on two other sides allow to obtain an homogeneous strain. The material parameter are given in Table 1

Table 1 Viscoplastic material parameters

We have proceeded to a time convergence study by computing the stress/strain response for two type of model. The first model is a standard 2D finite element model with quadratic fully integrated elements for the space domain and a radial return method for the local time integration of the constitutive equations (see for instance [51] for a detailed version of the radial return method). The radial return method is based on a first order implicit time approximation, for linear hardening laws the implicit resolution on a time increment leads to a linear problem whereas for nonlinear hardening laws local newton resolutions are needed. The time increment is controlled in the global resolution, each increment is solved by a standard newton scheme and we obtain a global/local scheme (global=equilibrium equation, local=evolutions equations).

The second model is an IGA time-discontinuous space-time model. The NURBS elements are also fully integrated in space and time and we consider approximations of order 2 and 3 in space and time. The time increment is here the size of the ST-IGA element in time. We can also play with the order of approximation and the continuity order (i.e. between NURBS elements) in space and time. Our implementation of the IGA does not allow us to consider different continuity orders or approximation orders for space and time separately for one field. Therefore we propose to compare the results of 3 cases. For the first one, every field (i.e. $\textbf{u},\varvec{\varepsilon }_p,\alpha$) is approximated with the same functions. For the second one, the plastic strain and the hardening parameters are approximated with lower degree functions (in space and time) than the kinematic field, we denote this by ST-IGA LD in the following figures. For the third one, the plastic strain and the hardening parameters are approximated with lower continuity functions (in space and time), we denote this by ST-IGA LC in the following figures.

For all models, we compute a stress error integrated over time. This error is defined by the following formula

$$\begin{aligned} e=\int _{t=0}^{T=0.25} \left( \varvec{\sigma }(t)-\varvec{\sigma }_{ref}(t) \right) ^2 dt \end{aligned}$$

(102)

where $\varvec{\sigma }_{ref}(t)$ is a reference solution computed on a material point with the help of Mathematica (function NDSolve with a maximum time increment of $1e-5\,s$).

The results are given on Fig. 1. It can seen that the convergence of the FE model with the return radial scheme is of order 1 as expected. For the time discontinuous ST-IGA models we obtain optimal convergence rate of order 2 and 3 in the case where the fields have the same approximations functions and in the case for which a lower continuity for $\varvec{\varepsilon }_p$ and $\alpha$ is used in the approximation (compare to $\textbf{u}$). However, it can be seen that in the case of a lower degree for $\varvec{\varepsilon }_p$ and $\alpha$ (compare to $\textbf{u}$) we are limited by the lowest degree in time and the results are similar to the FE model.

It can be remarked that for $p=3$ in the case of the ST-IGA model the convergence is non uniform (so as for the finite element model for the larger time increments). The interest of the ST-IGA approach can be clearly seen on this figure: for an error of $e=1.e-2$ there is one order of magnitude for the time increment size between the ST-IGA model and the standard FE model (the order of convergence is better but the initial error is also lower).

Figure 2 illustrate the stress/strain responses obtained with the two models. It can be seen that the ST-IGA model exhibits an oscillating behavior in time after the yield stress which is particularly pronounced for the model with a lower degree in the approximation functions. These oscillations disappears far from the yield stress except for the lower order model. Obviously, for smaller time increments this oscillations become negligible and all models converge to the reference solution.

Fig. 1

$L_2$ error on the stress response computed from a reference obtained with Mathematica

Fig. 2

Stress/strain responses for the FE model and the ST-IGA

5.2 Shear localization in tension in the case of softening viscoplasticity

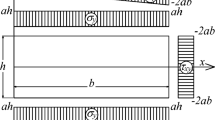
We now investigate a non homogeneous test case. The test corresponds to the extension of a rectangular 2D plate. The plate is $4\,$mm long and $2\,$mm large and we assume a plane strain hypothesis. The extension is imposed with a displacement of $0.28\,$mm at a constant rate of $0.6\,$mm/s on one side of the plate, the opposite side is clamped. For the hardening, we assume a linear hardening but with a softening behavior (i.e. $k_m<0$). The expected solution for this test is a localized cross shear plastic band started from the center. To correctly track this solution the yield stress of the element located in the center of the plate is reduced by 5%. Due to the symmetry conditions only a quarter of the plate is considered. The Fig. 3 shows the boundary conditions considered for this test. The material parameters used in this test are given in Table 2, the parameter $k_m$ is negative so as to obtain a softening hardening behavior.

Fig. 3

Plate extension: boundary conditions and dimensions

Table 2 Material parameters for softening viscoplasticity

Fig. 4

Force/displacement response for the plate extension for different mesh sizes (for space), the initial time increment is identical for all models: $dt_0=1.e{-3}\,$s (the time increment can be reduced or enlarged automatically during the iterations depending on convergence indicators)

Table 3 Value of the force for a displacement of $0.044\,$mm and for different time increments

As in the previous example, we propose here to compare the results of two type of models: time discontinuous ST-IGA models and standard IGA models with local integration of the viscoplastic flow rule with the radial return method. For the ST-IGA models we use as previously lower order of continuity (or lower degree) approximations for $\varvec{\varepsilon }_p$ and $\alpha$. Figure 4 shows the global force/displacement response of the 2D plate in extension. As expected, it can be seen that no mesh convergence (in space) is observed due to the fact that the localization of the shear band is directly related to the mesh size. It can be also remarked that ST-IGA and standard IGA models give very similar global results. The Table 3 gives a more detailed picture for the time convergence. The table report the value of the force for the maximum displacement and for three time increment. It can be seen that, as in the previous example, ST-IGA has a faster rate of convergence in time. ST-IGA and standard IGA do not converge exactly to the same value this is certainly due to the fact that the model are not strictly equivalent because we have a continuous field approximation for $\varvec{\varepsilon }_p$ and $\alpha$ in ST-IGA which is not the case in the standard IGA model (where $\varvec{\varepsilon }_p$ and $\alpha$ are only computed locally at each Gauss points and not approximated continuously over elements).

In the previous example we have seen that the convergence of the ST-IGA models is not optimal when the fields $\varvec{\varepsilon }_p,\alpha$ are approximated with functions of lower order than $\textbf{u}$ (ST-IGA LD) but it looks similar when we compare models with the same approximation functions or with lower continuity functions with similar degree for $\varvec{\varepsilon }_p,\alpha$ (ST-IGA LC). In this test, Fig. 5 clearly shows that only ST-IGA LC models can obtain the expected response. For the other two possibilities we see that we obtain unstable response with a drastic reduction for the step time. This result emphasis that controlling the continuity of the approximation with NURBS is of major importance in this type of multi-fields problems.

Fig. 5

Force/displacement responses for the plate extension with ST-IGA for different field approximations. LC=lower continuity for $\varvec{\varepsilon }_p, \alpha$, LD=lower degree for $\varvec{\varepsilon }_p, \alpha$ comparatively to $\textbf{u}$

Fig. 6

Field $\alpha$ for $u=0.045\,$mm with a similar mesh of 800 elements for both models

Fig. 7

Norm of the displacement field $\textbf{u}$ for $u=0.045\,$mm with a similar mesh of 800 elements for both models

Figures 6 and 7 show that the expected localized shear band is obtained with the ST-IGA LC model. Using the same mesh size for the space discretization, the shear band is very similar with ST-IGA compared to the standard IGA model with radial return integration for the viscoplastic evolution.

5.3 Homogeneous extension in the case of nonlinear viscosity

In a similar way that was done in Sect. 5.1, we investigate the case of an homogeneous extension. As previously we impose a time dependent displacement on one side of a unit square and symmetry boundary conditions on two other sides such as to obtain an homogeneous strain. The applied displacement is piecewise linear with $u(t)=\{0.8t/0.0625,\,\text {if}\,t\le 0.0625;0.8-0.8(t-0.0625)/0.0625,\,\text {if}\,0.0625<t\le 0.125\}$ such as to obtain a loading and unloading. The material parameter are given in Table 4.

We investigate the time convergence with the comparison of two models. The first one is a standard 2D finite element model with quadratic Lagrange elements (with full gauss integration) for displacement and linear discontinuous interpolation (between element) for the pressure. Pressure nodes are therefore condensed in the element formulation. The viscosity is solved locally, at Gauss points, with the help of a backward Euler scheme for the time integration and a local Newton scheme to resolve the nonlinear system that results from the time integration. The second model is a ST-IGA model with the time discontinuous formulation. The kinematic field and the viscous strain are approximated with the same NURBS functions of maximum continuity degree. For the pressure field we are limited with the stability condition, we adopt the same strategy as proposed in [52]. The pressure field is approximated on a coarser grid (for space only) than the other fields but with NURBS functions of the same degree and same continuity than the kinematic field. In practice we do not observe any stability problems due to the incompressibility. Compare to the case of viscoplasticity we do not investigate here the cases of lower degree or lower continuity for the viscosity (compare to the kinematic field). From numerical tests we do not observe any interest of using such approximations. To track the time convergence we adopt here a slightly different error. We define a stress error such that:

$$\begin{aligned} e=|\varvec{\sigma }(t=0.125)-\varvec{\sigma }_{ref}(t=0.125)| \end{aligned}$$

(103)

where $\varvec{\sigma }_{ref}(t)$ is a reference solution obtained with the help of NDSolve on Mathematica assuming a perfectly homogeneous strain/stress field (with a maximum time increment of $1e-5\,$s).

Table 4 Material parameters for nonlinear viscosity

The results are given in Fig. 8. As in the case of viscoplasticity we observe that the rate of (time) convergence are, at least locally, obtained as expected theoretically. ST-IGA models converge faster but are also more precise. It has to be noted that FE models with a time increment larger than 0.2 diverge systematically which is not the case of ST-IGA models. As in Fig. 1, one can also observe that the convergence is not uniform for ST-IGA model of order 3. We do not precisely know why, one possibility (if feasible) could be to investigate separately in the error the contribution of the continuity terms and the temporal integration inside the space-time element.

In Fig. 9, we have plotted the strain/stress responses obtained with the different models. It can be observed that the nonlinear stress/strain curves are perfectly captured by St-IGA models. Compare to viscoplasticity we do not observe oscillations in the responses.

Fig. 8

Stress error upon time increment for nonlinear viscosity

Fig. 9

Stress/strain response for the homogeneous tension test with nonlinear viscosity

5.4 Relaxation test on a plate with a hole in the case of nonlinear viscosity

We consider the case of a square plate of $2\,mmx2\,mm$ with a circular hole of $0.38\,mm$ radius in the center of the plate. The plate is clamped on one side and subjected to an extension on the opposite side imposed with a rigid displacement. The displacement is defined such that (relaxation): $u(t)=\{ 0.6t/0.1,\,\text {if }t\le 0.1; 0.6\,\text {if }t>0.1\}$. Due to symmetry conditions we consider only one quarter of the plate. The geometry and the boundary condition are schematized on Fig. 10. The same material parameters as in the previous example (see Table 4) are used. The test is in plane strain. The mesh for ST-IGA is obtained from a single patch representation with NURBS functions. The space mesh is shown at Fig. 11. The refinement is homogeneous and the space-time mesh is obtained as a simple extrusion operation of the space mesh. For this case the mesh building lead to degenerated elements at the top right corner and result in numerical artifacts when computing gradients. However for the test considered, this could be considered as unimportant and the solutions obtained with FE elements are very similar elsewhere excepted in the top right corner (non degenerated meshes are used for FE).

Fig. 10

Plate with hole relaxation test: boundary conditions and dimensions

Fig. 11

Space mesh for the plate with hole relaxation test

In this test we propose to investigate the impact of the numerical parameter $\alpha$ (perturbation parameter to impose $\det ({{\bar{\textbf{C}}_v}})=1$). We consider two models. The first one is a standard 2D FE model (as in the previous section) with a mixed formulation (quadratic interpolation for displacement and linear and discontinuous between elements for the pressure). In this model the viscosity is integrated with a backward euler scheme and no particular constraints are defined on $\det ({{\bar{\textbf{C}}_v}})$ for the time integration. The second model is a ST-IGA model of order 2 (with the time discontinuous formulation and a coarser mesh for the pressure field to ensure stability). For the ST-IGA model we consider the case $\alpha =0\,$MPa (similar to FE model: no restriction on $\det ({{\bar{\textbf{C}}_v}})$) and $\alpha >0\,$MPa.

On Fig. 12 we show the global relaxation of the plate for the different models (we plot the resulting force upon time). The mesh size for the space domain is similar for every models (the average mesh size is $0.022\,$mm), for the FE model the initial time increment is $\Delta t=1e-3\,$s and for the ST-IGA the initial mesh size in time is $\Delta t=3.3e-3\,$s (both the mesh size in time for ST-IGA and the time increment for FE can evolve depending on convergence). It can be first remarked that FE model and ST-IGA with $\alpha =0$ are perfectly in accordance. These models show pronounced nonlinear behavior at the end of the first step of loading and a very short stress relaxation. This nonlinear behavior is not observed when only the hyperelastic part of the model is used, indicating that a non expected behavior is obtained. A contrario, when $\alpha$ is not null we obtain a more expected behavior with a more progressive relaxation. It can also be remarked that $\alpha =1\,$MPa and $\alpha =10\,$MPa lead to the same response.

As suspected on the global response, the difference in terms of relaxation is due to the determinant of the viscous Cauchy-Green strain ${{\bar{\textbf{C}}_v}}$. Figure 13 illustrate the difference between the results obtained with a model without any particular restriction on the determinant (see Fig. 13a), after some iterations of integration the determinant can go far from its expected value of 1. However, incorporating in the formulation a penalization term can control the value of determinant (see Fig. 13b) with only small variations from the incompressible case. This result illustrates another advantage of space time methods: space-time formulation can incorporate specific penalization or stabilization terms in a straightforward way (in space and time).

Fig. 12

Force/time responses for the relaxation test for different values of the perturbation parameter $\alpha$

Fig. 13

Determinant of the viscous Cauchy-Green strain, $\det ({{\bar{\textbf{C}}_v}})$, at the end of the relaxation test on a plate with a hole (nonlinear viscoelastic behavior)

6 Conclusions

We proposed to investigate the interest of using space-time methods for nonlinear and time-dependent behaviors, formulated as standard generalized materials. This framework has enabled us to obtain space-time formulations that derive from the stationarity conditions of a space-time potential. This space-time potential exploits the convex structure behind the definition of a pseudo potential of dissipation. Moreover, by also exploiting the duality between thermodynamics forces and fluxes we have obtained formulations with natural primary variables (as for viscoplasticity for instance). The declination of time continuous or time discontinuous forms poses no major difficulties and can be done by introducing a modified potential that accounts of strain energy jumps at the time interfaces. Imposing the time continuity of the strain energy in the weak sense in the space-time potential leads in a straightforward manner to appropriate time continuity terms (with appropriate dimension and without adding any specific numerical parameter) at the interface even for multi-fields formulation. Numerical validated this approach by comparing space time results to standard finite-elements formulations. We can conclude from this study the following points. Firstly, space-time IGA allowed to obtain optimal rate of convergence. Therefore increasing the degree of interpolation of the space-time basis leads to higher order integration scheme without any supplementary effort of development. Secondly, the space-time formalisms have made it possible to introduce specific and supplementary constraints into the time integration. For instance in the case of nonlinear incompressible viscosity we were able to guaranty that the isochoric viscoelastic strain remain isochoric during the time integration. Thirdly, the isogeometric framework allows us to play on the order of continuity which help us to develop optimum approximations for the internal variables especially in the case of viscoplasticity. We were able to maintain the optimal order of convergence without obtaining instabilities due to the strain localization. These advantages open the way to new opportunities. Obviously, we can deal with more complex material models (with more internal variables). We can also extend the approach in a dynamics context and/or in a multi-physics framework without too many difficulties (at least from the point of view of the formulation, not from the numerical one). In this paper, we do not investigate the numerical performances as we think that many specific improvements must be taken into account with space-time methods before a comparison with standard finite-element makes sense (such as optimization of the integration in time, space-time parallelization, etc).