1 Introduction

Many real-world engineering structures can be categorized as thin-walled applications, and engineers often rely on computationally efficient shell elements to perform an initial analysis and determine the load-carrying capacity of the structure. While the linear elastic shell analysis is adopted in many cases, it is often insufficient due to the large-deformation nature of the problem or the nonlinear material behavior as a result of locally concentrated loading. In the latter, a high-fidelity elastoplastic constitutive model is needed to accurately capture the material degradation. An example of such a scenario encountered in engineering is low-cycle fatigue analysis, which deals with stresses beyond yielding and sophisticated material behaviors such as hardening. In such cases, a plasticity coupled shell analysis is required.

The incorporation of finite-to-large strain elastoplastic constitutive models into shell formulations is very challenging, and a variety of research efforts has been devoted to the advancement in this subject. In the modeling of the elastoplastic material response using thin shells (e.g., of the Kirchhoff–Love (KL) shell type), two approaches are typically adopted, one being the deployment of integration points in the through-thickness direction of the shell body and the use of 3D stress-based elastoplastic material models [1,2,3,4,5,6,7,8], and the other being the employment of stress resultant based plasticity models in which the constitutive material relations are directly formulated towards obtaining the stress resultants [9,10,11,12,13,14]. While the latter extends the 2D geometric description into constitutive models and seems to be a more straightforward path to take, the derivation of the inelastic constitutive models directly for stress resultants is rather complicated, even for the simplest case of \(J_2\) plasticity. The level of complexity arises when hardening is involved, leading to the so-called Ilyushin–Shapiro constitutive relations [13]. Due to the difficulties in the mathematical derivation and numerical implementation, researchers are widely in favor of the stress-based approach, where 3D plasticity models for solids with standard return mapping algorithms are directly applicable.

Although thin shell elements [15] are computationally efficient, they sometimes do not suffice in the complex structural design and analysis workflow, mainly due to the need to acquire 3D high-fidelity strains and stresses in order to comprehensively evaluate the structural integrity and multiaxial fatigue life [16, 17]. This, in turn, gives rise to the development of shell formulations of the continuum type [18,19,20,21,22,23] and the blended type [24,25,26,27,28], which features accurate predictions of the full 3D strain and stress tensors, including the components in the transverse directions and through the thickness of the shell body. Worth mentioning is a recently developed blended shell formulation [24,25,26] that couples KL shells and continuum shells in a non-matching and nonlinear analysis setting so that it can compute accurate 3D strains and stresses without compromising computational efficiency. The primary advantage of using continuum shells over solids to obtain high-fidelity 3D strains and stresses of thin-walled structures arises from the efficiency in the geometric modeling process. The continuum shells are formulated based on a reference surface, and therefore only the surface modeling of a thin-walled structure is needed. This greatly simplifies the modeling procedure compared to using solid elements, where a full 3D description of the geometry is required. An added benefit of the continuum shell approach is that it significantly eases the coupling mechanism between KL shells and the solid-like counterpart, since both are formulated under curvilinear coordinates with analogous definitions of surface tangential and normal vectors. More details of the coupling formulation can be found in Liu et al. [24].

As is commonly an issue in the analysis group, the process of geometry repair and the generation of an approximate finite element mesh from computer-aided design (CAD) consume the majority of the analysis time. This primarily results from the use of different technologies between the design and analysis parties and constitutes a major bottleneck to the interoperability between CAD and finite element analysis (FEA) technologies. Driven by the need in design and analysis alike, the advent of isogeometric analysis (IGA) [29] bridges the gap in the sense that it uses the same high-order spline basis functions to represent the original geometry and the physics-based solution fields in analysis. Moreover, the high-order continuities of splines offer other significant benefits beyond the perspective of exact geometric representations, such as the straightforward implementation of high-order differential operators [30,31,32,33,34], as is the case of Kirchhoff–Love thin shell formulations where \(C^1\) global smoothness is required [35,36,37,38,39,40,41,42]. Additionally, it has been shown that the use of spline-based IGA provides significantly improved per-degree-of-freedom solution accuracy over standard FEA [27, 31, 43,44,45,46,47,48,49,50,51,52], and the IGA approach has since been used to solve the most challenging science and engineering problems [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83]. Nevertheless, the development with regards to IGA-based plastic shell formulations has been rare. This includes a recently proposed isogeometric stress-based elastoplastic KL shell formulation with the plane stress assumption imposed in an iterative fashion [1, 2] and later applied to multi-patch analysis [84]. In addition, an isogeometric solid shell element formulated in an updated Lagrangian framework has been presented with emphasis on locking alleviation by resorting to the assumed natural strain technique [85], where the applied plasticity model pertains to the small strain regime.

The primary aim of this work is to extend the isogeometric large-deformation continuum shell formulation presented in Liu et al. [18] to the finite strain plasticity regime. The multiplicative decomposition of the deformation gradient into the elastic and plastic parts, along with the classical \(J_2\) von Mises plasticity with isotropic hardening [86], is adopted in a total Lagrangian framework. The standard backward Euler time integration scheme with return mapping is employed to solve the 3D elastoplastic constitutive equations.

This paper is organized as follows. In Sect. 2, we briefly review the isogeometric large-deformation continuum shell formulation. In Sect. 3, the finite strain plasticity model, along with details on the numerical implementation aspects, is given. A discussion on the adopted \(J_2\) plasticity model with isotropic hardening is also included. The proposed formulation is then applied in Sect. 4 to a variety of benchmark tests to demonstrate its accuracy and robustness. Finally, Sect. 5 concludes the paper with some remarks.

2 Isogeometric continuum shell formulation

We start the derivation by briefly introducing the isogeometric large-deformation continuum shell formulation [18, 24]. In the following, we use italic letters (e.g., a, A) to represent scalars, lowercase bold letters (e.g., \(\mathbf{a} \)) to represent vectors, and uppercase bold letters (e.g., \(\mathbf{A} \)) to represent second-order tensors. We refer the geometric variables denoted by to the reference (i.e., undeformed) configuration. Compact notations are used only when convenient for the presentation of general equations, while the detailed derivations are written in index notation. The Latin indices such as i, j, k,  and l take on values of \(\{1, 2, 3\}\), and the Greek indices such as \(\alpha \) and \(\beta \) take on values of \(\{1, 2\}\); summation convention of repeated indices is employed unless otherwise stated.

Fig. 1
figure 1

A schematic view of the mapping between the parametric, reference (i.e., undeformed) and current (i.e., deformed) configurations

Full size image

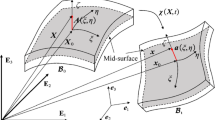
We describe a material point within the shell body in the reference configuration \(\varOmega _0\) by its position vector , with \(\xi _1\) and \(\xi _2\) the convective curvilinear coordinates in the in-plane directions, and \(\xi _3\) the through-thickness coordinate of the parameter space \(\mathrm {P}\) (cf. Fig. 1). Taking the bottom surface of the continuum shell as the reference surface, the undeformed position vector can be further described using the projected point at the bottom surface, , and the unit thickness director normal to the shell bottom surface, ,

(1)

where \(\xi _3 \in [0, t]\) and t denotes the total thickness of the shell. We denote as the in-plane base vectors of the bottom surface in the reference configuration, where \((\cdot )_{,\alpha }=\partial (\cdot )/\partial \xi _\alpha \). The unit normal vector can then be derived as

(2)

In order to describe the motion of an arbitrary material point in the continuum shell body, it is convenient to define a set of covariant base vectors. Specifically, the base vectors at any point in the original shell configuration can be expressed as , with \((\cdot )_{,i}=\partial (\cdot )/\partial \xi _i\), and further expanded as

(3)
(4)

Having defined the covariant base vectors, their dual base vectors (i.e., the contravariant base vectors) can be computed according to the Kronecker delta relation, . The position vector \(\mathbf{x} \left( \xi _1,\xi _2,\xi _3\right) \) in the current configuration \(\varOmega \) can be related to the reference position vector through the displacement vector \(\mathbf{u} \), i.e., . The deformed covariant base vectors can then be written as

(5)

Finally, we arrive at the deformation gradient between the reference and current configurations in a total Lagrangian framework, , from which the Green–Lagrange strain tensor can be easily computed as

$$\begin{aligned} \mathbf{E} = \frac{1}{2} \left( \mathbf{F} ^\text {T} \mathbf{F} - \mathbf{I} \right) \text { ,} \end{aligned}$$
(6)

with \(\mathbf{I} \) the second-order identity tensor. Let \({g}_{ij} = \mathbf{g} _{i} \cdot \mathbf{g} _{j}\) be the metric coefficients of the first fundamental form. The Green–Lagrange strain tensor then becomes

(7)

where the specific strain component \({E}_{ij}\) can be computed based on the reference local covariant vectors and the current displacement derivatives as

(8)

Equation (7) essentially describes the variation of surface metric tensors due to structural deformation.

With the Green–Lagrange strain tensor at hand, the energetically conjugate second Piola–Kirchhoff stress tensor \(\mathbf{S} \) can be obtained based on the adopted hyperelastic-based plasticity model, as elaborated in the next section. Note that, since material models are typically formulated with respect to the Cartesian coordinate system, the above strain tensor needs to be transformed from the curvilinear system to the element local system

(9)

where \({E}^{e}_{ij}\) are the coefficients of the Green–Lagrange strain tensor with respect to the local Cartesian base vectors defined as

(10)

Transformations of the stress tensor \(\mathbf{S} \) and the deformation gradient \(\mathbf{F} \) follow in an analogous fashion.

It is now straightforward to arrive at the variational formulation of the isogeometric continuum shell based on the principle of virtual work, in which the contribution of the body force is neglected for brevity:

$$\begin{aligned} \delta W \!=\! \delta W^\text {int} - \delta W^\text {ext} \!=\! \int _{\varOmega _0} \delta \mathbf{E} : \mathbf{S} \, \text {d} \varOmega _0 \!-\! \int _{\varGamma ^\text {h}_0} \delta \mathbf{u} \cdot \mathbf{h} \, \text {d} \varGamma ^\text {h}_0 \!=\! 0 \text { ,} \end{aligned}$$
(11)

where W, \(W^\text {int}\) and \(W^\text {ext}\) represent the total, internal and external work, respectively, \(\delta \) denotes the variation with respect to the virtual displacement variable \(\delta \mathbf{u} \), \(\varOmega _0\) is the shell volume in the reference configuration, , \(\mathbf{h} \) is the surface traction, and \(\varGamma ^\text {h}_0\) is the reference boundary to which \(\mathbf{h} \) is applied.

An incremental iterative solution scheme (e.g., cylindrical arc-length control [87]) can be adopted to solve the above nonlinear system, in which the derivation of the tangential stiffness necessitates the linearization of the internal work

(12)

Additional details of the formulation and numerical implementation aspects can be found in Liu et al. [18, 24].

3 Finite strain hyperelastic-based plasticity

The adopted finite strain hyperelastic plasticity model is based on the framework of multiplicative decomposition of the deformation gradient into the elastic and plastic contributions and the concept of intermediate stress-free configurations [88, 89]. To describe the plastic flow and nonlinear material response, the classical 3D \(J_2\) von Mises rate-independent plasticity model along with isotropic hardening is employed.

According to the notion of an intermediate stress-free configuration, the deformation gradient \(\mathbf{F} \) is decomposed as

$$\begin{aligned} \mathbf{F} = \mathbf{F} ^\text {e} \mathbf{F} ^\text {p} \text { ,} \end{aligned}$$
(13)

where \(\mathbf{F} ^\text {e}\) and \(\mathbf{F} ^\text {p}\) denote the elastic and plastic contributions of the deformation gradient, respectively. This decomposition can be regarded as a purely plastic deformation to an intermediate stress-free configuration, based on which the elastic response can be characterized.

Following the decomposition described in Eq. (13), the elastic left and plastic right Cauchy–Green (CG) deformation tensors are introduced respectively as

$$\begin{aligned} \mathbf{b} ^\text {e} = \mathbf{F} ^\text {e} \left( \mathbf{F} ^\text {e}\right) ^\text {T} \text { ,}\quad \mathbf{C} ^\text {p} = \left( \mathbf{F} ^\text {p}\right) ^\text {T} \mathbf{F} ^\text {p} \text { .} \end{aligned}$$
(14)

A crucial relationship can be found by rearranging Eqs. (13) and (14), which yields an alternative expression of the elastic left CG deformation tensor \(\mathbf{b} ^\text {e}\) as a function of the plastic right CG deformation tensor \(\mathbf{C} ^\text {p}\),

$$\begin{aligned} \mathbf{b} ^\text {e} = \mathbf{F} \left( \mathbf{C} ^\text {p} \right) ^{-1} \mathbf{F} ^\text {T} \text { .} \end{aligned}$$
(15)

Equation (15) dictates that the elastic deformation can be related to the plastic deformation through the deformation gradient. The rate of the elastic left CG deformation tensor, denoted as \(\dot{\mathbf{C }}^\text {p}\), is then written in Lie derivative form as

$$\begin{aligned} \mathcal {L}_v \mathbf{b} ^\text {e} = \mathbf{F} \left( \dot{\mathbf{C }}^\text {p} \right) ^{-1} \mathbf{F} ^\text {T} \text { .} \end{aligned}$$
(16)

We describe the total free energy in the form of the summation of the elastic and plastic strain energies in the following form

$$\begin{aligned} \varPhi \left( \mathbf{b} ^\text {e},J^\text {e},\alpha \right) =&\varPhi ^\text {e} \left( \mathbf{b} ^\text {e},J^\text {e} \right) +\varPhi ^\text {p} \left( \alpha \right) \nonumber \\ =&\int _{\varOmega _0} \left( \varPsi ^\text {e} \left( \mathbf{b} ^\text {e},J^\text {e}\right) + \varPsi ^\text {p} \left( \alpha \right) \right) \, \text {d} \varOmega _0 \text { ,} \end{aligned}$$
(17)

where the elastic strain energy density \(\varPsi ^\text {e}\) is defined in terms of the elastic left deformation tensor \(\mathbf{b} ^\text {e}\) and the determinant of the elastic deformation gradient \(J^\text {e}\), \(J^\text {e} = \det [\mathbf{F} ^\text {e}]\), and the plastic strain energy density \(\varPsi ^\text {p}\) is expressed as a function of the internal hardening variable \(\alpha \) in the case of isotropic hardening.

For the elastic description of the adopted elastoplastic model, we employ a material model of the isotropic hyperelastic type to describe the material behavior, of which the elastic strain energy density \(\varPsi ^\text {e}\) can be further split into the volumetric (i.e., shape preserving) and deviatoric (i.e., volume preserving) contributions as

$$\begin{aligned} \varPsi ^\text {e} = \varPsi _\text {vol}^\text {e} + \varPsi _\text {dev}^\text {e} \text { ,} \end{aligned}$$
(18)

where

$$\begin{aligned} \varPsi _\text {vol}^\text {e}&= \frac{\kappa }{2} \left( \frac{\left( J^\text {e} \right) ^2 -1}{2} - \text {ln} J^\text {e} \right) \text { ,} \end{aligned}$$
(19)
$$\begin{aligned} \varPsi _\text {dev}^\text {e}&=\frac{\mu }{2} \left( \text {tr} \left[ \hat{\mathbf{b }}^\text {e} \right] -3 \right) \text { ,} \end{aligned}$$
(20)

with \(\text {tr}[\cdot ]\) denoting the trace of a matrix, \(\hat{\mathbf{b }}^\text {e}=( J^{e} )^{-2/3}{} \mathbf{b} ^\text {e}\), \(\kappa \) and \(\mu \) being the bulk and shear moduli of the material, respectively. From the derived elastic strain energy density function \(\varPsi ^\text {e}\), the Cauchy stress \(\varvec{\sigma }\) can be directly computed [90] as

$$\begin{aligned} \varvec{\sigma }&= 2 J^{-1} \left( \frac{\partial \varPsi _\text {vol}^\text {e}}{\partial \varvec{b}^\text {e}} + \frac{\partial \varPsi _\text {dev}^\text {e}}{\partial \varvec{b}^\text {e}}\right) \varvec{b}^\text {e} \nonumber \\&= J^{-1} \left( \frac{\kappa }{2} \left( J^2-1 \right) \mathbf{I} + \mu \text {dev} \left[ \hat{\mathbf{b }}^\text {e} \right] \right) \nonumber \\&= J^{-1} \left( \varvec{\tau }_\text {vol} + \varvec{\tau }_\text {dev} \right) \text { ,} \end{aligned}$$
(21)
Table 1 The solution scheme of the \(J_2\) plasticity constitutive equations based on return mapping and backward Euler time integration
Full size table
Table 2 The solution algorithm for the fourth-order consistent elastoplastic tangent moduli
Full size table

where \(\text {dev} \left[ \cdot \right] =\left[ \cdot \right] -\frac{1}{3}\text {tr}\left[ \cdot \right] \mathbf{I} \), \(\varvec{\tau }_\text {vol}\) and \(\varvec{\tau }_\text {dev}\) are the volumetric and deviatoric parts of the Kirchhoff stress tensor \(\varvec{\tau }\), respectively. We emphasize that plastic flow is isochoric in von Mises plsticity, and thus \(J=J^\text {e}\). Accordingly, the superscript ‘e’ is neglected for brevity. Subsequently, the second Piola–Kirchhoff stress used in the isogeometric continuum shell formulation can be computed according to the pull-back operation

$$\begin{aligned} \mathbf{S} = J \mathbf{F} ^{-1} \varvec{\sigma } \mathbf{F} ^\text {-T} \text { .} \end{aligned}$$
(22)

In terms of the plastic deformation, we employ the classical Mises–Huber yield criterion, which is defined as a function of the deviatoric Kirchhoff stress \(\varvec{\tau }_\text {dev}\),

$$\begin{aligned} f \left( \varvec{\tau }_\text {dev},\alpha \right) = \Vert \varvec{\tau }_\text {dev} \Vert - \sqrt{\frac{2}{3}} k \left( \alpha \right) \text { ,} \end{aligned}$$
(23)

where \(k \left( \alpha \right) \) is the hardening function.

The associative flow rule emerging from the theory of maximum plastic dissipation can be expressed as

$$\begin{aligned} \left( \dot{\mathbf{C }}^\text {p} \right) ^{-1} = -\frac{2}{3} \gamma \text {tr} \left[ \mathbf{b} ^\text {e} \right] \mathbf{F} ^{-1} \mathbf{n} \mathbf{F} ^\text {-T} \text { ,} \end{aligned}$$
(24)

where \(\gamma \) is the plastic multiplier and \(\mathbf{n} = \varvec{\tau }_\text {dev} / \Vert \varvec{\tau }_\text {dev} \Vert \). Moreover, the evolution of the yield stress is characterized by the rate of the hardening variable, which is defined as

$$\begin{aligned} \dot{\alpha } = \sqrt{\frac{2}{3}} \gamma \text { .} \end{aligned}$$
(25)

The Karush–Kuhn–Tucker (KKT) conditions are employed to govern the loading/unloading conditions

$$\begin{aligned} \gamma \ge 0 \text { ,}\quad f \left( \varvec{\tau }_\text {dev},\alpha \right) \le 0 \text { ,}\quad \gamma f \left( \varvec{\tau }_\text {dev},\alpha \right) = 0 \text { .} \end{aligned}$$
(26)

In order to solve the above elastoplastic constitutive equations, we utilize a backward Euler time integration technique along with a standard return mapping algorithm. The detailed implementation is summarized in Tables 1 and 2.

4 Numerical examples

In this section, we select a number of challenging benchmark examples in the realm of finite-to-large strain plasticity to demonstrate the accuracy and robustness of the present isogeometric elastoplastic continuum shell formulation. Bicubic NURBS are utilized to represent the in-plane geometries, and quadratic B-splines with a single element discretization are used to describe the through-thickness kinematics of the continuum shell. A total of \(p+1\) Gaussian points are used in each direction for the integration of the governing equations, with p the polynomial order of the employed spline basis. A displacement-controlled algorithm is employed to iteratively solve the first two problems, while a cylindrical arc-length control algorithm [87] is adopted for the solution of the third problem. All the numerical examples were simulated on a hierarchical set of meshes, whereas only the meshes for the converged solutions were demonstrated.

4.1 Rectangular plate under uniaxial tension

The first benchmark example investigated here is concerned with the classical rectangular plate model subjected to uniaxial tension [1, 2, 91], which is used to test the formulation under plane stress necking. As illustrated in Fig. 2, the total length and width of the plate are \(L=50\) mm and \(W=10\) mm, respectively, and the thickness is \(t=1\) mm. The plate is fixed at one end and subjected to uniaxial tension at the other end. The material model employed is: Young’s modulus of \(E=1.89 \times 10^5\) MPa, Poisson’s ratio of \(\nu =0.29\), and a nonlinear isotropic hardening model of \(k(\alpha )=343+(680-343)(1-e^{-16.93\alpha })+300\alpha \). Due to symmetry, only a quarter of the plate is modeled. A mesh of 250 elements (i.e., 25 in the length direction and 10 in the width direction) is used to obtain the final solution.

The norm of the displacement vector divided by the total number of control points, \(U_{\text {norm}}=\sqrt{\frac{U^\text {T}U}{n_\text {cp}}}\), is recorded to quantitatively assess the accuracy of the present formulation. The obtained load-displacement curve is compared with the reference data [1, 2] and plotted in Fig. 3, where a very good agreement is reached. Figure 4 displays the evolution of the hardening variable \(\alpha \) on the deformed plate at several stages of the loading process. It can be seen that, once the material enters the yielding zone and before the ultimate strength is reached, plasticity initiates at the corners and the plate deforms uniformly as the plastic strain accumulates. At a certain stage after the ultimate strength is reached, the plastic strain starts to concentrate at the plate center where necking forms and branches out to the free edges until ultimate failure. Note that the proposed formulation is based on the theory of local plasticity, and therefore the results at the necking zone may be sensitive to the mesh density due to the significant softening in that region. In cases where solution singularity is expected, nonlocal gradient plasticity models are recommended [92] to alleviate this issue.

Fig. 2
figure 2

The geometry and problem setup of the rectangular plate under uniaxial tension. Due to symmetry, only a quarter of the plate is modeled

Full size image
Fig. 3
figure 3

The load–displacement curve of the tensile plate problem

Full size image
Fig. 4
figure 4

The contour plots of the hardening variable \(\alpha \) at various stages of the loading process in the tensile plate benchmark problem. The hardening variable \(\alpha \) is evaluated at the midsurface for visualization

Full size image
Fig. 5
figure 5

The geometry and problem setup of the hollow cylinder. Due to symmetry, only one octant of the cylinder is modeled

Full size image

4.2 Tensile hollow cylinder

The second numerical example considered here is a hollow cylinder model that is fixed at one end and subjected to uniaxial displacement increment at the other end. The same material properties are used as in the first numerical example. Only one octant of the cylinder is modeled leveraging on symmetry and discretized with a total of 500 elements (i.e., 20 elements in the circumferential direction and 25 elements in the length direction). The geometric details and problem setup can be found in Fig. 5.

Fig. 6
figure 6

The load–displacement curve of the hollow cylinder problem

Full size image
Fig. 7
figure 7

The contour plots of the hardening variable \(\alpha \) at various stages of the loading process in the hollow cylinder problem. The hardening variable \(\alpha \) is evaluated at the midsurface for visualization

Full size image

The effective stress, defined as the applied force divided by the cross-sectional area of the cylinder, is plotted against the displacement norm \(U_{\text {norm}}\) in Fig. 6, where the obtained results agree very well with the reference solutions [1, 2]. The evolution of the internal hardening variable at different loading stages is demonstrated in Fig. 7. Similar to the findings in the rectangular plate example, necking occurs at the central region of the cylinder when the ultimate strength is reached and accounts for the final failure of the model.

Fig. 8
figure 8

Pinched hemisphere problem setup and the corresponding mesh used in analysis. The radial displacements at points A and B are recorded

Full size image
Fig. 9
figure 9

The load–displacement curves of the pinched hemisphere problem

Full size image
Fig. 10
figure 10

The contour plots of the hardening variable \(\alpha \) at various stages of the loading/unloading process in the pinched hemisphere benchmark. Contours (a)–(c) are from the loading stage and contours (d)–(f) are from the unloading stage. The hardening variable \(\alpha \) is evaluated at the midsurface for visualization

Full size image

4.3 Pinched hemisphere

The pinched hemisphere problem at large elastoplastic deformations is one of the most challenging benchmark examples in both material and geometrically nonlinear shell analysis and has been investigated by a variety of research work [1, 9, 13, 85, 93, 94], to name a few. The radius and thickness of the hemisphere are \(R=100\) mm and \(t=5\) mm, respectively. The applied material model is: Young’s modulus of \(E=100\) N/mm\(^2\), Poisson’s ratio of \(\nu =0.2\), and a linear isotropic hardening model of \(k(\alpha )=2+30\alpha \). The hemisphere is subjected to two sets of inward and outward opposing point forces of \(P=35\) N at the bottom, respectively. Leveraging on symmetry, only a quarter of the hemisphere is modeled. The detailed geometry and problem setup, as well as the mesh corresponding to a total of 256 NURBS elements used for analysis, can be found in Fig. 8.

The loading/unloading response of the hemisphere is studied. The load–displacement relationship at points A and B in Fig. 8 is plotted in Fig. 9 along with comparisons to the reference results obtained from Başar and Itskov [93], Ambati et al. [1], and Alaydin et al. [2], where a satisfactory agreement is observed. The evolution of the internal hardening variable \(\alpha \) is also illustrated in Fig. 10 at various loading/unloading stages for demonstration purposes. As expected, the plastic strain is localized in the vicinity of the points where external forces are applied and retains itself permanently during unloading.

5 Conclusion

In this work, a large-deformation isogeometric continuum shell formulation that incorporates the theory of finite strain plasticity is developed in a total Lagrangian framework. The key characteristic of the method is the multiplicative decomposition of the deformation gradient into the elastic and plastic parts to properly model plasticity at the finite strain regime. The standard return mapping algorithm and the classical \(J_2\) von Mises plasticity model with nonlinear isotropic hardening are implemented for demonstration. A number of numerical benchmarks are used for testing and the obtained results are compared with published data in literature, which proves the solution accuracy of the present formulation. The proposed formulation enables us to obtain high-fidelity 3D strains and stresses in the finite strain plasticity regime while requiring only the surface modeling of thin-walled structures, which greatly reduces the complexity of the geometric modeling process.

The main limitations of the present formulation are that it is rather computationally expensive to solve problems with severe localized plasticity, as compared to computationally efficient KL shell formulations. The reasons are mainly twofold. For one thing, the present isogeometric continuum shell is essentially a solid formulated under curvilinear coordinates, whose solution requires significant computational resource. While not pursued in the current study, reduced quadrature schemes can be used for computational saving. For another, these solid-like formulations are prone to locking issues, especially in the modeling of thin-walled structures. While it is out of the scope of the current study, locking mitigation strategies are recommended to be used together with the present formulation. We plan to address these limitations in future work.

To summarize, although continuum shells are computationally costly compared to KL shells, the ability to accurately compute 3D stresses is clearly a significant advantage in structural failure analysis. It is envisioned that the developed large-deformation elastoplastic continuum shell formulation can be used in a blended shell [24,25,26] setting where critical structural components with yielding can be modeled using the developed continuum shells for accurate 3D stress prediction and other less critical structural components can be modeled using KL shells for computational efficiency.