1 Introduction

The need to model and understand new composite materials as led to the development of several microstructure modeling techniques. The ability to represent and simulate complex microstructures is valuable as it leads to faster prototyping and decision making. Analytical modeling of a theoretical assembly of constituents can provide a rough estimate of thermal and mechanical properties of a composite material but it requires specific conditions to assert validity of results obtained. When feasible, actual mechanical testing can provide an accurate evaluation of tested samples but is time consuming and requires complex and costly equipment. Hence popularity and thrive towards numerical modeling and analysis of composite materials. Finite Element Analysis (FEA) applied on Statistical Volume Elements (SVE) is a numerical approach that has generated a great deal of interest in the research community [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Constituent’s intrinsic properties along with their distribution, orientation and assembly are the major influences on the properties of SVEs. To be considered as accurately representative of the spatial distribution of constituent’s intrinsic properties, referred to as a Representative Volume Element (RVE), a single numerical sample or SVE must usually be of considerable size, which is limited by modelling and analysis issues. To overcome these limitations, a given microstructure is usually broken down into smaller but numerous SVEs which leads to a statistical representation of the composite properties. In this case, the set SVEs used is referred to as a Representative Volume Element (RVE). These SVEs can be generated from actual samples using scanning techniques [16,17,18,19] or generated from scratch based on predetermined material parameters. The latter option is interesting since it does not require actual physical samples. Microstructure modeling using the FEA approach as tremendously evolved over time. Indeed, many research papers have considered this approach towards assessing the influence of constituent’s shapes [1,2,3, 15], size [3, 7,8,9,10,11,12,13,14], orientation [1, 20, 21], volume fraction [7, 21] and distribution [22, 23] on composite materials mechanical and thermal properties.

Numerical analysis of a SVE usually starts with the generation of a geometric representation of its microstructure. Automatically generating the geometric representation of an ordered microstructure is straightforward since it can be performed based on a few simple operations. For example, a unidirectional fiber glass laminate can be defined as a set of equally spaced, unidimensional cylinders surrounded with an epoxy matrix. The generation process is much more complex when the material considered is composed of randomly distributed particles. Positioning and orienting each particle, according to specified distributions, while achieving a targeted volume fraction of particles comes with many challenges. One of these challenges is making sure that two particles do not intersect with each other. One simple solution to avoid these intersections is to assume that all particles are spherical in shape. Indeed, knowing the distance between two spheres and their radius, one can easily determine if they overlap or not. This method was first used along with a random number generator to randomly position spherical particles in a defined space [1, 2, 6, 8, 15, 24,25,26]. If a newly created particle overlaps an existing one, it is discarded, and a new particle is randomly generated. This generation method is referred to as the Random Adsorption Algorithm or RSA. However, it is obvious that the behavior of many material microstructures cannot be accurately modeled with spherical particles only. To circumvent this limitation, improved overlap detection methods relying on the parametric equations of primitive shapes such as ellipsoidal particles [1, 3, 25,26,27,28,29], cylindrical particles [1, 4, 7, 14, 21, 26, 29,30,31,32] and polyhedral particles [2, 15] have been developed. Even with these improved methods, automatically generating the geometric representation of a microstructure that features non-primitive shapes is still problematic due to the lack of shape independent overlap detection methods. Shape independent overlap detection can be accounted for with the aid of Computer Aided Design (CAD) tools. Indeed, computing the minimum distance between two volumes or assessing the intersection between two volumes are two basic features of modern CAD software. Moreover, using a CAD model to represent SVE microstructures brings other benefits such as, for example, easily altering the shape of a particle that crosses the borders of a SVE. Another efficient way to detect overlaps between two neighboring particles is to generate boundary meshes of these particles and to use this discretization to evaluate the overlap. Such surface meshes can be obtained by applying parametric mesh generation algorithms on primitive shapes or by applying CAD based automatic mesh generation algorithms. The second challenge associated with automatically generating the geometric representation of a microstructure is accurately reaching a specific targeted volume fraction of particles. For example, with the RSA, if a new particle overlaps an existing one it is discarded, and a new particle is randomly generated. With just a few particles inserted in a SVE, the chance that a new particle is accepted is high but, the more particles are added, the more this chance drops, sometimes reaching a point where there is no possible way to insert a new particle. This phenomenon restricts achievable volume fractions and this process is not representative of particle packing as it occurs along actually manufacturing the composite material. Indeed, with the RSA, once a particle is accepted, it remains rigidly fixed in space. The theoretical volume fraction achievable with mono-sized spherical particles is \(\frac{\Pi }{3\sqrt 2 } \approx 74.1\%\) in a cubic centered configuration or an hexagonal compact configuration [33]. With the same type of particles, a standard RSA can only reach volume fractions below 40% (38.5% [34], 38.2% [35]). To overcome this limitation, spherical particles relocation procedures were elaborated, which enables to reach volume fractions up to 50% if direct contact between particles is avoided and 60% if it allowed [6]. Such relocation procedures can be difficult to implement with non-spherical particles because the orientation of particles needs to be considered.

One alternative to the RSA is using rigid MultiBody Dynamics (MBD) methods to simulate the dynamic interaction of particles [36,37,38,39,40,41,42,43]. By allowing particles to move and collide with each other, higher compaction levels can be reached. With spherical particles, using MBD allows to reach volume fractions up to 65% [37]. Time managing along MBD can either be driven by collision events or by predetermined time stepping. Event-driven time managing methods are suitable for spherical particles and rely on kinematic equations to predict when two spheres come in contact. When two spheres collide, the collision response is evaluated, kinematic equations are updated, and the time parameter is incremented to the next collision. Time stepping time managing methods are suitable for any convex solid shapes and rely on a refined discretization of time with short time steps. At first, the boundary of solid shapes particles is meshed. This mesh is used to evaluate if two solids shapes are in contact. At each time step, a collision evaluation procedure is run to find which solids shapes are in contact. Collision responses are computed, and kinematic equations are updated. The next time step is evaluated and so forth. Time steps driven methods show the advantage of being usable with any kind of convex particles, but unlike event-driven methods, time step driven methods may miss collisions if the time step used is too long.

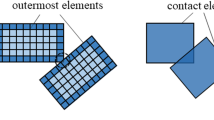
Generating geometric representations of SVEs is followed by automatically meshing these representations. SVEs are either meshed using unstructured mesh generation methods (Delaunay, advancing front, octree [44]) with quadratic tetrahedrons in most cases, or using structured voxel-based methods. Unstructured mesh generation methods generate mesh elements of varying sizes and shapes and thus allows for a better definition of curvature in comparison with voxel based discretizations. As mentioned in [45], using a CAD geometric representation of SVEs greatly facilitates the meshing process since robust and proven CAD based meshing tools can be used. Regardless of the unstructured meshing algorithm used, one important parameter that must be controlled is the size of mesh elements. Locally refining the size of mesh elements using an imposed size map will improve the accuracy of geometric representation and increase the accuracy of FEA computed fields. In addition, controlling the size of mesh elements can be mandatory to ensure convergence of automatic mesh generation algorithms in some cases. Indeed, situations may occur where element creation is impossible at a given location if surrounding mesh elements are not appropriately sized. However, reducing the size of mesh elements implies more mesh elements, which can also significantly increase the size of the FEA model and thus increase computing time and resources needed. If two particles are close to each other as illustrated in Fig. 1, the size of mesh elements between those particles must be adjusted to prevent badly shaped elements and to ensure mesh generation convergence. The same situation arises when a particle is close to SVE boundaries. This proximity can lead to an excessive number of mesh elements between the particle and the SVE boundary, or to automatic mesh generation failure, if this proximity is not taken into account in the imposed size map. Mesh element quality is another aspect that must be accounted for. Sharp angles between edges or faces of the SVE geometric representation will also results in badly shaped mesh elements as illustrated in Fig. 2. The effect of such sharp angles can be minimized by locally refining the size of mesh elements but cannot be completely avoided (Fig. 2b). If particles themselves do not feature sharp angles, the only situation where sharp angles can appear is when a particle crosses the SVE boundary. For example, if a cylindrical particle is almost parallel to one of the faces of a cubic SVE and is in contact with that face, it will generate such a sharp angle.

Fig. 1
figure 1

Illustration of mesh refinement to fill a gap between two particles

Full size image
Fig. 2
figure 2

Illustration of the effect of a sharp angle on mesh element quality (bad quality in red). a For constant sized mesh elements and b when locally refining the mesh size

Full size image

Controlling the minimum distance between particles, between particles and SVE boundaries and controlling the minimum angle between edges and faces can be accomplished along the generation of SVE geometry when using RSA. Indeed, a newly generated particle that is too close to another particle or too close to the SVE boundary can be rejected. The same principle can be applied for sharp angles.

Up to a certain volume fraction, non-conforming particles are rejected and replaced by new particles. This rejection comes at a cost since rejecting these particles likely impedes the targeted distributions of location and orientation of particles. If one considers that the particles of a given microstructure have a minimum distance separating them (for example if the particles are completely surrounded by matrix) then the exclusion problem will be localized in the areas close to the SVE’s border as illustrated in (Fig. 15). Indeed, particles are more prone to be excluded close to SVE boundaries as the minimum angle problem arises when a particle intersects these boundaries. Also, if the generation domain is larger than the SVE’s domain, minimum distance problems can occur at the borders of the SVE. With the MBD simulation approach, as introduced earlier, controlling minimum distance and sharp angles is not that simple due to the fact that a particle cannot be rejected and replaced if, at a given moment, it does not meet minimum distance and sharp angles criteria.

As mentioned above, the minimum distance and angle between two geometric objects must be controlled in order to ensure convergence of mesh generation, to limit the size of the model and to promote quality of numerical results. The question that arises is how should be processed particles that are close to SVE boundaries? From a geometric standpoint, the solution could consist in modifying the microstructure geometry in a way that eliminates closeness and sharp angles. One approach could be to move, to cut or to extend the geometry of particles to meet closeness and sharp angles criteria. This approach would be very complex to implement, especially if the approach should apply for any shape of particles. It would require complex geometric modification rules and would inevitably affect fidelity of the geometric representation. On the other end of the spectrum, the solution could be to keep the geometrical representation intact and adapt mesh generation in a way that avoids non convergence and avoids generating small or badly shaped mesh elements. The resulting mesh would not perfectly conform to the CAD model. It would require a set of custom meshing rules to generate and assign each element to the corresponding geometry (or material). In the end, it would also be a very complex approach to implement and it would induce a biased representation of the actual microstructure.

The aim of this study is to present a simple solution to meshing problem induced by particles that surround the SVE boundary, as introduced above. The proposed solution can be summarized though the following steps:

  • Remove particles that are located close to boundaries of the SVE. Remove particles that do not conform to the preestablished minimum distance and minimum angle criterions.

  • Mesh the SVE using robust CAD meshing algorithms.

  • Perform FEA and erode FEA results around the SVE boundary. This erosion consists in an elimination of results that are close the SVE boundary, which means only considering FEA results inside a core of the SVE in order to avoid boundary effects.

Indeed, taken as a whole, the CAD model of a SVE does not faithfully represent the simulated microstructure, due to boundary effects. However, at some distance from the SVE boundary, the CAD model is unaltered by boundary effects and, by the way, it is representative of the actual microstructure. This solution is inspired by a homogenization technique presented in [24] where SVEs are eroded to reduce boundary effects caused by FEA boundary conditions. It is shown in this reference that, as the erosion distance increases, boundary conditions effects are reduced. Furthermore, it is also demonstrated in this reference that the erosion technique approximately satisfies the Hill-Mandel homogenization condition and that the average loading of eroded SVEs is similar to that of complete SVEs.

In this paper, we present a new erosion based SVE generation and homogenization method along with a new SVE generation algorithm based on rigid MultiBody Dynamics (MBD). This new multibody dynamics SVE generation algorithm is introduced as a solution to reach higher volume fractions for non-spherical particles. These new methods are implemented using the Unified Topology Model (UTM) as described in [45]. Using the Unified Topology Model (UTM) [45, 46] benefits the automatic CAD—mesh—FEA modeling and analysis process thanks to a close data structure integration between CAD objects (geometrical, topological and co-topological entities) and FEA mesh elements, material properties and boundary conditions. As detailed in [45] the UTM notably allows fully automating the whole process, from CAD model generation up to FEA analysis and statistical calculations. The process detailed in [45] is synthesized in (Fig. 3): using the RSA algorithm, particles are randomly generated and inserted in the SVE if they satisfy geometrical criteria used to prevent subsequent meshing problems such as sharp angles and too fine mesh elements. Then, a mesh size map is defined in such a way that the mesh element size is small enough to prevent distorted elements but large enough to minimize the number of elements. The SVE is meshed, consistently with the imposed size map, using an automatic mesh algorithm, which is based the advancing front method. The process ends with FEA simulation and homogenization, which allows assessing material properties. See reference [45] for more details on this process.

Fig. 3
figure 3

Synthesis of the SVE automatic generation process presented in reference [45]

Full size image

To illustrate the potential and validity of the two new approaches proposed in this paper, multiple sets of fiberglass and epoxy SVEs will be generated and compared with previous results in [45].

The following section presents a complete description of the new erosion-based homogenization method. In Sect. 3, results for short glass fiber/epoxy composite SVEs generated with the RSA algorithm and progressively eroded with the erosion method are compared with non-eroded SVEs as presented in [45]. An original and alternative SVE generation method based on rigid multibody dynamics combined with erosion is detailed in Sect. 4. Results are presented in Sect. 5 for the same glass fiber composite using this new SVE generation method. The paper ends with conclusion remarks and perspective work in Sect. 6.

2 An erosion-based homogenization method

The aim of introducing erosion in SVE modelling is to avoid the boundary effects caused by a lack of participles close to the SVE boundary and by the effect of FEA boundary conditions. In the approach proposed, erosion is performed on FEA results, which makes that no subsequent FEA solving is required. Therefore, this erosion method can be applied in conjunction with any type of SVE generation method. In this new approach, erosion is performed by gradually eroding the SVE from its boundary towards its center using an erosion distance \(d_{e}\). In this erosion scheme, a mesh element is preserved if its center is located inside a cube with faces at distance \(d_{e}\) from the SVE boundary (Fig. 4).

Fig. 4
figure 4

Erosion of a unit cube SVE. a No erosion, b \(d_{e} = 0.1\), and c \(d_{e} = 0.2\)

Full size image

Volume averaged tensor \( \left \langle \underline{{\underline {A} }} \right \rangle _{V}\) of a given tensor field \(\underline{{\underline {a} }}\) defined at all points \(\underline {x}\) for a non-eroded SVE of volume \(V\) is obtained with Eq. (1).

$$ \left \langle \underline{{\underline {A} }} \right \rangle_{V} = \frac{1}{V}\mathop \int \limits_{V} \underline{{\underline {a} }} \left( {\underline {x} } \right)dV $$
(1)

The volume average of an eroded tensor field \(\left \langle \underline{{\underline {A} }} \right \rangle_{{V_{{d_{e} }} }}\) is redefined for the eroded SVE of volume \(V_{{d_{e} }}\) with Eq. (2).

$$ \left \langle \underline{{\underline {A} }} \right \rangle_{{V_{{d_{e} }} }} = \frac{1}{{V_{{d_{e} }} }}\mathop \int \limits_{{V_{{d_{e} }} }} \underline{{\underline {a} }} \left( {\underline {x} } \right)dV $$
(2)

Since the erosion method only consists in post-processing FEA results, it is possible to extract homogenized results for multiple value of \(d_{e}\) and evaluate their evolution as \(d_{e}\) increases.

3 Erosion based homogenization applied to SVEs generated with the RSA

3.1 Homogenization results

The effect of erosion on homogenized results is evaluated by making comparisons on SVEs generated with RSA, without erosion, as presented in a previous paper [45]. In the following sections, SVEs generated with RSA are identified with the prefix RSA. Table 1 lists the different sample configurations used with spherical and cylindrical particles. Spherical particles are labeled as S1, S2 and cylindrical particles are labeled as C1, C2. Targeted volume fractions are labeled as FV. Material properties of constituents are indicated in Table 2. Considering that particles are isotopically distributed, resulting SVEs are considered isotropic.

Table 1 Configurations of SVEs generated with the RSA
Full size table
Table 2 Material properties considered
Full size table

Figure 5 illustrates the evolution of the volume fraction of particles for numerical samples RSA_S1FV10 and RSA_C1FV10. When erosion distance is zero, the volume fraction of particles is 10%, which corresponds to the target volume fraction. As erosion distance increases, the volume fraction of particles increases until it reaches a plateau around \(d_{e} = 0.2\). This increase illustrates side effects induced by the particle insertion process with the RSA. Indeed, it is harder to insert a particle near faces of the SVE than in its core. Statistically a particle has a better chance of finding itself in the center of the SVE than close to its faces. Table 3 lists the volume fractions of microstructures generated with the RSA without erosion and volume fractions with erosion distance \(d_{e} = 0.2\). For all samples, the volume fractions with erosion distance \(d_{e} = 0.2\) are higher than corresponding volume fractions without erosion. Increasing the target volume fraction of particles reduces the gap between eroded and non-eroded volume fractions. Indeed, as the volume fraction increases, a particle has a higher chance of being close to SVE faces. A reduction in deviation is also observed when the size of SVEs is increased since particles are smaller, with respect to the erosion distance.

Fig. 5
figure 5

Evolution of the volume fraction of particles with erosion distance \(d_{e}\) for a RSA_S1FV10 and b RSA_C1FV10

Full size image
Table 3 Resulting volume fractions for SVEs generated with the RSA
Full size table

Kinematic Uniform Boundary Conditions (KUBC) and Static Uniform Boundary Conditions (SUBC) are used to evaluate the apparent elasticity modulus \(E_{app}\) [45]. In the present case, compressibility modulus \(K_{app}\) and shear modulus \(G_{app}\) are calculated using Eqs. (3)–(5) with the assumption of a macroscopically isotropic microstructure. The apparent elasticity modulus \(E_{app}\) is calculated from \(K_{app}\) and \(G_{app}\) using Eq. (5).

$$ K_{app} = \frac{{Tr\left( {\underline{\underline{\Sigma }} } \right)}}{{3Tr\left( {\underline{\underline{E}} } \right)}} $$
(3)
$$ G_{app} = \frac{1}{3}\left( {\frac{{{\Sigma }_{xy} }}{{2E_{xy} }} + \frac{{{\Sigma }_{yz} }}{{2E_{yz} }} + \frac{{{\Sigma }_{xz} }}{{2E_{xz} }}} \right) $$
(4)
$$ E_{app} = \frac{{9K_{app} G_{app} }}{{3K_{app} + G_{app} }} $$
(5)

The evolution of the volume fraction of particles \(F_{vol}\) with erosion distance \(d_{e}\) necessarily induces an evolution of the apparent modulus of elasticity \(E_{app}\). Indeed, if the volume fraction \(F_{vol}\) increases, it is reasonable to anticipate an increase of \(E_{app}\). However, this is not always the case. Figure 6 illustrates the evolution of \(E_{app}\) and \(F_{vol}\) as a function of \(d_{e}\) for two types of microstructures. One of the interesting observations that can be made on this figure is the progressive convergence of results with KUBC and SUBC. This convergence clearly illustrates a presence of side effects due to FEA boundary conditions and due to the method used for particles insertion. This observation also brings about an explanation about why SUBC results in Fig. 13a from [45], which are initially below the HS– limit without erosion, cross above the HS– limit when erosion distance increases. The underlying evolution of \(F_{vol}\) with \(d_{e}\) makes it possible to observe that \(E_{app}\) basically follows the evolution of \(F_{vol}\) with \(d_{e}\). Table 4 lists elasticity moduli obtained for non-eroded SVEs (\(d_{e} = 0\)) and for eroded SVEs with erosion distance \(d_{e} = 0.2\). When \(d_{e} = 0.2\), all results with KUBC are above the HS− limit and the difference ∆(%) between moduli with KUBC and SUBC is significantly reduced. It can also be observed that the standard deviation of elasticity modulus slightly increases with \(d_{e}\). However, the envelope formed by average results in KUBC and SUBC with their respective standard deviations is clearly narrower than that without erosion.

Fig. 6
figure 6

Evolution of \(E_{app}\) and \(F_{vol}\) as a function of erosion distance \(d_{e}\)

Full size image
Table 4 Apparent elasticity modulus \(E_{app}\) and analytics bounds for non-eroded and eroded SVEs generated with the RSA
Full size table

3.2 Homogenization analysis

As mentioned previously, mechanical properties of the simulated glass fiber composite are considered as isotropic. Compressibility modulus \(K_{app}\), shear modulus \(G_{app}\) and ultimately apparent elasticity modulus \(E_{app}\) are calculated based on this assumption. \(K_{app}\) is evaluated using a spherical load while \(G_{app}\) is evaluated using a deviatoric load. To ensure that the resulting modules are representative, several metrics are evaluated. In order to check whether the tensors of strain and stress are always spherical or deviatoric at a given erosion distance \(d_{e}\), the difference in loading as a function of the erosion distance is calculated as explained in [24]. The difference in spherical loading for each component \(\underline{{\underline{{{\updelta }^{S} }} }} \left( {a_{ij} } \right)\) of tensor \(\underline{{\underline {a} }}\) is calculated according to Eq. (6). The global difference in spherical loading \({\Delta }^{S} \left( {\underline{{\underline {a} }} } \right)\) is calculated using Eq. (7). The difference in deviatoric loading \({\Delta }^{D} \left( {\underline{{\underline {a} }} } \right)\) is evaluated in a similar way using Eqs. (8) and (9).

$$ \underline{{\underline{{\updelta ^{S} }} }} (a_{{ij}} ) = \left| {\frac{{3\left\langle {a_{{ij}} } \right\rangle _{{V_{{d_{e} }} }} }}{{\left\langle {a_{{11}} } \right\rangle _{{V_{{d_{e} }} }} + \left\langle {a_{{22}} } \right\rangle _{{V_{{d_{e} }} }} + \left\langle {a_{{33}} } \right\rangle _{{V_{{d_{e} }} }} }}} \right| - \updelta _{{ij}} $$
(6)
$$\begin{aligned} {\Delta }^{S} \left( {\underline{{\underline {a} }} } \right)&= \frac{1}{9}\left( \left| {{\updelta }^{S} \left( {a_{11} } \right)} \right| + \left| {{\updelta }^{S} \left( {a_{22} } \right)} \right| + \left| {{\updelta }^{S} \left( {a_{33} } \right)} \right|\right.\\ &\quad \left. + 2\left| {{\updelta }^{S} \left( {a_{12} } \right)} \right| + 2\left| {{\updelta }^{S} \left( {a_{23} } \right)} \right| + 2\left| {{\updelta }^{S} \left( {a_{13} } \right)}\right| \right) \end{aligned} $$
(7)
$$ \underline{{\underline{{\updelta ^{D} }} }} (a_{{ij}} ) = \left| {\frac{{3\left\langle {a_{{ij}} } \right\rangle _{{V_{{d_{e} }} }} }}{{\left\langle {a_{{12}} } \right\rangle _{{V_{{d_{e} }} }} + \left\langle {a_{{23}} } \right\rangle _{{V_{{d_{e} }} }} + \left\langle {a_{{13}} } \right\rangle _{{V_{{d_{e} }} }} }}} \right| - (1 - \updelta _{{ij}} ) $$
(8)
$$ \begin{aligned} {\Delta }^{D} \left({\underline{{\underline {a} }} } \right) &= \frac{1}{9}\left( \left|{{\updelta }^{D} \left( {a_{11} } \right)} \right| + \left|{{\updelta }^{D} \left( {a_{22} } \right)} \right| + \left|{{\updelta }^{D} \left( {a_{33} } \right)} \right|\right.\\ &\quad \left. + 2\left| {{\updelta }^{D} \left( {a_{12} } \right)} \right|+ 2\left| {{\updelta }^{D} \left( {a_{23} } \right)} \right| +2\left| {{\updelta }^{D} \left( {a_{13} } \right)} \right| \right)\end{aligned} $$
(9)

Figures 7, 8, 9 and 10 show the difference between spherical and deviatoric loadings for a complete SVE and results obtained with an increasing erosion distance, both with KUBC and SUBC. Tables 5 and 6 lists differences for \(d_{e} = 0.0\) and \(d_{e} = 0.2\). With KUBC at \(d_{e} = 0.0\), \({\Delta }^{S} \left( {\underline{{\underline {E} }} } \right)\) is close to zero while \({\Delta }^{D} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) is around 5% (Figs. 7, 9). The opposite tendency is observed with SUBC. As \(d_{e}\) increases, loading differences slightly increase (Figs. 8, 10). This increase is more pronounced for \(\underline{{\underline {E} }}\) in KUBC and for \(\underline{{\underline {{\Sigma }}}}\) in SUBC for both loading types. Loading differences for \(d_{e} = 0.2\) are more pronounced for microstructures made of cylindrical particles (Figs. 7b, 8b, 9b, 10b) than for microstructures made of spherical particles (Figs. 7a, 8a, 9a, 10a). However, load differences for \(d_{e} = 0.2\) remain relatively low.

Fig. 7
figure 7

Evolution of loading gap \({\Delta }^{S} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{S} \left( {\underline{{\underline {E} }} } \right)\) (KUBC—spherical loading) with erosion distance \(d_{e}\)

Full size image
Fig. 8
figure 8

Evolution of loading gap \({\Delta }^{S} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{S} \left( {\underline{{\underline {E} }} } \right) \)(SUBC—spherical loading) with erosion distance \(d_{e}\)

Full size image
Fig. 9
figure 9

Evolution of loading gap \({\Delta }^{D} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{D} \left( {\underline{{\underline {E} }} } \right)\) (KUBC—spherical loading) with erosion distance \(d_{e}\)

Full size image
Fig. 10
figure 10

Evolution of loading gap \({\Delta }^{D} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{D} \left( {\underline{{\underline {E} }} } \right)\) (SUBC—deviatoric loading) with erosion distance \(d_{e}\)

Full size image
Table 5 Loading gap on \(\underline{{\underline {{E }}}}\) (%)
Full size table
Table 6 Loading gap on \(\underline{{\underline {{\Sigma }}}}\) (%)
Full size table

To evaluate the variation of internal energy due to erosion, the difference in averaged elastic energy between the eroded SVE compared to the complete SVE is calculated. For each finite element \(K\), the elastic energy \(e^{pot}\) is calculated according to Eq. (10) where \({\mathcal{C}}\) is the stiffness tensor inside \(K\). The difference between the averaged elastic energy of an eroded SVE and a non-eroded SVE \({\Delta }^{{e^{pot} }} \left( {d_{e} } \right)\) is calculated following Eq. (11).

$$ e^{pot} = \frac{1}{2}\mathop \int \limits_{K} \underline {\underline {\epsilon } } :{\mathcal{C}}:\underline {\underline {\epsilon } } $$
(10)
$$ \Delta ^{{e^{{pot}} }} (d_{e} ) = \frac{{\left\langle {e^{{pot}} } \right\rangle _{{V_{{d_{e} }} }} - \left\langle {e^{{pot}} } \right\rangle _{V} }}{{\left\langle {e^{{pot}} } \right\rangle _{V} }} $$
(11)

The difference in elastic energy \({\Delta }^{{e^{pot} }} \left( {d_{e} } \right)\) for each SVE configuration for \(d_{e} = 0.2\) is listed in Table 7. Figure 11 illustrates the evolution of \({\Delta }^{{e^{pot} }} \left( {d_{e} } \right)\) for RSA_S1FV10 and RSA_C1FV10 cases. Boundary effects caused by particle insertion can be observed. Indeed, \({\Delta }^{{e^{pot} }}\) significantly drops between \(d_{e} = 0.0\) and \(d_{e} = 0.1\) and remains nearly constant for \(d_{e} > 0.1\). This drop is more important with cylindrical particles. This drop indicates that the elastic energy is higher close to the borders of SVEs, which can be explained by the fact that there are fewer particles in these areas. Figure 12 illustrates the distribution of elastic energy for a RSA_C1FV10 case.

Table 7 Difference in elastic energy \({\Delta }^{{e^{pot} }} \left( {d_{e} } \right)\)
Full size table
Fig. 11
figure 11

Evolution of \({\Delta }^{{e^{pot} }}\) with erosion distance \(d_{e}\) for RSA_S1FV10 and RSA_C1FV10 cases

Full size image
Fig. 12
figure 12

Distribution of elastic energy for a RSA_C1FV10 case under spherical KUBC loading

Full size image

To verify if the Hill-Mandel macro-homogeneity condition is verified, difference \({\Delta }^{Hill} \left( {d_{e} } \right)\) between the macroscopic work \(\underline{{\underline {E} }}_{{d_{e} }} :\underline{{\underline {{\Sigma }}}}_{{d_{e} }}\) and the volume averaged mesoscopic work \(\left \langle \underline {\underline {\epsilon } }_{{d_{e} }} :\underline{{\underline {{\upsigma }}}} \right \rangle_{{V_{{d_{e} }} }}\) based on the erosion distance is evaluated according to Eq. (12). This condition states that macroscopic work must be equal to the volume average of mesoscopic work.

$$ {\Delta }^{Hill} \left( {d_{e} } \right) = \frac{{ \left \langle\underline {\underline {\epsilon}} :\underline{{\underline{{\upsigma}}}} \right \rangle_{{V_{{d_{e} }} }} - \underline{{\underline {E} }}_{{d_{e} }} :\underline{{\underline {{\Sigma }}}}_{{d_{e} }} }}{{\underline{{\underline {E} }}_{{d_{e} }} :\underline{{\underline {{\Sigma }}}}_{{d_{e} }} }} $$
(12)

The difference between macroscopic work and the volume average of mesoscopic work as a function of the erosion distance is evaluated for each type of sample. Figure 13 illustrates the evolution of \({\Delta }^{Hill} \left( {d_{e} } \right)\) for a RSA_S1FV10 case and a RSA_C1FV10 case. For all SEVs considered, \({\Delta }^{Hill} \left( {d_{e} } \right)\) remains below ± 5%, which means that Hill's macro-homogeneity condition is therefore quite well satisfied.

Fig. 13
figure 13

Evolution of \({\Delta }^{Hill}\) with erosion distance \(d_{e}\) for a RSA_S1FV10 and b RSA_C1FV10

Full size image

3.3 Choosing the appropriate erosion distance

The choice of the appropriate erosion distance at which the mechanical properties are accounted requires finding the minimum distance at which boundary effects are negligible. A generalized method with which the optimal erosion distance could be found for any given microstructure is not reported in this work and remains to be studied and implemented. Such a method would require balancing the minimum erosion distance with the minimum variation of loading and potential energy. In the results presented above, mechanical properties could be evaluated for \(d_{e} = 0.2\) since, at this level, the variation of potential energy is low for all SVEs. In a more general perspective, a proper calibration of the targeted non-eroded volume fraction is necessary to obtain the correct eroded volume fraction using the RSA algorithm.

3.4 Benefits of the erosion method proposed

One problematic encountered when modeling SVEs is that the distance and angle between two particles and between a particle and the SVE border must stay below a minimum threshold to account for mesh generation issues. If this distance is too small, it will result in either a few numbers of ill shaped mesh elements or too many very small well shaped mesh elements. The same logic applies for small angles between particles and between a particle and the SVE border. Another problematic is boundary effects caused by FEA boundary conditions, which are inevitable when modeling non-periodic microstructures. The erosion method presented here alleviates these two problems by only considering results that are far enough from the SVEs borders. Thus, erosion makes it possible to faithfully generate microstructures with a high-volume fraction of particles, which could not be modeled otherwise considering minimum distance and angle criterions for inserting particles. The implementation of erosion is simple and does not require any modification of the geometric model, of the FEA mesh or FEA model since it is only based on processing FEA results. When using the erosion method, one must keep in mind that the eroded SVE is not guaranteed to be in perfect equilibrium with the boundary conditions applied to the non-eroded SVE. In the present case, this non equilibrium is illustrated by the difference \({\Delta }^{Hill} \left( {d_{e} } \right)\). Still, the benefits provided by the erosion method are significant considering that \({\Delta }^{Hill} \left( {d_{e} } \right)\) is below 5%.

4 Generation of SVEs based on rigid multibody dynamics

As mentioned in the introduction, one important drawback of the RSA is the relatively low volume fractions achievable. Indeed, once a particle is inserted with the RSA, it cannot move anymore, which limits the ability to pack particles. The following method uses a rigid MultiBody Dynamics (MBD) approach to position particles in a SVE. In this project, the simulation of motion and collision of rigid particles is carried out by a time-driven based algorithm. The equations governing dynamics of moving and colliding particles are updated at each time step \(T_{step}\). The opensource library Project Chrono [47] is used to perform these rigid multibody simulations. The first step of this process is creating the generation domain \({\Omega }_{gen}\). The dimensions of this domain are slightly larger than the SVE dimensions in order to avoid boundary effects caused by particles in contact with the borders of \({\Omega }_{gen}\). In this work, a SVE is a unit cube of material and \({\Omega }_{gen}\) is a cube that is slightly larger than this unit cube. \({\Omega }_{gen}\) boundaries are considered as rigid and impenetrable walls that act as impassible barriers. One by one, \({\Omega }_{gen}\) is filled with particles without any concern to interference between particles as illustrated in Fig. 14. Position \(P\left( {x,y,z} \right)\), orientation \(Ori\left( {\phi ,{\uptheta }} \right)\) and geometric parameters \(Geo_{{\mathcal{P}}}\) (radius, length, etc.) of particles are generated according to predetermined distributions. The volume fraction of particles \(F_{vol}\) is evaluated after each particle insertion in \({\Omega }_{gen}\) and particles are added until the targeted volume fraction \(F_{{vol_{target} }}\) is reached. Then, the boundary of each particle is tessellated using a surface Delaunay based triangulation method. These tessellations are used for detecting collisions between particles along MBD calculations. To enforce a minimum distance \(Dist_{min}\) between two particles, the tessellation is outwardly offset by \(Dist_{min} /2\). Therefore, if the tessellations of two particles are in contact (with no penetration) minimum distance \(Dist_{min}\) between these two particles is respected. The algorithm used for filling \({\Omega }_{gen}\) with particles is described in Algo 1.

Fig. 14
figure 14

Initial distribution of particles

Full size image

At this stage of the process, the resulting set of particles generated is not valid since there are many overlap occurrences. The next step of this generation process is to eliminate these overlaps (see Algo 2).

This step is carried out by MBD (based on Project Chrono in this work). A velocity vector is first applied to the center of mass of two overlapping particles in opposite directions in order to separate these two particles. Given enough space, overlapping particles will eventually separate from each other. The collision response model used considers that there is no kinetic energy loss in a collision between two particles. This eliminates eventual percolation effects that could occur when multiple particles collide and bond between each other through loss of kinetic energy. Once all overlap occurrences have been resolved this way, particles are gradually slowed down to reach a rest state. This rest state occurs when the velocity of a particle is very close to zero. Particles in rest state are faster to compute which accelerates the simulation. The simulation ends when all particles are at a rest state. The rigid multibody dynamic simulation algorithm is detailed in Algo 3.

First, the generation domain \({\Omega }_{gen}\) is created. Particles are inserted using the Filling algorithm (Algo 1) and overlaps are resolved using a MBD simulation (Algo 2). The SVEs domain is created, in this case, a unit cube labeled as \(M_{struct}\). Position and orientation of particles obtained with MBD are used to automatically generate the CAD representation of SVEs. CAD methods and tools used to generate this geometric representation are similar to those used in [45]. As mentioned in the introduction, to be inserted, a particle needs to meet minimal distance and angle criterions. A particle that does not conform to these criterions is removed and is not replaced by a new particle. Consequently, since the targeted volume fraction \(F_{{vol_{target} }}\) is respected during the MBD simulation, the actual resulting volume fraction will be lower than \(F_{{vol_{target} }}\). Excluded particles are mostly located close to SVEs borders as illustrated in Fig. 15. Before mesh generation, resulting CAD representations of SVEs are analyzed using different metrics such as volume fraction of each constituents, number of particles, and orientation tensor [48] for elongated particles.

Fig. 15
figure 15

Illustration of voids caused by the exclusion of non-conforming particles

Full size image

Mesh generation is carried out using 2D and 3D advancing front mesh generation algorithms as described in [45]. Beforehand, a mesh size map is generated with the objective of ensuring that a minimum number of mesh elements is generated between two distinct topological entities (for example between two particles). In this work, meshes used are composed of quadratic tetrahedrons. Boundary conditions are automatically applied to the faces of SVEs. As mentioned previously, Kinematic Uniform Boundary Conditions (KUBC) and Static Uniform Boundary Conditions (SUBC) are used to evaluate the apparent elasticity modulus \(E_{app}\). Again with the assumption of a macroscopically isotropic composite, spherical and deviatoric loads are used [45]. FEA simulation of SVEs is automatically performed with the use of the UTM linked to the open-source solver Code_Aster [49]. Like in Sect. 3 for SVEs generated with the RSA, material properties resulting from homogenization of entire and partially eroded SVEs are then calculated.

5 Homogenization results obtained for SVEs generated with MBD simulations

5.1 Homogenization results

To evaluate the effect of erosion on homogenized mechanical results, SVEs are generated with the multibody dynamics approach presented in the previous section (referred to with the prefix MBD) in the two following contexts:

  • with particles intersecting SVEs borders (referred to with the suffix INT)

  • without particles intersecting SVEs borders (referred to with the suffix NOI).

Table 8 lists the different configurations considered with spherical (S) and cylindrical (C) particles.

Table 8 RSA SVE configurations
Full size table

Figure 16 illustrates BREP models of each MBD configuration. Even though some of the SVEs were generated with the possibility that a particle intersects SVE borders (INT cases), it can be observed that there are few particles touching SVE borders. Indeed, compared with RSA based SVEs, the MBD generation approach does not generate a new particle to replace a non-conforming particle.

Fig. 16
figure 16

Illustration of BREP models for each MBD configuration

Full size image

Orientation tensors for SVEs with cylindrical particles are shown in Tables 9, 10, 11 and 12 for 4 configurations. These 4 tensors show that the orientation of cylindrical particles closely fits an isotropic distribution which is, in our case, an objective in the generation of non-spherical particles. This indicates that the MBD based generation of particles meets the isotropic distribution at which the particles were initially positioned.

Table 9 Orientation tensor for MDB_C1FV10_INT
Full size table
Table 10 Orientation tensor for MDB_C1FV10_NOI
Full size table
Table 11 Orientation tensor for MDB_C1FV30_NOI
Full size table
Table 12 Orientation tensor for MDB_C2FV30_NOI
Full size table

The volume fraction of particles obtained with a \(d_{e} = 0.0\) erosion distance (without erosion) and a \(d_{e} = 0.2\) erosion distance, along with the number of mesh elements generated are listed in Table 13. As expected, volume fraction for \(d_{e} = 0.0\) is significantly lower than the target volume fraction for each case, which explains given the nearly absence of particles close to the SVE boundary. When \(d_{e} = 0.2\), volume fraction obtained is close to the target volume fraction for each case. It can also be observed that not inserting a particle that intersects the SVE boundary (NOI cases) decreases the number of mesh elements. Indeed, for NOI cases the size map does not need to be refined close to the SVE boundary since nearly no particles are located there.

Table 13 Volume fractions and mesh statistics for MBD based SVEs
Full size table

Figure 17 illustrate the evolution of apparent elasticity modulus \(E_{app}\) as a function of the erosion distance. Table 14 lists \(E_{app}\) for SVEs eroded with \(d_{e} = 0.2\). Analytical bounds (Reuss, Voigt and Hashin–Shtrikman) are calculated according to the volume fraction of particles obtained after erosion. All modules are located inside these analytical bounds. The difference between \(E_{app}\) obtained with KUBC and SUBC conditions is very small. As for microstructures obtained with the RSA method, the more the erosion distance increases the more the apparent elasticity modules \(E_{app}\) with KUBC and SUBC converge towards the same value. The difference between results obtained with and without intersections (between INT and NOI cases) is small and standard deviations obtained show that this difference cannot be clearly related to a presence or absence of particles close to the SVE boundary. A comparison between Table 4 and Table 14 show that apparent elasticity moduli calculated for MBD_S1FV10 and MBD_C1FV10 microstructures are close to those calculated for RSA_S1FV10 and RSA_C1FV10 microstructures with \(d_{e} = 0.2\). Apparent elasticity moduli calculated for SVEs composed of 30% of particles (in volume) are much higher than those obtained for a 10% volume fraction. These moduli are more distant from HS bounds—which is expected given the high-volume fraction in particles.

Fig. 17
figure 17figure 17

Evolution of apparent elasticity modulus \(E_{app}\) as a function of the erosion distance \(d_{e}\)

Full size image
Table 14 Apparent elasticity modulus \(E_{app}\) and analytics bounds for non-eroded and eroded SVEs generated with MBD
Full size table

5.2 Analysis of homogenization results

Loading differences obtained for SVEs generated with MBD are similar to those observed with SVEs generated with the RSA. In addition, no clear difference can be made between loading differences observed for MBD_NOI and MBD_INT cases (Fig. 18). Figures 19, 20, 21 and 22 illustrates loading differences for MDB_S2FV30_NOI and MDB_C2FV30_NOI. As for the difference in elastic energy, the situation is similar for the MBD: \({\Delta }^{{e^{pot} }}\) significantly drops between \(d_{e} = 0.0\) and \(d_{e} = 0.1\) and remains nearly constant for \(d_{e} > 0.1\) (Fig. 23). Hill's macro-homogeneity condition is quite well satisfied Similar to what is observed for SVEs generated with the RSA, Hill's macro-homogeneity condition is quite well satisfied since \({\Delta }^{Hill} \left( {d_{e} } \right)\) remains below ± 5% for all SEVs considered.

Fig. 18
figure 18

Evolution of loading gap \({\Delta }^{S} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{S} \left( {\underline{{\underline {E} }} } \right)\) (KUBC—spherical loading) with erosion distance \(d_{e}\)—(NOI vs INT)

Full size image
Fig. 19
figure 19

Evolution of loading gap \({\Delta }^{S} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{S} \left( {\underline{{\underline {E} }} } \right) \)(KUBC—spherical loading) with erosion distance \(d_{e}\)

Full size image
Fig. 20
figure 20

Evolution of loading gap \({\Delta }^{S} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{S} \left( {\underline{{\underline {E} }} } \right) \)(SUBC—spherical loading) with erosion distance \(d_{e}\)

Full size image
Fig. 21
figure 21

Evolution of loading gap \({\Delta }^{S} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{S} \left( {\underline{{\underline {E} }} } \right) \)(KUBC—deviatoric loading) with erosion distance \(d_{e}\)

Full size image
Fig. 22
figure 22

Evolution of loading gap \({\Delta }^{S} \left( {\underline{{\underline {{\Sigma }}}} } \right)\) and \({\Delta }^{S} \left( {\underline{{\underline {E} }} } \right) \)(SUBC—deviatoric loading) with erosion distance \(d_{e}\)

Full size image
Fig. 23
figure 23

Evolution of \({\Delta }^{{e^{pot} }}\) with erosion distance \(d_{e}\) for MBD_S2FV30 and MBD_C2FV30 cases

Full size image

5.3 Choosing the appropriate erosion distance

As mentioned in Sect. 3.3, the choice of the appropriate erosion distance requires balancing the minimum erosion distance with the minimum variation of loading and potential energy. Size of particles with respect to the dimension of the generation domain \({\Omega }_{gen}\) can also affect the erosion distance. Large particles in a small \({\Omega }_{gen}\) will affect the particle’s distribution. Since \({\Omega }_{gen}\) is an impenetrable barrier, it affects the particle’s distribution by limiting their movements. Therefore, a small \({\Omega }_{gen}\) coupled with large particles will require a larger erosion distance to avoid a biased particle distribution than a large \({\Omega }_{gen}\) coupled with small particles. A generalized method with which the optimal ratio of particle size to \({\Omega }_{gen}\) size is not reported in this work and remains to be implemented.

5.4 Benefits of the MBD based method

It is important to outline that using the rigid multibody dynamics (MBD) generation method without erosion would not yield representative results as the volume fraction close to SVE borders is far below the targeted volume fraction. Indeed, the main limitation of the MBD generation method is the difficulty in inserting particles close to SVE boundaries, due to insertion criteria used. As demonstrated above, erosion, by only considering the representative core of SVEs, makes it possible to use rigid multibody dynamics as a method towards the automatic generation of microstructures. The interest of using MBD based methods is that it allows managing and positioning very slender particles, which could not be properly arranged with the RSA. Indeed, one of the potentials of MBD based methods is their ability to pack particles closer to each other while avoiding overlaps. Thus, combining MBD with erosion opens the path towards being able to model materials with more realistic shapes of particles.

6 Conclusion

Statistical volume element representation of particle based composite materials can be challenging when the targeted volume fraction is high or when particles are elongated. Densely packing particles with no overlaps has been the subject of many research papers and remains a tedious task when dealing with non-spherical particles. If not accounted for, the position and orientation of particles that are close to the faces SVEs can induce significant meshing problems in the form of ill shaped elements or incommensurable quantity of small elements. The proposed method is aimed at addressing these two problems. The spatial arrangement of particles is carried out in two main steps. First particles are randomly positioned according to pre-defined position and orientation distributions without considering overlaps. Overlapping particles are gradually moved using a multibody simulation which adds flexibility to the entire particle arrangement. Once all overlaps are resolved, a CAD model of the SVE is generated using a UTM based platform. Each particle is subjected to insertion criterions in order to promote mesh quality and mesh generation convergence. Any particles not meeting these criterions is rejected and not replaced. The SVE is meshed and FEA analysis is automatically performed, thanks to the UTM. To account for particle deficient areas created close to the borders of a SVE, an erosion-based homogenization method is used to evaluate volume averaged fields in the inner core of the SVE instead of inside the entire SVE. The erosion method is applied on FEA results obtained with the whole SVE and thus does not require any subsequent FEA analysis. Mechanical properties can be evaluated at different levels of erosion along with validation metrics. To illustrate the potential of this method, a short glass fiber/epoxy composite material is simulated and compared with results obtained on non-eroded SVEs generated with the RSA algorithm. Extending this methodology to various other shapes of particles and to flexible particles could be easily foreseen for future work.