1 Introduction

The objective of non-intrusive frameworks is to carry out advanced numerical methods as a result of efficient linear and non-linear solvers applied in the commercial software and used as “black boxes”. An example of the above is that it is feasible to operate the free open-source industrial finite elements software code-aster [12] with the Python interface. Advanced algorithms can be designed within this Python interface and call non-linear methods of code-aster to consider complex phenomena. In addition, depending on the perspective, the non-intrusivity might be the alternative to “enrich” a global model with those that are more detailed and without modifying the global one. For example, the global model could be the product of a long industrial process, which might not be altered easily. In this regard, methods considering local models without altering the global one can be perceived as non-intrusive.

The global/local approach [38] is a very good option for implementing the non-intrusive method [16]. In essence, the idea is to introduce some more localized details into a global and coarse model and potentially add non-linear behaviours in specific areas without altering the global model. Summarizing, a global and a local model connected through an interface coexist. The global/local approach is about an iterative Dirichlet-Neumann algorithm and an iteration consisting of two steps: (1) a problem in the local model with Dirichlet boundary conditions on the interface, and (2) a problem in the global model with Neumann boundary conditions on the interface. Connections with optimized Schwarz domain decomposition methods can be observed in [18]. The global/local structure has been expanded to a domain decomposition method [11] and has been implemented to different types of non-linearities such as crack propagation [11, 28, 32], structural joints and assemblies [19], local plasticity [16] and cycling visco-elastic behaviour [4]. It is possible to find other studies regarding different applications and improvements for non-intrusive frameworks and the global/local method in [1, 6, 15, 17, 18, 23].

Considering the St. Venant’s principle, the interface between the local and global models should be nowhere near the local details to avoid the inaccuracy of the Dirichlet boundary conditions from the linear global model close to the area of potential non-linearity. This problem could be solved by using Robin parameters on the interface. The first proposal to apply Robin parameters on the interface for a local plastic model can be found in [15]. Their idea is to design a “quasi-optimal” Robin parameter avoiding the full computation of the Schur complement of the complementary models. They prefer two-scale Robin parameters that include both short and long-range effects. Very recent works [1, 28] applied a global/local approach with Robin conditions for phase field modelling for mechanical and hydraulic fractures in porous media. They chose the Schur complement of the complementary domain and observed very good performance, improving drastically the convergence of the global/local algorithm.

Finally, a formal mathematical approach to Mixed Domain Decomposition Methods and the application for non-intrusive analysis with Robin Parameters can be found in [27, 28, 31].

This paper focuses on the global/local method with a non-intrusive implementation of Robin parameters on the interface. These Robin parameters are developed with a strip of elements linked to the interface similarly as [15]. The choice of these Robin parameters is crucial for the convergence of the method. The optimal choice is classically known but with an unaffordable cost as it would involve the computation of a Schur complement of a large model. Therefore, approximations are sought and we propose to carry out an optimization of the parameters to obtain a better convergence of the mixed method for the global/local analysis and study the impact of the Robin parameter as well.

The article is structured as follows: Section 2 formulates the global/local method as a Dirichlet-Neumann algorithm; Section 3 pursues the global/local method with the Robin parameters; Section  4 and subsequent sections illustrate the improvements of our implementation with numerical examples and different non-linear problems in 2D and 3D models, as well as the optimization of the Robin parameters.

2 Global/local problem formulation

2.1 Reference problem

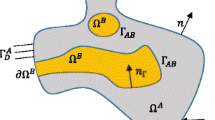
A mechanical model of a structure determined on a domain \(\varOmega _R\) is considered. This domain consists of two non-overlapping domains \(\varOmega _C\), the complementary domain, and \(\varOmega _L\), the local domain. \(\varOmega _C\) considers elastic linear isotropic assumptions with small perturbations, meanwhile in \(\varOmega _L\), the mechanical model may be non-linear, such as a crack propagation model or a plastic material. This local model allows embedding localized richer contents in the structure’s simple global model. \(\varGamma \) is noted as the interface between the complementary and local models.

Defining the admissible space of displacements as:

$$\begin{aligned} V\left( \varOmega _R\right) =\left\{ v\in H_1\left( \varOmega _R\right) ~v=u_d~\text {on}~\partial _u\varOmega _R\right\} \end{aligned}$$
(1)

.

The mechanical problem is equivalent to:

$$\begin{aligned} \text {Find}~u\in V\left( \varOmega _R\right) ,~ a_R(u,v)=l_R(v),~\forall v\in V_0\left( \varOmega _R\right) \end{aligned}$$
(2)

with \(a_R\) the bi-linear form representing the structure’s equilibrium and \(l_R\) the linear form symbolizing the Neumann boundary conditions. The Dirichlet boundary conditions are taken into account in the affine space \(V\left( \varOmega _R\right) \).

A discretization of standard finite elements with Lagrange shape functions is considered in order to obtain discrete models for which a conforming mesh in the interface between the complementary and local models is adopted.

A full elastic linear isotropic material over the whole domain \(\varOmega _R=\varOmega _C\cup \varOmega _L\) is considered to detail the methods and the equation. Under this type of hypothesis, the discrete problem becomes as follows:

$$\begin{aligned} \text {Find}~\mathbf {u}_R~\text {solution of}~ \mathbf {K}_R\mathbf {u}_R= \mathbf {f}_d^R\end{aligned}$$
(3)

with \(\mathbf {K}_R\) the stiffness matrix, \(\mathbf {u}_R\) the discrete unknown of displacements and \(\mathbf {f}_d^R\) the right-hand side conforming to the boundary conditions. The null Dirichlet conditions are expected to be eliminated.

Fig. 1
figure 1

Reference problem

Full size image

This reference problem can be seen as the coupling between the complementary model in \(\varOmega _C\) and the local model in \(\varOmega _L\), as presented in Figure  1. We note that \(\mathbf {K}_C\) and \(\mathbf {K}_L\) are the stiffness matrices of the complementary and local models respectively, \(\mathbf {u}_C\) and \(\mathbf {u}_L\) are the displacements in \(\varOmega _C\) and \(\varOmega _L\), \({\mathbf {f}_d^C}\) and \({\mathbf {f}_d^L}\) are the load vectors in \(\varOmega _C\) and \(\varOmega _L\). The perfect coupling of the two models to impose the continuity of the displacement is enforced with a Lagrange multiplier \(\varvec{\lambda }\) into the following Lagrangian:

$$\begin{aligned} {\mathcal {L}}\left( \mathbf {u}_C,\mathbf {u}_L,\varvec{\lambda }\right)= & {} \frac{1}{2}\mathbf {u}_C^T\mathbf {K}_C\mathbf {u}_C+ \frac{1}{2}\mathbf {u}_L^T\mathbf {K}_L\mathbf {u}_L-{\mathbf {f}_d^C}^T\mathbf {u}_C\nonumber \\&- {\mathbf {f}_d^L}^T\mathbf {u}_L+ \varvec{\lambda }^T\left( \mathbf {C}_C\mathbf {u}_C- \mathbf {C}_L\mathbf {u}_L\right) \end{aligned}$$
(4)

Where \(\mathbf {C}_C\) and \(\mathbf {C}_L\) are coupling operators. For conforming meshes, these are trace operators that extract displacements from \(\varOmega _C\) and \(\varOmega _L\) on the interface \(\varGamma \). They are sparse matrices filled with number ones in the indexes associated to the interface degrees of freedom.

The minimization of the Lagrangian leads to:

  • Equilibrium of the coarse model:

    $$\begin{aligned} \frac{\partial {\mathcal {L}}}{\partial \mathbf {u}_C} = \mathbf {K}_C\mathbf {u}_C+ \mathbf {C}_C^T\varvec{\lambda }- {\mathbf {f}_d^C}= 0 \end{aligned}$$
    (5)

  • Equilibrium of the local model:

    $$\begin{aligned} \frac{\partial {\mathcal {L}}}{\partial \mathbf {u}_L} = \mathbf {K}_L\mathbf {u}_L- \mathbf {C}_L^T\varvec{\lambda }- {\mathbf {f}_d^L}= 0 \end{aligned}$$
    (6)

  • Continuity of the interface displacements:

    $$\begin{aligned} \mathbf {C}_C\mathbf {u}_C- \mathbf {C}_L\mathbf {u}_L= 0 \end{aligned}$$
    (7)

Therefore we obtain the standard coupling system:

$$\begin{aligned} \text {Find}~\left( \mathbf {u}_C,\mathbf {u}_L,\varvec{\lambda }\right) ,~ \begin{bmatrix} \mathbf {K}_C&{} 0 &{} -\mathbf {C}_C^T\\ 0 &{} \mathbf {K}_L&{} \mathbf {C}_L^T\\ -\mathbf {C}_C&{} \mathbf {C}_L&{} 0 \end{bmatrix} \begin{bmatrix} \mathbf {u}_C\\ \mathbf {u}_L\\ \varvec{\lambda }\end{bmatrix} =\begin{bmatrix} {\mathbf {f}_d^C}\\ {\mathbf {f}_d^L}\\ 0 \end{bmatrix} \end{aligned}$$
(8)

This problem can be rewritten as two sub-problems: one over \(\varOmega _C\) with Neumann conditions of the interface \(\varGamma \) and the other problem over \(\varOmega _L\) with Dirichlet conditions on the interface \(\varGamma \):

$$\begin{aligned} \begin{aligned}&\text {Find}~\mathbf {u}_C,~\mathbf {K}_C\mathbf {u}_C= {\mathbf {f}_d^C}+ \mathbf {C}_C^T\varvec{\lambda }\\&\text {Find}~\left( \mathbf {u}_L,\varvec{\lambda }\right) ,~\begin{bmatrix} \mathbf {K}_L&{}\mathbf {C}_L^T\\ \mathbf {C}_L&{} 0 \end{bmatrix}\begin{bmatrix} \mathbf {u}_L\\ \varvec{\lambda }\end{bmatrix}=\begin{bmatrix} {\mathbf {f}_d^L}\\ -\mathbf {C}_C\mathbf {u}_C\end{bmatrix} \end{aligned} \end{aligned}$$
(9)

A Dirichlet-Neumann iterative algorithm is used to solve this problem. The iteration consists in the following two steps:

  1. 1.

    Knowing a \(\left( \mathbf {u}_L^n,\varvec{\lambda }^n\right) \) solution in \(\varOmega _L\) to solve a Neumann problem on \(\varOmega _C\):

    $$\begin{aligned} \text {Find}~\mathbf {u}_C^{n+1},~\mathbf {K}_C\mathbf {u}_C^{n+1}= {\mathbf {f}_d^C}+ \mathbf {C}_C^T\varvec{\lambda }^n\end{aligned}$$
    (10)
  2. 2.

    Knowing a \(\mathbf {u}_C^{n+1}\) solution in \(\varOmega _C\) to solve a Dirichlet problem on \(\varOmega _L\):

    $$\begin{aligned} \text {Find}~\left( \mathbf {u}_L^{n+1},\varvec{\lambda }^{n+1}\right) ,~\begin{bmatrix} \mathbf {K}_L&{}\mathbf {C}_L^T\\ \mathbf {C}_L&{} 0 \end{bmatrix}\begin{bmatrix} \mathbf {u}_L^{n+1}\\ \varvec{\lambda }^{n+1}\end{bmatrix}=\begin{bmatrix} {\mathbf {f}_d^L}\\ \mathbf {C}_C\mathbf {u}_C^{n+1}\end{bmatrix} \end{aligned}$$
    (11)

    and obtain \(\varvec{\lambda }^{n+1}\), the opposite of the reaction forces \(\varvec{\lambda }_L^{n+1}\) on the interface of the local model.

Remark 1

This type of algorithm could be considered with multiple local models and conceived as a non-overlapping domain decomposition [11].

2.2 Primal-dual global/local analysis

The subtlety of the global/local method is to slightly modify the problem in the complementary domain with the aim of not solving it in \(\varOmega _C\), but in a “global” domain \(\varOmega _G\), which corresponds to the union of \(\varOmega _C\) and an auxiliary domain \(\varOmega _A\). Globally, this auxiliary domain corresponds geometrically to the local domain \(\varOmega _L\) but coarsely meshed as the complementary model. As shown in Figure  2, the local model is substituted by an auxiliary model to obtain a global model.

Fig. 2
figure 2

Linear problem

Full size image

This can also be interpreted differently. Starting from a global model with a coarse mesh and an elastic linear isotropic material, this model can be enriched with localized details such as structural details (holes or a particular geometry) or complex non-linear behaviour (plasticity or cracks). This is especially suitable in an industrial design process where the global model may not be easily changed to incorporate localized details.

The complementary problem to be solved is defined as:

$$\begin{aligned} \text {Find}~\mathbf {u}_C^{n+1},~\mathbf {K}_C\mathbf {u}_C^{n+1}= {\mathbf {f}_d^C}+ \mathbf {C}_C^T\varvec{\lambda }^n\end{aligned}$$
(12)

The contribution of the auxiliary model is added to the two sides of the equation where the exponent \(n+1\) and n are omitted in order to simplify the notations:

$$\begin{aligned} \overline{\mathbf {K}}_C\overline{\mathbf {u}}_C+ \overline{\mathbf {K}}_A\overline{\mathbf {u}}_A= \underset{{\mathbf {f}_d^G}}{\underbrace{\overline{\mathbf {f}}_d^C+ \overline{\mathbf {f}}_d^A}} + \mathbf {C}_G^T\varvec{\lambda }+\underset{\mathbf {C}_G^T\varvec{\lambda }_A}{\underbrace{\overline{\mathbf {K}}_A\overline{\mathbf {u}}_A- \overline{\mathbf {f}}_d^A}} \end{aligned}$$
(13)

where the notation \(\overline{\square }_{X}\) means that the variable or operator \(\square \) specified in \(\varOmega _X\) is extended with zeros to the domain \(\varOmega _G\) for the rest of the degrees of freedom. In addition, \(\overline{\mathbf {f}}_d^A\) corresponds to the boundary conditions that could be implemented on the auxiliary model in order to represent an approximation of those on the local model. The term \(\overline{\mathbf {K}}_A\overline{\mathbf {u}}_A- \overline{\mathbf {f}}_d^A\) symbolizes the reaction forces of a Dirichlet problem on the auxiliary model with displacement \({\mathbf {u}_G}_{|\varGamma }\) imposed in \(\varGamma \) and a Neumann boundary condition through \(\overline{\mathbf {f}}_d^A\). For more details see [18].

Therefore, as \(\overline{\mathbf {u}}_C=\overline{\mathbf {u}}_A\) on the interface \(\varGamma \), the equation becomes as follows:

$$\begin{aligned} \begin{aligned} \mathbf {K}_G\mathbf {u}_G^{n+1}&= {\mathbf {f}_d^G}+ \mathbf {C}_G^T\varvec{\lambda }^n+ \mathbf {C}_G^T\varvec{\lambda }_A^n\\&= {\mathbf {f}_d^G}+ \mathbf {C}_G^T\mathbf {P}^{n}\end{aligned} \end{aligned}$$
(14)

with \(\mathbf {u}_G^{n+1}\) the displacement specified on the global model. The reaction forces \(\varvec{\lambda }_A^n\) are computed with displacement \(\mathbf {u}_G^n\) from the previous iteration of the algorithm. \(\mathbf {P}^{n}=\varvec{\lambda }_A^n-\varvec{\lambda }_L^n\) represents the correction of forces that will be applied to the global model in order to consider the local model. It can also be observed that \(\mathbf {P}^{n}\) verifies the following equations assuming exact solutions for the global and local problems [18]:

$$\begin{aligned} \begin{aligned} \mathbf {P}^{n}&= \varvec{\lambda }_A^{n+1}+\varvec{\lambda }_C^{n+1}\\ \mathbf {P}^{n+1}&= \mathbf {P}^{n}+\mathbf {r}^{n+1}~\text {with}~\mathbf {r}^{n+1}=-\left( \varvec{\lambda }_L^{n+1}+\varvec{\lambda }_C^{n+1}\right) \end{aligned} \end{aligned}$$
(15)

Under this notation, \(\mathbf {r}^{n+1}\) represents the disequilibrium of forces between the complementary model and the local model. When convergence is fulfilled, \(\mathbf {r}^{n+1}=0\) and the forces are balanced: the solution on \(\varOmega _C\cap \varOmega _L\) reaches the solution of the reference model.

The error indicator for the convergence of the method is the residual norm for each iteration normalized regarding the first residual obtained from global/local iterations, as presented in Eq. (16).

$$\begin{aligned} \eta =\frac{\Vert \mathbf {r}^{n+1}\Vert _2}{\Vert \mathbf {r}^{0}\Vert _2}\end{aligned}$$
(16)

2.3 Global/local algorithm

The iterations described above lead to the algorithm 1 of the global/local method.

Moreover, the case of matching meshes on the interface between auxiliary and local models is assumed. For the case of non-matching meshes, a projection step needs to be developed to communicate the displacement field from the global to the local model, and the reaction forces from the local to the global auxiliary domain.

This algorithm is no more than a fixed point for which the convergence is known to be slow. Full linear models can be considered as preconditioners for a Krylov solver to improve the convergence rate. In the case of a non-linear local model, quasi-Newton or Aitken’s relaxation must be taken into account [11, 18].

3 Global/Local method with robin parameters

As previously stated, the standard global/local analysis can be observed as a coupling of the complementary and local model by means of a Lagrange’s multiplier. This coupling problem can be solved with an iterative Dirichlet-Neumann fixed-point algorithm.

However, in the same way as Schwarz domain decomposition methods [14], Robin conditions can be introduced to enhance the convergence and obtain more flexibility. In fact, the kinematic compatibility between the complementary and local model is broken and replaced by Robin conditions written on the interface \(\varGamma \). The first studies in the global/local method with Robin conditions are introduced in [15] and reminded in [18]. The proposal in this paper is to go further and derive a complete mixed global/local method.

3.1 Derivation of global/local analysis with robin parameters

The mechanical problem is presented differently in this section as it follows a mixed domain decomposition framework. Instead of using a Lagrange’s multiplier specified on the interface \(\varGamma \), reaction forces \(\varvec{\lambda }_L\) and \(\varvec{\lambda }_C\) are considered as full unknowns on the interface. The conditions to be enforced at the interface are provided by writing the problem as a domain decomposition:

$$\begin{aligned} \begin{aligned}&\varvec{\lambda }_L+\varvec{\lambda }_C= 0&\text {Equilibrium of forces} \\&\mathbf {C}_L\mathbf {u}_L-\mathbf {C}_C\mathbf {u}_C= 0&\text {Continuity of displacements} \end{aligned} \end{aligned}$$
(17)

These two equations interpreting the interface behaviour are written with Robin conditions:

$$\begin{aligned} \begin{aligned}&\varvec{\lambda }_L+ \varvec{\lambda }_C- \mathbf {k}_C\left( \mathbf {C}_L\mathbf {u}_L- \mathbf {C}_C\mathbf {u}_C\right) = 0 \\&\varvec{\lambda }_L+ \varvec{\lambda }_C+ \mathbf {k}_L\left( \mathbf {C}_L\mathbf {u}_L- \mathbf {C}_C\mathbf {u}_C\right) = 0 \\ \end{aligned} \end{aligned}$$
(18)

\(\mathbf {k}_C\) and \(\mathbf {k}_L\) are Robin parameters, which are stiffness operators. Symmetric definite positive operators are selected to ensure the equivalence with Eq. (17) of the interface. These Robin conditions are determined and written on the interfaces, connecting reaction forces \(\varvec{\lambda }_C\) and \(\varvec{\lambda }_L\) to the interface displacements \(\mathbf {C}_L\mathbf {u}_L\) and \(\mathbf {C}_C\mathbf {u}_C\).

Thus, the new system to be solved is:

$$\begin{aligned} \begin{aligned}&\mathbf {K}_C\mathbf {u}_C= {\mathbf {f}_d^C}+ \mathbf {C}_C^T\varvec{\lambda }_C\\&\varvec{\lambda }_L+ \varvec{\lambda }_C- \mathbf {k}_C\left( \mathbf {C}_L\mathbf {u}_L- \mathbf {C}_C\mathbf {u}_C\right) = 0 \\&\mathbf {K}_L\mathbf {u}_L= {\mathbf {f}_d^L}+ \mathbf {C}_L^T\varvec{\lambda }_L\\&\varvec{\lambda }_L+ \varvec{\lambda }_C+ \mathbf {k}_L\left( \mathbf {C}_L\mathbf {u}_L- \mathbf {C}_C\mathbf {u}_C\right) = 0 \\ \end{aligned} \end{aligned}$$
(19)

Similarly, as the standard global/local method, the problem in the complementary model is generalized to the global model. Therefore, the first equation of the system becomes as follows:

$$\begin{aligned} \mathbf {K}_G\mathbf {u}_G= {\mathbf {f}_d^G}+ \mathbf {C}_G^T\varvec{\lambda }_C+ \mathbf {C}_G^T\varvec{\lambda }_A\end{aligned}$$
(20)

In addition, as \(\mathbf {u}_G\) and \(\mathbf {u}_C\) are equal on the interface \(\varGamma \), Robin conditions can also be written as:

$$\begin{aligned} \begin{aligned}&\varvec{\lambda }_L+ \varvec{\lambda }_C- \mathbf {k}_G\left( \mathbf {C}_L\mathbf {u}_L- \mathbf {C}_G\mathbf {u}_G\right) = 0 \\&\varvec{\lambda }_L+ \varvec{\lambda }_C+ \mathbf {k}_L\left( \mathbf {C}_L\mathbf {u}_L- \mathbf {C}_G\mathbf {u}_G\right) = 0 \end{aligned} \end{aligned}$$
(21)

with \(\mathbf {k}_G=\mathbf {k}_C\).

Remark 2

\(\varvec{\lambda }_C\) is the reaction force of a problem in the complementary domain. Therefore, it is preferable not to use the notation \(\varvec{\lambda }_G\) in order to avoid a confusion on the nature of \(\varvec{\lambda }_G\).

The first equation of the Robin conditions allows to obtain the expression of \(\varvec{\lambda }_C\) to incorporate it into the equilibrium of the global model, which led to:

$$\begin{aligned} \mathbf {K}_G\mathbf {u}_G= {\mathbf {f}_d^G}+ \mathbf {C}_G^T\varvec{\lambda }_A- \mathbf {C}_G^T\left( \varvec{\lambda }_L-\mathbf {k}_G\mathbf {C}_L\mathbf {u}_L- \mathbf {k}_G\mathbf {C}_G\mathbf {u}_G\right) \end{aligned}$$
(22)

The second equation of the Robin conditions allows to obtain the expression of \(\varvec{\lambda }_L\) to incorporate it into the equilibrium of the local model, which led to the following equation:

$$\begin{aligned} \left( \mathbf {K}_L+\mathbf {C}_L^T\mathbf {k}_L\mathbf {C}_L\right) \mathbf {u}_L= {\mathbf {f}_d^L}+ \mathbf {C}_L^T\left( \mathbf {k}_L\mathbf {C}_G\mathbf {u}_G- \varvec{\lambda }_C\right) \end{aligned}$$
(23)

Similarly as the global/local method, a fixed-point algorithm can be derived where an iteration consists of the following steps:

  1. 1.

    Global problem: knowing \(\left( \mathbf {u}_L^n,\varvec{\lambda }_L^n,\varvec{\lambda }_A^n\right) \), find \(\mathbf {u}_G^{n+1}\) solution of:

    $$\begin{aligned} \mathbf {K}_G\mathbf {u}_G^{n+1}= {\mathbf {f}_d^G}+ \mathbf {C}_G^T\underset{\mathbf {P}^{n}}{\underbrace{\left( \varvec{\lambda }_A^n- \left( \varvec{\lambda }_L^n-\mathbf {k}_G\mathbf {C}_L\mathbf {u}_L^n-\mathbf {k}_G\mathbf {C}_G\mathbf {u}_G^n\right) \right) }} \end{aligned}$$
    (24)
  2. 2.

    Auxiliary problems: computing the reaction forces on \(\varOmega _A\) and \(\varOmega _C\) on the interface \(\varGamma \):

    $$\begin{aligned} \begin{aligned} \varvec{\lambda }_A^{n+1}&= \mathbf {C}_A\left( \mathbf {K}_A{\mathbf {u}_G}_{|\varOmega _A} - {\mathbf {f}_d^A}\right) \\ \varvec{\lambda }_C^{n+1}&= \mathbf {C}_C\left( \mathbf {K}_C{\mathbf {u}_G}_{|\varOmega _C} - {\mathbf {f}_d^C}\right) \end{aligned} \end{aligned}$$
    (25)
  3. 3.

    Local problem: knowing \(\left( \mathbf {u}_G^{n+1},\varvec{\lambda }_C^{n+1}\right) \), find \(\mathbf {u}_L^{n+1}\) solution of:

    $$\begin{aligned} \left( \mathbf {K}_L+\mathbf {C}_L^T\mathbf {k}_L\mathbf {C}_L\right) \mathbf {u}_L^{n+1}= {\mathbf {f}_d^L}+ \mathbf {C}_L^T\left( \mathbf {k}_L\mathbf {C}_G\mathbf {u}_G^{n+1}- \varvec{\lambda }_C^{n+1}\right) \end{aligned}$$
    (26)

Remark 3

As to preserve the global model without any change, the contribution of \(\mathbf {u}_G\) is considered on the right-hand side of the previous equation with the term \(-\mathbf {C}_G^T\mathbf {k}_G\mathbf {C}_G\mathbf {u}_G^n\), due to the Robin parameter \(\mathbf {k}_G\). In fact, the contribution of Robin conditions leads to local changes of global stiffness operators regarding the interface degrees of freedom. For another framework of dealing with Robin conditions see [30]

As mentioned in the previous section, auxiliary problems are not needed if finite element codes can get reaction forces on an immersed surface. Nevertheless, if this is not the case, the auxiliary problem in \(\varOmega _C\) is still not necessary. Indeed, it can be computed from known and easy computations without assembling the operator \(\mathbf {K}_C\):

$$\begin{aligned} \begin{aligned} \varvec{\lambda }_C^{n+1}&= \mathbf {C}_C\left( \mathbf {K}_C{\mathbf {u}_G^{n+1}}_{|\varOmega _C}-{\mathbf {f}_d^C}\right) \\&= \mathbf {C}_G\left( \mathbf {K}_G\mathbf {u}_G^{n+1}-{\mathbf {f}_d^G}- \left( \overline{\mathbf {K}}_A\mathbf {u}_G^{n+1}-\overline{\mathbf {f}}_d^A\right) \right) \\&= \mathbf {C}_G\mathbf {C}_G^T\mathbf {P}^{n}-\varvec{\lambda }_A^{n+1}\\ \varvec{\lambda }_C^{n+1}&= \mathbf {P}^{n}- \varvec{\lambda }_A^{n+1}\end{aligned} \end{aligned}$$
(27)

The same relation as the standard global/local method is given where \(\mathbf {P}^{n}=\varvec{\lambda }_C^{n+1}+\varvec{\lambda }_A^{n+1}\). In addition, since \(\mathbf {P}^{n}= \varvec{\lambda }_A^n- \varvec{\lambda }_L^n+ \mathbf {k}_G\mathbf {C}_L\mathbf {u}_L^n- \mathbf {k}_G\mathbf {C}_G\mathbf {u}_G^n\), \(\mathbf {P}^{n+1}\) can be written in function of \(\mathbf {P}^{n}\), a new rest \(\mathbf {r}^{n+1}\) will appear:

$$\begin{aligned} \begin{aligned} \mathbf {P}^{n+1}&= \varvec{\lambda }_A^{n+1}- \varvec{\lambda }_L^{n+1}+ \mathbf {k}_G\mathbf {C}_L\mathbf {u}_L^{n+1}-\mathbf {k}_G\mathbf {C}_G\mathbf {u}_G^{n+1}\\&= \mathbf {P}^{n}- \varvec{\lambda }_C^{n+1}- \varvec{\lambda }_L^{n+1}+ \mathbf {k}_G\mathbf {C}_L\mathbf {u}_L^{n+1}-\mathbf {k}_G\mathbf {C}_G\mathbf {u}_G^{n+1}\\&= \mathbf {P}^{n}-\left[ \left( \varvec{\lambda }_C^{n+1}+\varvec{\lambda }_L^{n+1}\right) + \mathbf {k}_G\left( \mathbf {C}_G\mathbf {u}_G^{n+1}-\mathbf {C}_L\mathbf {u}_L^{n+1}\right) \right] \\&= \mathbf {P}^{n}+ \mathbf {r}^{n+1}\end{aligned} \end{aligned}$$
(28)

The new rest \(\mathbf {r}^{n+1}\) now incorporates a mixed contribution of the discontinuity of displacements and the disequilibrium of forces:

$$\begin{aligned} \mathbf {r}^{n+1}= -\underset{\text {Disequilibrium}}{\underbrace{\left( \varvec{\lambda }_C^{n+1}+\varvec{\lambda }_L^{n+1}\right) }} - \mathbf {k}_G\underset{\text {discontinuity}}{\underbrace{\left( \mathbf {C}_G\mathbf {u}_G^{n+1}-\mathbf {C}_L\mathbf {u}_L^{n+1}\right) }} \end{aligned}$$
(29)

3.2 Algorithm for global/local method with robin parameters

The mixed global/local methodology with Robin conditions can be located in Alg. 2.

The method error is calculated by using the same expression as for the primal-dual strategy presented in Eq. (16). However, each residual term in Eq. (16) is calculated differently for the mixed global/local analysis (it is estimated as a combination of interface forces and displacements). It could be interesting to take into consideration the error of the results reached when using the global/local analysis with mixed conditions and the results regarding the monolithic computation. This error is calculated as the rule of displacement difference on the interface between the global and the monolithic model, as presented in Eq. (30).

$$\begin{aligned} \eta _{Mono.} = \frac{\Vert \left( \mathbf {C}_G\mathbf {u}_G^{n+1}-\mathbf{u }_{Mono.} \right) \Vert _2}{\Vert \mathbf{u }_{Mono.}\Vert _2} \end{aligned}$$
(30)

Figure 3 shows a flowchart of the iterative method implementation of the global/local with Robin parameters.

Fig. 3
figure 3

Flowchart of the algorithm of the Global/Local Analysis with Robin Parameters

Full size image

4 Results for 2D structures using Global/local analysis with robin parameters

4.1 Description of the two cases - definition of the robin parameters

Code Aster [12] was used to implement the global/local algorithm with Robin parameters as two A-36 steel structures modelled with 2D plane stress formulation: a) an inverted T-Shape with a 10mm initial crack and b) an inverted T-Shape model with a circular cut to induce the plastic hardening behaviour. The properties used for the analysis correspond to: Yield stress of 250 (MPa), hardening ratio of 0.1 and 4 propagation steps with a maximum advance of 2 (mm) per step. Geometrical properties are presented in Figure 4a and Figure 4b.

Fig. 4
figure 4

Geometry of analyzed models

Full size image

The Robin parameter is chosen as the stiffness of an element strip [33], as presented in Figure 5. Robin operators \(\mathbf {k}_L\) and \(\mathbf {k}_G\) are determined independently: \(\mathbf {k}_L\) is the linear elastic stiffness of the strip on the side of the complementary model from the interface and \(\mathbf {k}_G\) is the linear elastic stiffness of the strip on the side of the local model from the interface. In addition, Aitken’s \(\delta ^2\) dynamic relaxation is used to accelerate the convergence in relation to a classical static relaxation.

Fig. 5
figure 5

Element strip of elements used for the analysis

Full size image

Remark 4

In the Code Aster implementation, the Robin operator is calculated as follows: the strip of elements is applied with a Young Modulus variable (\(\alpha _L E_L\)) for the local model, modifying the stiffness and considering coupled degrees of freedom on the interface. This strip of elements is connected directly to the interface and with fixed support boundary conditions. On the other hand, the strip of elements is used to compute the part on the right-hand side for the global model, which corresponds to the Robin conditions in Eq. (28). It is not assembled with the global stiffness. The strip of elements considers a Poisson ratio of 0.3, a Young Modulus variable (\(\alpha _G E_G\)) and fixed boundary conditions on the opposite side of the interface, as presented in Figure 5.

4.2 Results

Fig. 6
figure 6

Method error for Global/Local Analysis with Robin Parameters and cracked domain with 4 propagation steps

Full size image
Fig. 7
figure 7

Method error for Global/Local Analysis with Robin Parameters and plastic hardening domain

Full size image

It is clear that the global/local Analysis with Robin parameters converges slower with respect to the primal-dual Method (from 8 to 6 iterations compared to the primal-dual for the cracked model). For the hardening problem, it converges from 8 to 6 with respect to the primal-dual and considering the number of iterations. The Aitken \(\delta ^2\) dynamic relaxation converges both models rapidly, with a faster convergence rate for the primal-dual Method.

The complete global/local analysis results with the initial Robin operator are shown in Table  1 for non-linear/cracked behaviour.

Table 1 Results for both models and non-linear/cracked behaviour, using Aitken \(\delta ^2\) and the Initialized Robin Operator
Full size table

4.3 Summary of the results

As presented in Section 4, the mixed method converges slower with respect to the primal-dual method. Regarding computational times, these were 18 seconds for the cracked model and 10 seconds for the non-linear hardening problem. However, these times are referential and can be improved by optimizing the python code. Finally, as the analysis considers an arbitrary strip of elements used to start the Robin operator, an optimization process is carried out with the intention of reducing the number of iterations until convergence and analysing the results for different Robin parameter values. In addition, the strip of elements are very stiff and do not represent the neighbour structure, i.e., the theoretical optimum.

Remark 5

Is important to mention that non-linear plastic behaviour or crack tip propagation are not being transferred between the local and global models. The interfaces are considered far from the source of plasticity or the crack tip; Therefore, based on St. Venant’s principle, only the effects of these singularities are transmitted between models. In order to study specific aspects of the non-linear behaviour, the local model should be further analyzed. Finally, the “total” solution of the analysis should be considered as the superposition of the global linear model and the local non-linear model.

5 Optimization of the robin parameter Global/local analysis with robin conditions in 2D plane stress

5.1 Description of the optimization process

As presented in [25], the convergence of the global/local analysis with mixed conditions can be assured for a certain range of values for the Robin parameters. Within this range, an optimum that minimizes the number of iterations can be found. However, as presented in [13, 34], the value depends on the problem type, the applied loads, the boundary conditions and the form of the Robin operator used in the analysis. Therefore, in order to find the Robin operator that guarantees convergence and also minimizes the number of iterations until convergence, an optimization process is performed for the different problems presented. Optimization algorithms have been used widely in engineering problems and other scientific areas, such as the Basin-Hopping Algorithm [24, 29], already distributed within Scipy library [36].

Remark 6

The values of the Robin operator assuring the convergence of the non-intrusive method with Robin conditions can be estimated analytically for simple examples with few degrees of freedom. For industrial/real structures, the range of the values are not easily found directly, so these values are found by iterative methods as presented in [13, 20] or by using two scale strategies as shown in [15, 27].

For this article, the Basin-Hopping algorithm is used in the optimization process, allowing the specification of an initial “guess” of the problem within the search space and stochastically start the refinement of the solution until finding the best possible solution. The Basin-Hopping algorithm is based on the transformation of the “potential energy landscape” of an objective function, finding local minima using the Limited-Memory Broyden-Fletcher-Goldfarb-Shanno method (L-BFGS) [9]. This potential energy surface is being explored by means of random jumps for each evaluation based on the Boltzmann probability distribution. The number of random jumps is defined by a variable N, in which the probabilities for finding the best local minimum are increased for larger values of N. Therefore, the Basin-Hopping algorithm has been used successfully to find a minimum using N=110 or larger [37]. This parameter is also a measurement of the computational cost, because it is a direct measurement of the amount of random jumps between each solution. For our work, N has been defined as the default option provided in Scipy, with a value of N equal to 100. Finally, the L-BFGS method has a computational complexity of \({\mathcal {O}}(n^2)\) and must be repeated N times in accordance with the number of random jumps [8].

Nevertheless, a global optimum cannot be assured in metaheuristics, due to the non-convex nature of the problem. However, a good approximation of a global minimum solution can be found. This is due to the internal behaviour of the optimization process: it is stopped through an internal convergence criterion and not by founding a global minimum [3]. More information and applications on the different optimization algorithms can be seen in [2, 7, 10, 21, 22, 26, 35, 40], among others. Therefore, considering that the convergence of the method depends on the Robin parameters as presented in [25], the initial Robin parameter (calculated as the condensed stiffness on the interface estimated from an initial strip of elements and presented in Figure  5) can be modified by means of two factors: \(\alpha _G\) for the global model and \(\alpha _L\)for the local fine model, as shown in Eq. (31):

$$\begin{aligned} \mathbf {k}_L=\alpha _L {\mathbf {k}_L}^{init} \qquad \mathbf {k}_G=\alpha _G {\mathbf {k}_G}^{init} \end{aligned}$$
(31)

The optimization algorithm will be used to find an optimum value for \(\alpha _{G,L}\) that minimizes the number of iterations until convergence.

It is important to note that the search space for the values of \(\alpha _{G,L}\) to be used in the optimization process are constrained between 0 and 100 in order to find an overall optimum that minimizes the number of iterations, starting with the initial search direction \(\mathbf{k }_{G,L}^{init}\), i.e., \(\alpha _{G}=1\) and \(\alpha _{L}=1\).

The optimization problem is carried out using the initial configuration of the domains and considering the initialized Robin conditions and multiplied by the \(\alpha \) factor. The analysis contemplates linear elasticity behaviour for both problems for all optimization trials. Finally, the results for the optimum \(\alpha _{G,L}\) will be used for non-linear problems (all propagation steps and post-yielding hardening).

The following procedure is applied to perform the optimization of the Robin parameter, using the Basin-Hopping [29] algorithm, as well as for linear elastic initialized models, i.e., without plasticity or crack propagation:

  • Choose global and local models to be analysed considering the elastic linear behaviour, as presented in Figure 4a and Figure 4b.

  • Perform the analysis on the model considering the iterative non-intrusive scheme with \(\alpha _L=1\) and \(\alpha _G=1\) (Initial guess or initial trial for the Robin parameter).

    1. 1.

      Choose new values of \(\alpha _L\) and \(\alpha _G\) found in the local neighbourhood of the initial guess.

    2. 2.

      Perform the non-intrusive analysis using Robin parameters and recover the number of iterations until the analysis converges for each \(\alpha _L\) and \(\alpha _G\) in the neighbourhood of the current trial.

    3. 3.

      Study the convergence values of the previous neighbourhood and select random values in the best direction (gradient) found in the neighbour to proceed with updated \(\alpha _{G,L}\) trial.

  • When the optimization algorithm converges and the best solution for the linear model is obtained, the best factors \(\alpha ^{opt}_L\) and \(\alpha ^{opt}_G\) are recovered.

  • Apply \(\alpha ^{opt}_L\) and \(\alpha ^{opt}_G\) to the non-linear model (hardening or cracked model) and study the convergence.

5.2 Results

For the 2D cases, the optimization results are presented summarized in Table 2 for both models.

Table 2 Optimized \(\alpha \) results for initial cracked and perforated linear model
Full size table

The optimized \(\alpha \) found for the linear cases are used directly as an input for the non-linear cases. These results, regarding the evolution of the method error with respect to iterations, are introduced in Figure  8 for the cracked case and in Figure 9 for the plastic hardening case.

Fig. 8
figure 8

Method error for Global/Local Analysis with Optimized Robin Parameters and cracked domain

Full size image
Fig. 9
figure 9

Method error for Global/Local Analysis with Optimized Robin Parameters and plastic hardening domain

Full size image

Figure 8 and Figure 9 show that the number of iterations are reduced by 25% for the cracked case and 12.5% for the plastic hardening case respecting the non-optimized solution (initial guess of the Robin parameter). However, with regard to the primal-dual solution, the cracked optimized model equals the performance in terms of the number of iterations. For the non-linear hardening case, the optimized model with Robin parameters performs slower with respect to the primal-dual method. The results for the cracked model and non-linear hardening, using the optimized \(\alpha _{G,L}\) factors, are presented in Table  3.

Table 3 Results for optimized \(\alpha \), cracked behaviour (4 propagation steps) and post-yielding hardening
Full size table

5.3 Summary of the results

When optimizing the linear elastic analysis of each model (including the initial configuration of the local geometry) using the Basin-Hopping algorithm, the convergence of non-linear models is improved as expected. The optimized \(\alpha _L^{opt}\) and \(\alpha _G^{opt}\) used for the non-linear problems obtain better results with respect to the non-optimized problems, similar to the performance of the primal-dual method. This approximation using the linear elastic optimized model works for localized patches with non-linearities. However, the solution found with the Basin-Hopping algorithm for the linear models may not be the actual optimum for the non-linear models. Finally, as the Code Aster code with the python interface was implemented, the optimization times are elevated in comparison with the non-optimized \(\alpha \) case. However, these times can be optimized by using better coding practices and more efficiency in computing resources.

6 Global/local analysis with robin conditions for 3D structures

As presented in Section 5, the same approach will be applied in two models: a cantilever beam with an initial crack near the fixed support and a beam with two 50 (mm) perforations and non-linear hardening behaviour. The properties are the same as the previous case but including different lengths, loads applied and crack size, as shown in Figure  10. The crack propagates for the 3D case, including 3 propagation steps and 10 (mm) for maximum crack advance per step for the cracked domain.

Fig. 10
figure 10

3D cantilever cracked and non-linear hardening beam

Full size image

As the discretization carried out in the global and local 3D models are geometrically complex, incompatible meshes were generated. The incompatibility is managed by Code Aster projecting the fields between the models and the interface. The initial Robin parameter will be used in order to find the results for the non-optimized \(\alpha _{G,L}\) for both models, which are summarized in Table  4.

Table 4 Results for the optimization for 3D model with initial conditions and linear behaviour
Full size table

Results using the optimized Robin parameter, following the same procedure as shown in Sec. 5, are summarized in Table 5 and presented in Figure 11 for the cracked case and in Figure 12 for the plastic hardening case.

Fig. 11
figure 11

Method error for Global/Local Analysis Robin Parameters for 3D cracked domain and optimized \(\alpha _{G,L}\)

Full size image

The use of the optimized \(\alpha _{G,L}\) implies a reduction on the number of iterations from 10 to 9 for the cracked case with 3 propagation steps, meaning a 18% faster respect to the primal-dual and a 10% improvement in relation to the global/local with non-optimized Robin conditions. For the hardening problem, the optimized \(\alpha _{G,L}\) reduces the number of iterations from 10 to 8, which corresponds to an improvement of 20% with respect to the non-optimized Robin conditions and 11% improvement in comparison to the primal-dual solution. The complete results for the 3D analysis are presented in Table  5.

Fig. 12
figure 12

Method error for Global/Local Analysis Robin Parameters for 3D hardening domain and optimized \(\alpha _{G,L}\)

Full size image
Table 5 Results for the 3D cracked models 3 propagation steps
Full size table

The final deformed shape for the cracked model is presented in Figure 13 for the Global/Local 3D model with Robin conditions (optimized) and in Figure 14 for the hardening case.

Fig. 13
figure 13

Deformed shape of the 3D beam for Global/Local Analysis with Optimized Robin Parameters and cracked domain

Full size image
Fig. 14
figure 14

Deformed shape of the 3D beam for Global/Local Analysis with Optimized Robin Parameters and hardening domain

Full size image

6.1 Summary of the results

As in Section 5, the optimization improves the convergence with respect to the initialized Robin parameter.

The optimization process, when applied to the 3D cracked model, improves the convergence rate, resulting in better performances, considering the number of iterations with respect to the primal-dual methodology.

7 Discussion

In this article, the global/local non-intrusive analysis with Robin parameters was implemented in 2D and 3D problems with cracked and plastic hardening behaviour. Subsequently, results were optimized using the Basin-Hopping algorithm and compared to a primal-dual non-intrusive analysis.

The method presented in this study has a good convergence rate for 2D and 3D non-linear plastic hardening behaviour and cracked models. However, as for any mixed method, the selection of the Robin parameters is crucial for convergence. Our initial choice is based on studying the effect of a simple element strip, but it may not be very efficient compared to the primal-dual approach.

The optimization of the mixed global/local method was performed using the Basin-Hopping algorithm, allowing an improvement in the performance of the global/local analysis with Robin parameters. The optimized \(\alpha \) is different for each case, which is consistent with results presented in [34], indicating that the values of \(\alpha \) are specific to each model (geometry, behaviour, etc.), loads and boundary conditions.

Nevertheless, the optimization does not guarantee that the mixed global/local analysis works better with respect to the primal-dual non-intrusive analysis, although a local minimum could improve the mixed analysis results.

8 Future research

The Robin parameter and the flexibility added to the structure are a great advantage of the mixed model, as presented in [20]. Therefore, the non-intrusive analysis with Robin parameters can be studied for structures with geometric non-linear behaviour and large displacements.

Another topic to be studied further is to extend the analysis to larger structures, associated with multiple domains and with multiple stiffeners or variable cross sections. This is useful to study the convergence of the method in structures with strong modifications in the stiffness. Consequently, the original approximation of the Robin parameter may not be the best for each interface and these factors could be different for each analysis direction, as presented in [13].

Different crack propagation techniques must be considered in future studies, for example, the Cohesive Zone Model (CZM) and the Virtual Closing-Crack Technique (VCCT) to study the effectiveness of the global/local method with Robin parameters using this type of analysis. The feasibility of coupling the global/local method with phase field approaches to deal with crack propagation has been studied successfully in [17, 28].

The studied strategies for solving the global/local problem, i.e., primal-dual and with Robin conditions, work without problems for incompatible patches. Nevertheless, a sensitivity analysis can be performed to study the effect of incompatible meshes for different structures and behaviours, and the error that can be induced due the interpolation of forces and displacements in the different interfaces.

Basin-Hopping is a meta-heuristic that can be easily implemented, but as presented in [5], it may not be the fastest to obtain convergence. Therefore, a more efficient way to optimize the Robin parameters and reduce computational times must be studied and applied, such as the Particle Swarm Optimization [39] and exploiting the ability to evaluate multiple trials with parallel architecture. In addition, the efficiency of the algorithm on larger cases will be studied. For now, due to the small problems we studied, the iterative algorithm cannot compete with a full-scale computation. We expect that larger problems may reverse this trend.

Finally, the effect of the discretization for the 2D and 3D models, the degree of the shape functions used for the FEM method elements and also the coupling between 2D global models and 3D local non-linear models must be analyzed, in order to study the convergence of these elements and how affects the response.