Subdivision-based isogeometric analysis for second order partial differential equations on surfaces

Abstract

We investigate the isogeometric analysis approach based on the extended Catmull–Clark subdivision for solving the PDEs on surfaces. As a compatible technique of NURBS, subdivision surfaces are capable of the refinability of B-spline techniques, and overcome the major difficulties of the interior parameterization encountered by the isogeometric analysis. The surface is accurately represented as the limit form of the extended Catmull–Clark subdivision, and remains unchanged throughout the h-refinement process. The solving of the PDEs on surfaces is processed on the space spanned by the Catmull–Clark subdivision basis functions. In this work, we establish the interpolation error estimates for the limit form of the extended Catmull–Clark subdivision function space on surfaces. We apply the results to develop the approximation estimates for solving multiple second-order PDEs on surfaces, which are the Laplace–Beltrami equation, the Laplace–Beltrami eigenvalue equation and the time-dependent Cahn–Allen equation. Numerical experiments confirm the theoretical results and are compared with the classical linear finite element method to demonstrate the performance of the proposed method.

1 Introduction

A wide variety of partial differential equations (PDEs) defined on surfaces have been described as mathematical models of physical engineering phenomena. It is essential to study the numerical method of solving the Laplace–Beltrami equation, which is the main component of some physical models, such as the problems of the Navier–Stokes types [1] which are coupled with atmosphere/ocean models to study the long-term earth climate change. The eigenvalue problem based on the Laplace–Beltrami operator [2] is widely used not only in scientific computing but also in the fields of engineering and physics (such as quantum mechanics, laser, etc.). The Allen–Cahn equation was originally introduced by Allen–Cahn [3] to describe the motion of antiphase boundaries in crystalline solids. It is proposed as a simple (non-conservative) model for the phase separation process of binary alloys at a fixed temperature.

We recall that there exist numerous numerical methods for these PDEs on surfaces using the finite-difference methods [4] and spectral methods [5, 6], which are applicable to simple surfaces. In practical engineering, there is an urgent need for a more geometrically flexible method. Finite element analysis has become a widely accepted method (cf. a good review of various finite element methods on surfaces in [7]). As we all know, the finite element method involves the approximation of the differential geometric quantities of surfaces, which may increase the error of numerical approximation. This is because the variation of the Laplace–Beltrami operator needs to integrate the derivative product on the surface. Moreover, the traditional finite element method solves the problem through expensive and time-consuming manual intervention, and difficulties are encountered in the refining process (especially for complex geometries).

The isogeometric analysis (IGA), introduced by Hughes et al. [8, 9], can use non-uniform Rational B-Splines (NURBS) [10, 11] or T-splines [12,13,14] instead of standard finite elements. The concept of IGA shows great potential in the development of seamless integration between computer-aided design (CAD) and finite element method (FEM), which has higher accuracy than standard FEM. The h-refinement, p-refinement and even k-refinement can be easily achieved by knot insertion and/or order elevation, thereby improving the accuracy without changing the geometry, which eliminates the subsequent communication with the CAD system.

Solving the equations is an important issue in IGA. Discretization with single-patch NURBS-based IGA and implicit backward differentiation formula schemes was proposed to solve mean curvature (2nd order) and Willmore (4th order) flows in [15]. NURBS-based IGA was considered to numerically solve benchmark Laplace–Beltrami problems of the fourth and sixth order, as well as the corresponding eigenvalue problems, Cahn–Hilliard and crystal equations in [16]. The second-order PDEs on surfaces with IGA were considered in [17] where a priori error estimates under h-refinement in the general case of second order PDEs was proposed. A general theory and isogeometric finite element implementation based on structured NURBS and unstructured spline spaces for studying two coupled fourth-order nonlinear PDEs that live on an evolving two-dimensional manifold was presented in [18]. Toshniwal et al. [19] proposed the construction of a separate, smooth spline on unstructured quadrilateral meshes while ensuring isogeometric compatibility-requiring the geometric models to be members of the analysis-suitable spaces. Analysis-suitable T-splines (ASTS) including both extraordinary points and T-junctions were used to solve Kirchhoff-Love shell problems, where $C^1$-continuous non-negative spline basis functions were constructed near extraordinary points to obtain optimal convergence rates in [20].

As a compatible technique of NURBS, subdivision surfaces are capable of the refinability of B-spline techniques. Surface subdivision is a powerful technology originated from computer graphics, which provides a simple and efficient recursive refinement to construct smooth surfaces from arbitrary meshes [21,22,23]. Constructing surfaces through subdivision elegantly addresses some issues faced by computer graphics and CAD practitioners, where they need to handle control meshes of arbitrary topology, while maintaining surface smoothness and visual quality automatically. Subdivision surfaces easily admit multi-resolution extensions, thus enabling efficient hierarchical representations of complex surfaces. Subdivision technology not only can be easily used to treat the complex geometries but also preserve the features around boundaries by simple extensions, such as concave corners, convex corners, sharp creases and smooth creases etc.

Since subdivision algorithms can be used to define the basis on any mesh domain, they naturally become candidates for higher-order finite element calculations in engineering applications (see [24,25,26,27,28,29,30]). Recently, there have been some works on the application of the IGA approach based on the subdivision. Volumetric IGA based on Catmull–Clark solids was investigated in [31] where the boundary of the solid model was a Catmull–Clark surface with optional corners and creases to support the modeling phase. The use of Powell-Sabin splines in the context of IGA for the numerical solution of advection-diffusion-reaction equations was represented in [32], which focused on the accurate detection of internal and boundary layers. Truncated hierarchical Catmull–Clark subdivision [33] was developed to support local refinement and generalize truncated hierarchical B-splines to arbitrary topology. In the recent years, the subdivision-based IGA was studied in [34, 35], which was applied to solve linear and nonlinear PDEs on plane. The subdivision weights were optimised by minimising short-wavelength surface oscillations around extraordinary vertices to minimise finite element discretisation errors in [36]. A subdivision scheme for unstructured quadrilateral meshes with improved convergence rates in extraordinary regions for IGA was presented in [37]. A new non-uniform subdivision surface was introduced to generalize bi-cubic NURBS to arbitrary topology and was proved to be $G^1$ -continuous for any valence extraordinary points in [38]. A new tuned hybrid subdivision surface with globally $G^1$-continuous was introduced as a basis in IGA in [39].

In this work, we develop the isogeometric analysis based on Catmull–Clark subdivision (IGA-CC) method to approximate the PDEs on surfaces. The precise surface is patch-wisely represented by the limited form of the extended Catmull–Clark subdivision mesh, which has the flexibility of dealing with any topological structure, and remains unchanged, along with its parameterization, throughout the subdivision process equivalent to the h-refinement of NURBS. The solution space of the PDEs on surfaces is spanned by the extended Catmull–Clark subdivision basis functions. The convergence of the interpolation errors is studied in detail where we use the unique solvability of the interpolation problem on the support extension. We apply the theoretical results to several problems including the Laplace–Beltrami equation, the Laplace–Beltrami eigenvalue equation, and the time-dependent Allen–Cahn equation. The numerical results are completely consistent with the theoretical estimates. By comparing with the classical linear element finite element method, the convergence is studied in detail. The proposed IGA-CC method has the ability to accurately represent the surface geometries and improves the accuracy of the approximate PDE solutions on surfaces through the h refining process.

We organize the rest of this article in the following way. The required preliminaries and the extended Catmull–Clark subdivision are introduced in Sect. 2. In Sect. 3, we introduce three PDEs on surfaces that all involve the Laplace–Beltrami operator. In Sect. 4, we introduce spatial discretization based on the IGA-CC method. In Sect. 5, we study the interpolation error estimates for the limit form of the extended Catmull–Clark subdivision function space on surfaces, and a priori error estimates corresponding to the PDEs on surfaces. In Sect. 6, we present the numerical experiments. Some conclusions are given in Sect. 7.

2 Notations and preliminaries

In this section we firstly review in an abstract framework the surface parameterization and some surface differential operators. Then we briefly introduce the extended Catmull–Clark subdivision surface which is used to represent the physical domains. We also select these subdivision basis functions for numerically solving the PDEs on surfaces.

2.1 Surface parameterization and surface differential operators

Let ${{\mathcal {S}}}:= \{\mathbf{x}(u^1, u^2) \in {\mathbb {R}}^3: (u^1, u^2) \in {\mathscr {D}}\subset {\mathbb {R}}^2\}$ be a parametric surface. Assume that the surface ${{\mathcal {S}}}$ is sufficiently smooth and orientable. Let $g_{\alpha \beta }=\langle \mathbf{x}_{u^\alpha }, \mathbf{x}_{u^\beta }\rangle$ and $b_{\alpha \beta }=\langle \mathbf{n}, \mathbf{x}_{u^\alpha u^\beta }\rangle$ be the coefficients of the first and the second fundamental forms of ${{\mathcal {S}}}$ with

$$\begin{aligned}&\mathbf{x}_{u^{\alpha }} = \frac{\partial \mathbf{x}}{\partial u^{\alpha }}, \quad \mathbf{x}_{u^{\alpha }u^{\beta }} = \frac{\partial ^2 \mathbf{x}}{\partial u^{\alpha }\partial u^{\beta }}, \quad \alpha , \beta = 1, 2, \\[1mm]&\mathbf{n} = ( \mathbf{x}_{u^1}\times \mathbf{x}_{u^2})/\Vert \mathbf{x}_{u^1}\times \mathbf{x}_{u^2}\Vert , \end{aligned}$$

where $\langle \cdot , \cdot \rangle$, $\Vert \cdot \Vert$ and $\cdot \times \cdot$ stand for the usual inner product, Euclidean norm and cross product in ${\mathbb {R}}^3$ respectively. In what follows, we will make use of the following notations

$$\begin{aligned}&[g^{\alpha \beta }] = [g_{\alpha \beta }]^{-1},\ g = \mathrm{det}[g_{\alpha \beta }],\ [b^{\alpha \beta }] = [b_{\alpha \beta }]^{-1}, \\&b = \mathrm{det}[b_{\alpha \beta }]. \end{aligned}$$

The matrix form of Weingarten map is denoted as

$$\begin{aligned} \mathbf{S}=[b_{\alpha \beta }][g^{\alpha \beta }] = \frac{1}{g}\left[ \begin{array}{cc} b_{11}g_{22}-b_{12}g_{12} &{} b_{12}g_{11}-b_{11}g_{12} \\ b_{12}g_{22}-b_{22}g_{12} &{} b_{22}g_{11}-b_{12}g_{12} \end{array} \right] , \end{aligned}$$

which is a self-adjoint linear map on the tangent space $T_\mathbf{x}{{\mathcal {S}}}:=\mathrm{span}\{\mathbf{x}_{u^1},\mathbf{x}_{u^2} \}$. Then the eigenvalues $k_1$ and $k_2$ of $\mathbf{S}$ are the principal curvatures of ${{\mathcal {S}}}$, whose arithmetic average and product are the mean curvature H and the Gaussian curvature K, namely,

$$\begin{aligned}&H =\frac{k_1+k_2}{2}= \frac{\mathrm{tr}(\mathbf{S})}{2} = \frac{b_{11}g_{22}-2b_{12}g_{12}+b_{22}g_{11}}{2g},\\&\quad K =k_1k_2= \det (\mathbf{S}) = \frac{b_{11}b_{22}-b_{12}^{2}}{g}, \end{aligned}$$

respectively. Let $\mathbf{H} = H\mathbf{n}$, which is referred to the mean curvature normal.

Now we introduce several geometric differential operators of interest.

Tangential gradient operator. Suppose that $f\in C^1({{\mathcal {S}}})$, where $C^1({{\mathcal {S}}})$ stands for a function space consisting of $C^1$ smooth functions on ${{\mathcal {S}}}$, then the tangential gradient operator $\nabla _s$ acting on f is defined as

$$\begin{aligned} \nabla _s f = [\mathbf{x}_{u^1}, \mathbf{x}_{u^2}] [g^{\alpha \beta }] [f_{u^1}, f_{u^2}]^T \in {\mathbb {R}}^3. \end{aligned}$$

(1)

For a vector-valued function $\mathbf{f} = [f_1, \ldots , f_k]^T \in C^1({{\mathcal {S}}})^k$, the gradient $\nabla _s$ acting on $\mathbf{f}$ is defined as

$$\begin{aligned} \nabla _s \mathbf{f} = [\nabla _s f_1, \ldots , \nabla _s f_k] \in {\mathbb {R}}^{3\times k}. \end{aligned}$$

Divergence operator. Let $\mathbf{v} \in [C^1({{\mathcal {S}}})]^3$ be a smooth vector field on surface ${{\mathcal {S}}}$. Then the divergence operator $\mathrm{div}_s$ acting on $\mathbf{v}$ is defined as

$$\begin{aligned} \mathrm{div}_s (\mathbf{v}) = \frac{1}{\sqrt{g}}\left[ \frac{\partial }{\partial u^1}, \frac{\partial }{\partial u^2}\right] \left[ \sqrt{g}[ g^{\alpha \beta }][ \mathbf{x}_{u^1}, \mathbf{x}_{u^2} ]^T\mathbf{v}\right] . \end{aligned}$$

(2)

Laplace–Beltrami operator. Let $f\in C^2({{\mathcal {S}}})$. Then the Laplace–Beltrami operator (LBO) $\Delta _s$ acting on f is defined as

$$\begin{aligned} \Delta _s f = \mathrm{div}_s (\nabla _s f) . \end{aligned}$$

With the definitions of $\Delta _s$ and $\mathrm{div}_s$, we derive

$$\begin{aligned} \Delta _s f = \frac{1}{g}(g_{22}f_{11}+g_{11}f_{22}-2g_{12}f_{12}), \end{aligned}$$

(3)

where $f_{\alpha \beta } = f_{u^{\alpha }u^{\beta }} - (\nabla _s f)^{\mathrm{T}} \mathbf{x}_{u^{\alpha } u^{\beta }}, \ \alpha , \beta = 1,2$. Obviously, $\Delta _s$ is a second order differential operator, which relates to the mean curvature vector via the formula $\Delta _s \mathbf{x}=2\mathbf{H}$.

Theorem 2.1

(Green formula for LBO) Let ${{\mathcal {S}}}$ be an orientable surface, and $\Omega$ be a subregion of ${{\mathcal {S}}}$ with a piecewise smooth boundary $\partial {\Omega }$. Let $\mathbf{n}_c$ be the outward unit normal along the boundary $\partial {\Omega }$. Then for a given smooth vector field ${{\varvec{v}}} \in C^1(\Omega )$, we have

$$\begin{aligned} \int _{\Omega }\langle {{\varvec{v}}},\nabla _s f\rangle + f\, \mathrm{div}_{s}({{\varvec{v}}})\mathrm{d}A = \int _{\partial \Omega } f \langle {{\varvec{v}}},\mathbf{n}_c \rangle \mathrm{d} s. \end{aligned}$$

(4)

2.2 Extended Catmull–Clark subdivision surfaces

In this section we review the extended Catmull–Clark subdivision. It is a generalization of bicubic B-spline subdivision, which eliminates the rigid restriction on the topology of the control mesh, and can treat boundary features, such as concave/convex corners, and sharp/smooth creases. It can generate a smooth surface from a control mesh of arbitrary topology by using iterative refinement procedure. The control vertices of the refined meshes are generated from the control vertices of the previous step by a portfolio of weight coefficients, which is described in Fig. 2 ( [40]). This process subdivides each quadrilateral into four sub-quadrilaterals, where this sequence of meshes converges to a $C^1$ smooth limit surface composed of quadrilateral patches. For more clarity, the extended Catmull–Clark subdivision scheme is described as follows.

Fig 1

A control mesh for extended Catmull–Clark subdivision rules. Vertices are classified into 3 categories. Edges are classified into 3 categories and patches are classified into 3 categories

Fig 2

a and b are the vertex recomputation rules. c, d and e are the edge insertion point rules. f shows the face insertion point rule

Vertex Schemes. The vertices can be separated into three types: corner vertex, boundary vertex and interior vertex. For different type of vertex, the refined strategy is given as (see Fig. 1)

• 1. Interior vertex with N face valence: It is updated as the combination of its previous position with weight $1-7/(4N)$, the sum of all adjacent vertices with weight $3/(2N^2)$, and all the remaining 1-ring vertices with weight $1/(4N^2)$ (see Fig. 2a).

• 2. Boundary vertex: It is updated as the sum of its own previous position with weight 3/4 and the two adjacent boundary vertices with weight 1/8 (see Fig. 2b).

• 3. Corner vertex: It needs to be interpolated, meaning they are fixed.

Edge Schemes. The edges can be divided into boundary edge, sub-boundary edge and interior edge. The boundary edges lie on the boundaries, which are the features of control mesh in general. The sub-boundary edges are not boundary edges but adjacent to the boundary vertices. The rest are the interior edges. For the different type of edges, the refinement is performed as (see Fig. 1))

• 1. Sub-boundary edge: The newly added vertex on a sub-boundary edge is the combination of the boundary vertex with weight $\frac{3}{4} - \gamma$, another endpoint of this edge with weight $\gamma$, and the sum of the four wing vertices of this edge with weight 1/16, where $\gamma = 3/8-1/4\mathrm{cos} \theta _k$, $\theta _k = \pi /k$ for a boundary vertex, and $\theta _k = \alpha /k$ for a convex corner vertex, $\theta _k = (2 \pi -\alpha ) /k$ for a concave corner vertex. Here k denotes the face valence of the boundary vertex, $\alpha$ is the angle of the two boundary edges incident to the boundary vertex (see Fig. 2c).

• 2. Interior edges: Use the subdivision rule for the sub-boundary edge only by choosing $\gamma = 3/8$ (see Fig. 2d).

• 3. Boundary edge: The newly added vertex on a boundary edge is the average of its adjacent boundary vertices (see Fig. 2e).

Face Schemes. Insert a vertex at the centroid of each face (see Fig. 2f).

Each quadrilateral patch of the control mesh can be regarded as a parametric domain, which corresponds to only one quadrilateral patch of the limit surface. We divide the control mesh into interior patches, sub-boundary and boundary patches. The patches containing boundary vertices are named as boundary patches, the ones adjacent to boundary patches are called sub-boundary patches, and all others are called interior ones (see Fig. 1). For the two cases of boundary and sub-boundary patches , it is not difficult to find that several more subdivision times can change them into the calculable interior patches, where we described their computation in Section 4.3. Here we simply describe the evaluation method for the interior cases. If the four control vertices of an interior patch have valence four, the resulting surface patch is called regular. The regular patch can be exactly described by a bicubic B-spline, which is formulated by

$$\begin{aligned} \mathbf{x}(\xi ,\eta ) = \sum _{i=1}^{16} B_i(\xi ,\eta ) \mathbf{x}_i, \end{aligned}$$

(5)

where $(\xi , \eta )$ are the barycentric coordinates of the unit square $T = \{(\xi , \eta )\in {{\mathbb {R}}}^2: 0 \le \xi \le 1, 0 \le \eta \le 1 \}$, and the index i refers to the local sorting of 16 control vertices shown in Fig. 3a.

Fig 3

a A regular patch with its 16 control vertices. b An irregular patch over the shaded quadrilateral with an extraordinary vertex labeled ’1’ whose valence is 5. c Subdividing this irregular patch once generates 3 sub-patches which can be evaluated

If an interior patch is irregular, i.e., at least one of its vertices has a valence other than four, the resulting surface patch cannot be represented by a bicubic B-spline. We assume extraordinary vertices are isolated; that is, there is no edge in the interior patch such that both of its vertices are extraordinary. This assumption could be fulfilled by subdividing the mesh once. Under this assumption, any irregular interior patch has only one extraordinary vertex. For evaluating irregular patches, the mesh needs to be subdivided repeatedly until the parameter values of interest are interior to a regular patch. Hence, the basis functions given in (5) can be used to represent the geometry exactly. Each subdivision of an irregular patch produces three regular sub-patches and one irregular sub-patch (see Fig. 3b, c), then repeated subdivision of the irregular patch produces a sequence of regular sub-patches defined as

$$\begin{aligned} \begin{array}{ll} T_1^k = \{(\xi ,\eta ): \xi \in [2^{-k}, 2^{-k+1}], &{}~~ \eta \in [0, 2^{-k}]\}, \\ T_2^k = \{(\xi ,\eta ): \xi \in [2^{-k}, 2^{-k+1}], &{}~~ \eta \in [2^{-k},2^{-k+1}]\}, \\ T_3^k = \{(\xi ,\eta ): \xi \in [0, 2^{-k}], &{}~~ \eta \in [2^{-k}, 2^{-k+1}]\}, \end{array} \end{aligned}$$

(6)

with the subdivision level $k = \mathrm{floor}(\mathrm{min}(-\mathrm{log2}(\xi ), -\mathrm{log2}(\eta )))$. Obviously, these sub-patches can be mapped onto the unit square T through the transform

$$\begin{aligned} \begin{array}{lr} t_{1,k}(\xi ,\eta ) = (2^k \xi - 1, 2^k \eta ), &{} ~~~(\xi ,\eta ) \in T_1^k, \\ t_{2,k}(\xi ,\eta ) = (2^k\ \xi -1, 2^k \eta -1), &{} ~~~(\xi ,\eta ) \in T_2^k,\\ t_{3,k}(\xi ,\eta ) = (2^k\ \xi , 2^k \eta -1), &{} ~~~(\xi ,\eta ) \in T_3^k. \end{array} \end{aligned}$$

Hence the patch is defined by its restriction to each quadrilateral

$$\begin{aligned} \mathbf{x}(\xi , \eta )|_{T_{j}^{k}}= & {} \sum _{i = 1}^{16} B_{i}(t_{j,k}(\xi , \eta )) \mathbf{x}_{i}^{j,k},\nonumber \\&\quad j = 1, 2, 3; k = 1, 2, \ldots , \end{aligned}$$

(7)

where $\mathbf{x}_{i}^{j,k}$ are properly chosen from the control vertices $\bar{\mathbf{x}}^k = [\mathbf{x}_1^k, \ldots , \mathbf{x}_{2N+17}^k]^T$. $\bar{\mathbf{x}}^{k+1} = {\bar{A}} A^{k} \mathbf{x}^0$ where A and ${\bar{A}}$ are the subdivision matrices at corresponding subdivision steps. Stam [23] used the Jordan canonical form $A = S J S^{-1}$ where S and J have explicit forms so that the computation of $A^{k}$ is simplified to the computation of $J^{k}$. It makes computing cost nearly independent of k and hence very efficient.

3 PDEs on surfaces

We introduce three second-order PDEs defined on surfaces containing the Laplace–Beltrami operator. We also give their corresponding weak forms for the following numerical discretization.

3.1 Sobolev spaces on surfaces

Assume that ${{\mathcal {S}}}$ is a sufficiently smooth surface. For a given constant k and a function $f \in C^{\infty } ({{\mathcal {S}}})$, denote $\nabla ^{k} f$ the k-th order covariant derivative of function f, with the convention $\nabla ^{0}f = f$. Let

$$\begin{aligned} C_{k}({{\mathcal {S}}}) = \left\{ f \in C^{\infty }({{\mathcal {S}}}): \int _{s} |\nabla ^{j} f|^{2} \mathrm{d}A \le \infty ~\text {for}~j = 0,\ldots , k \right\} . \end{aligned}$$

We have the following definition of Sobolev space $H^{k}({{\mathcal {S}}})$.

Definition 3.1

Let ${{\mathcal {S}}}$ be a compact surface with at least k-th order smoothness. Sobolev space $H^{k}({{\mathcal {S}}})$ is the completion of $C_{k}({{\mathcal {S}}})$ in the sense of norm

$$\begin{aligned} \Vert f\Vert _{H^{k}({{\mathcal {S}}})} := \left( \sum \limits ^{k}_{j=0} \int _{s} |\nabla ^{j} f|^{2} \mathrm{d}A \right) ^{\frac{1}{2}}. \end{aligned}$$

(8)

For the compact surface ${\mathcal {S}}$, we have

$$\begin{aligned} C_{k}({{\mathcal {S}}}) = C^{\infty }({{\mathcal {S}}})\subset C^{k}({{\mathcal {S}}}) \subset H^{k}({{\mathcal {S}}}). \end{aligned}$$

For the sake of simplicity, we need introduce the following forms

$$\begin{aligned} (u, v) = \int _{s} uv \mathrm{d} A, \ \ \mathrm{and}\ \ (\nabla _{s} u , \nabla _{s} v) = \int _{s} \nabla _{s} u \cdot \nabla _{s} v \mathrm{d} A. \end{aligned}$$

3.2 Laplace–Beltrami equation

The Laplace–Beltrami equation with the homogenous Dirichlet boundary condition is written as

$$\begin{aligned} \left\{ \begin{array}{ll} - \Delta _{s} u = f, &{}\text {in}~{{\mathcal {S}}}, \\ [0.5em] u= 0, &{} \text {on}~\partial {{\mathcal {S}}}, \end{array} \right. \end{aligned}$$

(9)

where $\Delta _{s}$ is the Laplace–Beltrami operator. ${{\mathcal {S}}} \in {\mathbb {R}}^3$ is a bounded surface with piecewise smooth boundary $\partial {{\mathcal {S}}}$. Let $H^1_{0}({{\mathcal {S}}}) = \{ u \in H^{1}({{\mathcal {S}}}), u = 0 \ \mathrm{on} \ \partial {{\mathcal {S}}}$ }. The weak form of the problem (9) is given as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \mathrm{Find}\ u \in H^1_{0}({{\mathcal {S}}}) \ \mathrm{such\ that} \\ [0.5em] (\nabla _{s} u , \nabla _{s} v) = (f,v), \quad \forall v \in H^1_0({{\mathcal {S}}}). \end{array} \right. \end{aligned}$$

(10)

3.3 Laplace–Beltrami eigenvalue equation

The Laplace–Beltrami eigenvalue problem defined on a closed surface ${{\mathcal {S}}}$ is described as

$$\begin{aligned} \begin{array}{l} -\Delta _{s} u = \lambda u, \quad \text {in}~{{\mathcal {S}}}, \end{array} \end{aligned}$$

(11)

where the parameter $\lambda$ is unknown. The weak form of the problem (11) is given as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \mathrm{Find}\ u \in H^1_{0}({{\mathcal {S}}})\ \mathrm{and} \ \lambda \in {\mathbb {R}} \ \mathrm{such\ that} \\ [0.5em] (\nabla _{s} u , \nabla _{s} v) = \lambda (u,v), \quad \forall v \in H^1_0({{\mathcal {S}}}). \end{array} \right. \end{aligned}$$

(12)

Due to the symmetry and positive definiteness of the problem, all the eigenvalues $\lambda$ are real values and non negative, i.e. $\lambda \in {\mathbb {R}},\ \lambda \ge 0$.

3.4 Time-dependent Allen–Cahn equation

In this work, we consider the Allen–Cahn equation with the homogeneous Dirichlet boundary condition (13), which is the simplest special case of a more complicated phase field model for solidification of a pure material, that is

$$\begin{aligned} \left\{ \begin{array}{ll} u_{t}-\Delta _{s} u +\frac{1}{\varepsilon ^2} f(u) = g, &{} (\mathbf{x},t) \in {{\mathcal {S}}} \times [0,T], \\ [0.5em] \nabla _{s} u \cdot \mathbf{n} =0, &{} (\mathbf{x},t) \in \partial {{\mathcal {S}}} \times [0,T], \\ [0.5em] u(\mathbf{x},0) =u_{0}(\mathbf{x}), &{} \mathbf{x} \in {{\mathcal {S}}}, \end{array} \right. \end{aligned}$$

(13)

where ${\nabla _s}$ denote the tangent gradient operator on surface, and $\mathbf{n}$ is the unit outward normal of ${{\mathcal {S}}}$ along the boundary $\partial {{\mathcal {S}}}$. The time T is fixed as a constant parameter. The term $f(u) = {{\mathcal {F}}}^{\prime }(u)$ for some double well potential density function ${{\mathcal {F}}}$, which takes its global minimum value 0 at $u =\pm 1$. Here we choose the following widely used quartic density function ${{\mathcal {F}}}(u) = \frac{1}{4}(u^2-1)^2$. Here the function u(t) represents the concentration of one of the two metallic components of the alloy. The parameter $\varepsilon$ is an ’interaction length’, which is small compared to the characteristic dimensions on the laboratory scale. Then the weak form of the problem (13) reads: for all $t \in (0,T)$,

$$\begin{aligned} \left\{ \begin{array}{lllll} \mathrm{Find}\ u(t) \in H^1_{0}({{\mathcal {S}}}) \ \mathrm{such\ that} \\ \displaystyle \big (\frac{\partial u(t)}{\partial t}, v \big )+(\nabla _{s} u , \nabla _{s} v) + \frac{1}{\varepsilon ^2}(f(u),v)\\ \quad = (g,v), \quad \forall v \in H^1_0({{\mathcal {S}}}),\\ u(\mathbf{x},0) =u_{0}(\mathbf{x}). \end{array} \right. \end{aligned}$$

(14)

4 IGA-CC discrertization

In this section we proceed the IGA-CC discretization for the three problems introduced in Sect. 3. We describe the approximation in a uniform form for the three problems which are all second-order equations. For the time-dependent Allen–Cahn equation we focus on discussing its spatial discretization where the generalized-$\alpha$ method in the time direction discretization can be seen in a lot of references.

4.1 Function spaces

As described in Sect. 2.2, starting from an initial quadrilateral control mesh $M^0_h$ which serves as the control mesh of the extended Catmull–Clark subdivision, the vertex positions of the refined mesh $M^{k+1}_h$ are computed as the weighted average of the vertex positions of the unrefined mesh $M^k_h$ through $\hat{\mathbf{x}}^{k+1} = A \hat{\mathbf{x}}^k,\ \ k =0,1,\ldots$, where the subdivision matrix A describes the subdivision rules. Taking the infinite number of these subdivision process yields its limit representation denoted as ${\mathcal {S}}$. The limit surface ${\mathcal {S}}$ converges at extraordinary control vertices. The limit position for each control vertex can be found explicitly, which is described as Lemma 4.1 ( [40]).

Lemma 4.1

Let $\hat{\mathbf{x}}^0_0$ be a vertex with valence n of the initial control mesh $M^{(0)}_{h}$. Mark its 1-ring adjacent edgepoints with subscript p and 1-ring facepoints with subscript r, then all these vertices converge to a single position

$$\begin{aligned} {\mathbf{x}}_0:= & {} \frac{n}{n+5}\hat{\mathbf{x}}^0_0 + \frac{4}{n(n+5)} \sum \limits ^{n}_{j = 1} \hat{\mathbf{x}}^0_{p_j}\nonumber \\&+ \frac{1}{n(n+5)} \sum \limits ^{n}_{j = 1} \hat{\mathbf{x}}^0_{r_j}, \end{aligned}$$

(15)

as the subdivision step goes to infinity.

We employ the function space defined by the limit of the extended Catmull–Clark subdivision for describing the computation domain and performing the numerical simulation to arrive at a unified discretization of our problems which is $C^1$ continuous everywhere. We use ${{\mathcal {S}}}_h$ to denote the discretized representation of the limit form ${{\mathcal {S}}}$ where the discretization parameter h usually denotes the mesh size. The discretized form ${{\mathcal {S}}}_h = \bigcup ^{k}_{\alpha =1} e _{\alpha }, \mathring{e}_{\alpha } \bigcap \mathring{e}_{\beta } = \emptyset$ for $\alpha \ne \beta$, where $\mathring{e}_{\alpha }$ is the interior of the quadrilateral patch $e_{\alpha }$. Each patch $e_{\alpha }$ can be parameterized as

$$\begin{aligned} \mathbf{x}_{\alpha }: \ \ {\mathsf {e}} \rightarrow e_{\alpha }; \ \ (\xi , \eta ) \ \mapsto \ \mathbf{x}_{\alpha }(\xi , \eta ), \end{aligned}$$

where the unit reference square ${\mathsf {e}} = \{(\xi , \eta )\in {{\mathbb {R}}}^2: 0 \le \xi \le 1, 0 \le \eta \le 1 \}$, and $(\xi ,\eta )$ are the barycentric coordinates on it. The domain of each patch $e_{\alpha }$ on the quadrilaterization ${{\mathcal {S}}}_h$ can always be locally represented as an explicit bicubic B-spline according to the formula (7). Let the mesh ${{\mathcal {S}}}_h$ with control vertices $\{ \mathbf{x}_j \}_{j=1}^{n}$, we associate a basis function $\phi _j$ for every vertex $\mathbf{x}_j$, which is the corresponding basis function induced by the limit of the extended Catmull–Clark subdivision. Our finite element space is spanned by the set of basis functions $\phi _1, \ldots , \phi _n$, then the limit surface ${{\mathcal {S}}}$ is exactly represented with the extended subdivision patches,

$$\begin{aligned}&{{\mathcal {S}}} = \mathbf{x}(\xi , \eta ) = \mathbf{x}( x(\xi , \eta ),y(\xi , \eta ),z(\xi , \eta ))\nonumber \\&= \sum \limits ^{n}_{j=1} \phi _j(\xi , \eta ) \mathbf{x}_j. \end{aligned}$$

(16)

The boundaries of the surfaces are represented as the cubic B-spline curves which are preserved as the subdivision proceeds. Therefore Catmull–Clark subdivision elements can exactly represent geometries in the same way which is consistent with the concept of isogeometric strategy.

4.2 Applications to PDEs on surfaces

Let $\{\mathbf{x}_1, \ldots , \mathbf{x}_{n_0}\}$ be the set of interior control vertices, and $\{\mathbf{x}_{n_0+1}, \ldots , \mathbf{x}_{n}\}$ be the set of boundary control vertices. By means of the set of the basis functions $\phi _{j} \in H^{2}({{\mathcal {S}}}_h)$ induced by the limit form of the extended Catmull–Clark subdivision, we have the basis description for the unknowns $u^h$ to be determined

$$\begin{aligned} u^h = \sum ^{n_0}_{j=1} \phi _j u^h_j + \sum ^{n}_{j=n_0+1} \phi _j u^h_j. \end{aligned}$$

(17)

The finite element approximation for the Laplace–Beltrami equation (10) reads as

$$\begin{aligned} \left\{ \begin{array}{llll} \mathrm{Find}\ u^h \in H^{1}_{0}({{\mathcal {S}}}_h)\ \mathrm{such\ that} \\ [0.5em] (\nabla _{s} u^{h} , \nabla _{s} v) = (f,v), \quad \forall v \in H^{1}_{0}({{\mathcal {S}}}_h). \end{array} \right. \end{aligned}$$

(18)

Applying (17) to (18), and taking the test functions $v = \phi _{i},\ i = 1, \ldots , n_{0}$, it follows that

$$\begin{aligned} \sum \limits ^{n}_{j=1} u^h_j (\nabla _{s} \phi _{j}, \nabla _{s} \phi _{i}) = (f, \phi _i) \quad i = 1, \ldots , n_{0}, \end{aligned}$$

with the zero boundary conditions. Denote the stiffness matrix $\mathbf{K} =[(\nabla _{s} \phi _{j}, \nabla _{s} \phi _{i})]_{n_{0} \times n_{0}}$, and the right-hand side term vector $\mathbf{b} = [(f,\phi _1), \ldots , (f, \phi _{n_{0}})]^{\mathrm{T}}$, it yields a linear system

$$\begin{aligned} \mathbf{Ku} = \mathbf{b} \end{aligned}$$

(19)

where $\mathbf{u} =[u^{h}_{1}, \ldots , u^{h}_{n_{0}}]^{\mathrm{T}}$ is the unknown vector.

We proceed in a similar manner for the Laplace–Beltrami eigenvalue equation (12) as follows:

$$\begin{aligned} \left\{ \begin{array}{llll} \mathrm{Find}\ u^h \in H^{1}_{0}({{\mathcal {S}}}_h) \ \mathrm{and} \ \lambda ^{h} \in {\mathbb {R}} \ \mathrm{such\ that} \\ (\nabla _{s} u^h , \nabla _{s} v) =\lambda ^{h} (u^{h},v), \quad \forall v \in H^{1}_{0}({{\mathcal {S}}}_h). \end{array} \right. \end{aligned}$$

(20)

Applying (17) to (20), and taking the test functions $v = \phi _{i},\ i = 1, \ldots , n$, we have

$$\begin{aligned} \sum \limits ^{n}_{j=1} u^h_j (\nabla _{s} \phi _{j}, \nabla _{s} \phi _{i}) = \lambda ^{h} (f, \phi _i) \quad i = 1, \ldots , n. \end{aligned}$$

The eigenvalues $\lambda ^h$ are real since the bilinear forms are symmetric. It yields a linear system

$$\begin{aligned} \mathbf{Ku} = \lambda ^{h}{} \mathbf{b}, \end{aligned}$$

(21)

where $\mathbf{u}= [u^{h}_{1}, \ldots , u^{h}_{n}]^{\mathrm{T}}$ is the unknown vector, the stiffness matrix $\mathbf{K}= [(\nabla _{s} \phi _{j}, \nabla _{s} \phi _{i})]_{n \times n}$ and the load vector $\mathbf{b} = [(f,\phi _1), \ldots , (f, \phi _{n})]^{\mathrm{T}}$.

For the semi-discrete form of the Allen–Cahn equation (14), we have

$$\begin{aligned} \left\{ \begin{array}{lll} \mathrm{Find}\ u^h(t) \in H^{1}_{0}({{\mathcal {S}}}_h) \ \mathrm{such\ that} \\ \displaystyle \big (\frac{\partial u^{h}(t)}{\partial t}, v \big ) + (\nabla _{s} u^h(t), \nabla _{s} v)\\ +\frac{1}{\varepsilon ^2}(f(u^h(t)), v) =(g,v), \quad \forall v \in H^{1}_{0}({{\mathcal {S}}}_h). \end{array} \right. \end{aligned}$$

(22)

Applying (17) to (22), and taking the test functions $v = \phi _{i},\ i = 1, \ldots , n$, it follows that

$$\begin{aligned}&\sum \limits ^{n_{0}}_{j=1} \frac{\partial u^{h}_{j}(t)}{\partial t} (\phi _{j}, \phi _{i}) +u^h_j(t) (\nabla _{s} \phi _{j}, \nabla _{s} \phi _{i}) \\&\quad + \frac{1}{\varepsilon ^2}(f(u^h_{j}(t)), \phi _i) = (g,\phi _{i}) \quad i = 1, \ldots , n_{0}, \end{aligned}$$

with the homogenous Dirichlet boundary conditions. Denote the mass matrix $\mathbf{M} =[(\phi _{j}, \phi _{i})]_{n_{0} \times n_{0}}$, the stiffness matrix $\mathbf{K}= [(\nabla _{s} \phi _{j}, \nabla _{s} \phi _{i})]_{n_{0} \times n_{0}}$, the matrix $\mathbf{F} = \frac{1}{\varepsilon ^2}[(f,\phi _1), \ldots , (f, \phi _{n_0})]^{\mathrm{T}}$, and the matrix $\mathbf{G} = [(g,\phi _1), \ldots , (g, \phi _{n_0})]^{\mathrm{T}}$, it yields a linear system

$$\begin{aligned} \mathbf{M} \frac{\partial \mathbf{u}(t)}{\partial t} + \mathbf{Ku}(t) + \mathbf{F} = \mathbf{G}, \end{aligned}$$

(23)

where $\mathbf{u}(t)= [u^{h}_{1}(t), \ldots , u^{h}_{n_{0}}(t)]^{\mathrm{T}}$ is the unknown vector.

4.3 Precomputing the basis functions

The related basis functions and their derivatives need to be precomputed for each control patch of ${{\mathcal {S}}}_{h}$ before solving the linear systems. These computations of IGA-CC are not intuitive in comparison with standard linear elements since the required two-ring neighbors around each patch have arbitrary topological structure, and additional geometric data are reflected in the subdivision schemes around boundaries. However, the framework of these computations is the same standard process as the classical FEM. We classify the control mesh into interior patches, sub-boundary patches, and boundary patches. The patches containing boundary vertices are named as boundary patches. The patches adjacent to boundary patches are called sub-boundary patches. As described in Sect. 2.2, Stam’s fast algorithm is just applied to the interior patches, however it is obvious that the sub-boundary patches can be subdivided into four interior sub-patches by one time subdivision, and the boundary patches can be subdivided repeatedly till their sub-patches belong to the sub-boundary case. Therefore, the actual final calculation makes the region of interest fall into the standard bi-cubic spline patch.

The Stam’s fast evaluation scheme is always suitable for interior patches with only one extraordinary vertex. Therefore, it is necessary to first subdivide once each patch of the initial mesh. The evaluation of basis functions over their support elements uses general Gaussian integration, which just needs a few subdivision steps to bring Gaussian quadrature knots into a bi-cubic spline patch. The integrations for computing the matrix elements are computed by a 16-point Gaussian quadrature rule. That is, each quadrilateral is subdivided into four sub-quadrilaterals and a 4-point Gaussian quadrature rule is employed on each of the sub-quadrilaterals. The 4-point Gaussian quadrature rule has error bound $O(h^3)$, where h is the maximal edge length. We adopt the adaptive numerical method developed in our former work [35].

5 Error estimates

In this section we study the error estimation for the Laplace–Beltrami equation, the Laplace–Beltrami eigenvalue equation and the time-dependent Cahn–Allen equation. With the aim, we need provide the interpolation error estimate for the IGA-CC function space on surfaces.

5.1 Interpolation error estimate

Next we can formulate the interpolation problem. Let $\hat{\mathbf{x}}_{i}$ be the i-th control vertex of the control mesh $M_{h}$ of the extended Catmull–Clark subdivision, and $\mathbf{x}_{i}$ is the i-th vertex on the limit form ${{\mathcal {S}}}_{h}$ of the extended Catmull–Clark subdivision surface, where $i = 1,\ldots , n$. Denote $u(\mathbf{x}_{i})$ is the i-th interpolation function value, $v(\hat{\mathbf{x}}_{i})$ is the i-th control function value, and $\phi _{i}$ is the i-th basis function, where $i = 1,\ldots , n$. For the given function values $\{ u(\mathbf{x}_{i}) \}^{n}_{1}$, find the control function values $\{v({\hat{\mathbf{x}}}_{i})\}^{n}_{1}$ such that

$$\begin{aligned}&\sum \limits ^{n}_{i=1} v({\hat{\mathbf{x}}}_{i}) \phi _{i}(\mathbf{x}_{j}) = u(\mathbf{x}_{i}), \ j = 1,\ldots , n. \end{aligned}$$

(24)

The interpolation problem (24) always has a unique solution. It follows from (15) that equation (24) is equivalent to the following Lemma 5.1 (see [35] for details).

Lemma 5.1

Given a vertex $\hat{\mathbf{x}}_i$ of the control mesh $M_h$, with the valence $n_{i}$, let $\hat{\mathbf{x}}_{p_j} (j = 1,2,\ldots , n_i)$ be its 1-ring edgepoints on $M_h$, and $\hat{\mathbf{x}}_{r_j} (j = 1,2,\ldots , n_i)$ be its 1-ring facepoints on $M_h$. Denote $\mathbf{x}_i$ be the i-th control vertex of the discrete representation ${{\mathcal {S}}}_h$ for the limit surface ${{\mathcal {S}}}$, $u(\mathbf{x}_i)$ is the i-th interpolation function value, and $v(\hat{\mathbf{x}}_i)$ is the i-th control function value. The system

$$\begin{aligned}&\frac{n_i}{n_i+5}v(\hat{\mathbf{x}}_i) + \frac{4}{n_i(n_i+5)} \sum \limits ^{n_i}_{j = 1} v(\hat{\mathbf{x}}_{p_j}) \nonumber \\&\quad + \frac{1}{n_i(n_i+5)} \sum \limits ^{n_i}_{j = 1} v(\hat{\mathbf{x}}_{r_j}) = u(\mathbf{x}_i),\ \ i =1,\ldots , n, \end{aligned}$$

(25)

is always solvable uniquely.

Let $\Omega$ be a unit square parameter region of the physical domain ${{\mathcal {S}}}$. The geometric mapping G is sufficiently smooth and invertible, then denote

$$\begin{aligned} {{\mathcal {S}}} = G(\Omega ), \ \ \Omega = G^{-1} ({{\mathcal {S}}}). \end{aligned}$$

It provides a parameterization for the limit representation ${{\mathcal {S}}}$ of the extended Catmull–Clark subdivision surface. Therefore, each patch $e \in {{\mathcal {S}}}_h$ is mapped onto a unit square ${\mathsf {e}} \in \Omega$. We associate the domain set $\tilde{{\mathsf {e}}} \in \Omega$ as the support of ${\mathsf {e}}$ which is a unit of 1-ring neighbors of ${{\mathsf {e}}}$ on $\Omega$. Analogously, the support $\tilde{{\mathsf {e}}}$ is mapped onto ${\tilde{e}} = G (\tilde{{\mathsf {e}}})$, where ${\tilde{e}}$ is the set of 1-ring neighbors of e on the quadrangularization ${{\mathcal {S}}}_h$. The following lemma provides us the estimates for the projection change of the function variables between the parameter region and the physical domain.

Lemma 5.2

Let the indexes $m=0, 1,2$, and given $e \in {{\mathcal {S}}}_h$ and its corresponding support extension ${\tilde{e}}$, we have for the function $u \in H^2(e)$ and its projection ${\hat{u}} \in H^2({{\mathsf {e}}})$ on the parameter domain,

$$\begin{aligned}&|u(\mathbf{x})|_{{H^m}(e)} \le C | J_{G}|^{1/2}_{L^{\infty }({\mathsf {e}})}|\nabla G^{-1}|^{m}_{L^{\infty }({\mathsf {e}})}\nonumber \\&\quad \qquad \sum ^{m}_{i=0} |{\hat{u}}({\hat{x}})|_{H^i({\mathsf {e}})}, \end{aligned}$$

(26)

and

$$\begin{aligned}&|{\hat{u}}({\hat{x}})|_{{H^m}({{\mathsf {e}}})} \le C |J_{G^{-1}}|^{1/2}_{L^{\infty }(e)}\nonumber \\&\qquad \quad \sum ^{m}_{i=0} |\nabla G|^{i}_{L^{\infty }({{\mathsf {e}}})} |u(\mathbf{x})|_{H^i(e)}. \end{aligned}$$

(27)

Proof. We start proving the result (26). Observe that

$$\begin{aligned}&u= {\hat{u}} \circ G^{-1},\ \ {\hat{u}} = u \circ G, \nonumber \\&\quad \mathrm{and} \ \ \mathbf{x} = G({\hat{x}}), \ \ {\hat{x}} = G^{-1}(\mathbf{x}), \end{aligned}$$

(28)

and the definition of the norm on the surface (3.1). For the case $m=0$,

$$\begin{aligned} \begin{array}{l} |u(\mathbf{x})|_{{H^0}(e)} = \displaystyle \int _{e} |u(\mathbf{x})| \mathrm{d}{} \mathbf{x} = \int _{e} |{\hat{u}}\circ G^{-1}(\mathbf{x})| \mathrm{d}{} \mathbf{x} \\ [0.5em] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \displaystyle \int _{{\mathsf {e}}} | J_{G}|^{1/2} \cdot |{\hat{u}}({\hat{x}})| \mathrm{d} {\hat{x}} \le C |J_{G}|^{1/2}_{L^{\infty }({\mathsf {e}})} \cdot |{\hat{u}}({\hat{x}})|_{H^0({{\mathsf {e}}})}. \end{array} \end{aligned}$$

For the case $m=1$, note that $|\nabla _{s} u(\mathbf{x})| \le |\nabla G^{-1}|_{L^{\infty }({\mathsf {e}})} \cdot |\nabla {\hat{u}}({\hat{x}})|$, from which we obtain

$$\begin{aligned} |u(\mathbf{x})|_{{H^1}(e)}= & {} \displaystyle \int _{e} |\nabla _{s} u(\mathbf{x})| \mathrm{d}{} \mathbf{x} \le C |\nabla G^{-1}|_{L^{\infty }({\mathsf {e}})} \\&\quad \cdot \int _{e} |\nabla {\hat{u}}({{{\hat{x}}}})| \mathrm{d}{} \mathbf{x} \\&\quad \le C |J_{G}|^{1/2}_{L^{\infty }({\mathsf {e}})} \cdot |\nabla G^{-1}|_{L^{\infty }({\mathsf {e}})} |{\hat{u}}({\hat{x}})|_{H^1({{\mathsf {e}}})}. \end{aligned}$$

We can similarly proceed the case $m=2$. Next we consider the inequality (27). For $m=0$, we deduce that

$$\begin{aligned} |{\hat{u}}({\hat{x}})|_{{H^0}({{\mathsf {e}}})}= & {} \displaystyle \int _{{\mathsf {e}}} |{\hat{u}}({\hat{x}})| \mathrm{d}{{{\hat{x}}}} \\= & {} \int _{{\mathsf {e}}} | u\circ G({{\hat{x}}})| \mathrm{d}{{\hat{x}}} \\= & {} \displaystyle \int _{e} |J_{G^{-1}}|^{1/2} \cdot |u(\mathbf{x})| \mathrm{d} \mathbf{x}\\\le & {} C |J_{G^{-1}}|^{1/2}_{L^{\infty }(e)} \cdot |u(\mathbf{x})|_{H^0(e)}. \end{aligned}$$

and for $m=1$ we have that

$$\begin{aligned} |{\hat{u}}({\hat{x}})|_{{H^1}({{\mathsf {e}}})}= & {} \displaystyle \int _{{\mathsf {e}}} |\nabla {\hat{u}}({\hat{x}}) | \mathrm{d}{{{\hat{x}}}} \\\le & {} C |\nabla G|_{L^{\infty }({{\mathsf {e}}})} \cdot \int _{{{\mathsf {e}}}} |\nabla _{s} u(\mathbf{x})| \mathrm{d} {\hat{x}} \\\le & {} C|J_{G^{-1}}|^{1/2}_{L^{\infty }(e)} \cdot |\nabla G|_{L^{\infty }({{\mathsf {e}}})} | u(\mathbf{x})|_{H^1(e)}. \end{aligned}$$

We can similarly proceed the case $m=2$. It completes the proof.

Fig 4

Laplace–Beltrami problem on a quarter of a cylinder. a, b and c are three progressive h-refinement control meshes. The corresponding distribution of the errors $u-u^h$ resulting from the FEM-Linear and the IGA-CC is respectively shown in a’, b’, and c’ of the second row, and a”, b”, and c” of the third row

Fig 5

Laplace–Beltrami eigenvalue problem on a sphere. a, b and c are three progressive h-refinement control meshes. The corresponding distribution of the errors $u_{3}-u^h_{3}$ resulting from the FEM-Linear and the IGA-CC is respectively shown in a’, b’, and c’ of the second row, and a”, b”, and c” of the third row

Fig 6

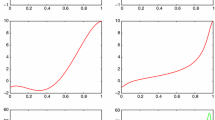
Convergence of $u-u^h$ for the IGA-CC and the FEM-Linear method. a Laplace–Beltrami problem on a quarter of a cylinder. b Laplace–Beltrami eigenvalue problem on a sphere. h along x-axis corresponds to the mesh sizes of the examples in Figs. 4 and 5. The triangles describe the $H^0$-norm convergence order, where $O(h^2)$ can be observed for both methods

Fig 7

Allen–Cahn problem on a cylinder. a, b and c are three progressive h-refinement control meshes. The corresponding distribution of the errors $u-u^h$ resulting from the FEM-Linear and the IGA-CC is respectively shown in a’, b’, and c’ of the second row, and a”, b”, and c” of the third row

Fig 8

Allen–Cahn problem on a hemisphere. a, b and c are three progressive h-refinement control meshes. The corresponding distribution of the errors $u-u^h$ resulting from the FEM-Linear and the IGA-CC is respectively shown in a’, b’, and ($c'$) of the second row, and a”, b”, and c” of the third row

Fig 9

Convergence of $u-u^h$ for the IGA-CC and the FEM-Linear method. a Allen–Cahn problem on a cylinder. b Allen–Cahn problem on a hemisphere. h along x-axis corresponds to the mesh sizes of the examples in Figs. 7 and 8. The triangles describe the $H^0$-norm convergence order, where $O(h^2)$ can be observed for both methods

Based on Lemma 5.1 and Lemma 26, we can achieve the interpolation error estimates for the extended Catmull–Clark function space on surfaces according to the same proof routine as the classical finite element method. Here we just represent the result as the following Theorem 5.3.

Theorem 5.3

Let the indexes $m=0, 1$, and given the mesh element $e \in {{\mathcal {S}}}_h$ and its corresponding support extension ${\tilde{e}}$. For $u \in H^2({\tilde{e}}) \cap L^2({{\mathcal {S}}})$, the interpolation error estimates for the limit form of the extended Catmull–Clark function space on surfaces read as

$$\begin{aligned} |u- \sqcap _{s} u|_{H^{m} (e)} \le C h^{2-m}_{e} \sum \limits ^{2}_{i=1}|u|_{H^{i}({\tilde{e}})}, \end{aligned}$$

(29)

where $h_{e}$ is the size of the mesh element $h_{e} = \mathrm{max} \{ h_{e^{\prime }} {e^{\prime }} \in {\tilde{e}} \}$, and C is a positive constant independent of $h_{e}$.

5.2 A priori error estimates

In this section we present the priori error results for the three equations introduced in Sect. 3. In what follows, assume that the limit surface ${{\mathcal {S}}}$ of the extended Catmull–Clark subdivision is convex, and its mesh h-refinement is quasi-uniform where the size of the mesh elements $h_{e} \simeq h,\ \forall e \in {{\mathcal {S}}}_{h}$. For the Laplace–Beltrami problem (10), the well-posedness is guaranteed with the boundedness of the bilinear form

$$\begin{aligned} |(\nabla _{s} u, \nabla _{s} v)| \le C \Vert u\Vert _{H^1({{\mathcal {S}}})} \Vert v\Vert _{H^1({{\mathcal {S}}})}, \ \ \forall u,v \in H^1({{\mathcal {S}}}), \end{aligned}$$

where C is a positive constant independent of h, and its coercivity

$$\begin{aligned} (\nabla _{s} u, \nabla _{s} u) \ge \nu \Vert u\Vert ^{2}_{H^1({{\mathcal {S}}})}, \ \ \forall u \in H_{0}^1({{\mathcal {S}}}), \end{aligned}$$

where $\nu$ is a positive constant independent of h. The problem (9) leads to the linear system (18), where the number of equations is equal to the number of unknowns, therefore there exists a unique solution $u_{h} \in H^{1}_{0}({{\mathcal {S}}}_{h})$ for (18). Recalling the interpolation error results of Theorem 5.3, we get its $H^1$ norm error estimate, then its $L^2$ norm error estimate using the standard Aubin-Niestche arguments as follows:

Theorem 5.4

Let u be a sufficiently smooth solution of the Laplace–Beltrami problem (9), and $u^h$ be its discrete solution obtained by the IGA-CC method, we have

$$\begin{aligned} | u - u^h |_{H^m({{\mathcal {S}}})} \le Ch^{2-m},\ \ m =0, 1, \end{aligned}$$

(30)

where C is a positive constant independent of h.

As for the Laplace–Beltrami eigenvalue problem (20), we need consider the errors of its eigenvalues $|\lambda _{n}-\lambda ^{h}_{n}|$ where $\lambda _{n}, \ n= 1,2,\ldots ,$ indicates the n-th exact eigenvalue and $\lambda ^{h}_{n}$ is its corresponding approximate value obtained from the IGA-CC method. The eigenvalues $\lambda _{n}$ are real values and non negative where we denote $\lambda _{1} \le \lambda _{2} \le \cdots \le \lambda _{n} \le \cdots$. With the method presented in [41] and Theorem 5.3, we similarly obtain the following error estimates:

Theorem 5.5

Let $\lambda _{n}$ be the n-th eigenvalue of the problem (11), and $\lambda _{n}^h$ be its discrete solution obtained by the IGA-CC method, we have

$$\begin{aligned} | \lambda _{n} - \lambda ^h_{n} | \le Ch^{2},\ \ \forall n \ge 1, \end{aligned}$$

(31)

where C is a positive constant independent of h.

In order to analyze the spatial approximation errors of the Allen–Cahn equation (22), we need find the convergence results of its corresponding elliptic projection. It means we consider the following approximate solutions of the elliptic equation with the Dirichlet boundary conditions

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{s} u + u = g, &{} \mathrm{in}\ {{\mathcal {S}}}, \\ u = 0, &{} \mathrm{on} \ \partial {{\mathcal {S}}}. \end{array} \right. \end{aligned}$$

(32)

Note that the error estimates of the problem (32) are not essential different from the Laplace–Beltrami problem (20), here we omit the details of the proofs. For the semi-discrete form (22) of the Allen–Cahn equation (13), on the basis of Theorem 5.4, we have the following $L^2$ norm estimate:

Theorem 5.6

Let u be a sufficiently smooth solution of the problem (13), and $u^h$ be its spatially discrete solution obtained by the IGA-CC method. Assume that the initial discrete data $u^{h}(0)$ satisfies

$$\begin{aligned} \Vert u^{h}(0) - u_{0}\Vert _{L^{2}({{\mathcal {S}}})} \le Ch^2, \end{aligned}$$

then the following error estimate holds, for $t \le T$,

$$\begin{aligned} \Vert u^{h}(t) - u(t)\Vert _{L^{2}({{\mathcal {S}}})} \le Ch^2, \end{aligned}$$

(33)

where the constant C is a positive constant independent of h and t.

6 Numerical examples

In this section, we represent some numerical experiments of solving the Laplace–Beltrami problem, the Laplace–Beltrami eigenvalue problem and the Cahn–Allen problem on different domain surfaces. We numerically approximate these problems by means of the IGA-CC method, and the linear finite element (FEM-Linear) method is also adopted in these examples.

6.1 Laplace–Beltrami equation

We firstly consider the Laplace–Beltrami equation

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{s} u = f, &{} \text {in}~{{\mathcal {S}}}, \\ [0.5em] u = 0, &{} \text {on}~{\partial {\mathcal {S}}}, \end{array} \right. \end{aligned}$$

(34)

on a quarter of a cylinder with radius 1 and height 2, i.e., ${{\mathcal {S}}}_{1} = \{(x,y,z): x^2+y^2 =1 \ \& \ x \ge 0 \ \& \ y \ge 0 \ \& \ 0 \le z \le 2 \}$. The exact solution is given as $u = (1-x)(1-y) \mathrm{sin} (\pi z)$ with the calculated f.

The computational domain is discretized by five progressive h-refinement meshes with the Catmull–Clark subdivision elements, where we show the first three discretization examples in Fig. 4. The total numbers of vertices/patches are 317/288, 1209/1152, and 4721/4608 in Fig. 4a–c respectively, where the maximum value for the vertex valence arrives at 8. They have the same limit surface ${{\mathcal {S}}}_{1}$. Figure 4 also plots the error distribution indicated by $u-u^h$ for the two numerical methods, where we can observe that the error fluctuation of the FEM-Linear method is bigger that the IGA-CC method.

The convergence rates of the errors versus different mesh sizes for both methods are depicted in Fig. 6a, from which we can see that the $H^0$-norm convergence rate of both methods is approximately 2. The test data are consistent with the theoretical results. As demonstrated in this figure, as for the same level of the mesh h-refinement, the approximation errors of the FEM-Linear discretization are approximately 2.0 times more than that of the IGA-CC discretization. It means that the IGA-CC approximation only requires a smaller number of degree of freedoms than the FEM-Linear to achieve the same accuracy.

6.2 Laplace–Beltrami eigenvalue equation

We consider the Laplace–Beltrami eigenvalue problem on a closed sphere with radius 1, i.e., ${{\mathcal {S}}}_{2} = \{(x,y,z): x^2+y^2+z^2=1\}$ as the second example, that is

$$\begin{aligned} \begin{array}{l} -\Delta _{s} u = \lambda u, \quad \text {in}~{{\mathcal {S}}}. \end{array} \end{aligned}$$

(35)

The exact values of the eigenvalues $\lambda _{n} = n(n+1)$, each with multiplicity $2n+1$, $n= 0,1,\ldots , \infty$, which correspond to the eigenfunctions $u^{h}_{n}$ ( [2]). We show the discrete solutions of the eigenfunction $u^{h}_{3}$ corresponding to the eigenvalue $\lambda _{3} = 12$ where the sphere is discretized by five progressive h-refinement meshes with the Catmull–Clark subdivision elements. We show the first three discretization examples in Fig. 5. The total numbers of vertices/patches are 898/896, 3586/3584, and 14338/14336 in Fig. 5a–c respectively, where the maximum value for the vertex valence arrives at 6. Figure 5 also reports the error distribution indicated by $u_{3}-u^h_{3}$ for the two numerical methods. It is observed that the accuracy of the IGA-CC is higher than that of the FEM-Linear by the profile of the error distribution.

The convergence rates of the errors $\lambda - \lambda ^{h}_{3}$ versus different mesh sizes for both methods are reported in Fig. 6b. Both methods exhibit a perfect accuracy of $O(h^2)$. The convergence rates obtained by both methods for the numerical solutions are in agreement with the theoretical results. We observe that the approximation errors of the FEM-Linear discretization are about 2.0 times more than that of the IGA-CC discretization. The IGA-CC method obtains the same level of accuracy more efficiently than the FEM-Linear method.

6.3 Allen–Cahn equation

In this problem, we consider the Allen–Cahn equation with the homogeneous Dirichlet boundary condition on two different domain surfaces, that is

$$\begin{aligned} \left\{ \begin{array}{ll} u_{t}-\Delta _{s} u +\frac{1}{\varepsilon ^2} f(u) = g(\mathbf{x},t), &{} (\mathbf{x},t) \in {{\mathcal {S}}} \times [0,T], \\ [0.5em] u(\mathbf{x},t) =0, &{} (\mathbf{x},t) \in \partial {{\mathcal {S}}} \times [0,T], \\ [0.5em] u(\mathbf{x},0) =u_{0}(\mathbf{x}), &{} \mathbf{x} \in {{\mathcal {S}}}, \end{array} \right. \end{aligned}$$

(36)

where we take $\varepsilon = 0.1$. We focus on the spatial discretization for this problem. One example of the Allen–Cahn problem is considered a cylinder with radius 1 and height 2, i.e., ${{\mathcal {S}}}_{3} = \{(x,y,z): x^2+y^2=1, 0 \le z \le 2 \}$. The exact solution is taken as $u(x,y,z,t) = e^{t} \mathrm{sin}^2 (x) \mathrm{cos} ^2(y) \mathrm{sin}(\pi z/2)$ with the calculated g, and $u_{0}$ is given by the exact solution. As the other example, we consider a hemisphere with radius 1, i.e., ${{\mathcal {S}}}_{4} = \{(x,y,z): x^2+y^2+z^2=1, z \ge 0 \}$ as the computational domain. The exact solution is taken as $u(x,y,z,t) = e^{t + \mathrm{sin} x +\mathrm{cos}y } (e^{\mathrm{sin}z}-1)$ with the calculated g, and $u_{0}$ is given by the exact solution. The results of both cases are computed at the fixed time $T = 0.02$.

In both examples, we numerically solve this problem using five progressive h-refinement meshes, then we get similar results. For the cylinder case, the limit surface ${{\mathcal {S}}}_{3}$ is discretized using 1152, 4608 and 18432 Catmull–Clark subdivision elements depicted respectively in Fig. 7a–c. The corresponding data for the number of control vertices are 317, 1209 and 4721 whose maximum valence is 8. For the hemisphere case, the limit surface ${{\mathcal {S}}}_{4}$ is discretized using 448, 1792 and 7168 Catmull–Clark subdivision elements respectively depicted in Fig. 8a–c. The corresponding data for the number of control vertices are 489, 1873 and 7329 whose maximum valence is 6. We report the error states between the exact and the numerical solutions also in these two figures, from which a bigger error fluctuation is introduced by the FEM-Linear contrast to the IGA-CC.

The $H^0$ norm errors at the fixed time $T = 0.02$ are plotted against the mesh sizes in Fig. 9. The convergence rates of $O(h^2)$ are observed in both cases, which are accordance with the predicted priori error estimates. The same convergence rates are reported for the FEM-Linear method. A similar phenomena can be found that the approximation errors of the FEM-Linear discretization are approximately 2.0 times more than that of the IGA-CC discretization. It means that the IGA-CC discretization is potentially more efficient. The approximation error is added by the discretization of the surface geometries using the linear finite elements, instead, exact representation of the surfaces can be achieved by means of the IGA-CC.

7 Conclusions

In this work, we present the capability of the IGA-CC method for the numerical approximation of PDEs defined on surfaces. We consider three problems including the Laplace–Beltrami harmonic equation, the Laplace–Beltrami eigenvalue equation and the time-dependent Allen–Cahn equation on different domain surfaces. These problems all involve the Laplace–Beltrami operator. The surfaces are accurately represented as the extended form of the Catmull–Clark subdivision patches. The finite element discretization for these PDEs is also induced from the extended Catmull–Clark subdivision function space on surfaces. Moreover, we develop corresponding interpolation error estimates, which are used to obtain a priori error estimates for these PDEs. We present numerous numerical examples consistent with the theoretical results and show the performance of IGA-CC by comparing with the standard linear finite elements.