1 Introduction

The advancement of full-field measurement techniques in solid mechanics is a source of numerous inverse problems arising from the identification of material properties and of their spatial variations [1,2,3,4]. A robust way to solve inverse problems in elasticity is to introduce constrained optimization problems based on the deviation between measurements and model predictions, and solve them iteratively [5,6,7,8,9,10]. In this case, there are a large number of parameters to be identified in the inverse problem. The total number of the optimization parameters is correlated with the mesh of the discretized problem domain. Due to the large number of the optimization parameters, the computational cost of optimization-based inverse problems is considerable. To identify the nonhomogeneous linear elastic property distribution of solids, an alternative is to explicitly express the linear elastic property in terms of the stress and strain and directly solve elastic properties of every element [11, 12]. Similar to the iterative inverse solvers, the computational cost of direct resolution methods depends on the number of unknown material properties defined in the discretization.

In 1989, a novel parameter identification method was proposed, referred to as the virtual fields method (VFM) [13]. This approach is based on the principle of the virtual work or principle of virtual power. Compared to the optimization-based approaches, the VFM does not require solving the inverse problem iteratively but relies on the selection of virtual fields to establish a system of equations involving the unknown material properties. Therefore, the computational cost can be significantly reduced. Due to this merit, the VFM has been applied to the characterization of a wide range of constitutive behaviors, including linear elasticity [14, 15], hyperelasticity [16, 17] or plasticity [18, 19]. Besides, the VFM has also been used to estimate the nonhomogeneous distribution of material properties in solids [20,21,22,23]. In [23], the authors proposed novel types of virtual fields to estimate the shear moduli of nonhomogeneous, incompressible linear elastic solids assuming that every nonhomogeneous region is known as a priori. In [20], the authors approximated the nonhomogeneous shear modulus distribution by the Fourier series and successfully estimated the shear modulus distribution. However, when there is a very large number of unknowns and the inverse problem becomes ill-posed, it may be needed to take into account prior knowledge about the material properties. For instance, it can be assumed that material properties remain within a given bounded interval or that the spatial variations of material properties cannot induce gradients larger than a given threshold. The downside of the VFM so far was not to take into account this prior knowledge. Regularization was always achieved by decreasing the number of unknowns, for instance, by tuning the degree of Fourier polynomials in [20].

In this work, novel inverse approaches introducing regularization methods into the VFM are proposed in order to ensure the uniqueness and convergence of the inverse problem resolution. This paper is organized as follows: In the Methods Section, we present the mathematical aspects of the proposed regularized VFM. In the Results Section, several simulated and experimental displacement datasets of nonhomogeneous elastic solids are used to test the feasibility of the proposed method. Subsequently, the proposed method and identification results are discussed in the Discussion Section. Finally, a summary of the salient results and of future directions is provided in the Conclusion Section.

2 Methods

2.1 Identification of spatially varying stiffness properties with the VFM

For a domain of interest \(\Omega\) across a solid at equilibrium in a quasi-static state, the principle of virtual work neglecting the body force may be written as:

$$- \int_{\Omega } {{\varvec{\upsigma}}} :{{\varvec{\upvarepsilon}}}^{*} dV + \int_{{\partial \Omega_{t} }} {\mathbf{t}} \cdot {\mathbf{u}}^{*} dS = 0$$
(1)

for any kinematically admissible u* where \({{\varvec{\upsigma}}}\) is the actual stress tensor computed related to the strain tensor \({{\varvec{\upvarepsilon}}}\) through constitutive equations. The strain components are calculated from gradients of the measured displacement field \({\mathbf{u}}\) and \({\mathbf{t}}\) is the traction vector field applied on the traction boundary \(\partial \Omega_{t}\). \({\mathbf{u}}^{*}\) and \({{\varvec{\upvarepsilon}}}^{*}\) are the kinematically admissible virtual displacement field and the associated virtual strain field, respectively.

For the sake of simplicity in developing the first version of the regularized VFM, we consider 2D solids in plane strain, but the method can easily extend to 3D. In plane strain, the linear elastic constitutive equations may be written such as:

$${{\varvec{\upsigma}}} = \frac{E}{(1 + \nu )}{{\varvec{\upvarepsilon}}} + \frac{E\nu }{{(1 + \nu )(1 - 2\nu )}}{\text{tr}}({{\varvec{\upvarepsilon}}}){\mathbf{I}}$$
(2)

for any kinematically admissible u* where E is the Young’s modulus and \(\nu\) the Poisson’s ratio. It is generally assumed that the Poisson’s ratio v is known a priori [20,21,22,23], which significantly simplifies further derivations. This simplification is especially admitted for nearly incompressible materials.

To identify the nonhomogeneous distribution of the Young’s modulus E, the domain of interest is discretized with a finite-element mesh and it is assumed that E is constant across each element as shown in Fig. 1.

Fig. 1
figure 1

a Discretization of the domain of interest across which the inverse problem is defined; b–d are the free body diagrams of the elements in the discretized domain

Full size image

For any arbitrary element in the discretized domain (Fig. 1), equilibrium can be represented through the free body diagram (Fig. 1b). For a single element, the principle of virtual work may be written such as,

$$- \int_{{\Omega^{e} }} {{\varvec{\upsigma}}} :{{\varvec{\upvarepsilon}}}^{*} dS + \int_{{\partial \Omega_{t}^{e} }} {\mathbf{t}} \cdot {\mathbf{u}}^{*} dl = 0$$
(3)

where \(\Omega^{e}\) and \(\partial \Omega_{t}^{e}\) are the area and the contour of the element, respectively. In this case, \({\mathbf{t}}\) are the reaction forces from neighboring elements, which are unknown. A classical approach in the VFM is to cancel out these unknown reaction forces by satisfying the following equation:

$${\mathbf{u}}^{ * } {\mathbf{ = 0}}{\text{ on }}\partial \Omega^{e}$$
(4)

However, this automatically zeroes the external virtual work, and so does the internal virtual work, Eq. (3) being reduced to:

$$\int_{{\Omega^{e} }} {\left( {\frac{E}{(1 + \nu )}{{\varvec{\upvarepsilon}}} + \frac{E\nu }{{(1 + \nu )(1 - 2\nu )}}tr({{\varvec{\upvarepsilon}}}){\mathbf{I}}} \right)} :{{\varvec{\upvarepsilon}}}^{*} dS = 0$$
(5)

It is not possible to estimate the Young’s modulus in this case since Eq. (5) holds for any value of Young’s modulus.

To avoid this caveat, we can consider equilibrium across a domain defined by two neighboring elements, as shown in Fig. 1c and apply the principle of virtual work with the following virtual displacement field:

$$\left\{ \begin{gathered} u_{x}^{ * } = 0 \hfill \\ u_{y}^{ * } = (x - x_{a} )(x - x_{b} )(y - y_{a} )(y - y_{b} ) \hfill \\ \end{gathered} \right.$$
(6)

The proposed virtual displacement field vanishes all the unknown tractions on the entire boundary of these two neighboring elements. Furthermore, this virtual displacement field yields the following the virtual strain field:

$$\begin{gathered} \varepsilon_{xx}^{{ \star }} = 0 \hfill \\ \varepsilon_{yy}^{{ \star }} = (x - x_{a} )(x - x_{b} )(2y - y_{a} - y_{b} ) \hfill \\ \varepsilon_{xy}^{{ \star }} = (y - y_{a} )(y - y_{b} )(2x - x_{a} - x_{b} )/2 \hfill \\ \end{gathered}$$
(7)

Therefore, Eq. (3) can be reduced to:

$$\begin{gathered} \int_{{\Omega^{1} }} {\sigma_{22} (x - x_{a} )(x - x_{b} )(2y - y_{a} - y_{b} )} dxdy + \int_{{\Omega^{1} }} {\sigma_{12} (y - y_{a} )(y - y_{b} )(2x - x_{a} - x_{b} )} dxdy + \hfill \\ \int_{{\Omega^{2} }} {\sigma_{22} (x - x_{a} )(x - x_{b} )(2y - y_{a} - y_{b} )} dxdy + \int_{{\Omega^{2} }} {\sigma_{12} (y - y_{a} )(y - y_{b} )(2x - x_{a} - x_{b} )} dxdy = 0 \hfill \\ \end{gathered}$$
(8)

Eventually, the relationship between the Young’s moduli of the two elements can be written as:

$$E_{2} = - E_{1} \frac{{\int_{{\Omega^{1} }} {\left[ {\left( {\frac{{\varepsilon_{yy} }}{1 + \nu } + \frac{{\upsilon \left( {\varepsilon_{xx} + \varepsilon_{yy} } \right)}}{(1 + \nu )(1 - 2\nu )}} \right)(x - x_{a} )(x - x_{b} )(2y - y_{a} - y_{b} ) + \frac{{\varepsilon_{xy} }}{1 + \nu }(y - y_{a} )(y - y_{b} )(2x - x_{a} - x_{b} )} \right]} dxdy}}{{\int_{{\Omega^{2} }} {\left[ {\left( {\frac{{\varepsilon_{yy} }}{1 + \nu } + \frac{{\varepsilon_{xx} + \varepsilon_{yy} }}{(1 + \nu )(1 - 2\nu )}} \right)(x - x_{a} )(x - x_{b} )(2y - y_{a} - y_{b} ) + \frac{{\varepsilon_{xy} }}{1 + \nu }(y - y_{a} )(y - y_{b} )(2x - x_{a} - x_{b} )} \right]} dxdy}}$$
(9)

If the Young’s modulus value is known for one element, the Young’s modulus value of the other element can be directly derived. This principle can be applied sequentially to each pair of elements, starting from the boundary. Scanning towards the interior enables the sequential identification of all the unknown moduli. For the sake of convenience, the direct VFM method is called the “DI” method in the following.

Remark 1

In Eq. (6), \(u_{x}\) rather than \(u_{y}\) is set to zero everywhere in \(\Omega_{1} \cup \Omega_{2}\). This is due to the fact that compression is applied in the y direction, as shown in Fig. 1a. This induces that the normal stress component in x direction is almost zero. If \(u_{y}\) was also zero, both the numerator and denominator in Eq. (9) would be almost zero.

2.2 Identification of spatially varying stiffness properties with the VFM using “local” regularization

The VFM approach introduced in the previous subsection is equivalent to a double differentiation of the original displacement data along the y direction. Since noise always exists in the measurements, it can be dramatically amplified through this approach. In order to overcome this issue, we introduce a regularization term by defining the following cost function:

$$\pi \left( {E_{2} } \right){ = }\left( {\int\limits_{{\Omega^{1} }} {\sigma_{ij} \varepsilon_{ij}^{*} dS + \int\limits_{{\Omega^{2} }} {\sigma_{ij} \varepsilon_{ij}^{*} dS} } } \right)^{2} + \alpha l_{12} \left| {E_{2} - E_{1} } \right|$$
(10)

where the second term, i.e. the regularization term, is supposed to reduce the spurious effects mentioned previously, and \(l_{12}\) is the length of the interface between two neighboring elements as presented in Fig. 2.

Fig. 2
figure 2

A illustration of two neighbouring elements

Full size image

In Eq. (10), we adopt the total variation diminishing (TVD) regularization approach. Unlike [7, 24], the TVD regularization is a discrete form since material properties are assumed to be constant across each element and discontinuous at the interface between neighboring elements. The detailed derivation of the discrete TVD regularization can be found in "Appendix".\(\alpha\) is the regularization factor controlling the significance of the regularization. The larger the regularization factor, the smoother the identification results. As the regularization factor for each small-scale optimization problem will not make significant influence on the final reconstructed material property map, we always sought for optimal regularization factors within a range of small values (0–0.1) and determined the optimal regularization factor based on the standard deviation of the reconstructed Young’s modulus distribution in a subregion of the background. For the sake of convenience, this regularized VFM method solved by the optimization method is called “OP” method in the following.

Since material properties can be explicitly expressed by the stress and strain for the linear elastic model, we can rewrite the cost function (10) such as:

$$\pi \left( {E_{2} } \right){ = }\left( {aE_{2} + bE_{1} } \right)^{2} { + }\alpha l_{12} \left| {E_{2} - E_{1} } \right|$$
(11)

where a is the integral at the denominator in Eq. (9) and b is the associated integral at the numerator. To find the global minima, we have \(d\pi /dE_{2} = 0\) yielding:

$$\begin{gathered} E_{2} = - \frac{b}{a}E_{1} - \frac{{\alpha l_{12} }}{{2a^{2} }}{\text{ if }}E_{2} \ge E_{1} \hfill \\ E_{2} = - \frac{b}{a}E_{1} + \frac{{\alpha l_{12} }}{{2a^{2} }}{\text{ if }}E_{2} < E_{1} \hfill \\ \end{gathered}$$
(12)

Thus, this identification problem can be solved by the explicit method even in the presence of the regularization term in the cost function. For the sake of convenience, this method is called “EX” method in the following.

Remark 2

Though the EX method is derived from the cost function (10), EX and OP methods are not equivalent since the global minima can be acquired in EX method. In the OP method, the global minima might not be ensured by the optimization scheme. Besides, in OP method, the bound of the optimization parameters can be easily set to ensure that the Young’s modulus can be varied within a reasonable range, while EX method is an unbounded method.

2.3 Identification of material properties on the boundary

To identify the Young’s modulus on the boundary (see Fig. 1d), we can adopt special virtual field written such as:

$${\mathbf{u}}^{ * } {\mathbf{ = 0}}{\text{ on }}\partial \Omega^{e} \backslash \partial \Omega_{t}^{e}$$
(13)

where \(\partial \Omega_{t}^{e}\) is the boundary of the element where tractions are applied. For instance, if we choose an element on the traction boundary as shown Fig. 1d, the prescribed virtual field can be chosen as

$$\left\{ \begin{gathered} u_{x}^{ * } = 0 \hfill \\ u_{y}^{ * } = (x - x_{a} )(x - x_{b} )(y - y_{b} ) \hfill \\ \end{gathered} \right.$$
(14)

Substituting Eq. (14) into Eq. (3), the Young’s modulus can be obtained by:

$$E = \frac{{\int_{{\partial \Omega^{e} }} {t_{i} u_{i}^{*} dl} }}{{\int_{{\Omega^{e} }} {\sigma_{ij} (E = 1)\varepsilon_{ij}^{*} } dS}}$$
(15)

Thereby, the Young’s moduli of each element on the traction boundary can be estimated by Eq. (15). For the OP method, the cost function of the element on the traction boundary is given by:

$$\pi \left( E \right){ = }\left( {\int_{{\Omega_{1} }} {\sigma_{ij} \varepsilon_{ij}^{*} dS - \int_{{\partial \Omega^{e} }} {t_{i} u_{i}^{*} dl} } } \right)^{2}$$
(16)

With the obtained Young’s moduli of the element on the traction boundary, we can scan from the boundary to the interior and identify sequentially all the unknown moduli.

2.4 Effect of unknown boundary conditions

For many biomedical imaging techniques, it is almost impossible to obtain the non-zero traction or force boundary information. In this case, the material property can merely be mapped relatively up to a multiplicative factor. For the proposed inverse approach, we can set the Young’s modulus of one element to be equal to one, start to solve the relative Young’s moduli of its neighboring elements and keep this procedure until the Young’s moduli of all the elements are obtained. To this end, the elastic property distribution can be recovered relatively to an unknown multiplicative constant.

Remark 3

It can be seen that the proposed iterative inverse method converts a large-scale optimization problem into multiple small-scale optimization problems. Thus, the solution to the inverse problem becomes unique, and the computational time is significantly reduced. Moreover, since there are merely several optimization parameters in each small-scale optimization problem, the convergence can be remarkably improved.

Remark 4

It should be noted that the proposed VFM method merely satisfies the local equilibrium, but it does not rigorously satisfy the global equilibrium. However, the obtained stress fields deviate of less than 10% from the target stress fields, demonstrating only small deviations from the global equilibrium.

To test the feasibility and performance of the proposed method, we will first utilize simulated data to test the proposed inverse approach. The flow chart of the testing procedure is shown in Fig. 3. Subsequently, we utilize the experimental data to test the feasibility of the proposed method. For the simulated testing, we add noise into the simulated displacement data. The noise level is defined as:

$${\text{noise level}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{NN} {\left( {\overline{u}_{i} - u_{i} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{NN} {\overline{u}_{i}^{2} } }}} \times 100\%$$
(17)

where \(u_{i}^{{}}\) and \(\overline{u}_{i}\) are the noisy and exact nodal displacements, respectively. \(NN\) is the total number of nodes in the discretized domain.

Fig. 3
figure 3

The flow chart of numerical testing for the proposed VFM approach

Full size image

3 Results

3.1 Synthetic data

3.1.1 Reconstruction of a three-layered structure

In the first example, we attempt to identify the elastic property distribution of a layered structure. The layered structure consists of three layers with different material properties. The Young’s moduli of each layer are 1 MPa, 3 MPa and 6 MPa from the top layer to the bottom layer, respectively. The Poisson’s ratio is set to 0.3 throughout the domain of interest and we assume it is known. The measured displacement is acquired by finite element simulation. The domain of interest is discretized by 100 by 100 elements with 10,000 unknown elastic parameters. In the forward problem used to generate the simulated displacement field, we applied traction on the top edge to induce 1% compression and restricted the vertical motion of the bottom edge. To avoid rigid body motion, we fixed the center point on the bottom edge. In the inverse problem, we scan the shear moduli from the elements on the top boundary to those on the bottom. The associated reconstructed results are shown in Fig. 4. We firstly employ the DI method. From the reconstructed results shown in Fig. 4, we observe that when there is no noise in the dataset, the DI method is capable of yielding the exact distribution. The slight artifacts at the corner of the layers are due to the numerical noise when computing the strain field. When we add noise into the displacement data, we observe that the strong artifacts occur in the middle and bottom layers. Nevertheless, we are still capable of delimiting each layer and estimating the thickness of each layer with high accuracy when the noise level is less than 0.5%. When the noise level is 0.5%, the interface between the middle and bottom layers is not very clear.

Fig. 4
figure 4

The reconstructed Young’s modulus distribution of the layered structure with different noise levels using the DI method

Full size image

Sequentially, we utilize the OP method and the corresponding reconstructed elastic property distribution is presented in Fig. 5. In this case, the BFGS (Broyden–Fletcher–Goldfarb–Shanno) method, a quasi-Newton method, was employed in the optimization scheme and the bounds of the optimized Young’s modulus were [0.1 MPa, 12 MPa]. The same setting was also utilized in the following numerical examples in the OP method. It can be seen that the reconstructed elastic property distribution is mapped well when the noise level is not larger than 0.1%. However, the interfaces between the middle and bottom layers are poorly identified in the presence of higher than 0.1% noise.

Fig. 5
figure 5

The reconstructed Young’s modulus distribution of the layered structure with different noise levels using the OP method

Full size image

Finally, we utilize the EX method to solve the same problem. The regularization factor utilized in this case is very small. Similar to the previous two methods, the modulus distribution is mapped well when the noise level is less than 0.1% (see Fig. 6). When the noise level increases, the top two layers can still be delimitated clearly, while the bottom two layers are not.

Fig. 6
figure 6

The reconstructed Young’s modulus distribution of the layered structure with different noise levels using the EX method

Full size image

From all the reconstructed results for the layered structure and relative error tables from Tables 1, 2 and 3, we observed that the top layer was generally reconstructed better than the other two layers. This was probably related to the fact that we scanned from top to bottom. The error in the recovered Young’s moduli accumulated from the top elements to the bottom ones.

Table 1 Relative error in the identified Young’s moduli of the three layers in Fig. 4
Full size table
Table 2 Relative error in the identified Young’s moduli of the three layers in Fig. 5
Full size table
Table 3 Relative error in the identified Young’s moduli of the three layers in Fig. 6
Full size table

3.1.2 Reconstruction of the structure with inclusions

In the second example, we tested the feasibility and performance of the proposed inverse approach by a case where there were inclusions embedded in the problem domain. We first tested a case with two circular inclusions in the domain as shown in Fig. 7a. In this case, we assumed the target Young’s modulus was 5 MPa and the Poisson’s ratio was 0.3 throughout the domain of interest. We still assumed that the Poisson’s ratio was known a priori. Similar to the previous case, we applied the uniform compression on the top surface, and restricted the motion in the vertical direction of the bottom edge. To prevent the rigid body motion, we fixed the middle point of the bottom edge. The domain of interest was discretized by 100 × 100 elements.

Fig. 7
figure 7

The reconstructed Young’s modulus distribution of the structure with different noise levels using the DI method

Full size image

The reconstructed results (see Fig. 7) with the DI method indicate that with small noise level (less than 0.1% noise), the inclusion can be mapped well in both the shape and the shear modulus value, though the mapped Young’s modulus value in the inclusion is still less than the target even when no noise is introduced. If the noise level becomes larger, the inclusion can still be observed in the reconstructed elastic property distribution. However, there are strong artifacts in the material property reconstruction. We also obverse that the artifacts are much stronger in the lower region of the domain since we start to map the shear moduli from the top surface to the bottom surface. Consequently, the error in the measured data accumulates from the top to the bottom, leading to strong artifacts on the lower region.

Using the OP method, it can be seen that the reconstructed results become slightly worse compared with the results acquired by the DI method (see Fig. 7) when the noise level is higher than 0.1%. Although the inclusions can be detected in Fig. 8d, e, the shape of the inclusions are not clearly recovered. The EX method yields better reconstruction quality than the OP method (see Fig. 9). Even in the presence of 0.5% noise, the two inclusions can be recovered well in the shape. In Tables 4, 5 and 6, we report the relative error within two circular inclusions, and we observe that the relative error of the identified Young’s moduli of the inclusions by the three methods are very close.

Fig. 8
figure 8

The reconstructed Young’s modulus distribution of the structure with different noise levels using the OP method

Full size image
Fig. 9
figure 9

The reconstructed Young’s modulus distribution of the structure with different noise levels using the EX method

Full size image
Table 4 Relative error in the identified Young’s moduli of the inclusions in Fig. 7
Full size table
Table 5 Relative error in the identified Young’s moduli of the inclusions in Fig. 8
Full size table
Table 6 Relative error in the identified Young’s moduli of the inclusions in Fig. 9
Full size table

We also present a case with one circular inclusion and one elliptical inclusion as shown in Fig. 10a. In this case, the Young’s moduli of the circular and elliptical inclusions are 5 MPa and 10 MPa, respectively. The domain of interest is discretized by 100 × 100 elements. Similar to the previous case, we apply the uniform compression on the top and restrict the vertical motion of the bottom edge. The DI method performs well in mapping the inclusions even with 0.5% noise. This is probably due to the fact that the two inclusions are very close to the top edge, hence less influenced by the accumulated error.

Fig. 10
figure 10

The reconstructed Young’s modulus distribution of the structure with different noise levels using the DI method

Full size image

For the OP method, we observe that the reconstructed inclusions are well preserved both in the shape and Young’s modulus values with the low noise introduced (see Fig. 11b, c). However, when the noise level is higher than 0.3%, the elliptic inclusion cannot be clearly observed in the domain. It seems that the reconstructed results are still worse than that acquired by the DI method. For the EX method (see Fig. 12), the identified Young’s modulus distribution is well recovered compared to the OP method. The relative error (see Tables 7, 8, 9) of the elliptic inclusion is larger than that of the circular inclusion in presence of noise.

Fig. 11
figure 11

The reconstructed Young’s modulus distribution of the structure with different noise levels using the OP method

Full size image
Fig. 12
figure 12

The reconstructed Young’s modulus distribution of the structure with different noise levels using the EX method

Full size image
Table 7 Relative error in the identified Young’s moduli of the inclusions in Fig. 10
Full size table
Table 8 Relative error in the identified Young’s moduli of the inclusions in Fig. 11
Full size table
Table 9 Relative error in the identified Young’s moduli of the inclusions in Fig. 12
Full size table

3.1.3 Influence of the virtual fields on the reconstruction

We also chose different virtual fields to investigate the sensitivity of the virtual fields to the reconstruction results. For comparison, we introduced the two following additional virtual displacement fields:

$$\begin{gathered} {\text{2nd}}\;{\text{ VF }}\left\{ \begin{gathered} u_{x} = (x - x_{a} )(x - x_{b} )(y - y_{a} )(y - y_{b} ) \hfill \\ u_{y} = (x - x_{a} )(x - x_{b} )(y - y_{a} )(y - y_{b} ) \hfill \\ \end{gathered} \right. \hfill \\ {\text{3rd }}\;{\text{VF }}\left\{ \begin{gathered} u_{x} = 0 \hfill \\ u_{y} = [(x - x_{a} )(x - x_{b} )(y - y_{a} )(y - y_{b} )]^{2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(18)

The reconstructed Young’s modulus distribution by the OP method are shown in Figs. 13 and 14. It can be seen than the influence of the virtual fields on the reconstruction is marginal, no matter if the displacement method is exact or noise. This can also be verified with the relative error reported in Tables 10 and 11.

Fig. 13
figure 13

The reconstructed Young’s modulus distribution using different virtual fields when the noise level is 0%. Note that the 1st virtual displacement field was the one we used previously (Eq. (6))

Full size image
Fig. 14
figure 14

The reconstructed Young’s modulus distribution using different virtual fields when the noise level is 0.5%. Note that the 1st virtual displacement field was the one we used previously (Eq. (6))

Full size image
Table 10 Relative error in the identified Young’s moduli of each layer or inclusion in Fig. 13
Full size table
Table 11 Relative error in the identified Young’s moduli of each layer or inclusion in Fig. 14
Full size table

3.1.4 Influence of the noise filter on the reconstruction of Young’s modulus distribution

Since the VFM method requires the strain field which is usually much noisier than the displacement fields, we considered two noise filtering approaches to smoothen the displacement fields: the Gaussian filter [25, 26] and the Median filter [27]. The reconstructed results (see Figs. 15, 16 and 17) demonstrate that noise filtering can smooth the recovered Young’s modulus distribution. In particular, the delimitation of the neighboring layers and the boundary of inclusions are well preserved when using the noise filtering approach. With the noise filtering approach, the Young’s modulus distribution is also recovered in the presence of 1% noise (see Fig. 18). However, the inclusions or layers were not detected without using noise filtering.

Fig. 15
figure 15

The reconstructed Young’s modulus distribution using the OP method with different noise filter approaches

Full size image
Fig. 16
figure 16

The reconstructed Young’s modulus distribution using the OP method with different noise filter approaches

Full size image
Fig. 17
figure 17

The reconstructed Young’s modulus distribution using the OP method with different noise filter approaches

Full size image
Fig. 18
figure 18

The reconstructed Young’s modulus distribution using the OP method with different noise filter approaches when the noise level is 1%

Full size image

3.1.5 Influence of the assumed Poisson’s ratio on the reconstruction of Young’s modulus distribution

In this paper, we assumed that the Poisson’s ratio was known for solving the inverse problem. It is important to examine the impact of the value of the Poisson’s ratio on the reconstructed results. Figure 19 indicates that the value of the assumed Poisson’s ratio does not influence significantly the Young’s modulus distribution. The relative error in the identified Young’s modulus is very close for different assumed Poisson’s ratio (Table 12).

Table 12 Relative error in the identified Young’s moduli of each layer or inclusion in Fig. 19
Full size table
Fig. 19
figure 19

The reconstructed Young’s modulus distribution using the OP method with different value of the assumed Poisson’s ratio

Full size image

3.2 Experimental data

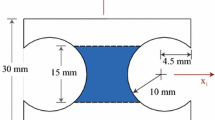
We also tested the proposed VFM on displacement data obtained experimentally with ultrasound. The simplified illustration of the experimental setup is shown in Fig. 20a. A stiff and circular inclusion was embedded in the soft background. More details on the experiment have been discussed in [12, 28]. Furthermore, the experimental dataset was filtered with a B-spline noise filtering approach. The target stiffness ratio between the stiff inclusion and the background was 3. The specimen was assumed as nearly incompressible in the inverse problem, with a Poisson’s ratio of 0.48. The reconstructed elastic property distributions using the DI, OP and EX methods are shown in Fig. 20. It can be seen that the three methods were capable of detecting the location of the inclusion accurately. Moreover, the Young’s modulus value of the recovered inclusion was very close to the target. The relative error of the Young’s modulus of the inclusion was less than 14% (see Table 13). Additionally, the DI and EX methods were capable of deriving more circular inclusion than the OP method. Nevertheless, the OP method induced less error in the Young’s modulus of the inclusion (see Table 13), although the shape of the inclusion was not well recovered compared with the other two approaches.

Fig. 20
figure 20

The reconstructed Young’s modulus distribution of a tissue mimicking phantom using the DI (c), OP (d) and EX (e) methods

Full size image
Table 13 Relative error in the identified Young’s moduli of the inclusion in Fig. 20
Full size table

4 Discussion

In this paper, we have presented a methodology to characterize the nonhomogeneous elastic property distribution of solids. The proposed method is based on the virtual fields method (VFM). We proposed direct and regularized VFM inverse approaches, and the feasibility of the proposed approaches were tested successfully by multiple numerical and experimental examples presented in the Results Section. All the inverse problems presented in this paper were solved within several seconds even by a personal computer. The reconstructed results using the simulated displacement fields demonstrate that these approaches are capable of detecting the nonhomogeneous region in the domain in the presence of low noise level. However, with a high noise level, the reconstruction of the elastic property distribution was poorly recovered. We also tested several different virtual fields and acquired roughly the same reconstruction results. Although we tested several different virtual fields in this study, there remain many other choices of possible virtual fields. When we worked with experimental results, both the shape and the stiffness ratio of the inclusion were well recovered. From the comparative study of the proposed VFM approaches, we observed that the DI and EX methods performed better than the OP method. We also observed that the reconstructed material property distribution deviated from the exact one even without any noise introduced. This was induced by numerical errors arising when deriving the strain field. The numerical error “propagated” from top to bottom elements and accumulated.

Compared to regularization, it seems that noise filtering significantly improves the quality of the reconstruction. The reason might be that the accuracy of any VFM method is highly dependent on the accuracy of the strain fields. By smoothing the displacement data, the smoothness of the associated strain field (the gradient of the displacement field) is improved remarkably. This subsequently improves the smoothness of the reconstructed Young’s modulus distribution.

In this paper, we started from the top edge and then mapped the interior elements (the same direction as the applied external loading). We used the axial direction for scanning because the axial deformation was more significant than the lateral deformation. Thus, the contribution of the axial strain to the virtual work was more significate. As a result, this scanning pattern appeared more accurate.

The primary advantage of the proposed method is the high efficiency to solve the inverse problem. In general, solving inverse problem requires solving a large-scale optimization problem. However, in this paper, we converted the large-scale optimization problem into multiple small-scale optimization problems. Thus, the computational cost was significantly reduced, and the convergence rate of the inverse problem was remarkably improved. In particular, since there are only fewer optimization parameters in each small-scale optimization problem, the uniqueness of the inverse problem can be improved as well.

The VFM method based on the Fourier series [20] utilized using the continuous Fourier function to smoothen the reconstructed results, while the regularized VFM method proposed here attempted to smoothen the reconstruction by adding an additional regularization term. Since the regularization was applied locally, the regularization did not significantly affect the final reconstruction results. Compared to the VFM method based on the Fourier series [20], the proposed method does not require solving a very large linear algebraic system, thus the computational time for the proposed method is remarkably reduced. However, the effect of the regularization on improving the smoothness of the reconstructed results is not significant, and much effort should be devoted to this question in the future.

Since the strain field is required in the proposed VFM approach, the proposed approach is very sensitive to noise. This needs to be addressed in future work. For that, the resolution and accuracy of the imaging facilities need to be improved. Alternatively, strategies on filtering the noisy displacement data could be employed. In fact, the experimental displacement field utilized in this work is filtered by a B-spline approach [12]. By using the filtering approach, the quality of the reconstruction might be improved. Another approach to improve the accuracy of the proposed VFM method could be to use the Split Bregman method [29] to solve the L1 norm regularized problems of Eq. 11. This method has shown great potential in solving a very broad class of L1- regularized problem. Further, a new formulation that is capable of avoiding calculation of the strain field should be proposed. In this paper, we merely tested the feasibility of the proposed method for examples with uniform mesh. For the irregular mesh, the proposed method should work as well and will be examined in the future work.

Besides, although reconstruction of the Young’s modulus or shear modulus distributions are the primary goals in elastography, we should also estimate the Poisson’s ratio in some cases. For the VFM, the Poisson’s ratio has been estimated by using the virtual fields expressed by either sinusoid or polynomial functions [30,31,32] in order to estimate the homogeneous material properties. To the best of our knowledge, there is no work on the identification of the nonhomogeneous Poisson’s ratio distribution using the VFM. For the anisotropic elastic model, since there are more elastic properties in the constitutive model, more virtual fields or measurements are required in the inverse algorithm. For the three-dimensional domain, the computational cost is usually more intensive, the reduction of the computational cost by the proposed inverse approach will also be investigated.

5 Conclusion

In this paper, we have proposed novel VFM-based inverse approaches to reconstruct the nonhomogeneous elastic property distribution of solids. The inverse approaches have been tested successfully for a number of simulated and experimental datasets. The reconstruction results have demonstrated that the proposed VFM approaches are capable of recovering inclusions even with a low level of noise. We also observed that the DI and EX methods perform much better than the OP method in characterizing the elastic property distribution. This is probably due to the fact that the OP method cannot guarantee a global minima. Nevertheless, the three proposed methods are capable of detecting the inclusions in the tissue mimicking phantom using the experimental data. The proposed method introduced the regularization into the VFM method. Although there is still limitation in the current version of the regularization based VFM, the introduction of the regularization might address the issue of the overfitting noisy data of the VFM. The proposed method also provides a computationally efficient way to solve the inverse problem in elasticity and has great potential in developing novel mechanics-based disease detection techniques in biomedical engineering.