A phase-field model of thermo-elastic coupled brittle fracture with explicit time integration

Abstract

The phase-field method is a very effective way to simulate arbitrary crack nucleation, propagation, bifurcation, and the formation of complex crack networks. The diffusion-based method is suitable for multi-field coupling fracture problems. In this paper, a parallel algorithm of the thermo-elastic coupled phase-field model is implemented in commercial finite element code Abaqus/Explicit. The algorithm is applied to simulate the dynamic and quasi-static brittle fracture of thermo-elastic materials. Further, it is adopted on a structured mesh combined with first-order explicit integrators. Several examples of the quasi-static and dynamic cases of single crack, as well as multi-crack initiation and propagation under thermal shock, are given to demonstrate the robustness of the algorithm. The source code and tutorials provide an effective way to simulate crack nucleation and propagation in multi-field coupling problems.

1 Introduction

In practical engineering, there are a lot of fracture processes of materials under thermal shock loads, such as hot ceramic sheets in cold water [1], the thermal shock of an $\alpha$-alumina porous capillary [2], and instantaneous thermal start-up of engine blades [3]. Usually, thermal shock occurs on a short time scale, accompanied by instantaneous temperature changes, and results in non-uniform volume change and stress distribution of brittle materials. Fracture of materials and a large number of cracks may be a severe consequence of thermal shock stress. The dynamic thermal shock fracture mechanism is very complicated due to the inertia effect and complex thermo-mechanical coupling [4].

Because of the complexity of the multi-field coupled fracture process in thermal shock, the numerical methods play an important role in fracture analysis. The boundary element method (BEM) [5], non-local damage models [6], and damage mechanics-based models [7] are used to reproduce multiple cracking modes in quenching tests. Besides, the thermal stress evolution and dynamic crack growth under thermal shock loading are studied by using the extended finite element method (XFEM) [8, 9]. However, these numerical models still have limitations in simulating compound dynamic crack growth.

The phase-field method, as a widely concerned method in recent years, can simulate arbitrary propagation, branching, and convergence of cracks based on the fundamental theory of Griffith’s elastic fracture mechanics [10,11,12,13]. Unlike other numerical methods such as XFEM [14, 15], no additional discontinuity is required in the phase-field method. Instead, the distribution of cracks is approximated by a phase-field variable which smoothes the crack boundary in a small area [16,17,18]. The main advantage of using the phase-field variable is that the evolution of the fracture surface follows the solution of coupled partial differential equations (PDEs). Thus, no additional tracking of the crack surface is required [19,20,21,22]. This description method of the crack surface is in sharp contrast to the complexity of many discrete fracture models and is especially beneficial to the three-dimensional complex fracture networks [23].

In the past ten years, the phase-field method has gained remarkable attention and research interest because of its flexible implementation [24,25,26]. A great deal of code has been developed for personal research. Unfortunately, most of the current articles do not give the source code of phase-field method implementation. Molnár and Gravouil [27] gave the code of two-dimensional (2D) and three-dimensional (3D) phase-field model based on implicit commercial software package Abaqus/Standard, which is a very excellent work and has a good effect on the application of the phase-field method in engineering practice. They also provide detailed and practical tutorials on their personal websites [28]. However, the source code of an explicit dynamic phase-field model based on mature commercial software is not yet available.

In this paper, a fully functional realization of the multi-field coupled phase-field model in Abaqus/Explicit is presented to study the dynamic evolution of multi-field coupled brittle fracture problems in thermoelastic solids. The work of this paper is inspired by Molnar and Gravouil’s work [27]. Also, as supplementary material, we provide the source code of Abaqus/VUEL and the other user subroutines, as well as several examples. The aim is to make the multi-field coupled diffusion crack propagation scheme applicable not only to numerical research but also to practical application.

In addition, the code provided here can be easily further developed for other multi-field coupling problems, such as mechanical-chemical coupling fracture of lithium batteries [29], fracture of porous media [30, 31], anisotropic failure of soft biological tissues [32] and solute-assisted fracture [33], etc. More practical, through equation analogy, new applications can be completed quickly without additional code development. A major advantage of current implementations is that they do not require additional updates and software, but only widely available Abaqus/Explicit packages and Fortran compilers. Its parallel framework can solve various fracture problems more efficiently.

This paper is organized as follows: the basic principle and governing equations of the phase-field method are reviewed for thermoelastic materials in Sect. 2. The governing equations are discretized in space and time, and how to implement in Abaqus/Explicit is explained in Sect. 3. Five typical dynamic and quasi-static numerical examples are presented in Sect. 4 to verify the correctness and efficiency of the numerical implementation. The concluding remarks are given in Sect. 5.

2 Problem statement

2.1 Variational formulation of thermo-elastic brittle fracture

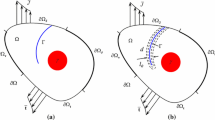
Consider the evolution of the deformation, fracture and temperature fields of an isotropic thermo-elastic solid body $\Omega \subset \mathbb {R}^\delta$ with external boundary $\partial \Omega \subset \mathbb {R}^{\delta -1}$ over a time period [0-$t_a$], as shown in Fig. 1. Here $\delta \in [1 - 3]$ is the dimension. Let $\partial {\Omega _ {\varvec{t}} }$, $\partial {\Omega _ {\varvec{u}} }$, $\partial {\Omega _ {\varvec{J}} }$ and $\partial {\Omega _ { \theta } }$ be the traction, displacement, heat flux and temperature boundaries, such that: $\partial {\Omega _ {\varvec{t}} } \cup \partial {\Omega _ {\varvec{u}} } = \partial \Omega$, $\partial {\Omega _ {\varvec{t}} } \cap \partial {\Omega _ {\varvec{u}} } = \emptyset$ and $\partial {\Omega _ {\varvec{J}} } \cup \partial {\Omega _ {\theta } } = \partial \Omega$, $\partial {\Omega _ {\varvec{J}} } \cap \partial {\Omega _ {\theta } } = \emptyset$. Let $\bar{\varvec{t}}:\partial {\Omega _{\varvec{t}} } \times [0,{t_a}] \rightarrow {\mathbb {R}^\delta }$ and $\bar{\varvec{u}}:\partial {\Omega _{\varvec{u}} } \times [0,{t_a}] \rightarrow {\mathbb {R}^\delta }$ be prescribed traction and displacement boundary conditions, and $\bar{\theta }:\partial {\Omega _{\theta } } \times [0,{t_a}] \rightarrow {\mathbb {R}^1 }$ and $\bar{\varvec{J}}:\partial {\Omega _{\varvec{J}} } \times [0,{t_a}] \rightarrow {\mathbb {R}^1 }$ be prescribed temperature and heat flux boundary conditions.

Fig. 1

Deformed configuration of the thermo-elastic brittle fracture problem: a sharp representation of discontinuities, and b dispersion representation of discontinuities

According to Ref. [34,35,36], the brittle fracture of thermoelastic solids involves finding saddle points for the following problems:

$$\begin{aligned} S\left[ \varvec{u},\dot{\varvec{u}},\theta ,\Gamma \right] : = \int _0^{{t_a}} {L\left[ \varvec{u},\dot{\varvec{u}},\theta ,\Gamma \right] } dt \end{aligned}$$

(1)

among all $\varvec{u}:=\Omega \times [0,t_a] \rightarrow {\mathbb {R}^\delta }$ and $\theta :=\Omega \times [0,t_a] \rightarrow {\mathbb {R}^1}$ that are bounded functions of $\Omega$ that satisfy:

$$\begin{aligned}&\varvec{u} = \bar{\varvec{u}},\quad \mathrm {on} \quad \partial {\Omega _{\varvec{u}}} \times \left[ {0,{t_a}} \right] \end{aligned}$$

(2a)

$$\begin{aligned}&\theta = \bar{\theta },\quad \mathrm {on} \quad \partial {\Omega _\theta } \times \left[ {0,{t_a}} \right] \end{aligned}$$

(2b)

The Lagrangian L is defined as follows:

$$\begin{aligned} L\left[ \varvec{u},\dot{\varvec{u}},\theta ,\Gamma \right] :=&\int _{\Omega /\Gamma } \left\{ \frac{1}{2}\rho \dot{\varvec{u}} \cdot \dot{ \varvec{u}} - {\psi _0}\left( {{\varvec{\varepsilon }}^e \left( \varvec{u}, \theta \right) } \right) + \rho \varvec{b} \cdot \varvec{u} \right. \nonumber \\&\left. +\, \rho c\dot{\theta }+ \nabla \cdot \varvec{J} - \gamma \right\} dV \nonumber \\&+\int _{\partial {\Omega _{\varvec{t}} }} {\bar{\varvec{t}} \cdot \varvec{u} d\Gamma } + \int _{\partial {\Omega _{\varvec{J}} }} {\bar{\varvec{J}} \cdot \varvec{n} d\Gamma } - {g_c}\left| \Gamma \right| \end{aligned}$$

(3)

where $\rho$ is the density of body, $\varvec{b}$ denotes the body force per unit mass, c is the specific heat capacity, $\gamma$ is the body heat source per unit volume, $g_c$ is the critical energy release rate, $\Gamma$ is the set of discontinuities as shown in Fig. 1a and $|\Gamma |$ is the length of $\Gamma$. ${\psi _0}\left( {{\varvec{\varepsilon }}^e \left( \varvec{u}, \theta \right) } \right) := \frac{\lambda }{2} (\mathrm {tr} \varvec{\varepsilon }^e)^2 + \mu \left\| \varvec{\varepsilon }^e\right\| ^2$ is the elastic strain energy density which depends on elastic strain:

$$\begin{aligned} \varvec{\varepsilon }^e = \varvec{\varepsilon } - \varvec{\varepsilon }^\theta \end{aligned}$$

(4)

where $\lambda$ and $\mu$ are Lame constants, and $\varvec{\varepsilon }$ is the total strain defined as:

$$\begin{aligned} \varvec{\varepsilon } := \frac{1}{2} \left( \nabla \varvec{u} + \nabla \varvec{u}^T \right) \end{aligned}$$

(5)

and $\varvec{\varepsilon }^\theta$ is the thermal strain tensor, which is proportional to the temperature difference:

$$\begin{aligned} \varvec{\varepsilon }^\theta := \alpha _{\theta } \Delta \theta \mathbf{I } \end{aligned}$$

(6)

where $\alpha _{\theta }$ is the thermal expansion coefficient of materials, and $\mathbf{I }$ is the identity tensor.

2.2 Phase-field description of diffuse crack

In the phase-field method, a damage variable $d: \Omega \rightarrow [0, 1]$ is introduced to describe the failure of the material. In particular, regions with $d = 0$ and $d = 1$ correspond to unbroken and fully broken states of the material. Thus the crack surface is dispersed, as shown in Fig. 1b. Let

$$\begin{aligned} \mathcal{T}^{\varvec{u}}&:= \left\{ {\varvec{u} \in H^1 \left( \Omega ; \mathbb {R}^\delta \right) \times [0,t_a]~|~\varvec{u}(\cdot ,t)=\bar{\varvec{u}}(\cdot ,t) ~\mathrm {on}~\partial \Omega _{\varvec{u}} } \right\} , \end{aligned}$$

(7a)

$$\begin{aligned} \mathcal{T}^\theta&:= \left\{ {\theta \in H^1 \left( \Omega ; \mathbb {R}^1 \right) \times [0,t_a]~|~\theta (\cdot ,t)=\bar{\theta }(\cdot ,t) ~\mathrm {on}~\partial \Omega _{\theta } } \right\} , \end{aligned}$$

(7b)

$$\begin{aligned} \mathcal{T}^d&:= \left\{ {d \in H^1 \left( \Omega ; [0,1] \right) \times [0,t_a] } \right\} , \end{aligned}$$

(7c)

then the regularized variational formulation reads: find $(\varvec{u}, \theta , d) \in \mathcal{T}^{\varvec{u}} \times \mathcal{T}^{\theta } \times \mathcal{T}^d$ that is the stationary point of $S_{l_c}\left[ \varvec{u},\dot{\varvec{u}},\theta ,\Gamma \right] : = \int _0^{{t_a}} {L_{l_c}\left[ \varvec{u},\dot{\varvec{u}},\theta ,\Gamma \right] } dt$, with

$$\begin{aligned} L_{l_c}\left[ \varvec{u},\dot{\varvec{u}},\theta ,\Gamma \right] :=&\int _{\Omega } \left\{ \frac{1}{2}\rho \dot{\varvec{u}} \cdot \dot{ \varvec{u}} - {\psi }\left( {{\varvec{\varepsilon }}^e \left( \varvec{u}, \theta \right) }, d\right) + \rho \varvec{b} \cdot \varvec{u} \right. \nonumber \\&\left. +\, \rho c\dot{\theta }+ \nabla \cdot \varvec{J} - \gamma \right\} dV \nonumber \\&+\int _{\partial {\Omega _{\varvec{t}} }} {\bar{\varvec{t}} \cdot \varvec{u} d\Gamma } + \int _{\partial {\Omega _{\varvec{J}} }} {\bar{\varvec{J}} \cdot \varvec{n} d\Gamma }\nonumber \\&- {g_c} \int _\Omega {\left( {\frac{{{d^2}}}{{2{l_c}}} + \frac{{{l_c}}}{2}{{\left\| {\nabla d} \right\| }^2}} \right) dV} \end{aligned}$$

(8)

where $l_c$ is a length scale which can be understood as characteristic crack width. When $l_c \rightarrow 0$, the regularized formulation converges to that with sharp crack representation. $\psi (\varvec{\varepsilon }^e, d)$ is the strain energy density degraded by the phase-field variable such that $\psi (\varvec{\varepsilon }^e, d=0) = \psi _0(\varvec{\varepsilon }^e)$ and that $\psi (\varvec{\varepsilon }^e, d_1) \ge \psi (\varvec{\varepsilon }^e, d_2)$ if $d_1 \le d_2$.

The strong form of the boundary value problem can be derived from Eq. (8):

$$\begin{aligned}&\mathrm {div\varvec{\sigma }} + \rho \varvec{b} = \rho \ddot{\varvec{u}}\quad&\mathrm {in}\quad \Omega \times \left[ {0,{t_a}} \right] \end{aligned}$$

(9a)

$$\begin{aligned}&\rho c\dot{\theta }+ \nabla \cdot \varvec{J} = \gamma \quad&\mathrm {in}\quad \Omega \times \left[ {0,{t_a}} \right] \end{aligned}$$

(9b)

$$\begin{aligned}&-\frac{{\partial \psi }}{{\partial d}} - \frac{{{g_c}}}{{{l_c}}}\left( {d - {l_c^2}\Delta d} \right) = 0\quad&\mathrm {in}\quad \Omega \times \left[ {0,{t_a}} \right] \end{aligned}$$

(9c)

$$\begin{aligned}&\varvec{\sigma } \cdot \varvec{n} = \bar{\varvec{t}}\quad&\mathrm {on}\quad \partial {\Omega _{\varvec{t}}} \times \left[ {0,{t_a}} \right] \end{aligned}$$

(9d)

$$\begin{aligned}&\varvec{J} \cdot \varvec{n} = \bar{J}\quad&\mathrm {on}\quad \partial {\Omega _J} \times \left[ {0,{t_a}} \right] \end{aligned}$$

(9e)

$$\begin{aligned}&\frac{\partial d}{\partial \varvec{n}} = 0 \quad&\mathrm {on}\quad \partial {\Omega } \times \left[ {0,{t_a}} \right] \end{aligned}$$

(9f)

where $\varvec{\sigma } = \varvec{\sigma } (\varvec{\varepsilon }^e,d):=\frac{\partial \psi }{\partial \varvec{\varepsilon }^e}$ is the Cauchy stress, and $\varvec{n}$ is the unit outer normal to $\partial \Omega$. Here, Eq. (9a) expresses the momentum conservation of solid, Eq. (9b) gives the evolution process of temperature, Eq. (9c) defines the phase-field evolution, and Eqs. (9d) to (9f) are Neumann boundary conditions for $\varvec{u}$, $\theta$ and d, respectively.

The heat flux $\varvec{J}$ is assumed to be proportional to the temperature gradient, and the thermal conductivity k is also degraded by the damage d to ensure no heat flux at the crack surface:

$$\begin{aligned} \varvec{J} = - k \cdot \nabla \theta ,\quad k = {\left( {1 - d} \right) ^2}{k_0} \end{aligned}$$

(10)

where $k_0$ is the inherent thermal conductivity for undamaged material.

Table 1 Three different expressions of strain energy density decomposition for phase-field models used to simulate crack growth [34]

2.3 Rate-dependent form of phase-field evolution

In order to adopt explicit time integral, we replace Eq. (9c) with a time-dependent form according to Ref. [34, 37]:

$$\begin{aligned} \dot{d} = \left\{ \begin{array}{ll} \frac{1}{\eta }{\left\langle { - \frac{{\partial \psi }}{{\partial d}} - \frac{{{g_c}}}{{{l_c}}}\left( {d - {l_c^2}\Delta d} \right) } \right\rangle _ + },&{} \quad d < 1\\ 0, &{}\quad \mathrm {otherwise} \end{array} \right. \end{aligned}$$

(11)

where $\eta$ is the viscous parameter that controls phase field evolution and ${\left\langle a \right\rangle _ \pm }: = \left( {a \pm \left| a \right| } \right) /2$ for any $a \in \mathbb {R}$.

The initial condition of the problem can be expressed as

$$\begin{aligned} \varvec{u}(\cdot , 0) = \varvec{u}_0, \quad \dot{\varvec{u}}(\cdot , 0) = \varvec{v}_0, \quad \theta (\cdot , 0) = \theta _0, \quad d(\cdot , 0) = d_0, \end{aligned}$$

(12)

where $\varvec{u}_0, \varvec{v}_0, \theta _0$ and $d_0$ are the initial displacement, velocity, temperature and damage field, respectively.

2.4 Three different models of energy decomposition

For the phase-field simulation of brittle fracture, the different elastic strain energy density functions can be selected, corresponding to different energy decomposition and degradation modes. Here we mainly review and discuss three common ways. Their elastic strain energy density functions have the following general forms:

$$\begin{aligned} \psi \left( {\varvec{\varepsilon }^e,d} \right) = {\left( {1 - d} \right) ^2}{\psi _ + }\left( \varvec{\varepsilon }^e \right) + {\psi _ - }\left( \varvec{\varepsilon }^e \right) \end{aligned}$$

(13)

where ${\psi _+ }\left( \varvec{\varepsilon }^e \right)$ and ${\psi _-}\left( \varvec{\varepsilon }^e \right)$ satisfy ${\psi _+ }\left( \varvec{\varepsilon }^e \right) + {\psi _- }\left( \varvec{\varepsilon }^e \right) = {\psi _ 0 }\left( \varvec{\varepsilon }^e \right)$. The expressions of ${\psi _ + }\left( \varvec{\varepsilon }^e \right)$ and ${\psi _-}\left( \varvec{\varepsilon }^e \right)$ for the three models are shown in Table 1.

It should be noted that an additional small number s with $0 < s \ll 1$ and $s=o(l)$ is added to the coefficient of ${\left( {1 - d} \right) ^2}{\psi _ + }\left( \varvec{\varepsilon }^e \right)$ to solve the singularity of stiffness matrix caused by complete fracture in Ref. [37,38,39]. That is, the $(1-d)^2$ in Eq. (13) is replaced by $[(1-d)^2 + s]$. In this model, we do not need to introduce such an additional parameter because we adopt a fully explicit time integration method and do not need to inverse the stiffness matrix.

3 Numerical implementation

In order to implement the phase-field method in Abaqus/Explicit, we first discretize the governing equations in space and time using the standard finite element method (FEM) discretization scheme and explicit integral operators. Then, the algorithm is implemented by using multiple user-defined subroutines.

3.1 Spatial-discrete Galerkin scheme

The solution domain $\Omega$ is discretized by using a mesh family $\{\mathcal{T}_h\}$, which has a feature mesh size of h. We can approximate $(\varvec{u},\theta ,d)$ with the standard first-order FEM shape function:

$$\begin{aligned}&{\varvec{u}^e}\left( {{\varvec{x}},t} \right) = {\sum \limits _{I = 1}^n {{{{N}}{{_{\varvec{u}}^e}_I}}\left( {\varvec{x}} \right) {\varvec{u}_I^e}\left( t \right) } }, \quad \theta ^e \left( {{\varvec{x}},t} \right) = \sum \limits _{I = 1}^n {{{N}_{\theta }^e}_I \left( {\varvec{x}} \right) {\theta _I^e}\left( t \right) }, \nonumber \\&d^e \left( {{\varvec{x}},t} \right) = \sum \limits _{I = 1}^n {{{N}_d^e}_I \left( {\varvec{x}} \right) {d_I^e}\left( t \right) } \end{aligned}$$

(14)

where $\varvec{u}^e$, $\varvec{\theta }^e$ and $d^e$ are the displacement, temperature and phase fields of the element e, respectively. $\varvec{u}_I^e$, $\varvec{\theta }_I^e$ and $d_I^e$ are the displacement, temperature and phase field values of node I in element e, respectively. n is the number of nodes in the element. ${{N}}{{_{\varvec{u}}^e}_I}$, ${{N}}{{_{\theta }^e}_I}$ and ${{N}}{{_{d}^e}_I}$ are the standard FEM shape functions [40].

Then the spatial discrete equations of the coupling problem with phase-field evolution are obtained by using the standard Galerkin approximation

$$\begin{aligned}&{\varvec{M\ddot{u}}} = {{\varvec{F}}^{{\mathrm{ext}}}}\left( {\varvec{b}}, {\bar{\varvec{t}}} \right) - {{\varvec{F}}^{{\mathrm{int}} }}\left( {{\varvec{u}},{\varvec{\theta }},{\varvec{d}}} \right) \nonumber \\&\varvec{C}_{\theta } \dot{\varvec{\theta }} = {{\varvec{Q}}^{\mathrm{ext}} \left( {\gamma ,\varvec{\bar{J}}} \right) } - {{\varvec{Q}}^{\mathrm{int}} \left( {{\varvec{\theta }},{\varvec{d}}} \right) }, \quad \varvec{C}_d \dot{\varvec{d}} = {\left\langle {{\varvec{Y}}\left( \mathcal{H} ({\varvec{u}}),{\varvec{d}} \right) } \right\rangle _ + } \end{aligned}$$

(15)

where $\varvec{u} = \{\varvec{u}^e\}$, $\varvec{\theta } = \{\theta ^e\}$ and $\varvec{d} = \{d^e\}$ are the displacement, temperature and phase-field vectors that contain the time-dependent nodal DOFs of $\varvec{u}$, $\theta$ and d in the whole solution domain. The expressions of the coefficient matrices in Eq. (15) are listed below:

(16a)

(16b)

(16c)

(16d)

(16e)

(16f)

(16g)

(16h)

where the operator represents matrix assembly from element to global in classic FEM, $N_e$ is the total number of the elements, ${N_s^{t}}$ and ${N_s^{J}}$ are the number of surface elements having the surface force and surface heat flow. ${\varvec{N}}{{_{\varvec{u}}^e}}$, ${\varvec{N}}{{_{\theta }^e}}$ and ${\varvec{N}}{{_{d}^e}}$ are the vectors of the FEM shape functions: ${\varvec{N}}{{_{\varvec{u}}^e}} = {\varvec{N}}{{_{\theta }^e}} = {\varvec{N}}{{_{d}^e}}= [N_1, \cdots ,N_b]$ (where $b=4$ for volume integral in 2D and surface integral in 3D, and $b=8$ for volume integral in 3D). ${\varvec{B}}{{_{\varvec{u}}^e}}$, ${\varvec{B}}{{_{\theta }^e}}$ and ${\varvec{B}}{{_{d}^e}}$ are the shape functions’ spacial derivatives [40]. $\varvec{K} = diag\left\{ {k,k,k} \right\}$ and $\varvec{K}_0 = diag\left\{ {k_0,k_0,k_0} \right\}$ are the damaged and undamaged body’s heat transfer coefficient matrix, respectively. The local gradient of the phase-field can be calculated by the following formula: ${\nabla d} = {\varvec{B}}{{_{d}^e}} {\varvec{d}}$. $\mathcal H$ is a so-called history variable which is defined as:

$$\begin{aligned} \mathcal{H} = \left\{ \begin{array}{ll} {\psi _ + }\left( {{\varvec{\varepsilon } ^e}} \right) &{}\quad \mathrm {if} \, {\psi _ + }\left( {{\varvec{\varepsilon } ^e}} \right) > {\mathcal{H}_n}\\ {\mathcal{H}_n}&{}\quad \mathrm {otherwise}, \end{array} \right. \end{aligned}$$

(17)

where $\mathcal{H}_n$ is the previously calculated history variable in the n-th increment step. This history variable couples the displacement and phase field. Furthermore, it enforces the irreversibility criterion of the phase-field variable ($\dot{d} \ge 0$).

3.2 Time-discrete scheme

To integrate over time, the time interval $[0,t_a]$ is discretized into several small time intervals: $0=t_0< t_1< \cdots < t_N = t_a$. The time increment in the k-th incremental step $\Delta t_k = t_k - t_{k-1}$ is defined. Because explicit time integral is used, the velocity vector should be calculated at the middle time of each time interval: $t_{k+\frac{1}{2}} =\frac{1}{2} (t_k + t_{k+1})$.

Since the displacement field is second-order in time, the temperature field and phase field are first-order in time. In order to adapt to the built-in time integration rules of Abaqus/Explicit for different degrees of freedom, we adopt different time integration schemes for different fields. In this paper, the displacement field is integrated using the explicit central-difference time integration rule, and the temperature field and phase field are integrated using the explicit forward-difference time integration rule with using the diagonal or “lumped” element capacity/mass matrices. The approximate solutions of $\varvec{u}(t_k)$, $\varvec{\dot{u}}(t_{k+\frac{1}{2}})$, $\varvec{\ddot{u}}(t_k)$, $\varvec{\theta }(t_k)$, $\varvec{\dot{\theta }}(t_k)$, $\varvec{d}(t_k)$ and $\varvec{\dot{d}}(t_k)$ are marked as $\varvec{u}_k$, $\varvec{v}_{k+\frac{1}{2}}$, $\varvec{a}_k$, $\varvec{\theta }_k$, $\varvec{p}_k$, $\varvec{d}_k$ and $\varvec{r}_k$, respectively.

(1) Central-difference method for displacement field integration. In this paper, we use central-difference method to calculate $\varvec{u}_{k+1}$, $\varvec{v}_{k+\frac{1}{2}}$, $\varvec{a}_{k+1}$ from $\varvec{u}_{k}$, $\varvec{v}_{k-\frac{1}{2}}$, $\varvec{a}_{k}$, $\varvec{d}_k$ and $\varvec{\theta }_k$ according to the following update formulas

$$\begin{aligned}&\varvec{a}_{k} = \varvec{M}^{-1}( {{\varvec{F}}^{{\mathrm{ext}}}}\left( {\varvec{b}}, \varvec{\bar{t}} \right) - {{\varvec{F}}^{{\mathrm{int}} }}\left( {{\varvec{u}_k},\varvec{\theta }_k,{\varvec{d}_k}} \right) ) \end{aligned}$$

(18a)

$$\begin{aligned}&\varvec{v}_{k+\frac{1}{2}} = \varvec{v}_{k-\frac{1}{2}} + \frac{\Delta t_{k+1} + \Delta t_{k}}{2} \varvec{a}_k \end{aligned}$$

(18b)

$$\begin{aligned}&\varvec{u}_{k+1} = \varvec{u}_{k} + \Delta t_{k+1} \varvec{v}_{k+\frac{1}{2}} \end{aligned}$$

(18c)

It should be pointed out that the central difference operator is not self-starting since the value of velocity $\varvec{v}_{-\frac{1}{2}}$ needs to be defined. To this end, the following two equations are used to determine the initial conditions of velocity.

$$\begin{aligned} \varvec{v}_{+\frac{1}{2}} = \varvec{v}_{0} + \frac{\Delta t_1}{2} \varvec{a}_0, \quad \varvec{v}_{-\frac{1}{2}} = \varvec{v}_{0} - \frac{\Delta t_0}{2} \varvec{a}_0 \end{aligned}$$

(19)

(2) Forward-difference method for temperature field integration. In this paper, the forward-difference method is adopted to calculate $\varvec{\theta }_{k+1}$, $\varvec{p}_{k+1}$ from $\varvec{\theta }_{k}$, $\varvec{d}_{k}$ and $\varvec{p}_{k}$ according to the following update formulas

$$\begin{aligned}&\varvec{p}_{k} = \varvec{C}_{\theta }^{-1} \cdot ( {\varvec{Q}}^{\mathrm{ext}}\left( \gamma , \varvec{\bar{J}} \right) - {{\varvec{Q}}^{\mathrm{int}}\left( {{\varvec{\theta }_k},{\varvec{d}_k}} \right) } ) \end{aligned}$$

(20a)

$$\begin{aligned}&\varvec{\theta }_{k+1} = \varvec{\theta }_{k} + {\Delta t_{k+1}} \varvec{p}_k \end{aligned}$$

(20b)

(3) Forward-difference method for phase-field integration. In this paper, the forward-difference method is adopted to calculate $\varvec{d}_{k+1}$, $\varvec{r}_{k+1}$ from $\varvec{d}_{k}$, $\varvec{u}_{k}$ and $\varvec{r}_{k}$ according to the following update formulas

$$\begin{aligned}&\varvec{r}_{k} = \varvec{C}_{d}^{-1} \cdot ({\left\langle {{\varvec{Y}}\left( {{\varvec{u}_k},{\varvec{d}_k}} \right) } \right\rangle _ + }) \end{aligned}$$

(21a)

$$\begin{aligned}&\varvec{d}_{k+1} = \varvec{d}_{k} + {\Delta t_{k+1}} \varvec{r}_k \end{aligned}$$

(21b)

Since the center and forward differential integrals are both explicit, the displacement field, temperature field, and phase field can be solved simultaneously by explicit coupling. Therefore, it is not necessary to perform an iterative solution or calculate a tangent stiffness matrix, and the solution process in each incremental step is very efficient. In addition, explicit integration is independent on each FEM node, so it is very suitable for multi-CPU parallel computing. The parallel performance of multi-CPU is studied in detail in “Appendix A”.

Fig. 2

Schematic diagram of multi-field coupled phase-field method in Abaqus/Explicit

3.3 Finite element implementation in Abaqus/Explicit

In order to implement the solution in Abaqus/Explicit, we duplicate a geometric model (including the mesh) as shown in Fig. 2. The solution domain of original model is marked as $\Omega _1$, and the replicated model is marked as $\Omega _2$. We solve the displacement and temperature field on $\Omega _1$ and the phase field on $\Omega _2$. Besides, $\Omega _1$ is also used to visualize the results. The reason for using this replication model is that there is not enough freedom in Abaqus/Explicit to solve two diffusion equations at the same time. The actived degrees of freedom (DOFs) are 1, 2, 3 and 11 in $\Omega _1$. Among them, DOFs 1, 2 and 3 are used to calculate the displacement field, and DOF 11 is used to calculate the evolution of temperature field. In order to maximize the use of Abaqus’s existing code, the coupling of displacement field and temperature field and stiffness degradation are realized in the user subroutine VUMAT. The actived DOF is 11 in $\Omega _2$ and the evolution of the phase field is realized in the user subroutine VUEL.

To transfer information among the three fields, we introduce the user subroutines VUSDFLD and VUFIELD. The detailed information transmission paths are shown in Fig. 2. It mainly involves transferring the contribution of displacement field to phase field evolution ($\mathcal H$) from $\Omega _1$ to $\Omega _2$, and transferring the phase-field variable d from $\Omega _2$ to $\Omega _1$.

Besides, the user subroutine VEXTERNALDB is used to synchronize variables in different regions of multi-CPU parallelism.

The above process and method are implemented in Abaqus/Explicit by writing Fortran 90 subroutines. The detailed tutorial of one element example is given in “Appendix B”. The source code and input files for the implementation of the above algorithm are provided in “Appendix C”.

4 Benchmark tests and numerical examples

4.1 One element tests

In this section, we use two typical one-element tests to verify the correctness of the code and study the influence of numerical parameters. The input file and source code are given for the convenience of readers to grasp and use.

4.1.1 Uniaxial tensile test

In this section, an example of uniaxial tension with a three-dimensional solid element is carried out to understand the phase-field model. The geometry parameters and boundary conditions of the model are shown in Fig. 3. The size of the element (also the model) is $1.0 \times 1.0 \times 1.0~\hbox {mm}$. The material properties and viscosity parameter of the model are listed in Table 2. The length scale parameter $l_c$ is set to $1.0~\mathrm {mm}$.

According to Ref. [27], although the size of $l_c$ here does not satisfy the relationship between $l_c$ and the mesh size, because we do not study the crack growth, but understand the essence of the phase-field model through the basic equation of phase-field evolution, so it is acceptable. The displacement load is applied linearly and the total simulation time is 0.01 s. We will prove later that in such a long time, loading can be regarded as a quasi-static process, which can be compared with the analytical solution given by Molnár and Gravouil [27].

Fig. 3

Comparison of numerical results and analytical solutions [27] under different viscosity parameters for one element test under uniaxial tensile load: a axial stress as a function of axial strain, and b damage phase field as a function of axial strain

Considering the quasi-static loading process and ignoring the viscous effect, the problem has an analytical solution, which can be found in Ref. [27]. In Fig. 3, the calculated axial stress versus axial strain curves and phase-field versus axail strain curves under different viscous parameters ($\eta = 1.0 \times {10^{-5}}~{\mathrm{kN \, s/mm^2}}$, $\eta = 1.0 \times {10^{-6}}~{\mathrm{kN \, s/mm^2}}$, $\eta = 1.0 \times {10^{-7}}~{\mathrm{kN \, s/mm^2}}$) are given and compared with the analytical solutions ($\eta =0$) [27]. We can find that the numerical results are in good agreement with the analytical solutions when the viscous parameter $\eta$ decreases gradually. In Fig. 4, the kinetic energy and external work of the system and their ratios versus time are given for $\eta = 1.0 \times {10^{-7}}~{\mathrm{kN}} \, {\mathrm{s/mm}}^{2}$. The results show that the ratio of kinetic energy to external work is always less than $0.001\%$, which indicates that this is a quasi-static process.

The input file and source code for this example can be found in the supplementary materials in “Appendix C”. See “Appendix B” for details of the execution of this example.

4.1.2 Tension–compression cycle test

The evolution process of phase-field under tension and compression cyclic loads is considered to verify the monotonicity of phase-field evolution and the different responses for compression loads of phase-field models with different energy decomposition modes. The material parameters and viscous parameter are listed in Table 2. The loading–unloading–reloading curve is shown in the upper right corner of Fig. 5a.

In Fig. 5, the curves of axial stress and axial strain and the curves of phase-field evolution with loading are given respectively under three phase field models. The arrows in the figure indicate the direction of the curve (that is, the direction of loading) and the numbers indicate the order of loading. It can be seen that the pure tensile responses of the three models are the same. However, their responses to compressive loads are different. Model A and B will be damaged under compressive loads, while Model C will not. Model A is more vulnerable to damage than model B under the same compressive load. At the same time, the compression and re-stretching process also shows that when the material has certain damage, not only the stresses but also the material stiffness is degraded. The evolution curve of phase-field variable d in Fig. 5b also shows that our phase-field model based on explicit time intergration satisfies the irreversibility criterion ($\dot{d} \ge 0$). The input file and source code for this example can be found in the supplementary materials in “Appendix C”.

Table 2 The material properties and viscosity parameter used in Sect. 4.1.1

Fig. 4

The curves of energy and energy ratio with time of uniaxial tension example

Fig. 5

A phase-field model of one element under a cyclic load of tension and compression: a axial stress as a function of axial strain (the loading curve of displacement-time is in the upper right corner); and b damage phase-field variable as a function of axial strain

Fig. 6

Single edge notched specimen problems: a geometry and boundary. b Crack pattern for pure tension $(\alpha = 90^{\circ })$. c Crack pattern for pure shear $(\alpha =0^{\circ })$. d Crack angle $(\beta )$ vs. loading direction $(\alpha )$ and the comparison with the work of Molnár and Gravouil [27] and Bourdin et al. [41]

Fig. 7

The crack propagation paths of single edge notched specimen problem for $\alpha =0^{\circ }$ with different viscosity parameters: a $\eta = 1 \times {10^{-6}}~{\mathrm{kN}} \, {\mathrm{s/mm}}^{2}$, b $\eta = 1 \times {10^{-7}}~{\mathrm{kN}} \, {\mathrm{s/mm}}^{2}$, and c $\eta = 1 \times {10^{-8}}~{\mathrm{kN}} \, {\mathrm{s/mm}}^{2}$

4.2 Single edge notched test

The third example is a single edge notched sample under tensile and shear loading. The geometry and boundary conditions are shown in Fig. 6a. Consider a specimen of $100~\mathrm {mm} \times 100~\mathrm {mm}$ with a single notched crack in the middle and a length of 50 mm. The bottom of the specimen is fixed, and the upper part is given a constant velocity $\varvec{v}$ in a certain direction $(\alpha )$. The material properties and viscosity parameter are listed in Table 3. The characteristic width of crack $l_c$ is chosen as 0.5 mm, and the mesh size is set as $h = l_c/2$. Besides, Model C is used for strain energy decomposition.

The crack patterns for the two limit cases are shown in Fig. 6b, c. While for the pure tensile loading ($\alpha = 90^{\circ }$) the crack is horizontal ( $\beta = 0^{\circ }$) for the pure shear loading ($\alpha = 0^{\circ }$) we see a curved crack path initiating with a deflection angle from the horizontal direction ( $\beta = 70.1^{\circ }$). The crack pattern is in good agreement with the works of Ziaei-Rad and Shen [34] and Miehe et al. [42]. The calculation results of the initial deflection angle of crack under different loading angles are compared with those of previous calculation results, as shown in Fig. 6d. We can see that our results are in good agreement with the works of Molnár and Gravouil [27] and Bourdin et al. [41].

Next, we use the example of $\alpha =0^{\circ }$ to study the viscosity parameter $\eta$ of the solution. Figure 7 shows the phase field contour calculated with three different values of $\eta$ at the same time ($\eta = 1.0 \times {10^{-6}}~{\mathrm{kN \, s/mm^2}}$, $\eta = 1.0 \times {10^{-7}}~{\mathrm{kN \, s/mm^2}}$, $\eta = 1.0 \times {10^{-8}}~{\mathrm{kN \, s/mm^2}}$) and the other parameters of the model are the same. The results show that the crack propagation paths are the same under different viscous parameters, and the crack propagation speed increases with the decrease of $\eta$.

Table 3 The material properties and viscosity parameter used in Sect. 4.2

4.3 Dynamic crack propagation

In this section, we use a classic Kalthoff experiment [43] to show the simulation ability of the model and code for dynamic crack propagation. The schematic diagram and geometric parameters of the model are shown in Fig. 8a. Due to symmetry, only half of the models are shown. The material properties and viscosity parameter used here are listed in Table 4. The mesh size h is 0.1 mm (To reduce the calculation consumption, the four-layer element is used in the thickness direction) and the characteristic length scale $l_c = 2h$. The notched part on the side of the specimen is impacted at a speed of 20 m/s to drive the crack growth. The results of Kalthoff and Winkler’s experiments [43] and previous numerical simulations [36, 44, 45] show that under the low-velocity impact, the crack will propagate along the direction of about 70-degree angle.

Fig. 8

The schematic diagram of the model for Kalthoff experiment [43] and the three typical crack growth paths obtained by simulation: a the model schematic diagram and geometric parameters; b the crack growth path at $t = 25\,\upmu \mathrm {s}$; c the crack growth path at $t = 50\,\upmu \mathrm {s}$; and d the crack growth path at $t = 100\,\upmu \mathrm {s}$

Fig. 9

The simulated crack path of Kalthoff experiment [43] under different step time increments and viscosity parameters: a $\Delta t = 0.01\,\upmu \mathrm {s}, \eta = 1.0 \times 10^{-7} \mathrm {kN} \, \mathrm {s/mm}^{2}$; b $\Delta t = 0.01\,\upmu \mathrm {s}, \eta = 1.0 \times 10^{-8} \mathrm {kN} \, \mathrm {s/mm}^{2}$; and c $\Delta t = 0.005\,\upmu \mathrm {s}, \eta = 1.0 \times 10^{-7} \mathrm {kN} \, \mathrm {s/mm}^{2}$

The simulated 3D crack growth paths at different times ($t = 25\,\upmu \mathrm {s}$, $t = 50\,\upmu \mathrm {s}$ and $t = 100\,\upmu \mathrm {s}$) are shown in Fig. 8b–d. The resulting crack propagation angle is $69^\circ$, which is very close to $70^\circ$. This shows that our phase-field model and code are suitable for typical dynamic fracture problems.

We also compare the crack paths of the Kalthoff experiment under different step time increments and viscosity parameters, as shown in Fig. 9. It can be found that the crack propagation paths under the three conditions have good consistency, and the crack deflection angles are very close ($69^{\circ }$, $70^{\circ }$, and $70^{\circ }$, respectively). This shows that (1) when the viscosity parameter is small, reducing the viscosity parameter does not affect the crack propagation path; (2) when the time increment is less than the requirement of stable time increment, reducing the time increment does not affect the crack propagation path.

Table 4 The material properties and viscosity parameter used for Kalthoff test

4.4 Quenching test

This example concerns a quenching test to verify the thermo-elastic coupled fracture process under thermal shock loading. Shao et al. [46] carried out a detailed experimental study on the quenching process. In the experiment, the ceramic plates were heated to different temperatures and then put into a low temperature water bath. Under the thermal shock load, a large number of parallel cracks were produced in the ceramic. In the quenching process, the shrinkage of ceramics with higher temperature before contact with water is more intense, showing a larger number of parallel cracks with alternating length. Many researchers have studied this problem numerically [4, 47].

Table 5 The material properties for quenching test problem

Fig. 10

The numerical results (left) of crack distribution in ceramics after cooling for 10 $\mathrm {ms}$ at different initial temperatures (i.e., different cooling temperature differences a $\Delta \theta = 250~\mathrm {K}$, b $\Delta \theta = 380~\mathrm {K}$ and c $\Delta \theta = 680~\mathrm {K}$) are compared with the experimental results (The experimental results are from Ref. [46])

Fig. 11

Statistical chart of the number of non-dimensional length range of cracks after cooling for 10 $\mathrm {ms}$ at various initial temperatures (i.e., various cooling temperature differences a $\Delta \theta = 250~\mathrm {K}$, b $\Delta \theta = 380~\mathrm {K}$ and c $\Delta \theta = 680~\mathrm {K}$) in the numerical simulation

According to the experimental settings, we take half-model for numerical simulation. The size of the sample is $50 \times 9.8~\mathrm {mm}$. The ambient temperature is $\theta _m = 300~\mathrm {K}$ (in the simulation, the surface temperature of the sample is kept at $300~\mathrm {K}$) and the initial temperature of the sample is $\theta _i = 550~\mathrm {K}$, $680~\mathrm {K}$ and $980~\mathrm {K}$ respectively (the corresponding temperature difference is $\Delta \theta = 250~\mathrm {K}$, $380~\mathrm {K}$ and $680~\mathrm {K}$). The material properties are listed in Table 5. In order to ensure that enough dense initial cracks are generated on the boundary, the mesh size h is set to 0.02 mm and the characteristic length scale $l_c = 2h$. The viscosity parameter is $\eta = 1.0 \times {10^{-8}}~{\mathrm{kN \, s/mm^2}}$. In this case, the crack initiation or propagation is mainly caused by thermal expansion and contraction. The time step used here is $1.8 \times {10^{-9}}~{\mathrm{s}}$.

Fig. 12

Comparisons between numerical results and experimental results [46] of the crack density, average crack length and crack distance with different temperature differences

Fig. 13

For $\Delta \theta = 380~(\mathrm {K})$, the distribution of temperature (left) and maximum principal stress (right) at $t = 10~\mathrm {ms}$

The final crack patterns at different initial temperatures (corresponding to different temperature difference) and their comparison with experimental results are given in Fig. 10. If short cracks are neglected, the crack patterns calculated by numerical method at different temperatures are in good agreement with the experimental results. In fact, shorter cracks may nucleate in the ceramic slab during the experiment, but due to the limitations of the experimental technology, they can not be clearly observed. Our simulations can well capture the key features of this problem: a large number of parallel short cracks nucleate, then selectively arrest and propagate. The parameter $l_c$ ensures that enough microcracks are initiated to simulate subsequent selective arresting and growth processes accurately. Figure 11 shows the statistics of the number of cracks in different crack length intervals (dimensionless by the height of the ceramic slab) of the numerical results. We can see that the more significant the temperature difference, the denser the cracks are. Especially the number of short cracks, which increases rapidly. That is, the more prominent the temperature difference is, the bigger the temperature gradient near the boundary of the ceramic slab is at the beginning, so the more significant the shrinkage caused by thermal stress is. Therefore, denser short cracks are needed in a short time to minimize the energy of the system.

Fig. 14

3D crack distribution of ceramic ball after fracture under thermal loading: a temperature distribution, b damage distribution on the surface of ceramic ball, and c 3D geometric structure of cracks

Fig. 15

Evolution of phase-field under thermal load of ceramic ball at different time: a–d the phase-field distribution on the middle section (top view) and e–h the 3D debris structure (the regions of $d > 0.95$ were removed to show the position of the cracks)

According to the statistical data, we further define the crack of more than $25\%$ sample height (H) as long crack. The number of long cracks and the average distance p and the average length of cracks a (nondimensionalized by the height of ceramic slab H) under different temperature differences ($\Delta \theta$) are summarized, as shown in Fig. 12. From the statistical results, it can be seen that the numerical results are in good agreement with the experimental results. At the same time, we also noticed that the crack length calculated by the numerical method is always smaller than the experimental value. This is mainly due to the numerical simulation of a relatively short period of time (10 ms) while the experimental time lasts for a long time (although the crack propagation mainly occurs in a short period of time when the ceramic slab is placed into cold water). We also show the temperature distribution and stress field distribution at the end of the simulation in Fig. 13. It can be seen that since the propagation direction of heat flux is consistent with the propagation direction of the crack, there is no obvious difference between the temperatures on both sides of the crack. Still, there is a noticeable temperature gradient along the propagation direction of crack. The distribution of the stress field shows the shielding effect of long crack to short crack, so only some cracks are dominant in competition and extend to a long distance.

4.5 Fragmentation of ceramic balls under thermal shock

In order to demonstrate the simulation ability of the algorithm and code for 3D complex thermo-mechanical coupling problems, in this example, we simulate the fracture and fragmentation process of a ceramic ball under thermal shock loading. Similar problems for 3D fracture process of balls have been studied by Klinsmann et al. in modeling crack initiation and propagation during Li insertion in storage particles [29]. The radius of the ceramic ball is 5.0 mm, and the material parameters are the same as those in the previous section. Initially, the temperature of the ceramic ball is 273 K. When the ambient temperature suddenly rises to 653 K (The corresponding temperature difference is $\Delta \theta = 380~\mathrm {K}$) the ceramic ball will crack and break under the action of thermal expansion. The characteristic crack width is chosen as $l_c=0.14~\mathrm {mm}$ and the mesh size is set as $h=l_c/2$. The viscosity parameter is $\eta = 1.0 \times {10^{-8}}~{\mathrm{kN}} \, {\mathrm{s/mm}}^{2}$

The 3D crack distributions of the ceramic ball after fracture under thermal loading are shown in Fig. 14. We can find that the ceramic ball was broken into 14 large pieces of ceramic fragments. Moreover, the broken form and the shape of the fragments of the ceramic ball have good symmetry. In order to study the fracture and fragmentation process of ceramic balls more precisely, we sliced the ceramic balls and observed the phase field evolution process on the slices, as shown in Fig. 15a–d. The process of 3D crack propagation and debris generation with time is also given, as shown in Fig. 15e–h (the regions of $d > 0.95$ were removed to show the position of the cracks). It can be found that the complete damage first occurs in the center of the ceramic ball and then gradually expands around it. When the crack extends near the surface of the ball, the crack bifurcates (in 3D space, it appears as a cone) and finally forms a 3D complex crack surface, as shown in Figs. 14 and 15e–h.

Fig. 16

Parallel performance study: a incremental steps every two minutes with different number of CPUs, and b calculating wall time consumption under different numbers of DOFs

5 Concluding remarks

In this paper, a phase-field model based on explicit time integration for thermo-elastic coupling problems was developed in the commercial finite element code Abaqus/Explicit to simulate brittle fracture in 3D solids. The implementation was carried out in the framework of a user-defined finite element subroutine (Abaqus/VUEL) and a user-defined material subroutine (Abaqus/VUMAT). Several examples are given to illustrate the practicability and robustness of this method for complex fracture problems under thermal shock: from one element to 3D thermal shock crack nucleation and propagation. The numerical results are in good agreement with the analytical solutions and existing experiments.

The influence of viscous parameters on numerical results is systematically studied. It is observed that this parameter does not affect the crack path or the initiation of crack propagation, but it leads to different crack velocities and stress peaks.

The source code and several benchmark examples are given as supplementary materials. Abaqus is one of the most widely used finite element software. This implementation makes it easy for engineers and researchers to simulate complex crack propagation, bifurcation, and crack network formation in multi-field coupling problems. Besides, the source code can be easily extended to simulate large deformation, crack propagation in plastic materials, and other multi-field coupled fracture problems.

Appendices

Appendix A: Parallel performance study

The phase-field model has high requirements for mesh density and usually requires large-scale calculations. Therefore, parallel computing is particularly important for the wide application of the phase field method. The explicit time integration schemes (including central-difference and forward-difference integration method) are suitable for increasing computational efficiency through parallel computing. In this paper, we implement them using multi-CPU sub-regional calculations. Here we use the example in Sect. 4.5 to study the efficiency of parallel computing. For parallel computing, the entire model is divided into several subdomains according to the number of CPUs that will be used. The information on the common boundary of each subdomain is stored in the public variables, which are synchronized in multiple CPUs via MPI functions in the user subroutine VEXTERNALDB.

Figure 16a shows the increment numbers every two minutes of the model with different number of CPUs. The model has 12,859,435 DOFs and 22,851 incremental steps. We can find that using multiple CPUs can greatly improve the efficiency of calculation, and the wall time is approximately inversely proportional to the number of CPUs used. Figure 16b shows the wall time consumed by the same model with the same number of CPUs (16) and different DOFs. It can be seen that the relationship between the wall time and the number of DOFs is basically linear, which is better than that of the implicit scheme.

Table 6 Solution dependent variables (SDVs) used for visualization

Appendix B: One element tutorial

Here we assume that users are familiar with Abaqus/Explicit and its user subroutines. Due to the limitation of page space, only some key modeling details are given.

Each problem has two files for calculation: an Abaqus input file (*.inp) and a FORTRAN source code file (*.for or *.f, depending on the operation system).

Due to the problem of the allocation of the common block (module) for every finite element mesh a new FORTRAN file should be created. Only two variables that should be modified in the provided example file are NodeNum (the number of the nodes in $\Omega _1$) and NumEle (the number of the elements in $\Omega _1$). Thus, in this example NodeNum = 8, and NumEle=1.

The Abaqus input file is generally written by the software itself. However, we should modify it before initiating the simulation.¹

In the first section, the parts are created. The nodes are given (*Node) and the elements are generated. After creating all the nodes, a command is given to define the phase-field element type (*User element, nodes=8, type=VU2, properties=3, coordinates=3, variables=16). This command creates an element with eight nodes with five material properties and sixteem status variables. The status variables are used to transport information from one step to the next. It contains the phase-field value and the history variable at each integration point. The meaning of the SDVs is listed in Table 6.

In the next line, we define the concerning DOFs, in this case only the eleventh (11). To create the elements after the command: *Element, type=VU2, the elements are given starting with the serial number then the nodes of the corners in a counterclockwise list: 1, 5, 6, 8, 7, 1, 2, 4, 3. To assign material parameters to the elements a set is created. After which the command *Uel property, elset=Set-part2-ele-1 and the properties are given in the next line (where Set-part2-ele-1 is the name of the set containing all the phase-field elements). The properties are given as follows: viscosity parameter ($\eta$), length scale parameter ($l_c$) and fracture surface energy ($g_c$).

For temperature and displacement elements, the user material subroutine VUMAT is used. We only need to specify the material parameters passed into the user subroutine in *.inp file through the following statement: *User Material, constants=3. The properties are given as follows: Young’s modulus (E) Poisson’s ratio ($\nu$) and thermal expansion coefficient ($\alpha _{\theta }$). The user subroutine VUSFLD is declared to be used by adding command *User Defined Field to the *.inp file. Command *Field, Variable=1, User declares that the user subroutine VUFIELD is used and that the scope is all nodes (Set-allnode). The loads and boundaries of the displacement and temperature fields (in $\Omega _1$) are defined usually as it is done in a normal input file.

See the *.inp file in “Appendix C” for more details.

Appendix C: Supplementary materials

The supplementary materials related to this article include the source code of Abaqus user subroutine and the input file of the one element example.