Crack-face frictional contact modelling in cracked piezoelectric materials

Abstract

Actuators, sensors, micro- and nano-electromechanical systems and other piezoelectirc components are generally constructed in block form or as a thin laminated composites. The study of the integrity of such materials in their various forms and small sizes is still a challenge nowadays. To gain a better understanding of these systems, this work presents a crack surface contact formulation that includes friction and thus makes it possible to study the integrity of these advanced materials under more realistic crack surface multifield operational conditions. The dual boundary element method (BEM) is used for modeling frictional crack surface contact on piezoelectric solids in the presence of electric fields, further taking into account the electrical semipermeable boundary conditions on the crack. The formulation uses contact operators over the augmented Lagrangian to enforce contact constraints on the crack surfaces. The BEM reveals to be a very suitable methodology for these interface interaction problems because it considers only the boundary degrees of freedom, what makes it possible to reduce the number of unknowns and to obtain accurate results with a much lower number of elements than formulations based on the standard finite element method or the eXtended finite element method. The capabilities of this methodology are illustrated by solving some benchmark problems.

1 Introduction

Piezoelectric materials exhibit a multifield coupling which allows for their use as actuators and sensors in many technological sectors of current interest, such as the aerospace and automotive industries, or the biomedical and the electronics industries. Actuators, sensors, micro- and nano-electromechanical systems and other PE components are generally constructed in block form or in a thin laminated composite. The study of the integrity of such materials in their various forms and small sizes is still a challenge nowadays [1,2,3].

Fig. 1

Fractured piezoelectric domain

In general, crack surface contact problems is a key aspect that should be considered to study integrity problems [4,5,6]. These pioneering (analytical) works showed that, when a closed crack is considered in an elastic material, it is necessary to know the contact condition of the crack surface to avoid, for instance, physically unrealistic interpenetration of the crack surfaces or over estimation of stress intensity factors. Moreover, the crack surface roughness also alters the direction of crack propagation [7] so it influences the crack path [8]. Consequently, several numerical methodologies have been developed to provide engineers with computational tools to consider crack surface frictional contact in fractured materials. Due to the extremely good accuracy that the Boundary Element Method (BEM) presents in fracture mechanics problems, several works [9,10,11,12,13,14] have studied the influence of contact during the last thirty years. This problem have also been tackled considering other numerical techniques like finite element (FE) formulations with enrichment functions, i.e., extended FE method (XFEM) [15,16,17,18], new advanced FE strategies [19] or a scaled boundary finite element methodologies (SBFEM) [2].

However, to the best of the authors’ knowledge, numerical framework has never been proposed for modeling crack face frictional contact problem in fractured piezoelectric materials. The BEM has been proven as one of the more suitable numerical formulation to study fracture in piezoelectric materials for the last twenty years [20,21,22,23,24,25]. The BEM considers only the boundary degrees of freedom involved in this multifield problem and allows us to obtain a very good accuracy with a low number of elements. During those years, some boundary element based formulations proposed how to consider nonlinear electrical and mechanical crack face boundary conditions in fractured piezoelectric (PE) materials [26, 27], or in magneto-electro-elastic (MEE) materials [28, 29], considering the crack-face electromagnetic boundary conditions for fracture of magnetoelectroelastic materials presented in [30]. Although several authors have modeled the case of normal contact conditions between crack faces [26, 31,32,33], frictional contact conditions were not considered in those works. Moreover, recent works on mulfield materials under contact conditions [34,35,36,37] have revealed the strong influence of friction on the contact pressures, stress and electric/magnetic fields.

In this context, this work presents a crack surface contact formulation which makes it possible to study the integrity of these advanced materials under more realistic crack surface multifield operational conditions. The dual BEM [38, 39] is used for modeling frictional crack surface contact on piezoelectric solids, in the presence of electric fields and using a singe-domain formulation that permits to easily include the more realistic semipermeable electrical boundary conditions on the crack, while avoiding the need to define multiple domains in order to incorporate the crack geometry [40]. The formulation, based on previous works [23, 26, 34,35,36], uses the BEM for computing the elastic influence coefficients and contact operators over the augmented Lagrangian to enforce contact constraints on the crack surface. The capabilities of this methodology are illustrated by solving some benchmark problems.

The remainder of this work is organized as follows. Section 2 presents the problem description. Sections 3 and 4 present the crack face mechanical and electrical contact boundary conditions, respectively. The literature on BEM formulations is quite extensive, so in Sect. 5 we briefly present the basic ideas of a dual boundary element formulation to tackle fracture problems in piezoelectric materials. The discrete crack surface contact nonlinear equations set is presented in Sect. 6 and the solution scheme is summarized in Sect. 7. Section 8 presents the numerical results and discussion and, finally, Sect. 9 concludes the paper.

2 Problem formulation

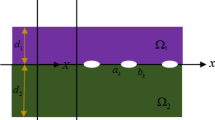
Let us consider a two-dimensional, homogeneous, anisotropic and linear piezoelectric (PE) cracked solid $\varOmega \subset \mathbb {R}^2$ with boundary $\partial \varOmega$ (see Fig. 1), in a Cartesian coordinate system $(x_i)$ ($i=1,2$). The mechanical equilibrium equations for this problem, in the absence of body forces, and the electric equilibrium equations under free electrical charge are

$$\begin{aligned} \begin{array} [c]{ll} \sigma _{ij,j}=0 &{}\quad \text {in}\quad \varOmega , \\ D_{i,i}=0 &{}\quad \text {in}\quad \varOmega , \end{array} \end{aligned}$$

(1)

where $\sigma _{ij}$ are the components of Cauchy stress tensor and $D_{i}$ are the electric displacements. The infinitesimal strain tensor $\gamma _{ij}$ and the electric field $E_{i}$ are defined as

$$\begin{aligned} \begin{array} [c]{ll} \gamma _{ij}=(u_{i,j}+u_{j,i})/2 &{}\quad \text {in}\quad \varOmega , \\ E_{i}=-\varphi _{,i} &{}\quad \text {in}\quad \varOmega , \end{array} \end{aligned}$$

(2)

with $u_{i}$ being the elastic displacement and $\varphi$ being the electric potential.

The elastic and electric fields are coupled through the linear constitutive law

$$\begin{aligned} \begin{array} [c]{ll} \sigma _{ij}=c_{ijkl}\gamma _{kl}-e_{lij}E_{l} &{}\quad \text {in}\quad \varOmega ,\\ D_{i}=e_{ikl}\gamma _{kl}+\epsilon _{il}E_{l} &{}\quad \text {in}\quad \varOmega , \end{array} \end{aligned}$$

(3)

where $c_{ijkl}$ and $\epsilon _{il}$ denote the components of the elastic stiffness tensor and the dielectric permittivity tensor, respectively; and $e_{ijk}$ are the PE coupling coefficients. These tensors satisfy the following symmetries: $c_{ijkl}=c_{jikl}=c_{ijlk}=c_{klij},\quad e_{kij}=e_{kji}, \quad \epsilon _{kl}=\epsilon _{lk}$, with the elastic constant and dielectric permittivity tensors being positive definite.

The boundary $\partial \varOmega$ is divided in two disjoint parts: $\partial \varOmega =\partial \varOmega _e \cup \partial \varOmega _c$, where $\partial \varOmega _e$ denotes the external boundary and $\partial \varOmega _c$ is the crack surface. Two partitions of the boundary $\partial \varOmega _e$ are considered to define the mechanical and the electrical boundary conditions. The first partition is: $\partial \varOmega _e=\partial \varOmega _{u} \cup \partial \varOmega _{p}$, i.e., $\partial \varOmega _u$ being the external boundary on which diplacements $\tilde{u}_i$ are prescribed and $\partial \varOmega _p$ with imposed tractions $\tilde{p}_i$. The second partition is: $\partial \varOmega _e=\partial \varOmega _{\varphi } \cup \partial \varOmega _{q}$, being the electrical potential $\tilde{\varphi }$ prescribed on $\partial \varOmega _\varphi$, and the electrical charges $\tilde{q}$ assumed on $\partial \varOmega _q$. Consequently, the Dirichlet boundary conditions are

$$\begin{aligned} \begin{array} [c]{ll} u_i=\tilde{u}_i &{}\quad \text {on}\quad \partial \varOmega _{u},\\ \varphi =\tilde{\varphi } &{}\quad \text {on}\quad \partial \varOmega _{\varphi }, \end{array} \end{aligned}$$

(4)

and the Neumann boundary conditions are given by

$$\begin{aligned}{}\begin{array}[c]{ll} \sigma _{ij}\nu _j=\tilde{p}_i &{}\quad \text {on}\quad \partial \varOmega _{p},\\ D_i\nu _i=\tilde{q} &{}\quad \text {on}\quad \partial \varOmega _{q}, \end{array} \end{aligned}$$

(5)

with $\nu _i$ being the outward unit normal to the boundary.

Finally, on the upper and lower crack faces (i.e. $\partial \varOmega _c=\partial \varOmega _c^+ \cup \partial \varOmega _c^-$) self equilibrated tractions and electric charges are considered: $\varDelta p_{i} = p_{i}^+ + p_{i}^-=0$ and $\varDelta q = q^+ + q^-=0$. However, aditional crack surface contact conditions have to be considered, as follows, on $\partial \varOmega _c$.

3 Crack face mechanical contact conditions

In order to avoid material interpepenetration between crack-faces, the unilateral contact law involves Signorini’s contact conditions on $\partial \varOmega _{c}$:

$$\begin{aligned} \begin{array} [c]{lll} \varDelta u_{\nu } \ge 0,&~p_{\nu }^+\ge 0,&~\varDelta u_{\nu }~p_{\nu }^+ = 0, \end{array} \end{aligned}$$

(6)

where $\varDelta u_{\nu } = u_{\nu }^+ - u_{\nu }^-$ and $p_{\nu }^+=\mathbf {p}^+\cdot \varvec{\nu }_c^+$, with $\varvec{\nu }_c^+$ being the unit normal on $\partial \varOmega _{c}^+$.

The normal contact constraints presented in (6) can be formulated as:

$$\begin{aligned} p_{\nu }^+ - \mathbb {P}_{\mathbb {R}_{+}}(\widehat{p}_{\nu }^{+} )=0, \end{aligned}$$

(7)

where $\mathbb {P}_{\mathbb {R}_{+}}(\cdot )$ is the normal projection function ($\mathbb {P}_{\mathbb {R}_{+}}(\cdot )=max(0,\cdot )$) and $\widehat{p}^{+}_{\nu }=p_{\nu }^+ - r_{\nu }\varDelta u_{\nu }$ is the augmented normal traction. The parameters $r_\nu$ is the normal dimensional penalization parameter ($r_\nu \in \mathbb {R}^+$).

In general, frictional contact condition on crack surfaces should be considered. So the Coulomb friction restriction can be summarized as:

$$\begin{aligned} \begin{array} [c]{llll} \varDelta u_{\tau }=-\lambda p_{\tau }^+,&~\lambda \ge 0,&~|p_{\tau }^+|\le \mu p_{\nu }^+,&~\lambda (p_{\tau }^+ - \mu p_{\nu }^+) = 0, \end{array} \end{aligned}$$

(8)

where $\lambda$ is an scalar, $\mu$ is the friction coefficient, $\varDelta u_{\tau } = u_{\tau }^+ - u_{\tau }^-$ and $p_{\tau }^+=\mathbf {p}^+\cdot \varvec{\tau }_c^+$, with $\varvec{\tau }_c^+$ being the unit tangential vector on $\partial \varOmega _{c}^+$.

The frictional contact constraints (8) can be also formulated using a contact operators as:

$$\begin{aligned} p_{\tau }^+ - \mathbb {P}_{\mathbb {E}_{\rho }}(\widehat{p}^{+}_{\tau })=0, \end{aligned}$$

(9)

where $\widehat{p}^{+}_{\tau }=p^{+}_{\tau } - r_\tau \varDelta u_{\tau }$ is the augmented tangential traction, $r_\tau$ being the tangential dimensional penalization parameter ($r_\tau \in \mathbb {R}^+$), and $\mathbb {P}_{\mathbb {E}_{\rho }}(\cdot ):\mathbb {R}\longrightarrow \mathbb {R}$ is the tangential projection function defined as

$$\begin{aligned} \mathbb {P}_{\mathbb {E}_{\rho }}(\widehat{p}^{+}_{\tau })=\left\{ \begin{array}{lll} \widehat{p}^{+}_{\tau } &{} \text {if} &{} |\widehat{p}^{+}_{\tau }| < \rho ,\\ \rho (\widehat{p}^{+}_{\tau }/|\widehat{p}^{+}_{\tau }|) &{} \text {if} &{} |\widehat{p}^{+}_{\tau }| \ge \rho , \end{array} \right. \end{aligned}$$

(10)

with $\rho =\mu p^{+}_{\nu }$, as it was defined in Eq. (7).

4 Crack face electrical contact conditions

The electrical boundary conditions on the crack-faces $\partial \varOmega _{c}$ can be defined in the general form as

$$\begin{aligned} q^+ = \kappa _c{\varDelta \varphi }/{\varDelta u_{\nu }}, \end{aligned}$$

(11)

where $\varDelta \varphi =\varphi ^+ - \varphi ^-$. In Eq. (4), $\kappa _c$ is the electrical permittivity of the medium between the crack faces and it is defined by the product of the relative permittivity of the considered medium ($\kappa _r$) and the permittivity of the vacuum ($\kappa _o = 8.85\,\times \,10^{-3}$ C/(GVm)): $\kappa _c = \kappa _r\kappa _o$. So, in contrast to the impermeable or the permeable crack-face boundary conditions, this expression presents a non-linear relation between mechanical displacements, electrical potential and electrical charges.

In order to consider both semi-permeable crack-face conditions and crack-face contact conditions, Eq. (4) is redefined as $q^+ = \tilde{\kappa }{\varDelta \varphi }/{\varDelta u_{\nu }}$,

$$\begin{aligned} \tilde{\kappa }=\left\{ \begin{array} [c]{lll} \kappa _{c} &{} \text { if } &{} \varDelta u_{\nu }>0,\\ \infty &{} \text { if } &{} \varDelta u_{\nu }=0. \end{array} \right. \end{aligned}$$

(12)

According to (12), the electrical contact condition shows that when there is no contact (i.e. crack opening displacements $\varDelta u_{\nu }>0$) on $\partial \varOmega _c$, the normal component of the electric displacement field is $q^+ = \kappa _{c}{\varDelta \varphi }/{\varDelta u_{\nu }}$, $\partial \varOmega _c$ being the permittivity parameter that allows us to impose permeable, impermeable or semipermeable crack face conditions. Nevertheless, when there is contact (i.e., $\varDelta u_{\nu }=0$, and consequently $\tilde{\kappa }=\infty$), electric potentials on the crack faces are the same: $\varDelta \varphi =0$.

5 Boundary integral equations

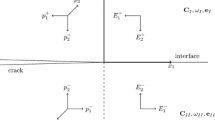
The dual formulation for the BE solution of crack problems considers both the extended displacement (EDBIE) and the extended traction (ETBIE) boundary integral representations to overcome the difficulty of having two coincident boundaries $\partial \varOmega _{c}^+$ and $\partial \varOmega _{c}^-$. In this way, the EDBIE is applied for collocation points $\varvec{\xi }$ on $\partial \varOmega _{e}$ and on either of the crack faces, say $\partial \varOmega _{c}^-$, to yield

(13)

where $\mathbf {x}$ is a boundary point, $u_J$ is the extended displacement vector (see Barnett and Lothe representation [41])

$$\begin{aligned} u_{J}=\left\{ \begin{array} [c]{ll} u_{j} &{} \qquad J\leqslant 2\\ \varphi &{} \qquad J=3, \end{array} \right. \end{aligned}$$

(14)

$p_J$ is the extended tractions vector

$$\begin{aligned} p_{J}=\left\{ \begin{array} [c]{ll} p_{j} &{} \qquad J\leqslant 2\\ q &{} \qquad J=3, \end{array} \right. \end{aligned}$$

(15)

$c_{IJ}$ depends on the local geometry of the boundary $\partial \varOmega$ at the collocation point $\varvec{\xi }$; $u_{IJ}^{*}$ and $p_{IJ}^{*}$ are the extended displacement fundamental solution and the extended traction fundamental solution at a boundary point $\mathbf {x}$ due to a unit extended source applied at point $\varvec{\xi }$, respectively [20] .

Consequently, the ETBIE is applied for collocation points $\varvec{\xi }$ on the other crack surface, $\partial \varOmega _{c}^+$,

(16)

to complete the set of equations to compute the extended displacements and tractions on $\partial \varOmega$. In Eq. (16) $s_{IJ}^{*}$ and $d_{IJ}^{*}$ are obtained by differentiation of $u_{IJ}^{*}$ and $p_{IJ}^{*}$ [20], as

$$\begin{aligned} d_{IJ}^{*}(\mathbf {x},\varvec{\xi })= & {} -N_s(\varvec{\xi }) C_{sIKr}u_{KJ,r}^{*}(\mathbf {x},\varvec{\xi }), \end{aligned}$$

(17)

$$\begin{aligned} s_{IJ}^{*}(\mathbf {x},\varvec{\xi })= & {} -N_s(\varvec{\xi }) C_{sIKr}p_{KJ,r}^{*}(\mathbf {x},\varvec{\xi }), \end{aligned}$$

(18)

with $N_s(\varvec{\xi })$ being the outward unit normal to the boundary at the source point and

$$\begin{aligned} C_{iJKl}=\left\{ \begin{array} [c]{ll} C_{ijkl}, &{} \qquad J,K = 1,2\\ e_{lij}, &{} \qquad J = 1,2; K=3\\ e_{ikl}, &{} \qquad J = 3; K=1,2\\ -\epsilon _{il}, &{} \qquad J,K=3, \end{array} \right. \end{aligned}$$

(19)

where the lowercase (elastic) and uppercase (extended) subscripts take values 1, 2 and 1, 2, 3, respectively. Furthermore, Symbols and in Eqs. (13) and (16) stand for the Cauchy Principal Value (CPV) and the Hadamard Finite Part (HFP) of the integral, respectively.

When the cracks are mechanically and electrically selfequilibrated, i.e., $\varDelta p_{I} = p_{I}^+ + p_{I}^-=0$ on $\partial \varOmega _{c}$ (the superscripts $+$ and − stand for the upper and lower crack surfaces), it would be enough to apply the EDBIE for collocation points $\varvec{\xi }$ on $\partial \varOmega _{e}$ and the ETBIE for collocation points $\varvec{\xi }$ on either side of the crack, say $\partial \varOmega _{c}^+$, to yield

(20)

(21)

Equations (20) and (21) yield a complete set of equations to compute the extended displacements and tractions on $\partial \varOmega _{e}$ and the extended crack opening displacements $\varDelta u_{I} = u_{I}^+ - u_{I}^-$ on $\partial \varOmega _{c}$. In Eq. (21), as previously discussed in Ref. [23], the free term $c_{IJ}$ has been set to 1 because of the additional singularity arising from the coincidence of the two crack surfaces.

6 Crack surface contact discrete equations

Numerical evaluation of the ETBIE requires $C^1$ continuity of the displacements. As in previous works [23], discontinuous quadratic elements with the two extreme collocation nodes shifted towards the element interior are used to mesh the cracks. The asymptotic behavior of the extended displacements near the crack tip is modelled via discontinuous quarter-point elements. For the rest of the boundaries, continuous quadratic elements are employed. A detailed justification of the discretization procedure can be found in [23].

A collocation procedure on boundary integral equations (20) and (21) leads to the following system of equations: $\mathbf {A} \mathbf {x}=\mathbf {F}$, where the boundary conditions have been imposed and all the unknowns have been passed to vector $\mathbf {x}$, to yield

$$\begin{aligned} \left[ \begin{array}{ccccc} \mathbf {A}_{\mathrm {x}_e}&\mathbf {A}_{\varDelta u_c}&\mathbf {A}_{\varDelta \varphi _c}&\mathbf {A}_{p_c}&\mathbf {A}_{q_c} \end{array}\right] \left\{ \begin{array}{c} \mathbf {x}_{e} \\ \varDelta \mathbf {u}_{c} \\ \varDelta \varvec{\varphi }_c\\ \mathbf {p}_{c} \\ \mathbf {q}_{c} \end{array}\right\} = \mathbf {F}. \end{aligned}$$

(22)

In expression (22), $\mathbf {x}_{e}$ collects the nodal external unknowns (i.e. the nodal unknowns on $\partial \varOmega _{e}$), $\varDelta \mathbf {u}_{c}$ and $\varDelta \varvec{\varphi }_{c}$ collect the nodal crack opening displacements and electric potentials, respectively, on $\mathbf {x}_{c}$, $\mathbf {p}_{c}$ contains the normal and tangential nodal contact tractions (i.e. ${\mathbf{p}}_\nu$ and ${\mathbf{p}}_\tau$) and $\mathbf {q}_{c}$ contains the nodal electric charges. Matrices $\mathbf {A}_{\mathrm {x}_e}$, $\mathbf {A}_{\varDelta u_c}$, $\mathbf {A}_{\varDelta \varphi _c}$, $\mathbf {A}_{p_c}$ and $\mathbf {A}_{q_c}$ are constructed with the columns of matrices yielded from the numerical integration of Eqs. (20) and (21).

The electric charge on every contact node i can be expressed in terms of the electric potential according to the electrical contact condition (4), as: $({\mathbf {q}_{c}})_{i} = -\tilde{\kappa }((\varDelta \mathbf {u}_{\nu })_{i})(\varDelta \varvec{\varphi }_{c})_{i}$. So equation (22) can be written as

$$\begin{aligned} \left[ \begin{array}{cccc} \mathbf {A}_{\mathrm {x}_e}&\mathbf {A}_{\varDelta u_c}&\tilde{\mathbf {A}}_{\varDelta \varphi _c}&\mathbf {A}_{p_c}\end{array}\right] \left\{ \begin{array}{c} \mathbf {x}_{e} \\ \varDelta \mathbf {u}_{c} \\ \varDelta \varvec{\varphi }_{c}\\ \mathbf {p}_{c} \end{array}\right\} = {\mathbf {F}}, \end{aligned}$$

(23)

being $\tilde{\mathbf {A}}_{\varDelta \varphi _c} = \mathbf {A}_{\varDelta \varphi _c} - {\tilde{\varvec{\kappa }}}(\varDelta \mathbf {u}_{\nu })\mathbf {A}_{q_c}$ and ${\tilde{\varvec{\kappa }}}(\varDelta \mathbf {u}_{\nu })$ a diagonal matrix, i.e.:

$$\begin{aligned} {\tilde{\varvec{\kappa }}}(\varDelta \mathbf {u}_{\nu })=diag \left( ~\tilde{\kappa }(({\varDelta \mathbf {u}_{\nu }})_{1}),\ldots ,\tilde{\kappa }(({\varDelta \mathbf {u}_{\nu }})_{i}),\ldots ,\tilde{\kappa }(({\varDelta \mathbf {u}_{\nu }})_{N_c})~\right) .\nonumber \\ \end{aligned}$$

(24)

Finally, the mechanical contact restrictions (7) and (9) are defined on every contact node i as:

$$\begin{aligned} ({\mathbf {p}_{\nu }})_{i} - \mathbb {P}_{\mathbb {R}_{+}}(~(\mathbf {p}_{\nu })_i - r_{\nu }(\varDelta \mathbf {u}_{\nu })_i~)=0, \end{aligned}$$

(25)

$$\begin{aligned} ({\mathbf {p}_{\tau }})_{i} - \mathbb {P}_{\mathbb {E}_{\rho }}(~(\mathbf {p}_{\tau })_i- r_{\tau }(\varDelta \mathbf {u}_{\tau })_i~)= 0, \end{aligned}$$

(26)

where $\mathbf {p}_{\nu }$ and $\mathbf {p}_{\tau }$ contain the normal and tangential contact tractions of every contact node i and $\varDelta \mathbf {u}_{\nu }$ and $\varDelta \mathbf {u}_{\tau }$ contain the normal and tangential nodal crack opening displacements, respectively.

7 Solution method

The nonlinear equations set (23–26) can be solved using different solution schemes according to [42, 43]. In this work, the system (23–26) will be solved using the Uzawa’s method. This iterative solution scheme is presented in [42, 44,45,46] and more recently in [47,48,49], for contact and wear problems, and in [34, 36], for multifield PE materials in contact.

To compute the variables on load step (k), $\mathbf {z}^{(k)}=(\mathbf {x}_{e}^{(k)},\varDelta \mathbf {u}_c^{(k)}, \varDelta \varvec{\varphi }_{c}^{(k)},\mathbf {p}_c^{(k)})$, when the variables on previous instant $\mathbf {z}^{(k-1)}$ are known:

• (I) Initialize $\mathbf {z}^{(0)}=\mathbf {z}^{(k-1)}$ and iterate using (n) index.

• (II) Solve:

  $$\begin{aligned}&\left[ \begin{array}{ccc} \mathbf {A}_{\mathrm {x}_e}&\mathbf {A}_{u_c}&(\mathbf {A}_{\varphi _c} - {\tilde{\varvec{\kappa }}}(\mathbf {p}_{\nu }^{(n)})\mathbf {A}_{q_c}) \end{array}\right] \left\{ \begin{array}{c} \mathbf {x}_{e} \\ \varDelta \mathbf {u}_{c} \\ \varDelta \varvec{\varphi }_c \end{array}\right\} ^{(n+1)}\nonumber \\&\quad = -\mathbf {A}_{p_c}~\mathbf {p}_c^{(n)} + \widetilde{\mathbf {F}}, \end{aligned}$$

  (27)

  where $\widetilde{\mathbf {F}}= \mathbf {F} - ({\tilde{\varvec{\kappa }}}^{(n)}/\varDelta \varvec{\varPhi }^{(n)}) \mathbf {A}_{q_c}$, ${\tilde{\varvec{\kappa }}}^{(n)}$ is a diagonal matrix that depends on the contact status of every contact node and $\varDelta \varvec{\varPhi }^{(n)}$ is a diagonal matrix defined as: $\varDelta \varvec{\varPhi }^{(n)}=diag ((\varDelta \varvec{\varphi }_c^{(n)})_{1},\ldots ,(\varDelta \varvec{\varphi }_c^{(n)})_{i},\ldots ,(\varDelta \varvec{\varphi }_c^{(n)})_{N_c})$.

• (III) Update contact tractions and contact status for every contact node i:

  $$\begin{aligned} (\mathbf {p}_{\nu }^{(n+1)})_{i}= & {} \mathbb {P}_{\mathbb {R}_{-}} \left( (\mathbf {p}_{\nu }^{(n)})_{i} + r_{\nu }(\varDelta \mathbf {u}_{\nu }^{(n+1)})_{i}\right) , \end{aligned}$$

  (28)
  $$\begin{aligned} (\mathbf {p}_{\tau }^{(n+1)})_{i}= & {} \mathbb {P}_{\mathbb {E}_{\rho }} \left( (\mathbf {p}_{\tau }^{(n)})_{i} - r_{\tau }~(\varDelta \mathbf {u}_{\tau }^{(n+1)})_{i}\right) , \end{aligned}$$

  (29)

  where $\rho =\mu |(\mathbf {p}_{\nu }^{(n+1)})_{i}|$. So if $(\mathbf {p}_{\nu }^{(n+1)})_{i}<0$, node i is assumed to be in contact.

• (IV) Update diagonal matrix ${\tilde{\varvec{\kappa }}}^{(n+1)}$ as a function of the contact status computed in previous step.

• (V) Compute the error $\varPsi (\mathbf {z}^{(n+1)})=max\{ \Vert \varDelta \mathbf {u}_c^{(n+1)}-\varDelta \mathbf {u}_c^{(n)}\Vert$, $\Vert \varvec{\varDelta }\varvec{\varphi }_{c}^{(n+1)}-\varDelta \varvec{\varphi }_{c}^{(n)}\Vert$, $\Vert \mathbf {p}_c^{(n+1)}-\mathbf {p}_c^{(n)}\Vert \}$.

  • (a) If $\varPsi (\mathbf {z}^{(n+1)}) \le \varepsilon$, the solution for the instant (k) is reached, so $\mathbf {z}^{(k)}=\mathbf {z}^{(n+1)}$.

  • (b) Otherwise, return to (II) evaluating: $\mathbf {p}_c^{(n)} = \mathbf {p}_c^{(n+1)}$ and $\varvec{\kappa }^{(n)}=\varvec{\kappa }^{(n+1)}$.

After the solution at step (k) is reached, the solution for the next step is achieved by setting: $\mathbf {z}^{(0)}=\mathbf {z}^{(k)}$ and returning to (I).

8 Numerical examples

The previously sketched formulation offers a suitable framework to study the influence of crack face frictional contact and nonlinear electric boundary conditions on fracture response of piezoelectric materials. In order to validate the formulation and to understand the influences of these factors, several benchmark problems have been studied.

8.1 Crack in unbounded domain

The first example corresponds to a finite straight crack along the $x_1$-direction in an infinite PZT-4 plane under a uniform far field stress or electric displacement (see Fig. 2). This example allows us to check the formulation under nonlinear electrical crack face boundary conditions. The material constants are shown in Table 1, the axis of symmetry of the material being the $x_2$-axis. Moreover, to mesh the crack, five quadratic elements are considered, crack tip elements being discontinuous quarter-point elements.

Fig. 2

Crack in an infinite domain under far field uniform stress ($\sigma _{22}$) and electric displacements ($D_2$)

Table 1 Material properties of PZT-4, from [20]

The obtained crack opening displacements in normal direction and electric potential increment along the crack due to an uniform electric displacements loading: $D_2=1 C/m^2$ are shown in Fig. 3a, b, respectively. Results in Fig. 3 are presented in a non-dimensional form, $\varDelta u_{\nu ,o}$ and $\varDelta \varphi _o$ being the crack opening displacements and the electric potential increment, respectively, obtained in [30] for impermeable crack-face electric boundary conditions . It can observed how the permittivity parameter $\kappa _c$ clearly affects the crack opening displacements and the electric potential increment along the crack. Moreover, the results are compared with the known exact analytical solution obtained by [30] for ideal crack-face electric boundary conditions (i.e., impermeable and permeable conditions), showing an excellent agreement. The extended crack opening displacement components $\varDelta u_{I}$ for the ideal crack-face electric boundary conditions can be written as

$$\begin{aligned} \varDelta u_{I} = 2\mathbf {Y}_{IJ}\left( \sigma _{J2}^{\infty } - \sigma _{J2}^{c}\right) \sqrt{a^2 - x_1^2}, \end{aligned}$$

(30)

where $\sigma _{J2}^{\infty }$ are the applied extended stresses, $\sigma _{J2}^{c}$ are the extended stresses on the crack surfaces and $\mathbf {Y}$ is the compliance (Irwin) matrix, as defined in [23]. In the expression above, the repeated indexes implies summation.

Fig. 3

Influence of the permittivity parameter $\kappa _c$ on: a the crack opening displacements and b the electric potential increment along the crack due to an uniform electric displacements loading: $D_2=1\,{\mathrm{C/m}}^2$

Same conclusions were observed in Fig. 4 for an uniform traction loading: $\sigma _{22}=1$ GPa, where it may be observed a perfect agreement between the numerical and the analytical solutions for impermeable and permeable crack-face electric boundary conditions. The increase of $\varDelta u_{\nu }$ caused by the increase of the $\kappa _c$ value in Fig. 4a is due to the fact that both the mechanical and the electrical fields are fully coupled, as it may be observed in the compliance (Irwin) matrix.

Fig. 4

Influence of the permittivity parameter $\kappa _c$ on: a the crack opening displacements and b the electric potential increment along the crack for uniform traction loading: $\sigma _{22}=1\,$GPa

To illustrate the convergence of the proposed solution scheme under nonlinear crack-face electrical boundary conditions, convergence studies have been included for the case of a Griffith crack in a piezoelectric material. Figure 5 shows the relative error evolution ($\varPsi (\mathbf {z}^{(n)})/\varPsi (\mathbf {z}^{(o)})$) with the number of iterations for several meshes and different values of the permittivity parameter ($\kappa _c$). Results reveal that the proposed methodology is robust and accurate. While the number of iterations is hardly affected by the number of elements used to mesh the crack, it is however significantly affected by the severity of the nonlinear crack-face electrical boundary conditions: a low number of iterations have been observed for fully permeable or fully impermeable electrical conditions, whereas a greater number of iterations are required for convergence when semipermeable conditions hold on the crack-faces.

Fig. 5

Error evolution for several meshes and different values of the permittivity parameter ($\kappa _c$)

The influence of the permittivity parameter $\kappa _c$ on extended stress intensity factors: $K_{I}$, $K_{II}$ and $K_{IV}$, for the uniform electric displacements loading is presented in Fig. 6. According to [23, 50], those extended stress intensity factors are determined from the nodal values from the extended crack opening displacements across the crack, as

$$\begin{aligned} \left( \begin{array}{c} K_{II} \\ K_{I} \\ K_{IV} \end{array}\right) = \sqrt{\frac{\pi }{8\bar{r}}}\mathbf {Y}^{-1} \left( \begin{array}{c} \varDelta u_{1} \\ \varDelta u_{2} \\ \varDelta \varphi \end{array}\right) , \end{aligned}$$

(31)

where, in this case, the $\bar{r}$ is the distance between the crack tip and the extreme node of the quarter-point elements and $K_{IV}$ denotes the electric displacement intensity factor.

Finally, results in Fig. 6 correspond to the crack subjected to an uniform remote electric displacements loading and depicts the intensity factors. Consequently, when the permittivity parameter $\kappa _c$ increases, i.e., when perfect permeable crack-face boundary conditions are considered, the extended stress intensity factors tend to zero.

Fig. 6

Influence of the permittivity parameter $\kappa _c$ on the intensity factors $K_{I}$, $K_{II}$ and $K_{IV}$ for the uniform electric displacements loading $D_2=1\,\mathrm{C/m}^2$

8.2 Inclined crack under compression

In order to validate this crack surface frictional contact formulation, another benchmark problem is solved. In this example, the formulation is applied for a mathematical degenerate case, i.e., elastic and isotropic material. Figure 7 shows a single crack of length 2a in an unbounded domain and subjected to a compressive remote stress $\sigma$ (i.e., $\sigma _{11}=-\sigma$). The analytical solution of this plane strain state is available in [4] for comparison. The mode-I stress intensity factor (SIF) $K_I=0$, as the crack surfaces remain closed under compression. However, the analytical solution for the mode-II SIF is

$$\begin{aligned} K_{II} = \sigma \sqrt{\pi a} \sin \alpha (\cos \alpha - \mu \sin \alpha ) \end{aligned}$$

(32)

where $\mu$ can be written as a function of the friction angle ($\phi$): $\mu =tan(\phi )$.

Fig. 7

A crack under compression in an unbounded domain

The material constants employed are: Young’s modulus $E= 70$GPa and Poisson’s ratio $\nu =0.2$. Results are presented in Fig. 8, where the normalized $K_{II}$ ($K_{II}/\sigma \sqrt{\pi a}$) is showed for various inclination angles ($\alpha$) of the crack and different friction angles ($\phi ={0^{\circ }, 15^{\circ }, 30^{\circ }, 45^{\circ }}$). An excellent agreement between analytical and numerical solutions can be observed. In this example, nonlinear crack-face mechanical boundary conditions (i.e. frictional contact) are considered for electroelastic problems. The convergence ratios observed for the Uzawa scheme in these examples are analogous to the ratios observed in [49] for frictional contact problems using the BEM in elastic problems.

Fig. 8

Numerical results vs. analytical solutions for normalized $K_{II}$ ($K_{II}/\sigma \sqrt{\pi a}$) for various inclination angles ($\alpha$) and different friction angles ($\phi$)

After validating the frictional contact methodology, this formulation is now applied for a piezoelectric material whose properties are presented in Table 1. In order to study only the influence of frictional contact conditions on cracked piezoelectric materials, Sects. 8.2 and 8.3 show two benchmark problems presented in the literature, where impermeable crack face boundary conditions (i.e., $\kappa _c=0$) are considered. Figure 9 shows the normalized stress ($K_{I}$, $K_{II}$) and electric ($K_{IV}$) intensity factors at the tip of the crack due to remote tension for different crack orientation angles ($\alpha$) and different friction angles ($\phi$). The extended stress intensity factors (ESIF), i.e., $K_{I}$, $K_{II}$ and $K_{IV}$, were computed according to (31). Due to the mechanical and electrical fully coupled compliance (Irwing) matrix, the crack-face tangential slip ($\varDelta u_{\tau }$) causes not null ESIFs values. The ESIFs in Fig. 9 show the same behavior that has been observed in Fig. 7: when the crack angle ($\alpha$) is equal or greater than the friction angle ($\phi$), i.e., $\alpha \ge \phi$, the crack-face is subject to stick conditions. So the values of the ESIFs become null. Results show again the enormous influence of friction on the stress and electric intensity factors and, consequently, on the integrity of these systems. Therefore, modeling friction is mandatory in order to obtain valid results.

Fig. 9

Normalized stress ($K_{I}$, $K_{II}$) and electric ($K_{IV}$) intensity factors at the tip of the crack due to remote tension for different crack orientation angles ($\alpha$) and different friction angles ($\phi$)

8.3 Branched crack

This example considers a branched crack in an unbounded plane, whose geometry is shown in Fig. 10. The material is PZT-4 and the material constants are given in Table 2. The axis of symmetry of the material is the $x_2$-axis and the main crack is along the $x_1$-axis with a branch with an angle $\theta$ initiating from one of the crack tips. Five quadratic elements are considered to mesh the main crack. Two equal length elements are used for the branch when its length is $b = a/10$ and nine elements when $b = a/2$. Crack tip elements are discontinuous quarter-point. The crack is under a uniform far field stress along the y-axis and the ESIF are evaluated in accordance to Eq. (31).

Fig. 10

A branched crack under uniform traction in an unbounded domain

Table 2 Material properties of PZT-4, from [21]

Crack branching is a common phenomenon in the fracture of brittle materials. However, the multifield coupling makes crack branching more complex for piezoelectric materials than for elastic materials. One of the pioneering works that studied this problem was published by Xu and Rajapakse [21]. They presented a theoretical framework which made it possible to study crack branching on piezoelectric materials. For instance, they presented the values of the ESIF versus the branch angle $\theta$ for different lengths of the branch when an uniform traction along the $x_2$-axis was applied. However, in those cases, no frictional contact conditions were considered on the crack faces. So, crack faces interpenetration were observed for some values of $\theta$ and consequently, over-or-under estimated values of the ESIFs were computed.

Figure 11 shows the normalized stress intensity factors $K_{I}$ at the tip of a branched crack due to remote tension. A comparison between the boundary element solution including frictionless contact and the analytical solution from [21] for different branched crack orientation angles ($\theta$) and branch lengths (b) is considered. We can observe negative values of $K_{I}$ on [21] when $\theta$ is greater than certain value (i.e., $\theta >90^{\circ }$ for $b = a/10$ and $\theta >80^{\circ }$ for $b = a/2$). Nevertheless, $K_{I}$ tends to zero for those branch angles when contact is considered. So crack closure is observed when $\theta >100^{\circ }$ for $b = a/10$ and $\theta >90^{\circ }$ for $b = a/2$.

Fig. 11

Normalized stress intensity factors $K_{I}$ at the tip of a branched crack due to remote tension: $K_{I}^b/K_{o}$, being $K_{o}=\sigma \sqrt{\pi a}$. Comparison between the boundary element solution including frictionless ($\mu =0$) contact and the analytical solution from [21] for different branched crack orientation angles ($\theta$) and branch lengths (b)

Fig. 12

Influence of frictional contact on the normalized stress ($K_{I}$, $K_{II}$) and electric ($K_{IV}$) intensity factors at the tip of a branched crack due to remote tension for different branched crack orientation angles ($\theta$), i.e. $K_{I}^b/K_{o}$, $K_{II}^b/K_{o}$ and $K_{IV}^b/K_{o}$, being $K_{o}=\sigma \sqrt{\pi a}$

Fig. 13

Curved crack in unbounded domain

Next, the influence of frictional contact on the ESIFs is studied in detail for a branch length $b = a/2$. Figure 12 presents the normalized stress ($K_{I}$, $K_{II}$) and electric ($K_{IV}$) intensity factors at the tip of a branched crack due to remote tension for different branch orientation angles and different friction angles ($\phi ={0^{\circ }, 15^{\circ }, 30^{\circ }, 45^{\circ }}$). Figure 12a shows the normalized stress intensity factor $K_{I}$ at the tip of a branched crack. As we would expect, friction does not affect $K_{I}$, only $\theta$ and the normal contact constraints. However, $K_{II}$ and $K_{IV}$ are clearly affected not only by the normal contact constraints, but also by friction. Figure 12b shows how the normalized stress intensity factors $K_{II}$ is affected by crack closure on the branch when $\theta >90^{\circ }$. Moreover, significant reduction on $K_{II}$ can be observed as the friction coefficient increases when compared to [21]. Same situation is presented on Fig. 12c for the electric intensity factors $K_{IV}$. However, in this case, the effect of contact is significantly stronger, i.e., a non-smooth peak on $K_{IV}$ is observed for the crack branching closure around $\theta \approx 90^{\circ }$. This is due to the combined effect of crack closure (i.e. crack-face contact) and the impermeable electrical crack-face boundary conditions (i.e. $\kappa _c=0$). Once again, the influence of friction and the need to incorporate this phenomenon in the model is clear from Fig. 12b, c.

Fig. 14

Influence of frictional contact on the normalized stress ($K_{I}$, $K_{II}$) and electric ($K_{IV}$) intensity factors at the tip of a curved crack due to remote tension for different curved crack angles ($\theta$)

8.4 Curved crack in unbounded domain

Finally, to show the use of the current procedure for curved crack geometries, this section presents a curved crack in an unbounded domain (see Fig. 13), where crack-face frictional contact conditions are considered. The crack region is under a uniform far field stress ($\sigma _{22}=1$ GPa) along the material and crack axis of symmetry. The material properties are the same as in the previous example and they were presented in Table 2. Several cracks for elastic stress loading are analyzed, with semi-angles $\theta$ between 0 and 120 degrees.

The computed values of the normalized ESIFs $K_{I}$, $K_{II}$ and $K_{IV}$ are shown versus $\theta$ in Fig. 14. Similarly to [23], the ratio $\chi$ between the dielectric constant $\epsilon _{22}$ and the piezoelectric constant $e_{22}$ has been used to represent a dimensionless value of $K_{IV}$. Computed values of $K_{I}$ and $K_{II}$ are shown in Fig. 14a, b, respectively, whereas the obtained values of $K_{IV}$ are shown in Fig. 14c. These results show the great influence that crack curvature has on the ESIFs. It may be observed that large values of $\theta$ ($\theta \ge 90^{\circ }$) imply crack closure. Moreover, Fig. 14b shows a significant reduction on $K_{II}$ when the friction coefficient increases. As we mentioned in the previous example, the electric intensity factor $K_{IV}$ presents a non-smooth peak due to the crack closure around $\theta \approx \,90^{\circ }$.

9 Conclusions

A dual boundary element formulation has been presented and further applied to study fracture phenomena in PE materials. The formulation avoids unrealistic assumptions usually considered for the boundary conditions on the crack surfaces. In particular, it accounts for both surface frictional contact between crack faces and electrically semipermeable boundary conditions. The accuracy and validity of the proposed formulation have been verified by comparison of the obtained numerical results against some classical benchmark problems, exhibiting an excellent agreement with the analytical solution available in the literature. The numerical examples presented reveal the key importance of including friction in the model in order to accurately compute the stress and electric intensity factors in situations where crack closure occurs. Finally, we would like to emphasize that, although the paper contains only examples for crack problems in infinite domains, the boundary element formulation is also valid for bounded domains.