An efficient boundary collocation scheme for transient thermal analysis in large-size-ratio functionally graded materials under heat source load

Abstract

This paper presents a boundary collocation scheme for transient thermal analysis in large-size-ratio functionally graded materials (FGMs) with heat source load. In the proposed scheme, Laplace transformation and the numerical inverse Laplace transformation (NILT) are implemented to avoid the troublesome time-stepping effect on numerical efficiency. The collocation Trefftz method (CTM) coupled with composite multiple reciprocity method is used to obtain the high accurate results in the solution of nonhomogeneous problems in Laplace-space domain. The extended precision arithmetic is introduced to overcome the ill-posed issues generated from the CTM simulation, the NILT process and the large-size-ratio FGM. Heuristic error analysis and numerical investigation are presented to demonstrate the effectiveness of the proposed scheme for transient thermal analysis. Several benchmark examples are considered under large-size-ratio FGMs with some specific spatial variations (quadratic, exponential and trigonometric functions). The proposed scheme is validated in comparison with known analytical solutions and COMSOL simulation.

1 Introduction

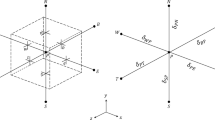
Owing to their excellent thermal properties, functionally graded materials (FGMs) [1,2,3] have been widely used in the high temperature environments such as aerospace, oil exploration, power generation and so on. With ever-increasing demand on engineering structure performances, great attentions have been focused on thermal analysis of large-size-ratio FGM structures, such as large-aspect-ratio FGMs (3D cuboid) and the FGMs consisting of the size-disparity components (airplane) as shown in Fig. 1.

Fig. 1

Typical examples on large-size-ratio FGM structures

For transient thermal analysis [4,5,6], several temporal discretization schemes and spatial discretization schemes can be selected. The most popular temporal discretization schemes are the time-stepping method [7,8,9], Laplace transformation technique [10, 11], the spectral collocation methods [12] and convolution quadrature method [13,14,15]. The spatial discretization schemes mainly include finite difference method [16, 17], finite element method (FEM) [18,19,20], boundary element method (BEM) [21,22,23], singular boundary method [24,25,26], weak-form meshless methods [27,28,29,30,31] and strong-form meshless methods [32,33,34,35,36] and so on. Any combination of these two discretization schemes can constitute a class of methods for simulating the transient thermal behavior under FGMs.

However, the accurate and efficient analysis of transient thermal problems exhibiting large-size-ratio FGM structures or the structures including sharp thermal gradients is currently an open issue of research in computational mechanics community. Very few studies have been reported on this topic. Recently, O’Hara et al. [37] proposed an advanced FEM with global–local enrichment functions and multi-scale scheme to analyze the transient thermal behavior under the structures including sharp thermal gradients. Some researchers introduced transformation technique or element-subdivision method into the BEM for simulating the thermal behavior under slender structures [38,39,40]. The authors proposed Laplace-transform boundary knot method in conjunction with extended precision arithmetic (EPA) [41, 42] for solving the transient thermal problems under slender FGMs with exponential variations [43]. It should be mentioned that the aforementioned first two schemes require the modification of the core algorithm to thermal simulation under large-size-ratio FGMs. The third scheme with the EPA is free for the modification of the core algorithm. However, it is restricted to the slender exponential FGMs without heat source loading.

In this study, a Trefftz-based collocation scheme [44, 45] is presented to transient thermal analysis in large-size-ratio FGMs with some specific spatial variations (quadratic, exponential and trigonometric functions [46, 47]) under heat source loading [48]. In the present scheme, it implements Laplace transformation technique to obtain series of the corresponding time-independent nonhomogeneous problems in Laplace-space domain. And then it employs the collocation Trefftz scheme in conjunction with composite multiple reciprocity technique [49, 50] to solve these Laplace-transformed nonhomogeneous problems with boundary-only collocation. Finally, the Fixed Talbot numerical inverse Laplace transform (NILT) [51] is implemented to retrieve the time-dependent numerical solutions of transient thermal conduction equations from the corresponding Laplace-domain solutions. Moreover, the extended precision arithmetic is introduced to alleviate the effect of the ill-posed issues generated from the CTM simulation, the NILT process and the large-size-ratio FGM.

A brief outline of the paper is as follows. In Sect. 2, the collocation scheme including the collocation Trefftz method in conjunction with composite multiple reciprocity method, Laplace transformation and the extended precision arithmetic (EPA) is introduced, and the heuristic error analysis of the proposed collocation scheme is presented. Section 3 investigates the numerical efficiency of the proposed approaches through several typical benchmark examples. Finally, some conclusions are presented in Sect. 4.

2 Methodology

2.1 Mathematical model

Consider transient thermal conduction problems in functionally graded materials under heat source load. The governing equation is stated as

$$ \nabla \cdot \left[ {{\mathbf{K}}\left( {\mathbf{x}} \right)\nabla u\left( {{\mathbf{x}},t} \right)} \right] + Q\left( {{\mathbf{x}},t} \right) = \rho \left( {\mathbf{x}} \right)c\left( {\mathbf{x}} \right)\frac{{\partial u\left( {{\mathbf{x}},t} \right)}}{\partial t},\quad {\mathbf{x}} \in\Omega $$

(1)

with the boundary and initial conditions:

Dirichlet/Essential condition

$$ u\left( {{\mathbf{x}},t} \right) = g_{1} \left( {{\mathbf{x}},t} \right),\quad {\mathbf{x}} \in \Gamma_{D} $$

(2a)

Neumann/Natural condition

$$ q({\mathbf{x}},t) = - {\mathbf{K}}\nabla u({\mathbf{x}},t) \cdot {\mathbf{n}} = g_{2} \left( {{\mathbf{x}},t} \right),\quad {\mathbf{x}} \in \Gamma_{N} $$

(2b)

Initial condition

$$ u({\mathbf{x}},0) = u_{0} ({\mathbf{x}}),\quad {\mathbf{x}} \in \Omega $$

(2c)

where $\Omega \subset \Re^{d}$ represents a large-size-ratio domain bounded by its boundary Γ, d is the dimension of the computational domain, $u\left( {{\mathbf{x}},t} \right)$ is the temperature on the coordinate x at time instant t, $\Gamma = \Gamma_{D} \cup \Gamma_{N}$,${\mathbf{n}} = \left\{ {n_{i} } \right\}$ represents the outward unit normal vector at boundary ${\mathbf{x}} \in \Gamma$, $g_{1} \left( {{\mathbf{x}},t} \right)$, $g_{2} \left( {{\mathbf{x}},t} \right)$ and $u_{0} ({\mathbf{x}})$ are known functions. ${\mathbf{K}} = \left\{ {K_{ij} \left( {\mathbf{x}} \right)} \right\}_{1 \le i,j \le d}$,$\rho \left( {\mathbf{x}} \right)$ and $c\left( {\mathbf{x}} \right)$ denote the thermal conductivity matrix, the mass density and the specific heat, respectively.

In this study, we assume that the thermal conductivity and the product of mass density and specific heat are, respectively, expressed by

$$ K_{ij} \left( {\mathbf{x}} \right) = k_{ij} f\left( {\mathbf{x}} \right),\quad {\mathbf{x}} \in \Omega ,\quad 1 \le i,\quad j \le d $$

(3)

$$ \rho \left( {\mathbf{x}} \right)c\left( {\mathbf{x}} \right) = \rho_{0} c_{0} f\left( {\mathbf{x}} \right),\quad {\mathbf{x}} \in \Omega $$

(4)

in which ${\mathbf{k}} = \left\{ {k_{ij} } \right\}_{1 \le i,j \le d}$ ($\Delta_{{\mathbf{k}}} = \det \left( {\mathbf{k}} \right) > 0$ and $k_{ij} = k_{ji}$), $k_{ij} ,\rho_{0} ,c_{0}$ are all real constants, and $f\left( {\mathbf{x}} \right)$ is the function of coordinates.

By employing the following variable transformation

$$ v\left( {{\mathbf{x}},t} \right) = \sqrt {f\left( {\mathbf{x}} \right)} u\left( {{\mathbf{x}},t} \right) $$

(5)

Equations (1)–(2) can be rewritten as

$$ \nabla \cdot \left[ {{\mathbf{k}}\nabla v\left( {{\mathbf{x}},t} \right)} \right] + \eta v\left( {{\mathbf{x}},t} \right) + \frac{{Q\left( {{\mathbf{x}},t} \right)}}{{\sqrt {f\left( {\mathbf{x}} \right)} }} = \rho_{0} c_{0} \frac{{\partial v\left( {{\mathbf{x}},t} \right)}}{\partial t} $$

(6)

$$ v\left( {{\mathbf{x}},t} \right) = \sqrt {f\left( {\mathbf{x}} \right)} g_{1} \left( {{\mathbf{x}},t} \right),\quad {\mathbf{x}} \in \Gamma_{D} $$

(7a)

$$ - {\mathbf{k}}\left[ {\sqrt {f\left( {\mathbf{x}} \right)} \nabla v({\mathbf{x}},t) - v({\mathbf{x}},t)\nabla \left( {\sqrt {f\left( {\mathbf{x}} \right)} } \right)} \right] \cdot {\mathbf{n}} = g_{2} \left( {{\mathbf{x}},t} \right),\quad {\mathbf{x}} \in \Gamma_{N} $$

(7b)

$$ v({\mathbf{x}},0) = \sqrt {f\left( {\mathbf{x}} \right)} u_{0} ({\mathbf{x}}),\quad {\mathbf{x}} \in \Omega $$

(7c)

where

$$ \eta = \sum\limits_{i,j = 1}^{d} {k_{ij} } \left( {\frac{{\frac{{\partial f\left( {\mathbf{x}} \right)}}{{\partial x_{i} }}\frac{{\partial f\left( {\mathbf{x}} \right)}}{{\partial x_{j} }}}}{{\left( {2f\left( {\mathbf{x}} \right)} \right)^{2} }} - \frac{{\frac{{\partial^{2} f\left( {\mathbf{x}} \right)}}{{\partial x_{i} \partial x_{j} }}}}{{2f\left( {\mathbf{x}} \right)}}} \right) $$

(8)

Actually, the parameter $\eta$ in Eq. (8) can be simplified with the following special forms of $f\left( {\mathbf{x}} \right)$:

• (i) Quadratic function $f\left( {\mathbf{x}} \right) = \left( {b_{0} + \sum\nolimits_{i = 1}^{d} {b_{i} x_{i} } } \right)^{2}$ with arbitrary constants $b_{0} ,b_{1} \ldots ,b_{d}$, then $\eta = 0$ can be determined according to Eq. (8).

• (ii) Exponential function $f\left( {\mathbf{x}} \right) = c_{1} e^{{\sum\nolimits_{i = 1}^{d} {2\varsigma_{i} x_{i} } }}$ with arbitrary constants $\varsigma_{i} \left( {i = 1,2, \ldots ,d} \right)$, $c_{1}$, then $\eta = - \sum\nolimits_{i = 1}^{d} {\sum\nolimits_{j = 1}^{d} {\varsigma_{i} } } k_{ij} \varsigma_{j}$ can be determined according to Eq. (8)

• (iii) Trigonometric function $f( {\mathbf{x}} ) = \prod\nolimits_{i = 1}^{d} (d_{i} \cos (\beta_{i} x_{i} )+ e_{i} \sin (\beta_{i} x_{i}) )^{2}$ with arbitrary constants $d_{i} ,e_{i} ,\beta_{i} \left( {i = 1,2, \ldots ,d} \right)$, then $\eta = \sum\nolimits_{i = 1}^{d} {k_{ii} \beta_{i}^{2} }$ can be determined according to Eq. (8) when $k_{ij} = 0\left( {i \ne j} \right)$.

2.2 Implementation procedure

For solving the transformed Eqs. (6)–(7), the following roadmap is implemented as shown in Fig. 2.

Fig. 2

Roadmaps of the boundary collocation scheme for the problems (6)–(7)

(a) Laplace transformation

Let Laplace transformation (LT) of $v\left( {{\mathbf{x}},t} \right)$ be defined as

$$ L\left( {v({\mathbf{x}},t)} \right) = \tilde{v}({\mathbf{x}},\varepsilon ) = \int\limits_{0}^{\infty } {v({\mathbf{x}},t)e^{ - \varepsilon t} dt} $$

(9)

By using Laplace transformation, the transient thermal problems (6)–(7) can be converted from time domain to Laplace-space domain as follows

$$ \nabla \cdot \left[ {{\mathbf{k}}\nabla \tilde{v}\left( {{\mathbf{x}},\varepsilon } \right)} \right] + \left( {\eta - \rho_{0} c_{0} \varepsilon } \right)\tilde{v}\left( {{\mathbf{x}},\varepsilon } \right) = - \rho_{0} c_{0} v\left( {{\mathbf{x}},0} \right) - \frac{{\tilde{Q}\left( {{\mathbf{x}},\varepsilon } \right)}}{{\sqrt {f\left( {\mathbf{x}} \right)} }} $$

(10)

$$ \tilde{v}\left( {{\mathbf{x}},\varepsilon } \right) = \sqrt {f\left( {\mathbf{x}} \right)} \tilde{g}_{1} \left( {{\mathbf{x}},\varepsilon } \right),\quad {\mathbf{x}} = \left( {x_{1} ,x_{2} } \right) \in \Gamma_{D} $$

(11a)

$$ - {\mathbf{k}}\left[ {\sqrt {f\left( {\mathbf{x}} \right)} \nabla \tilde{v}\left( {{\mathbf{x}},\varepsilon } \right) - \tilde{v}\left( {{\mathbf{x}},\varepsilon } \right)\nabla \left( {\sqrt {f\left( {\mathbf{x}} \right)} } \right)} \right] \cdot {\mathbf{n}} = \tilde{g}_{2} \left( {{\mathbf{x}},\varepsilon } \right),\quad {\mathbf{x}} = \left( {x_{1} ,x_{2} } \right) \in \Gamma_{N} $$

(11b)

(b) Boundary collocation technique

To simplify the time-independent nonhomogeneous problems (10)–(11), the domain mapping method (DMM) is introduced. By using the transformation

$$ \left\{ \begin{array}{l} \left( {\begin{array}{*{20}l} {y_{1} } \\ {y_{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {{1 \mathord{\left/ {\vphantom {1 {\sqrt {k_{11} } }}} \right. \kern-0pt} {\sqrt {k_{11} } }}} & 0 \\ {{{ - k_{12} } \mathord{\left/ {\vphantom {{ - k_{12} } {\sqrt {k_{11} \Delta_{k} } }}} \right. \kern-0pt} {\sqrt {k_{11} \Delta_{k} } }}} & {{{\sqrt {k_{11} } } \mathord{\left/ {\vphantom {{\sqrt {k_{11} } } {\sqrt {\Delta_{k} } }}} \right. \kern-0pt} {\sqrt {\Delta_{k} } }}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right),\quad d = 2 \hfill \\ \left( {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ {y_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 {\sqrt {k_{11} } }}} \right. \kern-0pt} {\sqrt {k_{11} } }}} & 0 & 0 \\ {{{ - k_{12} } \mathord{\left/ {\vphantom {{ - k_{12} } {\sqrt {k_{11} \Delta_{k} } }}} \right. \kern-0pt} {\sqrt {k_{11} \Delta_{k} } }}} & {{{\sqrt {k_{11} } } \mathord{\left/ {\vphantom {{\sqrt {k_{11} } } {\sqrt {\Delta_{k} } }}} \right. \kern-0pt} {\sqrt {\Delta_{k} } }}} & 0 \\ {\Upsilon_{1} } & {\Upsilon_{2} } & {\Upsilon_{3} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ \end{array} } \right),\quad d = 3 \hfill \\ \end{array} \right.,\quad {\mathbf{y}} = {\mathbf{k}}^{ - } {\mathbf{x}} $$

(12)

where $\Upsilon _{1} = {{\left( {k_{12} k_{13} - k_{23} k_{11} } \right)\sqrt {k_{11} } } \mathord{\left/ {\vphantom {{\left( {k_{12} k_{13} - k_{23} k_{11} } \right)\sqrt {k_{11} } } {\sqrt {w\Delta_{k} } }}} \right. \kern-0pt} {\sqrt {w\Delta_{k} } }}$, $\Upsilon_{2} = \left( {k_{12} k_{23} - k_{13} k_{22} } \right){{\sqrt {k_{11} } } \mathord{\left/ {\vphantom {{\sqrt {k_{11} } } {\sqrt {w\Delta_{k} } }}} \right. \kern-0pt} {\sqrt {w\Delta_{k} } }}$, $\Upsilon_{3} = {{\sqrt {k_{11} \Delta_{K} } } \mathord{\left/ {\vphantom {{\sqrt {k_{11} \Delta_{K} } } {\sqrt w }}} \right. \kern-0pt} {\sqrt w }}$, $w = k_{11} k_{33} \Delta_{k} - k_{11} k_{22} k_{13}^{2} + 2k_{11} k_{12} k_{13} k_{23} - k_{23}^{2} k_{11}^{2}$. One may rewrite Eqs. (10)–(11) as the following simplified form in the transformed ${\mathbf{y}}$ coordinate system

$$ \Re \tilde{v}\left( {{\mathbf{y}},\varepsilon } \right) = \tilde{W}\left( {{\mathbf{y}},\varepsilon } \right) $$

(13)

$$ \tilde{v}\left( {{\mathbf{y}},\varepsilon } \right) = \sqrt {f\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}}} \right)} \tilde{g}_{1} \left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}},\varepsilon } \right) = D\left( {{\mathbf{y}},\varepsilon } \right),\quad {\mathbf{y}} \in \Gamma_{D} $$

(14a)

$$ \begin{array}{*{20}l} { - {\mathbf{k}}\left[ {\sqrt {f\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}}} \right)} \nabla \widetilde{v}\left( {{\mathbf{y}},\varepsilon } \right) - \widetilde{v}\left( {{\mathbf{y}},\varepsilon } \right)\nabla \left( {\sqrt {f\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}}} \right)} } \right)} \right] \cdot {\mathbf{n}}} \hfill \\ {\quad = \tilde{g}_{2} \left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}},\varepsilon } \right) = E\left( {{\mathbf{y}},\varepsilon } \right)} \hfill \\ \end{array} ,\quad {\mathbf{y}} \in \Gamma_{N} $$

(14b)

where $\tilde{W}\left( {{\mathbf{y}},\varepsilon } \right) = - \rho_{0} c_{0} v\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}},0} \right) - \frac{{\widetilde{Q}\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}},\varepsilon } \right)}}{{\sqrt {f\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}}} \right)} }}$, and $\Re { = }\left( {\Delta + \eta - \rho_{0} c_{0} \varepsilon } \right)$ is a differential operator. If $\eta - \rho_{0} c_{0} \varepsilon > 0$, $\Re$ is Helmholtz operator; if $\eta - \rho_{0} c_{0} \varepsilon = 0$, $\Re$ is Laplace operator; if $\eta - \rho_{0} c_{0} \varepsilon < 0$, $\Re$ is modified Helmholtz operator.

Next the collocation Trefftz method (CTM) in conjunction with composite multiple reciprocity method (CMRM) is implemented to solve simplified time-independent nonhomogeneous problems (13)–(14) via boundary nodes. The corresponding Laplace-domain solution can be expressed as

$$ \tilde{v}\left( {{\mathbf{y}},\varepsilon } \right) = \widetilde{{v_{h} }}\left( {{\mathbf{y}},\varepsilon } \right) + \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) $$

(15)

where $\widetilde{{v_{h} }}\left( {{\mathbf{y}},\varepsilon } \right)$ and $\widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right)$ represent the homogeneous and the particular solution, respectively. If the particular solution $\widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right)$ satisfies

$$ \Re \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) = \tilde{W}\left( {{\mathbf{y}},\varepsilon } \right) $$

(16)

then the homogeneous solution can be solved by the corresponding homogeneous equation

$$ \Re \widetilde{{v_{h} }}\left( {{\mathbf{y}},\varepsilon } \right) = 0 $$

(17)

with the updated boundary conditions

$$ \widetilde{{v_{h} }}\left( {{\mathbf{y}},\varepsilon } \right) = D\left( {{\mathbf{y}},\varepsilon } \right) - \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) $$

(18a)

$$ \begin{aligned} & - {\mathbf{k}}\left[ {\sqrt {f\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}}} \right)} \nabla \widetilde{{v_{h} }}\left( {{\mathbf{y}},\varepsilon } \right) - \widetilde{{v_{h} }}\left( {{\mathbf{y}},\varepsilon } \right)\nabla \left( {\sqrt {f\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}}} \right)} } \right)} \right] \cdot {\mathbf{n}} \\ & \quad = E\left( {{\mathbf{y}},\varepsilon } \right){ + }{\mathbf{k}}\left[ {\sqrt {f\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}}} \right)} \nabla \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) - \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right)\nabla \left( {\sqrt {f\left( {\left( {{\mathbf{k}}^{ - } } \right)^{ - 1} {\mathbf{y}}} \right)} } \right)} \right] \cdot {\mathbf{n}} \\ \end{aligned} $$

(18b)

Let us get back to Eq. (16) for evaluating the particular solution $\widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right)$. In the CMRM, it applies the composite differential operators to both sides of Eq. (16) under the assumption of the smooth-enough functions $\widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right)$ and $\tilde{W}\left( {{\mathbf{y}},\varepsilon } \right)$, and then vanishes nonhomogeneous term $\tilde{W}\left( {{\mathbf{y}},\varepsilon } \right)$ by iterative differentiations

$$ \mathop {\lim }\limits_{m \to \infty } L_{m} \ldots L_{2} L_{1} \left\{ {\tilde{W}\left( {{\mathbf{y}},\varepsilon } \right)} \right\} \to 0, $$

(19)

where L₁, L₂, …L_m are differential operators of the same or different kinds. Under the assumption that the annihilation (19) is finite order or is truncated at certain order M, the representation can be modified as the following higher order homogeneous equation

$$ L_{M} \ldots L_{2} L_{1} \Re \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) \cong 0,\quad {\mathbf{y}} \in \Omega . $$

(20)

To guarantee the uniqueness of the solution, the following constraint conditions are imposed

$$ \left\{ {\begin{array}{*{20}l} {\Re \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) = \tilde{W}\left( {{\mathbf{y}},\varepsilon } \right)} \hfill \\ {L_{1} \Re \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) = L_{1} \tilde{W}\left( {{\mathbf{y}},\varepsilon } \right)} \hfill \\ \vdots \hfill \\ {L_{M - 1} \ldots L_{2} L_{1} \Re \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) = L_{M - 1} \ldots L_{2} L_{1} \tilde{W}\left( {{\mathbf{y}},\varepsilon } \right)} \hfill \\ \end{array} } \right.,\quad {\mathbf{y}} \in \partial \Omega $$

(21)

To solve Eqs. (20)–(21), the particular solution $\widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right)$ can be approximated by a sum of higher order homogeneous solutions,

$$ \widetilde{{v_{p} }}\left( {{\mathbf{y}},\varepsilon } \right) = \sum\limits_{i = 1}^{m} {\widetilde{{v_{h}^{i} }}} $$

(22)

where $\widetilde{{v_{h}^{i} }}$ represents the ith-order composite homogeneous solutions. Then the solution of nonhomogeneous problem (13)–(14) can be represented by $\tilde{v}\left( {{\mathbf{y}},\varepsilon } \right) = \sum\nolimits_{i = 0}^{M} {\widetilde{{v_{h}^{i} }}}$, where $\widetilde{{v_{h}^{0} }} = \widetilde{{v_{h} }}\left( {{\mathbf{y}},\varepsilon } \right)$.

For 2D problems, the ith-order homogeneous solutions $\widetilde{{v_{h}^{i} }}$ can be approximated by a linear combination of ith-order Trefftz functions with unknown coefficients $\left\{ {a_{j}^{i} } \right\}$

$$ \widetilde{{v_{h}^{i} }} = \sum\limits_{j = 1}^{N} {a_{j}^{i} u_{j}^{Ti} \left( {r_{{\mathbf{y}}} ,\theta_{{\mathbf{y}}} } \right)} ,\quad {\mathbf{y}} = \left( {r_{{\mathbf{y}}} \cos \theta_{{\mathbf{y}}} ,r_{{\mathbf{y}}} \sin \theta_{{\mathbf{y}}} } \right) $$

(23)

where N represents the number of boundary collocation nodes, $u_{j}^{Ti}$ denotes jth term of Trefftz function satisfying the ith-order homogeneous Eq. (20), one may find the different types of high-order Trefftz functions in “Appendix”. And the unknown coefficients $\left\{ {a_{j}^{i} } \right\}$ can be determined by imposing the boundary conditions (18) and constraint conditions (21).

For 3D problems, the directional Trefftz functions are constructed by using the following variable transformation $\vartheta : = q_{2} y_{2} + q_{3} y_{3}$, where $q_{2}^{2} + q_{3}^{2} = 1$. And then 3D Cartesian coordinates $\left( {y_{1} ,y_{2} ,y_{3} } \right)$ can be projected into two-dimensional polar coordinates $\left( {r^{*} ,\theta^{*} } \right): = \left( {\sqrt {y_{1}^{2} + \left( {q_{2}^{i} y_{2} + q_{3}^{i} y_{3} } \right)^{2} } ,\arctan \left( {\frac{{q_{2}^{i} y_{2} + q_{3}^{i} y_{3} }}{{y_{1} }}} \right)} \right),i = 1,2, \ldots M_{1}$, where $q_{2}^{i} = \cos \left( {{{2i\pi } \mathord{\left/ {\vphantom {{2i\pi } {M_{1} }}} \right. \kern-0pt} {M_{1} }}} \right),q_{3}^{i} = \sin \left( {{{2i\pi } \mathord{\left/ {\vphantom {{2i\pi } {M_{1} }}} \right. \kern-0pt} {M_{1} }}} \right)$ is a direction in the plane $\left( {y_{2} ,y_{3} } \right)$, and $M_{1}$ denotes the number of directions. Based on this variable transformation, the aforementioned 2D high-order Trefftz functions can be introduced to solve 3D problems.

Therefore, the ith-order homogeneous solutions $\widetilde{{v_{h}^{i} }}$ can be approximated by a linear combination of ith-order directional Trefftz functions with unknown coefficients $\left\{ {a_{j}^{i} } \right\}$

$$ \widetilde{{v_{h}^{i} }} = \sum\limits_{j = 1}^{N} {a_{j}^{i} u_{j}^{Ti} \left( {r^{*} ,\theta^{*} } \right)} , $$

(24)

Similar to 2D problem, the unknown coefficients $\left\{ {a_{j}^{i} } \right\}$ can also be determined by imposing the boundary conditions (18) and constraint conditions (21). After the determination of the coefficients $\left\{ {a_{j}^{i} } \right\}$, Laplace-domain solution $\tilde{v}\left( {{\mathbf{y}},\varepsilon } \right)$ at any point can be evaluated by using Eqs. (23) or (24).

(c) Numerical inverse Laplace transformation

Numerical inverse Laplace transformation (NILT) is implemented to convert the numerical solutions $\widetilde{v}\left( {{\mathbf{y}},\varepsilon } \right)$ in Laplace space domain to the time-dependent solutions $v_{s} \left( {{\mathbf{y}},t} \right)$ in time domain. Here the well-established Fixed Talbot algorithm [51] is implemented, and the approximate value $v\left( {{\mathbf{y}},t} \right)$ for time $t = T$ is given by

$$ v_{s} \left( {{\mathbf{y}},T} \right) = \frac{p}{{N_{FT} }}\left\{ {\frac{1}{2}\tilde{v}\left( {{\mathbf{y}},p} \right)e^{pT} + \sum\limits_{\mu = 1}^{{N_{FT} - 1}} {\text{Re} \left[ {e^{{T\omega \left( {\eta_{\mu } } \right)}} \tilde{v}\left( {{\mathbf{y}},\omega \left( {\eta_{\mu } } \right)} \right)\left( {1 + I\left( {\gamma \left( {\eta_{\mu } } \right)} \right)} \right)} \right]} } \right\} $$

(25)

where $\omega \left( {\eta_{\mu } } \right) = p\eta_{\mu } \left( {\cot \eta_{\mu } + I} \right)$, $\gamma \left( {\eta_{\mu } } \right) = \eta_{\mu } + \left( {\eta_{\mu } \cot \eta_{\mu } - 1} \right)\cot \eta_{\mu }$, $p = \frac{{2N_{FT} }}{5T}$, $I = \sqrt { - 1}$, and $\eta_{\mu } = \frac{\mu \pi }{{N_{FT} }}, \, \mu { = 1,2,} \ldots ,N_{FT} - 1$. For a specific time instant T, one may require to solve $N_{FT}$ boundary value problems with the corresponding Laplace transformation parameters $\varepsilon { = }p{\text{ and }}\omega \left( {\eta_{\mu } } \right)$.

Finally the inverse variable transformation of Eq. (5) is employed to obtain the final time-dependent solution $u\left( {{\mathbf{x}},T} \right)$.

2.3 Error analysis

This section presents error analysis of the proposed collocation scheme. In the present implementation procedure, all of Laplace transformation and variable transformation are analytical, and the numerical error appears mainly in the CTM + CMRM implementation of Step (b) and the NILT process of Step (c).

First, we discuss the numerical error generated in Step (c), i.e., Fixed Talbot numerical inverse Laplace transform (NILT). Abate et al. [52, 53] did extensive numerical experiments to investigate the parameter effect on numerical accuracy. According to his conclusion [53], the following heuristic error estimation of Fixed Talbot algorithm is obtained,

Remark 1

If the error of input data is $\frac{{\left\| {\tilde{v}_{N} - \tilde{v}} \right\|}}{{\left\| {\tilde{v}} \right\|}} \approx 10^{{ - M_{p} }}$ with positive integer N_FT = M_p, then the final error is $\left| {\frac{{v_{s} - v}}{v}} \right| \approx 10^{{ - 0.6M_{p} }}$. Therefore the efficiency of the Fixed Talbot algorithm is

$$ Eff\left( {FT} \right) \equiv \frac{{{\text{significant}}\;{\text{ digits}}\;{\text{ obtained}}}}{{{\text{precision}}\;{\text{ required}}}} \approx \frac{{0.6M_{p} }}{{M_{p} }} \approx 0.6. $$

(26)

It can be found from Remark 1 that the Fixed Talbot algorithm tends to demand highly precise input data $\tilde{v}_{N}$ in order to yield satisfactory accuracy in the following NILT calculations. For this requirement, we implement the collocation Trefftz scheme (CTM) in conjunction with composite multiple reciprocity method (CMRM) in Step (b) to obtain highly accurate solution in Laplace-space domain.

As we can see, the computational error in Step (b) is mainly generated from the CTM + CMRM solution of Laplace-transformed nonhomogeneous problems (13)–(14). Since 3D problems are transformed into 2D problems in the present numerical implementation, the error analysis of the CTM + CMRM in 2D problems is only considered. In the error analysis of the CTM + CMRM, we assume that the solution $\tilde{v} \in H^{1} \left( \Omega \right)$, the source term function $\tilde{W}$, and the boundary condition function $\tilde{g}_{1}$ are smooth enough on $\Omega$. At first, the following homogeneous equation with Dirichlet boundary condition under a polygonal domain is considered

$$ \Re \tilde{v} = 0, $$

(27)

$$ \left. {\tilde{v}} \right|_{\partial \Omega } = \tilde{g}_{1} . $$

(28)

When $\Re = \Delta$, we obtain a simplified error estimation from Theorem 3.2 in [54] and maximum principle of Laplace equation [55],

$$ \left\| {\tilde{v} - \tilde{v}_{N} } \right\|_{H} \le C_{1} \left\| {\tilde{v} - \tilde{v}_{N} } \right\|_{B} \le \frac{{C_{1} C_{2} }}{{N_{h}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}, $$

(29)

where $\left\| \bullet \right\|$ is the Sobolev norm and $H,B$ denotes the computational domain $\Omega$ and its boundary $\partial \Omega$, respectively. And $\tilde{v}_{N}$ is the corresponding approximation solution, $N_{h}$ denotes the boundary collocation number on $\partial \Omega$ for obtaining the homogeneous solution, $C_{1} ,C_{2}$ are constants independent of $N_{h}$.

When $\Re = \Delta + k^{2}$ and $k$ is not exactly equal (but may be very close) to an eigenvalue $\left\{ {\lambda_{i} } \right\}$ of Laplace operator, we obtain a simplified error estimation from Corollary 3.1 in [56].

$$ \left\| {\tilde{v} - \tilde{v}_{{n_{1} ,n_{2} }} } \right\|_{H} \le \frac{{C_{3} N_{h\hbox{max} }^{2} }}{\delta }\left[ {\frac{{\alpha_{ + }^{{n_{1} + 1}} }}{{\left( {n_{1} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} + \frac{{\alpha_{ - }^{{n_{2} + 1}} }}{{\left( {n_{2} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \right], $$

(30)

where $\delta { = }\mathop {\hbox{min} }\nolimits_{i} \left| {\frac{{k^{2} - \lambda_{i} }}{{k^{2} }}} \right| > 0$ represents the smallest relative distance between $k^{2}$ and the eigenvalues $\lambda_{i}$, and the solution domain $\Omega$ is divided by a piecewise straight line $\Gamma_{I}$ into two subdomains $\Omega^{ + }$ and $\Omega^{ - }$, the solution $\tilde{v}_{{n_{1} ,n_{2} }}$ can be represented as

$$ \tilde{v}_{{n_{1} ,n_{2} }} { = }\left\{ {\begin{array}{*{20}l} {\tilde{v}_{{n_{1} }}^{ + } = a_{0}^{0 + } J_{0} \left( {kr} \right) + \sum\nolimits_{i = 1}^{{n_{1} }} {J_{i} \left( {kr} \right)\left[ {a_{2i - 1}^{0 + } \cos i\theta + a_{2i + 1}^{0 + } \sin i\theta } \right],{\text{ in }}\Omega^{ + } } } \hfill \\ {\tilde{v}_{{n_{2} }}^{ - } = a_{0}^{0 - } J_{0} \left( {k\rho } \right) + \sum\nolimits_{i = 1}^{{n_{2} }} {J_{i} \left( {k\rho } \right)\left[ {a_{2i - 1}^{0 - } \cos i\theta + a_{2i + 1}^{0 - } \sin i\theta } \right],{\text{ in }}\Omega^{ - } } } \hfill \\ \end{array} } \right. $$

(31)

and $N_{h\hbox{max} } { = }\hbox{max} \left\{ {n_{1} ,n_{2} } \right\}$, $C_{3}$ is a bounded constant independent of $n_{1} ,n_{2} ,k,\delta$, $\frac{{ekr_{\hbox{max} }^{ + } }}{{2n_{1} }} \le \alpha_{ + }^{{}} < 1, \, \frac{{ek\rho_{\hbox{max} }^{ - } }}{{2n_{2} }} \le \alpha_{ - }^{{}} < 1$, in which $r_{\hbox{max} }^{ + } { = }\max_{{{\text{in}}\Omega^{ + } }} r$, $\rho_{\hbox{max} }^{ - } { = }\max_{{{\text{in}}\Omega^{ - } }} \rho$. Set $\alpha_{ + }^{{}} \le \left( {\frac{{C_{4} \delta }}{{2C_{3} N_{h\hbox{max} }^{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\left( {n_{1} + 1} \right)}}} \right. \kern-0pt} {\left( {n_{1} + 1} \right)}}}}$ and $\alpha_{ - }^{{}} \le \left( {\frac{{C_{4} \delta }}{{2C_{3} N_{h\hbox{max} }^{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\left( {n_{2} + 1} \right)}}} \right. \kern-0pt} {\left( {n_{2} + 1} \right)}}}}$, then the error estimation becomes

$$ \begin{aligned} \left\| {\tilde{v} - \tilde{v}_{{n_{1} ,n_{2} }} } \right\|_{H} &\le \frac{{C_{3} N_{h\hbox{max} }^{2} }}{\delta }\left[ {\frac{{\alpha_{ + }^{{n_{1} + 1}} }}{{\left( {n_{1} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} + \frac{{\alpha_{ - }^{{n_{2} + 1}} }}{{\left( {n_{2} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \right]\\ &\le \frac{{C_{4} }}{{2\left( {n_{1} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} + \frac{{C_{4} }}{{2\left( {n_{2} + 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} < \frac{{C_{4} }}{{N_{h\hbox{min} }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }},\end{aligned} $$

(32)

where the boundary node number $N_{h\hbox{min} } { = }\hbox{min} \left\{ {n_{1} ,n_{2} } \right\}$ for obtaining the homogeneous solution, $C_{4}$ is a bounded constant.

Next we turn to the following nonhomogeneous problem

$$ \Re \tilde{v} = \tilde{W}, $$

(33)

$$ \left. {\tilde{v}} \right|_{\partial \Omega } = \tilde{g}_{1} . $$

(34)

in which the source term $\tilde{W}$ can be eliminated by using differential operator $L_{1}$, namely, $L_{1} \left\{ {\tilde{W}} \right\}{ = }0$ on $\Omega$.

Theorem 1

Let$\tilde{v} = \tilde{v}_{h} + \tilde{v}_{p}$and$\tilde{v}_{L} = \tilde{v}_{Lh} + \tilde{v}_{Lp}$be the exact and numerical solution of the nonhomogeneous problem (39)–(40), where$\tilde{v}_{Lp}$is the particular solution of Eq. (38), and$\Re \tilde{v}_{Lp} = \tilde{W}$. Then

$$ \left\| {\tilde{v} - \tilde{v}_{L} } \right\|_{H} \le \frac{C}{{N^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}, $$

(35)

where$C$is a bounded constant and$N{ = }\hbox{min} \left\{ {N_{h} ,N_{p} } \right\}$, in which the boundary node number$N_{p}$for obtaining the particular solution.

Proof

Let $\hat{v}_{h}$ be the exact solution of the following problem

$$ \Re \hat{v}_{h} = 0, $$

(36)

$$ \left. {\hat{v}_{h} } \right|_{\partial \Omega } = \tilde{g}_{1} - \tilde{v}_{Lp} . $$

(37)

Let $\hat{v} = \hat{v}_{h} + \tilde{v}_{Lp}$, then we have

$$ \left\| {\tilde{v} - \tilde{v}_{L} } \right\|_{H} \le \left\| {\tilde{v} - \hat{v}} \right\|_{H} { + }\left\| {\hat{v} - \tilde{v}_{L} } \right\|_{H} . $$

(38)

By using Eqs. (35) or (38), we have

$$ \left\| {\hat{v} - \tilde{v}_{L} } \right\|_{H} { = }\left\| {\hat{v}_{h} - \tilde{v}_{Lh} } \right\|_{H} \le \frac{{C_{h} }}{{N_{h}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}. $$

(39)

when $\Re = \Delta$, $\tilde{v}_{Lh} { = }\tilde{v}_{{N_{h} }}$, $C_{h} { = }C_{1} C_{2}$; when $\Re = \Delta + k^{2}$, $\tilde{v}_{Lh} { = }\tilde{v}_{{n_{1h} ,n_{2h} }}$, $C_{h} { = }C_{4}$, $N_{h} { = }N_{h\hbox{min} }$. Notice that in $\Omega$

$$ \Re \left( {\tilde{v} - \hat{v}} \right) = \tilde{W} - \hat{W}, $$

(40)

and on $\partial \Omega$

$$ \left. {\left( {\tilde{v} - \hat{v}} \right)} \right|_{\partial \Omega } = \tilde{g}_{1} - \left( {\tilde{g}_{1} - \tilde{v}_{Lp} { + }\tilde{v}_{Lp} } \right){ = }0. $$

(41)

According to a priori estimate [55], we obtain

$$ \left\| {\tilde{v} - \hat{v}} \right\|_{H} \le C_{5} \left\| {\tilde{W} - \hat{W}} \right\|_{H} . $$

(42)

Consider the following problems

$$ L_{1} v{ = }0, $$

(43)

$$ \left. v \right|_{\partial \Omega } = \tilde{W}, $$

(44)

where $\tilde{W}$ and $\hat{W}$ are its exact and numerical solution, respectively.For $L_{1} { = }\Delta$, Eq. (42) can be rewritten by using Eq. (29)

$$ \left\| {\tilde{v} - \hat{v}} \right\|_{H} \le C_{5} \left\| {\tilde{W} - \hat{W}} \right\|_{H} \le \frac{{C_{5} C_{1} C_{2} }}{{N_{p}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}. $$

(45)

and then according to Eqs. (38), (39), (45), we get

$$ \begin{aligned}\left\| {\tilde{v} - \tilde{v}_{L} } \right\|_{H} &\le \left\| {\tilde{v} - \hat{v}} \right\|_{H} { + }\left\| {\hat{v} - \tilde{v}_{L} } \right\|_{H} \le \frac{{C_{h} }}{{N_{h}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{ + }\frac{{C_{5} C_{1} C_{2} }}{{N_{p}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}\\ &\le \frac{C}{{N^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}.\end{aligned} $$

(46)

For $L_{1} { = }\Delta + k_{1}^{2}$ and and $k_{1}$ is not exactly equal (but may be very close) to an eigenvalue $\left\{ {\lambda_{i} } \right\}$ of Laplace operator, Eq. (42) can be rewritten by using Eq. (32)

$$ \left\| {\tilde{v} - \hat{v}} \right\|_{H} \le C_{5} \left\| {\tilde{W} - \hat{W}} \right\|_{H} \le \frac{{C_{4} C_{5} }}{{N_{p}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}. $$

(47)

and then according to Eqs. (38), (39), (45), we get

$$ \begin{aligned}\left\| {\tilde{v} - \tilde{v}_{L} } \right\|_{H} &\le \left\| {\tilde{v} - \hat{v}} \right\|_{H} { + }\left\| {\hat{v} - \tilde{v}_{L} } \right\|_{H} \\ &\le \frac{{C_{h} }}{{N_{h}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{ + }\frac{{C_{4} C_{5} }}{{N_{p}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} \le \frac{C}{{N^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}.\end{aligned} $$

(48)

Therefore, the conclusion of the theorem is obtained.

It can be observed from Eq. (35) that the CTM + CMRM has polynomial convergence rate for nonhomogeneous problems (33)–(34), and its error decreases but the condition number of its resultant matrix increases as the boundary node number $N \to \infty$. In the literatures [9, 38, 44], numerical experiments show that the CTM + CMRM error tends to decrease exponentially and then oscillate slightly below a certain error level with an increase of $N$.

2.4 Extended precision arithmetic

This section introduces the extended precision arithmetic (EPA) to eliminate the ill-posed issues encountered in the implementation procedure and enhance the applicability of the proposed collocation scheme for transient thermal conduction analysis in large-size-ratio FGMs under heat source loading. Nowadays the common-used double-precision floating point arithmetic (F = 16) [42] has the machine epsilon $\varepsilon_{M} { = }2.22{\text{E}} - 16$, which lead to the following error estimation

$$ \varepsilon_{N} = \varepsilon_{M} \times \kappa , $$

(49)

where $\varepsilon_{N}$ denotes the computational error to measure the numerical accuracy, $\kappa$ represents the ratio between maximum value and minimum value in the present implementation. To guarantee the numerical error $\varepsilon_{N} \le 2.00{\text{E}} - 0 2$, the value $\kappa \le 9.00{\text{E + 13}}$. Unfortunately, with the increasing size ratio, both the CTM resultant matrix with moderate boundary nodes and the Fixed Talbot algorithm with small term $N_{FT}$ bring very large $\kappa$. It could be efficient to implement the EPA in the present implementation. So far, several open source libraries (GMP, MPFR and MPC, etc.) are available for serving on the extended precision arithmetic. Recently, Holoborodko [57] developed an easy-to-implement MATLAB toolbox, Advanpix Multi-precision Computing Toolbox (AMCT). In this study, the AMCT (version 3.9.0.9938) is used in the present computation. More details about the AMCT implementation can be found in Ref. [57].

3 Numerical example

In this section, the numerical accuracy and efficiency of the proposed collocation scheme are verified by 2D/3D large-size-ratio FGMs with three different types of specific spatial variations (quadratic, exponential and trigonometric functions) under heat source loading. Then the proposed scheme is applied to heat conduction problems under 2D/3D complex-shaped FGMs in comparison to the analytical results and COMSOL results. All the numerical examples are computed on a personal computer with Intel(R) Core(TM) i7-6700 CPU 3.40 GHz and 8 GB RAM. In order to measure the numerical accuracy of the proposed scheme, the relative error $rerr\left( u \right)$ and maximum relative error $Mrerr(u)$ is defined as follows,

$$ rerr = \left| {\frac{{u({\mathbf{x}}_{i} ,T) - \bar{u}({\mathbf{x}}_{i} ,T)}}{{\bar{u}({\mathbf{x}}_{i} ,T)}}} \right| $$

(50a)

$$ Mrerr = \mathop {\text{Max}}\limits_{{ 1\le i \le N_{T} }} \left( {\left| {\frac{{u({\mathbf{x}}_{i} ,T) - \bar{u}({\mathbf{x}}_{i} ,T)}}{{\bar{u}({\mathbf{x}}_{i} ,T)}}} \right|} \right) $$

(50b)

where $N_{T}$ represents the number of test nodes, $u({\mathbf{x}}_{i} )$ and $\bar{u}({\mathbf{x}}_{i} )$ denote the numerical and analytical solutions at test point ${\mathbf{x}}_{i}$ with the time instant T, respectively. Unless otherwise specified, the number of boundary nodes $N = N_{h} = N_{p} = 91$, the number of directions $M_{1} = 13$ in the plane $\left( {y_{2} ,y_{3} } \right)$, the frequency term in Fixed Talbot algorithm is $N_{FT} = 8$, and the multi-precision floating point arithmetic $F = 30$.

3.1 Numerical verifications

Example 1

Transient thermal conduction with inner heat sources under 2D large-aspect-ratio rectangular FGMs.

Consider transient thermal conduction problems with heat sources in 2D rectangle functionally graded materials $\Omega_{1} = \{ \left. {(x_{1} ,x_{2} )} \right| - \frac{{h_{1} }}{2} < x_{1} < \frac{{h_{1} }}{2},\frac{{h_{2} }}{2} < x_{2} < \frac{{h_{2} }}{2}\}$, which is shown in Fig. 3. The size of FGMs are set as the height $h_{2} = 0.1$ and the length $h_{1} = h_{2} \times SR$, where $SR$ represents the size ratio. Zero initial temperature and full Dirichlet boundary condition are considered in this example. The symbol “/” denotes the numerical accuracy less than the engineering accuracy (Mrerr > 10⁻²). The test points are uniformly distributed in the computational domains, and the number of test points NT = 121. Three kinds of FGMs with different types of material variations are investigated.

Fig. 3

Schematic configuration of rectangle FGMs with boundary nodes (·) in Example 1

Case 1.1: 2D FGM with quadratic variations

In this case, the thermal conductivity matrix ${\mathbf{K}}$, specific heat $c\left( {\mathbf{x}} \right)$ and mass density $\rho \left( {\mathbf{x}} \right)$ are quadratic functions, i.e. $f\left( {\mathbf{x}} \right) = \left( {2 + 8x_{1} + 2x_{2} } \right)^{2}$ in Eqs. (3) and (4), and ${\mathbf{k}} = \left[ {\begin{array}{*{20}c} 1 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} & 2 \\ \end{array} } \right]$, $\rho_{0} c_{0} { = }1$. Its analytical temperature distribution can be represented as

$$ u\left( {{\mathbf{x}},t} \right) = \frac{{te^{{x_{1} }} \sin x_{2} }}{{2 + 8x_{1} + 2x_{2} }} $$

(51)

and the heat source function $Q({{\mathbf{x}},t} ) = ( {( {t + 1} )e^{{x_{1} }} \sin x_{2} - te^{{x_{1} }} \cos x_{2} } )( {2 + 8x_{1} + 2x_{2} } )$. In the proposed implementation procedure, ${\mathbf{k}}^{ - } { = }\left( {\begin{array}{*{20}c} 1 & 0 \\ {{{ - \sqrt 7 } \mathord{\left/ {\vphantom {{ - \sqrt 7 } 7}} \right. \kern-0pt} 7}} & {{{2\sqrt 7 } \mathord{\left/ {\vphantom {{2\sqrt 7 } 7}} \right. \kern-0pt} 7}} \\ \end{array} } \right)$, $\Re { = }\Delta - \varepsilon$, $\tilde{W} = \frac{{{\text{e}}^{{y_{1} }} }}{{\varepsilon^{2} }}\cos \left( {\frac{{\sqrt 7 y_{2} + y_{1} }}{2}} \right) - \frac{1 + \varepsilon }{{\varepsilon^{2} }}{\text{e}}^{{y_{1} }} \sin \left( {\frac{{\sqrt 7 y_{2} + y_{1} }}{2}} \right)$, and the corresponding annihilating differential operator $L_{1} = \Delta$ in Eq. (20).

Case 1.2: 2D FGM with exponential variations

In this case, the thermal conductivity matrix ${\mathbf{K}}$, specific heat $c\left( {\mathbf{x}} \right)$ and mass density $\rho \left( {\mathbf{x}} \right)$ are exponential functions, i.e. $f\left( {\mathbf{x}} \right) = e^{{2x_{1} + x_{2} }}$ in Eqs. (3) and (4), and ${\mathbf{k}} = \left[ {\begin{array}{*{20}c} 1 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} & 2 \\ \end{array} } \right]$, $\rho_{0} c_{0} { = }10^{4}$. Its analytical temperature distribution can be represented as

$$ u\left( {{\mathbf{x}},t} \right) = te^{{x_{1} + 6x_{2} }} $$

(52)

and the heat source function $Q\left( {{\mathbf{x}},t} \right) = \left( {10^{4} - \frac{199t}{2}} \right)e^{{3x_{1} + 7x_{2} }}$. In the proposed implementation procedure, ${\mathbf{k}}^{ - } { = }\left( {\begin{array}{*{20}c} 1 & 0 \\ {{{ - \sqrt 7 } \mathord{\left/ {\vphantom {{ - \sqrt 7 } 7}} \right. \kern-0pt} 7}} & {{{2\sqrt 7 } \mathord{\left/ {\vphantom {{2\sqrt 7 } 7}} \right. \kern-0pt} 7}} \\ \end{array} } \right)$, $\Re { = }\Delta - \left( {10^{4} \varepsilon + 2} \right)$, $\tilde{W} = \left( {\frac{199}{{2\varepsilon^{2} }} - \frac{{10^{4} }}{\varepsilon }} \right)e^{{2y_{1} + \frac{{13\left( {\sqrt 7 y_{2} + y_{1} } \right)}}{4}}}$, and the corresponding annihilating differential operator $L_{1} = \Delta - \frac{185}{4}$ in Eq. (20).

Case 1.3: 2D FGM with trigonometric variations

In this case, the thermal conductivity matrix ${\mathbf{K}}$, specific heat $c\left( {\mathbf{x}} \right)$ and mass density $\rho \left( {\mathbf{x}} \right)$ are trigonometric functions, i.e. $f\left( {\mathbf{x}} \right) = \left( {\sin \left( {x_{2} + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}} \right)} \right)^{2}$ in Eqs. (3) and (4), and ${\mathbf{k}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 2 \\ \end{array} } \right]$, $\rho_{0} c_{0} { = }10^{2}$. Its analytical temperature distribution can be represented as

$$ u\left( {{\mathbf{x}},t} \right) = {\text{e}}^{{2x_{1} }} \sqrt 2 \sin \left( {x_{2} + \frac{3\pi }{4}} \right)t $$

(53)

and the heat source $Q\left( {{\mathbf{x}},t} \right) = \left( {2t + 100} \right){\text{e}}^{{2x_{1} }} \cos 2x_{2} \sin \left( {x_{2} + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}} \right)$. In the proposed implementation procedure, ${\mathbf{k}}^{ - } { = }\left( {\begin{array}{*{20}c} 1 & 0 \\ 0 & {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. \kern-0pt} 2}} \\ \end{array} } \right)$, $\Re { = }\Delta - \left( {10^{2} \varepsilon - 2} \right)$, $\tilde{W} = \frac{{ - \left( {2 + 10^{2} \varepsilon } \right){\text{e}}^{{2x_{1} }} \cos 2x_{2} }}{{\varepsilon^{2} }}$, and the corresponding annihilating differential operator $L_{1} = \Delta$ in Eq. (20).

Tables 1, 2 and 3 list the numerical results obtained by using the proposed collocation scheme with/without the extended precision arithmetic (EPA). It can be found from Tables 1, 2 and 3 that the proposed method with the EPA can enhance the applicability for the large-aspect-ratio FGMs with larger SR, in particular the FGMs with exponential and trigonometric material variations. It indicates that the EPA can alleviate the effect of ill-posed issues generated from the ill-conditioning resultant matrix, the NILT process and the large-size-ratio computational domain.

Table 1 Numerical errors obtained by the proposed collocation scheme with/without the EPA in Case 1.1 ($t = 100\,\text{s}$)

Table 2 Numerical errors obtained by the proposed collocation scheme with/without the EPA in Case 1.2 ($t = 1000\,\text{s}$)

Table 3 Numerical errors obtained by the proposed collocation scheme with/without the EPA in Case 1.3 ($t = 10\,\text{s}$)

To investigate the effect of $N$ and $N_{FT}$ on numerical accuracy, the proposed collocation scheme with large EPA (F = 80) is implemented in the solution of Cases 1.1–1.3. Figure 4 displays the convergence curves of Cases 1.1–1.3 by using the proposed scheme with two different NILT terms ($N_{FT} { = }15$ and 30). It can be observed from Fig. 4 that the proposed method can obtain the satisfactory numerical results with few boundary nodes and converge very fast. Moreover, with small NILT term number $N_{FT} { = }15$, the numerical accuracy can be improved at the beginning of increasing node number N($N \le 115$), and then it cannot improve any more with the further increasing node number N. This is because the numerical errors are mainly generated from NILT process in the present parameter setting with $N > 115$. At this time, increasing NILT term number becomes the most effective way to improve numerical accuracy.

Fig. 4

Convergence curves of Cases 1.1–1.3 by using the proposed scheme with two different NILT terms ($N_{FT} { = }15$ and 30) under large EPA (F = 80)

Example 2

Transient thermal conduction with inner heat sources under 3D large-aspect-ratio cuboid FGMs.

Consider transient thermal conduction problems with heat sources in 3D cuboid FGMs $\Omega_{2} = \{ \left. {(x_{1} ,x_{2} ,x_{3} )} \right| - \frac{{h_{1} }}{2} < x_{1} < \frac{{h_{1} }}{2},\frac{{h_{2} }}{2} < x_{2} < \frac{{h_{2} }}{2},\frac{{h_{3} }}{2} < x_{3} < \frac{{h_{3} }}{2}\}$, which is shown in Fig. 5. Set the length and width of 3D FGM $h_{1} = h_{2} = 0.1$ and the size ratio is defined as $SR = {{h_{3} } \mathord{\left/ {\vphantom {{h_{3} } {h_{1} }}} \right. \kern-0pt} {h_{1} }}$, and the number of boundary nodes $N = 162$, the number of test points $N_{T} = 216$.

Fig. 5

Schematic configuration of 3D cuboid FGMs with boundary nodes (·) in Example 2

Case 2.1: 3D FGM with quadratic variations

In this case, the thermal conductivity matrix ${\mathbf{K}}$, specific heat $c\left( {\mathbf{x}} \right)$ and mass density $\rho \left( {\mathbf{x}} \right)$ are quadratic functions, i.e. $f\left( {\mathbf{x}} \right) = x_{1}^{2} + 2x_{1} x_{3} + x_{3}^{2}$ in Eqs. (3) and (4), and ${\rm{k = }}\left[ {\begin{array}{*{20}{c}}5&0&0\\0&5&0\\0&0&5 \end{array}} \right]$, $\rho_{0} c_{0} { = }10$. Its analytical temperature distribution can be represented as

$$ u\left( {{\mathbf{x}},t} \right) = \left( {x_{1} + x_{2} - x_{3} } \right)t $$

(54)

and the heat source function $Q\left( {{\mathbf{x}},t} \right) = 10\left( {x_{1}^{3} - x_{3}^{3} - x_{1} x_{3}^{2} + x_{2} x_{3}^{2} + x_{1}^{2} x_{2} + x_{1}^{2} x_{3} + 2x_{1} x_{2} x_{3} } \right)$. In the proposed implementation procedure, ${\mathbf{k}}^{ - } = \left( \begin{array}{ccc}{{\sqrt 5}/ 5}& 0& 0 \\ 0& { \sqrt 5}/5&0\\0&0& {{\sqrt 5}/ 5}\\\end{array} \right)$, $\Re { = }\Delta - 10\varepsilon$, $\tilde{W} = - \frac{{10\left( {x_{1}^{2} - x_{3}^{2} + x_{1} x_{2} + x_{3} x_{2} } \right)}}{s}$, and the corresponding annihilating differential operator $L_{1} = \Delta$ in Eq. (20).

Case 2.2: FGM with exponential variations

In this case, the thermal conductivity matrix ${\mathbf{K}}$, specific heat $c\left( {\mathbf{x}} \right)$ and mass density $\rho \left( {\mathbf{x}} \right)$ are exponential functions, i.e. $f\left( {\mathbf{x}} \right) = e^{{0.2x_{1} + 0.4x_{2} + 0.2x_{3} }}$ in Eqs. (3) and (4), and ${\rm {k=}}\left[ {\begin{array}{*{20}{c}}3&0&0\\0&3&0\\0&0&3\end{array}} \right]$, $\rho_{0} c_{0} { = }1$. Its analytical temperature distribution can be represented as

$$ u\left( {{\mathbf{x}},t} \right) = \text{e}^{{5x_{1} + 4x_{2} + 0.1x_{3} - t}} $$

(55)

and the heat source function $Q\left( {{\mathbf{x}},t} \right) = - 1 3 1. 8 9e^{{5x_{1} + 4x_{2} + 0.1x_{3} }} e^{ - t}$. In the proposed implementation procedure, ${\mathbf{k}}^{ - } =\left( \begin{array}{ccc} {{\sqrt 3 }/3}& 0& 0\\0& { \sqrt 3 }/3& 0\\0&0&{ \sqrt 3 }/3\\\end{array} \right)$, $\Re { = }\Delta - \left( {\varepsilon - 0.18} \right)$, $\tilde{W} = - e^{{5.1x_{1} + 4.2x_{2} + 0.2x_{3} }} + \frac{{131.89e^{{5.1x_{1} + 4.2x_{2} + 0.2x_{3} }} }}{{\left( {\varepsilon + 1} \right)}}$, and the corresponding annihilating differential operator $L_{1} = \Delta - 4 3. 6 9$ in Eq. (20).

Case 2.3: FGM with trigonometric variations

In this case, the thermal conductivity matrix ${\mathbf{K}}$, specific heat $c\left( {\mathbf{x}} \right)$ and mass density $\rho \left( {\mathbf{x}} \right)$ are trigonometric functions, i.e. $f\left( {\mathbf{x}} \right) = \left( {\cos \left( {x_{3} } \right) - \sin \left( {x_{3} } \right)} \right)^{2}$ in Eqs. (3) and (4), and ${\mathbf{k}} = \left[ \begin{array}{ccc}7&0&0\\0 & 7& 0 \\0& 0& 7 \\\end{array} \right]$, $\rho_{0} c_{0} { = }100$, $t = 100\,\text{s}$. Its analytical temperature distribution can be represented as

$$ u\left( {{\mathbf{x}},t} \right) = \frac{{\left( {x_{1} x_{2} + x_{2} x_{3} + x_{1} x_{3} } \right)t}}{{\sqrt 2 \sin \left( {x_{2} + {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 4}} \right. \kern-0pt} 4}} \right)}} $$

(56)

and the heat source function $Q\left( {{\mathbf{x}},t} \right) = \sqrt 2 \left( {100 - 7t} \right)\left( {x_{1} x_{2} + x_{2} x_{3} + x_{1} x_{3} } \right)\sin \left( {x_{2} + {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 4}} \right. \kern-0pt} 4}} \right)$. In the proposed implementation procedure, ${\mathbf{k}}^{ - } = \left(\begin{array}{ccc}{\sqrt 7}/7& 0& 0\\0&{\sqrt 7}/7&0\\0&0&{\sqrt 7}/7\\\end{array} \right)$, $\Re { = }\Delta - \left( {10^{2} \varepsilon - 7} \right)$, $\tilde{W} = \left( {\frac{7 - 100\varepsilon }{{\varepsilon^{2} }}} \right)\left( {x_{1} x_{2} + x_{2} x_{3} + x_{1} x_{3} } \right)$, and the corresponding annihilating differential operator $L_{1} = \Delta$ in Eq. (20).

Figure 6 displays the convergence curves of Cases 2.1–2.3 by using the proposed scheme with two different NILT terms ($N_{FT} { = }8$ and 16). Similar to the conclusion in 2D cases (Example 1), the proposed method can also obtain the satisfactory numerical results with few boundary nodes and converge fast in 3D cases. Numerical errors are mainly generated from NILT process when $N > 194$ in the present parameter setting. At this time, increasing NILT term number becomes the most effective way to improve numerical accuracy. Moreover, Fig. 7 draws temperature distributions and relative errors of 3D cuboid FGMs with different size ratios ($SR = 15,30,60$) at time instant ($t = 1\,\text{s}$) in Case 2.2,

Fig. 6

Convergence curves of Cases 2.1–2.3 by using the proposed scheme with two different NILT terms ($N_{FT} { = }8$ and 16) under large EPA (F = 80)

Fig. 7

Temperature distributions and relative errors (rerr) of 3D cuboid FGMs with different size ratios ($SR = 15,30,60$) at time instant ($t = 1\,\text{s}$) in Case 2.2, top row: temperature, a$SR = 15$, b$SR = 30$, c$SR = 60$; bottom row: relative error, d$SR = 15$, e$SR = 30$, f$SR = 60$

3.2 Application to complex-shaped FGMs

Example 3

Transient thermal conduction analysis in double-head wrench.

Next consider transient thermal conduction in the double-head wrench. Figure 8 shows the real object of the double-head wrench and its simplified computational domain, where $h$ is the opening distance of the wrench. The thermal conductivity matrix ${\mathbf{K}}$, specific heat $c\left( {\mathbf{x}} \right)$ and mass density $\rho \left( {\mathbf{x}} \right)$ of the double-head wrench are quadratic functions, i.e. $f\left( {\mathbf{x}} \right) = \left( {1 + 4x_{1} + 2x_{2} } \right)^{2}$ in Eqs. (3) and (4), and ${\mathbf{k}} = \left[ {\begin{array}{*{20}c} 1 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} & 2 \\ \end{array} } \right]$, $\rho_{0} c_{0} { = }1$. The initial temperature is assumed to be $u({\mathbf{x}},0) = 0$, and the full Dirichlet boundary conditions can be obtained by using the following analytical solution

$$ u({\mathbf{x}},t) = \frac{{\sqrt 2 \sum\limits_{i = 1}^{100} {e^{{\frac{{ix_{2} }}{100}}} \sin \left( {\frac{{ix_{1} }}{100} + \frac{\pi }{4}} \right)\frac{t}{i}} }}{{1 + 4x_{1} + 2x_{2} }} $$

(57)

Fig. 8

a Real object of the double-head wrench and b its simplified computational domain with boundary nodes (·)

And the source function is

$$\begin{aligned} Q\left( {{\mathbf{x}},t} \right)&= - \sqrt 2 \left( \sum\limits_{i =1}^{100} \left( {\frac{it}{{10^{4} }} - \frac{1}{i}}\right){\text{e}}^{{\frac{{ix_{2} }}{100}}} \sin \left({\frac{{ix_{1} }}{100}+ \frac{\pi }{4}} \right) \right.\\&\left.\quad + \frac{it}{{10^{4} }}{\text{e}}^{{\frac{{ix_{2}}}{100}}} \sin \left( {\frac{{ix_{1} }}{100} + \frac{3\pi }{4}}\right) \right)\left( {1 + 4x_{1} + 2x_{2} } \right)\end{aligned} $$

In the proposed implementation procedure, ${\mathbf{k}}^{ - } { = }\left( {\begin{array}{*{20}c} 1 & 0 \\ {{{ - \sqrt 7 } \mathord{\left/ {\vphantom {{ - \sqrt 7 } 7}} \right. \kern-0pt} 7}} & {{{2\sqrt 7 } \mathord{\left/ {\vphantom {{2\sqrt 7 } 7}} \right. \kern-0pt} 7}} \\ \end{array} } \right)$, $\Re { = }\Delta - \varepsilon$, $\tilde{W} = \sum\nolimits_{i = 1}^{100} {\frac{{\frac{{2i^{2} }}{{10^{4} }}\cos \frac{{iy_{1} }}{100} - \varepsilon \left( {\cos \frac{{iy_{1} }}{100} + \sin \frac{{iy_{1} }}{100}} \right)}}{{i\varepsilon^{2} }}} e^{{\frac{{i\left( {\sqrt 7 y_{2} + y_{1} } \right)}}{200}}}$, and the corresponding annihilating differential operator $L_{1} = \Delta$ in Eq. (20).

In this example, the accuracy and efficiency of the proposed method are investigated in comparison with the COMSOL simulation. In the COMSOL simulation, two types of the meshes and the adaptive time stepping size are automatically generated by implementing the in-built code, which are shown in Fig. 9. Table 4 lists numerical results obtained by the proposed method and COMSOL software in Example 3 with different h (h = 1, 1.5, 2) at $t = 100\,\text{s}$. Table 5 presents numerical comparisons on computational costs of the proposed method and the COMSOL simulation in Example 3. It can be observed from Tables 4 and 5 that the proposed scheme provides more accurate solutions with fewer computational resources than the COMSOL software in Example 3.

Fig. 9

a Coarse and b refined meshes in the COMSOL simulation

Table 4 Numerical errors obtained by the proposed method and the COMSOL simulation ($t = 100\,\text{s}$)

Table 5 Numerical comparisons on computational costs of the proposed method and the COMSOL simulation in Example 3 ($t = 100\,\text{s}$)

Example 4

Transient thermal conduction analysis on the airplane.

To further validate the accuracy of the proposed method, we consider transient thermal conduction on the airplane as shown in Fig. 10. The thermal conductivity matrix ${\mathbf{K}}$, specific heat $c\left( {\mathbf{x}} \right)$ and mass density $\rho \left( {\mathbf{x}} \right)$ of the airplane are quadratic functions, i.e. $f\left( {\mathbf{x}} \right) = x_{1}^{2} - 2x_{1} x_{2} + x_{2}^{2}$ in Eqs. (3) and (4), and ${\rm{k = }}\left[ {\begin{array}{*{20}{c}}1&{1/4}&{1/3}\\{1/4}&1&{1/4}\\{1/3}&{1/4}&1\end{array}}\right]$, $\rho_{0} c_{0} { = 0} . 01$, $t = 1\,\text{s}$, and the number of test points $N_{T} = 8 3 4$. The initial temperature and the full Dirichlet boundary conditions can be obtained by using the following analytical solution

$$ u\left( {{\mathbf{x}},t} \right) = \left( {x_{1} + x_{2} } \right)t $$

(58)

Fig. 10

Schematic configuration of the airplane with boundary nodes (·) in Example 4

And the source function is

$$ Q\left( {{\mathbf{x}},t} \right) = \frac{{x_{1}^{3} + x_{2}^{3} - x_{2}^{2} x_{1} - x_{1}^{2} x_{2} }}{100} $$

In the proposed implementation procedure, ${\mathbf{k}}^{ - } = \left(\begin{array}{ccc}1&0&0\\{{\sqrt {15}}/{15}}& {{4\sqrt {15}}/{15}}& 0\\{- 4\sqrt {435} }/{435}&{ - 13\sqrt {435}}/870&6\sqrt {29}/{29} \\\end{array} \right)$, $\Re { = }\Delta - 0.01\varepsilon$,$\tilde{W} = - \frac{{\left( {x_{1}^{2} - x_{2}^{2} } \right)}}{100\varepsilon }$, and the corresponding annihilating differential operator $L_{1} = \Delta$ in Eq. (20). In addition, the number of boundary nodes $N = 841$ is considered in this example. Figure 11 plots the numerical and analytical temperature distributions on the airplane surface. Figure 12 displays the relative error of airplane surface, where the maximum relative error appeared in the central region of the wing on both sides is 1.91E−3. It reveals that the proposed collocation scheme also works well for transient thermal conduction analysis in 3D FGMs consisting of the size-disparity components.

Fig. 11

Temperature distributions on the airplane surface, a numerical solutions and b analytical solutions

Fig. 12

Relative error distribution on the airplane surface

Finally computation times of the proposed scheme for each example are listed in Table 6. It can be observed from Table 6 that all the present 2D numerical implementations can be done by the proposed collocation scheme in 150 s, and the present 2D numerical implementations can be done by the proposed collocation scheme in 400 s, except for Example 4. This is because the node requirement to well represent the airplane surface is three times more than that of 3D cuboid model.

Table 6 Computational times of the proposed scheme for each example

4 Conclusions

This paper presents a boundary collocation scheme for analyzing transient thermal conduction behavior in large-size-ratio functionally graded materials (FGMs) with heat source load. In the proposed scheme, it employs the Laplace transformation (LT) and the numerical inverse Laplace transformation (NILT) to convert the problem between time domain and Laplace-space domain to avoid the troublesome time-stepping effect. The boundary-only collocation scheme including the collocation Trefftz method and the composite multiple reciprocity method is implemented in the solution of Laplace-domain nonhomogeneous problems. More importantly, it introduces the extended precision arithmetic to alleviate the effect of ill-posed issues generated from the ill-conditioning resultant matrix, the NILT process and the large-size-ratio computational domain.

Heuristic error analysis and numerical investigation are presented to demonstrate that the proposed method with the EPA can enhance the applicability for the slender FGMs with larger SR, in particular the FGMs with exponential and trigonometric material variations. The proposed method can obtain the satisfactory results with few boundary nodes for complex-shaped FGMs with large size ratio, which requires less computational resource than the method used in the COMSOL simulation. Therefore the proposed collocation scheme can be considered as a competitive alternative for transient thermal conduction analysis in 2D/3D complex-shaped FGMs with large size ratio under heat source loading.

It is worth noting that the rigorous theoretical analysis of the proposed collocation scheme needs to be derived. In addition, this study only considers the thermal conductivity and the product of mass density and specific heat have the same special function variation, namely, the thermal diffusivity is a matrix with constant elements. This assumption allows the development of the proposed boundary collocation scheme without any domain discretization for thermal conduction analysis. Moreover, this method can provide benchmark solutions to other numerical methods. If thermal diffusivity is not a constant matrix, some additional approaches related to nonlinear problems, such as analog equation method, domain decomposition method, dual reciprocity method and so on, should be introduced. These issues are still under study and will be reported in a subsequent paper.

Appendix

Consider a two-dimensional problem with the domain

$$ \Omega = \left\{ {\left( {r,\theta } \right)\left| {0 \le r} \right. < R,0 \le \theta \le 2\pi } \right\} $$

(A1)

where $r,\theta$ denote the polar coordinates in 2D problems, it can be generated from the Cartesian coordinates $\left( {x,y} \right)$ with the origin at the center of 2D computational domain ${\mathbf{x}}_{c} = \left( {x_{c} ,y_{c} } \right)$, namely, $r = \sqrt {\left( {x - x_{c} } \right)^{2} + \left( {y - y_{c} } \right)^{2} }$ and $\theta = \arctan \left( {\frac{{y - y_{c} }}{{x - x_{c} }}} \right)$. The high-order Trefftz functions of common-used operators are listed as follows:

• (i) High-order Trefftz functions of Laplacian operator $\Delta^{n + 1}$

For Laplace equation $\Delta u = 0$, when n = 0, its Trefftz function are given in the literature as

$$ 1,r^{m} \cos \left( {m\theta } \right),r^{m} \sin \left( {m\theta } \right)\quad m = 1,2, \ldots ,\quad \left( {r,\theta } \right) \in \Omega $$

(A2)

which are known as zero-order Trefftz function $u^{T0}$. The corresponding nth order Trefftz function $u^{Tn}$ is presented as follows

$$ A_{n} r^{2n} ,A_{n} r^{m + 2n} \cos \left( {m\theta } \right),A_{n} r^{m + 2n} \sin \left( {m\theta } \right)\quad m = 1,2, \ldots ,\quad \left( {r,\theta } \right) \in \Omega $$

(A3)

where $A_{n} = \frac{{A_{n - 1} }}{{4n\left( {m + n} \right)}},A_{0} = 1$.

• (ii) High-order Trefftz functions of Helmholtz operator $\left( {\Delta + \lambda^{2} } \right)^{n + 1}$

In the Helmholtz operator, $\lambda > 0$ is a real number and assume that $\lambda^{2}$ is not an eigenvalue of Laplace operator. Then the zero-order Trefftz function $u^{T0}$ can be written as

$$ J_{0} \left( {\lambda r} \right),J_{0} \left( {\lambda r} \right)\cos \left( {m\theta } \right),J_{0} \left( {\lambda r} \right)\sin \left( {m\theta } \right)\quad m = 1,2, \ldots ,\quad \left( {r,\theta } \right) \in \Omega $$

(A4)

where $J_{0}$ is the Bessel function of the first kind. And the following functions are the corresponding nth order Trefftz functions $u^{Tn}$.

$$ \begin{aligned} & A_{n} \left( {\lambda r} \right)^{n} J_{n} \left( {\lambda r} \right),A_{n} \left( {\lambda r} \right)^{n} J_{m + n} \left( {\lambda r} \right)\cos \left( {m\theta } \right), \\ & A_{n} \left( {\lambda r} \right)^{n} J_{m + n} \left( {\lambda r} \right)\sin \left( {m\theta } \right),\quad m = 1,2, \ldots ,\quad \left( {r,\theta } \right) \in \Omega \\ \end{aligned} $$

(A5)

where $A_{n} = \frac{{A_{n - 1} }}{{2n\lambda^{2} }},A_{0} = 1$.

• (iii) High-order Trefftz functions of modified Helmholtz operator $\left( {\Delta - \lambda^{2} } \right)^{n + 1}$

In the modified Helmholtz operator, $\lambda$ is again a real number and $\lambda > 0$. Then the zero-order Trefftz function $u^{T0}$ can be given in the form

$$ I_{0} \left( {\lambda r} \right),I_{0} \left( {\lambda r} \right)\cos \left( {m\theta } \right),I_{0} \left( {\lambda r} \right)\sin \left( {m\theta } \right)\quad m = 1,2, \ldots ,\quad \left( {r,\theta } \right) \in \Omega $$

(A6)

where I₀ is the Bessel and Hankel functions with a purely imaginary argument. The corresponding nth order Trefftz function $u^{Tn}$ is presented as follows

$$ \begin{aligned} & A_{n} \left( {\lambda r} \right)^{n} I_{n} \left( {\lambda r} \right),A_{n} \left( {\lambda r} \right)^{n} I_{m + n} \left( {\lambda r} \right)\cos \left( {m\theta } \right), \\ & A_{n} \left( {\lambda r} \right)^{n} I_{m + n} \left( {\lambda r} \right)\sin \left( {m\theta } \right),\quad m = 1,2, \ldots ,\quad \left( {r,\theta } \right) \in \Omega \\ \end{aligned} $$

(A7)

where $A_{n} = \frac{{A_{n - 1} }}{{2n\lambda^{2} }},A_{0} = 1$.