Efficient searching in meshfree methods

Abstract

Meshfree methods such as the Reproducing Kernel Particle Method and the Element Free Galerkin method have proven to be excellent choices for problems involving complex geometry, evolving topology, and large deformation, owing to their ability to model the problem domain without the constraints imposed on the Finite Element Method (FEM) meshes. However, meshfree methods have an added computational cost over FEM that come from at least two sources: increased cost of shape function evaluation and the determination of adjacency or connectivity. The focus of this paper is to formally address the types of adjacency information that arises in various uses of meshfree methods; a discussion of available techniques for computing the various adjacency graphs; propose a new search algorithm and data structure; and finally compare the memory and run time performance of the methods.

1 Introduction

For performing engineering analysis and the closely related topic of geometric modeling, meshfree methods provide an alternative to mesh-based approximation techniques. In contrast to the Finite Element Method (FEM), where a function space is constructed on elements of a mesh, meshfree methods construct their function space on a set of particles, where the shape functions associated with a particle are compactly supported. Obviating the need for a disjoint polygonal or polyhedral domain decomposition makes them well suited for handling problems where generating and maintaining a mesh is difficult. While meshfree methods offer some advantages over FEM, they also possess several disadvantages, including increased computational time and, depending on implementation, memory overhead. This cost is attributed to the increased complexity of both shape function evaluation and determination of connectivity. There are three types of connectivity information required in geometric modeling and analysis as listed in Table 1, and discussed in detail in Sect. 3. The first type of connectivity arises in evaluating quadrature points and problems involving contact between bodies. The second type comes about when one has quantities at field points and wishes to project those values to the particle locations, e.g. stress or strain values. The third type is useful for determining the sparsity pattern and entries in the stiffness matrix of a Galerkin solution to a partial differential equation (PDE). The various connectivities are a type of graph and can be represented through an adjacency matrix [10].

Table 1 Adjacency types in geometric modeling and analysis

In FEM, a common approach is to use the isoparametric concept where the shape functions are formulated in a parent or natural coordinate system and then the geometric domain values are computed by applying an affine transformation. The description of the mesh can be used as a graph to provide the first two types of connectivity. Since Gauss quadrature is an efficient method for integrating FEM shape functions, they are normally defined in the parent domain, eliminating the need to find the reverse transformation from geometric to parent coordinates and evaluating Type 1 connectivity directly. If one uses conforming shape functions, Type 3 connectivity can also be quickly determined from the mesh. In the case of stiffness matrix assembly using the element viewpoint, explicit Type 3 information is not required. Since the parent element is fixed, the parent shape functions are fixed and simple to compute. In contrast, meshfree shape functions are constructed for the current point of interest based on the collection of surrounding particles that have a non-zero contribution at the point. Since this collection of contributing particles varies with the spatial position of the point to be evaluated and there is no predefined adjacency information, the construction of meshfree shape functions is more involved.

In the Galerkin solution of the governing PDEs describing physical problems, an integration over the domain is required to form a global system of equations. A common challenge with any integration scheme for meshfree methods is controlling the integration errors. Meshfree shape functions are of a non-polynomial rational form with overlapping supports, requiring special techniques for conducting integration [13]. A commonly used approach to reduce the integration error is to employ a higher order quadrature rule, consequently requiring a larger number of shape function evaluations compared to FEM.

While meshfree methods have received significant attention by researchers, the topic of efficient implementations have received significantly less attention. To summarize, the increased cost of meshfree analysis over FEM is due to: increased shape function evaluation cost, increased number of shape function evaluations in quadrature when using a background mesh, and dynamic or runtime evaluation of connectivity. This paper will only focus on the last topic, and an overview of prior contributions as they pertain to the present work are reviewed in Sect. 5. This unorthodox placement within the paper of a review of the state of the art is done because the authors feel that it is best understood once the background information in Sects. 4–4.2 have been presented.

This paper has three objectives and is organized as follows. Following a brief review of the Reproducing Kernel Particle Method (RKPM) in Sect. 2, the first objective is to provide a thorough review of the adjacency information that is commonly required in geometric modeling and analysis when employing a meshfree method, accomplished in Sect. 3. The second objective is to describe the various approaches that can be used for determining the adjacency information. Since the reader may not be familiar with data structure concepts from Computer Science, Sect. 4 is provided as background and to set the stage for a new data structure for meshfree searches in Sect. 4.2.2. The final objective is to demonstrate the effectiveness of the various approaches under various circumstances, in order to aid those using meshfree methods to select an appropriate search scheme for their problem, presented in Sect. 6, followed by a conclusion in Sect. 7. While this paper is focused on applications involving meshfree methods, the primary algorithm discussed is essentially a nearest neighbour search and therefore the data structures presented can be abstracted to any set of compact non-disjoint or disjoint objects. The data structures are capable of operations such as ray–object intersections, which occur in computer graphics, but are also of interest for meshfree methods when enforcing visibility conditions.

2 Preliminaries

Numerous meshfree methods have been developed, including the well-known Reproducing Kernel Particle Method (RKPM) [24], Element Free Galerkin (EFG) method [3], Meshfree Local Petrov Galerkin (MLPG) [1], HP-Clouds [14], and the Finite Point Method (FPM) [26]. A thorough review of meshfree methods is given in [19, 20, 22]. The data structures and algorithms discussed in this paper are applicable to many of the meshfree methods, but for completeness the RKPM formulation will be used.

2.1 RKPM shape functions

Following the general formulation, such as [19] and [25], we review the RKPM approximation. The problem domain is discretized by a collection of particles $\{\mathbf{x }_{I} :I{ \in } \{1,2,\ldots ,N\}\}$, each representing a certain volume and mass of material.

The RKPM approximation to a scalar function $u(\mathbf{y })$ is given as

$$\begin{aligned} u^{h}\left( \mathbf{y }\right) = \int _\varOmega \varPhi _{\rho } \left( \mathbf{y }- \mathbf{x }\right) u\left( \mathbf{x }\right) d\mathbf{x }, \end{aligned}$$

(1)

where $\varPhi _{\rho }$ is the corrected kernel and is given as

$$\begin{aligned} \varPhi _{\rho } \left( \mathbf{y }- \mathbf{x }\right) = C \left( \mathbf{y }-\mathbf{x };\mathbf{y }\right) \phi _{\rho } \left( \mathbf{y }-\mathbf{x }\right) , \end{aligned}$$

(2)

where $C\left( \mathbf{y }-\mathbf{x };\mathbf{y }\right)$ is known as the correction and $\phi _{\rho }$ is a compactly supported function. The correction term is taken as the polynomial

$$\begin{aligned} C\left( \mathbf{y }-\mathbf{x },\mathbf{y }\right) = \mathbf{c }^{T}\left( \mathbf{y }\right) \mathbf{P }\left( \mathbf{y }-\mathbf{x }\right) , \end{aligned}$$

(3)

where $\mathbf{c }$ is an unknown vector of coefficients and $\mathbf{P }$ is a vector of monomials. Enforcing consistency yields the following linear system:

$$\begin{aligned} \mathbf{M }\left( \mathbf{y }\right) \mathbf{c }\left( \mathbf{y }\right) = \mathbf{P }\left( 0\right) , \end{aligned}$$

(4)

where $\mathbf{M }$ is known as the moment matrix. Evaluation of Eq. 1 via nodal integration, is expressed as

$$\begin{aligned} \mathbf{M }\left( \mathbf{y }\right) = \sum _{I} \mathbf{P }\left( \mathbf{y }-\mathbf{x }_{I}\right) \mathbf{P }^{T}\left( \mathbf{y }-\mathbf{x }_{I}\right) \phi _{\rho } \left( \mathbf{y }-\mathbf{x }_{I}\right) \varDelta V_{I}. \end{aligned}$$

(5)

Solving for the correction weights $\mathbf{c }$ in Eq. 4 and using Eqs. 2 and 3 the corrected kernel can be expressed as:

$$\begin{aligned} \varPhi _{I}\left( \mathbf{y }\right) = \mathbf{P }^{T}\left( {\mathbf{y }-\mathbf{x }_I}\right) \mathbf{M }^{-1}\left( \mathbf{y }\right) \mathbf{P }\left( 0\right) \phi _{\rho } \left( \mathbf{y }-\mathbf{x }_{I}\right) . \end{aligned}$$

(6)

The meshfree approximation then has the following form

$$\begin{aligned} \hat{u}^{h}\left( \mathbf{y }\right) = \sum _{I} \varPsi _{I}\left( \mathbf{y }\right) u_I, \end{aligned}$$

(7)

where $\varPsi _{I}\left( \mathbf{y }\right)$ are the RKPM approximation functions, and $u_I$ are the nodal unknowns. The summation is taken over the set of particles that have non-zero shape functions at $\mathbf{y }$.

2.2 Computational efficiency

The form of the approximation in Eq. 7 appears identical to the FEM function approximation, however the meshfree approximation functions have several key differences. First, the meshfree approximation functions in general do not possess the Kronecker-$\delta$ property [20].

$$\begin{aligned} \varPsi _{I}\left( \mathbf{x }_{J}\right) \ne \delta _{IJ}. \end{aligned}$$

(8)

The computation of the meshfree shape functions are significantly more expensive, as a small linear system, Eq. 4, must be solved for every point of interest. In addition, the meshfree shape functions do not use a prescribed topological map as in FEM, but instead determine this information as part of the shape function calculation, augmenting the computational cost. The meshfree shape functions are non-polynomial rational functions, where those used in traditional FEM are polynomial functions. Compared to the FEM shape functions, which are predefined, the meshfree shape functions require the computation of a correction term at each point of interest in the domain. This correction term is a function of position and requires the knowledge of all the surrounding particles that have the given evaluation point in their support domain, i.e. Type 1 adjacency. Given this adjacency information the computation of the meshfree shape functions can be computed by Eq. 6, requiring the inversion of the moment matrix. While the moment matrix is not particularly large, the number of inversions required for a practical problem may be significant. To alleviate the computational cost of computing the inverse, a method to avoid the direct computation is given in [4]. Research to reduce cost of meshfree analysis by reducing the number of necessary shape function evaluations by nodal integration has been published in [11, 12]. To further reduce the computational performance gap between meshfree methods and FEM the computation of the adjacency information must be addressed.

3 Adjacency information

This section will expand on the three types of adjacency listed in Table 1. The finite set of particle locations discretizing the domain is denoted as $\mathbb {X}$, which is assumed to be indexed. The finite set of field points where shape functions will be computed will be denoted as $\mathbb {Y}$, which is also assumed to be indexed. We use the term evaluation point to refer to points in $\mathbb {Y}$, to distinguish them from the particle locations. Of course, one may want to evaluate shape functions at particle locations, so the two sets are not necessarily disjoint. As mentioned in Sect. 1, given these two sets there are three connectivities which commonly arise when employing a meshfree method, which can be conveniently denoted as sets. Any given type of connectivity is represented as a set of sets, indexed by either particle index, or evaluation point index. Each entry I in the connectivity is a set of indices of objects adjacent to I defined by the type of adjacency. The formal definitions that follow will make this clear.

Type 1::

Given an evaluation point, $\mathbf{y }_{J} \in \mathbb {Y}$ define the index set, $\varTheta ^{J}$, containing the indices of those particles that have a non-zero shape function at $\mathbf{y }_{J}$, which can be stated as

$$\begin{aligned} \varTheta ^{J} = \left\{ I \vert \mathbf{x }_I \in \mathbb {X} \wedge \varPsi _I \left( \mathbf{y }_{J}\right) \ne 0 \right\} . \end{aligned}$$

(9)

Evaluation point–particle adjacency, denoted $\varTheta$, is defined to be the set whose elements are the $\varTheta ^{J}$.

Type 2::

Given a particle, $\mathbf{x }_{I} \in \mathbb {X}$, define the index set, $\varLambda ^{I}$, containing the indices of those evaluation points that result in a non-zero shape function value with respect to particle $\mathbf{x }_I$, or more formally

$$\begin{aligned} \varLambda ^{I} = \left\{ J \vert \mathbf{y }_J \in \mathbb {Y} \wedge \varPsi _{I} \left( \mathbf{y }_{J}\right) \ne 0 \right\} . \end{aligned}$$

(10)

Particle–evaluation point adjacency, $\varLambda$, is the set whose elements are the $\varLambda ^I$. Figure 1 shows a graphical depiction of Eq. 10. The circles and squares represent points in $\mathbb {Y}$. The particle of interest $\mathbf{x }_I$ is shown as a triangle with its corresponding domain of influence represented by the circle. The index set of evaluation points that result in a non-zero shape function value with respect to particle $\mathbf{x }_I$ are denoted by the squares.

Fig. 1

Graphical depiction of $\varLambda ^{I}$, an element in Type 2, particle–evaluation point adjacency

Type 3::

Given a particle, $\mathbf{x }_{I}$, determine the index set of particles, $\varPi ^{I}$ whose support domain overlaps with the support of $\mathbf{x }_{I}$, specifically

$$\begin{aligned} \varPi ^{I} = \left\{ K \vert \mathbf{x }_K \in \mathbb {X} \wedge supp\left( \mathbf{x }_{I} \right) \cap supp \left( \mathbf{x }_K\right) \ne \emptyset \right\} . \end{aligned}$$

(11)

The particle–particle adjacency is given as the set $\varPi$ whose elements are the $\varPi ^{I}$.

The prescription in Eq. 11 is applicable in a continuous setting, however, in the solution of PDEs employing a numerical integration technique the discretization will result in particle to particle adjacencies that do not occur due to the discrete nature of the integration. This situation can be seen in Fig. 2. Here the lightly shaded symbols represent the integration grid and the particles are denoted by dark triangles and labeled $\mathbf{x }_{1}$, $\mathbf{x }_{2}$, and $\mathbf{x }_{3}$. According to Eq. 11 all three particles are neighbors, but since particles $\mathbf{x }_{1}$ and $\mathbf{x }_{2}$ do not share an evaluation point their respective discrete adjacency is broken. The lightly shaded rectangles and diamonds are the evaluation points in the overlapping supports yielding $\mathbf{x }_1$ and $\mathbf{x }_3$ as neighbors and $\mathbf{x }_2$ and $\mathbf{x }_3$ as neighbors, respectively. Therefore, we can restate Eq. 11 to define the discrete particle–particle adjacency as

$$\begin{aligned} \varPi ^{I} = \left\{ K \vert \mathbf{x }_K \in \mathbb {X} \wedge \varLambda ^{I} \cap \varLambda ^{K} \ne \emptyset \right\} . \end{aligned}$$

(12)

Fig. 2

Graphical depiction of Type 3, particle–particle adjacency

3.1 Relation between Type 1 and Type 2 adjacency

The Type 1 and Type 2 adjacencies are not mutually independent, they are duals of each other. Given the evaluation point to particle adjacency information, $\varTheta$, the particle to evaluation point information, $\varLambda ^{I}$, for particle I can be stated as

$$\begin{aligned} \varLambda ^{I} = \left\{ J \vert \mathbf{y }_{J} \in \mathbb {Y} \wedge I \in \varTheta ^{J} \right\} . \end{aligned}$$

(13)

Similarly, if the particle to evaluation point information, $\varLambda$, is known the evaluation point to particle information, $\varTheta ^{J}$, for evaluation point J is

$$\begin{aligned} \varTheta ^{J} = \left\{ I \vert \mathbf{x }_{I} \in \mathbb {X} \wedge J \in \varLambda ^{I} \right\} . \end{aligned}$$

(14)

Note that since Eq. 12 does not contain any information on evaluation points, it cannot be used, by itself, to construct Type 1 or Type 2 adjacency, and hence is itself insufficient for meshfree applications involving evaluation points. In a formulation in which exact integration over analytic geometric domains were used, this might not be the case, but the authors are un-aware of any such formulations. Given the insufficiency of Type 3 adjacency and its construction through Eq. 12, it will not be further discussed in this paper.

The dual nature of Type 1 and Type 2 adjacency means that either adjacency can be used to fulfill any role in which either type is required. However, some applications are more naturally addressed by one type than the other. It should be noted that it is possible to construct all three types of adjacency simultaneously. However, in a multi-threaded computation, this will lead to race conditions impeding efficient shared-memory parallel (SMP) performance. Similarly, use of one adjacency may be more convenient or efficient, again considering SMP environments. This paper will focus on solutions that both work naturally for their purpose and scale well in multi-threaded implementations.

3.2 Example uses of adjacency

The application dictates which of these sets will be needed. In a finite-dimensional Galerkin solution of PDEs the weak form of the governing equations need to be integrated resulting in the formation of a system of algebraic equations, commonly referred to as assembly. In the context of solid mechanics the coefficient matrix is known as the stiffness matrix whose entries depict the interaction between the degrees of freedom. Generally speaking there are two approaches that can be used to perform assembly, the evaluation point-wise or the particle-wise approach.

In the evaluation point-wise method, all contributions to the various matrix elements from the single evaluation point are computed and accumulated. Successively considering each evaluation point results in a complete stiffness matrix. This approach requires Type 1 adjacency, which is the information contained in $\varTheta$. The algorithm for the evaluation point-wise assembly is given in Algorithm 1.

In this assembly procedure each evaluation point is going to affect multiple degrees of freedom, which means multiple entries in the global matrix will be affected by the same evaluation point. This presents a race condition when parallelizing over the evaluation points as multiple evaluation points will need to write to the same location in memory.

Alternatively, the assembly procedure can be done on groups of evaluation points, as is often done in FEM. The group of evaluation points used are those which affect the same degrees of freedom. In finite elements this is simply the Gauss points contained within an element with the nodes being those of the element. Instead of adding the contributions of each evaluation point into the global matrix, a local or element matrix is created, which is then added to the global matrix. Note this approach also has a race condition on an SMP.

The second assembly procedure is based on the particle viewpoint. In this approach the particle to particle, $\varPi$, and particle to evaluation point, $\varLambda$, adjacencies are needed. The procedure is to iterate over the particles and for each particle, $\mathbf{x }_I$, determine the particle to particle adjacency $\varPi ^{I}$. Then for each particle in $\varPi ^{I}$ determine the evaluation points that are common between each particle pair and compute the entry in the global matrix. The algorithm for the particle-wise assembly is given in Algorithm 2.

This approach allows for straightforward parallelization over the particles. However, if the Type 1 connectivity information is not computed a priori a large number of redundant calculations will occur, since the same evaluation point will be in the domains associated with multiple particles. To avoid this the evaluation point to particle adjacency information, $\varTheta$, can be pre-computed and stored along with shape function values. Depending on the size of the problem this memory overhead could result in a large payoff in run time since the shape function values are needed not only during assembly, but often during post-processing.

The matrix assembly example assumes that all of the quadrature points and particles are known, and either Type 1 or Type 2 adjacency can easily be used. On the other hand, one may have a problem in which either the evaluation points or the particles are known only dynamically. Such applications would be contact problems, where additional quadrature points along boundaries in contact are determined during the course of the simulation. Another example would be dynamic refinement by particle insertion. Depending on how adjacency is stored and constructed, one type may be easier than the other.

A naive approach to determining the adjacency information contained in $\varTheta$ or $\varLambda$ would involve checking all the particles against all the evaluation points resulting in an $\mathcal {O}\left( N_{e}*N_{p}\right)$ algorithm and the particle to particle interactions, $\varPi$, would require $\mathcal {O}\left( \frac{N_{p}\left( N_{p} + 1\right) }{2}\right)$. These naive approaches are very inefficient as they have not exploited the fact that particles are compactly supported. In order to reduce this cost, a data structure that excludes most of the objects from the search can be utilized. Data structures of this type are of fundamental importance in many fields of computer science, such as computer graphics. The construction of this type of data structure requires either the space in which the objects reside to be partitioned or the set of objects themselves to be partitioned.

4 Data structures

A data structure is simply a method for organizing, storing, and retrieving data. Beginning programmers learn about the most fundamental data structure, an array, early in their studies. Copious other data structures have been developed by computer scientists over the years and it is a subject in and of itself. All data structures inherently balance a number of attributes: memory overhead, search times, access, retrieval, and dynamic size. Depending upon the application, one of these attributes may take precedence over the others, and data structures focused on optimizing that attribute can be developed. In the context of meshfree methods, there are two options for data to be stored to effect the three types of adjacency described in Sect. 3. One can store evaluation points, or one can store particles. The former have zero extent, but the latter carry volume information, in the form of the size of their support, that needs to be taken into account. Regardless of this choice, both Type 1 and Type 2 queries must account for the support size of the particles. Note that particle extent can be accounted for either in the construction of the data structure, when storing particles, or during a search. Therefore, three different viewpoints can be taken when developing a data structure for conducting adjacency queries in meshfree methods (Table 2).

Table 2 Data structure options for accounting for particle support

The key to efficient searching of a data structure is to reduce the number of potentially expensive detailed evaluations of the search condition. In meshfree methods, the search condition typically entails determining whether a given point is within the support of a particle. Given that evaluation points and particles are distributed in space, a natural approach to reduce the number of detailed support checks is to organize the data so that points and particles that are far from each other are excluded from detailed checks. The following sections will describe two basic approaches to partitioning the data, spatial partitioning and object partitioning. While the focus of this paper is in applications to meshfree methods, the data structures and associated algorithms will be presented in an abstract manor. The purpose of this is not to obfuscate the implementation details, but to provide the reader with a generic algorithm that could be applicable to problems outside the context of meshfree methods. In addition, the spatial partitioning data structures can be used to determine both Type 1 and Type 2 adjacency with only minor changes to the algorithm, so for brevity these subtleties have been abstracted allowing for a single algorithm associated with each data structure for both searching and construction. The specifics of applying these algorithms for answering the adjacency questions that arise in meshfree methods will be given in Sect. 4.1.4.

4.1 Spatial partitioning

Spatial partitioning data structures decompose the space in which the objects reside into disjoint regions and distribute the objects into the resulting partitions. A drawback to this type of structure arises for objects that have a non-zero spatial extent, or size. Often this results in an object overlapping multiple partitions, leading to multiple references to the same object. Pursuing the goal of using the data structure to reduce the candidate sets of objects to be checked, one generally ends up with a relatively fine subdivision, relative to the support size of the particles, and thus many particles have multiple references in nearby subdivisions. For a large collection of objects these references may result in a sizable memory footprint. In the context of meshfree methods, the particle supports are required to overlap, thereby guaranteeing that each spatial subdivision intersects multiple particle supports. To circumvent the memory issue while still using a spatial partitioning data structure two options exist. The first is to construct the data structure on the particles, but not account for their supports. The second is to construct the data structure on the evaluation points, which have zero volume. Three spatial partitioning structures will be discussed: grids, kd-trees, and the well-known octree/quadtrees. Further discussion on spatial partitioning data structures can be found in [7, 31].

4.1.1 Regular grids

The grid spatial subdivision was proposed as an acceleration method for generating images using ray tracing by Fujimoto and Iwata [16]. The concept of a grid is to subdivide an axis aligned space into equal sized rectilinear regions or cells. Each cell stores references to the objects that overlap it or are contained within it. While the grid data structure was originally designed to accelerate ray–object intersections, it can also be used during query operations occurring in meshfree methods, discussed in the following two sections.

4.1.1.1 Construction The algorithm for constructing a grid is given in Algorithm 3. The construction routine operates on the a set of geometric objects, $\mathbb {Y}$, with bounding box $\mathbf{B }$. The result of the construction is an array of grid cells $\mathbf{C }$, where each cell contains a set of references to those objects associated with the cell. The first task of the construction routine, Line 1, is to determine the resolution of the grid. The resolution of the grid can be a prescribed value by the user, but determining an optimal setting for this value is non-trivial and some choices can result in a subdivision that is either too coarse, causing poor performance, or an overly refined grid that results in a large memory footprint. To address this issue we use the approach to determine the resolution such that the total number of cells in the grid is linearly proportional to the number of objects in the grid and the cells are approximately cuboidal in three-dimensions or square in two-dimensions [29]. Using these conditions the resolution of the grid can be computed as shown by Eq. 15.

$$\begin{aligned} n_{i} = \left\lceil \varDelta y_{i} \left( \frac{\gamma N_{p}}{\prod _{j}^{d} \varDelta y_{j}} \right) ^{\frac{1}{d}} \right\rceil \quad i = 1,\ldots ,d \end{aligned}$$

(15)

Here $n_{i}$ is the number of cells along direction i, $\varDelta y_{i}$ is the ith extent of the grid, $N_{p}$ is the total number of objects in the grid, d is the spatial dimension, and $\gamma$ is a proportionality constant that linearly relates the number of objects to the total number of grid cells, i.e., $N_{cells} = \gamma N_{p}$. Choosing an appropriate value of $\gamma$ requires experimentation and will vary from problem to problem. The authors have found values ranging from one to ten to be a good choice for most problems. Choosing a larger value will result in a more refined grid, which could reduce the number of objects residing in a single cell. Given the resolution, Line 2 allocates an array of empty cells corresponding to the resolution. Determining the indices of a cell containing a specific coordinate is a linear interpolation problem along each spatial dimension as shown in Eq. 16.

$$\begin{aligned} \frac{i_j - i_j^{min}}{i_j^{max} - i_j^{min}} = \frac{y_j - y_j^{min}}{y_j^{max} - y_j^{min}} \quad j=1,\ldots ,d \end{aligned}$$

(16)

The upper and lower cell indices along the jth direction are defined by $i_j^{max}$ and $i_j^{min}$ respectively. The upper and lower limits of the grid are defined as $y_j^{max}$ and $y_j^{min}$ and $y_{j}$ representing the jth component of the known coordinate. Assuming a zero based indexing scheme for the cell numbering and solving for the unknown cell number $i_j$ leads to the following expression,

$$\begin{aligned} i_{j} = \left\lfloor \left( \frac{y_{j} - y^{min}_{j}}{\varDelta y_j} \right) n_{j} \right\rfloor \quad j=1,\ldots ,d \end{aligned}$$

(17)

Equation 17 does suffer from one pitfall in practical applications, which is the scenario where $y_j$ is greater than or equal $y_j^{max}$. This will result in $i_j = n_j$, but the cells are numbered such that $i_j \in \left[ 0,n_j - 1 \right]$. To handle this situation a simple routine to clamp the values to the interval $\left[ 0,n_j - 1\right]$ is used. With the ability to compute the indices of a cell associated with a single coordinate the cell numbers pertaining to those cells intersecting the geometric object can be determined by considering an axis aligned bounding box (AABB) encompassing the domain of $\mathbf{y }$, which provides two spatial locations that define the range of cells the particle intersects. The cells in this range are updated with a reference to $\mathbf{y }$.

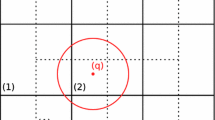
4.1.1.2 Searching The regular grid search algorithm, given in Algorithm 4, seeks to determine those objects that intersect the search domain, $\mathbf{S }$, defined here by a location and radial vector as shown in Fig. 3. The algorithm begins with an intersection test against the search domain and the bounding box of the grid. If no intersection occurs the search is terminated. Given an intersection does occur the cells that have a non-zero intersection with the search domain are determined and the objects residing in these cells are then queried to determine those that intersect the search domain.

Fig. 3

Search domain

4.1.2 Kd-tree

The kd-tree [5] is a popular variant of the more general Binary Space Partitioning (BSP) tree [15]. The kd-tree adaptively decomposes a space into disjoint rectilinear partitions. This differs from the uniform grid decomposition of the space in that it adapts to irregularly distributed objects. A kd-tree restricts the splitting plane to be orthogonal to one of the coordinate axes. This restriction allows for efficient construction with the sacrifice of how the space is divided.

4.1.2.1 Construction The general procedure for constructing a kd-tree for is given in Algorithm 5. The input to the construction routine is a set of geometric objects, $\mathbb {Y}$, with associated bounding box $\mathbf{B }$. The output of the construction algorithm is a kd-tree $\tau$. The routine begins by checking if the termination criteria has been met. Several options exist for the termination criteria. The first possibility uses a preset limit on the number of objects that a single kd-tree node is allowed to contain, commonly referred to as the bin size. Another possibility for the termination condition is restricting the height of the tree. In addition, the volume of the half space that a tree node represents could be restricted, this termination condition is useful when the geometric objects the tree is constructed upon are of a non-zero volume. Once the termination condition is satisfied the splitting of the tree node is stopped and a single leaf node is constructed and updated with references to the objects that are contained within the node. If the termination criteria is not met the algorithm proceeds to Line 4 where a splitting plane, ${\mathcal {P}}$, is determined. Several options for determining a split plane are shown below.

• Median splitting The splitting dimension is the dimension with the greatest variation. The splitting location is taken as the median of the coordinates along this dimension.

• Cyclic splitting Similar to the median splitting rules except the splitting axis is chosen in a cyclic manner. That is the root will start with the split axis being along the x-axis, the next level of the tree will then use the y-axis as the split directions and the next level using the z-axis.

• Midpoint splitting Similar to the median splitting rule, the split direction is determined by the greatest variation in the bounding box of the tree node being split. The split location is then taken as the mid-point of this side.

Given ${\mathcal {P}}$, the left and right half spaces can be defined. Line 7 computes the intersection of $\mathbb {Y}$ with $\mathcal {H}^{L}$ resulting in the subset $\mathbb {Y}^{L} = \{y_j \in \mathcal {H}^{L}\}$. The ConstructKDTree function is then called recursively at Line 8 with $\mathbb {Y}^{L}$ as the input, resulting in the left kd-tree node $\tau ^{L}$. A similar procedure is conducted for the right half space. Line 11 creates a single tree node and with references to the left and right child nodes.

4.1.2.2 Searching The kd-tree search algorithm is given in Algorithm 6. The inputs to the search routine are the constructed kd-tree, $\tau$, from Algorithm 5 that is rooted at tree node $\mathbf{r }$ and a search domain. The result of Algorithm 6 is the set of objects, $\varTheta \in \tau$, that have a non-zero intersection with the search domain $\mathbf{S }$. The search begins by checking if the root of the input kd-tree is a leaf node. If this condition is true the algorithm queries each item associated with the given leaf to determine those that intersect $\mathbf{S }$ appending them to the set $\varTheta$. Provided the root of the input kd-tree is not a leaf node the algorithm proceeds to Line 6, where the split plane associated with the given node is retrieved. The split plane, ${\mathcal {P}}$ is then used to define the left half space in Line 7. A intersection test between the search region, and the left half space $\mathcal {H}^{L}$ is performed. Since the search region is capable of intersecting both left and right half spaces each must be tested independently of the other. If either intersection occurs the respective child node is used as the input to a recursive call to Algorithm 6. The resulting sets from Lines 11 and 14 are combined as shown by the union operation at Line 15.

4.1.3 Octree

An octree is a three-dimensional space partitioning data structure that uses three mutually orthogonal planes to recursively decompose the space into eight axis-aligned boxes, or octants, at each step. The quad-tree is the two-dimensional analog to the octree, where instead of the eight axis-aligned boxes used by the octree, the quad-tree recursively partitions the space into four rectilinear regions or quadrants. An octree differs from a kd-tree in several ways. The kd-tree is a binary partitioning data structure in that at each level the space is decomposed into two sub-regions, where as the octree decomposes the space into eight sub-regions at each level. In general, an expression for the size of a kd-tree node is not possible due to the varying nature of the split location and direction. The extents of an octree node can be expressed as

$$\begin{aligned} \varDelta x^{s}_{i} = \frac{\varDelta x^{0}_{i}}{2^{s}} \quad i=1,\ldots ,d. \end{aligned}$$

(18)

Here $\varDelta x^{s}_i$ represents the extents of the octree node at level s of the tree with $\varDelta x^{0}$ representing the bounds of the root node. In Eq. 18 the depth value, s, is an identifier on the left side of the equals sign, but is the power when appearing on the right hand side.

4.1.3.1 Construction The general procedure for constructing an octree is given in Algorithm 7. The inputs to the construction routine are the set of geometric objects, $\mathbb {Y}$, and the bounding box, $\mathbf{B }$, encompassing $\mathbb {Y}$. The output of the construction algorithm is an octree $\tau$. The routine begins by checking if the termination criteria has been met. Several options exist for the termination criteria.Possible termination conditions include:

• if the number of objects within a leaf falls below a prescribed value

• if the number of subdivisions exceeds a prescribed value

• if the extents of the leaf reaches a minimum size, which is another form of the max subdivision criteria as the size of a tree node can be determined at each level of the tree provided the root node’s extents using Eq. 18.

Once the termination condition is satisfied a leaf node is constructed and updated with references to the objects that intersect it. If the termination criteria is not met the algorithm proceeds to Line 5 where three splitting planes, ${\mathcal {P}}_1$, ${\mathcal {P}}_2$, and ${\mathcal {P}}_3$, which partition the current tree node into eight equal sized octants. The partitioning is performed around the current tree node’s centroid. The next step involves partitioning the set of objects $\mathbb {Y}$ into eight subsets where the ith subset contains those objects that intersect child i of the current node. Following this partitioning the construction routine is recursively called as shown in Line 9. Once the recursion routine returns the constructed sub-tree is added to the current tree node.

4.1.3.2 Searching The octree search algorithm is given in Algorithm 8. The inputs to the search routine are the constructed octree, $\tau$, from Algorithm 7 that is rooted at tree node $\mathbf{r }$ and the search region. The result of Algorithm 8 is the set of objects in $\tau$, that intersect the search domain. The search begins by checking if the root of the input octree is a leaf node. If this condition is true the algorithm queries each object associated with the given leaf to determine those objects that intersect $\mathbf{S }$, appending those that intersect to the set $\varTheta$. Provided the root of the input octree is not a leaf node the algorithm proceeds to Line 6, where the child nodes that the search region intersects are determined. This determination is based on the three planes used to partition the current node $\mathbf{r }$ into octants. This child node is then retrieved and used as the first argument to a recursive call to Algorithm 8.

4.1.4 Meshfree details

Here we will bring to attention the way in which the above algorithms can be used to answer the adjacencies questions arising in meshfree methods and which data structures are most applicable. Each of the three data structures described can be used to determine either Type 1 or Type 2 adjacencies.

Using a spatial partitioning data structure for determining evaluation point to particle, Type 1, adjacency information the Case 1a or Case 1b viewpoint is taken with the space containing the particles being partitioned. For Case 1a the space encompassing the particle locations and their supports is used and only the particle locations for Case 1b is used. The concept of an intersection between the particles and a cell or node of the data structure is utilized in each construction algorithm. For the Case 1a this intersection is between the support of the particle, where as for Case 1b this intersection only takes into account the spatial position of the particle. Therefore the intersection used in the Case 1b construction can result in only a single intersection, i.e., a particle can associate with at most one cell or node. This differs from Case 1a where a particle support can intersect multiple cells or tree nodes.

The search is then conducted per evaluation point resulting in those particles that contribute at the given evaluation point. Each of the search algorithms requires a search domain. The search region for the Case 1a is the evaluation point location or a region with zero extent. The search method in Case 1b requires a search domain be assigned to the evaluation point. In general the particles are associated with a support size not the evaluation point. So a method to choose a bounds for the search must be applied. A solution that is guaranteed to work is to choose the supremum of the particle supports. However, this approach could result in a large number of particles needing to query the evaluation point if particle distribution is graded.

When determining the particle to evaluation point, Type 2, adjacency information the spatial partitioning data structures decompose the space containing the evaluation points and search per particle as described by Case 2. The only aspects that differentiate this case from Case 1 are the input arguments and the results. Here the construction is done on the evaluation point locations instead of the particle locations. The search for Case 2 is done per particle with the search region being the particle’s support domain.

4.2 Object partitioning

Object partitioning structures recursively subdivide the collection of primitives into disjoint sets. Therefore, object hierarchies do not suffer from the additional memory requirement associated with multiple references to the same object, since the object is at most referenced once. Data structures of this type have received little attention in the context of meshfree methods. This could be due to the fact that querying a single point is not a common operation; instead, all of the points of interest are evaluated at once making the spatial partitioning data structures constructed of evaluation points feasible. However, a data structure of this type is not feasible if all the evaluation points are not known apriori. This case may arise, for example, in problems involving contact, where the points of contact are part of the problem to be solved [21]. Another disadvantage of determining adjacency information on a per particle basis, is the race conditions that are present, which requires special attention to allow for parallelization. The race condition potentially arises when storing the shape functions from multiple particles at the same evaluation point. A final disadvantage to using a Case 2 structure for shape function computations occurs when one prefers to compute shape functions on the fly, rather than pre-compute and store them. In the former case, one would have to evaluate the set $\varTheta ^J$ from Eq. 14. This would be very costly. Alternatively a spatial partitioning data structure following the Case 1a or Case 1b mantra can be used as described in the previous sections. While these structures do address the challenges associated with the Case 2 variants, they do present their own challenges.

4.2.1 Bounding volume hierarchy

A well-known object partitioning data structure is the Bounding Volume Hierarchy (BVH). As object partitioning data structures are designed to partition objects with non-zero volume they naturally address the adjacency query corresponding with Case 1a. Bounding Volume Hierarchies, introduced in [27], partition the set of objects into a hierarchy of non-disjoint sets. References to the objects are stored in the leaves and each node stores a bounding box of the primitives in the nodes beneath it.

4.2.1.1 Construction The construction of a BVH is performed on the particles accounting for their support domains. The BVH construction shown in Algorithm 9 resembles the construction of the kd-tree in Algorithm 5. Comparison of the two algorithms shows the only apparent difference, with the exception of kd-tree being replaced by BVH, being the computation of the bounding-box at Line 1 of Algorithm 9. However, another significant difference exists that is masked by the abstract intersection between the particles in $\mathbb {X}$ and the half spaces. These intersections for the Case 1a kd-tree were between the support of the particles and the half spaces, but the intersections shown in Algorithm 9 are between the coordinates of the particles and the half spaces. Since the classification is based on a spatial position i.e. not on a volume there are no repeated references as in the Case 1a spatial partitioning structures. Once the set of particles have been placed in their respective tree node the newly created leaves must recompute their bounding boxes accounting for the support of the particle. In contrast to spatial partitioning data structures where the splitting plane defines one of the extents of a tree node’s bounding box, the extents of the bounding box for tree nodes can span across this plane overlapping one another.

4.2.1.2 Searching As the BVH is constructed of particles, the goal of the search algorithm is to query the BVH with an evaluation point and determine Type 1 adjacency. The search process shown in Algorithm 10 begins with a point inside test between the root’s bounding box and the evaluation point. If the point is not inside the root’s bounds then the search is terminated. Provided the evaluation point is inside the root’s bounding box the search proceeds by determining if the root is a leaf node. If the node is a leaf the algorithm iterates through the particles associated with the node and performs a containment query between the evaluation point and each particle. If the root has children then each child node of $\mathbf{r }$ is retrieved and a point inside test is used to determine if the search should proceed with a recursive search using that node. Once each child node has been processed the resulting sets are combined and returned. While the BVH search routine, shown in Algorithm 10, follows a similar procedure to that of the kd-tree search routine previously discussed several key differences exist. The first is the determination of whether a child node should be processed. This selection was done using a splitting plane in the kd-tree. This differs from the BVH which conducts a point inside bounding box test. Another difference is the combining of results from each subtree search. For the BVH these results are guaranteed to be disjoint allowing for a simple structure to be used for combining these results. However, the Case 1a kd-tree variant the results were not necessarily disjoint requiring a more sophisticated data structure or algorithm for combining the results.

4.2.1.3 Remarks Unlike the spatial partitioning data structures the BVH partitions the set of particles treating them as individual bounding boxes. Therefore, the BVH falls under the Case 1a description and is best suited for determining Type 1 adjacency. If the BVH were to be constructed of objects with no extents it would be identical to the kd-tree.

4.2.2 A new support tree structure

We now introduce a new data structure that can be classified as an object partitioning structure with a tree-type hierarchy. The proposed data structure will be composed of a root node, collection of internal nodes, and leaf nodes. The root node and internal nodes are identical in that they are composed of three child nodes, split plane and bounding box. The leaf nodes are similar, but instead of a split plane and child nodes they contain references to the data that is contained within them.

4.2.2.1 Construction The construction uses a divide-and-conquer algorithm, also referred to as top-down, that groups the objects according to a splitting heuristic. The algorithm begins with all the particles at the top level or root as illustrated in Fig. 4. The bounding box of the root node is taken as the minimum box that contains the particles and their supports. Construction proceeds with the determination of the location and direction to be used for the splitting of the objects. The current approach employs a mid-point splitting heuristic, where the split direction is determined by computing the largest deviation along the current node’s bounding box. The location is then taken to be the mid-point along this direction. Considering the domain coverage in Fig. 5a and the greatest deviation to be along the horizontal or x-direction, with the split plane shown as the blue vertical line.

Fig. 4

Domain coverage

With the split plane determined, the particles are classified as strictly left, intersecting the split plane, or strictly right. This classification is done by determining whether the given particle’s support bounding box overlaps the split plane. If the bounding box does overlap, the particle is classified as belonging to child one; if the bounding box does not overlap, then the particle is classified as belonging to child zero or two. This depends on which side of the split plane the support bounding box lies, with child zero corresponding to the left of the split plane and child two corresponding to the right. In Fig. 5b the magenta boxes represent the supports of the particles that belong to child one, those particles with dashed lines that are left of the blue line belong to child zero with the remaining particles belonging to child two. As the objects are partitioned and distributed to the appropriate child nodes, the bounding box for each new child node is updated to enclose the particles and their supports. This procedure is repeated for each child node until a termination criteria is met. The termination criteria used in this paper occurs when all the particles’ supports overlap the splitting plane. Pseudo code for the construction is given in Algorithm 11.

Fig. 5

Construction of support data structure. a Splitting plane location for root node, b partitioning of root into child leaves

Fig. 6

Particle distribution for example problems. a Scarlet Macaw, b Stanford Bunny

Fig. 7

Close-up view of the particle distribution of Scarlet Macaw skull

Fig. 8

Memory requirements corresponding to Case 1 data structures. Memory versus number of particles for a Scarlet Macaw and b Stanford Bunny

Fig. 9

Memory requirements corresponding to Case 2 data structures for Ex. 1 and 2. Memory versus number of evaluation points for a Scarlet Macaw and b Stanford Bunny

Fig. 10

Construction time corresponding to Case 1 data structures. Construction time versus number of particles for a Scarlet Macaw and b Stanford Bunny

Fig. 11

Construction time corresponding to Case 2 data structures. Construction time versus number of evaluation points for a Scarlet Macaw and b Stanford Bunny

Fig. 12

Search time versus number of evaluation points for Case 1 data structures for the Scarlet Macaw (a) and Stanford Bunny (b) discretized with 122,334 and 1,284,920 particles respectively

Fig. 13

Search time versus number of evaluation points for Case 2 structures for the Scarlet Macaw (a) and Stanford Bunny (b) discretized with 122,334 and 1,284,920 particles respectively

Fig. 14

Search time versus number of particles for Case 1 structures for both examples using 140,625 evaluation points for the Scarlet Macaw (a) and 8,000,000 evaluation points for the Stanford Bunny (b)

Fig. 15

Search time versus number of particles for Case 2 structures for both examples using 140,625 evaluation points for the Scarlet Macaw (a) and 8,000,000 evaluation points for the Stanford Bunny (b)

4.2.2.2 Searching Given a spatial location, the objective of the search algorithm is to determine the particles that contribute at the given point. The search begins with a containment check between the root’s bounding box and the provided point. If the containment inquiry returns false then the search is terminated. If the point is within the root’s bounding box, then a check is done to determine if the root is a leaf node. If the node is a leaf node the algorithm iterates through the particles associated with the node and performs a containment query between the point of interest and each particle. If the root has child nodes then the search point is checked against the root’s split plane to determine the side it lies and the child node corresponding to that side is tested for existence along with child node one. Each of these nodes if they exist are processed following the same procedure used on the root of the tree.

4.2.2.3 Dynamic insertion In order for the data structure to be applicable for analysis that employs refinement based on insertion of new particles i.e. h-refinement, a dynamic insertion algorithm is necessary. To add a particle to an existing tree, the algorithm follows a similar procedure to that of the construction algorithm. The particle must first traverse down the tree using the particles support bounding box and the current nodes’s split plane to determine which child node to proceed to. For each interior node traversed, the bounding box must be updated to enclose the support of the particle. Upon reaching a leaf, a reference to the particle is added to existing list of references and the bounding box for the leaf is updated. The leaf is then processed to test whether a split needs to occur following the procedure described in the construction algorithm. To avoid splitting prematurely a minimum split requirement can be enforced.

5 Related work

Most of the work related to improving the adjacency information searches in meshfree methods can be classified as one of the aforementioned cases coupled with the previously discussed data structures. An early overview of various techniques for fixed radius nearest neighbor searching are given in [6].

In [22, 23], a bucket algorithm is used to reduce the computational cost associated with determining adjacency information. The algorithm allows a maximum number of particles to reside within each bucket. The allowable number, also known as the bin size, is defined according to the size of the problem and the maximum number of particles allowed in a support domain. If the number of particles in the bucket exceeds the bin size the bucket is partitioned into two sub-buckets. The subdivision is repeated recursively on each sub-bucket until the number of particles in a bucket is less than or equal to the bin size. Generally speaking, the bucket algorithm is similar to the Case 1b kd-tree and octree.

The authors in [18] employ a strategy similar to the regular grid Case 2. Here the authors use a rectangular grid with each region containing a set of Gauss points, which is referred to as a Gauss region. Then given a particle the region containing the spatial coordinates of the particle can easily be computed. Once the Gauss region containing the particle is located the neighboring Gauss regions that have non-zero intersection with the particle’s domain of influence are determined and the Gauss points within the regions are queried to determine if they fall with the particle’s support domain.

An analysis of various techniques for increasing the efficiency of the shape function computations in RKPM and MLS is discussed in [2]. The authors note the bottleneck associated with determining adjacency information and suggest the use of a kd-tree. The authors do not explicitly state if the kd-tree is constructed on the particles, or the evaluation points. In their description of the kd-tree it is clear that they are using a variation that does not consider the volumes of the particles in the construction.

An approach based on hash tables and regular grids is discussed in [28]. The neighbour search problem as it pertains to SPH is addressed in [30]. Here the authors present a search algorithm, based on the plane sweep algorithm to efficiently answer the neighbour search problem. A block-based searching technique is introduced in [9] for efficient computation of partition of unity interpolants. The authors in [17] address the challenge of locating the particles contributing at an evaluation point using quadtrees and octrees constructed of particles accounting for their supports. The implementation of the search algorithms given in [17] for parallel computing are given in [8].

6 Performance comparison

In this section, the performance of the previously discussed data structures will be presented. A complete comparison of all the methods under a wide range of the various user-supplied parameters or algorithm choices is too voluminous for a journal article. Rather, we take the approach of making commensurate, as nearly as possible, choices for each of the methods so that we can make a fair comparison. Then, we show how the memory cost, search and construction times scale with the number or particles or evaluation points. For any given data set, any of the methods may be significantly improved by optimizing the selection of parameters. We will include a brief guide on our opinion in choosing a method.

Two meshfree domains are used to measure the construction time, search time, and memory footprint for each method on both structured and unstructured arrangements of particles. All of the data structures were implemented in C++ and run on an Intel Xeon CPU E5-2680 v2 @ 2.80 GHz with 64 GB of RAM. The unstructured data is two-dimensional and comes from the micro-CT scan of a Scarlet Macaw skull, shown in Fig. 6a, with discretizations ranging from 31,139 to 157,317 particles. Figure 7 shows a close up view of the particles and their distribution. Clearly, this particle distribution is graded and shows large regions with no particles, and small regions with varying particle density. It should provide a good test for both spatial and object partitioning data structures and their ability to handle a wide variation in particle distribution and spacing. The structured data example is a particle distribution of the Stanford Bunny,¹ with discretizations ranging from 196,017 to 3,793,349 particles as shown in Fig. 6b. It is worth recapping that the approaches of Case 1a and Case 1b seek to solve the same problem, namely determining what particles have non-zero contribution at a given evaluation point i.e., Type 1 connectivity. Case 2 is different, in that it is best suited for determining what evaluation points lie in the support of a given particle i.e., Type 2 connectivity. Before discussing the performance heuristics, the factors that impact these results for each of the data structures warrants a discussion. Recall from the previous sections that discussed the algorithms for constructing and searching the various data structures being discussed in this paper that all the construction routines required some user defined parameters, which can have significant impacts on the performance of the data structures. In addition to these parameters, the actual implementation of these data structures can have drastic effects on performance. In all of our implementations, an effort to program the best version of each method was made. The grid data structure required a method to determine the grid resolution. The numerical studies conducted in this paper determined the resolution with Eq. 15. The build factor, $\gamma$, used to determine the grid resolution was set to one resulting in the total number of grids being approximately equal to the number of particles. While using a larger value for $\gamma$ would result in a more refined grid and potentially better search times, this would also result in a larger memory footprint. Instead a smaller value of $\gamma$ could be used resulting in slower search times, but the memory costs would also be reduced. The kd-tree requires a splitting rule and termination criteria be defined. The kd-trees in this study used a mid-point splitting rule with the split axis corresponding to the dimension with the greatest deviation of a tree node’s bounding box. The termination criteria was satisfied when the number of objects associated within a tree node fell below a user defined threshold or if the volume of the node’s bounding box became less than the volume of the largest support size. While it is true that the first termination criteria will eventually be satisfied, the Case 1a kd-tree requires objects that overlap the splitting plane be associated with each child node requiring numerous references to the same object resulting in a large memory footprint as will be discussed in the next section. The Case 1b and Case 2 data structures do not suffer from this and a bin size of one was used for both kd-tree variants. As with the kd-tree, the BVH requires a splitting rule and termination criteria. The same splitting rule and similar termination conditions used for the kd-tree were employed for the BVH in this study. Differing from the Case 1a kd-tree, the BVH partitions the objects and therefore does not require multiple references to the same object and cannot create tree nodes of a size that is significantly smaller than particles’ support sizes reducing the potential growth in memory. Therefore no restriction on the volume of a tree node was necessary. Several bin sizes were tested and from these trials a bin size of one was chosen as it provided the best performance in regards to searching at a higher memory cost, but the memory cost were not considered substantial. Depending on the splitting rule used the proposed data structure may not need a termination criteria. By using a mid-point splitting rule the termination criteria is defined once all the objects overlap the splitting plane. This removes an element of user interaction and the potential for a poorly chosen value that could result in an ill-performing data structure. However, the use of a different splitting rule may require a different termination criteria. The implementation used in this paper employed a mid-point splitting rule and therefore did not require a user defined termination criteria.

6.1 Memory cost

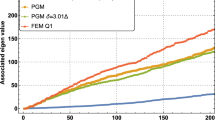
The memory usage for those data structures constructed based on Case 2 are independent of the number of particles, as they are constructed of evaluation points. The memory usage for the tree based data structures is dependent on both the termination criteria and for the BVH, Kd-tree, and Support tree the splitting method is also a factor. The memory for the Case 1a and Case 1b data structures are plotted on the same graph for each example in Fig. 8a, b, respectively. From the figures, it is clear that among the Case 1a implementations, the grid, depicted by the magenta line, exhibits the worst memory usage. However, for the Case 1b approaches, the grid appears to have the lowest memory footprint, which clearly is due to the fact that the particle support size is not taken into account. Considering only the Case 1a data structures the proposed Support Tree data structure, shown here by the green line, has the lowest memory impact for the second example, Fig. 8b, and is nearly identical to the kd-tree and octree for the first example with all three contending for the lowest memory impact. The grid data structure has the lowest memory footprint for Case 2 searches as shown in Fig. 9a, b.

6.2 Construction cost

Here, the time required to construct the various data structures is analyzed. A direct comparison of the three cases here is not feasible, as the data structures associated with Case 1a and Case 1b are constructed on the set of particles, where as those data structures associated with Case 2 are constructed on the set of evaluation points. The construction times for Case 1b approaches are significantly lower than Case 1a approaches, since accounting for particle support size is not necessary. For a mechanics problem using a meshfree approximation method the construction routines will generally occur once at the beginning of the simulation and could be conducted as a pre-processing step obviating the time from the main processing step entirely. However, if a refinement method is being used or evolving topologies are of interest the ability to quickly reconstruct the data structures could become important. The time required to construct the data structures is represented graphically in Figs. 10 and 11.

6.3 Search cost

In this section, we report the time it takes to search the various structures for computing the connectivities used in meshfree methods. Note that construction costs are one-time costs for a given problem, whereas the search times are accumulated over many calls. In general, many searches will be performed over the course of a computation. In some cases, for example constructing a stiffness matrix, the number of searches is known apriori, but in other cases, e.g. contact, the number of searches is not. Figures 12, 13, 14 and 15 show the time required to search the data structures for the given number of particles and evaluation points. For both examples the most efficient data structure is the regular grid constructed on the particles accounting for their support size.

6.4 Guide to choosing a search structure

As previously mentioned, one can tune any of these methods to improve search times or reduce memory cost, so it is not possible to recommend a single ‘best’ data structure. However, after many experiments, we can say that, in general, a grid structure or the support-tree structure will be a good choice. The grid, in one of the Case 1 scenarios, will substantially sacrifice memory for speed, or speed for memory. On the other hand, while it is not usually optimal in either speed or memory, the Support Tree does perform well in both regards in the two examples presented. If one needs or desires a single structure to be a work horse, performing well in most situations without user interaction, the support tree may be the best choice. Further, the Support Tree scales very well with number of particles stored, or in number of evaluation points searched. On the other hand, if either speed or memory footprint are paramount at the expense of all else, a properly tuned grid will likely be the best choice.

7 Conclusion

The computational expense associated with determining adjacency information presents a performance bottleneck for meshfree methods. The present work defined the three adjacency queries that commonly arise when employing a meshfree method. An overview of several data structures and the approaches to applying these within the context of meshfree methods were discussed. In addition to the discussion on existing data structures, a new data structure was proposed with the associated algorithms for construction, searching, and dynamic insertion.

The numerical results show the grid data structure is the best, both in memory and speed, for Case 2 searches, i.e. finding evaluation points within a given particle’s support. On the other hand, the newly proposed Support Tree showed good performance simultaneously in both memory usage and search speed and scaled very well with increasing problem sizes.

As previously mentioned, several of the data structures including the proposed data structure require the choice of a splitting plane during construction. A simple choice that was used for those structures presented in this paper is the mid-point splitting along the axis with greatest extent. While this does appear to provide good results and ease of implementation it may not result in an optimal partitioning, resulting in a negative impact on search times. The study of other heuristics was beyond the scoped of this paper, but the authors believe could result in the tree-based data structures out performing the grid in regards to query times. This belief is somewhat motivated by the performance gains seen in computer graphics where a cost function is employed to determine the best split plane.

Within this study, little was discussed on dynamically evolving domains such as those occurring in problems involving fracture and fragmentation. Obviously those data structures discussed within the context of Case 2 are not affected by such problems, but those Case 1a and Case 1b data structures are. The proposed work discussed a dynamic insertion algorithm, but the impact dynamic insertions will have on the performance of the structure still warrants further investigation.

Several remarks were made regarding parallel computing throughout the paper, but they were in the context of the shared memory paradigm. As modern infrastructures rely on the distributed memory paradigm, further examination of the applicability of the algorithms discussed should be addressed.