A new multi-layer approach for progressive damage simulation in composite laminates based on isogeometric analysis and Kirchhoff–Love shells. Part II: impact modeling

Abstract

In this two-part paper we introduce a new formulation for modeling progressive damage in laminated composite structures. We adopt a multi-layer modeling approach, based on isogeometric analysis, where each ply or lamina is represented by a spline surface, and modeled as a Kirchhoff–Love thin shell. Continuum damage mechanics is used to model intralaminar damage, and a new zero-thickness cohesive-interface formulation is introduced to model delamination as well as permitting laminate-level transverse shear compliance. In Part I of this series we focus on the presentation of the modeling framework, validation of the framework using standard Mode I and Mode II delamination tests, and assessment of its suitability for modeling thick laminates. In Part II of this series we focus on the application of the proposed framework to modeling and simulation of damage in composite laminates resulting from impact. The proposed approach has significant accuracy and efficiency advantages over existing methods for modeling impact damage. These stem from the use of IGA-based Kirchhoff–Love shells to represent the individual plies of the composite laminate, while the compliant cohesive interfaces enable transverse shear deformation of the laminate. Kirchhoff–Love shells give a faithful representation of the ply deformation behavior, and, unlike solids or traditional shear-deformable shells, do not suffer from transverse-shear locking in the limit of vanishing thickness. This, in combination with higher-order accurate and smooth representation of the shell midsurface displacement field, allows us to adopt relatively coarse in-plane discretizations without sacrificing solution accuracy. Furthermore, the thin-shell formulation employed does not use rotational degrees of freedom, which gives additional efficiency benefits relative to more standard shell formulations.

1 Introduction

Composite materials are increasingly adopted for structural lightweight applications in the aerospace field due to their high stiffness and strength properties. Nowadays laminated composites are used in the manufacturing of primary aircraft components including, as in the case of a new generation of long-range jet airliners, wing and fuselage structures. However, one of the most critical issues in the design of composite structures is their sensitivity to local damage caused by low velocity impacts, which may occur, for example, during normal operations, or even as a result of ground service or maintenance-related activity.

Because of the inherent heterogeneous nature of fiber-reinforced polymer composite materials and the complexity of their failure mechanisms, damage can occur at different length scales and often involves a simultaneous deterioration of the matrix material and separation of the layers that constitute the laminate, i.e., delamination. This damage mode, which often leads to a significant loss of strength of a structural component, may be difficult, if not impossible, to detect by visual inspection.

For these reasons, the response of composite laminates subjected to low velocity impact presents an important research direction. Experimental studies of Choi et al. [1] and a literature review from Richardson and Wisheart [2] identified delamination as a critical factor, which, owing to local instabilities of the disconnected lamina, severely affects post-impact behavior of structures subjected to compressive loads. These authors also stressed the fact that failure modes in composite laminates are interrelated, and that the development of comprehensive modeling approaches that can simultaneously and accurately capture intralaminar failure and delamination is of primary importance.

Several models have been proposed, starting from the early 1990’s, to predict damage growth in laminated composites subjected to low-velocity impact. Choi et al. [1, 3] developed finite element procedures to predict the extension of the delamination front based on the analysis of stresses in the plies. The references focused their attention on the interaction between matrix cracking and propagation of delamination. A prototype of a multi-layer modeling approach, where the plies are modeled as individual parts connected through discrete interfaces, was proposed in Allix et al. [4, 5] who developed a cohesive damage model in order to predict delamination under Mode I, Mode II, and mixed-mode openings. Several authors investigated the use of cohesive interfaces [6, 7] and cohesive elements [8, 9] to simulate the interaction between discrete plies in laminated structures, while Turon et al. [10, 11] developed a cohesive damage model in order to accurately predict delamination in composite laminates under multi-mode loading conditions. The use of discrete, connected interfaces, implemented either by means of surfaces or solid elements, allows for the development of multi-layer modeling techniques. As a result, a multi-layer representation combined with intralaminar damage modeling has become increasingly popular in recent years for progressive damage simulations of laminated composites.

A phenomenological Residual Stiffness Approach (RSA) [12, 13] is widely used as an intralaminar damage model. The RSA, which is developed in the framework of the Continuum Damage Mechanics (CDM), is based on a progressive reduction of the elastic properties of material as a function of the damage state, which is described in terms of the so-called damage variables that are evolved according to specific damage initiation and evolution criteria. Recent advances in the modeling of intralaminar damage include the introduction of the material nonlinearities [14] such as fiber kinking [15, 16] and nonlinear shear behavior [17]. Some authors [18, 19] also investigated the use of matrix plasticity to predict post-impact permanent indentation of the laminates. Several enhancements have been proposed in the past years for the intralaminar and interlaminar damage models. The proposed models make use of 3D solid linear [17,18,19,20] and higher-order [21] Finite Elements (FE) for the discretization of the continuum. Faggiani and Falzon [22] proposed a mixed model where, in order to reduce the problem size, solid elements were used in the impact region while continuum shell elements were employed elsewhere. Davila et al. [7] developed a 2D cohesive interface for the Reissner–Mindlin shell elements and applied it to simulate delamination in aerospace structural components under quasi-static loading conditions.

Nevertheless, despite these enhancements, simulation of impact on laminated composite structures is dominated by 3D linear hexahedral elements. While the computational costs can be kept at a manageable level (i.e., $\mathcal {O}(10^5)$ elements) for coupon-scale simulations, 3D solid element technology becomes prohibitively expensive for larger-size structural components. This was one of the motivating factors for the development of a computational approach based on Isogeometric Analysis (IGA) [23, 24] in the framework of the multi-layer shell modeling presented in detail in Part I of this paper. Because the individual plies of a laminate are sufficiently thin to be reasonably described using the Kirchhoff–Love shell theory, we took the work of [25, 26] on rotation-free shells, and its extension to CDM in [27], as the starting point. The individual lamina, modeled as thin shells and discretized using spline-based IGA with only displacement degrees of freedom, were connected with cohesive interfaces resulting in an accurate and efficient methodology that is able to simultaneously model intralaminar damage and delamination. The use of IGA has an added benefit of a natural connection to Computer-Aided Design (CAD), allowing the use of CAD or other geometric modeling software to model structural components and directly analyze them using the same geometry representation, without the need to generate FE meshes [28]. We note that an alternative approach to delamination modeling using IGA may be found in the recently proposed continuum or solid-like shell formulations [29, 30].

Part II of this two-part paper focuses on the application of the multi-layer IGA shell formulation to simulate damage in composite laminates due to low-velocity impact. The formulation developed in Part I of this article is augmented with a contact model between the impactor and laminate, which is presented in Sect. 2. In Sect. 3 the complete discrete formulation is summarized including intralaminar damage, delamination, and contact with the impactor. In Sect. numerical simulations of an impact test are carried out with the IGA-based formulation. In Sect. 5 the numerical results are compared with experimental data and two FE-based models. In Sect. 6 conclusions are drawn and future research directions are presented.

2 Contact algorithm

The ability of the method to handle contacts between the impactor and laminate, as well as between the lamina or sublaminates, is essential for carrying out simulation of impact on laminated composite structures. In what follows, we describe in detail the contact formulation employed in this work and its algorithmic implementation. The formulation is presented in the context of thin isogeometric shells. However, many of its constituents are applicable to a wider class of solid and structural models.

While several numerical techniques have been developed for contact and impact problems (see, e.g., [31] for a comprehensive review), the penalty formulation is the most commonly adopted methodology, especially for large-scale analyses, because, unlike in the case of Lagrange-multiplier or mortar-type methods [32], no additional unknowns are introduced in the formulation.

The penalty method is based on the introduction of a repulsive traction in order to enforce, albeit approximately, the non-interpenetration condition between the disconnected parts. The contact algorithm developed in this paper consists of two separate steps:

• 1. Search step, where pairs of candidate contact points are identified.

• 2. Penalization step, where a signed distance function is evaluated in order to verify if the contact criteria are satisfied.

By definition, a pair of candidate contact points are two material points belonging to two separate parts, or objects, that satisfy a user-defined search criterion. The existence of a pair of candidate contact points is only a necessary condition to determine whether the separate parts are in contact. The actual contact occurs only if the distance between the candidate points is smaller than a specified threshold. If both the search and penalization steps are successful, meaning that a pair of candidate contact points exists and the distance between them is small enough to satisfy the contact criterion, then contact traction is introduced in the multilayer-shell variational formulation. In what follows, we outline our methodology to detect interaction between separate parts represented by shell surfaces in 3D. We note that this two-step procedure is efficient because it allows one to perform the search step, which is computationally demanding, in a configuration of choice, such as, for example, the reference configuration at the beginning of the simulation. Conversely, the penalization step is much less expensive as it only requires evaluation of the distance between all the pairs of candidate contact points, and thus may be performed at every time-integration and/or nonlinear-iteration step.

2.1 Search step

A contact interface is defined as the intersection of two distinct surfaces, namely $\Gamma ^{1}$ and $\Gamma ^{2}$, which, in the framework of our modeling approach, correspond to NURBS surfaces representing two separate geometric entities. The purpose of the search step is to identify, for each point $\mathbf{x }_1 \in \Gamma ^{1}$, the corresponding candidate contact point $\mathbf{x }_2 \in \Gamma ^{2}$ defined according to a specific proximity criterion. From a theoretical standpoint, a pair of candidate contact points is defined as a subset of $\Gamma ^{1} \cap \Gamma ^{2}$. However, this definition is not appropriate in the framework of shell representations of 3D continuum. Indeed, in order to take the shell thickness into account, it is necessary to detect possible contact before the intersection of the surfaces occurs. We therefore introduce a search procedure in order to identify all the possible pairs of candidate contact points on all the surfaces where the contact is activated, while detection of the actual contact is deferred to the penalization step.

In our work, we developed a search algorithm based on the technique proposed in [33]. The search problem is formally defined in terms of finding the points $\mathbf{x }_1 \left( \varvec{\xi }_{\mathbf{x }_1} \right)$ and $\mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right)$ that satisfy:

$$\begin{aligned} \left\{ \begin{array}{ll} \text {f}_1 \left( \varvec{\xi }_{\mathbf{x }_2} \right) = \left( \mathbf{x }_1 - \mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right) \right) \cdot \mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right) _{,\xi _1} &{}= 0, \\ \text {f}_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right) = \left( \mathbf{x }_1 - \mathbf x _2 \left( \varvec{\xi }_{\mathbf{x }_2} \right) \right) \cdot \mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right) _{,\xi _2} &{}= 0.\\ \end{array} \right. \end{aligned}$$

(1)

The above nonlinear-equation system represents the condition that the distance vector $\mathbf{x }_1 - \mathbf x _2 \left( \varvec{\xi }_{\mathbf{x }_2} \right)$ is orthogonal to the tangent plane of $\Gamma ^{2}$ defined by the tangent vectors $\mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right) _{,\xi _1}$ and $\mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_1} \right) _{,\xi _2}$. Note that $\mathbf{x }_1$ is not explicitly written as a function of $\varvec{\xi }_{\mathbf{x }_1}$ because during the search step the point $\mathbf{x }_1$ is assumed fixed and its parametric coordinates constant.

Fig. 1

Three stages of the impact. a No contact, where $d \le -h$; b soft contact, where $d \in \left( -h,0 \right)$; c Hard contact, where $d \ge 0$. Solid black lines represent the shell middle surfaces, while dashed lines represent the actual surface with shell thickness taken into account

The Newton–Raphson iterative method is used to solve the nonlinear-equation system for the parametric coordinates $\varvec{\xi }_{\mathbf{x }_2}$, where each iteration takes on the form:

$$\begin{aligned} \varvec{\xi }^{i+1}_{\mathbf{x }_2} = \varvec{\xi }^{i}_{\mathbf{x }_2} - \left[ \mathbf{J } \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right) \right] ^{-1} \left[ \begin{array}{l} \text {f}_1 \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right) \\ \text {f}_2 \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right) \end{array} \right] , \end{aligned}$$

(2)

where i is the iteration index. The exact Jacobian matrix $\mathbf{J }$ of the Newton–Raphson iteration is given by

$$\begin{aligned} \mathbf{J } \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right) = \left[ \begin{array}{ll} \text {J}_{11} \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right) &{} \text {J}_{12} \left( \varvec{\xi }^{i}_\mathbf{x _2} \right) \\ \text {J}_{21} \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right) &{} \text {J}_{22} \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right) \end{array} \right] , \end{aligned}$$

(3)

where

$$\begin{aligned} \begin{aligned} \text {J}_{11} \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right)&= \mathbf{x }_1 \cdot \mathbf{x }_{2,\xi _1 \xi _1} - \mathbf{x }_{2,\xi _1} \cdot \mathbf{x }_{2,\xi _1} - \mathbf{x }_2 \cdot \mathbf{x }_{2,\xi _1 \xi _1}, \\ \text {J}_{12} \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right)&= \mathbf{x }_1 \cdot \mathbf{x }_{2,\xi _1 \xi _2} - \mathbf{x }_{2,\xi _2} \cdot \mathbf{x }_{2,\xi _1} - \mathbf{x }_2 \cdot \mathbf{x }_{2,\xi _1 \xi _2}, \\ \text {J}_{21} \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right)&= \mathbf{x }_1 \cdot \mathbf{x }_{2,\xi _2 \xi _1} - \mathbf{x }_{2,\xi _1} \cdot \mathbf{x }_{2,\xi _2} - \mathbf{x }_2 \cdot \mathbf{x }_{2,\xi _2 \xi _1}, \\ \text {J}_{22} \left( \varvec{\xi }^{i}_{\mathbf{x }_2} \right)&= \mathbf{x }_1 \cdot \mathbf{x }_{2,\xi _2 \xi _2} - \mathbf{x }_{2,\xi _2} \cdot \mathbf{x }_{2,\xi _2} - \mathbf{x }_2 \cdot \mathbf{x }_{2,\xi _2 \xi _2}. \end{aligned} \end{aligned}$$

(4)

As pointed out in [34], the IGA representation of contacting surfaces is beneficial for the search procedure because the surfaces are naturally parameterized (in our case, using NURBS functions), and the parameterization is smooth almost everywhere allowing for direct evaluation of the position-vector second derivatives. However, in general, the uniqueness of the nonlinear-system solution is not guaranteed, and it is often necessary to introduce additional constraints on the domain of the unknown solution vector $\varvec{\xi }_{\mathbf{x }_2}$. In practice, these constraints are enforced by reducing the search domain from the whole surface $\Gamma ^{2}$ to a smaller sub-domain located in the proximity of the point $\mathbf{x }_1$. Implementation details of the search step are discussed in Sect. 2.4.

2.2 Penalization step

The successful search step finds pairs of points $\mathbf{x }_1$ and $\mathbf{x }_2$ that satisfy the condition given by Eq. (1). However, these points are not necessarily in contact as they may be too far apart. Contact is thus introduced through a penalization step, where we first introduce the signed distance $d\left( \varvec{\xi }_{\mathbf{x }_1} , \varvec{\xi }_{\mathbf{x }_2} \right)$ defined as:

$$\begin{aligned} d = \left[ \mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right) - \mathbf{x }_1 \left( \varvec{\xi }_{\mathbf{x }_1} \right) \right] \cdot \mathbf{n }_2 \left( \mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right) \right) . \end{aligned}$$

(5)

Since the distance vector $\left( \mathbf{x }_2 - \mathbf x _1 \right)$ is, by definition, parallel to $\mathbf{n }_2$, the value of the distance function is null when the spatial locations $\mathbf{x }_1$ and $\mathbf{x }_2$ coincide in space and the surfaces are in contact at that location. We then define the contact pressure $P_k$ to be a non-linear function of d as:

$$\begin{aligned} P_k =\left\{ \begin{array}{ll} 0 &{}\text {if} \quad d \le -h, \\ \dfrac{k}{2h} \left( d + h \right) ^2 &{}\text {if} \quad d \in \left( -h,0 \right) ,\\ \dfrac{kh}{2} + kd &{}\text {if} \quad d \ge 0,\\ \end{array} \right. \end{aligned}$$

(6)

where k is the contact stiffness, while the absolute value of the parameter h determines the distance at which the candidate points are set to be in contact. In our implementation, the parameter h is chosen equal to the sum of the local half-thicknesses of the surfaces $\Gamma ^{1}$ and $\Gamma ^{2}$ at points $\mathbf{x }_1 \left( \varvec{\xi }_{\mathbf{x }_1} \right)$ and $\mathbf{x }_2 \left( \varvec{\xi }_{\mathbf{x }_2} \right)$. Note that the contact pressure $P_k$ in Eq. (6) is designed to be a smooth function of d in order to improve nonlinear convergence.

Using the contact pressure $P_k$ as above, we define the contact traction by multiplying $P_k$ with the normal vector $\mathbf{n }_2$ as:

$$\begin{aligned} \mathbf{t }^{\text {con}} = P_k \left( \mathbf{n }_2 \right) \mathbf{n }_2, \end{aligned}$$

(7)

and adding the following terms to the variational formulation of the multi-layer shell:

$$\begin{aligned} + \int _{\Gamma ^{\text {con}}_t} \left( \mathbf w _2 - \mathbf{w }_1 \right) \cdot P_k \left( \mathbf{n }_2 \right) \mathbf{n }_2 \, \mathrm {d}\Gamma . \end{aligned}$$

(8)

Equation (8) presents the nonlinear penalty-contact formulation, which weakly enforces the surface non-interpenetration condition. Given the definition of the contact pressure in Eq. (6), one can identify three stages of impact, namely, no-contact, soft contact, and hard contact. See Fig. 1 for an illustration and further description.

Fig. 2

Evaluation of the distance for the penalization step. a, b Asymmetric definition of the distance vector; c Symmetrization procedure

2.3 Symmetrization of the contact formulation

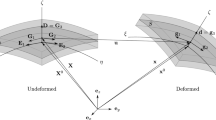
The contact formulation presented in the previous section introduces a dependence of the contact pressure, and, as a result, of the contact traction, on which surface, $\Gamma ^{1}$ or $\Gamma ^{2}$, is designated as the contact surface. The difference in the contact traction arises from the difference in the orientation of the normal vector on the two contacting surfaces. Consider, for example, the case of a curved and flat surface in contact, as shown in Fig. 2a, b. The signed distance function computed with the curved surface designated as $\Gamma ^{2}$ is clearly different from that computed by designating the flat surface as $\Gamma ^{2}$.

To minimize this dependence, we “symmetrize” the contact formulation by introducing a two-step search procedure illustrated in Fig. 2c and summarized in what follows.

• 1. Consider point $\mathbf{x }_1$ on $\Gamma ^{1}$:

  • (a) Do a search step, keeping $\mathbf{x }_1$ fixed, to find $\mathbf{x }_2$ on $\Gamma ^{2}$;

  • (b) Compute the contact pressure $P_k(\mathbf{n }_2 \left( \mathbf{x }_2 \right) )$ based on the distance function $d = \left( \mathbf{x }_2 - \mathbf x _1 \right) \cdot \mathbf{n }_2 \left( \mathbf{x }_2 \right)$.

• 2. Consider point $\mathbf{x }_2$ on $\Gamma ^{2}$ found in Step 1 above.

  • (a) Do a search step, keeping $\mathbf{x }_2$ fixed, to find $\bar{\mathbf{x }}_1$ on $\Gamma ^{1}$;

  • (b) Compute the contact pressure $\bar{P_k}(\mathbf{n }_1 \left( \bar{\mathbf{x }}_1 \right) )$ based on the distance $\bar{d} = \left( \bar{\mathbf{x }}_1 - \mathbf{x }_2 \right) \cdot \mathbf{n }_1 \left( \bar{\mathbf{x }}_1 \right)$.

• 3. Compute the final contact pressure by averaging $P_k$ and $\bar{P_k}$.

This symmetrization procedure provides significant advantages over the unsymmetrized case if the difference in the orientation of the normal vectors on the contacting surfaces is large.

Remark

In the last step of the symmetrization procedure it is also possible to average the contract traction vector directly. However, this option was not pursued in this work.

2.4 Increasing the efficiency of the search step

In order to increase the efficiency of the search step, we devised a two-level reduction of the search domain for a given pair of contact surfaces. The first step involves defining a search box: all the elements that are not included in a user-defined box region in 3D space are automatically excluded from the search domain. The second step involves defining a search list: for each element included in the search box, we create a list that includes only the elements that are closer to it than a specified threshold. The actual search step, which involves solution of the nonlinear system given by Eq. (1), is therefore performed only for the elements included in the search list.

A rigorous application of the contact algorithm requires one to perform a full search and penalization at each time step and at every iteration of the nonlinear solver in order to accurately account for the interaction between the contacting surfaces. However, in some situations, this requirement may be relaxed. For example, if the parts in contact are not subjected to large relative displacements during the deformation, search for the candidate contact points can be performed only once in the structure reference configuration. However, even if the search step is performed only once in the reference configuration, the penalization step must be performed continuously during the analysis to allow the surfaces to come in and out of contact as dictated by the governing equations.

3 Discrete formulation

As in Part I of this paper, we consider a laminated composite structure comprised of Np plies or sublaminates and Nc cohesive interfaces. In addition, we assume the structure also contains Ncon contact interfaces. For this case, the semi-discrete variational formulation may be stated as follows: Find the configuration $\mathbf{x }^h \in S^h_\text {x}$, such that, $\forall \mathbf{w }^h \in S^h_\text {w}$,

$$\begin{aligned} \begin{aligned}&\sum ^{Np}_{ip = 1} \quad \Bigg \{ \int _{{\left( \Gamma ^{S}_0 \right) }_{ip}} \mathbf{w }^h \cdot \rho _{0_{ip}} h_{th_{ip}} \left( \dfrac{d^2 \mathbf{x }^h}{dt^2} - \mathbf{f }^h \right) \, \mathrm {d}\Gamma \\&\quad + \int _{{\left( \Gamma ^{S}_0 \right) }_{ip}} \delta \overline{\varvec{\varepsilon }}^h \cdot \left( \mathbf{K }^{\text {exte}}_{ip} \overline{\varvec{\varepsilon }}^h + \mathbf{K }^{\text {coup}}_{ip} \overline{\varvec{\kappa }}^h \right) \, \mathrm {d}\Gamma \\&\quad + \int _{{\left( \Gamma ^{S}_0 \right) }_{ip}} \delta \overline{\varvec{\kappa }}^h \cdot \left( \mathbf{K }^{\text {coup}}_{ip} \overline{\varvec{\varepsilon }}^h + \mathbf{K }^{\text {bend}}_{ip} \overline{\varvec{\kappa }}^h \right) \, \mathrm {d}\Gamma \\&\quad - \int _{{\left( \Gamma ^{S}_t \right) }_h} \mathbf{w }^h \cdot \mathbf{h }^h \, \mathrm {d} \Gamma \Bigg \} \\&\quad + \sum ^{Nc}_{ic = 1} \quad \Bigg \{ \int _{{\left( \Gamma ^{\text {coh}}_t \right) }_{ic}} \Big [ \left( \mathbf{w }_{1_{ic}}^h + \dfrac{h_{\Gamma ^{1_{ic}} }}{2} \delta \mathbf{n }^h_{1_{ic}} \right) \\&\quad -\left( \mathbf{w }_{2_{ic}}^h + \dfrac{h_{\Gamma ^{2_{ic}} }}{2} \delta \mathbf{n }^h_{2_{ic}} \right) \Big ] \cdot \mathbf{t }^{\text {coh}} \, \mathrm {d}\Gamma \Bigg \} \\&\quad + \sum ^{Ncon}_{ic = 1} \quad \Bigg \{ \int _{{\left( \Gamma ^{\text {cont}}_t \right) }_{ic}} \left( \mathbf{w }^h_{2_{ic}} - \mathbf{w }^h_{1_{ic}} \right) \cdot \mathbf{t }^{\text {con}} \, \mathrm {d}\Gamma \Bigg \} \\&\quad - \int _{ \left( \Gamma ^{S}_0 \right) _{es} } \mathbf{w }^h \cdot \mathbf{K }^{\text {es}} \left( \mathbf{x }^h - \mathbf X ^h \right) \, \mathrm {d}\Gamma = 0. \end{aligned} \end{aligned}$$

(9)

As in Part I of this article, the trial and test function sets are comprised of NURBS basis functions that are defined on each ply, and are discontinuous from ply to ply. In the cohesive-interface terms of the above formulation the subscripts $1_{ic}$ and $2_{ic}$ are consistent with the notation introduced in Part I of this paper, while the subscripts $1_{ic}$ and $2_{ic}$ in the contact terms are consistent with the notation in Sect. 2. Intralaminar damage is implicitly embedded in the definition of the extensional, coupling, and bending stiffness matrices of each ply, and automatically accounts for their current damage state. Both the implicit and explicit versions of the Generalized-$\alpha$ method [35] are employed to integrate the semi-discrete Eq. (9) in time.

Remark

In the above formulation, the last term on the left hand side represents the elastic-support boundary conditions. The boundary conditions are defined on a subregion $\left( \Gamma ^{S}_0 \right) _{es}$ in the reference configuration. The matrix $\mathbf{K }^{\text {es}}$ is diagonal and may be expressed as:

$$\begin{aligned} \mathbf{K }^{\text {es}} = \left[ \begin{array}{lll} \text {K}^{\text {es}}_x &{} 0 &{} 0 \\ 0 &{}\text {K}^{\text {es}}_y &{} 0 \\ 0 &{}0 &{} \text {K}^{\text {es}}_z \end{array} \right] \end{aligned}$$

(10)

where $\text {K}^{\text {es}}_x$, $\text {K}^{\text {es}}_y$ and $\text {K}^{\text {es}}_z$ are the directional stiffness coefficients expressed in the global coordinate system. Although the elastic-support boundary conditions are not employed in the computations presented in the next section, they may be quite useful for representing the effect of frame-like supports employed in many impact tests.

4 Impact simulations

We simulate a composite-laminate impact test in order to validate our modeling procedures through comparison with experimental data and simulations of this test reported in the literature. $C^1$-continuous quadratic NURBS are employed for all the IGA-based simulations presented in this section. All the IGA-based computations are carried out using an in-house research software that implements all the methods presented in this two-part paper. In-house FE-based Abaqus/Explicit [36] simulations using 3D linear solid elements are also carried out for comparison.

Fig. 3

Experimental setup for the impact test

4.1 Experimental setup

Experimental setup of the impact test is shown in Fig. 3. The coupon measures 150 mm $\times$ 100 mm and is supported by a rigid frame with a rectangular open window at its center. The size of the unsupported test region is 125 mm $\times$ 75 mm. The plate is 4.16 mm thick and is composed of 16 unidirectional carbon/epoxy plies stacked using a symmetric lamination sequence $[ 0_2, 45_2, 90_2, -45_2 ]_{\text {s}}$. The impactor head is stiff and spherical, with a diameter of 16 mm and total mass of 2 kg.

Two cases with different impact-energy levels are considered, 6.5 and 25 J, with experimental investigations reported in [37] and [38], respectively. The experimental results in these references are commonly used for the purposes of model validation (see, e.g., [19]). For the lower energy case, the composite plate is made of T700/M21 material, while for the higher energy case the material employed is T700GC/M21.

Fig. 4

Schematic representation of the multi-layer shell model for the impact test. Each ply is represented by a flat surface discretized with $C^1$-continuous quadratic NURBS. The extensional, coupling and bending stiffnesses depend on the current damage state, and are computed according to the procedures introduced in Part I of this paper. Only half of the laminate is shown for clarity

4.2 Computational setup for IGA-based simulations

An illustration of the IGA-based multi-layer shell approach for the laminated-plate impact test is shown in Fig. 4. The lamina material properties employed in the simulations are reported in Table 1. The impactor is modeled as a hemispherical shell made from isotropic, stiff material to minimize compliance, with uniform thickness of 1.5 mm and density chosen to match the total mass of the experimental impactor. Zero normal displacement and tangential traction boundary conditions are employed on the plate subdomain supported by the rigid frame.

As proposed in [39], and discussed in Part I of this paper, a characteristic length $L_c$ is introduced in the intralaminar damage model in order to ensure that the strain energy dissipated during the damage process is independent of the discretization adopted for analysis. As before, we define $L_c = \sqrt{A_{\text {ele}}}$, where $A_{\text {ele}}$ is the surface area the shell element. The baseline mesh size employed for the IGA-based simulations is 1 mm near the impact location, and gradually increases to 1.5 mm outside the impact zone. The baseline IGA model is shown in Fig. 5a. A coarser discretization is also employed for the IGA-based 6.5 J impact-energy simulation in order to investigate the effect of the mesh size. The mesh size of the coarser isogeometric discretization is 1 mm near the impact location and gradually increases to 2.8 mm outside the area where damage is expected to occur. The distribution of $L_c$ in the problem domain is consistent with that of the mesh size.

Table 1 Lamina material properties used in the simulations for the T700/M21 material [37] and for the T700GC/M21 material [38]

Fig. 5

Representation of the a IGA and of the b in-house FE model created for the impact simulations

Table 2 Cohesive-interface properties used in the simulations for the (a) T700/M21 material [37] and for the (b) T700GC/M21 material [38]

Fig. 6

Impact force time history obtained for the a 6.5 J and b 25 J impact energy cases. Experimental data labeled (1) and (3) are reported, respectively, in [37] and [38]. Reference numerical results labeled (2) and (4) are reported in [19]

The cohesive-interface properties employed in the simulations are taken from [19] and reported in Table 2. A detailed discussion about the selection of the cohesive-interface stiffness may be found in [40]. As shown in Part I, a more compliant interface gives rise to more pronounced transverse-shear-induced localized deformations, which are inherently neglected in the pure Kirchhoff–Love shell theory. For IGA-based simulations we selected a cohesive-interface stiffness of $\text {K}^{\text {coh}} =10^4$ N/mm$^3$.

Cohesive-interface formulations, as a rule, require finer mesh resolution in order to correctly describe the delamination-front propagation. According to [40], three-to-ten elements are needed in the cohesive process zone, which is defined as the region between the crack tip and the point where cohesive traction reaches its maximum value. Several models [9, 40,41,42,43,44] were proposed for the estimation of the process-zone length $l^{\text {coh}}$. Here we make use of the following expressions for the normal and in-plane opening modes:

$$\begin{aligned} l^{\text {coh}}_{\text {n}}= & {} \text {M} E^{\prime }_{\text {n}} \dfrac{ \text {G}_{\text {C}_\text {n}} }{ \left( \text {t}^{0}_{\text {n}} \right) ^2}, \nonumber \\ l^{\text {coh}}_{\tau }= & {} \text {M} E^{\prime }_{\tau } \dfrac{ \text {G}_{\text {C}_\tau } }{ \left( \text {t}^{0}_{\tau } \right) ^2}, \end{aligned}$$

(11)

where $E^{\prime }$ is the equivalent elastic modulus and $\text {M}$ is a parameter that depends on the model adopted for the cohesive interface. Following [41], we chose $\text {M} = 9\pi /32$ in the simulations.

Fig. 7

IGA-based simulation results. Intralaminar matrix damage for plies 1 (bottom) to 7 (impact side) for the a 6.5 J and b 25 J impact energy cases. Contour plots of the matrix damage variable $d_2$

Fig. 8

IGA-based simulation results. Interlaminar damage for cohesive interfaces 1 (bottom) to 6 (impact side) for the a 6.5 J and b 25 J impact energy cases. Contour plots of the cohesive damage variable $d_\text {coh}$

The equivalent elastic modulus for an orthotropic material $E^{\prime }$ can conservatively be set equal to the elastic modulus in the transverse direction $E_3$, as suggested in [40]. Other authors [9, 43] proposed a definition of the the equivalent elastic modulus for an orthotropic material to be a function of the fiber-direction elastic modulus $E_1$, the transverse modulus $E_3$, the shear modulus $G_{31}$, and loading conditions. The equivalent elastic modulus is computed [42] under the hypothesis of the plane-stress state in an unbounded medium. For Mode I opening $E^{\prime }_{\text {n}}$ is computed as

$$\begin{aligned} \dfrac{1}{E^{\prime }_{\text {n}}} = \sqrt{\dfrac{1}{2E_1 E_2}} \sqrt{\sqrt{\dfrac{E_1}{E_3}} + \dfrac{E_1}{2} \left( -\dfrac{2\nu _{31}}{E_3} + \dfrac{1}{G_{13}} \right) }, \end{aligned}$$

(12)

while for Mode II opening $E^{\prime }_{\tau }$ is computed as

$$\begin{aligned} \dfrac{1}{E^{\prime }_{\tau }} = \sqrt{\dfrac{1}{2E_1}} \sqrt{\sqrt{\dfrac{1}{E_1 E_3}} + \left( -\dfrac{\nu _{31}}{E_3} + \dfrac{1}{2 G_{13}} \right) }. \end{aligned}$$

(13)

We note that for isotropic materials the equivalent elastic modulus $E^{\prime }$ obtained from either expression reduces to the classical elastic modulus E.

Substituting the values of $E^{\prime }$ given by Eqs. (12) and (13) computed for both T700/M21 and T700GC/M21 materials into Eq. (11), gives $l^{\text {coh}}_{\text {n}}=11.86$ mm, whereas a more conservative definition from [40] gives $l^{\text {coh}} = 8.4$ mm. As a result, NURBS meshes created for the impact simulations allow at least five (quadratic!) elements to resolve the cohesive process zone.

Ply grouping is adopted for the simulations in order to reduce the computational effort. This simplification is based on the assumption that delamination is triggered mainly due to transverse shear at the interface between the plies with different fiber orientations. We note that while delamination and compliance between the sub-plies of a single ply group is neglected, the intralaminar damage variables are still evaluated at the level of each ply in the group. This different treatment of interlaminar and intralaminar damage allows us to improve the simulation efficiency without degrading the solution accuracy.

An implicit version of the Generalized-$\alpha$ algorithm is employed with a time step of 2.5 and 10 $\upmu$s for the 25 and 6.5 J impact cases, respectively, to integrate the governing equations in time. Viscous regularization discussed in Part I of this paper is employed for both intralaminar and interlaminar damage variables. Viscous regularization parameters are set to $10^{-7}$ and 3 $\times 10^{-7}$ s for the 25 and 6.5 J impact cases, respectively, for both intralaminar and interlaminar damage variables.

5 Results and discussion

The IGA-based model is validated through the correlation of the impact-force time history with the experimental data available in the literature [19, 37, 38]. In addition, we compare the IGA predictions with the results obtained using an in-house FE model as well as an FE model developed by researchers in [19]. We refer to the latter as the reference FE model.

Fig. 9

Matrix failure for the a 6.5 J and b 25 J impact impact energy cases. Top: IGA-based results. Bottom: in-house FEM-based results. View from the impacted side

Fig. 10

Delamination for the a 6.5 J and b 25 J impact impact energy cases. Top: IGA-based results. Bottom: in-house FEM-based results. View from the impacted side

Fig. 11

Comparison of intralaminar matrix damage (top) and cohesive damage (bottom) for the 6.5 J impact case. a IGA-based results; b Reference FE results. Contour plots for the IGA case correspond to variables $d_2$ (top) and $d_\text {{coh}}$ (bottom). The dashed red line in the bottom-right panel defines the contour of the delaminated area obtained from the experiments reported in [37]

The in-house FE model, shown in Fig. 5b, is an Abaqus/Explicit model comprised of linear brick elements (C3D8R). The in-plane mesh has elements of size 0.5 mm near the impact location, and the element size is gradually increased to 1.5 mm away from the impact zone. Ply grouping is employed with one layer of elements per group. The impactor is modeled as a hemisphere of solid elements with steel elastic properties and mass scaled to 2 kg. Impactor-to-laminate contact is modeled as hard contact with the impactor surface as the master. The NASA CompDam subroutine [45, 46] is employed to model intralaminar damage. Delamination is modeled using the Abaqus built-in surface-based cohesive-interface formulation that implements a mixed-mode bilinear softening law. After delamination, ply-to-ply interactions are modeled via contact with friction.

The reference FE model is similar to its in-house counterpart, however, in contrast to the IGA-based and in-house FE models, it also employs a non-symmetric tension-compression material constitutive law and a model for matrix plasticity (see [19] for details).

The baseline discretization for the IGA-based simulations has 128,244 DOFs. This number is reduced to 62,766 DOFs for the coarser IGA-based simulation of the 6.5 J impact case. In contrast, the in-house FE discretization has 772,176 DOFs.

The impact force time histories for the 6.5 and 25 J impact energy cases are reported in Fig. 6a, b, respectively. The results obtained for the 6.5 J impact exhibit a good correlation with the experimental data [37] in terms of the maximum impact force. The IGA and in-house FE models overpredict the peak value by 6 and 9.7%, respectively. In addition, all numerical simulations show an excellent agreement with the experimental data for impact duration. No significant differences are found between the IGA simulation results for two different mesh discretizations (see Fig. 6a), suggesting the baseline IGA mesh is sufficiently fine for the prediction of the impact force.

The numerical results obtained for the 25 J impact case show a little more discrepancy compared to the experimental data [38] and to the reference FE model. The maximum impact force predicted by the IGA-based simulation is 4% larger compared to the in-house FE model, while no significant differences are found in terms of the impact duration. The IGA model overpredicts the peak force by 11.5% relative to the reference FE model and by 20.1% compared to the experimental data. The predicted duration of the impact event is 0.5 ms shorter compared to the experimental value. However, in the reference FE model, the authors adopted a non-symmetric constitutive law for the unidirectional composite, where the compressive elastic modulus is 23% smaller than the corresponding tensile value of 130 GPa. This can explain a somewhat softer response predicted by the reference FE model.

Remark

We note that the multilayer Kirchhoff–Love shells discretized with quadratic NURBS are able to produce impact-force time histories that are very similar to those for the solid linear-element FE models, while using a much smaller number of DOFs. For implicit computations this directly translates to significant cost savings in the direct solution of linear-equation systems, which typically dominates the overall analysis time. For explicit computations, provided assembly time per DOF is comparable for the IGA shells and linear solid elements, the costs savings will come from the overall lower DOF numbers and the higher stable time-step size associated with smooth higher-order discretizations (see [47, 48]). The higher per-DOF accuracy for IGA shells, and the direct link with CAD, make the present technology attractive to larger-scale simulations of impact damage, which we plan to pursue in the future work.

A ply-by-ply distribution of the intralaminar matrix damage variable is shown in Fig. 7a, b for the 6.5 and 25 J impact-energy cases, respectively. The results show a symmetric damage pattern within each ply. The most severe damage is predicted to develop on the back side of the laminate. This is because the matrix tensile stress in the lower lamina causes it to fail earlier compared to the lamina closer to the impacted side, where compressive stresses are dominant.

A interface-by-interface distribution of the interlaminar damage variable is shown in Fig. 8a, b for the 6.5 and 25 J impact-energy cases, respectively. The most severe delamination occurs in the lower half of the laminate, between the plies oriented at $90^{\circ }$ and $-45^{\circ }$. We note that localized compressive stress near the impact location prevents the plies to reach complete delamination. In the case of high-energy impact, the presence of the support frame causes the initiation of interlaminar damage at the interface closest to the back of the laminate.

A comparison of matrix damage and delamination between the IGA-based and in-house FE simulations is shown in Figs. 9 and 10, respectively, for both energy levels. The distribution of matrix and interlaminar damage predicted by the IGA-based model is also compared with the results of the reference FE model for the 6.5 J impact case, and the comparison is shown in Fig. 11. In addition, the dashed red line in the bottom-right panel in Fig. 11 defines the contour of the delaminated area obtained from the experiments reported in [37]. The model predictions and experimental results show a reasonable agreement in terms of the the size and shape of the damage and delamination regions. Discrepancies in the matrix damage are attributable to the difference in the intralaminar damage models adopted in the simulations, and to the fact the FE simulations are able to represent a full 3D state of stress at the lamina level. Compared to the IGA results, the in-house FE model predicts a more severe and extended delamination on all the ply interfaces, especially for the higher-energy impact case. This, in turn, explains a slightly softer response of the in-house FE model for the prediction of the peak force during impact for this case.

6 Conclusions

In this paper we showed that the proposed IGA-based formulation for progressive damage modeling in laminated composite structures, which is developed in the framework of multi-layer modeling using rotation-free Kirchhoff–Love shells, is an accurate and efficient alternative to the more traditional low-order solid-element FE approaches. In particular, the new IGA-based formulation is capable of reproducing impact-damage results using a fraction of the degrees of freedom required for traditional FE analysis. The reasons for this increased efficiency, besides the lack of rotational degrees of freedom in the discrete formulation, are as follows. Rotation-free Kirchhoff–Love shells, unlike solids or shear-deformable shells, do not suffer from transverse-shear locking in the limit of vanishing thickness. This property, in combination with higher-order accurate and smooth representation of the shell midsurface geometry and solution fields, allows one to adopt relatively coarse in-plane discretizations while maintaining good solution accuracy.

Excellent agreement with experimental data was obtained for the lower-energy impact case. In the case of higher-energy impact simulations, however, the numerical results obtained with both the IGA- and in-house FE-based models exhibited some discrepancies with the experimental data. These are likely related to the lack of a plasticity model for the matrix phase and to the use of a symmetric tension-compression constitutive law.

Finally, although strain localization and the associated mesh sensitivity was not observed in the examples computed in this paper, such phenomena may occur even in the context of smooth IGA discretizations, and would require appropriate modeling and numerical treatment, such as, for example, using nonlocal gradient-enhanced damage models [49,50,51,52].

In the future research efforts we plan to address the localization of deformation issue in the context of IGA shells (see [53] for preliminary results in this direction). We also plan to carry out impact and compression-after-impact analyses of larger-scale stiffened panels to assess the ability of the proposed IGA-based formulation to deliver accurate results in this setting.