Steady-state non-linear vibrations of plates using Zener material model with fractional derivative

Abstract

The paper is devoted to non-linear vibrations of plates, made of the Zener viscoelastic material modelled with the Caputo fractional derivative, and in particular to their response to harmonic excitation. The plate geometric non-linearity is of the von Kármán type. In the formulation shear effects and rotary inertia are considered, too. The problem is solved in the frequency domain. A one-harmonic form of the solution for plate displacements corresponding to the plate formulation is assumed. The amplitude equation is obtained from the time averaged principle of virtual work. The time averaging precedes the use of the harmonic balance method. In the space discretization the finite element method is used involving 8-noded rectangular plate elements with selective-reduced integration. Several numerical examples are analyzed and the response curves are found using a path-following method. The purpose of these analyses is to identify material features of the adopted model of viscoelasticity with the fractional derivative.

1 Introduction

In the view of continually growing requirements to reduce excessive and undesired vibrations in engineering, a variety of methods serving this purpose have been devised. Making use of special materials exhibiting damping properties is of the key importance in many of these methods. A variety of viscoelastic models can be applied to analyze physical behaviour of these materials. It is possible to use these materials as layers or single patches attached to some structural elements. Alternatively, materials used as structural ones do exhibit viscoelastic properties, too. That is why considerations of dynamic behaviour of such structural elements, i.e. beams, plates or shells, often taking into account geometric non-linearity, made from or containing fragments of viscoelastic materials became very urgent.

In the course of a non-linear analysis a large range of dynamic phenomena can be found. They include, besides ordinary type of resonance, internal resonance of three-to-one type, quasi-periodic vibrations and chaotic response, see for instance [12, 13]. The author was solving the problem of non-linear vibrations of the Kelvin–Voigt viscoelastic beams during axial movement and with additional non-linear spring support. The problem was further investigated in [14, 15] for the case of vibrations over a buckled state. In [16] the vibrations of viscoelastic microbeams were analyzed, too. Li and Cheng [27] also reported many non-linear phenomena including transition to chaos in the case of viscoelastic plates with high-order shear deformation included.

In the field of plates vibrations several further contributions can be found as well. A hereditary model of viscoelastic material to solve non-linear free vibrations of laminated plates was used by Kim and Kim [19]. In the paper [9] a special collocation method with radial basis functions was used to solve equations of free vibrations of laminated plates. Non-linear free and forced vibrations of sandwich plates with the Green-Rivlin material viscoelastic core were considered by Mahmoudkhani et al. [29], and the solutions were obtained using a few different models of non-linearity. Amabili [1] solved the problem of non-linear vibrations of simply supported plates made from the Kelvin–Voigt material, with inclusion of geometric imperfections. In recent years the Golla–Hughes–McTavish (GHM) material was applied to model viscoelastic properties for various types of plates. Sarangi and Ray [34] as well as Kumar and Ray [21] analyzed damping of non-linear vibrations in laminated plates. Transient non-linear vibrations of skew laminated composite plates and non-linear thin panels with piezoelectric active constrained damping patches or layers were considered in [18, 37]. The papers [20, 22, 33] were devoted to smart functionally graded plates including the active constraining in the form of piezoelectric layers. The problem of geometrically linear vibrations of thin laminated plates was solved with a three-dimensional fractional derivative model for viscoelasticity by Datta and Ray [7]. The Zener material with fractional derivative was also considered in [10] for linear transient vibrations of viscoelastic sandwich beams.

The use of fractional derivatives to model the hereditary properties of viscoelastic materials dates back to the beginning of twentieth century. But a physical foundation for this approach was laid much later, in the works of Bagley and Torvik [3, 4]. They found a link between molecular theories predicting the behaviour of viscoelastic polymers and the fractional calculus used to describe these phenomena. Since then the idea was used to generalize classical viscoelastic models—Kelvin–Voigt [8], Maxwell [30], Zener [2], which is also called standard linear solid [28], or a 3-parameter viscoelastic model [35]. It is generally agreed, that the introduction of fractional derivatives, where its order can be viewed as an additional material parameter, allows to reduce the number of classical physical parameters—thus, to simplify the model.

The main goal of the research reported in this paper is to show the possibility of solving, in a form of resonance curves, the steady-state vibrations problem for viscoelastic plates within the von Kármán geometric non-linearity. The Zener material with fractional derivative is taken into account. Bearing in mind the growing need for the reduction of vibrations in structural systems, one can conclude, that the analysis of various models of viscoelasticity is very important. The choice of the fractional Zener material in this paper is motivated in that, among the models capable of predicting all key properties of a viscoelastic body, it is the simplest possible one [17, 23]. It is the authors’ opinion that the presented approach and discussion of the model properties can be viewed as an attractive proposal to predict the dynamic behaviour of real viscoelastic materials and structural elements made of them. The suggested methodology of solution to the plate vibrations problem can also be applied in more practical cases, like laminated plates with viscoelastic layers used for the reduction of vibrations.

The paper is divided into the following sections. A summary of plate kinematics with the von Kármán geometric non-linearity is presented in Sect. 2. In Sect. 3 the formulation of the fractional Zener material is given. The physical equations for a plate with the Caputo fractional derivative are presented. Section 4 is devoted to the form of solution assumed in the analysis. A single-harmonic form consistent with plate and material description is proposed. Section 5 contains the most important element of the paper, i.e. the derivation of the amplitude equation from the virtual work. The equations of motion are expressed in the frequency domain in terms of amplitudes of plate displacements. A novel aspect in this derivation is the precedence of the time averaging with respect to the harmonic balance method and the space integration. The latter is done using the finite element method. Details of the adopted discretization are discussed in Sect. 6. The most complex matrices for the plate element resulting from the FE formulation are given in “Appendix”. Several analyses for simple cases of vibrating plates are presented in Sect. 7 with a discussion of results. Sect. 8 contains a summary and an outlook.

2 Geometrically non-linear plate

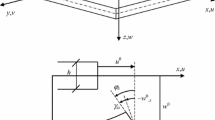
Let us analyze a plate of moderate thickness h with the von Kármán geometric non-linearity included to cover the moderate rotations regime. Shear deformation is taken into account in the formulation, too. Figure 1 shows appropriate kinematic variables, i.e. deflection at the mid-plane $w^{0}$, in-plane translations at the mid-plane $u^{0}$ and $v^{0}$ and two cross-section rotations $\varphi _{x}$ and $\varphi _{xy}$. For an arbitrary point at the cross-section the displacements are given by

$$\begin{aligned} u(x,y,z)= & {} u^{0}(x,y)+z\varphi _x (x,y) \nonumber \\ v(x,y,z)= & {} v^{0}(x,y)+z\varphi _y (x,y) \nonumber \\ w(x,y,z)= & {} w^{0}(x,y) \end{aligned}$$

(1)

Fig. 1

Plate kinematics

Functions of von Kármán strains, which result from the definition of displacement fields (1), are assembled into vectors and expressed using the following geometric relations

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_r= & {} \left\{ {\begin{array}{c} \varphi _{x,x} \\ \varphi _{y,y} \\ \varphi _{x,y} +\varphi _{y,x} \\ \end{array}} \right\} \end{aligned}$$

(2)

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_s= & {} \left\{ {\begin{array}{l} w_{,x}^0 +\varphi _x \\ w_{,y}^0 +\varphi _y \\ \end{array}} \right\} \end{aligned}$$

(3)

$$\begin{aligned} {{\varvec{\upvarepsilon }}}_p= & {} {{\varvec{\upvarepsilon }}}_{pl} +{{\varvec{\upvarepsilon }}}_{pn} =\left\{ {\begin{array}{l} u_{,x}^0 \\ v_{,y}^0\\ u_{,y}^0 +v_{,x}^0 \\ \end{array}} \right\} +\left\{ {\begin{array}{l} \frac{1}{2}\left( w_{,x}^0 \right) ^{2} \\ \frac{1}{2}\left( w_{,y}^0 \right) ^{2} \\ w_{,x}^0 w_{,y}^0 \\ \end{array}} \right\} \end{aligned}$$

(4)

The in-plane strains (4) are composed from linear and non-linear part.

The displacement vectors are defined as

$$\begin{aligned} \begin{array}{l} \mathbf{q}_r =\left\{ {\begin{array}{l} \varphi _x \\ \varphi _y \\ \end{array}} \right\} \\ \mathbf{q}_w =\left\{ {w^{0}} \right\} \\ \mathbf{q}_t =\left\{ {{\begin{array}{l} {u^{0}} \\ {v^{0}} \\ \end{array} }} \right\} \\ \end{array} \end{aligned}$$

(5)

and the strains (2)–(4) can now be given as

$$\begin{aligned} {{\varvec{\upvarepsilon }}}_r= & {} \mathbf{B}^{\prime }_r \mathbf{q}_r \end{aligned}$$

(6)

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_s= & {} \mathbf{B}^{\prime }_{sw} \mathbf{q}_w +\mathbf{B}^{\prime }_{sr} \mathbf{q}_r \end{aligned}$$

(7)

$$\begin{aligned} {{\varvec{\upvarepsilon }}}_{pl}= & {} \mathbf{B}^{\prime }_r \mathbf{q}_t \end{aligned}$$

(8)

$$\begin{aligned} {{\varvec{\upvarepsilon }}}_{pn}= & {} \left\{ {{\begin{array}{l} {\varepsilon _{pn1} } \\ {\varepsilon _{pn2} } \\ {\varepsilon _{pn3} } \\ \end{array} }} \right\} =\frac{1}{2}\left\{ {{\begin{array}{c} {{\mathbf{q}_w}^{T}{{\mathbf{B}^{\prime }}_{w1}}^{T}{\mathbf{B}^{\prime }}_{w1} \,\mathbf{q}_w } \\ {{\mathbf{q}_w }^{T}{{\mathbf{B}^{\prime }}_{w2}}^{T}{\mathbf{B}^{\prime }}_{w2}\, \mathbf{q}_w } \\ {{\mathbf{q}_w }^{T}{{\mathbf{B}^{\prime }}_{w1}}^{T}{\mathbf{B}^{\prime }}_{w2} \mathbf{q}_w +{\mathbf{q}_w}^{T}{{\mathbf{B}^{\prime }}_{w2}}^{T}{\mathbf{B}^{\prime }}_{w1} \mathbf{q}_w } \\ \end{array} }} \right\} \nonumber \\ \end{aligned}$$

(9)

where the appropriate matrices of differential operators take the form

$$\begin{aligned}&\mathbf{B}^{\prime }_r =\left[ {{\begin{array}{lll} {\frac{\partial }{\partial x}}&{} 0&{} {\frac{\partial }{\partial y}} \\ 0&{} {\frac{\partial }{\partial y}}&{} {\frac{\partial }{\partial x}} \\ \end{array} }} \right] ^{T} \end{aligned}$$

(10)

$$\begin{aligned}&\begin{array}{l} \mathbf{{B}'}_{sw} =\left[ {{\begin{array}{ll} {\frac{\partial }{\partial x}}&{} {\frac{\partial }{\partial y}} \\ \end{array} }} \right] ^{T} \\ \mathbf{{B}'}_{sr} =\left[ {\begin{array}{ll} 1&{}0 \\ 0&{}1 \\ \end{array}} \right] \\ \end{array} \end{aligned}$$

(11)

$$\begin{aligned}&\begin{array}{l} \mathbf{B}^{\prime }_{w1} =\left[ {\frac{\partial }{\partial x}} \right] \\ \mathbf{B}^{\prime }_{w2} =\left[ {\frac{\partial }{\partial y}} \right] \\ \end{array} \end{aligned}$$

(12)

The virtual strains required in the subsequent expression of the virtual work are

$$\begin{aligned} \delta {{\varvec{\upvarepsilon }} }_r= & {} \mathbf{B}^{\prime }_r \delta \mathbf{q}_r \end{aligned}$$

(13)

$$\begin{aligned} \delta {{\varvec{\upvarepsilon }} }_s= & {} \mathbf{B}^{\prime }_{sw} \delta \mathbf{q}_w +\mathbf{B}^{\prime }_{sr} \delta \mathbf{q}_r \end{aligned}$$

(14)

$$\begin{aligned} \delta {{\varvec{\upvarepsilon }} }_p= & {} \delta {{\varvec{\upvarepsilon }} }_{pl} +\delta {{\varvec{\upvarepsilon }} }_{pn} \end{aligned}$$

(15)

where the in-plane linear and nonlinear components are given as

$$\begin{aligned} \delta {{\varvec{\upvarepsilon }} }_{pl}= & {} \mathbf{B}^{\prime }_r \delta \mathbf{q}_t \end{aligned}$$

(16)

$$\begin{aligned} \delta {{\varvec{\upvarepsilon }} }_{pn}= & {} \left\{ {\begin{array}{l} \delta \varepsilon _{pn1} \\ \delta \varepsilon _{pn2} \\ \delta \varepsilon _{pn3} \\ \end{array}} \right\} =\left\{ {{\begin{array}{c} {{\delta \mathbf{q}_w}^{T}{{\mathbf{B}^{\prime }}_{w1} }^{T}{{\mathbf{B}^{\prime }}_{w1}}{} \mathbf{q}_w } \\ {{\delta \mathbf{q}_w }^{T}{{\mathbf{B}^{\prime }}_{w2} }^{T}{{\mathbf{B}^{\prime }}_{w2}} \mathbf{q}_w } \\ {{\delta \mathbf{q}_w} ^{T}{\mathbf{B}^{\prime }}_{w1} ^{T}{{\mathbf{B}^{\prime }}_{w2}}{} \mathbf{q}_w +{\delta \mathbf{q}_w }^{T}{{\mathbf{B}^{\prime }}_{w2} }^ {T}{{\mathbf{B}^{\prime }}_{w1}} \mathbf{q}_w } \\ \end{array} }} \right\} \nonumber \\ \end{aligned}$$

(17)

Let us also put together bending and torsional moments, two shear forces and in-plane forces, into the respective vectors of internal forces

$$\begin{aligned} \mathbf{M}= & {} \left\{ {{\begin{array}{lll} {M_x }&{} {M_y }&{} {M_{xy} } \\ \end{array} }} \right\} ^{T} \end{aligned}$$

(18)

$$\begin{aligned} \mathbf{Q}= & {} \left\{ {{\begin{array}{ll} {Q_x }&{} {Q_y } \\ \end{array} }} \right\} ^{T} \end{aligned}$$

(19)

$$\begin{aligned} \mathbf{N}= & {} \left\{ {{\begin{array}{lll} {N_x }&{} {N_y }&{} {N_{xy} } \\ \end{array} }} \right\} \end{aligned}$$

(20)

Fig. 2

Representation of Zener material: a classical, b fractional

3 Fractional Zener model of viscoelastic material

Viscoelasticity can be modelled using different approximations, starting with the simplest classical Maxwell and Kelvin–Voigt ones. It is known, that none of these two models with two material constants only is capable of predicting simultaneously all the important phenomena, as creep, relaxation, immediate elasticity, etc. Thus, more complex models were proposed and it was found that the simplest possible approximation to qualitatively describe viscoelasticity is given by Zener, e.g. [17, 23]. This three-parameter model involves two springs with stiffness $E_{1}$ and $E_{2}$ and a dashpot of viscosity c, see Fig. 2a.

Attempts were also made to generalize classical Maxwell and Kelvin–Voigt models in applications related to the dynamic behaviour of viscoelastic dampers. They led to inclusion of many more material parameters [5, 25, 31]. Contrary to this, it was shown, that the use of fractional derivative models can significantly reduce the required number of additional material parameters, while preserving the same level of accuracy in the description of real materials and that it remains correct over a broad range of excitation frequency [3, 11].

Thus, in the present paper the fractional Zener model, shown in Fig. 2b, is used. Instead of the classical dashpot, the Scott-Blair fractional damping element described by the damping coefficient c and the order of fractional derivative $\alpha$ is introduced. With $\alpha$ kept in the range [0,1] the Scott-Blair element exhibits properties intermediate between a spring $(\alpha =0)$ and a dashpot $(\alpha =1)$. The stress-strain relation for the fractional Zener model reads

$$\begin{aligned} \sigma +\tau D_t^\alpha \sigma =E_0 \varepsilon +\tau E_\infty D_t^\alpha \varepsilon \end{aligned}$$

(21)

where the initial and final stiffness values are given by $E_{0} =E_{1}$ and $E_\infty =E_{1}+E_{2}$, respectively, $\tau =c/{E_2 }$ is the relaxation time and $D_t^\alpha$ denotes the fractional derivative of the order $\alpha$ with respect to time t. It is worth to note, that the unit for the relaxation time in the case of fractional derivative formulation is second to the power $\alpha (\hbox {s}^{\alpha })$.

There are several possible definitions of fractional derivatives, for example Grünwald-Letnikov, Caputo or Riemann–Liouville ones. In the present formulation the Caputo definition is applied

$$\begin{aligned} D_t^\alpha f(t)=\frac{1}{\Gamma \left( {1-\alpha } \right) }\int \limits _a^t {\frac{df\left( \tau \right) }{d\tau }\frac{d\tau }{\left( {t-\tau } \right) ^{\alpha }}} \end{aligned}$$

(22)

with the special function $\Gamma$ present. Let us also note, that with zero initial conditions and for $a \rightarrow -\infty$ in (22) the result from the Caputo calculation becomes identical with the Riemann–Liouville one.

Taking into account the introduced definitions of the generalized stresses (18)–(20) and the generalized strains (2)–(4), one can write down the physical relations as

$$\begin{aligned} \mathbf{M}+\tau D_t^\alpha \mathbf{M}= & {} \mathbf{D}_0 {{\varvec{\upvarepsilon }} }_r +\tau \mathbf{D}_\infty D_t^\alpha {{\varvec{\upvarepsilon }} }_r \end{aligned}$$

(23)

$$\begin{aligned} \mathbf{Q}+\tau D_t^\alpha \mathbf{Q}= & {} \mathbf{A}_{q0} {{\varvec{\upvarepsilon }} }_s +\tau \mathbf{A}_{q\infty } D_t^\alpha {{\varvec{\upvarepsilon }} }_s \end{aligned}$$

(24)

$$\begin{aligned} \mathbf{N}+\tau D_t^\alpha \mathbf{N}= & {} \mathbf{A}_0 {{\varvec{\upvarepsilon }} }_l +\tau \mathbf{A}_\infty D_t^\alpha {{\varvec{\upvarepsilon }} }_l \end{aligned}$$

(25)

with the matrices of the material stiffness introduced

$$\begin{aligned} \mathbf{D}_i= & {} \frac{E_i h^{3}}{12\left( {1-\nu ^{2}} \right) }\left[ {\begin{array}{lll} 1&{}\quad \nu &{}\quad 0 \\ \nu &{}\quad 1 &{}\quad 0 \\ 0&{}\quad 0&{}\quad {\left( {1-\nu } \right) }/2 \\ \end{array}} \right] \end{aligned}$$

(26)

$$\begin{aligned} \mathbf{A}_{qi}= & {} \frac{\kappa E_i h^{2}}{2\left( {1+\nu } \right) }\left[ {{\begin{array}{ll} 1&{}\quad 0 \\ 0&{}\quad 1 \\ \end{array} }} \right] \end{aligned}$$

(27)

$$\begin{aligned} \mathbf{A}_i= & {} \frac{E_i h}{1-\nu ^{2}}\left[ {\begin{array}{lll} 1 &{}\quad \nu &{}\quad 0 \\ \nu &{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad {\left( {1-\nu } \right) }/2 \\ \end{array}} \right] \end{aligned}$$

(28)

where $i =0$ or $\infty$. The Poisson’s ratio of the material assumed as time-constant is denoted with $\nu$, while $\kappa$ stands for the shear correction factor, which for a plate is equal to 5/6.

4 Harmonic form of steady-state solution

For the purpose of analysis of plate vibrations the excitation is adopted in the form of loading transverse to the plate mid-plane, as the most common and realistic one in the plate theory. The steady-state vibrations will be considered, so for the harmonic excitation function $p_{w}$ the following time form is assumed

$$\begin{aligned} p_w (x,y,t)=p_{wc} (x,y)\cos \lambda t+p_{ws} (x,y)\sin \lambda t \end{aligned}$$

(29)

In (29) $p_{wc}$ and $p_{ws}$ are arbitrary space functions of force amplitudes and $\lambda$ is the frequency of excitation.

The resulting solution for rotation and deflection displacements components reads

$$\begin{aligned} \mathbf{q}_w (x,y,t)= & {} \left\{ {w^{0}} \right\} =\mathbf{q}_{wc} (x,y)\cos \lambda t+\mathbf{q}_{ws} (x,y)\sin \lambda t \end{aligned}$$

(30)

$$\begin{aligned} \mathbf{q}_r (x,y,t)= & {} \left\{ {\begin{array}{l} \varphi _x \\ \varphi _y \\ \end{array}} \right\} =\mathbf{q}_{rc} (x,y)\cos \lambda t+\mathbf{q}_{rs} (x,y)\sin \lambda t\nonumber \\ \end{aligned}$$

(31)

Due to the partly linear (in in-plane displacements) and partly non-linear (in deflections) nature of in-plane strains (4) one has to assume a higher order form of solution for the in-plane displacements

$$\begin{aligned}&{} \mathbf{q}_t (x,y,t)=\left\{ {\begin{array}{l} u^{0} \\ v^{0} \\ \end{array}} \right\} \nonumber \\&\quad =\mathbf{q}_{tc} (x,y)\cos ^{2}\lambda t+\mathbf{q}_{t0} (x,y)\cos \lambda t\sin \lambda t\nonumber \\&\qquad +\,\mathbf{q}_{ts} (x,y)\sin ^{2}\lambda t \end{aligned}$$

(32)

The accelerations resulting from (30)–(32) are given by

$$\begin{aligned} {{\ddot{\mathbf{q}}}}_w (x,y,t)= & {} -\lambda ^{2}{} \mathbf{q}_{wc} (x,y)\cos \lambda t-\lambda ^{2}{} \mathbf{q}_{ws} (x,y)\sin \lambda t \end{aligned}$$

(33)

$$\begin{aligned} {{\ddot{\mathbf{q}}}}_r (x,y,t)= & {} -\lambda ^{2}{} \mathbf{q}_{rc} (x,y)\cos \lambda t-\lambda ^{2}{} \mathbf{q}_{rs} (x,y)\sin \lambda t \end{aligned}$$

(34)

$$\begin{aligned} {\ddot{\mathbf{q}}}_t (x,y,t)= & {} -2\lambda ^{2}\left\{ \left[ {\mathbf{q}_{tc} (x,y)-\mathbf{q}_{ts} (x,y)} \right] \cos ^{2}\lambda t\right. \nonumber \\&\quad \left. +\,2\mathbf{q}_{t0} (x,y)\cos \lambda t\sin \lambda t \right. \nonumber \\&\quad \left. {-\,\left[ {\mathbf{q}_{tc} (x,y)-\mathbf{q}_{ts} (x,y)} \right] \sin ^{2}\lambda t} \right\} \end{aligned}$$

(35)

Now the expressions for inertia forces can be written down. For the in-plane movement

$$\begin{aligned} \mathbf{b}_t (x,y,t)= & {} 2\lambda ^{2}\left\{ {\mathbf{m}_t \left[ {\mathbf{q}_{tc} (x,y)-\mathbf{q}_{ts} (x,y)} \right] \cos ^{2}\lambda t+} \right. \nonumber \\&\quad \left. +\,2\mathbf{m}_t \mathbf{q}_{t0} (x,y)\cos \lambda t\sin \lambda t\right. \nonumber \\&\left. \quad -\,\mathbf{m}_t \left[ {\mathbf{q}_{tc} (x,y)-\mathbf{q}_{ts} (x,y)} \right] \sin ^{2}\lambda t \right\} \end{aligned}$$

(36)

for the deflections

$$\begin{aligned} \mathbf{b}_w (x,y,t)=\lambda ^{2}{} \mathbf{m}_w \mathbf{q}_{wc} (x,y)\cos \lambda t+\lambda ^{2}{} \mathbf{m}_w \mathbf{q}_{ws} (x,y)\sin \lambda t \end{aligned}$$

(37)

and for the rotations

$$\begin{aligned} \mathbf{b}_r (x,y,t)=\lambda ^{2}{} \mathbf{m}_r \mathbf{q}_{rc} (x,y)\cos \lambda t+\lambda ^{2}{} \mathbf{m}_r \mathbf{q}_{rs} (x,y)\sin \lambda t \end{aligned}$$

(38)

Expressions (36)–(38) include the following mass matrices

$$\begin{aligned} \mathbf{m}_w =[m], \quad \mathbf{m}_t =\left[ {\begin{array}{cc} m&{}0 \\ 0&{}m \\ \end{array}} \right] =m\mathbf{I}, \quad \mathbf{m}_r =\frac{1}{12}\left[ {{\begin{array}{cc} {mh^{2}}&{} 0 \\ 0&{} {mh^{2}} \\ \end{array} }} \right] =m_r \mathbf{I} \end{aligned}$$

where m and $m_{r}$ are the plate unit area mass and the rotary inertia of the unit area mass, respectively.

Taking into account the geometric relations (6)–(9) with the assumed form of displacements (30)–(32) allows to formulate the generalized strains as

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_r (x,y,t)= & {} {{\varvec{\upvarepsilon }} }_{rc} (x,y)\cos \lambda t+{{\varvec{\upvarepsilon }} }_{rs} (x,y)\sin \lambda t \end{aligned}$$

(39)

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_s (x,y,t)= & {} {{\varvec{\upvarepsilon }} }_{sc} (x,y)\cos \lambda t+{{\varvec{\upvarepsilon }} }_{ss} (x,y)\sin \lambda t \end{aligned}$$

(40)

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_p (x,y,t)= & {} {{\varvec{\upvarepsilon }} }_{pc} (x,y)\cos ^{2}\lambda t+{{\varvec{\upvarepsilon }} }_{p0} (x,y)\cos \lambda t\sin \lambda t\nonumber \\&\quad +\,{{\varvec{\upvarepsilon }} }_{ps} (x,y)\sin ^{2}\lambda t\nonumber \\= & {} \left[ {{{\varvec{\upvarepsilon }} }_{plc} (x,y)+{{\varvec{\upvarepsilon }} }_{pnc} (x,y)} \right] \cos ^{2}\lambda t\nonumber \\&\quad +\,\left[ {{{\varvec{\upvarepsilon }} }_{pl0} (x,y)+{{\varvec{\upvarepsilon }} }_{pn0} (x,y)} \right] \cos \lambda t\sin \lambda t\nonumber \\&\quad +\,\left[ {{{\varvec{\upvarepsilon }} }_{pls} (x,y)+{{\varvec{\upvarepsilon }} }_{pns} (x,y)} \right] \sin ^{2}\lambda t \end{aligned}$$

(41)

In (41)$_{3}$ the functions of amplitudes of in-plane strains are split into linear and non-linear parts.

With the physical law for the fractional Zener material model (23)–(25) and the strains (39)–(41) taken into account, one can introduce the time form for the internal forces (18)–(20) as

$$\begin{aligned} \mathbf{M}(x,y,t)= & {} \mathbf{M}_c (x,y)\cos \lambda t+\mathbf{M}_s (x,y)\sin \lambda t \end{aligned}$$

(42)

$$\begin{aligned} \mathbf{Q}(x,y,t)= & {} \mathbf{Q}_c (x,y)\cos \lambda t+\mathbf{Q}_s (x,y)\sin \lambda t \end{aligned}$$

(43)

$$\begin{aligned} \mathbf{N}(x,y,t)= & {} \mathbf{N}_c (x,y)\cos ^{2}\lambda t\nonumber \\&\quad +\,\mathbf{N}_0 (x,y)\cos \lambda t\sin \lambda t+\mathbf{N}_s (x,y)\sin ^{2}\lambda t\nonumber \\ \end{aligned}$$

(44)

Note, that the non-linearity of the in-plane strain (9) requires the higher-order harmonic expression for the in-plane forces (44).

The corresponding time forms of virtual displacements and virtual strains are

$$\begin{aligned} \delta \mathbf{q}_w (x,y,t)= & {} \delta \mathbf{q}_{wc} (x,y)\cos \lambda t+\delta \mathbf{q}_{ws} (x,y)\sin \lambda t \end{aligned}$$

(45)

$$\begin{aligned} \delta \mathbf{q}_r (x,y,t)= & {} \delta \mathbf{q}_{rc} (x,y)\cos \lambda t+\delta \mathbf{q}_{rs} (x,y)\sin \lambda t \end{aligned}$$

(46)

$$\begin{aligned} \delta \mathbf{q}_t (x,y,t)= & {} \delta \mathbf{q}_{tc} (x,y)\cos ^{2}\lambda t\nonumber \\&+\,\delta \mathbf{q}_{t0} (x,y)\cos \lambda t\sin \lambda t\nonumber \\&+\,\delta \mathbf{q}_{ts} (x,y)\sin ^{2}\lambda t \end{aligned}$$

(47)

$$\begin{aligned} \delta {{\varvec{\upvarepsilon }} }_s (x,y,t)= & {} \delta {{\varvec{\upvarepsilon }} }_{sc} (x,y)\cos \lambda t+\delta {{\varvec{\upvarepsilon }} }_{ss} (x,y)\sin \lambda t \end{aligned}$$

(48)

$$\begin{aligned} \delta {{\varvec{\upvarepsilon }} }_r (x,y,t)= & {} \delta {{\varvec{\upvarepsilon }} }_{rc} (x,y)\cos \lambda t+\delta {{\varvec{\upvarepsilon }} }_{rs} (x,y)\sin \lambda t \end{aligned}$$

(49)

$$\begin{aligned} \delta {{\varvec{\upvarepsilon }} }_p (x,y,t)= & {} \delta {{\varvec{\upvarepsilon }} }_{pc} (x,y)\cos ^{2}\lambda t\nonumber \\&+\,\delta {{\varvec{\upvarepsilon }} }_{p0} (x,y)\cos \lambda t\sin \lambda t+\delta {{\varvec{\upvarepsilon }} }_{ps} (x,y)\sin ^{2}\lambda t\nonumber \\= & {} \left[ {\delta {{\varvec{\upvarepsilon }} }_{plc} (x,y)+\delta {{\varvec{\upvarepsilon }} }_{pnc} (x,y)} \right] \cos ^{2}\lambda t\nonumber \\&+\,\left[ {\delta {{\varvec{\upvarepsilon }} }_{pl0} (x,y)+\delta {{\varvec{\upvarepsilon }} }_{pn0} (x,y)} \right] \cos \lambda t\sin \lambda t \nonumber \\&+\,\left[ {\delta {{\varvec{\upvarepsilon }} }_{pls} (x,y)+\delta {{\varvec{\upvarepsilon }} }_{pns} (x,y)} \right] \sin ^{2}\lambda t \end{aligned}$$

(50)

5 The amplitude equation

The general form of the principle of virtual work for a vibrating plate can be written as

$$\begin{aligned} L_e +L_m =L_i \end{aligned}$$

(51)

where $L_{m}$, $L_{e}$ and $L_{i}$ represent the work due to inertia, external and internal forces, respectively. The time-averaged virtual work of external loading can be expressed by

$$\begin{aligned} L_e =\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta \mathbf{q}_w^T (x,y,t)\mathbf{p}_w (x,y,t)dAdt} } \end{aligned}$$

(52)

The time-averaged form of the virtual work by three considered inertia forces is given by

$$\begin{aligned} L_m= & {} \frac{2}{T}\int \limits _0^T \int \limits _A {\delta \mathbf{q}_t^T (x,y,t)\mathbf{b}_t (x,y,t)dAdt} \nonumber \\&\quad + \frac{2}{T}\int \limits _0^T {\int \limits _A {\delta \mathbf{q}_w^T (x,y,t)\mathbf{b}_w (x,y,t)dAdt} } \nonumber \\&\quad +\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta \mathbf{q}_r^T (x,y,t)\mathbf{b}_r (x,y,t)dAdt} } \end{aligned}$$

(53)

And the virtual work due to internal forces takes the form

$$\begin{aligned} L_i= & {} \frac{2}{T}\int \limits _0^T \int \limits _A {\delta {{\varvec{\upvarepsilon }} }_r^T (x,y,t)\mathbf{M}(x,y,t)dAdt}\nonumber \\&\quad +\frac{2}{T}\int \limits _0^T \int \limits _A {\delta {{\varvec{\upvarepsilon }} }_s^T (x,y,t)\mathbf{Q}(x,y,t)dAdt}\nonumber \\&\quad +\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_p^T (x,y,t)\mathbf{N}(x,y,t)dAdt} } \end{aligned}$$

(54)

In the definitions (52)–(54) T denotes the vibrations period and A is the plate area.

The problem in hand is geometrically non-linear and, additionally, the adopted physical law involves time derivatives of stress and strain (23)–(25). Thus it was decided, that the best way in the derivation of the amplitude equation will be to begin with the time integration. To this end, the time-form expressions from Sect. 4 are inserted into the virtual work (52)–(54).

In the case of the external work term (52), after substitution of (29), one gets

$$\begin{aligned}&\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta \mathbf{q}_w^T (x,y,t)\mathbf{p}_w (x,y,t)dAdt} } \nonumber \\&\quad =\int \limits _A {\delta \mathbf{q}_{wc}^T (x,y)\mathbf{p}_{wc} (x,y)dA} +\int \limits _A {\delta \mathbf{q}_{ws}^T (x,y)\mathbf{p}_{ws} (x,y)dA} \end{aligned}$$

(55)

For the in-plane inertia terms, substitution of (36) and (47) into the first component of (53), yields

$$\begin{aligned}&\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta \mathbf{q}_t^T (x,y,t)\mathbf{b}_t (x,y,t)dAdt} } \nonumber \\&\quad =\lambda ^{2}\left\{ {\int \limits _A {\delta \mathbf{q}_{tc}^T (x,y)\mathbf{m}_t \left[ {\mathbf{q}_{tc} (x,y)-\mathbf{q}_{ts} (x,y)} \right] dA} +} \right. \nonumber \\&\qquad \left. +\,\int \limits _A \delta \mathbf{q}_{t0}^T (x,y)\mathbf{m}_t \mathbf{q}_{t0} (x,y)dA\right. \nonumber \\&\left. \qquad -\,\int \limits _A {\delta \mathbf{q}_{ts}^T (x,y)\mathbf{m}_t \left[ {\mathbf{q}_{tc} (x,y)-\mathbf{q}_{ts} (x,y)} \right] dA} \right\} \end{aligned}$$

(56)

The influence of deflection inertia, after substitution of (37) and (45) into the second term in (53), results in

$$\begin{aligned}&\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta \mathbf{q}_w^T (x,y,t)\mathbf{b}_w (x,y,t)dAdt} } \nonumber \\&\quad =\lambda ^{2}\left[ \int \limits _A {\delta \mathbf{q}_{wc}^T (x,y)\mathbf{m}_w \mathbf{q}_{wc} (x,y)dA}\right. \nonumber \\&\left. \qquad +\int \limits _A {\delta \mathbf{q}_{ws}^T (x,y)\mathbf{m}_w \mathbf{q}_{ws} (x,y)dA} \right] \end{aligned}$$

(57)

For the rotary inertia, substitution of (38) and (46) into the third component of (53) leads to

$$\begin{aligned}&\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta \mathbf{q}_r^T (x,y,t)\mathbf{b}_r (x,y,t)dAdt} } \nonumber \\&\quad =\int \limits _A {\delta \mathbf{q}_{rc}^T (x,y)\mathbf{m}_r \mathbf{q}_{rc} (x,y)dA} \nonumber \\&\qquad +\,\int \limits _A {\delta \mathbf{q}_{rs}^T (x,y)\mathbf{m}_r \mathbf{q}_{rs} (x,y)dA} \end{aligned}$$

(58)

Now let us consider the virtual work due to internal forces. Taking into account (42) and (49) in the first component of (54) results in

$$\begin{aligned}&\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_r^T (x,y,t)\mathbf{M}(x,y,t)dAdt} } \nonumber \\&\quad =\int \limits _A {\delta \mathbf{q}_{rc}^T (x,y)\mathbf{B}_r^{{\prime }T} \mathbf{M}_c (x,y)dA}\nonumber \\&\qquad +\int \limits _A {\delta \mathbf{q}_{rs}^T (x,y)\mathbf{B}_r^{{\prime }T} \mathbf{M}_s (x,y)dA} \end{aligned}$$

(59)

The second component of (54) after substitution of (43) and (48) yields

$$\begin{aligned}&\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_s^T (x,y,t)\mathbf{Q}(x,y,t)dAdt} } \nonumber \\&\quad =\int \limits _A {\left[ {\delta \mathbf{q}_{wc}^T (x,y)\mathbf{{B}'}_{sw}^T +\delta \mathbf{q}_{rc}^T (x,y)\mathbf{{B}'}_{sr}^T } \right] \mathbf{Q}_c (x,y)dA} \nonumber \\&\qquad +\,\int \limits _A {\left[ {\delta \mathbf{q}_{ws}^T (x,y)\mathbf{{B}'}_{sw}^T +\delta \mathbf{q}_{rs}^T (x,y)\mathbf{{B}'}_{sr}^T } \right] \mathbf{Q}_s (x,y)dA}\nonumber \\ \end{aligned}$$

(60)

From the third component of (54) with (44) and (50) taken into account one gets

$$\begin{aligned}&\frac{2}{T}\int \limits _0^T {\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_p^T (x,y,t)\mathbf{N}(x,y,t)dAdt} }\nonumber \\&\quad =\frac{3}{4}\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_{pc}^T (x,y)\mathbf{N}_c (x,y)dA} \nonumber \\&\qquad +\,\frac{1}{4}\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_{pc}^T (x,y)\mathbf{N}_s (x,y)dA} +\frac{1}{4}\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_{p0}^T (x,y)\mathbf{N}_0 (x,y)dA} \nonumber \\&\qquad +\,\frac{1}{4}\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_{ps}^T (x,y)\mathbf{N}_c (x,y)dA} +\frac{3}{4}\int \limits _A {\delta {{\varvec{\upvarepsilon }} }_{ps}^T (x,y)\mathbf{N}_s (x,y)dA}\nonumber \\ \end{aligned}$$

(61)

The functions of amplitudes of internal forces M, Q and N in (59)–(61) have to be expressed in terms strains amplitudes functions. To this end the physical relations for the fractional Zener model (23)–(25) given in Sect. 3 are applied. In this fragment of the paper the explicit indication of dependence of amplitude functions on the space co-ordinates x, y is skipped in the notation.

To express the fractional time derivatives of internal forces and strains present in the physical law (23)–(25) one needs the fractional time derivatives of trigonometric functions

$$\begin{aligned}&D_t^\alpha \sin \lambda t=\lambda ^{\alpha }\cos \lambda t \nonumber \\&D_t^\alpha \cos \lambda t=-\lambda ^{\alpha }\sin \lambda t \end{aligned}$$

(62)

$$\begin{aligned}&D_t^\alpha \cos ^{2}\lambda t\nonumber \\&\quad =\frac{1}{2}\left( {2\lambda } \right) ^{\alpha }\left( {C\cos ^{2}\lambda t-2S\sin \lambda t\cos \lambda t-C\sin ^{2}\lambda t} \right) \nonumber \\&D_t^\alpha \left( {\sin \lambda t\cos \lambda t} \right) \nonumber \\&\quad =\frac{1}{2}\left( {2\lambda } \right) ^{\alpha }\left( {S\cos ^{2}\lambda t+2C\sin \lambda t\cos \lambda t-S\sin ^{2}\lambda t} \right) \nonumber \\&D_t^\alpha \sin ^{2}\lambda t\nonumber \\&\quad =-\frac{1}{2}\left( {2\lambda } \right) ^{\alpha }\left( {C\cos ^{2}\lambda t-2S\sin \lambda t\cos \lambda t-C\sin ^{2}\lambda t} \right) \end{aligned}$$

(63)

where:

$$\begin{aligned} C=\cos \frac{\alpha \pi }{2}, \quad S=\sin \frac{\alpha \pi }{2} \end{aligned}$$

The relations for moments (42) and rotational strains (39) as well as their time derivatives computed with (62) taken into account are substituted into the physical law (23) to get the equation

$$\begin{aligned}&{} \mathbf{M}_c \left[ {\left( {1+\tau ^{\alpha }\lambda ^{\alpha }C} \right) \cos \lambda t-\tau ^{\alpha }\lambda ^{\alpha }S\sin \lambda t} \right] \nonumber \\&\qquad +\,\mathbf{M}_s \left[ {\left( {1+\tau ^{\alpha }\lambda ^{\alpha }C} \right) \sin \lambda t+\tau ^{\alpha }\lambda ^{\alpha }S\cos \lambda t} \right] \nonumber \\&\quad =\mathbf{D}_0 \left( {{{\varvec{\upvarepsilon }} }_{rc} \cos \lambda t+{{\varvec{\upvarepsilon }} }_{rs} \sin \lambda t} \right) \nonumber \\&\qquad +\,\tau ^{\alpha }\lambda ^{\alpha }{} \mathbf{D}_\infty \left[ \left( {C\cos \lambda t-S\sin \lambda t} \right) {{\varvec{\upvarepsilon }} }_{rc} +\left( S\cos \lambda t\right. \right. \nonumber \\&\qquad \left. \left. +\,C\sin \lambda t \right) {{\varvec{\upvarepsilon }} }_{rs} \right] \end{aligned}$$

(64)

Using the harmonic balance method leads to a system of two equations, which correspond to cosine and sine amplitudes, respectively

$$\begin{aligned}&{} \mathbf{M}_c \left( {1+\tau ^{\alpha }\lambda ^{\alpha }C} \right) +\mathbf{M}_s \tau ^{\alpha }\lambda ^{\alpha }S\nonumber \\&\quad =\left( {\mathbf{D}_0 +\tau ^{\alpha }\lambda ^{\alpha }C\mathbf{D}_\infty } \right) {{\varvec{\upvarepsilon }} }_{rc} +\tau ^{\alpha }\lambda ^{\alpha }S\mathbf{D}_\infty {{\varvec{\upvarepsilon }} }_{rs}\nonumber \\&-\,\mathbf{M}_c \tau ^{\alpha }\lambda ^{\alpha }S+\mathbf{M}_s \left( {1+\tau ^{\alpha }\lambda ^{\alpha }C} \right) \nonumber \\&\quad =-\tau ^{\alpha }\lambda ^{\alpha }S\mathbf{D}_\infty {{\varvec{\upvarepsilon }} }_{rc} +\left( {\mathbf{D}_0 +\tau ^{\alpha }\lambda ^{\alpha }C\mathbf{D}_\infty } \right) {{\varvec{\upvarepsilon }} }_{rs} \end{aligned}$$

(65)

The functions of amplitudes of moments resulting from the solution of (65) take the form

$$\begin{aligned} \mathbf{M}_c (x,y)= & {} \mathbf{D}_{\alpha 1} {{\varvec{\upvarepsilon }} }_{rc} (x,y)+\mathbf{D}_{\alpha 2} {{\varvec{\upvarepsilon }} }_{rs} (x,y) \nonumber \\ \mathbf{M}_s (x,y)= & {} -\mathbf{D}_{\alpha 2} {{\varvec{\upvarepsilon }} }_{rc} (x,y)+\mathbf{D}_{\alpha 1} {{\varvec{\upvarepsilon }} }_{rs} (x,y) \end{aligned}$$

(66)

The new physical matrices in (66) are defined as

$$\begin{aligned} \mathbf{D}_{\alpha 1}= & {} d_M \left[ {\left( {1+\tau ^{\alpha }\lambda ^{\alpha }C} \right) \mathbf{D}_0 +\tau ^{\alpha }\lambda ^{\alpha }\left( {C+\tau ^{\alpha }\lambda ^{\alpha }} \right) \mathbf{D}_\infty } \right] \nonumber \\ \mathbf{D}_{\alpha 2}= & {} -d_M \tau ^{\alpha }\lambda ^{\alpha }S\left[ {\mathbf{D}_0 -\mathbf{D}_\infty } \right] \end{aligned}$$

(67)

where

$$\begin{aligned} d_M =\left[ {\left( {1+\tau ^{\alpha }\lambda ^{\alpha }C} \right) ^{2}+\tau ^{2\alpha }\lambda ^{2\alpha }} \right] ^{-1} \end{aligned}$$

After similar operations done on the shear force law (24) the following definitions are obtained

$$\begin{aligned} \mathbf{Q}_c (x,y)= & {} \mathbf{A}_{\alpha q1} {{\varvec{\upvarepsilon }} }_{rc} (x,y)+\mathbf{A}_{\alpha q2} {{\varvec{\upvarepsilon }} }_{rs} (x,y) \nonumber \\ \mathbf{Q}_s (x,y)= & {} -\mathbf{A}_{\alpha q2} {{\varvec{\upvarepsilon }} }_{rc} (x,y)+\mathbf{A}_{\alpha q1} {{\varvec{\upvarepsilon }} }_{rs} (x,y) \end{aligned}$$

(68)

with the new physical matrices

$$\begin{aligned} \mathbf{A}_{\alpha q1}= & {} d_M \left[ {\left( {1+\tau ^{\alpha }\lambda ^{\alpha }C} \right) \mathbf{A}_{q0} +\tau ^{\alpha }\lambda ^{\alpha }\left( {C+\tau ^{\alpha }\lambda ^{\alpha }} \right) \mathbf{A}_{q\infty } } \right] \nonumber \\ \mathbf{A}_{\alpha q2}= & {} -d_M \tau ^{\alpha }\lambda ^{\alpha }S\left[ {\mathbf{A}_{q0} -\mathbf{A}_{q\infty } } \right] \end{aligned}$$

(69)

Derivation of expressions for the in-plane forces is more complex due to the quadratic-trigonometric expressions (41) and (44). They are substituted into the physical law (25) to get the following equation

$$\begin{aligned}&{} \mathbf{N}_c \cos ^{2}\lambda t+\mathbf{N}_0 \cos \lambda t\sin \lambda t+\mathbf{N}_s \sin ^{2}\lambda t\nonumber \\&\qquad +\,\frac{1}{2}\left( {2\tau \lambda } \right) ^{\alpha }\left( C\cos ^{2}\lambda t-2S\cos \lambda t\sin \lambda t -\,C\sin ^{2}\lambda t \right) \left( {\mathbf{N}_c -\mathbf{N}_s } \right) \nonumber \\&\qquad +\,\frac{1}{2}\left( {2\tau \lambda } \right) ^{\alpha }\left( S\cos ^{2}\lambda t+2C\cos \lambda t\sin \lambda t - S\sin ^{2}\lambda t \right) \mathbf{N}_0 \nonumber \\&\quad =\mathbf{A}_0 {{\varvec{\upvarepsilon }} }_{pc} \cos ^{2}\lambda t+\mathbf{A}_0 {{\varvec{\upvarepsilon }} }_{p0} \cos \lambda t\sin \lambda t+\mathbf{A}_0 {{\varvec{\upvarepsilon }} }_{ps} \sin ^{2}\lambda t\nonumber \\&\qquad +\,\frac{1}{2}\left( {2\tau \lambda } \right) ^{\alpha }\left( C\cos ^{2}\lambda t-2S\cos \lambda t\sin \lambda t\right. \nonumber \\&\left. \qquad -\,C\sin ^{2}\lambda t \right) \mathbf{A}_\infty \left( {{{\varvec{\upvarepsilon }} }_{pc} -{{\varvec{\upvarepsilon }} }_{ps} } \right) \nonumber \\&\qquad +\,\frac{1}{2}\left( {2\tau \lambda } \right) ^{\alpha }\left( {S\cos ^{2}\lambda t+2C\cos \lambda t\sin \lambda t-S\sin ^{2}\lambda t} \right) \mathbf{A}_\infty {{\varvec{\upvarepsilon }} }_{p0}\nonumber \\ \end{aligned}$$

(70)

and the harmonic balance method applied to squared-cosine, sine-cosine and squared-sine terms, respectively, results in the following set of three equations

$$\begin{aligned}&\left[ {2+C\left( {2\tau \lambda } \right) ^{\alpha }} \right] \mathbf{N}_c +S\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{N}_0 -C\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{N}_s \nonumber \\&\quad =\left[ {2\mathbf{A}_0 +C\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{A}_\infty } \right] {{\varvec{\upvarepsilon }} }_{pc} \nonumber \\&\qquad +\,S\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{A}_\infty {{\varvec{\upvarepsilon }} }_{p0} -C\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{A}_\infty {{\varvec{\upvarepsilon }} }_{ps} \nonumber \\&-\,S\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{N}_c +\left[ {1+C\left( {2\tau \lambda } \right) ^{\alpha }} \right] \mathbf{N}_0 +S\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{N}_s \nonumber \\&\quad =-S\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{A}_\infty {{\varvec{\upvarepsilon }} }_{pc} +\left[ {\mathbf{A}_0 +C\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{A}_\infty } \right] {{\varvec{\upvarepsilon }} }_{p0} \nonumber \\&\qquad +\,S\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{A}_\infty {{\varvec{\upvarepsilon }} }_{ps} \nonumber \\&-\,C\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{N}_c -S\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{N}_0 +\left[ {2+C\left( {2\tau \lambda } \right) ^{\alpha }} \right] \mathbf{N}_s \nonumber \\&\quad =-C\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{A}_\infty {{\varvec{\upvarepsilon }} }_{pc} -S\left( {2\tau \lambda } \right) ^{\alpha }{} \mathbf{A}_\infty {{\varvec{\upvarepsilon }} }_{p0}\nonumber \\&\qquad +\,\left[ {2\mathbf{A}_0 +C\left( {2\tau \lambda } \right) ^{\alpha }\mathbf{A}_\infty } \right] {{\varvec{\upvarepsilon }} }_{ps} \end{aligned}$$

(71)

Finally, the expressions for the functions of in-plane forces amplitudes are obtained from the solution of (71) in the form

$$\begin{aligned}&{} \mathbf{N}_c (x,y)=\mathbf{A}_{\alpha 1} {{\varvec{\upvarepsilon }} }_{pc} (x,y)+\mathbf{A}_{\alpha 3} {{\varvec{\upvarepsilon }} }_{p0} (x,y)+\mathbf{A}_{\alpha 4} {{\varvec{\upvarepsilon }} }_{ps} (x,y) \nonumber \\&{} \mathbf{N}_0 (x,y)=2\mathbf{A}_{\alpha 3} {{\varvec{\upvarepsilon }} }_{pc} (x,y)+\mathbf{A}_{\alpha 2} {{\varvec{\upvarepsilon }} }_{p0} (x,y)-2\mathbf{A}_{\alpha 3} {{\varvec{\upvarepsilon }} }_{ps} (x,y) \nonumber \\&{} \mathbf{N}_s (x,y)=\mathbf{A}_{\alpha 4} {{\varvec{\upvarepsilon }} }_{pc} (x,y)+\mathbf{A}_{\alpha 3} {{\varvec{\upvarepsilon }} }_{p0} (x,y)+\mathbf{A}_{\alpha 1} {{\varvec{\upvarepsilon }} }_{ps} (x,y) \end{aligned}$$

(72)

There are four new physical matrices present in (72)

$$\begin{aligned} \mathbf{A}_{\alpha 1}= & {} \mathbf{A}_0 +t_{\alpha 1} (\mathbf{A}_\infty -\mathbf{A}_0 )\nonumber \\ \mathbf{A}_{\alpha 2}= & {} \mathbf{A}_0 +2t_{\alpha 1} (\mathbf{A}_\infty -\mathbf{A}_0 ) \nonumber \\ \mathbf{A}_{\alpha 3}= & {} -t_{\alpha 2} (\mathbf{A}_\infty -\mathbf{A}_0 ) \nonumber \\ \mathbf{A}_{\alpha 4}= & {} -t_{\alpha 1} (\mathbf{A}_\infty -\mathbf{A}_0 ) \end{aligned}$$

(73)

where

$$\begin{aligned} t_{\alpha 1}= & {} d_N \left( {2\tau \lambda } \right) ^{\alpha }\left[ {\left( {2\tau \lambda } \right) ^{\alpha }+C} \right] \\ t_{\alpha 2}= & {} d_N \left( {2\tau \lambda } \right) ^{\alpha }S \\ d_N= & {} \left[ {2+4\left( {2\tau \lambda } \right) ^{\alpha }C+2\left( {2\tau \lambda } \right) ^{2\alpha }} \right] ^{-1} \end{aligned}$$

In the further derivations also a component-wise format of the physical matrices (73) will be useful. Making use of the structure of the basic matrices $\mathbf{A}_{0}$ and $\mathbf{A}_{\infty }$ in (28) one can write down,

$$\begin{aligned} \mathbf{A}_{\alpha i} =\left[ {{\begin{array}{ccc} {a_{\alpha i11} }&{}\quad {a_{\alpha i12} }&{}\quad 0 \\ {a_{\alpha i12} }&{}\quad {a_{\alpha i22} }&{}\quad 0 \\ 0&{}\quad 0&{}\quad {a_{\alpha i33} } \\ \end{array} }} \right] , \quad i=1-4 \end{aligned}$$

(74)

It is worth to note, that setting $\alpha =1.0$ turns the fractional integral (22) into the classical one. Indeed, the physical relations (66), (68) and (72) for the fractional Zener material, which involve the physical matrices (67), (69) and (73), include, as a particular case for $\alpha =1.0$, the classical Zener material with the classical integer integral of the order one.

6 Finite element discretization

Plates considered in this paper are discretized using 8-noded rectangular elements with selective reduced integration for the shear terms. These elements were effectively used in [34] and some other papers to analyze the laminated plates with the GHM viscoelastic material.

Fig. 3

8-noded rectangular plate element

An element with the dimensions 2a and 2b and with the introduced numbering of nodes is depicted in Fig. 3. The vectors of nodal displacements amplitudes coinciding with the displacement field in (5) are introduced:

• the in-plane translations amplitudes in three 16-component vectors $\mathbf{q}_{tec}$, $\mathbf{q}_{te0}$, $\mathbf{q}_{tes}$

  $$\begin{aligned} \mathbf{q}_{tek} =\left\{ {{\begin{array}{lllllll} {u_{k1}^0 }&{} {v_{k1}^0 }&{} {u_{k2}^0 }&{} {v_{k2}^0 }&{} \ldots &{} {u_{k8}^0 }&{} {v_{k8}^0 } \\ \end{array} }} \right\} ^{T}, \quad k=c,~0\,\, \hbox {or}\,\, s\nonumber \\ \end{aligned}$$

  (75)

• the deflections amplitudes in two 8-component vectors $\mathbf{q}_{wec}$, $\mathbf{q}_{wes}$

  $$\begin{aligned} \mathbf{q}_{wek} =\left\{ {{\begin{array}{llll} {w_{j1}^0 }&{} {w_{j2}^0 }&{} \ldots &{} {w_{j8}^0 } \\ \end{array} }} \right\} ^{T}, \quad j=c\,\, \hbox {or}\,\, s \end{aligned}$$

  (76)

• the rotations amplitudes in two 16-component vectors $\mathbf{q}_{rec}$, $\mathbf{q}_{res}$

  $$\begin{aligned} \mathbf{q}_{rek} =\left\{ {{\begin{array}{llllllll} {\varphi _{xj1}}&{} {\varphi _{yj1}}&{} {\varphi _{xj2}}&{} {\varphi _{yj2}}&{} \ldots &{} {\varphi _{xj8}}&{} {\varphi _{yj8}} \\ \end{array} }} \right\} ^{T}, \quad j=c \,\,\hbox {or}\,\, s\nonumber \\ \end{aligned}$$

  (77)

The dimensionless local co-ordinates

$$\begin{aligned} \xi= & {} \frac{x}{a} \\ \eta= & {} \frac{y}{b} \end{aligned}$$

are introduced and the following bi-quadratic shape functions of the isoparametric element are used

$$\begin{aligned} \begin{array}{ll} N_1 =-\frac{1}{4}\left( {1+\xi } \right) \left( {1+\eta } \right) \left( {1-\xi -\eta } \right) &{}\quad N_5 =\frac{1}{2}\left( {1+\xi } \right) \left( {1-\eta } \right) \left( {1+\eta } \right) \\ N_2 =-\frac{1}{4}\left( {1+\xi } \right) \left( {1-\eta } \right) \left( {1-\xi +\eta } \right) &{}\quad N_6 =\frac{1}{2}\left( {1-\xi } \right) \left( {1-\eta } \right) \left( {1+\xi } \right) \\ N_3 =-\frac{1}{4}\left( {1-\xi } \right) \left( {1-\eta } \right) \left( {1+\xi +\eta } \right) &{}\quad N_7 =\frac{1}{2}\left( {1-\xi } \right) \left( {1+\eta } \right) \left( {1-\eta } \right) \\ N_4 =-\frac{1}{4}\left( {1-\xi } \right) \left( {1+\eta } \right) \left( {1-\xi +\eta } \right) &{}\quad N_8 =\frac{1}{2}\left( {1+\xi } \right) \left( {1+\eta } \right) \left( {1-\xi } \right) \end{array}\nonumber \\ \end{aligned}$$

(78)

to form the matrices

$$\begin{aligned} \mathbf{N}_w= & {} \left[ {{\begin{array}{llllllll} {N_1 }&{} {N_2 }&{} {N_3 }&{} {N_4 }&{} {N_5 }&{} {N_6 }&{} {N_7 }&{} {N_8 } \\ \end{array} }} \right] \nonumber \\ \mathbf{N}_t= & {} \mathbf{N}_r =\left[ {{\begin{array}{llllllll} {\mathbf{N}_1 }&{} {\mathbf{N}_2 }&{} {\mathbf{N}_3 }&{} {\mathbf{N}_4 }&{} {\mathbf{N}_5 }&{} {\mathbf{N}_6 }&{} {\mathbf{N}_7 }&{} {\mathbf{N}_8 } \\ \end{array} }} \right] \end{aligned}$$

(79)

where

$$\begin{aligned} \mathbf{N}_j =\left[ {{\begin{array}{ll} {N_j }&{} 0 \\ 0&{} {N_j } \\ \end{array} }} \right] \quad j=1{-}8 \end{aligned}$$

(80)

With (75)–(77) and (79) in hand, the element displacements amplitudes are

$$\begin{aligned} \mathbf{q}_{tc} (x,y)= & {} \mathbf{N}_t (x,y)\mathbf{q}_{tec} \nonumber \\ \mathbf{q}_{t0} (x,y)= & {} \mathbf{N}_t (x,y)\mathbf{q}_{te0} \nonumber \\ \mathbf{q}_{ts} (x,y)= & {} \mathbf{N}_t (x,y)\mathbf{q}_{tes} \end{aligned}$$

(81)

$$\begin{aligned} \mathbf{q}_{wc} (x,y)= & {} \mathbf{N}_w (x,y)\mathbf{q}_{wec} \nonumber \\ \mathbf{q}_{ws} (x,y)= & {} \mathbf{N}_w (x,y)\mathbf{q}_{wes} \end{aligned}$$

(82)

$$\begin{aligned} \mathbf{q}_{rc} (x,y)= & {} \mathbf{N}_r (x,y)\mathbf{q}_{rec} \nonumber \\ \mathbf{q}_{rs} (x,y)= & {} \mathbf{N}_r (x,y)\mathbf{q}_{res} \end{aligned}$$

(83)

The matrices of shape functions derivatives can be used to express the strain amplitudes (39)–(41). The rotational strains are

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_{rc} (x,y)= & {} \mathbf{B}_r (x,y)\mathbf{q}_{rec} \nonumber \\ {{\varvec{\upvarepsilon }} }_{rs} (x,y)= & {} \mathbf{B}_r (x,y)\mathbf{q}_{res} \end{aligned}$$

(84)

and with (6) the matrix $\mathbf{B}_{r}$ is

$$\begin{aligned} \mathbf{B}_r =\mathbf{B}_r^{\prime }{} \mathbf{N}_r =\left[ {{\begin{array}{llll} {\mathbf{B}_{r1} }&{} {\mathbf{B}_{r2} }&{} \ldots &{} {\mathbf{B}_{r8} } \\ \end{array} }} \right] \end{aligned}$$

(85)

where

$$\begin{aligned} \mathbf{B}_{ri} =\left[ {{\begin{array}{cc} {\frac{\partial N_i }{\partial x}}&{} 0 \\ 0&{} {\frac{\partial N_i }{\partial y}} \\ {\frac{\partial N_i }{\partial y}}&{} {\frac{\partial N_i }{\partial x}} \\ \end{array} }} \right] , \quad i=1-8 \end{aligned}$$

(86)

A row-wise layout of the matrix (85) will be useful, too:

$$\begin{aligned} \mathbf{B}_r =\left[ {{\begin{array}{c} {\mathbf{B}_{rx} } \\ {\mathbf{B}_{ry} } \\ {\mathbf{B}_{rxy} } \\ \end{array} }} \right] =\left[ {{\begin{array}{ccccccc} {\frac{\partial N_1 }{\partial x}}&{} 0&{} {\frac{\partial N_2 }{\partial x}}&{} 0&{} \ldots &{} {\frac{\partial N_8 }{\partial x}}&{} 0 \\ 0&{} {\frac{\partial N_1 }{\partial y}}&{} 0&{} {\frac{\partial N_2 }{\partial y}}&{} \ldots &{} 0&{} {\frac{\partial N_8 }{\partial y}} \\ {\frac{\partial N_1 }{\partial y}}&{} {\frac{\partial N_1 }{\partial x}}&{} {\frac{\partial N_2 }{\partial y}}&{} {\frac{\partial N_2 }{\partial x}}&{} \ldots &{} {\frac{\partial N_8 }{\partial y}}&{} {\frac{\partial N_8 }{\partial x}} \\ \end{array} }} \right] \end{aligned}$$

(87)

The shear strains can be given as

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_{sc} (x,y)= & {} \mathbf{B}_{sw} (x,y)\mathbf{q}_{wec} +\mathbf{B}_{sr} (x,y)\mathbf{q}_{rec} \nonumber \\ {{\varvec{\upvarepsilon }} }_{ss} (x,y)= & {} \mathbf{B}_{sw} (x,y)\mathbf{q}_{wes} +\mathbf{B}_{sr} (x,y)\mathbf{q}_{res} \end{aligned}$$

(88)

where

$$\begin{aligned} \mathbf{B}_{sw}= & {} {\mathbf{B}_{sw}}^{\prime }{} \mathbf{N}_w =\left[ \begin{array}{llll} {\mathbf{B}_{sw1} }&{} {\mathbf{B}_{sw2} }&{} \ldots &{} {\mathbf{B}_{sw8}} \\ \end{array} \right] \nonumber \\ \mathbf{B}_{sr}= & {} {\mathbf{B}_{sr}}^{\prime }{} \mathbf{N}_r =\left[ \begin{array}{llll} {\mathbf{B}_{sr1} }&{} {\mathbf{B}_{sr2} }&{} \ldots &{} {\mathbf{B}_{sr8}} \\ \end{array} \right] \end{aligned}$$

(89)

$$\begin{aligned} \mathbf{B}_{swi}= & {} \left[ \begin{array}{l} {\frac{\partial N_i }{\partial x}} \\ {\frac{\partial N_i }{\partial y}} \\ \end{array} \right] , \quad i=1-8 \nonumber \\ \mathbf{B}_{sri}= & {} \left[ \begin{array}{ll} {N_i} &{} 0 \\ 0&{} {N_i} \\ \end{array} \right] \end{aligned}$$

(90)

The discretization of the linear in-plane strains components leads to

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_{plc} (x,y)= & {} \mathbf{B}_r (x,y)\mathbf{q}_{tec} \nonumber \\ {{\varvec{\upvarepsilon }} }_{pl0} (x,y)= & {} \mathbf{B}_r (x,y)\mathbf{q}_{te0} \nonumber \\ {{\varvec{\upvarepsilon }} }_{pls} (x,y)= & {} \mathbf{B}_r (x,y)\mathbf{q}_{tes} \end{aligned}$$

(91)

with the same matrix $\mathbf{B}_{r}$ as in (85).

Let us now consider the particular elements of the non-linear in-plane strains components

$$\begin{aligned} {{\varvec{\upvarepsilon }} }_{pnc} (x,y)= & {} \left\{ {{\begin{array}{lll} {\varepsilon _{pnc1} (x,y)}&{} {\varepsilon _{pnc2} (x,y)}&{} {\varepsilon _{pnc3} (x,y)} \\ \end{array} }} \right\} ^{T} \nonumber \\ {{\varvec{\upvarepsilon }} }_{pn0} (x,y)= & {} \left\{ {{\begin{array}{lll} {\varepsilon _{pn01} (x,y)}&{} {\varepsilon _{pn02} (x,y)}&{} {\varepsilon _{pn03} (x,y)} \\ \end{array} }} \right\} ^{T} \nonumber \\ {{\varvec{\upvarepsilon }} }_{pns} (x,y)= & {} \left\{ {{\begin{array}{lll} {\varepsilon _{pns1} (x,y)}&{} {\varepsilon _{pns2} (x,y)}&{} {\varepsilon _{pns3} (x,y)} \\ \end{array} }} \right\} ^{T} \end{aligned}$$

(92)

With (9) taken into account one gets

$$\begin{aligned} \varepsilon _{pnk1} (x,y)= & {} \frac{1}{2}{} \mathbf{q}_{wek} ^{T}\mathbf{B}_{w1} ^{T}(x,y)\mathbf{B}_{w1} (x,y)\mathbf{q}_{wek} \nonumber \\ \varepsilon _{pnk2} (x,y)= & {} \frac{1}{2}{} \mathbf{q}_{wek} ^{T}\mathbf{B}_{w2} ^{T}(x,y)\mathbf{B}_{w2} (x,y)\mathbf{q}_{wek} \nonumber \\ \varepsilon _{pnk1} (x,y)= & {} \frac{1}{2}{} \mathbf{q}_{wek} ^{T}\left[ \mathbf{B}_{w1} ^{T}(x,y)\mathbf{B}_{w2} (x,y)\right. \nonumber \\&\left. +\,\mathbf{B}_{w2} ^{T}(x,y)\mathbf{B}_{w1} (x,y) \right] \mathbf{q}_{wek}\nonumber \\ \end{aligned}$$

(93)

where k  stands for c, s or 0. The appropriate shape functions matrices are

$$\begin{aligned} \mathbf{B}_{w1}= & {} {\mathbf{B}_{w1}}^{\prime }{} \mathbf{N}_w =\left[ {{\begin{array}{llll} {\mathbf{B}_{w11} }&{} {\mathbf{B}_{w12} }&{} \ldots &{} {\mathbf{B}_{w18} } \\ \end{array} }} \right] \nonumber \\ \mathbf{B}_{w2}= & {} {\mathbf{B}_{w2}}^{\prime }{} \mathbf{N}_w =\left[ {{\begin{array}{llll} {\mathbf{B}_{w21} }&{} {\mathbf{B}_{w22} }&{} \ldots &{} {\mathbf{B}_{w28} } \\ \end{array} }} \right] \end{aligned}$$

(94)

including

$$\begin{aligned} \begin{array}{l} \mathbf{B}_{w1j} =\left[ {\frac{\partial N_j }{\partial x}} \right] \\ \mathbf{B}_{w2j} =\left[ {\frac{\partial N_j }{\partial y}} \right] \\ \end{array}, \quad j=1-8 \end{aligned}$$

(95)

Now the mass and stiffness matrices of the plate element can be derived. After the discretization the three inertia terms (57)–(59) in the virtual work result in the following matrix expression

$$\begin{aligned} \begin{array}{l} \left\{ {\delta \mathbf{q}_e } \right\} ^{T}\left( {-\lambda ^{2}} \right) \left[ {\mathbf{M}_e } \right] \left\{ {\mathbf{q}_e } \right\} \\ \quad =\left\{ {{\begin{array}{l} {\delta \mathbf{q}_{tec} } \\ {\delta \mathbf{q}_{te0} } \\ {\delta \mathbf{q}_{tes} } \\ {\delta \mathbf{q}_{wec} } \\ {\delta \mathbf{q}_{wes} } \\ {\delta \mathbf{q}_{rec} } \\ {\delta \mathbf{q}_{res} } \\ \end{array} }} \right\} ^{T}\left( {-\lambda ^{2}} \right) \left[ {\begin{array}{ccccccc} \mathbf{M}_t &{}0&{}-\mathbf{M}_t &{}0&{}0&{}0&{}0 \\ 0&{}\mathbf{M}_t &{}0&{}0&{}0&{}0&{}0 \\ -\mathbf{M}_t &{}0&{}\mathbf{M}_t &{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}\mathbf{M}_w &{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}\mathbf{M}_w &{}0&{}0 \\ 0&{}0&{}0&{}0&{}0&{}\mathbf{M}_r &{}0 \\ 0&{}0&{}0&{}0&{}0&{}0&{}\mathbf{M}_r \\ \end{array}} \right] \\ \qquad \times \left\{ {{\begin{array}{l} {\mathbf{q}_{tec} } \\ {\mathbf{q}_{te0} } \\ {\mathbf{q}_{tes} } \\ {\mathbf{q}_{wec} } \\ {\mathbf{q}_{wes} } \\ {\mathbf{q}_{rec} } \\ {\mathbf{q}_{res} } \\ \end{array} }} \right\} \\ \end{array} \end{aligned}$$

(96)

where the mass matrices are

$$\begin{aligned} \mathbf{M}_t= & {} \int \limits _A {m\mathbf{N}_t ^{T}{} \mathbf{N}_t dA} \nonumber \\ \mathbf{M}_w= & {} \int \limits _A {m\mathbf{N}_w ^{T}{} \mathbf{N}_w dA} \nonumber \\ \mathbf{M}_r= & {} \int \limits _A {m_r \mathbf{N}_r ^{T}{} \mathbf{N}_r dA} \end{aligned}$$

(97)

The expression (96) is linear in displacements. Hence, in the linearization of the amplitude equation the term—$\lambda ^{2}{} \mathbf{M}_{e}$ will be included directly in the tangent matrix, while—$\lambda ^{2}{} \mathbf{M}_{e}\mathbf{q}_{e}$ will enter the residual vector.

Let us now consider the stiffness terms. The contribution of moments (59) to the amplitude equation after the discretization produces four stiffness matrices related to rotation degrees of freedom of the element. The resulting expression has the following form

$$\begin{aligned} \left[ {\begin{array}{ll} {\delta \mathbf{q}_{rec}^T }&{} {\delta \mathbf{q}_{res}^T } \\ \end{array} } \right] \left[ {{\begin{array}{ll} {\mathbf{K}_{r1} }&{} {\mathbf{K}_{r2} } \\ {-\mathbf{K}_{r2} }&{} {\mathbf{K}_{r1} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\mathbf{q}_{rec} } \\ {\mathbf{q}_{res} } \\ \end{array} }} \right\} \end{aligned}$$

(98)

The element stiffness matrices in (98) yielding from the moments amplitudes (66) and the discretization of rotational strains (84) are given by

$$\begin{aligned} \mathbf{K}_{ri} =\int \limits _A {\mathbf{B}_r^T \mathbf{D}_i \mathbf{B}_r dA} , \quad i=1,2 \end{aligned}$$

(99)

The shear forces contribution (60) to the amplitude equation is expressed by deflection and rotation degrees of freedom. The discretization yields

$$\begin{aligned}&\left[ {{\begin{array}{llll} {\delta \mathbf{q}_{wec}^T }&{} {\delta \mathbf{q}_{wes}^T }&{} {\delta \mathbf{q}_{rec}^T }&{} {\delta \mathbf{q}_{res}^T } \\ \end{array} }} \right] \left[ {{\begin{array}{cccc} {\mathbf{K}_{sw1} }&{} -{\mathbf{K}_{sw2} }&{} {\mathbf{K}_{swr1} }&{} {\mathbf{K}_{swr2} } \\ {\mathbf{K}_{sw2} }&{} {\mathbf{K}_{sw1} }&{} {-\mathbf{K}_{swr2} }&{} {\mathbf{K}_{swr1} } \\ {\mathbf{K}_{swr1} ^{T}}&{} {\mathbf{K}_{swr2} ^{T}}&{} {\mathbf{K}_{sr1} }&{} {\mathbf{K}_{sr2} } \\ {-\mathbf{K}_{swr2} ^{T}}&{} {\mathbf{K}_{swr1} ^{T}}&{} {-\mathbf{K}_{sr2} }&{} {\mathbf{K}_{sr1} } \\ \end{array} }} \right] \nonumber \\&\quad \times \left\{ {{\begin{array}{l} {\mathbf{q}_{wec} } \\ {\mathbf{q}_{wes} } \\ {\mathbf{q}_{rec} } \\ {\mathbf{q}_{res} } \\ \end{array} }} \right\} \end{aligned}$$

(100)

Using the expression for shear forces amplitudes (68) and the discretization of shear strain amplitudes (88) leads to the following expressions for the matrices in (100)

$$\begin{aligned} \mathbf{K}_{swi}= & {} \int \limits _A {\mathbf{B}_{sw}^T \mathbf{A}_{qi} \mathbf{B}_{sw} dA} , \quad i=1,2 \end{aligned}$$

(101)

$$\begin{aligned} \mathbf{K}_{swri}= & {} \int \limits _A {\mathbf{B}_{sw}^T \mathbf{A}_{qi} \mathbf{B}_{sr} dA} , \quad i=1,2 \end{aligned}$$

(102)

$$\begin{aligned} \mathbf{K}_{sri}= & {} \int \limits _A {\mathbf{B}_{sr}^T \mathbf{A}_{qi} \mathbf{B}_{sr} dA} , \quad i=1,2 \end{aligned}$$

(103)

The in-plane virtual strains present in the in-plane forces contribution to the amplitude equation (61) include linear and non-linear expressions, resulting from (91) and (92), respectively. These strains are also used to define the in-plane forces in (72). Taking this into account it becomes evident, that the contribution (61) to the amplitude equation results in four groups of terms:

• (i) linear in $\mathbf{q}_{tec}$, $\mathbf{q}_{te0}$, $\mathbf{q}_{tes}$,

• (ii) mixed non-linear with products of $\mathbf{q}_{tec}$, $\mathbf{q}_{te0}$, $\mathbf{q}_{tes}$ and $\mathbf{q}_{wec}$, $\mathbf{q}_{wes}$

• (iii) quadratic in $\mathbf{q}_{wec}$ ,$\mathbf{q}_{wes}$,

• (iv) cubic in $\mathbf{q}_{wec}$, $\mathbf{q}_{wes}$,

Within each group are one has to take into account each of the five components in (61). For the linear terms (i) one gets

$$\begin{aligned} \left[ {{\begin{array}{lll} {\delta \mathbf{q}_{tec}^T }&{} {\delta \mathbf{q}_{te0}^T }&{} {\delta \mathbf{q}_{tes}^T } \\ \end{array} }} \right] \left[ {{\begin{array}{lll} {\mathbf{K}_{l1} }&{} {\mathbf{K}_{l3} }&{} {\mathbf{K}_{l4} } \\ {-\mathbf{K}_{l3} }&{} {\mathbf{K}_{l2} }&{} {\mathbf{K}_{l3} } \\ {\mathbf{K}_{l4} }&{} {-\mathbf{K}_{l3} }&{} {\mathbf{K}_{l1} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\mathbf{q}_{tec} } \\ {\mathbf{q}_{te0} } \\ {\mathbf{q}_{tes} } \\ \end{array} }} \right\} \end{aligned}$$

(104)

where

$$\begin{aligned} \mathbf{K}_{l1}= & {} \frac{1}{4}\left( {3\mathbf{K}_{t1} +\mathbf{K}_{t4} } \right) \nonumber \\ \mathbf{K}_{l2}= & {} \frac{1}{4}{} \mathbf{K}_{t2} \nonumber \\ \mathbf{K}_{l3}= & {} -\frac{1}{2}{} \mathbf{K}_{t3} \nonumber \\ \mathbf{K}_{l4}= & {} \frac{1}{4}\left( {\mathbf{K}_{t1} +3\mathbf{K}_{t4} } \right) \nonumber \\ \mathbf{K}_{tj}= & {} \int \limits _A {\mathbf{B}_r^T \mathbf{A}_j \mathbf{B}_r dA} , \quad j=1-4 \end{aligned}$$

(105)

The linear dependence of (98), (100) and (104) on nodal displacements is evident and we can write down these three contributions together in a short form

$$\begin{aligned} \left\{ {\delta \mathbf{q}_e } \right\} ^{T}\left[ {\mathbf{K}_{el} } \right] \left\{ {\mathbf{q}_e } \right\} \end{aligned}$$

(106)

similarly to the inertia terms in (96). The product $\mathbf{K}_{el} \mathbf{q}_{e}$ constitutes a part of the residual vector and the linear stiffness matrix $\mathbf{K}_{el}$ has to be directly included in the tangent matrix of the linearization of the amplitude equation.

The other three groups of contributions from the in-plane forces are non-linear in displacements amplitudes. The mixed non-linear ones (ii) yield

$$\begin{aligned} \left[ {{\begin{array}{ll} {\delta \mathbf{q}_{wec}^T }&{} {\delta \mathbf{q}_{wes}^T } \\ \end{array} }} \right] \left[ {{\begin{array}{lll} {\mathbf{K}_{wtc} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{wtc0} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{wtcs} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) } \\ {\mathbf{K}_{wtsc} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{wts0} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{wts} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\mathbf{q}_{tec} } \\ {\mathbf{q}_{te0} } \\ {\mathbf{q}_{tes} } \\ \end{array} }} \right\} \end{aligned}$$

(107)

the quadratic ones (iii)

$$\begin{aligned}&\left[ {{\begin{array}{lll} {\delta \mathbf{q}_{tec}^T }&{} {\delta \mathbf{q}_{te0}^T }&{} {\delta \mathbf{q}_{tes}^T } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\mathbf{K}_{twc} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{twcs} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) } \\ {\mathbf{K}_{tw0c} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{tw0s} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) } \\ {\mathbf{K}_{twsc} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{tws} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) } \\ \end{array} }} \right] \nonumber \\&\quad \times \left\{ {{\begin{array}{l} {\mathbf{q}_{wec} } \\ {\mathbf{q}_{wes} } \\ \end{array} }} \right\} \end{aligned}$$

(108)

and, finally, the cubic ones (iv)

$$\begin{aligned}&\left[ {{\begin{array}{ll} {\delta \mathbf{q}_{wec}^T }&{} {\delta \mathbf{q}_{wes}^T } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\mathbf{K}_{wc} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{wcs} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) } \\ {\mathbf{K}_{wsc} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) }&{} {\mathbf{K}_{ws} \left( {\mathbf{q}_{wec} ,\mathbf{q}_{wes} } \right) } \\ \end{array} }} \right] \nonumber \\&\quad \times \left\{ {{\begin{array}{l} {\mathbf{q}_{wec} } \\ {\mathbf{q}_{wes} } \\ \end{array} }} \right\} \end{aligned}$$

(109)

The matrices appearing in (107)–(109) are defined in “Appendix” in (122)–(124).

The products of particular stiffness matrices K and the respective displacements vectors q in (107)–(109) are the vectors which enter the global residual vector. To compute tangent matrix components, necessary in the numerical solution of the derived non-linear amplitude equation, one still requires linearization of (107)–(109). After some elementary mathematics the following expressions are obtained

$$\begin{aligned}&\left[ {{\begin{array}{ll} {\delta \mathbf{q}_{wec}^T }&{} {\delta \mathbf{q}_{wes}^T } \\ \end{array} }} \right] \left[ {{\begin{array}{lllll} {\mathbf{K}_{wtc} }&{} {\mathbf{K}_{wtc0} }&{} {\mathbf{K}_{wtcs} }&{} {\mathbf{K}_{nlc} }&{} {\mathbf{K}_{nlcs} } \\ {\mathbf{K}_{wtsc} }&{} {\mathbf{K}_{wts0} }&{} {\mathbf{K}_{wts} }&{} {\mathbf{K}_{nlcs} }&{} {\mathbf{K}_{nls} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\Delta \mathbf{q}_{tec} } \\ {\Delta \mathbf{q}_{te0} } \\ {\Delta \mathbf{q}_{tes} } \\ {\Delta \mathbf{q}_{wes} } \\ {\Delta \mathbf{q}_{wes} } \\ \end{array} }} \right\} \end{aligned}$$

(110)

$$\begin{aligned}&\left[ {{\begin{array}{lll} {\delta \mathbf{q}_{tec}^T }&{} {\delta \mathbf{q}_{te0}^T }&{} {\delta \mathbf{q}_{tes}^T } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {2\mathbf{K}_{twc} }&{} {2\mathbf{K}_{twcs} } \\ {2\mathbf{K}_{tw0c} }&{} {2\mathbf{K}_{tw0s} } \\ {2\mathbf{K}_{twsc} }&{} {2\mathbf{K}_{tws} } \\ \end{array} }} \right] \left\{ {{\begin{array}{ll} {\Delta \mathbf{q}_{wec} } \\ {\Delta \mathbf{q}_{wes} } \\ \end{array} }} \right\} \end{aligned}$$

(111)

$$\begin{aligned}&\left[ {{\begin{array}{ll} {\delta \mathbf{q}_{wec}^T }&{} {\delta \mathbf{q}_{wes}^T } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\left( {2\mathbf{K}_{wc} +\mathbf{K}_{nc} } \right) }&{} {\left( {2\mathbf{K}_{wcs} +\mathbf{K}_{ncs} } \right) } \\ {\left( {2\mathbf{K}_{wsc} +\mathbf{K}_{ncs} } \right) }&{} {\left( {2\mathbf{K}_{ws} +\mathbf{K}_{ns} } \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\mathbf{q}_{wec} } \\ {\mathbf{q}_{wes} } \\ \end{array} }} \right\} \nonumber \\ \end{aligned}$$

(112)

The final form of additional matrices present in (110) and (112) is specified in “Appendix” in (125) and (126).

To complete the discretized amplitude equation, the virtual work of excitation forces (55) is found as

$$\begin{aligned} \left\{ {\delta \mathbf{q}_e} \right\} ^{T}\left\{ {\mathbf{P}_e } \right\} =\left\{ {{\begin{array}{l} {\delta \mathbf{q}_{tec} } \\ {\delta \mathbf{q}_{te0} } \\ {\delta \mathbf{q}_{tes} } \\ {\delta \mathbf{q}_{wec} } \\ {\delta \mathbf{q}_{wes} } \\ {\delta \mathbf{q}_{rec} } \\ {\delta \mathbf{q}_{res} } \\ \end{array} }} \right\} ^{T}\hbox { }\left\{ {{\begin{array}{l} \mathbf{0} \\ \mathbf{0} \\ \mathbf{0} \\ {\mathbf{P}_{wec} } \\ {\mathbf{P}_{wes} } \\ \mathbf{0} \\ \mathbf{0} \\ \end{array} }} \right\} \end{aligned}$$

(113)

where the load amplitude vectors take the form

$$\begin{aligned} \mathbf{P}_{wec}= & {} \int \limits _A {\mathbf{N}_w ^{T}{} \mathbf{p}_{wc} dA} \nonumber \\ \mathbf{P}_{wes}= & {} \int \limits _A {\mathbf{N}_w ^{T}{} \mathbf{p}_{ws} dA} \end{aligned}$$

(114)

The vector of element loading $\mathbf{P}_{e}$ constitutes a part of the residual vector.

Remark 1

Surface integrals in stiffness and mass matrices derived above are evaluated using the double Gauss quadrature. The mass matrices (97) including shape functions directly are computed using its 5-point version. The stiffness matrices, where the derivatives of shape functions are present, (99), (105) and (122)–(126) are computed using the 4-point version of the quadrature. Only the matrices (101)–(103) in the shear contribution are computed using the reduced integration with 3-point version of the Gauss integration scheme to eliminate the problem of shear locking.

Remark 2

Expressions (96), (106)–(109) and (113) put together constitute the non-linear amplitude equation, which can be written in the general form

$$\begin{aligned} \mathbf{R}\left( {\mathbf{q},\lambda } \right) =0 \end{aligned}$$

(115)

and solved to find the response curves. These solutions are non-linear, including turning points, and can be obtained using the Newton-Raphson method only partially. To overcome the problems due to the complex nature of these curves, path-following methods can be applied [24].

The idea of path following methods was first presented by Riks [32]. Then it was successfully applied in computation schemes (e.g. [6, 36]), especially for equilibrium paths in non-linear static and stability analyses. Lewandowski [24] proposed to use it also in finding highly non-linear response curves in steady-state vibration analyses. This idea is followed in this paper and the procedure for the spherical hyperplane constraint equation is taken after Stanić et al. [38], where it was used to solve the equilibrium path in the stability analysis of structural elements.

7 Numerical analyses

Results of solved numerical examples are presented in this section with the purpose to illustrate the efficiency of the proposed approach to analysis of plate steady-state vibrations. The main goal of the presentation is to show influences of various physical parameters on the dynamic characteristics. Relatively simple cases are considered on purpose and focus is mainly on the inherent features of the Zener model with the Caputo fractional derivative applied to the geometrically non-linear steady-state vibrations of plates.

7.1 Example 1—sensitivity to the FE mesh density

As an introduction let us check the influence of the number of finite elements on the response curves. Harmonically forced vibrations of a moderately thick square plate with immovable simple supports on all four edges, presented in Fig. 4, are considered. The plate dimensions are: edge length 1.0 m and depth 0.1m. The viscoelastic material data for a fictitious polymer are taken from [10] as: $E_{0}=7\times 10^{6}~\hbox {N/m}^{2}$, $E_{\infty }=10\times 10^{6}~\hbox {N/m}^{2}$, $\tau =0.01~\hbox {s}^{\alpha }$ and $\rho =1250~\hbox {kg/m}^{3}$. The order of the fractional derivative is taken as $\alpha =0.8$. The excitation is assumed as a point load applied at the plate centre.

Fig. 4

Square plate loaded by the concentrated force at the centre

The force time form is expressed as

$$\begin{aligned} P_w =P_{wc} \cos \lambda t \end{aligned}$$

(116)

with the amplitude $P_{wc}$ equal to 2000 N.

The plate is discretized using four different mesh sizes. We focus our attention on the total amplitude of deflection q at the plate centre point (where the excitation force is applied) which is given by

$$\begin{aligned} q=\sqrt{q_{wc} ^{2}+q_{ws} ^{2}} \end{aligned}$$

(117)

where $q_{wc}$ and $q_{ws}$ are sine and cosine amplitudes of the deflection corresponding to (30).

Within the considered range of excitation frequency $\lambda =[0,~100]~\hbox {rad/s}$ lies the analytical value of the first natural frequency of linear vibrations for the analyzed plate. For the Young’s modulus $E={E}_{0}$ it is $\omega _{1ex}=40.8 \,\,\hbox {rad/s}$. The results for both component amplitudes $q_{wc}$, $q_{ws}$ and for the total amplitude q are presented in Figs. 5, 6 and 7, respectively. It can be noted that the response curves for the total amplitude in Fig. 7 correspond well to the resonance zone in the vicinity of the exact value of $\omega _{1ex}$.

Fig. 5

Example 1—response curves of cosine deflection $q_{c}$ for varying FE mesh sizes

Fig. 6

Example 1—response curves of cosine deflection $q_{s}$ for varying FE mesh sizes

Fig. 7

Example 1—response curves of total deflection q for varying FE mesh sizes

Results of static deflection $q_{st}$ of the plate, the maximum amplitude $q_{max}$ and the corresponding excitation frequency $\lambda _{max}$, which is called the resonance frequency, are presented in Table 1 for four analyzed FE meshes. The relative differences between results for a given mesh and the results for the finest analyzed mesh with 64 elements are given, too. This comparison, combined with the graphic representation in Figs. 5, 6 and 7 allows to conclude, that the meshes of 36 and 64 elements yield response curves with insignificant discrepancy. The percentage difference is 1.7% for a relatively small value of static deflection and not more than 0.2% for the most interesting parameters at the response curves related to the resonance zone. Thus, henceforth the 36-element mesh will be applied.

7.2 Example 2—influence of fractional derivative order

In this example the harmonically forced vibrations of a plate with the geometry and loading form as in Example 1 but with varying order of the fractional derivative in the Zener material model are analyzed. Four cases of the excitation amplitude and the relaxation time are considered:

• Case 1 excitation amplitude $P_{wc}=500~\hbox {N}$, relaxation time $\tau =0.0175~\hbox {s}^{\alpha }$

• Case 2 excitation amplitude $P_{wc}=1000~\hbox {N}$, relaxation time $\tau =0.0125~\hbox {s}^{\alpha }$

• Case 3 excitation amplitude $P_{wc}=1500~\hbox {N}$, relaxation time $\tau =0.0100~\hbox {s}^{\alpha }$

• Case 4 excitation amplitude $P_{wc}=2000~\hbox {N}$, relaxation time $\tau =0.00875~\hbox {s}^{\alpha }$

Table 1 Results of mesh sensitivity in Example 1

In each of these cases the response curves are computed for a range of fractional derivative order: $\alpha =1.0,~0.9,~0.8$  and  0.7. The total deflection amplitude (119) under the centrally applied concentrated force is considered. The response curves for all the cases are presented in Figs. 8, 9, 10 and 11.

Inspection of the presented results indicates that the decreasing order of the fractional derivative decreases the damping properties of the Zener fractional viscoelastic material, as was expected, because the Scott-Blair fractional damping element is then steadily transformed into a spring-like elastic one. This leads to larger vibrations amplitudes, inevitably increases the geometric non-linear effects in the plate and is manifested in a larger inclination of response curves sections in the vicinity of the resonance zone. Even the Case 1 in Fig. 8, with a very small amplitude of excitation force, exhibits an almost linear behaviour for the classical Zener model with $\alpha =1.0$ and the decrease of the fractional derivative order transforms vibrations into a non-linear regime.

Fig. 8

Example 2—response curves for Case 1, $P_{wc}=500~\hbox {N}$, $\tau =0.0175~\hbox {s}^{\alpha }$

Fig. 9

Example 2—response curves for Case 2, $P_{wc}=1000~\hbox {N}$, $\tau =0.0125~\hbox {s}^{\alpha }$

Fig. 10

Example 2—response curves for Case 3, $P_{wc}=1500~\hbox {N}$, $\tau =0.0100~\hbox {s}^{\alpha }$

Fig. 11

Example 2—response curves for Case 4, $P_{wc}=2000~\hbox {N}$, $\tau =0.00875~\hbox {s}^{\alpha }$

7.3 Example 3—effect of geometric non-linearity and relaxation time

Here we continue with the analysis of the simply supported square plate, of the same dimensions, excitation form and physical properties, except for the relaxation time and the order of fractional derivative, as in Example 1. Now two cases of relaxation time, $\tau =0.010~\hbox {s}^{\alpha }$ and $0.015~\hbox {s}^{\alpha }$, are considered and four different values of the excitation force amplitude, $P_{wc}=500~\hbox {N}$, $1000~\hbox {N}$, $1500~\hbox {N}$ and $2000~\hbox {N}$ are taken into account. The order of fractional derivative is taken as $\alpha =0.8$.

Fig. 12

Example 3—resonance curves for: a Case 1—$\tau =0.010~\hbox {s}^{\alpha }$, b Case 2—$\tau =0.015~\hbox {s}^{\alpha }$

The response curves computed for the leading amplitude (117)—that of the deflection at the centre point, are presented in Fig. 12a, b. The increasing effect of the geometric non-linearity, more emphasized with the increasing value of the excitation amplitude, is evident in the results for both cases of relaxation time. To indicate this level of non-linearity, the comparison of the proposed non-linear model with the geometrically linear behaviour for the case with $\tau =0.010~\hbox {s}^{\alpha }$ and $\mathbf{P}_{wc}=2000~\hbox {N}$ is presented in Fig. 13.

Inspection of the curves in Fig. 12 for two different relaxation times also indicates some effect of this value on the behaviour of the plate. Seemingly, the larger relaxation time, the more non-linear output is obtained. To investigate this aspect in more detail let us now continue with the analysis of the plate from Fig. 4 for four considered excitation amplitudes, two orders of fractional derivative $\alpha =1.0$ and 0.8 as well as a broader range of relaxation time values. The results in the form of response curves are presented in Figs. 14 and 15, where for each combination of force amplitude and order of fractional derivative, the curves for three selected different values of relaxation time are shown.

Fig. 13

Example 3—effect of geometrical non-linearity for $\tau =0.010~s^{\alpha }$ and $\mathbf{P}_{wc}=2000~\hbox {N}$

Fig. 14

Example 3—resonance curves for $\alpha =1.0$ and: a $P_{wc}=500~\hbox {N}$, b $P_{wc}=1000~\hbox {N}$, c $P_{wc}=1500~\hbox {N}$, d $P_{wc}=2000~\hbox {N}$

Inspection of these graphs reveals an interesting behaviour. In all the analyzed cases, with the decreasing relaxation time, no monotonic decrease of the maximum amplitude at the resonance peak is observed. Evidently, there exists a critical value of the relaxation time $\tau$, for which the peak deflection amplitude $q_{max}$ reaches its smallest value. This characteristic point on a resonance curve has also its corresponding excitation frequency $\lambda _{max}$. Viewing the structure of physical matrices (67), (69) and (73) one should conclude, that it is indeed a question of a critical value of the product $\tau \lambda _{max}$, that can be of interest. This issue was further investigated.

Now the response curves were computed for more cases of the relaxation time, force amplitude and order of fractional derivative. Some of these results are presented in Figs. 16 and 17. The graphs in this figures show the relation between the value of the product $\tau \lambda _{max}$ and the corresponding resonance peak amplitude $q_{max}$ obtained for $\alpha =1.0$ and 0.8. The dots in the figures represent the pairs obtained from the response curves, while the solid lines are the best spline fits for the set of computed points. From the graphical representation of the spline approximations, the critical pairs of $\tau \lambda _{max}$ and $q_{max}$ were found. These pairs are presented in Table 2 for two cases of $\alpha =1.0$ and 0.8 depicted in Figs. 16 and  17 as well as for $\alpha =0.9$ and 0.7.

Fig. 15

Example 3—resonance curves for $\alpha =0.8$ and: a $P_{wc}=500~\hbox {N}$, b $P_{wc}=1000~\hbox {N}$, c $P_{wc}=1500~\hbox {N}$, d $P_{wc}=2000~\hbox {N}$

Fig. 16

Example 3—relations between the critical relaxation time and extreme resonance peak characteristics for $\alpha =1.0$ and: a $P_{wc}=500~\hbox {N}$, b $P_{wc}=1000~\hbox {N}$, c $P_{wc}=1500~\hbox {N}$, d $P_{wc}=2000~\hbox {N}$

It can be observed, that for the lowest considered value of the excitation amplitude $P_{wc}=500~\hbox {N}$ and the order of the fractional derivative $\alpha =1.0$, where the plate behaviour can be considered as linear, the critical value of $\tau \lambda _{max}$ equal to 0.983 is very close to unity. With the increasing excitation and/or the decreasing order of the fractional derivative, the geometrically non-linear effects in the plate are more and more pronounced and the value of the critical parameter $\tau \lambda _{max}$ is decreasing, getting further and further from unity. It is accompanied by the increase of plate deflections, from about 40% of the plate thickness for $\alpha =1.0$ and $\mathbf{P}_{wc}=500~\hbox {N}$ up to almost 150% of the plate thickness for the force amplitude $\alpha =0.7$ and $P_{wc}=2000~\hbox {N}$. Apparently, this unusual behaviour should be attributed to the fractional Zener model of viscoelasticity in the plate material. For the first time such characteristics were reported in [39] for vibrating beams. It is worth to note, that these results are of practical use if one takes into account the findings from [26], where the authors showed that the temperature influence on the damping properties of the Zener viscoelastic material is mostly manifested in the varying damping coefficient c, what changes the relaxation time $\tau$ only.

Fig. 17

Example 3—relations between the critical relaxation time and extreme resonance peak characteristics for $\alpha =0.8$ and: a $P_{wc}=500~\hbox {N}$, b $P_{wc}=1000~\hbox {N}$, c $P_{wc}=1500~\hbox {N}$, d $P_{wc}=2000~\hbox {N}$

7.4 Example 4—numerical comparison with Kelvin–Voigt model

In this example a square simply supported plate with immovable edges, as analyzed in [1] is considered. The plate has the dimensions: the edge length $a=0.3~\hbox {m}$ and the thickness $h= 0.001~\hbox {m}$. In the paper [1] this plate was analyzed with the Kelvin–Voigt model of viscoelasticity, with the elastic modulus $E=70\times 10^{9}~\hbox {N/m}^{2}$ and the retardation time $\tau _{c}=0.00039~\hbox {s}$. The material density was assumed as $\rho =1250~\hbox {kg/m}^{3}$. The retardation time corresponds to the relaxation time used here, divided by the factor 2, so we assume $\tau =0.00078~\hbox {s}$. The modulus E is assumed to be equal to the relaxed elastic modulus of the Zener material, i.e. $E_{0}=70\times 10^{9}~\hbox {N/m}^{2}$. The two remaining parameters present in the fractional Zener material model are now treated as independently varying values and their influence on the response curves is investigated for four cases:

$$\begin{aligned} E_{\infty }=1.0\times 10^{11}~\hbox {N/m}^{2}, \quad {\alpha }=1.0\\ E_{\infty }=1.1\times 10^{11}~\hbox {N/m}^{2}, \quad {\alpha }=1.0\\ E_{\infty }=1.1\times 10^{11}~\hbox {N/m}^{2}, \quad {\alpha }=0.9\\ E_{\infty }=1.1\times 10^{11}~\hbox {N/m}^{2}, \quad {\alpha }=0.8\\ \end{aligned}$$

The plate is loaded at the mid-point by the force with the amplitude $P_{ws}=1.74~\hbox {N}$ and the response as the total amplitude of the plate deflection $q_{w}$ (117) at the same point is analyzed. The results are calculated in the dimensionless format, as they are presented in [1]—the amplitude of deflection is divided by the plate thickness h to get the reference amplitude $q_{wr}$, whereas the excitation frequency is divided by the first natural frequency of the plate $\omega _{1}$ to get the reference frequency $\lambda _{r}$. The analytical result for $\omega _{1}=333.16~\hbox {rad/s}$.

In the present calculations the plate is divided into 64 finite elements forming a regular mesh of 8x8 elements.

The response curves for four considered cases are shown in Fig. 18. For the purpose of a better comparison the scale and the axes range therein are adopted in the way identical to the presentation in [1]. Additionally, a set of results selected for the resonance peak and for the excitation frequency $\lambda$ equal to the natural frequency $\omega _{1}$ is presented in Table 3. The results in [1] were given graphically only, thus the values in the last row of Table 3 were assessed by interpolation.

From the presented analysis one can conclude that the increasing non-relaxed modulus $E_{\infty }$ has an effect in the increased damping in the Zener model—the peak deflection amplitudes decrease. Also, as in the previous examples, the increasing order of the fractional derivative $\alpha$ leads to a decrease in the material damping.

Table 2 Values of critical parameter $\tau \lambda _{max}$ and the peak amplitude $q_{max}$ in Example 3

Fig. 18

Example 4—response curves for four considered cases of material parameters combinations and $E_{0}=0.7\times 10^{11}~\hbox {N/m}^{2}$, $\tau =0.00078~\hbox {s}$ (the figure format identical to [1] to allow for a graphical comparison)

Table 3 Selected results of Example 4, comparison with [1]

Also, one can observe, that it is possible to tune the parameters of the fractional Zener model to obtain the results coinciding with the Kelvin–Voigt model. In the analyzed example a good agreement is achieved for $E_{\infty }=1.0\times 10^{11}~\hbox {N/m}^{2}$ and $\alpha =1.0$. In this case the relative difference between the models in the excitation frequency corresponding to the peak value is about 5.3% only, while the computed deflection amplitudes agree with the discrepancy smaller than 1%.

It is worth to point out, that the fractional Zener model with its four material parameters gives more practical possibilities to represent a real behaviour of viscoelastic materials. This is due to the fact, that it can be used to predict correctly the basic rheological response of real materials, as indicated in the literature, e.g. [17, 23].

8 Conclusions

A novel approach to formulate the problem of geometrically non-linear vibrations of plates in frequency domain was presented. The viscoelasticity of the plate material was assumed as the Zener model with the Caputo fractional derivative. To overcome the problems with the involved physical law including fractional derivatives of stress and strain, the approach with time averaging carried out before the harmonic balance method and the space integration was proposed. In this way a non-linear amplitude equation with plate displacement amplitudes was obtained and solved using a standard path-following method.

In the course of analysis of numerical results for several simple examples of vibrating plates some expected conclusions were drawn. They are related to the level of non-linearity observed in response curves taking into account different values of excitation force magnitude or different order of fractional derivative, which controls the transformation of Scott-Blair element between the classical spring and the classical dashpot. Surprisingly, there are also some unexpected findings which concern the influence of relaxation time on the damping properties of the fractional Zener viscoelastic material and the resonance frequency in the geometrically non-linear regime. Due to the complexity of the formulation, there exists a certain critical value of the relaxation time, which implies the highest level of damping. This inherent feature of the Zener model can be viewed as an interesting alternative in attempts related to numerical modeling of real viscoelastic materials.

There are no apparent difficulties to note in a possible future application of the presented approach to analyze the steady-state vibrations of laminated plates with viscoelastic layers as well as to other, more intricate models of viscoelasticity.

Appendix: Matrices in non-linear components of residual vector and tangent matrix

Let us introduce some notation to simplify the formulae:

• (1) new geometric matrices using the matrices from (94)

  $$\begin{aligned} \mathbf{B}_1= & {} \mathbf{B}_{w1} ^{T}{} \mathbf{B}_{w1} \nonumber \\ \mathbf{B}_2= & {} \mathbf{B}_{w2} ^{T}{} \mathbf{B}_{w2} \nonumber \\ \mathbf{B}_3= & {} \mathbf{B}_{w1} ^{T}{} \mathbf{B}_{w2} +\mathbf{B}_{w2} ^{T}{} \mathbf{B}_{w1} \end{aligned}$$

  (118)

• (2) new physical matrices using the row vectors from (87) and physical parameters from (74)

  $$\begin{aligned} \begin{array}{l} \mathbf{H}_{i1} =a_{i11} \mathbf{B}_{rx} +a_{i12} \mathbf{B}_{ry} \\ \mathbf{H}_{i2} =a_{i12} \mathbf{B}_{rx} +a_{i22} \mathbf{B}_{ry} \\ \mathbf{H}_{i3} =a_{i11} \mathbf{B}_{rxy} \\ \end{array}, \quad i= 1{-}4 \end{aligned}$$

  (119)

• (3) products of physical matrices H (119) and displacements

  $$\begin{aligned} \begin{array}{l} \mathbf{H}_{ijc} =\mathbf{q}_{wec} \mathbf{H}_{ij} \\ \mathbf{H}_{ijs} =\mathbf{q}_{wes} \mathbf{H}_{ij} \\ \end{array}, \quad i= 1{-}4, \hbox {j}=1{-}3 \end{aligned}$$

  (120)

• (4) products of physical matrices and displacements using physical parameters from (74) and matrices (118)

  $$\begin{aligned} \begin{array}{l} \mathbf{G}_{i1c} =\mathbf{q}_{wec}^T \left( {a_{i11} \mathbf{B}_1 +a_{i12} \mathbf{B}_2 } \right) \\ \mathbf{G}_{i2c} =\mathbf{q}_{wec}^T \left( {a_{i12} \mathbf{B}_1 +a_{i22} \mathbf{B}_2 } \right) \\ \mathbf{G}_{i3c} =a_{i33} \mathbf{q}_{wec}^T \mathbf{B}_3 \\ \mathbf{G}_{i1s} =\mathbf{q}_{wes}^T \left( {a_{i11} \mathbf{B}_1 +a_{i12} \mathbf{B}_2 } \right) \\ \mathbf{G}_{i2s} =\mathbf{q}_{wes}^T \left( {a_{i12} \mathbf{B}_1 +a_{i22} \mathbf{B}_2 } \right) \\ \mathbf{G}_{i3s} =a_{i33} \mathbf{q}_{wes}^T \mathbf{B}_3 \\ \end{array}, \quad i= 1{-}4 \end{aligned}$$

  (121)

Now the matrices from (107) can be defined as

$$\begin{aligned}&\mathbf{K}_{wtc} =\frac{1}{4}\int \limits _A {\left[ {\mathbf{B}_1 \left( {3\mathbf{H}_{11c} +\mathbf{H}_{41c} +\hbox {2}{} \mathbf{H}_{31s} } \right) } \right. } \nonumber \\&\quad \left. +\,\mathbf{B}_2 \left( {3\mathbf{H}_{12c} +\mathbf{H}_{42c} +\hbox {2}{} \mathbf{H}_{32s} } \right) \right. \nonumber \\&\left. \quad +\,\mathbf{B}_3 \left( {3\mathbf{H}_{13c} +\mathbf{H}_{43c} +\hbox {2}{} \mathbf{H}_{33s} } \right) \right] dA \nonumber \\&\mathbf{K}_{wtc0} =\frac{1}{4}\int \limits _A {\left[ {\mathbf{B}_1 \left( {-2\mathbf{H}_{31c} +\mathbf{H}_{21s} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_2 \left( {-2\mathbf{H}_{32c} +\mathbf{H}_{22s} } \right) +\mathbf{B}_3 \left( {-2\mathbf{H}_{33c} +\mathbf{H}_{23s} } \right) dA} \right] \nonumber \\&\mathbf{K}_{wtcs} =\frac{1}{4}\int \limits _A {\left[ {\mathbf{B}_1 \left( {3\mathbf{H}_{41c} +\mathbf{H}_{11c} -\hbox {2}{} \mathbf{H}_{31s} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_2 \left( {3\mathbf{H}_{42c} +\mathbf{H}_{12c} -\hbox {2}{} \mathbf{H}_{32s} } \right) +\mathbf{B}_3 \left( {3\mathbf{H}_{43c} +\mathbf{H}_{13c} -\hbox {2}{} \mathbf{H}_{33s} } \right) dA} \right] \nonumber \\&\mathbf{K}_{wtsc} =\frac{1}{4}\int \limits _A {\left[ {\mathbf{B}_1 \left( {3\mathbf{H}_{41s} +\mathbf{H}_{11s} +\hbox {2}{} \mathbf{H}_{31c} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_2 \left( {3\mathbf{H}_{42s} +\mathbf{H}_{12s} +\hbox {2}{} \mathbf{H}_{32c} } \right) +\mathbf{B}_3 \left( {3\mathbf{H}_{43s} +\mathbf{H}_{13s} +\hbox {2}{} \mathbf{H}_{33c} } \right) } \right] dA \nonumber \\&\mathbf{K}_{wts0} =\frac{1}{4}\int \limits _A {\left[ {\mathbf{B}_1 \left( {2\mathbf{H}_{31s} +\mathbf{H}_{21c} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_2 \left( {2\mathbf{H}_{32s} +\mathbf{H}_{22c} } \right) +\mathbf{B}_3 \left( {2\mathbf{H}_{33s} +\mathbf{H}_{23c} } \right) } \right] dA \nonumber \\&\mathbf{K}_{wts} =\frac{1}{4}\int \limits _A {\left[ {\mathbf{B}_1 \left( {3\mathbf{H}_{11s} +\mathbf{H}_{41s} -\hbox {2}{} \mathbf{H}_{31c} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_2 \left( {3\mathbf{H}_{12s} +\mathbf{H}_{42s} -\hbox {2}{} \mathbf{H}_{32c} } \right) +\mathbf{B}_3 \left( {3\mathbf{H}_{13s} +\mathbf{H}_{43s} -\hbox {2}{} \mathbf{H}_{33c} } \right) } \right] dA \nonumber \\ \end{aligned}$$

(122)

The matrices in (108) take the form

$$\begin{aligned}&\mathbf{K}_{twc} =\frac{1}{8}\int \limits _A {\left[ {\mathbf{B}_{rx} \left( {3\mathbf{G}_{11c} +\mathbf{G}_{41c} -\hbox {2}{} \mathbf{G}_{31s} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_{ry} \left( {3\mathbf{G}_{12c} +\mathbf{G}_{42c} -\hbox {2}{} \mathbf{G}_{32s} } \right) +\mathbf{B}_{rxy} \left( {3\mathbf{G}_{13c} +\mathbf{G}_{43c} -\hbox {2}{} \mathbf{G}_{33s} } \right) } \right] dA \nonumber \\&\mathbf{K}_{twcs} =\frac{1}{8}\int \limits _A {\left[ {\mathbf{B}_{rx} \left( {3\mathbf{G}_{41s} +\mathbf{G}_{11s} -\hbox {2}{} \mathbf{G}_{31c} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_{ry} \left( {3\mathbf{G}_{42s} +\mathbf{G}_{12s} -\hbox {2}{} \mathbf{G}_{32c} } \right) +\mathbf{B}_{rxy} \left( {3\mathbf{G}_{43s} +\mathbf{G}_{13s} -\hbox {2}{} \mathbf{G}_{33c} } \right) } \right] dA \nonumber \\&\mathbf{K}_{twc0} =\frac{1}{8}\int \limits _A {\left[ {\mathbf{B}_{rx} \left( {2\mathbf{G}_{31c} +\mathbf{G}_{21s} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_{ry} \left( {2\mathbf{G}_{32c} +\mathbf{G}_{22s} } \right) +\mathbf{B}_{rxy} \left( {2\mathbf{G}_{33c} +\mathbf{G}_{23s} } \right) } \right] dA \nonumber \\&\mathbf{K}_{tws0} =\frac{1}{8}\int \limits _A {\left[ {\mathbf{B}_{rx} \left( {-2\mathbf{G}_{31s} +\mathbf{G}_{21c} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_{ry} \left( {-2\mathbf{G}_{32s} +\mathbf{G}_{22c} } \right) +\mathbf{B}_{rxy} -\left( {2\mathbf{G}_{33s} +\mathbf{G}_{23c} } \right) } \right] dA \nonumber \\&\mathbf{K}_{twsc} =\frac{1}{8}\int \limits _A {\left[ {\mathbf{B}_{rx} \left( {3\mathbf{G}_{41c} +\mathbf{G}_{11c} +\hbox {2}{} \mathbf{G}_{31s} } \right) +} \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_{ry} \left( {3\mathbf{G}_{42c} +\mathbf{G}_{12c} +\hbox {2}{} \mathbf{G}_{32s} } \right) +\mathbf{B}_{rxy} \left( {3\mathbf{G}_{43c} +\mathbf{G}_{13c} +\hbox {2}{} \mathbf{G}_{33s} } \right) } \right] dA \nonumber \\&\mathbf{K}_{tws} =\frac{1}{8}\int \limits _A {\left[ {\mathbf{B}_{rx} \left( {3\mathbf{G}_{11s} +\mathbf{G}_{41s} +\hbox {2}{} \mathbf{G}_{31c} } \right) +} \right. } \nonumber \\&\quad \left. +\,\mathbf{B}_{ry} \left( {3\mathbf{G}_{12s} +\mathbf{G}_{42s} +\hbox {2}{} \mathbf{G}_{32c} } \right) +\mathbf{B}_{rxy} \left( 3\mathbf{G}_{13s}\right. \right. \nonumber \\&\quad \left. \left. \quad +\,\mathbf{G}_{43s} +\hbox {2}{} \mathbf{G}_{33c} \right) \right] dA \end{aligned}$$

(123)

The matrices in (109) are defined as

$$\begin{aligned}&\mathbf{K}_{wc} =\frac{1}{8}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {\mathbf{q}_{wec} \left( {3\mathbf{G}_{11c} +\mathbf{G}_{41c} -\hbox {2}{} \mathbf{G}_{31s} } \right) +\mathbf{q}_{wes} \left( {2\mathbf{G}_{31c} +\mathbf{G}_{21s} } \right) } \right] } \right. } \nonumber \\&\quad +\,\mathbf{B}_2 \left[ {\mathbf{q}_{wec} \left( {3\mathbf{G}_{12c} +\mathbf{G}_{42c} -\hbox {2}{} \mathbf{G}_{32s} } \right) +\mathbf{q}_{wes} \left( {2\mathbf{G}_{32c} +\mathbf{G}_{22s} } \right) } \right] \nonumber \\&\quad \left. {+\,\mathbf{B}_3 \left[ {\mathbf{q}_{wec} \left( {3\mathbf{G}_{13c} +\mathbf{G}_{43c} -\hbox {2}{} \mathbf{G}_{33s} } \right) +\mathbf{q}_{wes} \left( {2\mathbf{G}_{33c} +\mathbf{G}_{23s} } \right) } \right] } \right\} dA \nonumber \\&\mathbf{K}_{wcs} =\frac{1}{8}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {\mathbf{q}_{wec} \left( {3\mathbf{G}_{41s} +\mathbf{G}_{11s} -\hbox {2}{} \mathbf{G}_{31c} } \right) +\mathbf{q}_{wes} \left( {-2\mathbf{G}_{31s} +\mathbf{G}_{21c} } \right) } \right] } \right. } \nonumber \\&\quad +\,\mathbf{B}_2 \left[ {\mathbf{q}_{wec} \left( {3\mathbf{G}_{42s} +\mathbf{G}_{12s} -\hbox {2}{} \mathbf{G}_{32c} } \right) +\mathbf{q}_{wes} \left( {-2\mathbf{G}_{32s} +\mathbf{G}_{22c} } \right) } \right] \nonumber \\&\quad \left. {+\,\mathbf{B}_3 \left[ {\mathbf{q}_{wec} \left( {3\mathbf{G}_{43s} +\mathbf{G}_{13s} -\hbox {2}{} \mathbf{G}_{33c} } \right) +\mathbf{q}_{wes} \left( {-2\mathbf{G}_{33s} +\mathbf{G}_{23c} } \right) } \right] } \right\} dA\nonumber \\&\mathbf{K}_{wsc} =\frac{1}{8}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {\mathbf{q}_{wec} \left( {2\mathbf{G}_{31c} +\mathbf{G}_{21s} } \right) +\mathbf{q}_{wes} \left( {3\mathbf{G}_{41c} +\mathbf{G}_{11c} +\hbox {2}{} \mathbf{G}_{31s} } \right) } \right] } \right. }\nonumber \\&\quad +\,\mathbf{B}_2 \left[ {\mathbf{q}_{wec} \left( {2\mathbf{G}_{32c} +\mathbf{G}_{22s} } \right) +\mathbf{q}_{wes} \left( {3\mathbf{G}_{42c} +\mathbf{G}_{12c} +\hbox {2}{} \mathbf{G}_{32s} } \right) } \right] \nonumber \\&\quad \left. {+\,\mathbf{B}_3 \left[ {\mathbf{q}_{wec} \left( {2\mathbf{G}_{33c} +\mathbf{G}_{23s} } \right) +\mathbf{q}_{wes} \left( {3\mathbf{G}_{43c} +\mathbf{G}_{13c} +\hbox {2}{} \mathbf{G}_{33s} } \right) } \right] } \right\} dA\nonumber \\&\mathbf{K}_{ws} =\frac{1}{8}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {\mathbf{q}_{wec} \left( {-2\mathbf{G}_{31s} +\mathbf{G}_{21c} } \right) +\mathbf{q}_{wes} \left( {3\mathbf{G}_{11s} +\mathbf{G}_{41s} +\hbox {2}{} \mathbf{G}_{31c} } \right) } \right] } \right. }\nonumber \\&\quad +\,\mathbf{B}_2 \left[ {\mathbf{q}_{wec} \left( {-2\mathbf{G}_{32s} +\mathbf{G}_{22c} } \right) +\mathbf{q}_{wes} \left( {3\mathbf{G}_{12s} +\mathbf{G}_{42s} +\hbox {2}{} \mathbf{G}_{32c} } \right) } \right] \nonumber \\&\quad \left. +\,{\mathbf{B}_3 \left[ {\mathbf{q}_{wec} \left( {-2\mathbf{G}_{33s} +\mathbf{G}_{23c} } \right) +\mathbf{q}_{wes} \left( {3\mathbf{G}_{13s} +\mathbf{G}_{43s} +\hbox {2}{} \mathbf{G}_{33c} } \right) } \right] } \right\} dA\nonumber \\ \end{aligned}$$

(124)

Linearization of the residual vector with respect to displacements leads to several additional matrices.

The matrices in (110) not defined earlier are:

$$\begin{aligned}&\mathbf{K}_{nlc} =\frac{1}{4}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {\mathbf{H}_{11} \left( {3\mathbf{q}_{tec} +\mathbf{q}_{tes} } \right) -\hbox {2}{} \mathbf{H}_{31} \mathbf{q}_{te0} +\mathbf{H}_{41} \left( {3\mathbf{q}_{tes} +\mathbf{q}_{tec} } \right) } \right] } \right. } \nonumber \\&\quad +\,\mathbf{B}_2 \left[ {\mathbf{H}_{12} \left( {3\mathbf{q}_{tec} +\mathbf{q}_{tes} } \right) -\hbox {2}{} \mathbf{H}_{32} \mathbf{q}_{te0} +\mathbf{H}_{42} \left( {3\mathbf{q}_{tes} +\mathbf{q}_{tec} } \right) } \right] \nonumber \\&\quad \left. {+\,\mathbf{B}_3 \left[ {\mathbf{H}_{13} \left( {3\mathbf{q}_{tec} +\mathbf{q}_{tes} } \right) -\hbox {2}{} \mathbf{H}_{33} \mathbf{q}_{te0} +\mathbf{H}_{43} \left( {3\mathbf{q}_{tes} +\mathbf{q}_{tec} } \right) } \right] } \right\} dA \nonumber \\&\mathbf{K}_{nlcs} =\frac{1}{4}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {2\mathbf{H}_{31} \left( {\mathbf{q}_{tec} -\mathbf{q}_{tes} } \right) +\mathbf{H}_{21} \mathbf{q}_{te0} } \right] } \right. } \nonumber \\&\quad \left. {+\,\mathbf{B}_2 \left[ {2\mathbf{H}_{32} \left( {\mathbf{q}_{tec} -\mathbf{q}_{tes} } \right) +\mathbf{H}_{22} \mathbf{q}_{te0} } \right] }\right. \nonumber \\&\left. {+\,\mathbf{B}_3 \left[ {2\mathbf{H}_{33} \left( {\mathbf{q}_{tec} -\mathbf{q}_{tes} } \right) +\mathbf{H}_{23} \mathbf{q}_{te0} } \right] } \right\} dA \nonumber \\&\mathbf{K}_{nls} =\frac{1}{4}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {\mathbf{H}_{11} \left( {\mathbf{q}_{tec} +3\mathbf{q}_{tes} } \right) +\hbox {2}{} \mathbf{H}_{31} \mathbf{q}_{te0} +\mathbf{H}_{41} \left( {\mathbf{q}_{tes} +3\mathbf{q}_{tec} } \right) } \right] } \right. } \nonumber \\&\quad +\,\mathbf{B}_2 \left[ {\mathbf{H}_{12} \left( {\mathbf{q}_{tec} +3\mathbf{q}_{tes} } \right) +\hbox {2}{} \mathbf{H}_{32} \mathbf{q}_{te0} +\mathbf{H}_{42} \left( {\mathbf{q}_{tes} +3\mathbf{q}_{tec} } \right) } \right] \nonumber \\&\quad \left. {+\,\mathbf{B}_3 \left[ {\mathbf{H}_{13} \left( {\mathbf{q}_{tec} +3\mathbf{q}_{tes} } \right) +\hbox {2}{} \mathbf{H}_{33} \mathbf{q}_{te0} +\mathbf{H}_{43} \left( {\mathbf{q}_{tes} +3\mathbf{q}_{tec} } \right) } \right] } \right\} dA \end{aligned}$$

(125)

The matrices in (112) not defined earlier are

$$\begin{aligned} \mathbf{K}_{nc}= & {} \frac{1}{8}\int \limits _A \left\{ \mathbf{B}_1 \left[ \left( {3\mathbf{G}_{11c} +\mathbf{G}_{41c} -\hbox {2}{} \mathbf{G}_{31s} } \right) \mathbf{q}_{wec} +\left( 3\mathbf{G}_{41s} +\mathbf{G}_{11s}\right. \right. \right. \nonumber \\&\left. \left. \left. -\,\hbox {2}\mathbf{G}_{31c} \right) \mathbf{q}_{wes} \right] +\,\mathbf{B}_2 \left[ \left( 3\mathbf{G}_{12c} +\mathbf{G}_{42c}\right. \right. \right. \nonumber \\&\left. \left. -\,\hbox {2}{} \mathbf{G}_{32s} \right) \mathbf{q}_{wec} +\left( 3\mathbf{G}_{42s} +\mathbf{G}_{12s} -\hbox {2}{} \mathbf{G}_{32c} \right) \mathbf{q}_{wes} \right] \nonumber \\&+\,\mathbf{B}_3 \left[ {\left( {3\mathbf{G}_{13c} +\mathbf{G}_{43c} -\hbox {2}{} \mathbf{G}_{33s} } \right) }{} \mathbf{q}_{wec}\right. \nonumber \\&\left. {\left. +\,\left( {3\mathbf{G}_{43s} +\mathbf{G}_{13s} -\hbox {2}\mathbf{G}_{33c} } \right) \mathbf{q}_{wes} \right] } \right\} dA \nonumber \\ \mathbf{K}_{ncs}= & {} \frac{1}{8}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {\left( {2\mathbf{G}_{31c} +\mathbf{G}_{21s} } \right) \mathbf{q}_{wec} +\left( {-2\mathbf{G}_{31s} +\mathbf{G}_{21c} } \right) \mathbf{q}_{wes} } \right] } \right. }\nonumber \\&+\,\mathbf{B}_2 \left[ {\left( {2\mathbf{G}_{32c} +\mathbf{G}_{22s} } \right) \mathbf{q}_{wec} +\left( {-2\mathbf{G}_{32s} +\mathbf{G}_{22c} } \right) \mathbf{q}_{wes} } \right] \nonumber \\&\left. {+\,\mathbf{B}_3 \left[ {\left( {2\mathbf{G}_{33c} +\mathbf{G}_{23s} } \right) \mathbf{q}_{wec} +\left( {-2\mathbf{G}_{33s} +\mathbf{G}_{23c} } \right) \mathbf{q}_{wes} } \right] } \right\} dA \nonumber \\ \mathbf{K}_{ns}= & {} \frac{1}{8}\int \limits _A {\left\{ {\mathbf{B}_1 \left[ {\left( {3\mathbf{G}_{41c} +\mathbf{G}_{11c} +\hbox {2}{} \mathbf{G}_{31s} } \right) \mathbf{q}_{wec}}\right. } \right. }\nonumber \\&{\left. {\left. {+\,\left( {3\mathbf{G}_{11s} +\mathbf{G}_{41s} +\hbox {2}{} \mathbf{G}_{31c} } \right) \mathbf{q}_{wes} } \right] } \right. }\nonumber \\&+\,\mathbf{B}_2 \left[ \left( {3\mathbf{G}_{42c} +\mathbf{G}_{12c} +\hbox {2}{} \mathbf{G}_{32s} } \right) \mathbf{q}_{wec}\right. \nonumber \\&\left. +\,\left( 3\mathbf{G}_{12s} +\mathbf{G}_{42s}+\,\hbox {2}{} \mathbf{G}_{32c} \right) \mathbf{q}_{wes} \right] \nonumber \\&\left. +\,\mathbf{B}_3 \left[ \left( {3\mathbf{G}_{43c} +\mathbf{G}_{13c} +\hbox {2}{} \mathbf{G}_{33s} } \right) \mathbf{q}_{wec} \right. \right. \nonumber \\&\left. \left. +\left( {3\mathbf{G}_{13s} +\mathbf{G}_{43s} +\hbox {2}{} \mathbf{G}_{33c} } \right) \mathbf{q}_{wes} \right] \right\} dA \end{aligned}$$

(126)