Shear correction factors for layered plates and shells

Abstract

In this paper layered composite shells subjected to static loading are considered. The theory is based on a multi-field functional, where the associated Euler–Lagrange equations include besides the global shell equations formulated in stress resultants, the local in-plane equilibrium in terms of stresses and a constraint which enforces the correct shape of warping through the thickness. Within representative volume elements warping displacements are interpolated with layerwise cubic functions in thickness direction and constant shape throughout the reference surface. Elimination of warping and Lagrange parameters by static condensation leads to a material matrix for the stress resultants and to shear correction factors for layered plates and shells. For linear elasticity the computation can be done once in advance. The condensed material matrix is used in displacement based elements along with the enhanced strain method or in mixed hybrid elements with the usual 5 or 6 nodal degrees of freedom. This allows standard geometrical boundary conditions and the elements are applicable also to shell intersection problems. The interlaminar shear stresses are evaluated via the constitutive law by back substitution of the eliminated parameters. The computed transverse shear stresses are automatically continuous at the layer boundaries and zero at the outer surfaces. Furthermore, the integrals of the shear stresses coincide exactly with the shear forces without introduction of further constraints.

1 Introduction

A survey on models to compute the complicated three-dimensional stress state in laminated plates and shells is given e.g., in [1, 2]. In the following only a few papers out of a large number are discussed.

Shell elements which account for the layer sequence of a laminated structure are able to predict the deformation behaviour of the reference surface sufficiently accurate. This holds also for the layerwise linear shape of the in-plane stresses through the thickness, if the shell is not too thick. In contrast to that only averaged transverse shear strains through the thickness are obtained within the Reissner–Mindlin theory. As a consequence only the average of the transverse shear stresses is accurate. Neither the shape of the stresses is correct nor the boundary conditions at the outer surfaces are fulfilled. Within the Kirchhoff theory the transverse shear strains are set to zero. For this approach $C^1$-continuous shape functions are necessary, whereas Reissner–Mindlin elements require only $C^0$-continuity. On the other hand arrangements to avoid shear locking are necessary.

In several papers the equilibrium equations are exploited within a post-processing procedure to obtain the interlaminar stresses, e.g., [3, 4] for the transverse shear stresses. The essential restriction of the approach is the fact that these stresses are not embedded in the variational formulation and an immediate extension to geometrical and physical nonlinearity is not possible. Furthermore first and second derivatives of the in-plane stresses require bi-quadratic or bi-cubic shape functions.

In [5] a proper generalized decomposition and layer-wise approach for the modelling of composite plate structures is proposed. The authors in [6–8] present linear plate elements based on mixed-enhanced approaches. On basis of the first-order shear deformation theory resultant shear stresses and enhanced incompatible modes are used as primary variables.

In [9] refined theories with seven unknown kinematic quantities have been presented. The standard displacement field is enhanced by layer-wise (zig-zag) functions through the thickness, see also [10].

Higher order plate and shell formulations and layerwise approaches represent a wide class of advanced models, e.g., [11–16]. In [17] recommendations for an optimal choice for the thickness interpolation are given. For geometrical nonlinear formulations we refer to e.g., [18–21]. These theories are associated with global layerwise degrees of freedom which makes the general handling complicated for practical problems, e.g., when structures with intersections occur.

The use of brick elements or so-called solid shell elements, e.g., [22, 23] represents a computationally expensive approach. For a sufficient accurate evaluation of the interlaminar stresses each layer must be discretized with several elements $(\approx$4–10) in thickness direction. Especially for non-linear practical problems with a multiplicity of load steps and several iterations in each load step this is not a feasible approach.

The notion of a shear correction factor was first introduced by Timoshenko [24]. For inhomogeneous plates and shells shear factors have been computed e.g., in [6, 25–34], and references therein. The factors are especially important for a frequency analysis of vibrating plates and shells.

Based on above discussion we propose a shell formulation which is characterized by the following features and new developments.

• (i) The underlying shell theory is based on the Reissner–Mindlin kinematics with inextensible director field. This leads in the basic version to averaged transverse shear strains through the thickness when exploiting the Green–Lagrangian strain tensor. The displacements of the Reissner–Mindlin kinematics are enriched by warping displacements which are interpolated with layerwise cubic functions through the thickness. We propose a multi–field functional, where the associated Euler–Lagrange equations include besides the usual shell equations in terms of stress resultants the in-plane equilibrium in terms of stresses and a constraint which enforces the correct shape of warping through the thickness. Based on a previous paper [35] we present the following enhancements and improvements.

• (ii) The global shell equations are extended to geometrical nonlinearity. In [35] quasi linear dependent columns are added to avoid singular matrices. This approximation is overcome by a reformulation of the shape functions for the independent quantities. As an add-on the necessary pivot change formulated in [35] is automatically obtained.

• (iii) The material matrix for the stress resultants is computed in representative volume elements (RVE). Elimination of warping parameters and Lagrange parameters is achieved by static condensation. For linear elasticity the computation can be done once as a pre-processing, which reduces the computing time significantly. The condensation affects only the transverse shear stiffness. In this context shear correction factors for layered plates and shells are defined. The resulting material matrix is used to compute the stiffness matrix of displacement based elements combined with the enhanced strain method or of mixed hybrid elements with the usual 5 or 6 nodal degrees of freedom. This is an essential feature since standard geometrical boundary conditions can be applied and the element is applicable also to shell intersection problems.

• (iv) The interlaminar shear stresses are computed via the constitutive law by back substitution of the condensed parameters using the stored matrices of the elimination procedure. One obtains a shape which is automatically continuous at the layer boundaries and zero at the outer surfaces. Furthermore, the integrals of the shear stresses coincide identically with the shear forces computed with the material law for the stress resultants.

The paper is organized as follows. In Sect. 2 the variational formulation is presented. The kinematics and the constitutive equations for the stress resultants are specified. Furthermore, thickness integration of the in–plane equilibrium and the derivation of a constraint are carried out. A constrained optimization problem is formulated and variation and associated Euler–Lagrange equations are derived. The material matrix for the stress resultants is computed in a RVE in Sect. 3. In Sect. 4 several linear test examples with different layer sequences and a stiffened cylindrical shell as nonlinear example are investigated. For various laminates shear correction factors are computed and compared, if possible, with results from the literature. The influence of the factors on eigenfrequencies of vibrating plates is investigated.

2 Variational formulation

2.1 Kinematics

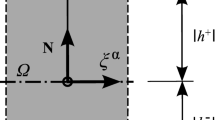
Let $\mathcal{B}$ be the three-dimensional Euclidean space occupied by a shell with thickness h. With $\xi ^i$ we denote a convected coordinate system of the body, where for the thickness coordinate holds $h^- \le \xi ^3 \le h^+$. The reference surface $\Omega$ of the shell is defined with $\xi ^3=0$ and the coordinate on the boundary $\Gamma = \Gamma _u \bigcup \Gamma _\sigma$ is denoted by s. In the following the summation convention is used for repeated indices, where Latin indices range from 1 to 3 and Greek indices range from 1 to 2. Commas denote partial differentiation with respect to the coordinates $\xi ^i$.

The position vector of the reference surface is denoted by $\mathbf{{X}}(\xi ^1,\xi ^2)$. Furthermore, the vector field $\bar{\mathbf{D}}(\xi ^1, \xi ^2)$ with $|\bar{\mathbf{D}} (\xi ^1, \xi ^2)| = 1$ which is perpendicular to $\Omega$ is introduced. The director field of the current configuration with position vector $\mathbf{{x}}(\xi ^1, \xi ^2)$ follows from $\mathbf{{d}}(\xi ^1, \xi ^2) = \mathbf{{R}} \, \bar{\mathbf{D}}$, where $\mathbf{{R}} ({\varvec{\varphi }})$ denotes a rotation tensor. With $\mathbf{{d}} \cdot \mathbf{{x}},_\alpha \ne 0$ the Reissner–Mindlin theory accounts for averaged transverse shear strains. Within the vector $\mathbf{{v}} := [\mathbf{{u}}, {\varvec{\varphi }}]^T$ the displacements $\mathbf{{u}}(\xi ^1, \xi ^2) = \mathbf{{x}} -\mathbf{{X}}$ and the rotational parameters ${\varvec{\varphi }}(\xi ^1, \xi ^2)$ of the reference surface are summarized.

Based on the introduced kinematic assumptions one can derive the shell strains evaluating the Green–Lagrangian strain tensor. The membrane strains $\varepsilon _{\alpha \beta }$, curvatures $\kappa _{\alpha \beta }$ and transverse shear strains $\gamma _\alpha$

$$\begin{aligned}&\varepsilon _{\alpha \beta } = \dfrac{1}{2}\left( \mathbf{{x}},_\alpha \cdot \mathbf{{x}},_\beta - \mathbf{{X}},_\alpha \cdot \mathbf{{X}},_\beta \right) \nonumber \\&\kappa _{\alpha \beta } = \dfrac{1}{2}\left( \mathbf{{x}},_\alpha \cdot \mathbf{{d}},_\beta + \mathbf{{x}},_\beta \cdot \mathbf{{d}},_\alpha - \mathbf{{X}},_\alpha \cdot \bar{\mathbf{D}},_\beta -\mathbf{{X}},_\beta \cdot \bar{\mathbf{D}},_\alpha \right) \\&\gamma _\alpha = \mathbf{{x}},_\alpha \cdot \mathbf{{d}} - \mathbf{{X}},_\alpha \cdot \bar{\mathbf{D}} \nonumber \end{aligned}$$

(1)

are organized in the vector

$$\begin{aligned} {\varvec{\varepsilon }}(\mathbf{{v}}) = [\varepsilon _{11},\varepsilon _{22},2 \varepsilon _{12}, \kappa _{11},\kappa _{22},2 \kappa _{12},\gamma _{1},\gamma _{2}]^T \,. \end{aligned}$$

(2)

So-called warping displacements $\tilde{\mathbf{u}} = [\tilde{u}_1, \tilde{u}_2]^T$ are superposed on the linear shape of the Reissner–Mindlin theory. The shape of $\tilde{\mathbf{u}}$ through the thickness is chosen as

$$\begin{aligned} \tilde{\mathbf{u}} (\xi ^3) = {\varvec{\Phi }}(\xi ^3) \, {\varvec{\alpha }}\,. \end{aligned}$$

(3)

The vector ${\varvec{\alpha }}$ is constant throughout the representative volume element as is defined in Sect. 3.1 and contains alternating the discrete warping ordinates in 1- and 2-direction of the nodes in thickness direction. For N layers this leads to $M = 6 \cdot N + 2$ components in ${\varvec{\alpha }}$, see Fig. 1. The interpolation matrix contains cubic hierarchic functions

$$\begin{aligned}&{\varvec{\Phi }}(\xi ^3) = \left[ \phi _1 \, \mathbf{{1}}_2 \quad \phi _2 \, \mathbf{{1}}_2 \quad \phi _3 \, \mathbf{{1}}_2 \quad \phi _4 \, \mathbf{{1}}_2 \right] \, \mathbf{{a}}^i \nonumber \\&\phi _1 = \dfrac{1}{2}\,(1-\zeta ) \qquad \phi _2 = 1-\zeta ^2 \qquad \phi _3 = \dfrac{8}{3}\,\zeta \, (1-\zeta ^2) \qquad \nonumber \\&\phi _4 = \dfrac{1}{2}\,(1+\zeta ) \,, \end{aligned}$$

(4)

where $-1 \le \zeta \le 1$ is a normalized thickness coordinate of layer i. Furthermore,

$$\begin{aligned} \mathbf{{a}}^i =\left[ \mathbf{{0}}_{8 \times 6 \cdot (i-1)} \mid \mathbf{{1}}_8 \mid \mathbf{{0}}_{8 \times 6\cdot (N-i)} \right] _{8 \times M} \end{aligned}$$

(5)

is an assembly matrix, which relates the 8 degrees of freedom of layer i to the M components of ${\varvec{\alpha }}$ and $\mathbf{{1}}_n$ denotes a unit matrix of order n.

Fig. 1

Laminate with N layers

2.2 Constitutive equations for the stress resultants

Assuming orthotropic material behaviour the constitutive equations are introduced in an orthonormal coordinate system and $S^{33}=0$ in the following standard manner

$$\begin{aligned} \begin{array}{rcl} \left[ \begin{array}{l} S^{11} \\ S^{22} \\ S^{12} \\ S^{13} \\ S^{23} \end{array} \right] &{}=&{}\left[ \begin{array}{lllll} C_{11} &{} \quad C_{12} &{} \quad C_{13} &{} \quad 0&{} \quad 0 \\ C_{21} &{} \quad C_{22} &{} \quad C_{23} &{} \quad 0&{} \quad 0 \\ C_{31} &{} \quad C_{32} &{} \quad C_{33} &{} \quad 0&{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad C_{44}&{} \quad C_{45} \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad C_{54}&{} \quad C_{55} \end{array} \right] \quad \left[ \begin{array}{r} E_{11} \\ E_{22} \\ 2E_{12} \\ 2E_{13} \\ 2E_{23} \\ \end{array} \right] \\ \mathbf{{S}} &{}=&{} \mathbf{{C}} \; \mathbf{{E}} \,. \end{array} \end{aligned}$$

(6)

Due to the varying fibre orientation the material constants $C_{ij} = C_{ji}$ differ for each individual layer. The layer strains of a point in shell space with coordinates $\xi ^3$ are obtained with

$$\begin{aligned} \mathbf{{E}} = \mathbf{{A}}_1 \, {\varvec{\varepsilon }}+ \mathbf{{A}}_2 \, {\varvec{\alpha }}\end{aligned}$$

(7)

where

(8)

The first part $\mathbf{{A}}_1 \, {\varvec{\varepsilon }}$ emanates from the Reissner–Mindlin kinematic, whereas the second part $\mathbf{{A}}_2 \, {\varvec{\alpha }}$ follows from the superposed warping displacements.

Now the relation of the stress resultants to $\mathbf{{S}}$ is defined by thickness integration of the specific internal virtual work and $\delta \mathbf{{E}} = \mathbf{{A}}_1 \, \delta {\varvec{\varepsilon }}+ \mathbf{{A}}_2 \, \delta {\varvec{\alpha }}$. This yields

$$\begin{aligned} \int \limits _{h^-}^{h^+} \delta \mathbf{{E}}^T \mathbf{{S}} \, \bar{\mu }\,\text {d}\xi ^3 = \delta {\varvec{\varepsilon }}^T {\varvec{\sigma }}_1 + \delta {\varvec{\alpha }}^T {\varvec{\sigma }}_2 \end{aligned}$$

(9)

with

$$\begin{aligned} {\varvec{\sigma }}_1 := \int \limits _{h^-}^{h^+} \mathbf{{A}}_1^T \mathbf{{S}} \, \bar{\mu }\,\text {d}\xi ^3 \quad {\varvec{\sigma }}_2 := \int \limits _{h^-}^{h^+} \mathbf{{A}}_2^T \mathbf{{S}} \, \bar{\mu }\,\text {d}\xi ^3 \,, \end{aligned}$$

(10)

where $\bar{\mu }$ denotes the determinant of the shifter tensor. The integrals are computed in a RVE with rectangular shape, thus $\bar{\mu }= 1$ holds, see Sect. 3.1. The components of

$$\begin{aligned} {\varvec{\sigma }}_1 =\left[ n^{11},n^{22},n^{12}, m^{11},m^{22},m^{12},q^{1},q^{2}\right] ^T \end{aligned}$$

(11)

are membrane forces $n^{\alpha \beta }= n^{\beta \alpha }$, bending moments $m^{\alpha \beta } = m^{\beta \alpha }$ and shear forces $q^\alpha$. The components of ${\varvec{\sigma }}_2$ are higher order stress resultants.

Now, inserting (6) with (7) into (10) yields the constitutive law for the stress resultants

$$\begin{aligned} \left[ \begin{array}{l} {\varvec{\sigma }}_1\\ {\varvec{\sigma }}_2 \end{array} \right] =\left[ \begin{array}{ll} \mathbf{{D}}_{11} &{}\quad \mathbf{{D}}_{12}\\ \mathbf{{D}}_{21} &{}\quad \mathbf{{D}}_{22} \end{array} \right] \quad \left[ \begin{array}{l} {\varvec{\varepsilon }}\\ {\varvec{\alpha }}\end{array} \right] \end{aligned}$$

(12)

with

$$\begin{aligned} \mathbf{{D}}_{\alpha \beta } = \int \limits _{h^-}^{h^+} \, \mathbf{{A}}_\alpha ^T \, \mathbf{{C}} \, \mathbf{{A}}_\beta \, \bar{\mu }\, \,\text {d}\xi ^3 = \mathbf{{D}}^T_{\beta \alpha }\,. \end{aligned}$$

(13)

At first, $\mathbf{{D}}_{11}$ reads

$$\begin{aligned} \mathbf{{D}}_{11} = \displaystyle \int \limits _{h^-}^{h^+}\mathbf{{A}}_1^T \mathbf{{C}} \, \mathbf{{A}}_1\, \, \bar{\mu }\,\text {d}\xi ^3 =\left[ \begin{array}{lll} \mathbf{{D}}_m &{} \quad \mathbf{{D}}_{mb} &{} \quad \mathbf{{0}} \\ \mathbf{{D}}^T_{mb} &{} \quad \mathbf{{D}}_b &{} \quad \mathbf{{0}} \\ \mathbf{{0}} &{} \quad \mathbf{{0}} &{} \quad \mathbf{{D}}_s \end{array} \right] _{(8\times 8)} \end{aligned}$$

(14)

The submatrices for membrane, bending and shear are obtained by summation over N layers and analytical integration in each layer leading to well–known expressions. For symmetric layer sequences the coupling matrix $\mathbf{{D}}_{mb}$ vanishes. In $\mathbf{{D}}_s$ shear correction factors are not introduced.

Inserting (6–8) into (13) the matrices $\mathbf{{D}}_{22}$ and $\mathbf{{D}}_{21}$ can now be assembled with the contributions of the layers

$$\begin{aligned} \mathbf{{D}}_{22} = \sum \limits _{i=1}^N \mathbf{{a}}^{iT} \, \mathbf{{D}}^i_{22} \, \mathbf{{a}}^{i} \quad \mathbf{{D}}_{21} = \sum \limits _{i=1}^N \mathbf{{a}}^{iT} \, \mathbf{{D}}^i_{21} \end{aligned}$$

(15)

where

$$\begin{aligned} \begin{array}{rclrcl} \mathbf{{D}}^i_{22} &{}=&{} \displaystyle \int \limits _{-1}^{+1} \mathbf{{A}}^T_{2s} \, \mathbf{{C}}_s \, \mathbf{{A}}_{2s} \, \bar{\mu }\, \frac{h^i}{2} \, \,\text {d}\zeta &{} \quad \mathbf{{C}}_s &{}=&{} \left[ \begin{array}{ll} C_{44}&{} \quad C_{45} \\ C_{54}&{} \quad C_{55} \end{array} \right] \\ \mathbf{{D}}^i_{21} &{}=&{} \displaystyle \int \limits _{-1}^{+1} \mathbf{{A}}^T_{2s} \, \mathbf{{C}}_s \, \, \mathbf{{A}}_{1s} \, \bar{\mu }\, \frac{h^i}{2} \, \,\text {d}\zeta &{}\quad \mathbf{{A}}_{1s} &{}=&{} \left[ \begin{array}{ll} \mathbf{{0}}_{2 \times 6} &{}\mathbf{{1}}_2 \end{array} \right] \,. \end{array} \end{aligned}$$

(16)

With $\bar{\mu }= 1$ only powers of $\zeta$ occur in (16) and analytical integration is possible. A numerical integration with three Gauss integration points also leads to exact results. Due to the interpolation functions with local layerwise support it follows that $\mathbf{{D}}_{22}$ is banded and thus is sparse. In $\mathbf{{D}}_{21}$ only the last two columns are populated.

2.3 Equilibrium equations and a constraint

Neglecting body forces the equilibrium equations for the in–plane directions read

$$\begin{aligned} \left[ \begin{array}{l} S^{11},_1 + S^{12},_2 + S^{13},_3 \\ S^{12},_1 + S^{22},_2 + S^{23},_3 \end{array} \right] = \mathbf{{f}} = \mathbf{{0}} \,. \end{aligned}$$

(17)

In (17) the in-plane stresses $S^{\alpha \beta }$ as well as transverse shear stresses $S^{\alpha 3}$ enter. The coordinate system, as is introduced in Sect. 3.1, is orthogonal and constant. This allows partial derivatives instead of covariant derivatives.

For the in-plane stresses holds with (6–8)

$$\begin{aligned} \left[ \begin{array}{l} S^{11} \\ S^{22} \\ S^{12} \end{array} \right] =\left[ \begin{array}{lll} C_{11} &{} C_{12} &{} C_{13} \\ C_{21} &{} C_{22} &{} C_{23} \\ C_{31} &{} C_{32} &{} C_{33} \end{array} \right] \quad \left[ \begin{array}{l} \varepsilon _{11} + \xi ^3 \, \kappa _{11} \\ \varepsilon _{22} + \xi ^3 \, \kappa _{22} \\ 2 \varepsilon _{12} + \xi ^3 \, 2 \kappa _{12} \\ \end{array} \right] _{\,.} \end{aligned}$$

(18)

Introducing

$$\begin{aligned} \begin{array}{rcl} \bar{\mathbf{C}}_{23} &{}=&{} \left[ \begin{array}{llllll} C_{11} &{} C_{12} &{} C_{13} &{}C_{31} &{} C_{32} &{} C_{33} \\ C_{31} &{} C_{32} &{} C_{33} &{}C_{21} &{} C_{22} &{} C_{23} \end{array} \right] \\ {\varvec{\lambda }}_\varepsilon &{}=&{} \left[ \begin{array}{r} \varepsilon _{11},_1 \\ \varepsilon _{22},_1 \\ 2\varepsilon _{12},_1 \\ \varepsilon _{11},_2 \\ \varepsilon _{22},_2 \\ 2\varepsilon _{12},_2 \\ \end{array} \right] {\varvec{\lambda }}_\kappa = \left[ \begin{array}{r} \kappa _{11},_1 \\ \kappa _{22},_1 \\ 2\kappa _{12},_1 \\ \kappa _{11},_2 \\ \kappa _{22},_2 \\ 2\kappa _{12},_2 \\ \end{array} \right] \end{array} \end{aligned}$$

(19)

the derivatives of the in-plane stresses yield

$$\begin{aligned} \begin{array}{rcl} \left[ \begin{array}{l} S^{11},_1 + S^{12},_2\\ S^{12},_1 + S^{22},_2 \end{array} \right]= & {} \left[ \begin{array}{rr} \bar{\mathbf{C}}_{23} &{} \quad \xi ^3 \, \bar{\mathbf{C}}_{23} \end{array} \right] \left[ \begin{array}{r} \quad {\varvec{\lambda }}_\varepsilon \\ {\varvec{\lambda }}_\kappa \end{array} \right] \\ \mathbf{{f}}_1&{}=&{} \mathbf{{C}}_{23} \, {\varvec{\lambda }}\,. \end{array} \end{aligned}$$

(20)

Furthermore we introduce

$$\begin{aligned} {\varvec{\sigma }}_2 = -\displaystyle \int \limits _{h^-}^{h^+} {\varvec{\Phi }}^T \left[ \begin{array}{l} S^{13},_3 \\ S^{23},_3 \end{array} \right] \, \bar{\mu }\, \,\text {d}\xi ^3 \quad \mathbf{{D}}_{23} := - \displaystyle \int \limits _{h^-}^{h^+} {\varvec{\Phi }}^T \mathbf{{C}}_{23} \, \bar{\mu }\,\text {d}\xi ^3 \,, \end{aligned}$$

(21)

where the reformulation of (10)$_2$ with $\bar{\mu }= 1$ to (21)$_1$ is obtained with integration by parts and consideration of stress boundary conditions $S^{\alpha 3}(h^-) = S^{\alpha 3}(h^+) =0$.

The evaluation of $\mathbf{{D}}_{23}$ is performed by summation over layers considering (4)

$$\begin{aligned} \mathbf{{D}}_{23} = - \sum \limits _{i=1}^N \mathbf{{a}}^{iT} \, \mathbf{{D}}^i_{23} \end{aligned}$$

(22)

and

$$\begin{aligned} \mathbf{{D}}^i_{23}= & {} \displaystyle \int \limits _{-1}^{+1} {\varvec{\phi }}^{iT} \, \mathbf{{C}}_{23} \, \bar{\mu }\, \frac{h^i}{2} \, \,\text {d}\zeta \quad \nonumber \\ {\varvec{\phi }}^{i}= & {} \left[ \begin{array}{llll} \phi _1 \, \mathbf{{1}}_2&\quad \phi _2 \, \mathbf{{1}}_2&\quad \phi _3 \, \mathbf{{1}}_2&\quad \phi _4 \, \mathbf{{1}}_2 \end{array} \right] \,. \end{aligned}$$

(23)

Again the integral (23)$_1$ can be computed by analytical integration or numerical Gauss integration with three integration points.

Now the integral form of $\mathbf{{f}} = \mathbf{{0}}$ according to (17) is formulated with $\delta \tilde{\mathbf{u}} = {\varvec{\Phi }}\, \delta {\varvec{\alpha }}$. Considering (20) and (21) it follows

$$\begin{aligned} \int \limits _{h^-}^{h^+} \delta \tilde{\mathbf{u}}^T \, \mathbf{{f}} \, \bar{\mu }\,\text {d}\xi ^3 = - \delta {\varvec{\alpha }}^T ({\varvec{\sigma }}_2 + \mathbf{{D}}_{23} \, {\varvec{\lambda }}) = 0 \end{aligned}$$

(24)

and with $\delta {\varvec{\alpha }}\ne \mathbf{{0}}$ one obtains

$$\begin{aligned} {\varvec{\sigma }}_2 + \mathbf{{D}}_{23} \, {\varvec{\lambda }}= \mathbf{{0}} \,, \end{aligned}$$

(25)

which describes equilibrium of higher order stress resultants.

The warping displacements have to fulfill an orthogonality condition. To specify this constraint we introduce the equilibrium of virtual in-plane stresses considering (20)

$$\begin{aligned} \left[ \begin{array}{l} \delta S^{11},_1 + \delta S^{12},_2 \\ \delta S^{12},_1 + \delta S^{22},_2 \end{array} \right] = \mathbf{{C}}_{23} \, \delta {\varvec{\lambda }}= \delta \mathbf{{f}}_1 = \mathbf{{0}} \,. \end{aligned}$$

(26)

The integral form of $\delta \mathbf{{f}}_1 = \mathbf{{0}}$ yields with $\tilde{\mathbf{u}} = {\varvec{\Phi }}\, {\varvec{\alpha }}$

$$\begin{aligned} \int \limits _{h^-}^{h^+} \delta \mathbf{{f}}^T_1 \tilde{\mathbf{u}} \, \bar{\mu }\, \,\text {d}\xi ^3 = \delta {\varvec{\lambda }}^T \int \limits _{h^-}^{h^+} \mathbf{{C}}_{23}^T {\varvec{\Phi }}\, \bar{\mu }\, \,\text {d}\xi ^3 \, {\varvec{\alpha }}= 0 \,. \end{aligned}$$

(27)

With

$$\begin{aligned} \mathbf{{D}}_{32} = - \int \limits _{h^-}^{h^+} \mathbf{{C}}_{23}^T \, {\varvec{\Phi }}\, \bar{\mu }\,\,\text {d}\xi ^3 = \mathbf{{D}}_{23}^T \end{aligned}$$

(28)

Eq. (27) reads $-\delta {\varvec{\lambda }}^T \mathbf{{D}}_{32} \, {\varvec{\alpha }}= 0$ and with $\delta {\varvec{\lambda }}\ne \mathbf{{0}}$ one obtains the constraint

$$\begin{aligned} \mathbf{{g}}({\varvec{\alpha }}) = \mathbf{{D}}_{32} \, {\varvec{\alpha }}= \mathbf{{0}} \,. \end{aligned}$$

(29)

This orthogonality condition enforces the correct shape of $\tilde{\mathbf{u}}$ through the thickness. It has the descriptive meaning that the superposed warping displacements must not lead to additional membrane forces and bending moments.

2.4 Functional and Euler–Lagrange equations

We introduce the constrained optimization problem

$$\begin{aligned} \Pi ({\varvec{\theta }}) = \displaystyle \int \limits _{\Omega } [W({\varvec{\varepsilon }}, {\varvec{\alpha }}) + {\varvec{\lambda }}^T \, \mathbf{{g}}({\varvec{\alpha }}) ] \,\text {d}A + \Pi _{ext} (\mathbf{{u}}) \quad \rightarrow \quad \hbox {stat.} \end{aligned}$$

(30)

with independent quantities ${\varvec{\theta }}:= [\mathbf{{v}}, {\varvec{\alpha }}, {\varvec{\lambda }}]^T$. The strain energy density $W({\varvec{\varepsilon }},{\varvec{\alpha }})$ per area element is obtained with thickness integration of

$$\begin{aligned} W (\mathbf{{E}}) = \frac{1}{2} \displaystyle \int \limits _{h^-}^{h^+} \mathbf{{E}}^T \, \mathbf{{C}} \, \mathbf{{E}} \, \bar{\mu }\,\text {d}\xi ^3 \end{aligned}$$

(31)

and leads with $\mathbf{{E}} = \mathbf{{A}}_1 \, {\varvec{\varepsilon }}+ \mathbf{{A}}_2 \, {\varvec{\alpha }}$ and (13) to the quadratic form

$$\begin{aligned} W({\varvec{\varepsilon }},{\varvec{\alpha }}) = \dfrac{1}{2} \left[ \begin{array}{l} {\varvec{\varepsilon }}\\ {\varvec{\alpha }}\end{array} \right] ^T \left[ \begin{array}{ll} \mathbf{{D}}_{11} &{} \mathbf{{D}}_{12} \\ \mathbf{{D}}_{21} &{} \mathbf{{D}}_{22} \end{array} \right] \, \left[ \begin{array}{l} {\varvec{\varepsilon }}\\ {\varvec{\alpha }}\end{array} \right] _{\,.} \end{aligned}$$

(32)

The Lagrange term ${\varvec{\lambda }}^T \mathbf{{g}}$ is formulated with the vector of Lagrange multipliers ${\varvec{\lambda }}$ to account for the constraint $\mathbf{{g}} ({\varvec{\alpha }})= \mathbf{{0}}$. The shell is loaded statically by surface loads $\bar{\mathbf{p}}$ in ${\Omega }$ and by boundary forces $\bar{\mathbf{t}}$ on the boundary $\Gamma _\sigma$. Hence, the potential of the external loads reads

$$\begin{aligned} \Pi _{ext} (\mathbf{{u}}) = - \int \limits _{\Omega } \mathbf{{u}}^T \bar{\mathbf{p}} \,\text {d}A - \int \limits _{\Gamma _\sigma } \mathbf{{u}}^T \bar{\mathbf{t}} \, \,\text {d}s \,. \end{aligned}$$

(33)

Furthermore, the area element of the reference surface is given with $\,\text {d}A = j \, \,\text {d}\xi ^1 \,\,\text {d}\xi ^2$ where $j = |\mathbf{{X}},_1 \times \mathbf{{X}},_2|$.

With admissible variations $\delta {\varvec{\theta }}=[\delta \mathbf{{v}}, \delta {\varvec{\alpha }}, \delta {\varvec{\lambda }}]^T$ and $\delta \mathbf{{v}} := [\delta \mathbf{{u}}, \delta {\varvec{\varphi }}]^T$ the stationary condition for functional (30) yields

$$\begin{aligned}&\delta \Pi ({\varvec{\theta }}, \delta {\varvec{\theta }}) = \displaystyle \int \limits _{\Omega } \, \left[ \begin{array}{l} \delta {\varvec{\varepsilon }}\\ \delta {\varvec{\alpha }}\\ \delta {\varvec{\lambda }}\end{array} \right] ^T \left[ \begin{array}{lll} \mathbf{{D}}_{11} &{} \quad \mathbf{{D}}_{12} &{} \quad \mathbf{{0}} \\ \mathbf{{D}}_{21} &{} \quad \mathbf{{D}}_{22} &{} \quad \mathbf{{D}}_{23} \\ \mathbf{{0}} &{} \quad \mathbf{{D}}_{32} &{} \quad \mathbf{{0}} \end{array} \right] \, \left[ \begin{array}{l} {\varvec{\varepsilon }}\\ {\varvec{\alpha }}\\ {\varvec{\lambda }}\end{array} \right] \,\text {d}A \nonumber \\&\qquad +\, \delta \Pi _{ext} = 0\nonumber \\&\displaystyle \delta \Pi _{ext} = \displaystyle -\int \limits _{\Omega } \delta \mathbf{{u}}^T \bar{\mathbf{p}} \,\text {d}A -\int \limits _{\Gamma _\sigma } \delta \mathbf{{u}}^T \, \bar{\mathbf{t}} \,\text {d}s \,, \end{aligned}$$

(34)

where the virtual shell strains

$\delta {\varvec{\varepsilon }}= [\delta \varepsilon _{11},\delta \varepsilon _{22},2 \delta \varepsilon _{12}, \delta \kappa _{11},\delta \kappa _{22}, 2 \delta \kappa _{12},\delta \gamma _{1},\delta \gamma _{2}]^T$ read

$$\begin{aligned} \begin{array}{rcl} &{}&{}\delta \varepsilon _{\alpha \beta } = \dfrac{1}{2}(\delta \mathbf{{x}},_\alpha \cdot \mathbf{{x}},_\beta + \delta \mathbf{{x}},_\beta \cdot \mathbf{{x}},_\alpha )\\ &{}&{}\delta \kappa _{\alpha \beta } = \dfrac{1}{2}(\delta \mathbf{{x}},_\alpha \cdot \mathbf{{d}},_\beta + \delta \mathbf{{x}},_\beta \cdot \mathbf{{d}},_\alpha + \delta \mathbf{{d}},_\alpha \cdot \mathbf{{x}},_\beta + \delta \mathbf{{d}},_\beta \cdot \mathbf{{x}},_\alpha )\\ &{}&{}\delta \gamma _\alpha = \delta \mathbf{{x}},_\alpha \cdot \, \mathbf{{d}} + \delta \mathbf{{d}} \cdot \mathbf{{x}},_\alpha \,. \end{array} \end{aligned}$$

(35)

Finally we derive the Euler–Lagrange equations associated with the introduced functional. For this purpose variational equation (34) is rewritten with (12) and (29) as

$$\begin{aligned}&\delta \Pi ({\varvec{\theta }}, \delta {\varvec{\theta }})\nonumber \\&\quad = \displaystyle \int \limits _{\Omega } [\delta {\varvec{\varepsilon }}^T {\varvec{\sigma }}_1 + \delta {\varvec{\alpha }}^T \big ({\varvec{\sigma }}_2 + \mathbf{{D}}_{23} \, {\varvec{\lambda }}\big ) + \delta {\varvec{\lambda }}^T \mathbf{{g}} ] \,\text {d}A + \delta \Pi _{ext}\nonumber \\&\quad = 0 \,. \end{aligned}$$

(36)

Integration by parts is applied to the first term in (36) using (11) and (35). Hence, applying standard arguments of variational calculus yields as Euler–Lagrange equations the equilibrium of stress resultants and stress couple resultants

$$\begin{aligned} \dfrac{1}{j} \, (j \, \mathbf{{n}}^\alpha ),_\alpha + \bar{\mathbf{p}} = \mathbf{{0}} \quad \dfrac{1}{j} \, (j \, \mathbf{{m}}^\alpha ),_\alpha + \mathbf{{x}},_\alpha \times \mathbf{{n}}^\alpha = \mathbf{{0}} \qquad \hbox {in} \quad \Omega \,, \end{aligned}$$

(37)

the constraint $\mathbf{{g}} = \mathbf{{0}} \; \hbox {in} \, \Omega$ (29) and with ${\varvec{\sigma }}_2 + \mathbf{{D}}_{23} \, {\varvec{\lambda }}= \mathbf{{0}} \; \hbox {in} \, \Omega$ the equilibrium of higher order stress resultants (25). Furthermore one obtains the static boundary conditions

$$\begin{aligned} j\, (\mathbf{{n}}^\alpha \, \nu _\alpha ) - \bar{\mathbf{t}} = \mathbf{{0}} \quad j \, (\mathbf{{m}}^\alpha \, \nu _\alpha ) = \mathbf{{0}} \quad \hbox {on} \quad \Gamma _\sigma \,. \end{aligned}$$

(38)

Here, $\nu _\alpha$ are components of the outward normal vector on $\Gamma _\sigma$ and

$$\begin{aligned} \mathbf{{n}}^\alpha = n^{\alpha \beta } \, \mathbf{{x}},_\beta + q^\alpha \, \mathbf{{d}} + m^{\alpha \beta } \, \mathbf{{d}},_\beta \quad \mathbf{{m}}^\alpha = \mathbf{{d}} \times m^{\alpha \beta } \, \mathbf{{x}},_\beta \,. \end{aligned}$$

(39)

The geometric boundary conditions $\mathbf{{v}} = \bar{\mathbf{v}}$ on $\Gamma _u$ have to be fulfilled as constraints.

3 Finite element formulation

3.1 Representative volume element

Fig. 2

RVE at an integration point of a shell and reference surface of the RVE

The evaluation of the matrices defined in the last section is carried out in representative volume elements (RVEs) which are located at the integration points of the shell reference surface $\Omega$, see Fig. 2. For linear elasticity and constant thickness h the computation can be done in advance for one RVE only. An orthonormal coordinate system is introduced in the center of the square reference surface $\Omega _i$ with edge length $\ell$. An investigation on a proper choice of $\ell$ is performed in Sect. 4.2.2. Normalized coordinates $-1 \le \xi \le 1$ and $-1 \le \eta \le 1$ are defined with $\xi = \frac{2}{\ell } \, \xi ^1$ and $\eta = \frac{2}{\ell } \, \xi ^2$, which yields a constant Jacobian matrix

$$\begin{aligned} \mathbf{{J}} = \left[ \begin{array}{ll} \frac{\partial \xi ^1}{\partial \xi } &{} \frac{\partial \xi ^2}{\partial \xi }\\ \frac{\partial \xi ^1}{\partial \eta } &{} \frac{\partial \xi ^2}{\partial \eta } \end{array} \right] = \left[ \begin{array}{ll} \frac{\ell }{2} &{} 0\\ 0 &{} \frac{\ell }{2} \end{array} \right] _{\,.} \end{aligned}$$

(40)

The approximation for ${\varvec{\theta }}^h :=[{\varvec{\varepsilon }}^h, {\varvec{\alpha }}^h, {\varvec{\lambda }}^h]^T$ in $\Omega _i$ is chosen as

$$\begin{aligned} \begin{array}{rcl} &{}&{}\left[ \begin{array}{l} {\varvec{\varepsilon }}^h \\ {\varvec{\alpha }}^h \\ {\varvec{\lambda }}^h \end{array} \right] = \left[ \begin{array}{lllll} \mathbf{{N}}^1_\varepsilon &{}\quad \mathbf{{N}}^2_\varepsilon &{} \quad \mathbf{{0}} &{} \quad \mathbf{{0}} &{} \quad \mathbf{{N}}^3_\varepsilon \\ \mathbf{{0}} &{} \quad \mathbf{{0}} &{} \quad \mathbf{{0}} &{} \quad \mathbf{{N}}_\alpha &{} \quad \mathbf{{0}} \\ \mathbf{{0}} &{} \quad \mathbf{{N}}^1_\lambda &{} \quad \mathbf{{N}}^2_\lambda &{} \quad \mathbf{{0}} &{} \quad \mathbf{{N}}^3_\lambda \end{array} \right] \left[ \begin{array}{c} \hat{{\varvec{\varepsilon }}}\\ \hat{{\varvec{\lambda }}}_1 \\ \hat{{\varvec{\lambda }}}_2 \\ \hat{{\varvec{\alpha }}}\\ \hat{{\varvec{\lambda }}}_3 \end{array} \right] \\ &{}&{}{\varvec{\theta }}^h = \mathbf{{N}}_\theta \; \hat{{\varvec{\theta }}}\,, \end{array} \end{aligned}$$

(41)

where for the parameters $\hat{{\varvec{\varepsilon }}}\in \mathbb {R}^{8}, \hat{{\varvec{\lambda }}}_1 \in \mathbb {R}^{6}, \hat{{\varvec{\lambda }}}_2 \in \mathbb {R}^{4}, \hat{{\varvec{\alpha }}}\in \mathbb {R}^M$ and $\hat{{\varvec{\lambda }}}_3 \in \mathbb {R}^{8}$ holds. The interpolation matrices $\mathbf{{N}}^1_\varepsilon = \mathbf{{1}} _8$, $\mathbf{{N}}^2_\varepsilon$ and $\mathbf{{N}}^3_\varepsilon$ are specified in dependence on Ref. [36]

$$\begin{aligned}&\mathbf{{N}}_\varepsilon ^2 = \left[ \begin{array}{lll} \mathbf{{N}}^{m2}_\varepsilon &{} \quad \mathbf{{0}} &{} \quad \mathbf{{0}} \\ \mathbf{{0}} &{} \quad \mathbf{{N}}^{b2}_\varepsilon &{} \quad \mathbf{{0}} \\ \mathbf{{0}} &{} \quad \mathbf{{0}} &{} \quad \mathbf{{N}}^{s2}_\varepsilon \end{array} \right] _{8 \times 6} \mathbf{{N}}^{m2}_\varepsilon = \mathbf{{N}}^{b2}_\varepsilon = \left[ \begin{array}{ll} \eta &{} \quad 0 \\ 0 &{} \quad \xi \\ 0 &{} \quad 0 \end{array} \right] \nonumber \\&\mathbf{{N}}^{s2}_\varepsilon = \left[ \begin{array}{ll} \eta &{} \quad 0 \\ 0 &{} \quad \xi \end{array} \right] \nonumber \\&\mathbf{{N}}_\varepsilon ^3 = \left[ \begin{array}{ll} \mathbf{{N}}_\varepsilon ^{m3} &{} \quad \mathbf{{0}}_{3 \times 4} \\ \mathbf{{0}}_{3 \times 4} &{} \quad \mathbf{{N}}_\varepsilon ^{b3} \\ \mathbf{{0}}_{2 \times 4} &{} \quad \mathbf{{0}}_{2 \times 4} \end{array} \right] _{8 \times 8} \mathbf{{N}}^{m3}_\varepsilon = \mathbf{{N}}^{b3}_\varepsilon = \left[ \begin{array}{llll} \xi &{} \quad 0 &{} \quad 0&{} \quad 0 \\ 0 &{} \quad \eta &{} \quad 0&{} \quad 0 \\ 0 &{} \quad 0 &{} \quad \xi &{} \quad \eta \end{array} \right] _{\,.} \end{aligned}$$

(42)

The coefficient matrices $\mathbf{{T}}^0_\varepsilon , (\mathbf{{T}}^0_\sigma )^{-1}$ and the quantities $\bar{\xi }, \bar{\eta }, j_0/j$, as are used in [36], can be discarded due to the rectangular shape of $\Omega _i$.

The warping displacements ${\varvec{\alpha }}^h$ are constant in $\Omega _i$ with $\mathbf{{N}}_\alpha = \mathbf{{1}}_M$. This also holds for the derivatives of membrane strains and curvatures ${\varvec{\lambda }}^h = [{\varvec{\lambda }}^h_\varepsilon ,{\varvec{\lambda }}^h_\kappa ]^T$ with

$$\begin{aligned} \begin{array}{rclrcl} \mathbf{{N}}_\lambda ^1 &{}=&{} \left[ \begin{array}{lll} \mathbf{{N}}_\lambda ^{11}&{}\quad \mathbf{{0}}_{6 \times 2}&{}\quad \mathbf{{0}}_{6\times 2} \\ \mathbf{{0}}_{6 \times 2}&{}\quad \mathbf{{N}}_\lambda ^{11}&{}\quad \mathbf{{0}}_{6\times 2} \end{array} \right] &{}\quad \mathbf{{N}}^{11}_\lambda &{}=&{} \dfrac{2}{\ell } \left[ \begin{array}{ll} 0 &{}\quad 0 \\ 0 &{}\quad 1 \\ 0 &{}\quad 0 \\ 1 &{}\quad 0 \\ 0 &{}\quad 0 \\ 0 &{}\quad 0 \end{array} \right] \\ \mathbf{{N}}_\lambda ^2 &{}=&{} \left[ \begin{array}{ll} \mathbf{{N}}_\lambda ^{21} &{}\quad \mathbf{{0}}_{6 \times 2} \\ \mathbf{{0}}_{6 \times 2} &{}\quad \mathbf{{N}}_\lambda ^{21} \end{array} \right] &{} \mathbf{{N}}_\lambda ^{21} &{}=&{} \left[ \begin{array}{llllll} 1&{}\quad 0 \\ 1&{}\quad 0 \\ 0&{}\quad 1 \\ 0&{}\quad 1 \\ 0&{}\quad 1 \\ 1&{}\quad 0 \\ \end{array} \right] \\ \mathbf{{N}}_\lambda ^3 &{}=&{} \left[ \begin{array}{ll} \mathbf{{N}}_\lambda ^{31} &{}\quad \mathbf{{0}}_{6 \times 4} \\ \mathbf{{0}}_{6 \times 4} &{}\quad \mathbf{{N}}_\lambda ^{31} \end{array} \right] &{} \mathbf{{N}}_\lambda ^{31} &{}=&{} \dfrac{2}{\ell } \left[ \begin{array}{llll} 1 &{}\quad 0 &{}\quad 0&{}\quad 0 \\ 0 &{}\quad 0\quad &{}\quad 0&{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1&{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0&{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0&{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0&{}\quad 1 \\ \end{array} \right] _{\,.} \end{array} \end{aligned}$$

(43)

The components of $\mathbf{{N}}_\lambda ^{11}$ and $\mathbf{{N}}_\lambda ^{31}$ are obtained computing the derivatives of the membrane strains and curvatures in (41) with respect to $\xi ^\alpha$ considering (40). When multiplying $\bar{\mathbf{C}}_{23}$ from (19) with $\mathbf{{N}}_\lambda ^{21}$, one obtains the reduced form of $\bar{\mathbf{C}}_{23}$ as is used in [35] as an approximation to avoid singular matrices. Here, $\mathbf{{N}}^2_\lambda \, \hat{{\varvec{\lambda }}}_2$ describes an independent part of the interpolation.

Remark: In all computed examples the parameters associated with $\mathbf{{N}}_\varepsilon ^{s2}$ in (42) are zero, such that this matrix and the associated parameters could be taken out. Furthermore the shape function matrix $\mathbf{{N}}_\lambda ^{1}$ in (41) has negligible influence on the results.

We insert ${\varvec{\theta }}^h = \mathbf{{N}}_\theta \, \hat{{\varvec{\theta }}}$ according to (41) and the corresponding equation for the virtual quantities $\delta {\varvec{\theta }}^h = \mathbf{{N}}_\theta \, \delta \hat{{\varvec{\theta }}}$ in variational Eq. (34), which now reads

$$\begin{aligned}&\delta \Pi ({\varvec{\theta }}^h, \delta {\varvec{\theta }}^h) = \displaystyle \int \limits _{\Omega } \, \frac{1}{\ell ^2} \displaystyle \int \limits _{\Omega _i} \, \delta {\varvec{\theta }}^{hT} \mathbf{{D}} \, {\varvec{\theta }}^h \, \,\text {d}A_i \, \,\text {d}A + \delta \Pi _{ext} = 0 \quad \nonumber \\&\mathbf{{D}} = \left[ \begin{array}{lll} \mathbf{{D}}_{11} &{} \quad \mathbf{{D}}_{12} &{} \quad \mathbf{{0}} \\ \mathbf{{D}}_{21} &{} \quad \mathbf{{D}}_{22} &{} \quad \mathbf{{D}}_{23} \\ \mathbf{{0}} &{} \quad \mathbf{{D}}_{32} &{} \quad \mathbf{{0}} \\ \end{array} \right] \end{aligned}$$

(44)

or

$$\begin{aligned}&\delta \Pi ({\varvec{\theta }}^h, \delta {\varvec{\theta }}^h) = \displaystyle \int \limits _{\Omega } \, \delta \hat{{\varvec{\theta }}}^T \mathbf{{H}} \, \hat{{\varvec{\theta }}}\,\text {d}A + \delta \Pi _{ext} = 0\nonumber \\&\mathbf{{H}} = \dfrac{1}{\ell ^2} \int \limits _{\Omega _i} \, \mathbf{{N}}^T_\theta \, \mathbf{{D}} \, \mathbf{{N}}_\theta \, \,\text {d}A_i \end{aligned}$$

(45)

with a constant and symmetric matrix $\mathbf{{D}}_{J \times J}$, where $J= 20+M$. Since only powers of $\xi$ and $\eta$ occur, the integration for $\mathbf{{H}}_{K \times K}$, where $K = 26 + M$ and $\,\text {d}A_i = \ell ^2/4 \, \,\text {d}\xi \, \,\text {d}\eta$, can be carried out analytically. A $2 \times 2$ Gauss integration also leads to correct results. It is important to note, that although $\mathbf{{D}}$ is singular, $\mathbf{{H}}$ is regular.

The parameters $\hat{{\varvec{\beta }}}:=[\hat{{\varvec{\lambda }}}_1,\hat{{\varvec{\lambda }}}_2, \hat{{\varvec{\alpha }}},\hat{{\varvec{\lambda }}}_3]^T$ in $\hat{{\varvec{\theta }}}=[\hat{{\varvec{\varepsilon }}}, \hat{{\varvec{\beta }}}]^T$ are independent quantities in the RVEs, and thus are not continuous in $\Omega$. Furthermore $\delta \Pi _{ext}$ does not depend on $\hat{{\varvec{\beta }}}$. For this reason a static condensation of $\hat{{\varvec{\beta }}}$ from the set of equations

$$\begin{aligned} \left[ \begin{array}{cc} \mathbf{{H}}_{11} &{} \quad \mathbf{{H}}_{12} \\ \mathbf{{H}}_{21} &{} \quad \mathbf{{H}}_{22} \\ \end{array} \right] \, \left[ \begin{array}{cc} \hat{{\varvec{\varepsilon }}}\\ \hat{{\varvec{\beta }}}\end{array} \right] = \left[ \begin{array}{cc} {\varvec{\sigma }}_1 \\ {\varvec{0}} \end{array} \right] \end{aligned}$$

(46)

is possible. Here $\mathbf{{H}}_{\alpha \beta }$ are the submatrices of $\mathbf{{H}}$, where $\mathbf{{H}}_{11} = \mathbf{{D}}_{11}$ according to Eq. (14) holds. The right hand side of (46) contains the vector of stress resultants, since the lateral surfaces of the RVEs are not stress free. The elimination yields

$$\begin{aligned} \hat{{\varvec{\beta }}}= - \mathbf{{H}}^{-1}_{22} \, \mathbf{{H}}_{21}\, \hat{{\varvec{\varepsilon }}}\end{aligned}$$

(47)

and the material law for the stress resultants

$$\begin{aligned} {\varvec{\sigma }}_1 = \tilde{\mathbf{D}} \, \hat{{\varvec{\varepsilon }}}\quad \tilde{\mathbf{D}} :=\mathbf{{H}}_{11} - \mathbf{{H}}_{12} \, \mathbf{{H}}^{-1}_{22} \, \mathbf{{H}}_{21} \,. \end{aligned}$$

(48)

Due to the interpolation in thickness direction with local layerwise support $\mathbf{{H}}_{22}$ is sparse. Thus the effort for the static condensation is even for examples with many layers comparatively small. The sequence of the sub-vectors in ${\varvec{\theta }}^h$ and $\hat{{\varvec{\theta }}}$ in Eq. (41) is interchanged. This causes a pivot change in $\mathbf{{H}}$ and only enables the static condensation.

The condensed matrix $\tilde{\mathbf{D}}_{8 \times 8}$ possesses the same structure as $\mathbf{{D}}_{11}$, see eq. (14).

$$\begin{aligned} \tilde{\mathbf{D}} = \left[ \begin{array}{ccc} \tilde{\mathbf{D}}_m &{} \quad \tilde{\mathbf{D}}_{mb} &{} \quad \mathbf{{0}} \\ \tilde{\mathbf{D}}^T_{mb} &{} \quad \tilde{\mathbf{D}}_b &{} \quad \mathbf{{0}} \\ \mathbf{{0}} &{} \quad \mathbf{{0}} &{} \quad \tilde{\mathbf{D}}_s \end{array} \right] \begin{array}{rcl} \tilde{\mathbf{D}}_m &{}=&{} \mathbf{{D}}_m \\ \tilde{\mathbf{D}}_b &{}=&{} \mathbf{{D}}_b \\ \tilde{\mathbf{D}}_{mb} &{}=&{} \mathbf{{D}}_{mb} \end{array} \quad \tilde{\mathbf{D}}_s = \left[ \begin{array}{cc} \tilde{D}_{s11} &{} \quad \tilde{D}_{s12} \\ \tilde{D}_{s12} &{} \quad \tilde{D}_{s22} \end{array} \right] \end{aligned}$$

(49)

Only the shear stiffness $\mathbf{{D}}_s = \mathbf{{D}}^T_s$ with components $D_{s\alpha \beta }$ is affected by the static condensation. In this context shear correction factors are defined as

$$\begin{aligned} k_1 = \frac{\tilde{D}_{s11}}{D_{s11}} \quad k_2 = \frac{\tilde{D}_{s22}}{D_{s22}} \quad k_{12} = \frac{\tilde{D}_{s12}}{0.5 \, (D_{s11}+D_{s22})} \,. \end{aligned}$$

(50)

Since $D_{s12}$ may take the value zero, the average of the diagonal terms is taken as reference value for $k_{12}$. For a homogeneous laminate the well-known value $k_1 =k_2 = 5/6$, as is derived in [37, 38], is obtained with (50). Furthermore, $k_{12}=0$ holds for a homogeneous and isotropic laminate and for various anisotropic laminates with certain stacking sequences. It is pointed out that $k_{12} = \sqrt{k_1 \, k_2}$, as is assumed in several papers, does not hold here.

If the element coordinate system and the coordinate system of the RVE do not coincide, e.g., for unstructured meshes, $\tilde{\mathbf{D}}$ has to be transformed to the element coordinate system. The evaluation of the stresses is performed via constitutive law (6) and layer strains (7). For this purpose the eliminated parameters are obtained by back substitution using Eq. (47). In doing so, the parameters $\hat{{\varvec{\varepsilon }}}$ have to be transformed to the coordinate system of the RVE. The transformations are standard and therefore are not displayed here.

3.2 Linearized variational equations

Identifying the parameters $\hat{{\varvec{\varepsilon }}}$ in the RVEs with the finite element approximation of the shell strains shell ${\varvec{\varepsilon }}^h$ according to (2), variational equation (45) now reads with the static condensation (47–48)

$$\begin{aligned} \delta \Pi ({\varvec{\varepsilon }}^h, \delta {\varvec{\varepsilon }}^h) := g({\varvec{\varepsilon }}^h, \delta {\varvec{\varepsilon }}^h)\!=\! \displaystyle \int \limits _{\Omega } \, \delta {\varvec{\varepsilon }}^{hT} \, \tilde{\mathbf{D}} \, {\varvec{\varepsilon }}^h \,\text {d}A + \delta \Pi ^h_{ext} \! =\! 0 \,. \end{aligned}$$

(51)

Eq. (51) represents the principle of virtual work as variational basis for geometrical nonlinear shell elements based on the displacement method. The finite element approximations for ${\varvec{\varepsilon }}^h$ and $\delta {\varvec{\varepsilon }}^h$ are inserted in (51) and the resulting nonlinear set of equations is iteratively solved using Newton’s method. For this purpose linearization is applied which yields

$$\begin{aligned} \begin{array}{rcl} \,\text {L}\, [g({\varvec{\varepsilon }}^h, \delta {\varvec{\varepsilon }}^h), \Delta {\varvec{\varepsilon }}^h] &{}:=&{} g({\varvec{\varepsilon }}^h, \delta {\varvec{\varepsilon }}^h) + \,\text {D}g \cdot \Delta {\varvec{\varepsilon }}^h\\ &{}=&{} \, \displaystyle \sum _{e=1}^{numel} \, \delta \mathbf{{v}}^T \, [\mathbf{{K}}_T \, \Delta \mathbf{{v}} + (\mathbf{{f}}_{int} - \mathbf{{f}}_{ext})] \,. \end{array} \end{aligned}$$

(52)

Here, numel denotes the total number of finite shell elements to discretize the problem. Furthermore, $\delta \mathbf{{v}}$ and $\Delta \mathbf{{v}}$ are the virtual element displacement vector and the incremental element displacement vector, respectively. The vector of internal element forces $\mathbf{{f}}_{int}$ and the tangential element stiffness matrix $\mathbf{{K}}_T$ for 4–node elements, applying the assumed strain method for the transverse shear strains [39] and the enhanced strain method [40] for the membrane strains and curvatures are specified e.g., in [41]. The element vector $\mathbf{{f}}_{ext}$ of the external loads $\bar{\mathbf{p}}$ in $\Omega$ and $\bar{\mathbf{t}}$ on $\Gamma _\sigma$ corresponds to the one of a standard displacement method. When discarding the parameters of the enhanced strain formulation a pure displacement based finite shell element is contained as special case.

The basis for mixed hybrid shell elements is given with ${\varvec{\theta }}:= [\mathbf{{v}}, {\varvec{\sigma }}, {\varvec{\varepsilon }}, {\varvec{\alpha }}, {\varvec{\lambda }}]^T$ and an extension of functional (30)

$$\begin{aligned}&\Pi ({\varvec{\theta }}) = \displaystyle \int \limits _{\Omega } [W({\varvec{\varepsilon }}, {\varvec{\alpha }}) + {\varvec{\sigma }}^T({\varvec{\varepsilon }}_g(\mathbf{{v}})- {\varvec{\varepsilon }}) + {\varvec{\lambda }}^T \, \mathbf{{g}}({\varvec{\alpha }}) ] \nonumber \\&\qquad \qquad \,\text {d}A + \Pi _{ext} (\mathbf{{u}}) \; \rightarrow \; \hbox {stat.} \end{aligned}$$

(53)

with the second term of the integrand. Here, ${\varvec{\varepsilon }}_g$ and ${\varvec{\varepsilon }}$ denote geometrical and physical shell strains, respectively. The variation and associated Euler–Lagrange equations are derived in Ref. [35]. The associated finite element formulation leads with static condensation of $[{\varvec{\sigma }}^h, {\varvec{\varepsilon }}^h, {\varvec{\alpha }}^h, {\varvec{\lambda }}^h]$ on element level to Eq. (52). The tangential element stiffness matrix $\mathbf{{K}}_T$ and the vector of internal element forces $\mathbf{{f}}_{int}$ are specified in [42] and in an extended version for laminated shells in [36]. In both papers a remarkable robustness of the mixed hybrid element in nonlinear applications is shown. In comparison to displacement based elements much bigger load steps with less iterations are possible.

The developed element formulation has been implemented in an extended version of the general finite element program FEAP [43].

Fig. 3

Simply supported layered plate

Table 1 Shear correction factors for different lay-ups

4 Examples

4.1 Preface

Several plate examples and one shell example with carbon fibre reinforced polymer (CFRP) layers and laminated wooden layers are considered in this section. The material constants assuming transversal isotropic material behaviour as special case of orthotropy are specified along with the respective example. The present quadrilateral shell element is based on variational equation (51) and can be applied to finite deformation problems. Shear locking is avoided applying the assumed strain approach [39].

For the plate examples we use the notation depicted in Fig. 3. All considered plates are simply supported (soft support). The origin of the x, y, z–coordinate system coincides with the plate centre. The fibre direction $0^\circ$ corresponds to the x–direction.

Furthermore, 3D reference solutions are computed using 8-noded solid shell elements with three displacement degrees of freedom at the nodes, see Ref. [23]. Due to the applied assumed strain interpolation for the transverse shear strains [39] these elements possess an orientation which must coincide with the thickness direction of the shell. Furthermore, 5 parameters are used for the so-called enhanced strain interpolation. Each layer must be discretized with several elements to obtain sufficient accurate results.

Table 2 Eigenfrequencies of a layered plate

4.2 Evaluation of shear correction factors

4.2.1 Comparison with literature results

In this section we compare shear correction factors according to Eq. (50) with results of Whitney [25, 26]. The material constants, chosen by Withney (here in SI units), are

$$\begin{aligned} \begin{array}{rcllrcll} &{}&{}E_{1} = 172369 &{}\text {N/mm}^2 \qquad &{} \quad G_{12} = 3447 &{}\text {N/mm}^2 \\ &{}&{}E_{2} = 6895 &{}\text {N/mm}^2 &{} \quad G_{23} = 1379 &{}\text {N/mm}^2 \\ &{}&{}\nu _{12} = 0.25 &{} &{} \nu _{23} = 0.25 \,. \end{array} \end{aligned}$$

(54)

It is pointed out that due to the independent choice of $G_{23}$ and $\nu _{23}$ these constants do not fulfill all conditions for transversal isotropy. According to Table 1 five different layer sequences with equal layer thickness within a total thickness $h = 1$ mm are investigated. Only for the third example holds: each $0^\circ$ layer has a thickness h / 10 and each $90^\circ$ layer has a thickness of h / 8.

Fig. 4

Influence of $\ell /h$ on the shear correction factors

Present factors are slightly different from the literature results. When setting the elasticity parameters $C_{12}=C_{21}$ and $C_{33}$ in (19)$_1$ to zero, we can verify the comparative results for cross-ply laminates. Thereby the simplifying assumption of cylindrical bending, as is used in [25, 26], is taken into account. Furthermore, the ansatz $\tilde{D}_{s12} = k_{12} \, D_{s12}$ with $k_{12} = \sqrt{k_1 \, k_2}$ is used in [25]. From this equation $\tilde{D}_{s12} = 0$ follows, since $D_{s12} = 0$ holds for all examples of Table 1. For the angle–ply laminates a transition to [25] can not be shown. Here, we verify present results for the last example via a frequency analysis of a vibrating plate, see Sect. 4.3.

4.2.2 Influence of the RVE-length

For the cross-ply laminate $[0^\circ /90^\circ /90^\circ /0^\circ ]$ the influence of the RVE-length $\ell$ on the shear correction factors is investigated. The converged values according to Table 1 $k_1=0.5936$ and $k_2=0.7788$ are obtained as $\ell /h$ exceeds certain values, see Fig. 4. Furthermore, in this range present factors are independent of the total thickness h. Similar results are obtained for other stacking sequences. Based on these investigations all further computations are performed with the ratio $\ell /h=100$. The factors in Table 1 are also based on this value.

4.3 Influence of shear correction factors on eigenfrequencies

4.3.1 Simply supported CFRP plate

Eigenfrequencies of a simply supported square plate are computed in this section to verify the correctness of the computed shear factors. The plate length and the total thickness read $L=1000$ mm and $h = 50$ mm, respectively. Additional to the material data (54) a density $\rho$ = 1500 kg/m$^3$ is chosen. The last example of Table 1 with a $[30^\circ /{-30^\circ }/-30^\circ /{30^\circ }]$ stacking sequence is investigated. The shell results are obtained using a regular $80 \times 80$ mesh of 4-node elements. A 3D reference solution is computed using the 8-noded solid shell element [23] and a regular $80 \times 80 \times (4 \times 4)$ mesh. The first 10 eigenfrequencies are listed in Table 2. Present results using the factors of Table 1 show deviations of less than $0.4 \, \%$ in comparison to the reference solution. In contrast to that use of the factors [25] in a 4-node Reissner–Mindlin shell element (R.M. shell) with assumed transverse shear strains [39] lead with increasing frequency to increasing deviations. This becomes even more evident when using $k_1=k_2 = 5/6$ for homogeneous plates. Plots of the normalized eigenvectors computed with the present element are depicted in Fig. 5.

Fig. 5

Eigenvectors 1–5 and 6–10 using present element

4.3.2 Simply supported timber plate

The significance of the shear correction factors for a correct evaluation of eigenfrequencies is demonstrated with this example. Now a simply supported square plate with $L/h=4800/120$ (mm) is considered. The plate consists of 8 layers of equal thickness and $[45^\circ /{-45^\circ }/45^\circ /{-45^\circ }/{-45^\circ }/45^\circ /{-45^\circ }/45^\circ ]$ stacking sequence. The material parameters assuming transversal isotropic behaviour and the density for glued-laminated timber are chosen as

$$\begin{aligned}&E_{1} = 11600 \, \text {N/mm}^2 \quad G_{12} = 720 \, \text {N/mm}^2\nonumber \\&E_{2} = 390 \, \text {N/mm}^2 ~~~~\quad G_{23} = 100 \, \text {N/mm}^2\nonumber \\&\nu _{12} = 0.03\nonumber \\&\rho = 530 \,\text {kg/m}^3 .\nonumber \end{aligned}$$

(55)

Literature results for the shear factors are not available. Again a 3D reference solution is computed using solid shell [23] and a regular $80 \times 80 \times (8 \times 4)$ mesh. For the shell solutions a mesh of $80 \times 80$ 4-node elements is used.

For this example the computed factors $k_1=k_2=0.3427$ deviate considerable from $k_1=k_2=5/6$ for homogeneous plates, see Table 3. As consequence the deviations from the reference solution grow up to approximately $8 \, \%$ when computing the first 10 eigenfrequencies using $k_1=k_2=5/6$ in a quadrilateral Reissner–Mindlin shell element (R.M. shell). In contrast to that the deviations are less than $0.3 \,\%$ when using present factors. Plots of the normalized eigenvectors computed with the new element are depicted in Fig. 6.

Table 3 Eigenfrequencies of a layered plate

Fig. 6

Eigenvectors 1-5 and 6-10 using present element

4.4 Displacement and stress evaluations in layered plates

With this example a simply supported square plate subjected to a constant load $\bar{p} = 0.1 \, \text {N/mm}^2$ is considered. For the comparative computation with solid shell elements the loading is also applied via the middle surface. The geometrical data are: $L=1000$ mm and $h = 20$ mm. The material parameters for carbon fiber reinforced polymers are as follows

$$\begin{aligned} \begin{array}{rcllrcll} &{}&{}E_{1} = 125000 \, &{}\text {N/mm}^2 \qquad &{} \quad G_{12} = 4800 \, &{}\text {N/mm}^2 \\ &{}&{}E_{2} = 7400 \, &{}\text {N/mm}^2 &{} \quad G_{23} = 2700 \, &{}\text {N/mm}^2 \\ &{}&{}\nu _{12} = 0.34 \,. \end{array} \end{aligned}$$

(56)

We investigate four different layer sequences as are displayed in Table 4. A subscript s refers to symmetry of the total lay-up. The layer thickness is constant in each lay-up.

The output of warping displacements and of interlaminar shear stresses is performed at the center of selected elements with coordinates $(x_p, y_p)$, see Fig. 3. These values are specified in the following Figure captions. In below depicted diagrams present solutions and the solid shell solutions are denoted by 2D and 3D, respectively. As the 3D solutions are evaluated at the nodes using a standard smoothing technique, a corresponding adjustment of the 3D-meshes is necessary.

Table 4 Plate with 4 different layer sequences

Fig. 7

$\tau _{xz}(x_p = 9/21 \cdot L, y_p = 0, z)$ for the 5-layer cross-ply laminate

Fig. 8

$\tau _{yz}(x_p = 0, y_p = 9/21 \cdot L, z)$ for the 5-layer cross-ply laminate

Fig. 9

$\tau _{xz}(x,y,z=0)$ in N/mm$^2$ for the 5-layer cross-ply laminate using a distorted mesh

Remark: With the present element formulation continuity of the transverse shear stresses at the layer boundaries is automatically obtained. We do not apply any smoothing technique. Furthermore, at the outer surfaces the zero stress boundary conditions are fulfilled in an exact way. The integrals of the shear stress distributions coincide identically with the stress resultants $q^1$ and $q^2$ computed via (48).

Fig. 10

$\tau _{xz}(x,y,z=0)$ in N/mm$^2$ for the 5-layer cross-ply laminate using a regular mesh

Fig. 11

$\tilde{u}_x (x_p = 9/21 \cdot L, y_p = 0, z)$ for the 5-layer cross-ply laminate

Fig. 12

$\tau _{xz}(x_p = 9/21 \cdot L, y_p=0, z)$ for the 3-layer angle-ply laminate

Fig. 13

$\tau _{xz}(x_p = 7/32 \cdot L, y_p = 9/32\cdot L, z)$ for the 3-layer angle-ply laminate

Fig. 14

$\tau _{yz}(x_p =7/32 \cdot L, y_p = 9/32\cdot L, z)$ for the 3-layer angle-ply laminate

Fig. 15

$\tau _{xz}(x_p = 9/21 \cdot L, y_p=0, z)$ for the 8-layer angle-ply laminate

Fig. 16

$\tau _{xz} (x_p= 7/32 \cdot L, y_p = 9/32\cdot L, z)$ for the 8-layer angle-ply laminate

Fig. 17

$\tilde{u}_x (x_p \!=\!7/32 \cdot L, y_p \!=\! 9/32\cdot L, z)$ for the 8-layer angle-ply laminate

Fig. 18

$\tau _{xz}(x_p\!=\! 9/21 \cdot L, y_p\!=\!0, z)$ for the 20-layer angle-ply laminate

Fig. 19

$\tau _{xz} (x_p =7/32 \cdot L, y_p = 9/32\cdot L, z)$ for the 20-layer angle-ply laminate

Fig. 20

$\tilde{u}_x (x_p = 7/32 \cdot L, y_p = 9/32\cdot L, z)$ for the 20-layer angle-ply laminate

Fig. 21

Stiffened cylindrical shell and finite element mesh

Fig. 22

Load deflection curve of the stiffened cylindrical shell

Fig. 23

Final deformed configuration of the stiffened cylindrical shell

4.4.1 Cross–ply laminate with 5 layers

At first a 5 layer cross-ply laminate with $[0^\circ /90^\circ /0^\circ /90^\circ /0^\circ ]$ stacking sequence is investigated. The applied discretizations for both models using regular meshes are given in Figs. 7 and 8. The influence of mesh distortion on the results has also been investigated. We compare results for $\tau _{xz}(z=0)$ using a distorted mesh (1594 elements, 1675 nodes—generated with a meshing scheme based on an advancing front technique, Fig. 9) with a regular mesh (1600 elements, 1681 nodes, Fig. 10) for a quarter of the plate. In the diagrams and plots there is good agreement between the different models. A typical zig-zag shape of the warping displacements $\tilde{u}_x$ is depicted in Fig. 11. One should note that the warping ordinates are several orders less than the maximum in-plane displacements of the Reissner–Mindlin kinematic.

Table 5 Comparison of relative computing times

4.4.2 Angle-ply laminate with 3 layers

The angle-ply lay-up $[45^\circ /-45^\circ /45^\circ ]$ is considered next. The applied discretizations using regular meshes for the two models and the coordinates of the stress evaluation are given in Figs. 12, 13 and 14. The shape of $\tau _{yz}(x_p=0, y_p= 9/21 \cdot L, z)$ corresponds to the distribution of $\tau _{xz}$ in Fig. 12, and therefore is not displayed. Instead of this we present the stress evaluation at the coordinates given in Fig. 13. It shows the interesting effect that a drop of $\tau _{xz}$ in the middle layer takes place. The evaluation of $\tau _{yz}$ at the same coordinates yields a distribution as in a homogeneous plate, Fig. 14.

4.4.3 Angle-ply laminate with 8 layers

In Figs. 15 and 16 the used regular meshes are specified for an 8 layer laminate $[45^\circ /-45^\circ /45^\circ /-45^\circ ]_s$. The coordinates $(x_p,y_p)$ for the evaluation of $\tau _{xz}$ are chosen as in the previous example. The snapback behaviour of $\tau _{xz}$ in Fig. 16 is associated with the relative complicated shape of the warping displacements in Fig. 17.

Fig. 24

$\tau _{13}$ of the middle surface in N/mm$^2$ for the present formulation

Fig. 25

$\tau _{1 3}$ of the middle surface in N/mm$^2$ for the element formulation [4]

4.4.4 Angle-ply laminate with 20 layers

Finally a 20 layer laminate $[-45^\circ /45^\circ /-45^\circ /45^\circ /-45^\circ /45^\circ /-45^\circ /45^\circ /-45^\circ /0^\circ ]_s$ is investigated. The applied shell and solid shell discretizations using regular meshes can be seen in Figs. 18 and 19. The coordinates $(x_p,y_p)$ for the evaluation of $\tau _{xz}$ are chosen as in the previous example. Both diagrams show good agreement for the shear stresses of the two models. The warping displacements $\tilde{u}_x$ are depicted in Fig. 20. One can see, that with an increasing number of layers the shape approaches the distribution in a homogeneous plate. In Table 5 relative computing times (stiffness computation and solution of the system of equations) for the 2D and 3D models and different mesh densities are displayed. The 3D meshes are generated with 4 elements in thickness direction of each layer. The fast direct solver PARDISO [44] is used along with a Windows PC (2 Intel Xeon E5-2620v2, 6 cores, 2.1 GHz). In each row of the table the 3D times are normalized with respect to the 2D times. The table shows that fully 3D computations are costly, which restricts the applicability to small problems.

Fig. 26

$\tau _{13}(\xi ^1_p,\xi ^2_p, \xi ^3)$ of the stiffened cylindrical shell

4.5 Stiffened cylindrical shell

The last example represents a stiffened cylindrical shell. Figure 21 shows a cross-section of the structure and a coarse finite element mesh of half the structure considering symmetry conditions. Radius and length of the cylinder are $R=1000\, \text {mm}$, $L=2000\, \text {mm}$ and the shell thickness is $h = 10 \,\text {mm}$. The shell is free at $y=z=0$ and clamped at $y=L$. A concentrated force F acts at the coordinates $(x,y,z)=(0,0,R)$. The skin of the structure consists of a $[0^\circ /90^\circ /0^\circ ]$ lay-up, where $0^\circ$ refers to the tangential direction and $90^\circ$ to the length direction of the cylinder. The stiffeners with geometrical data $d=50\, \text {mm}$ and $h=10\, \text {mm}$ are arranged in radial direction. The stiffener in the symmetry axis has a thickness of $2\, h$. The stiffeners are homogeneous and the fibre direction coincides with the length direction. Again the data for CFRP–layers (56) are taken. A reference solution is obtained with the element formulation [4] where the transverse shear stresses are computed within a post processing procedure and thus are not embedded in the variational formulation. For both element formulations a $24 \times 16$ mesh is used for the skin and a $2 \times 16$ mesh for each stiffener.

The nonlinear load deflection curves are computed using an arc length procedure with displacement control, see Fig. 22. The kinks are caused by buckling of the stiffeners as can be seen in Fig. 23. The final deformed configuration is characterized by large deformations.

For a load $F = 100$ kN plots of the shear stresses $\tau _{13}(\xi ^1,\xi ^2)$ of the middle surface, where $\xi ^2 \equiv y$, are depicted in Figs. 24 and 25. The stiffeners are turned off in the plots. Again for $F = 100$ kN in Fig. 26 the shape of $\tau _{13}(\xi ^1_p,\xi ^2_p)$ through the thickness at a point P with coordinates $\xi ^1_p = (13/96 \cdot \pi /2) \cdot R$ and $\xi ^2_p = 7/64 \cdot L$ is displayed. Here, a refined mesh with $48 \times 32$ elements for the skin and $2 \times 32$ elements for each stiffener is used. In the diagrams and plots one can state good agreement between the two models.

5 Conclusions

In this paper the kinematics of shells is extended as warping deformations are superposed on the linear shape of the Reissner–Mindlin theory. The theory is based on a multi-field functional, where the associated Euler–Lagrange equations include besides the global shell equations formulated in stress resultants, the local in-plane equilibrium in terms of stresses and a constraint which enforces the correct shape of warping through the thickness. The material matrix for the stress resultants is computed in representative volume elements applying static condensation. For linear elasticity and constant shell thickness this can be done once in advance. As a by product shear correction factors for layered shear elastic shells are obtained. Present factors are independent of the total thickness of the laminate. The importance of the factors for a correct evaluation of eigenfrequencies is shown. The interlaminar shear stresses are evaluated via the constitutive law by back substitution of the condensed parameters. The computed transverse shear stresses are automatically continuous at the layer boundaries. Also the stress boundary conditions at the outer surfaces are fulfilled and the integrals of the shear stresses coincide exactly with the shear forces without introduction of further constraints. The computed displacements and stresses show good agreement with the results of costly 3D computations. Likewise comparisons with a post processing procedure are performed. In contrast to that approach, here the interlaminar shear stresses are embedded in the variational formulation.