A damage analysis for brittle materials using stochastic micro-structural information

Abstract

In this work, a micro-crack informed stochastic damage analysis is performed to consider the failures of material with stochastic microstructure. The derivation of the damage evolution law is based on the Helmholtz free energy equivalence between cracked microstructure and homogenized continuum. The damage model is constructed under the stochastic representative volume element (SRVE) framework. The characteristics of SRVE used in the construction of the stochastic damage model have been investigated based on the principle of the minimum potential energy. The mesh dependency issue has been addressed by introducing a scaling law into the damage evolution equation. The proposed methods are then validated through the comparison between numerical simulations and experimental observations of a high strength concrete. It is observed that the standard deviation of porosity in the microstructures has stronger effect on the damage states and the peak stresses than its effect on the Young’s and shear moduli in the macro-scale responses.

1 Introduction

In continuum mechanics, the mathematical description of material inelastic behavior such as plasticity and damage models are typically phenomenological, and connection to the underlined physics at smaller length scale is lacking. In recent years, multi-scale modeling has been introduced into the mechanics of inelasticity, such as plasticity and damage mechanics. Hill [1] defined the concept of stochastic representative volume element (SRVE) methods as a microscopic cell containing sufficient micro-scale features while possessing statistical homogeneity and ergodic properties. Hazanov [2] discussed the role of Hill’s principle and its applications in micromechanics of composite materials, where Hill condition was generalized for arbitrary materials, in particular for nonlinear inelastic composites with imperfect interfaces. Huget [3, 4] derived the upper and lower bounds of the effective moduli and compliance tensors by partitioning the domain of microstructure, named partition theorem. As the domain of consideration is smaller than the size of RVE, the maximum error of the approximated effective modulus can be estimated. Similar to the partition theorem, Ostoja-Starzewski [5] proposed a technique of scale separation to define a RVE, where the meso-scale over which the homogenization is carried out separates the microscale from the macroscale (RVE). Two hierarchies of bounds under Dirichlet and Neumann boundary conditions as the mesoscale grows were derived. Xu and Graham-Brady [6] developed a stochastic computational method to evaluate global effective properties and local probabilistic behavior of random elastic media based on the stochastic decomposition of random field.

In the area of multi-scale damage modeling, Lee et al. [7] proposed a hierarchical multi-scale model to relate the evolution of damages at the macro- and micro- scales. Fish et al. [8] developed a non-local theory for describing damage phenomena based on two-scale asymptotic expansion. Due to the high computational cost in solving the characteristic functions in the asymptotic expansion type approach, Dascalu et al. [9] constructed damage laws based on micro-mechanical energy balance on representative elementary volume with evolving micro-cracks. Ren and Chen et al. [10] proposed micro-cracks informed damage models based on an energy bridging method, in which damage evolution is treated as a consequence of micro-crack propagation.

The randomness of microstructures has been considered in the material model construction. The early work in the stochastic micro-mechanical modeling is the parallel element model [11, 12]. This model was proposed to describe the progressive damage evolution of a brittle rod subjected to uniaxial loading. Sfantos and Aliabadi [13] developed a multi-scale damage model for a polycrystalline brittle material where the randomly oriented anisotropic grains are considered. The material degradation is assumed to be caused by the initiation, propagation and coalescence of cracks on the grain boundaries. Wriggers and Moftah [14] considered a geometrical multi-scale model of concrete, where the random distribution of aggregate sizes follows the Fuller curve [15], while the locations of the aggregates are subjected to a uniform probability distribution. Xia and Curtin [16] introduced the multi-scale technique to model the failure of fiber-reinforced aluminum composites using a Green’s function method to calculate the load transferred from broken to unbroken fibers.

In the literature, the concepts of SRVE have been widely discussed. For elastic materials, the existence of RVE has been clearly defined. However, the fundamental study on material failure under the SRVE framework is limited. In this paper, material degradation caused by the formation of micro-cracks is studied under the framework of SRVE. The hierarchies of the homogenized damage evolutions with respect to different RVE sizes are derived, where the damage evolutions are evaluated based on the fracture mechanics. Furthermore, a two-parameter stochastic damage model is developed. This model contains volumetric and deviatoric failures with the consideration of the statistical variations of micro-voids and the associated crack evolution. The damage evolution law is obtained based on the Helmholtz free energy equivalence between cracked microstructure and homogenized continuum. The characteristic length scale in the proposed stochastic damage model is also investigated under the framework of the SRVE. The proposed micro-crack informed stochastic damage analysis is applied to modeling of the high strength concrete structures.

This paper is organized as follows. In Sect. 2, the framework of SRVE is reviewed and an energy-bridging homogenization method is introduced to determine the micro-crack informed damage evolution. In Sect. 3, the issue of size effect is addressed under the framework of SRVE and a scaling law is introduced to the damage evolution function to resolve the mesh-dependency deficiency. In Sect. 4, a volumetric-deviatoric decoupled stochastic damage model is proposed and then the proposed stochastic damage model is demonstrated via an implementation of the stochastic damage laws into the Advanced Fundamental Concrete (AFC) model. In Sect. 5, numerical triaxial compression tests are conducted to validate the proposed stochastic damage analysis. Conclusions are made in Sect. 6.

2 Stochastic representative volume element (SRVE)

The definition of SRVE given by Hill [1] is: (a) “entirely typical of the whole mixture on average” and (b) the one that “contains a sufficient number of inclusions for the overall moduli to be effectively independent of the surface values of traction and displacement, so long as these values are macroscopically uniform”. The statement of (a) is about the material’s statistical nature, while (b) describes that the effective material moduli should be independent of the prescribed boundary conditions in the RVE. Generally speaking, the following conditions are required for the SRVE to exist [1, 5, 17, 18]:

• (1) The micro-structure is periodic in a random sense.

• (2) The given micro-structure is sufficiently large so that the RVE is statistically representative for the entire micro-structure.

• (3) The spatial correlation lengths in the micro-structure are small enough with respect to the dimension of the macro-structure.

To describe the characteristics of SRVE, three conditions are considered, the Hill condition, ergodicity and the principle of the minimum potential energy [5]. The first two are requirements for SRVE, and the last one is the nature of continuum mechanics.

Hill [1] defined the following condition for heterogeneous elastic materials:

$$\begin{aligned} \overline{{\varvec{\upsigma } }:\varvec{\upvarepsilon }} ={ \bar{\varvec{\upsigma }}}:{\bar{\varvec{\upvarepsilon }}} \end{aligned}$$

(1)

where ${\varvec{\upsigma } }\equiv {\varvec{\upsigma } }\left( \mathbf{x} \right)$ and $\varvec{\upvarepsilon }\equiv \varvec{\upvarepsilon }\left( \mathbf{x} \right)$ are stresses and strains, and the overbar “$-$” denotes the spatial average operator defined as :

$$\begin{aligned} \bar{{f}}=\frac{1}{V}\int _{\Omega } {f\left( \mathbf{x} \right) } \hbox {d}\Omega \end{aligned}$$

(2)

in which $\Omega$ is the occupied domain, V is the volume of the occupied domain.

There are two types of boundary conditions that satisfy the Hill condition in (1): the pure Dirichlet and the pure Neumann boundary conditions with zero body forces. The pure Dirichlet boundary condition corresponds to prescribing displacements $\mathbf{u}_{\Omega }^D$ on the entire boundary $\partial \Omega$ of the microscopic cell as expressed in the following form:

$$\begin{aligned} \mathbf{u}_\Omega ^D ={\varvec{\upvarepsilon }}_0 \cdot \mathbf{x}\hbox { on }\partial \Omega \end{aligned}$$

(3)

where ${\varvec{\upvarepsilon }}_0$ is the homogenized strain tensor and x is the spatial coordinates. Note that the homogenized strain is equal to the spatially averaged strain over the domain $\Omega$ if there is no internal crack in the body:

$$\begin{aligned} {\bar{\varvec{\upvarepsilon }}}_\Omega ^D =\frac{1}{V}\int _{\Omega } {\varvec{\upvarepsilon }_\Omega ^D } \hbox {d}\Omega =\frac{1}{2V}\int _{\partial \Omega } {\left( {\mathbf{u}_\Omega ^D \otimes \mathbf{n}+\mathbf{n}\otimes \mathbf{u}_\Omega ^D } \right) } \hbox {d}\Gamma =\varvec{\upvarepsilon }_0 \end{aligned}$$

(4)

With the above definitions, it can be easily shown

$$\begin{aligned} U=\frac{1}{2}\overline{{\varvec{\upsigma } }_\Omega ^D :\varvec{\upvarepsilon }_\Omega ^D } =\frac{1}{2}{\bar{\varvec{\upsigma }}}_\Omega ^D :{\bar{\varvec{\upvarepsilon }}}_\Omega ^D \end{aligned}$$

(5)

To describe random material properties via specific samples, one needs to consider the concept of ergodicity. A random process in an SRVE is said to be ergodic if the spatial average is the same as the ensemble average of the sequence of the events:

$$\begin{aligned} \bar{{f}}\!=\!\mathop {\lim }\limits _{V\rightarrow \infty } \frac{1}{V}\int _{\Omega } {f\left( {\mathbf{x},\theta } \right) } \hbox {d}\Omega \!=\!\int _\Theta {f\left( {\mathbf{x},\theta } \right) } \rho \left( \theta \right) \hbox {d}\theta =\left\langle f \right\rangle \nonumber \\ \end{aligned}$$

(6)

where $\theta$ is the random variable in the probability space, $\left\langle {\bullet } \right\rangle$ denotes the operator of the ensemble average, $\Theta$ is the concerned domain in the probability space and $\rho \left( \theta \right)$ is the probability density function. The above definition implies that the occupied domain of the microscopic cell should be very large (mathematically infinite) compared with the size of micro-scale features, such that the microscopic cell can be considered as the SRVE, which is statistically representative for the entire micro-structure.

In the microstructures, if the fluctuations of the mechanical fields are finite and the concerned spatial and probabilistic domains are sufficiently large, these fields (such as averaged stress or strain field) are ergodic. This is because that the average of the fluctuations vanishes over infinite domains. If the microstructure possesses the ergodic property as shown in (6), it can be shown that the stress and strain fields are statistically uncorrelated:

$$\begin{aligned} U= & {} \frac{1}{2}\overline{{\varvec{\upsigma } }_\Omega ^D :\varvec{\upvarepsilon }_\Omega ^D } =\frac{1}{2}{\bar{\varvec{\upsigma }}}_\Omega ^D :{\bar{\varvec{\upvarepsilon }}}_\Omega ^D \nonumber \\= & {} \frac{1}{2}\left\langle {{\varvec{\upsigma } }_\Omega ^D :\varvec{\upvarepsilon }_\Omega ^D } \right\rangle =\frac{1}{2}\left\langle {{\varvec{\upsigma } }_\Omega ^D } \right\rangle :\left\langle {\varvec{\upvarepsilon }_\Omega ^D } \right\rangle \end{aligned}$$

(7)

Alternatively, one can apply the pure Neumann boundary condition on the entire boundary of the microscopic cell:

$$\begin{aligned} \mathbf{t}_\Omega ^N ={\varvec{\upsigma } }_0 \cdot \mathbf{n}\hbox { on }\partial \Omega \end{aligned}$$

(8)

where ${\varvec{\upsigma } }_0$ is a constant homogenized stress tensor. Under this type of boundary condition, a similar result can be obtained for the case of pure Neumann boundary condition [3]:

Fig. 1

Homogenization of a microscopic cell

$$\begin{aligned} U=\frac{1}{2}\overline{{\varvec{\upsigma } }_\Omega ^N :\varvec{\upvarepsilon }_\Omega ^N } =\frac{1}{2}{\bar{\varvec{\upsigma }}}_\Omega ^N :{\bar{\varvec{\upvarepsilon }}}_\Omega ^N =\frac{1}{2}\left\langle {{\varvec{\upsigma } }_\Omega ^N :\varvec{\upvarepsilon }_\Omega ^N } \right\rangle =\frac{1}{2}\left\langle {{\varvec{\upsigma } }_\Omega ^N } \right\rangle :\left\langle {\varvec{\upvarepsilon }_\Omega ^N } \right\rangle \end{aligned}$$

(9)

where

$$\begin{aligned} {\bar{\varvec{\upsigma }}}_\Omega ^N =\frac{1}{V}\int _{\Omega } {{\varvec{\upsigma } }_\Omega ^N } \hbox { d}\Omega =\frac{1}{V}\int _{\partial \Omega } {{\varvec{\upsigma } }_0 \cdot \mathbf{n}\otimes \mathbf{x}} \hbox { d}\Gamma ={\varvec{\upsigma } }_0 \end{aligned}$$

(10)

As the Hill condition is fulfilled and the microstructure possesses the ergodic property, one can further derive the hierarchies of mesoscale bounds for linear elastic microstructures [3–5]. Under the pure boundary conditions (3) and (8), the strain energy density of a linear problem can be obtained through the calculation of average strains and stresses. The relationships between the average strains and average stresses resulting from the Dirichlet boundary condition can be defined as:

$$\begin{aligned} {\bar{\varvec{\upsigma }}}_\Omega ^D ={\tilde{\mathbf{C}}}_\Omega ^D :{\bar{\varvec{\upvarepsilon }}}_\Omega ^D \end{aligned}$$

(11)

where ${\tilde{\mathbf{C}}}_\Omega ^D$ is the effective stiffness tensor under the Dirichlet boundary condition.

By substituting (11) into (5), the strain energy density can be rewritten as

$$\begin{aligned} U=\frac{1}{2}{\bar{\varvec{\upvarepsilon }}}_\Omega ^D :{\tilde{\mathbf{C}}}_\Omega ^D :{\bar{\varvec{\upvarepsilon }}}_\Omega ^D \end{aligned}$$

(12)

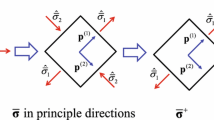
In this section, we introduce the free energy as the basis in constructing stochastic damage model from the cracked microstructure. Ren and Chen et al. [10] introduced the Helmholtz free energy relationship between cracked microstructure and damage continuum (Fig. 1) as follows

$$\begin{aligned} \tilde{\Psi }_{\Omega _y }^D =\frac{1}{V_y }\left( {\int _{\Omega _y } {\Psi _{\Omega _y }^D \hbox {d}\Omega \;+} \int _{\Gamma _c } {\frac{1}{2}{} \mathbf{h}_{\Omega _y }^D \cdot \mathbf{u}_{\Omega _y }^D } \hbox {d}\Gamma } \right) \end{aligned}$$

(13)

where $\Omega _y$ is the domain of the microstructural RVE with volume $V_{y}, \Gamma _c$ is the crack surface, $\mathbf{h}_{\Omega _y }^D$ is the cohesive traction on the crack surface, $\Psi _{\Omega _y }^D =(1/2) {\varvec{\upsigma } }_{\Omega _y }^D{:}\,\varvec{\upvarepsilon }_{\Omega _y }^D$ is the Helmholtz free energy density in the cracked RVE, the tilde “$\sim$” denotes the homogenized quantities with $\tilde{\Psi }_{\Omega _y }^D$ the homogenized Helmholtz free energy density

$$\begin{aligned} \tilde{\Psi }_{\Omega _y }^D =\frac{1}{2}{\tilde{\varvec{\upsigma } }}_{\Omega _y }^D :{\tilde{\varvec{\upvarepsilon }}}_{\Omega _y }^D \end{aligned}$$

(14)

Here ${\tilde{\varvec{\upsigma }}}_{\Omega _y }^D$ and ${\tilde{\varvec{\upvarepsilon } }}_{\Omega _y }^D$ are the homogenized stress and strain tensors, respectively, defined as:

$$\begin{aligned} {\tilde{\varvec{\upsigma }}}_{\Omega _y }^D= & {} \frac{1}{V_y }\int _{\partial \Omega _y } {\mathbf{t}_{\Omega _y }^D \otimes \mathbf{x}} \hbox { d}\Gamma =\frac{1}{V_y }\int _{\partial \Omega _y } {{\varvec{\upsigma } }_{\Omega _y }^D \cdot \mathbf{n}\otimes \mathbf{x}} \hbox { d}\Gamma \nonumber \\\end{aligned}$$

(15)

$$\begin{aligned} {\tilde{\varvec{\upvarepsilon }}}_{\Omega _y }^D= & {} \frac{1}{2V_y }\int _{\partial \Omega _y } {\left( {\mathbf{u}_{\Omega _y }^D \otimes \mathbf{n}+\mathbf{n}\otimes \mathbf{u}_{\Omega _y }^D } \right) } \hbox {d}\Gamma \end{aligned}$$

(16)

Note that the homogenized stresses and strains are related to the averaged stresses and strains as follows

$$\begin{aligned} \bar{\varvec{\upsigma }}_{\Omega _y }^D= & {} {\tilde{\varvec{\upsigma } }}_{\Omega _y }^D \end{aligned}$$

(17)

$$\begin{aligned} {\bar{\varvec{\upvarepsilon }}}_{\Omega _y }^D= & {} \frac{1}{V_y }\int _{\Omega _y } {\varvec{\upvarepsilon }_{\Omega _y }^D } \hbox { d}\Omega ={\tilde{\varvec{\upvarepsilon } }}_{\Omega _y }^D -\frac{1}{V_y }\int _{\Gamma _c } {\left( {\mathbf{n}\otimes \mathbf{u}_{\Omega _y }^D +\mathbf{u}_{\Omega _y }^D \otimes \mathbf{n}} \right) } \hbox { d}\Gamma \nonumber \\ \end{aligned}$$

(18)

With the right hand side of (13) computed in the cracked RVE, it is utilized as the Helmholtz free energy of the damaged continuum [10]. For example, the isotropic damage model can be defined as:

$$\begin{aligned} \tilde{\Psi }_{\Omega _y }^D =(1-d_{\Omega _y }^D )\tilde{\Psi }_{0\_\Omega _y }^D \end{aligned}$$

(19)

where $d_{\Omega y}^D$ is the damage parameter and $\tilde{\Psi }_{\Omega _y \_0}^D$ is the Helmholtz free energy of the undamaged continuum with moduli ${\tilde{\mathbf{C}}}_{0\_\Omega _y }^D$:

$$\begin{aligned} \tilde{\Psi }_{0\_\Omega _y }^D =\frac{1}{2}{\tilde{\mathbf{e}}}_{\Omega _y }^D :{\tilde{\mathbf{C}}}_{0\_\Omega _y }^D :{\tilde{\mathbf{e}}}_{\Omega _y }^D \end{aligned}$$

(20)

As such, the damage evolution function is obtained as $d_{\Omega _y }^D =1-\tilde{\Psi }_{\Omega _y }^D /\tilde{\Psi }_{0\_\Omega _y }^D$.

3 Size effect of micro-crack informed damage modeling

3.1 The cause of size effect

Consider a 2-D square domain partitioned into 4 equal-size sub-squares as shown in Fig. 2. Each sub-domain is defined as $\Omega _y^i$ with volume $V_y^i =V_y/4$, and $\cup _{i=1}^4 \Omega _y^i =\Omega _y$. The subscript ’y’ denotes the coordinate system in the micro-scale. A consistent Dirichlet boundary condition is imposed to the boundary of each sub-domain as:

$$\begin{aligned} \mathbf{u}_{\Omega _y^i }^D =\varvec{\upvarepsilon }_0 \cdot \mathbf{x}\hbox { }\forall \mathbf{x}\in \partial \Omega _y^i ,\hbox { }i = \hbox {1,}\ldots , 4 \end{aligned}$$

(21)

Fig. 2

Partitions of a microscopic cell in domain $\Omega _y$

The fields of the sub-domains are denoted as $\mathbf{u}_{\Omega _y^i }^D ,\hbox { }{\varvec{\upsigma } }_{\Omega _y^i }^D, \hbox {and }\varvec{\upvarepsilon }_{\Omega _y^i }^D$, which are kinematically admissible, and the fields of the entire domain are denoted as $\mathbf{u}_{\Omega _y }^D ,\hbox { }{\varvec{\upsigma } }_{\Omega _y }^D \hbox {, and }\varvec{\upvarepsilon }_{\Omega _y }^D$. Note that the averaged strains of the sub-domains are the same as the overall averaged strains of the entire domain when the consistent Dirichlet boundary condition is imposed:

$$\begin{aligned} {\bar{\varvec{\upvarepsilon }}}_{\Omega _y^i }^D =\varvec{\upvarepsilon }_0 ={\bar{\varvec{\upvarepsilon }}}_{\Omega _y }^D \end{aligned}$$

(22)

To investigate the size effect for the micro-crack informed (MCI) damage modeling, we first introduce the principle of minimum total potential energy. Let ${\hat{\mathbf{u}}}$ be the perturbation from the equilibrated displacement field u, and consider a positive functional $F\left( {\mathbf{u},{\hat{\mathbf{u}}}} \right)$ as follows:

$$\begin{aligned} F\left( {\mathbf{u},{\hat{\mathbf{u}}}} \right)= & {} \hbox { }\frac{1}{2}\int _{\Omega _y } {\left( {\varvec{\upvarepsilon }-{\hat{{\varvec{\upvarepsilon }}}}} \right) :\mathbf{C}:\left( {\varvec{\upvarepsilon }-{\hat{\varvec{\upvarepsilon }}}} \right) \hbox {d}\Omega }\nonumber \\&+\frac{1}{2}\int _{l_c } {\left( {[\mathbf{u}]-[{\hat{\mathbf{u}}}]} \right) {k}^{\prime }\left( {[\mathbf{u}]-[{\hat{\mathbf{u}}}]} \right) } \hbox {d}S\ge 0 \end{aligned}$$

(23)

where $[\mathbf{u}]$ and $[{\hat{\mathbf{u}}}]$ are displacement jumps across the crack surface. Considering the RVE of uniform thickness, we then denote $l_c$ the length of fracture process zone, ${k}^{\prime }\left( {\ge 0} \right)$ the coefficient of cohesive law, i.e. ${k}^{\prime }=\hbox { }f_t /[\mathbf{u}]-k$ for linear cohesive law, in which $f_t$ is the material tensile strength and k a constant denoting the slope of the cohesive law.

Using (23), the principle of minimum total potential energy can be expressed as:

$$\begin{aligned}&\frac{1}{2}\int _{\Omega _y } {{\varvec{\upsigma } }:\varvec{\upvarepsilon }d\Omega } +\frac{1}{2}\int _{l_c } {[\mathbf{u}]{k}^{\prime }[\mathbf{u}]} \hbox { }ds-\int _{\partial \Omega _y } {\mathbf{u}\cdot \mathbf{t}} \hbox { d}\Gamma \nonumber \\&\quad \le \frac{1}{2}\int _{\Omega _y } {{\hat{\varvec{\upsigma }}}:{ \hat{\varvec{\upvarepsilon }}}d\Omega } +\frac{1}{2}\int _{l_c } {[{ \hat{\mathbf{u}}}]{k}^{\prime }[{\hat{\mathbf{u}}}]} \hbox { }ds-\int _{\partial \Omega _y } {{\hat{\mathbf{u}}}\cdot \mathbf{t}} \hbox { d}\Gamma \end{aligned}$$

(24)

Performing the partitioning of the RVE as aforementioned, replacing the perturbation terms by the kinematically admissible sub-domain fields $\mathbf{u}_{\Omega _y^i }^D \hbox { and }\varvec{\upvarepsilon }_{\Omega _y^i }^D$ where compatibility is satisfied on the sub-cell boundaries, and considering that the consistent Dirichlet boundary condition is imposed in the sub-cells, we have:

$$\begin{aligned}&\frac{1}{V_y }\left( {\int _{\Omega _y } {\Psi _{\Omega _y }^D } \hbox {d}\Omega +\frac{1}{2}\int _{\Gamma _c } {\mathbf{u}_{\Omega _y}^D \cdot \mathbf{h}_{\Omega _y}^D ds} -\int _{\partial \Omega _y } {\mathbf{u}_{\Omega _y}^D \cdot \mathbf{t}_{\Omega _y}^D } \hbox {d}\Gamma } \right) \nonumber \\&\quad \le \frac{1}{V_y }\sum _{i=1}^4 \left( \frac{1}{2}\int _{\Omega _y^i } {\Psi _{\Omega _y^i }^D } \hbox {d}\Omega +\frac{1}{2}\int _{\Gamma _c^i } {\mathbf{u}_{\Omega _y^i }^D \cdot \mathbf{h}_{\Omega _y^i }^D ds}\right. \nonumber \\&\left. \qquad -\int _{\partial \Omega _y^i } {\mathbf{u}_{\Omega _y^i }^D \cdot \mathbf{t}_{\Omega _y}^D } \hbox {d}\Gamma \right) \end{aligned}$$

(25)

Here the following conditions have been applied to the above inequality:

$$\begin{aligned}&\frac{1}{2}\int _{l_c } {[\mathbf{u}]{k}^{\prime }[\mathbf{u}]} \hbox { }ds=\frac{1}{2}\int _{\Gamma _c } {\mathbf{u}\cdot \mathbf{h}ds} \hbox {, }\frac{1}{2}\int _{l_c } {[{\hat{\mathbf{u}}}]{k}^{\prime }[{\hat{\mathbf{u}}}]} \hbox { }ds\nonumber \\&\quad =\frac{1}{2}\int _{\Gamma _c } {{\hat{\mathbf{u}}}\cdot { \hat{\mathbf{h}}}ds} \end{aligned}$$

(26)

Note that by considering that the displacement field $\mathbf{u}_{\Omega _y^i }^D$ and the surface traction $\mathbf{t}_{\Omega _y }^D$ are continuous across the interfaces of any two neighboring sub-domains, and $\mathbf{u}_{\Omega _y }^D =\mathbf{u}_{\Omega _y^i }^D$ on the overall boundary of the entire domain, we have:

$$\begin{aligned} \int _{\partial \Omega _y } {\mathbf{t}_{\Omega _y }^D } \cdot \mathbf{u}_{\Omega _y }^D \hbox { d}\Gamma =\sum _{i=1}^4 {\int _{\partial \Omega _y^i } {\mathbf{t}_{\Omega _y }^D } \cdot \mathbf{u}_{\Omega _y^i }^D \hbox { d}\Gamma } \end{aligned}$$

(27)

Thus, we can deduce from (25) to yield the following form:

$$\begin{aligned}&\frac{1}{V_y }\left( {\int _{\Omega _y } {\Psi _{\Omega _y}^D } \hbox {d}\Omega +\frac{1}{2}\int _{\Gamma _c } {\mathbf{u}_{\Omega _y}^D \cdot \mathbf{h}_{\Omega _y}^D ds} } \right) \nonumber \\&\quad \le \frac{1}{V_y }\sum _{i=1}^4 {\left( {\frac{1}{2}\int _{\Omega _y^i } {\Psi _{\Omega _y^i }^D } \hbox {d}\Omega +\frac{1}{2}\int _{\Gamma _c^i } {\mathbf{u}_{\Omega _y^i }^D \cdot \mathbf{h}_{\Omega _y^i }^D ds} } \right) } \end{aligned}$$

(28)

Using the relationship between the Helmholtz free energy of the homogenized continuum and the microscopic free energy and cohesive energy in (13), we obtain the following inequality in terms of the Helmholtz free energy, namely:

$$\begin{aligned} \tilde{\Psi }_{\Omega _y}^D \le \frac{1}{4}\sum _{i=1}^4 {\tilde{\Psi }_{\Omega _y^i }^D } \end{aligned}$$

(29)

Here we consider a sub-division of domain $\Omega _{y}$ into four equal-size sub-domains denoted as $\Omega _y /4$. Note that since the sizes of the 4 subdomains are equal, $\Omega _y^i$ is replaced by $\Omega _y /4$ in the following stochastic analysis. With ergodicity, we have:

$$\begin{aligned} \left\langle {\tilde{\Psi }_{\Omega _y }^D } \right\rangle \le \left\langle {\tilde{\Psi }_{\Omega _y /4}^D } \right\rangle \end{aligned}$$

(30)

Applying (19) to (30), it yields:

$$\begin{aligned} \left\langle {\left( {1-d_{\Omega _y }^D } \right) \tilde{\Psi }_{0\_\Omega _y }^D } \right\rangle \le \left\langle {\left( {1-d_{\Omega _y /4}^D } \right) \tilde{\Psi }_{0\_\Omega _y /4}^D } \right\rangle \end{aligned}$$

(31)

Furthermore, assume that the undamaged material moduli are homogeneous:

$$\begin{aligned} \tilde{\Psi }_{{0}\_\Omega _y }^D =\tilde{\Psi }_{0\_\Omega _y /4}^D =\frac{1}{2}{\tilde{\varvec{\upvarepsilon }}}_{\Omega _y }^D :\mathbf{C}_{0\_\Omega _y }^D :{\tilde{\varvec{\upvarepsilon } }}_{\Omega _y }^D \end{aligned}$$

(32)

We then obtain:

$$\begin{aligned} \left\langle {d_{\Omega _y }^D } \right\rangle \ge \left\langle {d_{\Omega _y /4}^D } \right\rangle \end{aligned}$$

(33)

Repeating the same procedures of partitioning the RVEs, the hierarchy of the damage parameter inequality can be obtained:

$$\begin{aligned} \left\langle {d_{\Omega _y }^D } \right\rangle \ge \left\langle {d_{\Omega _y /4}^D } \right\rangle \ge \cdots \ge \left\langle {d_{\Omega _y /\infty }^D } \right\rangle \end{aligned}$$

(34)

The above inequalities agree with the phenomenological Weibull-type representation of brittle solids: the larger the specimen the more likely it is to fail. With fixed characteristic length of the structure, e.g. employing the same fracture cohesive law which is independent of the structural dimension, a larger structure fails easier.

Fig. 3

Periodic micro-structure with micro-cracks

Now, consider the deterministic case: a micro-structure containing micro-cracks as shown in Fig. 3. As the micro-structure is periodic, we can modify (29) as:

$$\begin{aligned} \tilde{\Psi }_{\Omega _y }^D \le \tilde{\Psi }_{\Omega _y/4}^D \end{aligned}$$

(35)

As illustrated in Fig. 4b, c, consider an enlarged micro-structure with a single crack proportionally enlarged in which the total HFE of the system in Fig. 4b is equal to that in Fig. 4c, that is:

$$\begin{aligned} 4\left( {\frac{1}{4}V_y } \right) \tilde{\Psi }_{\Omega _y/4}^D =V_y \tilde{\Psi }_{\Omega _y}^{D\_Coarse} \end{aligned}$$

(36)

Here $V_y \tilde{\Psi }_{\Omega _y}^{D\_Coarse}$ denotes the energy of the enlarged micro-structure as given in Fig. 4c. One can see that by substituting (36) into (35), the micro-structure with a single crack has lager energy density than the one with 4 smaller cracks. The cases of Fig. 4a, c can be viewed as two different mesh discretizations of the material described by the same constitutive law as shown in Fig. 5a, c, respectively. The superscript “Coarse” signifies its underlined coarse mesh representation as shown in Fig. 5c.

Fig. 4

Illustration of the size effect of periodic micro-structures: (a) Large RVE with multiple small cracks, (b) Multiple small RVEs each with single crack, (c) Large RVE with large single crack

Repeating the same procedures, the HFE inequalities associated with mesh refinement of material described by the damage law read:

$$\begin{aligned} V_y \tilde{\Psi }_{\Omega _y}^{D\_Coarse} \ge \cdots \ge V_y \tilde{\Psi }_{\Omega _y}^{D\_fine} \end{aligned}$$

(37)

The above inequalities reveal that the free energy of the discrete system of damaged material reduces as the mesh is refined, referred to as the mesh dependency as shown in Fig. 6.

Meshfree refinement of material subjected to the same damage law implicitly imposes a condition that the underlined RVEs with different dimensions have the same homogenized stress-strain relationship. This requires a critical crack opening displacement in the micro-cracks to be proportional to the RVE size and thus yields mesh dependency in (37). To remedy the mesh dependency, some approaches such as introducing non-local theories in the finite element models [19–21], embedding non-locality in the kernel function support in meshfree method [22], or employing the implicit gradient operator [23] have been proposed. In this work, we introduce a scaling law in the damage evolution function to resolve the mesh-dependency deficiency as will be discussed in the next sub-section.

Fig. 5

Illustration of the mesh dependency with different discretizations: (a) FEM model with fine discretization, (b) Subdivisions of the FEM model, (c) FEM model with coarse discretization

Fig. 6

Mesh dependency of stress and strain curves

3.2 A remedy for mesh dependency by considering size effect

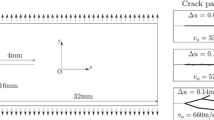
Consider a 3-point bending test on a notched beam as shown in Fig.  7. The overall behavior of the beam is governed by the Mode I crack initiated at the vertex of the notch. In this example, we consider that the damage evolution is driven only by the tensile damage due to the bending condition and the substantial strength in compression of the concrete. The material properties of the Young’s modulus and Poisson’s ratio are 21.5 GPa and 0.22, respectively. For this problem, only half of the beam is modeled for numerical simulations due to the symmetric conditions.

Fig. 7

A notched beam subjected to three-point bending

As discussed before, the solution of a problem with material degradation exhibits mesh dependency if a characteristic length independent to the mesh size is not defined. Consider a concrete sample with three different microscopic cell sizes, $5\times 5$, $2.5\times 2.5$ and $1.25\times 1.25\,\mathrm{mm^2}$ as shown in Fig. 8. The concrete sample is simplified as a 2-phase material consisting voids and matrix for the numerical study.

Fig. 8

Samples of different microscopic cell sizes

In this work, various sizes of microscopic cells corresponding to macro-structural discretizations with coarse, medium and fine meshes are considered to study the size effect. For this purpose, a dimensionless parameter, $\lambda$, is defined as follows:

$$\begin{aligned} \lambda =\frac{l_{mic} }{l_{mac} }=\frac{l}{L} \end{aligned}$$

(38)

where $l_{mic}$ is the microscopic length parameter and $l_{mac}$ is the macroscopic length parameter. Here we chose the microscopic cell size $l=5$ mm, 2.5 mm and 1.25 mm as the microscopic length parameters and the beam depth L as the macroscopic length parameter. The normalized RVE sizes are the physical RVE sizes divided by the depth of the notched beam shown in Fig. 7, which is $L =$ 0.1 m.

Fig. 9

Average homogenized stress-strain curves of different RVE sizes

Fig. 10

Average damage evolution curves of different RVE sizes

The homogenized stress and strain curves under the uniaxial tension are plotted in Fig. 9. The corresponding damage evolution curves obtained by using the energy bridging method are plotted in Fig.  10. The mesh dependency, in the homogenized stress-strain curves and consequently the nominal strengths, is due to the influence of the internal length scale, i.e., the void size and the cohesive crack law do not scale with the overall dimensions of the microscopic cells. Fig. 11 demonstrates the mesh dependency of the calculated nominal strength which can be fitted to the size effect law proposed by Bazant [24]:

$$\begin{aligned} \textstyle {\upsigma _N} =\frac{Bf_u }{\sqrt{1+\beta }},\hbox { }\beta =\frac{l}{l_0} \end{aligned}$$

(39)

where $f_u$ is the tensile strength of concrete, l is the specimen dimension, and B and $l_{0}$ are material parameters identified by experiments or numerical simulations.

Fig. 11

The size effect curve of nominal strength

Fig. 12

Mesh dependent load–disp. curves using inconsistent microscopic cell sizes

As being pointed out previously, if the discretization is refined without considering the relationship between microstructure dimension and mesh size, the solutions exhibit mesh dependency. Fig. 12 shows a strong mesh dependency induced by the standard procedure in the conventional damage mechanics, where the damage evolution law obtained from the microscopic cell size 5 mm$^{2}$ was used for all three levels of mesh refinement. The damage evolution function extracted from this microscopic cell size 5 mm$^{2}$ is only consistent with the coarse discretization but not for the medium and fine discretizations.

To resolve the mesh-dependency artifact, modified damage evolution with a scaling law is introduced:

$$\begin{aligned} d=\frac{\upvarepsilon -\upvarepsilon _i }{\upvarepsilon _u -\upvarepsilon _i},\hbox { }\textstyle \upvarepsilon _i =\textstyle \upvarepsilon _i \left( \lambda \right) , \textstyle \upvarepsilon _u =\textstyle \upvarepsilon _u \left( \lambda \right) \end{aligned}$$

(40)

where $\upvarepsilon _i$ and $\upvarepsilon _u$ are the damage initiation strain and the rupture strain, respectively, and they are considered as functions of the dimensionless parameter $\lambda$. The damage initiation strain $\upvarepsilon _i$ is assumed to be in a form similar to (39) expressed as:

$$\begin{aligned} \textstyle \upvarepsilon _i =\frac{A}{\sqrt{1+\alpha \lambda }} \end{aligned}$$

(41)

and the term $\left( {\upvarepsilon _u -\upvarepsilon _i } \right)$ is assumed of the form [10]:

$$\begin{aligned} \left( {\textstyle \upvarepsilon _{u} - \textstyle \upvarepsilon _{i} } \right) =C\lambda ^{n} \end{aligned}$$

(42)

where A, $\alpha$, C and n are constants obtained by fitting the three mesh dependent damage evolution curves in Fig. 10:

$$\begin{aligned} A= & {} 0.53336\times \hbox {10}^{-4},\hbox { }\quad \alpha ={9}.{38776} \nonumber \\ C= & {} 0.\hbox {48918}\times \hbox {10}^{-4},\hbox { }\quad n={-0.43116} \end{aligned}$$

(43)

The corrected (scaled) damage evolution curves and the uncorrected damage evolution curves are compared in Fig. 13. By introducing the corrected damage evolution function with a scaling law, the mesh insensitive results are obtained as shown in Fig. 14. This approach avoids conducting many RVE analyses for different mesh refinements in the continuum scale simulations to achieve the converged solution.

Fig. 13

Fitted and computed damage evolution curves of various RVE sizes

Fig. 14

Mesh independent load–disp. curves using scaled damage evolution law

4 Implementation of stochastic damage laws into AFC model

4.1 A volumetric-deviatoric decoupled stochastic damage model

In this work, a volumetric-deviatoric decoupled damage model is adopted to describe the pressure-shear driven material failure. Such volumetric-deviatoric decomposition approach has been proposed and been applied to concrete materials [25–28]. The damage model is described by using the decoupled Helmholtz free energy (HFE) formulation:

$$\begin{aligned} \tilde{\Psi }=(1-d_{vol} )\tilde{\Psi }_{0\_vol} +(1-d_{dev} )\tilde{\Psi }_{0\_dev} \end{aligned}$$

(44)

where $\tilde{\Psi }$ is the total effective HFE, $d_{vol}$ and $d_{dev}$ are volumetric and deviatoric damage parameters, respectively, and $\tilde{\Psi }_{0\_vol}$ and $\tilde{\Psi }_{0\_dev}$ are volumetric and deviatoric parts of the undamaged HFE, respectively.

The undamaged effective free energy can be expressed in terms of homogenized material moduli and homogenized stress (${\tilde{\varvec{\upsigma }}})$ and strain (${\tilde{\mathbf{e}}})$:

$$\begin{aligned}&\tilde{\Psi }_0 =\frac{1}{2}{\tilde{\mathbf{e}}}:{\tilde{\mathbf{C}}}_0 :{\tilde{\mathbf{e}}}=\frac{1}{2}{\tilde{\varvec{\upsigma } }}_0 :{\tilde{\mathbf{e}}}=\tilde{\Psi }_{0\_vol} +\tilde{\Psi }_{0\_dev} \end{aligned}$$

(45)

$$\begin{aligned}&\tilde{\Psi }_{0\_vol} =\frac{1}{2}{\tilde{\varvec{\upsigma } }}_{0\_vol} :{\tilde{\mathbf{e}}}_{vol} , \tilde{\Psi }_{0\_dev} =\frac{1}{2}{\tilde{\varvec{\upsigma } }}_{0\_dev} :{\tilde{\mathbf{e}}}_{dev} \end{aligned}$$

(46)

$$\begin{aligned}&{\tilde{\varvec{\upsigma }}}_{0\_vol} =\frac{1}{3}tr({\tilde{\varvec{\upsigma } }}_0 )\mathbf{1},\hbox { }{\tilde{\varvec{\upsigma }}}_{0\_dev} ={ \tilde{\varvec{\upsigma } }}_0 -{\tilde{\varvec{\upsigma } }}_{0\_vol} \end{aligned}$$

(47)

$$\begin{aligned}&{\tilde{\mathbf{e}}}_{vol} =\frac{1}{3}tr({\tilde{\mathbf{e}}})\mathbf{1},\hbox { }{\tilde{\mathbf{e}}}_{dev} ={\tilde{\mathbf{e}}}-{\tilde{\mathbf{e}}}_{vol} \end{aligned}$$

(48)

The terms with subscript “0” denote their undamaged states, “dev” denotes deviatoric and “vol” denotes volumetric. The Helmholtz free energy is further decomposed into elastic and plastic parts:

$$\begin{aligned}&\tilde{\Psi }_{0\_vol} =\tilde{\Psi }_{0\_vol}^e +\tilde{\Psi }_{0\_vol}^p\quad (a) \nonumber&\tilde{\Psi }_{0\_vol} =\tilde{\Psi }_{0\_vol}^e +\tilde{\Psi }_{0\_vol}^p \quad (b) \nonumber \\\end{aligned}$$

(49)

$$\begin{aligned}&\tilde{\Psi }^{e}=(1-d_{vol} )\tilde{\Psi }_{0\_vol}^e +(1-d_{dev} )\tilde{\Psi }_{0\_dev}^e\quad (a)\nonumber&\tilde{\Psi }^{p}=(1-d_{vol} )\tilde{\Psi }_{0\_vol}^p +(1-d_{dev} )\tilde{\Psi }_{0\_dev}^p \quad (b)\nonumber \end{aligned}$$

(50)

where the superscript “e” denotes elastic and “p” denotes plastic.

In the proposed model, the damage evolution is assumed to be related to the elastic Helmholtz free energy [29]. The elastic Helmholtz free energy $\tilde{\Psi }^{e}$ can be obtained through the homogenization process. Examples of imposing the shear and tension boundary conditions on the RVE are shown in Fig. 15. By modeling crack propagations in the RVEs and computing the history of HFE [10], the deviatoric and volumetric damage evolution functions of the homogenized continuum can be obtained as:

$$\begin{aligned} d_{dev}= & {} \left( {1-\frac{{\tilde{\Psi }}^{e}}{{\tilde{\Psi }}_{0\_dev}^e }} \right) \end{aligned}$$

(51)

$$\begin{aligned} d_{vol}= & {} \left( {1-\frac{{\tilde{\Psi }}_{vol}^e }{{\tilde{\Psi }}_{0\_vol}^e }} \right) \end{aligned}$$

(52)

Fig. 15

Different loading cases for microscopic cell analyses: (a) Under pure shear, (b) Under tension

4.2 Advanced fundamental concrete (AFC) model

To validate the proposed stochastic damage model in this paper, a high strength concrete material [30] is considered. The micro-structural geometries are constructed using the computerized tomography (CT) scans as shown in Fig. 16. The adopted numerical simulation model is simplified as a two-phase material: the matrix and voids. The effects of aggregates and the interface between aggregates and the cement are neglected, since the roughness of the aggregate shape is sufficiently high to provide an appropriate bonding of the interface, and the uniformity of the aggregate distribution on the specimen makes the crack propagation path less dependent on the interface. The procedures for obtaining the stochastic damage evolution functions extracted from the misco-scale fracture modeling are illustrated in Fig. 17.

Fig. 16

Sampled CT scans of a high strength concrete

Fig. 17

The procedures of the multi-scale modeling

Fig. 18

Construction of numerical model through image segmentation

For the construction of the micro-structural geometry, a two-phase level set method is introduced for the image based void segmentation [31] as illustrated in Fig. 18. The corresponding numerical discretization of the micro-structural geometry can then be obtained. Before conducting the macro-scale simulations, the damage evolution functions need to be determined. To quantify the heterogeneity of the microstructure, the overall porosities of the RVE samples are considered, where the porosity is defined as:

$$\begin{aligned} Porosity\equiv P=\frac{A_{void} }{A_{cell} } \end{aligned}$$

(53)

Here $A_{void}$ is the total area of the voids and $A_{cell}$ is the area of the microscopic cell.

The porosity is considered as a random variable subjected to some assumed stochastic measures. Figure 19 shows the probability density distribution of the porosity, which is obtained by using Kernel Density estimation (KDE) [32, 33] with 1600 samples.

Here, to describe the statistical variation of material properties the random variable, the normalized overall porosity, $\xi$ of the RVE is defined as:

$$\begin{aligned} \xi =\frac{P-\mu _P }{\textit{STD}_P } \end{aligned}$$

(54)

where P is the overall porosity of the RVE, $\mu _P$ and $STD_P$ are the mean value and the standard deviation of P, respectively.

The fracture mechanics based numerical simulation of the micro-structural failure processes is then conducted. The extrinsically enriched Reproducing Kernel Particle method (RKPM) [34] with cohesive law is employed for the RVE fracture analyses. The stochastic Helmholtz free energies calculated in the stochastic RVEs are related to the stochastic Helmholtz free energies of the homogenized continuum based on the energy bridging of equation (13). Finally, the stochastic damage evolution functions are extracted from the loss of Helmholtz free energy in the RVEs following (19). Due to the random variations in the heterogeneity of microstructures, the macro-scale damage parameter is considered as a random function which exhibits stochastic variations. The conventional stochastic methods are introduced to evaluate the uncertainty for the investigated concrete materials.

Fig. 19

Approximation of PDF by using Kernel Density estimation

The proposed stochastic damage model is then incorporated into the Advanced Fundamental Concrete (AFC) model [25, 26], in which the damage evolution functions will be replaced by the ones obtained by the proposed stochastic damage model, while the plasticity part remains in its original form. In this modified AFC model, the yield surface is expressed as:

$$\begin{aligned} F({\varvec{\upsigma } }_{dev} , I_{1})= & {} \left\| {{\varvec{\upsigma } }_{dev}} \right\| \!-\!\left\{ {\hat{{C}}}_{1}^{*} -\left[ {C_2^{*} \!+\!\left( {C_{1}^{*} -C_2^{*} } \right) d^{*} } \right] e^{A_n I_{1} }\right. \nonumber \\&\left. -C_4^*I_{1} \right\} \left( {1\!+\!C_3^*\ln \left( {\dot{\upvarepsilon }_n } \right) } \right) \end{aligned}$$

(55)

where $I_{1}$ is the first invariant of the stress tensor, $C_i^*$ and $d^{*}$ are random parameters and $A_{n}$ is a constant. The damage evolution function $d^{*}$ will be determined through homogenization of stochastic RVE. The random parameters $C_{1}^{*} \sim C_4^*$ are assumed in the following form:

$$\begin{aligned} C_i^*= & {} C_i \left( {1+\alpha _i \xi } \right) ,\quad i=1\sim 4 \nonumber \\ d^{*}= & {} d\left( {1+\beta \xi } \right) \end{aligned}$$

(56)

Fig. 20

Modified yield surface of AFC model

Fig. 21

RVE analyses under shear boundary condition. a Homogenized stress-strain curves. b Damage evolution curves

Fig. 22

RVE analyses under uniaxial tension boundary condition. a Homogenized stress-strain curves. b Damage evolution curves

where $\xi$ is a random variable as defined in (54) and $\alpha _i$ and $\beta$ are constants. If $\xi$ is a random variable with zero mean and unit variance, $\alpha _i$ and $\beta$ will be the standard deviations of the parameters $C_i^*$ and $d^{*}$ normalized by their averages. The parameters $C_i$ and d can be regarded as the mean values of $C_i^*$ and $d^{*}$ respectively. Note that d is the average damage evolution function in terms of strains, which can be obtained by averaging the curves in Figs. 21b and 22b. More details of the parameter $C_i^*$ for the practical use will be discussed later in Sect. 5. Here, we also slightly modify the AFC model, where a bi-linear hardening law is introduced to the parameter $\hat{{C}}_{1}^{*}$:

$$\begin{aligned} \hat{{C}}_{1}^{*} =C_1^{*} \left( {1+h\bar{{e}}_p } \right) \end{aligned}$$

(57)

in which h is the hardening parameter, and $\bar{{e}}_p$ is the effective plastic strain. The hardening law is introduced to provide stiffness after the material yields. Here a two-stage hardening rules are adopted:

$$\begin{aligned} \left\{ {{\begin{array}{ll} {h=h_a ,}&{}\quad \hbox {at initial yield point} \\ {h=h_b ,}&{}\quad \hbox {when }\left\| {{\varvec{\upsigma } }_{dev} } \right\| =\upsigma _d^*=\upsigma _d \left( {1+\gamma \xi } \right) \\ \end{array}}}\right. \end{aligned}$$

(58)

where $h_{a}$, $h_{b}$ and $\gamma$ are constants and $\upsigma _d$ is the damage initiation stress which is assumed to be a function of the first invariant of the stress tensor ($I_{1})$:

$$\begin{aligned} \textstyle \upsigma _d=a_1 +a_2 I_1 +a_3 I_1^2 \end{aligned}$$

(59)

Fig. 23

Failure patterns of an RVE sample under different loading conditions. a Under pure shear. b Under uniaxial tension

Fig. 24

Peak stress-porosity curves. a Peak shear stress versus porosity. b Peak tensile stress versus porosity

Note that $\upsigma _d$ is not only dependent on equation (59) but also on the elastic HFE, since the $\upsigma _d$ is the stress when the damage is initiated and the damage evolution is related to the HFE. When $\left\| {{\varvec{\upsigma } }_{dev}} \right\|$ reaches the critical value, the parameter $\hat{{C}}_{1}^{*}$ becomes

$$\begin{aligned} {\hat{{C}}}_{1}^{*} ={C^{\prime }}_1^{*} \left( {1+h_b \bar{{e}}_p } \right) , \quad {C^{\prime }}_1^{*} =C_1^{*} \left( {1+h_a \bar{{e}}_p^d } \right) \end{aligned}$$

(60)

in which $\bar{{e}}_p^d$ is the effective plastic strain when $\left\| {{\varvec{\upsigma } }_{dev}} \right\| =\upsigma _d^{*}$.

Figure 20 illustrates the characteristics of the yield criterion as $I_{1}<0$. As can be seen in this figure, the initial yield stress is the difference between the constants $C_{1}$ and $C_{2}$. Beyond the initial yield point, the material hardening provides sufficient stiffness for the yield surface to grow. At some point, the damage is initiated and the hardening rule is changed.

5 Validation of the proposed stochastic damage model

In this section, a high strength concrete material is tested under tri-axial compression with different confinement pressures, namely, 20, 50, 100, and 300 MPa, and the test data are fitted into the AFC model as described in Sect. 4. The material properties used in the microscopic level are: Young’s modulus $E=24.5$ MPa, and the Poisson’s ratio $v=0.16$. A linear cohesive law with the tensile strength 3.48 MPa and fracture energy 1.0 N/m is employed. These parameters are curve-fitted to the means of the homogenized stress-strain curves and experimental data. We introduced reproducing kernel particle method (RKPM) with crack enrichments to model crack propagation in the RVE [34, 35]. In the enriched RKPM, a cubic B-spline kernel function and linear basis functions are employed.

We model crack propagations in 11 RVE samples at the collocation points as shown in Fig. 19 with cell dimension 5x5 mm$^{2}$. The deviatoric and volumetric damage evolution functions are extracted by the RVE analyses with shear and uniaxial tensile Dirichlet boundary conditions, respectively, as discussed in Sects. 3 and 4. The stress-strain curves and the damage evolution functions for the corresponding RVE analyses with different microstructures are plotted in Figs. 21 and 22. The failure patterns of a RVE sample under the tensile and shear loading cases are shown in Fig. 23. The curves relating the peak shear and tensile stresses to porosity are plotted in Fig. 24. In the numerical simulation, the modified AFC model in conjunction with the damage evolution functions described in this paper is employed. The RVE samples are selected at 11 sampling points. Each sampling point corresponds to a damage evolution function as shown in Fig. 21b and 22b. After the results of RVE analyses are obtained, the solution in terms of random variables can be determined by introducing the approximation in the random space. Consequently, the statistical moments such as mean and standard deviation of the solution can be obtained.

Table 1 Normalized STDs of the homogenized material properties

Table 2 Parameters of the modified AFC model

Fig. 25

Comparison of the tri-axial compression tests. a 20 MPa confinement stress. b 50 MPa confinement stress. c 100 MPa confinement stress. d 300 MPa confinement stress

As shown in Table 1, the normalized standard deviations (STD’s) of the homogenized Young’s and shear moduli of 1600 samples are 3.4 and 4.6 % respectively, and the normalized standard deviation (standard deviation divided by the average value) of the porosity is 18.51 %, while the normalized STD’s of the peak shear and tensile stresses based on the 11 RVE analyses are 11.61 and 14.83 %, respectively. The normalized STD’s of the peak stresses are slightly smaller than the one of the porosity, and the normalized STD’s for the homogenized Young’s modulus and shear modulus are much smaller than the normalized STD’s of the peak stresses. This is due to the fact that homogenized moduli are determined by the elastic response while the peak stresses are affected by the fracture processes and are more sensitive to the void distribution in the microstructures. Furthermore, the parameters in (56) have been characterized based on the RVE analyses. The normalized standard deviation (STD) of the parameters $C_{1}^{*} \sim C_{4}^{*}$ and $\upsigma _d^*$ are assumed to be the same as the normalized STD of the homogenized damage parameter $d^{*}$:

$$\begin{aligned} \alpha _1 =\alpha _2 =\alpha _3 =\alpha _4 =\gamma =-\beta =-0.1{15} \end{aligned}$$

(61)

The other material parameters characterized using the trial testing data are listed in Table 2. Consequently, the characterized Young’s and shear moduli are expressed as

$$\begin{aligned} E^{*}= & {} \left\langle {\tilde{E}} \right\rangle \left( {1-k_1 \xi } \right) ,k_1 =0.034, \nonumber \\ G^{*}= & {} \left\langle {\tilde{G}} \right\rangle \left( {1-k_2 \xi } \right) ,k_2 =0.046 \end{aligned}$$

(62)

where $\left\langle {\tilde{E}} \right\rangle$ and $\left\langle {\tilde{G}} \right\rangle$ are the means of the effective Young’s modulus and shear modulus and the $k_{1}$ and $k_{2}$ are the normalized STD’s.

The characterized stochastic AFC model aforementioned is then used for the macro-scale modeling of concrete specimen under triaxial compressions. The comparisons between the numerical simulations and the experiment observations are plotted in Fig. 25. For the numerical simulations, three curves are obtained through the stochastic analysis for each confinement stress. One is the average of the principal stress difference, which is the difference between the major principal stress and the confinement stress, and the other two are the average plus and minus STD. In the comparison, the numerical results agree well with the experimental data. Note that for high confinement stresses, such as 100 and 300 MPa, the material exhibits high rigidity after reaches the yield point. This behavior is appropriately captured by the bi-linear hardening law in the AFC model.

Here we observe how the statistical variations in the microstructure (porosity) affect the statistical variations in the material and damage properties of macro-structure. From numerical macro-scale triaxial tests, the normalized STD’s (normalized by average) of the equivalent Young’s and shear moduli are 0.038 and 0.049, respectively. These two values are very close to the ones obtained from the RVE analyses, i.e. 0.034 and 0.046 as shown in (62). Furthermore, we compare the STD of the overall damage evolution in triaxial tests with the STD of the damage evolution from the RVE analyses. For the former, the STD of the overall damage is evaluated at the point of 14 % axial strain. The STD of the overall damage under 50, 100 and 300 MPa confining stresses are 0.115, 0.111 and 0.112, respectively. These values are very close to the normalized STD $\beta$, which is 0.115 as shown in (61), of the damage evolution obtained from the RVE analyses. These results show that the normalized STD’s for the homogenized Young’s modulus and shear modulus are much smaller than the ones in the damage state. High STD of porosity does not affect much for the material moduli but the damage state and consequently the peak stresses. This is due to the fact when the RVE size is sufficiently large the material moduli will tend to be deterministic as being discussed in the literature. On the other hand, the damage state and peak stresses are affected by the fracture processes which is more sensitive to the void distribution in the microstructures.

6 Conclusions

This study aims to develop a stochastic damage model for brittle materials. A two-parameter damage model is considered under the framework of SRVE, which employs the deviatoric and volumetric damage laws for brittle materials. The proposed stochastic damage model is implemented into the AFC model. In this approach, the material damage on the macro-scale has been considered as the consequence of the crack formation and coalescence on the micro-scale.

This work is the extension of the micro-crack informed damage model proposed by Ren and Chen et al. [10] with the consideration of statistical variations in the voids geometry and distributions. The characteristics of the SRVE have been investigated. The size effect of the proposed damage analysis is analyzed by using the principle of the minimum potential energy. The analysis confirms that the larger the specimen the more likely it is to fail. This size effect associated with the dimension of SRVE serves as the basis in explaining the mesh dependency phenomenon in continuum analysis of materials with softening. The quantified size effect provided a remedy for the mesh dependency issue by introducing a size scaling law into the damage evolution function to achieve mesh insensitive results in damage mechanics modeling.

From RVE and macro-scale modeling we observe that the normalized STD’s for the homogenized Young’s modulus and shear modulus are much smaller than the ones in the damage state. High STD of porosity does not affect much for the material moduli but the damage state and consequently the peak stresses. This is due to the fact when the RVE size is sufficiently large the material moduli will tend to be deterministic as being discussed in the literature. On the other hand, the damage state and peak stresses are affected by the fracture processes which is more sensitive to the void distribution in the microstructures.

Finally, the proposed stochastic damage model was validated through modeling of concrete specimen under triaxial compression, which shows good agreement with experimental results.