Modified SFEM for computational homogenization of heterogeneous materials with microstructural geometric uncertainties

Abstract

In the current work we examine the application of the stochastic finite element method (SFEM) to the modeling of representative volume elements for heterogeneous materials. Uncertainties in the geometry of the microstructure result in the random nature of the solution fields thus requiring use of the stochastic version of the finite element method. For considering large differences in the material properties of matrix and inclusions a standard SFEM approach proves not stable and results in high numerical errors compared to a brute-force Monte-Carlo evaluation. Therefore in order to stabilize the SFEM we propose an alternative Gauss integration rule as resulting from a truncation of the probability density function for the random variable. In addition we propose new basis functions substituting the common polynomial chaos expansion, resulting in higher accuracy for the standard deviation in the homogenized stress at the macro scale.

1 Introduction

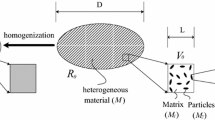
The effective macroscopic properties of heterogeneous materials result from the response of the underlying microstructure and can be estimated using homogenization techniques. Various analytical approaches based on multiscale methods, perturbation methods and asymptotic estimations are proposed e.g. in [2–5]. Alternatively computational homogenization can be applied to a wide range of complex problems, as e.g. the response of heterogeneous magneto-active polymers [7, 20, 42], which can not be properly modeled using only analytical methods. A number of applications for computational homogenization can be found in [1, 17, 24, 27, 45].

Due to its high efficiency and simple extension to complex problems we choose in this study computational homogenization to determine the macroscopic behavior of heterogeneous materials.

Computational homogenization involves two main ingredients—transfer of the macroscopic loading to the microscale and averaging the corresponding response of the microstructure to obtain the macroscopic properties.

Thereby transfer of the macroscopic loading to the microscale is performed by applying either Neumann, periodic or Dirichlet boundary conditions (satisfying the Hill-Mandel condition) to the representative volume element (RVE) of the microstructure.

A challenging aspect in computational homogenization is the modeling of the microstructure, which is often assumed to be periodic. We use the computational homogenization formulation proposed in [20], which theoretical aspects are discussed in [7]. Thereby the proposed framework requires two separate FE models—a macroscopic model and a model of the underlying microstructure (RVE).

Due to the heterogeneity of the microstructure and the often complex phase distribution the mesh generation for the microscopic model is not a trivial task. Alternatively [45] proposes to introduce the material heterogeneity on the integration point level. As mentioned in [27] this yields sufficient accuracy for the homogenized stress but suffers from the improper description of the stress distribution over the RVE. The later aspect was used as motivation for the development of a XFEM based homogenization framework [24, 27]. This method was initially developed in [28] for crack propagation problems of the underlying discretization. However the integration rule still has to be fitted to the geometry. More details can be found in [14].

XFEM is also suitable to describe matrix-inclusion interfaces, open interfaces inside the media and holes in the material. Spieler [42] successfully applied this method to complex magneto-elastic problems.

We consider the random microstructure of a heterogeneous material, i.e. the random geometry of the RVE. Thus neither the usual FEM with a geometry dependent mesh, nor traditional XFEM can be applied. Here the most suitable option is the approach proposed in [45].

A lot of works are devoted to periodic media. However, most of real composites can possess random microstructures. In many applications the uncertainties results from the random position of inclusions in the RVE.

Analytical estimates for the averaged effective properties of random heterogeneous material can be found in [6, 15–17]. The framework proposed in [6] is based on averaging the energy function for the case of aligned, ellipsoidal particles distributed randomly with “ellipsoidal” symmetry.

A simple estimate of the lower and upper bounds of the macroscopic properties of the material with random distribution of inclusions is proposed in [3]. This estimate is based on the solution of a purely deterministic problem which is found as an asymptotic expansion in powers of a small parameter.

To date the most common methods applied to problems with uncertainties are the perturbation method, Monte-Carlo simulation and Stochastic FEM.

A number of results in stochastic homogenization were obtained by Sakata et al. [37–40]. He considered a material with random position of inclusions (defined by a small parameter $\varepsilon$) and obtained the mechanical properties as function of the parameter $\varepsilon$ by using the first-order perturbation method. This method is based on the assumption that the uncertainty is small, i.e. the inclusion is located in the center, but its position can be changed by a very small value. The deterministic solution is assumed to coincide with the mean value and is obtained analytically. Likewise the homogenized quantities for the deterministic problem are obtained analytically. Introducing a small perturbation into the deterministic solution and further differentiation allows to obtain the sensitivity matrix. This method provides only linearized solutions and is restricted to problems with small uncertainties. Higher order generalizations of this method are discussed in [37] and are found to be not efficient enough.

The formulation of the perturbation method is very close to the multiscale method used in [3] and can be naturally combined with upper and lower bound estimates.

The Monte-Carlo simulation (MC) is a “brute-force” technique which involves the independent solution of the problem for each particular model configuration (called sample). In the case of a sufficient high number of samples this technique can guarantee good convergence for any problem. Monte-Carlo simulation does not require a stochastic model and all probabilistic measures are obtained statistically from the set of independent solutions. MC is a very effective tool in stochastic homogenization [8, 9, 23, 44] due to its capability to handle problems where other methods fails. Furthermore Monte-Carlo simulation is often used to verify solutions obtained with more sophisticated techniques as the perturbation method or SFEM.

Recent results in stochastic homogenization for a problem similar to the one considered in this paper were obtained in [25, 26] using a combination of the FE$^2$ method with Monte-Carlo simulation. The considered RVE includes a few types of uncertainties such as in the geometry of the microstructure as well as in its mechanical properties.

A high number of samples needed to reach a required accuracy results in high computational costs and long simulation times, which constitute the main disadvantages of the MC method.

The Stochastic FEM (SFEM) is introduced in the classical treatise [18] for problems including different types of uncertainties. This method can be applied to problems with random material properties and random loading or boundary conditions. It has a number of application to the diffusion problem, stochastic plasticity, and thermo-mechanical problems [10–13, 19, 21, 22, 30, 33–36, 43].

The stochastic finite element method states that the nodal values of the solution field (e.g. nodal displacements) are not anymore deterministic but random variables (RV). Accordingly all uncertainties in the model are represented in terms of random variables and random fields. Due to the fact that the probability density functions of the introduced random variables and their supports are usually unknown, the solution of the resulting stochastic problem is highly complex. However it can be strongly simplified by the introduction of a set of independent orthogonal basic random variables with known density function and correspondent probabilistic measures. Then all other random variables are represented as a nonlinear mapping of the basic variables, which is represented in terms of orthogonal polynomials called Polynomial Chaos [18]. The unknown coefficients of the polynomial chaos expansion (PCE) are obtained by applying the stochastic Galerkin method, which merely differs from the usual Galerkin method by the definition of the inner product in the probability space. A brief description of the SFEM framework is presented in Sect. 3.

In many problems considering heterogeneous materials the physical properties are unknown and there is no expression describing their distribution over the domain [11, 18, 21, 22, 35, 43]. However information about their averaged properties and their covariance matrix (characterizing the intensity of local random fluctuations) is always available. The Karhunen-Loeve expansion (KLE) is a technique compensating this lack of information by transformation the covariance matrix to the more convenient form of the random field. The KLE presents the spectral decomposition of the covariance matrix which yields an expression in terms of random variables and eigenvectors. This expression can be directly used in the MC simulation to generate samples or as part of the SFEM framework.

In comparison to the perturbation method SFEM is not restricted to a small randomness or linearized solution. And in contrast to the Monte-Carlo simulation SFEM is considered to be more efficient, because it requires to solve the problem only once.

The aim of this paper is the development of an accurate homogenization strategy for random heterogeneous materials with geometrical uncertainties in the microstructure. To this end we combine the SFEM as presented in [18] with the computational homogenization approach [20]. In Sect. 3 we introduce a general SFEM formulation for continuous nonlinear mechanical problems. The stochastic RVE including uncertainties in the geometry is introduced in Sect. 4. Introduction of geometrical uncertainties into SFEM is demonstrated for an example of a RVE with random position of inclusions.

The first modification of the standard SFEM involving truncated Gaussian random variables and a new Gauss integration rule is presented in Sect. 5. The second modification of SFEM considering non-polynomial bases in the stochastic domain is discussed in Sect. 6. Section 7 presents simulation results obtained using SFEM with both modifications, comparison of different bases and comparison with the Monte-Carlo simulation. Accuracy and weak points of the method are discussed in Sect. 8. Modification of the RVE considering further seven examples of geometrical uncertainties are introduced in Sect. 9, followed by the discussion of the simulation results. Finally, Sect. 10 concludes the paper.

2 Notation

In this work we distinguish between deterministic and random variables, vectors and tensors, matrices and operators. We use the following notation:

• Second order tensors and vectors are emphasized by bold (e.g. $\mathbf {F}$) and bold italic (e.g. $\varvec{{x}}$) scripts respectively.

• Random variables, second order tensors and vectors are represented [31, 41] as functions of the elementary event $\omega$, e.g. $\chi (\omega )$, $\mathbf {F}(\omega )$, $\varvec{{\theta }}(\omega )$.

• Random fields are any functions of the spatial coordinates $\varvec{{x}}$ and the elementary event $\omega$ (e.g. $G(\varvec{{x}},\omega )$).

• Capital calligraphic letters are used for the domains of functions and sets [e.g. $\mathcal {D}$, $\mathcal {S}$, $\mathcal {F}$].

• Bold calligraphic letters denote function space like e.g. the Hilbert space $\varvec{\mathcal {H}}$.

• Differential operators are denoted by capital upright letters, e.g. $\mathrm {D}(\varvec{{x}},\omega )$.

• In particular $\mathrm{Div}$ and $\mathrm{Grad}$ denote divergence and gradient operators applied in the reference configuration of a geometrically nonlinear continuous deformable body.

Fig. 1

Physical, stochastic and product spaces $\varvec{\mathcal {H}}$, $\varvec{\mathcal {Q}}$ and $\varvec{\mathcal {W}}$ with corresponding physical, stochastic and product domains $\mathcal {D}$, $\mathcal {S}$ and $\mathcal {V}$

3 Stochastic finite element method

We consider SFEM as a special case of the Galerkin method. To this end we introduce two spaces—the physical space, where we apply the usual spatial FEM discretization, and the probability space, with discretization described in the sequel.

Following [18] we introduce the Hilbert (inner product) space $\varvec{\mathcal {H}}$ of functions defined over a physical domain $\mathcal {D}$ with values on the real line $\mathbb {R}$. Examples for spatial basis functions in $\varvec{\mathcal {H}}$ are the well-known piece-wise linear or quadratic shape functions.

Let (${\Omega }$,$\mathcal {F}$,$\mathbb {P}$) be the probability space with total mass equal to unity. ${\Omega }$ is the space of elementary events $\omega$ or the sample space. $\mathcal {F}$ is a $\sigma$-algebra in ${\Omega }$, $\mathbb {P}$ is a probability measure [31, 41].

Any random variable $\chi (\omega )$ can be defined as a function mapping ${\Omega }$ into the real line [18].

$$\begin{aligned} \chi (\omega ):{\Omega } \rightarrow \mathbb {R}. \end{aligned}$$

Let $\varvec{\mathcal {Q}}$ be the Hilbert space of random variables called the stochastic space, so that $\forall \chi (\omega ):~\chi (\omega )\in \varvec{\mathcal {Q}}$.

In the stochastic space we can choose a subset of independent random variables as coordinates. For convenience the random variables in this subset will be Gaussian, denoted by $\theta _i(\omega )$ that are collected in the vector $\varvec{{\theta }}(\omega )$. Then all other random variables and random fields will be expressed as a nonlinear mapping of this set.

We can visualize the stochastic space with Gaussian random variables $\theta _i(\omega )$ as coordinates in the same way as the physical space with coordinates $x_1$, $x_2$ and $x_3$. The domain for the Gaussian random variables in the stochastic space is called the stochastic domain $\mathcal {S}$. A random field (any function of the spatial coordinates $\varvec{{x}}$ and the event $\omega$) may be described as a function defined on the product space $\varvec{\mathcal {W}}=\varvec{\mathcal {H}} \times \varvec{\mathcal {Q}}$ over the domain $\mathcal {V}$, see Fig. 1. This space is Hilbert as well.

The main property of a Hilbert space is the existence of an inner product denoted by $\langle ,\rangle$. In $\varvec{\mathcal {H}}$ the inner product (a scalar) of two functions over $\mathcal {D}$ [18] is defined as

$$\begin{aligned} \big \langle g_1(\varvec{{x}}),g_2(\varvec{{x}}) \big \rangle := \int \limits _\mathcal {D} g_1(\varvec{{x}})g_2(\varvec{{x}}) \mathrm {d}\varvec{{x}}. \end{aligned}$$

(1)

A similar inner product of two elements in $\varvec{\mathcal {Q}}$ (called expectation) i.e. of two functions over ${\Omega }$ is represented as the Lebesgue integral

$$\begin{aligned} \big \langle g_1(\omega ),g_2(\omega ) \big \rangle := \int \limits _{\Omega } g_1(\omega )g_2(\omega ) \mathrm {d}\mathbb {P}. \end{aligned}$$

(2)

It can be written more conveniently as the Riemann integral

$$\begin{aligned} \big \langle g_1(\omega ),g_2(\omega ) \big \rangle= & {} \big \langle g_1 \big (\varvec{{\theta }}(\omega )\big ), g_2\big (\varvec{{\theta }}(\omega )\big ) \big \rangle \nonumber \\:= & {} \int \limits _\mathcal {S} g_1(\varvec{{\theta }})g_2(\varvec{{\theta }}) f_{\Theta } \mathrm {d}\varvec{{\theta }}, \end{aligned}$$

(3)

where the weight function $f_{\Theta }$ is the joint probability density function (JPDF) of the basis random variables $\theta _i(\omega )$ that are collected in the vector $\varvec{{\theta }}(\omega )$. For independent Gaussian variables the JPDF is well-known; for the case of two independent random variables $\theta _1$ and $\theta _2$ it is depicted in Fig. 2.

Fig. 2

JPDF for two independent Gaussian random variables

Based on the definitions given in the above the inner product in the product space $\varvec{\mathcal {W}}$ results in

$$\begin{aligned} \big \langle g_1(\varvec{{x}},\omega ),g_2(\varvec{{x}},\omega ) \big \rangle := \int \limits _\mathcal {D}\int \limits _\mathcal {S} g_1(\varvec{{x}},\varvec{{\theta }})g_2(\varvec{{x}},\varvec{{\theta }}) \mathrm {d}\varvec{{x}} f_{\Theta } \mathrm {d}\varvec{{\theta }}. \end{aligned}$$

(4)

We introduce next a random differential operator $\mathrm {D}(\varvec{{x}},\omega )$ with correspondent data $f(\varvec{{x}},\omega )$, i.e. a random field

$$\begin{aligned} \mathrm {D}(\varvec{{x}},\omega )\varvec{{u}}(\varvec{{x}},\omega )=f(\varvec{{x}},\omega ). \end{aligned}$$

(5)

Thus the solution $\varvec{{u}}(\varvec{{x}},\omega )$ satisfying the random differential operator is in general also a random field.

The Bubnov–Galerkin method includes two steps: firstly, representing the unknown functions by their projections onto some basis

$$\begin{aligned} \varvec{{u}}(\varvec{{x}},\omega )=\sum \limits _{i=1}^\infty \varvec{{u}}_i\varphi _i(\varvec{{x}},\omega ) \end{aligned}$$

(6)

Whereby, for an approximation, the first n coefficients $\varvec{{u}}_i$ are computed from the system

$$\begin{aligned} \big \langle \varvec{{u}}(\varvec{{x}},\omega ), \varphi _j(\varvec{{x}},\omega ) \big \rangle =\sum \limits _{i=1}^n\varvec{{u}}_i \big \langle \varphi _i(\varvec{{x}},\omega ),\varphi _j(\varvec{{x}},\omega ) \big \rangle , \end{aligned}$$

(7)

where $j=1,2~\ldots ~n$.

Secondly, projecting the differential equation onto the same basis

$$\begin{aligned} \big \langle \mathrm {D}(\varvec{{x}},\omega )\varvec{{u}}(\varvec{{x}},\omega )-f(\varvec{{x}},\omega ), \varphi _i(\varvec{{x}},\omega ) \big \rangle =0. \end{aligned}$$

(8)

For the numerical implementation the number n of basis functions $\varphi _i(\varvec{{x}},\omega )$ is finite and thus the solution obtained is approximate.

Restricting this procedure to the space $\varvec{\mathcal {H}}$ results in the deterministic Galerkin method. Selecting piece-wise basis functions e.g. based on Legendre polynomials as shape functions $N_i(\varvec{{x}})$ collected in $\varvec{{N}}(\varvec{{x}})$, renders the familiar spatial FEM.

On the other hand if we focus on the stochastic domain only, we obtain the stochastic Galerkin method. Due to their orthogonality the basis functions in the stochastic domain are typically expressed in terms of the Polynomial Chaos Expansion (PCE). If we restrict ourselves to Gaussian variables, Polynomial Chaos will be represented by the so called Hermite polynomials $H_i\big ( \varvec{{\theta }}(\omega ) \big )$ that are collected in the vector $\varvec{{H}}\big ( \varvec{{\theta }}(\omega ) \big )$. They are orthogonal with respect to their expectation.

$$\begin{aligned} \Big \langle H_i\big ( \varvec{{\theta }}(\omega ) \big ),H_j\big ( \varvec{{\theta }}(\omega ) \big ) \Big \rangle = \big \langle H_i^2\big ( \varvec{{\theta }}(\omega ) \big ) \big \rangle \delta _{ij}. \end{aligned}$$

(9)

In the physical-stochastic product space $\varvec{\mathcal {W}}$ the basis functions will be represented as a tensor product of the set of spatial FEM basis in terms of the piece-wise defined Legendre polynomials and the set of stochastic Galerkin basis functions in terms of the Hermite polynomials

$$\begin{aligned} \varvec{{\varphi }}(\varvec{{x}},\omega )=\varvec{{N}}(\varvec{{x}})\otimes \varvec{{H}}\big ( \varvec{{\theta }}(\omega ) \big ), \end{aligned}$$

(10)

or component-wise

$$\begin{aligned} \varphi _{\varvec{{i}}}(\varvec{{x}},\omega )=\varphi _{kl}(\varvec{{x}},\omega )=N_k(\varvec{{x}})H_l\big ( \varvec{{\theta }}(\omega ) \big ), \end{aligned}$$

(11)

where $\varvec{{i}}$ is a multi-index containing index combinations $\varvec{{i}}=\{k,l\}$.

In this work we focus on nonlinear mechanical problems described by the differential operator

$$\begin{aligned}&\mathrm {D}(\varvec{{x}},\omega )\varvec{{u}}(\varvec{{x}},\omega ):=- \mathrm{Div}\,\mathbf {P}\big ( \varvec{{u}}(\varvec{{x}},\omega ) \big ),\nonumber \\&f(\varvec{{x}},\omega ):=\varvec{{f}}(\varvec{{x}},\omega ), \end{aligned}$$

(12)

where $\varvec{{u}}(\varvec{{x}},\omega )$ denotes the random displacement field, $\mathbf {P}$ is the Piola stress and $\varvec{{f}}(\varvec{{x}},\omega )$ denotes random body forces.

Projection onto the basis $\varphi _{\varvec{{i}}}(\varvec{{x}},\omega )$ leads to

$$\begin{aligned}&\varvec{{R}}=\varvec{{F}}^{ext}-\varvec{{F}}^{int} \rightarrow \varvec{{0}},\nonumber \\&\varvec{{F}}^{int}_{\varvec{{i}}}=\big \langle \mathbf {P} \cdot \mathrm{Grad}\, \varphi _{\varvec{{i}}}(\varvec{{x}},\omega ) \big \rangle ,\nonumber \\&\varvec{{F}}^{ext}_{\varvec{{i}}}=\big \langle \varvec{{f}}(\varvec{{x}},\omega ),\varphi _{\varvec{{i}}}(\varvec{{x}},\omega ) \big \rangle , \end{aligned}$$

(13)

where $\varvec{{R}}$ is the residual and $\langle ~,~\rangle$ is the inner product in $\varvec{\mathcal {W}}$. Here for the simplicity of exposition only the Dirichlet problem is considered.

An iterative procedure (Newton method) is used to find the solution.

$$\begin{aligned}&\varvec{{R}}^k(\varvec{{U}})+\left. \frac{\partial \varvec{{R}}^k}{\partial \varvec{{U}}}\right| _{\varvec{{U}}} \cdot \mathrm {d} \varvec{{U}}^k \rightarrow \varvec{{0}},\nonumber \\&\mathbf {K}^k:=-\left. \frac{\partial \varvec{{R}}^k}{\partial \varvec{{U}}}\right| _{\varvec{{U}}} ,\nonumber \\&\mathrm {d} \varvec{{U}}^k = \left[ \mathbf {K}^k \right] ^{-1} \varvec{{R}}^k ,\nonumber \\&\varvec{{U}}^{k+1}=\varvec{{U}}^{k}+\mathrm {d} \varvec{{U}}^k, \end{aligned}$$

(14)

where $\varvec{{U}}$ is a vector of coefficients in the finite approximation of (6)

$$\begin{aligned} \varvec{{U}}=\begin{bmatrix} \varvec{{u}}_1\\ \varvec{{u}}_2\\ \vdots \\ \varvec{{u}}_n \end{bmatrix}, \end{aligned}$$

The explicit expression for the stiffness matrix $\mathbf {K}$ is given as follows:

$$\begin{aligned} \mathbf {K}_{\varvec{{ij}}}=\left\langle \frac{\partial \mathbf {P}}{\partial \mathbf {F}} \overline{:}\left[ \mathrm{Grad}\, \varphi _{\varvec{{i}}}(\varvec{{x}},\omega ) \otimes \mathrm{Grad}\, \varphi _{\varvec{{j}}}(\varvec{{x}},\omega ) \right] \right\rangle , \end{aligned}$$

(15)

where $\overline{:}$ denotes the non-standard double contraction of a fourth order tensor $\mathbf {A}$ and a second order tensor $\mathbf {B}$ represented component-wise by $\big [ \mathbf {A}\overline{:}\mathbf {B}\big ]_{ik}=\big [\mathbf {A}\big ]_{ijkl}\big [\mathbf {B}\big ]_{jl}$.

Note that SFEM differs from common FEM only by the definition of the inner product over an extended (physical-stochastic) domain. However since additional stochastic dimensions are introduced the system size increases considerably.

For the evaluation of the integrals in the product space $\varvec{\mathcal {W}}$ we use Legendre–Gauss quadrature in the physical domain and Hermite–Gauss quadrature in the stochastic domain respectively, thus resulting in a very high accuracy.

4 Basic example: stochastic RVE

The effective properties of heterogeneous materials on the macro level can be obtained from the response of the underlying microstructure [7, 20]. Homogenization theory typically considers two separate scales: the macro-scale, which describes the continuum body, and the micro-scale characterized by a RVE. From scanning electron microscopy (Fig. 3) we often conclude that the microstructure is random. A realistic RVE model has to capture this uncertainty in the geometry of the microstructure.

Following [20] we study composites with (almost) periodic microstructures. As an example we initially consider for demonstration a RVE that includes only one circular particle (Fig. 4), however we do not restrict the position of the inclusion to the center of the RVE. Thus we here introduce only two random parameters $\xi _1(\omega )$ and $\xi _2(\omega )$ in terms of the elementary event $\omega$ with normal distribution describing the random position of the inclusion within the RVE.

Fig. 3

Scanning electron microscopy of an iron particle filled elastomer (Courtesy of Bastian Walter, chair of Applied Mechanics, University of Erlangen-Nuremberg)

Fig. 4

2D stochastic representative volume element with two random parameters describing the random position of the inclusion

For the sake of demonstration we consider the material behavior of the matrix and inclusion to be isotropic, compressible and hyperelastic. The Neo-Hookean energy potential $\varPsi$ for such material is given in the form:

$$\begin{aligned} \varPsi (\mathbf {F})=\frac{1}{2}\mu \left[ \mathbf {F}:\mathbf {F} - 3 - 2\ln J \right] +\frac{1}{2}\lambda \ln ^2 J, \end{aligned}$$

(16)

resulting in

$$\begin{aligned} \mathbf {P}=\frac{\partial \varPsi }{\partial \mathbf {F}}=\mu \mathbf {F} + \left[ \lambda \ln J -\mu \right] \mathbf {F}^{-t}, \end{aligned}$$

(17)

where $\mathbf {P}$ is the Piola stress, $\mathbf {F}$ is the deformation gradient, $\mathbf {F}^{-t}$ denotes the transposed inverse of $\mathbf {F}$, $J=\det {\mathbf {F}}$ is the Jacobian determinant, $\mu$ and $\lambda$ are Lamé parameters. The Lamé parameters are related to the shear modulus $G=\mu$ and the Poisson’s ratio $\nu =\frac{\lambda }{2[\lambda +\mu ]}$.

We model an inclusion as a jump in the elastic properties. Thereby we assume for simplicity a constant Poisson’s ratio $\nu =0.25$. Then only the shear modulus is a random field and is explicitly given as

$$\begin{aligned} G(\varvec{{x}},\omega )=G_m+\frac{1}{2}[G_i-G_m]\big [ 1-\tanh k z\big (\varvec{{x}},\omega \big )\big ], \end{aligned}$$

(18)

where $G_m$ and $G_i$ are shear moduli of the matrix and the inclusion, respectively; k is a coefficient of smoothness; $z\big (\varvec{{x}},\omega \big )$ is the level-set function, which indicates whether the material point with coordinates $\varvec{{x}}$ belongs to the matrix or to the inclusion ($z<0$: inclusion, $z>0$: matrix).

For the here considered simplest case of a circular inclusion with constant radius the definition of $z\big (\varvec{{x}},\omega \big )$ is the equation

$$\begin{aligned} z\big (\varvec{{x}},\omega \big )=r\left[ \sqrt{\frac{\left[ x_1-\xi _1(\omega ) \right] ^2}{r^2} + \frac{\left[ x_2-\xi _2(\omega ) \right] ^2}{r^2}}-1\right] , \end{aligned}$$

(19)

where r is the (deterministic) radius of the inclusion.

For convenience we represent the random parameters $\xi _1(\omega )$ and $\xi _2(\omega )$ in terms of the orthogonal, zero mean and unit variance Gaussian random variables (RV) $\theta _1(\omega )$ and $\theta _2(\omega )$.

$$\begin{aligned} \xi _1(\omega )= & {} m_1+\sigma _1\theta _1(\omega ) ,\nonumber \\ \xi _2(\omega )= & {} m_2+\sigma _2\theta _2(\omega ) , \end{aligned}$$

(20)

where $m_i$ and $\sigma _i$, respectively, are the mean value and the standard deviation (STD) of the random parameters.

If the inclusion intersects with the boundary of the RVE or even is outside, the volume fraction changes and affects the results. In order to reduce the influence of this effect we force the inclusion to be fully contained in the RVE for $\xi _i \in [-3\sigma _i,~~ 3\sigma _i]$ by choosing $\sigma _1=\sigma _2=0.15$ and $m_1=m_2=0$.

For the basic example please note that, unlike for the case of periodic boundary conditions, the homogenized stress is not deterministic when Dirichlet boundary conditions are applied.

Remark

It is strongly recommended to not use quadratic level-set functions like

$$\begin{aligned} \bar{z}\big (\varvec{{x}},\omega \big )=\big [ x_1-\xi _1(\omega ) \big ]^2 + \big [ x_2-\xi _2(\omega ) \big ]^2 -r^2, \end{aligned}$$

due to the fact that the smoothing level depends in this case not only on the parameter k but also on the radius of the inclusion.

In the case of the quadratic level-set function $\bar{z}\big (\varvec{{x}},\omega \big )$ the transition between the matrix and the inclusion gets smoother with a smaller inclusion radius (see Figs. 5 and 6). If the radius is variable (see Sect. 9) then simulations provide incorrect stress statistics. This results from the form of the level-set function $\bar{z}\big (\varvec{{x}},\omega \big )$ describing for a given values of $\xi _1(\omega ),~\xi _2(\omega )$ an elliptic paraboloid in the $x_1,x_2,\bar{z}\big (\varvec{{x}},\omega \big )$-space (see Fig. 7). Thus the values of $\bar{z}\big (\varvec{{x}},\omega \big )$ are related to the square of the distance between the point $(x_1,x_2)$ and the inclusion’s center. Therefore the transition between the matrix and the inclusion, as described by a hyperbolic tangent of the level-set function, is not uniform. In contrast the level-set function in the form (19) represents (if plotted versus the spatial coordinates) a cone-like surface (Fig. 8) and corresponds to the distance between the point $(x_1,x_2)$ and the inclusion’s boundary. Further it can be easily modified for the case of an elliptic inclusion and the case of multiple inclusions (see Sect. 9).

Fig. 5

Transition between the matrix and the inclusion defined for the sake of demonstration as $1-\tanh (k\bar{z})$ where $\bar{z}\big (\varvec{{x}},\omega \big )$ is the quadratic level-set function. Please note the different angles of plotted curves and different sizes of the transition region resulting from dependence of the smoothing level on the inclusion’s radius

Fig. 6

Transition between the matrix and the inclusion defined for the sake of demonstration as $1-\tanh (kz)$ where $z\big (\varvec{{x}},\omega \big )$ is the cone level-set function (19). Please note the equal angles of all curves in the diagram

Fig. 7

Quadratic level-set function versus spatial coordinates

Fig. 8

Level-set function of the form (19) versus spatial coordinates

Note that for the advanced examples in Sect. 9 the formulation of $z\big (\varvec{{x}},\omega \big )$ needs to be modified further.

In Stochastic FEM, due to its randomness, it is impossible to provide a mesh matching the geometry of the inclusion. We will thus rather use a discretization with a regular mesh due to its simplicity, efficiency and low computational costs. The heterogeneity in elastic properties is treated at the integration point level. As mentioned in [27, 45] this strategy yields a reasonable rate of convergence for the homogenized parameters of the RVE but suffers a slow rate of convergence for the quality of the stress distribution within the RVE. The possible alternative is to use the XFEM technique. However the traditional XFEM cannot be directly applied to the stochastic problem, whereas the special stochastic XFEM proposed in [29] drastically increases computational costs and requires further study (see discussion in Sect. 8).

The distribution of the shear modulus and an example for the regular FEM discretization are presented in Fig. 9 for a realization with $\xi _1(\omega )=\xi _2(\omega )=0$. To study accuracy and convergence we consider the case of uniaxial tension in horizontal direction with applied displacement $U=2.5 \,\%$ for the sake of demonstration.

Fig. 9

Shear modulus $G(\varvec{{x}})$ corresponding to the case of a centered inclusion ($k=30,~~r=0.4$)

5 Modification I: truncated RV and new integration rule

With a view to the proper description of uncertainties in the geometry we define the level-set function (19) and introduce it into the shear modulus (see Sect. 18). On the one hand due to the huge difference in elastic properties (i.e. the jump in the shear modulus) of matrix and inclusion the KLE suffers from the Gibbs phenomenon and causes numerical instabilities. However in contrast to the works in [10–13, 19, 21, 22, 30, 33–36, 43] the material properties are not exclusively given by their mean and covariance, but explicitly by their analytical expression (18), thus allowing us to avoid the KLE completely. Note in the case that no analytical expression for the random field is available the application of the KLE is possible and necessary. On the other hand the discontinuity in the shear modulus causes a sophisticated behavior of the solution field and requires to increase the number of basis functions in $\varvec{{H}}\big ( \varvec{{\theta }}(\omega ) \big )$. In the stochastic domain this results in the application of higher order Hermite polynomials and correspondingly in the need to increase the number of Gauss integration points.

By increasing the degree of Hermite polynomials the standard SFEM proves not stable due to numerical errors in the integrals’ evaluation. In the case of higher order Hermite polynomials, for example such as fifth order $H_5\big (\varvec{{\theta }}(\omega )\big )$, the evaluation of the stiffness matrix involves integrals of the polynomials $\left[ H_5\big (\varvec{{\theta }}(\omega )\big )\right] ^2$ and $\left[ H_5\big (\varvec{{\theta }}(\omega )\big )\right] ^4$. Weights of the Gauss-Hermite quadrature versus the integration point abscissa for the 1D-case are plotted in Fig. 10 and the values of the polynomials $\left[ H_5\big (\theta (\omega )\big )\right] ^2$ and $\left[ H_5\big (\theta (\omega )\big )\right] ^4$ evaluated at the integration points multiplied by the corresponding weights are plotted in Figs. 11 and 12. Theoretically, values which correspond to $|\theta (\omega )| \ge 3$ should have a negligible influence, however, they are strongly sensitive to computational errors and as becomes clear in Figs. 11 and 12, they are obviously dominating.

Fig. 10

Weights and integration points of the Gauss–Hermite quadrature

Fig. 11

Values of the Hermite polynomials raised to the power two at the integration points after multiplication by the weight factors

Fig. 12

Values of the Hermite polynomials raised to the power four at the integration points after multiplication by the weight factors

To avoid this problem we therefore propose to change the integration rule to one with integration points restricted to the range $[-3,3]$. This will be achieved by a change of the basis random variables. Please note that the Gauss integration rule, the probability density function of the basis random variable and the orthogonal polynomials are closely related and thus can not be changed independently. So, e.g. simple truncation of the integration range yields inconsistent solutions due to the fact, that the total probability mass gets less than one, axioms of the probability theory are not satisfied, and the Hermite polynomials are not orthogonal in a finite range. On the other hand the accurate numerical integration is performed by using the Gauss integration rule which is obtained uniquely from the support and the probability density function of the basic RV. Moreover the set of orthogonal polynomials required for both the generation of the Gauss integration rule and the Galerkin approximation in the SFEM framework also depends on the RV.

Thereby we introduce new random variables, which are a truncated version of the Gaussian RV with values only in the interval $[-3,3]$. From a physical point of view this truncation is reasonable because in the basis example values $|\theta (\omega )| \rightarrow \infty$ correspond to the inclusion lying partially or completely outside the RVE. From a mathematical point of view we perform a certain truncation anyway by evaluating integrals numerically. According to the well-known 3-sigma rule, most of the values drawn from a normal distribution lie within three standard deviations, i.e. in the range $[-3,3]$:

$$\begin{aligned} p=\int \limits _{-3}^3 f_{{\Theta }}\mathrm {d}\theta =0.9973. \end{aligned}$$

Outside the range $[-3,3]$ the new probability density function is set to zero, while its values inside the range $[-3,3]$ are obtained by a rescaling of the Gaussian density function $f_{{\Theta }}\rightarrow \frac{1}{p} f_{{\Theta }}$ (Fig. 13).

Fig. 13

Probability density functions for the normal Gaussian and truncated Gaussian RVs

The integral over the stochastic domain $\mathcal {S}$ in expression (3) includes the weight function $f_{{\Theta }}$ which is the joint probability density function (JPDF). Previously for the case of Gaussian RV we used the well-known Hermite–Gauss quadrature which fits exactly to this weight function. After the truncation of the JPDF we have to introduce a modified integration rule fitting this new weight function.

According to the framework given in [32] we can easily construct the Gauss integration rule from the set of polynomials which are orthogonal with respect to the current weight function. Orthogonal polynomials are computed using the Gram–Schmidt (orthogonalization) process. These new polynomials [limited Hermite polynomials denoted by $\varvec{{L}}\big (\theta (\omega )\big )$] are close to the Hermite polynomials $\varvec{{H}}\big (\theta (\omega )\big )$, but all their roots belong to the range $\theta (\omega )\in [-3,~3]$ (see Fig. 14).

Fig. 14

The first 12 limited Hermite polynomials $\varvec{{L}}\big (\theta (\omega )\big )$

According to [32] the nodes of the integration rule coincide with the roots of the orthogonal polynomials. Furthermore the weights can be obtained easily using the values and derivatives of these polynomials:

$$\begin{aligned} w_i^{(n)}=\frac{a_n}{a_{n-1}}\frac{\displaystyle \int \nolimits _{-3}^{3} L_{n-1}^2(\theta ) f_{{\Theta }} \mathrm {d}\theta }{\displaystyle \left. \frac{\mathrm {d}L_{n}(\theta )}{\mathrm {d}\theta }\right| _{\displaystyle \theta _i} L_{n-1}(\theta _i)}, \end{aligned}$$

(21)

where $w_i^{(n)}$ is the $i{\text {th}}$ weight factor of the n-point integration rule, $a_n$ is the coefficient of $\theta ^n$ in $L_n(\theta )$, $\theta _i$ is the $i{\text {th}}$ integration point [$i{\text {th}}$ root of the $L_n(\theta )$].

Fig. 15

Weights and integration points of the truncated Gauss–Hermite quadrature

Fig. 16

Values of the limited Hermite polynomials raised to the power two at the integration points after multiplication by the weight factors

Fig. 17

Values of the limited Hermite polynomials raised to the power four at the integration points after multiplication by the weight factors

Weights of the new Gauss quadrature versus integration points are plotted in Fig. 15 and values of the polynomials $\left[ L_5\big (\theta (\omega )\big )\right] ^2$ and $\left[ L_5\big (\theta (\omega )\big )\right] ^4$ evaluated at integration points and multiplied by the corresponding weights are plotted in Figs. 16 and 17.

Please note that the new integration points are much more densely distributed in the range of interest and that the maximum value of the polynomial in Fig. 17 is 75 times smaller than the correspondent value in Fig. 12 and belong to the range $[-3,3]$. Values of the integrals $\int _{-\infty }^{\infty }\left[ H_5(\theta )\right] ^2\mathrm {d}\theta$ and $\int _{-\infty }^{\infty }\left[ H_5(\theta )\right] ^4\mathrm {d}\theta$ differ dramatically by a ratio of 4000, in contrast values of the integrals of limited Hermite polynomials $\int _{-3}^{3}\left[ L_5(\theta )\right] ^2\mathrm {d}\theta$ and $\int _{-3}^{3}\left[ L_5(\theta )\right] ^4\mathrm {d}\theta$ obtained with the new quadrature display a ratio of 42. According to the fact that the integrals $\int _{-\infty }^{\infty }\left[ H_5(\theta )\right] ^2\mathrm {d}\theta$ and $\int _{-3}^{3}\left[ L_5(\theta )\right] ^2\mathrm {d}\theta$ result from the expression for the residual, while the integrals $\int _{-\infty }^{\infty }\left[ H_5(\theta )\right] ^4\mathrm {d}\theta$ and $\int _{-3}^{3}\left[ L_5(\theta )\right] ^4\mathrm {d}\theta$ appear only in the expressions for the stiffness matrix, their ratio is critically important for the stabilization of the numerical procedure.

Furthermore due to the fact that the limited Hermite polynomials are orthonormal in the domain $\mathcal {S}$ we may implement them together with the truncated Gaussian RV straightforwardly in the SFEM framework as outlined in the above. Thus the Galerkin basis functions in (10) can be rewritten in the modified form:

$$\begin{aligned} \varvec{{\varphi }}(\varvec{{x}},\omega )=\varvec{{N}}(\varvec{{x}})\otimes \varvec{{L}}\big ( \varvec{{\theta }}(\omega ) \big ). \end{aligned}$$

(22)

The proposed changes to the numerical procedure strongly increase the accuracy and stabilize the iterative procedure. Results of the simulation performed using the new basic random variables are collected in Chapter 7.

6 Modification II: non-polynomial basis

The displacement mean value and its standard deviation obtained using the SFEM show good agreement with the brute-force Monte-Carlo simulation performed with 961 uniformly distributed samples. Furthermore the mean value of the von Mises stress distribution in the RVE obtained with both methods are close (relative error measured based on Eq. (30) for the basic example is less than 0.7 %). However the SFEM has a deteriorated agreement with the MC simulation in the standard deviation of the von Mises stress. For more details see Figs. 27 and 29 that illustrates the relative error in the mean stress and relative error in the stress STD respectively. In addition, Figs. 31 and 32 depict the distribution of the stress STD over the volume of the RVE for the MC simulation and SFEM respectively.

This inaccuracy results from the oscillating behavior of the higher order polynomial interpolation at the edges of an interval in $\mathcal {S}$. Note that this phenomenon is known as Runge’s phenomenon and is likewise observed in Maclaurin series, polynomial interpolation with equispaced interpolation points and in asymptotic methods as the perturbation series, where it is treated e.g. using the rational approximation [2, 3, 5]. For the sake of illustration we plot the nodal displacements versus random variables $\theta _1(\omega )$ and $\theta _2(\omega )$ for the node number 96 with coordinates $(-0.375, 0.25)$. The random variable is interpreted as a position of the inclusions center. E.g. values of the random variables $\theta _1(\omega )=0$ and $\theta _2(\omega )=0$ correspond to the position of the inclusion exactly in the center of the RVE.

As a reference Fig. 18 shows the exact behavior of the displacement field as obtained using the Monte-Carlo method. Please note that the solution field is not smooth everywhere. The set of points, where the function is only $C^0-$continuous, is called weak discontinuity and is highlighted by the white curve.

In contrast Fig. 19 represents the approximate solution obtained using the stochastic finite element method with polynomial basis, where $\mathrm{card}\, \varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )=5$. Note the strong oscillations of the solution field (Runge’s phenomenon) visible at the sides and especially in the corners of the domain $\mathcal {S}$. The same behavior is demonstrated by the standard Hermite polynomials, thus this effect is general for all polynomial bases. Runge’s phenomenon is associated solely with the polynomial approximation, therefore we propose new non-polynomial basis functions instead of usual PCE techniques as used before.

Fig. 18

Nodal displacement of the node number 96 (Monte-Carlo simulation)

Fig. 19

Nodal displacement of the node number 96 (SFEM with polynomial basis, $\mathrm{card}\, \varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )=5$)

A polynomial basis has several important properties, but in many applications special bases such as trigonometric, hyperbolic, trigonometric-hyperbolic or quasi-polynomials can be advantageous. Here we select a few sets of independent functions, i.e. polynomials, trigonometric, exponential functions and their combinations from the generic expression:

$$\begin{aligned} g_k(\theta )=\theta ^{n_k}\exp \big ( [\alpha _k+i~\beta _k]\theta \big ), \end{aligned}$$

(23)

where $n_k$ is a non-negative integer number, $\alpha _k$ and $\beta _k$ are some real numbers and i is the imaginary unit.

Selected sequences are orthonormalized using the Gram-Schmidt process. These bases are then used in SFEM and compared with the Monte-Carlo simulation. Thereby the modified Gauss integration rule as introduced in the above is used.

A few examples of the selected sequences are shown in Fig. 20. The first sequence considered is the set of polynomials, which yields after orthonormalising the limited Hermite polynomials $\varvec{{L}}(\theta )$ as discussed in the above.

$$\begin{aligned} \varvec{{g}}(\theta ):=\{\theta ^n\}. \end{aligned}$$

(24)

In the next set we replace  $\theta ^n$ by $\theta ^{n-1}\sin \left( \frac{1}{2}\frac{\pi }{3}\theta \right)$   $\forall n\ge 1$.

$$\begin{aligned} \varvec{{g}}(\theta ):=\left\{ 1,~\sin \left( \frac{1}{2}\frac{\pi }{3}\theta \right) \theta ^{n-1}\right\} . \end{aligned}$$

(25)

This increases the accuracy of the solution by almost 20 % (see Table 1). We examined all options between sequence (25) and the trigonometric basis (26)

$$\begin{aligned} \varvec{{g}}(\theta ):=\left\{ \cos \left( n\frac{\pi }{3} \theta \right) ,~\sin \left( \frac{2n-1}{2}\frac{\pi }{3}\theta \right) \right\} . \end{aligned}$$

(26)

and observed that the sequence with lower values at the ends of the interval provides higher accuracy. Thereby the best results were obtained using the trigonometric functions in Eq. (26) denoted as Fourier basis $\varvec{{F}}\big (\theta (\omega )\big )$.

Fig. 20

Basic sequences used to obtain orthonormal bases in stochastic domain $\mathcal {S}$. a Equation (24), after orthonormalization yields $\varvec{{L}}\big ( \theta (\omega ) \big )$. b Equation (25). c Equation (26), after orthonormalization yields $\varvec{{F}}\big ( \theta (\omega ) \big )$. d Equation (27). e Equation (28), after orthonormalization yields $\varvec{{Q}}\big ( \theta (\omega ) \big )$. f Equation (29)

Table 1 Comparison relative error of different bases

However a disadvantage of the sequence (26) is the property

$$\begin{aligned} \left. \frac{\partial g(\theta )}{\partial \theta }\right| _{\pm 3}=0, \end{aligned}$$

which does not correspond to the function behavior in Fig. 18, thus making the approximation on the boundary inexact. To increase the accuracy we finally discuss the following sequences:

$$\begin{aligned} \varvec{{g}}(\theta ):= & {} \left\{ 1,~\cos \left( \frac{2n-1}{2}\frac{\pi }{3} \theta \right) ,~\sin \left( n\frac{\pi }{3}\theta \right) \right\} , \end{aligned}$$

(27)

$$\begin{aligned} \varvec{{g}}(\theta ):= & {} \left\{ 1,~\sin \left( \frac{2n-1}{2}\frac{\pi }{3}\theta \right) ,~\sin \left( \frac{2n-1}{2}\frac{\pi }{3}\theta \right) \theta \right\} , \end{aligned}$$

(28)

$$\begin{aligned} \varvec{{g}}(\theta ):= & {} \left\{ \cos \left( n\frac{\pi }{3} \theta \right) ,~\cos \left( n\frac{\pi }{3} \theta \right) \theta \right\} . \end{aligned}$$

(29)

From the proposed sequences the set (28) provides results very close to the sequence (26), but improves the approximation on the boundary. For the proposed model the basis involving the sequence in Eq. (28) [called quasi Fourier and denoted by $\varvec{{Q}}\big (\theta (\omega )\big )$] provides the most accurate results for the homogenized quantities. In contrast sequences (27) and (29) do not improve the method’s accuracy and are found inefficient.

Fig. 21

Nodal displacement of the node number 96 (SFEM with Fourier basis, $\mathrm{card}\, \varvec{{F}}\big (\varvec{{\theta }}(\omega )\big )=5$)

For comparison the nodal displacements at node 96 as obtained using five Fourier basis functions and five quasi Fourier basis functions are shown in Figs. 21 and 22 respectively.

Fig. 22

Nodal displacement of the node number 96 (SFEM with quasi Fourier basis, $\mathrm{card}\, \varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=5$)

7 Basic example: simulation results

The solution fields from the simulation with nine stochastic basis functions are compared with the Monte-Carlo simulation. The relative error is determined by:

$$\begin{aligned} A_{error}= \frac{\left| A_{SFEM}-A_{MC} \right| }{\max \nolimits _{\forall \varvec{{x}}\in \mathcal {D}} \left| A_{MC} \right| }, \end{aligned}$$

(30)

where $A_{error}$ is the relative error for the quantity A distributed over $\mathcal {D}$, $A_{SFEM}$ and $A_{MC}$ are solution fields obtained using SFEM and Monte-Carlo simulation, respectively.

Fig. 23

Mean displacement relative error, $\mathrm{card}\, \varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )=9$

Fig. 24

Mean displacement relative error, $\mathrm{card}\, \varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=9$

The error distribution of the displacement in x-direction and the true (Cauchy) von Mises stress in the case of uniaxial tension are plotted in Figs. 23, 24, 25, 26, 27, 28, 29, and 30. The Figs. 23, 25, 27, 29 correspond to the solution with nine limited Hermite polynomials [$\mathrm{card}\, \varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )=9$], and the Figs. 24, 26, 28, 30 correspond to the solution with 9 quasi Fourier basis functions [$\mathrm{card}\, \varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=9$].

Fig. 25

Displacement STD relative error, $\mathrm{card}\, \varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )=9$

Fig. 26

Displacement STD relative error, $\mathrm{card}\, \varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=9$

Fig. 27

Mean von-Mises stress relative error, $\mathrm{card}\, \varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )=9$

Fig. 28

Mean von-Mises stress relative error, $\mathrm{card}\, \varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=9$

Fig. 29

Von-Mises stress STD relative error, $\mathrm{card}\, \varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )=9$

Fig. 30

Von-Mises stress STD relative error, $\mathrm{card}\, \varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=9$

Table 1 summarizes the comparison of the relative errors of different bases. Please note that the first 4 columns correspond to the maximum value of the relative error over the domain $\mathcal {D}$, while the last two columns correspond to the homogenized quantities, which are volume averages over the domain $\mathcal {D}$.

The most important values in this study are the stress mean value, which will be used to obtain the macroscopic tangent stiffness, and the stress standard deviation, which shows fluctuations of the mechanical properties in the heterogeneous material with random microstructure. Figures 29 and 30 show the stress standard deviation for both types of basis functions. Note that the polynomial basis has a two times lower accuracy than the quasi Fourier basis.

Figures 31, 32 and 33 represent the distribution of the von Mises stress standard deviation obtained from the Monte-Carlo simulation, SFEM with limited Hermite polynomials and SFEM with quasi Fourier basis, respectively. The quasi Fourier basis has obviously a better agreement with the results from the Monte-Carlo simulation as compared to the polynomial basis $\varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )$.

Fig. 31

Von-Mises stress STD, Monte-Carlo simulation

Fig. 32

Von-Mises stress STD, $\mathrm{card}\, \varvec{{L}}\big (\varvec{{\theta }}(\omega )\big )=9$

Note that the bases $\varvec{{Q}}\big (\theta (\omega )\big )$ and $\varvec{{F}}\big (\theta (\omega )\big )$ compared to the polynomial basis $\varvec{{L}}\big (\theta (\omega )\big )$ both provide a relative error 2.7 times less in mean displacements, 1.5 times less in displacement STD, 2.75 times less in von Mises stress mean value, and two times in von Mises stress STD. Comparing the homogenized von Mises stress mean value the Fourier and quasi Fourier bases provide a three times higher accuracy. Moreover the relative error in homogenized stress STD is 1.7 times less in the simulation with Fourier basis and 2.6 times less with the quasi Fourier basis.

Fig. 33

Von-Mises stress STD, $\mathrm{card}\, \varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=9$

Fig. 34

Mean Homogenized Stress convergence

Table 2 Relative error of the SFEM with Fourier basis

Table 3 Relative error of the SFEM with Quasi Fourier basis

Convergence is studied for the cases of Fourier $\varvec{{F}}\big (\theta (\omega )\big )$ and quasi Fourier $\varvec{{Q}}\big (\theta (\omega )\big )$ bases. With increasing number of basis functions the results obtained with the SFEM are converging to the values obtained with the Monte-Carlo simulation. The rate of convergence is shown in Fig. 34 for the mean value of homogenized stress and in Fig. 35 for the standard deviation of the homogenized stress. Detailed information about the relative errors in displacement and stresses as well as in homogenized quantities are presented in Tables 2 and 3 for the Fourier and quasi Fourier bases respectively.

Fig. 35

Homogenized Stress STD convergence

Figure 35 demonstrates the main advantage of the quasi Fourier basis in comparison to the Fourier basis: the standard deviation of the homogenized stress is 1.5 times closer to the exact solution. Another interesting fact is that the solution with an even number of basis functions is inaccurate in terms of the homogenized stress standard deviation (because we start to count basis functions from zero, functions with an even number are odd).

Please note that the quasi Fourier basis is strongly advantageous in the case of a small number of basis functions. Thus for the case of $\mathrm{card}\, \varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=3$ and $\mathrm{card}\,\varvec{{F}}\big (\varvec{{\theta }}(\omega )\big )=3$ the quasi Fourier basis proves three times more accurate. For the case of $\mathrm{card}\,\varvec{{Q}}\big (\varvec{{\theta }}(\omega )\big )=5$ and $\mathrm{card}\,\varvec{{F}}\big (\varvec{{\theta }}(\omega )\big )=5$ the accuracy gain is around 2 times, and with an increase of the cardinality up to 9 it is deteriorating to only 1.5 times. With the increase of the number of Fourier basis functions the size of the area with incorrect approximation is decreasing rapidly and their influence according to the small weights of the side integration points is getting negligible. Thus for a high number of basis function the advantage of the quasi Fourier basis will be neglected as compared to the Fourier basis.

Fig. 36

Nodes selected to visualize the nodal displacement versus random variables obtained using the Monte-Carlo method

Fig. 37

Nodal displacement of the central node (number 145)

8 Discussion on weak discontinuities

By changing the integration rule and the stochastic basis we stabilize convergence and strongly increase the accuracy. But the comparison with the Monte-Carlo simulation shows some disagreement in the stress standard deviation. It is definitely lower for the homogenized stresses (which are the main point of interest in this study) but still quite high. This inaccuracy results from a weak discontinuity (discontinuous directional derivative) in displacements (Fig. 18) and a strong discontinuity (discontinuous function) in stresses which cannot be described properly with smooth continuous basis functions.

There is a set of techniques to solve problems with discontinuities—XFEM, GFEM, and Discontinuous Galerkin. But their implementation is very difficult in the current context, because we are restricted in the choice of integration points. A detailed discussion is as follows:

For the sake of illustration we plot the nodal displacements versus random variables $\theta _1(\omega )$ and $\theta _2(\omega )$ for the central node 145 and several offset nodes: node number 19 with coordinates $(-0.875, -0.875)$, node number 96 (Fig. 18) with coordinates $(-0.375, 0.25)$ and node number 563 with coordinates $(0.0625,-0.5)$ shown in Fig. 36. Figures 18, 37, 38 and 39 show the exact behavior of the displacement field as obtained using the Monte-Carlo method.

The white curves in Figs. 18, 37 and 39 highlight the weak discontinuity. This discontinuity forms an elliptic shape and occupies different regions for different nodes. It results from the jump in stiffness between matrix and inclusion. For example, the corner node 19 at $(-0.875,-0.875)$ displays no discontinuity because the matrix-inclusion interface does not reach this node in the simulation (Fig. 38).

Fig. 38

Nodal displacement of the node number 19

Fig. 39

Nodal displacement of the node number 563

On the one hand it is a well-known fact that discontinuous Galerkin (as well as XFEM) requires independent integration over the domains separated by the discontinuity. On the other hand in order to obtain a consistent solution we need a uniform integration rule for each nodal variable. The analogy is obtained if we imagine that our stochastic dimension is time. In dynamic problems in the case of implicit time integration we typically have to avoid the use of different time steps for different nodes. Exactly the same conclusions can be drawn here. Each integration point in the stochastic domain corresponds to a specific model configuration (sample). Taking different integration points we obtain solutions for absolutely different models or rather realizations.

Fig. 40

Geometrical uncertainties for the advanced examples (b)–(g)

But due to the fact that the discontinuity appearing in our problem is unique for each node, it is impossible to introduce such unique integration rule, which will fit all configurations for all nodal variables.

However this does not mean, that the XFEM integration into the SFEM framework is impossible. There have been some recent developments in this field [29]. However the form of the enrichment, the high dimensional integration rules for the enriched elements and the division of the elements in the high dimensional tetrahedrons are non-trivial and require further development.

Thus we have only two options to treat problems with discontinuities. One way is to change the coefficient k in Eq. (18). This makes the distribution of the shear modulus more smooth and strongly increases the accuracy of the method (no weak discontinuity appears anymore). But a small value of k corresponds to a large transition region and very smooth shear modulus distribution that can no longer be considered an inclusion. Due to the fact that the physical model is affected, this option should be avoided if possible.

Another option is to increase the number of basis functions. It doesn’t change the physical model, but increases the size of the stiffness matrix.

With the increase of the number of basis function the SFEM results are converging to the Monte-Carlo simulation. Figs. 34 and 35 illustrate the convergence of the standard SFEM with Hermite polynomial and modified SFEM with Fourier and quasi Fourier basis functions. Please note that the number of basis functions, as in usual FEM, is restricted by the computer capacity.

One has to notice that increasing the number of basis functions strongly increases the size of the problem. If d is the number of degrees of freedom of the deterministic FE model, s is the number of the random parameters, n is the number of the basis functions in the stochastic domain, then the number of degrees of freedom of the stochastic FE model D can be estimated as:

$$\begin{aligned} D=d \, n^s. \end{aligned}$$

In the proposed model 10 basis functions result in a 100 times larger stiffness matrix. Thus this method sets higher requirements to the computational capacity, in particular to the memory. However, it is still less time consuming than the Monte-Carlo simulation. Please note that the increase of the stochastic dimensions’ number s results in an exponential increase of the problem size D. This phenomenon is well-known as the curse of dimensionality.

9 Advanced examples

In this section we discuss several advanced numerical examples for different cases of geometrical uncertainties. In contrast to the previous basic example in all advanced examples we apply periodic boundary conditions to the RVE, which are commonly considered to be the most accurate. The applied macroscopic deformation gradient describes a 25 % uniaxial stretch

$$\begin{aligned} \mathrm {\overline{\mathbf {F}}}~ \widehat{=}\begin{bmatrix} 1.25&~~ 0\\ 0&~~ 1 \end{bmatrix}, \end{aligned}$$

which clearly requires a geometrically nonlinear formulation.

We perform a parameter study for the following cases (see Figs. 4 and 40):

• (a) The inclusion is (as in the previous study) circular with area A. The source of the uncertainties is the randomness in position.

• (b) A centered elliptic inclusion with given area A. The orientation of the major axis is random and is given by the angle $\varphi (\omega )$ with values $0 \le \varphi (\omega ) \le \frac{\pi }{2}$.

• (c) A centered elliptic inclusion with given area A and axes parallel to the coordinate axes. The random parameter $\rho (\omega )$ with values $0.5 \le \rho (\omega )\le 2$ defines the ratio between the radii of the ellipse: $\rho (\omega )=\frac{r_1}{r_2}$.

• (d) A centered elliptic inclusion with random orientation of the axes and random ratio between the radii. The level-set function includes two random parameters with values $0 \le \varphi (\omega ) \le \frac{\pi }{2}$ and $0.5 \le \rho (\omega )\le 2$.

• (e) A centered circular inclusion with random radius $0.28\le r(\omega ) \le 0.52$.

• (f) Two equal circular inclusions with total area A and with their centers on the diagonal of a rectangular RVE. The distance between the inclusion’s centers and the center of the RVE is described by the random parameter $e(\omega )$ such that $0.125\le e(\omega ) \le 0.575$.

• (g) Two equal circular inclusions with total area A and with their centers on the line l passing through the center of the RVE. The distance between the inclusion’s centers and the center of the RVE is described by the random parameter $e(\omega )$:  $0.125\le e(\omega ) \le 0.575$, the angle between the line l and the x-axis is $\varphi (\omega )$ which belongs to the interval $[0,\frac{\pi }{2}]$.

The level-set function for the example (a) has already been introduced in Chap. 4.

In example (b) the level-set function for an elliptic inclusion is defined as

$$\begin{aligned}&\widetilde{x}_1=x_1\cos \big (\varphi (\omega )\big )+x_2 \sin \big (\varphi (\omega )\big ),\nonumber \\&\widetilde{x}_2=-x_1\sin \big (\varphi (\omega )\big )+x_2\cos \big (\varphi (\omega )\big ),\nonumber \\&z\big (\varvec{{x}},\omega \big )=\sqrt{r_1 r_2}\left[ \sqrt{\frac{\widetilde{x}_1^2}{r_1^2}+\frac{\widetilde{x}_2^2}{r_2^2}}-1 \right] . \end{aligned}$$

(31)

For the case (c) the level-set function has to satisfy the following restrictions:

$$\begin{aligned} r_1 r_2=\frac{A}{\pi }=\mathrm {const},\quad \frac{r_1}{r_2}=\rho (\omega ), \end{aligned}$$

resulting in

$$\begin{aligned}&r_1^2=\rho (\omega )\frac{A}{\pi },\nonumber \\&r_2^2=\frac{A}{\rho (\omega )~\pi },\nonumber \\&z\big (\varvec{{x}},\omega \big )=\sqrt{\frac{A}{\pi }}\left[ \sqrt{\frac{x_1^2}{r_1^2}+\frac{x_2^2}{r_2^2}}-1 \right] . \end{aligned}$$

(32)

In the case (d) we have a combination of the two previous cases:

$$\begin{aligned}&r_1^2=\rho (\omega )\frac{A}{\pi },\nonumber \\&r_2^2=\frac{A}{\rho (\omega )~\pi },\nonumber \\&\widetilde{x}_1=x_1\cos \big (\varphi (\omega )\big )+x_2\sin \big (\varphi (\omega )\big ),\nonumber \\&\widetilde{x}_2=-x_1\sin \big (\varphi (\omega )\big )+x_2\cos \big (\varphi (\omega )\big ),\nonumber \\&z\big (\varvec{{x}},\omega \big )=\sqrt{\frac{A}{\pi }}\left[ \sqrt{\frac{\widetilde{x}_1^2}{r_1^2}+\frac{\widetilde{x}_2^2}{r_2^2}}-1 \right] . \end{aligned}$$

(33)

For the case (e) the level-set function is represented by

$$\begin{aligned} z\big (\varvec{{x}},\omega \big )=r(\omega )\left[ \sqrt{\frac{x_1^2}{r(\omega )^2}+\frac{x_2^2}{r(\omega )^2}}-1\right] . \end{aligned}$$

(34)

For the two next examples we have to define separate level-set functions for each inclusion. In the case (f) they are given by

$$\begin{aligned}&\varphi =\frac{\pi }{4},\nonumber \\&\widetilde{x}_{11}=x_1-e(\omega )\cos (\varphi ),\nonumber \\&\widetilde{x}_{12}=x_1+e(\omega )\cos (\varphi ),\nonumber \\&\widetilde{x}_{21}=x_2-e(\omega )\sin (\varphi ),\nonumber \\&\widetilde{x}_{22}=x_2+e(\omega )\sin (\varphi ),\nonumber \\&z_1\big (\varvec{{x}},\omega \big )=r\left[ \sqrt{\frac{\widetilde{x}_{11}^2}{r^2}+\frac{\widetilde{x}_{21}^2}{r^2}}-\sqrt{\frac{1}{2}}\right] ,\nonumber \\&z_2\big (\varvec{{x}},\omega \big )=r\left[ \sqrt{\frac{\widetilde{x}_{12}^2}{r^2}+\frac{\widetilde{x}_{22}^2}{r^2}}-\sqrt{\frac{1}{2}}\right] . \end{aligned}$$

(35)

The case (g) differs from this equation only in the value of $\varphi$ which is not anymore constant but represents the random parameter $\varphi (\omega )$.

However two separate level-set functions cannot directly be substituted into Eq. (18). We need some trick to merge them in one, and the resulting level-set function has to satisfy the following conditions:

$$\begin{aligned} \{z\big (\varvec{{x}},\omega \big )<0\}= & {} \bigcup _i\{z_i\big (\varvec{{x}},\omega \big )<0\},\nonumber \\ \{z\big (\varvec{{x}},\omega \big )>0\}= & {} \bigcap _i\{z_i\big (\varvec{{x}},\omega \big )>0\},\nonumber \\ \{z\big (\varvec{{x}},\omega \big )=0\}= & {} \bigcup _i\{z_i\big (\varvec{{x}},\omega \big )=0\}\setminus \bigcup _j\{z_j\big (\varvec{{x}},\omega \big )<0\}.\nonumber \\ \end{aligned}$$

(36)

Fig. 41

Merged level-set function versus spatial coordinates

Fig. 42

Homogenized stress versus random variables $\varvec{{\theta }}(\omega )$, example (a). Observe the comparable small STD due to the insensitivity of the result on the position of the inclusion if periodic boundary conditions are applied

Fig. 43

Homogenized stress versus random variables $\varvec{{\theta }}(\omega )$, example (b)

Fig. 44

Homogenized stress versus random variables $\varvec{{\theta }}(\omega )$, example (c)

Fig. 45

Homogenized stress versus random variables $\varvec{{\theta }}(\omega )$, example (d)

Fig. 46

Homogenized stress versus random variables $\varvec{{\theta }}(\omega )$, example (e)

Fig. 47

Homogenized stress versus random variables $\varvec{{\theta }}(\omega )$, example (f)

Fig. 48

Homogenized stress versus random variables $\varvec{{\theta }}(\omega )$, example (g)

Table 4 Comparison of the SFEM with Fourier basis and the Monte-Carlo simulation for advanced examples

This statement can be read as follows: if the region is occupied by at least one inclusion, i.e. at least one level-set function in this region has values less than zero, the resulting level-set function in this region has to be negative. In the case that all level-set functions are positive in some region, i.e. no one level-set function indicates an inclusion, the region belongs to the matrix and the resulting level-set function has to be positive. The third condition states that the curve $z\big (\varvec{{x}},\omega \big )=0$ (in other words the inclusion boundary) cannot cross the region inside another inclusion.

Please note that the earlier discussed formulation of the level-set function posseses the important property that all its values are proportional to the shortest distance from the point $(x_1,x_2)$ to the inclusion’s boundary (see Sect. 4). The level-set function obtained by merging is expected to keep this property thereby necessitating additional restrictions on the merging procedure.

The merging of two level-set functions satisfying restrictions (36) is depicted in Fig. 41. In Eq. (37) we represent the closed form expression defining the merging of two level-set functions into only one:

$$\begin{aligned} z\big (\varvec{{x}},\omega \big )=\min _{\forall \varvec{{x}}\in \mathcal {D}} \Big (z_1\big (\varvec{{x}},\omega \big ), z_2\big (\varvec{{x}},\omega \big )\Big ). \end{aligned}$$

(37)

This expression can be easily extended to the case of multi-inclusion level-set functions:

$$\begin{aligned} z\big (\varvec{{x}},\omega \big )=\min _{\forall \varvec{{x}}\in \mathcal {D}} \Big (z_1\big (\varvec{{x}},\omega \big ),~\ldots ~ z_n\big (\varvec{{x}},\omega \big )\Big ). \end{aligned}$$

For all examples we use the Fourier basis (26) introduced in Chap. 6. The quasi Fourier basis is advantageous only for example (a) due to the particular form of the solution fields. The Fourier basis is more general and provides very accurate results for the models (b)–(g), so there is no need to construct special and more sophisticated bases. In examples (b), (c), (e), (f) we introduce only one random parameter and the number of basis functions in the stochastic domain is set to 12 ($\mathrm{card}\, \varvec{{F}}\big (\varvec{{\theta }}(\omega )\big )=12$). For the sake of reducing computational effort we use in examples (a), (d) and (g) which require two random parameters only 9 basis functions for each stochastic dimension [$\mathrm{card}\, \varvec{{F}}\big (\varvec{{\theta }}(\omega )\big )=9$].

Please note that due to the periodic boundary conditions the position of the inclusion does not matter, thus as a verification of our method the standard deviation of the homogenized stress in example (a) has to be zero. The absolute values of the stress standard deviation for this example in both SFEM and Monte-Carlo simulations are much smaller than in the other examples and result from the method’s accuracy. Since small numbers are subtracted and divided, this yields a comparable high relative error.

The homogenized von Mises stresses versus the random variables are presented in Figs. 42, 43, 44, 45, 46, 47 and 48. The colors of the points correspond to the weights (probabilities) of these points while computing the mean value and the standard deviation. Please note the very good agreement between the Monte-Carlo simulation and the SFEM results in all examples, however with the exception of example (a). Please keep in mind that the high relative error in example (a) results from the small STD of the homogenized stress and not from the method’s inaccuracy. More detailed information is provided in Table 4.

10 Summary & conclusions

In the present work we apply the SFEM for the computational homogenization of heterogeneous materials with geometrical uncertainties in the microstructure. To this end, we introduce a basic example for a stochastic RVE including uncertainties in the geometry which result from the random position of an inclusion.

The matrix–inclusion interface is modeled as a jump in the elastic properties of the media described in terms of a random level-set function. Thus the geometrical uncertainties result in an expression for the shear modulus presenting a random field. For convenience random parameters are presented in terms of Gaussian random variables.

The so defined basic example is used to study the method’s accuracy and to compare different modifications proposed in this paper.

The standard SFEM formulation proves unstable due to the Gibbs phenomenon and the numerical errors resulting from the standard integration scheme. With a view to avoid the numerical instability we refuse from the KLE and introduce new random variables which are a truncated version of the standard Gaussian RVs. The correspondent set of polynomials which are orthogonal with respect to the new (truncated) probability density function (called limited Hermite polynomials) and a new Gauss integration rule are proposed.

This change of the variables and integration rule stabilizes the solution especially in the case of a high number of basis functions.

The standard polynomial basis in the stochastic space $\varvec{\mathcal {Q}}$ known as the PCE suffers from the Runge’s phenomenon—strong oscillation of the solution field on the edges of an interval. In order to avoid the Runge’s phenomenon we also study non-polynomial bases.

The highest accuracy in comparison to the brute-force Monte-Carlo simulation is obtained with the Fourier basis which provides 2–3 times higher accuracy in displacements and stresses, 3 times higher accuracy in mean value of the homogenized stress and 1.5 times higher accuracy in the standard deviation of the homogenized stress.

In particularly for the basic example of the stochastic RVE we present a further improved basis denoted as quasi Fourier basis. This basis fits much better to the behavior of the displacement field on the edges of the stochastic domain $\mathcal {S}$ resulting in ${\approx \!{2.5}}$ lower relative error in the stress standard deviation in comparison to the polynomial basis and in ${\approx \!1.5}$ times lower relative error in comparison to the Fourier basis (Table 1 and Fig. 35). All simulations are performed with different number of stochastic basis functions (a convergence study is presented in Figs. 34 and 35). By the increase of the number of basis functions the error decreases as the geometric progression with ratio 2. The quasi Fourier basis is found strongly advantageous for a low number of basis functions. With the increase of the number of basis functions from 3 to 9 the gain in accuracy of the quasi Fourier basis in comparison to the Fourier basis deteriorates from 3 times to 1.5 times. All results are collected in the Tables 1, 2 and 3.

The influence of weak discontinuities and various potentially possible techniques for their treatment are discussed.

Additionally seven advanced examples for a stochastic RVE with periodic boundary conditions and different types of geometrical uncertainties were introduced to study the accuracy of the method on a wide range of problems. The absolute value of the error in all examples is less than 1e$-$4, the relative error in comparison to the brute-force Monte-Carlo simulation is less than 7e$-$3 for the standard deviation of the homogenized stress and less than 5e$-$4 for the mean value of the homogenized stress.

Thus the SFEM in combination with the here proposed modifications was proven highly accurate and efficient in the application to computational homogenization of nonlinear heterogeneous materials with random microstructure.