Pizza and 2-Structures

Abstract

Let ${\mathcal {H}}$ be a Coxeter hyperplane arrangement in n-dimensional Euclidean space. Assume that the negative of the identity map belongs to the associated Coxeter group W. Furthermore assume that the arrangement is not of type $A_1^n$. Let K be a measurable subset of the Euclidean space with finite volume which is stable by the Coxeter group W and let a be a point such that K contains the convex hull of the orbit of the point a under the group W. In a previous article the authors proved the generalized pizza theorem: that the alternating sum over the chambers T of ${\mathcal {H}}$ of the volumes of the intersections $T\cap (K+a)$ is zero. In this paper we give a dissection proof of this result. In fact, we lift the identity to an abstract dissection group to obtain a similar identity that replaces the volume by any valuation that is invariant under affine isometries. This includes the cases of all intrinsic volumes. Apart from basic geometry, the main ingredient is a theorem of the authors where we relate the alternating sum of the values of certain valuations over the chambers of a Coxeter arrangement to similar alternating sums for simpler subarrangements called 2-structures introduced by Herb to study discrete series characters of real reduced groups.

1 Introduction

The 2-dimensional pizza theorem is the following result: Given a disc in the plane, choose a point on this disc and cut the disc by 2k equally spaced lines passing through the point, where $k \ge 2$. The alternating sum of the areas of the resulting slices is then equal to zero. This was first proved by Goldberg [10]. Frederickson gave a dissection proof [9] based on dissection proofs of Carter-Wagon in the case $k=2$ (see [5]) and of Allen Schwenk (unpublished) in the cases $k=3,4$. Frederickson deduced dissection proofs of a similar sharing result for the pizza crust and of the so-called calzone theorem, which is the analogue of the pizza theorem for a ball in ${\mathbb {R}}^3$ that is cut by one horizontal plane and by 2k equally-spaced vertical planes all meeting at one point in the ball.

To generalize the pizza problem, consider a finite central hyperplane arrangement ${\mathcal {H}}$ in ${\mathbb {R}}^n$ and fix a base chamber of this arrangement. Each chamber T has a sign $(-1)^{T}$ determined by the parity of the number of hyperplanes separating it from the base chamber. If K is a measurable subset of ${\mathbb {R}}^n$ of finite volume, what can we say about the pizza quantity $\sum _T (-1)^T{{\,\textrm{Vol}\,}}(T\cap K)$, where the sum runs over all the chambers T of ${\mathcal {H}}$? The original pizza theorem is the case where $n=2$, ${\mathcal {H}}$ has the type of the dihedral arrangement $I_2(2k)$ and K is a disc containing the origin. The calzone theorem is the case where $n=3$, ${\mathcal {H}}$ has the type of the product arrangement $I_2(2k)\times A_1$ and K is a ball containing the origin.

The following generalization of the pizza and calzone theorems was proved in [7, Thm. 1.2] by analytic means. We recently learned that Brailov had proved independently this result in the case of a ball for the type $B_{n}$ arrangement using similar methods [4].

Theorem 1.1

(Ehrenborg–Morel–Readdy) Let ${\mathcal {H}}$ be a Coxeter arrangement with Coxeter group W that contains the negative of the identity map, denoted by $-{{\,\textrm{id}\,}}$. Assume that ${\mathcal {H}}$ is not of type $A_{1}^{n}$. Let K be a set of finite measure that is stable by the group W. Then for every point $a\in {\mathbb {R}}^n$ such that K contains the convex hull of $\{w(a) : w \in W\}$, we have

$$\begin{aligned} \sum _T (-1)^T{{\,\textrm{Vol}\,}}(T\cap (K+a))=0. \end{aligned}$$

The proof of this result uses an expression for $\sum _T(-1)^T{{\,\textrm{Vol}\,}}(T\cap (K+a))$ as an alternating sum of pizza quantities over subarrangements of ${\mathcal {H}}$ of the form $\{e_1^\perp ,\ldots ,e_n^\perp \}$ with $(e_1,\ldots ,e_n)$ an orthonormal basis of ${\mathbb {R}}^n$, in other words, subarrangements of type $A_1^n$.

In the paper [6], we study a different sum $\sum _T (-1)^T\nu ({\overline{T}})$, where $\nu$ is a valuation defined on closed convex polyhedral cones of ${\mathbb {R}}^n$ that takes integer values. Under the same condition that ${\mathcal {H}}$ is a Coxeter arrangement, we rewrite this quantity as an alternating sum of similar quantities for certain subarrangements of ${\mathcal {H}}$ that are products of rank 1 and rank 2 arrangements [6, Thm. 3.2.1], and then deduce an expression for it. These subarrangements, called 2-structures, were introduced by Herb [13] to study characters of discrete series of real reductive groups. In fact, the identity of [6, Thm. 3.2.1] is valid for any valuation and its proof uses only basic properties of Coxeter systems and closed convex polyhedral cones.

In this paper we use the setting of 2-structures and [6, Cor. 3.2.4] (recalled in Theorem 2.5) to obtain a dissection proof of the higher-dimensional pizza theorem of [7, Thm. 1.2] that is independent of the results and methods of [7]:

Theorem 1.2

(Abstract pizza theorem; see Theorem 3.5.) With the notation and hypotheses of Theorem 1.1, we have

$$\begin{aligned} \sum _{T}(-1)^T[{\overline{T}}\cap (K+a)] = \sum _{T}(-1)^T[T\cap (K+a)] = 0, \end{aligned}$$

where the brackets denote classes in the abstract dissection group of Definition 3.1.

As we take into account lower-dimensional sets when defining our abstract dissection group, this result implies generalizations of the higher-dimensional pizza theorem to all the intrinsic volumes when K is convex.

The idea of the proof of Theorem 1.2 is the following: by expanding the expression using 2-structures, we can reduce to a sum where each term is a similar expression for an arrangement that is a product of arrangements of types $A_1$ and $I_2(2^k)$. We then adapt the dissection proof of Frederickson to an arrangement of type $I_2(2m)\times {\mathcal {H}}'$. We also explain how to keep track of lower-dimensional regions of the dissection. If our product arrangement contains at least one dihedral factor, then its contribution is zero, and we immediately get a dissection proof of the result. However, if all the product arrangements that appear are of type $A_1^n$, then their individual contributions are not zero. We need one extra step in the proof to show that the contributions cancel. This uses a slight refinement of the Bolyai–Gerwien Theorem explained in Sect. 4.

An interesting point to note is that the shape of the pizza plays absolutely no role in this proof, as long as it has the same symmetries as the arrangement and contains the convex hull of $\{w(a) : w \in W\}$. In particular, we no longer need to assume that it is measurable and of finite volume.

The plan of the paper is as follows. Section 2 contains a review of 2-structures and of the results from [6] that we will need. Section 3 contains the statement and proof of the abstract pizza theorem (Theorem 3.5), and Sect. 4, as we already mentioned, contains a Bolyai–Gerwien type result that is needed in the proof of the abstract pizza theorem.

Let us mention some interesting questions that remain open:

• (1) The paper [7] proves the pizza theorem for more general arrangements (the condition is that the arrangement ${\mathcal {H}}$ is a Coxeter arrangement and that the number of hyperplanes is greater than the dimension n and has the same parity as that dimension), but only in the case of the ball; see [7, Thm. 1.1]. Is it possible to give a dissection proof of this result?

• (2) Mabry and Deiermann [19] show that the two-dimensional pizza theorem does not hold for a dihedral arrangement having an odd number of lines. More precisely, they determine the sign of the quantity $\sum _T(-1)^T{{\,\textrm{Vol}\,}}(T\cap K)$, where K is a disc containing the origin, and show that it vanishes if and only if the center of K lies on one of the lines. Their methods are analytic. As far as we know, there exists no dissection proof of this result either. The higher-dimensional case where ${\mathcal {H}}$ is a Coxeter arrangement and the number of its hyperplanes does not have the same parity as n also remains wide open.

2 Review of 2-Structures and of the Basic Identity

Let V be a finite-dimensional real vector space with an inner product $(\cdot ,\cdot )$. For every $\alpha \in V$, we denote by $H_\alpha$ the hyperplane $\alpha ^\perp$ and by $s_\alpha$ the orthogonal reflection in the hyperplane $H_\alpha$.

We say that a subset $\Phi$ of V is a normalized pseudo-root system if:

• (a) $\Phi$ is a finite set of unit vectors;

• (b) for all $\alpha ,\beta \in \Phi$, we have $s_\beta (\alpha )\in \Phi$ (in particular, taking $\alpha =\beta$, we get that $-\alpha \in \Phi$).

Elements of $\Phi$ are called pseudo-roots. The rank of $\Phi$ is the dimension of its span.

We call such objects pseudo-root systems to distinguish them from the (crystallographic) root systems that appear in representation theory. If $\Phi '$ is a root system then the set $\Phi ={\{\alpha / {\Vert \alpha \Vert } : \alpha \in \Phi '\}}$ is a normalized pseudo-root system. Not every normalized pseudo-root system arises in this manner; see for instance the pseudo-root systems of type $H_{3}$ and $H_{4}$.

We say that a normalized pseudo-root system $\Phi$ is irreducible if, whenever $\Phi =\Phi _1\sqcup \Phi _2$ with $\Phi _1$ and $\Phi _2$ orthogonal, we have either $\Phi _1=\varnothing$ or $\Phi _2=\varnothing$. Every normalized pseudo-root system can be written uniquely as a disjoint union of pairwise orthogonal irreducible normalized pseudo-root systems. Irreducible normalized pseudo-root systems are classified: they are in one of the infinite families $A_n$ ($n\ge 1$), $B_n/C_n$ ($n\ge 2$),¹$D_n$ ($n\ge 4$), $I_2(m)$ ($m\ge 3$) or one of the exceptional types $E_6$, $E_7$, $E_8$, $F_4$, $H_3$ or $H_4$, with types $I_2(3)$ and $A_2$ isomorphic, as well as types $I_2(4)$ and $B_2$. (See [12, Chap. 5] or Table 1 in [1, Appendix A].)

We say that a subset $\Phi ^+\subset \Phi$ is a positive system if there exists a total ordering < on the ${\mathbb {R}}$-vector space V such that $\Phi ^+=\{\alpha \in \Phi : \alpha >0\}$ (see [16, Sect. 1.3]). The Coxeter group of $\Phi$ is the group of isometries W of V generated by the reflections $s_\alpha$ for $\alpha \in \Phi$. This group preserves $\Phi$ by definition of a normalized pseudo-root system, and it acts simply transitively on the set of positive systems by [16, Sect. 1.4]. In particular, the Coxeter group W is finite.

Let E be a finite set of unit vectors of V such that $E\cap (-E)= \varnothing$. The corresponding hyperplane arrangement is the set of hyperplanes ${\mathcal {H}}=\{H_e : e\in E\}$. A chamber of ${\mathcal {H}}$ is a connected component of $V - \bigcup _{e\in E}H_e$; we denote by ${\mathscr {T}}({\mathcal {H}})$ the set of chambers of ${\mathcal {H}}$. Fix a chamber $T_0$ to be the base chamber. For a chamber $T \in {\mathscr {T}}({\mathcal {H}})$ we denote by $S(T,T_0)$ the set of $e \in E$ such that the two chambers T and $T_0$ are on different sides of the hyperplane $H_e$, and define the sign of T to be $(-1)^T=(-1)^{|S(T,T_0)|}$.

We say that ${\mathcal {H}}$ is a Coxeter arrangement if it is stable by the orthogonal reflections in each of its hyperplanes. In that case, the set $\Phi =E\cup (-E)$ is a normalized pseudo-root system. We call its Coxeter group the Coxeter group of the arrangement. The map sending a positive system $\Phi ^+\subset \Phi$ to the set $\{v\in V : \forall \alpha \in \Phi ^+ \, (v,\alpha ) > 0\}$ is a bijection from the positive systems in $\Phi$ to the chambers of ${\mathcal {H}}$. See for example [3, Chap. V § 4 No. 8 Proposition 9 p. 99] and the discussion following it. Conversely, if $\Phi \subset V$ is a normalized pseudo-root system with Coxeter group W and $\Phi ^+\subset \Phi$ is a positive system, then ${\mathcal {H}}=\{H_\alpha : \alpha \in \Phi ^+\}$ is a Coxeter hyperplane arrangement, and in that case we always take the base chamber $T_0$ to be the chamber corresponding to $\Phi ^+$.

We now define product arrangements. Let $V_1$ and $V_2$ be two finite-dimensional real vector spaces equipped with inner products, and suppose that we are given hyperplane arrangements ${\mathcal {H}}_1$ and ${\mathcal {H}}_2$ on $V_1$ and $V_2$ respectively. We consider the product space $V_1\times V_2$, where the factors are orthogonal. The product arrangement ${\mathcal {H}}_1\times {\mathcal {H}}_2$ is then the arrangement on $V_1\times V_2$ with hyperplanes $H\times V_2$ for $H\in {\mathcal {H}}_1$ and $V_1\times H'$ for $H'\in {\mathcal {H}}_2$. If ${\mathcal {H}}_1$ is the empty arrangement, then we write $V_1\times {\mathcal {H}}_2$ instead of the confusing $\varnothing \times {\mathcal {H}}_2$. Similarly, if ${\mathcal {H}}_2$ is the empty arrangement, we write ${\mathcal {H}}_1\times V_2$. If the arrangements ${\mathcal {H}}_1$ and ${\mathcal {H}}_2$ arise from normalized pseudo-root systems $\Phi _1\subset V_1$ and $\Phi _2\subset V_2$, then their product ${\mathcal {H}}_1\times {\mathcal {H}}_2$ arises from the normalized pseudo-root system $\Phi _1\times \{0\}\cup \{0\}\times \Phi _2\subset V_1\times V_2$. We also denote this pseudo-root system by $\Phi _1\times \Phi _2$.

The notion of 2-structures was introduced by Herb for root systems to study the characters of discrete series representations; see, for example, the review article [13]. The definition we give here is Definition B.2.1 of [6]. It has been slightly adapted to work for pseudo-root systems.

Definition 2.1

Let $\Phi$ be a normalized pseudo-root system with Coxeter group W. A 2-structure for $\Phi$ is a subset $\varphi$ of $\Phi$ satisfying the following properties:

• (a) The subset $\varphi$ is a disjoint union $\varphi =\varphi _1\sqcup \varphi _2\sqcup \cdots \sqcup \varphi _r$, where the $\varphi _i$ are pairwise orthogonal subsets of $\varphi$ and each of them is an irreducible pseudo-root system of type $A_1$, $B_2$ or $I_2(2^k)$ for $k\ge 3$.

• (b) Let $\varphi ^+=\varphi \cap \Phi ^+$. If $w\in W$ is such that $w(\varphi ^+)=\varphi ^+$ then $\det (w) = 1$.

We denote by ${\mathcal {T}}(\Phi )$ the set of 2-structures for $\Phi$.

Proposition 2.2

Let $\Phi$ be a normalized pseudo-root system with Coxeter group W.

(i):

The group W acts transitively on the set of 2-structures ${\mathcal {T}}(\Phi )$.

(ii):

The pseudo-root system $\Phi$ and its 2-structures have the same rank if and only if there exists $w\in W$ whose restriction to ${{\,\textrm{Span}\,}}(\Phi )$ is equal to $-{{\,\textrm{id}\,}}_{{{\,\textrm{Span}\,}}(\Phi )}$.

Proof

• (i) See the start of Section 4 of [13] and Proposition B.2.4 of [6].

• (ii) For $\Phi$ arising from a root system $\Phi '$, these two conditions are equivalent to the fact that $\Phi '$ is spanned by strongly orthogonal roots; see, for example, the top of page 2559 of [14]. For general pseudo-root systems, see the classification of 2-structures in Section B.4 of [6].

$\square$

To each 2-structure $\varphi \subset \Phi$, we can associate a sign $\epsilon (\varphi )=\epsilon (\varphi ,\Phi ^+)$ (see the start of Section 5 and Lemma 5.1 of [14] and Definition B.2.8 of [6]).

We next introduce the abstract pizza quantity. Let ${\mathcal {H}}$ be a central hyperplane arrangement on V. Let ${\mathcal {C}}_{\mathcal {H}}(V)$ be the set of closed convex polyhedral cones in V that are intersections of closed half-spaces bounded by hyperplanes H where $H\in {\mathcal {H}}$, and let $K_{\mathcal {H}}(V)$ be the quotient of the free abelian group $\bigoplus _{K\in {\mathcal {C}}_{\mathcal {H}}(V)}{\mathbb {Z}}[K]$ on ${\mathcal {C}}_{\mathcal {H}}(V)$ by the relations $[K]+[K']=[K\cup K']+[K\cap K']$ for all $K,K'\in {\mathcal {C}}_{\mathcal {H}}(V)$ such that $K\cup K'\in {\mathcal {C}}_{\mathcal {H}}(V)$. For $K\in {\mathcal {C}}_{\mathcal {H}}(V)$, we still denote the image of K in $K_{\mathcal {H}}(V)$ by [K].

Definition 2.3

Suppose that we have fixed a base chamber of ${\mathcal {H}}$. The abstract pizza quantity of ${\mathcal {H}}$ is

$$\begin{aligned} P({\mathcal {H}})=\sum _{T\in {\mathscr {T}}({\mathcal {H}})}(-1)^T[{\overline{T}}]\in K_{\mathcal {H}}(V). \end{aligned}$$

Remark 2.4

By Lemma 3.2.3 of [6], we have

$$\begin{aligned} P({\mathcal {H}})=\sum _{T\in {\mathscr {T}}({\mathcal {H}})}(-1)^T[T]. \end{aligned}$$

We use this alternative definition of $P({\mathcal {H}})$ in our proofs.

The following result is Corollary 3.2.4 of [6]. It shows how to evaluate the pizza quantity for a Coxeter arrangement in terms of the associated 2-structures.

Theorem 2.5

Let $\Phi \subset V$ be a normalized pseudo-root system. Choose a positive system $\Phi ^+\subset \Phi$ and let ${\mathcal {H}}$ be the hyperplane arrangement $(H_\alpha )_{\alpha \in \Phi ^+}$ on V with base chamber corresponding to $\Phi ^+$. For every 2-structure $\varphi \in {\mathcal {T}}(\Phi )$, we write $\varphi ^+=\varphi \cap \Phi ^+$ and we denote by ${\mathcal {H}}_\varphi$ the hyperplane arrangement $(H_\alpha )_{\alpha \in \varphi ^+}$ with base chamber corresponding to $\varphi ^+$. Then we have

$$\begin{aligned} P({\mathcal {H}})=\sum _{\varphi \in {\mathcal {T}}(\Phi )}\epsilon (\varphi ) P({\mathcal {H}}_\varphi ). \end{aligned}$$

If $\varphi \in {\mathcal {T}}(\Phi )$ then the closures of the chambers of ${\mathcal {H}}_\varphi$ are elements of ${\mathcal {C}}_{\mathcal {H}}(V)$, so $P({\mathcal {H}}_\varphi )$ makes sense as an element of $K_{\mathcal {H}}(V)$.

3 A Dissection Proof of the Higher-Dimensional Pizza Theorem

Definition 3.1

Let ${\mathcal {C}}(V)$ be a nonempty family of subsets of V that is stable by finite intersections and affine isometries and such that, if $C\in {\mathcal {C}}(V)$ and D is a closed affine half-space of V, then $C\cap D\in {\mathcal {C}}(V)$. Furthermore, we assume that ${\mathcal {C}}(V)$ is closed with respect to Cartesian products, that is, if $C_{i} \in {\mathcal {C}}(V_{i})$ for $i=0,1$ then $C_{0} \times C_{1} \in {\mathcal {C}}(V_{0} \times V_{1})$. For example, we could take ${\mathcal {C}}(V)$ to be the family of all convex subsets of V, or of all closed (or compact) convex subsets, or of all convex polyhedra.

We denote by K(V) the quotient of the free abelian group $\bigoplus _{C\in {\mathcal {C}}(V)}{\mathbb {Z}}[C]$ on ${\mathcal {C}}(V)$ by the relations:

• $[\varnothing ]=0$;

• $[C\cup C']+[C\cap C']=[C]+[C']$ for all $C,C'\in {\mathcal {C}}(V)$ such that $C\cup C'\in {\mathcal {C}}(V)$;

• $[g(C)]=[C]$, for every $C\in {\mathcal {C}}(V)$ and every affine isometry g of V.

For $C\in {\mathcal {C}}(V)$, we still denote the image of C in K(V) by [C].

Definition 3.2

A valuation on ${\mathcal {C}}(V)$ with values in an abelian group A is a function ${\mathcal {C}}(V)\longrightarrow A$ that can be extended to a morphism of groups $K(V)\longrightarrow A$.

Remark 3.3

Define ${\mathcal {B}}(V)$ to be the relative Boolean algebra generated by ${\mathcal {C}}(V)$, that is, the smallest collection of subsets of V that contains ${\mathcal {C}}(V)$ and is closed under finite unions, finite intersections and set differences. Groemer’s Integral Theorem states that a valuation on ${\mathcal {C}}(V)$ can be extended to a valuation on the Boolean algebra B(V); see [11] and also [18, Chap. 2]. Applying this to the valuation $C \longmapsto [C]$ with values in K(V), we see that we can make sense of [C] for any $C\in {\mathcal {B}}(V)$. For instance, we have $[C_1 \cup C_2] = [C_1] + [C_2] - [C_1 \cap C_2]$ and $[C_1 - C_2] = [C_1] - [C_1 \cap C_2]$. Moreover, if ${\mathcal {C}}(V)$ is the set of all convex polyhedra in V, then ${\mathcal {B}}(V)$ contains all polyhedra (convex or not), and also half-open polyhedra.

Next we have the following straightforward lemma, whose proof we omit, which states that the class symbol is well-behaved with respect to Cartesian products.

Lemma 3.4

The two class identities $[C_{0}] = [D_{0}]$ and $[C_{1}] = [D_{1}]$ in $K(V_{0})$ and $K(V_{1})$, respectively, imply that $[C_{0} \times C_{1}] = [D_{0} \times D_{1}]$ in $K(V_{0}) \times K(V_{1})$.

Let ${\mathcal {H}}$ be a central hyperplane arrangement on V with fixed base chamber. If $K\in {\mathcal {C}}(V)$, we have a morphism of groups $e_K:K_{\mathcal {H}}(V)\longrightarrow K(V)$ induced by the map ${\mathcal {C}}_{\mathcal {H}}(V) \longrightarrow {\mathcal {C}}(V)$, $C\longmapsto C\cap K$.

We denote by $P({\mathcal {H}},K)$ the image of $P({\mathcal {H}})$ by this morphism $e_K$; in other words, we have

$$\begin{aligned} P({\mathcal {H}},K)&= \sum _{T\in {\mathscr {T}}({\mathcal {H}})}(-1)^T[{\overline{T}}\cap K]. \end{aligned}$$

By Remark 2.4, we also have

$$\begin{aligned} P({\mathcal {H}},K)&= \sum _{T\in {\mathscr {T}}({\mathcal {H}})}(-1)^T[T\cap K]. \end{aligned}$$

We state the main theorem of this paper. First for $u,v \in V$ define the half-open line segment (u, v] by $\{(1-\lambda ) u + \lambda v : 0 < \lambda \le 1\}$. Our main result is the following:

Theorem 3.5

(The Abstract Pizza Theorem) Let ${\mathcal {H}}$ be a Coxeter hyperplane arrangement with Coxeter group W in an n-dimensional space V such that $-{{\,\textrm{id}\,}}_V\in W$. Let $K\in {\mathcal {C}}(V)$ and $a\in V$. Suppose that K is stable by the group W and contains the convex hull of the set $\{w(a) : w\in W\}$.

• (i) If ${\mathcal {H}}$ is not of type $A_1^{n}$, we have $P({\mathcal {H}},K+a)=0$ in K(V).

• (ii) If ${\mathcal {H}}$ has type $A_1^{n}$, $\Phi$ is the normalized pseudo-root system corresponding to ${\mathcal {H}}$ and $\Phi ^+=\{e_1,\ldots ,e_n\}$ where $\Phi ^+\subset \Phi$ is the positive system corresponding to the base chamber of ${\mathcal {H}}$, then the following identity holds:

  $$\begin{aligned} P({\mathcal {H}},K+a)&= \left[ \prod _{i=1}^n(0,2(a,e_i)e_i]\right] . \end{aligned}$$

  (3.1)

Here we are using Remark 3.3 to make sense of the right-hand side of Eq. (3.1).

The conditions on K are satisfied if for example K is convex, contained in ${\mathcal {C}}(V)$, stable by W and $0\in K+a$. Indeed, the last condition implies that $-a\in K$; as $-{{\,\textrm{id}\,}}_V\in W$ by assumption, this in turns implies that $a\in K$, hence that K contains the convex hull of the set $\{w(a) : w \in W\}$.

We will give the proof of Theorem 3.5 at the end of the section. This proof does not use Theorem 1.2 of [7], so we obtain a new proof of that result.

Let $V_0,\ldots ,V_n$ denote the intrinsic volumes on V (see [21, Sect. 4.2]).

Lemma 3.6

Let $(v_1,\ldots ,v_k)$ be an orthogonal family of vectors in V. Then

$$\begin{aligned} V_i((0,v_1]\times \ldots \times (0,v_k])=0, \end{aligned}$$

for $0\le i\le k-1$.

Proof

By Lemma 14.2.1 of [22] or Proposition 4.2.3 of [18], it suffices to prove that, if $a<b$ are real numbers, the 0th intrinsic volume of the half-open segment $(a,b]\subset {\mathbb {R}}$ is 0. As the 0th intrinsic volume is the Euler-Poincaré characteristic with compact support, this is clear. $\square$

Corollary 3.7

We keep the notation and hypotheses of Theorem 3.5. If ${\mathcal {H}}$ is not of type $A_1^n$, we have

$$\begin{aligned} \sum _{T\in {\mathscr {T}}({\mathcal {H}})}(-1)^T V_i(T\cap (K+a))=0, \end{aligned}$$

(3.2)

for every $0 \le i \le n$, where K is assumed to be convex if $i\not =n$. If ${\mathcal {H}}$ has type $A_1^n$ and K is convex then Eq. (3.2) holds for $0 \le i \le n-1$.

Proof

If ${\mathcal {H}}$ is not of type $A_1^n$, then Eq. (3.2) actually holds for any valuation on ${\mathcal {C}}(V)$ that is invariant under the group of affine isometries; this includes the intrinsic volumes.

Suppose that ${\mathcal {H}}$ is of type $A_1^n$. Then we know that Eq. (3.1) holds. The result then follows from Lemma 3.6. $\square$

Remark 3.8

Theorem 3.5 immediately implies generalizations to our higher-dimensional case of the “thin crust” and “thick crust” results of Confection 3 and Leftovers 1 of [19] for an even number of cuts.

We obtain the “thin crust” result by evaluating the $(n-1)$st intrinsic volume on $P({\mathcal {H}},K+a)$. Note that this result holds for a pizza of any (convex) shape and even in the case where we only make n cuts, where n is the dimension.

To generalize the “thick crust” result, consider two sets $K\subset L$ stable by W and in ${\mathcal {C}}(V)$. If $a\in V$ is such that K contains the convex hull of the set $\{w(a) : w\in W\}$, then

$$\begin{aligned} P({\mathcal {H}},(L - K)+a)=P({\mathcal {H}},L+a)-P({\mathcal {H}},K+a)=0, \end{aligned}$$

so in particular

$$\begin{aligned} \sum _{T\in {\mathscr {T}}({\mathcal {H}})}(-1)^T{{\,\textrm{Vol}\,}}(T\cap ((L - K)+a))=0. \end{aligned}$$

The case where K and L are balls with the same center is the “thick crust” result.

We now state and prove some lemmas that will be used in the proof of Theorem 3.5.

Lemma 3.9

Let ${\mathcal {H}}_i$ be a hyperplane arrangement on $V_i$ for $i=0,1$. Assume furthermore that ${\mathcal {H}}_1 = \{H_e\}_{e \in E_1}$ has type $A_1^r$ and $\dim (V_1) = r$. Let $E_{1} = \{e_1, \ldots , e_r\}$ be the index set of ${\mathcal {H}}_{1}$. Let ${\mathcal {H}}$ and V be the Cartesian products ${\mathcal {H}}_0 \times {\mathcal {H}}_{1}$ and $V_0 \times V_1$, respectively. Then for every $K\in {\mathcal {C}}(V)$ that is stable under the orthogonal reflections in the hyperplanes $V_0 \times H_{e_1}, \ldots , V_0 \times H_{e_r}$ and for every $a\in V_1$, if $L=K+a$, we have the identity

$$\begin{aligned} P({\mathcal {H}},L)&= P\left( {\mathcal {H}}_0\times V_1,L\cap (V_0\times (0,2(a,e_1)e_1]\times \cdots \times (0,2(a,e_r)e_r])\right) , \end{aligned}$$

where ${\mathcal {H}}_0\times V_1$ is the product of ${\mathcal {H}}_0$ and the empty hyperplane arrangement on $V_1$.

Fig. 1

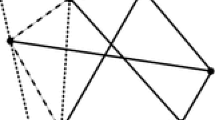
A schematic sketch of $V_0 \times V_1$ for the proof of Lemma 3.9

Proof

By a straightforward induction, we may assume that $r=\dim V_1=1$. Also, after changing the sign of $e_1$, we may assume that $(a,e_1)\ge 0$. See Fig. 1 for a sketch of the situation. Let T be a chamber of the arrangement ${\mathcal {H}}_0$. The classes of the two regions $(T\times {\mathbb {R}}_{> 0}e_1) \cap L$ and $(T\times {\mathbb {R}}_{< 0}e_1) \cap L$ of ${\mathcal {H}}$ occur with opposite signs in the pizza quantity $P({\mathcal {H}}, L)$. Note that the region $(T\times {\mathbb {R}}_{> 2(a,e_1)}e_1) \cap L$ is the orthogonal reflection of the region $(T \times {\mathbb {R}}_{< 0}e_1) \cap L$ in the affine hyperplane $H_{e_1} + (a,e_1)e_1=H_{e_1}+a$. Hence these regions have the same class in K(V) which cancels in the pizza quantity $P({\mathcal {H}},L)$, and the class of the region $(T \times (0,2(a,e_1)e_1]) \cap L= (T\times V_1)\cap L\cap (V_0\times (0,2(a,e_1)e_1])$ remains. As the map $T\longmapsto T\times V_1$ is a sign-preserving bijection from ${\mathscr {T}}({\mathcal {H}}_0)$ to ${\mathscr {T}}({\mathcal {H}}_0\times V_1)$, this completes the proof. $\square$

We now consider the case of a hyperplane arrangement that is the product of a 2-dimensional dihedral arrangement and another arrangement. Suppose that $V=V_0\times V_1$, where the factors are orthogonal, and that ${\mathcal {H}}={\mathcal {H}}_0\times {\mathcal {H}}_1$, where ${\mathcal {H}}_i$ is a hyperplane arrangement in $V_i$. Suppose also that $\dim V_0 = 2$ and that ${\mathcal {H}}_0$ is an arrangement of type $I_2(2m)$ with Coxeter group $W_0$ where $m\ge 2$. We view $W_0$ as a group of isometries of V by making $w\in W_0$ act on $V=V_0\times V_1$ by $w\times {{\,\textrm{id}\,}}_{V_1}$. We also choose a family ${\mathcal {C}}(V)$ as in Definition 3.1.

Let $a\in V_0$. We will describe a dissection of $V_0$. The case where $m=4$ is shown in Fig. 2. We call $L_0,\ldots ,L_{2m-1}$ the lines of ${\mathcal {H}}_0$ (numbered so that the angle between $L_0$ and $L_i$ is an increasing function of i) and we assume that the point a is in a chamber between $L_{m-1}$ and $L_{m}$. Choose a closed half-space D bounded by $L_0$ and containing a (this choice is unique if $a\not \in L_0$). Then, for $0\le i\le 2m-1$, we denote by $T_i$ the unique chamber of ${\mathcal {H}}$ contained in D and with boundary contained in $L_i\cup L_{i+1}$. We assume that $(-1)^{T_0}=1$ for concreteness. The point a is in the closure of the chamber $T_{m-1}$.

We write ${\mathscr {T}}_+=\{T\in {\mathscr {T}}({\mathcal {H}}_0) : (-1)^T=1\}$ and ${\mathscr {T}}_-=\{T\in {\mathscr {T}}({\mathcal {H}}_0) : (-1)^T=-1\}$. Let $W_a$ be the group of affine isometries generated by the orthogonal reflections in the lines $L+a$, for $L\in {\mathcal {H}}_0$. We take $R_0(a)$ to be the convex hull of the points w(0) for $w\in W_a$. This is the shaded polygon on Fig 2, where the darker slices are the intersections with the closures of chambers in ${\mathscr {T}}_+$. We have the inclusion $R_0(a)\subset \bigcup _{i=0}^{2m-2}{\overline{T}}_i$. Finally we set

$$\begin{aligned} R_{0,\pm }(a)=R_{0}(a) \cap \bigcup _{T\in {\mathscr {T}}_{\pm }}T. \end{aligned}$$

Lemma 3.10

The following three identities hold in $K(V_{0} \times V_{1})$:

(i):

Let $K \in {\mathcal {C}}(V)$ such that K is stable by $W_0$ and let $L=K+a$. Then

$$\begin{aligned} \sum _{T\in {\mathscr {T}}} (-1)^{T} [L \cap ((T - R_0(a))\times V_1)] = 0. \end{aligned}$$

(ii):

Let $K \in {\mathcal {C}}(V)$ such that K is stable by $W_0$ and let $L=K+a$ then

$$\begin{aligned} P({\mathcal {H}},L)= & {} P(V_0\times {\mathcal {H}}_1,L\cap (R_{0,+}(a)\times V_1))\\ {}{} & {} - P(V_0\times {\mathcal {H}}_1,L\cap (R_{0,-}(a)\times V_1)). \end{aligned}$$

(iii):

If $K_1\subset V_1$ is such that $R_0(a)\times K_1\in {\mathcal {C}}(V)$, then

$$\begin{aligned}{}[R_{0,+}(a)\times K_1]=[R_{0,-}(a)\times K_1]. \end{aligned}$$

Fig. 2

A picture of the regions in the proof of Lemma 3.10(i) for the case of $I_2(8)$

Proof

We begin by proving (i). For $0\le i\le 2m-1$, we denote by $R_{i,\pm }$ the unique chamber of ${\mathcal {H}}$ not contained in D and with boundary contained in $L_i\cup L_{i+1}$, that is, the image of $T_i$ by the symmetry with center 0; we write $R_{i,+}$ if this chamber has sign $+1$, or equivalently if i is even, and $R_{i,-}$ if this chamber has sign $-1$, or equivalently if i is odd. For every $0 \le j \le m-1$, we denote by $R_{2j,-}$ and $R_{2j+1,+}$ the orthogonal reflection in the line $L_{2j+1}^\perp +a$ of $R_{2j,+}$ and $R_{2j+1,-}$, respectively. Note that $R_{2j,-}\subset T_{2j+1}$ and $R_{2j+1,+}\subset T_{2j}$. For $0 \le j \le m-1$ again, we denote by $S_{j,+}$ the interior of $T_{2j} -(R_0(a)\cup R_{2j+1,+})$ and by $S_{j,-}$ the interior of $T_{2j+1} - (R_0(a)\cup R_{2j,-})$. Then $T_{2j} - R_0(a)$ is the disjoint union of $R_{2j+1,+}$, $S_{j,+}$ and an open ray $D_{2j}$ starting at an extremal point of $R_0(a)$ (the image of 0 by the orthogonal reflection in the line $L_{2j+1}^\perp +a$) and parallel to $L_{2j}$. Similarly $T_{2j+1} - R_0(a)$ is the disjoint union of $R_{2j,-}$, $S_{j,-}$ and an open ray $D_{2j+1}$ starting at the same extremal point of $R_0(a)$ and parallel to $L_{2j+2}$. See Fig. 2 for the case $m=4$, where the rays $D_{2j}$ and $D_{2j+1}$ are dashed.

The union $\bigcup _{T\in {\mathscr {T}}_+}T$ is equal to the disjoint union of the set $R_{0,+}(a)$, the regions $R_{i,+}$ for $0\le i\le 2m-1$, the regions $S_{j,+}$ for $0\le j\le m-1$ and the rays $D_{2j}$ for $0\le j\le m-1$. On the other hand, the union $\bigcup _{T\in {\mathscr {T}}_-}T$ is equal to the disjoint union of the set $R_{0,-}(a)$, the regions $R_{i,-}$ for $0\le i\le 2m-1$, the regions $S_{j,-}$ for $0\le j\le m-1$ and the rays $D_{2j+1}$ for $0\le j\le m-1$. Consider the following four observations:

• For $0\le i\le 2m-1$ the region $R_{i,-}$ is the image of $R_{i,+}$ by the orthogonal reflection in the affine line $L_{2\lfloor i/2 \rfloor +1}^\perp +a$.

• For $0\le j\le m-1$ the region $S_{j,-}$ is the image of $S_{j,+}$ by the rotation with center a and angle ${\pi }/{m}$.

• For $0\le j\le m-2$ the ray $D_{2j+3}$ is the image of the ray $D_{2j}$ by the rotation with center a and angle ${2\pi }/{m}$.

• The ray $D_{2m-2}$ is the image of $D_1$ by the orthogonal reflection in the affine line $L_m+a$.

Each of them is of the form: the set X is the image of the set Y under an affine isometry g belonging to the group $W_a$. Since the set $L = K+a$ is invariant under g, we obtain that the set $L \cap (X \times V_1)$ is the image of $L \cap (Y \times V_1)$, and hence that $[L \cap (X \times V_1)] = [L \cap (Y \times V_1)]$. Statement (i) follows by summing over all pairs of sets X and Y.

Next we prove (ii). There is a bijection ${\mathscr {T}}({\mathcal {H}}_0)\times {\mathscr {T}}({\mathcal {H}}_1){\mathop {\longrightarrow }\limits ^{\sim }}{\mathscr {T}}({\mathcal {H}})$ where $(T,T') \longmapsto T\times T'$ and $(-1)^{T\times T'}=(-1)^{T}(-1)^{T'}$ for all $T\in {\mathscr {T}}({\mathcal {H}}_0)$ and $T'\in {\mathscr {T}}({\mathcal {H}}_1)$. Hence

$$\begin{aligned} P({\mathcal {H}},L)= \sum _{T'\in {\mathscr {T}}({\mathcal {H}}_1)} \sum _{T\in {\mathscr {T}}(\mathcal {H}_0)} (-1)^{T} (-1)^{T'} [L \cap (T\times {T'})] . \end{aligned}$$

(3.3)

Fix $T'\in {\mathscr {T}}({\mathcal {H}}_1)$ for a moment. The fact that K is stable by $W_{0}$ implies that $K \cap (V_0 \times {T'})$ is also stable by $W_{0}$. Hence applying statement (i) to the set $(K \cap (V_0 \times {T'})) + a = L \cap (V_0 \times {T'})$ yields

$$\begin{aligned} \sum _{T\in {\mathscr {T}}(\mathcal {H}_0)} (-1)^{T} [L \cap ((T - R_0(a))\times {T'})]= 0 . \end{aligned}$$

(3.4)

Multiplying Eq. (3.4) with the sign $(-1)^{T'}$, summing over all $T'\in {\mathscr {T}}({\mathcal {H}}_1)$, and subtracting the result from Eq. (3.3) yields

$$\begin{aligned} P({\mathcal {H}},L)&= \sum _{T'\in {\mathscr {T}}({\mathcal {H}}_1)} \sum _{T\in {\mathscr {T}}(\mathcal {H}_0)} (-1)^{T} (-1)^{T'} [L \cap ((T \cap R_0(a)) \times {T'})] \\&= \sum _{T'\in {\mathscr {T}}({\mathcal {H}}_1)}(-1)^{T'} [L\cap (R_{0,+}(a)\times T')]- \sum _{T'\in {\mathscr {T}}({\mathcal {H}}_1)}(-1)^{T'}[L\cap (R_{0,-}(a)\times {T'})]\\&= P(V_0\times {\mathcal {H}}_1,L\cap (R_{0,+}(a)\times V_1)) - P(V_0\times {\mathcal {H}}_1,L\cap (R_{0,-}(a)\times V_1)). \end{aligned}$$

Finally we consider (iii). By Lemma 3.4, it suffices to show that, if we take ${\mathcal {C}}(V_0)$ to be the set of convex polygons in $V_0$, then $[R_{0,+}(a)]=[R_{0,-}(a)]$ in $K(V_0)$. This follows from Corollary 4.2 and from the fact that the intrinsic volumes of $R_{0,+}(a)$ and $R_{0,-}(a)$ are equal (which is an easy calculation), but we also give a direct proof. We consider the following dissection of the polygon $R_0(a)$; see Fig. 3 for the case $m=4$. For $0\le i\le 2m-1$ let $P_i$ be the image of 0 by the orthogonal reflection in the line $L_i^\perp +a$; note that $P_i$ is a boundary point of $R_0(a)$, and that it is on $L_i$. We describe the pieces of the dissection of $R_0(a)$:

• For $1 \le i \le m-2$ consider the pair of isosceles triangles $B_{i,+}$ and $B_{i,-}$ that have one side equal to the segment $[0,P_{2i}]$, angles equal to ${\pi }/{2m}$ at the vertices 0 and $P_i$, and such that $B_{i,\pm }$ is in a chamber with sign $\pm 1$; in other words, the triangle $B_{i,-}$ is in the chamber $T_{2i-1}$, and $B_{i,+}$ is in the chamber $T_{2i}$.

• Let $B_{0,+}$ be the isosceles triangle contained in $T_0$ with one side equal to the segment $[0,P_0]$ and angles equal to ${\pi }/{2m}$ at the vertices 0 and $P_0$.

• Consider the isosceles triangle contained in $T_{2m-3}$ with one side equal to the segment $[0,P_{2m-2}]$ and angles equal to ${\pi }/{2m}$ at the vertices 0 and $P_{2m-2}$; this splits into an isosceles triangle $B_{0,-}$ congruent to $B_{0,+}$ and an isosceles trapezoid $B_{m-1,-}$ having one edge equal to $[0,P_{2m-2}]$.

• Let $B_{m-1,+}$ be the image of $B_{m-1,-}$ by the orthogonal reflection in the line $L_{2m-2}$; then $B_{m-1,+}$ is contained in the chamber $T_{2m-2}$.

Fig. 3

The dissection of the polygon $R_0(a)$ in the case of $I_2(8)$. The darker shaded regions are the intersections with the chambers which have a positive sign

To finish the dissection of $R_0(a)$, we note that, for $0\le i\le 2m-3$, we still have a quadrilateral piece $Q_i$ left over in $T_i\cap R_0(a)$. Then for $1 \le i \le 2m-3$ the quadrilateral $Q_{i}$ is the image of $Q_{i-1}$ by the rotation with center a and angle ${\pi }/{m}$. Indeed, this is true for the intersections of these quadrilaterals with the boundary of $R_0(a)$ (which consist of two edges with endpoints $P_{i-1}$ and $P_{i+1}$), and it is easy to calculate the angles at the vertices of this intersection and to see that they correspond: If $1\le i\le 2m-2$ and i is even, respectively odd, the angle of $Q_{i-1}$ at $P_i$ is ${(i-1)\pi }/{2m}$, respectively ${i\pi }/{2m}$. If $0 \le i \le 2m-3$ and i is even, respectively odd, the angle of $Q_i$ at $P_i$ is ${(2m-2-i)\pi }/{2m}$, respectively ${(2m-1-i)\pi }/{2m}$.

This is Frederickson’s dissection; see pages 28–31 of [9]. That paper is only interested in giving a dissection proof that the alternating sum of the areas is equal to zero. Hence it can safely ignore line segments of area zero, whereas we are proving an identity in $K(V_{0})$ and have to be careful with all regions, including lower dimensional ones.

The set $R_{0,+}(a)$ is the disjoint union of the following subsets:

• For $0\le i\le m-2$ let $B'_{i,+}$ be the intersection of the triangle $B_{i,+}$ with the interior of the chamber containing $B_{i,+}$. In other words, $B'_{i,+}$ is the union of the interior of $B_{i,+}$ and the relative interior of one of its two equal sides.

• Let $B'_{m-1,+}$ be the intersection of the trapezoid $B_{m-1,+}$ and $T_{2m-2}$. That is, $B'_{m-1,+}$ is the union of the interior of $B_{m-1,+}$ and the intersection of its boundary with the boundary of $R_0(a)$, minus the two extremal points of this intersection.

• For $0\le j\le m-2$ let $Q'_{2j}$ be the intersection of the quadrilateral $Q_{2j}$ and $T_{2j}$. That is, $Q'_{2j}$ is the union of the interior of $Q_{2j+1}$ and the intersection of its boundary with the boundary of $R_0(a)$, minus the two extremal points of this intersection.

As for the set $R_{0,-}(a)$, it is the disjoint union of the following subsets:

• Let $B'_{0,-}$ be the union of the interior of the triangle $B_{0,-}$ and the relative interior of the side that it shares with $Q_{2m-3}$.

• For $1\le i\le m-2$ let $B'_{i,-}$ be the intersection of the triangle $B_{i,-}$ with the interior of the chamber containing $B'_{i,-}$. That is, $B'_{i,-}$ is the union of the interior of $B_{i,-}$ and the relative interior of one of its two equal sides.

• Let $B'_{m-1,-}$ be the intersection of the trapezoid $B_{m-1,-}$ and $T_{2m-3}$.

• For $0\le j\le m-2$ let $Q'_{2j+1}$ be the intersection of the quadrilateral $Q_{2j+1}$ and $T_{2j+1}$. That is, $Q'_{2j+1}$ is the union of the interior of $Q_{2j+1}$ and the intersection of its boundary with the boundary of $R_0(a)$, minus the two extremal points of this intersection.

We obtain that $[R_{0,+}(a)]=[R_{0,-}(a)]$ since the regions $B'_{i,+}$ and $B'_{i,-}$ are isometric for every $0 \le i \le m-1$, as are the regions $Q_{2j}$ and $Q_{2j+1}$ for $0 \le j \le m-2$. $\square$

Lemma 3.11

Suppose that we have $V=V_1^{(1)}\times \cdots \times V_1^{(r)}\times V_2^{(1)}\times \cdots \times V_2^{(s)}$, where the factors of the product are pairwise orthogonal, and that ${\mathcal {H}}$ is a product ${\mathcal {H}}_1^{(1)}\times \cdots \times {\mathcal {H}}_1^{(r)}\times {\mathcal {H}}_2^{(1)}\times \cdots \times {\mathcal {H}}_2^{(s)}$, where each ${\mathcal {H}}_i^{(j)}$ is a hyperplane arrangement on $V_i^{(j)}$. Suppose further that:

(a):

If $1 \le j \le r$ then $V_1^{(j)}$ is 1-dimensional, and we have a unit vector $e^{(j)}$ in $V_1^{(j)}$ yielding the hyperplane arrangement ${\mathcal {H}}_1^{(j)} = \{0\}$.

(b):

If $1 \le j \le s$ then $V_2^{(j)}$ is 2-dimensional, and the arrangement ${\mathcal {H}}_2^{(j)}$ is of type $I_2(2m^{(j)})$ for some $m^{(j)} \ge 2$.

Let $a\in V$ and $K\in {\mathcal {C}}(V)$. Suppose that K is stable by the Coxeter group W and contains the convex hull of the set $\{w(a) : w\in W\}$. Then the following two statements hold:

(i):

If $s\ge 1$ we have $P({\mathcal {H}},K+a)=0$ in K(V).

(ii):

If $s=0$ we have in K(V) the identity

$$\begin{aligned} P({\mathcal {H}},K+a)&= \left[ (0,2(a,e^{(1)})e^{(1)}]\times \cdots \times (0,2(a,e^{(r)})e^{(r)}]\right] . \end{aligned}$$

Proof

Let $L=K+a$. Since $-{{\,\textrm{id}\,}}_V\in W$ we have $-a\in K$ and so $0\in L+a$; also, the sets $\{w(a) : w\in W\}$ and $\{w(-a) : w\in W\}$ are equal. Let $W_a$ be the group of affine isometries of V generated by the orthogonal reflections in the hyperplanes $a+H$, for $H\in {\mathcal {H}}$. The conditions on K imply that L is stable by $W_a$ and contains the convex hull of the set $\{u(0) : u\in W_a\}=\{w(-a)+a : w\in W\}$.

Write $a=(a_1^{(1)},\ldots ,a_1^{(r)},a_2^{(1)},\ldots ,a_2^{(s)})$, with $a_i^{(j)}\in V_i^{(j)}$. For $1 \le i \le r$ let $S^{(i)}$ denote the half-open line-segment $(0, 2(a,e^{(i)}) e^{(i)}]$. For $1 \le j \le s$ we consider subsets $R_{+1}^{(j)} = R_{0,+}\big (a_2^{(j)}\big )$ and $R_{-1}^{(j)} = R_{0,-}\big (a_2^{(j)}\big )$ of $V_2^{(j)}$ as in Lemma 3.10. By Lemmas 3.9 and 3.10(ii), we have that

$$\begin{aligned} P({\mathcal {H}},L)&= \sum _{(\epsilon _1,\ldots ,\epsilon _s)\in \{\pm 1\}^s} \epsilon _1\cdots \epsilon _s \left[ L \cap \left( S^{(1)} \times \cdots \times S^{(r)} \times R_{\epsilon _1}^{(1)}\times \cdots \times R_{\epsilon _s}^{(s)}\right) \right] . \end{aligned}$$

Consider the polyhedron

$$\begin{aligned} P = [0,2 (a,e^{(1)}) e^{(1)}] \times \cdots \times [0,2 (a,e^{(r)}) e^{(r)}] \times R_0\big (a_2^{(1)}\big ) \times \cdots \times R_0\big (a_2^{(s)}\big ). \end{aligned}$$

Then P is the convex hull of the set $\{u(0) : u\in W_a\}$ by definition of the polygons $R_0\big (a_2^{(j)}\big )$, hence it is contained in L and so is its subset $S^{(1)} \times \cdots \times S^{(r)} \times R_{\epsilon _1}^{(1)}\times \cdots \times R_{\epsilon _s}^{(s)}$ for every $(\epsilon _1,\ldots ,\epsilon _s)\in \{\pm 1\}^s$. So we obtain

$$\begin{aligned} P({\mathcal {H}},L)&= \sum _{(\epsilon _1,\ldots ,\epsilon _s)\in \{\pm 1\}^s} \epsilon _1\cdots \epsilon _s \left[ S^{(1)} \times \cdots \times S^{(r)} \times R_{\epsilon _1}^{(1)}\times \cdots \times R_{\epsilon _s}^{(s)}\right] . \end{aligned}$$

If $s=0$ this implies statement (ii). Suppose that $s\ge 1$. By point (iii) of Lemma 3.10, we know that

$$\begin{aligned} \left[ S^{(1)} \times \cdots \times S^{(r)} \times R_{\epsilon _1}^{(1)}\times \cdots \times R_{\epsilon _s}^{(s)}\right] = \, \left[ S^{(1)} \times \cdots \times S^{(r)} \times R_{+1}^{(1)}\times \cdots \times R_{+1}^{(s)}\right] \end{aligned}$$

for every $(\epsilon _1,\ldots ,\epsilon _s)\in \{\pm 1\}^s$. As $\sum _{(\epsilon _1,\ldots ,\epsilon _s)\in \{\pm 1\}^s} \epsilon _1 \cdots \epsilon _s = 0$, this finishes the proof of (i). $\square$

Proof of Theorem 3.5

Statement (ii) is exactly Lemma 3.11(ii). We now prove statement (i), so we assume that ${\mathcal {H}}$ is not of type $A_1^{n}$. By Theorem 2.5, we have

$$\begin{aligned} P({\mathcal {H}},K+a)=\sum _{\varphi \in {\mathcal {T}}(\Phi )}\epsilon (\varphi ) P({\mathcal {H}}_\varphi ,K+a) . \end{aligned}$$

By definition, any 2-structure for $\Phi$ is of type $A_1^r\times \prod _{k\ge 2}I_2(2^k)^{s_k}$ with $\sum _{k\ge 2}s_k$ finite and, as W acts transitively on the set of 2-structures (Proposition 2.2(i)), the integers r and $s_k$, for $k\ge 2$, do not depend on the 2-structure but only on $\Phi$. Also, by Proposition 2.2(ii), we have $\dim V=r+\sum _{k\ge 2}2s_k$, so we are in the situation of Lemma 3.11. Suppose that $\sum _{k\ge 2}s_k\ge 1$. Then by Lemma 3.11(i) we have $P({\mathcal {H}}_\varphi ,K+a)=0$ for every $\varphi \in {\mathcal {T}}(\Phi )$ and hence $P({\mathcal {H}},K+a)=0$. Assume now that $\sum _{k\ge 2}s_k=0$, that is, $s_{k} = 0$ for every k. Statement (ii) of the same lemma implies that

$$\begin{aligned} P({\mathcal {H}},K+a)=\sum _{\varphi \in {\mathcal {T}}(\Phi )}\epsilon (\varphi ) \Bigg [\prod _{e\in \varphi \cap \Phi ^+}(0,2(a,e)e]\Bigg ]. \end{aligned}$$

(3.5)

This is an alternating sum of classes of half-open rectangular parallelotopes in V. So we can apply Theorem 4.1 to prove that $P({\mathcal {H}},K+a)=0$ in K(V). We know that $V_i(P({\mathcal {H}},K+a))=0$ if $0\le i\le n-1$ by Lemma 3.6, so it remains to prove that $V_n(P({\mathcal {H}},K+a))=0$, that is, that the alternating sum of the volumes of the parallelotopes $\prod _{e\in \varphi \cap \Phi ^+}(0,2(a,e)e]$ is equal to zero. This follows from Theorem 1.2 of the paper [7]. However, we now give a direct proof (that does not use analysis) using the method of that corollary. Let $f:V\longrightarrow {\mathbb {R}}$ be the function defined by

$$\begin{aligned} f(a)&= \sum _{\varphi \in {\mathcal {T}}(\Phi )}\epsilon (\varphi ) \prod _{e\in \varphi \cap \Phi ^+} 2(a,e) . \end{aligned}$$

Note that f is a polynomial homogeneous of degree n on V. Furthermore Eq. (3.5) implies that

$$\begin{aligned} {{\,\textrm{Vol}\,}}(P({\mathcal {H}},K+a)) =f(a), \end{aligned}$$

for every convex subset K of V of finite volume that is stable by W and every $a\in V$ such that $0\in K+a$. The polynomial f satisfies $f(w(a))=\det (w)f(a)$ for every $w\in W$ and every $a\in V$ (this is easy to see; see for example Corollary 2.3 of [7]), so it vanishes on every hyperplane of ${\mathcal {H}}$. But if $f\not =0$, then the vanishing set of f must be of degree at most n, which contradicts the fact that, as ${\mathcal {H}}$ is not of type $A_1^{n}$, we have $|{\mathcal {H}}|>n$. Hence we must have $f=0$, and this gives the desired result. $\square$

Remark 3.12

In the paper [15], Hirschhorn et al. proved that if a circular pizza is cut into 4m slices by 2m cuts at equal angles to each other and if m people share the pizza by each taking every mth slice then they receive equal shares. If $m=4$, Frederickson gives a dissection-based proof of this fact on page 32 of [9], and Proposition 9.1 of [7] generalizes the result to pizzas of more general shapes. We cannot lift this result to the group K(V), because it does not hold in that group. For example, if we consider the pizza of Fig. 3, then it is not true in general that the sums of the perimeters of the pizza pieces in all the shares will be equal.

However, we can lift the generalization of the Hirschhorns’s result to the quotient $K_0(V)$ of the group K(V) by the subgroup generated by all the elements [C] with $C\in {\mathcal {C}}(V)$ contained in a line of V. More precisely, consider a Coxeter arrangement of type $I_2(2m)$ in ${\mathbb {R}}^2$ with m even and let W be the Coxeter group of this arrangement. Let $T_0,\ldots ,T_{4m-1}$ be the chambers of ${\mathcal {H}}$, indexed so that that $T_i$ and $T_{i+1}$ share a wall. Let $K\in {\mathcal {C}}(V)$ and $a\in V$. Suppose that K is stable by W and contains the convex hull of the set $\{w(a) : w\in W\}$. Then the quantity

$$\begin{aligned} \sum _{i=0}^3[T_{r+mi}\cap (K+a)] \in K_0(V), \end{aligned}$$

is independent of $0 \le r \le m-1$. (This implies the Hirschhorns’s result even in the case where k is odd: Just apply the previous statement with $m=2k$, and share the pizza between k people by giving the pth person the eight slices contained in the chambers $T_{2p+mi}$ and $T_{2p+1+mi}$, for $0 \le i \le 3$.)

Let us prove this result. Let $0 \le r \le m-2$. We want to show that

$$\begin{aligned} \sum _{i=0}^3[T_{r+im}\cap (K+a)]= \sum _{i=0}^3[T_{r+1+im}\cap (K+a)], \end{aligned}$$

in $K_0(V)$. Suppose that we know that

$$\begin{aligned} \sum _{i=0}^3[T_{r+im}\cap R_+(a)\cap (K+a)]= \sum _{i=0}^3[T_{r+1+im}\cap R_-(a)\cap (K+a)] \end{aligned}$$

(3.6)

in $K_0(V)$, where $R_{+}(a)$ and $R_{-}(a)$ are given by

$$\begin{aligned} R_\pm (a)=(V-R_0(a))\cap \bigcup _{\begin{array}{c} T\in {\mathscr {T}}({\mathcal {H}}) \\ (-1)^T=\pm 1 \end{array}} T. \end{aligned}$$

Then it remains to see that

$$\begin{aligned} \sum _{i=0}^3[T_{r+im}\cap R_0(a)\cap (K+a)]= \sum _{i=0}^3[T_{r+1+im}\cap R_0(a)\cap (K+a)], \end{aligned}$$

in that same quotient. But now all the regions appearing in the sums are polygons, so the equality of the sums of their classes in $K_0(V)$ is equivalent to the equality of the sums of their areas, by the Bolyai–Gerwien Theorem; see [2, Sect. 5]. This last equality follows either from Proposition 9.1 of [7], or from the Hirschhorns’s result. (The Hirschhorns only consider the case of a circular pizza, but, by Eq. (3.6), their result for a circular pizza implies the result for the polygonal pizza $R_0(a)$.)

We first suppose that r is even. To prove Eq. (3.6), we suppose that $T_0,\ldots ,T_{2m-1}$ denote the same chambers as in the proof of Lemma 3.10, and we use the notation of that proof. In particular, for $0\le i\le 2m-1$, the chamber $T_{2m+i}$ is equal to the region $R_{i,\epsilon }$, where $\epsilon$ is the sign $(-1)^{i}$. We have $T_r\cap R_+(a)=S_{r/2,+}\cup R_{r+1,+}$, $T_{r+m}\cap R_+(a)=S_{(r+m)/2,+}\cup R_{r+m+1,+}$, $T_{r+2m}\cap R_+(a)=T_{r+2m}=R_{r,+}$ and $T_{r+3m}\cap R_+(a)= T_{r+3m}=R_{r+m,+}$. On the other hand, we have $T_{r+1}\cap R_-(a)=S_{r/2,-}\cup R_{r,-}$, $T_{r+1+m}\cap R_-(a)=S_{(r+m)/2,-}\cup R_{r+m,-}$, $T_{r+1+2m}\cap R_-(a)=T_{r+1+2m}=R_{r+1,-}$ and $T_{r+1+3m}\cap R_-(a)= T_{r+1+3m}=R_{r+m+1,-}$. This implies Eq. (3.6).

We now consider the case where r is odd. We again suppose that $T_0,\ldots ,T_{2m-1}$ denote the same chambers as in the proof of Lemma 3.10 and the notation of that lemma, but we use a different dissection, that is illustrated in Fig, 4 in the case $m=4$. For $0\le i\le 2m-2$, we consider the same region $R_{i,\pm }$ as in the proof of Lemma 3.10, but we denote by $R'_{2m-1,-}$ the chamber $T_{2m-1}$. For every $1 \le j \le m-1$, we denote by $R'_{2j-1,+}$ (respectively, $R'_{2j,-}$) the orthogonal reflection of $R_{2j,+}$ (respectively, $R_{2j+1,-}$) in the line $L_{2j}^\perp +a$; note that $R'_{2j-1,+}\subset T_{2j}$ and $R'_{2j,-}\subset T_{2j-1}$. We also denote by $R'_{0,-}$ (respectively, $R'_{2m-1,+}$) the orthogonal reflection of $R_{0,+}$ (respectively, $R'_{2m-1,-}$) in the line $L_{m}^\perp +a$. For $1 \le j \le m-1$ again, we denote by $S'_{j,-}$ the interior of $T_{2j-1} -(R_0(a)\cup R'_{2j,-})$ and by $S'_{j,+}$ the interior of $T_{2j} - (R_0(a)\cup R'_{2j-1,+})$. Finally, we denote by $S'_{0,-}$ the interior of $T_{4m-1}-(R_0(a)\cup R'_{0,-})$ and $S'_{0,+}$ the interior of $T_0-(R_0(a)\cup R'_{2m-1,+})$.

Fig. 4

The dissection that we use for odd r in the case of $I_2(8)$

For $0\le i\le 2m-2$, the chamber $T_{2m+i}$ is then equal to the region $R_{i,\epsilon }$, where $\epsilon$ is the sign $(-1)^{i}$; also, the chamber $T_{2m-1}$ is equal to $R'_{2m-1,-}$. We have $T_r\cap R_-(a)=S_{(r+1)/2,-}\cup R_{r+1,-}$, $T_{r+m}\cap R_-(a)=S_{(r+m+1)/2,-}\cup R_{r+m+1,-}$, $T_{r+2m}\cap R_-(a)=T_{r+2m}=R_{r,-}$ and $T_{r+3m}\cap R_-(a)= T_{r+3m}=R_{r+m,-}$. On the other hand, we have $T_{r+1}\cap R_+(a)=S_{(r+1)/2,+}\cup R_{r,+}$, $T_{r+1+m}\cap R_+(a)=S_{(r+1+m)/2,+}\cup R_{r+m,+}$, $T_{r+1+2m}\cap R_+(a)=T_{r+1+2m}=R_{r+1,+}$ and $T_{r+1+3m}\cap R_+(a)= T_{r+1+3m}=R_{r+m+1,+}$. This implies Eq. (3.6).

As in Frederickson’s article, there should also be a dissection-based proof of the equality of areas that we use to finish the proof, but we were not courageous enough to look for it.

4 The Bolyai–Gerwien Theorem

The classical Bolyai–Gerwien Theorem states that two polygons are scissors congruent if and only if they have the same area. There is also a well-known generalization in higher dimensions that applies to parallelotopes; it follows from the characterization of translational scissors congruences in arbitrary dimensions, and was proved independently by Jessen-Thorup and Sah; see the beginning of Section 7 of [17] or Theorem 1.1 in Chapter 4 of [20]. In this section, we state a slight refinement of this generalization, Theorem 4.1, that keeps track of lower-dimensional faces; in other words, we do not want to ignore the boundaries.

As in the previous sections, let V be an n-dimensional real vector space with an inner product $(\cdot ,\cdot )$. If $(v_1,\ldots ,v_r)$ is a linearly independent list of elements of V, we define the parallelotope

$$\begin{aligned} P(v_1,\ldots ,v_r)=\left\{ \sum _{i=1}^r a_i v_i : 0\le a_i\le 1\right\} . \end{aligned}$$

We denote by ${\mathcal {P}}(V)$ the set of all convex polytopes in V (including lower-dimensional ones) and by ${\mathcal {Z}}(V)$ the subfamily of polytopes that are translates of parallelotopes of the form $P(v_1,\ldots ,v_r)$. The set ${\mathcal {P}}(V)$ satisfies the conditions of Definition 3.1, so we can define an abelian group $K_{\mathcal {P}}(V)$ as in that definition. We denote by $K_{\mathcal {Z}}(V)$ the subgroup of $K_{\mathcal {P}}(V)$ generated by the classes [P] for $P\in {\mathcal {Z}}(V)$. Remark 3.3 implies that, if $\mathcal {P_{\textrm{ext}}}(V)$ is the relative Boolean algebra generated by ${\mathcal {P}}(V)$, then we can define the class [P] in $K_{\mathcal {P}}(V)$ of any element P in $\mathcal {P_{\textrm{ext}}}(V)$. We denote by $\mathcal {Z_{\textrm{ext}}}(V)$ the set of elements P of $\mathcal {P_{\textrm{ext}}}(V)$ such that $[P]\in K_{\mathcal {P}}(V)$ is in the subgroup $K_{\mathcal {Z}}(V)$. For example, the set $\mathcal {Z_{\textrm{ext}}}(V)$ contains ${\mathcal {Z}}(V)$, and it also contains all half-open parallelotopes.

Recall $V_0,\ldots ,V_n$ denotes the intrinsic volumes on V; see [21, Sect. 4.2]. These are valuations on the set of all compact convex subsets of V, and in particular on ${\mathcal {P}}(V)$, so they induce morphisms of groups from $K_{\mathcal {P}}(V)$ to ${\mathbb {R}}$, which we still denote by $V_0,\ldots ,V_n$. Note that $V_0$ is the Euler-Poincaré characteristic with compact support, so the image of $K_{\mathcal {P}}(V)$ is ${\mathbb {Z}}$.

The main result of this section is the following isomorphism.

Theorem 4.1

The morphism $(V_0,V_1,\ldots ,V_n):K_{\mathcal {Z}}(V)\longrightarrow {\mathbb {Z}}\times {\mathbb {R}}^n$ is an isomorphism. In particular, if $P,P'\in \mathcal {Z_{\textrm{ext}}}(V)$ are such that $V_i(P)=V_i(P')$ for every $0 \le i \le n$, then $[P]=[P']$ in $K_{\mathcal {Z}}(V)$.

We will give the proof of the theorem at the end of this section.

Corollary 4.2

Suppose that $\dim (V)=2$. Then the triple $(V_0,V_1,V_2)$ induces an isomorphism from $K_{\mathcal {P}}(V)$ to ${\mathbb {Z}}\times {\mathbb {R}}^2$. In particular, if $P,P'$ are two elements of $\mathcal {P_{\textrm{ext}}}(V)$, then their classes in $K_{\mathcal {P}}(V)$ are equal if and only if $V_i(P)=V_i(P')$ for all $0 \le i \le 2$.

Proof

By Theorem 4.1 it suffices to prove that $K_{\mathcal {P}}(V)=K_{\mathcal {Z}}(V)$. As points and segments are parallelotopes, it suffices to prove that every polygon P is scissors congruent to a parallelogram, which follows from the Bolyai–Gerwien Theorem (see [2, Sect. 5]). $\square$

Remark 4.3

• (1) If we take the quotient $K_{{\mathcal {P}},0}(V)$ of $K_{\mathcal {P}}(V)$ by the subgroup generated by the classes of lower-dimensional polytopes, then two polytopes have the same class in $K_{{\mathcal {P}},0}(V)$ if and only if they are scissors congruent, and the Bolyai–Gerwien Theorem (see [2, Sect. 5]), says that, if $\dim (V)=2$, the area $V_2$ induces an isomorphism from $K_{{\mathcal {P}},0}(V)$ to ${\mathbb {R}}$.

• (2) If $\dim (V)\ge 3$, then $K_{\mathcal {Z}}(V)\not = K_{\mathcal {P}}(V)$. Otherwise, every element of ${\mathcal {P}}(V)$ of positive volume would be scissors congruent to an element of ${\mathcal {Z}}(V)$, hence to a cube, and this is not true by the negative solution to Hilbert’s third problem (see for example [2]).

Let ${\mathcal {Z}}'(V)$ be the set of translates of parallelotopes of the form $P(v_1,\ldots ,v_r)$, for $(v_1,\ldots ,v_r)$ a linearly independent family of elements of V such that $r\le n-1$, and let $K'_{\mathcal {Z}}(V)$ be the subgroup of $K_{\mathcal {Z}}(V)$ generated by the classes of elements of ${\mathcal {Z}}'(V)$. We also write $\mathcal {Z_{\textrm{ext}}'}(V)$ for the set of $P\in \mathcal {Z_{\textrm{ext}}}(V)$ such that $[P]\in K'_{\mathcal {Z}}(V)$.

If $P,P'\in {\mathcal {Z}}(V)$, we write $P\sim P'$ if there exist $P_1,\ldots ,P_r,Q_1,\ldots ,Q_s\in \mathcal {P_{\textrm{ext}}}(V)$, $a_1,\ldots ,a_r$, $b_1,\ldots ,b_s\in V$ and $R,R'\in \mathcal {Z_{\textrm{ext}}'}(V)$ such that

$$\begin{aligned}{} & {} P\sqcup Q_1\sqcup \cdots \sqcup Q_s=R\sqcup P_1\sqcup \cdots \sqcup P_r \text { and } \\{} & {} P'\sqcup (Q_1+b_1)\sqcup \cdots \sqcup (Q_s+b_s)=R'\sqcup (P_1+a_1)\sqcup \cdots \sqcup (P_r+a_r). \end{aligned}$$

It is not hard to see that this is an equivalence relation, and that equivalent parallelotopes have the same volume.

Lemma 4.4

Let $W,W'$ be subspaces of V such that $V=W\times W'$. We do not assume that W and $W'$ are orthogonal. Let $P,P'\in {\mathcal {Z}}(W)$ and $S,S'\in {\mathcal {Z}}(W')$ such that $P\sim P'$ and $S\sim S'$. Then the relation $P\times S\sim P'\times S'$ holds.

Proof

As $\sim$ is transitive and as W and $W'$ play symmetric roles, it suffices to treat the case where $S=S'$. We choose $P_1,\ldots ,P_r,Q_1,\ldots ,Q_s\in \mathcal {P_{\textrm{ext}}}(W)$, $a_1,\ldots ,a_r,b_1,\ldots ,b_s\in W$ and $R,R'\in \mathcal {Z_{\textrm{ext}}'}(W)$ such that

$$\begin{aligned}{} & {} P\sqcup Q_1\sqcup \cdots \sqcup Q_s=R\sqcup P_1\sqcup \cdots \sqcup P_r \text { and } P'\sqcup (Q_1+b_1)\sqcup \cdots \sqcup (Q_s+b_s) \\{} & {} \quad = R'\sqcup (P_1+a_1)\sqcup \cdots \sqcup (P_r+a_r). \end{aligned}$$

Then

$$\begin{aligned} (P\times S)\sqcup (Q_1\times S)\sqcup \cdots \sqcup (Q_s\times S) =(R\times S)\sqcup (P_1\times S)\sqcup \cdots \sqcup (P_r\times S), \end{aligned}$$

and

$$\begin{aligned}{} & {} (P'\times S)\sqcup ((Q_1\times S)+b_1)\sqcup \cdots \sqcup ((Q_s\times S)+b_s) \\{} & {} \quad = (R'\times S)\sqcup ((P_1\times S)+a_1)\sqcup \cdots \sqcup ((P_r\times S)+a_r). \end{aligned}$$

As $R\times S$ and $R'\times S$ are in $\mathcal {Z_{\textrm{ext}}'}(V)$, this implies that $P\times S\sim P'\times S$. $\square$

For two real numbers $a, b \in {\mathbb {R}}$ recall that the half open interval is given by $(a,b] = \{t\in {\mathbb {R}}:a<t\le b\}$ and the closed interval by $[a,b] = \{t\in {\mathbb {R}}:a\le t\le b\}$.

Lemma 4.5

Let $(v_1,\ldots ,v_n)$ and $(w_1,\ldots ,w_n)$ be bases of V, and let $P=P(v_1,\ldots ,v_n)$ and $P'=P(w_1,\ldots ,w_n)$. Then $V_n(P)=V_n(P')$ if and only if there exists an isometry g of V such that $P\sim g(P')$.

In particular, if $V={\mathbb {R}}^n$, then, for every $P\in {\mathcal {Z}}(V)$, the classes of P and of $(0,1]^{n-1}\times (0,V_n(P)]$ in $K_{\mathcal {Z}}(V)$ are equal modulo $K'_{\mathcal {Z}}(V)$.

Proof

We already know that $V_n(P)=V_n(P')$ if $P\sim g(P')$ with g an isometry of V. We prove the converse by induction on n. It suffices to show that, for every basis $(v_1,\ldots ,v_n)$ of V, there exists an orthonormal basis $(e_1,\ldots ,e_n)$ of V and $a\in {\mathbb {R}}_{\ge 0}$ such that $P(v_1,\ldots ,v_n)\sim P(e_1,\ldots ,e_{n-1},a\cdot e_n)$; we then must have $a=V_n(P(v_1,\ldots ,v_n))$. There is nothing to prove if $n=0$, and the claim is clear if $n=1$. Suppose that $n=2$. The classical proofs that two parallelograms that have the same basis and the same height are scissors congruent and that rectangles that have parallel sides and the same area are scissors congruent use only translations to move the pieces of the decompositions (see for example [8, Prop. 35] and Figure 30 on page 52 of [2]; we reproduce the relevant decompositions in Figures 5 and 6). As the boundaries of the polygons that we ignore when we are talking about scissors congruence are in $\mathcal {Z_{\textrm{ext}}'}(V)$ when $\dim (V)=2$, this gives the claim.

Fig. 5

Proof of Lemma 4.5

Fig. 6

Proof of Lemma 4.5

Suppose that $n\ge 3$. Let $(v_1,\ldots ,v_n)$ be a basis of V, and let $P=P(v_1,\ldots ,v_n)$. By the claim for $n=2$ and Lemma 4.4, there exists an orthonormal basis $(e_1,e_2)$ of ${{\,\textrm{Span}\,}}(v_1,v_2)$ and $a\in {\mathbb {R}}_{\ge 0}$ such that $P\sim P(e_1,a\cdot e_2,v_3,\ldots ,v_n)$. Applying the $n=2$ case in ${{\,\textrm{Span}\,}}(e_1,v_3)$ and Lemma 4.4, we can find $v'_3\in {{\,\textrm{Span}\,}}(e_1,v_3)$ orthogonal to $e_1$ such that $P\sim P(e_1,a\cdot e_2,v'_3,v_4,\ldots ,v_n)$. Now applying the $n=2$ case in ${{\,\textrm{Span}\,}}(e_2,v'_3)$, noting that this space is orthogonal to $e_1$, and using Lemma 4.4, we can find a unit vector $e_3\in {{\,\textrm{Span}\,}}(e_2,v'_3)$ that is orthogonal to $e_1$ and $e_2$ and $b\in {\mathbb {R}}_{\ge 0}$ such that $P\sim P(e_1,e_2,b\cdot e_3,v_4,\ldots ,v_n)$. Continuing in this way, we finally obtain the claim.

We prove the last sentence of the lemma. If P is a translate of $P(v_1,\ldots ,v_k)$ with $k\le n-1$, then the classes of P and of $(0,1]^{n-1}\times (0,V_n(P)]$ are both in $K'_{\mathcal {Z}}(V)$. Suppose that P is a translate of $P(v_1,\ldots ,v_n)$, with $(v_1,\ldots ,v_n)$ a basis of V. By the first assertion, there exists an isometry g of V such that $g\cdot P\sim [0,1]^{n-1}\times [0,V_n(P)]$, so the classes of P and of $[0,1]^{n-1}\times [0,V_n(P)]$ in $K_{\mathcal {Z}}(V)$ are equal modulo $K'_{\mathcal {Z}}(V)$. As the difference between the classes of $[0,1]^{n-1}\times [0,V_n(P)]$ and of $(0,1]^{n-1}\times (0,V_n(P)]$ is in $K'_{\mathcal {Z}}(V)$, the result follows. $\square$

Lemma 4.6

(i):

Let H be a hyperplane of V. The inclusion ${\mathcal {Z}}(H)\subset {\mathcal {Z}}(V)$ induces a morphism $K_{\mathcal {Z}}(H)\longrightarrow K_{\mathcal {Z}}(V)$ whose image is $K'_{\mathcal {Z}}(V)$.²

(ii):

The subgroup $K'_{\mathcal {Z}}(V)$ is the kernel of the morphism $V_n:K_{\mathcal {Z}}(V)\longrightarrow {\mathbb {R}}$.

Proof

• (i) The existence of the morphism $K_{\mathcal {Z}}(H)\longrightarrow K_{\mathcal {Z}}(V)$ is clear, as well as the fact that its image is contained in $K'_{\mathcal {Z}}(V)$. Conversely, any translate of $P(v_1,\ldots ,v_k)$ with $k\le n-1$ can be moved by an affine isometry to lie in H, so its class is in the image of $K_{\mathcal {Z}}(H)$.

• (ii) We may assume that $V={\mathbb {R}}^n$. Any polytope in ${\mathcal {Z}}'(V)$ has volume zero, so $K'_{\mathcal {Z}}(V)$ is included in the kernel of $V_n$. We prove the reverse inclusion. Let x be an element of ${{\,\textrm{Ker}\,}}V_n$, and write $x=\sum _{i=1}^r\alpha _i[P_i]$, with $\alpha _i\in \{\pm 1\}$ and $P_i\in {\mathcal {Z}}(V)$. We want to show that $x\in K'_{\mathcal {Z}}(V)$. By Lemma 4.5, for every $1 \le i \le r$, the class of $P_i$ is equal to the class of $(0,1]^{n-1}\times (0,V_n(P_i)]$ modulo $K'_{\mathcal {Z}}(V)$. So x is equal modulo $K'_{\mathcal {Z}}(V)$ to the sum

  $$\begin{aligned} \sum _{i=1}^{r} \alpha _i[(0,1]^{n-1}\times (0,V_n(P_i)]]= [(0,1)^{n-1}\times (0,V_+]]-[(0,1]^{n-1}\times (0,V_-]], \end{aligned}$$

  where $V_{\pm }=\sum _{1\le i\le r,\ \alpha _i=\pm 1}{{\,\textrm{Vol}\,}}(P_i)$. As $V_+-V_-=V_n(x)=0$ by assumption, we conclude that $x\in K'_{\mathcal {Z}}(V)$.

$\square$

Proof of Theorem 4.1

Let $V_*=(V_0,V_1,\ldots ,V_n):K_{\mathcal {Z}}(V)\longrightarrow {\mathbb {Z}}\times {\mathbb {R}}^n$. Then the morphism $V_*$ sends the class of a point to $(1,0,\ldots ,0)$, so its image contains the factor ${\mathbb {Z}}$. Denote by $(e_1,\ldots ,e_n)$ the canonical basis of ${\mathbb {R}}^n$. If $i\in \{1,\ldots ,n\}$ and $a\in {\mathbb {R}}_{\ge 0}$, then by Lemma 3.6$V_*$ sends the class of the half-open rectangular parallelotope $(0,1]^{i-1}\times (0,a]\times \{0\}^{n-i}$ to $(0,a\cdot e_i)\in {\mathbb {Z}}\times {\mathbb {R}}^n$, so the image of $V_*$ contains ${\mathbb {R}}\cdot e_i$. This shows that $V_*$ is surjective.

We now prove the injectivity of $V_*$ by induction on $\dim (V)$. If $\dim (V)=0$, the result is clear. Suppose that $\dim (V)>0$ and that we know the result for spaces of smaller dimension. Let $x\in K_{\mathcal {Z}}(V)$ such that $V_i(x)=0$ for $0\le i\le n$. In particular, we have $V_n(x)=0$, so $x\in K'_{\mathcal {Z}}(V)$ by Lemma 4.6(ii). Let H be a hyperplane of V. Then x is in the image of the morphism $K_{\mathcal {Z}}(H)\longrightarrow K_{\mathcal {Z}}(V)$ by Lemma 4.6(ii); choose a preimage $y\in K_{\mathcal {Z}}(H)$ of x. If $0\le i\le n-1$, then we have $V_i(y)=V_i(x)$ because intrinsic volumes do not depend on the dimension of the ambient space (see the top of page 214 of [21]), so $V_i(y)=0$. It follows from the induction hypothesis that $y=0$, and we conclude that $x=0$. $\square$