Abstract
We prove that the stack-number of the strong product of three n-vertex paths is \(\Theta (n^{1/3})\). The best previously known upper bound was O(n). No non-trivial lower bound was known. This is the first explicit example of a graph family with bounded maximum degree and unbounded stack-number. The main tool used in our proof of the lower bound is the topological overlap theorem of Gromov. We actually prove a stronger result in terms of so-called triangulations of Cartesian products. We conclude that triangulations of three-dimensional Cartesian products of any sufficiently large connected graphs have large stack-number. The upper bound is a special case of a more general construction based on families of permutations derived from Hadamard matrices. The strong product of three paths is also the first example of a bounded degree graph with bounded queue-number and unbounded stack-number. A natural question that follows from our result is to determine the smallest \(\Delta _0\) such that there exists a graph family with unbounded stack-number, bounded queue-number and maximum degree \(\Delta _0\). We show that \(\Delta _0\in \{6,7\}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Stack layouts are ubiquitous objects at the intersection of combinatorics, geometry and topology with applications in computational complexity [14, 15, 26, 34], RNA folding [38], graph drawing in two [5, 56] and three dimensions [59], traffic light scheduling [45], and fault-tolerant multiprocessing [19, 55].
For a graphFootnote 1G and ordering \((v_1,\dots ,v_n)\) of V(G), two edges \(v_iv_j,v_kv_\ell \in E(G)\) cross with respect to \((v_1,\dots ,v_n)\) if \(i<k<j<\ell \). For \(s\in \mathbb {N}_0\), an s-stack layout of G consists of an ordering \((v_1,\ldots ,v_n)\) of V(G) together with a function \(\phi :E(G) \rightarrow \{1,\dots ,s\}\) such that for each \(a\in \{1,\dots ,s\}\) no two edges in \(\phi ^{-1}(a)\) cross with respect to \((v_1,\dots ,v_n)\); see Fig. 1 for an example. Each set \(\phi ^{-1}(a)\) is called a stack. Edges in a stack behave in a last-in-first-out manner (hence the name). Stack layouts can also be viewed topologically via embeddings into books (first defined by Ollmann [50]). The stack-number \({{\,\textrm{sn}\,}}(G)\) of a graph G is the minimum \(s\in \mathbb {N}_0\) for which there exists an s-stack layout of G (also known as page-number, book-thickness, or fixed outer-thickness).
Stack layouts have been studied for planar graphs [9, 17, 41, 62, 63], graphs of given genus [31, 42, 49], treewidth [29, 30, 35, 58], minor-closed graph classes [12], 1-planar graphs [2, 7, 8, 16], and graphs with a given number of edges [48], amongst other examples.
This paper studies stack layouts of 3-dimensional products. As illustrated in Fig. 2, for graphs \( G_1 \) and \( G_2 \), the Cartesian product \(G_1\square G_2\) is the graph with vertex-set \( V(G_1) \times V(G_2) \) with an edge between two vertices (x, y) and \( (x',y') \) if \(x=x'\) and \( yy' \in E(G_2) \), or \(y=y'\) and \(xx'\in E(G_1) \). The strong product \(G_1 \boxtimes G_2\) is the graph obtained from \(G_1\square G_2\) by adding edges \((x,y)(x',y')\) and \((x,y')(x',y)\) for all edges \(xx' \in E(G_1)\) and \(yy' \in E(G_2)\). Since the Cartesian and strong products are associative, we may write \(G_1\square G_2\square G_3\) and \(G_1\boxtimes G_2\boxtimes G_3\) (identifying pairs of the forms \(((v_1, v_2), v_3)\) and \((v_1, (v_2, v_3))\) with the triple \((v_1, v_2, v_3)\)).
Let \(P_n\) denote the n-vertex path. Our first main result is the following tight bound on the stack-number of the strong product of three paths (the 3-dimensional grid plus crosses).
Theorem 1.1
\({{\,\textrm{sn}\,}}(P_n \boxtimes P_n \boxtimes P_n) \in \Theta (n^{1/3})\).
Note that \((P_n \boxtimes P_n) \square P_n\) and \((P_n \square P_n) \boxtimes P_n\) both have bounded stack-number, as we now explain. Bernhart and Kainen [10] showed that if \(G_1\) and \(G_2\) are graphs with bounded stack-number and \(G_1\) is bipartite with bounded maximum degree, then the stack-number of \(G_1 \square G_2\) is bounded. Pupyrev [54] showed that if additionally \(G_2\) has bounded pathwidth, then the stack-number of \(G_1 \boxtimes G_2\) is also bounded. Since the Cartesian product is commutative, these results imply that \((P_n \boxtimes P_n) \square P_n\) and \((P_n \square P_n) \boxtimes P_n\) indeed have bounded stack-number. This shows that in Theorem 1.1, we cannot replace even one ‘strong product’ by a ‘Cartesian product’.
No non-trivial lower bound on \({{\,\textrm{sn}\,}}(P_n\boxtimes P_n\boxtimes P_n)\) was previously known. Indeed, Theorem 1.1 provides the first explicit example of a graph family with bounded maximum degree and unbounded stack-number. Malitz [48] first proved that graphs of maximum degree 3 have unbounded stack-number (using a probabilistic argument). Further motivation for Theorem 1.1 is provided in Sect. 2 where we present various connections to related graph parameters, shallow/small minors and growth.
We now discuss the lower bound in Theorem 1.1. We actually prove a stronger result that depends on the following definitions. For graphs \(G_1\) and \(G_2\), a triangulation of \(G_1\square G_2\) is any graph obtained from \(G_1\square G_2\) by adding the edge \((x,y)(x',y')\) or \((x,y')(x',y)\) for each \(xx'\in E(G_1)\) and \(yy'\in E(G_2)\). A triangulation of \(G_1 \square G_2 \square G_3\) is any graph obtained by triangulating all subgraphs induced by sets of the form \(\{v_1\} \times V(G_2) \times V(G_3)\), \(V(G_1) \times \{v_2\} \times V(G_3)\), and \(V(G_1)\times V(G_2) \times \{v_3\}\) with \(v_i \in V(G_i)\); see Fig. 2(c) for an example.
For directed graphs \(G_1\) and \(G_2\), if \(U_i\) is the undirected graph underlying \(G_i\), then let  be the triangulation of \(U_1 \square U_2\) containing the edge \((x,y)(x',y')\) for all directed edges \((x,x')\in E(G_1)\) and \((y,y')\in E(G_2)\). Similarly, for directed graphs \(G_1\), \(G_2\), and \(G_3\), let
be the triangulation of \(U_1 \square U_2\) containing the edge \((x,y)(x',y')\) for all directed edges \((x,x')\in E(G_1)\) and \((y,y')\in E(G_2)\). Similarly, for directed graphs \(G_1\), \(G_2\), and \(G_3\), let  be the appropriate triangulation of \(U_1\square U_2\square U_3\). When using the notation
be the appropriate triangulation of \(U_1\square U_2\square U_3\). When using the notation  or
or  , if some \(G_i\) is a path \(P_n\), then \(P_n\) is a directed path.
, if some \(G_i\) is a path \(P_n\), then \(P_n\) is a directed path.
Every triangulation of \(G_1\square G_2\) is a subgraph of \(G_1\boxtimes G_2\) and every triangulation of \(G_1\square G_2 \square G_3\) is a subgraph of \(G_1\boxtimes G_2 \boxtimes G_3\). So the next result immediately implies the lower bound in Theorem 1.1.
Theorem 1.2
Let \(T_1\), \(T_2\), and \(T_3\) be n-vertex trees with maximum degree \(\Delta _1\), \(\Delta _2\), and \(\Delta _3\) respectively, where \(\Delta _1\ge \Delta _2\ge \Delta _3\). Then for every triangulation G of \(T_1\square T_2\square T_3\),
Theorem 1.2 is similar in spirit to a recent result of Dujmović et al. [22], who showed that if \(S_n\) is the n-leaf star, then

Their proof actually establishes the following stronger resultFootnote 2:
Theorem 1.3
[22] For every triangulation G of \(P_n\square P_n\),
Theorem 1.2 has the advantage over Theorem 1.3 in that it applies to bounded degree graphs (for example when each \(T_i\) is a path). Moreover, the lower bound in Theorem 1.1 (as a function of the number of vertices) is much stronger than the lower bound of Theorem 1.3.
We prove Theorem 1.2 by relating the stack-number of a graph to the topological properties of its triangle complex. The triangle complex of a graph G, denoted by \({{\,\textrm{Tr}\,}}(G)\), is the 2-dimensional simplicial complex with 0-faces corresponding to vertices of G, 1-faces corresponding to edges of G, and 2-faces corresponding to triangles of G. For topological spaces X and Y, define
where C(X, Y) denotes the space of all continuous functions \(f:X \rightarrow Y\). In Sects. 3 and 4, respectively, we prove the following two lemmas.
Lemma 1.4
For all n-vertex trees \(T_1\), \(T_2\), and \(T_3\), and for every triangulation G of \(T_1 \square T_2 \square T_3\),
Lemma 1.5
For every graph G such that every vertex is in at most c triangles,
Lemma 1.4 has a natural geometric consequence: A straight-line drawing of a graph represents each vertex by a distinct point in the plane, and represents each edge by the line segment between its endpoints, such that the only vertices an edge intersects are its own endpoints. Let \(T_1\), \(T_2\), and \(T_3\) be n-vertex trees and let G be a triangulation of \(T_1 \square T_2 \square T_3\). Lemma 1.4 implies that for every straight-line drawing of G, there exists a point in the plane within \(\Omega (n)\) triangles of G.
Theorem 1.2 (and thus the lower bound in Theorem 1.1) follows from Lemmas 1.4 and 1.5 since (using the notation from Theorem 1.2) each vertex of G is in at most \(2(\Delta _1\Delta _2 + \Delta _1\Delta _3 + \Delta _2\Delta _3)\le 6\Delta _1\Delta _2\) triangles. So Lemma 1.5 is applicable with \(c=6\Delta _1\Delta _2\).
The lower bound on \({{\,\textrm{sn}\,}}(G)\) in Theorem 1.2 is non-trivial only if \(\Delta _1\Delta _2\in o(n)\). Nevertheless, we have the following result with no assumption on the maximum degree. Theorems 1.2 and 1.3 imply that the stack-numbers of triangulations of \(P_n \square P_n \square P_n\) and \(S_n \square P_n \square P_n\) grow with \(n\). Moreover, \(S_n \square S_n\) contains a subgraph isomorphic to a \(1\)-subdivision of \(K_{n, n}\), so its stack-number grows with \(n\) as well (see [13, 32]). Since every sufficiently large connected graph contains a copy of \(P_n\) or \(S_n\), we deduce the following.
Corollary 1.6
For every \(s\in \mathbb {N}\), there exists \(n\in \mathbb {N}\) such that for all n-vertex connected graphs \(G_1\), \(G_2\), and \(G_3\), if G is any triangulation of \(G_1\square G_2\square G_3\), then \({{\,\textrm{sn}\,}}(G) > s\).
The best previously known upper bound on \({{\,\textrm{sn}\,}}(P_n\boxtimes P_n\boxtimes P_n)\) was O(n), which follows from Theorem 1 of Dujmović et al. [24] or from Corollary 1 of Pupyrev [54]. The upper bound in Theorem 1.1 follows from a more general result in Sect. 5, which says that for every graph G with bounded stack-number and bounded maximum degree, \({{\,\textrm{sn}\,}}(G \boxtimes P_n)\in O(n^{1/2-\varepsilon })\) for some \(\varepsilon >0\) that depends on the chromatic number of G. The proof is based on families of permutations derived from Hadamard matrices.
Our final results concern maximum degree. Theorem 1.2 implies that  is a family of graphs with maximum degree 12, unbounded stack-number and bounded queue-number (defined in Sect. 2). It is natural to ask what is the smallest bound on the maximum degree in such a family. We prove the answer is 6 or 7.
is a family of graphs with maximum degree 12, unbounded stack-number and bounded queue-number (defined in Sect. 2). It is natural to ask what is the smallest bound on the maximum degree in such a family. We prove the answer is 6 or 7.
Theorem 1.7
The least integer \(\Delta _0\) such that there exists a graph family with maximum degree \(\Delta _0\), unbounded stack-number and bounded queue-number satisfies \(\Delta _0 \in \{6, 7\}\).
The proof of the upper bound in Theorem 1.7 uses the same topological machinery used to prove Theorem 1.2, and is based on the tessellation of \(\mathbb {R}^3\) by truncated octahedra. The proof of the lower bound exploits a connection with clustered colouring.
2 Connections
This section provides further motivation for our results by discussing connections with related graph parameters, minors and growth.
Consider a graph G. The geometric thickness of G is the minimum \(k\in \mathbb {N}_0\) for which there is a straight-line drawing of G and a partition of E(G) into k plane subgraphs; see [4, 20, 29]. A k-stack layout of G defines such a drawing and edge-partition, where the vertices are drawn on a circle in the order given by the stack layout. Thus the geometric thickness of G is at most its stack-number. The slope-number of G is the minimum \(k\in \mathbb {N}_0\) for which there is a straight-line drawing of G with k distinct edge slopes; see [3, 4, 23, 27, 46, 51]. Since edges of the same slope do not cross, the geometric thickness of G is at most its slope-number.
Note that  has slope-number and geometric thickness at most 6 (simply project the natural 3-dimensional representation to the plane). Hence Theorem 1.1 provides a family of graphs with bounded slope-number, bounded geometric thickness, and unbounded stack-number. Eppstein [32] previously constructed a graph family with bounded geometric thickness and unbounded stack-number, but not with bounded slope-number (since the graphs in question have unbounded maximum degree).
has slope-number and geometric thickness at most 6 (simply project the natural 3-dimensional representation to the plane). Hence Theorem 1.1 provides a family of graphs with bounded slope-number, bounded geometric thickness, and unbounded stack-number. Eppstein [32] previously constructed a graph family with bounded geometric thickness and unbounded stack-number, but not with bounded slope-number (since the graphs in question have unbounded maximum degree).
For a graph G and ordering \((v_1,\dots ,v_n)\) of V(G), two edges \(v_iv_j,v_kv_\ell \in E(G)\) nest with respect to \((v_1,\dots ,v_n)\) if \(i< k< \ell <j\). For \(q\in \mathbb {N}_0\), a q-queue layout of G consists of an ordering \((v_1,\ldots ,v_n)\) of V(G) together with a function \(\phi :E(G) \rightarrow \{1,\dots ,q\}\) such that for each \(a\in \{1,\dots ,q\}\) no two edges in \(\phi ^{-1}(a)\) nest with respect to \((v_1,\dots ,v_n)\). Each set \(\phi ^{-1}(a)\) is called a queue. Edges in a queue behave in a first-in-first-out manner (hence the name). The queue-number \({{\,\textrm{qn}\,}}(G)\) of a graph G is the minimum \(q\in \mathbb {N}_0\) for which there exists a q-queue layout of G.
Stack and queue layouts are considered to be dual to each other [43]. However, for many years it was open whether there is a graph family with bounded queue-number and unbounded stack-number, or bounded stack-number and unbounded queue-number. Theorem 1.3 by Dujmović et al. [22] resolved the first question, since they also showed that  . Observe that a \(4\)-queue layout of
. Observe that a \(4\)-queue layout of  can be obtained by taking the lexicographical ordering \((v_1, \ldots , v_{n^3})\) of the vertices and letting \(\phi (v_i v_j)\) be determined by which of the sets \(\{1\}\), \(\{n, n+1\}\), \(\{n^2, n^2 + 1\}\), \(\{n^2 + n\}\) contains \(|i - j|\). By Theorem 1.1,
can be obtained by taking the lexicographical ordering \((v_1, \ldots , v_{n^3})\) of the vertices and letting \(\phi (v_i v_j)\) be determined by which of the sets \(\{1\}\), \(\{n, n+1\}\), \(\{n^2, n^2 + 1\}\), \(\{n^2 + n\}\) contains \(|i - j|\). By Theorem 1.1,  is therefore another graph family with queue-number at most 4 and unbounded stack-number. It remains open whether there is a graph family with bounded stack-number and unbounded queue-number.
is therefore another graph family with queue-number at most 4 and unbounded stack-number. It remains open whether there is a graph family with bounded stack-number and unbounded queue-number.
While stack-number is not bounded by a function of queue number in general, it is of interest to find graph classes for which this property holds. In Sect. 6, we show that the class of graphs with maximum degree 5 has this property, but the class of graphs with maximum degree 7 does not. Bipartite graphs are another class where stack-number is bounded by a function of queue-number [25, 53]. On the other hand, \(3\)-colourable graphs do not have this property, since  and
and  are \(3\)-colourable with bounded queue-number and unbounded stack-number by Theorems 1.2 and 1.3.
are \(3\)-colourable with bounded queue-number and unbounded stack-number by Theorems 1.2 and 1.3.
We now discuss the behaviour of stack- and queue-number with respect to taking minors. Let G, H, and J be graphs. Let \(r,s\in \mathbb {N}_0\) and let \(k\ge 0\) be a half-integer (that is, \(2k\in \mathbb {N}_0\)). H is a minor of G if a graph isomorphic to H can be obtained from G by vertex deletions, edge deletions, and edge contractions. A model of H in G is a function \(\mu \) with domain V(H) such that: \(\mu (v)\) is a connected subgraph of G; \(\mu (v)\cap \mu (w)=\emptyset \) for all distinct \(v,w\in V(G)\); and \(\mu (v)\) and \(\mu (w)\) are adjacent for every edge \(vw \in E(H)\). Observe that H is a minor of G if and only if G contains a model of H. For \(r\in \mathbb {N}_0\), if there exists a model \(\mu \) of H in G such that \(\mu (v)\) has radius at most r for all \(v \in V(H)\), then H is an r-shallow minor of G. For \(s\in \mathbb {N}_0\), if there exists a model \(\mu \) of H in G such that \(|V(\mu (v))|\le s\) for all \(v \in V(H)\), then H is an s-small minor of G. We say that J is an \(({\le }\,s)\)-subdivision of H if J can be obtained from H by replacing each edge by a path with at most s internal vertices. If every path that replaces an edge has exactly s vertices, then J is the s-subdivision of H. We say that H is a k-shallow topological minor of G if a subgraph of G is isomorphic to a \(({\le }\,2k)\)-subdivision of H. Note that if a graph H is an s-small minor or an s-shallow topological minor of a graph G, then H is an r-shallow minor of G whenever \({s\le r}\).
Blankenship and Oporowski [13] conjectured that stack-number is ‘well-behaved’ under shallow topological minors in the following sense:
Conjecture 2.1
[13] There exists a function f such that for every graph G and half-integer \(k\ge 0\), if H is any k-shallow topological-minor of G, then \({{\,\textrm{sn}\,}}(H) \le f({{\,\textrm{sn}\,}}(G),k)\).
Dujmović et al. [22] disproved Conjecture 2.1. Their proof used the following lemma by Dujmović and Wood [28].
Lemma 2.2
[28] For every graph G, if \(s = 1+2\lceil \log _2{{\,\textrm{qn}\,}}(G)\rceil \) then the s-subdivision of \(G\) has a 3-stack layout.
Lemma 2.2 implies that the 5-subdivision of  admits a 3-stack layout. Using Theorem 1.3, Dujmović et al. [22] concluded there exists a graph class \(\mathcal {G}\) with bounded stack-number for which the class of (5/2)-shallow topological minors of graphs in \(\mathcal {G}\) has unbounded stack-number. Thus stack-number is not well-behaved under shallow topological minors. We now prove an analogous result for small minors.
admits a 3-stack layout. Using Theorem 1.3, Dujmović et al. [22] concluded there exists a graph class \(\mathcal {G}\) with bounded stack-number for which the class of (5/2)-shallow topological minors of graphs in \(\mathcal {G}\) has unbounded stack-number. Thus stack-number is not well-behaved under shallow topological minors. We now prove an analogous result for small minors.
Theorem 2.3
There exists a graph class \(\mathcal {G}\) with bounded stack-number for which the class of 2-small minors of graphs in \(\mathcal {G}\) has unbounded stack-number.
Proof
Lemma 2.2 implies that the 5-subdivision of  admits a 3-stack layout. Since
admits a 3-stack layout. Since  has maximum degree at most 12 and \(12 \lceil {5}/{2}\rceil +1=37\), it follows that
has maximum degree at most 12 and \(12 \lceil {5}/{2}\rceil +1=37\), it follows that  is a 37-small minor of its 5-subdivision. Let \(\mathcal {G}_0\) be the class of graphs with stack-number at most \(3\), and for each \(i \in \mathbb {N}_0 \), let \(\mathcal {G}_{i+1}\) be the class of \(2\)-small minors of graphs in \(\mathcal {G}_i\). Thus, \(\mathcal {G}_{37}\) contains all \(37\)-small minors of graphs in \(\mathcal {G}_0\), including all graphs of the form
is a 37-small minor of its 5-subdivision. Let \(\mathcal {G}_0\) be the class of graphs with stack-number at most \(3\), and for each \(i \in \mathbb {N}_0 \), let \(\mathcal {G}_{i+1}\) be the class of \(2\)-small minors of graphs in \(\mathcal {G}_i\). Thus, \(\mathcal {G}_{37}\) contains all \(37\)-small minors of graphs in \(\mathcal {G}_0\), including all graphs of the form  . Hence, there exists \(i\in \{0,\dots ,37\}\) such that stack-number is bounded for \(\mathcal {G}_i\) and unbounded for \(\mathcal {G}_{i+1}\). \(\square \)
. Hence, there exists \(i\in \{0,\dots ,37\}\) such that stack-number is bounded for \(\mathcal {G}_i\) and unbounded for \(\mathcal {G}_{i+1}\). \(\square \)
In contrast to Theorem 2.3, queue-number is well-behaved under small minors. In fact, the following lemma shows it is even well-behaved under shallow minors, which is a key distinction between these parameters.
Lemma 2.4
[44] For every graph G and for every r-shallow minor H of G,
We now compare stack and queue layouts with respect to growth. The growth of a graph G is the function \(f_G:\mathbb {N}\rightarrow \mathbb {N}\) such that \(f_G(r)\) is the maximum number of vertices in a subgraph of G with radius at most r. Similarly, the growth of a graph class \(\mathcal {G}\) is the function \(f_{\mathcal {G}}:\mathbb {N}\rightarrow \mathbb {N}\cup \{\infty \}\) where \(f_{\mathcal {G}}(r)=\sup {\{f_G(r): G\in \mathcal {G}\}}\). A graph class \(\mathcal {G}\) has linear/quadratic/cubic/polynomial growth if \(f_{\mathcal {G}}(r)\in O(r)/O(r^2)/O(r^3)/O(r^d)\) for some \(d\in \mathbb {N}\). Let \(\mathbb {Z}_n^d\) be the d-fold strong product \(P_n\boxtimes \dots \boxtimes P_n\). Every subgraph of \(\mathbb {Z}^d_n\) with radius at most r has at most \((2r+1)^d\) vertices. Thus \((P_n\boxtimes P_n\boxtimes P_n)_{n\in \mathbb {N}}\) has cubic growth, so Theorem 1.1 implies that graph classes with cubic growth can have unbounded stack-number. In contrast, we now show that graphs with polynomial growth have bounded queue-number. Krauthgamer and Lee [47] established the following characterisation of graphs with polynomial growth.
Theorem 2.5
[47] Let G be a graph with growth \(f_G(r) \le c r^d\) for some \(c,d>0\). Then G is isomorphic to a subgraph of \(\mathbb {Z}_n^{\lfloor c' \cdot d \log d\rfloor }\) for some n, and for some \(c'\) depending only on c.
It follows from the upper bound on the queue-number of products by Wood [60] that \({{\,\textrm{qn}\,}}(\mathbb {Z}^d_n)\le ( 3^d-1)/2\). Theorem 2.5 therefore implies the following.
Corollary 2.6
If a graph G has growth \(f_G(r)\le cr^d\) for some \(c,d>0\), then \({{\,\textrm{qn}\,}}(G)\le 2^{c'd\log d}\), for some \(c'\) depending only on c.
3 Proof of Lemma 1.4
The topological arguments in this paper exclusively involve finite 2-dimensional topological simplicial complexesFootnote 3, and so for brevity we refer to such an object as simply a complex. The proof of Lemma 1.4 relies on a Topological Overlap Theorem of Gromov [36]. To use it we need a technical variation of the overlap parameter. For a complex X and topological space Y, define
where \(X^{=2}\) denotes the set of 2-dimensional cells of X. We now state the 2-dimensional case of Gromov’s theorem.
Theorem 3.1
[36, p. 419, topological \(\Delta \)-inequality] There exists \(\alpha >0\) such that
for every integer \(n \ge 3\).
We use Theorem 3.1 in combination with the following straightforward lemma to lower bound \({{\,\textrm{overlap}\,}}(X,\mathbb {R}^2)\) for a complex X in terms of \({{\,\textrm{overlap}\,}}_{\triangle }({{\,\textrm{Tr}\,}}(K_n),X)\).
Lemma 3.2
For every complex \(X_0\) and for all topological spaces X and Y,
Proof
Let \(f_0:X_0 \rightarrow X\) be a continuous function such that
Let \(f:X \rightarrow Y\) be an arbitrary continuous function. Then \(f_0 \circ f:X_0 \rightarrow Y\) is continuous and so there exists \(p_0 \in Y\) such that
But
It follows that
as desired. \(\square \)
A family \(\mathcal {B}\) of subcomplexes of a complex X is a bramble over XFootnote 4 if:
-
every \(B \in \mathcal {B}\) is non-empty,
-
\(B_1 \cup B_2\) is path-connectedFootnote 5 for every pair of distinct \(B_1,B_2 \in \mathcal {B}\),
-
\(B_1 \cup B_2 \cup B_3\) is simply connectedFootnote 6 for every triple of distinct \(B_1,B_2, B_3 \in \mathcal {B}\).
The congestion \({{\,\textrm{cong}\,}}(\mathcal {B})\) of a bramble \(\mathcal {B}\) is the maximum size of a collection of elements in \(\mathcal {B}\) that all share a point in common; that is,
Lemma 3.3
There exists \(\beta >0\) such that for every complex X and bramble \(\mathcal {B}\) over X,
Proof
Let \(\mathcal {B}=\{B_1,\ldots ,B_n\}\). Let \(X_0= {{\,\textrm{Tr}\,}}(K_n)\) be the triangle complex of the complete graph with vertex set \(\{v_1,\ldots ,v_n\}\). We construct a continuous map \(f:X_0 \rightarrow X\) as follows. Let \(p_i \in B_i\) be chosen arbitrarily, and set \(f(v_i)=p_i\) for every \(i \in \{1,\dots ,n\}\). Extend f to the 1-skeleton of \(X_0\) by mapping each edge \(v_i v_j\) to a path \(\pi _{ij} \subseteq B_i \cup B_j\) from \(p_i\) to \(p_j\).
Finally, we need to continuously extend f to the interior of every 2-simplex \(F_{ijk}\) of \(X_0\) with vertices \(v_i\), \(v_j\), and \(v_k\). Since \(B_i \cup B_j \cup B_k\) is simply connected, and the boundary of \(F_{ijk}\) is mapped to a closed curve in \(B_i \cup B_j \cup B_k\), there is such an extension such that \(f(F_{ijk}) \subseteq B_i \cup B_j \cup B_k\).
Consider arbitrary \(p \in X\) and let \(I = \{i \in \{1,\dots ,n\} \mid p \in B_i\}\). Then \(|I| \le {{\,\textrm{cong}\,}}(\mathcal {B})\) and
It follows that \({{\,\textrm{overlap}\,}}_{\triangle }(X_0,X) \le {3n^2}{{\,\textrm{cong}\,}}(\mathcal {B})/2\). Thus by Theorem 3.1 and Lemma 3.2,
where \(\alpha \) is from Theorem 3.1. It follows that \(\beta = {2}\alpha /3\) satisfies the lemma. \(\square \)
Lemma 3.3 allows one to lower bound \({{\,\textrm{overlap}\,}}(X,\mathbb {R}^2)\) by exhibiting a bramble with size large in comparison to its congestion. To simplify the verification of the conditions in the definition of a bramble we use a simple consequence of van Kampen’s theorem.Footnote 7
Lemma 3.4
Let \(B_1,B_2\) be subcomplexes of a complex X. If \(B_1\) and \(B_2\) are simply connected, and \(B_1 \cap B_2\) is non-empty and path-connected, then \(B_1 \cup B_2\) is simply connected.
Corollary 3.5
Let X be a complex. Let \(\mathcal {B}\) be a family of subcomplexes of X such that:
-
every \(B \in \mathcal {B}\) is simply connected,
-
\(B_1 \cap B_2\) is path-connected for every pair of distinct \(B_1,B_2 \in \mathcal {B}\),
-
\(B_1 \cap B_2 \cap B_3\) is non-empty for every triple of distinct \(B_1,B_2, B_3 \in \mathcal {B}\).
Then \(\mathcal {B}\) is a bramble over X.
Proof
The first condition in the definition of a bramble trivially holds. The second condition holds since \(B_1 \cup B_2\) is simply connected for all distinct \(B_1,B_2 \in \mathcal {B}\) by Lemma 3.4.
It remains to show \(B_1 \cup B_2 \cup B_3\) is simply connected for all distinct \(B_1,B_2, B_3 \in \mathcal {B}\). Since \(B_1 \cup B_2\) and \(B_3\) are simply connected, this follows from Lemma 3.4 as long as \(B_3 \cap (B_1 \cup B_2) = (B_3 \cap B_1) \cup (B_3 \cap B_2)\) is non-empty and path-connected. By the assumptions of the corollary, each of \(B_3\cap B_1\) and \(B_3 \cap B_2\) is path-connected and they share a point in common. Thus their union is path-connected as desired. \(\square \)
We are now ready to prove Lemma 1.4.
Proof of Lemma 1.4
Let G be any triangulation of \(T_1 \square T_2 \square T_3\), where \(T_1\), \(T_2\), and \(T_3\) are n-vertex trees. To simplify our notation we assume that \(T_1\), \(T_2\), and \(T_3\) are vertex-disjoint. We denote by \(\widehat{T}_i\) the 1-dimensional complex corresponding to \(T_i\), to avoid confusion between discrete and topological objects.
For \(u \in V(T_1)\), let G(u) be the subgraph of G induced by all the vertices of G with the first coordinate u. That is, \(V(G(u))=\{(u,u_2,u_3) \mid u_2 \in V(T_2),\,u_3 \in V(T_3)\}\). So G(u) is isomorphic to a triangulation of \(T_2 \square T_3\). Let \(X(u) = {{\,\textrm{Tr}\,}}(G(u))\). As a topological space, X(u) is homeomorphic to \(\widehat{T}_2 \times \widehat{T}_3\). Define G(u) and X(u) for \(u \in V(T_2) \cup V(T_3)\) analogously.
For \((u_1,u_2,u_3) \in V(G)\), let \(B(u_1,u_2,u_3)=X(u_1) \cup X(u_2) \cup X(u_3)\), and let \(\mathcal {B}= \{B(u_1,u_2,u_3) \mid (u_1,u_2,u_3) \in V(G) \}\). We claim that \(\mathcal {B}\) is a bramble over \({\text {Tr(G)}}\). It suffices to check that it satisfies the conditions of Corollary 3.5.
To verify the first condition for \( \mathcal {B} \), we use Corollary 3.5 to show that \(\{X(u_1),X(u_2),X(u_3)\}\) is a bramble over \({\text {Tr(G)}}\) for every \((u_1,u_2,u_3) \in V(G)\). Note that each \(\widehat{T}_i\) is simply connected. As the product of simply connected spaces is simply connected, it follows that X(u) is simply connected for every \(u \in V(T_1) \cup V(T_2) \cup V(T_3)\). Consider now \((u_1,u_2,u_3) \in V(G)\). Then \(X(u_1) \cap X(u_2)\) is homeomorphic to \(\widehat{T}_3\) and is path-connected. Similarly, \(X(u_1) \cap X(u_3)\) and \(X(u_2) \cap X(u_3)\) are path-connected. Finally, \(X(u_1) \cap X(u_2) \cap X(u_3)\) consists of a single point (and is path-connected). By Corollary 3.5 the set \(\{X(u_1),X(u_2),X(u_3)\}\) is a bramble. In particular, \(B(u_1,u_2,u_3)=X(u_1) \cup X(u_2)\cup X(u_3)\) is simply connected. Thus the first condition in Corollary 3.5 for \( \mathcal {B} \) holds.
For the second condition, consider distinct \(B(u_1,u_2,u_3), B(v_1,v_2,v_3) \in \mathcal {B}\). Let \(R = B(u_1,u_2,u_3) \cap B(v_1,v_2,v_3)\) for brevity. Assume first, for simplicity, that \(u_i \ne v_i\) for \(i \in \{1,2,3 \}\). Then
Each set \(X(u_i) \cap X(v_j)\) in this decomposition is path-connected, since it is homeomorphic to \(\widehat{T}_k\) for \(\{k\} = \{1,2,3\} \setminus \{i,j\}\). Moreover, when ordering these sets,
each pair of consecutive sets share a point, for example, \((u_1,v_2,u_3) \in (X(u_1) \cap X(v_2)) \cap (X(u_3) \cap X(v_2)).\) It follows that their union is path-connected.
It remains to consider the case \(u_i= v_i\) for some \(i \in \{1,2,3 \}\). Assume \(i=1\) without loss of generality. If \(u_2 \ne v_2\) and \(u_3 \ne v_3\) then \(R = X(u_1) \cup (X(u_2) \cap X(v_3)) \cup (X(v_2) \cap X(u_3))\). Each of the sets in this decomposition is again path-connected and the second and third sets intersect the first, implying that their union is path-connected. Finally, if say \(u_2=v_2\) then \(R= X(u_1) \cup X(u_2)\) and is again a union of path-connected intersecting sets. This verifies the second condition of Corollary 3.5 for \( \mathcal {B} \).
For the last condition, for any \(B(u_1,u_2,u_3), B(v_1,v_2,v_3),B(w_1,w_2,w_3) \in \mathcal {B}\),
and so \(B(u_1,u_2,u_3) \cap B(v_1,v_2,v_3) \cap B(w_1,w_2,w_3) \ne \emptyset \). By Corollary 3.5, \(\mathcal {B}\) is a bramble.
As noted above, \(|\mathcal {B}|=n^3\). Moreover, for every \(p \in {{\,\textrm{Tr}\,}}(G)\) and every \(i \in \{1,2,3\}\) there exists at most one \(v_i \in V(T_i)\) such that \(p \in X(v_i)\). Thus \({{\,\textrm{cong}\,}}(\mathcal {B}) \le 3n^2\), and by Lemma 3.3,
as desired. \(\square \)
Note that \({{\,\textrm{Tr}\,}}(P_n\boxtimes P_n \boxtimes P_n)\) has a natural affine embedding into \(\mathbb {R}^3\) with vertices mapped to points in \(\{1,\dots ,n\}^{3}\). Since any line in a direction sufficiently close to an axis direction intersects this complex in \(n+O(1)\) points, projecting along such a direction we obtain an affine map \({{\,\textrm{Tr}\,}}(G) \rightarrow \mathbb {R}^2\) that covers every point at most \(n+O(1)\) times. Thus \({{\,\textrm{overlap}\,}}({{\,\textrm{Tr}\,}}(P_n \boxtimes P_n \boxtimes P_n), \mathbb {R}^2) \le n+O(1)\) and so the bound in Lemma 1.4 cannot be substantially improved.
4 Proof of Lemma 1.5
The proof of Lemma 1.5 depends on the following result.
Lemma 4.1
Let \(T_1,\dots ,T_m\) be pairwise vertex-disjoint pairwise intersecting triangles in \(\mathbb {R}^2\) with all the vertices on a circle S. Assume that the edges of \(T_1,\dots ,T_m\) can be partitioned into k non-crossing sets. Then \(m\le k^3\).
Proof
Number the vertices of \(T_1,\dots ,T_m\) by \(1,\dots ,3m\) in clockwise order starting at an arbitrary point on S. By assumption there is a function \(\phi :\bigcup _i E(T_i) \rightarrow \{1,\dots ,k\}\) such that \(\phi (e_1)\ne \phi (e_2)\) for all crossing edges \(e_1,e_2\in \bigcup _i E(T_i)\). Say the vertices of \(T_i\) are \((a_i,b_i,c_i)\) with \(a_i<b_i<c_i\). Define the function \(f :\{1,\dots ,m\}\rightarrow \{1,\dots ,k\}^3\) by \(f(i)=(\phi (a_ib_i),\phi (a_ic_i),\phi (b_ic_i))\). Suppose for the sake of contradiction that \(f(i)=f(j)\) for distinct \(i,j\in \{1,\dots ,m\}\). Thus \(a_ib_i\) does not cross \(a_jb_j\), \(a_ic_i\) does not cross \(a_jc_j\), and \(b_ic_i\) does not cross \(b_jc_j\). Without loss of generality, \(a_i<a_j\). Then \(a_j<c_i\) since \(T_i\) and \(T_j\) intersect. If \(c_i<c_j\) then \(a_ic_i\) crosses \(a_jc_j\), so \(a_i<a_j<b_j<c_j<c_i\). Now consider \(b_i\). If \(a_i<b_i<a_j\) or \(c_j<b_i<c_i\), then \(T_i\) and \(T_j\) do not intersect. So \(a_j<b_i<c_j\). If \(a_j<b_i<b_j\), then \(a_ib_i\) crosses \(a_jb_j\). Otherwise, \(b_j<b_i<c_j\) implying \(b_jc_j\) crosses \(b_ic_i\). This contradiction shows that \(f(i)\ne f(j)\) for distinct \(i,j\in \{1,\dots ,m\}\). Hence \(m\le k^3\). \(\square \)
Proof of Lemma 1.5
Let \(k={{\,\textrm{sn}\,}}(G)\), and let \((v_1,\ldots ,v_n)\) together with a function \(\phi :E(G) \rightarrow \{1,\dots ,k\}\) be a k-stack layout of G. Let \(p_1, p_2,\ldots , p_n\) be pairwise distinct points chosen on a circle S in \(\mathbb {R}^2\), numbered in cyclic order around S. Let \(X = {{\,\textrm{Tr}\,}}(G)\). Define a continuous function \(f:X \rightarrow \mathbb {R}^2\) by setting \(f(v_i)=p_i\) for all \(i \in \{1,\dots ,n\}\), extending f affinely to 2-simplices of X (triangles of G), and, for simplicity, mapping every edge of G that does not belong to a triangle continuously to a curve internally disjoint from S and its interior, so that every point of \(\mathbb {R}^2\) belongs to at most two such curves.
Let \(m'= {{\,\textrm{overlap}\,}}(X,\mathbb {R}^2)\). Then there exists \(p \in \mathbb {R}^2\) such that \(|f^{-1}(p)| \ge m'\). If \(m' \le 2\) the lemma trivially holds, and so we assume \(m'>2\). Since the restriction of f to each simplex of X is injective, there exist triangles \(T_1,T_2,\ldots , T_{m'} \subseteq \mathbb {R}^2\) corresponding to images of distinct 2-simplices of X so that \(p \in \bigcap _{i=1}^{m'}T_i\). Let \(m = \lceil {m'}/({3c-2})\rceil >{m'}/({3c})\). Since every triangle shares a vertex with at most \(3c-3\) others, we may assume that \(T_1,T_2,\ldots , T_{m}\) are pairwise vertex-disjoint by greedily selecting vertex-disjoint triangles among \(T_1,T_2,\ldots , T_{m'}\). By Lemma 4.1, \(m \le k^3\). Thus
\(\square \)
This lemma completes the proof of the lower bound in Theorem 1.1 as well as Theorem 1.2.
We finish this section by showing that Lemma 4.1 is best possible up to a constant factor.
Proposition 4.2
For infinitely many \(k\in \mathbb {N}\), there is a set of \((k/3)^3\) pairwise intersecting and pairwise vertex-disjoint triangles with vertices on a circle in \({\mathbb {R}}^2\), such that the edges of the triangles can be k-coloured with crossing edges assigned distinct colours.
This result is implied by the following (with \(k=3\cdot 2^\ell \)).
Lemma 4.3
Let S be a circle in \(\mathbb {R}^2\) partitioned into three pairwise disjoint arcs A, B, C. For every \(\ell \in \mathbb {N}_0\) there is a set \(\mathcal {T}\) of \(8^\ell \) triangles, each with one vertex in each of A, B, C, such that the AB-edges can be \(2^\ell \)-coloured with crossing edges assigned distinct colours, the BC-edges can be \(2^\ell \)-coloured with crossing edges assigned distinct colours, and the CA-edges can be \(2^\ell \)-coloured with crossing edges assigned distinct colours.
Proof
We proceed by induction on \(\ell \). The claim is trivial with \(\ell =0\). Assume that for some integer \(\ell \ge 0\), there is a set \(\mathcal {T}\) of \(8^\ell \) triangles satisfying the claim. Let X be the set of \(2^\ell \) colours used for the AB-edges. Let Y be the set of \(2^\ell \) colours used for the BC-edges. Let Z be the set of \(2^\ell \) colours used for the CA-edges. Let \(X'=\{x',x'\,|\,x\in X\}\) be a set of \(2^{\ell +1}\) colours. Let \(Y'=\{y',y'\,|\,y\in Y\}\) be a set of \(2^{\ell +1}\) colours. Let \(Z'=\{z',z''\,|\,z\in Z\}\) be a set of \(2^{\ell +1}\) colours. Let \(\mathcal {T}'\) be the set of triangles obtained by replacing each \(T\in \mathcal {T}\) by eight triangles as follows. Say the vertices of T are u, v, w where \(u\in A\), \(v\in B\), and \(w\in C\). Replace u by \(u_1,\dots ,u_8\) in clockwise order in A, replace v by \(v_1,\dots ,v_8\) in clockwise order in B, and replace w by \(w_1,\dots ,w_8\) in clockwise order in C. By this we mean that if p, q are consecutive vertices in the original ordering, then \(p_1,\dots ,p_8,q_1,\dots ,q_8\) are consecutive vertices in the enlarged ordering. Add the triangles \(u_1v_4w_6,u_2v_3w_5,u_3v_2w_8,u_4v_1w_7,u_5v_8w_2,u_6v_7w_1,u_7v_6w_4,u_8v_5w_3\) to \(\mathcal {T}'\). Say uv is coloured \(x\in X\), vw is coloured \(y\in Y\), and wv is coloured \(z\in Z\). Colour each of \(u_1v_4,u_2v_3,u_3v_2,u_4v_1\) by \(x'\in X'\), and colour each of \(u_5v_8,u_6v_7,u_7v_6,u_8v_5\) by \(x''\in X'\). Colour each of \(v_1w_7,v_3w_5,v_5w_3,v_7w_1\) by \(y'\in Y'\), and colour each of \(v_2w_8,v_4w_6,v_6w_4,v_8w_2\) by \(y''\in Y'\). Colour each of \(w_1u_6,w_2u_5,w_5u_2,w_6u_1\) by \(z'\in Z'\), and colour each of \(w_3u_8,w_4u_7, w_7u_4,w_8u_3\) by \(z''\in Z'\). As illustrated in Fig. 3, crossing edges are assigned distinct colours. Thus \(\mathcal {T'}\) is the desired set of \(8^{\ell +1}\) triangles. \(\square \)
Construction in the proof of Lemma 4.3
5 Upper Bound
This section proves the upper bound in Theorem 1.1 showing that \(P_n\boxtimes P_n\boxtimes P_n\) has an \(O(n^{1/3})\)-stack layout. Assume \(V(P_n) = \{1,\dots ,n\}\) and \(E(P_n) = \{i(i+1)\mid i \in \{1,\dots ,{n-1}\}\}\). We start with a sketch of the construction. Take a particular \(O(1)\)-stack layout and a proper \(4\)-colouring of \(P_n \boxtimes P_n\). In the corresponding ordering of \(V(P_n \boxtimes P_n)\) replace each vertex \((x, y)\) by vertices \(((x, y, z_1), \ldots , (x, y, z_n))\) where \((z_1, \ldots , z_n)\) is a permutation of \(\{1,\dots ,n\}\) determined by the colour of \((x, y)\). An appropriate choice of the permutations ensures that the edges of \(P_n \boxtimes P_n \boxtimes P_n\) can be partitioned into \(O(n^{1/3})\) stacks. See Fig. 4 for an illustration of the case \(n=8\).
A proper \(4\)-colouring of \(P_8 \boxtimes P_8\) and four permutations of \(\{1, \ldots , 8\}\). For \(n=8\), the stack layout of the graph \(P_n \boxtimes P_n \boxtimes P_n\) is obtained from a stack layout of \(P_n \boxtimes P_n\) by replacing each vertex by a permutation of vertices on the corresponding copy of \(P_n\). The permutation is determined by the colour of the vertex
We actually prove a more general result, Theorem 5.1 below, which relies on the following definition from the literature. An s-stack layout \(((v_1,\dots ,v_n),\psi )\) of a graph G is dispersable [1, 10, 54] (also called pushdown [26, 34]) if \(\psi ^{-1}(a)\) is a matching in G for each \(a\in \{1,\dots ,s\}\). The dispersable stack-number \({{\,\textrm{dsn}\,}}(G)\) is the minimum \(s \in \mathbb {N}_0\) for which there is a dispersable s-stack layout of G. For example, \({{\,\textrm{dsn}\,}}(P_n\boxtimes P_n)= 8\) since in the 4-stack layout of \(P_n \boxtimes P_n\) illustrated in Fig. 1, each stack is a linear forest; putting alternative edges from each path in distinct stacks produces a dispersable 8-stack layout. In general, \(\max {\{\Delta (G),{{\,\textrm{sn}\,}}(G)\}}\le {{\,\textrm{dsn}\,}}(G)\le (\Delta (G)+1){{\,\textrm{sn}\,}}(G)\) by Vizing’s Theorem. So a graph family has bounded dispersable stack-number if and only if it has bounded stack-number and bounded maximum degree.
Theorem 5.1
Let \(G\) be a graph with chromatic number \(\chi \) and dispersable stack-number \(d\). Let \(n \in \mathbb {N}\) and \(p = \max {\{2^{\lceil \log _2 \chi \rceil }, 2\}} \). Then
Since \(\chi (P_n \boxtimes P_n) \le 4\) and \({{\,\textrm{dsn}\,}}(P_n \boxtimes P_n) = 8\), Theorem 5.1 implies that
Furthermore, \(\chi (G) \le \Delta (G) + 1 \le {{\,\textrm{dsn}\,}}(G) + 1\). So Theorem 5.1 shows that graphs G with bounded dispersable stack-number satisfy \({{\,\textrm{sn}\,}}(G \boxtimes P_n)\in O(n^{1/2-\varepsilon })\) for some \(\varepsilon >0\).
For an even positive integer \(p\), an Hadamard matrix of order \(p\) is a \(p \times p\) matrix \(H\) with all entries in \(\{+1, -1\}\) such that every pair of distinct rows differs in exactly \(p/2\) entries. An example of an Hadamard matrix of order \(4\) is
Sylvester [57] proved that the order of an Hadamard matrix is \(2\) or is divisible by \(4\). He also constructed an Hadamard matrix whose order is any power of 2. Paley [52] constructed an Hadamard matrix of order \(q+1\) for any prime power \(q\equiv 3\) (mod 4), and an Hadamard matrix of order \(2(q+1)\) for any prime power \(q\equiv 1\) (mod 4). The Hadamard Conjecture proposes that there exists an Hadamard matrix of order \(p\) whenever \(p\) is divisible by 4. This conjecture has been verified for numerous values of p; see [21] for example.
To prove Theorem 5.1, we construct a stack layout of \( G \boxtimes P_n \) from a d-dispersable stack layout of G by replacing each vertex by a copy of the corresponding path \(P_n\). To determine the orderings of these paths, we use a family of permutations without long common subsequences by Beame et al. [6]. To avoid many pairwise crossing edges between two paths, it is necessary to choose permutations without long common subsequences. However, this is not sufficient because of the edges in \(G\boxtimes P_n\) between the i-th vertex and the \((i+1)\)-th vertex in distinct paths. To deal with this, the following lemma provides additional properties of the construction by Beame et al. [6].
Lemma 5.2
Assume there exists an Hadamard matrix of order \(p\). Let \(m \in \mathbb {N}\) and \(n = m^{p-1}\). Then there exist permutations \(\pi _1, \ldots , \pi _p :\{1,\dots ,n\} \rightarrow \{1,\dots ,n\}\) such that for all distinct \(k, \ell \in \{1,\dots ,p\}\),
and for each \(k \in \{1,\dots ,p\}\) there exists a \((2p-3)\)-stack layout of \(P_{n}\) using the vertex ordering \((\pi _k^{-1}(1), \ldots , \pi _k^{-1}(n))\).
Proof
Since there exists an Hadamard matrix of order \(p\), there exist \(\pm 1\)-vectors \(h_{1}, \ldots , h_p\) of length \(p\) each, such that any two of them differ in exactly \(p/2\) entries. Denote \(h_{k} = (h_{k}(0), \ldots , h_{k}(p-1))\) for each \(k\in \{1,\dots ,p\}\). By possibly negating all entries in some of these vectors, we may assume \(h_{k}(p-1) = +1\) for all \(k \in \{1,\dots ,p\}\).
For each \(i \in \{1,\dots ,n\}\), let \(d(i, 0), \ldots , d(i, p-2) \in \{0, \ldots , m-1\} \) denote the digits of \(i-1\) in base \(m\), so that
Note that the mapping \(\{1,\dots ,n\} \ni i \mapsto (d(i, 0), \ldots , d(i, p-2)) \in \{0, \ldots , m-1\}^{p-1}\) is bijective. For all \(k \in \{1,\dots ,p\}\), \(i \in \{1,\dots ,n\}\), and \(a \in \{0,\ldots ,p-2\}\), let
Observe that for any \(k, \ell \in \{1,\dots ,p\}\) and \(a \in \{0, \ldots , p-2\}\), if \(h_{k}(a)=-h_{\ell }(a)\) then \(d_{k}(i, a)+d_{\ell }(i, a)=m-1\) for all \(i \in \{1,\dots ,n\}\). For every \(k \in \{1,\dots ,p\}\), define \(\pi _k\) by
Note that each \(\pi _k\) is an involution; that is, \(\pi _k = \pi _k^{-1}\).
We claim that \(\pi _1, \ldots ,\pi _p\) satisfy the lemma. Fix distinct \(k, \ell \in \{1,\dots ,p\}\). For \(i, j \in \{1,\dots ,n\}\) and \(a \in \{0, \ldots , p-2\}\), define \(\tau _a(i, j) = d_{k}(i, a) + d_{\ell }(j, a)\), and let
Since \(\pi _{k}(i) + \pi _{\ell }(j) = 2+\sum _{a=0}^{p-2} \tau _a(i, j)m^a\), the value of \(\tau (i, j)\) determines the value of \(\pi _{k}(i) + \pi _{\ell }(j)\). As such, to prove the first part of the lemma it suffices to show that
Let \(A^+=\{a \in \{0, \ldots , p-2\}\,|\,h_{k}(a) = h_{\ell }(a)\}\) and \(A^- =\{a \in \{0, \ldots , p-2\}\, |\,h_{k}(a) = -h_{\ell }(a)\}\). Since \(h_{k}\) and \(h_{\ell }\) differ in exactly \(p/2\) entries and \(h_{k}(p-1) = +1 = h_{\ell }(p-1)\), we have \(|A^+| = p/2-1\) and \(|A^-| = p/2\).
Let \(i \in \{1,\dots ,n\}\). For every \(a \in A^-\), we have \(\tau _a(i, i)= m-1\) since \(h_{k}(a)=-h_{\ell }(a)\). For every \(a \in A^+\) we have \(d_{k}(i, a) = d_{\ell }(i, a) \in \{0, \ldots , m-1\}\), and thus \(\tau _a(i, i)\) is an even integer between \(0\) and \(2m-2\). Hence
Now, let \(i, j \in \{1,\dots ,n\}\) be such that \(j-i=1\). In particular, we have \(j > 1\), so there exists \(c \in \{0, \ldots , p-2\}\) such that \(d(j, c) \ne 0\). Let \(c_{i, j}\) denote the least such \(c\). As \(j-i=1\) and \(d(j, 0), \ldots , d(j, p-2)\) are the digits of \(j - 1\) in base \(m\), the value of \(c_{i, j}\) determines the value of \(d(j, a) - d(i, a)\) for each \(a \in \{0, \ldots , p-2\}\):
Hence for any \(c \in \{0, \ldots , p-2\}\) and \(a \in A^-\), for all pairs \((i, j)\) with \(j-i=1\) and \(c_{i, j} = c\), the value of \(\tau _a(i, j) = d_k(i, a) + d_{\ell }(j, a)\) is determined and is independent of \(i\) and \(j\): if \(h_{k}(a) = +1\), \(h_{\ell }(a) = -1\), then \(\tau _a(i, j) = m-1-(d(j, a) - d(i, a))\), and if \(h_{k}(a) = -1\) and \(h_{\ell }(a) = +1\), then \(\tau _a(i, j) = m-1+(d(j, a) - d(i, a))\).
Let \(a \in A^+\). If \(a < c_{i,j}\), then \(d(i, a) = m - 1\) and \(d(j, a) = 0\) whence \(\{d_{k}(i, a), d_{\ell }(j, a)\} = \{0, m-1\}\) and thus \(\tau _a(i, j) = m-1\). If \(a = c_{i, j}\), then \(|d_{k}(i, a) - d_{\ell }(j, a)| = 1\) since \(d(j, c_{i, j}) - d(i, c_{i, j}) = 1\), and thus \(\tau _a(i, j)\) is an odd integer between \(1\) and \(2m-3\). If \(a > c_{i, j}\), then \(d_{k}(i, a) = d_{\ell }(j, a)\) since \(d(i, a) = d(j, a)\), and thus \(\tau _a(i, j)\) is an even integer between \(0\) and \(2m-2\). In each of these three cases we can see that, for any \(c \in \{0, \ldots , p-2\}\) and \(a \in A^+\), there are at most \(m\) possible values of \(\tau _a(i, j)\) for pairs \((i, j)\) with \(j - i = 1\) and \(c_{i, j} = c\).
Summarizing, for any \(a, c \in \{0, \ldots , p-2\}\),
Hence
By a symmetric argument,
Therefore
which completes the proof of the first part of the lemma.
It remains to show that for each \(k \in \{1,\dots ,p\}\), the set \(E(P_n)\) can be partitioned into \(2p-3\) stacks with respect to \((\pi _k^{-1}(1), \ldots , \pi _k^{-1}(m^{p-1}))\). Partition \(E(P_n)\) into sets \(E_0, \ldots , E_{p-2}\) where \(E_a\) consists of all edges \(i(i+1)\) such that \(i\) is divisible by \(m^a\) but not by \(m^{a+1}\). By our construction of \(\pi _k\), any edge in \(E_0\) is between two consecutive vertices in \((\pi _k^{-1}(1), \ldots , \pi _k^{-1}(m^{p-1}))\), so the set \(E_0\) is a valid stack. Now it suffices to show that for every \(a \in \{1, \ldots , p-2\}\), the set \(E_a\) can be partitioned into two stacks. Fix \(a \in \{1, \ldots , p-2\}\), and partition \((\pi _k^{-1}(1), \ldots , \pi _k^{-1}(m^{p-1}))\) into blocks \(B_{a,1}, \ldots ,B_{a,m^{p-1-a}}\) each consisting of \(m^a\) consecutive elements, so that \(B_{a, j} = \{\pi _k^{-1}((j-1)m^a + 1), \ldots , \pi _k^{-1}(jm^a)\}\). By our construction of \(\pi _k\), each block \(B_{a, j}\) consists of \(m^a\) consecutive integers, where the largest integer in the block is divisible by \(m^a\). Furthermore, every edge \(i(i+1) \in E_a\) is between two consecutive blocks \(B_{a,j}\) and \(B_{a,j+1}\). Assign the edge \(i(i+1)\) to a set \(E_a^0\) when \(j\) is even and to a set \(E_a^1\) when \(j\) is odd. The resulting sets \(E_a^0\) and \(E_a^1\) are indeed stacks; in fact, no two edges cross or nest in these sets. Thus \(E(P_n)\) can be partitioned into \(2p-3\) stacks. \(\square \)
Theorem 5.1 is a consequence of the following technical variant.
Lemma 5.3
Assume there exists an Hadamard matrix of order \(p\). Let \(m \in \mathbb {N}\) and \(n=m^{p-1}\). Let \(G\) be a \(p\)-colourable graph with a dispersable \(d\)-stack layout. Then
Before proving Lemma 5.3, we show that it implies Theorem 5.1.
Proof of Theorem 5.1
Let \(m=\lceil n^{1/(p-1)}\rceil \). Since \(p\) is a power of 2, there exists an Hadamard matrix of order \(p\). Since \(P_n \subseteq P_{m^{p-1}}\), Lemma 5.3 implies
\(\square \)
Proof of Lemma 5.3
Let \(\rho :V(G) \rightarrow \{1,\dots ,p\}\) be a proper colouring of \(G\). Let \(\pi _1,\dots ,\pi _p\) be the permutations of \(\{1,\dots ,n\}\) given by Lemma 5.2. For each \(v \in V(G)\), let \(P^v\) denote the path in \(G \boxtimes P_n\) induced by \(\{v\} \times \{1,\dots ,n\}\), and let \(\overrightarrow{P^v} = \bigl (\bigl (v, \pi _{\rho (v)}^{-1}(1)\bigr ), \ldots \bigl (v, \pi _{\rho (v)}^{-1}(n)\bigr )\bigr )\). Let \(N = |V(G)|\), and let \(((v_1, \ldots , v_N), \psi )\) be a dispersable \(d\)-stack layout of \(G\). Let \(\overrightarrow{V} = (\overrightarrow{P^{v_1}}; \overrightarrow{P^{v_2}}; \ldots ; \overrightarrow{P^{v_N}})\) be an ordering of \(V(G \boxtimes P_{n})\). By our choice of the permutations \(\pi _1,\ldots ,\pi _p\), for each \(v \in V(G)\), the set \(E(P^{v})\) can be partitioned into \(2p-3\) stacks. Since the paths \(P^v\) occupy disjoint parts of \(\overrightarrow{V}\), it follows that \(\bigcup _{v \in V(G)} E(P^v)\) admits a partition into \(2p-3\) stacks with respect to \(\overrightarrow{V}\).
We partition the set \(E(G \boxtimes P_{n}) \setminus \bigcup _{v \in V(G)} E(P^v)\) into sets \(E_{u v}\) indexed by the edges of \(G\). For an edge \(uv \in E(G)\), let \(E_{uv}=\{xy \in E(G\boxtimes P_n)\mid x \in V(P^u),\, y \in V(P^v)\}\). For each \(xy \in E_{uv}\), let \(\gamma (xy)=\psi (uv)\). We claim that for all \(k \in \{1,\dots ,d\}\), \(\gamma ^{-1}(k)\) can be partitioned into at most \((2p-1)n^{1/2-1/(2p-2)}\) stacks with respect to \(\overrightarrow{V}\). Since \(\psi \) is a dispersable stack-layout, it suffices to show that for every \(uv\in E(G)\), \(E_{uv}\) can be partitioned into at most \((2p-1)n^{1/2-1/(2p-2)}\) stacks.
Fix an edge \(u v \in E(G)\). For each edge \(e = (u, i)(v, j) \in E_{uv}\), define
By our choice of the permutations \(\pi _1, \ldots ,\pi _p\), the size of the image of \(\phi \) is at most \(({2p-1})n^{1/2-1/(2p-2)}\). It remains to show that \(\phi \) partitions \(E_{uv}\) into stacks with respect to \(\overrightarrow{V}\). Let \(e = (u, i)(v, j)\) and \(e' = (u, i')(v, j')\) be two edges from \(E_{uv}\) which cross. Without loss of generality, assume that the vertices are in the order \((u, i), (u', i'),(v, j), (v', j')\) in \(\overrightarrow{V}\). This means that \(\pi _{\rho (u)}(i) < \pi _{\rho (u)}(i')\) and \(\pi _{\rho (v)}(j) < \pi _{\rho (v)}(j')\), so \(\phi (e) = \pi _{\rho (u)}(i) + \pi _{\rho (v)}(j) < \pi _{\rho (u)}(i') + \pi _{\rho (v)}(j') = \phi (e')\), so \(\phi (e) \ne \phi (e')\). Hence \(\phi \) partitions \(E_{u v}\) into \((2p-1)n^{1/2-1/(2p-2)}\) stacks, as required. \(\square \)
Note that when p is not a power of 2 but there exists an Hadamard matrix of order p, Lemma 5.3 gives a stronger bound than Theorem 5.1.
6 Smaller Maximum Degree
This section proves Theorem 1.7, which says that if \(\Delta _0\) is the minimum integer for which there exists a graph family with maximum degree \(\Delta _0\), unbounded stack-number and bounded queue-number, then \(\Delta _0\in \{6,7\}\). These upper and lower bounds are respectively proved in Theorems 6.1 and 6.4 below.
Theorem 6.1
There exists a graph family with maximum degree \(7\), unbounded stack-number and bounded queue-number.
The construction for Theorem 6.1 is based on a tessellation of \(\mathbb {R}^3\) with truncated octahedra, first studied by Fedorov [33]. Let \(Q_0\) denote the convex hull of all points \((x, y, z) \in \mathbb {R}^3\) such that \(\{|x|, |y|, |z|\} = \{0, 1, 2\}\); see Fig. 5. A truncated octahedron is any polyhedron embedded in \(\mathbb {R}^3\) that is geometrically similar to \(Q_0\). At each corner of a truncated octahedron three faces meet: one square and two regular hexagons. Let \(Q_0 + (x, y, z)\) be the translation of \(Q_0\) by a vector \((x, y, z)\).
Let \(\mathcal {T}_\infty \) be the family of translations of \(Q_0\) defined as
\(\mathcal {T}_\infty \) is a 3-dimensional tessellation; that is, a family of interior-disjoint polyhedra whose union is \(\mathbb {R}^3\). A corner of \(\mathcal {T}_\infty \) is any corner of a truncated octahedron from \(\mathcal {T}_\infty \); edges and faces of \(\mathcal {T}_\infty \) are defined similarly. Every (hexagonal or square) face of \(\mathcal {T}_\infty \) is shared by two truncated octahedra in \(\mathcal {T}_\infty \). At each edge of \(\mathcal {T}_\infty \) a square face and two hexagonal faces meet, and at each corner of \(\mathcal {T}_\infty \) two square and four hexagonal faces meet.
We construct an infinite graph \(G_\infty \) whose vertices are points in \(\mathbb {R}^3\) and edges are line segments between their endpoints. \(G_\infty \) is the union of copies of the plane graphs \(J_{\Diamond }\) and  (depicted in Fig. 6), where the copies of \(J_{\Diamond }\) are placed at the square faces of \(\mathcal {T}_\infty \) and the copies of
(depicted in Fig. 6), where the copies of \(J_{\Diamond }\) are placed at the square faces of \(\mathcal {T}_\infty \) and the copies of  are placed at the hexagonal faces of \(\mathcal {T}_\infty \). Each copy of \(J_{\Diamond }\) or
are placed at the hexagonal faces of \(\mathcal {T}_\infty \). Each copy of \(J_{\Diamond }\) or  is contained within its corresponding face so that the exterior cycle coincides with the union of the edges contained in that face, black vertices are at the corners of the face, and each edge of the face is split into equal segments by \(10\) vertices from the exterior face. A vertex of \(G_\infty \) is called a corner vertex if it coincides with a corner of \(\mathcal {T}_\infty \), an edge vertex if it lies on an edge of \(\mathcal {T}_\infty \) and is not a corner vertex, or a face vertex if it is neither a corner vertex nor an edge vertex.
is contained within its corresponding face so that the exterior cycle coincides with the union of the edges contained in that face, black vertices are at the corners of the face, and each edge of the face is split into equal segments by \(10\) vertices from the exterior face. A vertex of \(G_\infty \) is called a corner vertex if it coincides with a corner of \(\mathcal {T}_\infty \), an edge vertex if it lies on an edge of \(\mathcal {T}_\infty \) and is not a corner vertex, or a face vertex if it is neither a corner vertex nor an edge vertex.
Lemma 6.2
The maximum degree of \(G_\infty \) is \(7\).
Proof
Let \(v\in V(G_\infty )\). We proceed by case analysis. If \(v\) is a face vertex, then its degree is at most \(7\) because \(J_{\Diamond }\) and  have maximum degree \(7\).
have maximum degree \(7\).
Now suppose \(v\) is a corner vertex. Since \(v\) belongs to four edges of \(\mathcal {T}_\infty \), it is adjacent to four edge vertices in \(G_{\infty }\). Furthermore, v is adjacent to a face vertex in each of the two copies of \(J_{\Diamond }\) containing \(v\) and is not adjacent to any face vertex in a copy of  . Therefore, \(v\) has degree \(6\).
. Therefore, \(v\) has degree \(6\).
It remains to consider the case when v is an edge vertex. Let \(\varepsilon \) be the edge of the tessellation \(\mathcal {T}_\infty \) that contains \(v\). Let \(v_0 \ldots v_{11}\) be the path induced by the vertices of \(G_\infty \) which lie on \(\varepsilon \), so that \(v_0\) and \(v_{11}\) are corner vertices and \(v_1, \ldots ,v_{10}\) are edge vertices (and one of them is \(v\)). The vertices \(v_1, \ldots , v_{10}\) and all their neighbours lie in one copy of \(J_{\Diamond }\) and two copies of  . The degrees of the vertices \(v_1, \ldots , v_{10}\) in the copy of \(J_{\Diamond }\) containing them are \(3,3,5,5,3,3,5,5,3,3\), respectively, and their degrees in each copy of
. The degrees of the vertices \(v_1, \ldots , v_{10}\) in the copy of \(J_{\Diamond }\) containing them are \(3,3,5,5,3,3,5,5,3,3\), respectively, and their degrees in each copy of  containing them are \(4,4,3,3,4,4, 3,3,4, 4\), respectively. Since \(3 + 2\cdot 4=5+2\cdot 3=11\), for each \(i \in \{1, \ldots , 10\}\), the total sum of degrees of \(v_i\) in the copy of \(J_{\Diamond }\) and the two copies of
containing them are \(4,4,3,3,4,4, 3,3,4, 4\), respectively. Since \(3 + 2\cdot 4=5+2\cdot 3=11\), for each \(i \in \{1, \ldots , 10\}\), the total sum of degrees of \(v_i\) in the copy of \(J_{\Diamond }\) and the two copies of  is \(11\). However, we counted the vertices \(v_{i-1}\) and \(v_{i+1}\) thrice, so the degree of \(v_i\) in \(G_\infty \) is \(11 - 4 = 7\), as required. \(\square \)
is \(11\). However, we counted the vertices \(v_{i-1}\) and \(v_{i+1}\) thrice, so the degree of \(v_i\) in \(G_\infty \) is \(11 - 4 = 7\), as required. \(\square \)
Let \([a, b]\) denote the closed interval \(\{x \in \mathbb {R}\mid a \le x \le b\}\). Observe that for every \((i, j, k) \in \mathbb {Z}^3\), the cube \( [4i-2,4i+2]\times [4j-2,4j+2] \times [4k-2,4k+2]\) contains the same finite number of vertices of \(G_\infty \). For every \(n\in \mathbb {N}\), let \(\mathcal {F}_n\) be the set of all faces of \(\mathcal {T}_\infty \) contained in \([4, 4n+2]^3\) and let \(G_n\) be the subgraph of \(G_\infty \) induced by the vertices lying on the faces in \(\mathcal {F}_n\). Then \(|V(G_n)| \in \Theta (n^3)\). Furthermore, \((G_n)_{n \in \mathbb {N}}\) has cubic growth as the distance between any pair of adjacent vertices in \(G_n\) is \(O(1)\). By Corollary 2.6 and Lemma 6.2, \((G_n)_{n\in \mathbb {N}}\) has bounded queue-number and maximum degree \(7\). Thus Theorem 6.1 follows from the next lemma.
Lemma 6.3
\({{\,\textrm{sn}\,}}(G_n) \in \Omega (n^{1/3})\).
Proof
\(J_{\Diamond }\) and  are plane graphs in which every internal face is a triangle. Therefore, every subgraph induced by a face of \(\mathcal {T}_\infty \) has a triangle complex homeomorphic to that face (and to a closed disk). Furthermore, since faces intersect only at their edges and corners, every subgraph of \(G_n\) induced by a union of faces from \(\mathcal {F}_n\) has a triangle complex homeomorphic to that union.
are plane graphs in which every internal face is a triangle. Therefore, every subgraph induced by a face of \(\mathcal {T}_\infty \) has a triangle complex homeomorphic to that face (and to a closed disk). Furthermore, since faces intersect only at their edges and corners, every subgraph of \(G_n\) induced by a union of faces from \(\mathcal {F}_n\) has a triangle complex homeomorphic to that union.
For \(a \in \{1, 2, 3\}\) and \(i \in \{1,\dots ,n\}\), let \(X^a_i\) be the union of all faces \(F \in \mathcal {F}_n\) such that \(4i \le x_a \le 4i + 2\) for all \((x_1, x_2, x_3) \in F\). Each set \(X^a_i\) is homeomorphic to a closed disk (see Fig. 7). Let \(L^a_i\) denote the subgraph of \(G_n\) induced by \(X^a_i \cap V(G_\infty )\). As observed earlier, \(X^a_i\) as a union of faces from \(\mathcal {F}_n\) is homeomorphic to \({{\,\textrm{Tr}\,}}(L^a_i)\). Hence we identify \(X^a_i\) with \({{\,\textrm{Tr}\,}}(L^a_i)\).
Observe that there are \((2n-1)^3\) hexagonal faces in \(\mathcal {F}_n\), each of which is contained in a different cube of the form \([2x+2, 2x+4] \times [2y+2, 2y+4] \times [2z+2, 2z+4]\) with \((x, y, z) \in \{1,\dots ,2n-1\}^3\). Furthermore, each square face has its centre in a corner of one of these cubes (but not every corner is a centre of a square face). Hence, for \((i, j) \in \{1,\dots ,n\}^2\), the intersection \(X^1_i \cap X^2_j\) is the union of the \(2n-1\) hexagonal faces from \(\mathcal {F}_n\) contained in \([4i, 4i+2] \times [4j, 4j+2] \times \mathbb {R}\). These hexagons form a sequence such that any pair of consecutive hexagons share an edge. The intersection \(X^1_i \cap X^2_j\) is thus path-connected. Symmetric arguments show that
Furthermore, for \((i, j, k) \in \{1,\dots ,n\}^3\), the intersection \(X^1_i \cap X^2_j \cap X^3_k\) is the hexagonal face contained in \([4i, 4i+2] \times [4j, 4j+2] \times [4k, 4k+2]\), so in particular
Let \(\mathcal {B} = \{B(i, j, k)\}_{(i, j, k) \in \{1,\dots ,n\}^3}\) where \(B(i, j, k) = X^1_i \cup X^2_j \cup X^3_k\). We claim that \(\mathcal {B}\) is a bramble over \({{\,\textrm{Tr}\,}}(G_n)\). We proceed by verifying the preconditions of Corollary 3.5.
Let \((i, j, k) \in \{1,\dots ,n\}^3\). We first show that \(B(i, j, k)\) is simply connected. We have \(B(i, j, k) = X^1_i \cup X^2_j \cup X^3_k\), and each of \(X^1_i\), \(X^2_j\) and \(X^3_k\) is homeomorphic to a closed disk and is thus simply connected. By (6.1) and (6.2), the sets \(X^1_i \cap X^2_j\) and \(X^1_i \cap X^2_j \cap X^3_k\) are path-connected. Hence, by Lemma 3.4, \(B(i, j, k)\) is simply connected.
Now, let \((i_1, i_2, i_3), (j_1, j_2, j_3) \in \{1,\dots ,n\}^3\), and let \(B_1 = B(i_1, i_2, i_3)\) and \(B_2 = B(j_1, j_2, j_3)\). We now show that \(B_1 \cap B_2\) is path-connected. We have
By (6.1), \(X^a_{i_a} \cap X^b_{j_b}\) is path-connected when \(a \ne b\). Furthermore, if \(\{a, b, c\} = \{1, 2, 3\}\), then, by (6.2), \(X^a_{i_a} \cap X^b_{j_b}\) intersects \(X^{a}_{i_{a}} \cap X^{c}_{j_{c}}\) and \(X^c_{i_c} \cap X^b_{j_b}\). Hence, the union of all \(X^a_{i_a} \cap X^{b}_{j_b}\) with \(a \ne b\) is path-connected. Furthermore, for each \(a \in \{1, 2, 3\}\), the intersection \(X^a_{i_a} \cap X^a_{j_a}\) is \(X^a_{i_a}\) if \(i_a = j_a\), or an empty set if \(i_a \ne j_a\). In the former case, \(X^a_{i_a} \cap X^a_{j_a}\) intersects \(X^a_{i_a} \cap X^b_{j_b}\) for \(b \in \{1, 2, 3\} \setminus \{a\}\). Hence, \(B_1 \cap B_2\) is indeed path-connected.
Finally, for any \((i_1, j_1, k_1), (i_2, j_2, k_2), (i_3, j_3, k_3) \in \{1,\dots ,n\}^3\), the intersection \(B(i_1, j_1, k_1)\cap B(i_2, j_2, k_2) \cap B(i_3, j_3, k_3)\) contains \(X^1_{i_1} \cap X^2_{j_2}\cap X^3_{k_3}\) which is non-empty by (6.2). Hence, by Corollary 3.5, \(\mathcal {B}\) is a bramble.
By definition, \(|\mathcal {B}| = n^3\). Moreover, for every \(p \in {{\,\textrm{Tr}\,}}(G_n)\) and every \(a \in \{1, 2, 3\}\) there exists at most one \(i \in \{1,\dots ,n\}\) such that \(p \in {{\,\textrm{Tr}\,}}(L^a_i)\). Thus \({{\,\textrm{cong}\,}}(\mathcal {B}) \le 3n^2\). By Lemma 3.3,
Since the maximum degree of \(G_n\) is \(7\), each vertex is contained in at most \(\left( {\begin{array}{c}7\\ 2\end{array}}\right) = 21\) triangles. Therefore, by Lemma 1.5,
\(\square \)
We now prove the lower bound for \(\Delta _0\) (defined at the start of the section).
Theorem 6.4
Every graph class with maximum degree \(5\) and bounded queue-number has bounded stack-number.
The proof of Theorem 6.4 depends on the following definitions. For \(k,c\in \mathbb {N}\), a graph G is k-colourable with clustering c if each vertex of G can be assigned one of k colours such that each monochromatic component has at most c vertices. Here a monochromatic component is a maximal monochromatic connected subgraph. The clustered chromatic number of a graph class \(\mathcal {G}\) is the minimum \(k\in \mathbb {N}\) such that for some \(c\in \mathbb {N}\) every graph in \(\mathcal {G}\) is k-colourable with clustering c. See [61] for a survey on clustered graph colouring. Haxell et al. [40] proved that the class of graphs with maximum degree at most 5 has clustered chromatic number 2 (which is best possible, since  has maximum degree \(6\) and clustered chromatic number 3 by the Hex Lemma). Thus, Theorem 6.4 is an immediate consequence of the following result.
has maximum degree \(6\) and clustered chromatic number 3 by the Hex Lemma). Thus, Theorem 6.4 is an immediate consequence of the following result.
Theorem 6.5
Every graph class \(\mathcal {G}\) with bounded queue-number and clustered chromatic number at most 2 has bounded stack-number.
The proof of Theorem 6.5 depends on the following lemmas.
Lemma 6.6
[25, 53] For every bipartite graph G,
Lemma 6.7
For every graph G and \(t\in \mathbb {N}\),
Proof
We may assume that G is connected and \(V(K_t)=\{1,\dots ,t\}\). If \(|V(G)|=1\) then the claim holds since \({{\,\textrm{sn}\,}}(G)=0\) and \({{\,\textrm{sn}\,}}(G\boxtimes K_t)={{\,\textrm{sn}\,}}(K_t)\le \lceil {t}/{2} \rceil \); see [10]. Now assume that \(|V(G)|\ge 2\) and thus \(E(G)\ne \emptyset \). Let \(s={{\,\textrm{sn}\,}}(G)\ge 1\). Let \((v_1,\dots ,v_n)\) together with \(\psi :E(G)\rightarrow \{1,\dots ,s\}\) be an s-stack layout of G. For each \(k \in \{1,\dots ,s\}\), let \(G_k\) be the spanning subgraph of G with \(E(G_k)=\psi ^{-1}(k)\). Thus \(G_k\) admits a 1-stack layout and is therefore outerplanar. Hakimi et al. [37] proved that every outerplanar graph has an edge-partition into three star forests. For each \(k\in \{1,\dots ,s\}\), let \(G_{k,1},G_{k,2},G_{k,3}\) be an edge-partition of \(G_k\) into three star forests.
Consider the vertex-ordering
We now define the stack assignment. An edge \((u,i)(v,j)\in E(G\boxtimes K_t)\) is an intra-\(K_t\) edge if \(u=v\), otherwise \(uv\in E(G)\) and it is a cross-\(K_t\) edge. We use separate stacks for the intra-\(K_t\) edges and the cross-\(K_t\) edges. Since the intra-\(K_t\) edges induce copies of \(K_t\) that are disjoint with respect to the vertex-ordering, we may partition them into \({{\,\textrm{sn}\,}}(K_t)=\lceil {t}/{2}\rceil \) stacks. Now for some \(k\in \{1,\dots ,s\}\) and \(j\in \{1,2,3\}\), consider the spanning subgraph \(\tilde{G}_{k,j}\) of \(G_{k,j}\boxtimes K_t\) that contains only the cross-\(K_t\) edges. By the construction of \(G_{k,t}\), edges from different components in \(\tilde{G}_{k,j}\) do not cross with respect to the above vertex-ordering. Moreover, as each component of \(\tilde{G}_{k,t}\) that contains an edge is obtained from a star by blowing-up each vertex with t non-adjacent vertices and replacing each edge with a copy of \(K_{t,t}\), it is thus isomorphic to a bipartite graph of the form \(K_{t,r}\) for some multiple r of t. As such, we may partition the edges of \(\tilde{G}_{k,j}\) into t stacks. Therefore, we may partition the cross-\(K_t\) edges into 3st stacks, as required. \(\square \)
Proof of Theorem 6.5
By assumption, there exist \(c,\ell \in \mathbb {N}\) such that for every graph \(G\in \mathcal {G}\), we have \({{\,\textrm{qn}\,}}(G)\le c\) and G is 2-colourable with each monochromatic component having at most \(\ell \) vertices. Contracting each monochromatic component to a single vertex gives a bipartite \(\ell \)-small minor H of G. Lemma 2.4 implies \({{\,\textrm{qn}\,}}(H) \le 2\ell (2c)^{2\ell }\). Lemma 6.6 implies \({{\,\textrm{sn}\,}}(H) \le 4\ell (2c)^{2\ell }\). By construction, G is isomorphic to a subgraph of \(H \boxtimes K_{\ell }\). Thus \({{\,\textrm{sn}\,}}(G) \le {{\,\textrm{sn}\,}}(H\boxtimes K_\ell )\), which is at most \(3\ell {{\,\textrm{sn}\,}}(H) + \lceil {{\ell }/{2}\rceil }\le 12\ell ^2(2c)^{2\ell } + \lceil {{\ell }/{2}\rceil }\) by Lemma 6.7. Hence \(\mathcal {G}\) has bounded stack-number. \(\square \)
7 Open Problems
We finish with some open problems:
-
Does there exist a graph class with bounded stack-number and unbounded queue-number? This is equivalent to the question of whether graphs with stack-number 3 have bounded queue-number [28].
-
Do graphs with queue-number 2 (or 3) have bounded stack-number [22]?
-
Do graph classes with quadratic (or linear) growth have bounded stack-number?
-
Does there exist a graph family with unbounded stack-number, bounded queue-number and maximum degree 6?
-
The best known lower bound on the maximum stack-number of n-vertex graphs with fixed maximum degree \(\Delta \) is \(\Omega (n^{1/2-1/\Delta })\), proved by Malitz [48] using a probabilistic argument. Is there a constructive proof of this bound?
-
The best upper bound on the stack-number of n-vertex graphs with fixed maximum degree \(\Delta \) is \(O(n^{1/2})\), also due to Malitz [48]. Closing the gap between the lower and upper bounds is an interesting open problem. For example, the best bounds for graphs of maximum degree 3 are \(\Omega (n^{1/6})\) and \(O(n^{1/2})\).
Notes
All graphs in this paper are simple and, unless explicitly stated otherwise, undirected and finite. Let V(G) and E(G) denote the vertex-set and edge-set of a graph G. Let \(\mathbb {N}=\{1,2,\dots \}\) and \(\mathbb {N}_0=\mathbb {N}\cup \{0\}\).
See [11, Sect. 12] for background on simplicial complexes.
This definition is inspired by the definition of a bramble in a graph, which is used in graph minor theory. A bramble of a graph is only required to satisfy the first and second among the conditions we impose.
A topological space X is path-connected if there is a path joining any two points of X; that is, for all \(x,y \in X\) there exists a continuous map \(f:[0,1] \rightarrow X\) such that \(f(0)=x\) and \(f(1)=y\).
A topological space is simply connected if it is path-connected and any two paths with the same endpoints can be continuously transformed into each other.
References
Alam, J.M., Bekos, M.A., Dujmović, V., Gronemann, M., Kaufmann, M., Pupyrev, S.: On dispersable book embeddings. Theoret. Comput. Sci. 861, 1–22 (2021)
Alam, M.J., Brandenburg, F.J., Kobourov, S.G.: On the book thickness of 1-planar graphs (2015). arXiv:1510.05891
Ambrus, G., Barát, J., Hajnal, P.: The slope parameter of graphs. Acta Sci. Math. (Szeged) 72(3–4), 875–889 (2006)
Barát, J., Matoušek, J., Wood, D.R.: Bounded-degree graphs have arbitrarily large geometric thickness. Electron. J. Comb. 13, # R3 (2006)
Baur, M., Brandes, U.: Crossing reduction in circular layouts. In: 30th International Workshop on Graph-Theoretic Concepts in Computer Science (Bad Honnef 2004). Lecture Notes in Computer Science, vol. 3353, pp. 332–343. Springer, Berlin (2004)
Beame, P., Blais, E., Huynh-Ngoc, D.-T.: Longest common subsequences in sets of permutations (2009). arXiv:0904.1615
Bekos, M.A., Bruckdorfer, T., Kaufmann, M., Raftopoulou, Ch.N.: The book thickness of 1-planar graphs is constant. Algorithmica 79(2), 444–465 (2017)
Bekos, M.A., Da Lozzo, G., Griesbach, S.M., Gronemann, M., Montecchiani, F., Raftopoulou, Ch.: Book embeddings of nonplanar graphs with small faces in few pages. In: 36th International Symposium on Computational Geometry. Leibniz International Proceedings in Informatics, vol. 164, # 16. Leibniz-Zent. Inform., Wadern (2020)
Bekos, M.A., Kaufmann, M., Klute, F., Pupyrev, S., Raftopoulou, Ch., Ueckerdt, T.: Four pages are indeed necessary for planar graphs. J. Comput. Geom. 11(1), 332–353 (2020)
Bernhart, F., Kainen, P.C.: The book thickness of a graph. J. Comb. Theory Ser. B 27(3), 320–331 (1979)
Björner, A.: Topological methods. In: Handbook of Combinatorics, vol. 2, pp. 1819–1872. Elsevier, Amsterdam (1995)
Blankenship, R.L.: Book Embeddings of Graphs. PhD thesis, Louisiana State University and Agricultural & Mechanical College (2003)
Blankenship, R., Oporowski, B.: Drawing subdivisions of complete and complete bipartite graphs on books. Tech. Rep. 1999-4. Department of Mathematics, Louisiana State University (1999)
Bourgain, J.: Expanders and dimensional expansion. C. R. Math. Acad. Sci. Paris 347(7–8), 357–362 (2009)
Bourgain, J., Yehudayoff, A.: Expansion in \({\rm SL}_2(\mathbb{R} )\) and monotone expanders. Geom. Funct. Anal. 23(1), 1–41 (2013)
Brandenburg, F.J.: Book embeddings of \(k\)-map graphs (2020). arXiv:2012.06874
Buss, J.F., Shor, P.: On the pagenumber of planar graphs. In: 16th ACM Symposium on Theory of Computing (Washington 1984), pp. 98–100. ACM, New York (1984)
Camarena, O.A.: The van Kampen theorem (2021). https://www.matem.unam.mx/omar/groupoids/vankampen.pdf
Chung, F.R.K., Leighton, F.T., Rosenberg, A.L.: Embedding graphs in books: a layout problem with applications to VLSI design. SIAM J. Algebr. Discrete Methods 8(1), 33–58 (1987)
Dillencourt, M.B., Eppstein, D., Hirschberg, D.S.: Geometric thickness of complete graphs. J. Graph Algorithms Appl. 4(3), 5–17 (2000)
Đoković, D.Ž., Golubitsky, O., Kotsireas, I.S.: Some new orders of Hadamard and skew-Hadamard matrices. J. Comb. Des. 22(6), 270–277 (2014)
Dujmović, V., Eppstein, D., Hickingbotham, R., Morin, P., Wood, D.R.: Stack-number is not bounded by queue-number. Combinatorica 42(2), 151–164 (2021)
Dujmović, V., Eppstein, D., Suderman, M., Wood, D.R.: Drawings of planar graphs with few slopes and segments. Comput. Geom. 38(3), 194–212 (2007)
Dujmović, V., Morin, P., Yelle, C.: Two results on layered pathwidth and linear layouts. J. Graph Algorithms Appl. 25(1), 43–57 (2021)
Dujmović, V., Pór, A., Wood, D.R.: Track layouts of graphs. Discrete Math. Theor. Comput. Sci. 6(2), 497–521 (2004)
Dujmović, V., Sidiropoulos, A., Wood, D.R.: Layouts of expander graphs. Chic. J. Theoret. Comput. Sci. 2016, # 1 (2016)
Dujmović, V., Suderman, M., Wood, D.R.: Graph drawings with few slopes. Comput. Geom. 38(3), 181–193 (2007)
Dujmović, V., Wood, D.R.: Stacks, queues and tracks: layouts of graph subdivisions. Discrete Math. Theor. Comput. Sci. 7, 155–201 (2005)
Dujmović, V., Wood, D.R.: Graph treewidth and geometric thickness parameters. Discrete Comput. Geom. 37(4), 641–670 (2007)
Dujmović, V., Wood, D.R.: On the book thickness of \(k\)-trees. Discrete Math. Theor. Comput. Sci. 13(3), 39–44 (2011)
Endo, T.: The pagenumber of toroidal graphs is at most seven. Discrete Math. 175(1–3), 87–96 (1997)
Eppstein, D.: Separating geometric thickness from book thickness (2001). arXiv:math/0109195
Fedorov, E.S.: Introduction to the Theory of Figures. St, Petersburg (1885). (in Russian)
Galil, Z., Kannan, R., Szemerédi, E.: On \(3\)-pushdown graphs with large separators. Combinatorica 9(1), 9–19 (1989)
Ganley, J.L., Heath, L.S.: The pagenumber of \(k\)-trees is \(O(k)\). Discrete Appl. Math. 109(3), 215–221 (2001)
Gromov, M.: Singularities, expanders and topology of maps. Part 2: from combinatorics to topology via algebraic isoperimetry. Geom. Funct. Anal. 20(2), 416–526 (2010)
Hakimi, S.L., Mitchem, J., Schmeichel, E.: Star arboricity of graphs. Discrete Math. 149(1–3), 93–98 (1996)
Haslinger, Ch., Stadler, P.F.: RNA structures with pseudo-knots: graph-theoretical, combinatorial, and statistical properties. Bull. Math. Biol. 61(3), 437–467 (1999)
Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge (2002)
Haxell, P., Szabó, T., Tardos, G.: Bounded size components—partitions and transversals. J. Comb. Theory Ser. B 88(2), 281–297 (2003)
Heath, L.S.: Embedding planar graphs in seven pages. In: 25th Annual Symposium on Foundations of Computer Sciences (Singer Island 1984), pp. 74–83. IEEE (1984)
Heath, L.S., Istrail, S.: The pagenumber of genus \(g\) graphs is \(O(g)\). J. Assoc. Comput. Mach. 39(3), 479–501 (1992)
Heath, L.S., Leighton, F.T., Rosenberg, A.L.: Comparing queues and stacks as mechanisms for laying out graphs. SIAM J. Discrete Math. 5(3), 398–412 (1992)
Hickingbotham, R., Wood, D.R.: Shallow minors, graph products and beyond planar graphs (2021). arXiv:2111.12412
Kainen, P.C.: The book thickness of a graph II. Congr. Numer. 71, 127–132 (1990)
Keszegh, B., Pach, J., Pálvölgyi, D., Tóth, G.: Drawing cubic graphs with at most five slopes. Comput. Geom. 40(2), 138–147 (2008)
Krauthgamer, R., Lee, J.R.: The intrinsic dimensionality of graphs. Combinatorica 27(5), 551–585 (2007)
Malitz, S.M.: Graphs with \(E\) edges have pagenumber \(O(\sqrt{E})\). J. Algorithms 17(1), 71–84 (1994)
Malitz, S.M.: Genus \(g\) graphs have pagenumber \(O(\sqrt{g})\). J. Algorithms 17(1), 85–109 (1994)
Ollmann, L.T.: On the book thicknesses of various graphs. Congr. Numer. 8, 459 (1973)
Pach, J., Pálvölgyi, D.: Bounded-degree graphs can have arbitrarily large slope numbers. Electron. J. Comb. 13, # N1 (2006)
Paley, R.E.A.C.: On orthogonal matrices. J. Math. Phys. 12, 311–320 (1933)
Pemmaraju, S.V.: Exploring the Powers of Stacks and Queues via Graph Layouts. PhD thesis, Virginia Polytechnic Institute and State University (1992)
Pupyrev, S.: Book embeddings of graph products (2020). arXiv:2007.15102
Rosenberg, A.L.: The DIOGENES approach to testable fault-tolerant arrays of processors. IEEE Trans. Comput. 32(10), 902–910 (1983)
Shahrokhi, F., Székely, L.A., Sýkora, O., Vrt’o, I.: The book crossing number of a graph. J. Graph Theory 21(4), 413–424 (1996)
Sylvester, J.J.: Thoughts on inverse orthogonal matrices, simultaneous sign-successions, and tessellated pavements in two or more colours, with applications to Newton’s rule, ornamental tile-work, and the theory of numbers. Lond. Edinb. Dublin Philos. Mag. J. Sci. 34(232), 461–475 (1867)
Vandenbussche, J., West, D.B., Yu, G.: On the pagenumber of \(k\)-trees. SIAM J. Discrete Math. 23(3), 1455–1464 (2009)
Wood, D.R.: Bounded degree book embeddings and three-dimensional orthogonal graph drawing. In: 9th International Symposium on Graph Drawing (Vienna 2001). Lecture Notes in Computer Science, vol. 2265, pp. 312–327. Springer, Berlin (2002)
Wood, D.R.: Queue layouts of graph products and powers. Discrete Math. Theor. Comput. Sci. 7(1), 255–268 (2005)
Wood, D.R.: Defective and clustered graph colouring. Electron. J. Comb. DS, # 23 (2018)
Yannakakis, M.: Embedding planar graphs in four pages. J. Comput. System Sci. 38(1), 36–67 (1989)
Yannakakis, M.: Planar graphs that need four pages. J. Comb. Theory Ser. B 145, 241–263 (2020)
Acknowledgements
This work was initiated at the Workshop on Graph Product Structure Theory (BIRS21w5235) at the Banff International Research Station, 21–26 November 2021. Thanks to the other organisers and participants. Thanks to both referees for many helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Csaba D. Tóth
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Norin is supported by an NSERC Discovery Grant. Hickingbotham is supported by an Australian Government Research Training Program Scholarship. Wood is supported by the Australian Research Council. Eppstein is supported in part by NSF grant CCF-2212129.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Eppstein, D., Hickingbotham, R., Merker, L. et al. Three-Dimensional Graph Products with Unbounded Stack-Number. Discrete Comput Geom 71, 1210–1237 (2024). https://doi.org/10.1007/s00454-022-00478-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-022-00478-6



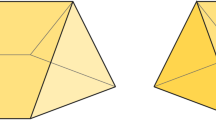



 , (c) a triangulation of
, (c) a triangulation of 




