1 History and Results

Helly’s theorem, dated from 1923 [13], is a cornerstone result in convex geometry. Its finitary version states that the intersection of a finite family of convex sets is empty if and only if there exists a subfamily of \(d+1\) sets such that its intersection is empty. In 1982, Bárány et al. [4] introduced the following quantitative versions of Helly’s theorem: there exist positive constants \(v(d),\delta (d)\) such that for a finite family \(\mathcal {F}\) of convex bodies (that is, compact convex sets with non-empty interior) in \(\mathbb {R}^d\), one may select 2d members such that their intersection has volume at most \(v(d){{\,\textrm{vol}\,}}(\bigcap \mathcal {F})\), or has diameter at most \(\delta (d){{\,\textrm{diam}\,}}(\bigcap \mathcal {F})\).

The problem of finding the optimal values of \(\delta (d)\) and v(d) has enjoyed special interest in recent years (see e.g. the excellent survey article [3]). In [4] (see also [5]) the authors proved that \(v(d) \le d^{2 d^2}\) and \(\delta (d) \le d^{2d}\), and they conjectured that \(v(d) \approx d^{c_1 d}\) and \(\delta (d) \approx c_2 d^{1/2}\) for some positive constants \(c_1, c_2 >0\).

For the volume problem, in a breakthrough paper, Naszódi [17] proved that \(v(d) \le e^{d+1} d^{2d+1/2}\), while \(v(d) \ge d^{d/2}\) must hold. Improving upon his ideas, Brazitikos [6] found the current best upper bound for volume: \(v(d) \le (c d)^{3d/2}\) for a constant \(c>0\).

For the diameter question, Brazitikos [8] proved the first polynomial bound on \(\delta (d)\) by showing that \(\delta (d) \le c d^{11/2}\) for some \(c>0\). In 2021, Ivanov and Naszódi [14] found the best known upper bound, \(\delta (d) \le (2d)^{3}\), and also proved that \(\delta (d) \ge c d^{1/2}\). Thus, the value conjectured in [4] for \(\delta (d)\) would be asymptotically sharp.

In the present note, we show that given a finite family \(\mathcal {F}\) of closed convex sets, one can select at most 2d members such that their intersection sits inside a scaled version of \(\bigcap \mathcal {F}\) for a suitable location of the origin. Clearly, it suffices to prove this statement for the special case when \(\mathcal {F}\) consists of closed halfspaces intersecting in a convex body. As an application, we obtain an improvement on the diameter bound, \(\delta (d) \le 2d^2\), and retrieve the best known bound for v(d). The crux of the argument is the following sparse approximation result for polytopes, which is a strengthening of [14, Thm. 2].

Theorem 1.1

Let \( \lambda > 0\) and \(Q \subset \mathbb {R}^d\) be a convex polytope such that \(Q \subseteq - \lambda Q\). Then there exist at most 2d vertices of Q whose convex hull \(Q'\) satisfies

$$\begin{aligned}Q \subseteq - ( \lambda + 2)d \, Q'.\end{aligned}$$

We immediately obtain the following corollary.

Corollary 1.2

Assume that \(Q=-Q\) is a symmetric convex polytope in \(\mathbb {R}^d\). Then we may select a set of at most 2d vertices of Q with convex hull \(Q'\) such that

$$\begin{aligned}Q \subseteq 3 d \, Q'.\end{aligned}$$

As usual, let \(B^d\) denote the unit ball of \(\mathbb {R}^d\) and let \(S^{d-1}\) be the unit sphere of \(\mathbb {R}^d\). A standard consequence of Fritz John’s theorem [16] states that if \(K\subset \mathbb {R}^d\) is a convex body in John’s position, that is, the largest volume ellipsoid inscribed in K is \(B^d\), then \(B^d \subseteq K \subseteq d B^d \subseteq - d K\) (see e.g. [2]). Thus, we derive

Corollary 1.3

Assume that \( Q \subset \mathbb {R}^d\) is a convex polytope in John’s position. Then there exists a subset of at most 2d vertices of Q whose convex hull \(Q'\) satisfies

$$\begin{aligned}Q \subseteq - 2 d^2 \, Q'.\end{aligned}$$

For \(n \in \mathbb {N}^+\), we will use the notation \([n] = \{1, \ldots ,n\}\). For a family of sets \(\{ K_1, \ldots , K_n\} \subset \mathbb {R}^d\) and for a subset \(\sigma \subset [n]\), let

$$\begin{aligned}K_\sigma = \bigcap _{i \in \sigma } K_i,\end{aligned}$$

as in [14]. Also, let \(\left( {\begin{array}{c}[n]\\ \le k\end{array}}\right) \) stand for the set of all subsets of [n] with cardinality at most k. Using this terminology, we are ready to state our quantitative Helly-type result.

Theorem 1.4

Let \(\{K_1,\ldots ,K_n\}\) be a family of closed convex sets in \(\mathbb {R}^d\) with \(d \ge 2\) such that their intersection \(K = K_1 \cap \cdots \cap K_n\) is a convex body. Then there exists a \(\sigma \in \left( {\begin{array}{c}[n]\\ \le 2d\end{array}}\right) \) such that

$$\begin{aligned} {{\,\textrm{vol}\,}}_d K_{\sigma } \le (cd)^{3d/2} {{\,\textrm{vol}\,}}_d K \quad \text {and}\quad {{\,\textrm{diam}\,}}K_{\sigma } \le 2 d^2 {{\,\textrm{diam}\,}}K \end{aligned}$$

for some constant \(c > 0\).

To conclude the section we formulate the following conjecture, which was essentially stated already in [4]. This would imply the asymptotically sharp bound for v(d), see the remark after the proof of Theorem 1.4.

Conjecture 1.5

Assume that \(\{u_1, \ldots , u_n \}\subset S^{d-1}\) is a set of unit vectors satisfying the conditions of Fritz John’s theorem. That is, there exist positive numbers \(\alpha _1, \ldots , \alpha _n\) for which \(\sum _{i=1}^n \alpha _i u_i =0\) and \(\sum _{i=1}^n \alpha _i u_i \otimes u_i = I_d\), the identity operator on \(\mathbb {R}^d\). Then there exists a subset \(\sigma \subset [n]\) with cardinality at most 2d so that

$$\begin{aligned}B^d \subset cd {{\,\textrm{conv}\,}}{\{ u_i: i \in \sigma \}}\end{aligned}$$

with an absolute constant \(c>0\).

That the above estimate would be asymptotically sharp is shown by taking \(n=d+1\) and letting \(\{u_1, \ldots , u_n \}\) to be the set of vertices of a regular simplex inscribed in \(S^{d-1}\).

Note that we study quantitative Helly-type questions that require selecting at most 2d sets, which is the smallest cardinality for which such estimates may hold. Versions obtained by relaxing this cardinality bound have been studied e.g. by Brazitikos [7], Dillon and Soberón [9], and Ivanov and Naszódi [14]. In particular, an estimate which matches Theorem 1.1 asymptotically was given in [14] when selecting \(2d+1\) vertices of the polytope, and an asymptotically sharp estimate for the quantitative Helly-type theorem for the diameter was proved in [9] for sufficiently large sub-families. Further quantitative Helly-type results have been studied in [15] (for log-concave functions) and [11] (continuous versions).

2 Proofs

Proof of Theorem 1.1

The condition \(Q \subseteq -\lambda Q\) ensures that \(0 \in {{\,\textrm{int}\,}}Q\). Among all simplices with d vertices from the set of vertices of Q and one vertex at the origin, consider a simplex \(S = {{\,\textrm{conv}\,}}{\{0,v_1,\ldots ,v_d\}}\) with maximal volume. We write S in the form

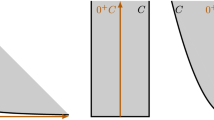
$$\begin{aligned} S = \left\{ x \in \mathbb {R}^d : x = \alpha _1 v_1 + \cdots + \alpha _d v_d \text { for } \alpha _i \ge 0 \text { and } \sum _{i=1}^d \alpha _i \le 1\right\} . \end{aligned}$$
(1)

For every \(i \in [d]\), let \(H_i\) be the hyperplane spanned by \(\{0, v_1,\ldots ,v_d\} \setminus \{v_i\}\), and let \(L_i\) be the closed strip between the hyperplanes \(v_i + H_i\) and \( -v_i + H_i\). Define \(P = \bigcap _{i \in [d]} L_i\) (see Fig. 1). Note that

$$\begin{aligned} P = \{ x \in \mathbb {R}^d : {{\,\textrm{vol}\,}}_d({{\,\textrm{conv}\,}}( \{0,x,v_1,\ldots ,v_d\} \setminus \{v_i\} )) \le {{\,\textrm{vol}\,}}_d(S) \ \text { for all }i \in [d]\}. \end{aligned}$$
(2)

This follows from the volume formula

$$\begin{aligned}{{\,\textrm{vol}\,}}_d({{\,\textrm{conv}\,}}{\{0,w_1,\ldots ,w_d\}}) = \frac{1}{d!}|{\det (w_1 \, w_2 \, \ldots \, w_d)}|\end{aligned}$$

for arbitrary \(w_1,\ldots ,w_d \in \mathbb {R}^d\), which implies that for all \(x \in \mathbb {R}^{d}\) of the form \( x = c v_i + w\) with \(w \in H_i\), \(i \in [d]\),

$$\begin{aligned}{{\,\textrm{vol}\,}}_d({{\,\textrm{conv}\,}}( \{0,x,v_1,\ldots ,v_d\} \setminus \{v_i\} )) = |c| {{\,\textrm{vol}\,}}_d(S).\end{aligned}$$

Next, we show that

$$\begin{aligned} P = \{ x \in \mathbb {R}^d : x = \beta _1 v_1 + \cdots + \beta _d v_d \text { for } \beta _i \in [-1,1] \}. \end{aligned}$$
(3)

Indeed, since \(v_1,\ldots ,v_d\) are linearly independent, we may consider the linear transformation A with \(A(v_i) = e_i\) for \(i \in [d]\). Note that

$$\begin{aligned}{} & {} A(P) = \bigcap _{i \in [d]} A(L_i) = \{ x \in \mathbb {R}^d : x = \beta _1 e_1 + \cdots + \beta _d e_d \text { for } \beta _i \in [-1,1]\}. \end{aligned}$$
Fig. 1
figure 1

Positions of the convex body Q, the simplex S of maximal volume, its homothetic copy \(S'\), and the parallelotope P

Full size image

Thus, (3) holds. Since S is chosen maximally, (2) shows that for any vertex w of Q, \(w \in P\). By convexity,

$$\begin{aligned} Q \subseteq P. \end{aligned}$$
(4)

Let \(S' = -2dS + (v_1 + \cdots + v_d)\). By (1),

$$\begin{aligned} S'=\left\{ x \in \mathbb {R}^d : x = \gamma _1v_1 + \cdots + \gamma _dv_d \text { for } \gamma _i \le 1 \text { and } \sum _{i= 1}^{d} \gamma _i \ge -d \right\} . \end{aligned}$$
(5)

Then, from (3) and (5),

$$\begin{aligned} P \subseteq S'. \end{aligned}$$
(6)

Let \(u =({1}/{d})(v_1 + \cdots + v_d)\) be the centroid of the facet\({{\,\textrm{conv}\,}}{\{v_1, \ldots , v_d\}}\) of S. Let y be the intersection of the ray from 0 through \(-u\) and the boundary of Q. By Carathéodory’s theorem, we can choose \(k \le d\) vertices \(\{v_1',\ldots ,v_k'\}\) of Q such that \(y \in {{\,\textrm{conv}\,}}{\{v_1',\ldots ,v_k'\}}\). Set \(Q'= {{\,\textrm{conv}\,}}{\{v_1,\ldots ,v_d,v_1',\ldots ,v_k'\}}\).

Note that \([y,u] \subseteq Q'\), which implies \(0 \in Q'\). Thus,

$$\begin{aligned} S \subseteq Q'. \end{aligned}$$
(7)

Since \(Q \subseteq - \lambda Q\), we have that \(-u \in \lambda Q\). Since \( \lambda y\) is on the boundary of \( \lambda Q\), we also have that \(-u \in [0, \lambda y]\). We know that \(0, \lambda y \in \lambda Q'\), so

$$\begin{aligned} u \in - \lambda Q'. \end{aligned}$$
(8)

Combining (4), (6), (7), and (8):

$$\begin{aligned} Q \subseteq P \subseteq S'= -2dS + d u\subseteq -2d \, Q' - \lambda d \, Q'= -(\lambda + 2) d \, Q'. \end{aligned}$$
(9)

\(\square \)

Proof of Theorem 1.4

As shown in [4], we may assume that the family \(\{K_1,\ldots ,K_n\}\) consists of closed halfspaces such that \(K = \bigcap K_i\) is a d-dimensional polytope. Let T be the affine transformation sending K to John’s position. Let \({\widetilde{K}}_i = T{K}_i\) for \(i \in [n]\), \({\widetilde{K}} = TK\), and for some \(\sigma \subset [n]\), let \({\widetilde{K}}_{\sigma } = \bigcap _{i \in \sigma } {\widetilde{K}}_i\). We claim that there exists \(\sigma \in \left( {\begin{array}{c}[n]\\ \le 2d\end{array}}\right) \) such that the following two properties hold:

$$\begin{aligned} \widetilde{K}_{\sigma }&\subseteq -2d^2 \widetilde{K}, \end{aligned}$$
(10)
$$\begin{aligned} {{\,\textrm{vol}\,}}_d {\widetilde{K}}_{\sigma }&\le (cd)^{3d/2} {{\,\textrm{vol}\,}}_d {\widetilde{K}} \end{aligned}$$
(11)

for some constant \(c > 0\). Estimates (10) and (11) are affine invariant, so this will suffice to prove Theorem 1.4.

Recall that since \({\widetilde{K}}\) is in John’s position, \(B^d \subseteq {\widetilde{K}} \subseteq d B^d\) (see [2] or [12, Thm. 5.1]). Setting \(Q = ({\widetilde{K}})^{\circ }\), this yields that \((1/d)B^d \subseteq Q \subseteq B^d\) (here and later on, \(K^\circ \) stands for the polar set: \(K^\circ = \{ x \in \mathbb {R}^d: \langle x, y \rangle \le 1 \text { for all } y \in K \}\).) In particular, \(Q \subseteq -d\,Q\). Hence, we may apply Theorem 1.1 to Q with \(\lambda = d\), we obtain a subset of at most 2d vertices of Q such that their convex hull \(Q'\) satisfies

$$\begin{aligned} Q \subseteq -(d + 2)d\, Q' \subseteq - 2 d^2\, Q'. \end{aligned}$$
(12)

The family of closed halfspaces supporting the facets of \((Q')^{\circ }\) is a subset of \(\{{\widetilde{K}}_1,\ldots , {\widetilde{K}}_n\}\) with at most 2d elements. Thus, we can choose \(\sigma \in \left( {\begin{array}{c}[n]\\ \le 2d\end{array}}\right) \) such that \({\widetilde{K}}_{\sigma } = (Q')^{\circ }\). Taking the polar of (12), we obtain

$$\begin{aligned}{\widetilde{K}}_{\sigma } \subseteq - (d+2)d\, {\widetilde{K}} \subseteq -2d^2\, {\widetilde{K}},\end{aligned}$$

which shows (10).

Let P be the parallelotope enclosing Q from the proof of Theorem 1.1 and set \(P' = -({1}/({2d^2}))P\). Statement (9) implies

$$\begin{aligned}Q' \supseteq P'.\end{aligned}$$

Since S is chosen maximally, the volume of S is at least the volume of the simplex obtained from the Dvoretzky–Rogers lemma [10] (see also [17, Lem. 1.4]):

$$\begin{aligned} {{\,\textrm{vol}\,}}_d(S) \ge \frac{1}{\sqrt{d!}\,d^{d/2}}. \end{aligned}$$
(13)

Using (13),

$$\begin{aligned} {{\,\textrm{vol}\,}}_d(P')= (2d^2)^{-d} {{\,\textrm{vol}\,}}_d(P)= (2d^2)^{-d} \cdot 2^{d} d! {{\,\textrm{vol}\,}}_d(S)\ge d^{-5d/2} (d!)^{1/2}. \end{aligned}$$
(14)

Note that \(P'\) is centrally symmetric, so we can use the Blaschke–Santaló inequality (see [1, Thm. 1.5.10]) for \(P'\):

$$\begin{aligned} {{\,\textrm{vol}\,}}_d (P') \cdot {{\,\textrm{vol}\,}}_d ((P')^{\circ }) \le {{\,\textrm{vol}\,}}_d (B_2^d)^2. \end{aligned}$$
(15)

Using the inclusions \({\widetilde{K}} \supseteq B_2^d\) and \({\widetilde{K}}_{\sigma } = (Q')^{\circ } \subseteq (P')^{\circ }\), as well as (14) and (15):

$$\begin{aligned} \frac{{{\,\textrm{vol}\,}}_d {\widetilde{K}}_{\sigma }}{{{\,\textrm{vol}\,}}_d {\widetilde{K}}}\le \frac{ {{\,\textrm{vol}\,}}_d( (P')^{\circ })}{{{\,\textrm{vol}\,}}_d( B_2^d)}\le \frac{ {{\,\textrm{vol}\,}}_d( B_2^d)}{ {{\,\textrm{vol}\,}}_d(P')}\le \frac{\pi ^{d/2} d^{5d/2} (d!)^{-1/2} }{\Gamma ((d/2) + 1)}\le (cd)^{3d/2} \end{aligned}$$
(16)

for some absolute constant \(c > 0\). This shows (11) and concludes the proof. \(\square \)

Remark

We briefly explain how Conjecture 1.5 would imply the asymptotically optimal bound on v(d). First note that the estimate (12) would hold with the factor cd instead of \(2d^2\). Then, in the rest of the proof of Theorem 1.4, we could replace all instances of the factor \(2 d^2\) with cd. In particular, one would get the linear upper bound \(\delta (d) \le c d\) from the improvement of (10), while the rest of the calculations would show that the final quotient in (16) is at most \((c' d)^{d/2}\) for some absolute constant \(c' > 0\).