Abstract
This paper proposes a new mathematical and computational tool for inferring the geometry of shapes known only through approximations such as triangulated or digital surfaces. The main idea is to decouple the position of the shape boundary from its normal vector field. To do so, we extend a classical tool of geometric measure theory, the normal cycle, so that it takes as input not only a surface but also a normal vector field. We formalize it as a current in the oriented Grassmann bundle \(\mathbb {R}^3 \times \mathbb {S}^2\). By choosing adequate differential forms, we define geometric measures like area, mean and Gaussian curvatures. We then show the stability of these measures when both position and normal input data are approximations of the underlying continuous shape. As a byproduct, our tool is able to correctly estimate curvatures over polyhedral approximations of shapes with explicit bounds, even when their natural normal are not correct, as long as an external convergent normal vector field is provided. Finally, the accuracy, convergence and stability under noise perturbation is evaluated experimentally onto digital surfaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We address in this paper the problem of defining a notion of curvature on non-smooth sets, with the goal of estimating the curvatures of a smooth surface through a non-smooth approximation such as a triangulation or a digitization. In order to tackle this problem, there are two main issues: (i) the first one is to define consistent notions of curvatures; (ii) the second is to show that these newly defined curvatures are stable, namely that one can can estimate the curvatures of a smooth object from an approximation. This problem has various applications in computer science, in particular in geometry processing, computer graphics or digital imaging where discrete surfaces are ubiquitous.
There is a long history on the generalization of the curvatures in non-smooth geometry. One important work on this topic is the seminal paper of Federer [12], who first defined curvature measures for sets with positive reach. This generalizes the notion of Gaussian and mean curvatures for convex and smooth objects, but it unfortunately does not apply to triangulations. Using the notion of normal cycle introduced by Wintgen [34], this notion was then extended to a wider class of objects including triangulations, digitized objects and subanalytic sets [15]. The normal cycle of a general shape in \(\mathbb {R}^n\) is a current in the Grassmann bundle \(\mathbb {R}^n\times {{\,\mathrm{Gr}\,}}(1,n)\) (where the \({{\,\mathrm{Gr}\,}}(1,n)\simeq \mathbb {S}^{n-1}\) factor stands for the normal cone) that encodes the geometry of the shape and allows to define curvature measures.
The stability of curvature measures has been well investigated the last 25 years. It is known that the curvature measures of a smooth object can be approximated by the ones of a triangulation, provided that the points and the normals of the triangulation are close to the ones of the smooth object [9, 14]. There exist different kinds of stability or convergence results for curvatures or curvature measures, including anisotropic curvature measures, which were introduced to estimate principal curvatures and directions [9, 26]. We may also quote the work of [5] which extends the normal cycle to arbitrary cloud of points by using offset surfaces, also with stability results. However these approaches do not provide a sound definition of curvatures when the naive normals do not converge toward smooth normals [5, 17]. This is the case for instance for the famous counterexample of the Schwarz lantern (see Sect. 3.3) that converges to a cylinder in the Hausdorff sense, but whose normals diverge. It also fails utterly in the case of digital approximations of surfaces, since the naive normal vectors take only six different possible values, parallel to the axes.
The key idea of this article is to replace the normal vector field of a surface S by another vector field \(\mathbf {u}\) which we assume to be geometrically more meaningful. For instance if S is a digitization of a smooth surface X, one may take for \(\mathbf {u}\) a local average of the naive normals of X. The contribution of the paper is therefore the following:
-
We extend the notion of normal cycle of a surface to a couple \((S,\mathbf {u})\) where S is a piecewise \(C^1\)-surface of \(\mathbb {R}^3\) and \(\mathbf {u}\) is a piecewise \(C^1\) unit vector field and we call it the corrected normal current \({{\,\mathrm{N}\,}}(S,\mathbf {u})\). Our corrected normal current \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) allows to define new curvature measures that we call corrected curvature measures.
-
We derive stability results for our corrected curvature measures with explicit bounds. In particular, we show that the corrected curvature measures of \((S,\mathbf {u}) \) approximate well Federer’s curvature measures of a smooth surface X, provided that S is close to X in the Hausdorff sense and that \(\mathbf {u}\) is close to the normal vector field of X.
-
We apply our results to the digital case and show that that it allows to define convergent pointwise estimators for the mean and Gaussian curvature with explicit convergence rates. We show that our estimators outperform also in practice state-of-the-art methods like digital integral invariants [7].
1.1 Alternative Approach with Varifolds
Another notable mathematical tool for representing generic shapes is the varifold, which has been introduced to solve shape optimization problems like Plateau’s problem [2]. A d-varifold is a Radon measure on \(\mathbb {R}^n\times {{\,\mathrm{Gr}\,}}(d,n)\), where \({{\,\mathrm{Gr}\,}}(d,n)\) denotes the Grassmannian manifold of unoriented d-planes in \(\mathbb {R}^n\). Its first variation is indeed related to the mean curvature vector field [1]. Varifolds were recently proposed for surface approximation and mean curvature estimation in [3].
Both approaches, the one with (corrected) normal cycles and the one with varifolds, are similar in that they rely on the Grassmann bundle. They differ however since \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) is an (oriented) integral current which possesses an additional combinatorial structure, which can be integrated against ambient invariants forms, yielding all the geometric curvatures, whereas the varifold defined in [3] is by definition unoriented and yields a vector valued mean curvature. Our framework is therefore less universal (for instance it does not encompass point clouds, which are a strong focus of the varifold approach). However, our explicit yet flexible construction allows us to use the homotopy lemma and compute actual convergence rates, which are further refined in a few test cases and which result in extremely efficient approximation rates. Furthermore, our results concern both Gaussian and mean curvature and can be extended to deal with principal curvatures and directions.
1.2 Related Works in Geometry Processing
Since accurate geometry estimations is an important step in many geometry processing tasks like sharp features extraction, surface approximation, shape segmentation, shape matching and identification, mesh denoising, the problem of having stable yet accurate normal and curvature estimations on discrete surfaces has been widely studied. We mention here some representative approaches.
The first methods for estimating curvatures on polyhedral meshes (generally triangulated surfaces) were based on local formula using a simple neighborhood of vertices (e.g. see [33] for a survey). However it was quickly shown that even the classical angle defect method for Gaussian curvature estimation does not converge in most of the cases [35]. Polynomial fitting was also popular to estimate curvatures, but, again, even the popular osculating jets of [4] are convergent under hypotheses that are not met in practice (like vertices lying on the ideal continuous surface).
For triangulated meshes, it was noted that convergence of normals was essential for getting convergence of area or other quantities [27]. Other authors then show the equivalence of convergence of normal fields, metric tensors, area, and Laplace–Beltrami operator [17]. This induces the weak convergence of mean curvatures, but only if the naive normals of the mesh are convergent.
Recognizing the weaknesses of local fitting approaches, integral methods (like in geometric measure theory) were explored also in this field. Integral invariants were studied as a way to estimate curvatures onto a mesh, by a proper eigendecomposition of a local covariance matrix [28, 29]. Unfortunately, this method is sensitive to errors in position. The Voronoi covariance measure is another way to compute geometric information from arbitrary compacts [24], with stability results. It indeed carries information related to curvature, but it is unclear if it induces pointwise convergence of curvature estimates.
Our work is significantly different from all the previous approaches. Our definition of curvatures is valid for surfaces that are union of cells homeomorphic to a disk, equipped with a vector field that only needs to be \(C^1\) per cell. We provide stability results for curvature measures with respect to a smooth surface. And given a convergent corrected normal vector field, we exhibit pointwise convergence for mean and Gaussian curvatures onto digital surfaces. Note that there exists convergent normal vectors onto digital surfaces [11, 22], so our mathematical framework is effective and gives convergent mean and Gaussian curvatures. Last but not least, our experiments show that they are not only convergent but outperform the state-of-the-art.
1.3 Detailed Outline of the Paper
In Sect. 2, we formalize this new integral with currents in \(\mathbb {R}^3 \times \mathbb {S}^2\), which we view as the set of couples (position, unit normal vector). The unit sphere \(\mathbb {S}^2\) stands for the oriented Grassmannian \({{\,\mathrm{Gr}\,}}(1,3)\), the set of unit vectors in \(\mathbb {R}^3\). Note that \({{\,\mathrm{Gr}\,}}(1,3)\) can be identified by duality to \({{\,\mathrm{Gr}\,}}(2,3)\), the set of oriented planes. The advantage in using currents is that they encompass both discrete and continuous objects. To each couple \((S,\mathbf {u})\) where S is a surface and \(\mathbf {u}\) a unit vector field along S we associate a current \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) in \(\mathbb {R}^3 \times \mathbb {S}^2\) (Definition 2.8). Intuitively we may view the current as a piecewise smooth oriented 2-surface in \(\mathbb {R}^3 \times \mathbb {S}^2\subset \mathbb {R}^6\). In particular, when the vector field \(\mathbf {u}\) is the naive normal field of S and \(S=\partial V\) is the boundary of a domain of \(\mathbb {R}^3\), then \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) corresponds to the normal cycle of V [26]. Then it is known that the integral of invariant forms over the normal cycle yields the area, mean and Gaussian curvature integrals over S. (However, the local convergence is only true when the normal cone approximates the smooth normal, whereas using \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) gives us the flexibility we need.)
In Sect. 3, we define our geometric measures, or corrected Lipschitz–Killing curvature forms as the integral on \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) of the classical invariant forms on \(\mathbb {R}^3\times \mathbb {S}^2\) (Definition 3.1). We further show that these measures have explicit and simple expressions in the specific but crucial case of polyhedral surfaces and a corrected normal vector field that is constant per face (Proposition 3.8). They reduce to finite sums of quantities attached to each discrete cell of S, i.e., face for area measure, edge for mean curvature measure, and vertex for Gaussian curvature measure. We illustrate with the case of the Schwarz lantern, known to be problematic even for the area, and we show how our corrected measures give very accurate or even exact curvature measures for several natural choices of the corrected normal field \(\mathbf {u}\).
We then provide in Sect. 4 a stability result for our corrected curvature measures (Theorem 4.2). More precisely, we show that the corrected curvatures of some \((S,\mathbf {u})\) approximate well the curvature measures of a surface \(X=\partial V\) of class \(C^2\) provided that the surface S is close to X in the Hausdorff sense and that the vector field \(\mathbf {u}\) approximates well the geometric normal \(\mathbf {n}\) of X. This result relies on several notions of Geometric Measure Theory: it uses the notion of reach [12] introduced by Federer that allows the projection of the support of \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) onto the one of the normal cycle \({\text {N}}(V)\); the affine homotopy formula [13] for currents is a key tool that allows to bound the flat norm between the normal cycle \({\text {N}}(V)\) and the corrected normal cycle \({{\,\mathrm{N}\,}}(S,\mathbf {u})\); the result also makes use of the Constancy Theorem [25] that allows to solve multiplicity issues that appear when projecting the support of \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) onto the one of \({\text {N}}(V)\).
As a byproduct, in the difficult case of digital surface approximations to smooth surface, we show that our normalized definitions of mean and Gaussian curvatures converge pointwise to the mean and Gaussian curvatures of the continuous surface S, provided \(\mathbf {u}\) is estimated by a multigrid convergent normal estimator (Theorem 5.4). The theoretical convergence speed is \(\mathcal {O}(h^{{1}/{3}})\) if h is the sampling step of the digitized surface, and equals the best known bound for curvature estimation \(\mathcal {O}(h^{{1}/{3}})\) for digital integral invariant method [7].
Following this stability and convergence results, we confront theory with practice in Sect. 6 and present an experimental evaluation of our new curvature estimator (defined from curvature measures) in the case of digital surfaces, which is a good testbed for our framework since naive normals of S never converge toward the normals of the continuous surface X (a problem known as metrication in the case of the area measure). We show that our estimators outperform also in practice state-of-the-art methods like digital integral invariants [7] and convergence speeds in \(\mathcal {O}(h^{{2}/{3}})\) are reached in practice.
We conclude in Sect. 7 and outline several research directions, especially the extension of our work to anisotropic curvature measures.
2 Normal Cycle Corrected by a Vector Field \(\mathbf {u}\)
We introduce in this section the notion of corrected normal current for piecewise \(C^1\) surfaces endowed with a vector field in the three dimensional space, called the corrected normal.
2.1 Corrected Surface
We assume in the following that S is a closed piecewise \(C^1\) oriented surface of \(\mathbb {R}^3\), namely \(S=\bigcup _{i=1}^n S_i\) where each \(S_i\) is a compact surface homeomorphic to a disc. Furthermore, we assume that we have the following combinatorial structure: (i) each \(S_i\) is called a face of S; (ii) for every \(i\ne j\), \(S_{i,j}=S_i\cap S_j\) is either empty or a point or a non-degenerated connected \(C^{1}\) curve; when not empty or reduced to a point, it is called an edge of S; (iii) the intersection of three (or more) faces of S is either empty or equal to a point that is called a vertex in the latter case.
Note that the orientation of S is equivalent to having an abstract orientation of the combinatorial structure. Indeed, each face \(S_i\) induces naturally an orientation of its bounding curves \(S_{i,j}\), where j ranges over the faces \(S_j\) adjacent to \(S_i\). This orientation turns \(S_{i,j}\) into a directed edge, and can be represented in space by the unit vector field \(\mathbf {e}_{i j}\) along \(S_{i j}\), which is tangent to \(S_{i,j}\). If we are given a normal vector field \(\mathbf {n}_i\) on \(S_i\) respecting its orientation, then \(\mathbf {n}_i\times \mathbf {e}_{i j}\) points toward the inside of \(S_i\). Note that the adjacent face \(S_j\) induces the opposite orientation on \(S_{i,j}\): \(\mathbf {e}_{j i} = - \mathbf {e}_{i j}\).
We say that \(\mathbf {u}:S\setminus \{S_{i,j}:i\ne j\}\rightarrow \mathbb {S}^2\) is a corrected normal vector field on S if: (i) its restriction \(\mathbf {u}_i\) to the relative interior of the face \(S_i\) is of class \(C^1\), and extends continuously to \(S_i\); (ii) along any curve \(S_{i,j} = S_i\cap S_j\), \(\mathbf {u}_i\) and \(\mathbf {u}_j\) are not antipodal; (iii) at any vertex \(p=S_{i_1}\cap \ldots \cap S_{i_k}\), the corrected normals \(\mathbf {u}_{i_1},\ldots ,\mathbf {u}_{i_k}\) lie in the same hemisphere. Note that, in this definition, we do not require \(\mathbf {u}\) to be continuous or even defined on the edges.
Definition 2.1
(corrected surface) We say that the couple \((S,\mathbf {u})\) is a corrected surface if \(S\subset \mathbb {R}^3\) is a surface that satisfies the above assumptions and \(\mathbf {u}\) is a corrected normal vector field on S.
Example 2.2
When S consists of a single \(C^1\) face, we can choose the vector \(\mathbf {u}\) to be the usual normal vector \(\mathbf {n}\). This generalizes easily to a piecewise \(C^1\) surface. The non-degeneracy across vertices or edges prohibits cusps or cuspidal edges.
Example 2.3
When S is an oriented polyhedral surface, we may choose \(\mathbf {u}\) to be the (unit) normal vector on each face. Here again, non-degeneracy across edges (resp. vertices) means that the dihedral angles are between \(-\pi \) and \(+\pi \) (resp. is a graph over the plane bounding the hemisphere).
Example 2.4
We can also consider any \(C^1\) unit vector field \(\mathbf {u}\) along S, even when S is a polyhedral surface, e.g. S can be a digital surface and \(\mathbf {u}\) can be a bilinear interpolation at the normals given at the vertices (in which case \(\mathbf {u}\) usually ceases to have unit length throughout, hence should be normalized).
2.2 Combinatorial Structure
Starting with the combinatorial structure of the surface S, i.e., the set of its vertices V, edges E and oriented faces F, together with their incidence relations, we define a new (abstract) combinatorial surface \(S^*\) over which the corrected normal current will be constructed. A similar construction exists for convex polyhedra, and is known under various names: expansion, cantellation, or complete truncation.Footnote 1
The idea behind the construction is that each inner edge is blown up into a strip (i.e., a combinatorial quadrilateral), while each inner vertex of degree d is blown up into a face with d edges, see Fig. 1. More precisely,
-
the vertices of \(V^*\) are the flags \( \{(p,f) \in V \times F:p \in f \} \),
-
the edges of \(E^*\) are the flags \( \{(e,f) \in E \times F: e\in f \} \),
-
the set \(F^*\) is the set \(\mathring{V}\cup \mathring{E}\cup F \), where \(\mathring{V}\) (resp. \(\mathring{E}\)) denotes the set of inner vertices (resp. edges).
The incidence relations are completely determined by describing the faces as an ordered list of vertices. Since a face \(f^* \in F^*\) is either a vertex p, an edge e of a face f of S, we consider separately all three cases.
-
Whenever the face corresponds to an inner vertex \(p \in V\), we denote it \(S^*_p\) and let \(S_1,\ldots ,S_n\) be an ordered list of the faces incident to p (the order is induced from the orientation and is unique, up to circular permutation). Then \(S^*_p\) is described by its vertices \(p^*_1,\ldots ,p^*_n\) where \(p^*_i = (p,S_i)\).
-
Whenever the face corresponds to an inner edge \(S_{i,j}=S_i \cap S_j \in E\), and \(S_{i,j}\) joins the vertices p, q, with the convention that \(S_i\) induces the orientation \(p \rightarrow q\) on \(S_{i,j}\), and \(S_j\) the opposite orientation. Then \(S^*_{i,j}\) is the quadrilateral face joining \( (p^*_i,p^*_j,q^*_j,q^*_i) \) where \(p^*_k = (p,S_k) \) and \(q^*_k = (q,S_k) \).
-
Whenever the face \(S^*_i\) corresponds to \(S_i \in F\), and the vertices of \(S_i \) (in order) are \(p_1,\ldots ,p_n\), then \(S^*_i\) is given by its vertices \(p^*_1,\ldots ,p^*_n\) where \(p^*_k = (p_k,S_i) \).
We slightly modify this definition by dividing all the faces \(S^*_p\) into triangles. More precisely, let \(S^*_p\) be a face of \(S^*\) corresponding to a vertex p of S. The boundary of this face is composed of \(\ell =\mathrm {d}(p)\) edges that are common with faces \(S^*_{i,j}\) and denoted by \(s_1,\dots ,s_\ell \),: (i) we add a vertex \(p^*\) at the interior of the face \(S^*_p\); (ii) for every \(1\le i\le \ell \), we add the triangle with vertex \(p^*\) and opposite edge \(s_i\); (iii) we add the edges corresponding to these triangles, see Fig. 1.
Expansion/cantellation at a degree three vertex, followed by subdivision of the face \(S^*_p\) corresponding to an original vertex p. The vertex p gives rise to a new face \(S^*_p\) (further subdivided); edges \(S_{i,j}=S_i\cap S_j\) give rise to new quadrilateral faces \(S^*_{i,j}\); faces \(S_i\) yield new faces \(S^*_i\)
2.3 Corrected Normal Cone
We need to define the notion of corrected normal cone which is the image by a continuous map of the combinatorial surface \(S^*\) into \(\mathbb {R}^3\times \mathbb {S}^2\). Its construction uses the corrected normal \(\mathbf {u}\) and is done so that the corrected normal cone inherits the orientation of \(S^*\).
Definition 2.5
Let \((S,\mathbf {u})\) be a corrected surface and \(S^*\) be the combinatorial surface of S whose orientation is inherited from S. The corrected normal cone \({\text {NC}}(f^*,\mathbf {u})\) of a face \(f^*\) of \(S^*\) is defined by:
-
if \(f^*=S^*_i\) corresponds to a face \(S_i\) in S, then \({\text {NC}}(f^*,\mathbf {u})={\text {NC}}(S_i,\mathbf {u})\) is the image of \(S_i\) by the map \(p \mapsto (p, \mathbf {u}(p))\);
-
if \(f^*=S^*_{i,j}\) corresponds to an edge \(S_{i,j}\) of S, then
$$\begin{aligned} {\text {NC}}(S_{i,j},\mathbf {u})=\{(p,n):p\in S_{i,j} \text {~and~}n \in {\text {Arc}}(\mathbf {u}_i(p),\mathbf {u}_j(p)) \}, \end{aligned}$$where \({\text {Arc}}(\mathbf {u}_i(p),\mathbf {u}_j(p))\) denotes the unique geodesic arc (on the sphere) between \(\mathbf {u}_i(p)\) and \(\mathbf {u}_j(p)\);
-
if \(f^*\) is a triangle of \(S^*_p\), then \({\text {NC}}(f^*,\mathbf {u})\) denotes the spherical triangle with vertices \(\mathbf {u}(p)\), \(\mathbf {u}_i(p)\), and \(\mathbf {u}_{i+1}(p)\) of area strictly less than \(2\pi \), where \(\mathbf {u}(p)\in \mathbb {S}^2\) is the normalized average of the \(\mathbf {u}_i(p)\).
Remark that for each oriented face \(f^*\) of \(S^*\), the corrected normal cone \({\text {NC}}(f^*,\mathbf {u})\) inherits from the orientation of \(f^*\).
Definition 2.6
(corrected normal cone) The corrected normal cone \({\text {NC}}(S,\mathbf {u})\) is the polygonal chain built as the sum of the \({\text {NC}}(f^*,\mathbf {u})\), where \(f^*\) ranges over the faces of \(S^*\).
Remark that for every face \(f^*\), \({\text {NC}}(f^*,\mathbf {u})\) is a surface of class at least \(C^1\) in \(\mathbb {R}^3\times \mathbb {S}^2\). The corrected normal cone \({\text {NC}}(S,\mathbf {u})\) can be seen globally as the image by a continuous map of the combinatorial surface \(S^*\) into \(\mathbb {R}^3\times \mathbb {S}^2\). However it may not be an embedding nor even an immersion over edges and vertices; indeed, the image may have multiplicity above the vertices, and singularities above the edges.
Remark 2.7
The corrected normal cone \({\text {NC}}(S^*_p,\mathbf {u})\) above a vertex p of S is made of \(\mathrm {d}(p)\) spherical triangles, each of them having \(\mathbf {u}(p)\) as a vertex. Note that the algebraic sum of these oriented triangles do not depend on this arbitrary point \(\mathbf {u}(p)\). The corrected normal cone \({\text {NC}}(S^*_p,\mathbf {u})\) can be seen as a set of point \(n\in \{p\}\times \mathbb {S}^2\) with an integer multiplicity \(\mu (p)\).
2.4 Corrected Normal Current
We may now define our variant of normal cycle, defined as a current with support given by the corrected normal cone. For the reader unfamiliar with the notion of currents, we recall briefly the main notions in Sect. 4.3.
Definition 2.8
(corrected normal current) Let \((S,\mathbf {u})\) be a corrected surface. The corrected normal current \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) of \((S,\mathbf {u})\) associates to every differential 2-form \(\omega \) of \(\mathbb {R}^3\times \mathbb {S}^2\) the real number
where \(f^*\) ranges over all the faces of \(S^*\).
The following proposition is an obvious consequence of the construction but is the heart of the notion introduced in this paper. Thanks to this property, the corrected normal current is globally coherent. In particular, this property will be central in the proof of stability results.
Proposition 2.9
If S has no boundary, then the corrected normal current \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) has no boundary.
Proof
By construction \({\text {NC}}(S,\mathbf {u})\) is the continuous image of a combinatorial surface \(S^*\). This comes from the coincidence of incident faces along their boundaries. Now, if S has no boundary, neither does \(S^*\), nor \({{\,\mathrm{N}\,}}(S,\mathbf {u})\). \(\square \)
Remark 2.10
Whenever \(S=\partial V\) is a piecewise smooth or planar surface, which is the boundary of a domain in \(\mathbb {R}^3\), and \(\mathbf {u}\) is chosen as the unit normal on faces pointing toward the outside, then \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) coincides with the normal cycle \({\text {N}}(V)\) of S [15, 36]. The corrected normal current thus generalizes the normal cycle.
Remark 2.11
For the sake of consistency and subsequent proofs, we have assumed that the vector field \(\mathbf {u}\) has unit length. Note that it is sometimes useful to relax that requirement to nonzero vector fields, for example when using linear interpolation to construct a smooth vector field from few samples. Indeed unit length is not required to define the corrected normal cone over a face of \(S_i\). However over an edge \(S_{i,j}\) or a vertex, it asks for different interpolation formulas, which we will not delve into in this article. Nevertheless, if \(\mathbf {u}\) is continuous, edge and vertex contributions have zero Lebesgue measure, and the integral formulas below can be defined. Moreover they will converge to the same limit as \(\mathbf {u}\) tends to the smooth normal \(\mathbf {n}\), even if \(\mathbf {u}\) is not of unit length. This case will be illustrated in a forthcoming article.
The corrected normal current of a planar curve, seen as a discrete curve in \(\mathbb {R}^3\). The Grassmann bundle \(\mathbb {R}^2\times {{\,\mathrm{Gr}\,}}(1,\mathbb {R}^2)=\mathbb {R}^2\times \mathbb {S}^1\) is represented as \(\mathbb {R}^3\) where the third coordinates is the angle \(\theta \). The smooth planar curve is a circular arc lifting to a piece of a helix. Its approximation by a digital curve can be lifted as the normal cycle (in purple), in which case the normal on each edge follows the axes (hence lies at height \(k\pi /2\) for some integer k); therefore the extra circular arcs at the vertices are vertical edges of length \(\pm \pi /2\). On the contrary, corrected normals on the digital curve are closer to the smooth normals; as a result, the corresponding lift (in blue) is also closer to the helix in \(\mathbb {R}^3\), and the vertical edges are shorter. Obviously, the corrected current is closer to the smooth lift. Note that the combinatorial structure of the current is extremely simple: each vertex is blown up into an edge
3 Corrected Curvature Measures
Our goal is to obtain geometric information on the surface S, namely its area and curvatures, which are independent of the position of S in space. It is classically known in the smooth case that the area and curvature measures can be computed by integrating the invariant forms on the normal cycle; it also extends to discrete surfaces (see [15]). These invariant forms [34, 36] form a basis of the 2-forms in \(\mathbb {R}^3 \times \mathbb {S}^2\) that are invariant by the action of the rigid motions of \(\mathbb {R}^3\). They yield the area, the mean curvature and the Gaussian curvature.
3.1 Invariant Forms, Curvature Measures, Curvature Estimators
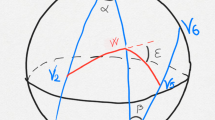
Let us now recall the expression of the invariant differential 2-forms of \(\mathbb {R}^3\times \mathbb {S}^2\) (see [26] for more details). Let \((p,\mathbf {w})\) be any point in the oriented Grassmann bundle \(\mathbb {R}^3\times \mathbb {S}^2\). Clearly the tangent plane of \(\mathbb {R}^3\times \mathbb {S}^2\) at the point \((p,\mathbf {w})\) is a space of dimension 5 spanned by the following vectors:
where \(\mathbf {e}_1\) and \(\mathbf {e}_2\) are any vectors such that \((\mathbf {e}_1,\mathbf {e}_2, \mathbf {w})\) form a direct orthonormal frame of \(\mathbb {R}^3\). The set of differential 2-forms of \(\mathbb {R}^3\times \mathbb {S}^2\) that are invariant under the action of rigid motions is a vector space of dimension four spanned by the following forms:
where \(\varvec{\varepsilon }^\flat (\varvec{\xi })\) denotes the scalar product of \(\varvec{\varepsilon }\) and \(\varvec{\xi }\).
Definition 3.1
Let \(k\in \{0,1,2,\Omega \}\). The kth Lipschitz–Killing corrected curvature measure of S with respect to \(\mathbf {u}\) associates to every Borel set B the real number
where \(\pi :\mathbb {R}^3\times \mathbb {S}^2 \rightarrow \mathbb {R}^3\) denotes the projection on the position space.
Remark 3.2
When S is smooth and \(\mathbf {u}= \mathbf {n}\) the standard normal, \(\mu _0\) is the area density \(\mathrm {d}A\), while \(\mu _1\) and \(\mu _2\) are respectively the mean curvature and Gaussian curvature densities, \(- 2 H \, \mathrm {d}\mathcal {H}^2\) and \(K \, \mathrm {d}\mathcal {H}^2\) (up to a scalar factor). This result is reproven below.
Remark 3.3
The measure \(\mu _\Omega \) induced by the symplectic form \(\omega _\Omega \) plays a different role. Instead of measuring metric data, it tests whether a surface in the \(\mathbb {R}^3\times \mathbb {S}^2\) is indeed the normal bundle of a surface in \(\mathbb {R}^3\). Quite logically, it vanishes identically on smooth surfaces as soon as \(\mathbf {u}=\mathbf {n}\). For an approximated surface, it measures how far the corrected normal \(\mathbf {u}\) is from being normal to the faces. While pointwise never true, its averaged value yields a measure of the quality of the choice of corrected normal.
In order to recover classical geometric invariants, we further define:
Definition 3.4
For any Borel set B such that \(\mu _0(B) \ne 0\), the normalized corrected mean curvature \(\hat{H}^{\mathbf {u}}\) of S with respect to \(\mathbf {u}\) is defined as \(\hat{H}^{\mathbf {u}}(B) := -\mu _1(B) / (2\mu _0( B ))\), and the normalized corrected Gaussian curvature \(\hat{G}^{\mathbf {u}}\) of S with respect to \(\mathbf {u}\) is defined as \(\hat{G}^{\mathbf {u}}(B) :=\mu _2(B) / \mu _0( B )\).
3.2 Calculation of the Corrected Curvature Measures
Let \((S,\mathbf {u})\) be a corrected surface. We recall that \(S=\bigcup _{i=1}^n S_{i}\) is a union of faces of class \(C^1\), that the edges \(S_{i,j}\) are of class \(C^1\) and the set \(\mathcal {E}(S)\) of edges of S is finite. The surface S is oriented. In order to state the proposition we need to introduce the following notations.
3.2.1 Notations
At every point p of the interior of a face \(S_i\), we denote by \(\mathbf {n}(p)\) the unit oriented normal vector, by \(T_pS\) the plane tangent to S, by \(\mathbf {e}_1(p)\) a vector of \(T_pS\) given by \(\mathbf {e}_1=(\mathbf {n}\times \mathbf {u})/\Vert \mathbf {n}\times \mathbf {u}\Vert \) if \(\mathbf {n}\) and \(\mathbf {u}\) are not collinear, and given by one of the principal directions otherwise. We also introduce \(\mathbf {e}_2=\mathbf {u}\times \mathbf {e}_1\) and \(\mathbf {e}_2'=\mathbf {n}\times \mathbf {e}_1 \in T_pS\). Note that \((\mathbf {e}_1, \mathbf {e}_2, \mathbf {u})\) is a moving frame of \(\mathbb {R}^3\) associated with \(\mathbf {u}\), while \((\mathbf {e}_1,\mathbf {e}_2^{\,\prime },\mathbf {n})\) is a Darboux frame associated to the surface \(S_i\).
At every point p on an edge \(S_{i,j}\), we denote by \(\mathbf {e}(p)=\mathbf {e}_{i j}(p)\) the unit vector along the edge \(S_{i,j}\) orientedFootnote 2 as the boundary of \(S_i\), by \(\varPsi (p)=\angle (\mathbf {u}_i(p), \mathbf {u}_j(p))\) the corrected dihedral angle between the faces \(S_i\) and \(S_j\), and \(\mathbf {e}_1(p) = (\mathbf {u}_i \times \mathbf {u}_j)/\Vert \mathbf {u}_i \times \mathbf {u}_j\Vert \). (The last vector is only defined when \(\mathbf {u}_i(p)\) and \(\mathbf {u}_j(p)\) are not collinear; however, whenever that happens, \(\varPsi (p)\) vanishes and \({\text {NC}}(p,\mathbf {u})\) drops in dimension, hence does not contribute to the integrals. Without loss of generality, we will assume that \(\mathbf {e}_1\) is always well defined.)
In order to integrate differential forms over manifolds (more details are provided in Sect. 4.3), we will use the notion of Hausdorff measure. In the following, we denote by \(\mathcal {H}^m\) the m-dimensional Hausdorff measure.
Proposition 3.5
The corrected Lipschitz–Killing curvature measures of S with respect to \(\mathbf {u}\) associates to every Borel set B the quantities
where \({\text {Area}}{({\text {NC}}(p,\mathbf {u}))}\) is the sum of the algebraic areas of each spherical triangle where the sign is induced by its orientation.
Proof
We recall that \(\mathbf {u}\) is of class \(C^1\). The measures have absolutely continuous and atomic parts; by additivity of the integral, we may consider separately the contributions of faces, edges and vertices.
Above the Faces. Remark that for any face \(S_i\) of S the map \(\varGamma _{\mathbf {u}}:p \in S_i \mapsto (p,\mathbf {u}(p))\) is a diffeomorphism between \(S_i\) and the corrected normal cone \({\text {NC}}(S_i,\mathbf {u})\). The change of variable formula implies that
Hence, the computation of the curvature measures amounts to computing the pull-back by \(\varGamma _{\mathbf {u}}\) of the corresponding curvature forms. In order to do that, we consider the orthonormal frame \((\mathbf {e}_1,\mathbf {e}_2')\) of the tangent plane \(T_pS\) at p. Using the fact that \(\mathrm {d}\varGamma _\mathbf {u}(p)=(\mathrm {Id},\mathrm {d}\mathbf {u}(p))\), one gets
Similarly, we evaluate \(\varGamma _\mathbf {u}^{\,*} \omega _1\) and \(\varGamma _\mathbf {u}^{\,*} \omega _2\) in the same basis:
Finally,
Above the Edges. Let \(p:[0,L]\rightarrow S_{i,j}\) be the arc length parameterization of \(S_{i,j}\) that satisfies \(\dot{p}(t)=\mathbf {e}(p(t))\) (the dot denoting the derivative w.r.t. t). Then the corrected normal cone \({\text {NC}}(S,\mathbf {u})\cap \pi ^{-1}(S_{i,j})\) above the edge \(S_{i,j}\) can be parameterized by
with
Note that the map \(\phi \) preserves the orientation. In order to shorten the equations below, we often (but not always) omit to specify that the quantities are considered at the point p or p(t). Note also that the reference frame at \((p, \mathbf {v})\) is \((\mathbf {e}_1,\mathbf {e}_2,\mathbf {v})\), where \(\mathbf {e}_2 = \mathbf {v} \times \mathbf {e}_1\). Finally,
where \(\lambda =\partial (\varPsi \circ p)/\partial t\), while \(\partial \mathbf {v}/ \partial s = - \varPsi \mathbf {e}_2\). We then get
We may note that \(\mu _0\) vanishes identically above the edges, since \({\text {Span}}{({\partial \phi }/{\partial \psi },{\partial \phi }/{\partial t})}\) projects to a line on the position component. Note that this calculation can be easily localized over a Borel set B: if we calculate \(\mu _1(B \cap S_{i,j})\), it amounts to add the indicator function of B in the integrand. Similarly, one gets
By differentiating the expression \(\langle {\mathbf {u}_i}\,|\,{\mathbf {e}_1}\rangle =0\), we write \(\langle {\mathrm {d}\mathbf {u}_i \cdot \mathbf {e}}\,|\,{\mathbf {e}_1}\rangle =-\langle {\mathbf {u}_i }\,|\,{\mathrm {d}\mathbf {e}_1\cdot \mathbf {e}}\rangle \). Similarly, one has \(\langle {\mathrm {d}(\mathbf {e}_1 \times \mathbf {u}_i) \cdot \mathbf {e}}\,|\,{\mathbf {e}_1}\rangle =-\langle {\mathbf {e}_1 \times \mathbf {u}_i }\;|\;{\mathrm {d}\mathbf {e}_1 \cdot \mathbf {e}}\rangle \) and thus
We note that the angle \(\psi \) between the two vectors \(\mathbf {u}_i\) and \(\mathbf {u}_j\) belongs to \([0,\pi ]\) so that \(\sin \psi \ge 0\). Since \((\mathbf {u}_i,\mathbf {u}_j,\mathbf {e}_1)\) is a direct frame, we have \(\det {(\mathbf {u}_i,\mathbf {u}_j,\mathbf {e}_1)}=\sin \psi \). Therefore \(\mathbf {u}_i\), \(\mathbf {u}_j\), and \(\mathbf {e}_1\times \mathbf {u}_i\) are all orthogonal to \(\mathbf {e}_1\), so they belong to the same plane and we have
This leads to
Finally,

Above the Vertices. When p is a vertex, its contribution is restricted to \(\mu _2\), since the position is constant in \({\text {NC}}(p)\). Since \(\omega _2\) measures the area in the velocity component, the vertex adds a Dirac mass at p to \(\mu _2\), with coefficient equal to the (signed) area of \({\text {NC}}(p)\). \(\square \)
Remark 3.6
In the smooth case, there are no edges nor vertices, and taking \(\mathbf {u}= \mathbf {n}\) (and hence \(\mathbf {e}_2'=\mathbf {e}_2\)), the formulas simplify. We recover
while
since \(\mathrm {d}\mathbf {n}\) is symmetric on \(T_p S\).
Remark 3.7
Similarly to [9], we can consider a vector-valued equivariant two-form on the Grassmann bundle defined for each fixed pair of vectors \(\mathbf {X},\mathbf {Y}\in \mathbb {R}^3\). This leads to an anisotropic curvature measure \(\mu ^{\mathbf {X},\mathbf {Y}}\) which converges to the second fundamental form by the same theorems in Sect. 4. Study of this measure allows to compute and approximate principal curvatures and principal directions. This will be the topic of a forthcoming article.
In the case of polyhedral surfaces with a normal constant per face, we have the following simplifications, which we will use in our experiments (Sect. 6).
Proposition 3.8
Let S be a polyhedral surface and \(\mathbf {u}\) a vector field constant on each planar face of S. Then the corrected Lipschitz–Killing curvature measures are
where \(\alpha (f)\) is the angle between the corrected normal \(\mathbf {u}\) and the naive normal \(\mathbf {n}\), \(\varPsi \) is the oriented angle between the corrected normal \(\mathbf {u}_i\) and \(\mathbf {u}_j\) incident to the edge \(S_{i,j}\) and \(\mathbf {e}_1 = ({\mathbf {u}_i \times \mathbf {u}_j})/{\Vert \mathbf {u}_i \times \mathbf {u}_j \Vert }\), while \(\mathbf {e}\) is the oriented unit tangent to the edge.
3.3 The Schwarz Lantern
To illustrate the remarkably fast rate of convergence of our approach, let us apply it to the Schwarz lantern L, a \(C^0\) approximation by triangles of a cylinder C of radius r and height h, known for its failure to converge in curvature and even area (see Fig. 3.3). The failure occurs because the normals do not converge to the cylinder’s (see [26] for the definition of the Schwarz lantern and an analysis of the problem). We will use two different choices of corrected normals on the Schwarz lantern.
The Schwarz lantern. The vertical cylinder of height h and radius r is cut horizontally along \(m+1\) evenly spaced circles; each circle is replaced by a regular n-gon (here \(m=6\) and \(n=7\)). However, consecutive polygons are not parallel but rather obtained one from another by a screw motion of vertical translation h/m and angle \({\pi }/n\). Any vertex is connected to the two nearby vertices above and the two nearby vertices below (except for the top and bottom levels)
We first consider the corrected normals to be constant on each triangle T and equal to the cylinder’s at the top (or bottom) of the triangle. Then the angle \(\alpha \) between the corrected normal and the face’s normal satisfies \(\tan \alpha = ({2 m r}/{h})\sin ^2({\pi }/({2n}))\), so that the corrected area of the lantern is
Edges are either horizontal, in which case the corrected normal is identical on the faces above and below, or slanted, in which case the two normals \(\mathbf {u}_i,\mathbf {u}_j\) are horizontal (so that \(\mathbf {e_1} = \mathbf {u}_i \times \mathbf {u}_j\) is vertical) and at angular distance \(\varPsi = \pi /n\). For an edge e, the scalar product \(\langle {\mathbf {e}}\,|\,{\mathbf {e_1}}\rangle \ell (e)\) is then h/m, thus \(\mu _1(e) = {\pi h}/({n m})\). Since there are exactly 2nm such edges, \(\int _L\mu _1=2 \pi h=2\int _C({2r})^{-1}\mathrm {d}A\). Finally, at a vertex p, the corrected normals are all horizontal, so that \({\text {NC}}(p)\) has measure zero, as expected. We have thus an exact result for the mean and Gaussian corrected curvature measures and a \(\mathcal {O}(1/n^2)\) convergent one for the area.
Now consider the same triangulation with a different corrected normal \(\mathbf {u}\), defined as follows: at every vertex, it is the same (horizontal) normal as the one to the cylinder; along edges and faces, it is defined by linear interpolation followed by normalization to one. It is easy to see that these normals coincide with the normal to the cylinder of the horizontal projection \(\pi \) on C: \(\mathbf {u}(p) = r^{-1}\pi (p)\). On a face, \(\mathbf {e}_1=\mathbf {u}\times \mathbf {n}\) and \(\mathbf {e}'_2 = \mathbf {n}\times \mathbf {e}_1\). Since \(\mathrm {d}\pi \) is the projection to the tangent plane to the cylinder, we have that \( \mathrm {d}\mathbf {u}\cdot \mathbf {e}_1 = r^{-1} \mathbf {e}_1\) and \( \mathrm {d}\mathbf {u}\cdot \mathbf {e}'_2 = r^{-1} \langle {\mathbf {u}}\,|\,{\mathbf {n}}\rangle \mathbf {e}_2 \).
The field \(\mathbf {u}\) being continuous on the edges and at the vertices, the curvature measures are carried only by the faces. Using Proposition 3.5, we get:
-
the corrected area measure \(\mu _0 = \langle {\mathbf {u}}\,|\,{\mathbf {n}}\rangle \,\mathrm {d}\mathcal {H}^2\) is no other than the pullback of the area form on the cylinder by the horizontal projection, i.e., \( \pi ^*\mathrm {d}A_C \); hence \(\mu _0\) measures the area of the projected lantern L onto the cylinder C, and globally gives exactly the area of the cylinder;
-
for \(\mu _1\), we have that
$$\begin{aligned} \mu _1=\langle {\mathrm {d}\mathbf {u}\cdot \mathbf {e}_2^{\,\prime }}\,|\,{\mathbf {e}_2}\rangle + \langle {\mathbf {u}}\,|\,{\mathbf {n}}\rangle \langle {\mathrm {d}\mathbf {u}\cdot \mathbf {e}_1}\,|\,{\mathbf {e}_1}\rangle \,\mathrm {d}\mathcal {H}^2= \frac{2}{r}\langle {\mathbf {u}}\,|\,{\mathbf {n}}\rangle \,\mathrm {d}\mathcal {H}^2= \frac{2}{r}\mu _0, \end{aligned}$$hence we obtain exactly twice the mean curvature density of the cylinder;
-
the corrected Gaussian curvature measure is also a pullback; but we may directly notice that the corrected normal is horizontal, hence stays on the equator of \(\mathbb {S}^2\); therefore \(\mu _2\) vanishes identically as in the previous example.
4 Stability of the Corrected Curvature Measures
We show in this section that the corrected curvatures of \((S,\mathbf {u})\) approximate well the curvature measures of a surface \(X\) of class \(C^2\) provided that the surface S is close to \(X\) in the Hausdorff sense and that the vector field \(\mathbf {u}\) approximates well the normal \(\mathbf {n}_X\) of \(X\). In order to be able to compare the two surfaces S and \(X\), one first need to recall the notion of reach introduced by Federer [12]. Remark that this notion was originally introduced in order to define the notion of curvature measures.
4.1 Background on Sets with Positive Reach
The distance function \(d_K\) of a compact set K of \(\mathbb {R}^d\) associates to any point x of \(\mathbb {R}^d\) its distance to K, namely \(d_K(x):=\min _{y\in K}d(x,y)\), where d is the Euclidean distance on \(\mathbb {R}^d\). For a given real number \(\varepsilon >0\), we denote by \(K^\varepsilon :=\{x\in \mathbb {R}^d:d_K(x)\le \varepsilon \}\) the \(\varepsilon \)-offset of K. The Hausdorff distance \(d_{H }(K,K')\) between two compact sets K and \(K'\) is the minimum number \(\varepsilon \) such that \(K\subset K'^\varepsilon \) and \(K'\subset K^\varepsilon \).
The medial axis of K is the set of points of \(x \in \mathbb {R}^d\) such that the distance d(x, K) is realized by at least two points y and \(y'\) in K. The reach of K, denoted by \({\text {reach}}(K)\), is the infimum distance between K and its medial axis. As a consequence, whenever the reach is positive and \(\varepsilon <{\text {reach}}(K)\), the projection map
is well defined. It is well know that smooth compact submanifolds have positive reach [12, 26]. The following proposition will be useful for stating our main theorem.
Proposition 4.1
Let \(X\) be a compact submanifold of class \(C^2\) of \(\mathbb {R}^d\). Then
where \(\rho _X\) is the largest absolute value of the principal curvatures of \(X\). Furthermore \(\pi _X\) is differentiable on \(X^\varepsilon \) for any \(\varepsilon < \mathrm {reach}(X)\) and
where \(\rho _X(x)\) is the largest absolute value of the principal curvatures of \(X\) at the point x.
4.2 Stability Result
We provide in this section a stability result on the curvature measures, namely we show that the corrected curvature measures of \((S,\mathbf {u})\) approximate the curvature measures of X provided that S and X are close in the Hausdorff sense and that \(\mathbf {u}\) is close to the unit normal vector of X. In order to state the result, we denote by \(\mu _k^{S,\mathbf {u}}\) the corrected curvature measures of \((S,\mathbf {u})\) and by \(\mu _k^X\) the curvature measures of X, where \(k\in \{0,1,2,\Omega \}\). Note that the curvature measures of X coincide with the corrected curvature measures of \((X,\mathbf {n})\) where \(\mathbf {n}\) is the geometric oriented unit normal of X.
Theorem 4.2
Let \(X\) be a compact surface of \(\mathbb {R}^3\) of class \(C^2\), of normal vector \(\mathbf {n}\), bounding a volume V, and \(S =\bigcup _i S_i\) be a piecewise \(C^{1,1}\) surface bounding a volume W, \(\mathbf {u}\) a corrected normal vector field on S. We assume the following two conditions:
-
there exists an open set U of the form \(U=\pi _X^{-1}(V)\) such that \(U\cap S\ne \emptyset \) and \(\pi _{X}:U\cap S \rightarrow X\) is injective;
-
\(\varepsilon :=d_{H }(S,X) < \mathrm {reach}(X)\) is the position error.
Then the corrected curvature measures of \((S,\mathbf {u})\) are close to the curvature measures of \(X\) in the following way: for any connected union \(B=\bigcup _{i\in I}S_i\) of faces \(S_i\) of S, one has

where  (\(i\sim j\) whenever \(S_i\) is adjacent to \(S_j\)), \(\eta :=\sup _{p\in S}\Vert \mathbf {u}(p) - \mathbf {n}(\pi _X(p) )\Vert \) is the normal error, \(\rho _{B}\) is the maximum absolute value of the principal curvatures of \(X\cap \pi _X(B)\), \(\mathrm {L}_\mathbf {u}\) is the maximum of the Lipschitz constants of \(\mathbf {u}\) over each face \(S_i\), \(d_{\max }\) is the maximum vertex degree, \(N_v^S(B)\) and \(N_v^S(\partial B)\) are the number of vertices of S that respectively belong to B and \(\partial B\).
(\(i\sim j\) whenever \(S_i\) is adjacent to \(S_j\)), \(\eta :=\sup _{p\in S}\Vert \mathbf {u}(p) - \mathbf {n}(\pi _X(p) )\Vert \) is the normal error, \(\rho _{B}\) is the maximum absolute value of the principal curvatures of \(X\cap \pi _X(B)\), \(\mathrm {L}_\mathbf {u}\) is the maximum of the Lipschitz constants of \(\mathbf {u}\) over each face \(S_i\), \(d_{\max }\) is the maximum vertex degree, \(N_v^S(B)\) and \(N_v^S(\partial B)\) are the number of vertices of S that respectively belong to B and \(\partial B\).
Remark 4.3
It may seem quite restrictive to evaluate the measures \(\mu _k^{S,\mathbf {u}}\) and \(\mu _k^X\) on union of faces instead of generic Borel sets. In particular, these faces may be large, which contradicts the idea behind the normalized corrected curvature  of Definition 3.4. However, the faces can be subdivided at measure in order to give neighborhoods as small as necessary (extra edges and vertices will carry no curvature). Working on faces ensures a minimum of regularity in our theorem, without loss of generality.
of Definition 3.4. However, the faces can be subdivided at measure in order to give neighborhoods as small as necessary (extra edges and vertices will carry no curvature). Working on faces ensures a minimum of regularity in our theorem, without loss of generality.
Theorem 4.2 allows us to estimate the rate of convergence of curvature measures for a sequence of approximations  together with their corrected normals vector fields. However, some terms may prove difficult, especially \(N_v^S(B)\) and \(N_v^S(\partial B)\) which will tend to infinity very fast. We give below two corollaries of the previous stability result. The first one is specific to the case where the corrected normal field \(\mathbf {u}\) is continuous. The second case concerns digital surface approximations, where \(\mathbf {u}\) is constant per face.
together with their corrected normals vector fields. However, some terms may prove difficult, especially \(N_v^S(B)\) and \(N_v^S(\partial B)\) which will tend to infinity very fast. We give below two corollaries of the previous stability result. The first one is specific to the case where the corrected normal field \(\mathbf {u}\) is continuous. The second case concerns digital surface approximations, where \(\mathbf {u}\) is constant per face.
Corollary 4.4
Under the same assumptions as in Theorem 4.2, if \(\mathbf {u}\) is continuous over the whole surface S, one has

Corollary 4.5
When S is a digital surface approximation with an estimated normal vector field \(\mathbf {u}\) constant per face, we have the following simplified estimate:

where B is an union of \(N_s\) surfels of edge size h, with \(N_b\) boundary edges.
Proof
In the digital case, a vertex has at most six neighbors so \(d_{\max } \le 6\). (We then major \(6^3/(2\pi )\) by 35.) Since \(\mathbf {u}\) is constant per-face, we have  . Furthermore, the length of each edge is h, the area of each face is \(h^2\), \(N_v^S(B)\le 4 N_s\) and the number of edges is less than \(4N_s\). The formula follows. \(\square \)
. Furthermore, the length of each edge is h, the area of each face is \(h^2\), \(N_v^S(B)\le 4 N_s\) and the number of edges is less than \(4N_s\). The formula follows. \(\square \)
Estimation of curvatures on digital surfaces is studied in more details in Sect. 5. The remaining of this section is devoted to the proof of Theorem 4.2.
4.3 Notions of Geometric Measure Theory
4.3.1 Currents
We denote by \(D_m\) the set of m-differential forms on \(\mathbb {R}^d\). This set can be endowed with the \(C^\infty \)-topology [31] and the set of m-currents on \(\mathbb {R}^d\) is then by definition its topological dual. Therefore a current \(T:D_m\rightarrow \mathbb {R}\) is a continuous linear map. The support of a current \(T:D_m\rightarrow \mathbb {R}\) is the smallest closed set K such that \(\mathrm {spt}(\omega )\cap K = \varnothing \Rightarrow T(\omega )=0\). The boundary \(\partial T\) of a m-current T is the \((m-1)\)-current defined by \(\partial T(\omega ) = T(\mathrm {d}\omega )\), where \(\mathrm {d}\) is the exterior derivative.
When U and V are open sets in Euclidean spaces, \(f:U\rightarrow V\) is of class \(C^\infty \), T is a m-current on U and \(f_{|\mathrm {spt}(T)}\) is proper, one define the m-current \(f_\sharp T\) by \(f_\sharp T(\omega )=T(f^*\omega )\) (see [13, 4.1.9]). This notion is extended when f is a locally Lipschitz map (see [13, 4.1.14]).
Note that if a subset S of \(\mathbb {R}^d\) is m-rectifiable, then it is of class \(C^1\) \(\mathcal {H}^m\)-almost everywhere and it is possible to integrate differential forms over it, and thus to define currents of the form
where \((e_1,\dots ,e_m)\) is any direct orthonormal basis of the tangent space at x.
4.3.2 Integral Currents
There exist several categories of currents, but we are mainly mentioning the one we use in this paper. An m-current T is said to be rectifiable if its support \(S=\mathrm {spt}(T)\) is m-rectifiable, compact and oriented and if for every \(\omega \in D_m(\mathbb {R}^d)\), one has
where \(\mu (x)\in \mathbb {Z}\) is the multiplicity and satisfies \(\int _S \mu (x)\,\mathrm {d}\mathcal {H}^m(x) < \infty \). When \(\mu (x)=k\) is constant, we denote \(T=k \cdot S\). Note that a current can be rectifiable without having its boundary rectifiable. A current T is said to be integral if both T and \(\partial T\) are rectifiable.
4.3.3 Flat Norm and Mass
We can also define semi-norms over the set of currents. The mass M(T) of a m-current T is given by
where \(\Vert \omega (x)\Vert ^*=\sup {\{ \omega (x)(\xi _1,\dots ,\xi _m):\xi _i \in \mathbb {R}^d,\,\Vert \xi _i\Vert \le 1\}}\). The flat norm \(\mathcal {F}(T)\) of T is given by
4.3.4 Constancy Theorem
A key tool in the proof is the Constancy Theorem (see [13, 4.1.14] or [25, 3.13]). This theorem is important since it implies that the multiplicity of a current supported on a \(C^1\) submanifold is constant. We state it for integral currents in the case where there is no boundary, even though it is true in a much more general setting.
Theorem 4.6
(Constancy Theorem) Let X be an m-dimensional oriented submanifold of \(\mathbb {R}^d\) of class \(C^1\) with no boundary. If T is an integral current supported in X with no boundary, then there exists an integer \(\lambda \) such that
4.4 Proof of Theorem 4.2
The proof is based on the homotopy formula for currents and is in the same spirit as the proof of [9]. We recall that the projection map \(\pi _X:X^\varepsilon \rightarrow X\) is well defined and differentiable since \(\varepsilon < \mathrm {reach}(K)\). We first build the Lipschitz map
Lemma 4.7
\(f_\sharp {{\,\mathrm{N}\,}}(S,\mathbf {u}) ={\text {N}}(X)\).
Proof
By definition, \(f_\sharp {{\,\mathrm{N}\,}}(S,\mathbf {u}) \) is a 2-current supported in the set \(\mathrm {spt}({\text {N}}(X))\). Since \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) has no boundary, \(f_\sharp {{\,\mathrm{N}\,}}(S,\mathbf {u})\) also has no boundary. Furthermore, \(\mathrm {spt}({\text {N}}(X))\) is of class \(C^1\), so by the Constancy Theorem (Theorem 4.6), one has \(f_\sharp {{\,\mathrm{N}\,}}(S,\mathbf {u}) = \lambda \cdot {\text {N}}(X)\), where \(\lambda \) is an integer. We know by assumption that there exists an open set U such that \(\pi _X:U\cap S \rightarrow X\) is injective. This implies that the restriction of f to \(\mathrm {spt}({{\,\mathrm{N}\,}}(S,\mathbf {u}))\) is one-to-one onto its image, so the constant \(\lambda =1\). \(\square \)
We denote by \(D={{\,\mathrm{N}\,}}(S,\mathbf {u})\,{\llcorner }\,(B \times \mathbb {R}^3)\) the restriction of the current \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) to \(B\times \mathbb {R}^3\). By Lemma 4.7, one has
Let h be the affine homotopy between f and the identity:
In the remainder of the proof, in order to shorten equations, we put \(x=(p,\mathbf {u})\). Using the affine homotopy formula for locally Lipschitz map (see [23, p. 187] or [13, 4.1.14]), one has
where \(E=h_\sharp (D \times [0,1])\) and \(F=h_\sharp (\partial D \times [0,1])\) are respectively 3-current and 2-current that satisfy
where the norm of the linear map Df(x) is \(\Vert Df(x)\Vert =\sup _{\Vert h\Vert =1}Df(x)\cdot h\). By definition of the flat norm one has
The following lemmas bound the terms involved in the right hand side term of the previous equation.
Lemma 4.8
For every \(x \in \mathrm {spt}(D)\), one has
Proof
Clearly, by definition of the Euclidean norm, one has
We can write \(f=g\circ \pi _X \circ p_1\), where \(p_1:X^\varepsilon \times \mathbb {R}^3\rightarrow X^\varepsilon \) is the projection and \(g:X\rightarrow \mathrm {spt}({\text {N}}(X))\) is given by \(g(p)=(p,\mathbf {n}_X(p))\). Since for any \(p\in X\), one has \(\Vert D\mathbf {n}_X(p)\Vert \le \rho _X(p)\), one gets \(\Vert Dg(p)\Vert \le \sqrt{1+\rho _B^2}\le 1+\rho _B\). Using the fact that \(\Vert D\pi _X(x)\Vert \le 1/(1-\rho _X(\pi _X(x))\varepsilon )\) for every x in \(X^\varepsilon \), one has by composition:
The conclusion follows from the fact that the upper bound is greater than 1. \(\square \)
Lemma 4.9
Proof
We can decompose the mass of D into three terms: the mass \(M^f\) above the relative interior of the faces \(S_i\) of S, the mass \(M^e\) above the relative interior of the edges of \(S_{i,j}\), and the mass \(M^v\) above the vertices of S.
Above the Faces of S. We recall that the corrected normal cone \({\text {NC}}(S_i^0,\mathbf {u})\) above the interior \(S_i^0\) of the face \(S_i\) is parameterized by \(\varGamma _\mathbf {u}:p\in S_i^0 \mapsto (p, \mathbf {u}(p))\). Since \(\mathbf {u}\) is \(\mathrm {L}_\mathbf {u}\)-Lipschitz on each face \(S_i\), the map \(\varGamma _\mathbf {u}\) is \(\sqrt{1+ \mathrm {L}^2_\mathbf {u}}\)-Lipschitz. The mass above \(S_i^0\) is given by the General Area-Coarea Formula [25, 3.13]
where \(J_2(\varGamma _\mathbf {u})\) denotes the 2-Jacobian. Summing over all the faces \(S_i^0\) of S, one has
Above the Edges of S. We recall that \(\pi :\mathrm {spt}{({{\,\mathrm{N}\,}}(s,\mathbf {u}))}\rightarrow \mathbb {R}^3\), defined by \(\pi (p,n)=p\), denotes the restriction to the support of \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) of the projection onto the position component. Note that the support of \({{\,\mathrm{N}\,}}(S,\mathbf {u})\) above an edge \(S_{i,j}\) is given by \(\mathrm {spt}{({{\,\mathrm{N}\,}}(S,\mathbf {u})}\,{\llcorner }\,(S_{i,j}\times \mathbb {R}^3)) = \pi ^{-1}(S_{i,j})\). The Coarea Formula thus gives:
The third line follows from the fact that the 1-Jacobian of \(\pi \) satisfies \(J_1(\pi )=1\) and that \(\pi ^{-1}(p)\) is an arc of circle of length \(2\arcsin {(\Vert u_i(p)-u_j(p)\Vert /2)}\). Summing over all the edges \(S_{i,j}\) one has
Above the Vertices of S. Let \(p\in B\) be a vertex of S. The support of the corrected cycle \({{\,\mathrm{N}\,}}(S,\mathbf {u})\,{\llcorner }\,(\{p\}\times \mathbb {R}^3)\) above p obviously lies in the set \(\{p\}\times \mathbb {S}^2\). By construction, the multiplicity \(\mu (\mathbf {n})\) of a point \((p,\mathbf {n})\) lying in this support is an integer that satisfies \(|\mu (\mathbf {n})|\le \deg (p)\), where \(\deg (p)\) is the degree of p, namely the number of edges \(S_{i,j}\) incident to p.
By definition, one has \(\Vert \mathbf {u}_i(p)-\mathbf {u}_j(p)\Vert \le \delta _\mathbf {u}\) for every pair of adjacent faces i and j containing p, which implies that the length of the boundary of the normal component of the support of \({{\,\mathrm{N}\,}}(S,\mathbf {u})\,{\llcorner }\,(\{p\}\times \mathbb {R}^3)\) is at most \(L=\delta _\mathbf {u}\deg (p)\). By the isoperimetric inequality on the sphere, since the support of the normal component above the point p lies in half a sphere, its area is at most \(L^2/(2\pi )\le \delta _{\mathbf {u}}^2 \deg (p)^2/ (2 \pi )\). Therefore, one has
Summing over all the vertices of \(S\cap \partial B\), one has
\(\square \)
Lemma 4.10
Proof
Since \(B=\bigcup _{i\in I}S_i\) is a connected union of faces \(S_i\), its boundary is a union of edges \(S_{i,j}\) where \(i\in I\) and \(j\notin I\). The boundary \(\partial D\) of the restricted current \(D={{\,\mathrm{N}\,}}(S,\mathbf {u})\,{\llcorner }\,(B\times \mathbb {R}^3)\) is supported on curves of two different kinds.
Above the relative interior of each \(S_{i,j}\subset \partial B\), the support D is parameterized by \(\varGamma _{\mathbf {u}_j}:S_{i,j}^0\rightarrow \mathbb {R}^3\times \mathbb {R}^3\). One then has
Above a vertex p of \(S\cap \partial B\), the support of the D is the union of at most \(\deg (p)\) arcs of circles. Each such arc of circle is a geodesic between two vectors \(\mathbf {u}_{j_1}(p)\) and \(\mathbf {u}_{j_2}(p)\), and is of length less than \(2\arcsin {(\Vert \mathbf {u}_{j_1}(p)-\mathbf {u}_{j_2}(p)\Vert /2)}\le 2 \arcsin (\delta _\mathbf {u}/2)\). Therefore
The result follows by summing over all the vertices and edges of \(\partial B\). \(\square \)
End of proof of Theorem 4.2
Plugging the results of Lemmas 4.8, 4.9, and 4.10 with (1), one gets:
For every form \(\omega \in \{\omega _0,\omega _1,\omega _2,\Omega \}\), one has \(\Vert \omega \Vert \le 2\) and \(\Vert \mathrm {d}\omega \Vert \le 4\). Let \(i\in \{0,1,2\}\). One has
which implies the result.\(\square \)
5 Convergence of Curvatures on Digital Surfaces
Digital surfaces come from the sampling of Euclidean shapes in a regular grid. They appear naturally when analyzing 3D images (coming from tomography or MRI). But for estimating curvatures, the digital surfaces are the most challenging among all discrete surfaces. As boundaries of union of cubes, their geometric normals can take only six possible directions. We show in this section how our normalized corrected curvatures provide accurate pointwise approximations of the curvatures of the original Euclidean shape. More precisely, we show their multigrid convergence and give an explicit speed of convergence.
We begin by recalling useful notions of digital geometry and establishing a few lemmas linking the local geometry of the digitized surface and the local geometry of the continuous surface. We will then use the stability result of the previous section to establish multigrid convergence results.
In this section, let V be a compact domain of \(\mathbb {R}^3\) whose boundary \(X := \partial V\) is of class \(C^3\). We assume that the reach of X is greater than \(\rho >0\). Let \(h>0\) be the sampling gridstep of the regular grid \(h \mathbb {Z}^3\). The Gauss digitization of V is defined as \(\mathtt {G}_{h}(V) := V \cap h \mathbb {Z}^3\). Digital sets are subsets of \(h \mathbb {Z}^3\). Let us denote \(Q^h_z\) the axes-aligned cube of edge length h centered on a point \(z \in h \mathbb {Z}^3\). Digital sets can thus be seen as a union of such cubes in \(\mathbb {R}^3\). We can now defined the digitized surface \(X_h\) of \(X := \partial V\) at step h as the topological boundary of the Gauss digitization of V, seen as a union of cubes:
We call surfel any square of edge length h that is the face of some \(Q^h_z\), with \(z \in \mathtt {G}_{h}(V)\) and that is included in \(X_h\). We call linel any edge of a surfel.
In order to apply the stability result presented in the previous section, a few requirements are necessary: (i) the object \(S := X_h\) should be a surface (i.e., a 2-manifold), and (ii) there exists an open set U of the form \(U=\pi _X^{-1}(V)\) such that \(U\cap S\ne \emptyset \) and \(\pi _{X}:U\cap S\rightarrow X\) is injective.
Concerning point (i), unfortunately, \(X_h\) is not a 2-manifold in general, even for smooth and convex shapes V [32]. However \(X_h\) is almost a 2-manifold since the places where it is not a 2-manifold tends to zero quickly as h tends to zero. We recall [19, Thm. 2]:
Theorem 5.1
Let \(h < 0.198 \rho \), letting \(y \in X_h\), then the digital surface \(X_h\) is locally homeomorphic to a 2-disk around y if either (i) y does not belong to a linel of \(X_h\), or (ii) y belongs to a linel s of \(X_h\) and \(s \cap X =\varnothing \), or (iii) y belongs to a linel s of \(X_h\) and there exists \(p \in s \cap X\) but the angle \(\alpha _y\) between s and the normal to X at p satisfies \(\alpha _y \ge 1.260h / \rho \).
So \(X_h\) may not be a manifold only when the normal of X is very close to one of the axes. It is possible to fix locally the manifoldness of digital surfaces by making it well-composed, either by subsampling the grid and doing majority interpolation [32], or repairing the digital surface by adding voxels [30] or by splitting vertices and edges [16]). All these transformations affect a very small part of the digital surface according to the previous theorem. Therefore from now on we shall assume that \(X_h\) is a 2-manifold.
As for point (ii), [19, Thm. 3] gives a positive answer to the existence of an open set U where the projection is injective. Indeed the area on X, where the projection \(\pi _X:U \cap X_h \rightarrow X\) is not injective is proportional to \({\text {Area}}(S)h\) and tends to zero.
The following results relate combinatorial properties of \(X_h\) to geometric properties. In all the sections, we denote by \(\mathbb {B}_p^R\) the ball centered at p and of radius R.
Lemma 5.2
Let p be an arbitrary point of \(X_h\). Let B be the surfels of \(X_h\) that lie in \(X_h \cap \mathbb {B}_p^R\). Then the numbers \(N_s\) of surfels and \(N_b\) of boundary linels of B (the ones bordering only one surfel of B) follow these bounds for radius \(R=Kh^\alpha \):
The proof of Lemma 5.2 relies on the following intermediary lemma.
Lemma 5.3
Under the same assumptions as in Lemma 5.2, one has
Proof of Lemma 5.3
Let \(x \in X_h \cap \partial \mathbb {B}_p^R\). We denote by \(\varepsilon \) the Hausdorff distance between X and its Gauss digitization \(X_h\). It is known that \(\varepsilon = \mathcal {O}(h)\). We put \(p'=\pi (p)\) and \(x'=\pi (x)\). We denote by \(\mathcal {C}\) the geodesic starting at the point \(p'\) and passing through \(x'\). We first assume that \(x'\in \mathbb {B}_p^R\). In that case, the geodesic curve \(\mathcal {C}\) is extended until it reaches a point \(\tilde{x}\in \partial \mathbb {B}_p^R\). Note that such a curve always exist if R is small enough. In the following of the proof, we denote by \(\mathcal {C}_{a,b}\) the shortest path on X between any two points a and b and by \(\ell (\mathcal {C}_{a,b})\) its length. Since the length of a curve is greater than its chord, we have
If R is small enough, then the line segment \([p',\tilde{x}]\) belongs to the offset \(X^r\) of X, where \(r=\mathrm {reach}(X)\) is the reach of X. By using the Lipschitz property of the projection map \(\pi \) onto X (see Proposition 4.1), one gets
where \(\tilde{\varepsilon }=\max _{w\in [p',\tilde{x}]}\Vert w-\pi (w)\Vert = \mathcal {O}(R^2)\). Since \(\Vert p'-\tilde{x}\Vert \le \Vert p-\tilde{x}\Vert +\Vert p'-p\Vert \le R + \varepsilon \), one gets
Since the curve is longer than its chord, \(R=\mathcal {O}(h^\alpha )\), \(\varepsilon =\mathcal {O}(h)\), we have
If \(x'\notin \mathbb {B}_p^R\), the same result holds with a similar proof. In that case the geodesic curve \(\mathcal {C}\) does not have to be extended and \(\tilde{x}=\mathcal {C}\cap \mathbb {B}_p^R\). We deduce that \(\Vert x-\tilde{x}\Vert =\mathcal {O}(h^{3\alpha }+h)\), which ends the proof. \(\square \)
Proof of Lemma 5.2
Let us first bound \(N_i\). Since X is of class \(C^2\), the intersection of X with a ball of radius \(R=Kh^\alpha \) is contained in a box of dimensions \((2R)\times (2R) \times \mathcal {O}(R^2)\). It is known that the digitized surface \(X_h\) is at an Hausdorff distance less than \({h\sqrt{3}}/{2}\) from X [19, Thm. 1]. Hence the set B is included in a set of dimensions \((2R+2h)\times (2R+2h)\times (\mathcal {O}(R^2)+2h)\). Since \(\alpha \in (0,1)\), we have h in \(\mathcal {O}(h^\alpha )\). Furthermore, since \(R=Kh^\alpha \), the set B is thus included in a domain of volume \(\mathcal {O}(h^\alpha h^\alpha h^{\min (2\alpha ,1)})\). This implies that the number of voxels intersecting B is less than \(\mathcal {O}(h^{\min (4\alpha ,2\alpha +1)-3})\). This also implies that \(N_s=\mathcal {O}(h^{\min (4\alpha ,2\alpha +1)-3})\).
Let us now bound \(N_b\). Every point \(x\in \partial B\) belongs to a surfel that intersects \(X_h \cap \partial \mathbb {B}_p^R\), so is at a distance less than \(h\sqrt{2}/2\) from \(X \cap \partial \mathbb {B}_p^R\). By Lemma 5.3, one has
Since the length of \(X \cap \partial \mathbb {B}_p^R\) is in \(\mathcal {O}(R)\), the volume of \(( X \cap \partial \mathbb {B}_p^R)^{\mathcal {O}(h+ h^{3\alpha })}\) is \(\mathcal {O}(R(h+ h^{3\alpha })^2)\). The number of boundary edges \(N_b\) is of the same order than the number of cubes of size h intersecting this volume so
We may now state our convergence result for the normalized corrected curvatures onto digitized surfaces.
Theorem 5.4
Let V be a compact domain of \(\mathbb {R}^3\) whose boundary \(X:=\partial V\) is of class \(C^{2,1}\). Let \(X_h\) be the boundary of the Gauss digitization of V with step h. Suppose that the normal estimator satisfies \(\delta _\mathbf {u}=\mathcal {O}(h^\beta )\) with \(\beta \le 1\) and \(\eta =\mathcal {O}(h^{{2}/{3}})\). Let \(p\in X_h\) and B be the set of surfels of \(X_h\) contained in the ball centered at p and of radius \(K h^\alpha \) (for arbitrary \(K>0\) and \(\alpha \in (0,1)\)). Then
where \(\gamma '= \min {( \alpha ,2 \beta -4/3,\beta -\alpha -1/3,2\alpha +2\beta -7/3,5\alpha +\beta -7/3)}\).
Remark 5.5
Note that for any \(\beta \in {}]3/4,1[\), there exists \(\alpha \in {}]7/6-\beta ,\beta -1/3[\) such that \(\gamma '>0\), which implies that we have the convergence of the pointwise mean and Gaussian curvature measures.
Proof
This proof relies on Corollary 4.5. We know that the Hausdorff \(\varepsilon \) between X and the boundary of its Gauss discretization \(X_h\) is no greater than \(h{\sqrt{3}}/{2}\), so \(\varepsilon =\mathcal {O}(h)\). By plugging \(\varepsilon =\mathcal {O}(h)\), \(\delta _\mathbf {u}=\mathcal {O}(h^\beta )\), \(\eta =\mathcal {O}(h^{{2}/{3}})\) with \(\beta \le 1\) in Corollary 4.5, one gets
Furthermore, since we are in the hypotheses of Lemma 5.2, we have bounds for \(N_s=\mathcal {O}(h^{4\alpha -3}+h^{2\alpha -2})\) and \(N_b=\mathcal {O}\bigl (h^{\alpha -1} + h^{7\alpha -3}\bigr )\). This leads to
where
Using the fact that there exists a constant C such that \( \mu _0^X(\pi _X(B)) \ge C h^{2 \alpha }\), one gets
Similarly, for \(k=1,2\),
Finally, we can relate our normalized mean curvature with the ratio of the mean curvature measure and the area measure:
It remains to relate this ratio of measures to the mean curvature at \(p':=\pi _X(p)\). Recall that the surface is of class \(C^{2,1}\). From the proof of the preceding lemma, we know that there are two real numbers \(R_1\) and \(R_2\) with \( D_{R_1}(p') \subset \pi _X(B)\subset D_{R_2}(p') \), where \(D_r(p')\) is the geodesic disk centered at \(p'\) of radius r, with \(R_1,R_2 = \mathcal {O}(h^\alpha )\) and \(R_2 - R_1 = \mathcal {O}(h + h^{3\alpha } )\). Then we can write in geodesic polar coordinates
Since H is K-Lipschitz on \( D_{R_1}(p')\) for some \(K>0\) one has
Similarly, the difference between the integrals over the two geodesic disks satisfies
so that
and
Finally,
The same holds for the Gaussian curvature.\(\square \)
Remark 5.6
The above bound \(\eta = \mathcal {O}(h^{2/3})\) has been established in [22] for the normal vector estimator based on digital integral invariants. Note that \(\beta = 1\) is the optimal convergence rate, since it is the one obtained by taking the ground truth normal, i.e., taking the normal at the projection on X. There is yet no formal proof that any digital normal vector estimator is Lipschitz (which implies \(\beta = 1\)). However, we have run simulations and both Voronoi Covariance measure [11, 24] and digital Integral Invariant [22] appear to be Lipschitz normal estimator (see Fig. 4).
Remark 5.7
If we choose \(\mathbf {u}\) as the normals estimated by digital integral invariant normal estimator and we assume \(\beta =1\), then the previous theorem implies that, when the set B of surfels is taken in a ball of center p and radius \(Kh^{{1}/{3}}\), then the mean corrected curvature \(\hat{H}_\mathbf {u}(B)\) (resp. the Gaussian corrected curvature \(\hat{G}_\mathbf {u}(B)\)) tends to the mean curvature \(H( \pi _X( p))\) (resp. to the Gaussian curvature \(G(\pi _X(p))\)) with a speed \(\mathcal {O}(h^{1/3})\). In the terminology of [18], \( \hat{H}_\mathbf {u}\) (resp. \(\hat{G}_\mathbf {u}\)) is a multigrid convergent mean (resp. Gaussian) curvature estimator.
In the following section, we perform a comparative evaluation of our curvature estimators. Although we have checked that they are indeed convergent for a radius \(Kh^{{1}/{3}}\) with a speed at least \(\mathcal {O}(h^{{1}/{3}})\), we will run our experiments with a much smaller radius \(Kh^{1/2}\) (see Figs. 5 and 6). Indeed it provides not only faster estimators but also a slightly better error bound in practice, closer to \(\mathcal {O}(h^{2/3})\). The reason is still investigated.
Experimental evaluation of the asymptotic error of mean curvature along a digitized polynomial shape (“Goursat”, see the next section) as a function of the gridstep h. Convergence behavior is observed when reading the graph from right to left, where smaller values of h are located. We check two different exponents \(\alpha \) of the computation radius \(Kh^\alpha \): \(\alpha =1/3\) and \(\alpha =1/2\). Thick lines represent \(\ell _\infty \)-error, thin lines represent \(\ell _2\)-error. Theoretically \(\alpha ={1}/{3}\) should be the best choice and implies a \(\ell _\infty \)-error of \(\mathcal {O}(h^{1/3})\). In practice, the error is smaller and seems below \(\mathcal {O}(h^{1/2})\). Furthermore, even better results are achieved when choosing \(\alpha =1/2\)
Experimental evaluation of the asymptotic error of Gaussian curvature along a digitized polynomial shape (“Goursat”, see next section) as a function of the gridstep h. Convergence behavior is observed when reading the graph from right to left, where smaller values of h are located. We check two different exponents \(\alpha \) of the computation radius \(Kh^\alpha \): \(\alpha =1/3\) and \(\alpha =1/2\). Thick lines represent \(\ell _\infty \)-error, thin lines represent \(\ell _2\)-error. Theoretically \(\alpha =1/3\) should be the best choice and implies an \(\ell _\infty \)-error of \(\mathcal {O}(h^{1/3})\). In practice, the error is smaller and seems below \(\mathcal {O}(h^{1/2})\). Furthermore, even better results are achieved when choosing \(\alpha ={1/2}\)
6 Experimental Evaluation on Digital Surfaces
We present here a series of experiments which demonstrates that the corrected measures provide accurate and stable curvature information. We do not evaluate experimentally the accuracy of measures themselves (which are already established through our main theorem), but the much more difficult problem of pointwise mean and curvature inference. As a stressful testbed that maximizes the difficulty of estimating curvatures, we evaluate the accuracy of the normalized corrected mean curvature \(\hat{H}\) and the normalized Gaussian curvature \(\hat{G}\) on digital surfaces (see Definition 3.4). Indeed, their canonical normal vectors can only take six different values. Last, we compare our new approach with the state-of-the-art method of [7, 22], which is based on digital integral invariants. We also show that the normal cycle approach [8, 9, 34, 36] is neither accurate nor convergent for digital surfaces.
6.1 Methodology of Evaluation on Digitizations of Polynomial Surfaces
We evaluate the accuracy of our geometric estimators on the digitization of implicitly defined polynomial shapes X, in order to have ground-truth curvatures. Let us detail our methodology for evaluating our new curvature estimators.
6.1.1 Ground-Truth Surfaces
We shall test shapes whose boundary is at least twice differentiable. As a representative example, we choose the “Goursat” implicit polynomial shape \(X := \{ (x,y,z) \in \mathbb {R}^3:P(x,y,z) \ge 0 \}\), with \(P(x,y,z):=4-0.015(x^4+y^4+z^4)+x^2+y^2+z^2\).
Its minimal, mean and maximal mean curvatures are respectively approximately \(-0.1070,0.0956,0.3448\). Its minimal, mean and maximal Gaussian curvatures are respectively approximately \(-0.0337,0.0080,0.1189\). Its reach is greater than 2.9.
6.1.2 Input Digitized Surfaces
We digitize a shape X using Gauss digitization \(G_h(X) := X \cap h\mathbb {Z}^3\) at several gridsteps h. If we see the discrete set \(G_h(X)\) as a union of axis-aligned cubes of edge-length h centered on those points, its topological boundary is then a union of axis-aligned squares of edge-length h that forms a digital surface (e.g. see [19]). We denote it by \({\partial _{h} X}\). As illustrated in Fig. 7, digitized surfaces \(\partial _h X\) tends toward the smooth surface \(\partial X\) in Hausdorff distance. In fact they are a Hausdorff approximation of \({\partial X}\) at distance less than \(h\sqrt{3}/2\) [19]. However their natural normal vectors \(\mathbf {n}\) do not tend toward the normal vectors of the smooth surface, since they can take only six different values whatever is h.
6.1.3 Input Corrected Normal Vector Field \(\mathbf {u}\)
We must estimate the field \(\mathbf {u}\) solely from the input digitized surface \({\partial _{h} X}\). We will use several normal vector estimators in the experiments, in order to show the importance of having a convergent estimator but also to show that our method gives stable results for any convergent \(\mathbf {u}\):
-
Trivial normal estimator (TN): this estimator just replicates \(\mathbf {n}\) (i.e., \(\mathbf {u}= \mathbf {n}\)). We use it in experiments since our measures become then equivalent to the normal cycle [8, 9, 34, 36].
-
Digital Integral Invariant normal estimator (II): this estimator provides a convergent normal vector field \(\mathbf {u}\) for a certain family of parameters [22]. It depends on a radius of integration parameter \(r:=k h^\alpha \). As shown by our experiments, the values \(\alpha =0.5\) and \(r=3\) provide both good and stable results.
-
Voronoi Covariance Measure normal estimator (VCM): this estimator provides a convergent normal vector field \(\mathbf {u}\) for a certain family of parameters [10, 11]. It depends on a radius of integration parameter \(r:=k h^\alpha \), which we set exactly as parameter r of II, and on a distance of computation \(R:=Kh^\alpha \), where \(K=10\) gives good results.
6.1.4 Estimated Curvatures
We will estimate the accuracy and stability of the following curvatures estimators:
-
Normalized corrected mean curvature (\(\hat{H}^{\mathbf {u}}\)) and Gaussian curvature (\(\hat{G}^{\mathbf {u}}\)): since they are ratios of measures, we must choose a Borel set on which measures are computed. For any point \(p\in {\partial _{h} X}\), we simply compute \(\hat{H}^{\mathbf {u}}(p) :=\hat{H}(B_\rho (p))=\mu _1(B_\rho (p))/\mu _0(B_\rho (p))\) and \(\hat{G}^{\mathbf {u}}(p):=\hat{G}(B_\rho (p))=\mu _2(B_\rho (p))/\mu _0(B_\rho (p))\), where \(\rho :=mh^{\beta }\). As shown by our experiments, the values \(\beta =1/2\) and \(m=3\) provide both good and stable results. We use the corrected normal field \(\mathbf {u}\) given either by II or VCM normal estimators (in both cases, \(r=3h^{1/2}\) is used).
-
Digital integral invariant mean and Gaussian curvature estimators (\(\hat{H}^{II }\)) and (\(\hat{G}^{II }\)): both are parameterized by the radius \(r'\) of integration. Experiments show that for \(r'=k'h^{\alpha '}\), we must set \(\alpha '={1/3}\) (and no greater value) to get convergence and set \(k'=6\) to minimize estimation errors.
-
Normal Cycle mean and Gaussian curvatures (\(\hat{H}^{NC }\)) and (\(\hat{G}^{NC }\)): they are defined similarly with \(\hat{H}^{\mathbf {u}}\) and \(\hat{G}^{\mathbf {u}}\) except that we use the Trivial Normal estimator to compute \(\mathbf {u}\), i.e., \(\hat{H}^{NC }:=\hat{H}^{\mathbf {n}}\) and \(\hat{G}^{NC }:=\hat{G}^{\mathbf {n}}\).
6.1.5 Measuring \(\ell _2\)- and \(\ell _\infty \)-Errors
Curvatures are estimated at the centroid p of each surfel element (the squares that form the digitized shape boundary), and are compared to the curvatures of the point \(q \in {\partial X}\) that is closest to p. Note that \(q=\pi (p)\) since p is in the reach of \({\partial X}\). For instance, letting \(\sigma \) be the set of centroids of the surfel of \({\partial _{h} X}\), we define the errors between \(\hat{H}\) and H as:
Note that when \(\ell _\infty \)-error tends to zero as h tends to zero implies the classical multigrid convergence. It also implies that \(\ell _2\)-error tends to zero.
6.1.6 Robustness to Noise
In practical application, input data are rarely perfect digitizations and may be corrupted by noise. We have used a noise model parameterized by a probability p, which perturbates the input voxels according to their distance to the exact digitized boundary. More precisely, if \(\delta \) is the discrete distance of the voxel to its nearest boundary point (minimum distance is 1), then this voxel has a probability of \(p^\delta \) to be flipped inside/out.
6.2 Evaluation of Mean Curvature Estimator \(\hat{H}^{\mathbf {u}}\)
6.2.1 Asymptotic Behavior of \(\hat{H}^{\mathbf {u}}\) and Normal Cycle \(\hat{H}^{NC }\)
First we measure both the \(\ell _\infty \)- and \(\ell _2\)-errors of our proposed mean curvature estimator \(\hat{H}^{\mathbf {u}}\). We further test several normal estimators for \(\mathbf {u}\): II, VCM, and TN. Results are displayed in Fig. 8. Graphs show an experimental convergence speed of \( \mathcal {O}(h^{2/3})\), II and VCM normals. It shows also that the normal cycle method is not convergent, since \(\hat{H}^{\mathbf {u}}\) with TN corresponds to the normal cycle mean curvature \(\hat{H}^{NC }\).
6.2.2 Comparative Evaluation of \(\hat{H}^{\mathbf {u}}\) and \(\hat{H}^{II }\)
We now compare the \(\ell _\infty \)- and \(\ell _2\)-errors of \(\hat{H}^{\mathbf {u}}\) with the ones of \(\hat{H}^{II }\), which is the state-of-the-art method for digital surface curvature estimation. We use the II normal estimator for \(\hat{H}^{\mathbf {u}}\) with \(r=3h^{1/2}\). Results are shown in Fig. 8. First it confirms that \(\hat{H}^{II }\) is not convergent if its parameter r follows some \(\Theta (h^{1/2})\). Secondly we do obtain a convergence speed of \(\Theta (h^{1/3})\) for bigger radii \(r=\Theta (h^{1/3})\). Last our new estimator \(\hat{H}^{\mathbf {u}}\) has a much faster convergence, approximately \(\Theta (h^{2/3})\), despite the fact that both the integration radius r for \(\mathbf {u}\) and the integration radius \(\rho \) for \(\hat{H}^{\mathbf {u}}\) are much smaller, i.e., \(3h^{1/2}\).
(Left) Asymptotic errors of mean curvature estimations by \(\hat{H}^{\mathbf {u}}\) along the “Goursat” shape, when changing the digital normal vector estimator: II and VCM are convergent normal estimators (see text), TN is the canonical normal vector, and it corresponds to the Normal Cycle mean curvature estimator (\(\hat{H}^{NC }\)). (Right) Respective asymptotic errors of mean curvature estimations by \(\hat{H}^{\mathbf {u}}\) and \(\hat{H}^{II }\) along the “Goursat” shape. In both figures, \(\ell _\infty \)-errors are drawn with thick lines, \(\ell _2\)-errors are drawn with thin lines
We further illustrate the differences of the two estimators \(\hat{H}^{\mathbf {u}}\) and \(\hat{H}^{II }\) by displaying the estimated mean curvatures and the localization of errors on several digitizations of “Goursat” on Fig. 9. It is clear that errors are mostly localized on places of extremal curvatures, but our estimator converges much faster everywhere visibly and does not oscillate around the correct value.
Illustration of the accuracy of mean curvature estimators \(\hat{H}^{\mathbf {u}}\) and \(\hat{H}^{II }\) at different resolutions: 1st row is ground-truth H, 2nd row is our approach \(\hat{H}^{\mathbf {u}}\), 3rd row is its local estimation error \(|\hat{H}^{\mathbf {u}}-H|\), 4th row is integral invariant approach \(\hat{H}^{II }\), 5th row is its local estimation error \(|\hat{H}^{II }-H|\). Curvatures are displayed with colors from dark blue (\(-0.3\)) to white to red (0.3), except a black band at \([-0.01;0.01]\). Errors are displayed with colors from white (0) to red (0.025) to black (0.05)
Last, we measure the stability of both estimators with respect to their parameters. For \(\hat{H}^{\mathbf {u}}\), we measure the \(\ell _\infty \)-error when changing k in the radius \(r:=kh^{{1/2}}\) and changing m in the radius \(\rho :=mh^{{1/2}}\). For \(\hat{H}^{II }\) we simply change k in the radius \(r:=kh^{{1/3}}\). See Fig. 10. First, the results show that the exponents chosen for the gridstep are consistent (best results are achieved for the same constant at a finer scale). It confirms that integral invariant methods require a radius of integration that is much larger asymptotically. Secondly it shows that our method is more stable with respect to parameter settings. We have almost the same errors in the range \((k,m) \in [2.5,4 ]\times [2.5, 6 ]\).
Stability of \(\hat{H}^{\mathbf {u}}\) and \(\hat{H}^{II }\) with respect to parameters and gridstep. Estimator \(\hat{H}^{\mathbf {u}}\) is parameterized by the integration radius \(r:=kh^{1/2}\) of its normal estimator \(\mathbf {u}=II \) and by the measure radius \(\rho :=m h^{{1/2}}\). We plot \(\ell _2\)- and \(\ell _\infty \)-errors of \(\hat{H}^{\mathbf {u}}- H\) as a function of k and m. Estimator \(\hat{H}^{II }\) is parameterized by the integration radius \(r':=k' h^{1/3}\). We plot \(\ell _2\)- and \(\ell _\infty \)-errors of \(\hat{H}^{II }- H\) as a function of \(k'\) (displayed as 2d plot to make easier the comparison)
6.2.3 Evaluation of \(\hat{H}^{\mathbf {u}}\) on Digital Shapes
We also run our method on digitizations of classical shapes (“dragon” and “octaflower”), trying several parameters (here we checked several initial gridsteps) such that Integral Invariant and Normal Cycle methods give the best possible results. Outputs are displayed in Figs. 11 and 12. It is clear that both \(\hat{H}^{NC }\) and \(\hat{H}^{II }\) oscillate around the correct solution (see black random or moiré patterns on both figures, whichever the resolution). On the contrary, \(\hat{H}^{\mathbf {u}}\) is stable in zero-curvature regions (like on the octaflower) while accurately delineating the small scales of the Chinese dragon.
Comparison of mean curvature estimators \(\hat{H}^{\mathbf {u}}\), \(\hat{H}^{NC }\), and \(\hat{H}^{II }\) on classical digital shapes at two different resolutions. We choose parameters according to Sect. 6.1, setting \(h=1\) for “dragon \(256^3\)” and naturally \(h=0.5\) for “dragon \(512^3\)”. Curvatures are displayed with colors from dark blue (\(-0.3\)) to white to red (0.3), except a black band at \([-0.01;0.01]\)
Comparison of mean curvature estimators \(\hat{H}^{\mathbf {u}}\), \(\hat{H}^{NC }\), and \(\hat{H}^{II }\) on classical digital shapes at two different resolutions. We choose parameters according to Sect. 6.1, setting \(h=0.5\) for “octaflower \(256^3\)” and naturally \(h=0.25\) for “octaflower \(512^3\)”. Curvatures are displayed with colors from dark blue (\(-0.2\)) to white to red (0.2), except a black band at \([-0.005;0.005]\)
6.2.4 Robustness to Noise of \(\hat{H}^{\mathbf {u}}\)
Last we have checked the robustness to noise of our mean curvature estimator \(\hat{H}^{\mathbf {u}}\). Experiments show that our method is mostly sensitive to the quality of the input corrected normal vector field \(\mathbf {u}\). On the one hand VCM normal estimator is relatively accurate but more unstable than II normal estimator. On the other hand, II normal estimator is inaccurate at places with sharp features (as one can see on the outer parts of the screw of “octaflower”). We should certainly in this case use smarter normal estimators, like the AT normal vector method of [6], which is able to compute piecewise smooth normal vector field, or a normal estimator which takes into account the digital nature of the input shape, like the plane-probe algorithms of [20, 21].
Robustness to noise of our mean curvature estimator \(\hat{H}^{\mathbf {u}}\). Noise with parameter p (see text) was added to the digital shape“octaflower \(256^3\)”. The gridstep was set to \(h=0.5\) for parameterizing the estimators. Curvatures are displayed with colors from dark blue (\(-0.2\)) to white to red (0.2), except a black band at \([-0.005;0.005]\)
(Left) Asymptotic errors of Gaussian curvature estimations by \(\hat{G}^{\mathbf {u}}\) along the “Goursat” shape, when changing the digital normal vector estimator: II and VCM are convergent normal estimators (see text), TN is the canonical normal vector, and it corresponds to the Normal Cycle Gaussian curvature estimator (\(\hat{G}^{NC }\)). (Right) Respective asymptotic errors of Gaussian curvature estimations by \(\hat{G}^{\mathbf {u}}\) and \(\hat{G}^{II }\) along the “Goursat” shape. In both figures, \(\ell _\infty \)-errors are drawn with thick lines, \(\ell _2\)-errors are drawn with thin lines
Illustration of the accuracy of Gaussian curvature estimators \(\hat{G}^{\mathbf {u}}\) and \(\hat{G}^{II }\) at different resolutions: 1st row is ground-truth G, 2nd row is our approach \(\hat{G}^{\mathbf {u}}\), 3rd row is its local estimation error \(|\hat{G}^{\mathbf {u}}-G|\), 4th row is integral invariant approach \(\hat{G}^{II }\), 5th row is its local estimation error \(|\hat{G}^{II }-G|\). Curvatures are displayed with colors from dark blue (\(-0.1\)) to white to red (0.1), except a black band at \([-0.002;0.002]\). Errors are displayed with colors from white (0) to red (0.0125) to black (0.025)
Comparison of Gaussian curvature estimators \(\hat{G}^{\mathbf {u}}\), \(\hat{G}^{NC }\), and \(\hat{G}^{II }\) on classical digital shapes at two different resolutions. We choose parameters according to Sect. 6.1, setting \(h=1\) for “dragon \(256^3\)” and naturally \(h=0.5\) for “dragon \(512^3\)”. Curvatures are displayed with colors from dark blue (\(-0.05\)) to white to red (0.05), except a black band at \([-0.0005;0.0005]\)
Comparison of Gaussian curvature estimators \(\hat{G}^{\mathbf {u}}\), \(\hat{G}^{NC }\), and \(\hat{G}^{II }\) on classical digital shapes at two different resolutions. We choose parameters according to Sect. 6.1, setting \(h=0.5\) for “octaflower \(256^3\)” and naturally \(h=0.25\) for “octaflower \(512^3\)”. Curvatures are displayed with colors from dark blue (\(-0.05\)) to white to red (0.05), except a black band at \([-0.0005;0.0005]\)
Robustness to noise of our Gaussian curvature estimator \(\hat{G}^{\mathbf {u}}\). Noise with parameter p (see the text) was added to the digital shape“octaflower \(256^3\)”. The gridstep was set to \(h=0.5\) for parameterizing the estimators. Curvatures are displayed with colors from dark blue (\(-0.05\)) to white to red (0.05), except a black band at \([-0.0005;0.0005]\)
Computation of principal directions (represented as sticks) and principal curvatures (same colormap as in “Goursat” figures) with a corrected anisotropic curvature measure. Top row: first (left) and second (right) principal directions with \(\mathbf {u}=VCM \). Second row: expected first (left) and second (right) principal directions
6.3 Evaluation of Gaussian Curvature Estimator \(\hat{G}^{\mathbf {u}}\)
6.3.1 Asymptotic Behavior of \(\hat{G}^{\mathbf {u}}\) and Normal Cycle \(\hat{G}^{NC }\)
Then we measure both the \(\ell _\infty \)- and \(\ell _2\)-errors of our proposed Gaussian curvature estimator \(\hat{G}^{\mathbf {u}}\). We further test several normal estimators for \(\mathbf {u}\): II, VCM, and TN. Results are displayed on Fig. 14. Graphs show again an experimental convergence speed of \(\mathcal {O}(h^{2/3})\) for II and VCM normals. It shows also that the normal cycle method is not convergent, since \(\hat{G}^{\mathbf {u}}\) with TN corresponds to the normal cycle Gaussian curvature \(\hat{G}^{NC }\).
6.3.2 Comparative Evaluation of \(\hat{G}^{\mathbf {u}}\) and \(\hat{G}^{II }\)
We compare the \(\ell _\infty \)- and \(\ell _2\)-errors of \(\hat{G}^{\mathbf {u}}\) with the ones of \(\hat{G}^{II }\), which is also the state-of-the-art method for digital surface curvature estimation. We pick the same parameterization as in the previous paragraph for all estimators. We observe the same behaviour of \(\hat{G}^{\mathbf {u}}\) with respect to \(\hat{G}^{II }\): much faster convergence speed with small integration radii.
We further illustrate the differences of the two estimators \(\hat{G}^{\mathbf {u}}\) and \(\hat{G}^{II }\) by displaying the estimated Gauss curvatures and the localization of errors on several digitizations of “Goursat” in Fig. 15. It is clear that errors are mostly localized on places of extremal curvatures, but our estimator converges much faster everywhere visibly and does not oscillate around the correct value.
6.3.3 Evaluation of \(\hat{G}^{\mathbf {u}}\) on Digital Shapes
We also check Gaussian curvature estimators \(\hat{G}^{\mathbf {u}}\), \(\hat{G}^{NC }\), and \(\hat{G}^{II }\) on the same classical shapes as in the previous subsection. Results are displayed in Figs. 16 and 17; keeping the same parameters as above. We also observe the oscillations and moiré patterns in \(\hat{H}^{II }\) estimations. Furthermore the Normal Cycle estimator \(\hat{G}^{NC }\) is clearly incorrect and gives only extremal results. This is because \(\hat{G}^{NC }\) takes into account solely six possible normals.
6.3.4 Robustness to Noise of \(\hat{G}^{\mathbf {u}}\)
Last we have checked the robustness to noise of our Gaussian curvature estimator \(\hat{G}^{\mathbf {u}}\). Experiments show that our method is mostly sensitive to the quality of the input corrected normal vector field \(\mathbf {u}\). On the one hand VCM normal estimator is relatively accurate but more unstable than II normal estimator. On the other hand, II normal estimator may be inaccurate at places with sharp features (as one can see on the outer parts of the screw of “octaflower”). As already said in the previous section, we should certainly in this case use smarter normal estimators [6, 20, 21].
6.4 Practical Computation Times of Our Curvature Estimators
We note first that the computation times of the measures \(\mu _0\), \(\mu _1\), \(\mu _2\), \(\mu _\Omega \), and \(\mu _{\mathbf {X},\mathbf {Y}}\) per cell are linear with the number of cells and are extremely fast. Their running times are negligible with respect to the estimation of corrected normal vector field or their integration in a ball a radius \(\rho \) (\(2\%\) when \(N \approx 1e^3\), \(0.01\%\) when \(N \approx 4e^6\)). Secondly, computation times for Gaussian curvature estimator \(\hat{G}^{\mathbf {u}}\) or principal directions is almost the same as the one of \(\hat{H}^{\mathbf {u}}\) and \(\hat{G}^{II }\), and are thus not displayed.
We have plotted the measured computation times of our mean curvature estimator \(\hat{H}^{\mathbf {u}}\), first as a function of the number of surfels of the digitized boundary, and after as a function of the accuracy (see Fig. 19). Running times for all estimators were measured with a mono-threaded CPU implementation on an average server (Intel Xeon Gold 6128 processor, 3.4 GHz, cache memory 19.25 Mb, each thread is evaluated at 6785.92 bogomips). In both cases, our approach clearly outperforms the digital Integral Invariant approach of [7, 22]. We have not compared with the execution times of Normal Cycle method, since \(\hat{H}^{NC }\) is not accurate. Note that using VCM normal estimator instead of II normal estimator to compute \(\mathbf {u}\) is faster for large digital shapes, but requires more memory.
To sum up, our method has an experimental complexity in \(\Theta (n^{3/2})\) compared to Integral Invariant method that has an experimental complexity in \(\Theta (n^{2})\). Our code could be further optimized in the integration step of the measures \(\mu _k\) by reusing the results of a neighboring point, as it is already done in Integral Invariant method. Last, for a given accuracy, our method is even much faster (5000 times faster than II to achieve 0.0065 \(\ell _2\)-accuracy).
7 Conclusion
We have proposed a sound mathematical framework for defining area and curvature measures over rather general surfaces. We have also shown that these measures are stable with an error proportional to the sum of the position error and the normal error. This framework induce sound definitions of curvatures on polyhedral surfaces, which are easy and fast to compute. We have evaluated extensively the numerical accuracy of our approach on digital surfaces, which are polyhedral surfaces with bad naive normals. It shows that our method is also effective and accurate in practice.
We are currently adapting the anisotropic curvature measures introduced in [8, 9] (see also textbook [26]) to our framework. These new measures give estimates of principal curvatures and principal directions, which are also stable and convergent by the same principles stated in Sect. 4. These works will be the focus of a forthcoming paper. Preliminary results are displayed in Fig. 20. We are also currently investigating smooth corrected normal vector field obtained by interpolation, which may reveal to be even more accurate than piecewise constant corrected normal vector field, both theoretically and practically.
Notes
So that \(\mathbf {e}_{ji}(p)=- \mathbf {e}_{ij}(p)\).
References
Allard, W.K.: On the first variation of a varifold. Ann. Math. 95, 417–491 (1972)
Almgren, F.J., Jr.: Plateau’s Problem: An Invitation to Varifold Geometry. W.A. Benjamin, New York (1966)
Buet, B., Leonardi, G.P., Masnou, S.: A varifold approach to surface approximation. Arch. Ration. Mech. Anal. 226(2), 639–694 (2017)
Cazals, F., Pouget, M.: Estimating differential quantities using polynomial fitting of osculating jets. Comput. Aided Geom. Design 22(2), 121–146 (2005)
Chazal, F., Cohen-Steiner, D., Lieutier, A., Thibert, B.: Stability of curvature measures. Comput. Graph. Forum 28(5), 1485–1496 (2009)
Coeurjolly, D., Foare, M., Gueth, P., Lachaud, J.-O.: Piecewise smooth reconstruction of normal vector field on digital data. Comput. Graph. Forum 35(7), 157–167 (2016)
Coeurjolly, D., Lachaud, J.-O., Levallois, J.: Multigrid convergent principal curvature estimators in digital geometry. Comput. Vis. Image Underst. 129, 27–41 (2014)
Cohen-Steiner, D., Morvan, J.-M.: Restricted Delaunay triangulations and normal cycle. In: 19th Annual Symposium on Computational Geometry (San Diego 2003), pp. 312–321. ACM, New York (2003)
Cohen-Steiner, D., Morvan, J.-M.: Second fundamental measure of geometric sets and local approximation of curvatures. J. Differ. Geom. 74(3), 363–394 (2006)
Cuel, L., Lachaud, J.-O., Mérigot, Q., Thibert, B.: Robust geometry estimation using the generalized Voronoi covariance measure. SIAM J. Imaging Sci. 8(2), 1293–1314 (2015)
Cuel, L., Lachaud, J.-O., Thibert, B.: Voronoi-based geometry estimator for 3D digital surfaces. In: Discrete Geometry for Computer Imagery. Lecture Notes in Comput. Sci., vol. 8668, pp. 134–149. Springer, Cham (2014)
Federer, H.: Curvature measures. Trans. Am. Math. Soc. 93, 418–491 (1959)
Federer, H.: Geometric Measure Theory. Classics in Mathematics. Springer, Berlin (1996)
Fu, J.H.G.: Convergence of curvatures in secant approximations. J. Differ. Geom. 37(1), 177–190 (1993)
Fu, J.H.G.: Curvature measures of subanalytic sets. Am. J. Math. 116(4), 819–880 (1994)
Gonzalez-Diaz, R., Jimenez, M.-J., Medrano, B.: 3D well-composed polyhedral complexes. Discrete Appl. Math. 183, 59–77 (2015)
Hildebrandt, K., Polthier, K., Wardetzky, M.: On the convergence of metric and geometric properties of polyhedral surfaces. Geom. Dedicata. 123, 89–112 (2006)
Klette, R., Rosenfeld, A.: Digital Geometry. Elsevier, Amsterdam (2004)
Lachaud, J.-O., Coeurjolly, D., Levallois, J.: Robust and convergent curvature and normal estimators with digital integral invariants. In: Modern Approaches to Discrete Curvature. Lecture Notes in Math., vol. 2184, pp. 293–348. Springer, Cham (2017)
Lachaud, J.-O., Provençal, X., Roussillon, T.: An output-sensitive algorithm to compute the normal vector of a digital plane. Theoret. Comput. Sci. 624, 73–88 (2016)
Lachaud, J.-O., Provençal, X., Roussillon, T.: Two plane-probing algorithms for the computation of the normal vector to a digital plane. J. Math. Imaging Vision 59(1), 23–39 (2017)
Lachaud, J.-O., Thibert, B.: Properties of Gauss digitized shapes and digital surface integration. J. Math. Imaging Vision 54(2), 162–180 (2016)
Lin, F., Yang, X.: Geometric Measure Theory–An Introduction. Advanced Mathematics (Beijing/Boston), vol. 1. International Press, Boston (2002)
Mérigot, Q., Ovsjanikov, M., Guibas, L.: Voronoi-based curvature and feature estimation from point clouds. IEEE Trans. Visual Comput. Graphics 17(6), 743–756 (2011)
Morgan, F.: Geometric Measure Theory. A Beginner’s Guide. Elsevier/Academic Press, Amsterdam (2016)
Morvan, J.-M.: Generalized Curvatures. Springer, Berlin (2008)
Morvan, J.-M., Thibert, B.: Approximation of the normal vector field and the area of a smooth surface. Discrete Comput. Geom. 32(3), 383–400 (2004)
Pottmann, H., Wallner, J., Huang, Q.-X., Yang, Y.-L.: Integral invariants for robust geometry processing. Comput. Aided Geom. Design 26(1), 37–60 (2009)
Pottmann, H., Wallner, J., Yang, Y.-L., Lai, Y.-K., Hu, S.-M.: Principal curvatures from the integral invariant viewpoint. Comput. Aided Geom. Design 24(8–9), 428–442 (2007)
Siqueira, M., Latecki, L.J., Tustison, N., Gallier, J., Gee, J.: Topological repairing of 3D digital images. J. Math. Imaging Vision 30(3), 249–274 (2008)
Spivak, M.: Calculus on Manifolds. CRC Press, Boca Raton (2018)
Stelldinger, P., Latecki, L.J., Siqueira, M.: Topological equivalence between a 3D object and the reconstruction of its digital image. IEEE Trans. Pattern Anal. Mach. Intell. 29(1), 126–140 (2007)
Surazhsky, T., Magid, E., Soldea, O., Elber, G., Rivlin, E.: A comparison of Gaussian and mean curvatures estimation methods on triangular meshes. In: 2003 IEEE International Conference on Robotics and Automation (Taipei 2003), pp. 1021–1026. IEEE (2003)
Wintgen, P.: Normal cycle and integral curvature for polyhedra in Riemannian manifolds. In: Differential Geometry (Budapest 1979). Colloq. Math. Soc. Janos Bolyai, vol. 31, pp. 805–816 (1982)
Xu, G.: Convergence analysis of a discretization scheme for Gaussian curvature over triangular surfaces. Comput. Aided Geom. Design 23(2), 193–207 (2006)
Zähle, M.: Curvatures and currents for unions of sets with positive reach. Geom. Dedicata. 23(2), 155–171 (1987)
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Kenneth Clarkson
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work has been partly funded by CoMeDiC ANR-15-CE40-0006 research grant. The authors thank the anonymous reviewer for his thoughtful comments and suggestions.
Rights and permissions
About this article
Cite this article
Lachaud, JO., Romon, P. & Thibert, B. Corrected Curvature Measures. Discrete Comput Geom 68, 477–524 (2022). https://doi.org/10.1007/s00454-022-00399-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-022-00399-4