Combinatorics of Antiprism Triangulations

Abstract

The antiprism triangulation provides a natural way to subdivide a simplicial complex $\Delta$, similar to barycentric subdivision, which appeared independently in combinatorial algebraic topology and computer science. It can be defined as the simplicial complex of chains of multi-pointed faces of $\Delta$, from a combinatorial point of view, and by successively applying the antiprism construction, or balanced stellar subdivisions, on the faces of $\Delta$, from a geometric point of view. This paper studies enumerative invariants associated to this triangulation, such as the transformation of the h-vector of $\Delta$ under antiprism triangulation, and algebraic properties of its Stanley–Reisner ring. Among other results, it is shown that the h-polynomial of the antiprism triangulation of a simplex is real-rooted and that the antiprism triangulation of $\Delta$ has the almost strong Lefschetz property over ${{\mathbb {R}}}$ for every shellable complex $\Delta$. Several related open problems are discussed.

1 Introduction

Barycentric subdivision provides a natural way to triangulate a simplicial complex $\Delta$, of fundamental importance in algebraic topology. Because of its especially nice enumerative and algebraic properties, it has also been studied intensely from the point of view of enumerative and algebraic combinatorics; see [11, 12, 20, 22, 23, 28, 29] and [30, Chap. 9]. For instance, Brenti and Welker [11] described in explicit combinatorial terms the transformation of the h-vector (a fundamental enumerative invariant) of $\Delta$, under barycentric subdivision, and showed that the h-polynomial (the generating polynomial for the h-vector) of the barycentric subdivision of $\Delta$ has only real roots (and in particular, log-concave and unimodal coefficients) for every simplicial complex $\Delta$ with nonnegative h-vector.

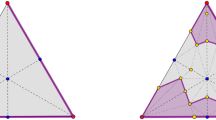
A similar, but combinatorially more intricate and much less studied than barycentric subdivision, way to subdivide $\Delta$ is provided by the antiprism triangulation, denoted here by $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$. To give the reader a hint on the comparison between the two triangulations, we recall that the barycentric subdivision of a geometric simplex $\Sigma$ can be constructed by inserting a vertex in the interior of $\Sigma$ and coning over its proper faces, which have been barycentrically subdivided by induction. The antiprism triangulation $\mathrm{sd}_{{\mathcal {A}}}(\Sigma )$ instead can be constructed by inserting another simplex of the same dimension in the interior of $\Sigma$, whose vertices are in a given one-to-one correspondence with those of $\Sigma$, and joining each nonempty face of that simplex with the antiprism triangulation of the complementary face of $\Sigma$. Figure 1 shows the antiprism triangulation of a 2-dimensional simplex (the labeling of faces is explained in Sect. 4). As an abstract simplicial complex, the barycentric subdivision of $\Delta$, denoted here by $\mathrm{sd}(\Delta )$, has faces which correspond bijectively to the ordered partitions of the faces of $\Delta$; in particular, the vertices and facets of $\mathrm{sd}(\Delta )$ correspond bijectively to the nonempty faces and the permutations of the facets of $\Delta$, respectively. The faces of $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ instead correspond bijectively to certain multi-pointed ordered partitions of the faces of $\Delta$; in particular, the vertices and facets of $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ correspond bijectively to the pointed faces and the ordered partitions of the facets of $\Delta$, respectively.

The antiprism triangulation was introduced by Izmestiev and Joswig [19] as a technical device in their effort to understand combinatorially branched coverings of manifolds, and arose independently and was studied under the name chromatic subdivision in computer science (specifically, in theoretical distributed computing); see [21] and references therein. This paper aims to show that, as is the case with barycentric subdivision, the antiprism triangulation has very interesting enumerative and algebraic properties and that its study leads to combinatorial problems which are often more challenging than the corresponding ones for the barycentric subdivision. We denote by $h (\Delta ,x)$ the h-polynomial of a simplicial complex $\Delta$ and by $\sigma _n$ the (abstract) simplex on an n-element vertex set. Our main motivation comes from the following conjectural analogue of the main result of [11].

Fig. 1

Antiprism triangulation of the 2-simplex

Conjecture 1.1

The polynomial $h(\mathrm{sd}_{{\mathcal {A}}}(\Delta ), x)$ is real-rooted for every simplicial complex $\Delta$ with nonnegative h-vector.

This conjecture is part of the general problem to understand when the h-polynomial of a triangulation of a simplicial complex is real-rooted. The present study of antiprism triangulations has partly motivated the study of this problem for the much more general class of uniform triangulations [5]. Although we are unable to fully settle Conjecture 1.1 in this paper, we reduce it to an interlacing relation between the members of two concrete infinite sequences of polynomials (see Conjecture 5.3), given the following important special case of the conjecture and [5, Thm. 1.2].

Theorem 1.2

The polynomial $h (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n), x)$ is real-rooted and has a nonnegative, real-rooted and interlacing symmetric decomposition with respect to $n-1$ for every positive integer n.

We also prove the unimodality of $h (\mathrm{sd}_{{\mathcal {A}}}(\Delta ), x)$ for every Cohen–Macaulay simplicial complex $\Delta$ and show that the peak appears in the middle, by studying Lefschetz properties of the Stanley–Reisner ring of $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$. The following result is an analogue of the main result of [22] for the barycentric subdivision.

Theorem 1.3

The complex $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ has the almost strong Lefschetz property over ${{\mathbb {R}}}$ for every shellable simplicial complex $\Delta$. Moreover, for every $(n-1)$-dimensional Cohen–Macaulay simplicial complex $\Delta$, the h-vector of $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ is unimodal, with the peak being at position n/2, if n is even, and at $(n-1)/2$ or $(n+1)/2$, if n is odd.

This paper is structured as follows. The antiprism triangulation $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ is described combinatorially as an abstract simplicial complex and defined geometrically as a triangulation, using either the antiprism construction, or balanced stellar subdivisions (crossing operations), in Sect. 4. The antiprism construction is defined in Sect. 3, where its face enumeration is studied within the framework of uniform triangulations, introduced in [5]. These results are then applied in Sect. 5 to find combinatorial interpretations and recurrences for the basic enumerative invariants of the antiprism triangulation of the simplex. The face enumeration of antiprism triangulations turns out to be related to traditional combinatorial themes, such as ordered set partitions, colorings and the enumeration of permutations by excedances (for example, the number of facets of $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ is equal to the number of ordered partitions of an n-element set). Section 5 also proves Theorem 1.2 and describes combinatorially the transformation of the h-vector of a simplicial complex, under antiprism triangulation. The proof of Theorem 1.2 is different from all proofs of the corresponding result for the barycentric subdivision known to the authors; it exploits the recurrence for the h-polynomial of $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ and uses the concept of interlacing sequence of polynomials. Theorem 1.3 is proved in Sect. 7; the method generally follows those of [22, 27], with certain complications and shortcuts.

Basic background and definitions, together with some preliminary technical results, are included in Sect. 2 for simplicial complexes, their triangulations and face enumeration, and for the unimodality and real-rootedness of polynomials and their symmetric decompositions, and in Sect. 6 for Lefschetz properties of simplicial complexes. Open problems, other than those proposed earlier in the paper, and further directions for research are discussed in Sect. 8.

2 Preliminaries

This section includes preliminaries on simplicial complexes and triangulations, their basic enumerative invariants and the unimodality of polynomials and related properties. Throughout this paper we set ${{\mathbb {N}}}:= \{0, 1, 2,\dots \}$ and $[n] := \{1, 2,\ldots ,n\}$ for $n \in {{\mathbb {N}}}$. We also denote by ${{\mathfrak {S}}}_n$ the symmetric group of permutations of [n] and by |V| and $2^V$ the cardinality and the powerset, respectively, of a finite set V.

2.1 Simplicial Complexes

We start with several definitions and refer to Stanley’s book [37] for background and more information.

Let V be a finite set. An (abstract) simplicial complex $\Delta$ on the vertex set V is a collection of subsets of V that is closed under inclusion and such that $\{v\} \in \Delta$ for every $v\in V$. Throughout this article, we assume that all simplicial complexes are finite. The elements of $\Delta$ are called faces and the inclusionwise maximal ones are called facets. The dimension of a face $F \in \Delta$ is defined as $\dim (F) = |F|-1$; the dimension of $\Delta$, denoted by $\dim (\Delta )$, is the maximum dimension of its faces. Zero-dimensional and one-dimensional faces of $\Delta$ are called vertices and edges, respectively. We say that $\Delta$ is pure if all facets of $\Delta$ have the same dimension. As in [5], we denote by $\sigma _n$ the abstract $(n-1)$-dimensional simplex $2^V$ on an n-element vertex set V (often taken to be [n]).

The cone over $\Delta$ is the simplicial complex consisting of the faces of $\Delta$, together with all sets $F \cup \{u\}$ for $F \in \Delta$, where $u \notin V$ is a new vertex, called the apex. We will denote this cone by $u *\Delta$. More generally, the (simplicial) join of two simplicial complexes $\Delta _1$ and $\Delta _2$ with disjoint vertex sets is defined as $\Delta _1 *\Delta _2 = \{ F_1 \cup F_2: F_1 \in \Delta _1,\, F_2\in \Delta _2\}$. Given a face $F \in \Delta$, the link and the star of F in $\Delta$ are defined as the simplicial complexes

$$\begin{aligned} \mathrm{link}_\Delta (F)&= \{ G \in \Delta : F \cup G \in \Delta ,\, F \cap G = \varnothing \}\quad \text {and}\\ \mathrm{star}_\Delta (F)&= \{ G \in \Delta :F \cup G \in \Delta \}, \end{aligned}$$

respectively. For $G_1, G_2,\ldots ,G_m \subseteq V$ we set

$$\begin{aligned} \langle G_1, G_2,\ldots ,G_m \rangle =\{F: F \subseteq G_i \text { for some } i \in [m]\}. \end{aligned}$$

In the sequel, $\Delta$ is a pure $(n-1)$-dimensional simplicial complex with vertex set V and ${{\mathbb {F}}}$ is a field. Let A be the polynomial ring ${{\mathbb {F}}}[x_v{:}\,v\in V]$ and write $x_F=\prod _{v\in F}x_v$ for $F\subseteq V$. The Stanley–Reisner ring (or face ring) of $\Delta$ (over ${{\mathbb {F}}}$) is defined as the quotient ring ${{\mathbb {F}}}[\Delta ]=A/I_\Delta$, where $I_\Delta =(x_F:F\subseteq V,\,F \notin \Delta )$ is the ideal of A known as the Stanley–Reisner ideal (or face ideal) of $\Delta$. The ring ${{\mathbb {F}}}[\Delta ]$ is graded by degree; subscripts on ${{\mathbb {F}}}[\Delta ]$ and its (standard) graded quotients will always refer to homogeneous components.

A linear system of parameters (l.s.o.p. for short) for ${{\mathbb {F}}}[\Delta ]$ is a sequence $\Theta =\theta _1,\ldots ,\theta _n$ of linear forms in ${{\mathbb {F}}}[\Delta ]$ such that the quotient ${{\mathbb {F}}}[\Delta ]/\Theta {{\mathbb {F}}}[\Delta ]$ has finite dimension, as a vector space over ${{\mathbb {F}}}$. The complex $\Delta$ is called Cohen–Macaulay over ${{\mathbb {F}}}$ if ${{\mathbb {F}}}[\Delta ]$ is a free module over the polynomial ring ${{\mathbb {F}}}[\Theta ]$ for some (equivalently, for every) l.s.o.p. $\Theta$ for ${{\mathbb {F}}}[\Delta ]$ and shellable if there exists a linear ordering $G_1, G_2,\ldots ,G_m$ of the facets of $\Delta$ such that for each $2 \le j \le m$, the set

$$\begin{aligned} \{F \subseteq G_j:F \not \subseteq G_i \text { for } 1 \le i < j\} \end{aligned}$$

has a unique minimal element, with respect to inclusion. Even though shellable simplicial complexes constitute a proper subclass of that of Cohen–Macaulay complexes, the sets of possible f-vectors for the two classes of simplicial complexes coincide (see, e.g., [37, Thm. 3.3]).

Given an $(n-1)$-dimensional simplicial complex $\Delta$, the f-vector of $\Delta$ is defined as the sequence $f(\Delta ) = (f_{-1}(\Delta ), f_0(\Delta ),\ldots ,f_{n-1}(\Delta ))$, where $f_i (\Delta )$ denotes the number of i-dimensional faces of $\Delta$. The h-vector of $\Delta$ is defined as $h(\Delta )=(h_0(\Delta ), h_1(\Delta ),\ldots ,h_n(\Delta ))$, where $h_i(\Delta )$ is given by the formula

$$\begin{aligned}h_i(\Delta ) =\sum _{j=0}^i(-1)^{i-j}{n-j \atopwithdelims ()i-j} f_{j-1}(\Delta ), \end{aligned}$$

and $h(\Delta ,x) = \sum _{i=0}^n h_i(\Delta ) x^i$ is the h-polynomial of $\Delta$. Equivalently, the latter can be defined by the formula

$$\begin{aligned} h(\Delta , x)= \sum _{i=0}^n f_{i-1} (\Delta ) x^i (1-x)^{n-i}=\sum _{F \in \Delta } x^{|F|}(1-x)^{n-|F|}. \end{aligned}$$

(1)

Assume now that $\Delta$ triangulates an $(n-1)$-dimensional ball, meaning that the geometric realization of $\Delta$ is homeomorphic to an $(n-1)$-dimensional ball (we also say that $\Delta$ is an $(n-1)$-dimensional simplicial ball). The boundary complex of $\Delta$ is then defined as

$$\begin{aligned} \partial \Delta =\langle F \in \Delta :F\subseteq G \text { for a unique facet } G \in \Delta \rangle . \end{aligned}$$

The set $\Delta ^\circ = \Delta \setminus \partial \Delta$ consists of the interior faces of $\Delta$ and $h^\circ (\Delta ,x)$ is defined by the sum on the far right of (1) in which $\Delta$ has been replaced by $\Delta ^\circ$. The following well-known statement is a special case of [33, Lem. 6.2].

Proposition 2.1

[33] We have $x^n h (\Delta ,1/x) = h^\circ (\Delta , x)$ for every triangulation $\Delta$ of an $(n-1)$-dimensional ball.

2.2 Triangulations

Let $\Delta$ and $\Delta '$ be simplicial complexes. We say that $\Delta '$ is a triangulation of $\Delta$ if there exist geometric realizations $K'$ and K of $\Delta '$ and $\Delta$, respectively, such that $K'$ geometrically subdivides K. Let $L \in K$ be a simplex and F be the corresponding face of $\Delta$. Then, $K'$ restricts to a triangulation $K'_L$ of L. The subcomplex $\Delta '_F$ of $\Delta '$ which corresponds to $K'_L$ is a triangulation of the abstract simplex $2^F$, called the restriction of $\Delta '$ to F. The carrier of a face $G \in \Delta '$ is the smallest face $F \in \Delta$ such that $G \in \Delta '_F$.

A fundamental enumerative invariant of a triangulation of a simplex is the local h-polynomial. Given a triangulation $\Gamma$ of an $(n-1)$-dimensional simplex $2^V$, this polynomial is defined [36, Defn. 2.1] by the formula

$$\begin{aligned} \ell _V (\Gamma , x) = \sum _{F \subseteq V}(-1)^{n - |F|} h (\Gamma _F, x). \end{aligned}$$

By the principle of inclusion–exclusion,

$$\begin{aligned} h (\Gamma , x)= \sum _{F \subseteq V}\ell _F (\Gamma _F, x). \end{aligned}$$

(2)

Stanley [36] showed that $\ell _V (\Gamma , x)$ has nonnegative and symmetric coefficients, so that $x^n\ell _V (\Gamma , 1/x) = \ell _V (\Gamma ,x)$, for every triangulation $\Gamma$ of $2^V$, and that it has unimodal coefficients for every regular triangulation, meaning that $\Gamma$ can be realized as the collection of projections on a geometric simplex of the lower faces of a simplicial polytope of one dimension higher.

The barycentric subdivision of a simplicial complex $\Delta$ is defined as the simplicial complex $\mathrm{sd}(\Delta )$ on the vertex set $\Delta \setminus \{\varnothing \}$ whose faces are the chains $F_0 \subsetneq F_1 \subsetneq \ldots \subsetneq F_k$ of nonempty faces of $\Delta$. The carrier of such a chain is its top element $F_k$. To describe the h-polynomial and local h-polynomial of $\mathrm{sd}(\sigma _n)$, we need to recall a few definitions from permutation enumeration. An excedance of a permutation $w \in {{\mathfrak {S}}}_n$ is an index $i \in [n-1]$ such that $w(i) > i$. Let $\mathrm{exc}(w)$ be the number of excedances of w. The polynomial

$$\begin{aligned} A_n(x)=\sum _{w \in {{\mathfrak {S}}}_n} x^{\mathrm{exc}(w)} \end{aligned}$$

is called the nth Eulerian polynomial; see [38, Sect. 1.4] for more information on this important concept. Similarly, the nth derangement polynomial is defined by the formula

$$\begin{aligned} d_n(x)=\sum _{w \in {{\mathfrak {D}}}_n}x^{\mathrm{exc}(w)}, \end{aligned}$$

where ${{\mathfrak {D}}}_n$ the set of all derangements (permutations without fixed points) in ${{\mathfrak {S}}}_n$. Then, $h (\mathrm{sd}(\sigma _n),x) = A_n(x)$ and $\ell _V(\mathrm{sd}(\sigma _n), x) = d_n(x)$ for every n (see [36, Sect. 2]), where V is the vertex set of $\sigma _n$.

Let ${{\mathcal {F}}}= (f_{{\mathcal {F}}}(i,j))$ be a triangular array of nonnegative integers, defined for $0 \le i \le j$. A triangulation $\Delta '$ of a simplicial complex $\Delta$ is called ${{\mathcal {F}}}$-uniform if for every $(n-1)$-dimensional face $F \in \Delta$, the restriction $\Delta '_F$ has exactly $f_{{\mathcal {F}}}(k,n)$ faces of dimension $k-1$ for all $0 \le k \le n$. The barycentric subdivision is a prototypical example of an ${{\mathcal {F}}}$-uniform triangulation, for a suitable array ${{\mathcal {F}}}$; the antiprism triangulation is another. The class of ${{\mathcal {F}}}$-uniform triangulations was introduced and studied in [5]. The h-polynomial and local h-polynomial of an ${{\mathcal {F}}}$-uniform triangulation of an $(n-1)$-dimensional simplex depend only on ${{\mathcal {F}}}$ and n and will be denoted by $h_{{\mathcal {F}}}(\sigma _n, x)$ and $\ell _{{\mathcal {F}}}(\sigma _n, x)$, respectively.

2.3 Polynomials

We recall some basic definitions and useful facts about unimodal and real-rooted polynomials. A polynomial $p(x)= a_0 + a_1 x + \cdots + a_n x^n \in {{\mathbb {R}}}[x]$ is called

• symmetric, with center of symmetry n/2, if $a_i = a_{n-i}$ for all $0 \le i \le n$,

• unimodal, with a peak at position k, if $a_0 \le a_1 \le \ldots \le a_k \ge a_{k+1} \ge \ldots \ge a_n$,

• alternatingly increasing with respect to n, if $a_0 \le a_n\le a_1\le a_{n-1} \le \ldots \le a_{\lceil n/2 \rceil }$,

• $\gamma$-positive, with center of symmetry n/2, if $p(x) = \sum _{j=0}^{\lfloor n/2 \rfloor } \gamma _jx^j (1+x)^{n-2j}$ for some nonnegative real numbers $\gamma _0, \gamma _1,\ldots ,\gamma _{\lfloor n/2 \rfloor }$.

Gamma-positivity implies palindromicity and unimodality; see [3] for a survey about this very interesting concept.

A polynomial $p(x) \in {{\mathbb {R}}}[x]$ is real-rooted if all complex roots of p(x) are real, or p(x) is the zero polynomial. A real-rooted polynomial, with roots $\alpha _1\ge \alpha _2\ge \ldots$, is said to interlace another real-rooted polynomial, with roots $\beta _1\ge \beta _2\ge \ldots$, if

$$\begin{aligned} \ldots \le \alpha _2 \le \beta _2 \le \alpha _1 \le \beta _1. \end{aligned}$$

By convention, the zero polynomial interlaces and is interlaced by every real-rooted polynomial and constant polynomials interlace all polynomials of degree at most one. Background on real-rooted polynomials and the theory of interlacing can be found in [9, 15, 35] and references therein. We recall here the crucial facts that every real-rooted polynomial with nonnegative coefficients is unimodal and that (see [15, Lem 3.4]) if two real-rooted polynomials p(x) and q(x) have positive leading coefficients and p(x) interlaces q(x), then $p(x) + q(x)$ is real-rooted as well and it is interlaced by p(x) and interlaces q(x). Moreover, every symmetric real-rooted polynomial with nonnegative coefficients is $\gamma$-positive.

A sequence $(p_0(x), p_1(x),\dots ,p_m(x))$ of real-rooted polynomials is called interlacing if $p_i(x)$ interlaces $p_j(x)$ for $0 \le i < j \le m$. The following lemma will be used for the proof of Theorem 1.2 in Sect. 5.1.

Lemma 2.2

• (a) ([8, Lem. 2.3], [39, Prop. 3.3]) Let $p_1(x), p_2(x),\dots ,p_m(x)$ be real-rooted polynomials in ${{\mathbb {R}}}[x]$. If $p_1(x)$ interlaces $p_m(x)$ and $p_i(x)$ interlaces $p_{i+1}(x)$ for all $i \in [m-1]$, then $(p_1(x), p_2(x),\dots ,p_m(x))$ is an interlacing sequence.

• (b) (cf. [15, Lem. 3.4]) If $(p_1(x), p_2(x),\dots ,p_m(x))$ is an interlacing sequence of real-rooted polynomials in ${{\mathbb {R}}}[x]$ with positive leading coefficients, then so is $(p_1(x) + p_2(x) + \cdots + p_m(x),\dots ,p_{m-1}(x) + p_m(x), p_m(x))$.

• (c) Let $(p_1(x), p_2(x),\ldots ,p_m(x))$ be an interlacing sequence of real-rooted polynomials in ${{\mathbb {R}}}[x]$ with positive leading coefficients. Then, $p_1(x) + p_2(x) + \cdots + p_m(x)$ interlaces $c_1 p_1(x) + c_2 p_2(x) + \cdots +c_m p_m(x)$ for all positive real numbers $c_1 \le c_2 \le \ldots \le c_m$. In particular, $p_1(x) + p_2(x)+\cdots + p_{m-1}(x)$ interlaces $p_1(x) + 2p_2(x) + \cdots + mp_m(x)$.

Proof

We only need to prove part (c) and for that, we proceed by induction on m. The case $m=1$ being trivial, let us assume that the result holds for a positive integer $m-1$, consider a sequence $(p_1(x),p_2(x),\dots ,p_m(x))$ and positive real numbers $c_1 \le c_2\le \ldots \le c_m$ as in the statement of the lemma and set $s_m(x) := p_1(x) + p_2(x) + \cdots + p_m(x)$. Since the sequence $(p_1(x),\ldots ,p_{m-2}(x),p_{m-1} + p_m(x))$ is also interlacing [15, Lem. 3.4], the induction hypothesis implies that $s_m(x)$ interlaces $c_1 p_1(x) + \cdots + c_{m-2} p_{m-2}(x) + c_{m-1} (p_{m-1}(x) + p_m(x))$. Since $s_m(x)$ also interlaces $(c_m - c_{m-1}) p_m(x)$ (because each of its summands does so), it must interlace the sum of these two polynomials. This completes the induction.

For the second statement, let $s_{m-1}(x) := p_1(x) +p_2(x) + \cdots + p_{m-1}(x)$. From the first statement $s_{m-1}(x)$ interlaces $p_1(x) + 2p_2(x) + \cdots + (m-1)p_{m-1}(x)$. Since $s_{m-1}(x)$ also interlaces $mp_m(x)$, it must interlace the sum of these two polynomials and the proof follows. $\square$

Every polynomial $p(x) \in {{\mathbb {R}}}[x]$ of degree at most n can be written uniquely in the form $p(x) = a(x) +xb(x)$, where a(x) and b(x) are symmetric with centers of symmetry n/2 and $(n-1)/2$, respectively. We say that p(x) has a nonnegative symmetric decomposition with respect to n, if a(x) and b(x) have nonnegative coefficients. Following [10], we also say that p(x) has a real-rooted symmetric decomposition (respectively, real-rooted and interlacing symmetric decomposition) with respect to n, if a(x) and b(x) are real-rooted (respectively, if a(x) and b(x) are real-rooted and $x^n p(1/x)$ interlaces p(x)). By [10, Thm. 2.6], if p(x) has a nonnegative, real-rooted and interlacing symmetric decomposition with respect to n, then b(x) interlaces a(x) and each one of them interlaces p(x). The alternatingly increasing property for p(x), defined earlier, with respect to n is equivalent to the unimodality of both a(x) and b(x).

3 The Antiprism Construction

The antiprism triangulation of a simplicial complex can be defined geometrically by iterating the antiprism construction. This section reviews the latter and studies its face enumeration, in the framework of uniform triangulations [5]. The results will be applied in Sect. 5, but may be of independent interest too.

Let $V = \{v_1, v_2,\ldots ,v_n\}$ be an n-element set and $\Delta$ be a triangulation of the boundary complex of the simplex $2^V$. We pick an n-element set $U = \{u_1, u_2,\ldots ,u_n\}$ which is disjoint from the vertex set of $\Delta$ and denote by $\Gamma _{{\mathcal {A}}}(\Delta )$ the collection of faces of $\Delta$ together with all sets of the form $E \cup G$, where $E = \{ u_i: i \in I\}$ is a nonempty face of the simplex $2^U$ for some $\varnothing \subsetneq I \subseteq [n]$ and G is a face of the restriction of $\Delta$ to the face $F = \{ v_i: i \in [n] \setminus I\}$ of $\partial (2^V)$ which is complementary to E. The collection $\Gamma _{{\mathcal {A}}}(\Delta )$ is a simplicial complex which contains $2^U$ and $\Delta$ as subcomplexes; we call it the antiprism over $\Delta$. When $\Delta = \partial (2^V)$ is the trivial triangulation, the antiprism $\Gamma _{{\mathcal {A}}}(\partial (2^V))$ is combinatorially isomorphic to the Schlegel diagram [41, Sect. 5.2] of the n-dimensional cross-polytope behind any of its facets. For general $\Delta$, the antiprism $\Gamma _{{\mathcal {A}}}(\Delta )$ is a triangulation of $\Gamma _{{\mathcal {A}}}(\partial (2^V))$: the carrier of a face $E \cup G$, as above, is the union of E with the carrier of G, the latter considered as a face of the triangulation $\Delta$ of $\partial (2^V)$. Since $\Gamma _{{\mathcal {A}}}(\partial (2^V))$ triangulates the simplex $2^V$, $\Gamma _{{\mathcal {A}}}(\Delta )$ is a triangulation of $2^V$ as well with boundary complex equal to $\Delta$.

Remark 3.1

Given a triangulation $\Gamma$ of the $(n-1)$-dimensional simplex $2^V$, an analogous procedure defines a triangulation, say $\Delta _{{\mathcal {A}}}(\Gamma )$, of the $(n-1)$-dimensional sphere which contains $2^U$ and $\Gamma$ as subcomplexes and which we may call the antiprism over $\Gamma$. This construction was employed in [2, Sect. 4], in order to relate the $\gamma$-vector of a flag triangulation of the sphere to the local $\gamma$-vector of a flag triangulation of the simplex, and in [4, Sect. 4], in order to interpret geometrically binomial Eulerian polynomials (see Example 3.5) and certain analogues for r-colored permutations. The connection between the two constructions is that $\Delta _{{\mathcal {A}}}(\Gamma ) = \Gamma \cup \Gamma _{{\mathcal {A}}}(\partial \Gamma )$.

The following statement is closely related to [4, Prop. 4.1].

Proposition 3.2

The simplicial complex $\Gamma _{{\mathcal {A}}}(\Delta )$ triangulates the $(n-1)$-dimensional simplex $2^V$ for every triangulation $\Delta$ of the boundary complex $\partial (2^V)$. Moreover,

$$\begin{aligned} h (\Gamma _{{\mathcal {A}}}(\Delta ), x)=\sum _{F \subsetneq V} x^{|F|} h (\Delta _F, 1/x). \end{aligned}$$

Proof

We have already commented on the first sentence. For the second, using Proposition 2.1 and the definition of the h-polynomial we find that

$$\begin{aligned} x^n h (\Gamma _{{\mathcal {A}}}(\Delta ), 1/x)&=h^\circ (\Gamma _{{\mathcal {A}}}(\Delta ), x)\,=\!\sum _{G \in \Gamma _{{\mathcal {A}}}(\Delta )^\circ }\!\! x^{|G|}(1-x)^{n-|G|} \\&=\sum _{\varnothing \ne E \subseteq U}\sum _{\begin{array}{c} G \in \Gamma _{{\mathcal {A}}}(\Delta )\\ G \cap U = E \end{array}}\!\! x^{|G|} (1-x)^{n-|G|}. \end{aligned}$$

By definition of $\Gamma _{{\mathcal {A}}}(\Delta )$, the inner sum is equal to $x^{|E|} h (\Delta _F, x)$, where $F \subsetneq V$ is the face of $2^V$ which is complementary to E. Replacing x by 1/x results in the proposed expression for $h (\Gamma _{{\mathcal {A}}}(\Delta ),x)$ and the proof follows. $\square$

We now turn our attention to uniform triangulations of $\partial (2^V)$.

Proposition 3.3

For every ${{\mathcal {F}}}$-uniform triangulation $\Delta$ of the boundary complex of an $(n-1)$-dimensional simplex $2^V$:

$$\begin{aligned} h (\Gamma _{{\mathcal {A}}}(\Delta ), x)&= \sum _{k=0}^{n-1}{n \atopwithdelims ()k} x^k h_{{\mathcal {F}}}(\sigma _k, 1/x) \end{aligned}$$

(3)

$$\begin{aligned}&=\sum _{k=0}^{n-1} {n \atopwithdelims ()k}\ell _{{\mathcal {F}}}(\sigma _k, x)( (1+x)^{n-k} - x^{n-k}) , \end{aligned}$$

(4)

$$\begin{aligned} \ell _V(\Gamma _{{\mathcal {A}}}(\Delta ), x)&=\sum _{k=0}^{n-1}{n \atopwithdelims ()k} \ell _{{\mathcal {F}}}(\sigma _k, x)( (1+x)^{n-k} - 1 - x^{n-k}), \end{aligned}$$

(5)

$$\begin{aligned} h (\Gamma _{{\mathcal {A}}}(\Delta ), x) - h(\Delta , x)&=\sum _{k=0}^{n-1} {n \atopwithdelims ()k} \ell _{{\mathcal {F}}}(\sigma _k, x)( (1+x)^{n-k} - 1 - x -\cdots - x^{n-k})\end{aligned}$$

(6)

$$\begin{aligned}&=\sum _{k=0}^{n-1}{n \atopwithdelims ()k} h_{{\mathcal {F}}}(\sigma _k, x)( x^{n-k} - x (x-1)^{n-k-1}). \end{aligned}$$

(7)

In particular, if all restrictions of $\Delta$ to proper faces of $2^V$ are regular triangulations, then the polynomials $\ell _V(\Gamma _{{\mathcal {A}}}(\Delta ),x)$ and $h (\Gamma _{{\mathcal {A}}}(\Delta ), x) - h (\Delta , x)$ are unimodal and $h (\Gamma _{{\mathcal {A}}}(\Delta ), x)$ is alternatingly increasing with respect to $n-1$.

Proof

Equation (3) follows directly from Proposition 3.2. To deduce (4) from that, we use (2) to express $h_{{\mathcal {F}}}(\sigma _k, 1/x)$ in terms of local h-polynomials, apply the symmetry property of the latter and change the order of summation to obtain

$$\begin{aligned} h(\Gamma _{{\mathcal {A}}}(\Delta ), x)&=\sum _{k=0}^{n-1} {n \atopwithdelims ()k} x^k \sum _{j=0}^k {k \atopwithdelims ()j}\ell _{{\mathcal {F}}}(\sigma _j, 1/x)=\sum _{k=0}^{n-1} {n \atopwithdelims ()k} \sum _{j=0}^kx^{k-j} {k \atopwithdelims ()j} \ell _{{\mathcal {F}}}(\sigma _j, x) \\&=\sum _{j=0}^{n-1} \ell _{{\mathcal {F}}}(\sigma _j, x)\sum _{k=j}^{n-1} {n \atopwithdelims ()k} {k \atopwithdelims ()j} x^{k-j} \\&=\sum _{j=0}^{n-1} {n \atopwithdelims ()j} \ell _{{\mathcal {F}}}(\sigma _j, x) \sum _{k=j}^{n-1} {n-j \atopwithdelims ()n-k} x^{k-j} \\&=\sum _{j=0}^{n-1} {n \atopwithdelims ()j}\ell _{{\mathcal {F}}}(\sigma _j, x)( (1+x)^{n-j} - x^{n-j}). \end{aligned}$$

For the fourth and fifth step we have used the identity ${n \atopwithdelims ()k} {k \atopwithdelims ()j} = {n \atopwithdelims ()j} {n-j\atopwithdelims ()n-k}$ and the binomial theorem, respectively.

Alternatively, (4) follows from an application of Stanley’s locality formula [36, Thm. 3.2] to $\Gamma _{{\mathcal {A}}}(\Delta )$, considered as a triangulation of the antiprism $\Gamma _{{\mathcal {A}}}(\partial (2^V))$ over the boundary complex of $2^V$. Equation (5) follows when combining (4) with

$$\begin{aligned} h(\Gamma _{{\mathcal {A}}}(\Delta ), x)=\ell _V(\Gamma _{{\mathcal {A}}}(\Delta ), x)+\sum _{k=0}^{n-1} {n \atopwithdelims ()k} \ell _{{\mathcal {F}}}(\sigma _k, x), \end{aligned}$$

(8)

the latter being (2) applied to $\Gamma _{{\mathcal {A}}}(\Delta )$. Equation (6) follows from (4) and

$$\begin{aligned} h(\Delta , x)=\sum _{k=0}^{n-1} {n \atopwithdelims ()k}\ell _{{\mathcal {F}}}(\sigma _k, x)(1 + x + x^2 + \cdots + x^{n-k-1}), \end{aligned}$$

(9)

which is also a consequence of [36, Thm. 3.2]; see [20, (4.2)]. Equation (7) follows from (6) by expressing $\ell _{{\mathcal {F}}}(\sigma _k, x)$ in terms of the h-polynomials $h_{{\mathcal {F}}}(\sigma _j, x)$, changing the order of summation and computing the inner sum, just as in the proof of (4); we leave the details of this computation to the interested reader.

For the last statement we note that, by the regularity assumption, $\ell _{{\mathcal {F}}}(\sigma _k, x)$ is (symmetric with center of symmetry k/2 and) unimodal for $0 \le k < n$. As a result, (5) and (6) imply the unimodality of $\ell _V(\Gamma _{{\mathcal {A}}}(\Delta ), x)$ and $h (\Gamma _{{\mathcal {A}}}(\Delta ), x) - h (\Delta , x)$, respectively, and (6) and (9) imply that the symmetric decomposition

$$\begin{aligned} h (\Gamma _{{\mathcal {A}}}(\Delta ), x)= h (\Delta , x) + (h (\Gamma _{{\mathcal {A}}}(\Delta ), x) - h (\Delta , x)) \end{aligned}$$

of $h(\Gamma _{{\mathcal {A}}}(\Delta ), x)$ with respect to $n-1$ is nonnegative and unimodal. The latter statement is equivalent to $h (\Gamma _{{\mathcal {A}}}(\Delta ),x)$ being alternatingly increasing. $\square$

Remark 3.4

Let $\Delta$ be as in Proposition 3.3. Since coning a simplicial complex does not affect the h-polynomial, the right-hand side of (9) is also an expression for $h (u*\Delta ,x)$, where $u *\Delta$ denotes the cone of $\Delta$ with apex u. The formula

$$\begin{aligned} h (u *\Delta , x)= \sum _{k=0}^{n-1} {n \atopwithdelims ()k} h_{{\mathcal {F}}}(\sigma _k, x) (x-1)^{n-k-1} \end{aligned}$$

can be derived from that by expressing $\ell _{{\mathcal {F}}}(\sigma _k, x)$ in terms of the h-polynomials $h_{{\mathcal {F}}}(\sigma _j, x)$, changing the order of summation and computing the inner sum, just as in the proof of (4) and (7) or, alternatively, by adapting the argument in the proof of Proposition 3.2. When $\Delta$ is the barycentric subdivision of $\partial \sigma _n$, this yields the recursion

$$\begin{aligned} A_n(x) =\sum _{k=0}^{n-1} {n \atopwithdelims ()k} A_k(x) (x-1)^{n-k-1} \end{aligned}$$

for the Eulerian polynomial $A_n(x)$, valid for $n \ge 1$. This appears as (2.7) in [16].

Example 3.5

Suppose again that $\Delta$ is the barycentric subdivision of $\partial \sigma _n$. Then (3) yields that

$$\begin{aligned} h (\Gamma _{{\mathcal {A}}}(\Delta ), x)= \sum _{k=0}^{n-1} {n \atopwithdelims ()k} x^k A_k(1/x)= 1+ x \sum _{k=1}^{n-1} {n \atopwithdelims ()k} A_k(x)={\widetilde{A}}_n(x) - xA_n(x) \end{aligned}$$

and $h (\Gamma _{{\mathcal {A}}}(\Delta ), x) - h_{{\mathcal {F}}}(\partial \sigma _n)= {\widetilde{A}}_n(x) - (1+x) A_n(x)$, where

$$\begin{aligned} {\widetilde{A}}_n(x) := 1 + x \sum _{k=1}^n {n \atopwithdelims ()k} A_k(x) \end{aligned}$$

is the nth binomial Eulerian polynomial studied, for instance, in [4, 32]. From (8) we compute further that $\ell _V(\Gamma _{{\mathcal {A}}}(\Delta ), x) = {\widetilde{A}}_n(x) - (1+x) A_n(x) - d_n(x)$, where $d_n(x) = \ell _{{\mathcal {F}}}(\sigma _n, x)$ is the nth derangement polynomial (see Sect. 2.2).

Therefore, by Proposition 3.3, ${\widetilde{A}}_n(x) - xA_n(x)$ is alternatingly increasing with respect to $n-1$ and ${\widetilde{A}}_n(x) - (1+x)A_n(x)$ is symmetric and unimodal.

4 The Antiprism Triangulation

This section briefly describes combinatorially and geometrically the antiprism triangulation of a simplicial complex. For more information we refer to [19, Appendix A.1] and [21], where these descriptions are given in variant forms. We first review the corresponding descriptions of the barycentric subdivision, which we will parallel to treat the antiprism triangulation.

Let $\Delta$ be a simplicial complex. Consider the (simple, undirected) graph ${{\mathcal {G}}}(\Delta )$ on the node set of nonempty faces of $\Delta$ for which two nodes are adjacent if one is contained in the other. The barycentric subdivision $\mathrm{sd}(\Delta )$ is defined as the clique complex of ${{\mathcal {G}}}(\Delta )$, meaning the abstract simplicial complex whose vertices are the nodes of ${{\mathcal {G}}}(\Delta )$ and whose faces are the sets consisting of pairwise adjacent nodes. This is equivalent to the definition already given in Sect. 2.2.

Geometrically, $\mathrm{sd}(\Delta )$ can be described as a triangulation of $\Delta$ as follows. Assume that all faces of $\Delta$ of dimension at most j have been triangulated, for some $j \in {{\mathbb {N}}}$. Then, triangulate each $(j+1)$-dimensional face of $\Delta$ by inserting one point in the interior of that face and coning over its boundary, which is already triangulated. By repeating this process, starting at $j=0$ and moving to higher dimensional faces, we get a triangulation of $\Delta$ which is combinatorially isomorphic to $\mathrm{sd}(\Delta )$. Alternatively, $\mathrm{sd}(\Delta )$ can be constructed by applying successively the operation of stellar subdivision to each face of $\Delta$ of positive dimension, starting from the facets and moving to lower dimensional faces in any order which respects reverse inclusion. A stellar subdivision on a face $F \in \Delta$ replaces $\mathrm{star}_\Delta (F)$ by the join of $\mathrm{link}_\Delta (F)$ with the cone over $\partial (2^F)$.

The antiprism triangulation can be defined similarly, if the nonempty faces of $\Delta$ are replaced by pointed faces and coning is replaced by the antiprism construction of Sect. 3. Recall that a pointed subset of a set V is any pair (S, v) such that $v \in S\subseteq V$. Similarly, a pointed face of a simplicial complex $\Delta$ is any pair (F, v) such that $F \in \Delta$ is a face and $v \in F$ is a chosen vertex.

Definition 4.1

Let $\Delta$ be a simplicial complex. We denote by ${{\mathcal {G}}}_{{\mathcal {A}}}(\Delta )$ the (simple, undirected) graph on the node set of pointed faces of $\Delta$ for which two distinct pointed faces (F, v) and $(F',v')$ are adjacent if

• $F = F'$, or

• $F \subsetneq F'$ and $v' \in (F' \setminus F)$, or

• $F' \subsetneq F$ and $v \in (F \setminus F')$.

The antiprism triangulation of $\Delta$, denoted by $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$, is the abstract simplicial complex defined as the clique complex of ${{\mathcal {G}}}_{{\mathcal {A}}}(\Delta )$.

Examples of antiprism triangulations are shown in Figs. 1 and 2.

Fig. 2

Antiprism triangulation of the cone over the boundary of the 2-simplex

The faces of $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ can be described explicitly, in combinatorial terms [21, Sect. 2]. Given a set S, an ordered set partition (or simply, ordered partition) of S is any sequence of nonempty, pairwise disjoint sets (called blocks) whose union is equal to S. A multi-pointed ordered partition of S is defined as a pair $(\pi ,\tau )$, where $\pi =(B_1,B_2,\ldots ,B_m)$ and $\tau =(C_1,C_2,\ldots ,C_m)$ are ordered partitions of S and of a subset of S, respectively, with the same number of blocks, such that $C_i$ is a nonempty subset of $B_i$ for every $i\in [m]$. We think of such a pair as an ordered partition of S, together with a choice of a nonempty subset for every block. The sum of the cardinalities of these subsets $C_i$ (total number of chosen elements) will be called the weight of $(\pi , \tau )$. Then, the $(k-1)$-dimensional faces of $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ are in one-to-one correspondence with the multi-pointed ordered partitions of faces of $\Delta$ of weight k. More specifically, the multi-pointed ordered partition $(\pi ,\tau )$, with $\pi = (B_1,B_2,\ldots ,B_m)$ and $\tau =(C_1,C_2,\ldots ,C_m)$, corresponds to the face of $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ with vertices the pointed faces (F, v) of $\Delta$, where $F=B_1\cup B_2\cup \cdots \cup B_i$ for some $i\in [m]$ and $v\in C_i$. The faces of the antiprism triangulation of the simplex $2^V$ are the multi-pointed ordered partitions of subsets of V; they will be referred to as multi-pointed partial ordered partitions of V. Note that the facets of $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ are in one-to-one correspondence with the ordered partitions of the facets of $\Delta$ (since all elements in the blocks should be chosen). Figure 1 shows the antiprism triangulation of the 2-simplex, including some faces labeled by multi-pointed ordered partitions.

As was the case with barycentric subdivision, $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ can be constructed geometrically by applying the antiprism construction of Sect. 3 to its faces, starting from the edges and moving to faces of higher dimension in any order which respects inclusion. This process is slightly different from the one in [19, 21] which uses crossing operations on the faces of $\Delta$ instead, starting from facets and moving to faces of lower dimension in any order which respects reverse inclusion. A crossing operation (also known as a balanced stellar subdivision [7]) on a face $F \in \Delta$ replaces $\mathrm{star}_\Delta (F)$ by the join of $\mathrm{link}_\Delta (F)$ with the antiprism (as defined in Sect. 3) over $\partial (2^F)$. Both approaches result in a triangulation which is combinatorially isomorphic to $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$. Under this isomorphism, the carrier of a multi-pointed ordered partition of a face $F \in \Delta$ is equal to F. As a result, the interior faces of the antiprism triangulation of the simplex $2^F$ are in one-to-one correspondence with the multi-pointed ordered partitions of F. A type of operation more general than stellar and balanced stellar subdivision was introduced in [18] and was applied there to all faces of a fixed dimension to produce a triangulation of $\Delta$.

5 Face Enumeration

This section studies the rich enumerative combinatorics of antiprism triangulations and proves Theorem 1.2. Following the notation of [5], we denote by $h_{{\mathcal {A}}}(\sigma _n, x)$ and $\ell _{{\mathcal {A}}}(\sigma _n, x)$ the h-polynomial and local h-polynomial of $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$, respectively. These two polynomials play an important role in this study. The main difficulty for proving the real-rootedness of $h_{{\mathcal {A}}}(\sigma _n, x)$ comes from the fact that we know of no simpler recurrence relation for it than that of Proposition 5.1. Some of the combinatorial interpretations of $h_{{\mathcal {A}}}(\sigma _{n}, x)$ extend to describe the effect of the antiprism triangulation on the h-polynomial of any simplicial complex.

5.1 The Antiprism Triangulation of a Simplex

As discussed in Sect. 4, the number of $(k-1)$-dimensional faces of the antiprism triangulation $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ is equal to the number of multi-pointed partial ordered set partitions of [n] of weight k. We now give a recurrence and combinatorial interpretations for the h-polynomial of $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$. For the first few values of n,

$$\begin{aligned} h_{{\mathcal {A}}}(\sigma _n, x)\;= {\left\{ \begin{array}{ll} 1, &{} \text {if }\,n = 0, \\ 1, &{} \text {if }\,n = 1, \\ 1 + 2x, &{} \text {if }\,n=2 ,\\ 1 + 9x + 3x^2, &{} \text {if }\,n=3, \\ 1 + 28 x + 42 x^2 + 4x^3, &{} \text {if }\,n=4 ,\\ 1 + 75 x + 310 x^2 + 150 x^3 + 5x^4, &{}\text {if }\,n=5, \\ 1 + 186 x + 1725 x^2 + 2300 x^3 + 465 x^4 + 6x^5,&{} \text {if }\,n=6, \\ 1 + 441 x + 8211 x^2 + 23625 x^3 + 13685 x^4 +1323 x^5 + 7x^6, &{} \text {if }\,n=7. \end{array}\right. } \end{aligned}$$

We first need to introduce some more terminology. Let $\varphi = (\pi , \tau )$ be a multi-pointed partial ordered set partition of [n]. Thus, $\pi = (B_1, B_2,\ldots ,B_m)$ is an ordered partition of a subset S of [n] and $\tau = (C_1,C_2,\ldots ,C_m)$, where $C_i$ is a nonempty subset of $B_i$ for every $i \in [m]$. We will say that $\varphi$ is proper if $C_i$ is a proper subset of $B_i$ for every $i \in [m]$. We will use the same terminology with the adjective ‘partial’ dropped, when $S = [n]$. The excedance set of a permutation $w \in {{\mathfrak {S}}}_n$ is defined as the set of indices $i \in [n-1]$ such that $w(i) > i$; see [13] for more information on this concept.

Proposition 5.1

• (a) We have

  $$\begin{aligned} h_{{\mathcal {A}}}(\sigma _n, x)=\sum _{k=0}^{n-1}{n \atopwithdelims ()k} x^k h_{{\mathcal {A}}}(\sigma _k, 1/x) \end{aligned}$$

  for every positive integer n.

• (b) The coefficient of $x^k$ in $h_{{\mathcal {A}}}(\sigma _n, x)$ is equal to:

• the number of proper multi-pointed partial ordered set partitions of [n] of weight k,

• the number of ways to choose a subset $S \subseteq [n]$ and an ordered set partition $\pi$ of S and to color k elements of S black and the remaining elements white, so that no block of $\pi$ is monochromatic,

• the number of ordered set partitions $\pi =(B_1, B_2,\ldots ,B_m)$ of [n] for which the union $\bigcup _{i=1}^{\lfloor m/2\rfloor } B_i$ has exactly k elements,

• ${n \atopwithdelims ()k}$ times the number of permutations in ${{\mathfrak {S}}}_n$ with excedance set equal to [k],

• the explicit expression

  $$\begin{aligned} {n \atopwithdelims ()k}\sum _{j=1}^{k+1}(-1)^{k+1-j} j! S(k+1,j) j^{n-k-1}, \end{aligned}$$

where S(n, k) are Stirling numbers of the second kind.

Proof

Part (a) follows from Proposition 3.3, as a special case of (3). For part (b), we first note that from (5) of the same proposition and (2) we get

$$\begin{aligned} \ell _{{\mathcal {A}}}(\sigma _n, x)=\sum _{m=0}^{n-1}{n \atopwithdelims ()m} \ell _{{\mathcal {A}}}(\sigma _m, x)( (1+x)^{n-m} - 1 - x^{n-m}) \end{aligned}$$

for $n \ge 1$ and

$$\begin{aligned} h_{{\mathcal {A}}}(\sigma _n, x)=\sum _{m=0}^n{n \atopwithdelims ()m} \ell _{{\mathcal {A}}}(\sigma _m, x), \end{aligned}$$

respectively. By induction on n, the former equality implies that the coefficient of $x^k$ in $\ell _{{\mathcal {A}}}(\sigma _n, x)$ is equal to the number of proper multi-pointed ordered set partitions of [n] of weight k. This and the latter equation yield the first interpretation of $h_{{\mathcal {A}}}(\sigma _n, x)$ claimed in part (b). The second interpretation is a restatement of the first (where black elements correspond to the chosen elements in the blocks of the multi-pointed partition).

The third interpretation can be deduced from the first as follows. Let Q(n, k) denote the collection of proper multi-pointed partial ordered partitions of [n] of weight k. Each element of Q(n, k) is a triple consisting of a subset $S \subseteq [n]$, an ordered partition $\pi =(B_1,B_2,\ldots ,B_r)$ of S and a choice of nonempty proper subset $C_i$ of $B_i$ for every $i\in [r]$, such that the union $\bigcup _{i=1}^r C_i$ has cardinality k. From such a triple one can define an ordered partition of [n] by listing the blocks $C_1,\ldots ,C_r, B_1 \setminus C_1,\ldots ,B_r \setminus C_r$ in this order and, if nonempty, adding $[n] \setminus S$ at the end as the last block. It is straightforward to verify that the resulting map is a bijection from Q(n, k) to the collection of ordered partitions of [n] described in the third proposed interpretation.

For the last two claimed interpretations, let us denote by c(n, k) the number of permutations in ${{\mathfrak {S}}}_n$ with excedance set equal to [k], for $k\in \{0, 1,\ldots ,n\}$. Then, $c(n,n) = 0$ and, as a consequence of Lemma 2.2 and Theorem 2.5 in [13] (see also Sect. 3 of this reference), $c(n,k) = c(n,n-k-1)$ and

$$\begin{aligned} c(n, k)=1+ \sum _{m=1}^k {k+1 \atopwithdelims ()m} c(n-k-1+m, m) \end{aligned}$$

for $k \in \{0, 1,\ldots ,n-1\}$. In view of $c(n,k)= c(n,n-k-1)$, the latter equality can be rewritten as

$$\begin{aligned} c(n, k)=1 +\! \sum _{m=1}^{n-k-1} {n-k\atopwithdelims ()m} c(k+m, m). \end{aligned}$$

(10)

On the other hand, writing $h_{{\mathcal {A}}}(\sigma _n, x) =\sum _{k=0}^n p_{{\mathcal {A}}}(n,k) x^k$ for $n \in {{\mathbb {N}}}$, the recursion of part (a) gives that

$$\begin{aligned} p_{{\mathcal {A}}}(n, k)=\sum _{m=k}^{n-1} {n \atopwithdelims ()m}p_{{\mathcal {A}}}(m, m-k) \end{aligned}$$

for $k \in \{0, 1,\ldots ,n-1\}$. Setting

$$\begin{aligned} p_{{\mathcal {A}}}(n,k)={n \atopwithdelims ()k} {\bar{p}}_{{\mathcal {A}}}(n,k), \end{aligned}$$

the last recursion can be rewritten as

$$\begin{aligned} {n \atopwithdelims ()k} {\bar{p}}_{{\mathcal {A}}}(n,k)&=\sum _{m=k}^{n-1}{n\atopwithdelims ()m}{m\atopwithdelims ()k}{\bar{p}}_{{\mathcal {A}}}(m, m-k),\quad \ \ \text {i.e.,}\\ {\bar{p}}_{{\mathcal {A}}}(n,k)&=\sum _{m=k}^{n-1}{n-k\atopwithdelims ()m-k}{\bar{p}}_{{\mathcal {A}}}(m,m-k)=\sum _{m=0}^{n-k-1}{n-k\atopwithdelims ()m} {\bar{p}}_{{\mathcal {A}}}(k+m,m). \end{aligned}$$

Comparing this recursion to (10) we get that ${\bar{p}}_{{\mathcal {A}}}(n,k)=c(n,k)$ for all n and all $0\le k\le n$. This proves the next to last interpretation, claimed in part (b). The last interpretation follows from this and the explicit formula for c(n, k) obtained in [13, Prop. 6.5]. $\square$

The following statement is the main result of this section.

Theorem 5.2

The polynomial $h_{{\mathcal {A}}}(\sigma _n, x)$ is real-rooted and interlaces $h_{{\mathcal {A}}}(\sigma _{n+1}, x)$ for every $n \in {{\mathbb {N}}}$. Moreover, $h_{{\mathcal {A}}}(\sigma _n, x)$ has a nonnegative, real-rooted and interlacing symmetric decomposition with respect to $n-1$, for every positive integer n.

Proof

We consider the polynomials

$$\begin{aligned} q_{n,r} (x) := \sum _{k=0}^n {n \atopwithdelims ()k}x^{k+r} h_{{\mathcal {A}}}(\sigma _{k+r}, 1/x), \end{aligned}$$

shown in Table 1 for small values of $n, r \in {{\mathbb {N}}}$. By part (a) of Proposition 5.1 and the definition of $q_{n,r}(x)$ we have

$$\begin{aligned} q_{n,0} (x)&= h_{{\mathcal {A}}}(\sigma _n, x) +x^n h_{{\mathcal {A}}}(\sigma _n, 1/x), \end{aligned}$$

(11)

$$\begin{aligned} q_{0,r} (x)&=x^r h_{{\mathcal {A}}}(\sigma _r, 1/x) \end{aligned}$$

(12)

for every positive integer n and every $r \in {{\mathbb {N}}}$, respectively. We claim that

$$\begin{aligned} {{\mathcal {Q}}}_n:=(q_{n,0}(x),q_{n-1,1}(x),\ldots ,q_{1,n-1}(x), q_{0,n}(x),q_{0,n+1}(x)) \end{aligned}$$

is an interlacing sequence of real-rooted polynomials for every $n \in {{\mathbb {N}}}$. In particular, selecting the first and last two terms, we have the interlacing sequence

$$\begin{aligned} \bigl (h_{{\mathcal {A}}}(\sigma _n, x) + x^n h_{{\mathcal {A}}}(\sigma _n, 1/x), x^n h_{{\mathcal {A}}}(\sigma _n, 1/x), x^{n+1}h_{{\mathcal {A}}}(\sigma _{n+1}, 1/x)\bigr ) \end{aligned}$$

of real-rooted polynomials for every $n \in {{\mathbb {N}}}$. Before we prove the claim let us observe that, since $x^n h_{{\mathcal {A}}}(\sigma _n, 1/x)$ and $x^{n+1} h_{{\mathcal {A}}}(\sigma _{n+1}, 1/x)$ have degrees n and $n+1$, respectively, the statement that the former polynomial interlaces the latter is equivalent to the statement that $h_{{\mathcal {A}}}(\sigma _n, x)$ interlaces $h_{{\mathcal {A}}}(\sigma _{n+1},x)$. Similarly, since $h_{{\mathcal {A}}}(\sigma _n, x) + x^nh_{{\mathcal {A}}}(\sigma _n, 1/x)$ is symmetric of degree n, the statement that this polynomial interlaces $x^{n+1} h_{{\mathcal {A}}}(\sigma _{n+1}, 1/x)$ is equivalent to each of the statements that the same polynomial is interlaced by $x^n h_{{\mathcal {A}}}(\sigma _{n+1}, 1/x)$ and that it interlaces $h_{{\mathcal {A}}}(\sigma _{n+1}, x)$.

We now prove the claim by induction on n. This is true for $n=0$, since ${{\mathcal {Q}}}_0 = (1, x)$. We assume that it holds for $n-1 \in {{\mathbb {N}}}$. The standard recurrence for the binomial coefficients shows that $q_{n,r} (x) = q_{n-1,r} (x) +q_{n-1,r+1}(x)$ for every $r \in {{\mathbb {N}}}$. Writing this in the form

$$\begin{aligned} q_{n-r,r} (x)=q_{n-r-1,r} (x) +q_{n-r-1,r+1} (x) \end{aligned}$$

and iterating, we get

$$\begin{aligned} q_{n-r,r} (x)=q_{n-r-1,r} (x) + q_{n-r-2,r+1}(x) + \cdots + q_{0,n-1} (x) + q_{0,n} (x) \end{aligned}$$

(13)

for $r \in \{0, 1,\ldots , n\}$. This means that the first $n+1$ terms of ${{\mathcal {Q}}}_n$ are the partial sums of the reverse of ${{\mathcal {Q}}}_{n-1}$ and hence they form an interlacing sequence, by part (b) of Lemma 2.2. Thus, by part (a) of this lemma, to complete the induction it suffices to show that $q_{n,0} (x)$ and $q_{0,n} (x)$ interlace $q_{0,n+1} (x)$. As already discussed, and in view of (11) and (12), this is equivalent to showing that $h_{{\mathcal {A}}}(\sigma _n, x) + x^n h_{{\mathcal {A}}}(\sigma _n, 1/x)$ and $h_{{\mathcal {A}}}(\sigma _n, x)$ interlace $h_{{\mathcal {A}}}(\sigma _{n+1}, x)$. To verify this we note that, setting $r=0$ in (13), comparing with (11) and (12), and replacing n with $n+1$, we get

$$\begin{aligned} q_{n,0} (x) + q_{n-1,1} (x) + \cdots + q_{0,n} (x)= h_{{\mathcal {A}}}(\sigma _{n+1}, x). \end{aligned}$$

(14)

Since the sum of the terms of an interlacing sequence is interlaced by the first term, we conclude that $h_{{\mathcal {A}}}(\sigma _n, x) + x^nh_{{\mathcal {A}}}(\sigma _n, 1/x)$ interlaces $h_{{\mathcal {A}}}(\sigma _{n+1}, x)$. Finally, applying part (c) of Lemma 2.2 to the interlacing sequence ${{\mathcal {Q}}}_{n-1}$ we conclude that the sum of the first n terms of this sequence, which equals $h_{{\mathcal {A}}}(\sigma _n, x)$, interlaces the sum of the partial sums of the reverse of ${{\mathcal {Q}}}_{n-1}$, which equals $h_{{\mathcal {A}}}(\sigma _{n+1}, x)$. This completes the proof of the claim.

Finally, note that $x^n h_{{\mathcal {A}}}(\sigma _n, 1/x)$ and $x^{n+1} h_{{\mathcal {A}}}(\sigma _{n+1}, 1/x)$ are the last two terms of ${{\mathcal {Q}}}_n$. Since this sequence is interlacing, the two polynomials are real-rooted and the former interlaces the latter. As already discussed, this means that $h_{{\mathcal {A}}}(\sigma _n, x)$ is real-rooted and interlaces $h_{{\mathcal {A}}}(\sigma _{n+1}, x)$. Similarly, the sum of the first n terms of the sequence ${{\mathcal {Q}}}_{n-1}$ interlaces the last term. In view of (12) and (14), this means that $h_{{\mathcal {A}}}(\sigma _n, x)$ interlaces $x^n h_{{\mathcal {A}}}(\sigma _n, 1/x)$ and, equivalently, that $h_{{\mathcal {A}}}(\sigma _n, x)$ is interlaced by $x^{n-1} h_{{\mathcal {A}}}(\sigma _n, 1/x)$. Since we already know from Proposition 3.3 that $h_{{\mathcal {A}}}(\sigma _n, x)$ has a nonnegative symmetric decomposition with respect to $n-1$, this decomposition must be real-rooted and interlacing by [10, Thm. 2.6]. $\square$

Table 1 Some polynomials $q_{n,r}(x)$

Let us write $\theta _{{\mathcal {A}}}(\sigma _n, x) := h_{{\mathcal {A}}}(\sigma _n, x) - h_{{\mathcal {A}}}(\partial \sigma _n, x)$. As mentioned in the proof of Proposition 3.3, the expression $h_{{\mathcal {A}}}(\sigma _n, x) = h_{{\mathcal {A}}}(\partial \sigma _n, x)+ \theta _{{\mathcal {A}}}(\sigma _n, x)$ is the (nonnegative) symmetric decomposition of $h_{{\mathcal {A}}}(\sigma _n, x)$ with respect to $n-1$. Thus, $h_{{\mathcal {A}}}(\partial \sigma _n, x)$ and $\theta _{{\mathcal {A}}}(\sigma _n, x)$ are real-rooted by Theorem 5.2. Although the latter appears to be a very special case of Conjecture 1.1, according to [5, Thm. 1.2], it would imply the conjecture if the following statement (which we have verified computationally for $n \le 20$) also turns out to be true.

Conjecture 5.3

The polynomial $h_{{\mathcal {A}}}(\sigma _{n-1}, x)$ interlaces $\theta _{{\mathcal {A}}}(\sigma _n, x)$ for every positive integer n.

Remark 5.4

The polynomial $h_{{\mathcal {A}}}(\sigma _n, x) + x^n h_{{\mathcal {A}}}(\sigma _n, 1/x)$, shown to be real-rooted in the proof of Theorem 5.2, is equal to the h-polynomial of a flag triangulation of the $(n-1)$-dimensional sphere. Indeed, let $\Gamma =\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$, so that $h(\Gamma , x) = h_{{\mathcal {A}}}(\sigma _n, x)$. Then, in the notation of Sect. 3, in particular Remark 3.1, $\Delta = \Delta _{{\mathcal {A}}}(\Gamma )$ is a flag triangulation of the $(n-1)$-dimensional sphere and $h(\Delta , x) = h(\Gamma , x) + h^\circ (\Gamma , x)= h(\Gamma , x) + x^n h(\Gamma , 1/x) =h_{{\mathcal {A}}}(\sigma _n, x) + x^n h_{{\mathcal {A}}}(\sigma _n, 1/x)$.

Remark 5.5

The polynomial

$$\begin{aligned} {\bar{p}}_{{\mathcal {A}}}(\sigma _n, x):=\sum _{k=0}^n{\bar{p}}_{{\mathcal {A}}}(n,k) x^k =\sum _{k=0}^n c(n,k) x^k, \end{aligned}$$

where, as in the proof of Proposition 5.1, c(n, k) is the number of permutations in ${{\mathfrak {S}}}_n$ with excedance set equal to [k], was shown to be symmetric and unimodal in [13, Sect. 3]. For the first few values of n,

$$\begin{aligned} {\bar{p}}_{{\mathcal {A}}}(\sigma _n, x)= {\left\{ \begin{array}{ll} 1, &{} \text {if }\, n = 1 ,\\ 1 + x, &{} \text {if }\, n=2, \\ 1 + 3x + x^2, &{} \text {if }\, n=3, \\ 1 + 7x + 7x^2 + x^3, &{} \text {if }\, n=4, \\ 1 + 15 x + 31 x^2 + 15 x^3 + x^4, &{}\text {if }\, n=5 ,\\ 1 + 31 x + 115 x^2 + 115 x^3 + 31 x^4 + x^5,&{} \text {if }\, n=6 ,\\ 1 + 63 x + 391 x^2 + 675 x^3 + 391 x^4 + 63 x^5 +x^6, &{} \text {if }\, n=7. \end{array}\right. } \end{aligned}$$

The following statement is stronger than the real-rootedness of $h_{{\mathcal {A}}}(\sigma _n, x)$.

Conjecture 5.6

The polynomial ${\bar{p}}_{{\mathcal {A}}}(\sigma _n, x)$ is real-rooted and interlaces ${\bar{p}}_{{\mathcal {A}}}(\sigma _{n+1}, x)$ for every $n \in {{\mathbb {N}}}$. In particular, ${\bar{p}}_{{\mathcal {A}}}(\sigma _n, x)$ is $\gamma$-positive for every $n \in {{\mathbb {N}}}$.

5.2 The Local h-Polynomial

We now focus on the local h-polynomial $\ell _{{\mathcal {A}}}(\sigma _n, x)$ of the antiprism triangulation of $\sigma _n$. For the first few values of n,

$$\begin{aligned} \ell _{{\mathcal {A}}}(\sigma _n, x)= {\left\{ \begin{array}{ll} 1, &{} \text {if }\,n = 0 ,\\ 0, &{} \text {if }\,n = 1 ,\\ 2x, &{} \text {if }\,n=2, \\ 3x + 3x^2, &{} \text {if }\,n=3, \\ 4x + 30 x^2 + 4x^3, &{} \text {if }\,n=4 ,\\ 5x + 130 x^2 + 130 x^3 + 5x^4, &{}\text {if }\,n=5 ,\\ 6x + 435 x^2 + 1460 x^3 + 435 x^4 + 6x^5,&{} \text {if }\,n=6, \\ 7x + 1281 x^2 + 10535 x^3 + 10535 x^4 + 1281 x^5+ 7x^6,&{}\text {if }\,n=7. \end{array}\right. } \end{aligned}$$

We now provide a recurrence, combinatorial interpretations and formulas for the polynomials $\ell _{{\mathcal {A}}}(\sigma _n, x)$.

Proposition 5.7

• (a) We have

  $$\begin{aligned} \ell _{{\mathcal {A}}}(\sigma _n, x)=\sum _{k=0}^{n-1}{n \atopwithdelims ()k} \ell _{{\mathcal {A}}}(\sigma _k, x)( (1+x)^{n-k} - 1 - x^{n-k}) \end{aligned}$$

  (15)

  for every positive integer n. In particular, $\ell _{{\mathcal {A}}}(\sigma _n, x)$ is unimodal for every $n\in {{\mathbb {N}}}$.

• (b) The coefficient of $x^k$ in $\ell _{{\mathcal {A}}}(\sigma _n, x)$ is equal to:

• the number of proper multi-pointed ordered set partitions of [n] of weight k,

• the number of ways to choose an ordered set partition $\pi$ of [n] and to color k elements of [n] black and the remaining $n-k$ white, so that no block of $\pi$ is monochromatic,

• the number of ordered set partitions $(B_1, B_2,\ldots ,B_m)$ of [n] having an even number of blocks for which the union $\bigcup _{i=1}^{m/2}B_i$ has exactly k elements,

• ${n \atopwithdelims ()k}$ times the number of derangements in ${{\mathfrak {S}}}_n$ with excedance set equal to [k],

• the explicit expression

  $$\begin{aligned} {n \atopwithdelims ()k} \sum _{j \ge 1} (j!)^2 S(k,j) S(n-k,j), \end{aligned}$$

  where S(n, k) are Stirling numbers of the second kind.

Proof

The recurrence of part (a) follows from Proposition 3.3, as a special case of (5). The unimodality of $\ell _{{\mathcal {A}}}(\sigma _n, x)$ follows directly from the recurrence by induction on n (and, alternatively, from the regularity of the antiprism triangulation of the simplex; see the proof of Proposition 7.2).

For part (b), the first interpretation was already shown in the proof of Proposition 5.1 and the second is a restatement of the first. The third interpretation follows from the first and the proof of the corresponding result of Proposition 5.1 by noting that in the provided bijection the set $[n] \setminus S$ is always empty. Furthermore, the fifth interpretation follows from the second one since there are ${n \atopwithdelims ()k}$ ways to choose the k black elements of [n] and for every such choice and every $j \ge 1$, there are $j! S(k,j)\cdot j! S(n-k,j)$ ways to choose an ordered partition of [n] with j blocks, none of which is monochromatic.

Finally, we deduce the fourth interpretation from the corresponding result of part (b) of Proposition 5.1. Let us use the notation adopted in the proof of that proposition, write $\ell _{{\mathcal {A}}}(\sigma _n, x) = \sum _{k=0}^n \ell _{{\mathcal {A}}}(n,k) x^k$ for $n \in {{\mathbb {N}}}$ and set

$$\begin{aligned} \ell _{{\mathcal {A}}}(n,k)={n \atopwithdelims ()k} {\bar{\ell }}_{{\mathcal {A}}}(n,k). \end{aligned}$$

Then, by the second interpretation, considering the elements $1, 2,\ldots ,k$ colored black and the other elements of [n] colored white, ${\bar{\ell }}_{{\mathcal {A}}}(n,k)$ is equal to the number of ordered set partitions of [n] with no monochromatic block. By Proposition 5.1, under the same coloring convention, ${\bar{p}}_{{\mathcal {A}}}(n,k)$ is equal to the number of ways to choose a set $[k] \subseteq S \subseteq [n]$ and an ordered set partition of S with no monochromatic block. These interpretations imply that

$$\begin{aligned} {\bar{p}}_{{\mathcal {A}}}(n,k)=\sum _{i=0}^{n-k} {n-k\atopwithdelims ()i} {\bar{\ell }}_{{\mathcal {A}}}(n-i,k) \end{aligned}$$

for all n, k. Denoting by d(n, k) the number of derangements in ${{\mathfrak {S}}}_n$ with excedance set equal to [k], it should also be clear that

$$\begin{aligned} c(n,k)=\sum _{i=0}^{n-k} {n-k \atopwithdelims ()i} d(n-i,k) \end{aligned}$$

for all n, k. By Proposition 5.1, we have ${\bar{p}}_{{\mathcal {A}}}(n,k) = c(n,k)$ for all n, k. Therefore, the two expressions for these numbers above and an easy induction show that ${\bar{\ell }}_{{\mathcal {A}}}(n,k) =d(n,k)$ for all n, k and the proof follows. $\square$

Following notation introduced in the previous proof, we set ${\bar{\ell }}_{{\mathcal {A}}}(\sigma _n, x) := \sum _{k=0}^n {\bar{\ell }}_{{\mathcal {A}}}(n,k) x^k$. We note that, since the polynomial $\ell _{{\mathcal {A}}}(\sigma _n, x)$ is symmetric with center of symmetry n/2, so is ${\bar{\ell }}_{{\mathcal {A}}}(\sigma _n, x)$.

Conjecture 5.8

• (a) The polynomial $\ell _{{\mathcal {A}}}(\sigma _n, x)$ is real-rooted and interlaces $\ell _{{\mathcal {A}}}(\sigma _{n{+}1}, x)$ for every $n \in {{\mathbb {N}}}$.

• (b) The polynomial ${\bar{\ell }}_{{\mathcal {A}}}(\sigma _n, x)$ is real-rooted and interlaces ${\bar{\ell }}_{{\mathcal {A}}}(\sigma _{n+1},x)$ for every $n \in {{\mathbb {N}}}$. In particular, ${\bar{\ell }}_{{\mathcal {A}}}(\sigma _n, x)$ is $\gamma$-positive for every $n \in {{\mathbb {N}}}$.

The following statement confirms a general conjecture of [2], claiming that all flag triangulations of simplices have $\gamma$-positive local h-polynomials, in the special case of antiprism triangulations and provides evidence in favor of Conjecture 5.8(a). The $\gamma$-positivity of $\ell _{{\mathcal {A}}}(\sigma _n, x)$ follows from that of the polynomial $\theta _{{\mathcal {A}}}(\sigma _n, x) := h_{{\mathcal {A}}}(\sigma _n, x) -h_{{\mathcal {A}}}(\partial \sigma _n, x)$, which appeared in Conjecture 5.3 and [20, Thm. 4.4].

Proposition 5.9

The polynomial $\ell _{{\mathcal {A}}}(\sigma _n, x)$ is $\gamma$-positive for every $n \in {{\mathbb {N}}}$.

Proof

[20, Thm. 4.4] applied to $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ asserts that

$$\begin{aligned} \ell _{{\mathcal {A}}}(\sigma _n, x)=\sum _{k=0}^n{n \atopwithdelims ()k} \theta _{{\mathcal {A}}}(\sigma _k, x) d_{n-k}(x), \end{aligned}$$

where $d_n(x)$ is the nth derangement polynomial discussed in Sect. 2.2. The polynomial $\theta _{{\mathcal {A}}}(\sigma _{k}, x)$ is symmetric, with center of symmetry k/2, and, as discussed after the proof of Theorem 5.2, it has nonnegative coefficients and only real roots. As a result, it is $\gamma$-positive, with center of symmetry k/2. The same property is shared by the derangement polynomial $d_k(x)$; see [3, Thm. 2.13]. Therefore, the right-hand side of the previous formula for $\ell _{{\mathcal {A}}}(\sigma _n, x)$ is a sum of $\gamma$-positive polynomials, each with center of symmetry $k/2 + (n-k)/2 = n/2$, and the proof follows. $\square$

A combinatorial interpretation of $\theta _{{\mathcal {A}}}(\sigma _n, x)$ can be deduced from Proposition 5.7.

Corollary 5.10

The coefficient of $x^k$ in $\theta _{{\mathcal {A}}}(\sigma _n, x)$ equals the number of ways to choose an ordered set partition $\pi$ of [n] and to color k elements of [n] black and the remaining $n-k$ white, so that no block of $\pi$ is monochromatic and there is a black element which is larger than a white element in the last block of $\pi$.

Proof

As a consequence of [20, Lem. 4.1] (and as already discussed in the proof of Proposition 3.3), we have

$$\begin{aligned} \theta _{{\mathcal {A}}}(\sigma _n, x)= \ell _{{\mathcal {A}}}(\sigma _n,x) - \sum _{m=0}^{n-2} {n \atopwithdelims ()m}\ell _{{\mathcal {A}}}(\sigma _m, x)(x + x^2 + \dots + x^{n-m-1}) \end{aligned}$$

for every positive integer n. By the second interpretation of $\ell _{{\mathcal {A}}}(\sigma _n, x)$ provided by Proposition 5.7 (b), the coefficient of $x^k$ in the sum on the right-hand side is equal to the number of ways to choose an ordered set partition $\pi$ of [n] and to color k elements of [n] black and the remaining $n-k$ white, so that no block of $\pi$ is monochromatic and every black element in the last block of $\pi$ is smaller than every white element of that block. Thus, the proposed interpretation of $\theta _{{\mathcal {A}}}(\sigma _n, x)$ follows from the previous equation and Proposition 5.7. $\square$

5.3 Face-Vector Transformations

The general results of [5] on uniform triangulations of simplicial complexes imply that there exist nonnegative integers $q_{{\mathcal {A}}}(n,k)$ and $p_{{\mathcal {A}}}(n,k,j)$ for $n, k, j \in {{\mathbb {N}}}$ with $k, j \le n$ such that

$$\begin{aligned} f_{j-1}(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))&= \sum _{k=j}^n q_{{\mathcal {A}}}(k,j) f_{k-1}(\Delta )\quad \text {and}\nonumber \\ h_j(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))&=\sum _{k=0}^n p_{{\mathcal {A}}}(n,k,j) h_k(\Delta ) \end{aligned}$$

(16)

for every $(n-1)$-dimensional simplicial complex $\Delta$ and every $j \in \{0, 1,\dots ,n\}$. The former equation is easy to explain; a simple counting argument (see the proof of [5, Thm. 4.1]) shows its validity when $q_{{\mathcal {A}}}(n,k)$ is defined as the number of $(k-1)$-dimensional faces in the interior of the antiprism triangulation of $\sigma _n$. This yields the following statement.

Proposition 5.11

For all integers $n \ge 1$ and $k \in \{0,1,\dots ,n\}$, $q_{{\mathcal {A}}}(n,k)$ is equal to the number of multi-pointed ordered set partitions of [n] of weight k. Moreover, we have the explicit formula

$$\begin{aligned} q_{{\mathcal {A}}}(n,k)= {n \atopwithdelims ()k} \sum _{j=0}^k j! S(k,j) j^{n-k} \end{aligned}$$

where, as usual, S(k, j) is a Stirling number of the second kind.

Proof

The proposed combinatorial interpretation follows from our previous discussion and that in Sect. 4. To verify the formula, we note that there are ${n \atopwithdelims ()k} \cdot j! S(k,j)$ ways to choose a k-element subset S of [n] and an ordered partition of S with j blocks and, for each such choice there are $j^{n-k}$ ways to distribute the remaining $n-k$ elements of [n] in the blocks so as to form a multi-pointed ordered set partition of [n] with set of chosen elements equal to S. $\square$

Equation (16) and the nonnegativity of the coefficients $p_{{\mathcal {A}}}(n,k,j)$ which appear there are less obvious. Various interpretations, an explicit formula and a recurrence are given for these numbers in [5] in the general framework of uniform triangulations. In particular, as shown in [5, Cor. 5.6] (and originally by the second and third author of this paper), the recurrence

$$\begin{aligned} p_{{\mathcal {A}}}(n,k,j)= p_{{\mathcal {A}}}(n,k-1,j) +p_{{\mathcal {A}}}(n-1,k-1,j-1) - p_{{\mathcal {A}}}(n-1,k-1,j)\nonumber \\ \end{aligned}$$

(17)

holds for all $k, j \in \{0, 1,\dots ,n\}$ with $k \ge 1$. We will also keep in mind that $p_{{\mathcal {A}}}(n,0,j) = p_{{\mathcal {A}}}(n,j)$ is the coefficient of $x^j$ in $h_{{\mathcal {A}}}(\sigma _n, x)$. This observation is the special case $\Delta = \sigma _n$ of (16). The following combinatorial interpretations of $p_{{\mathcal {A}}}(n,k,j)$ generalize some of those given for $p_{{\mathcal {A}}}(n,k)$ in Proposition 5.1.

Proposition 5.12

For all integers $n \ge 1$ and $k \in \{0, 1,\dots ,n\}$, $p_{{\mathcal {A}}}(n,k,j)$ is equal to:

• the number of ways to choose a set $[k] \subseteq S \subseteq [n]$ and an ordered set partition $\pi$ of S and to color j elements of S black and the remaining elements white, so that the following condition holds: if a block B of $\pi$ is monochromatic, then

$\circ$:

B is the first block of $\pi$,

$\circ$:

$B \subseteq [k]$, and

$\circ$:

all elements of B are colored black;

• the number of ordered set partitions $(B_1,B_2,\dots ,B_m)$ of [n] for which the following conditions hold:

$\circ$:

if m is even, then $\bigcup _{i=1}^{\lfloor m/2\rfloor } B_i$ has exactly j elements, and

$\circ$:

if m is odd, then the union of $\bigcup _{i=1}^{\lfloor m/2 \rfloor } B_i$ and $B_m\cap [k]$ has exactly j elements.

Proof

Let Q(n, k, j) be the collection of triples of sets S, partitions of S and colorings of the elements of S described in the first proposed combinatorial interpretation of $p_{{\mathcal {A}}}(n,k,j)$ and let q(n, k, j) be the cardinality of Q(n, k, j). We will show that $p_{{\mathcal {A}}}(n,k,j) = q(n,k,j)$. This is true for $k=0$ by the first combinatorial interpretation of $p_{{\mathcal {A}}}(n,j) = p_{{\mathcal {A}}}(n,0,j)$ provided by Proposition 5.1. Thus, it suffices to show that the numbers q(n, k, j) satisfy recurrence (17) or, equivalently, that

$$\begin{aligned} q(n,k-1,j)=q(n,k,j) + q(n-1,k-1,j)-q(n-1,k-1,j-1) \end{aligned}$$

for $k \ge 1$. By definition, $q(n,k-1,j)$ is the number of triples in $Q(n,k-1,j)$, each one consisting of a set S, a partition of S and a coloring of the elements of S having certain properties. Clearly, we have $k\notin S$ for exactly $q(n-1,k-1,j)$ of these triples. Moreover, we have $k \in S$ for exactly $q(n,k,j)-q(n-1,k-1,j-1)$ of them, since for exactly $q(n-1,k-1,j-1)$ of the triples in Q(n, k, j) there is a monochromatic block which contains k. This proves the first interpretation.

As an alternative proof, by computing the coefficient of $x^j$ in the right-hand side of [5, (12)] we get the explicit expression

$$\begin{aligned} p_{{\mathcal {A}}}(n,k,j)= \sum _{r=0}^n \sum _{i=0}^j {k \atopwithdelims ()i} {n-k \atopwithdelims ()n-r-i} \ell _{{\mathcal {A}}}(r,j-i). \end{aligned}$$

The double sum on the right side is also equal to q(n, k, j) since to choose a set S, a partition $\pi$ and a coloring as in the statement of the proposition so that a monochromatic block B has exactly i elements, if present, and there is a total of r elements in the remaining blocks of $\pi$, there are ${k \atopwithdelims ()i}{n-k \atopwithdelims ()n-r-i}$ ways to choose the i elements of B and the $n-r-i$ elements of [n] not in the blocks of $\pi$ and for each such choice, by Proposition 5.7, there are $\ell _{{\mathcal {A}}}(r,j-i)$ ways to choose the blocks of $\pi$ other than B. To prove the second interpretation, it suffices to find a bijection from Q(n, k, j) to the collection of ordered set partitions described there. Such a bijection can be constructed as an obvious extension of the one provided in the proof of Proposition 5.1 for the special case $k=0$. More specifically, the elements of the monochromatic block, if present, of a colored ordered partition in Q(n, k, j) should be included in the last block of the ordered partition produced by the bijection; the details are left to the interested reader. $\square$

6 Lefschetz Properties

This section reviews basic definitions and background on Lefschetz properties for simplicial complexes and includes some preliminary technical results, which will be applied in the following section in the context of antiprism triangulations.

Let $\Delta$ be an $(n-1)$-dimensional simplicial complex which is Cohen–Macaulay over an infinite field ${{\mathbb {F}}}$ and let $s \le n$ be a positive integer. We say that $\Delta$ has the s-Lefschetz property (over ${{\mathbb {F}}}$) if there exists a linear system of parameters $\Theta$ for ${{\mathbb {F}}}[\Delta ]$ and a linear form $\omega \in {{\mathbb {F}}}[\Delta ]$, such that the multiplication maps

$$\begin{aligned} \cdot \omega ^{s-2i}:({{\mathbb {F}}}[\Delta ]/\Theta {{\mathbb {F}}}[\Delta ])_i\rightarrow ({{\mathbb {F}}}[\Delta ]/\Theta {{\mathbb {F}}}[\Delta ])_{s-i} \end{aligned}$$

are injective for all $0 \le i \le \lfloor (s-1)/2 \rfloor$. Following [22], we call $\Delta$ almost strong Lefschetz (over ${{\mathbb {F}}}$) if it has the $(n-1)$-Lefschetz property. Usually, if $\Delta$ has the n-Lefschetz property and, additionally, the above multiplication maps are isomorphisms, one says that $\Delta$ is strong Lefschetz (or $\Delta$ has the strong Lefschetz property). Lefschetz properties are an important tool in the area of face enumeration of simplicial complexes; various classes of simplicial complexes, the most prominent probably being boundary complexes of simplicial polytopes [34], are known to have such properties. Barycentric subdivisions of shellable simplicial complexes were shown in [22] to be almost strong Lefschetz over ${{\mathbb {F}}}$.

The proof of Theorem 1.3, which follows similar lines, is fairly elementary and does not require heavy machinery. Since it is rather lengthy, we now explain the main steps to guide the reader through it. The main idea to show that the antiprism triangulation of a shellable simplicial complex is almost strong Lefschetz is to use induction on the number of facets and the dimension. The inductive step (see Theorem 7.6) essentially follows from a short exact sequence and some standard arguments for commutative diagrams. The hardest part is the base of the induction, namely to prove the almost strong Lefschetz property for the antiprism triangulation of a simplex (see Theorem 7.4). The main idea there is to show that $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ is almost strong Lefschetz if and only if so is its boundary complex (Proposition 7.2). Since the boundary complex can be realized as the boundary complex of a simplicial polytope (Proposition 7.3), the claim follows from [34]. To prove Proposition 7.2, we provide an explicit sequence of edge contractions which preserve the almost strong Lefschetz property and transform $\partial \mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ into $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$. It is known that Lefschetz properties behave well if the mentioned edge contractions are sufficiently nice. Before we can make this more precise, we need to introduce some definitions.

Let $\Delta$ be a simplicial complex on a vertex set V which is endowed with a total order <. Given an edge $e=\{a,b\}\in \Delta$ with $a<b$, the contraction ${{\mathcal {C}}}_\Delta (e)$ of $\Delta$ with respect to e is the simplicial complex on the vertex set $V\setminus \{b\}$ which is obtained from $\Delta$ by identifying vertices a and b, i.e.,

$$\begin{aligned} {{\mathcal {C}}}_\Delta (e) := \{F \in \Delta :b \notin F\}\cup \{(F \setminus \{b\})\cup \{a\}:b \in F \in \Delta \}. \end{aligned}$$

We say that $\Delta$ satisfies the Link Condition with respect to e if

$$\begin{aligned} \mathrm{link}_\Delta (e)=\mathrm{link}_\Delta (\{a\}) \cap \mathrm{link}_\Delta (\{b\}). \end{aligned}$$

Proposition 6.1

Let ${{\mathbb {F}}}$ be an infinite field and let $\Delta$ be an $(n-1)$-dimensional Cohen–Macaulay complex over ${{\mathbb {F}}}$. Suppose $\Delta$ satisfies the Link Condition with respect to an edge $e \in \Delta$. If ${{\mathcal {C}}}_\Delta (e)$ is Cohen–Macaulay over ${{\mathbb {F}}}$ of dimension $n-1$ and both $\mathrm{link}_\Delta (e)$ and ${{\mathcal {C}}}_\Delta (e)$ are strong (respectively, almost strong) Lefschetz over ${{\mathbb {F}}}$, then so is $\Delta$.

We note that since, e.g., by Reisner’s criterion [31], the Cohen–Macaulay property is inherited by links, it is guaranteed that $\mathrm{link}_{\Delta }(e)$ is Cohen–Macaulay. On the contrary, the contraction of an edge does not even need to be pure. Proposition 6.1 was proved in [27, Prop. 3.2] for the strong Lefschetz property if ${{\mathbb {F}}}$ is an arbitrary infinite field of any characteristic (see also [6, Thm. 2.2] for the same result in characteristic zero). Since it is not entirely obvious, although reasonable to believe, that the proofs go through for the almost strong Lefschetz property, we sketch the main steps of the proof.

Proof

Let V be the vertex set of $\Delta$ and $e = \{a,b\} \in \Delta$, where $a < b$. Following [27], we consider the shift operator

$$\begin{aligned} C_e(F)= {\left\{ \begin{array}{ll} (F \setminus \{b\}) \cup \{a\}, &{}\text { if }\, b \in F, a \notin F,\,\text {and }\, (F \setminus \{b\}) \cup \{a\}\notin \Delta ,\\ F, &{}\text { otherwise,} \end{array}\right. } \end{aligned}$$

which goes back to [14], and set $\mathrm{shift}_e(\Delta ) = \{C_e(F): F \in \Delta \}$. Since the Link Condition holds for e, [27, Lem. 2.1] implies that

$$\begin{aligned} \mathrm{shift}_e(\Delta )= {{\mathcal {C}}}_\Delta (e) \cup \{\{b\}\cup F:F \in a *\mathrm{link}_\Delta (e)\}. \end{aligned}$$

This implies that $\mathrm{shift}_e(\Delta ) = {{\mathcal {C}}}_\Delta (e)\cup \mathrm{star}_\Delta (e)$ and, as a result, there is the exact sequence of ${{\mathbb {F}}}[x_v{:}\,v \in V]$-modules

$$\begin{aligned} 0 \rightarrow {{\mathbb {F}}} [\mathrm{star}_\Delta (e)] \rightarrow {{\mathbb {F}}} [\mathrm{shift}_e(\Delta )]\rightarrow {{\mathbb {F}}} [{{\mathcal {C}}}_\Delta (e)] \rightarrow 0, \end{aligned}$$

(18)

where the first map is given by multiplication with $x_b$. Since $\mathrm{link}_\Delta (e)$ is $(n-3)$-Lefschetz, so is $\mathrm{star}_\Delta (e)$ (see, e.g., [22, Lem. 2.1]). Hence, there exist $\Theta =(\theta _1,\theta _2,\dots ,\theta _n)$ and a linear form $\omega \in {{\mathbb {F}}}[x_v{:}\,v\in V]$ such that $\Theta$ is an l.s.o.p. for ${{\mathbb {F}}} [\mathrm{star}_\Delta (e)]$, ${{\mathbb {F}}} [\mathrm{shift}_e(\Delta )]$, and ${{\mathbb {F}}} [{{\mathcal {C}}}_\Delta (e)]$ simultaneously, and $\omega$ is an $(n-1)$- and $(n-3)$-Lefschetz element for ${{\mathcal {C}}}_\Delta (e)$ and $\mathrm{star}_\Delta (e)$, respectively, with respect to $\Theta$. Hence, from (18) we get the commutative diagram

$$\begin{aligned} \begin{array}{ccccccccc} 0&{}\rightarrow &{} {{\mathbb {F}}}(\mathrm{star}_\Delta (e))_{\ell -1} &{}\rightarrow &{} {{\mathbb {F}}}(\mathrm{shift}_e(\Delta ))_\ell &{}\rightarrow &{} {{\mathbb {F}}}({{\mathcal {C}}}_\Delta (e))_\ell &{}\rightarrow &{} 0\\ &{} &{} &{} &{} &{} &{} &{}&{}\\ &{} &{} \downarrow \omega ^{n-3-2(\ell -1)}&{} &{}\ \ \downarrow \omega ^{n-2\ell -1}&{} &{} \ \downarrow \omega ^{n-2\ell -1}&{} &{} \\ &{} &{} &{} &{} &{} &{} &{}&{}\\ &{}&{} {{\mathbb {F}}}(\mathrm{star}_\Delta (e))_{n-2-\ell } &{}\rightarrow &{} {{\mathbb {F}}}(\mathrm{shift}_e(\Delta ))_{n-1-\ell }&{}\rightarrow &{} {{\mathbb {F}}}({{\mathcal {C}}}_\Delta (e))_{n-1-\ell }&{}\rightarrow &{}0 \end{array} \end{aligned}$$

for $0\le \ell \le \lfloor (n-1)/2\rfloor$, where we have written ${{\mathbb {F}}}(\mathrm{star}_\Delta (e))$ for ${{\mathbb {F}}}[\mathrm{star}_\Delta (e)]/\Theta$ and similarly for ${{\mathbb {F}}}(\mathrm{shift}_e(\Delta ))$ and ${{\mathbb {F}}}({{\mathcal {C}}}_\Delta (e))$, and we have set ${{\mathbb {F}}}(\mathrm{star}_\Delta (e))_{-1}=0$.

Since the left and right vertical maps are injective by assumption, so is the middle map by the snake lemma. Thus, $\mathrm{shift}_e(\Delta )$ has the almost strong Lefschetz property. Moreover, since $\Delta$ satisfies the Link Condition with respect to e, we conclude from [27, Lem. 2.2] that $I_{\mathrm{shift}_e(\Delta )}$ is an initial ideal of $I_\Delta$ with respect to a certain term order. Finally, $\Delta$ has the $(n-1)$-Lefschetz property by [40, Prop. 2.9]. Wiebe’s orginal result was for ${\mathfrak {m}}$-primary homogeneous ideals having the strong Lefschetz property. However, the same proof works in our setting. $\square$

Given a simplicial complex $\Delta$ and face $U = \{u_1, u_2,\dots ,u_n\} \in \Delta$, we say that $\Delta$ satisfies the strong Link Condition with respect to U if

$$\begin{aligned} \mathrm{link}_\Delta (F)\cap \mathrm{link}_\Delta (G)=\mathrm{link}_\Delta (F\cup G) \end{aligned}$$

(19)

for all $F,G\subseteq U$ with $F \cap G = \varnothing$. Note that, in this case, (19) holds for all (not necessarily disjoint) subsets $F,G\subseteq U$. The following technical lemma relates the strong Link Condition to the usual Link Condition.

Lemma 6.2

Let $\Delta$ be a simplicial complex which satisfies the strong Link Condition with respect to the face $U = \{u_1, u_2,\dots ,u_n\}$. Then, ${{\mathcal {C}}}_\Delta (\{u_{n-1},u_n\})$ satisfies the strong Link Condition with respect to $U \setminus \{u_n\}$. In particular, all edges of $2^U$ can be contracted successively so that at each step, the Link Condition is satisfied with respect to the contracted edge.

Proof

To simplify notation, we set $\Delta ' = {{\mathcal {C}}}_\Delta (\{u_{n-1},u_n\})$ and let $U' = U \setminus \{u_n\} \in \Delta '$ be the contraction of U. We consider disjoint sets $F, G \subseteq U'$ and observe that, by definition of $\Delta '$,

$$\begin{aligned} \begin{aligned} \mathrm{link}_{\Delta '}(F)&=\{H \in \mathrm{link}_\Delta (F):u_n\notin H\} \\&\,\,\,\quad \cup \{(H \setminus \{u_n\}) \cup \{u_{n-1}\}:u_n\in H\in \mathrm{link}_\Delta (F),\ u_{n-1}\notin H\} \end{aligned} \end{aligned}$$

(20)

if $u_{n-1} \notin F$, and

$$\begin{aligned} \begin{aligned} \mathrm{link}_{\Delta '}(F)&=\{H \in \mathrm{link}_\Delta (F):u_n\notin H\} \\&\,\,\,\quad \cup \{ H \setminus \{u_{n-1}\}: H \in \mathrm{link}_{\Delta }((F \setminus \{u_{n-1}\})\cup \{u_n\}) \} \end{aligned} \end{aligned}$$

(21)

if $u_{n-1}\in F$. The inclusion

$$\begin{aligned} \mathrm{link}_{\Delta '}(F\cup G) \subseteq \mathrm{link}_{\Delta '}(F) \cap \mathrm{link}_{\Delta '}(G) \end{aligned}$$

holds trivially. To prove the reverse inclusion, we consider a face $H \in \mathrm{link}_{\Delta '}(F) \cap \mathrm{link}_{\Delta '}(G)$ and distinguish two cases.

Case 1: $u_{n-1}\notin F\cup G$. By (20) for $\mathrm{link}_{\Delta '}(F)$ and $\mathrm{link}_{\Delta '}(G)$, four cases can occur. First, assume that $H \in \mathrm{link}_\Delta (F) \cap \mathrm{link}_\Delta (G)$. Then, by the strong Link Condition, $H\in \mathrm{link}_{\Delta }(F\cup G)$ and hence $H \in \mathrm{link}_{\Delta '}(F\cup G)$ by (20). Next, suppose that $H = (H' \setminus \{u_n\})\cup \{u_{n-1}\}$ for some $H' \in \mathrm{link}_\Delta (F)\cap \mathrm{link}_\Delta (G)$ with $u_n \in H'$, $u_{n-1}\notin H$. Then, the strong Link Condition implies that $H' \in \mathrm{link}_\Delta (F\cup G)$ and hence $H \in \mathrm{link}_{\Delta '}(F\cup G)$ by (20). Finally, assume that $H \in \mathrm{link}_\Delta (F)$ and that $H = (H' \setminus \{u_n\}) \cup \{u_{n-1}\}$ for some $H' \in \mathrm{link}_\Delta (G)$ with $u_n \in H'$ and $u_{n-1} \notin H'$. Then, $F\cup H\in \Delta$ and $G \cup (H \setminus \{u_{n-1}\}) \cup \{u_n\} \in \Delta$. From the strong Link Condition, we conclude that $H \setminus \{u_{n-1}\} \in \mathrm{link}_\Delta (F\cup G\cup \{u_n\})$, i.e., $(H \setminus \{u_{n-1}\}) \cup \{u_n\} \in \mathrm{link}_{\Delta }(F\cup G)$. This, together with (20) applied to $\mathrm{link}_{\Delta '}(F\cup G)$, implies again that $H\in \mathrm{link}_{\Delta '}(F\cup G)$. The remaining case follows by symmetry from the previous one.

Case 2: $u_{n-1}\in F\cup G$. Since $F \cap G = \varnothing$, we may assume without loss of generality that $u_{n-1} \in F$ and $u_{n-1} \notin G$. Since $H \in \mathrm{link}_{\Delta '}(F)$ and $u_{n-1} \in F$, we must have $u_{n-1} \notin H$. From (20), which applies to $\mathrm{link}_{\Delta '}(G)$, and the fact that $u_{n-1} \notin H$ we conclude that $H \in \mathrm{link}_\Delta (G)$. Two subcases can occur. Suppose first that $H \in \mathrm{link}_\Delta (F)$. Then, the strong Link Condition implies that $H \in \mathrm{link}_\Delta (F\cup G)$ and thus $H \in \mathrm{link}_{\Delta '}(F\cup G)$ by (21), applied to $\mathrm{link}_{\Delta '}(F \cup G)$. Otherwise, $H \notin \mathrm{link}_\Delta (F)$ and we must have $H \in \mathrm{link}_{\Delta }((F \setminus \{u_{n-1}\}) \cup \{u_n\})$ by (21). This implies that $H \cup (F \setminus \{u_{n-1}\}) \cup \{u_n\} \in \Delta$. Since $H \cup G\in \Delta$, from the strong Link Condition we infer that $H \cup (F \setminus \{u_{n-1}\}) \cup \{u_n\} \cup G \in \Delta$. Since $u_{n-1} \in F$, we conclude that $H \cup F \cup G \in \Delta '$ and so, once again, $H \in \mathrm{link}_{\Delta '}(F\cup G)$. This completes the proof of the first statement.

For the second statement we note that if $\Delta$ satisfies the strong Link Condition with respect to U, then it also satisfies the Link Condition with respect to any edge of $2^U$. Hence, the claim follows from successive applications of the first statement. $\square$

7 Lefschetz Properties of Antiprism Triangulations

This section aims to prove Theorem 1.3, i.e., to show that the antiprism triangulation of any shellable simplicial complex has the almost strong Lefschetz property over ${{\mathbb {R}}}$. From this we will infer that the h-vector of the antiprism triangulation of any Cohen–Macaulay simplicial complex is unimodal and will locate its peak.

We first show that the antiprism triangulation of the simplex $\sigma _n$ has the almost strong Lefschetz property over ${{\mathbb {R}}}$. The next lemma will be crucial. Recall that the (strong) Link Condition was defined in Sect. 6.

Lemma 7.1

Consider an $(n-1)$-dimensional simplex $2^V$ and a triangulation $\Delta$ of its boundary complex $\partial (2^V)$. Then, the antiprism $\Gamma _{{\mathcal {A}}}(\Delta )$ satisfies the strong Link Condition with respect to the set of its interior vertices. In particular, $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ satisfies the strong Link Condition with respect to the set of its interior vertices.

Proof

Set $V = \{v_1,v_2,\dots ,v_n\}$ and let $U = \{u_1,u_2,\dots ,u_n\}$ be the set of interior vertices of $\Gamma _{{\mathcal {A}}}(\Delta )$, linearly ordered so that $\{u_i, v_i\}\notin \Gamma _{{\mathcal {A}}}(\Delta )$ for every $i \in [n]$.

Let $E = \{u_i : i \in I\} \subseteq U$ for some $I \subseteq [n]$ be nonempty and let ${\bar{E}}=\{u_j:j\in [n]\setminus I\}$ and ${\bar{F}} = \{v_j :j \in [n]\setminus I\}$ be the faces of the simplices $2^U$ and $2^V$, respectively, which are complementary to E. Then, by definition of $\Gamma _{{\mathcal {A}}}(\Delta )$,

$$\begin{aligned} \mathrm{link}_{\Gamma _{{\mathcal {A}}}(\Delta )}(E)=\Delta _{{\mathcal {A}}}(\Delta _{{\bar{F}}}), \end{aligned}$$

where the new vertices added for the $\Delta _{{\mathcal {A}}}$ construction (see Remark 3.1) are the elements of ${\bar{E}}$ and $\Delta _{{\bar{F}}}$ is the restriction of $\Delta$ to the (proper) face ${\bar{F}} \in 2^V$. This directly implies that $\Gamma _{{\mathcal {A}}}(\Delta )$ satisfies the strong Link Condition with respect to U. $\square$

Given a Cohen–Macaulay simplicial complex $\Delta$ over a field ${{\mathbb {F}}}$, we say that the contraction of an edge $e \in \Delta$ is admissible over ${{\mathbb {F}}}$ if $\Delta$ satisfies the Link Condition with respect to e and $\mathrm{link}_{\Delta }(e)$ is strong Lefschetz over ${{\mathbb {F}}}$. The following proposition is, essentially, a consequence of Lemmas 6.2 and 7.1.

Proposition 7.2

There exists a sequence of admissible edge contractions over ${{\mathbb {R}}}$ which transforms $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ into the cone over its boundary. In particular, $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ is almost strong Lefschetz over ${{\mathbb {R}}}$, if $\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _{n}))$ is strong Lefschetz over ${{\mathbb {R}}}$.

Proof

As before, we let $V=\{v_1,\ldots ,v_n\}$ and $U =\{u_1,\ldots ,u_n\}$ be the vertices of $\sigma _n$ and the interior vertices of $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$, respectively. By Lemma 7.1, $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ satisfies the strong Link Condition with respect to U. Thus, using Lemma 6.2, we can successively contract edges from U, each satisfying the Link Condition, until we reach a single vertex u. The resulting complex is clearly the cone $u *\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$. If we can verify that the intermediate complexes, appearing in this sequence of contractions, are Cohen–Macaulay over ${{\mathbb {R}}}$ and that the links of the contracted edges are strong Lefschetz, then Proposition 6.1 implies that $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ is almost strong Lefschetz, if so is the cone $u *\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$.

To prove the missing statements, we use the fact that $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ can be constructed from $\sigma _n$ by crossing operations on its faces, starting at the facet V and moving to faces of lower dimension (see Sect. 4). From this it follows that the intermediate complexes can be constructed by first contracting the corresponding edges in the antiprism $\Gamma _{{\mathcal {A}}}(\partial (2^V))$ and then performing crossing operations on its boundary faces. The antiprism $\Gamma _{{\mathcal {A}}}(\partial (2^V))$ is a regular triangulation of $2^V$ and so is any subcomplex obtained from it by the performed edge contractions. Since, in addition, any crossing operation can be realized by a sequence of stellar subdivisions (see the proof of [7, Thm. 8]), which are well known to preserve regularity, we conclude that any intermediate complex in the sequence of edge contractions from $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ to the cone $u *\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$ is a regular triangulation of $2^V$ and, in particular, Cohen–Macaulay over ${{\mathbb {R}}}$. Moreover, the regularity of the intermediate complexes implies that the link of any interior edge that is contracted is a polytopal sphere and hence strong Lefschetz over ${{\mathbb {R}}}$ [34]. Using Proposition 6.1, we conclude that $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ is almost strong Lefschetz over ${{\mathbb {R}}}$, if so is $u *\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$. By [22, Lem. 2.1], this is the case if $\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$ is strong Lefschetz over ${{\mathbb {R}}}$. $\square$

The next statement suffices to conclude that $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ has the almost strong Lefschetz property over ${{\mathbb {R}}}$.

Proposition 7.3

The simplicial complex $\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$ is combinatorially isomorphic to the boundary complex of a simplicial polytope. In particular, it is strong Lefschetz over ${{\mathbb {R}}}$.

Proof

We use again the fact that $\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$ can be constructed from $\partial \sigma _n$ by a sequence of crossing operations (see Sect. 4). As already mentioned, it was shown in the proof of [7, Thm. 8] that every crossing operation can be expressed as a sequence of stellar subdivisions. Since those preserve polytopality, the first statement follows. The second follows from the first and [34]. $\square$

The next result follows by combining Propositions 7.2 and 7.3.

Theorem 7.4

The simplicial complex $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ is almost strong Lefschetz over ${{\mathbb {R}}}$.

Remark 7.5

Since the restriction of the antiprism triangulation $\mathrm{sd}_{{\mathcal {A}}}(\sigma _n)$ to a face F of $\sigma _n$ is the antiprism triangulation of $2^F$, we can apply the edge contractions from the proof of Proposition 7.2 to the subdivided faces of $\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$, ordered by decreasing dimension. Clearly, the simplicial complex obtained in this way is combinatorially isomorphic to the barycentric subdivision of $\partial \sigma _n$. Using similar arguments as in the proof of Proposition 7.2, one can show that all edge contractions are admissible. Indeed, let $\Delta '$ be the simplicial complex obtained from $\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$ after i edge contractions. Consider a face $F \in \sigma _n$ and let $\Delta '_F$ be the restriction of $\Delta '$ to F (which is the subcomplex of $\Delta '$ consisting of all faces with carrier contained in F). If $G \in \Delta '_F$ is a face having all vertices in the interior of $\Delta '_F$, then it can easily be verified that

$$\begin{aligned} \mathrm{link}_{\Delta '}(G) = \mathrm{link}_{\Delta '_F}(G)*\{\{u_{H_1},\ldots ,u_{H_r}\}:F\subsetneq H_1\subsetneq \ldots \subsetneq H_r\subsetneq [n]\}, \end{aligned}$$

(22)

where $u_H$ denotes the last interior vertex in the sequence of contractions of a face $H \in \sigma _n$. If G is the edge to be contracted in $\Delta '$, then the previous equation, combined with the proof of Proposition 7.2, implies that $\Delta '$ satisfies the Link Condition with respect to G. We further note that the second complex on the right-hand side of (22) is isomorphic to the barycentric subdivision of $\mathrm{link}_{\partial \sigma _n}(F)$, which itself is the barycentric subdivision of the boundary complex of an $(n-2-|F|)$-dimensional simplex. Thus, by [22, Prop. 2.3] and the proof of Proposition 7.2, both simplicial complexes on the right-hand side of (22) are strong Lefschetz over ${{\mathbb {R}}}$. From this fact and [6, Thm. 1.2 (i)], it follows that $\mathrm{link}_{\Delta '}(G)$ is strong Lefschetz over ${{\mathbb {R}}}$.

The previous discussion shows that there exists a sequence of admissible edge contractions transforming $\partial (\mathrm{sd}_{{\mathcal {A}}}(\sigma _n))$ into $\partial (\mathrm{sd}(\sigma _n))$. This provides another proof of the second statement of Proposition 7.3. Moreover, the analogous edge contraction can be applied to the edge links. This shows that the antiprism triangulation of $\partial \sigma _n$ is strongly edge decomposable (see [27, Defn. 1.1]), since so is the barycentric subdivision of $\partial \sigma _n$.

With Proposition 7.3 at hand, the key observation to complete the proof of the first statement of Theorem 1.3 is that the proof of [22, Thm. 1.1], showing that the barycentric subdivision of any shellable simplicial complex is almost strong Lefschetz over an infinite field (in particular, over ${{\mathbb {R}}}$), works for every uniform triangulation which fulfills this property for simplices. For the interested reader, and to keep this article as self-contained as possible, we provide a sketch of the proof.

Theorem 7.6

The complex $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ is almost strong Lefschetz over ${{\mathbb {R}}}$ for every shellable simplicial complex $\Delta$.

Proof

Let $\dim (\Delta ) = n-1$, as usual. The proof proceeds by double induction on n and the number of facets of $\Delta$. At the base of the induction, either $\Delta$ consists only of vertices, in which case there is nothing to show, or $\Delta$ is a simplex, in which case the result follows from Proposition 7.3.

For the inductive step we assume that $n \ge 2$, let V be the vertex set of $\Delta$ and let $A= {{\mathbb {R}}}[x_v{ :}\, v\in V]$. Consider a shelling $G_1,G_2,\dots ,G_m = G$ of $\Delta$ and set ${\widetilde{\Delta }}:=\langle G_1,\dots ,G_{m-1}\rangle$ and $\tau :={\widetilde{\Delta }}\cap 2^G$. There is the following exact sequence of A-modules:

$$\begin{aligned} 0\rightarrow {{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}(\Delta )]\rightarrow {{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}({\widetilde{\Delta }})]\oplus {{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}(2^G)]\rightarrow {{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}(\tau )]\rightarrow 0. \end{aligned}$$

(23)

One now chooses generic linear forms $\Theta =\theta _1, \theta _2,\dots ,\theta _n$ so that $\Theta$ is an l.s.o.p. for ${{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}(\Delta )]$, ${{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}({\widetilde{\Delta }})]$, and ${{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}(2^G)]$ simultaneously and $\theta _1,\theta _2,\dots ,\theta _{n-1}$ is an l.s.o.p. for ${{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}(\tau )]$. Dividing out by $\Theta$ in (23) gives rise to an exact sequence

$$\begin{aligned}\mathrm{Tor}_1({{\mathbb {R}}}[\mathrm{sd}_{{\mathcal {A}}}(\tau )],A/\Theta )&{\mathop {\rightarrow }\limits ^{\delta }} {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))\rightarrow {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}({\widetilde{\Delta }}))\oplus {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(2^G))\\&\rightarrow {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(\tau ))\rightarrow 0, \end{aligned}$$

where we have written ${{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))$ for ${{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}(\Delta )]/\Theta$ and similarly for ${{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}({\widetilde{\Delta }}))$, ${{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(\tau ))$, and ${{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(2^G))$. Next, one shows that $\mathrm{Tor}_1({{\mathbb {R}}} [\mathrm{sd}_{{\mathcal {A}}}(\tau )],A/\Theta )_i=0$ for $0 \le i \le \lfloor ({n-2})/{2}\rfloor$. This is done exactly as in the proof of [22, Thm. 1.1]. Since all maps in the previous exact sequence preserve the grading, one gets the commutative diagram

$$\begin{aligned} \begin{array}{ccccccc} {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))_i &{}\rightarrow &{} {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}({\widetilde{\Delta }}))_i\oplus {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(2^G))_i\\ &{} &{} &{} &{} &{} &{}\\ \downarrow \omega ^{n-2i-1}&{} &{}\ \ \downarrow (\omega ^{n-2i-1},\omega ^{n-2i-1})&{} &{} \\ &{} &{} &{} &{} &{} &{}\\ {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))_{n-1-i} &{}\rightarrow &{} {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}({\widetilde{\Delta }}))_{n-1-i}\oplus {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(2^G))_{n-1-i} \end{array} \end{aligned}$$

where $\omega$ is a degree one element in A. The induction hypothesis implies that the multiplication map on the right-hand side is injective for a generic $\omega$. One concludes that the multiplication

$$\begin{aligned} \omega ^{n-2i-1}:\,{{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))_i\rightarrow {{\mathbb {R}}}(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))_{n-1-i} \end{aligned}$$

is injective for $0 \le i\le \lfloor ({n-2})/{2}\rfloor$ and the proof follows. $\square$

To complete the proof of Theorem 1.3, we need the following properties of the numbers $p_{{\mathcal {A}}}(n,k,j)$, discussed in Sect. 5.3.

Lemma 7.7

Let $n,k,j\in {{\mathbb {N}}}$ with $k,j\le n$. We have

$$\begin{aligned} p_{{\mathcal {A}}}(n,k,j)&=p_{{\mathcal {A}}}(n,n-k,n-j), \end{aligned}$$

(24)

$$\begin{aligned} p_{{\mathcal {A}}}(n,k,0)&\le p_{{\mathcal {A}}}(n,k,1) \le \ldots \le p_{{\mathcal {A}}}(n,k,\lfloor n/2\rfloor ),\quad \text {and}\nonumber \\ p_{{\mathcal {A}}}(n,k,n)&\le p_{{\mathcal {A}}}(n,k,n-1)\le \ldots \le p_{{\mathcal {A}}}(n,k,\lceil n/2\rceil ). \end{aligned}$$

(25)

Proof

Equation (24) follows from [5, Prop. 4.6 (a)]; let us provide here a direct bijective proof. Let Q(n, k, j) be defined as in the proof of Proposition 5.12, so that $p_{{\mathcal {A}}}(n,k,j) =|Q(n,k,j)|$. Also, let ${\widetilde{Q}}(n,n-k,n-j)$ be the set of triples defining $Q(n,n-k,n-j)$, except that the set S which is partitioned satisfies $\{k+1,\dots ,n\} \subseteq S \subseteq [n]$, instead of $[n-k] \subseteq S \subseteq [n]$, and that the monochromatic block, if present, must be contained in $\{k+1,\ldots ,n\}$. Since, clearly, $|{\widetilde{Q}}(n,n-k,n-j)| = p_{{\mathcal {A}}}(n,n-k,n-j)$, to prove (24) it suffices to find a bijection from Q(n, k, j) to ${\widetilde{Q}}(n,n-k,n-j)$. Given a triple in Q(n, k, j), consisting of an ordered partition of $[k]\subseteq S \subseteq [n]$ and a suitable coloring of the elements of S, we construct a triple in ${\widetilde{Q}}(n,n-k,n-j)$ as follows. We first switch the colors of all elements of S from white to black and vice versa. If the first block was monochromatic, we delete it from the partition. The block $[n] \setminus S$, if nonempty, is then added to the constructed ordered partition as its new first block, with all its elements colored black. We leave to the reader to verify that this process gives a well-defined map. The inverse map can be constructed by the same procedure, applied to the triples in ${\widetilde{Q}}(n,n-k,n-j)$.

For (25), we note that the proof of [22, Cor. 4.4] works, with the symmetry of [11, Lem. 2.5] replaced by that of (24). $\square$

We recall that a sequence $(a_0, a_1,\dots ,a_s) \in {{\mathbb {N}}}^{s+1}$ is an M-sequence if it is the Hilbert function of a standard graded ${{\mathbb {F}}}$-algebra, where ${{\mathbb {F}}}$ is a field. Macaulay [24] provided a characterization of M-sequences by means of numerical conditions (see, e.g., [37]). Theorem 7.6 has the following numerical consequences for the h-vector of the antiprism triangulation of a Cohen–Macaulay complex.

Corollary 7.8

Let $\Delta$ be a Cohen–Macaulay simplicial complex of dimension $n\!-\!1$ and let $g(\mathrm{sd}_{{\mathcal {A}}}(\Delta )) \!=\!(1, h_1(\mathrm{sd}_{{\mathcal {A}}}(\Delta )) \!-\!h_0\!(\mathrm{sd}_{{\mathcal {A}}}(\Delta )),\!\dots ,\!h_{\lfloor n/2\rfloor }\!(\mathrm{sd}_{{\mathcal {A}}}(\Delta )) \!-\! h_{\lfloor n/2\rfloor \! -\! 1}(\mathrm{sd}_{{\mathcal {A}}}(\Delta )))$.

• (a) $g(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))$ is an M-sequence.

• (b) $h(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))$ is unimodal. The peak is at position n/2, if n is even, and at position $(n-1)/2$ or $(n+1)/2$, if n is odd.

• (c) $h_i(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))\le h_{n-1-i}(\mathrm{sd}_{{\mathcal {A}}}(\Delta ))$ for all $0 \le i \le \lfloor (n-2)/2\rfloor$.

Proof

Parts (a) and (c) follow by standard arguments used when one works with Lefschetz properties, see, e.g., [17, Sects. 3.1–3.2]. For part (b), the proof of [22, Cor. 4.7] works, with Lemma 7.7 replacing [22, Cor. 4.4 (ii)]. $\square$

We conclude this section by recording the following properties of the Stanley–Reisner ring of the antiprism triangulation of any simplicial complex.

Proposition 7.9

Let $\Delta$ be a simplicial complex.

• (a) $\dim ({{\mathbb {F}}} [\mathrm{sd}_{{\mathcal {A}}}(\Delta )]) =\dim ({{\mathbb {F}}}[\Delta ])$.

• (b) $\mathrm{depth} ({{\mathbb {F}}} [\mathrm{sd}_{{\mathcal {A}}}(\Delta )]) = \mathrm{depth} ({{\mathbb {F}}}[\Delta ])$.

• (c)
  $$\begin{aligned}\mathrm{reg}({{\mathbb {F}}}[\mathrm{sd}_{{\mathcal {A}}}(\Delta )])= {\left\{ \begin{array}{ll} \dim (\Delta ), &{}\text{ if } {\widetilde{H}}_{\dim (\Delta )}(\Delta ;{{\mathbb {F}}}) = 0,\\ \dim (\Delta )+1,&{}\text{ if } {\widetilde{H}}_{\dim (\Delta )}(\Delta ;{{\mathbb {F}}}) \ne 0. \end{array}\right. } \end{aligned}$$

Proof

Part (a) is clear, since $\dim (\mathrm{sd}_{{\mathcal {A}}}(\Delta )) =\dim (\Delta )$. Part (b) follows from [26, Thm. 3.1], since $\Delta$ and $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$ have homeomorphic geometric realizations. Part (c) follows from an application of Hochster’s formula [25, Cor. 5.12]; one can also mimic the detailed argument for the barycentric subdivision given in the proof of [23, Prop. 2.6]. $\square$

8 Further Directions

This section concludes with comments, open problems and further directions for research.

1. The question asking which uniform triangulations transform h-polynomials with nonnegative coefficients into polynomials with only real roots was raised in [5]. This property has been verified for several examples, including the prototypical one of the barycentric subdivision [11], and is conjectured in this paper for the antiprism triangulation. We believe that this property is not uncommon among uniform triangulations.

For instance, consider any word $w = w_1 w_2 \cdots w_d$ with $w _i \in \{a, b\}$ for every $i \in [d]$ and let $\Delta$ be a d-dimensional simplicial complex. Let $\mathrm{sd}_w(\Delta )$ be the triangulation of $\Delta$ defined inductively as follows. Assume that all faces of $\Delta$ of dimension less than j have been triangulated, for some $j \in [d]$. Then, triangulate each j-dimensional face $F \in \Delta$ by the antiprism construction, if $w_j = a$, and by the coning construction, if $w_j = b$, over the already triangulated boundary of F. By applying this process for $j = 1, 2,\dots ,d$, in this order, we get a triangulation $\mathrm{sd}_w(\Delta )$ of $\Delta$ which coincides with $\mathrm{sd}_{{\mathcal {A}}}(\Delta )$, when $w = aa \cdots a$, and with $\mathrm{sd}(\Delta )$, when $w = bb \cdots b$. It seems plausible that this triangulation has the same property for every w, but it is not easy to deduce such a statement from the results of [5] and this paper. Example 3.5 corresponds to the word $w = bb \cdots ba$.

2. The symmetric polynomials $\ell _{{\mathcal {A}}}(\sigma _n, x)$ and ${\bar{p}}_{{\mathcal {A}}}(\sigma _n, x)$ were shown and conjectured, respectively, to be $\gamma$-positive in Sect. 5. It is an interesting (and possibly challenging) open problem to find explicit combinatorial interpretations of the corresponding $\gamma$-coefficients. Similar remarks apply to the symmetric polynomials $h_{{\mathcal {A}}}(\partial \sigma _n, x)$ and $\theta _{{\mathcal {A}}}(\sigma _n, x) = h_{{\mathcal {A}}}(\sigma _n, x) -h_{{\mathcal {A}}}(\partial \sigma _n, x)$, shown to be real-rooted, and hence $\gamma$-positive, in Sect. 5.

3. The local h-polynomial of the barycentric subdivision of any CW-regular subdivision of the simplex was shown to be $\gamma$-positive in [20]. Does this hold if ‘barycentric subdivision’ and ‘CW-regular subdivision’ are replaced by ‘antiprism triangulation’ and ‘CW-regular simplicial subdivision’, respectively?

4. The h-polynomial of the barycentric subdivision of any doubly Cohen–Macaulay simplicial complex and the barycentric subdivision of any triangulation of a ball were shown to have a nonnegative real-rooted symmetric decomposition in [10, Sect. 5] and [5, Sect. 8], respectively. Do these statements hold if ‘barycentric subdivision’ is replaced by ‘antiprism triangulation’?

Note added in revision. After this paper was written, the almost strong Lefschetz property was established for a very broad class of triangulations of Cohen–Macaulay polyhedral complexes (including antiprism triangulations of Cohen–Macaulay simplicial complexes) by Adiprasito and Yashfe [1, Thm. 46] using completely different methods and tools, including the partition complex.