Abstract
Let P be a lattice polytope with the \(h^{*}\)-vector \((1, h^*_1, \ldots , h^*_s)\). In this note we show that if \(h_s^* \le h_1^*\), then the Ehrhart ring \({\mathbb {k}}[P]\) is generated in degrees at most \(s-1\) as a \({\mathbb {k}}\)-algebra. In particular, if \(s=2\) and \(h_2^* \le h_1^*\), then P is IDP. To see this, we show the corresponding statement for semi-standard graded Cohen–Macaulay domains over algebraically closed fields.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(R=\bigoplus _{i \in \mathbb {N}} R_i\) be a noetherian graded commutative ring. Throughout the paper, we assume that \({\mathbb {k}}:= R_0\) is a field. If \(R ={\mathbb {k}}[R_1]\), that is, R is generated by \(R_1\) as a \({\mathbb {k}}\)-algebra, we say R is standard graded. If R is finitely generated as a \({\mathbb {k}}[R_1]\)-module, we say R is semi-standard graded.
If R is a semi-standard graded ring of Krull dimension d, its Hilbert series is of the form
for some integers \(h_0, h_1, \ldots , h_s\) with \(\sum _{i=0}^s h_i \ne 0\) and \(h_s \ne 0\). We call the vector \((h_0,h_1,\ldots , h_s)\) the h-vector of R. We always have \(h_0=1\) and \(\deg R=\sum _{i=0}^s h_i\). If R is Cohen–Macaulay, then \(h_i \ge 0\) for all i. We have the following.
Theorem 1.1
Let R be a semi-standard graded Cohen–Macaulay domain with the h-vector \((h_0, h_1, h_2)\). Assume that \({\mathbb {k}}\) is algebraically closed. If \(h_2 \le h_1\), then R is standard graded. If further \(h_2 < h_1\) and \({\text {char}}{\mathbb {k}}=0\), then R is Koszul.
In fact, Theorem 2.1 states that, under the same situation, if the h-vector of R is \((h_0,h_1,\ldots , h_s)\) with \(h_s \le h_1\), then R is generated in degrees at most \(s-1\) as a \({\mathbb {k}}\)-algebra. So the first statement of Theorem 1.1 follows. To see the latter statement, we can use [5, Thm. 5.2 (1)], since we know R is standard graded now.
An important class of semi-standard graded Cohen–Macaulay domains are the Ehrhart rings of lattice polytopes, which we now recall. Let \(P \subset \mathbb {R}^d\) be a lattice polytope. Its Ehrhart ring \({\mathbb {k}}[P]\) is the monoid algebra of the monoid of lattice points in the cone \(C = {{\,\mathrm{cone}\,}}{(\{1\} \times P)}\subset \mathbb {R}^{d+1}\) over P. The additional coordinate in the construction of C yields a natural grading on \({\mathbb {k}}[P]\), such that \({\mathbb {k}}[P]\) is semi-standard graded, and its Hilbert series is the Ehrhart series of P. In particular, the h-vector of \({\mathbb {k}}[P]\) is the \(h^*\) -vector of P (for general information about this notion and its background, see [1]). Hence the Krull dimension \(\dim {\mathbb {k}}[P]\) equals \(\dim P+1\).
It is well known that \({\mathbb {k}}[P]\) is a normal domain, and by Hochster’s Theorem [12, Thm. 1], it is Cohen–Macaulay. We refer the reader to the monograph by Bruns and Gubeladze [2] for more information on Ehrhart rings. The index of the last non-zero entry of the \(h^*\)-vector is called the degree of P. We always have \(\deg P \le \dim P\). The \(h^*\)-vector of P is sometimes denoted by \((h_0^*, h_1^*, \ldots ,h^*_{\dim P})\), even if \(\deg P<\dim P\). In this case, \(h_i^*=0\) for all \(i > \deg P\). We also remark that there is no direct relation between \(\deg P\) and \(\deg {\mathbb {k}}[P]=\sum _{i=0}^d h_i^*\), the latter being the multiplicity of \({\mathbb {k}}[P]\), which also equals the normalized volume \({{\,\mathrm{Vol}\,}}P\) of P.
A lattice polytope P is called IDP (an abbreviation for “integer decomposition property”) if for every \(k \in \mathbb {N}\) and every lattice point \(p \in kP \cap \mathbb {Z}^d\), there exist k lattice points \(p_1, \dotsc , p_k \in P \cap \mathbb {Z}^d\) with \(p = \sum _i p_i\). Clearly, P is IDP if and only if \({\mathbb {k}}[P]\) is standard graded. Hence we obtain the following (here we do not have to assume that \({\mathbb {k}}\) is algebraically closed, since we can replace \({\mathbb {k}}[P]\) by \({\overline{{\mathbb {k}}}}[P] \cong {\overline{{\mathbb {k}}}} \otimes _{\mathbb {k}}{\mathbb {k}}[P]\)):
Corollary 1.2
Let \(P \subset \mathbb {R}^d\) be a lattice polytope of degree 2 with \(h^*\)-vector \((1, h^*_1, h^*_2)\). If \(h^*_2 \le h^*_1\), then P is IDP. If further \(h^*_2 < h^*_1\), the Ehrhart ring \({\mathbb {k}}[P]\) is Koszul for a filed \({\mathbb {k}}\) of characteristic 0.
Note that if \(P \subset \mathbb {R}^2\) is a lattice polygon, then it has degree at most 2, and it always satisfies \(h^*_2 \le h^*_1\). Therefore, the former half of this corollary can be seen as an extension of the well-known fact that lattice polygons are IDP. See also Remark 3.3 (i) below. We give an example to show that the bound in Corollary 1.2 is sharp:
Example 1.3
Let P be the 3-simplex with vertices
It is Reeve’s simplex (cf. [1, Exam. 3.22]) and its \(h^*\)-vector is (1, 0, 1). It is not IDP, and hence the bound \(h^{*}_2 \le h^{*}_1\) is sharp.
In the latter part of the present paper, we take a more combinatorial approach. Especially, keeping Corollary 1.2 in mind, we analyze the results of [9], and give several (counter)examples of the related statements.
2 Proofs of the Main Results
Let \(R=\bigoplus _{i \in \mathbb {N}} R_i\) be a noetherian graded commutative ring such that \({\mathbb {k}}:= R_0\) is an algebraically closed field. We are going to regard R as a module over \(S := {{\,\mathrm{Sym}\,}}_{\mathbb {k}}R_1\). Note that S is isomorphic to the polynomial ring \({\mathbb {k}}[x_1, \ldots , x_n]\) with \(n=\dim _{\mathbb {k}}R_1\). Moreover, R is standard graded if and only if R is a quotient ring of S, and R is semi-standard graded if and only if R is finitely generated as an S-module. For a finitely generated graded S-module M, \(i \in \mathbb {N}\) and \(j \in \mathbb {Z}\), set
In particular, \(\beta _{0,j}^S(M)\) is the number of S-module generators for M in degree j.
2.1 A Bound on the Degrees of the Generators
Assume that R is semi-standard graded, and has the h-vector \((h_0, h_1, \ldots , h_s)\). The goal of this section is to obtain a bound on the degrees of the generators of R as an S-module. If R is Cohen–Macaulay, it is well known that the generators have degree at most s. Our result is a sufficient criterion when this bound can be improved by one:
Theorem 2.1
Let R be a semi-standard graded Cohen–Macaulay domain with h-vector \((h_0, h_1, h_2, \dotsc , h_s)\), and \(S := {{\,\mathrm{Sym}\,}}_{\mathbb {k}}R_1\). Then it holds that
In particular, if \(h_s \le h_1\), then R is generated by elements of degree \(\le s-1\) as an S-module, and hence as a \({\mathbb {k}}\)-algebra.
Note that Theorem 1.1 amounts to the special case \(s = 2\) and \(p = 0\). This result and its proof have been inspired by Green’s Theorem of the Top Row, [7, Thm. 4.a.4]. For the proof of Theorem 2.1, we are going to use the following version of Green’s vanishing theorem:
Theorem 2.2
([6, Thm. 1.1]) Let \(\mathfrak {p}\subset S\) be a homogeneous prime ideal, which does not contain any linear forms. Let M be a torsion-free finitely generated graded \(S/\mathfrak {p}\)-module and let \(q \in \mathbb {Z}\) be the minimal integer such that \(M_q \ne 0\). Then it holds that
In addition, we need the following result:
Theorem 2.3
([2, Thm. 6.18], [3, Thm. 4.4.5]) Let M be a finitely generated graded Cohen–Macaulay module over \(S={\mathbb {k}}[x_1, \ldots , x_n]\) with \(d = \dim M\). Define \(M' := {{\,\mathrm{Ext}\,}}_S^{n - d}(M, \omega _S)\). Then
-
(i)
\(M'\) is also Cohen–Macaulay, \({{\,\mathrm{Ann}\,}}M' = {{\,\mathrm{Ann}\,}}M\), and \(M'' \cong M\);
-
(ii)
\(\beta ^S_{p,q}(M') = \beta ^S_{n - d - p, n - q}(M)\);
-
(iii)
\(H_{M'}(t) = (-1)^{d}H_M(t^{-1})\).
Here, \(\omega _S:=S(-n)\) denotes the canonical module of S, and \(H_M(t)\) denotes the Hilbert series \(\sum _{i\in \mathbb {Z}}(\dim _{\mathbb {k}}M_i)\cdot t^i\) of M.
Proof of Theorem 2.1
Let \(d := \dim R\). By [3, Prop. 3.6.12], \(\omega _R := {{\,\mathrm{Ext}\,}}_S^{n-d}(R, \omega _S)\) is a canonical module for R. Using Theorem 2.3 with \(M=R\) and \(M' =\omega _R\), we have
and the Hilbert series of \(\omega _R\) is
In particular, \(\omega _R\) has no elements in degrees below \(d-s\) and we have that \(\dim _{\mathbb {k}}(\omega _R)_{d-s} = h_s\). Now, since R is a domain and \(\omega _R\) is a canonical module, it is torsion-free over R by Theorem 2.3 (i), and thus it satisfies the hypothesis of Theorem 2.2. Applying that result to \(\omega _R\) (note that \(q=d-s\) in the notation there) yields that
Finally, note that \(h_1 = n - d\), and the proof is completed. \(\square \)
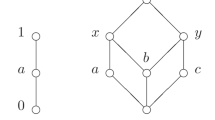
The poset P of Remark 2.4
Remark 2.4
Another important example of a semi-standard graded ring appearing in combinatorial commutative algebra is the face ring \(A_P\) of a simplicial poset P. See [15] for details. For the simplicial poset P given in Fig. 1, we have
where \(\deg x =\deg y=\deg z=1\) and \(\deg u=\deg v=2\), and \({\widehat{0}}, w \in P\) correspond to \(1, yz \in A_P\), respectively. It is easy to see that \(A_P\) is a 2-dimensional Cohen–Macaulay reduced semi-standard graded ring with the h-vector (1, 1, 1), but it is not standard graded. It means that Theorem 2.1 indeed requires the assumption that R is a domain.
3 Further Discussion on Ehrhart Rings
3.1 Direct Applications of Theorem 2.1
We now apply Theorem 2.1 in the setting of Ehrhart theory. Let \(P \subset \mathbb {R}^n\) be a lattice polytope. We write \(M(P)\subset \mathbb {Z}^{n+1}\) for the affine monoid generated by the lattice points in \( \{1\} \times P\subset \mathbb {R}^{n+1}\), and \({\widehat{M}}(P)\subset \mathbb {Z}^{n+1}\) for its integral closure inside \(\mathbb {Z}^{n+1}\). Let \(R={\mathbb {k}}[P]\) be the Ehrhart ring of P and \({\mathbb {k}}[R_1]\) its subalgebra generated by \(R_1\). Then R and \({\mathbb {k}}[R_1]\) are the monoid algebras of the monoids \({\widehat{M}}(P)\) and \(M(P)\), respectively. It is well known that \({\widehat{M}}(P)\) is generated by elements of degree at most \(\min { \{ \deg P, \dim P-1 \}}\) as a module over \(M(P)\) (cf. [2, Thm. 2.52]). Equivalently, \(R={\mathbb {k}}[P]\) is generated by elements of at most that degree as a \({\mathbb {k}}[R_{1}]\)-module, and hence in particular as a \({\mathbb {k}}\)-algebra.
Since \({\mathbb {k}}[P]\) is always Cohen–Macaulay, Theorem 2.1 allows us to improve this bound under an additional assumption as follows. Clearly, this generalizes Corollary 1.2.
Corollary 3.1
Suppose \(P \subset \mathbb {R}^n\) is a lattice polytope of degree s with \(h^*\)-vector \((1, h^*_1, \dotsc , h^*_s)\). If \(h^*_s \le h^*_1\), then \({\widehat{M}}(P)\) is generated by elements of degrees \(\le s - 1\) as an \(M(P)\)-module.
Let \(P^\circ \) be the relative interior of P. The lattice points in \(P^\circ \) are closely related to the canonical module of \({\mathbb {k}}[P]\) (cf. [3, Thm. 6.3.5 (b)]). In general, it holds that \(h^{*}_{\dim P} \le h^{*}_1\) (because \(h^{*}_{\dim P} = \#\,(P^\circ \cap \mathbb {Z}^n) \le \#\,(P \cap \mathbb {Z}^n) - (\dim P +1) = h^{*}_1\)), therefore this corollary extends the above mentioned fact that \({\widehat{M}}(P)\) is generated in degrees at most \(\min {\{ \deg P, \dim P-1 \}}\).
If P is IDP, then \(R = {\mathbb {k}}[P]\) is the quotient ring of \(S = {{\,\mathrm{Sym}\,}}_{\mathbb {k}}R_1\) by a certain prime ideal \(I \subseteq S\), which is called the toric ideal of P. It is known that I is generated by polynomials of degree at most \(\deg P + 1\le \dim P+ 1\) (Sturmfels, cf. [2, Cor. 7.27]), and again we can improve these bounds by one:
Corollary 3.2
Let P be an IDP lattice polytope and let \(I \subset S\) be its toric ideal.
-
(i)
If \(h^*_s \le h^*_1 - 1\), then I is generated in degrees \(\le \deg P\).
-
(ii)
If P is not a clean simplex, then I is generated in degrees \(\le \dim P\).
Recall that a clean simplex is a lattice simplex where the only lattice points on its boundary are the vertices.
Proof
-
(i)
Apply Theorem 2.1 to \(R = {\mathbb {k}}[P]\) with \(p = 1\).
-
(ii)
If I has a generator in degree \(\dim P+ 1\), then it holds that \(\deg P = \dim P\) by the above mentioned fact that I is generated in degrees at most \(\deg P + 1\le \dim P+ 1\). Moreover, the hypothesis of part (i) needs to be violated, hence it holds that \(h^{*}_{\dim P} \ge h^{*}_1\). It follows that \(h^{*}_{\dim P} = h^{*}_1\), which is equivalent to P being a clean simplex. \(\square \)
Remark 3.3
-
(i)
Let \(P \subset \mathbb {R}^2\) be a lattice polygon. Then we have \(\deg P \le 2\) and P is IDP. Moreover, Koelman [13] showed that the toric ideal of P is generated by quadrics if and only if \(h^*_2 < h^*_1\). Hence Corollary 3.2 (i) is an extension of one implication of his result. In particular, the result of [13] shows that the bound \(h^*_2 < h^*_1\) is sharp.
-
(ii)
In [14], Schenck also applied the theory of Green to the study of Ehrhart rings \({\mathbb {k}}[P]\). However, the focus of [14] is different from ours. More precisely, he always assumed that \({\mathbb {k}}[P]\) is standard graded (i.e., P is IDP), and treated the case the toric ideal is generated by quadrics.
3.2 Combinatorial Proofs
Corollary 1.2 is a purely combinatorial statement, and hence one might hope for a combinatorial proof. As a first step, we prove a weak variant of Corollary 1.2 which admits an elementary proof.
We remind the reader that a lattice polytope \(P \subset \mathbb {R}^n\) is called spanning [11], if \(( \{1\} \times P) \cap \mathbb {Z}^{n+1}\) generates the lattice \(\mathbb {Z}^{n+1}\). Every IDP polytope is spanning, but the converse is far from being true. Algebraically, for the Ehrhart ring \(R={\mathbb {k}}[P]\), P is spanning if and only if the field of fractions of R coincides with that of \({\mathbb {k}}[R_{1}]\).
Proposition 3.4
Let \(P \subset \mathbb {R}^n\) be a d-dimensional lattice polytope with \(h^{*}\)-vector \((h^{*}_0, h^{*}_1, \dotsc )\). If \(h^{*}_1 + h^{*}_d \ge \sum _{i=2}^{d-1}h^{*}_i\), then P is spanning.
Proof
Let L be the lattice generated by the lattice points in P, and q the index of L in \(\mathbb {Z}^n\). Further, let \({\widetilde{P}}\) be the polytope P considered in the lattice L (see [11]). We write \({\widetilde{h}}^{*}\) for the \(h^{*}\)-vector of \({\widetilde{P}}\). It holds that
Moreover, it holds that \(h^{*}_1={\widetilde{h}}^{*}_1\), \(h^{*}_d={\widetilde{h}}^{*}_d\), and \(h^{*}_i \ge {\widetilde{h}}^{*}_i\) for \(1 \le i \le d\) (see [11, Sect. 3.2]). Now (1) and the assumption that \( \sum _{i=2}^{d-1} h^{*}_i \le h^{*}_1 + h^{*}_d\) imply that
Since \(1+h^{*}_1 + h^{*}_d \ge 1\), we have \(q=1\), and it means that P is spanning. \(\square \)
In the next corollary, (i) is just a weak version of Corollary 1.2, but (ii) and (iii) are new.
Corollary 3.5
With the above notation, the following hold:
-
(i)
If \(\deg P = 2\) and \(h^{*}_1 \ge h^{*}_2\), then P is spanning.
-
(ii)
If \(\dim P= 3\) and \(h^{*}_1 + h^{*}_3 \ge h^{*}_2\), then P is spanning.
-
(iii)
If \(\dim P = 4\), \(\deg P\ge 3\), and \(h^{*}_1 + h^{*}_4 \ge h^{*}_2 + h^{*}_3\), then P is spanning. In this case, it holds that \(h^{*}_1 = h^{*}_2 = h^{*}_3 = h^{*}_4\).
Proof
Only the very last statement is not immediate from Proposition 3.4. If \(\dim P = 4\), then \(h^{*}_4 \le h^{*}_1\). By assumption and Proposition 3.4, P is spanning, and hence by [10, Thm. 1.4] it holds that \(h^{*}_1 \le h^{*}_i\) for \(1 \le i < \deg P\). As \(\deg P\ge 3\) it holds that \(h^{*}_1 \le h^{*}_2\) and \(h^{*}_3 > 0\), and thus \(h^{*}_1 < h^{*}_2 + h^{*}_3\). It follows that \(h^{*}_4 \ne 0\), so \(\deg P= 4\). Hence we have that \(h^{*}_4 \le h^{*}_1 \le h^{*}_2\) and \(h^{*}_1 \le h^{*}_3\). These inequalities, together with \(h^{*}_1 + h^{*}_4 \ge h^{*}_2 + h^{*}_3\), imply that \(h^{*}_1 = h^{*}_2 = h^{*}_3 = h^{*}_4\). \(\square \)
Unfortunately, these are the only cases where Proposition 3.4 can be applied, due to the following observation:
Proposition 3.6
If \(d:=\dim P \ge 5\) and \(\deg P \ge 3\), then \(h^{*}_1 + h^{*}_d < \sum _{i=2}^{d-1} h^{*}_i\).
Proof
Set \(s:=\deg P\). If \(h^{*}_d=0\) (i.e., \(s < d\)), then we have
where the first \(\le \) follows from [16, Prop. 4.1] and the second follows from the assumption that \(d \ge 5\) and \(s \ge 3\). If \(h^{*}_d \ne 0\), we have \(h^{*}_i \ge h^{*}_1\) for all \(1 \le i \le d-1\) by [8, Thm. 1.1]. Hence
Here we use the assumption that \(d \ge 5\). \(\square \)
3.3 About Polytopes of Degree 2
One can combine our Corollary 1.2 with the results of [9] to obtain the following web of implications for lattice polytopes of degree 2:
Theorem 3.7
Let \(P \subset \mathbb {R}^n\) be a lattice polytope of degree 2 with \(h^{*}\)-vector \((1, h^{*}_1, h^{*}_2)\), and let \({\widetilde{P}}\) denote the polytope P considered as a lattice polytope inside the lattice generated by the lattice points in P. Then the following implications hold:

Here, we say that a lattice polytope P is level if its Ehrhart ring \(R={\mathbb {k}}[P]\) is level, that is, its canonical module \(\omega _R\) is generated in a single degree as an R-module. The levelness of P is a combinatorial property of the monoid \({\widehat{M}}(P)\) (c.f. [9, Prop. 4.3]), and does not depend on the base field \({\mathbb {k}}\).
Proof
-
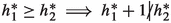 : This is elementary.
: This is elementary. -
 : We show the contrapositive. Assume that \(\deg {\widetilde{P}}= 1\). Denote the \(h^*\)-vector of \({\widetilde{P}}\) by \({\tilde{h}}^*\). The volume of \({\widetilde{P}}\) divides the volume of P, since the latter is normalized with respect to a finer lattice. Thus we have that $$\begin{aligned} (1 + {\tilde{h}}^*_1 + {\tilde{h}}^*_2) \mid (1 + h^*_1 + h^*_2). \end{aligned}$$
: We show the contrapositive. Assume that \(\deg {\widetilde{P}}= 1\). Denote the \(h^*\)-vector of \({\widetilde{P}}\) by \({\tilde{h}}^*\). The volume of \({\widetilde{P}}\) divides the volume of P, since the latter is normalized with respect to a finer lattice. Thus we have that $$\begin{aligned} (1 + {\tilde{h}}^*_1 + {\tilde{h}}^*_2) \mid (1 + h^*_1 + h^*_2). \end{aligned}$$On the other hand, we have that \({\tilde{h}}^*_1 = h^*_1\) and by assumption, \({\tilde{h}}^*_2 = 0\). It follows that \((1+h^*_1) \mid h^*_2\).
-
\(h^{*}_1 \ge h^{*}_2\ \Longrightarrow \) IDP: This is Corollary 1.2.
-
IDP \(\Longrightarrow \) spanning: This is well known (and elementary), and it does not need the assumption \(\deg P \le 2\).
-
spanning \(\Longrightarrow ~\!\!\deg {\widetilde{P}}\ne 1\): \(\deg {\widetilde{P}}= \deg P = 2 \ne 1\).
-
\(\deg {\widetilde{P}}\ne 1~\!\!\Longrightarrow \) level: Under this hypothesis, the degree of \({\widetilde{P}}\) is either 0 or 2. We distinguish those cases:
- \(\deg {\widetilde{P}}= 0\)::
-
In this case \(h^*_1 = 0\), the claim follows from [9, Lem. 2.1].
- \(\deg {\widetilde{P}}= 2\)::
-
Let R and \({\widetilde{R}}\) denote the Ehrhart rings of P and \({\widetilde{P}}\), respectively. Then \(\deg {\widetilde{R}}= 1 + h^*_1 + {\tilde{h}}^*_2 > 1 + h^*_1\) by assumption, and thus R is level by [9, Prop. 3.4].
-
level \(\Longrightarrow ~\!\!\deg {\widetilde{P}}\ne 1\): This follows from more general Lemma 3.8 below.\(\square \)
Lemma 3.8
Let \(P \subset \mathbb {R}^n\) be a lattice polytope. If P is level, then \(\deg {\widetilde{P}}\ne \deg P - 1\).
Proof
Let \(c(P) := \min {\{\ell \in \mathbb {Z}_{>0} :\ell P^\circ \cap \mathbb {Z}^n \ne \emptyset \}}\). It is well known that \(\deg P= \dim P+ 1 - c(P)\).
We are going to use [9, Prop. 4.3], which we recall for convenience: If P is level, then for any \(k \ge c(P)\) and \(\alpha \in kP^\circ \cap \mathbb {Z}^n\), there exist \(\beta \in c(P)P^\circ \cap \mathbb {Z}^n\) and \(\gamma \in (k - c(P))P \cap \mathbb {Z}^n\) such that
Now, assume that \(\deg {\widetilde{P}}= \deg P - 1\), and note that this implies \(c({\widetilde{P}}) = c(P) + 1\). Let \(L \subset \mathbb {Z}^n\) be the sublattice spanned by the lattice points in P. As \(P \ne {\widetilde{P}}\), this is a proper sublattice of \(\mathbb {Z}^n\). Choose \(\alpha \in c({\widetilde{P}})P^\circ \cap L\). Then, if P were level, there would exist \(\beta \) and \(\gamma \) as above. As \(\beta \in c(P)P^\circ \cap \mathbb {Z}^n\), it follows that  has no interior lattice points). Further, \(\gamma \) lies in \((c({\widetilde{P}}) - c(P))P = P\) and thus \(\gamma \in L\). But this contradicts \(\beta + \gamma = \alpha \in L\). \(\square \)
has no interior lattice points). Further, \(\gamma \) lies in \((c({\widetilde{P}}) - c(P))P = P\) and thus \(\gamma \in L\). But this contradicts \(\beta + \gamma = \alpha \in L\). \(\square \)
We provide some examples to show that all the implications are strict and that there are no other implications. In each example, the claimed properties can conveniently be verified using normaliz [4].
Example 3.9
( spanning, IDP, \(h^{*}_1 \ge h^{*}_2\)). Consider the 4-polytope P with vertices
spanning, IDP, \(h^{*}_1 \ge h^{*}_2\)). Consider the 4-polytope P with vertices
Its \(h^{*}\)-vector is (1, 2, 5), so it satisfies  , but \(h^{*}_1 \ngeq h^{*}_2\). To see that it is not spanning (and thus not IDP), consider the vector
, but \(h^{*}_1 \ngeq h^{*}_2\). To see that it is not spanning (and thus not IDP), consider the vector
It lies in \(2P \cap \mathbb {Z}^4\), but the sum of its coordinates is odd, while the coordinate sum of each vertex of P is even. Hence v cannot lie in the lattice spanned by them.
Example 3.10
(IDP and spanning  ). Let P be the 3-simplex with vertices
). Let P be the 3-simplex with vertices
It is IDP and its \(h^{*}\)-vector is (1, 5, 6), so \(h^{*}_1+1\mid h^{*}_2\) and \(h^{*}_1 \ngeq h^{*}_2\).
Example 3.11
(spanning  IDP). It is well known that this implication does not hold in general. For an example with degree 2, see [2, Exe. 2.24]. This is a very-ample (and thus spanning) 3-polytope which is not IDP. Its \(h^{*}\)-vector is (1, 4, 5), so it has degree 2.
IDP). It is well known that this implication does not hold in general. For an example with degree 2, see [2, Exe. 2.24]. This is a very-ample (and thus spanning) 3-polytope which is not IDP. Its \(h^{*}\)-vector is (1, 4, 5), so it has degree 2.
Example 3.12
( , spanning). Let P be the polytope of Example 1.3 with \(h^{*}\)-vector (1, 0, 1). In this case \({\widetilde{P}}\) is a unit simplex and thus \(\deg {\widetilde{P}}= 0 \ne 1\). However, P is not spanning and it holds that \(h^{*}_1+1\mid h^{*}_2\).
, spanning). Let P be the polytope of Example 1.3 with \(h^{*}\)-vector (1, 0, 1). In this case \({\widetilde{P}}\) is a unit simplex and thus \(\deg {\widetilde{P}}= 0 \ne 1\). However, P is not spanning and it holds that \(h^{*}_1+1\mid h^{*}_2\).
Example 3.13
( and IDP
and IDP  ). Let P be the 3-simplex with vertices
). Let P be the 3-simplex with vertices
Its \(h^{*}\)-vector is (1, 6, 9), so it satisfies  , but \(h^{*}_1 \ngeq h^{*}_2\). Moreover, it is IDP.
, but \(h^{*}_1 \ngeq h^{*}_2\). Moreover, it is IDP.
References
Beck, M., Robins, S.: Computing the Continuous Discretely. Undergraduate Texts in Mathematics. Springer, New York (2007)
Bruns, W., Gubeladze, J.: Polytopes, Rings, and \(K\)-Theory. Springer Monographs in Mathematics. Springer, Dordrecht (2009)
Bruns, W., Herzog, J.: Cohen–Macaulay Rings. Cambridge Studies in Advanced Mathematics, vol. 39. Cambridge University Press, Cambridge (1993)
Bruns, W., Ichim, B., Römer, T., Sieg, R., Söger, Ch.: Normaliz. Algorithms for Rational Cones and Affine Monoids. https://www.normaliz.uni-osnabrueck.de
Conca, A., Iyengar, S.B., Nguyen, H.D., Römer, T.: Absolutely Koszul algebras and the Backelin–Roos property. Acta Math. Vietnam. 40(3), 353–374 (2015)
Eisenbud, D., Koh, J.: Some linear syzygy conjectures. Adv. Math. 90(1), 47–76 (1991)
Green, M.L.: Koszul cohomology and the geometry of projective varieties. J. Differ. Geom. 19(1), 125–171 (1984)
Hibi, T.: A lower bound theorem for Ehrhart polynomials of convex polytopes. Adv. Math. 105(2), 162–165 (1994)
Higashitani, A., Yanagawa, K.: Non-level semi-standard graded Cohen–Macaulay domain with \(h\)-vector \((h_0, h_1, h_2)\). J. Pure Appl. Algebra 222(1), 191–201 (2018)
Hofscheier, J., Katthän, L., Nill, B.: Spanning lattice polytopes and the uniform position principle (2017). arXiv:1711.09512
Hofscheier, J., Katthän, L., Nill, B.: Ehrhart theory of spanning lattice polytopes. Int. Math. Res. Not. IMRN 2018(19), 5947–5973 (2018)
Hochster, M.: Rings of invariants of tori, Cohen–Macaulay rings generated by monomials, and polytopes. Ann. Math. 96, 318–337 (1972)
Koelman, R.J.: A criterion for the ideal of a projectively embedded toric surface to be generated by quadrics. Beiträge Algebra Geom. 34(1), 57–62 (1993)
Schenck, H.: Lattice polygons and Green’s theorem. Proc. Am. Math. Soc. 132(12), 3509–3512 (2004)
Stanley, R.P.: \(f\)-vectors and \(h\)-vectors of simplicial posets. J. Pure Appl. Algebra 71(2–3), 319–331 (1991)
Stanley, R.P.: On the Hilbert function of a graded Cohen–Macaulay domain. J. Pure Appl. Algebra 73(3), 307–314 (1991)
Acknowledgements
The authors thank Kazuma Shimomoto for many inspiring discussions throughout this project. They also thank anonymous reviewers for their careful reading and valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: János Pach
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was partially supported by JSPS Grant-in-Aid for Scientific Research (C) 19K03456.
Rights and permissions
About this article
Cite this article
Katthän, L., Yanagawa, K. Graded Cohen–Macaulay Domains and Lattice Polytopes with Short h-Vector. Discrete Comput Geom 68, 608–617 (2022). https://doi.org/10.1007/s00454-021-00342-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-021-00342-z




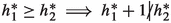 : This is elementary.
: This is elementary. : We show the contrapositive. Assume that
: We show the contrapositive. Assume that