Taking a Detour; or, Gioan’s Theorem, and Pseudolinear Drawings of Complete Graphs

Abstract

We describe a uniform approach to two known graph drawing results including Gioan’s theorem, stating that any two good drawings of a complete graph with the same rotation system are isomorphic up to Reidemeister moves of type 3, and a characterization of pseudolinear drawings of the complete graph via an excluded configuration: a bad $K_4$. Our approach yields a new and short self-contained proof of Gioan’s theorem, and a short proof of the pseudolinearity characterization using a previous result. As a bonus we obtain an extension of Gioan’s theorem to the family of graphs $K_n-M$, where M is a non-perfect matching in $K_n$, $n \ge 5$.

1 Introduction

This paper includes unified proofs of two known results in topological graph theory. The first result is Gioan’s theorem, announced in a 2005 WG paper by Gioan [7]; the paper only contains a sketch of the proof, and the first complete proof, due to Arroyo et al. [2], did not appear until 2018.¹ Gioan’s original proof sketch is based on a logical approach, while the proof in [2] uses more traditional graph drawing methods. Recall that a drawing of a graph is good if every pair of edges intersects at most once (a common endpoint counts as an intersection, so adjacent edges do not cross). The rotation of a vertex in a drawing is the cyclic permutation of edges incident to the vertex, as we pass through the edges around the vertex clockwise. The rotation system of the drawing is the collection of all rotations of vertices in the drawing. Two drawings of a graph are rotation-equivalent if they have the same rotation system, and they are isomorphic if there is a homeomorphism of the sphere that transforms one drawing into the other.² Unless we state otherwise, graphs are labeled, and the homeomorphisms of the drawings are required to respect the labeling.

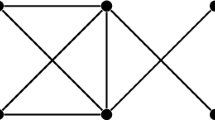
If two drawings are isomorphic, they are rotation-equivalent up to reversing the rotations at all vertices (corresponding to an orientation-reversing homeomorphism of the sphere). The converse is clearly not true: whenever we have a 3-gon bounded by three crossings, we can move one of the sides over the opposite crossing, as in Fig. 1. This changes the isomorphism type of the drawing, but does not affect the rotation system.

Fig. 1

A slide move (Reidemeister move of type 3)

The move in Fig. 1 is called a slide move.³ Gioan’s theorem states that up to slide moves, two rotation-equivalent, good drawings of a complete graph are isomorphic.⁴

Theorem 1.1

(Gioan’s theorem [2, 7])   Any two rotation-equivalent, good drawings of a complete graph are isomorphic up to slide moves.

We give a new proof of Gioan’s theorem. We also show that Gioan’s theorem can be extended to incomplete graphs, namely the family $K_n-M$, where M is a non-perfect matching in $K_n$, $n \ge 5$, if we strengthen the assumption of rotation-equivalence slightly. Both results can be found in Sect. 3.

The proofs of Gioan’s theorem and its extension are based on a lemma which allows us to detour edges without destroying the goodness of a drawing; we state and prove this result in Sect. 2. The same lemma can be used to give relatively short and conceptually simple proofs of another group of results. A drawing of a graph is x -monotone, or just monotone, if every edge intersects every vertical line at most once. A pseudoline arrangement is a collection of curves that go from $-\infty$ to $\infty$ such that every pair of curves crosses exactly once (and does not intersect otherwise). Pseudoline arrangements have been very useful in analyzing straight-line arrangements, which they generalize, since they abstract away from the geometry of the arrangement. We say a drawing of a graph is pseudolinear if it is isomorphic in the plane to a drawing that can be extended to a pseudoline arrangement, so that every edge of the graph lies on a unique pseudoline.

Let us consider $K_4$ as an example. Figure 2 shows all good drawings of $K_4$ in the plane, up to homeomorphism of unlabeled graphs.⁵ All but the last are rectilinear (so x-monotone and pseudolinear); the last drawing is x-monotone, but not pseudolinear: the edges involved in the crossing cannot be extended to pseudolines, since one end of the pseudoline will be stuck inside an inner region (and no homeomorphism will change that). We call this last drawing of $K_4$ the bad $K_4$. (If we were working with homeomorphisms in the sphere or the projective plane, then the bad $K_4$ would be pseudolinear, since it is homeomorphic to the second $K_4$ on those surfaces.) We observe that the bad $K_4$ is the only good drawing of $K_4$ in which the crossing is incident to the outer region.

Fig. 2

Non-isomorphic ood drawings of $K_4$ in the plane; the bad $K_4$ is on the right

The presence of a bad $K_4$ is the only obstruction to a good drawing of a complete graph being pseudolinear. This result was first announced without proof in [1]; a full version of that paper has not appeared yet.

Theorem 1.2

(Aichholzer et al. [1])   A good drawing of a complete graph in the plane is pseudolinear if and only if it does not contain a bad $K_4$.

While the proof of Theorem 1.2 has not appeared yet, a proof of an equivalent result was published around the same time, phrased in somewhat different terms. In a drawing of $K_n$, a triangle is a closed region bounded by a $K_3$ subgraph of $K_n$; the triangle is convex if for every pair of vertices u and v lying in the triangle (including boundary vertices, since the triangle is closed), the edge uv lies within the triangle. Call a drawing of $K_n$ face-convex if every triangle in $K_n$ is convex.⁶

Theorem 1.3

(Arroyo et al. [2])   A drawing of a complete graph is face-convex if and only if it is pseudolinear.

There are two obstacles to a triangle in a good drawing being convex: a bad $K_4$, and two vertices uv in the interior of the triangle, so that uv crosses two sides of the triangle. Therefore, Theorem 1.2 implies Theorem 1.3. The second obstacle forces the presence of a bad $K_4$: suppose there were no bad $K_4$, and let xy be one of the triangle edges crossed by uv; then the edges between $\{x,y\}$ and $\{u,v\}$ must lie inside the triangle, so the $K_4$ induced by $\{u,v,x,y\}$ has the crossing between uv and xy on its outer region, so it must be bad. Hence, Theorem 1.3 also implies Theorem 1.2, and the two results are equivalent.

Our proof of Theorem 1.2 is based on the following result, which the authors of [1] also cite as a starting point.⁷

Theorem 1.4

(Balko et al. [4])   An x-monotone, good drawing of a complete graph is pseudolinear if and only if it does not contain a bad $K_4$.

The gap between Theorems 1.2 and 1.4 is then covered by the following result.

Theorem 1.5

  A good drawing of a complete graph without a bad $K_4$ is isomorphic in the plane to an x-monotone drawing.

Since a bad $K_4$ is not pseudolinear, Theorem 1.5 together with Theorem 1.4 imply Theorem 1.2. In the other direction, Theorem 1.2 also implies Theorem 1.5, because every pseudoline drawing is isomorphic in the plane to a wiring diagram which is x-monotone (see [8]).

The new proofs in this paper are based on combining two ideas. The first is a graph redrawing tool, the detour lemma, presented in Sect. 2, which allows us to reroute edges in a good drawing, without destroying the goodness of the drawing. To apply this tool we work with a spanning star of the complete graph.⁸ In a good drawing of a complete graph with a given rotation system, the order and direction in which an edge intersects this spanning graph is entirely determined (Lemma 3.1). This restriction on good drawings significantly simplifies reasoning about them. In Sect. 3 we prove Gioan’s theorem and its extension, and in Sect. 4 we give a proof of Theorem 1.5.

2 Detours

A bigon consists of two simple curves $\delta$ and $\gamma$ which have the same two distinct endpoints, and do not intersect otherwise. We say two simple curves $\delta$ and $\gamma$, typically edges, bound a bigon if there are curves $\delta '\subseteq \delta$ and $\gamma ' \subseteq \gamma$ such that $\delta '$ and $\gamma '$ form a bigon, and $\delta -\delta '$ and $\gamma -\gamma '$ do not intersect the boundary of the bigon $\delta ' \cup \gamma '$. We say a bigon is empty if it does not contain any vertices in its interior.

Fig. 3

An edge e with a homotopic detour $\delta _e$ (dashed) for $\gamma _e$, the subarc of e between the endpoints of $\delta _e$. Arcs $\gamma _e$ and $\delta _e$ form a bigon, but e and $\delta _e$ do not bound that bigon, since e has additional crossings with $\delta _e$. There is, however, an empty bigon bounded by e and $\delta _e$ contained in the bigon $\delta _e\cup \gamma _e$

In a good drawing of a graph, a detour of an edge e is a curve $\delta _e$ that has both its endpoints on e and such that $\delta _e$ forms a bigon with $\gamma _e \subseteq e$, the arc along e connecting the two endpoints of $\delta _e$ on e. We also say that $\delta _e$ is a detour of $\gamma _e$. We call the detour homotopic if the bigon bounded by $\delta _e \cup \gamma _e$ is empty, and no edges in the bigon either end at an endpoint of $\delta _e$ or cross the boundary of the bigon at an endpoint of $\delta _e$. The bigon $\delta _e\cup \gamma _e$ may not be a bigon bounded by e and $\delta _e$, since it is possible that e has additional intersections with $\delta _e$. If the bigon $\delta _e \cup \gamma _e$ is empty, however, then there is a bigon bounded by $\delta _e$ and e contained in the region bounded by $\delta _e \cup \gamma _e$, and therefore empty again, see Fig. 3. The reason is that since e cannot cross itself, and $\delta _e \cup \gamma _e$ is empty, any crossing of e with $\delta _e$ must be paired with another crossing of e with $\delta _e$. We can therefore work with the minimal bigon between $\delta _e$ and a subarc of e contained in the original bigon. This minimal bigon is then bounded by e and $\delta _e$.

Lemma 2.1

(detour lemma⁹)   Let $\delta _e$ be a homotopic detour of the arc $\gamma _e$ on edge e in a good drawing of a graph. Let F be the set of edges which cross $\delta _e$ at least twice. Then we can apply a sequence of slide moves and homeomorphisms of the plane so that in the resulting drawing e is routed arbitrarily close to $\delta _e$, without intersecting it. The slide moves and homeomorphisms only affect a small open neighborhood of the region bounded by $\gamma _e \cup \delta _e$, and only edges in F and the $\gamma _e$ part of e are redrawn.

Since homeomorphisms and slide moves do not affect the goodness of a drawing, we know that the final drawing in Lemma 2.1 is good. For an example of applying the detour lemma to redraw a detour, see Fig. 5. We should mention that it is possible that the set F contains e.

Proof

Every time an edge enters the bigon $\delta _e\cup \gamma _e$ it must leave it again, since there are no vertices inside the empty bigon. Since the drawing is good, there can be only one crossing of an edge with $\gamma _e$. This leaves two ways an edge can cross through the bigon: transversely, one crossing with each side of the bigon, $\delta _e$ and $\gamma _e$; or laterally, both crossings are with the same side, which then must be $\delta _e$.

Let us first look at the case that some edge $f \in F$ crosses the bigon laterally. Then there is an arc $\gamma _f\subseteq f$ which lies inside the region bounded by the bigon $\delta _e\cup \gamma _e$ and which has both its endpoints on $\delta _e$, and otherwise does not intersect the closed curve $\delta _e\cup \gamma _e$. Then $\gamma _f$ and a subarc $\delta '_e\subseteq \delta _e$ bound a bigon; choose $f \in F$ and $\gamma _f$ so that the resulting bigon is minimal (that is, it encloses no other bigon of this type). Figure 4 illustrates the set-up.

Any edge that crosses the boundary of the bigon $\delta '_e\cup \gamma _f$ must do so transversely, that is, there are no two consecutive crossings with $\gamma _f$ or $\delta '_e$. For $\gamma _f$ this follows from the drawing being good, for $\delta '_e$ this follows from the minimality of the bigon we chose. We distinguish two cases:

• The bigon $\delta '_e \cup \gamma _f$ does not enclose any crossings. In this case, we can apply a homeomorphism of the plane to move $\gamma _f$ to the other side of $\delta '_e$ making it follow $\delta '_e$ closely.

• The bigon $\delta '_e\cup \gamma _f$ does contain a crossing. In this case, the bigon must contain a crossing c such that c and the two arcs connecting it to $\gamma _f$ bound an empty triangle (we will argue this presently); we can then slide $\gamma _f$ beyond c; repeating this we obtain a drawing of $\gamma _f$ such that $\delta '_e\cup \gamma _f$ does not enclose any crossings, and we continue as in the first case. See Fig. 5.

How do we know that the required c exists? Start with an arbitrary crossing $c_1$ inside the bigon, see Fig. 6. If the two arcs connecting $c_1$ to $\gamma _f$ contain a crossing, then there must be a crossing along at least one of the arcs. Let $c_2$ be the closest such crossing to $\gamma _f$. Then the arc from $c_2$ to $\gamma _f$ has no crossings. If the other arc from $c_2$ to $\gamma _f$ contains crossings, we pick the closest such crossing $c_3$ to $\gamma _f$. We continue this process to obtain a sequence of crossings. Starting with $c_2$, at least one of the arcs incident to the crossing must be free of crossings. This implies that the sequence of triangles formed by the two arcs at the crossing and $\gamma _f$ is nested (starting with $c_2$). Since we are strictly reducing the number of crossings contained inside the triangle, this sequence must stop in a finite number of steps with a crossing c for which both arcs connecting it to $\gamma _f$ do not contain a crossing.

At this point all crossings of $f\in F$ with the bigon are transverse. This is not possible, since f, by definition of F, has to cross $\delta _e$ at least twice, forcing two crossings of f with $\gamma _e$ (and therefore e), contradicting goodness of the drawing. Hence, F is empty, and all crossings of edges with $\delta _e\cup \gamma _e$ are transverse; this case we saw how to handle earlier when rerouting $\gamma _f$ along $\delta '_e$; we apply the same procedure here, to $\gamma _e$ and $\delta _e$. $\square$

Fig. 4

A detour $\delta _e$ (dashed) for $\gamma _e$, the subarc of e between the endpoints of $\delta _e$. Edge f and $\delta _e$ bound a minimal bigon $\delta '_e$ with $\gamma _f$. Edges of F in gray

Fig. 5

Detouring $\gamma _e$ along $\delta _e$: after three slide moves, $\delta _e\cup \gamma _e$ contains no more crossings, and we can redraw $\gamma _e$ on the other side of $\delta _e$, following it closely

Fig. 6

The bigon $\delta '_e\cup \gamma _f$ contains crossings. To find a crossing that bounds a triangle with $\gamma _f$ we start with (arbitrary) crossing $c_1$ and then keep following one of the incident arcs which contains crossings up to the crossing closest to $\gamma _f$ (after $c_1$ that choice is unique)

Remark 2.2

How many slide moves does the detour lemma need? Suppose the bigon $\delta _e \cup \gamma _e$ contains k crossings in its interior. For an edge $f\in F$, each arc of f may have to be pushed past all k crossings inside the bigon, leading to at most k slide moves for each arc $\gamma _f$ for each edge $f\in F$. At this point, we need at most another k slide moves for $\gamma _e$.

3 Gioan’s Theorem

To use the detour lemma to prove Gioan’s theorem, we need to find homotopic detours; we do so by comparing two drawings of an edge relative to a spanning star. For that purpose we introduce the notion of a directed crossing: if we (arbitrarily) orient all edges in a graph, we can distinguish between an edge e crossing another edge f from left-to-right, or from right-to-left (as we traverse f in the direction we chose). We talk about a directed crossing.

Lemma 3.1

(Gioan [7], Kynčl [12])   A rotation system of a good drawing of a $K_5$ uniquely determines its isomorphism type on the sphere. The order and direction of crossings between pairs of edges in the $K_5$ are uniquely determined (given the orientation of the edges).

Probably the easiest way of proving the lemma is to inspect the five non-isomorphic drawings of $K_5$ on the sphere, and note that their rotation systems differ, see [12]. The lemma also follows from Corollary B.2 in Appendix B.

Suppose we have a star S(w) centered at w, and two drawings, e and $e'$, of an edge uv between two neighbors u and v of w. We say the two drawings are equivalent with respect to the drawing of S(w), if following either drawing from u to v results in the same sequence of directed crossings with edges in S(w).

Lemma 3.2

If we have two drawings e and $e'$ of an edge uv that are equivalent with respect to a drawing D of a star S(w), and both $D \cup \{e\}$ and $D \cup \{e'\}$ are good drawings, then e and $e'$ bound an empty bigon.

As one of the referees pointed out, the lemma can also be deduced from a classical result by Hass and Scott on curves on surfaces [10, Lemma 3.1]. That proof requires some heavier machinery, so we prefer to include our own more elementary argument.

Proof

The edges of S(w), the star edges, split e and $e'$ into sequences of arcs. Since e and $e'$ are equivalent, the jth arc of each sequence connects the same sides of the same star edges. If the jth arc of e crosses the jth arc of $e'$ for some j, let j be minimal with this property, and let c be the first such crossing along the jth arc of e. Otherwise, no jth arc of e crosses a jth arc of $e'$, and we choose j so that the jth arcs of e and $e'$ are the final arcs of e and $e'$, and c is v, the common endpoint of those arcs.

Following e and $e'$ from their starting point u to c gives us two subarcs, $\gamma \subseteq e$ and $\gamma ' \subseteq e'$, connecting u to c; note that while $\gamma$ and $\gamma '$ intersect in c, they do not cross in c (since they end there), so we do not consider c a crossing of $\gamma$ and $\gamma '$. See Fig. 7.

If $\gamma$ and $\gamma '$ do not cross, then $\gamma$ and $\gamma '$ bound a bigon, and that bigon is empty, since both $\gamma$ and $\gamma '$ cross the same star edges in the same order and direction, so none of the star edges can cross exactly one of them, which would be necessary for a vertex to lie inside the bigon. If e and $e'$ bound the bigon $\gamma \cup \gamma '$, we are done; otherwise, we can choose a minimal bigon bounded by e and $e'$ inside the region enclosed by $\gamma$ and $\gamma '$. Since the bigon bounded by $\gamma$ and $\gamma '$ is empty, so is the minimal bigon, and we are done.

If $\gamma$ and $\gamma '$ cross, such a crossing cannot occur between the parts of $\gamma$ and $\gamma '$ that belong to the jth arcs, by the choice of c. So an ith arc of $\gamma$ crosses $\gamma '$ or an ith arc of $\gamma '$ crosses $\gamma$, where $i < j$, and both may happen. Without loss of generality, let us assume the first case holds, illustrated in Fig. 7. Since the ith arcs of $\gamma$ and $\gamma '$ do not cross each other, but $\gamma '$ does cross the ith arc of $\gamma$, there must be a bigon bounded by $\gamma$ and $\gamma '$ in the quadrilateral consisting of the two ith arcs of $\gamma$ and $\gamma '$ and the arcs along the star edges that connect the endpoints of those two arcs (unless the ith arc is the first or last arc, in which case the boundary has three sides—this case is shown in Fig. 7; two sides are not possible, since c is a crossing). As before, there must then be a bigon bounded by e and $e'$ within that quadrilateral. Since the quadrilateral cannot contain a vertex, this bigon is empty. $\square$

Fig. 7

The star S(w). The fourth arcs of e and $e'$ cross in c. Curves $\gamma \subseteq e$ and $\gamma ' \subseteq e'$ connect u to c. The third arc of $\gamma '$ crosses the first arc of $\gamma$

Proof of Theorem 1.1

Let D and $D'$ be two rotation-equivalent good drawings of a complete graph. By applying a homeomorphism, we can assume that the star S(v) on v and all its neighbors in the complete graph are drawn the same way in both D and $D'$. Moreover, by rotating the edges in $D'$ incident to a vertex u, we can ensure that the two drawings of each edge (in D and $D'$) have consecutive ends in the rotation at u, for all vertices u. Rotating the edges in $D'$ can be done using a homeomorphism.

Since the vertex locations in both drawings are the same, we can speak about two drawings of an edge, one in D, one in $D'$, being the same or not. Using the detour lemma we will show that there is a sequence of slide moves and homeomorphisms that turns D into $D'$. Since a homeomorphism followed by a slide move can be replaced by a slide move followed by another homeomorphism, and two homeomorphisms in sequence are equivalent to a single homeomorphism, this implies the result.

We use induction on the number of edges in which D and $D'$ differ. Suppose an edge e is drawn differently in D and $D'$, and let $E_{=}$ be the set of edges whose drawings in D and $D'$ are the same (initially, $S(v) \subseteq E_{=}$). We use e and $e'$ to denote the drawing of e in D and $D'$, respectively, overloading the symbol e. Using a homeomorphism, if necessary, we can perturb the drawing of $e'$ slightly so that e and $e'$ intersect only finitely often. Since the rotation systems of D and $D'$ agree, e and $e'$ are equivalent with respect to S(v), so, by Lemma 3.2, there are arcs $\gamma _e \subseteq e$ and $\delta _e \subseteq e'$ such that e and $e'$ bound an empty bigon $\gamma _e \cup \delta _e$. If either, or both, the endpoints of $\delta _e$ are vertices of the edge, we note that there can be no edges that end at such a vertex inside the bigon, since we made the ends of e and $e'$ consecutive at their endpoints.

In other words, $\delta _e$ is a homotopic detour for $\gamma _e$, and we can apply Lemma 2.1 to redraw D so that e is routed arbitrarily close to $\delta _e$, and the number of crossings between e and $e'$ is reduced by at least two. We repeat this process, until e and $e'$ have no more crossings. By Lemma 3.2, e and $e'$ are the boundaries of an empty bigon, and we can apply Lemma 2.1 one more time to redraw e as $e'$. Since $e'$ was good with respect to all edges in $E_{=}$, none of the edges in $E_{=}$ gets modified in the redrawing, so $e = e'$ can now be added to $E_{=}$. $\square$

Remark 3.3

How many slide moves are required to turn two rotation-equivalent drawings of the complete graph into each other? By Theorem A.1, in the appendix, we can assume that two drawings of an edge e cross at most $O(n^6)$ times, which means we apply the detour lemma at most $O(n^6)$ times for each edge e of G (the redrawing reduces the number of crossings between the two drawings). Since there are fewer than $n^2$ edges, this gives us a bound of $O(n^8)$ on the number of applications of the detour lemma. By Lemma 2.2 every edge f of G requires at most $O(n^{10})$ slide moves in an application of the detour lemma (f can have at most $O(n^6)$ arcs crossing $\delta _e$ laterally, and there are at most $k\le n^4$ crossings overall). Since there are at most $n^2$ edges, this gives us $O(n^{12})$ slide moves per application of the detour lemma, leading to $O(n^{20})$ slide moves overall. Improved accounting may lead to better bounds, but at least we can say that the bound is polynomial.

3.1 An Extension of Gioan’s Theorem¹⁰

Can Gioan’s theorem be extended to non-complete graphs? This seems unlikely, at first glance, and it is easy to construct counterexamples. Figure 8 shows that a $K_5-K_2$ can have different drawings for which the rotation system is the same, but the pairs of edges that cross are not. In particular, these drawings are not isomorphic, so Gioan’s theorem, as we stated it, does not generalize to $K_5-K_2$, or any $K_n-K_2$, for $n \ge 5$.

Fig. 8

Three drawings of $K_5-K_2$ with the same rotation system; the drawings are not isomorphic, but become isomorphic if viewed as unlabeled graphs

Remark 3.4

One could attempt to salvage the result by allowing the underlying homeomorphism to ignore the vertex labels. Clearly, the three drawings shown in Fig. 8 are isomorphic if viewed as drawings of unlabeled graphs. It is easy to destroy such a homeomorphism by replacing an outer vertex with a very small $K_3$ (or larger complete graph), which lies inside the triangle. This leads to three drawings of $K_7-K_2$, for which the rotation systems are the same, but the three drawings cannot be made isomorphic by slide moves, even if we do not require vertex labels to be respected. For this reason, we do not further pursue this idea.

Let us try a different approach. We phrased Gioan’s theorem in terms of rotation systems, but Gioan originally stated his theorem for weak isomorphism types. Two drawings of a graph are weakly isomorphic if the same set of pairs of edges cross in both drawings. If two drawings are isomorphic, they are weakly isomorphic, but the converse need not be the case in general. For complete graphs, the rotation system of a drawing determines the weak isomorphism type [11, 15], and vice versa (up to all rotations reversing) [7, 12]. For incomplete graphs, that changes. In Appendix B, we show that for a $K_5-2K_2 = W_4$, a wheel with four spokes, its weak isomorphism type determines its isomorphism type.

Lemma 3.5

The weak isomorphism type of a good drawing of a $K_5-2K_2 = W_4$ uniquely determines its isomorphism type on the sphere.

This lemma allows us to extend Gioan’s theorem to complete graphs minus a non-perfect matching. The following result holds even if the matching is perfect.

Corollary 3.6

Let M be a matching in a $K_n$, $n \ge 5$. Then the weak isomorphism type of $K_n-M$ determines its rotation system (up to all rotations reversing).

Proof

For $n = 5$, this follows from Lemma 3.5 and Corollary B.2. For $n > 5$, all vertices have degree at least four. Let q be an arbitrary vertex and pick four arbitrary neighbors $\{a,b,c,d\}$ of q. Then the five vertices $\{q,a,b,c,d\}$ induce either a $K_5$, a $K_5-K_2$, or $K_5-2K_2 = W_4$ subgraph of $K_n-M$. In any case, q and the four edges qa, qb, qc, and qd belong to a $W_4$-subgraph of $K_5-M$, so the rotation of the four edges at q is determined by Lemma 3.5 (up to reversing the rotation). Suppose the rotation is abcd. We can then determine the full rotation at q (up to reversing): for every neighbor x of q we determine the rotation of $\{a,b,c,x\}$ at q. It will be one of axbc, abxc, or abcx (up to reversing). In the first two cases, we can easily combine this with abcd to conclude that the rotation at q is axbcd or abxcd, respectively. In the final case, the rotation could be abcdx or abcxd. We can easily figure out which, by determining the rotation of, for example, $\{c,d,x,a\}$ at q. Continuing like this, we can find the full rotation at every vertex, up to reversing. This gives us a rotation system for $K_n-M$, in which each rotation may be reversed. Since any two vertices have at least three common neighbors, though, we can use these to synchronize all rotations, so that either all, or none of them reverse. $\square$

When we review the proof of Theorem 1.1 to see what properties of the underlying (complete) graph we used, we find that we only need three properties: (i) the rotation system is determined (which it is, by Corollary 3.6 if we fix the weak isomorphism type of the drawing), (ii) the graph contains a spanning star S(w), and (iii) we can determine, for any two edges in S(w), in which order and direction they cross an edge f.

For a complete graph minus a matching, property (i) is satisfied by Corollary 3.6. If M is not a perfect matching, then $K_n-M$ contains a spanning star, so (ii) is satisfied. Finally, for (iii) we note that the graph induced by f and the two edges from S(w) induce a subgraph of $K_n-M$ which contains $K_5-2K_2 = W_4$ as a subgraph, so (iii) follows from Lemma 3.5. We conclude that Gioan’s theorem—phrased in terms of weak isomorphism type—holds for $K_n-M$.

Corollary 3.7

Let M be a non-perfect matching in $K_n$, $n \ge 5$. Any two weakly isomorphic, good drawings of a $K_n-M$ are isomorphic up to slide moves.

Can Gioan’s theorem be extended even further? The obviously missing case in Corollary 3.7 is a complete graph minus a perfect matching (so n is even). The first case to investigate here would be $K_6-3K_2$. Our method heavily relies on the existence of a spanning star, so it is not immediately clear whether it applies here. A complete list of good drawings of $K_6-3K_2$ may help to settle that specific case, see Remark B.1.

We can also consider removing two incident edges from a $K_5$, which results in the house X-graph $K_5-P_3$. This graph has two non-isomorphic plane drawings, so the weak isomorphism type does not determine its rotation, and it is also easy to see that a rotation system of a good drawing of this graph does not determine its weak isomorphism type. To proceed farther with removing adjacent edges then would either require strengthening our assumption to have both rotation system and weak isomorphism type, or to investigate the relationship between rotation system and weak isomorphism type of $K_n-P_3$ for larger n.

We leave Gioan’s theorem with one final remark. If two drawings of a graph are isomorphic up to slide rules, then clearly their rotation system and weak isomorphism type are the same. If an edge f crosses two edges g and h which do not cross each other, then slide moves cannot change the order and direction in which f crosses g and h. It follows that the order and direction in which an edge f crosses the edges of a star S(w) is not changed by slide moves. Hence, if there is a spanning star S(w), then the requirement that order and direction of crossing with S(w) do not change is a necessary and sufficient condition for there to be a sequence of slide moves turning one drawing of the graph into another (assuming they have the same rotation system and weak isomorphism type). So our method seems to be optimal in case there is a spanning star.

4 Pseudolinearity of Complete Graphs

For the proof of Theorem 1.5, we introduce one more notion: a drawing of a graph is x-bounded if for every edge uv, the curve representing uv lies entirely between u and v (with respect to x-coordinates). In the proof we will show how to modify the drawing using the detour lemma, and homeomorphisms, to make the drawing x-bounded, and then x-monotone.

Proof of Theorem 1.5

Fix a good drawing of the complete graph that does not contain a bad $K_4$. We will prove the result by induction on the number of vertices in the graph. In the base case we have at most four vertices. For $n \le 3$, $K_n$ has a unique drawing, which is isomorphic (in the plane) to a rectilinear, and, therefore, x-monotone drawing. Figure 2 shows that all non-isomorphic drawings of $K_4$ are isomorphic (in the plane) to an x-monotone drawing. So we can assume that $n \ge 5$.

We claim that the drawing contains a vertex incident to the outer region. If the outer region were not incident to any vertices, then there must be a crossing c incident to the outer region. Let e and f be the edges crossing in c. The graph induced by the endpoints of e and f is a $K_4$ with its crossing incident to the outer region, a bad $K_4$, which is not possible. So we can let v be a vertex incident to the outer region. Isomorphically redraw the graph so that S(v), the star centered at v, is drawn using straight-line segments, all neighbors of v lie on the same horizontal line, and v lies below that line, see Fig. 9. Moreover, we can ensure that no edge is drawn in the half-plane below v, that is, the horizontal line through v is not crossed by any edges.

We show how to make the drawing x-monotone using the detour lemma, so only using homeomorphisms and slide moves; neither of these change whether the drawing contains a bad $K_4$. In the first step we aim for an x-bounded drawing.

For $x \ne v$, let $\ell _x$ be the ray at v extending vx. Consider an edge xy between two neighbors of v, with x to the left of y. We already know that xy cannot cross below v. It also cannot cross any edge vw where w is to the left of x or to the right of y; if it did, then the $K_4$ induced by $\{v,x,y,w\}$ would be bad (the crossing between xy and vw is incident to the outer region of the $K_4$). Hence, xy can only cross edges vw with w between x and y.

Suppose that xy crosses $\ell _x$ or $\ell _y$, say $\ell _x$, without loss of generality. Since xy cannot cross vx, the drawing of the complete graph being good, it must cross $\ell _x$ beyond x. Let us first consider the possibility that xy attaches at x from the left side of $\ell _x$. We claim that for any edge xz that attaches to x in the wedge formed by xy and $\ell _x$ to the left of $\ell _x$ we must have that z lies to the right of x: if z were to the left of x, then xz cannot cross vy (as we argued earlier); it also cannot cross vx and xy, since those edges are adjacent to xz, and xy does not cross vz, so xz is caught in the cycle vxy and cannot reach z. See the left illustration in Fig. 10.

Fig. 9

Stretching S(v). Rays extending edges of S(v) are dotted

Fig. 10

Moving ends at x to the right side

Fig. 11

Stuck again

We can then take xy and all edges that end in the wedge between xy and $\ell _x$ and rotate them to the right side of $\ell _x$ (without changing the cyclic order of edges attaching to x, so the rotation at x remains the same), see Fig. 10. Repeating this for all edges xy, with $x,y\ne v$, we can ensure that an edge xy leaves its endpoints in the correct direction (towards the other endpoint). Now consider $\ell _x$. If xy crosses $\ell _x$ it must do so an even number of times (since xy leaves towards the right, must end to the right, and does not cross vx or pass below v). We can pick two crossings of xy with $\ell _x$ which are consecutive along $\ell _x$ (when ignoring crossings with edges other than xy); the subarc of $\ell _x$ connecting these two crossings is a detour for the subarc of xy between those same crossings, and we can apply the detour lemma to reroute xy along $\ell _x$, removing (at least) two crossings between xy with $\ell _x$. Repeating this process, we can remove all crossings of xy with $\ell _x$. Applying this redrawing for all edges and each endpoint, we obtain a drawing in which edges xy only cross rays $\ell _z$ where z lies between x and y. Assuming that the rays are reasonably close to vertical, the drawing is x-bounded; moreover, by construction, the drawing is good, and isomorphic (in the plane) to the original drawing.

In the second step we show how to turn the x-bounded drawing into an x-monotone drawing. Suppose some edge xy, where x is to the left of y, crosses a ray $\ell _z$ more than once. Let z be the left-most vertex with this property. We know that z must lie between x and y. Since x and y lie on opposite sides of $\ell _z$ (and xy does not pass below v), xy must cross $\ell _z$ an odd number of times, so at least three times. As we traverse xy and record crossings with $\ell _z$, these crossings are either with vz or with $\ell _z - vz$. Since xy can cross vz only once, this means that xy must cross $\ell _z-vz$ twice consecutively, unless xy crosses $\ell _z$ exactly three times, and the crossing with vz is the second (middle) crossing. In that case, xy first crosses $\ell _z-vz$ from left to right, then vz from right to left, and then $\ell _z-vz$ again from left to right. But then xy can no longer reach y, so this case is not possible, see Fig. 11.

Fig. 12

Directions of two consecutive crossings. Left: xy crosses $\ell _z-vz$ right-to-left followed by left-to-right. Right: xy crosses $\ell _z-vz$ left-to-right followed by right-to-left

We are left with two cases depending on whether the two consecutive crossings with $\ell _z-vz$ occur in the directions right-to-left followed by left-to-right, or vice versa (if there are more than three crossings, both cases may apply). Figure 12 illustrates both scenarios. In both scenarios, we have found a detour for xy along an arc of $\ell _z-vz$. We need to argue that in both cases the corresponding bigon is empty, to ensure the detour is homotopic, allowing us to apply the detour lemma.

In the first case the detour is homotopic, since the arc of xy between the two crossings cannot cross any ray between vx and vz, since it would have to do so twice (once with the arc of xy between x and vz), which contradicts the choice of z. If we are not in the first case, we must be in the second case, and xy crosses vz from left to right. Then the arc of $\ell _z-vz$ between the two consecutive crossings with xy is a homotopic detour: there cannot be a $z'$ such that the detour crosses $vz'$, since then xy would have to cross $vz'$ twice (once with the detour, and once with the arc of xy connecting vz to y). In either case, we have found a homotopic detour for xy, which allows us to remove two crossings of xy with $\ell _z$. Repeating this process, we can ensure that xy crosses every $\ell _z$ with z between x and y exactly once, and no other $\ell _z$, since xy cannot cross $\ell _x$ and $\ell _y$ as we saw earlier. We have shown that every edge intersects every $\ell _z$ at most once. We can now replace the drawings of edges between neighboring $\ell _z$ by straight-line segments without changing how often two edges cross (in every wedge, and, therefore, overall). Assuming the $\ell _z$ are sufficiently close to vertical (which we can ensure by moving v downwards), the drawing of the complete graph is now x-monotone. Since the drawing was obtained by a sequence of homeomorphisms (of the plane) and slide moves, the drawing remains good, and it still contains no bad $K_4$.

As in the proof of Gioan’s theorem, we can reorder the homeomorphisms and slide moves so that all slide moves get performed first, after which the drawing is isomorphic in the plane to an x-monotone drawing. To make that final x-monotone drawing isomorphic (in the plane) to the original drawing, we need to undo the slide moves (in reverse order). Suppose we have an empty triangle formed by crossings a, b, c with the crossings occurring in order $a<b<c$ from left to right. It does not matter which of the sides we slide over the opposite crossing, the resulting drawings are the same (up to homeomorphism), so we may as well slide edge e through ac over b. For this we simply redraw e by replacing ac with a detour along abc without crossing ab or bc. We conclude that the original drawing is isomorphic (in the plane) to an x-monotone drawing. $\square$

5 Conclusion

The main goal of this paper was to showcase the combination of the detour lemma with Kynčl’s spanning star approach. The approach yielded two known and one new result, the extension of Gioan’s theorem to the family $K_n-M$. What other results can be proven with this method? One immediate candidate is the link between x-monotone and pseudolinear drawings. We currently bridge this gap by referring to a result using different techniques. Can this gap be bridged with the techniques of this paper?

A more philosophical goal of the paper was to make the case that graph redrawing arguments can lead to constructive, and conceptually simple proofs. Along those lines, I also attempted a proof of Levi’s lemma, see [17]. A tempting open question here is suggested by Lemma 3.2; that lemma proves the special case of Hass and Scott’s classical result on curves on surfaces [10, Lemma 3.1] which we need for this paper, namely the planar case. Can our proof technique be extended to give a full graph-redrawing proof of Hass and Scott’s Lemma 3.1? Such a proof could be a first step in recasting and reproving the results of the Hass and Scott paper in graph-drawing terms.

Appendices

A Crossings in Simultaneous Drawings

The usual perturbation/general position argument can be invoked to show that during the redrawings performed in this paper, different drawings of the same edge intersect only finitely often. To bound the number of slide moves in applications of the detour lemma asymptotically, we need a more precise statement, which the following theorem supplies.¹¹ The result applies to cone graphs, graphs that have a spanning vertex.

Theorem A.1

  Suppose $D_1$ and $D_2$ are good drawings of the same cone graph G on n vertices. Then there is a good drawing $D'_2$ isomorphic to $D_2$ such that

• (i) the vertices of G have the same locations in $D_1$ and $D_2'$,

• (ii) any two edges in $D_1 \cup D_2'$ are drawn the same way, or cross at most $O(n^6)$ times,

• (iii) if $D_1$ and $D_2$ have the same rotation system, then the ends of $e_1 \in D_1$ and $e_2 \in D_2$, both corresponding to the same edge $e\in E(G)$, are consecutive at their vertices in $D_1 \cup D_2'$, or e is drawn the same way in both $D_1$ and $D_2'$.

Proof

Since G is a cone graph, there is a vertex w such that S(w) spans all of G. For a good drawing D of G we can do the following: cut the sphere along the edges of S(w). This results in a disk bounded by two copies of each edge of S(w) and $n-1$ copies of v (this is Kynčl’s star-cut representation [11]). Isomorphically redraw the disk, so that its boundary is a convex polygon. Since the drawing D was good, each edge of G crosses each boundary edge at most once, so an edge of G consists of at most n arcs in the star-cut drawing. Replacing each crossing with a degree-4 dummy vertex gives us a plane graph. Triangulating that drawing yields a 3-connected plane graph with a unique embedding (up to orientation-preserving homeomorphisms) by Whitney’s theorem [13]. We can now apply Tutte’s spring embedding theorem [18] to find a straight-line embedding of the plane graph in which the bounding convex polygon remains the same. Removing the edges we added, and converting dummy vertices back into crossings, gives us a drawing isomorphic to D in which every arc is a polygonal-arc consisting of at most $n^2$ straight-line segments (since each arc can cross at most $\left( {\begin{array}{c}n\\ 2\end{array}}\right) <n^2$ other arcs). Since each edge of G consists of at most n arcs, each edge of G consists of at most $n^3$ straight-line segments.

We now build star-cuts drawings for both $D_1$ and $D_2$ using the same convex (geometric) polygon based on S(w). Slightly perturbing points inside the disk, we can ensure there is no overlap between edges or crossing points. In this simultaneous drawing, there are at most $n^6$ crossings between any two edges (independently of whether they are based on $D_1$ or $D_2$).

We now glue the pieces of S(w) back together, to obtain a drawing D which contains a drawing $D'_1$ isomorphic to $D_1$ and a drawing $D^*_2$ isomorphic to $D_2$, and in this joint drawing S(w) is drawn the same way. In particular, all vertices are in the same location. Since $D_1$ and $D'_1$ are isomorphic, we can apply a homeomorphism of the plane to $D=D'_1\cup D^*_2$ that turns $D'_1$ into $D_1$. The result of that homeomorphism on $D^*_2$ is the drawing $D'_2$ we need for (i) and (ii).

Claim (iii) is achieved by homeomorphisms: in a small neighborhood of each vertex, rotate the edges of $D'_2$ until they satisfy (iii). This will introduce at most one crossing between any two edges incident to the same vertex belonging to different drawings, so the asymptotic analysis is not affected. $\square$

B Good Drawings of $W_4$

Recall that we want to prove Lemma 3.5: the weak isomorphism type of a good drawing of $W_4$ determines the drawing up to isomorphism. The most direct approach would be to study all non-isomorphic drawings of $W_4$ and prove that their weak isomorphism types differ.

There are two obstacles: (i) when listing non-isomorphic drawings, we typically do so for non-labeled graphs, so one has to take into account that there may be non-trivial automorphisms of the drawing (of the unlabeled graph); the drawings in Fig. 8 show that this difference matters; and (ii) there are no reliable lists of non-isomorphic good drawings of $W_4$. There is a such list in the paper by Gronau and Harborth [9], $W_4$ is $G_{31}$ in their list; however, there are at least two obvious mistakes in that list (the 11th drawing of $W_4$ shows a degree-2 vertex, and the 15th drawing looks like it has two degree-4 vertices). This is probably due to copying mistakes, but makes this a less than ideal basis for a proof. Hence, we opt for a direct proof.

Remark B.1

It would be highly desirable to have a tool that is able to generate all good drawings (maybe even bad [5] drawings) of small graphs (labeled and unlabeled) automatically, in some verifiable manner. There are algorithms in the literature (going as far back as Eggleton [6]), but implementations tend to focus on drawings of small complete, or small complete bipartite graphs.

Proof of Lemma 3.5

Fix a good drawing of $W_4$. The drawing determines a weak isomorphism type. We have to show that we can reconstruct the drawing, up to isomorphism, from the weak isomorphism type. It is sufficient to determine the rotation at each vertex, and the order and direction in which edges cross each other (for this, we fix an arbitrary orientation of the edges). Let q be the unique vertex of degree 4. Edges incident to q are called spokes, the remaining edges are cycle edges.

Claim 1: The rotation at q is determined. Let uv and xy be two disjoint cycle edges. Then the two 3-cycles quv and qxy intersect in q; the underlying curves of those two cycles may touch or cross in q: they touch, if edges qu, uv, qv cross edges qx, xy, qy an even number of times, otherwise they cross, and we can tell which, based on the weak isomorphism type. This test tells us whether qu and qv are neighbors in the rotation at q or not. If they are not neighbors, the rotation at q has to be uxvy (possibly requiring an orientation-reversing homeomorphism). Otherwise, there are two possible rotations: uvxy or uvyx (again up to isomorphism). We can tell which is the case, by checking whether qu and qx are neighbors (using the other two triangles at q).

Claim 2: The rotation at all cycle vertices is determined. Fix a cycle vertex u; for one of the two cycle edges uv incident to u, edges qu and qv must be neighbors in the rotation at q (they cannot both be opposite to qu in the rotation at q). Up to isomorphism, there are then four possible good drawings of the four spokes together with uv, as shown in Fig. 13.

The weak isomorphism type tells us which of the four cases we are in. Vertex u is incident to two cycle edges: uv, and a second edge e, which is either ux or uy. In all four cases, we know whether the other endpoint of e lies inside the triangle quv or not, and the weak isomorphism type tells us how often e crosses edges qu, uv, qv. From this, we can determine if the end of e at u is inside or outside the triangle, determining the rotation at u.

Claim 3: For every pair of edges, the direction of crossing is determined. Only pairs of independent edges can cross, so consider a pair of independent edges which cross. Suppose one of the two edges is a spoke qx, then the other edge must be a cycle edge uv. Consider the triangle quv. We know (using rotation at q and weak isomorphism type), whether x lies inside or outside of quv, and we know whether qx starts inside or outside quv. This tells us in which direction qx crosses uv. Otherwise, we have two cycle edges uv and xy which cross. Applying an orientation-preserving homeomorphism if necessary, we can choose the direction of crossing in this case. Since a good drawing of a $C_4$ can have at most one crossing, this happens at most once.

Claim 4: The order of crossing along each edge is determined. We argue the cases of spokes and cycle edges separately.

Consider a spoke qx (with at least two crossings, otherwise the order of crossings is trivial). In a good drawing of a $W_4$ a spoke can only cross two edges, the two cycle edges uv and vy (with $x\ne y,v,y$), so qx must cross both. The triangle quv splits the sphere into two regions, and we (arbitrarily) call the region containing the end of qx at q the inside of quv; so x will lie on the outside of quv, as shown in the left illustration of Fig. 14. If vy starts inside quv (something we can tell using the rotation at v), then qx crosses vy before it crosses uv. Otherwise, vy starts outside of quv. In this case, qx can cross uv and vy in either order, but the order depends on the direction of vy crossings qx, something we already know. Hence, we can determine the order.

We are left with the case of a cycle edge, call it xy; again, we assume it has at least two crossings. Let quv be the triangle on the remaining two spokes. In a good drawing of the $W_4$ the cycle edge xy can only cross edges qu, qv, and uv, and it must cross at least two of them (otherwise the order is trivial). In this case, we think of x as lying on the outside of quv, and xy crosses the boundary two or three times. In the case of two crossings, the order of crossings along xy is directly determined by the direction of the crossings (going inside quv first, then leaving again, second). In the case of three crossings, there are two orders consistent with the directions; see the two illustrations in the middle and on the right in Fig. 14; the vertices are relabeled $\{a,b,c\}=\{q,u,v\}$ to reduce the number of cases. Now y is incident to two of $\{a,b,c\}$, so it must be incident to a or b. Let us assume that there is an edge ya (the case yb is the same). If the edge ay starts inside the triangle abc, we are in the left case, otherwise, we are in the right case (since ay cannot cross xy). Since we know the rotation at a (by Claim 3), we can decide which case we are in, and determine the order of crossings along xy. $\square$

Fig. 13

The four good drawings of triangle quv with all four spokes

Fig. 14

Left: triangle quv with spoke qx crossing uv; vy can start inside or outside. Middle, right: triangle quv (labels renamed abc) and edge xy; directions of crossing of xy with ab, bc, and ac are the same in both drawings, the order of crossing is not

Corollary B.2

For $G\in \{K_5, K_5-K_2\}$, the weak isomorphism type of a good drawing of G determines the drawing up to isomorphism.

Proof

Fix a good drawing of G. Suppose an edge f is crossed by edges g and h (which the weak isomorphism type tells us). Then g and h must have a shared endpoint (since G contains no three independent edges). Then $\{e,g,h\}$ are part of a $W_4$-subgraph of G, and by Lemma 3.5 the order and direction of crossing of g and h with f is determined. Using this, we can find the order of all edges crossing f. $\square$