An Exploration of Locally Spherical Regular Hypertopes

Abstract

Hypertope is a generalization of the concept of polytope, which in turn generalizes the concept of a map and hypermap, to higher rank objects. Regular hypertopes with spherical residues, which we call regular locally spherical hypertopes, must be either of spherical, euclidean, or hyperbolic type. That is, the type-preserving automorphism group of a locally spherical regular hypertope is a quotient of a finite irreducible, infinite irreducible, or compact hyperbolic Coxeter group. We classify the locally spherical regular hypertopes of spherical and euclidean type and investigate finite hypertopes of hyperbolic type, giving new examples and summarizing some known results.

1 Introduction

Much of the recent work in the area of polytopes and hypertopes was inspired by the influential paper [17] by Branko Grünbaum, in which he defines the concept of a polystroma (coming from a Greek word for a layer or stratum) which generalizes the concept of a polytope by stripping it of its geometric properties while retaining its combinatorial structure.

This concept, further developed and formalized in [13, 27, 28], evolved through a number of publications by various authors in the eighties and nineties to that what was eventually named an abstract polytope. The comprehensive text [25] on the subject by McMullen and Schulte was published in 2002.

Of particular interest are highly symmetric such objects, known as regular abstract polytopes, which can be built from quotients of Coxeter groups with linear diagrams satisfying a certain condition known as the intersection property. In [16], Fernandes, Leemans and Weiss showed that it is natural to generalize this further, using the concept of a thin residually connected incidence geometry, by allowing objects that can be constructed from quotients of any Coxeter group. When the groups have non-linear Coxeter diagrams additional conditions (specified in Sect. 2) must be satisfied in order for such objects to have natural properties which generalize the concepts of both polytope and hypermap. While regular hypermaps had been thoroughly studied (starting with the seminal paper [10] by Corn and Singerman) and much data, including the determination of all regular and chiral hypermaps of small genus, is available in the literature (see for example [8]), very little is known about their higher dimensional analogues, the hypertopes. With this paper we hope to show how fundamental and how rich the theory of regular hypertopes is.

The structure of the paper is as follows. In Sect. 2 we give a brief overview of the basic theory (more details can be found in recent paper [16] by the same authors) and state some essential theorems that we will make use of in subsequent sections. We introduce the concept of a locally spherical hypertope but will only be interested in regular such objects in this paper. In Sect. 3 we give some general results on quotients of Coxeter groups and show how they can be used to construct regular locally spherical hypertopes. These hypertopes must be of either spherical, euclidean, or hyperbolic type and are respectively covered in Sects. 4, 5, and 6. In Sect. 4 we list all finite hypertopes of spherical type. In Sect. 5, we show that finite locally spherical hypertopes of euclidean type are toroids and review the relevant literature for the types of toroidal hypertopes that have already been classified, as well as for general results about normal subgroups of euclidean Coxeter groups. In Sect. 6 we survey the literature on locally spherical polytopes of hyperbolic type and provide some new examples of locally spherical hypertopes which are proper in the sense that their Coxeter diagrams are not linear.

2 Preliminaries

The concept of a hypertope, introduced recently in [16], is a generalization of an abstract polytope. There are different but equivalent ways to define (abstract) polytopes, one of which being that its faces form a partially ordered set that is a thin, residually connected geometry. This had been generalized in [16] to include structures built from a set of (what we still call) faces that do not form a partially ordered set.

We start with the definition of an incidence system$\Gamma := (X, *, t, I)$ as a 4-tuple having

• X as a set whose elements are called the elements, or faces, of $\Gamma$;

• I as a set whose elements are called the types of $\Gamma$;

• $t:X\rightarrow I$ as a type function, associating to each element $x\in X$ of $\Gamma$ a type $t(x)\in I$;

• $*$ as a binary relation on X called incidence, that is reflexive, symmetric and such that for all $x,y\in X$, if $x*y$ and $t(x) = t(y)$ then $x=y$.

The incidence graph of $\Gamma$ is the graph whose vertex set is X and where two vertices are joined provided the corresponding elements of $\Gamma$ are incident, omitting loops. A flag is a set of pairwise incident elements of $\Gamma$. The type of a flag F is $\{t(x) : x \in F\}$ and the rank of F is |F|. An i-face is an element of type i and a chamber is a flag of type I. An element x is incident to a flag F, and we write $x*F$ for that, provided x is incident to all elements of F. An incidence system $\Gamma$ is a geometry or incidence geometry if every flag of $\Gamma$ is contained in a chamber. The rank of $\Gamma$ is the cardinality of I. If $\Gamma = (X, *, t, I)$ is an incidence geometry and F is a flag of $\Gamma$, the residue of F in $\Gamma$ is the incidence geometry $\Gamma _F := (X_F, *_F, t_F, I_F)$ where $X_F := \{ x \in X : x * F,\, x \notin F\}$; $I_F := I {{\setminus }} t(F)$; $t_F$ and $*_F$ are the restrictions of t and $*$ to $X_F$ and $I_F$.

An incidence system $\Gamma$ is connected if its incidence graph is connected. It is residually connected when each residue of rank at least two of $\Gamma$ (including $\Gamma$ itself) has a connected incidence graph. It is called thin when every residue of rank one of $\Gamma$ contains exactly two elements. A hypertope is a thin, residually connected geometry. Residues of hypertopes are hypertopes.

We are particularly interested in the study of hypertopes having the highest possible level of symmetry. We will need to consider a notion of automorphism that allows permutation of types. Let $\Gamma =(X,*, t,I)$ be an incidence system. An automorphism of $\Gamma$ is a permutation $\alpha$ of X such that

• for each x, $y\in X$, $x*y$ if and only if $\alpha (x)*\alpha (y)$;

• for each x, $y\in X$, $t(x)=t(y)$ if and only if $t(\alpha (x))=t(\alpha (y))$.

An automorphism $\alpha$ induces a bijection on I. An automorphism $\alpha$ of $\Gamma$ is called type-preserving when for each $x\in X$, $t(\alpha (x))=t(x)$. The set of type-preserving automorphism of $\Gamma$ is a group denoted by ${\text {Aut}}_I\Gamma$. The set of automorphisms of $\Gamma$ is a group denoted by ${\text {Aut}}{\Gamma }$. A hypertope $\Gamma$ is regular if ${\text {Aut}}_I\Gamma$ acts regularly on the chambers (i.e., the action is semi-regular and transitive).

The Coxeter diagram of a regular hypertope $\Gamma = (X, *, t, I)$ is a graph whose vertices are the elements of I and a pair of elements $\{i,j\}$ are joined by an edge with label k whenever the residue of type $\{i,j\}$ is a k-gon with $k>2$. Observe that flag-transitive hypertopes with linear diagrams are precisely the regular abstract polytopes as the linearity of diagram induces a partial order on the set of its faces. We say that a flag-transitive hypertope is proper if it has a non-linear Coxeter diagram. For the class of hypertopes, the Coxeter diagram coincides with the Buekenhout diagram [4] for the diagram geometry defined by the hypertope.

A regular hypertope is irreducible if its Coxeter diagram is connected. Otherwise it is called reducible.

Let $I := \{0, \ldots , n-1\}$. When C is a chamber of a thin geometry, we let $C_i$ denote the chamber i-adjacent to C, that is, the chamber that differs from C only in its i-face. Given a regular hypertope $\Gamma$ and a chamber C of $\Gamma$, for each $i\in I$ let $\rho _i$ denote the automorphism mapping C to $C_i$. Then $\{\rho _0,\ldots , \rho _{n-1}\}$ is a generating set for ${\text {Aut}}_I\Gamma$ and $G_i=\langle \rho _j:j\ne i\rangle$ is the stabilizer of the i-face of C. Moreover $({\text {Aut}}_I\Gamma ,\{ \rho _0,\ldots , \rho _{n-1}\})$ is a C-group [16, Thm. 4.1], that is, $\{ \rho _0,\ldots , \rho _{n-1}\}$ is a set of involutions generating ${\text {Aut}}_I\Gamma$ and satisfying the following condition, called the intersection property:

$$\begin{aligned} \forall \, I, J \subseteq \{0, \ldots , n {-} 1\}\quad \ \langle \rho _i : i \in I\rangle \cap \langle \rho _j : j \in J\rangle = \langle \rho _k : k \in I \cap J\rangle . \end{aligned}$$

This property establishes that the group of type-preserving automorphisms of a regular hypertope is a smooth quotient of a Coxeter group. The Coxeter diagram of a C-group $(G,\{ \rho _0,\ldots , \rho _{n-1}\})$ is a graph with n vertices corresponding to the generators of G and with a k-edge between the vertices i and j whenever the order of $\rho _i\rho _j$ is k and $k>2$ (usually the label is omitted when $k=3$).

From now on, we will omit the generators from the notation of a C-group and simply denote it by G whenever from the context it is clear what the generating set is.

The subgroups $G_i$, $i\in \{0,\ldots , n-1\}$, of the group $\langle \rho _0,\ldots , \rho _{n-1}\rangle$ generated by involutions, are called the maximal parabolic subgroups of $\langle \rho _0,\ldots , \rho _{n-1}\rangle$. We denote by $G_{i,j}$ the subgroup of G generated by all the generators of G except $\rho _i$ and $\rho _j$. When all maximal parabolic subgroups, together with their respective generators, are C-groups the following proposition gives the conditions on their intersections for the group generated by all involutions be a C-group.

Proposition 2.1

[15, Prop. 6.1] Let G be a group generated by n involutions $\rho _0,\ldots , \rho _{n-1}$. Suppose that $G_i$ is a C-group for every $i\in \{0,\ldots ,n{-}1\}$. Then G is a C-group if and only if $G_i \cap G_j = G_{i,j}$ for all $0\le i,j \le n{-}1$.

The following proposition shows how, starting from a group G, and particularly from a C-group, we can construct an incidence system whose type-preserving automorphism group is G.

Proposition 2.2

(Tits 1956 [30]) Let n be a positive integer and $I:= \{0,\ldots ,n{-}1\}$. Let G be a group together with a family of subgroups ($G_i$)$_{i \in I}$, X the set consisting of all cosets $G_ig$ with $g \in G$ and $i \in I$, and $t:X \rightarrow I$ defined by $t(G_ig) = i$. Define an incidence relation $*$ on $X\times X$ by

$$\begin{aligned} G_ig_1 * G_jg_2 \quad \text {if and only if}\quad G_ig_1 \cap G_jg_2 \ne \emptyset . \end{aligned}$$

Then the 4-tuple $\Gamma := (X, *, t, I)$ is an incidence system having a chamber. Moreover, the group G acts by right multiplication on $\Gamma$ as a group of type-preserving automorphisms. Finally, the group G is transitive on the flags of type J with $J\subseteq I$ and $|J| \le 2$.

The incidence system constructed by the proposition above will be denoted by $\Gamma (G; (G_i)_{i\in I})$ and might not be a geometry, but if it is a geometry we call it a coset geometry. An incidence system constructed from a C-group using Proposition 2.2 does not give, in general, a regular hypertope (some examples can be found in [16]). It might not give a geometry at all (see Example 3.3). Nevertheless we have the following result which proves that from a C-group we can get a hypertope when the incidence system arising from Proposition 2.2 is flag-transitive.

Theorem 2.3

[16, Thm. 4.6]   Let $G=\langle \rho _0,\ldots ,\rho _{n-1}\rangle$ be a C-group of rank n and let $\Gamma :=\Gamma (G;(G_i)_{i\in I})$ with $G_i:=\langle \rho _j:j \in I{\setminus }\{i\}\rangle$ for all $i\in I:=\{0, \ldots , n{-}1\}$. If G is flag-transitive on $\Gamma$, then $\Gamma$ is a regular hypertope.

An incidence system constructed from a C-group $G=\langle \rho _0, \ldots , \rho _{n-1}\rangle$ of maximal parabolic subgroups $G_i=\langle \rho _j:j\ne i\rangle$ will be denoted by $\Gamma (G;\{\rho _0, \ldots , \rho _{n-1}\})$.

If we apply the construction of Proposition 2.2 to string C-groups, that is, groups with linear Coxeter diagram, then we necessarily get a polytope (as shown in the following theorem). For this reason there is a one to one correspondence between string C-groups and regular abstract polytopes.

Theorem 2.4

[1, 27, 28]   Let $G=\langle \rho _0, \ldots , \rho _{n-1}\rangle$ be a string C-group of rank r and let $\Gamma :=\Gamma (G;\{\rho _0, \ldots , \rho _{n-1}\})$. Then $\Gamma$ is thin, residually connected and regular. Moreover, $\Gamma$ has a linear Coxeter diagram.

Note that constructing polytopes from a set of generators of a string C-group and from the same set of generators taken in reverse order, in general results in two different polytopes; the two polytopes are said to be dual. As hypertopes, we will consider them “the same”. Indeed, as incidence geometries, they have the same set X of elements. Only the type function changes. A re-ordering of the types does not change the combinatorial structure of the hypertope. Hence, we classify the hypertopes up to isomorphism and re-ordering of the types. Consequently, in what follows the classification of hypertopes is given up to a graph isomorphism of their Coxeter diagrams.

Example 2.5

As an example of a proper (infinite) hypertope ${\mathcal {H}}$ we give that of a semi-regular tessellation of $\mathbb {E}^3$ by cubes of two colors. The hypertope is constructed from the Coxeter group with the following diagram (the generators $\rho _i$ are represented by dots labeled by i):

Bi-coloring the cubes of the cubic tessellation of $\mathbb {E}^3$ alternately with red and yellow, we define elements of type 0 as the red cubes, elements of type 2 as the yellow cubes, elements of type 3 as the points of the lattice $\mathbb {Z}^3 \subset \mathbb {E}^3$, and elements of type 1 as the edges joining vertices at distance 1 of each other. Incidence is defined as follows: A 3-element is incident to an i-element ($i=0, 1, 2$) if it is contained in that element. A 1-element is incident to an i-element ($i = 0, 2$) if it is an edge of the corresponding cube. A 0-element is incident to a 2-element if they have a square in common.

Every Coxeter group is a type-preserving automorphism group of a regular hypertope [30, Sect. 3] which we will call the universal hypertope associated with the Coxeter group. The type-preserving automorphism group of every regular hypertope ${\mathcal {H}}$, as explained above, is a quotient of a Coxeter group ${\mathcal {C}}$. The universal hypertope associated with the Coxeter group ${\mathcal {C}}$ is then called the universal cover of the hypertope${\mathcal {H}}$ and the Coxeter diagram of ${\mathcal {H}}$ is the diagram of its universal cover. The hypertope ${\mathcal {H}}$ is said to be of type ${\mathcal {C}}$. We note that there is basically no difference between Coxeter diagrams and the diagrams of regular hypertopes.

An irreducible regular hypertope (resp. polytope) is of euclidean type if its Coxeter diagram is the same as the Coxeter diagram of an infinite irreducible Coxeter group of euclidean type (resp. with linear diagram). Similarly, an irreducible regular hypertope (resp. polytope) is of spherical type if its Coxeter diagram is the same as the Coxeter diagram of a finite irreducible Coxeter group (resp. with linear diagram). Therefore, a hypertope is of euclidean type (resp. spherical type) if and only if the type-preserving automorphism group of its universal cover is an irreducible affine (resp. finite) Coxeter group. A regular hypertope is spherical if its Coxeter diagram is a union of diagrams of finite irreducible Coxeter groups. A locally spherical regular hypertope is a hypertope whose proper residues are spherical hypertopes. These definitions are in agreement with definitions of spherical and locally spherical polytopes in [25, Sect. 6B]. A projective hypertope (resp. polytope) is a regular hypertope obtained by factoring a spherical hypertope (resp. polytope) by a central symmetry (provided it exists). In Sect. 6 we will define a hypertope to be of hyperbolic type only for locally spherical hypertopes and see that locally spherical hypertopes are one of the spherical, euclidean, or hyperbolic type.

In the remainder of the paper we will restrict the discussion to irreducible locally spherical hypertopes.

3 Quotients of Regular Locally Spherical Hypertopes

In the classification of regular hypertopes with a given diagram, quotient relations play an important role. In what follows, we extend to regular hypertopes some results known for abstract regular polytopes. The following theorem is a generalization of [25, Thm. 2E17], called the quotient criterion.

Theorem 3.1

Let $G:=\langle \rho _0, \ldots , \rho _{n-1}\rangle$ be a group generated by involutions and $H := \langle \delta _0, \ldots , \delta _{n-1}\rangle$ be a C-group. If the mapping $\sigma :G\rightarrow H$ with $\sigma (\rho _i) = \delta _i$ for each $i=0, \ldots , n{-}1$ is a homomorphism which is one-to-one on $G_i$ for each $i=0, \ldots , n{-}1$, then G is also a C-group.

Proof

By Proposition 2.1 we need to prove that $G_i\cap G_j=G_{i,j}$ for every $i,j\in \{0,\ldots , n{-}1\}$. Let $x\in G_i\cap G_j$. Then $\sigma (x)\in H_i\cap H_j$. Since by hypothesis H is a C-group, $H_i\cap H_j=H_{i,j}$ (by Proposition 2.1). Therefore $\sigma (x) \in H_{i,j}$ and $\sigma (x)$ has a pre-image in $G_{i,j}$. Then, $\sigma$ induces one-to-one homomorphism on $G_i$ and one-to-one homomorphism on $G_j$ so that x is the only pre-image of $\sigma (x)$ in $G_i$ and in $G_j$. Therefore $x \in G_{i,j}$. $\square$

Let $\Gamma := (X, *, t, I)$ be an incidence system and N a normal subgroup of ${\text {Aut}}_I\Gamma$. The quotient of$\Gamma$with respect toN is an incidence system $\Gamma$$/N:=(\bar{X}, *_N, t_N, I)$ where

• $\bar{X}$ is the set $\{F \cdot N:F\in X\}$ of orbits of N in X;

• for $F_1,F_2\in X$, $(F_1 \cdot N) *_N (F_2 \cdot N)$ if and only if there exist a face F in $F_1\cdot N$ and a face G in $F_2\cdot N$ such that $F*G$; and

• $t_N(F \cdot N)=t(F)$.

Theorem 3.2

Let ${\mathcal {U}}$ be a regular hypertope and $U:=\langle \delta _0, \ldots , \delta _{n-1}\rangle$ be its type-preserving automorphism group. Let $N{\triangleleft }U$ be such that $N\cap U_i = \{1\}$ for all $i=0,\ldots , n{-}1$. Let $H_i=\langle \delta _jN :j\in \{0,\ldots ,n{-}1\}{\setminus } \{i\}\rangle$ for all $i=0,\ldots ,n{-}1$. If $\Gamma (U/N;\{ H_0, \ldots , H_{n-1}\})$ is a flag-transitive coset geometry then it is a regular hypertope and it is isomorphic to ${\mathcal {U}}/N$.

Proof

The group U/N with the generators $\{ \delta _0N, \ldots , \delta _{n-1}N\}$ is a group generated by involutions and since $N\cap U_i = \{1\}$ for all $i=0, \ldots , n{-}1$, the mapping $\sigma :U/N \rightarrow U$ with $\sigma (\delta _iN) = \delta _i$ satisfies the hypotheses of Theorem 3.1. Therefore U/N is a C-group. Theorem 2.3 then implies that ${{\mathcal {U}}}/N$ is a hypertope. $\square$

The following example shows that in the previous theorem flag-transitivity is required for the quotient to be a geometry.

Example 3.3

Starting from the hypercube, a spherical polytope of type $B_4=\langle \rho _0,\rho _1,\rho _2,\rho _3\rangle$ (see Table 1 for notation), we can construct the universal spherical hypertope of type $D_4=\langle \tilde{\rho }_0,\rho _1,\rho _2,\rho _3\rangle$, where $\tilde{\rho }_0=\rho _1^{\rho _0}$, in the following way. The 1-skeleton of the hypercube is a bipartite graph whose vertex-set can therefore be colored using two colors, say black and white. Elements of type 0 (respectively 1) are the black (respectively white) vertices. Elements of type 3 are the cubes¹ of the hypercube. Elements of type 2 are the square faces of the hypercube. Factoring $D_4$ by its normal subgroup $N=\langle (\tilde{\rho _0}\rho _1\rho _2\rho _3)^3\rangle =\{\pm 1\}$ (the group generated by a longest element in $D_4$ represented in the following figure by a red path) has the effect of identifying pairs of opposite vertices, and pairs of disjoint cubes (Fig. 1).

Fig. 1

Longest element representation for the hypertope of type $D_4$

Now, given a cube C and a cube disjoint from it, there are four pairs of opposite white vertices and four pairs of black vertices incident to them. Take a pair of white vertices W and a pair of black vertices B such that their incidence in the whole geometry is via the edge joining the two disjoint cubes. The set $\{C, W, B\}$ is a flag of $D_4/N$ that is not contained in any chamber of $D_4/N$. Hence this quotient does not give a hypertope.

Theorem 3.4

Let ${\mathcal {H}}:={\mathcal {H}}(G;\{\rho _0, \ldots , \rho _{n-1}\})$ be a regular locally spherical hypertope and ${\mathcal {U}}=(U;\{ \delta _0, \ldots , \delta _{n-1}\})$ be its universal cover. Then there exists a subgroup $N{\triangleleft }U$ such that $N\cap U_i = \{1\}$ for each $i=0,\ldots , n{-}1$ and $G \cong U/N$. Finally, ${{\mathcal {H}}}\cong {{\mathcal {U}}}/N$.

Proof

The mapping $\delta _i\mapsto \rho _i$, for $i=0,\ldots , n{-}1$, induces an epimorphism $\sigma :U \rightarrow G$ and $N:={\text {Ker}}{\sigma }$ has the required properties. $\square$

4 Regular Hypertopes of Spherical Type

A regular hypertope of spherical type is a quotient of a universal hypertope of spherical type by a normal subgroup (by Theorem 3.4). As in the case of Coxeter groups, it is sufficient to classify irreducible regular hypertopes, the reducible ones being direct sums of irreducible hypertopes, corresponding to the connected components of the Coxeter diagram. Coxeter diagrams of irreducible regular hypertopes of spherical type are those of the finite irreducible Coxeter groups, the list of which can be seen in Table 1. In [22] all normal subgroups of finite and affine Coxeter groups are characterized using graph homomorphisms. A homomorphism $\varphi :G\rightarrow H$ is a graph homomorphism between Coxeter groups $G=\langle \rho _0,\ldots ,\rho _{r-1}\rangle$ and $H=\langle \delta _0,\ldots ,\delta _{n-1}\rangle$, if the following conditions are satisfied:

• for each $i\in \{0,\ldots , r{-}1\}$ either $\varphi (\rho _i)=\delta _j$ for some $j\in \{0,\ldots , n{-}1\}$ or $\varphi (\rho _i )=1_H$; and

• for each $i\in \{0,\ldots , n{-}1\}$, $\delta _i=\varphi (\rho _j )$ for some $j\in \{0,\ldots , r{-}1\}$.

The following theorem characterizes the normal subgroups of the finite Coxeter groups. Recall that in a Coxeter group, a product of all the generating reflections gives a so-called Coxeter element. Taking a different order of generators in a product produces conjugate Coxeter elements. Thus, they have same order h and if h is even, any Coxeter element to the power h/2 is an involution. The normal subgroup $N=\{\pm 1\}$ in the theorem below is the group generated by the longest element of the Coxeter group, that is any Coxeter element to the power h/2.

Theorem 4.1

[22, Thm. 0.1] If G is an irreducible finite Coxeter group and N is a normal subgroup of G, then either $N=\{\pm 1\}$ or $N={\text {Ker}}{\varphi }$ where $\varphi$ is a graph homomorphism between G and a finite Coxeter group.

Table 1 Locally spherical hypertopes of spherical type

The rotation subgroup of G denoted by $G^+$ is always a normal subgroup of G. The other normal subgroups of Coxeter groups arising from graph automorphisms are listed in Tables 2 and 3 of [22].

Theorem 4.2

There exists a unique regular hypertope for each of the diagrams $A_n$, $D_n$, $E_6$, and $I_2$. There are exactly two regular hypertopes for each of the diagrams $B_n$, $E_7$, $E_8$, $F_4$, $H_3$, and $H_4$.

Proof

Let ${\mathcal {H}}$ be a regular hypertope of rank n having one of the diagrams of the irreducible finite Coxeter groups listed in Table 1 (and [25, Table 3B1]). By Theorem 3.4, ${\mathcal {H}}$ is a quotient of its universal cover ${\mathcal {U}}=(U;(U_0,\ldots ,U_{n-1}))$ by a normal subgroup N such that $N\cap U_i = \{1\}$ for each $i=0, \ldots , n{-}1$. Tables 2 and 3 of [22] list all non-trivial normal subgroups of finite irreducible Coxeter groups different from their rotation subgroups. All normal subgroups listed in [22, Table 3] have a non-trivial intersection with at least one maximal parabolic subgroup $U_i$ of the universal cover. Thus N must be one of the groups of [22, Table 2]. We now deal with each of the diagrams in Table 1 separately.

First suppose that ${\mathcal {U}}$ is of one of the types $A_n$, $D_n$ (n odd), and $E_6$. [22, Table 2] shows that there are no normal subgroups besides the rotation subgroups. Thus ${\mathcal {H}}\cong {\mathcal {U}}$.

Now suppose that ${\mathcal {U}}$ is the universal regular hypertope of type $D_n$ ($n\ge 4$, n even). Let us prove that the number of chambers of ${\mathcal {H}}$ must be $2^{n-1}n!$ and therefore that ${\mathcal {H}}\cong {\mathcal {U}}$. We proceed by induction. Assume that $n=4$. By [9, Lem. 2.3] the smallest hypertope with diagram isomorphic to a star-shaped diagram with three unlabeled edges has at least 120 chambers. On the other hand the number of chambers of the 4-hypertope of type $D_4$ must be a divisor of $2^3\cdot 4!=192$ and hence the number of chambers must be exactly 192. Now let $n>4$. Let 0, 1, and 2 be the three types corresponding to the nodes of the Coxeter diagram, as follows.

Let $x_i$ be an i-face with $i\in \{0,1,2\}$. The residue of $x_i$ is an $(n{-}1)$-simplex when $i\in \{1,2\}$. By induction assume that the residue of $x_0$ is a regular hypertope with $2^{n-2}(n{-}1)!$ chambers. Let $i\in \{1,2\}$. The residue of $x_i$ is an $(n{-}1)$-simplex and therefore has n 0-faces. Suppose that the hypertope has exactly n 0-faces. Then $x_1$ and $x_2$ are both incident to all 0-faces, which is not possible as this would imply that the residue of type $\{0\}$ would have n elements, and therefore the geometry would not be thin. Thus the hypertope has at least $n{+}1$ 0-faces and therefore the number of chambers must be at least $2^{n-2}(n{-}1)!(n{+}1)$. Hence its group of type-preserving automorphisms must have the largest possible size, that is, $2^{n-1}n!$

Let ${\mathcal {U}}$ be the Coxeter group with diagram $B_n$. We now prove that the number of chambers of ${\mathcal {H}}$ is either $2^{n}n!$ or $2^{n-1}n!$ corresponding to the universal and the projective regular polytopes of this type, respectively. This is equivalent to saying that there are exactly two regular hypertopes with diagram $B_n$, namely ${\mathcal {U}}$ and ${\mathcal {U}}/\{\pm 1\}$. This is well known for $B_4$ and we now assume it is true for rank less than n. We may assume that a vertex-figure has type $B_{n-1}$ and hence has either $2^{n-2}(n{-}1)!$ or $2^{n-1}(n{-}1)!$ chambers, while a facet has at least $n{+}1$ vertices. Therefore the number of chambers of a regular hypertope of type $B_n$ is greater than $2^{n-2}n!$ as wanted.

The remaining cases can be dealt with Magma [2]. If ${\mathcal {U}}$ has a linear diagram $F_4$, $H_3$, or $H_4$ then using Table 1 we see that in each case there is only one possibility for N, that is $\{ \pm 1\}$. Thus for each diagram there are exacly two possibilities for ${\mathcal {H}}$, either the universal or the projective hypertope isomorphic to ${\mathcal {U}}/\{\pm 1\}$. If ${\mathcal {U}}$ has one of the diagrams $E_7$ or $E_8$, using Table 1 we see that either ${\mathcal {H}}\cong {\mathcal {U}}$ or ${\mathcal {H}}\cong {\mathcal {U}}/\{\pm 1\}$. Using Magma, we can easily check that all these cases give hypertopes. $\square$

Theorem 4.3

All proper residues of regular hypertopes of spherical type are spherical hypertopes.

Proof

Only projective hypertopes can have projective residues, but for that to happen a Coxeter element needs to be in a proper residue which is impossible. $\square$

Hence all locally spherical regular hypertopes of spherical type are either spherical or projective hypertopes. Table 1 gives the complete list. Observe that there are hypertopes (in fact polytopes) of euclidean type that have proper sections which are projective, such as, e.g., the polytope $\{\{4,3\}_6,\{3,4\}_3\}$ (see [29]). Other examples can be found in [18].

5 Locally Spherical Regular Hypertopes of Euclidean Type

In this section we consider regular hypertopes whose Coxeter diagrams correspond to infinite irreducible Coxeter groups of euclidean type listed in the left column of Table 2. Theorem 4.2 implies that all proper residues of regular hypertopes of euclidean type are either spherical or projective. Here we only consider those with spherical residues.

Let us start with a simple but important observation following from Theorem 3.2.

Corollary 5.1

Every locally spherical regular hypertope of euclidean type is a quotient of its universal cover by a normal subgroup that lies in the translation subgroup of the automorphism group of its universal cover.

Proof

Let ${\mathcal {H}}$ be a hypertope of euclidean type and ${\mathcal {U}}$ its universal cover. Then, by [22, Thm. 0.2] and Theorem 3.2, the only possibility for the normal subgroup N of the Coxeter group of euclidean type to avoid the maximal parabolic subgroups (in order to keep the same Coxeter diagram) is that N lies in the translation subgroup of the Coxeter group. $\square$

In analogy with regular toroidal polytopes (toroids), we say that a regular toroidal hypertope of rank$n{+}1$ or $(n{+}1)$-toroid is a quotient of a regular universal hypertope of rank $n{+}1$ of euclidean type by a normal subgroup of its translational symmetries (in ${\mathbb {E}}^n$). It follows from Corollary 5.1 that any finite regular hypertope of euclidean type is a toroidal hypertope which we will briefly call a toroid.

Rank 3 toroids have been classified. They must have the following linear or triangular Coxeter diagrams.

The first two diagrams are those of regular tessellations on a torus and the last one is that of a regular hypermap on a torus. The regular (and also chiral) toroidal maps have been classified by Coxeter [11] and hypermaps by Cacciari [7]. Up to duality, they belong to the following families: $\{4,4\}_{(s,0)}$ with $s\ge 2$; $\{4,4\}_{(s,s)}$ with $s\ge 1$; $\{3,6\}_{(s,0)}$ with $s\ge 2$; $\{3,6\}_{(s,s)}$ with $s\ge 1$; $(3,3,3)_{(s,0)}$ with $s\ge 2$, and $(3,3,3)_{(s,s)}$ with $s\ge 2$. The vectors in the subscripts determine in each case the translation subgroup used, and the restriction on s guaranties that the hypertopes are large enough so that they do not degenerate.

Finite toroidal polytopes (hypertopes with linear diagram) for higher ranks had been classified by McMullen and Schulte [24] (see also [25, 6D and 6E]). We denote by $\Lambda ^n$ the group of all translations of ${\mathbb {E}}^n$ with integral translation vectors, and think of it as the lattice $\mathbb {Z}^n$, and by $\Lambda ^n_{\mathbf{s}}$ the sublattice generated by ${\mathbf{s}}:=(s^k,0^{n-k})$.

• Polytopes of type ${\tilde{C}}_n$, also known as cubic $(n+1)$-toroids (corresponding to regular tessellations of n-torus by n-cubes) belong to one of the following three infinite families $\{\tilde{C}_n\}_{\mathbf{s}}=\{4,3^{n-2},4\}_{\mathbf{s}}$ where

  $$\begin{aligned} {\mathbf{s}}=(s^k,0^{n-k}) \quad \text {with}\quad s\ge 2\ \text {and}\ k=1,2, n, \end{aligned}$$

  and where the quotient, by $\Lambda ^n_{\mathbf{s}}$, of the standard cubical lattice $\{4,3^{n-2},4\}$ with vertex-set $\mathbb Z^n$ is denoted simply by $\{4,3^{n-2},4\}_{\mathbf{s}}$.

• Polytopes of type $\tilde{F}_4$, belong to one of the following two infinite families of 5-toroids $\{\tilde{F}_4\}_{\mathbf{s}}=\{3,3,4,3\}_{\mathbf{s}}$ where

  $$\begin{aligned} {\mathbf{s}}=(s^k,0^{4-k})\quad \text {with}\quad s\ge 2 \ \text {and} \ k=1, 2, \end{aligned}$$

  and where similarly the quotient, by $\Lambda ^4_{\mathbf{s}}$, of the regular tessellation $\{3,3,4,3\}$ with vertex-set $\mathbb Z^4\cup (({1}/{2},{1}/{2},{1}/{2},{1}/{2})+\mathbb Z^4)$ is denoted by $\{3,3,4,3\}_{\mathbf{s}}$.

Using the methods of McMullen and Schulte and the notation as above, in [14] Ens classified finite rank 4 toroidal hypertopes with non-linear diagrams as follows.

• Finite toroidal hypertopes of rank 4 and type $\tilde{B}_3$, belong to one of the following three infinite families of type $\{\tilde{B}_3\}_{\mathbf{s}}$ where

  $$\begin{aligned} {\mathbf{s}}=(2s,0,0) \ \text {or} \ (s,s,0) \ \text {with} \ s\ge 2, \quad \text {or}\quad \mathbf{{s}}=(2s,2s,2s) \ \text {with}\ s \ge 1. \end{aligned}$$

• Finite toroidal hypertopes of rank 4 and type $\tilde{A}_3$, belong to one of the following three infinite families of type $\{\tilde{A}_3\}_{\mathbf{s}}=(3,3,3,3)_{\mathbf{s}}$ where

  $$\begin{aligned} {\mathbf{s}}=(2s,0,0) \ \text {or} \ (s,s,0)\ \text {with} \ s\ge 2, \quad \text {or}\quad \mathbf{{s}}=(2s,2s,2s) \ \text {with}\ s \ge 1. \end{aligned}$$

To complete the classification of finite locally spherical euclidean hypertopes it is necessary, as proven in Sect. 3, to enumerate normal subgroups of the corresponding Coxeter groups which have trivial intersection with the maximal parabolic subgroups of the Coxeter group. In fact the enumeration of all normal subgroups of Coxeter groups of euclidean type can be found in [22, Sect. 7] and the lattice subgroups in Table 5. Corollary 5.1 together with Maxwell’s results can be used to construct finite toroids of each hypertope of euclidean type.

In the forthcoming paper [21] we extend the results of McMullen and Schulte on toroidal polytopes to that on hypertopes, thus completing the geometric classification of toroidal hypertopes in each rank.

Table 2 Diagrams of locally spherical hypertopes of euclidean and hyperbolic types

6 Locally Spherical Hypertopes of Hyperbolic Type

A locally spherical regular hypertope is of hyperbolic type if the irreducible residues of the type-preserving automorphism group of its universal cover are compact hyperbolic Coxeter groups (that is, groups generated by hyperbolic reflections with compact fundamental domain). Compact hyperbolic Coxeter groups exist only in ranks 3, 4, and 5. The complete list of their diagrams is given in Table 2 (see, for example [20, Sect. 6.9] or [25, 3C]). Examining all possible Schläfli symbols for locally spherical regular hypertopes we easily see that universal locally spherical hypertopes are either of spherical, euclidean, or of hyperbolic type.

The rank 3 hypertopes have the following Coxeter diagrams:

where p, q are integers with $3\le p,q <\infty$ and ${1}/{p}+{1}/{q}<{1}/{2}$, or

where k, l, m are integers with $3\le k,l,m <\infty$ and ${1}/{k}+{1}/{l}+{1}/{m}<1$. There are infinitely many finite rank 3 polytopes (non-degenerate maps) arising from the tessellations of the hyperbolic plane (having the rank 3 linear diagrams above), and infinitely many finite (non-degenerate, proper) hypermaps arising from the rank 3 triangular diagrams above. These had been extensively studied and written about in literature. In the seminal paper [10], Corn and Singerman showed that every regular (which they call reflexive) hypermap of that kind is a quotient of the universal hypermap obtained from the group $\langle x,y:x^k=y^m=(xy)^l=1\rangle$ and that the universal hypermap is regular.

Corollary 4C5 in [25] implies that in ranks 4 and 5 there are infinitely many finite locally spherical polytopes of hyperbolic type. Unfortunately, examples of these are not easy to find as the proof is non-constructive. However, a number of polytopes for certain types can be found in literature.

Using modular reduction of the Coxeter group [3, 5, 3], with moduli given by primes in $\mathbb Z[\tau ]$ (where $\tau$ is the golden ratio), Monson and Schulte constructed infinitely many finite regular locally spherical polytopes of type $\{3,5,3\}$ (see [26, Prop. 5.1]).

There is an infinite family of locally spherical polytopes of hyperbolic type $\{4,3,5\}$ (described in [3, 7.1]) with automorphism groups $D_s^6 \rtimes [3,5]$, $s \ge 2$, where $D_s=I_2(s)$ denotes the dihedral group of order 2s.

Table 3 Small regular locally spherical 4-hypertopes of hyperbolic type

There are also two locally spherical polytopes of hyperbolic type $\{5,3,5\}$ with respective type-preserving automorphism groups $J_1\times J_1$ and $J_1\times J_1\times L_2(19)$. They were constructed by Hartley and Leemans in [19]. Another example of the same type is the classical regular star-polytope $\{{5}/{2},3,5\}$ in euclidean 4-space obtained by a sequence of several stellations of $\{5,3,3\}$ (see [12, 14.2]). As an abstract polytope it is a finite locally spherical polytope of hyperbolic type $\{5,3,5\}$. It has 120 dodecahedral facets (which in euclidean 4-space are realized as great stellated dodecahedra whose 2-faces are pentagrams $\{{5}/{2}\}$), 120 icosahedral vertex-figures, and the group of order 14400. The automorphism group of the polytope, which is $H_4=[5,3,3]=[5,3,5\,|\,3]$ (here we used the extended Schläfli symbol where the number 3 following | indicates that the polytope has triangular holes), can be obtained from [5, 3, 5] (the symmetry group of the regular tessellation $\{5,3,5\}$ of the hyperbolic 3-space) by imposing the extra relation

$$\begin{aligned} (\rho _0 \rho _1 \rho _2 \rho _3 \rho _2 \rho _1)^3=id \end{aligned}$$

(see [23, p. 435]). Similarly $\{{5}/{2},3,3,5\}$, obtained from $\{3,3,3,5\}$ (see [23, Sect. 6]), can be seen as a locally spherical rank 5 polytope of hyperbolic type $\{5,3,3,5\}$ arising from regular tessellation of hyperbolic 4-space by 120-cells) and imposing the extra relation

$$\begin{aligned} (\rho _0 \rho _1 \rho _2 \rho _3 \rho _4 \rho _3 \rho _2 \rho _1)^3=id \end{aligned}$$

(see [23, pp. 441–442]).

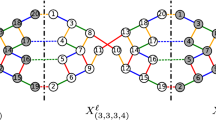
In Table 3 we give a list of small regular finite locally spherical hypertopes of rank 4 of hyperbolic type. Here, by extension of the notation for hypermaps, we denote by (p, q, r, s) the hypertope with a square diagram whose successive edges have labels p, q, r, and s. Furthermore, the hypertope of type $\bigl \{5,{}^3_3\bigr \}$ is the hypertope with diagram $\bigl [5,{}^3_3\bigr ]$ in Table 2. In particular, we computed the smallest example of each type using Magma. For each hypertope we specify the type-preserving automorphism group in the second column (here we note that $\cdot$ stands for a non-split extension).

Our computations searching for small rank 5 hyperbolic proper hypertopes were inconclusive as the groups involved seem to be too large for a successful application of the LowIndexNormalSubgroups function of Magma.