Rounding Meshes in 3D

Abstract

Let ${\mathcal {P}}$ be a set of n polygons in ${\mathbb {R}}^3$, each of constant complexity and with pairwise disjoint interiors. We propose a rounding algorithm that maps ${\mathcal {P}}$ to a simplicial complex ${\mathcal {Q}}$ whose vertices have integer coordinates. Every face of ${\mathcal {P}}$ is mapped to a set of faces (or edges or vertices) of ${\mathcal {Q}}$ and the mapping from ${\mathcal {P}}$ to ${\mathcal {Q}}$ can be done through a continuous motion of the faces such that: (i) the $L_\infty$ Hausdorff distance between a face and its image during the motion is at most 3/2, and (ii) if two points become equal during the motion, they remain equal through the rest of the motion. In the worst case the size of ${\mathcal {Q}}$ is $O(n^{13})$ and the time complexity of the algorithm is $O(n^{15})$ but, under reasonable assumptions, these complexities decrease to $O(n^{4}\sqrt{n})$ and $O(n^{5})$. Furthermore, these complexities are likely not tight and we expect, in practice on non-pathological data, $O(n\sqrt{n})$ space and time complexities.

1 Introduction

Rounding 3D polygonal structures is a fundamental problem in computational geometry. Indeed, many implementations dealing with 3D polygonal objects, in academia and industry, require as input pairwise-disjoint polygons whose vertices have coordinates given with fixed-precision representations (usually with 32 or 64 bits). On the other hand, many algorithms and implementations dealing with 3D polygonal objects in computational geometry output polygons whose vertices have coordinates that have arbitrary-precision representations. For instance, when computing boolean operations on polyhedra, some new vertices are defined as the intersection of three faces and their exact coordinates are rational numbers whose numerators and denominators are defined with roughly seven times the number of bits used for representing each input coordinate. When applying a rotation to a polyhedron, the new vertices have coordinates that involve trigonometric functions. When sampling algebraic surfaces, the vertices are obtained as solutions of algebraic systems and they may require arbitrary-precision representations since the distance between two solutions may be arbitrarily small (depending on the degree of the surface).

This discrepancy between the precision of the input and output of many geometric algorithms is an issue, especially in industry, because it often prevents the output of one algorithm from being directly used as the input to a subsequent algorithm.

In this context, there exists no solution for rounding the coordinates of 3D polygons with the constraint that their rounded images do not properly intersect and that every input polygon and its rounded image remain close to each other (in Hausdorff distance). In practice, coordinates are often rounded without guarding against changes in topology and there is no guarantee that the rounded faces do not properly intersect one another.

The same problem in 2D for segments, referred to as snap rounding, has been widely studied and admits practical and efficient solutions [1, 5,6,7,8,9,10,11, 14]. Given a set of possibly intersecting segments in 2D, the problem is to subdivide their arrangement and round the vertices so that no two disjoint segments map to segments that properly intersect. For clarity, all schemes consider that vertices are rounded on the integer grid. It is well known that rounding the endpoints of the edges of the arrangement to their closest integer point is not a good solution because it may map disjoint segments to properly intersecting segments. Snap rounding schemes propose to further split the edges when they share a pixel (a unit square centered on the integer grid). In such schemes, disjoint edges may collapse but this is inevitable if the rounding precision is fixed and if we bound the Hausdorff distance between the edges and their rounded images. Furthermore, it is NP-hard to determine whether it is possible to round simple polygons with fixed precision and bounded Hausdorff distance, and without changing the topological structure [13].

In dimension three, results are extremely scarse, despite the significance of the problem. Goodrich et al. [5] proposed a scheme for rounding segments in 3D, and Milenkovic [12] sketched a scheme for polyhedral subdivisions but, as pointed out by Fortune [4], both schemes have the property that rounded edges can cross. Fortune [3] suggested a high-level rounding scheme for polyhedra but in a specific setting which does not generalize to polyhedral subdivisions [4]. Finally, Fortune [4] proposed a rounding algorithm that maps a set ${\mathcal {P}}$ of n disjoint triangles in ${\mathbb {R}}^3$ to a set ${\mathcal {Q}}$ of triangles with $O(n^4)$ vertices on a discrete grid such that: (i) every triangle of ${\mathcal {P}}$ is mapped to a set of triangles in ${\mathcal {Q}}$ at $L_\infty$ Hausdorff distance at most 3/2 from the original face, and (ii) the mapping preserves or collapses the vertical ordering of the faces. Unfortunately, this rounding scheme is very intricate and, moreover, it uses a grid precision that depends on the number n of triangles: the vertices coordinates are rounded to integer multiples of about 1/n.

The difficulty of snap rounding faces in 3D is described by Fortune [4]: First, it is reasonable to round every vertex to the center of the voxel containing it (a voxel is a unit cube centered on the integer grid). But, by doing so, a vertex may traverse a face and to avoid that, it might be necessary to add beforehand a vertex on the face, which requires triangulating it. Newly formed edges may cross older edges when snapping; to avoid this, new vertices are added to these edges, in turn requiring further triangulating of faces. It is not known whether such schemes terminate.

To better understand the difficulty of the problem, consider the following simple but flawed algorithm. First project all the input faces onto the horizontal plane, subdivide the projected edges as in 2D snap rounding, triangulate the resulting arrangement, lift this triangulation vertically on all faces, and then round all vertices to the centers of their voxels. For an input of size n, this yields an output of size $\Theta (n^4)$ in the worst case and an $L_\infty$ Hausdorff distance of at most 1/2 between the input faces and their rounded images. Unfortunately, this algorithm does not work in the sense that edges may cross: indeed, consider two almost vertical close triangles whose projections on the horizontal plane are triangles that are rounded in 2D to the same segment; such triangles in 3D may be rounded into properly overlapping vertical triangles. Fortune [4] solved this problem by using a finer grid to round the vertices and to avoid vertical rounding of the faces.

Contributions

We present in this paper the first algorithm for rounding a set of interior-disjoint polygons into a simplicial complex whose vertices have integer coordinates and such that the geometry does not change too much: namely, (i) the Hausdorff distance between every input face and its rounded image is bounded by a constant (3/2 for the $L_\infty$ metric), and (ii) the relative positions of the faces are preserved in the sense that there is a continuous motion that deforms all input faces into their rounded images such that if two points collapse at some time, they remain identical up to the end of the motion (see Theorem 3.1). This ensures, in particular, that if a line stabs two input faces far enough from their boundaries, the line will stab their rounded images in the same order or in the same point.

The worst-case complexity of our algorithm is polynomial but unsatisfying as our upper bound on the output simplicial complex is $O(n^{13})$ for an input of size n (see Proposition 5.2). However, this upper bound decreases to $O(n^{4}\sqrt{n})$ under the assumption that, roughly speaking, the input is a nice discretization of a constant number of surfaces that satisfy some reasonable assumptions on their curvature (see Proposition 5.8 for details). The corresponding time complexity reduces from $O(n^{15})$ to $O(n^{5})$. It is also very likely that these bounds are not tight and, in practice on realistic non-pathological data, we anticipate time and space complexities of $O(n\sqrt{n})$ (see Remark 5.9).

We present the algorithm in Sect. 3, its proof of correctness in Sect. 4, and its complexity analysis in Sect. 5.

2 Preliminaries

Notation

The coordinates in the Euclidean space ${\mathbb {R}}^3$ are referred to as x, y, and z and $\vec {\imath },\vec {\jmath },\vec {k}$ is the canonical basis. We use several planes parallel to the axes to project or intersect some faces: the xy-plane is called the floor, the xz-plane is called the back wall and a plane parallel to the yz-plane is called a side wall. Projections on the floor and on the back wall are always considered orthogonal to the plane of projection. Two polygons, edges, or vertices are said to properly intersect if their intersection is non-empty and not a common face of both. Two polygons (resp. segments) intersect transversally if their relative interiors intersect and if they are not coplanar (resp. colinear).

General Position Assumption

For the sake of simplicity, we assume, without loss of generality, some general position on our input set of polygons ${\mathcal {P}}$. Precisely, we assume:

($\alpha$):

No faces are parallel to the axes of coordinates and no vertices project along the y-axis on an edge (except the endpoints of that edge).

($\beta$):

No supporting plane of a face translated by vector $\vec {\jmath }$ or $-\vec {\jmath }$ contains a vertex.

Let ${{\mathcal {I}}}$ denote the intersection, if not empty, of the supporting plane of a face with the translation by $\pm \vec {\jmath }$ of the supporting plane of another face. By assumption ($\beta$), ${{\mathcal {I}}}$ is a line.

($\gamma$):

No vertices project along the y-axis onto such a line ${{\mathcal {I}}}$.

($\delta$):

For any point A on a face and with half-integer x- and y-coordinates, $A\pm \vec {\jmath }$ does not belong to another face. More generally, no line ${{\mathcal {I}}}$ crosses any vertical line defined by half-integer x- and y-coordinates.

This general position assumption is done with no loss of generality because it can be achieved by a sequence of four symbolic perturbations of decreasing importance: (i) the input faces are translated in the x-direction by $\epsilon _1$, (ii) translated in the y-direction by $\epsilon _2$, (iii) the vector $\vec {\jmath }$ is scaled by a factor $1+\epsilon _3$, and (iv) the faces are rotated by an angle $\epsilon _4$ around a line that is not parallel to the coordinate axes. As shown below, enforcing $\epsilon _1\gg \epsilon _2\gg \epsilon _3\gg \epsilon _4$ yields that our perturbation scheme removes all degeneracies.

Consider an intersection ${\mathcal {I}}$ as defined above; ${\mathcal {I}}$ can be a line or a plane. If ${\mathcal {I}}$ is a line L that induces a degeneracy of type ($\delta$), this degeneracy is avoided by a translation (i) in the x-direction if L is not parallel to the xz-plane, and by a translation (ii) in the y-direction, otherwise. Then, perturbations (iii) and (iv) of smaller scales do not reintroduce this degeneracy [2]. If the intersection ${\mathcal {I}}$ is a plane, this remains the case after perturbations (i) and (ii), but the intersection becomes empty after a small enough perturbation (iii) and it remains empty after perturbation (iv). Hence, degeneracies of type ($\delta$) are avoided by our scheme of perturbations. Degeneracies of type ($\beta$) and ($\gamma$) are not affected by perturbations (i) and (ii), but they are avoided by the scaling of type (iii). Indeed, if ${\mathcal {I}}$ is a line then, viewed in projection on the back wall, the scaling of type (iii) translates the line. Finally, degeneracies of type ($\alpha$) are not affected by perturbations (i)–(iii), but they are avoided by a rotation of type (iv).

3 Algorithm

We first describe the main algorithm in Sects. 3.1 and 3.2 and then two algorithmic refinements in Sect. 3.3 which we present separately for clarity. Our algorithm has the following property.

Theorem 3.1

Given a set ${\mathcal {P}}$ of polygonal faces in 3D in general position that do not properly intersect, the algorithm outputs a simplicial complex ${\mathcal {Q}}$ whose vertices have integer coordinates and a mapping $\sigma$ that maps every face F of ${\mathcal {P}}$ onto a set of faces (or edges or vertices) of ${\mathcal {Q}}$ such that there exists a continuous motion that moves every face F into $\sigma (F)$ such that: (i) the $L_\infty$ Hausdorff distance between F and its image during the motion never exceeds 3/2, and (ii) if two points on two faces become equal during the motion, they remain equal through the rest of the motion.

Fig. 1

Projection of Step 1. a Two 3D faces. b Their intersection with a side wall $x=cst$. c After the projection of Step 1, face $F_i$ is partially projected onto $F_j$, $j<i$, i.e., $R_{ij}$ is replaced by the faces $R'_{ij}$, $X_{ij1}$ and $X_{ij2}$. d–f Other scenarios: d $R_{ij}$ is replaced by $R'_{ij}$ and only $X_{ij1}$; e $F_i$ is also partially projected onto $F_k$, $j<k<i$; f if instead $j<i<k$, it is $F_k$ that is partially projected onto $F_i$

3.1 Sketch

We first give a high-level description of our algorithm and the intuition of its design. The algorithm is organized in four steps. In Step 1, we locally deform the input faces by partially projecting some of them on some others, so that no two resulting faces have two distinct points aligned in the y-direction at distance less than 1 (see Fig. 1). In Step 2 (see Fig. 2), we project all the edges vertically onto all faces and subdivide the faces accordingly. We then project all the resulting edges on the back wall. For every vertex of their arrangement, we round its x-coordinate to the nearest integer, say $c\in {\mathbb {Z}}$, and consider the so-called narrow slab bounded by the two side-wall planes $x=c\pm 1/2$. The wide slabs are the regions bounded by two consecutive narrow slabs and we partition all the faces by the narrow and wide slabs.

Eventually, in every narrow slab bounded by the planes $x=c\pm 1/2$, we will round the x-coordinates of all vertices to c (which amounts to projecting all the faces on the plane $x=c$) and then round the y- and z-coordinates with a 2D snap rounding scheme; this process may turn some edges into polylines and for those edges that were (before rounding) in the boundary planes ($x=c\pm 1/2$), their incident faces in the adjacent wide slabs need to be subdivided accordingly. Thus, in Step 3 (see Fig. 3), in every narrow slab, we project all the faces on its center side-wall plane, split the edges as if we were 2D snap rounding them, and lift these vertices back on the original edges.

On the other hand, in every wide slab (see Fig. 4), due to the subdivision of Step 2, the faces are trapezoids whose projections on the floor are pairwise identical or interior disjoint. We triangulate them from the bottom-left vertex to the top-right vertex (with respect to the x- and y-coordinates) and further triangulate with the vertices that come from the simulation of 2D snap rounding in the adjacent narrow slabs. In Step 4, we simply round all vertices to their closest integer grid points.

During the snapping motion of Step 4, no vertex traverses a face, no two edges properly intersect and, in particular, no two triangles get rounded to properly intersecting (possibly overlapping and vertical) triangles. Indeed, roughly speaking, in narrow slabs, we inherit the good properties of the 2D snap rounding scheme, and in wide slabs, there is no vertex strictly inside the slab and edges do not properly intersect during the snapping motion because: (i) no two boundary edges of the trapezoids properly intersect by the definition of the slabs in Step 2, (ii) the edges of triangles that are rounded vertically do not intersect other edges by the distance property of Step 1, and (iii) the triangulation edges incident to two triangles that are not rounded vertically do not intersect other edges by the property of the triangulation in Step 3; these key properties of our algorithm are proven in Lemma 4.5.

Fig. 2

Partition of Step 2. a Projection of the faces on the floor. b Lift of the floor arrangement onto the 3D faces followed by the subdivision of the faces. c Projection on the back wall and arrangement (here no new intersections occur for clarity). d Partition of the space into slabs and subdivision of the faces by their side-wall boundaries

3.2 Detailed Algorithm

We now precisely describe the algorithm. In every step of the algorithm, faces are subdivided and/or modified. We denote by ${\mathcal {P}} _{i}$ the set of faces at the end of Step i and by $\sigma _{i}$ the mapping from the faces of ${\mathcal {P}} _{i-1}$ to those of ${\mathcal {P}} _{i}$ (with ${\mathcal {P}} _{0}={\mathcal {P}}$ and ${\mathcal {P}} _4={\mathcal {Q}}$). These mappings are trivial and not explicitly described, except in Step 1. Let $\sigma =\sigma _4\circ \cdots \circ \sigma _1$ be the global mapping from the faces of ${\mathcal {P}}$ to those of the output simplicial complex ${\mathcal {Q}}$.

1. Project the Faces That Are Close to One Another. Refer to Fig. 1. Order all the input faces arbitrarily from ${\bar{F}}_1$ to ${\bar{F}}_n$: ${\mathcal {P}} =\{{\bar{F}}_i:1\leqslant i\leqslant n\}$. During the process, we modify the faces iteratively. For clarity, we denote by $F_1,\ldots ,F_n$ the faces that are iteratively modified, which we initially set to $F_i={\bar{F}}_i$ for all i. Roughly speaking, for i from 2 to n, we project $F_i$ along y onto $F_1,\ldots ,F_{i-1}$, in order, but only the points that project at distance at most 1. Furthermore, we create, if needed, new faces that connect the boundary of the projected points to their pre-image. More precisely, Step 1 consists of the following three substeps (a)–(c).

• (a) For i from 2 to n and for j from 1 to $i-1$, do

  • Let $R_{ij}$ be the polygonal region that consists of the points $p_i\in F_i$ whose projection onto $F_j$ along the y-direction lies within distance less than 1 from $p_i$, i.e., $R_{ij}=\{p_i\in F_i : \exists \,\alpha \in (-1,1),\, \exists \, p_j\in F_j,\,p_i=p_j+\alpha \vec {\jmath }\}$.

  • Modify $F_i$ by removing $R_{ij}$ from it.

  Let ${\tilde{F}}_1,\ldots ,{\tilde{F}}_n$ be the resulting faces at the end of the two nested loops and let $R'_{ij}$ be the projection of $R_{ij}$ on ${\tilde{F}}_j$ along the y-direction.

• (b) For i from 2 to n, consider on ${\bar{F}}_i$ the set of $R_{ij}$, $i>j$, and consider their edges, in turn. We define new faces that connect some edges of $R_{ij}$ and $R'_{ij}$, which we refer to as connecting faces (see faces $X_{ij\xi }$ in Fig. 1). If an edge e is a common edge of $R_{ij}$ and ${\tilde{F}}_i$, we define a new face as the convex hull of e and its projection on ${F}_j$ along y (as faces $X_{ij1}$ and $X_{ij2}$ in Fig. 1c). If e is a common edge of $R_{ij}$ and $R_{ik}$ and if e projects (along y) on ${\tilde{F}}_j$ and on ${\tilde{F}}_{k}$ into two distinct segments $e_j$ and $e_{k}$, respectively, we define a new face as the convex hull of $e_j$ and $e_{k}$ (as face X in Fig. 7); however, if e belongs to that face, we split it in two at e (as faces $X_{ij1}$ and $X_{ik1}$ in Fig. 1e). Structural properties of the connecting faces are discussed in Sect. 3.4.

• (c) For j from 1 to $n-1$, subdivide ${\tilde{F}}_j$ by the arrangement of edges of the $R'_{ij}$, $i=j+1,\ldots ,n$.

To summarize, we have removed from every input face ${\bar{F}}_i$ the regions $R_{ij}$, $j=1,\ldots ,i-1$, we subdivided the resulting faces ${\tilde{F}}_j$ by the edges of all $R'_{ij}$, $i=j+1,\ldots ,n$, and we created new connecting faces. Finally, we defined $\sigma _{{{1}}}$ to map every input face ${\bar{F}}_i$ to the union of the resulting subdivided face ${\tilde{F}}_i$, all the regions $R'_{ij}$, $j=1,\ldots ,i-1$ (subdivided as in ${\tilde{F}}_j$), and all the connecting faces that are defined by the $R_{ij}$, $j=1,\ldots ,i-1$.

2. Partition the Space into Slabs. Refer to Fig. 2. Project all the faces of ${\mathcal {P}} _{{{1}}}$ on the floor, compute their arrangement, lift all the resulting edges onto all faces of ${\mathcal {P}} _{{{1}}}$, and subdivide the faces accordingly; let ${\mathcal {P}} _{{{1}}}'$ be the resulting subdivision. Then, project all edges of ${\mathcal {P}} _{{{1}}}'$ on the back wall and compute their arrangement (but do not lift the resulting edges back on ${\mathcal {P}} _{{{1}}}'$).

The closed region bounded by the two side walls $x=c \pm {1}/{2}$, $c\in {\mathbb {Z}}$, is called a narrow slab${\mathcal {S}} _c$, if it contains (at least) a vertex of the back wall arrangement. A wide slab is a closed region bounded by two consecutive narrow slabs.

We subdivide all faces of ${\mathcal {P}} _{{{1}}}'$ by intersecting them with the side-wall boundaries of all slabs, resulting in ${\mathcal {P}} _{{{2}}}$. Note that if two narrow slabs share a side-wall plane, this plane is a wide slab in between these two narrow slabs. However, we treat such wide slabs as if they had infinitesimal width; their two side-wall boundaries are considered combinatorially distinct although they coincide geometrically. Thus, for instance, an edge of ${\mathcal {P}} _{{{1}}}'$ intersects such a wide slab boundary in two combinatorially distinct points that geometrically coincide.

Fig. 3

Step 3a: triangulation in a narrow slab. a Faces in a narrow slab. b Their projections onto the side wall $x=c$. c In that plane, the edges are split as in 2D snap rounding and the faces are triangulated. d The triangulation is lifted back on the 3D faces; in red are the dummy vertices, i.e., the new vertices that lie on the side-wall boundaries of the narrow slab

3. Triangulate the Faces. We triangulate all the faces of ${\mathcal {P}} _{{{2}}}$ in every slab in turn. We first consider narrow slabs and then wide slabs. This order matters because, when triangulating faces in narrow slabs, we split some edges at some new vertices; when such edges and new vertices lie in the side-wall boundaries of the narrow slabs, they also belong to the adjacent wide slabs and these new vertices are to be considered in these wide slabs.

• (a) Narrow slabs.   Refer to Fig. 3. Project along the x-axis all the faces in a narrow slab ${\mathcal {S}} _c$ on the side wall $x=c$ that bisects the slab, and compute the arrangement of the projected edges. In that side wall, denote as hot all the pixels that contain a vertex of that arrangement and split every edge that intersects a hot pixel at its intersections with the pixel boundary.¹ Triangulate the resulting arrangement² and lift it back (still along the x-axis) onto all the faces in the slab and subdivide them accordingly. The subdivision vertices that lie on the side-wall boundaries of ${\mathcal {S}} _c$ are referred to as dummy vertices to distinguish them from the other vertices.

• (b) Wide slabs.   Refer to Fig. 4. Not considering the dummy vertices of Step 3a, all faces are trapezoids such that the parallel edges lie on the two side-wall boundaries of the wide slab; any two trapezoids are either identical, disjoint, or share exactly one edge or vertex, and the same holds for their projections on the floor. The dummy vertices lie on the trapezoid edges that lie on the side-wall boundaries of the wide slab. Not considering the dummy vertices, all trapezoids that project on the floor onto one and the same trapezoid are triangulated so that all the diagonals project on the floor onto one and the same diagonal, say from the bottom-left vertex to the top-right vertex in the xy-plane. Trapezoids can have dummy vertices only on the edges on the side walls; thus, after splitting a trapezoid in two triangles, each triangle can have dummy vertices on at most one of its edges. For every such triangle, we further triangulate it by adding an edge connecting every dummy vertex to the opposite vertex of the triangle. As mentioned above, if a wide slab has zero width, we treat it as if it had infinitesimal width, with two combinatorially distinct side walls, one defined by each of its adjacent narrow slabs. Note that a non-dummy vertex defined as the intersection of a 3D edge with these side walls, is thus combinatorially duplicated, one on each side wall, but a dummy vertex is not duplicated on both side walls, since it is defined by one or the other adjacent narrow slab.

4. Snap All Vertices to the centers of their voxels. Vertices that are on the boundary of a narrow slab ${\mathcal {S}} _c$ are snapped onto the side wall $x=c$ that bisects the slab; this is well defined even when two narrow slabs share a side-wall boundary because we have considered (in Step 2) two combinatorial instances of such side walls, one associated to each of the narrow slabs. Vertices that lie on the common boundary of two voxels inside a narrow slab ${\mathcal {S}} _c$ are associated to voxels according to the vertex-pixel associations when snap rounding in 2D the projections of the edges in ${\mathcal {S}} _c$ onto its bisecting side wall $x=c$.

Fig. 4

Step 3b: triangulation in a wide slab of four trapezoids (produced by the Step 2 subdivision of two triangles). a Trapezoids, without dummy vertices, have identical or interior-disjoint floor projections (the top trapezoid and the middle-bottom one have identical floor projections). b Trapezoid triangulations, without dummy vertices, with diagonals from “bottom-left” to “top-right”. c Further triangulations with the dummy vertices

3.3 Algorithm Refinements

We present here two algorithmic refinements that we did not describe above for clarity.

3.3.1 Faces in Narrow Slabs (Steps 2 and 3a)

When snapping all vertices to their voxel centers in Step 4, any planar polygon in a narrow slab ${\mathcal {S}} _c$ is transformed into a planar polygon in the side wall $x=c$. Depending on how the vertices move toward their voxel centers, the polygon may not remain planar during the motion, but it is planar at the end of the motion. Hence, the output will be unchanged if, in Step 3a, we avoid triangulating the faces, that is, we avoid triangulating the arrangement in the side wall $x=c$ and only lift the new vertices of the arrangement onto the edges in ${\mathcal {S}} _c$. Still, after snapping the vertices in Step 4, the resulting polygons in the side wall $x=c$ should be triangulated so that the algorithm returns a simplicial complex. Doing so improves the complexity of the algorithm but it is nonetheless convenient for the proof of correctness to consider the triangulations of the faces in Step 3a.

Furthermore, in narrow slabs, we can avoid subdividing the faces (including the connecting faces) by the vertical projections of edges in Step 2; however, the edges in the narrow slab boundary planes should be subdivided as in their adjacent wide slabs. Unlike before, this can change the output, but we do not need these faces to be subdivided in Step 2. However, since slabs are defined by the lifted edges, this means in Step 2 to vertically lift the edges on all the faces, without subdividing them, to define the slabs, and to subdivide the faces by the lifted edges only in the wide slabs.

3.3.2 Connecting Faces (Steps 2 and 3)

We argue that, (i) we do not need to project on the floor the edges (of the connecting faces) that are parallel to the y-axis (Step 2), (ii) we do not need to subdivide these edges in any way (Steps 2 and 3), nor to subdivide the other edges of the connecting faces by the vertical projections of the edges of ${\mathcal {P}} _{{{1}}}$ (Step 2), and (iii) we do not need to triangulate the connecting faces (Step 3).

First observe that all the points on an edge (of a connecting face) that is parallel to the y-axis or on any one of its lifted copies (along z) have the same x-coordinate as the edge endpoints, which are also the endpoints of other edges (not parallel to the y-axis) of the connecting face. Thus, considering these edges in Step 2 would not create any additional slab.

As mentioned in Sect. 3.3.1, we do not need to subdivide, in narrow slabs, the connecting faces by the vertical projections of the edges of ${\mathcal {P}} _{{{1}}}$, in Step 2. The resulting faces are trapezoids with two edges of length at most 1 that are parallel to the y-axis. In Step 3a, the connecting faces in narrow slabs are subdivided according to their projection on a side wall (and the hot pixels in that plane). Similarly as in Sect. 3.3.1, triangulating these faces will not change the rounding of these polygons. Furthermore, not subdividing their edges that are parallel to the y-axis does not change the resulting trapezoids either (since any subdivision vertex lies in the same voxel as one of its endpoints).

In wide slabs, the edges (of a connecting face) that traverse the slab cannot be subdivided (by construction) by the vertical projections of the edges of ${\mathcal {P}} _{{{1}}}$ and, similarly as above, subdividing the edges that are parallel to the y-axis and triangulating the face do not change the rounding of these polygons.

Note that we should however triangulate the connecting faces at the end of the algorithm in order to obtain a simplicial complex. These triangulations can trivially be done without creating proper intersections in between the edges because the connecting faces that need to be triangulated are parallelograms with two edges of length 1 and parallel to the y-axis; edges are not properly intersecting at the end of Step 4, thus the edges that lie in such a parallelogram are all equal to one diagonal and we can triangulate the parallelogram accordingly.

3.4 Properties of the Faces of ${\mathcal {P}} _{{{1}}}$

Observe first that, in Step 1a, $R_{ij}$, $i>j$, is polygonal since its boundary consists of (i) segments of the boundary of $F_i$, (ii) segments of the boundary of $F_j$ projected onto $F_i$ along the y-direction, and (iii) segments of the intersection of $F_i$ and the translated copies of $F_j$ by vectors $\pm \vec {\jmath }$. This also implies that, in projection on the back wall, an edge e of $R_{ij}$ lies in an edge $e'$ of the boundary of an input face ${\bar{F}}_u$ or of ${\bar{F}}_u\cap ({\bar{F}}_v\pm \vec {\jmath })$ for some u and v. Furthermore, u and v are less than or equal to i because $F_i$ and $F_j$ do not depend on ${\bar{F}}_u$ for $u>i$. However, the distance between e and $e'$ is not bounded from above by a constant, as depicted in Fig. 5.

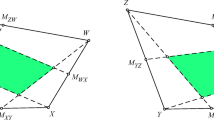
In Step 1b, connecting faces are defined as trapezoids that intersect any side wall in segments of length at most 1 that are parallel to the y-axis. However, it should be noted that connecting faces may overlap, as depicted in Fig. 6, and that a connecting face may not contain the edge of $R_{ij}$ that defines it, as depicted in Fig. 7.

Fig. 5

View in a side wall: the boundary edge e of $R_{87}$ can be far away from the edge $e'={\bar{F}}_1\cap ({\bar{F}}_2-\vec {\jmath })$ that coincides with e on the back wall

Fig. 6

Example of overlapping connecting faces $X_{31}$ and $X_{41}$, viewed inside a side wall: a Four input faces; b$F_2$ is not projected onto $F_1$ because they are far from each other, then $F_3$ is first projected onto $F_1$ and then onto $F_2$; c $F_4$ is projected onto $F_1$ and it is not further projected onto $F_2$ (which is too far) nor $F_3$ (which is now empty)

Fig. 7

A connecting face X induced by the common edge e of $R_{31}$ and $R_{32}$, such that it does not contain e. View inside a side wall: a The three input faces; b$F_2$ is projected onto $F_1$, then c$F_3$ is projected onto $F_1$ and $F_2$

4 Proof of Correctness

We prove here Theorem 3.1. We focus on Step 1 of the algorithm in Sect. 4.1, on Step 4 in Sect. 4.2, and we wrap up in Sect. 4.3.

4.1 Step 1

We first state the main properties of Step 1 and then a technical lemma, which will be used in Lemma 4.5. The intuition of the proof of Lemma 4.1 is quite straightforward but the proof is surprisingly long and technical, thus we first give a sketch and postpone the actual proof to Sect. 4.1.1.

Lemma 4.1

Every point of the faces of ${\mathcal {P}}$ can be continuously moved so that every face F of ${\mathcal {P}}$ is continuously deformed into $\sigma _1(F)$ so that (i) the $L_\infty$ Hausdorff distance between F and its image during the motion never exceeds 1 and (ii) if two points on two faces become equal during the motion, they remain equal through the rest of the motion.

Proof (sketch)

The motion is decomposed into n successive phases, considering the projection of each $F_i$ in turn. For a particular $F_i$, the naive way of moving $R_{ij}$ to $\sigma _1(R_{ij})$ is to move $R_{ij}$ to $R'_{ij}$, by moving each point of $R_{ij}$ along the y-direction and at constant speed, and to transform edge $e_\zeta$ into face $X_\zeta$ for every edge $e_\zeta$ of the boundary of $R_{ji}$ that defines a connecting face $X_\zeta$. However, this does not define a function since segments are mapped to faces. The definition of a continuous motion requires a bit of technicality but the straightforward underlying idea is to subdivide $R_{ij}$ by considering, for each edge $e_{\zeta }$, a tiny quadrilateral inside $R_{ij}$ and bounded by $e_{\zeta }$. We then transform continuously each tiny quadrilateral bounded by $e_{\zeta }$ into the connecting face $X_{\zeta }$ and move the complement of these quadrilaterals, which is a slightly shrunk version of $R_{ij}$, into $R'_{ij}$. This can be done so that when two distinct points become equal during the motion, they remain equal through the rest of the motion. The formal proof is detailed in Sect. 4.1.1. $\square$

Lemma 4.2

If a line L parallel to the y-axis intersects the relative interior of a face of ${\mathcal {P}} _{{{1}}}$ in a single point p then the distance along L from p to any other face of ${\mathcal {P}} _{{{1}}}$ is at least 1.

Fig. 8

For the proof of Lemma 4.2

Proof

If a line L parallel to the y-axis intersects the relative interior of a face F of ${\mathcal {P}} _{{{1}}}$ in a single point p, this face is not a connecting face. Assume for a contradiction that L intersects another face $F'$ of ${\mathcal {P}} _{{{1}}}$ at some point $p'$ that is at distance less than 1 from p (see Fig. 8a).

Consider first the case where $F'$ is not a connecting face. Since non-connecting faces are not parallel to the y-axis, there exists a line $L'$ parallel to the y-axis (and close to L) that intersects the relative interiors of both F and $F'$ in two points at distance less than 1. However, this is impossible after Step 1.

Consider now the case where $F'$ is a connecting face (see Fig. 8, b and c). It follows from Step 1b of the algorithm that any point $p'\in F'$ lies on a segment (not necessarily entirely in $F'$) of length at most 2, parallel to the y-axis and with its endpoints on two non-connecting faces of ${\mathcal {P}} _{{{1}}}$. Consider the shortest such segment. Unless this segment has length 2 and p is its midpoint, p is at distance less than 1 from one of the segment endpoints, say $p''$ (see Fig. 8b); considering instead of $F'$ the non-connecting face $F''$ supporting this endpoint yields a contradiction as shown above. By definition, if the segment has length 2 (see Fig. 8c), its midpoint p must lie on a common edge e of some $R_{ij}$ and $R_{ij'}$ such that p projects on ${\tilde{F}}_j$ and on ${\tilde{F}}_{j'}$ into two points at distance 1 from p in the directions $\vec {\jmath }$ and $-\vec {\jmath }$, respectively. During Step 1, $R_{ij}$ and $R_{ij'}$ are removed from the input face ${\bar{F}}_i$, thus the resulting face ${\tilde{F}}_i$ does not contain p in its interior (and not at all if p is in the interior of edge e). If the input face that contains F is distinct from ${\bar{F}}_i$, then the fact that p belongs to $R_{ij}\cap R_{ij'}\subset {\bar{F}}_i$ and to the interior of F contradicts the assumption that the input faces do not properly intersect. Otherwise, $F\subseteq {\bar{F}}_i$ and thus $F\subseteq {\tilde{F}}_i$, which contradicts the fact that p belongs to the interior of F but not to the interior of ${\tilde{F}}_i$, and concludes the proof. $\square$

4.1.1 Proof of Lemma 4.1

Recall that ${\bar{F}}_1,\ldots ,{\bar{F}}_n$ denote the input faces of ${\mathcal {P}}$ and that we initially set $F_i={\bar{F}}_i$. In Step 1, for i from 2 to n and for j from 1 to $i-1$, we modify $F_i$ by projecting its subset $R_{ij}$ onto $R'_{ij}\subset F_j$, and by adding the corresponding connecting faces. When we start these projections of $F_i$ onto $F_j$ for j from 1 to $i-1$, the faces $F_j$ are no longer modified and we have $F_j={\tilde{F}}_j$ until the end of Step 1. Thus $R_{ij}$ only depends on ${\bar{F}}_i$ and ${\tilde{F}}_1,\ldots ,{\tilde{F}}_{j}$, $j<i$.

Subdivision of$R_{ij}$. For all i and all $j<i$, we project parallelly to y the $R_{ij}$ on the back wall, triangulate the resulting arrangement, lift the triangulation back onto the $R_{ij}$, and subdivide the $R_{ij}$ accordingly. Let $T_1,\ldots ,T_g$ denote the resulting triangles. An edge of $T_u\subset R_{ij}$ is called blue if it is part of a boundary edge of $R_{ij}$ that defines a connecting face; it is called red otherwise. A vertex of $T_u$ is called blue if it is incident to a blue edge, otherwise, it is red.

Ordering Property. Consider two triangles $T_b\subset R_{bj}\subset {\bar{F}}_b$, $b>j$, and $T_r\subset R_{rj}\subset {\bar{F}}_r$, $r>j$ and $r\ne b$, that are on the same side of ${\tilde{F}}_j$ (with respect to y) and that project onto the same triangle on the back wall (or equivalently on ${\tilde{F}}_j$). We prove the following ordering property: if a blue edge$e_b$of$T_b$and a red edge$e_r$of$T_r$coincide in that projection, then$T_b$is farther away than$T_r$from${\tilde{F}}_j$with respect toy (i.e., any line parallel to the y-axis, that intersects these triangles, intersects ${\tilde{F}}_j$, $T_r$ and $T_b$ in that order). Roughly speaking, this property holds because the two triangles incident to the red edge project on ${\tilde{F}}_j$ and thus, if the blue edge was in between the red edge and ${\tilde{F}}_j$, as in Fig. 9, the two triangles incident to the blue edge would also project on ${\tilde{F}}_j$, implying that the edge should be red and not blue.

More formally, since $R_{bj}$ only depends on ${\bar{F}}_b$ and ${\tilde{F}}_1,\ldots ,{\tilde{F}}_{j}$, the face ${\bar{F}}_r$, $r>j$, plays no role in the definition of $R_{bj}$. Thus the boundary edges of ${\bar{F}}_r$ do not overlap the edges of $R_{bi}$ in projection on the back wall, by items ($\alpha$) and ($\gamma$) of the general position assumption. In particular, $e_r$ cannot be a boundary edge of ${\bar{F}}_r$. Thus, since $e_r$ is a red edge, either (a) $e_r$ lies on a common edge of $R_{rj}$ and some $R_{rj'}$ (on ${\bar{F}}_r$) such that $e_r$ projects (along y) on ${\tilde{F}}_j$ and on ${\tilde{F}}_{j'}$ onto the same segment $e_{rj}=e_{rj'}$, or (b) $e_r$ is induced by the subdivision of the $R_{rk}$ into triangles.

Fig. 9

Counterexample for the proof of the ordering property

Refer to Fig. 9. In case (a), since input faces are interior disjoint, the segment $e_{rj}=e_{rj'}$ is on the common boundary of the input faces ${\bar{F}}_j$ and ${\bar{F}}_{j'}$. Hence, $e_r$ is a common edge of some triangles $T_{r}\subset R_{rj}$ and $T'_{r}\subset R_{rj'}$ that respectively project in Step 1 onto two triangles $T_j\subset {\tilde{F}}_j$ and $T_{j'}\subset {\tilde{F}}_{j'}$ that share edge $e_{rj}=e_{rj'}$. Assume for contradiction that edge $e_b$ is in between $e_r$ and $e_{rj}$ (i.e., in their convex hull). Since $e_b$ is a blue edge, the triangle $T'_{b}\subset {\bar{F}}_b$ that shares edge $e_b$ with $T_b$ exists and projects in Step 1 onto a triangle $T_{b'}\ne T_{j'}$. Consider any line parallel to the y-axis that intersects the interior of the four triangles $T_{b'}$, $T_{j'}$, $T'_{b}$ and $T'_{r}$ in points $p_{b'}$, $p_{j'}$, $p'_b$ and $p'_r$, respectively. By definition, segment $p'_rp_{j'}$ has length less than 1 and contains $p'_b$. Thus $\Vert p'_bp_{j'}\Vert <1$ and since $T'_{b}$ projects in Step 1 onto $T_{b'}\ne T_{j'}$, we have $b'<j'$. Furthermore, $j'<r$ by definition of $R_{rj'}$. Thus $b'<j'<r$ and since $T'_{r}$ projects on $T_{j'}$ instead of $T_{b'}$, $\Vert p'_rp_{b'}\Vert >1$ while $\Vert p'_bp_{b'}\Vert <1$. Hence, $p_{b'}$, $p_{j'}$, $p'_b$ and $p'_r$ appear in that order on their supporting line. It follows that $\Vert p_{j'}p_{b'}\Vert <1$ and thus $T_{j'}$ should have been projected on $T_{b'}$ in Step 1, which contradicts the definition of $R_{rj'}$, and thus $e_b$ is not in between $e_r$ and $e_{rj}$. Since $e_r$ and $e_b$ are on the same side of ${\tilde{F}}_j$, $e_b$ is farther away than $e_r$ from ${\tilde{F}}_j$. Case (b) is similar: the only difference is that $T_{j'}$ lies in ${\tilde{F}}_j$ instead of ${\tilde{F}}_{j'}$ but $T_j$ and $T_{j'}$ are still incident. The ordering property follows.

Motions of the$T_i$. In Step 1, each of the triangles $T_1,\ldots ,T_g$ is projected onto some face. We consider all the vertices of the $T_1,\ldots ,T_g$ in the order of all the red vertices ordered by their increasing distances (along y) to the faces they are projected to, followed by all the blue vertices ordered similarly. (By our general position assumption, these distances are well defined.) In turn, we move each red vertex to its image on the face it projects to, and we move all the points of its incident triangles among $T_1,\ldots ,T_g$ according to their barycentric coordinates (see Fig. 10a).

Fig. 10

Motions of the $T_i$

We now consider each blue vertex in turn and all its incident triangles among $T_1,\ldots ,T_g$. For each such blue vertex b and incident triangle T, we consider the two edges of T incident to b. If they are both blue (see Fig. 10b), we choose arbitrarily any point p strictly inside T. Otherwise, for each red edge incident to b, we consider the point p on this edge at distance $\epsilon$ from b (see Fig. 10c), for some sufficiently small global parameter $\epsilon >0$. Then, we move all these particular points (simultaneously for all triangles $T_1,\ldots ,T_g$ incident to b) to the point to which b projects to; all the points of the triangles $T_1,\ldots ,T_g$ incident to b move accordingly to their barycentric coordinates (after re-triangulating these triangles with respect to the new points p we considered).

Because of the ordering property and the considered ordering of the red and blue vertices, any two distinct points remain distinct during any one of these motions, except possibly at the end.

Finally, consider, as in Fig. 7, a common edge e of $R_{ij}$ and $R_{ij'}$ (on ${\bar{F}}_i$) such that e projects (along y) on ${\tilde{F}}_j$ and on ${\tilde{F}}_{j'}$ into two distinct segments $e_j$ and $e_{j'}$, respectively, that are on the same side of ${\bar{F}}_i$ with respect to y (i.e., e does not belong to the convex hull of $e_j$ and $e_{j'}$). In Step 1b, we define a connecting face as the convex hull of $e_j$ and $e_{j'}$. However, since e is a blue edge and has thus not yet been moved at this stage, $R_{ij}$ and $R_{ij'}$ have currently been deformed into a set of faces that contain the convex hull of e and $e_j$, and the convex hull of e and $e_{j'}$. These two faces overlap in between e and, say, $e_j$. In this final phase, we simply retract these overlapping parts into segment $e_j$ and move all the points in the other faces incident to e accordingly to their barycentric coordinates.

Hausdorff Distance. The property that the Hausdorff distance between a face and its image during the motion never exceeds 1 (for the $L_{\infty }$ metric) is straightforward since, (i) any line parallel to y that intersects a triangle $T_i$ also intersects its image during the motion, (ii) the image of $T_i$ during the motion remains in the convex hull of $T_i$ and its projection (parallel to y) on ${\tilde{F}}_j$, and (iii) all the points of $T_i$ are at distance at most 1 along y from ${\tilde{F}}_j$ (by definition of $R_{ij}$).

4.2 Step 4

In the following, we consider in the snapping phase of Step 4 a continuous motion of the vertices such that every vertex moves on a straight line toward the center of its voxel at a speed that is constant for each vertex and so that all vertices start and end their motions simultaneously. The other points in a face move accordingly to their barycentric coordinates in the face. Note that, in every voxel that contains a vertex, the motion is a homothetic transformation whose factor goes from one to zero. During that motion, we consider that narrow and wide slabs respectively shrink and expand accordingly. We prove in Lemmas 4.4 and 4.5 that no proper intersections occur during that motion in between faces, edges and vertices. We refer to Sect. 3.1 for the intuition behind these proofs. We first recall the standard snap-rounding result for segments in two dimensions. A pixel is called hot if it contains a vertex of the arrangement of segments.

Theorem 4.3

[7, Thm. 1] Consider a set of segments in 2D split in fragments at the hot pixel boundaries and a deformation that (i) contracts homothetically all hot pixels at the same speed ³ and (ii) moves the fragments outside the hot pixels according to the motions of their endpoints. During the deformation, no fragment endpoint ever crosses over another fragment.

Lemma 4.4

When moving all vertices to the center of their voxels in Step 4, no two faces, edges, or vertices of ${\mathcal {P}} _{{{3}}}$ properly intersect in narrow slabs.

Proof

Consider all the faces of ${\mathcal {P}} _{{{3}}}$ in a narrow slab ${\mathcal {S}} _c$ and the arrangement of their projections (along the x-axis) onto the side wall $x=c$. In that side wall, a pixel that contains a vertex of the arrangement is hot and every edge (in that side wall) that intersects a hot pixel is split at the pixel boundary (Step 3a). By Theorem 4.3, when moving in that side wall all the projected vertices to the centers of their pixels, the topology of the arrangement does not change except possibly at the end of the motion, where edges and vertices may become identical.

It follows that the property that every face of ${\mathcal {P}} _{{{3}}}$ in ${\mathcal {S}} _c$ projects onto a single face of the arrangement in the side wall $x=c$, which holds by construction at the beginning of the motion (Step 3a), holds during the whole motion of the vertices in 3D and of their projections in the side wall $x=c$.

Furthermore, the motion preserves the ordering of the x-coordinates of the vertices in ${\mathcal {S}} _c$, until the end when they all become equal to c. Together with the previous property, this implies that, in a narrow slab, during the snapping motion, (i) no vertices and edges intersect the relative interior of a face and (ii) if two edges intersect in their relative interior, it is at the end of the motion and they become identical. Furthermore, (iii) no vertices intersect the relative interior of an edge because, in Step 3a, we have split every edge that intersects a hot pixel in projection in the side wall $x=c$. This concludes the proof. $\square$

Lemma 4.5

When moving all vertices to the center of their voxels in Step 4, no two faces, edges, or vertices of ${\mathcal {P}} _{{{3}}}$ properly intersect in wide slabs.

Proof

By construction (Step 2), all the vertices in a wide slab are on its side-wall boundaries and, in these side walls, no two edges or vertices properly intersect during the motion, by Lemma 4.4. Thus, we only have to consider edges that connect the two side-wall boundaries of a wide slab and show that such edges do not properly intersect during the snapping motion. Note that input faces are not vertical (i.e., not parallel to the z-axis) by assumption and connecting faces are not vertical in wide slabs since they are parallel to the y-axis and they intersect both side-wall boundaries of the wide slab.

Initially, these edges project on the floor onto edges that do not properly intersect pairwise (by definition of the slabs in Step 2). Thus, by Theorem 4.3, the projections on the floor of two edges either (i) coincide throughout the whole motion, or (ii) they do not properly intersect and do not coincide throughout the whole motion except possibly at the end when they may coincide. In the first case, throughout the whole motion, the edges belong to the same moving vertical plane and they do not properly intersect since they do not initially; indeed, since faces are initially not vertical, edges may intersect in a vertical plane only if they are boundary edges of trapezoids of ${\mathcal {P}} _{{{2}}}$, and such edges do not properly intersect on the back wall by definition of wide slabs. Hence, only in the latter case (ii), two edges may properly intersect during the motion; furthermore, the first time this may happen is at the end of the motion and then, the two edges belong to the same vertical plane.

Applying again Theorem 4.3 to the back-wall projection of the boundary edges of the trapezoids (but not their triangulating edges), we get that if two boundary edges of trapezoids properly intersect in 3D during the motion, it is at the end and they must coincide in the back-wall projection. Since two edges that coincide in two projections are equal, we get that boundary edges of trapezoids cannot properly intersect throughout the motion. It remains to prove that there are no proper intersections that involve the edges triangulating the trapezoids.

Consider for a contradiction two edgeseand$e'$that properly intersect in a vertical planeVat time$t_1$, the end of the motion. Since boundary edges of the trapezoids do not properly intersect, we can assume without loss of generality that one of the two edges, say e, is a triangulation edge. Consider the trapezoid that initially contains e and its image F, at time $t_1$, which is a set of triangles. We prove below that, at time $t_1$, the edge$e'$properly intersects (at least) one of the two boundary edges of F.

Fig. 11

For the proof of Lemma 4.5: for a contradiction, two edges e and $e'$ that properly intersect in a vertical plane V at time $t_1$, the end of the motion

Assume for a contradiction that $e'$ properly intersects none of the two boundary edges of F and refer to Fig. 11a. Consider all the edges of the triangulation of F that are properly intersected by $e'$ and the sequence of triangles (of that triangulation) that are incident to these edges; let T and $T'$ denote the first and last triangles of that sequence. All these triangles except possibly one, T or $T'$, must be in the vertical plane V; this is trivial for all triangles but T and $T'$ and, if neither T nor $T'$ lies in V, then edge $e'$ properly intersects the surface formed by these triangles, contradicting the property that $t_1$ is the first time a proper intersection may occur.

As in Fig. 11a, assume without loss of generality that T, the bottommost triangle of the sequence, lies in the vertical plane V at time $t_1$. Let $M'$ be the endpoint of $e'$ that lies in T and let $M_1M_2$ be the edge of T that supports $M'$. At time $t_1$, $M_1$ and $M_2$ are vertically aligned and $M'$ is in between them. Thus, before the snapping motion starts, at time $t=t_0$, $M_1, M_2$ and $M'$ must lie in the same vertical column of pixels (in the side wall—see Fig. 11b) and $M'$ must be vertically in between $M_1$ and $M_2$ (otherwise $M'$ would never get vertically in between $M_1$ and $M_2$ during the motion).⁴ Moreover, the distance along the y-axis in between $M'$ and segment $M_1M_2$ is initially at least 1 by Lemma 4.2. Thus, $M'$ and the point on $M_1M_2$ that realizes this distance are at distance 1 and lie initially on opposite sides of the column of pixels, as in Fig. 11b’.⁵ They thus have half-integer x- and y-coordinates, which contradicts item $(\delta )$ of our general position assumption.

Hence, at time $t=t_1$, edge $e'$ properly intersects one of the boundary edges, say r, of trapezoid F. Since boundary edges do not properly intersect, $e'$ must be a triangulation edge of its trapezoid $F'$ and we can apply the same argument as above on edges $e'$ and r, instead of e and $e'$. We get that r properly intersects a boundary edge $r'$ of $F'$, which is a contradiction. $\square$

4.3 Wrap Up, Proof of Theorem 3.1

First, by construction, the algorithm outputs faces that have integer coordinates.

Second, there is a continuous motion of every input face F into $\sigma (F)$ so that the Hausdorff distance between F and its image during the motion never exceeds 3/2 for the $L_\infty$ metric. Indeed, by Lemma 4.1, the Hausdorff distance never exceeds 1 between F and its image during the motion in Step 1; in Steps 2 and 3 the faces are only subdivided; and the Hausdorff distance between any face of ${\mathcal {P}} _{{{3}}}$ and its image during the motion of Step 4 clearly never exceeds 1/2 since vertices are moved to the centers of their respective voxels.

Third, if two points on two faces become equal during the motion, they remain equal through the rest of the motion. This is proven in Lemma 4.1 for the motion of Step 1 and this also holds for the motion of Step 4 since, by Lemmas 4.4 and 4.5, if two faces, edges or vertices intersect during this motion, they share a common face of both, whose motion is uniquely defined by its vertices (actually, we show in the proofs of Lemmas 4.4 and 4.5 that no two distinct points become equal except possibly at the end of the motion).

Finally, the algorithm outputs a simplicial complex by Lemmas 4.4 and 4.5.

5 Complexity

We first analyze in Sect. 5.1 the complexity of our algorithm in the worst case (Proposition 5.2) and then, in Sect. 5.2, its complexity under some reasonable assumptions on the input (Proposition 5.8). We finally argue in Remark 5.9 that we can anticipate time and space complexities of $O(n\sqrt{n})$ in practice on realistic non-pathological data.

5.1 Worst-Case Complexity

We start by proving the complexity of the algorithm in terms of n, as a warm up. We then refine the analysis in Proposition 5.2 in terms of other parameters.

Lemma 5.1

Given a set of polygons of total complexity O(n), the algorithm outputs a simplicial complex of complexity $O(n^{13})$ in time $O(n^{15})$.

Proof

Let n be the number of input edges. Consider in the back wall the arrangement ${{\mathcal {A}}}$ of the $O(n^2)$ lines that support the projections of the n input edges and the intersections ${\bar{F}}_k\cap ({\bar{F}}_\ell \pm \vec \jmath )$. At the end of Step 1, each of the O(n) input faces is subdivided by the projection (on the face) of these $O(n^2)$ lines, which define $N_3=O(n^3)$ lines in total. In addition, the connecting faces are also bounded by the $N_4=O(n^4)$ lines that are parallel to the y-axis and incident in the back wall to the $O(n^4)$ vertices of ${{\mathcal {A}}}$.

In Step 2, we project and lift the above $N_3=O(n^3)$ lines onto the O(n) planes supporting the input faces, and project these $O(n^4)$ lines onto the back wall. Indeed, as mentioned in Sect. 3.3.2, we do not need to project and lift the $N_4=O(n^4)$ lines parallel to the y-axis that support the edges of the connecting faces, and we do not need to lift the edges onto the connecting faces. This induces an arrangement of $O(n^4)$ lines, which has $O(n^8)$ vertices. There are thus $O(n^8)$ slabs.

Faces in narrow slabs are not subdivided in Step 2 (see Sect. 3.3.1). Thus, there are bounded by (i) the $N_3=O(n^3)$ above lines, altogether for all narrow slabs, (ii) for each narrow slab, the O(n) intersections between the input faces and the slab boundaries, and (iii) the edges parallel to the y-axis of the connecting edges.

We prove that these edges define $O(n^{12})$ hot pixels in total over all narrow slabs, in Step 3a. According to Sect. 3.3.2, the edges of type (iii) need not to be subdivided and thus play no role in the complexity analysis.⁶ The edges of type (i) define $O(n^6)$ hot pixels in total over all narrow slabs because their arrangement after projection on a side wall has size $O(n^6)$ and each vertex (counted with multiplicity if more than two edges intersect in a same point) defines a unique hot pixel in the $O(n^8)$ narrow slabs; indeed, if the restrictions to a narrow slab of two lines intersect in projection on a side wall, their parts outside that narrow slab do not intersect in projection. All other pairs of edges (between types (i) and (ii), and among type (ii)) define $O(n^4)$ hot pixels for each narrow slab, hence $O(n^{12})$ hot pixels in total. As we will see below, the total number of trapezoids in wide slabs is $O(n^{12})$, thus the total number of hot pixels defined by vertices on the walls in between slabs is also $O(n^{12})$. Hence, there are $O(n^{12})$ hot pixels in total and the complexity of the subdivision after snapping is thus $O(n^{12})$ in total over all narrow slabs. Moreover, these $O(n^{12})$ hot pixels define $O(n^{13})$ dummy vertices in total, since only the edges of type (ii) are subdivided by dummy vertices (see Sect. 3.3.2).

In every wide slab, there are $O(n^4)$ trapezoids defined by the lifting in Step 2 of the $N_3=O(n^3)$ lines on O(n) faces and $O(n^3)$ connecting faces defined in Step 1. Indeed, connecting faces are not subdivided (see Sect. 3.3.2) and a wide slab intersects the back wall arrangement ${{\mathcal {A}}}$ in $O(n^2)$ edges (since there are no vertices in the slab) and each edge may induce O(n) connecting faces (one for each input face). This defines $O(n^{12})$ trapezoids in total over all wide slabs, to which should be added the $O(n^{13})$ edges induced by the dummy vertices. Hence, the complexity of the subdivision after snapping is $O(n^{13})$ in total over all narrow and wide slabs.

All the arrangements and triangulations performed by the algorithm can be done in time complexities that match their worst sizes. However, this does not match the complexity of the output because the complexity of the arrangements in narrow slabs may be larger before than after snapping. Before snapping, there are $O(n^{12})$ hot pixels that subdivide $O(n^3)$ lines in total over all narrow slabs (since edges of type (iii) are not subdivided). The total complexity before snapping and the running time are thus in $O(n^{15})$. $\square$

We now refine the previous complexity analysis in terms of the following parameters. We define the z-cylinder of a face F as the volume defined by all the lines parallel to the z-axis that intersect F; similarly for x- and y-cylinders. Over all input faces F, let $f_d$ be the maximum number of input faces that are (i) intersected by one such cylinder of F and (ii) at distance at most d from F. Denote by $f=f_\infty$ the maximum number of faces intersected by one such cylinder. Let $g_1$ be maximum number of input faces that are intersected by the boundary of a voxel. Finally, let $w_x$ be the maximum number of input faces that are intersected by any side wall $x=c$. Typically, we can hope that “nice” input will be such that $w_x=O(\sqrt{n})$ and that $g_1$ and $f_1<f$ are in O(1) (see Remark 5.9). However, under some reasonable assumptions, we only prove that $w_x$ and $g_1$ are in $O(\sqrt{n})$ and that $f_1<f=O(\root 4 \of {n})$ (see Lemma 5.7).

Proposition 5.2

Given a set of polygons of total complexity O(n), the algorithm outputs a simplicial complex of complexity $O(nw_xf^7f_1^3g_1) \subset O(n^{13})$ in time $O(nw_xf^8f_1^4g_1) \subset O(n^{15})$.

Proof

The proof is similar to the proof of Lemma 5.1. For each face, we first count the number of subdivision edges created by the algorithm without considering any intersection; to avoid confusion, we refer to these edges as unsplit edges.

Number of Slabs. After projection on the back wall, the edges of $R_{ij}$ and $R'_{ij}$, in Step 1, are pieces of the boundary edges of the input faces ${\bar{F}}_k$ and of the segments of intersection ${\bar{F}}_k\cap ({\bar{F}}_\ell \pm \vec \jmath )$. In a y-cylinder of a face F, only f faces project on the back wall and thus there are $O(ff_1)$ such edges. Thus, at the end of Step 1, every input face ends up supporting $O(ff_1)$ unsplit edges. In Step 2, we thus lift $O(f^2 f_1)$ unsplit edges onto every face. Every unsplit edge on a given face F may only intersect, after projection on the back wall, edges that lie on the faces that intersect the y-cylinder of F; there are O(f) such faces and $O(f^2f_1)$ unsplit edges on each of them, thus every unsplit edge may intersect $O(f^3f_1)$ edges on the back wall. There are $O(nf^2f_1)$ unsplit edges in total, hence, in Step 2, the back wall arrangement has complexity $O(nf^5f_1^2)$. The number of narrow and wide slabs is thus $O(nf^5f_1^2)$.

Complexity in Narrow Slabs. At the end of Step 2, since faces in narrow slabs are not subdivided in Step 2 (see Sect. 3.3.1), the faces in narrow slabs are bounded by (i) the $O(ff_1)$ above unsplit edges for each of the O(n) input faces, (ii) for each narrow slab ${\mathcal {S}} _c$, the $O(w_x)$ intersections in between the input faces and the slab boundaries, and (iii) the edges parallel to the y-axis of the connecting edges.

We prove that these edges define $O(nw_xf^6f_1^3)$ hot pixels in total over all narrow slabs, in Step 3a. As before, edges of type (iii) play no role. Every edge on a given input face F may only intersect, after projection on a side wall, edges that lie on faces that intersect the x-cylinder of F. There are O(f) such faces and, on each of them, there are $O(ff_1)$ edges of type (i). Thus every edge of type (i) may intersect $O(f^2f_1)$ edges of type (i) after projection on a side wall. There are $O(nff_1)$ edges of type (i), thus pairs of edges of type (i) define $O(nf^3f_1^2)$ hot pixels in total over all narrow slabs (similarly as in Lemma 5.1).

For counting the hot pixels induced by other pairs of edges, we consider the $O(w_x)$ edges of type (ii) in a given slab ${\mathcal {S}} _c$. Such an edge in a face F may intersect, after projection on a side wall, the edges that lie on faces that intersect ${\mathcal {S}} _c$ and the x-cylinder of F. There are $f_1$ such faces and each contains $O(ff_1)$ edges of type (i) and at most two edges of type (ii) in ${\mathcal {S}} _c$. The number of hot pixels in ${\mathcal {S}} _c$ induced by an edge of type (ii) and an edge of types (i)–(ii) is thus $O(w_x ff_1^2)$. Summing over all $O(nf^5f_1^2)$ narrow slabs gives $O(nw_xf^6f_1^4)$ hot pixels induced by the edges of types (i)–(iii), over all narrow slabs.

As we will see below, the total number of trapezoids in wide slabs is $O(nw_xf^7f_1^3)$, which induces up to the same number of hot pixels defined by vertices on the walls in between slabs.

Since $f_1\leqslant f$, the total number of hot pixels and the complexity of the subdivision after snapping is thus $O(nw_xf^7f_1^3)$. Furthermore, the number of hot pixels times $O(g_1)$ bounds the total number of dummy vertices since $g_1$ bounds the number of input faces that intersect the boundary of a voxel, and an input face in a narrow slab has at most two edges of type (ii) (those subdivided by dummy vertices). Hence, there are $O(nw_xf^7f_1^3g_1)$ dummy vertices in total.

Complexity in Wide Slabs. At most $w_x$ input faces are intersected by any wide slab and we lift, in Step 2, $O(f^2f_1)$ unsplit edges on each of these faces. These edges do not intersect since we consider a wide slab. In every wide slab, at the end of Step 2, there are thus $O(w_xf^2f_1)$ trapezoids plus the connecting faces. Similarly as in Lemma 5.1, there are $O(w_xff_1)$ connecting faces: the number $O({f}f_1)$ of unsplit edges on an input face at the end of Step 1 times the number $O(w_x)$ of input faces that intersect the slab. Summing over the $O(nf^5f_1^2)$ wide slabs, there are thus $O(nw_xf^7f_1^3)$ trapezoids, to which should be added the $O(nw_xf^7f_1^3g_1)$ edges induced by the dummy vertices. The complexity of the subdivision after snapping is thus $O(nw_xf^7f_1^3g_1)$ in total over all wide slabs.

Time Complexity. Before snapping, there are $O(nw_xf^7f_1^3)$ hot pixels. The boundary of each hot pixel intersects $O(g_1)$ input faces and thus subdivides $O(g_1ff_1)$ unsplit edges of types (i)–(ii) in total over all narrow slabs. Similarly as in the proof of Lemma 5.1, the total complexity before snapping and the running time are thus in $O(nw_xf^8f_1^4g_1)$. $\square$

5.2 Complexity Under Some Assumptions

We consider, in Proposition 5.8, the complexity of our algorithm for approximations of “nice” surfaces, defined as follows.

Definition 5.3

An $(\varepsilon ,\kappa )$-sampling of a surface ${\mathcal {S}}$ is a set of vertices on ${\mathcal {S}}$ such that there is at least 1 and at most $\kappa$ vertices strictly inside any ball of radius $\varepsilon$ centered on ${\mathcal {S}}$. It is straightforward that an $(\varepsilon ,\kappa )$-sampling of a fixed compact surface has $\Theta (n)$ vertices with $n=\varepsilon ^{-2}$ (the constant hidden in the $\Theta$ complexity depends on $\kappa$ and on the area of the surface).

Definition 5.4

The Delaunay triangulation of a set of points ${\mathcal {P}}$ restricted to a surface ${\mathcal {S}}$ is the set of simplices of the Delaunay triangulation of ${\mathcal {P}}$ whose dual Voronoi faces intersect ${\mathcal {S}}$. If ${\mathcal {P}} \subset {\mathcal {S}}$, we simply refer to the restricted Delaunay triangulation of ${\mathcal {P}}$ on ${\mathcal {S}}$.

Definition 5.5

(nice surfaces) A surface ${\mathcal {S}}$ is k-monotone (with respect to z) if every line parallel to the z-axis intersects ${\mathcal {S}}$ in at most k points. Let $\Delta$ and k be any two positive constants. A surface ${\mathcal {S}}$ is nice if it is a compact smooth k-monotone surface such that the Gaussian curvature of ${\mathcal {S}}$ is larger than a positive constant in a ball of radius $\Delta$ centered at any point $p\in {\mathcal {S}}$ where the tangent plane to ${\mathcal {S}}$ is vertical.

For instance, a compact smooth algebraic surface whose silhouette (with respect to the vertical direction) is a single convex curve is nice for suitable choices of $\Delta$ and k.

Remark 5.6

The following complexities are asymptotic when n goes to infinity (or $\varepsilon$ to zero) with hidden constants depending on the surface areas, $\Delta$, and k. It is important to notice that these complexities are independent from the voxel size, which can go to zero with no changes in the complexities. Of course if the grid size and the surface are fixed, the total number of voxels intersecting the surface is constant and so is the size of a rounding.

The following lemma is a technical though rather straightforward result.

Lemma 5.7

The restricted Delaunay triangulation ${\mathcal {T}}$ of an $(\varepsilon ,\kappa )$-sampling of a nice surface has complexity $O(n)=O(\varepsilon ^{-2})$. Any plane $x=c$ intersects at most $O(\sqrt{n})=O(\varepsilon ^{-1})$ faces of ${\mathcal {T}}$. Furthermore, for any face f of ${\mathcal {T}}$, the set of vertical lines through f intersects at most $O(n^{{1}/{4}})=O(\varepsilon ^{-1/2})$ faces of ${\mathcal {T}}$.

Proof

Since ${\mathcal {S}}$ is k-monotone, we can assume without loss of generality that any plane $x=c$, for some constant $c\in {\mathbb {R}}$, intersects ${\mathcal {S}}$ in at most one component. Indeed, this assumption will affect the actual overall complexity by a factor at most k/2.

Observe first that the edges of ${\mathcal {T}}$ have length less than $2\varepsilon$. Indeed, if there is a Delaunay edge of length at least $2\varepsilon$, there is a ball centered on ${\mathcal {S}}$ that contains this edge and that contains no vertices strictly inside it (by definition of restricted Delaunay triangulations). This ball has radius at least $\varepsilon$, contradicting the $(\varepsilon ,\kappa )$-sampling assumption. The $(\varepsilon ,\kappa )$-sampling of ${\mathcal {S}}$ ensures that there are O(1) vertices at distance at most $2\varepsilon$ from every vertex, hence the triangulation has complexity $O(n)=O(\varepsilon ^{-2})$.

Intersection with a plane$x=c$.   Since the edges of ${\mathcal {T}}$ have length less than $2\varepsilon$, any edge that intersects a plane $x=c$ has a vertex in between the two planes $x=c\pm \varepsilon$. We prove in the following that the area of ${\mathcal {S}}$ in that region is of order $O(\varepsilon )$ and thus that the number of sampling points in that region is $O(\varepsilon ^{-1})=O(\sqrt{n})$.

Fig. 12

For the proof of Lemma 5.7

Observe first that if ${\mathcal {S}}$ intersects a plane $x=c$ in a curve of perimeter $\ell$ and if, at any point p on that curve, the plane tangent to ${\mathcal {S}}$ makes an angle at least $\alpha$ with the plane $x=c$, then the area of ${\mathcal {S}}$ in between $x=c$ and $x=c+\varepsilon$ is in $O({\ell \varepsilon }/{\alpha })$ when $\varepsilon$ tends to zero (see Fig. 12a). Consider a point $q\in {\mathcal {S}}$ where the tangent plane is parallel to the side-wall plane $x=c$ and assume without loss of generality that q is located at the origin. Refer to Fig. 12b. It follows from the assumptions that there exists a constant $\delta >0$ such that, for any $0<c<\delta$, (i) the intersection of ${\mathcal {S}}$ with the plane $x=c$ has perimeter at most $\sqrt{c}$ up to some constant and (ii) the plane tangent to ${\mathcal {S}}$ at any point on that curve and the plane $x=c$ make an angle at least $\alpha >{c}/{\sqrt{c}}=\sqrt{c}$ up to some constant. Hence the area of ${\mathcal {S}}$ in between $x=c$ and $x=c-\varepsilon$ is in $O(\sqrt{c}\,\varepsilon /{\sqrt{c}})=O(\varepsilon )$.

On the other hand, for any $c>\delta$, the intersection of ${\mathcal {S}}$ with the plane $x=c$ has perimeter $\ell =O(1)$ and the plane tangent to ${\mathcal {S}}$ at any point on that curve and the plane $x=c$ make an angle at least $\alpha ={\delta }/{\sqrt{\delta }}=\sqrt{\delta }=\Omega (1)$. Hence the area of ${\mathcal {S}}$ in between $x=c$ and $x=c+\varepsilon$ is in $O({\ell \varepsilon }/{\sqrt{\delta }})=O(\varepsilon )$, which concludes the proof that any plane $x=c$ intersects at most $O(\sqrt{n})=O(\varepsilon ^{-1})$ faces of ${\mathcal {T}}$.

Intersection with the z-cylinder of a face.   Consider a face f of ${\mathcal {T}}$ and its z-cylinder defined as the set of vertical lines through f. Similarly as above, the z-cylinder of f intersects a face $f'$ only if a vertex of $f'$ lies in the z-cylinder enlarged by $\varepsilon$. Since the edges of f have length at most $2\varepsilon$, this enlarged z-cylinder is contained in the z-cylinder defined by a square of edge length $3\varepsilon$ in the xy-plane. In that z-cylinder, the height span of ${\mathcal {S}}$ is $O(\sqrt{\varepsilon })$ (see Fig. 12b), hence the area of ${\mathcal {S}}$ in the cylinder is $O(\varepsilon \sqrt{\varepsilon })$. The number of sampling points in the cylinder is thus $O({\varepsilon \sqrt{\varepsilon }}/{\varepsilon ^2})=O(\varepsilon ^{-1/2})=O(n^{{1}/{4}})$. $\square$

Proposition 5.8

Given the arrangement of the restricted Delaunay triangulations of the $(\varepsilon ,\kappa )$-samplings of a constant number of nice surfaces, the algorithm outputs a simplicial complex of complexity $O(n^4\sqrt{n})$ in time $O(n^5)$.

Proof

Consider the restricted Delaunay triangulations of the $(\varepsilon ,\kappa )$-samplings of two surfaces. By definition of $(\varepsilon ,\kappa )$-samplings, it is straightforward that any triangle of one triangulation intersects a constant number of triangles of the other triangulation. Hence, the complexities of Lemma 5.7 hold for the arrangement of the two triangulations, and similarly for a constant number of triangulations. Thus, for the arrangement of triangulations, Lemma 5.7 yields $w_x=O(\sqrt{n})$, and similarly $g_1=O(\sqrt{n})$, and $f_1<f=O(\root 4 \of {n})$ (as defined in Sect. 5.1) and plugging these values in the complexities of Proposition 5.2 yields the result. $\square$

Remark 5.9

In practice on realistic non-pathological data, one can anticipate a better complexity of $O(n\sqrt{n})$ for the size of the output and for the time complexity. Indeed, if the size of the voxels is small compared to the input model (say the edge lengths), we can expect that there are O(1) faces at distance at most $\sqrt{3}$ (the diagonal of a voxel) from any given face, thus $f_1$ and $g_1$ are in O(1). Furthermore, we can expect that the x-, y- or z-cylinders of most faces will intersect a constant number of other faces and that the few that intersect a non-constant number of faces will not impact the final complexities, hence we anticipate that f will behave as O(1). Finally, assuming that $w_x=O(\sqrt{n})$ as in the proof of Lemma 5.7, Proposition 5.2 yields space and time complexities of $O(n\sqrt{n})$.

6 Conclusion

The algorithm we presented is reasonably simple, however, its worst-case complexity, even under reasonable assumptions (Propositions 5.2 and 5.8), is prohibitive in practice. Hence, the question of whether our estimated practical complexity of $O(n\sqrt{n})$ (Remark 5.9) is correct on real data is crucial for applications. Furthermore, it would be interesting to design heuristics for improving the practical efficiency of the algorithm. Another issue is that faces can drift arbitrarily far when the snap rounding scheme is applied repeatedly. Several approaches were presented to address this issue in 2D [8, 10, 14] but the problem in 3D is naturally entirely open.