1 Introduction

Finiteness results are not uncommon in the study of lattice polytopes. Most of these are proven by fixing the dimension, showing an upper bound for the volume and then using the following result by Lagarias and Ziegler.

Theorem 1.1

([44, Thm. 2]) Up to unimodular equivalence, there are finitely many d-dimensional lattice polytopes having volume lower than a constant K.

Note that working up to unimodular equivalence, i.e., up to affine lattice-preserving maps in \(GL_d({\mathbb {Z}}) \times {\mathbb {Z}}^d\) is an obvious requirement which we will often avoid to mention.

Once it is known that a family of lattice polytopes is finite, it is tempting to give a complete description of it. Most of the times this seems not to be possible in full generality, and it is instead done explicitly only fixing “small enough” parameters, first and foremost the dimension. A well-known example of such a finiteness result is the finiteness of d-dimensional lattice polytopes having a fixed positive number of interior lattice points, which follows from a volume bound proven by Hensley [35]. This result paved the way to explicit classifications of families of lattice polytopes having a fixed number of interior lattice points. The best example is probably the massive classification of reflexive polytopes (which have one interior lattice point) up to dimension four performed by Kreuzer and Skarke to study mirror symmetric Calabi–Yau manifolds [42, 43]. Another example of polytopes having exactly one interior point are the smooth Fano polytopes, fully enumerated up to dimension nine [9, 10, 41, 46, 48, 51, 59]. Without additional restrictions, lattice polytopes having one and two interior lattice points are classified in dimension three [6, 40].

In the last years, many other examples of these kind of results were provided. In [2, 4] is proven that in each dimension there are finitely many hollow lattice polytopes that are maximal up to inclusion, and they are classified in dimension three. In [18] the finiteness of smooth polytopes having fixed number of lattice points is shown in each dimension. Such polytopes are enumerated in dimension three, up to 16 lattice points [45, 47]. A finiteness result in dimension three for polytopes of width larger than one and fixed number of interior points is proven in [14], and an explicit enumeration has been performed up to 11 lattice points [15, 16].

All the aforementioned results are proven via bounding the volume of the considered family of polytopes and applying Theorem 1.1. In this paper we take a natural step, and use Lagarias and Ziegler’s Theorem to perform a systematic enumeration of all lattice polytopes of fixed dimension and volume that are within computational reach. This is done by giving an alternative proof of Theorem 1.1 which has the advantage of being efficiently implementable. The key is to build the polytopes “from below”, starting with a simplex and progressively adding vertices, instead of “from above” as the original proof of Theorem 1.1 suggests, carving out all the possible lattice polytopes from a big cube.

A result with a similar taste, but only in dimension two, has been achieved by Castryck [26]. With a “moving out” technique, he gives a different proof of a finiteness result and classifies all lattice polygons having up to 30 interior lattice points.

The paper has the following structure. In Sect. 2 we give an introduction to point configurations, building the necessary tools for the rest of the paper. In Sect. 3 we give an independent proof of Theorem 1.1, which leads to an algorithm, whose implementation is discussed in Sect. 4. In Sect. 5 we discuss the results of the classification and compare them with existing ones. In Sect. 6 we specialize the classification to smooth polytopes. In this setting our classification extends other ones performed in dimension three, and creates a database of small smooth polytopes. We give a structure theorem for d-dimensional smooth polytopes having at most \(3d-4\) lattice points (Theorem 6.10), which we immediately apply to fully categorize smooth polytopes having normalized volume at most 10 (Proposition 6.14). In Sect. 7 we use the classification together with existing volume bounds for simplices with a fixed number of interior lattice points to classify all the three-dimensional lattice simplices having up to 11 interior lattice points (Corollary 7.5). In Sect. 8, we use the classification of the preceding section to give conjectural Ehrhart inequalities for three-dimensional lattice polytopes (Conjecture 8.7). In the final Sect. 9, we look for interesting examples contained in the database, and we observe the commonness of polytopes which are spanning, very ample, IDP, have a unimodular cover/triangulation (see Appendix C).

2 Invitation to Point Configurations and Volume Vectors

In this section we sketch some basic concepts and results regarding point configurations, triangulations and volume vectors of lattice polytopes. This material will be used in Sect. 3 for proving Theorem 1.1. We use [27, Chap. 4] as a reference, but we also refer to [44, Chap. 6] for details.

A point configuration is a finite set of points \({\mathcal {A}}\) in an affine space \({\mathbb {R}}^d\). We say that a point configuration \({\mathcal {A}}\) is independent if none of its points is an affine combination of the rest, otherwise we say that \({\mathcal {A}}\) is dependent. A point configuration has corank one if it has a unique (up to scalar multiplication) dependence relation \(\sum _{{\mathbf {p}}\in {\mathcal {A}}} \lambda _{\mathbf {p}}{\mathbf {p}}= {\mathbf {0}}\). Such dependence relation defines a partition of \({\mathcal {A}}\) into the sets

$$\begin{aligned} J_+ :=\{{\mathbf {p}}\in {\mathcal {A}}: \lambda _{\mathbf {p}}> 0 \}, \quad J_0 :=\{{\mathbf {p}}\in {\mathcal {A}}: \lambda _{\mathbf {p}}= {\mathbf {0}}\}, \quad J_- :=\{{\mathbf {p}}\in {\mathcal {A}}: \lambda _{\mathbf {p}}< {\mathbf {0}}\}. \end{aligned}$$

Such partition is unique, up to switching \(J_+\) with \(J_-\). Given any point configuration \({\mathcal {A}}\) one can consider the polytope P defined as the convex hull of the points of \({\mathcal {A}}\), i.e., \(P_{\mathcal {A}}:=\mathrm {conv}({\mathcal {A}})\). If \({\mathcal {A}}\) has corank one then \(P_{\mathcal {A}}\) has exactly two different triangulations in simplices having vertices on A.

Lemma 2.1

([27, Lem. 2.4.2]) If a point configuration \({\mathcal {A}}\) has corank one, then the following are the only two triangulations of \(P_{\mathcal {A}}\) in simplices having vertices in \({\mathcal {A}}\):

$$\begin{aligned} {\mathcal {T}}_+:=\{C \subset {\mathcal {A}}: J_+ \not \subseteq C\} \quad \mathrm{and} \quad {\mathcal {T}}_-:=\{C \subset {\mathcal {A}}: J_- \not \subseteq C\}. \end{aligned}$$

Note that, assuming \(P_{\mathcal {A}}\) full-dimensional, the full-dimensional simplices in \({\mathcal {T}}_+\) and \({\mathcal {T}}_-\) are \(|J_+|\) and \(|J_-|\) respectively, i.e., the signature of \({\mathcal {A}}\) is the pair of numbers of simplices of the two ways to triangulate \(P_{\mathcal {A}}\) discussed above. If the unique dependence relation of a corank one point configuration \({\mathcal {A}}\) is entirely supported on \({\mathcal {A}}\), i.e., if \(J_0\) is empty, then we say that \({\mathcal {A}}\) is a circuit. In particular every proper subset of a circuit is an independent point configuration. If \({\mathcal {A}}\) is a circuit the pair \((J_+,J_-)\) is classically called the Radon partition or the oriented circuit of \({\mathcal {A}}\).

Being interested in lattice polytopes, we move our focus to point configurations contained in the lattice \({\mathbb {Z}}^d\). Given a full-dimensional lattice polytope P in \({\mathbb {R}}^d\), we denote by \({{\,\mathrm{Vol}\,}}(P)\) its normalized volume \({{\,\mathrm{Vol}\,}}(P) :=d! {{\,\mathrm{vol}\,}}(P)\), where \({{\,\mathrm{vol}\,}}(P)\) is the standard Euclidean volume. In other words, we set the normalized volume of any lattice simplex S with vertices \({\mathbf {v}}_1,\ldots ,{\mathbf {v}}_{d+1}\) to be

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(S) :=\left| \det \begin{bmatrix} 1 &{} \dots &{} 1 \\ {\mathbf {v}}_1 &{} \dots &{} {\mathbf {v}}_{d+1} \\ \end{bmatrix} \right| . \end{aligned}$$

Then the notion of volume can be extended to arbitrary polytopes via triangulations. The notion of volume can be extended in a finer way to polytopes, via volume vectors. For this we adopt the notation used in [14].

Definition 2.2

Let \({\mathcal {A}}= \{ {\mathbf {p}}_1 , \ldots , {\mathbf {p}}_n \}\) in \({\mathbb {Z}}^d\), with \(n \ge d+1\). Then the volume vector of \({\mathcal {A}}\) is defined as

$$\begin{aligned} \bigl (w_{i_1,\ldots ,i_{d+1}}\bigr )_{1 \le i_1< \ldots < i_{d+1} \le n } \in {\mathbb {Z}}^{\left( {\begin{array}{c}n\\ d+1\end{array}}\right) }, \end{aligned}$$
(1)

where

$$\begin{aligned} \bigl (w_{i_1,\ldots ,i_{d+1}}\bigr ) :=\det \begin{bmatrix} 1 &{} \dots &{} 1 \\ {\mathbf {p}}_{i_1} &{} \dots &{} {\mathbf {p}}_{i_{d+1}} \\ \end{bmatrix}. \end{aligned}$$

Note that we are assuming that \({\mathcal {A}}\) has an intrinsic order on the elements. The volume vector is a powerful invariant, which encodes most of the data of a point configuration.

Proposition 2.3

([14, Prop. 5]) Let \({\mathcal {A}}\) and \({\mathcal {A}}'\) be the point configurations \({\mathcal {A}}=\{{\mathbf {p}}_1,\ldots ,{\mathbf {p}}_n\}\) and \({\mathcal {A}}'=\{{\mathbf {p}}_1',\ldots ,{\mathbf {p}}_n'\}\) in \({\mathbb {Z}}^d\), and suppose that (with respect to a given ordering) they have the same volume vector (1). Then:

  1. (1)

    There is a unique unimodular affine map \(t:{\mathbb {R}}^d \rightarrow {\mathbb {R}}^d\) with \(t({\mathcal {A}}) = {\mathcal {A}}'\) (respecting the order of points).

  2. (2)

    If, moreover, \(\gcd _{1 \le i_1< \cdots < i_{d+1} \le n } (w_{i_1,\ldots ,i_{d+1}}) = 1\), then t is additionally lattice-preserving. In particular, \(P_{\mathcal {A}}\) and \(P_{{\mathcal {A}}'}\) are unimodularly equivalent lattice polytopes.

We now restrict our interest to point configurations in \({\mathbb {Z}}^d\) having \(d+2\) elements. We always assume that the point configuration is full-dimensional, i.e., it affinely spans \({\mathbb {R}}^d\). Note that this is equivalent to assume the configuration to have corank one. In this case, we can simplify, and modify slightly, the notation for the entries of the volume vector. If \({\mathcal {A}}= \{ {\mathbf {p}}_1, \ldots , {\mathbf {p}}_{d+2}\}\), then we denote the volume vector of \({\mathcal {A}}\) as

$$\begin{aligned} w_{\mathcal {A}}= (w_1 , \ldots , w_{d+2}), \text{ where } w_i :=(-1)^{i+1} w_{1,\ldots ,{\hat{i}},\ldots ,d+2}. \end{aligned}$$
(2)

The change of sign allows us to simplify the statement in the following lemma.

Lemma 2.4

([14, Eq. (2)]) Let \({\mathcal {A}}=\{{\mathbf {p}}_1,\ldots ,{\mathbf {p}}_{d+2}\}\) be a corank one point configuration. Then its volume vector \(w_{\mathcal {A}}= (w_1 , \ldots , w_{d+2})\) sums up to zero and encodes the unique linear relation in \({\mathcal {A}}\):

$$\begin{aligned} \sum _{i=1}^{d+2} w_i {\mathbf {p}}_i = {\mathbf {0}}\quad {and} \quad \sum _{i=1}^{d+2} w_i = 0. \end{aligned}$$

One may think the equality of \(\sum _{i=1}^{d+2} w_i = 0\) in the following way. The positive \(w_i\)’s are the normalized volumes of the full dimensional simplices in \({\mathcal {T}}_+\), while the negative \(w_i\)’s equal to (minus) the normalized volumes of the full-dimensional simplices in \({\mathcal {T}}_-\). The equality follows by noting that \({\mathcal {T}}_+\) and \({\mathcal {T}}_-\) are both triangulations of the same polytope. This is clarified by the following example.

Example 2.5

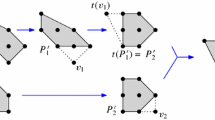
Let \({\mathcal {A}}\) be the point configuration given by the columns of the matrix below.

$$\begin{aligned} \begin{bmatrix} 0 &{} \quad 1 &{} \quad 1 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ \end{bmatrix}. \end{aligned}$$

Then, \({\mathcal {A}}\) is the vertex set of the polytope \(P_{\mathcal {A}}\) depicted below.

figure a

The volume vector of \({\mathcal {A}}\) is \(w_{\mathcal {A}}= (1,-1,-1,-1,2)\). Note that the positive entries (1, 2) in \(w_{\mathcal {A}}\) correspond exactly to the normalized volumes of the two tetrahedra in \({\mathcal {T}}_+\), while the negative entries \((-1,-1,-1)\) correspond exactly to (minus) the volumes of the three tetrahedra in \({\mathcal {T}}_-\).

figure b

In particular the entries of \(w_{\mathcal {A}}\) sum up to zero. We can furthermore check that they encode the unique affine linear relation in \({\mathcal {A}}\), indeed:

$$\begin{aligned} {\mathbf {p}}_1 - {\mathbf {p}}_2 - {\mathbf {p}}_3 - {\mathbf {p}}_4 + 2 {\mathbf {p}}_5 = {\mathbf {0}}. \end{aligned}$$

3 An Implementable Proof for the Lagarias–Ziegler Theorem

In this section we give an alternative algorithmic proof of Theorem 1.1. This algorithm will be then implemented for a complete enumeration of lattice polytopes with “reasonably small” volume and dimension, which is described in the following sections.

The original proof given in [44] is divided in two parts, one proving the result for simplices, another extending it to polytopes. The “simplicial” part of the result is easily deduced by putting the matrix of the vertices of a simplex in a normal form. This part of the proof, as given in [44], can be easily implemented, so we can use it as the first step of the algorithm, adding only some small improvements (see Algorithm 1). For the convenience of the reader we quickly sketch the theoretical argument used.

Lemma 3.1

There are finitely many equivalence classes of d-dimensional lattice simplices having volume lower than a constant K.

Proof

Let S be the d-dimensional lattice simplex with vertices \({\mathbf {v}}_0, {\mathbf {v}}_1,\ldots , {\mathbf {v}}_{d+1}\). We can suppose \(v_0\) to be the origin of the lattice. In this way \({{\,\mathrm{vol}\,}}(S)=|{\det (M)}|\), where M is the \(d \times d\) matrix whose columns are the vertices \({\mathbf {v}}_1,\ldots ,{\mathbf {v}}_{d+1}\). We now take M to the upper-triangular form (Hermite normal form)

$$\begin{aligned} M' :=\begin{bmatrix} a_{1,1} &{}\quad a_{1,2} &{}\quad \cdots &{}\quad a_{1,d} \\ &{} \quad a_{2,2} &{}\quad \cdots &{}\quad a_{2,d} \\ &{} &{} \quad \ddots &{} \quad \vdots \\ &{} &{} &{}\quad a_{d,d} \\ \end{bmatrix}, \end{aligned}$$

where on the jth column \( 0 \le a_{i,j} < a_{j,j}\) for \(i=1,\ldots ,j\), and \(a_{i,j}=0\) for \(i=j+1,\ldots ,d\). Since the simplex \(S'\), whose vertices are the origin and the columns of \(M'\), is affinely equivalent to S, \({{\,\mathrm{Vol}\,}}(S)=\prod _{i=1}^{d}a_{i,i}\). Since all the entries of \(M'\) are positive, there are finitely many possible values for all the entries \(a_{i,i}\), and consequently, for all the entries of \(M'\). \(\square \)

From now on, our proof diverges from the original one. In particular, we now focus our attention on the case of d-dimensional polytopes having \(d+2\) vertices. We prove the result for this special case using the theory developed in the previous section and then we deduce the general case as a corollary.

Proposition 3.2

There are finitely many equivalence classes of d-dimensional lattice polytopes having \(d+2\) vertices and volume lower than a constant K.

Proof

Let P be a lattice polytope with \(d+2\) vertices such that \({{\,\mathrm{Vol}\,}}(P) < K\). We call \({\mathcal {A}}\) the point configuration given by the vertices of \(P=P_{\mathcal {A}}\), it has corank one. Let \(w_{\mathcal {A}}\) be the volume vector of \({\mathcal {A}}\). Since the volume of P is bounded by K, the sum of the positive entries of \(w_{\mathcal {A}}\) is at most K. Similarly, the sum of the negative entries in \(w_{\mathcal {A}}\) is at least \(-K\). In particular there are finitely many possible volume vectors that can be the volume vector of \({\mathcal {A}}\). By Lemma 2.4 the previous statement means there are finitely many possible dependence relations which can be (up to multiplication by a scalar factor) the only dependence relation on \({\mathcal {A}}\). This proves that, if S is any d-dimensional lattice simplex with \({{\,\mathrm{Vol}\,}}(S) < K\), then the set

$$\begin{aligned} \{ {\mathbf {p}}\in {\mathbb {Z}}^d : {{\,\mathrm{Vol}\,}}(\mathrm {conv}(S \cup \{{\mathbf {p}}\})) \le K \} \end{aligned}$$

is finite. Finally, we note that P is completely determined by the choice of \(d+1\) affinely independent and ordered vertices, plus the unique linear relation among its \(d+2\) vertices. The convex hull of \(d+1\) affinely independent vertices of P is a d-dimensional simplex having normalized volume strictly smaller than K. By Lemma 3.1, there are finitely many such simplices. \(\square \)

From this we are able to deduce the Lagarias–Ziegler theorem.

Proof of Theorem 1.1

A d-dimensional lattice polytope P of volume \({{\,\mathrm{Vol}\,}}(P) \le K\) has at most \(K+d\) vertices. One can verify this by constructing P starting with a full-dimensional lattice simplex in P, and progressively “grow” it by adding the vertices of P, taking the convex hull each time. At each step the volume is a positive integer and will increase by another positive integer. Suppose the vertices of P are ordered so that \({\mathbf {v}}_0,\ldots ,{\mathbf {v}}_d\) are affinely independent. Then

$$\begin{aligned} P= \mathrm {conv}\left( \bigcup _{i=d+2}^n P_i \right) , \end{aligned}$$

where \(P_i :=\mathrm {conv}({\mathbf {v}}_0,\ldots ,{\mathbf {v}}_d,{\mathbf {v}}_i)\) with \(d+2 \le i \le n\). For each i, \(P_i\) is a d-dimensional polytope with \(d+2\) vertices, while \(S:=\mathrm {conv}({\mathbf {v}}_0,\ldots ,{\mathbf {v}}_d)\) is a d-dimensional simplex. Since \({{\,\mathrm{Vol}\,}}(S) \le {{\,\mathrm{Vol}\,}}(P_i) \le {{\,\mathrm{Vol}\,}}(P) \le K\), we conclude by Lemma 3.1 and Proposition 3.2. \(\square \)

4 Implementation

In this section we describe the implementation of the results described in the previous section. Note that both the proofs of Theorem 1.1 for simplices and for polytopes admit a straightforward algorithmic implementation. In order to have feasible running times, we are going to optimize the algorithms with some careful tweaking. The results of such implementation will be described in Sect. 5.

We denote by \({\mathcal {P}}_V^d\) and \({\mathcal {S}}_V^d\) the sets of d-dimensional polytopes and simplices having normalized volume V. Note that, as usual, these sets are considered up to unimodular equivalence. Computationally speaking, this is not a problem: each polytope can be indeed put in a normal form, and \({\mathcal {P}}_V^d\) can be thought of as the set of these forms.

Algorithm 1 fully enumerates all the elements of \({\mathcal {S}}_V^d\). To speed things up, we can “recycle” the enumeration of \({\mathcal {S}}_V^{d-1}\), the case \({\mathcal {S}}_V^1\) being trivial.

figure c

We now discuss the implementation for the complete enumeration of the elements of \({\mathcal {P}}_V^d\). We denote by \({\mathcal {P}}_{\le K}^d\) the set of all d-dimensional lattice polytopes of normalized volume at most K, i.e., \({\mathcal {P}}_{\le K}^d :=\bigcup _{V = 1}^K {\mathcal {P}}_V^d\). Similarly, we set \({\mathcal {S}}_{\le K}^d :=\bigcup _{V = 1}^K {\mathcal {S}}_V^d\). The algorithm works as follows. The simplices of \({\mathcal {S}}_{\le K}^d\) are used as starting objects for the enumeration. The possible volume vectors of point configurations of cardinality \(d+2\) are then calculated and used to iteratively add new vertices to the simplex. This is possible because the volume vector of a point configuration with \(d+2\) points encodes the unique affine dependence among them (Lemma 2.4). In order to optimize the implementation, the volume vectors have to be chosen carefully. We use the sign-changed definition of the volume vector given in (2). We denote by \({\mathcal {W}}_K^d\) the set

$$\begin{aligned} {\mathcal {W}}_K^d :=\left\{ (w_1,\ldots ,w_{d+2}) \in [-K,K]^{d+2} : \sum _{w_i > 0} w_i = - \sum _{w_i< 0} w_i < K \right\} \cap {\mathbb {Z}}^{d+2}. \end{aligned}$$

It contains all the possible volume vectors of point configurations of \(d+2\) points whose convex hull has normalized volume at most K. Once a simplex S is fixed, we can add new vertices to it using only the volume vectors having \({{\,\mathrm{Vol}\,}}(S)\) as the first entry. To make the computation even faster one can assume that \({{\,\mathrm{Vol}\,}}(S)\) is, in absolute value, the highest entry in the volume vector. This means that each polytope would be built starting only with the biggest simplex it contains. Using the volume vectors to determine the growing step of the classification algorithm also provides a handy way to deal with symmetries. Algorithm 2 requires \({\mathcal {S}}_{\le K}^d\) and \({\mathcal {W}}_K^d\) as inputs, and returns \({\mathcal {P}}_{\le K}^d\) as output. \({\mathcal {S}}_{\le K}^d\) is obtained by iterating Algorithm 1 for values of V ranging from 1 to K, while \({\mathcal {W}}_K^d\) can be trivially computed. Given a simplex \(S=\mathrm {conv}({\mathbf {v}}_0,\ldots ,{\mathbf {v}}_{d}) \in {\mathcal {S}}_{\le K}^d\) and a volume vector \(w=(w_1,\ldots ,w_{d+2}) \in {\mathcal {W}}_K^d\) such that \(w_{d+2}={{\,\mathrm{Vol}\,}}(S)\), we define \({\mathbf {p}}_{S,w}\) to be the point of \({\mathbb {R}}^d\) such that w is the volume vector of the point configuration \(\{{\mathbf {v}}_0,\ldots ,{\mathbf {v}}_{d},{\mathbf {p}}_{S,w}\}\). Thanks to Lemma 2.4, \({\mathbf {p}}_{S,w}\) is uniquely determined, indeed

$$\begin{aligned} {\mathbf {p}}_{S,w} = \frac{- \sum _{i=0}^{d} w_{i+1} {\mathbf {v}}_i }{{{\,\mathrm{Vol}\,}}(S)}. \end{aligned}$$

Note that, in general, \({\mathbf {p}}_{S,w}\) is not a lattice point. At every iteration of Algorithm 2, all the points \({\mathbf {p}}_{S,w}\) that are lattice points are stored in a temporary variable \({\mathcal {X}}_S\). After that, the elements of \({\mathcal {X}}_S\) are used to “grow” S in all the possible ways. This is done in the second part of the main loop. A variable called s is used to count how many iterations the growing process needs. One can think of s as the variable counting the \(size \) of the lattice polytopes, i.e., their number of lattice points. In particular, at every iteration over s, only the lattice polytopes of size s will be processed and “grown” by adding one lattice point. Consider that this process ramifies and becomes slower, indeed starting with a single simplex, adding different points obviously generates different polytopes. In order to minimize the number of iterations we use some Ehrhart theory, which guarantees a simple structure for the polytopes for which the number of lattice points is maximal with respect to the volume. This is done via Lemma 4.1. In order to state it correctly, we need some definitions.

Given a d-dimensional lattice polytope \(P \subset {\mathbb {R}}^d\), we define the lattice pyramid \(\mathrm {Pyr}(P)\) as the \((d+1)\)-dimensional polytope

$$\begin{aligned} \mathrm {Pyr}(P) :=\mathrm {conv}\bigl (P \times \{0\} \cup \{(0,\ldots ,0,1)\}\bigr ) \subset {\mathbb {R}}^{d+1}. \end{aligned}$$

Moreover, we say that a d-dimensional lattice polytope P is an exceptional simplex if P can be obtained via the \((d-2)\)-fold iterations of the lattice pyramid construction over the second dilation of a unimodular simplex, that is,

$$\begin{aligned} P \cong \mathrm {Pyr}\bigl (\ldots (\mathrm {Pyr}(\mathrm {conv}((0,0), (2,0),(0,2))))\ldots \bigr ). \end{aligned}$$

We say that a d-dimensional lattice polytope \(P \subseteq {\mathbb {R}}^d\) is a Lawrence prism with heights \(a_0, \ldots , a_{d-1}\) if there exist nonnegative integers \(a_0, \ldots , a_{d-1}\) such that

$$\begin{aligned} P \cong \mathrm {conv} (\{ {\mathbf {0}}, a_0 {\mathbf {e}}_d , {\mathbf {e}}_1 , {\mathbf {e}}_1 + a_1 {\mathbf {e}}_d , \ldots , {\mathbf {e}}_{d-1}, {\mathbf {e}}_{d-1} + a_{d-1} {\mathbf {e}}_d \}), \end{aligned}$$

where \({\mathbf {e}}_1,\ldots ,{\mathbf {e}}_d\) denote the standard basis of \({\mathbb {R}}^d\).

Lemma 4.1

Let P be a d-dimensional lattice polytope. Then \(|P \cap {\mathbb {Z}}^d| \le d + {{\,\mathrm{Vol}\,}}(P)\), with equality if and only if P is either an exceptional simplex or a Lawrence prism.

Proof

The first part of the lemma is also known as Blichfeldt’s Theorem [17] (but it can be easily deduced also with some basic Ehrhart theory, see Proposition 8.1). A polytope for which the equality \(|P \cap {\mathbb {Z}}^d| = d + {{\,\mathrm{Vol}\,}}(P)\) is attained, must have \(h^*\)-polynomial \(h^*_P(t) = 1 + ({{\,\mathrm{Vol}\,}}(P)-1) t\), which has degree one. The rest of the statement is exactly the characterization of lattice polytopes having \(h^*\)-polynomial of degree one by Batyrev–Nill [11]. \(\square \)

Thanks to this lemma, we know that the variable s can range between \(|S \cap {\mathbb {Z}}^d|\) and \(K+d-1\). At every iteration over s the algorithm selects all the lattice polytopes of size s, grows them into larger ones, which are then stored into a set \({\mathcal {Q}}_S\). The union of all the \({\mathcal {Q}}_S\) for all the simplices \(S \in {\mathcal {S}}_{\le K}^d\) will be the complete list of d-dimensional lattice polytopes having volume at most K, except possibly some Lawrence prisms. Those are easy to classify and can be added “manually” as the last step of the algorithm.

figure d

Beside the optimizations discussed in this section, other small improvements above have been added to the actual implementations of Algorithms 1 and 2. Such expedients are obvious verifications, such as not trying to add points to lattice polytopes of volume K or not trying to add the same point twice, and are not reported in the pseudocode, in order to keep it essential.

5 Results and Comparison with Existing Classifications

In this section we discuss the results of the classification, and compare it with other existing ones. Algorithms 1 and 2 have been implemented in Magma [20] on Intel Core i7-2600 CPU 3.40 GHz. The total running time for all the classifications was roughly one year in total.

Note that the implementation can be easily parallelized and run on large clusters, but this was beyond the resources of the author and the aims of the paper. The implementation has therefore been performed in low dimensions (up to six) and finding a compromise between a large enough volume and a fast enough running time. The classifications are therefore far from any kind of computational limit, and, on request, they can easily be pushed forward.

The two-dimensional case of the classification is not of particular interest, as lattice polygons up to 30 interior lattice points have been classified in [26] and the hollow ones, i.e., the ones without interior lattice points, can be easily described. Indeed, a hollow lattice polygon can either be the convex hull of two lattice segments in two consecutive lines, or the exceptional simplex. For completeness, and for making comparisons, this case has been computed anyway, but the computation has been stopped after a few hours.

Specifically, we fully enumerate the elements of \({\mathcal {S}}_{\le K}\) and \({\mathcal {P}}_{\le K}^d\) for the following couples d and K:

  • \(d = 2\) and \(K = 50\),

  • \(d = 3\) and \(K = 36\),

  • \(d = 4\) and \(K = 24\),

  • \(d = 5\) and \(K = 20\),

  • \(d = 6\) and \(K = 16\).

Having in mind applications to Ehrhart theory, the enumeration of \({\mathcal {S}}_{\le K}^3\) has been performed for \(K=1000\) and discussed in Sect. 7.

We report here the outcome of the implementation of Algorithm 2, while applications and implications are discussed in the following sections.

Theorem 5.1

Up to unimodular equivalence there are

  • \(408 \, 788\) two-dimensional lattice polytopes having volume at most 50;

  • \(6 \, 064 \, 034\) three-dimensional lattice polytopes having volume at most 36;

  • \(989 \, 694\) four-dimensional lattice polytopes having volume at most 24;

  • \(433 \, 273\) five-dimensional lattice polytopes having volume at most 20;

  • \(117 \, 084\) six-dimensional lattice polytopes having volume at most 16.

Their distribution according to their volume, can be read from the tables in Appendix C.

The resulting database is available at https://github.com/gabrieleballetti/small-lattice-polytopes. An immediate application of a classification result such as this one, is to double check existing classifications. For example, Theorem 5.1 has already been used to correct mistakes in a recent classification result by Hibi and Tsuchiya. In [38] they give a characterization for all the lattice polytopes of any dimension, having normalized volume lower than or equal to four. By comparing their results with the classification above it turned out that some polytopes in dimension four and five were missing from their lists. The current version has been corrected with the missing polytopes.

In dimension three our classification has large intersections with several existing ones. In particular we checked that it agrees with:

  1. (1)

    the classification of three-dimensional lattice polytopes with one interior lattice point [40];

  2. (2)

    the classification of three-dimensional lattice polytopes with two interior lattice points [6];

  3. (3)

    the classification of three-dimensional lattice polytopes with width larger than one and having up to eleven lattice points [16].

Additionally, our classification fully contains:

  1. (4)

    the 12 hollow three-dimensional lattice polytopes which are maximal up to inclusion classified in [2, 4];

  2. (5)

    the classification of three-dimensional smooth polytopes (see Sect. 6 for a definition), having up to 16 lattice points, which have been classified in several steps [18, 45, 47].

The fact that our classification contains the 12 hollow three-dimensional lattice polytopes of [2, 4] which are maximal up to inclusion is not surprising. On the contrary, the classification of three-dimensional polytopes was pushed up to normalized volume 36 in order to compare the two classifications. Indeed the largest hollow maximal three-dimensional polytope has volume 36 (this is interesting on its own, as it seems to suggest a “hollow case” of Conjecture 7.2). We remark that our classification does not give an independent proof of this fact. On the other hand, it is remarkable that Algorithm 2 seems to be faster than the algorithms used to classify smooth polytopes in [18, 45, 47].

6 Smooth Polytopes

A natural property in the study of lattice polytopes (especially when it is motivated by toric geometry) is the smoothness property. A lattice polytope P in \({\mathbb {R}}^d\) is called smooth if it is simple and if its primitive edge directions at every vertex form a basis of \({\mathbb {Z}}^d\). Sometimes, smooth polytopes are also called Delzant. The word “smooth” comes in fact from the toric varieties realm: a lattice polytope is smooth if and only if the associated projective toric variety is smooth (see [31, Sect. 2.1]).

The most important open problem regarding smooth polytopes is the so called Oda’s conjecture, for which we need to introduce the notion of Integer Decomposition Property. We say that a d-dimensional lattice polytope P is IDP, or has the Integer Decomposition Property, if for every integer \(n \ge 1\) and every lattice point \({\mathbf {p}}\in nP \cap {\mathbb {Z}}^d\) there are lattice points \({\mathbf {p}}_1, \ldots , {\mathbf {p}}_n \in P \cap {\mathbb {Z}}^d\) such that \({\mathbf {p}}= {\mathbf {p}}_1 + \cdots + {\mathbf {p}}_n\). Polytopes having this property are often referred to as integrally closed, but one should not confuse them with normal polytopes, which are those which are IDP when considered as lattice polytopes with respect to the lattice affinely spanned by their lattice points. Being IDP is also a very natural property (one can think of it as a discrete counterpart of convexity), which is of interest in algebraic geometry, combinatorics, commutative algebra and optimization.

In the nineties Oda [49] formulated several problems on Minkowski sums of lattice polytopes. One of them is nowadays known in the following form as Oda’s Conjecture.

Conjecture 6.1

(Oda’s conjecture)Every smooth lattice polytope is IDP.

This seemingly innocuous statement is actually open even in low dimensions, and in many stronger forms.

In [18] Bogart et al. prove that for every nonnegative integers d and n there are, modulo unimodular equivalence, only finitely many d-dimensional smooth polytopes with n lattice points. This can be seen as evidence for the validity of Conjecture 6.1, as it would follow from it as a corollary (it is indeed easy to verify that there are finitely many IDP polytopes once dimension and number of lattice points are fixed). As an application of their result they classify smooth three-dimensional polytopes having up to 12 lattice points (see also [45]). This was later extended by Lundman [47] who classified all the lattice polytopes having up to 16 lattice points.

Theorem 6.2

([47, Thm. 1]) Up to unimodular equivalence there exist exactly 103 smooth three-dimensional lattice polytopes \(P \subseteq {\mathbb {R}}^3\) such that \(|P \cap {\mathbb {Z}}^3| \le 16\).

The largest polytope in Lundman’s classification has normalized volume 23. As a consequence, the following result enlarges the current census of “small” three-dimensional polytopes.

Theorem 6.3

Up to unimodular equivalence there exist exactly \(1 \, 588\) smooth three-dimensional lattice polytopes \(P \subseteq {\mathbb {R}}^3\) such that \({{\,\mathrm{Vol}\,}}(P) \le 36\). The 103 polytopes having at most 16 lattice points are a subset of them. The distribution of smooth three-dimensional polytopes by their volume is summarized in Table 3.

This highlights why Algorithm 2 may seem more efficient than the ones used to classify smooth polytopes in [18, 45, 47], although it is not shaped to deal with smooth polytopes. Moreover, Algorithm 2 can be freely used in higher dimensions. In particular, we can easily obtain results analogous to Theorem 6.3 up to dimension six.

Theorem 6.4

Up to unimodular equivalence there are

  • \(1 \, 530\) two-dimensional smooth polytopes having normalized volume at most 50;

  • \(1 \, 588\) three-dimensional smooth polytopes having normalized volume at most 36;

  • 738 four-dimensional smooth polytopes having normalized volume at most 24;

  • 412 five-dimensional smooth polytopes having normalized volume at most 20;

  • 127 six-dimensional smooth polytopes having normalized volume at most 16.

The distribution of the classified smooth polytopes by their volume is summarized in Appendix A.

Note that, in dimension two, volume and number of lattice points are strictly correlated. It is easy to prove that, for a two-dimensional polytope P,

$$\begin{aligned} |P \cap {\mathbb {Z}}^2| - 2 \le {{\,\mathrm{Vol}\,}}(P) \le 2|P \cap {\mathbb {Z}}^2|-5. \end{aligned}$$

One can see it as a consequence of some basic results of Ehrhart theory, developed in the following section. As a consequence, the classification of two-dimensional smooth polytopes contains all those having up to 27 lattice points. This extends [18, Thm. 32].

Corollary 6.5

Up to unimodular equivalence there are exactly 458 two-dimensional smooth polytopes having up to 27 lattice points.

Conjecture 6.1 can now be easily verified on the classified polytopes.

Theorem 6.6

Conjecture 6.1 holds for all the smooth polytopes of Theorem 6.4.

By observing Tables 2, 3, 4, 5 and 6 in Appendix A, one can notice that, in each dimension \(d \le 6\), there are only two smooth polytopes of normalized volume lower than or equal to d. They are the unimodular simplex \(\Delta _d\), defined as the convex hull of the origin and the standard basis, which has volume one, and the prism \(\Delta _{d-1} \times \Delta _{1}\), which has volume d. We now verify that this is always the case, for all d. This is indeed a consequence of the combinatorics of simple polytopes.

We are going to use two classical results for simple polytopes. The first is Barnette’s Lower Bound Theorem for simple polytopes.

Theorem 6.7

([8, Thms. 1–2])Let P be a d-dimensional simple polytope. Denote by \(f_0\) and \(f_{d-1}\) the number of vertices and facets of P, respectively. Then,

$$\begin{aligned} f_0 \ge (d-1)f_{d-1} - (d+1)(d-2). \end{aligned}$$

If \( d\ge 4\), the equality can hold only if P has been obtained from a simplex via successive truncations of vertices.

After that we are going to use a description of simple polytopes with \(d+2\) facets, which can be found (in a dual version for simplicial polytopes) in Grünbaum’s textbook.

Theorem 6.8

([32, Thm. 6.1.1]) There exist \(\lfloor {d}/{2} \rfloor \) combinatorial types of d-dimensional simple polytopes with \(d+2\) facets. These are exactly \(\Delta _{d-i} \times \Delta _{i}\) for \(i=1,\ldots ,\lfloor {d}/{2} \rfloor \).

As a corollary of this result, we describe the combinatorics of simple lattice polytopes having few lattice points.

Lemma 6.9

Let P be a simple d-dimensional lattice polytope having at most \(3d-4\) lattice points. Then P is either combinatorially equivalent to the simplex \(\Delta _d\), or to the prism \(\Delta _{1} \times \Delta _{d-1}\).

Proof

P has at most \(3d-4\) vertices. By plugging this number into the inequality of Theorem 6.7, we get an upper bound for the number of facets \(f_{d-1}\) that P can have:

$$\begin{aligned} f_{d-1} \le d+2. \end{aligned}$$

Since \(f_{d-1} = d+1\) if and only if P is a simplex, we can focus on the case \(f_{d-1} = d+2\). By Theorem 6.8, P is combinatorially equivalent to the product \(\Delta _i \times \Delta _{d-i}\), for some \(1 \le i \le \lfloor {d}/{2} \rfloor \). In particular, P has \(f_0 = (i+1)(d-i+1)\) vertices. Fixing d, this quantity is growing in i (for \(i \le {d}/{2}\)), so the inequality

$$\begin{aligned} f_0 = (i+1)(d-i+1) \le 3d-4 \end{aligned}$$

is satisfied if and only if \(i=1\). \(\square \)

Now, by adding the constraint of being a smooth polytope, we can get a simple description of smooth polytopes having few lattice points.

Theorem 6.10

Let P be a smooth d-dimensional lattice polytope having at most \(3d-4\) lattice points. Then P is either the unimodular simplex \(\Delta _d\) or a Lawrence prism with heights \(a_0,\ldots ,a_{d-1}\) with \(a_i \ge 1\) for all i, and \(\sum _{i=0}^{d-1} a_i = 2d-4\).

Proof

If P is a simplex, the statement is trivial. By Lemma 6.9, P is combinatorially equivalent to \(\Delta _1 \times \Delta _{d-1}\), in particular P has two facets F and \(F'\) which are \((d-1)\)-dimensional simplices. Since faces of smooth polytopes are smooth, F and \(F'\) are dilations of \(\Delta _{d-1}\). The tth dilation of a \((d-1)\)-dimensional simplex has \(\left( {\begin{array}{c}d+t-1\\ d-1\end{array}}\right) \) lattice points (see e.g. [13, Thm. 2.2]), which is lower than or equal to \(3d-4\) only for \(t=1\). This proves that both F and \(F'\) are unimodularly equivalent to \(\Delta _{d-1}\). Since P is smooth we can assume that

$$\begin{aligned} F = \Delta _{d-1} = \mathrm {conv}{({\mathbf {0}},{\mathbf {e}}_1,\ldots ,{\mathbf {e}}_{d-1})}, \end{aligned}$$

and that \({\mathbf {e}}_d\) is a lattice point of P. Let \(E_0,\ldots ,E_{d-1}\) be the edges of P that are neither in F nor in \(F'\), labeled so that \({\mathbf {e}}_i\) is a vertex of \(E_i\) for \(i=1,\ldots ,d-1\), while \({\mathbf {0}}\) and \({\mathbf {e}}_d\) are in \(E_0\) (\({\mathbf {e}}_d\) might be not a vertex). Let moreover \({\mathbf {p}}_i\) be the first lattice point met while traveling from \({\mathbf {e}}_i\) along \(E_i\), for \(i=0,\ldots ,d-1\), so that \({\mathbf {p}}_0={\mathbf {e}}_d\). The statement follows by proving that

$$\begin{aligned} \mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,\ldots ,{\mathbf {e}}_{d-1},{\mathbf {p}}_0,\ldots ,{\mathbf {p}}_{d-1})= F \times \Delta _1. \end{aligned}$$

By the smoothness assumption, the simplex \(\mathrm {conv}(F \cup {\mathbf {p}}_i)\) is unimodular for all i. This proves that all the \({\mathbf {p}}_i\)’s are at height one, i.e.,

$$\begin{aligned} {\tilde{F}} :=\mathrm {conv}({\mathbf {p}}_0,\ldots ,{\mathbf {p}}_{d-1}) = P \cap \{x_d = 1\}. \end{aligned}$$

The combinatorics of P implies that \({\tilde{F}}\) equals \(tF \times {1}\) for a dilation factor t, but by the same argument as above, \(t=1\). \(\square \)

Having a Lawrence prism structure is very restricting. Lattice points and volume of a Lawrence prism P are linked by the formula \(|P \cap {\mathbb {Z}}^d| = d + {{\,\mathrm{Vol}\,}}(P)\) (see Lemma 4.1).

Corollary 6.11

In dimension d the only smooth polytopes having normalized volume at most d are the unimodular simplex \(\Delta _d\) and the prism \(\Delta _{d-1} \times [0,1]\). They have normalized volume 1 and d, respectively.

Lawrence prisms have a very restrictive geometry. It is easy to show (for example using pushing or pulling triangulations) that they have a quadratic triangulation, i.e., a triangulation which is regular unimodular and flag. We refer to [33] for definitions and terminology about triangulations. The existence of quadratic triangulations for a smooth polytope is a central question in toric geometry as it implies that the associated projective toric variety has a defining ideal generated by quadrics (see [57]). This problem and several of its variations are sometimes known as Bögvad Conjecture.

Corollary 6.12

Let P be a d-dimensional smooth polytope satisfying one of the following equivalent conditions:

  • \(|P \cap {\mathbb {Z}}^d| \le 3d-4\),

  • \({{\,\mathrm{Vol}\,}}(P) \le 2d-4\).

Then P has a quadratic triangulation. In particular it is IDP.

Another consequence is the following finiteness result, independent of the dimension.

Corollary 6.13

There are finitely many smooth polytopes of normalized volume V, for any fixed integer \(V>1\).

By putting together this and our classification, we can easily classify all smooth polytopes having normalized volume up to 10.

Proposition 6.14

Let P be a smooth polytope having normalized volume at most 10. Then P is either a Lawrence prism, or one of the following 14 polytopes:

  1. (2.a)

    \(\mathrm {conv}({\mathbf {0}},2{\mathbf {e}}_1,2{\mathbf {e}}_2)\),

  2. (2.b)

    \(\mathrm {conv}({\mathbf {0}},3{\mathbf {e}}_1,3{\mathbf {e}}_2)\),

  3. (2.c)

    \(\mathrm {conv}({\mathbf {0}},2{\mathbf {e}}_1,2{\mathbf {e}}_2,2{\mathbf {e}}_1+2{\mathbf {e}}_2)\),

  4. (2.d)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,-2{\mathbf {e}}_1 + {\mathbf {e}}_2, -4{\mathbf {e}}_1 + {\mathbf {e}}_2)\),

  5. (2.e)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,3{\mathbf {e}}_1+2{\mathbf {e}}_2,2{\mathbf {e}}_1+3{\mathbf {e}}_2,3{\mathbf {e}}_1+3{\mathbf {e}}_2)\),

  6. (2.f)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,2{\mathbf {e}}_1+{\mathbf {e}}_2,{\mathbf {e}}_1+2{\mathbf {e}}_2,2{\mathbf {e}}_1+2{\mathbf {e}}_2)\),

  7. (2.g)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,3{\mathbf {e}}_1+{\mathbf {e}}_2,{\mathbf {e}}_1+2{\mathbf {e}}_2,4{\mathbf {e}}_1+2{\mathbf {e}}_2)\),

  8. (2.h)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_1+2{\mathbf {e}}_2,-2{\mathbf {e}}_1+2{\mathbf {e}}_2)\),

  9. (3.a)

    \(\mathrm {conv}({\mathbf {0}},3{\mathbf {e}}_1,3{\mathbf {e}}_2,3{\mathbf {e}}_3)\),

  10. (3.b)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_1+{\mathbf {e}}_2,{\mathbf {e}}_3,{\mathbf {e}}_1+{\mathbf {e}}_3,-2{\mathbf {e}}_2+{\mathbf {e}}_3,{\mathbf {e}}_1-2{\mathbf {e}}_2+{\mathbf {e}}_3)\),

  11. (3.c)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_3,-2{\mathbf {e}}_2+{\mathbf {e}}_3,2{\mathbf {e}}_1-2{\mathbf {e}}_2+{\mathbf {e}}_3)\),

  12. (3.d)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_1+{\mathbf {e}}_2,{\mathbf {e}}_3,{\mathbf {e}}_1+{\mathbf {e}}_3,{\mathbf {e}}_2+{\mathbf {e}}_3,{\mathbf {e}}_1+{\mathbf {e}}_2+{\mathbf {e}}_3)\),

  13. (4.a)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_3,{\mathbf {e}}_4,{\mathbf {e}}_1+{\mathbf {e}}_3,{\mathbf {e}}_1+{\mathbf {e}}_4,{\mathbf {e}}_2+{\mathbf {e}}_3,{\mathbf {e}}_2+{\mathbf {e}}_4)\),

  14. (5.a)

    \(\mathrm {conv}({\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_3,{\mathbf {e}}_4,{\mathbf {e}}_5,{\mathbf {e}}_1+{\mathbf {e}}_4,{\mathbf {e}}_1+{\mathbf {e}}_5,{\mathbf {e}}_2+{\mathbf {e}}_4,{\mathbf {e}}_2+{\mathbf {e}}_5,{\mathbf {e}}_3+{\mathbf {e}}_4,{\mathbf {e}}_3+{\mathbf {e}}_5)\).

7 Classifications of 3-Simplices with Few Interior Lattice Points

In this section we show how the classification of polytopes (in particular simplices) with small volume can be used to enumerate all those having a fixed small number of interior lattice points.

It is natural to wonder how large the volume of a d-dimensional polytope P can be when we fix the number of its interior lattice points to be a nonnegative integer k. In case \(k=0\), i.e., when P is hollow, the answer is clear. One can indeed fit an arbitrarily large d-dimensional hollow polytope in the “slab” \([0,1] \times {\mathbb {R}}^{d-1}\). But in case \(k \ne 0\) the answer is different: Hensley [35] proved that if P is not hollow, then its volume is bounded by a constant depending only on the dimension d and the number of interior lattice points k. In dimension two this was already known, thanks to a sharp bound proven by Scott in 1976 (see Theorem 8.3 in the next section). Hensley’s bound has been improved first by Lagarias–Ziegler [44], later by Pikhurko [50], who gave the best currently known bound.

Theorem 7.1

Let P be a d-dimensional lattice polytope having k interior lattice points, \(k\ge 1\). Then

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(P) \le d! \cdot (8d)^d \cdot 15^{d\cdot 2^{2d+1}}\cdot k. \end{aligned}$$

Although it grows linearly with k (which is the conjectured behavior, see Conjecture 7.2), the bound is expected to be very rough. The current largest known volume of a d-dimensional lattice polytope having k interior points, \(k\ge 1\), is given by the ZPW simplex defined as

$$\begin{aligned} S^d_k:=\mathrm {conv}\bigl ({\mathbf {0}},s_1 {\mathbf {e}}_1,\ldots ,s_{d-1}{\mathbf {e}}_{d-1},(k+1)(s_d-1){\mathbf {e}}_d\bigr ) \end{aligned}$$
(3)

first described by Zaks–Perles–Wills [60] (hence the nameFootnote 1). Here \((s_i)_{i\in {\mathbb {Z}}_{\ge 1}}\) is the Sylvester sequence, defined by the following recursion:

$$\begin{aligned} s_1=2,\quad s_i=s_1\cdots s_{i-1}+1. \end{aligned}$$

It has been conjectured that, once d and k are fixed, the ZPW simplex \(S_k^d\) maximizes the volume among all k-point d-dimensional polytopes. This conjecture has been explicitly stated in [6], but has been already hinted at some of the previously cited works [35, 44, 60].

Conjecture 7.2

([6, Conj. 1.5]) Fix \(d\ge 3\) and \(k\ge 1\). A d-dimensional lattice polytope P having k interior lattice points satisfies

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(P)\le (k+1)(s_d-1)^2. \end{aligned}$$
(4)

With the exception of the case when \(d=3\), \(k=1\), this inequality is an equality if and only if \(P=S^d_k\).

The case when \(d=3\), \(k=1\) has been addressed in [40]: in addition to the ZPW simplex \(S^3_1\), the maximum normalized volume of 72 is also attained by the simplex

$$\begin{aligned} \mathrm {conv}((0,0,0), (2,0,0), (0,6,0), (0,0,6)). \end{aligned}$$

In recent years, Conjecture 7.2 has been proven for several families of lattice polytopes. The explicit classifications [6, 40] settle the cases \(d=3\) and \(k \in \{1,2\}\). Averkov–Krümpelmann–Nill [3] proved it for simplices with one interior point, while Balletti–Kasprzyk–Nill [7] for reflexive polytopes. Recently Averkov [1] proved it for simplices having a facet with one lattice point in its relative interior. For all these families the bound for the volume is sharp as they include the ZPW simplices.

We now use our classification to enumerate all the three-dimensional simplices having few interior lattice points, in this way we will be able to verify Conjecture 7.2 in these additional cases. The idea is to use volume bounds to make sure that our classification contains all lattice polytopes having small number of interior points. Note that using the general bounds, even the best known ones (Theorem 7.1) would be futile: one would have to classify all the simplices having up to normalized volume \(3.4 \times 10^{456}\), in order to be sure that the classification contains all the three-dimensional polytopes with one interior lattice point. Luckily some better bounds are known in special cases.

Theorem 7.3

([50]) Let S be a three-dimensional lattice simplex having k interior lattice points, with \(k \ge 1\). Then

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(S) \le \frac{29791}{352} k \le 85k. \end{aligned}$$

We now use Algorithm 1 to classify all the elements in \({\mathcal {S}}_{\le 1000}^3\).

Proposition 7.4

There are \(28 \, 015 \, 923\) three-dimensional simplices having normalized volume at most \(1 \, 000\).

As an immediate corollary, we are able to fully enumerate the three-dimensional simplices having up to 11 interior lattice points.

Corollary 7.5

All the 3-simplices having up to 11 interior lattice points are in \({\mathcal {S}}_{\le 1000}^3\). Their distribution by number of interior lattice points is summarized in Table 1.

Note that Corollary 7.5 can be seen as an extension of existing classifications of three-dimensional simplices performed up to two interior lattice points. The 225 three-dimensional simplices with one interior lattice point have been enumerated by Borisov and Borisov [19, p. 278], while the 471 with two interior lattice points are classified in [6, Thm. 3.4].

Table 1 Numbers of three-dimensional polytopes and simplices having few interior lattice points
Full size table

Conjecture 7.2 can be now verified on the classified objects. In a similar way, we are going to verify that these satisfy a conjecture known as the Duong Conjecture [29, Conj. 1–2]. It concerns a special class of three-dimensional lattice simplices. We call a lattice polytope clean, if the only lattice points on its boundary are the vertices.

Conjecture 7.6

(Duong conjecture) Let S be a three-dimensional clean simplex having k interior lattice points, with \(k \ge 1\). Then

$$\begin{aligned} {{\,\mathrm{Vol}\,}}(S) \le 12k + 8, \end{aligned}$$

where the equality is attained if and only if S is the Duong simplex, defined as

$$\begin{aligned} D^3_k:=\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(3,6k+1,12k+8)). \end{aligned}$$

Theorem 7.7

Conjectures 7.2 and 7.6 hold for three-dimensional simplices having up to 11 interior lattice points.

8 Conjectural Ehrhart Inequalities in Dimension Three

In this section we use the classification of three-dimensional polytopes to estimate the behavior of their \(h^*\)-polynomials. We begin with a quick introduction to Ehrhart theory and refer the more interested reader to Beck and Robins’ book [13].

Given a d-dimensional lattice polytope P in \({\mathbb {R}}^d\), one can associate a function \(t \mapsto |tP \cap {\mathbb {Z}}^d|\), which counts the number of lattice points in tP, the tth dilation of P, where t is a positive integer. Ehrhart [30] proved that this function behaves polynomially, i.e., that there exists a polynomial \(\mathrm {ehr}_P\), which we call the Ehrhart polynomial of P, satisfying \(\mathrm {ehr}_P(t)=|tP \cap {\mathbb {Z}}^d|\) for \(t \ge 1\).

Its generating function is the rational function

$$\begin{aligned} 1 + \sum _{t \ge 1} \mathrm {ehr}_P(t) z^t =\frac{\sum _{i \ge 0}h^*_i z^i}{(1-z)^{d+1}}, \end{aligned}$$

where \(h^*_i=0\) for any \(i \ge d+1\). We call the polynomial \(h^*_P(z)=h^*_0 + h^*_1 z + \cdots + h^*_s z^s\) the \(h^*\)-polynomial of P (sometimes also the \(\delta \)-polynomial), and we set the degree of P to be s, the degree of its \(h^*\)-polynomial. In the following we will often identify the \(h^*\)-polynomial with the vector of its coefficients \((h^*_0,h^*_1,\ldots ,h^*_d)\), which is called the \(h^*\)-vector (or \(\delta \)-vector) of P. Some properties of the \(h^*\)-polynomial are well known, and listed in the following proposition.

Proposition 8.1

The coefficients \(h^*_0,h^*_1,\ldots ,h^*_d\) of the \(h^*\)-polynomial of P are nonnegative integers satisfying the following conditions:

  1. (1)

    \(h^*_0=1\);

  2. (2)

    \(h^*_1=|P \cap {\mathbb {Z}}^d| - d - 1\);

  3. (3)

    \(h^*_d = |P^\circ \cap {\mathbb {Z}}^d|\);

  4. (4)

    \(\sum _{i=0}^d h^*_i={{\,\mathrm{Vol}\,}}(P)\).

The nonnegativity part of the statement above is a result of Stanley [53], while the rest can be derived from Ehrhart’s original approach. Combinatorial interpretations for the other coefficients are possible, but they are not as natural as the ones above. One of the biggest challenges in Ehrhart theory is to characterize the \( h^*\)-vectors of lattice polytopes.

Question 8.2

For each d, which vectors \((h^*_0,h^*_1,\ldots ,h^*_d)\) are \(h^*\)-vectors of some d-dimensional lattice polytope?

This question is broadly open even in dimension three. In two dimensions the answer to Question 8.2 was first given by Scott [52].

Theorem 8.3

The vector with integer entries \((1,h^*_1,h^*_2)\) is the \(h^*\)-vector of a two-dimensional lattice polytope if and only if one of the following conditions holds:

  1. (1)

    \(h^*_2=0\);

  2. (2)

    \(0 < h^*_2\le h^*_1\le 3h^*_2+3\);

  3. (3)

    \((1,h^*_1,h^*_2)=(1,7,1)\).

The last condition is fulfilled only by the exceptional triangle

$$\begin{aligned} 2\Delta _2 =\mathrm {conv}({\mathbf {0}},2{\mathbf {e}}_1,2{\mathbf {e}}_2). \end{aligned}$$

A generalized version of Theorem 8.3 has been proven in each dimension and for degree two polytopes in [58]. This has been generalized further to every degree in [5], showing that there are inequalities for the \(h^*\)-coefficients that are universal, i.e., not depending on dimension and degree.

Some relations among the coefficients of an \(h^*\)-polynomial are known, and summarized in the following proposition. The first one can be deduced directly from Proposition 8.1, the others come from works by Stanley [54] and Hibi [36].

Proposition 8.4

Let P be a d-dimensional lattice polytope of degree s with its \(h^*\)-vector \(h^*(P)=(h^*_0,\ldots ,h^*_d)\). Then:

  1. (1)

    \(h^*_d \le h^*_1\);

  2. (2)

    \(h^*_{d-1} + \cdots + h^*_{d-i} \le h^*_2 + \dots + h^*_{i+1}\), for \(i=1,\ldots , d-1\);

  3. (3)

    \(h^*_{0} + \dots + h_{i} \le h_{s} + \cdots + h_{s-i}\), for \(i=0,1,\ldots , s\);

  4. (4)

    if \(h^*_d > 0\), then \(h^*_1 \le h^*_i\), for \(i=1,2,\ldots ,d-1\).

Recently Stapledon [55, 56] proved existence of infinite new classes of inequalities, giving explicit formulas in small dimensions.

In dimension three, the known inequalities are far from giving a complete picture of all possible \(h^*\)-vectors. Nevertheless this case has been proven provided \(h^*_3=0\), i.e., for hollow lattice polytopes. In this case a polytope has degree two, and Treutlein’s result [58] gives a necessary condition, while Henk–Tagami [34] prove the sufficiency part.

Theorem 8.5

([58, Thm. 2], [34, Prop. 2.10]) A vector \((1,h^*_1,h^*_2,0)\) with integer entries is the \(h^*\)-vector of a three-dimensional lattice polytope if and only if one of the following conditions holds:

  1. (1)

    \(h^*_2 = 0\);

  2. (2)

    \( 0 \le h^*_1 \le 3h^*_2 + 3\);

  3. (3)

    \((1,h^*_1,h^*_2,0) = (1,7,1,0)\).

The last condition is satisfied only by the exceptional simplex

$$\begin{aligned} \mathrm {conv}({\mathbf {0}},2{\mathbf {e}}_1,2{\mathbf {e}}_2,{\mathbf {e}}_3). \end{aligned}$$

In the following we use the classification of three-dimensional lattice polytopes to conjecture a set of sharp inequalities describing the behavior of three-dimensional polytopes with interior points, i.e., the polytopes whose Ehrhart coefficient \(h^*_3\) is nonzero. An immediate way to do this is by plotting the \(h^*\)-vectors of classified polytopes (see Appendix B), and try to understand which inequalities seem to be satisfied.

In what follows, we frequently need to calculate the \(h^*\)-vector of families of lattice simplices depending on a parameter. The following lemma is an example. Its proof outlines how these kind of results can be proven, and similar results will be given without proof in the rest of the section.

Lemma 8.6

The ZPW simplex

$$\begin{aligned} S^3_k :=\mathrm {conv}((0,0,0),(2,0,0),(0,3,0),(0,0,6k+6)), \end{aligned}$$

has the \(h^*\)-vector \((1,16k+19,19k+16,k)\).

Proof

From Proposition 8.1, we can write the \(h^*\)-vector of any three-dimensional lattice polytope P in terms of number of lattice points, number of interior lattice points and volume as

$$\begin{aligned} \bigl (1,|P \cap {\mathbb {Z}}^d|-4, {{\,\mathrm{Vol}\,}}(P)-|P \cap {\mathbb {Z}}^d|-|P^\circ \cap {\mathbb {Z}}^3|+3, |P^\circ \cap {\mathbb {Z}}^3|\bigr ). \end{aligned}$$

The normalized volume \({{\,\mathrm{Vol}\,}}(S^3_k)\) of \(S^3_k\) can be calculated trivially and equals \(36(k+1)\). For the number of interior lattice point we project \(S^3_k\) along \({\mathbf {e}}_3\), and we deduce that they have to be all of the form (1, 1, a) for \(a \ge 1\). Note that \((1,1,k+1)\) can be written as a convex combination of the vertices (2, 0, 0), (0, 3, 0) and \((0,0,6k+6)\) with weights \(\frac{1}{2}, \frac{1}{3},\frac{1}{6}\), respectively, in particular it is on the boundary of \(S^3_k\). Therefore the interior points are all those of the form (1, 1, a), with \(1 \le a \le k\), and there are exactly k of them. With a similar (and easier) argument, one can count the lattice points in the relative interior of lower-dimensional faces of \(S^3_k\). By summing everything up, we get \(|P \cap {\mathbb {Z}}^d|=16k+23\), and hence the claim follows. \(\square \)

Conjecture 8.7

Let P be a three-dimensional lattice polytope having at least one interior lattice point. Then its \(h^*\)-vector \((1,h^*_1,h^*_2,h^*_3)\) satisfies the following inequalities.

  1. (1)

    \(h^*_3 \le h^*_1\),

  2. (2)

    \(h^*_1 \le h^*_2\),

  3. (3)

    \(h^*_2 \le 19h^*_3+16\),

  4. (4)

    \(h^*_2 - h^*_1 \le 9 h^*_3 + 9\),

  5. (5)

    \( 5 h^*_3 h^*_1 + 4 h^*_1 + 4 \le 4 {h^*_3}^2 + 4 h^*_3 h^*_2 + 5 h^*_2\).

Moreover, the fourth inequality holds in the stronger formFootnote 2

  1. (4*)

    \(h^*_2 - h^*_1 \le 9 h^*_3 + 7\),

unless P is one of the following exceptional cases (listed together with their \(h^*\)-vectors):

  1. (i)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(2,19,25))\), (1, 3, 20, 1)

  2. (ii)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(3,19,28))\), (1, 4, 22, 1)

  3. (iii)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(3,13,19),(1,-2,-3))\), (1, 5, 22, 1)

  4. (iv)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(4,7,11),(-5,-7,-15))\), (1, 7, 24, 1)

  5. (v)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(2,2,3),(-21,-8,-25))\), (1, 11, 28, 1)

  6. (vi)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(5,17,42))\), (1, 11, 29, 1)

  7. (vii)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(5,7,17),(1,-2,-5))\), (1, 12, 29, 1)

  8. (viii)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(7,2,9),(-7,-3,-15))\), (1, 13, 30, 1)

  9. (ix)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(0,0,1),(5,42,-25))\), (1, 14, 31, 1)

  10. (x)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(5,23,45))\), (1, 8, 34, 2)

  11. (xi)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(3k+3,9k+8,18k+15))\), \((1,4k+3,13k+11,k)\)

  12. (xii)

    \(\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(3,12k+8,18k+15))\), \((1,4k+3,13k+11,k)\)

where, in the last two cases, \(k \in {\mathbb {Z}}_{\ge 1}\). Inequalities (3) and (5) both become equalities if and only if, for some \(k \ge 1\), P is one of the ZPW simplices

$$\begin{aligned} S^3_k :=\mathrm {conv}((0,0,0),(2,0,0),(0,3,0),(0,0,6k+6)), \end{aligned}$$

having the \(h^*\)-vector \((1,16k+19,19k+16,k)\), or the special “almost-ZPW” simplex

$$\begin{aligned} {\tilde{S}}^3_1:=\mathrm {conv}((0,0,0),(2,0,0),(0,6,0),(0,0,6)), \end{aligned}$$

having the \(h^*\)-vector (1, 35, 35, 1).

Inequalities (1) and (4*) become equalities if and only if, for some \(k\ge 1\), P is one of the Duong simplices

$$\begin{aligned} D^3_k:=\mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(3,6k+1,12k+8)) \end{aligned}$$

having the \(h^*\)-vector \((1,k,10k+7,k)\).

Inequalities (1) and (2) of Conjecture 8.7 are already known to be true, as they are a consequence of Proposition 8.4. Note that Conjecture 8.7 generalizes the three-dimensional case of Conjecture 7.2, for the maximal volume of polytopes having interior lattice points, and Conjecture 7.6 (Duong Conjecture). Moreover, it generalizes [6, Conj. 6.1], on the maximal \(h^*\)-coefficients of lattice polytopes with interior lattice points.

Note that inequality (5) of Conjecture 8.7 is non-linear. However, fixing \(h^*_3\) to be larger than one, the inequalities are linear and define a pentagon (see Fig. 1). In the special case when \(h^*_3=1\) equalities (2) and (5) coincide. We now give a vertex representation of such a pentagon.

Proposition 8.8

For each \(h^*_3 \in {\mathbb {Z}}_{>1}\), inequalities (1), (2), (3), (4*), (5) define a pentagon in \({\mathbb {R}}^4\) with vertices

$$\begin{aligned} {\mathbf {v}}_1&:=(1,h^*_3,h^*_3,h^*_3),\\ {\mathbf {v}}_2&:=(1,4h^*_3+4,4h^*_3+4,h^*_3),\\ {\mathbf {v}}_3&:=(1,16h^*_3+19,19h^*_3+16,h^*_3),\\ {\mathbf {v}}_4&:=(1,10h^*_3+9,19h^*_3+16,h^*_3),\\ {\mathbf {v}}_5&:=(1,h^*_3,10h^*_3+7,h^*_3). \end{aligned}$$

Moreover,

  • \({\mathbf {v}}_1\) is realized as the \(h^*\)-vector of the polytope

    $$\begin{aligned} \mathrm {conv}((0,0,0),(1,0,0),(0,1,0),(3,3h^*_3,3h^*_3+1)), \end{aligned}$$

  • \({\mathbf {v}}_2\) is realized as the \(h^*\)-vector of the polytope

    $$\begin{aligned} \mathrm {conv}((0,0,0),(1,0,0),(2,3,0),(2,3,3+3h^*_3)), \end{aligned}$$

  • \({\mathbf {v}}_3\) is realized as the \(h^*\)-vector of the ZPW simplex \(S^3_{h^*_3}\),

  • \({\mathbf {v}}_5\) realized as the \(h^*\)-vector of the Duong simplex \(D^3_{h^*_3}\).

Fig. 1
figure 1

The pentagon defined by Conjecture 8.7, for a fixed \(h^*_3\). The dashed lines represent inequalities (3), (4*) and (5), which are conjectural. Note that the vertex \({\mathbf {v}}_4\) seems not to be realized as the \(h^*\)-vector of any lattice polytope, anyway there are other realizable \(h^*\)-vectors which are very close to it (see Proposition 8.9 and the previous discussion)

Full size image

Note that we do not have a candidate polytope realizing the vertex \({\mathbf {v}}_4\), for each value of \(h^*_3\). From the data available, it seems like such an \(h^*\)-vector is never attained for any number of interior points. In order to show that inequalities (3) and (4*) are actually sharp, we give examples of polytopes having, for each \(h^*_3\), the \(h^*\)-vector “close enough” to \({\mathbf {v}}_4\). We remark that, in this way, there should be an additional inequality in Conjecture 8.7 cutting out the vertex \({\mathbf {v}}_4\), and creating two additional ones. The distance of the two new vertices from \({\mathbf {v}}_4\) is fixed and does not depend on the value of \(h^*_3\), so we decided not to include it.

Proposition 8.9

For each positive integer value of \(h^*_3\), the \(h^*\)-vectors

$$\begin{aligned}&(1,10h^*_3+11,19h^*_3+16,h^*_3),\quad \ (1,10h^*_3+9,19h^*_3+15,h^*_3),\\&\quad \ (1,10h^*_3+7,19h^*_3+14,h^*_3) \end{aligned}$$

are attained, respectively, by the polytopes

$$\begin{aligned}&\mathrm {conv}\bigl ((1,0,0),(2,0,0),(0,1,0),(0,3,0),(0,0,6h^*_3+5),(1,0,3h^*_3+3)\bigr ),\\&\mathrm {conv}\bigl ((0,0,0),(1,0,0),(0,1,0),(9h^*_3+8,6h^*_3+5,18h^*_3+15),\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \,\, (12h^*_3+10,8h^*_3+7,24h^*_3+20)\bigr ),\\&\mathrm {conv}\bigl ((0,0,0),(1,0,0),(0,1,0),(6h^*_3+5,3h^*_3+3,18h^*_3+15),\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (8h^*_3+5,4h^*_3+3,24h^*_3+14)\bigr ). \end{aligned}$$

Proof

Using the same technique as in Lemma 8.6, one can prove that the simplices

  • \(S^3_{h^*_3}\),

  • \(\mathrm {conv}\bigl ( (0,0,0),(1,0,0),(0,1,0),(12h^*_3+10,6h^*_3+6,36h^*_3+30) \bigr )\),

  • \(\mathrm {conv}\bigl ( (0,0,0),(1,0,0),(0,1,0),(12h^*_3+8,6h^*_3+5,36h^*_3+24)\bigr )\),

have \(h^*\)-vectors respectively equal to

  • \((1,16h^*_3+19,19h^*_3+16,h^*_3)\),

  • \((1,16h^*_3+14,19h^*_3+15,h^*_3)\),

  • \((1,16h^*_3+ 9,19h^*_3+14,h^*_3)\).

From this, one can obtain the three polytopes starting with the simplices, and successively cutting out unimodular simplices. At each cut, \(h^*_1\) drops by one, while \(h^*_2\) stays the same. \(\square \)

As a final observation for this section, we plot heat diagrams of the distribution of \(h^*\)-vectors of three-dimensional lattice polytopes having one and two interior lattice points. From Fig. 2 one can note that Conjecture 8.7 seems to describe accurately the behavior of \(h^*\)-vectors in dimension three, and that most of the \(h^*\)-vectors seem to be in the center of the pentagon.

Fig. 2
figure 2

Heat diagrams for \(h^*\)-vector of three-dimensional polytopes with one and two interior lattice points (from [6, 40]). Each \(h^*\)-vector is colored according to the number of lattice polytopes attaining it

Full size image

9 Final Examples

In this final section we use the classification to check explicitly how common are some of the most studied properties of lattice polytopes.

In the literature it is possible to find a vast multitude of hierarchies ordering lattice polytopes with a chain of progressively more restricting properties. Having the Integer Decomposition Property (defined in Sect. 6), plays usually a central role in such a hierarchy, due to its importance in algebraic and optimization contexts. Here we additionally focus on the following properties.

Definition 9.1

Let \(P \subset {\mathbb {R}}^d\) be a d-dimensional lattice polytope. We say that P is spanning if its lattice points affinely span \({\mathbb {Z}}^d\), i.e., if

$$\begin{aligned} {\mathbb {Z}}((P-{\mathbf {p}}) \cap {\mathbb {Z}}^d) = {\mathbb {Z}}^d, \end{aligned}$$

for any \({\mathbf {p}}\in P \cap {\mathbb {Z}}^d\). We say that P is very ample if for each vertex \({\mathbf {v}}\) of P the lattice points in the tangent cone \({\mathbb {R}}_{\ge 0} (P-{\mathbf {v}})\) are sums of lattice points of \(P-{\mathbf {v}}\), i.e., if

$$\begin{aligned} {\mathbb {R}}_{\ge 0} (P-{\mathbf {v}}) \cap {\mathbb {Z}}^d = {\mathbb {Z}}_{\ge 0}((P-{\mathbf {v}}) \cap {\mathbb {Z}}^d). \end{aligned}$$

We say that P has a unimodular cover if there exist unimodular lattice simplices \(S_1,\ldots ,S_n \subset {\mathbb {R}}^d\) such that \(P = S_1 \cup \ldots \cup S_n\). Finally, we say that P has a unimodular triangulation if P admits a triangulation in unimodular lattice simplices.

It is easy to verify that such properties are given in ascending order of restrictiveness, with the IDP property being in the middle, i.e.,

figure e

Notice that in dimension two all these properties are always satisfied by all polytopes. On the other hand, in higher dimensions the reverse implications are known to be false. While counterexamples to the last implication (very ampleness implies spanning) are easy to produce, the first example of a very ample but not IDP lattice polytope was given in dimension five by Bruns and Gubeladze [23], who later gave an example in dimension three [24, Exercise 2.24]. Examples of IDP polytopes not having a unimodular cover have also been given by Bruns and Gubeladze in dimension five [22]. The first example of a three-dimensional polytope which has a unimodular but does not have a unimodular triangulation has been given by Kantor and Sarkaria [39], although the first example, in dimension four, appears in [25].

By looking at the database of three-dimensional polytopes classified in this paper, we can easily find examples of lattice polytopes which are spanning but not very ample, examples of lattice polytopes which are very ample but not IDP, and examples of IDP lattice polytopes not admitting a unimodular triangulation. Additionally we can be sure that the following examples are the smallest possible, i.e., having smallest possible dimension and volume.

Theorem 9.2

The polytope

$$\begin{aligned} \mathrm {conv}(\{{\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_3,{\mathbf {e}}_1+{\mathbf {e}}_2+3{\mathbf {e}}_3\}) \end{aligned}$$

is spanning but not very ample. The polytope

$$\begin{aligned} \mathrm {conv}(\{{\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_1 + {\mathbf {e}}_2 + 2 {\mathbf {e}}_3,{\mathbf {e}}_1 + {\mathbf {e}}_2 + 3 {\mathbf {e}}_3, {\mathbf {e}}_1 - {\mathbf {e}}_3,{\mathbf {e}}_2 - {\mathbf {e}}_3,{\mathbf {e}}_3\}) \end{aligned}$$

is very ample but not IDP. The polytope

$$\begin{aligned} \mathrm {conv}(\{{\mathbf {0}},{\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_1 + {\mathbf {e}}_2, {\mathbf {e}}_3, {\mathbf {e}}_1 + 2 {\mathbf {e}}_2 - {\mathbf {e}}_3, 3 {\mathbf {e}}_1 + {\mathbf {e}}_2 - {\mathbf {e}}_3, -2 {\mathbf {e}}_1 - {\mathbf {e}}_2 + {\mathbf {e}}_3\}) \end{aligned}$$

has a unimodular cover but does not have a unimodular triangulation. Such examples are of minimal volume in dimension three.

The last example also appears in [28]. No IDP polytope without a unimodular cover has been found in dimension three, but not all the enumerated three polytopes could be checked, as the algorithm implemented for checking the existence of a unimodular cover is computationally expensive. The presence of such polytopes in higher dimension has already been mentioned, but it makes sense to wonder whether being IDP and having a unimodular cover are equivalent properties in dimension three.

Question 9.3

Is there a three-dimensional IDP polytope that does not have a unimodular cover?

In this last part of the paper we discuss properties of the \(h^*\)-vectors of very ample lattice polytopes. We call a sequence \(a_0, a_1 , \ldots , a_n\) of real numbers unimodal if, for some \(0 \le k \le n\),

$$\begin{aligned} a_0 \le \cdots \le a_{k-1} \le a_k \ge a_{k+1} \ge \cdots \ge a_n. \end{aligned}$$

We call \(a_0, a_1 , \ldots , a_n\) log-concave if, for all \( 1 \le i \le n-1\),

$$\begin{aligned} a_{i-1} a_{i+1} \le a_i^2. \end{aligned}$$

If all the \(a_i\) are nonnegative, then log-concavity implies unimodality. It is a long standing open problem (originally posed by Stanley) to understand whether all IDP polytopes have unimodal, or even log-concave, \(h^*\)-vector (see Braun’s survey [21]). In [37, p. 39] it is shown that, by relaxing the IDP property to very ampleness, it is possible to lose log-concavity. This is done by giving an example of nine-dimensional very ample (but non-IDP) lattice polytope.

By looking at our database it turns out that this kind of examples can be small and exist already in dimension three, as the polytope

$$\begin{aligned} \mathrm {conv}({\mathbf {0}},e_1,e_2,e_3,e_1+e_3,e_2+e_3,e_1+e_2+16e_3,e_1+e_2+17 e_3) \end{aligned}$$

is very ample and has \(h^*\)-vector (1, 4, 17, 0), which is not log-concave. This example can be easily generalized by considering the three-dimensional lattice polytope

$$\begin{aligned} Q :=\mathrm {conv}({\mathbf {0}},e_1,e_2,e_3,e_1+e_3,e_2+e_3,e_1+e_2+ke_3,e_1+e_2+(k+1) e_3), \end{aligned}$$

where k is a nonnegative integer. It is easy to verify that Q is a very ample lattice polytope with \(h^*\)-vector \((1,4,k+1,0)\), which, for \(k \ge 16\), is not log-concave. Note that Q fails to be IDP for \(k \ge 4\). This kind of construction is called segmental fibration and has been used in [12] to generate non-IDP but very ample polytopes.