Computational Aspects of the Colorful Carathéodory Theorem

Abstract

Let $C_1,\dots ,C_{d+1}\subset \mathbb {R}^d$ be $d+1$ point sets, each containing the origin in its convex hull. We call these sets color classes, and we call a sequence $p_1, \dots , p_{d+1}$ with $p_i \in C_i$, for $i = 1, \dots , d+1$, a colorful choice. The colorful Carathéodory theorem guarantees the existence of a colorful choice that also contains the origin in its convex hull. The computational complexity of finding such a colorful choice (ColorfulCarathéodory) is unknown. This is particularly interesting in the light of polynomial-time reductions from several related problems, such as computing centerpoints, to ColorfulCarathéodory. We define a novel notion of approximation that is compatible with the polynomial-time reductions to ColorfulCarathéodory: a sequence that contains at most k points from each color class is called a k-colorful choice. We present an algorithm that for any fixed $\varepsilon > 0$, outputs an $\lceil \varepsilon d\rceil$-colorful choice containing the origin in its convex hull in polynomial time. Furthermore, we consider a related problem of ColorfulCarathéodory: in the nearest colorful polytope problem (Ncp), we are given sets $C_1,\dots ,C_n\subset \mathbb {R}^d$ that do not necessarily contain the origin in their convex hulls. The goal is to find a colorful choice whose convex hull minimizes the distance to the origin. We show that computing a local optimum for Ncp is PLS-complete, while computing a global optimum is NP-hard.

1 Introduction

Let $P\subset \mathbb {R}^d$ be a point set. Carathéodory ’s well-known theorem [14, Thm. 1.2.3] states that the containment of each point in ${{\mathrm{conv}}}(P)$ can be witnessed by a “small” subset of P. Moreover, the standard proof of this result is constructive and gives a polynomial-time algorithm if the coefficients of the original convex combination are known. In the following, we say that P embraces a point ${\varvec{q}}\in \mathbb {R}^d$ or is ${\varvec{q}}$-embracing if and only if ${\varvec{q}}$ is in the convex hull of P. Similarly, we say P ray-embraces ${\varvec{q}}$ if and only if ${\varvec{q}}$ is in the cone spanned by P.

Theorem 1.1

(Carathéodory’s theorem) Let $P=\{{\varvec{p}}_1,\dots ,{\varvec{p}}_n\} \subset \mathbb {R}^d$ be a set of n points.

• (Convex version) If P embraces the origin, there is an affinely independent subset $P' \subseteq P$ that embraces the origin.

• (Cone version) If P ray-embraces a point ${\varvec{b}}\in \mathbb {R}^d$, there is a linearly independent subset $P' \subseteq P$ that ray-embraces ${\varvec{b}}$. $\square$

Fig. 1

The colorful Carathéodory theorem in two dimensions: all color classes embrace the origin and the marked points form a ${\varvec{0}}$-embracing colorful choice

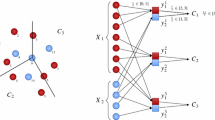
As we will discuss in Sect. 2, the standard proof of Theorem 1.1 is constructive and can be interpreted as a polynomial-time algorithm. Bárány  [3] generalized Carathéodory ’s theorem by introducing colors: now, multiple point sets embrace the origin, and we think of these point sets as color classes. Then, there is a sequence of points, one from each color class, that also embraces the origin. This is called a colorful choice. See Fig. 1 for an example.

Theorem 1.2

(Colorful Carathéodory’s theorem [3]) Let $C_1,\dots ,C_{d+1} \subset \mathbb {R}^d$ be point sets that all embrace the origin. There exists a colorful choice that embraces the origin.

Proof

Let C, $|C|\le d+1$, be a colorful choice of $C_1,\dots ,C_{d+1}$. Let $\Phi (C)$ be the minimum $\ell _2$-distance between any point in ${{\mathrm{conv}}}(C)$ and the origin. If $\Phi (C) = 0$, then ${\varvec{0}} \in {{\mathrm{conv}}}(C)$, and we are done. Now, assume $\Phi (C) > 0$. Let ${\varvec{c}}$ be the point in ${{\mathrm{conv}}}(C)$ with minimum $\ell _2$-distance to the origin. Furthermore, let $h^-$ be the open halfspace that contains the origin and that is bounded by the hyperplane through ${\varvec{c}}$ that is orthogonal to ${\varvec{c}}$ interpreted as a vector. Since ${\varvec{c}}$ minimizes the distance to the origin, it is contained in a facet of ${{\mathrm{conv}}}(C)$. Note that ${\varvec{c}}$ is not necessarily contained in the interior of a facet. Theorem 1.1 implies that there is a d-subset $F \subset C$ of C with ${\varvec{c}}\in {{\mathrm{conv}}}(F)$. Let $i^\times$ be the color of the point that is missing in F. The halfspace $h^-$ contains the origin, and thus it contains at least one point ${\varvec{c}}_{i^\times } \in C_{i^\times }$ with color $i^\times$. Now, set $C' = (F \cup \{{\varvec{c}}_{i^\times }\})$. Since ${{\mathrm{conv}}}(C')$ contains ${\varvec{c}}$ and a point in $h^-$, we have $\Phi (C') < \Phi (C)$. Thus, if $\Phi (C) > 0$, there is always a way to strictly decrease it. The situation is depicted in Fig. 2. Because there is only a finite number of colorful choices, there is a colorful choice $C^\star$ with $\Phi (C^\star ) = 0$. $\square$

Fig. 2

Proof of the colorful Carathéodory theorem: if the potential function is larger than 0, it can be decreased by swapping one point with another point of the same color

The convex version of Theorem 1.1 can be derived directly from Theorem 1.2 by setting $C_1=\dots =C_{d+1}=P$. There are many different variants and generalizations of the colorful Carathéodory theorem (see [16]).

We denote with ColorfulCarathéodory the computational problem of finding a ${\varvec{0}}$-embracing colorful choice under the conditions of Theorem 1.2. ColorfulCarathéodory is particularly interesting in the light of its applications: let $P \subset \mathbb {R}^d$ be a point set. We call a partition of P into r sets $P_1,\dots ,P_r$ a Tverberg r-partition if the convex hulls of the $P_i$ have a point in common. By Tverberg’s theorem [29], there always exists a Tverberg $\lceil |P| / (d+1)\rceil$-partition. We denote the computational problem of finding such a partition by Tverberg. Sarkaria’s proof [26] of Tverberg’s theorem can be interpreted as polynomial-time reduction of Tverberg to ColorfulCarathéodory. Moreover, Tverberg’s theorem directly implies the centerpoint theorem [24] that guarantees the existence of centerpoints, a popular generalization of the median to higher dimensions. We call a point ${\varvec{q}}\in \mathbb {R}^d$ a centerpoint for P if any closed halfspace that contains ${\varvec{q}}$ also contains at least $\lceil |P| / (d+1) \rceil$ points from P. Consider a Tverberg r-partition $P_1,\dots ,P_r$ of P for $r = \lceil |P| / (d+1) \rceil$. Then any point in $\bigcap _{i=1}^r {{\mathrm{conv}}}(P_i) \ne \emptyset$ is a centerpoint. Hence, the computational problem of computing centerpoints, Centerpoint, can again be reduced in polynomial time to ColorfulCarathéodory. Furthermore, the key argument of Sarkaria’s proof of Tverberg’s theorem can also be used to prove the colorful Kirchberger theorem [2]: given n Tverberg r-partitions $\mathcal {T}_1, \dots , \mathcal {T}_n$ for disjoint d-dimensional point sets of size n and $r = \lceil n / (d+1) \rceil$, a Tverberg r-partition $\mathcal {T}$ can be constructed by taking exactly one point from each $\mathcal {T}_i$ and putting it in the set of $\mathcal {T}$ with the same index as in $\mathcal {T}_i$. Again, the proof can be interpreted as a polynomial-time reduction to ColorfulCarathéodory from ColorfulKirchberger, the computational problem corresponding to the colorful Kirchberger theorem. We discuss these reductions in more detail in Sect. 3.1.

In contrast to Carathéodory ’s theorem, the complexity of ColorfulCarathéod ory is still unsettled. Since a solution always exists and can be verified in polynomial-time, ColorfulCarathéodory is contained in the complexity class total function NP (TFNP). This already implies that ColorfulCarathéodory is not NP-hard unless ${\small {\textsf {NP}}} = {\small {\textsf {coNP}}}$ [15, Thm. 2.1], [10, Lem. 4]. In a recent result, Meunier et al.  [17] showed that ColorfulCarathéodory is contained in the intersection of two important subclasses of TFNP: polynomial parity argument in a directed graph (PPAD) and polynomial-time local search (PLS). Moreover, Meunier and Sarrabezolles [18] have shown that a related problem is PPAD-complete: given $d+1$ pairs of points $P_1,\dots ,P_{d+1}\in \mathbb {Q}^d$ and a colorful choice that embraces the origin, find another colorful choice that embraces the origin. Complementary to this result, we show in Sect. 5 that a related problem is PLS-complete, the nearest colorful polytope problem (Ncp): given n color classes $C_1,\dots ,C_n$, find a colorful choice whose distance to the origin cannot be decreased by swapping one point with another point of the same color. This problem is motivated by Bárány ’s proof of Theorem 1.2. Furthermore, we show that the global search variant of Ncp is NP-hard, which answers a question by Bárány and Onn [4]. This question was also answered independently by Meunier and Sarrabezolles [18].

Despite the recent improvements on the upper bounds on the complexity of ColorfulCarathéodory, a polynomial-time algorithm remains elusive. Hence, approximation algorithms are of interest. This was first considered by Bárány and Onn [4] who described how to find a colorful choice whose convex hull is “close” to the origin under several general position assumptions. We call a set $\varepsilon$-close to the origin if its convex hull has $\ell _2$-distance at most $\varepsilon$ to ${\varvec{0}}$. Let in the following $\varepsilon , \rho > 0$ be parameters. Given $d+1$ sets $C_1,\dots ,C_{d+1}\in \mathbb {Q}^d$ such that

• (i) each $C_i$, $i \in [d+1]$, contains a ball of radius $\rho$ centered at the origin in its convex hull, and

• (ii) all points ${\varvec{p}}\in C_i$, $i \in [d+1]$, fulfill $1\le \Vert {\varvec{p}}\Vert \le 2$.

Then, the algorithm by Bárány and Onn iteratively computes a sequence of colorful choices such that the $\ell _2$-distances of their convex hulls to the origin strictly decrease until a colorful choice that embraces the origin is found. In particular, if stopped earlier, a colorful choice that is $\varepsilon$-close to ${\varvec{0}}$ can be computed in time $\text {poly}(L, \log (1/\varepsilon ),1/\rho )$ on the Word-Ram with logarithmic costs. Here, L denotes the length of the bit-encoding of the input points. Note that if $1/\rho = \hbox {O}(\text {poly}(L))$, the algorithm actually finds a colorful choice that embraces the origin in polynomial-time. The Bárány–Onn algorithm is essentially the algorithm from the proof of the convex version of Theorem 1.2, and the main contribution is a careful analysis.

In the same spirit, Barman [5] showed that if the points have constant norm, a colorful choice that is $\varepsilon$-close to the origin can be found in $d^{\hbox {O}(1/\varepsilon ^2)}L$ time, where L is again the length of the input encoding. The algorithm uses the following approximate version of Carathéodory ’s theorem as a main ingredient: let $P \subset \mathbb {R}^d$ be a ${\varvec{0}}$-embracing point set. Then, for any $\varepsilon > 0$, there exists a subset $P' \subseteq P$ of size $c_{\varepsilon } = \hbox {O}(\max _{{\varvec{p}}\in P} \Vert {\varvec{p}}\Vert / \varepsilon ^2)$ that is $\varepsilon$-close to ${\varvec{0}}$. This immediately implies a simple brute-force algorithm: let $C_1,\dots , C_{d+1} \subset \mathbb {Q}^d$ be point sets with ${\varvec{0}} \in {{\mathrm{conv}}}(C_i)$, for $i \in [d+1]$, and assume all points have constant norm. Let further $C \subseteq \bigcup _{i=1}^{d+1} C_i$ be a ${\varvec{0}}$-embracing colorful choice whose existence is guaranteed by Theorem 1.2. Then, the approximative version of Carathéodory ’s theorem asserts that there is a subset $C' \subseteq C$ of size $c_{\varepsilon }$ that is $\varepsilon$-close to the origin. We can now guess $C'$ by trying out all $\left( {\begin{array}{c}d+1\\ c_{\varepsilon }\end{array}}\right)$ possibilities for the colors in $C'$, and for each color i, we try all $|C_i|$ possibilities of picking a point with color i. For each choice of $C'$, we can check whether it is $\varepsilon$-close to the origin by solving a convex quadratic program. Solving one convex quadratic program needs $\hbox {O}({{\mathrm{poly}}}(d)L)$ time [11, 13]. Hence, assuming that each color class is of size $\hbox {O}(d)$, we can compute an $\varepsilon$-close colorful choice in $d^{\hbox {O}(1/\varepsilon ^2)}L$ time.

It is desirable to approximate ColorfulCarathéodory in a way that is compatible with the polynomial-time reductions to it. Then, good enough approximation algorithms for ColorfulCarathéodory can be converted to approximation algorithms for Tverberg, Centerpoint, and ColorfulKirchberger. Both approximation algorithms above relax the requirement that the resulting colorful choice embraces the origin. However, in the polynomial-time reductions from Tverberg, Centerpoint, and ColorfulKirchberger to ColorfulCarathéodory, it is crucial that the colorful choice embrace the origin. If the convex hull is only close to the origin but does not contain it, the reductions break down, and it is not immediate how to fix them. On the other hand, allowing multiple points from each color class has a natural interpretation in the polynomial-time reductions to ColorfulCarathéodory and leads to approximation algorithms for the other problems. Let $C_1,\dots ,C_{d+1} \subset \mathbb {R}^d$ be point sets that embrace the origin and let $k \in \mathbb {N}$ be a number. We call a set $C \subseteq \bigcup _{i=1}^{d+1} C_i$ a k-colorful choice if it contains at most k points from each $C_i$. In Sect. 3.1, we assume an oracle that computes ${\varvec{0}}$-embracing k-colorful choices, and we give precise bounds on the quality of the approximation algorithms for Tverberg, Centerpoint, and ColorfulKirchberger depending on k. We obtain these bounds by combining this oracle with the polynomial-time reductions. Furthermore, in Sect. 3, we present an algorithm that computes for any fixed $\varepsilon > 0$, a ${\varvec{0}}$-embracing $\lceil \varepsilon d\rceil$-colorful choice.

2 Preliminaries: Embracing Equivalent Points

Throughout the paper, vectors or points are set in boldface. The origin is denoted by ${\varvec{0}}$, the canonical basis of $\mathbb {R}^d$ is denoted by ${\varvec{e}}_1,\dots ,{\varvec{e}}_d$, and the all-ones vector $\sum _{i=1}^{d} e_i$ is denoted by ${\varvec{1}}$. For a set of points $P = \bigl \{{\varvec{p}}_1, \dots , {\varvec{p}}_n \bigr \} \subset \mathbb {R}^d$, we denote by

• $\mathrm{span}(P) = \bigl \{\sum _{i = 1}^n \phi _i {\varvec{p}}_i \,|\,\phi _i \in \mathbb {R}\bigr \}$ its linear span and the subspace orthogonal to ${{\mathrm{span}}}(P)$ by ${\mathrm{span}(P)}^\perp = \bigl \{v \in \mathbb {R}^d \,|\,\forall p \in {{\mathrm{span}}}(P): \langle v, p \rangle = 0\bigr \}$;

• ${{\mathrm{aff}}}(P) = \bigl \{\sum _{i = 1}^n \alpha _i {\varvec{p}}_i \,|\,\alpha _i \in \mathbb {R}, \sum _{i = 1}^n \alpha _i = 1 \bigr \}$ its affine hull;

• ${{\mathrm{pos}}}(P) = \bigl \{\sum _{i=1}^n \psi _i {\varvec{p}}_i \,|\,\psi _i \in \mathbb {R}_+ \bigr \}$ all linear combinations with nonnegative coefficients. We call ${{\mathrm{pos}}}(P)$ the positive span of P and we call a combination with nonnegative coefficients a positive combination;

• ${{\mathrm{conv}}}(P) = \bigl \{\sum _{i = 1}^n \lambda _i {\varvec{p}}_i \,|\,\lambda _i \in \mathbb {R}_+, \sum _{i=1}^n \lambda _i = 1 \bigr \}$ its convex hull;

• $\dim P$ the dimension of ${{\mathrm{span}}}(P)$;

Unless noted otherwise, all algorithms are analyzed in the Real-Ram model of computation [23, Chap. 1.4].¹ We begin with a constructive version of Theorem 1.1.

Lemma 2.1

(Constructive version of Carathéodory’s theorem) Suppose that $P \subset \mathbb {R}^d$ is a ${\varvec{0}}$-embracing point set. Given the coefficients of the convex combination of ${\varvec{0}}$ with the points in P, a ${\varvec{0}}$-embracing affinely independent subset $P' \subseteq P$ can be computed in $\mathrm{O}(d^3 |P| + |P|^2)$ time.

Proof

The standard proof of Theorem 1.1 is already constructive. We repeat it briefly before analyzing its running time when interpreted as an algorithm.

Assume P is affinely dependent. Let ${\varvec{p}}_1,\dots ,{\varvec{p}}_n$ denote the points in P and let $\alpha _1,\dots ,\alpha _n \in \mathbb {R}$ be coefficients of a nontrivial affine dependency, i.e., let

$$\begin{aligned} {\varvec{0}} = \alpha _1 {\varvec{p}}_1 + \dots + \alpha _n {\varvec{p}}_n \end{aligned}$$

(1)

with $\sum _{i=1}^{n} \alpha _i = 0$ and $\alpha _i > 0$ for some $i \in [n]$. Furthermore, because ${\varvec{0}} \in {{\mathrm{conv}}}(P)$, there are coefficients $\lambda _1,\dots ,\lambda _n \in \mathbb {R}_+$ such that

$$\begin{aligned} {\varvec{0}} = \lambda _1 {\varvec{p}}_1 + \dots + \lambda _n {\varvec{p}}_n \end{aligned}$$

(2)

and $\sum _{i=1}^{n} \lambda _i = 1$. Let $c \in \mathbb {R}$ be a factor that is to be specified. Scaling (1) by $c \in \mathbb {R}$ and subtracting it from (2), we obtain

$$\begin{aligned} {\varvec{0}} = \sum _{i=1}^{n} \lambda _i {\varvec{p}}_i - c \sum _{i=1}^{n} \alpha _i {\varvec{p}}_i = \sum _{i=1}^{n} \lambda '_i {\varvec{p}}_i, \end{aligned}$$

where $\lambda '_i = \lambda _i - c \alpha _i$. Thus, let $i^\star = {{\mathrm{arg\,min}}}\bigl \{\lambda _i/\alpha _i \,|\,i \in [n], \alpha _i > 0\bigr \}$, where ties are broken arbitrarily, and set $c = \lambda _{i^\star } / \alpha _{i^\star }$. Then, $\sum _{i=1}^{n} \lambda '_i {\varvec{p}}_i$ is a convex combination of ${\varvec{0}}$ with the points in $P \setminus \{{\varvec{p}}_{i^\star }\}$. Indeed by definition of $i^\star$, we have $\lambda '_i = \lambda _i - c \alpha _i \ge 0$, $\sum _{i=1}^{n} \lambda '_i = \sum _{i=1}^{n} (\lambda _i - c \alpha _i) = \sum _{i=1}^{n} \lambda _i = 1$, and $\lambda '_{i^\star }= 0$. A repeated removal of points until the remaining set is affinely independent implies the statement.

It remains to show the running time. We compute in each iteration a linear dependency by Gaussian elimination in $\hbox {O}(d^3)$ time.² By our assumption, we know the convex coefficients $\lambda _1,\dots ,\lambda _n$ and thus, we can find the point ${\varvec{p}}_{i^\star }\in P$ in $\hbox {O}(n)$ time. Furthermore, we can compute the new coefficients $\lambda '_i \in \mathbb {R}_+$, $i \in [n] \setminus \{i^\star \}$, from $\lambda _1,\dots ,\lambda _n$, the coefficients of the affine dependency, and the index $i^\star$ in $\hbox {O}(n)$ time. Hence, one iteration takes $\mathrm{O}({d^3 + n})$ time and since there are $\mathrm{O}({n})$ iterations, the algorithm needs in total $\mathrm{O}({d^3 n + n^2})$ time. $\square$

In Sect. 3, we present two approximation algorithms that follow the same strategy: begin with a complete color class and then replace a subset by points from other color classes while maintaining the property that the origin is embraced. We conclude this section with the necessary tools to implement the replacement step.

Fig. 3

The blue points constitute the linearly dependent set $\overline{C}$. The removal of ${\varvec{c}}^\times$ maintains the embrace of the origin

Let $C \subset \mathbb {R}^d$ be a ${\varvec{0}}$-embracing point set. We say C is minimally ${\varvec{0}}$-embracing if $C \setminus \{{\varvec{c}}\}$ is not ${\varvec{0}}$-embracing for all points ${\varvec{c}}\in C$.

Lemma 2.2

Let $C \subset \mathbb {R}^d$ be an affinely independent ${\varvec{0}}$-embracing set. Then, a subset $C'$ of C is linearly dependent if and only if $C'$ embraces the origin.

Proof

Clearly, all ${\varvec{0}}$-embracing subsets of C must be linearly dependent. Let now $C'$ be a linearly dependent subset of C. We need to show that $C'$ is ${\varvec{0}}$-embracing. Assume without loss of generality that $C'$ is a proper subset and let ${\varvec{c}}^\times \in C \setminus C'$ be a missing point. We prove that the set $\overline{C} = C \setminus \{{\varvec{c}}^\times \}$ is ${\varvec{0}}$-embracing. A repeated application of this argument then implies the statement.

Since $C' \subseteq \overline{C}$, the set $\overline{C}$ is linearly dependent. Thus, we can write ${\varvec{0}}$ as a nontrivial linear combination $\sum _{{\varvec{c}}\in \overline{C}} \phi _{\varvec{c}}{\varvec{c}}$ of the points in $\overline{C}$, where $\phi _{{\varvec{c}}} \in \mathbb {R}$, for all ${\varvec{c}}\in \overline{C}$. Furthermore, since C is affinely independent, so is $\overline{C}$, and hence $\sum _{{\varvec{c}}\in \overline{C}} \phi _{\varvec{c}}\ne 0$. By rescaling the coefficients, we obtain an affine combination of ${\varvec{0}}$. This implies ${{\mathrm{aff}}}(\overline{C}) = {{\mathrm{span}}}(\overline{C})$. Now, because $\overline{C} = C \setminus \{{\varvec{c}}^\times \}$ and because C is affinely independent, the point ${\varvec{c}}^\times$ is not contained in the affine hull of $\overline{C}$ and thus not in the linear span of $\overline{C}$. Then, there exists a hyperplane h that contains ${{\mathrm{span}}}(\overline{C})$ but not ${\varvec{c}}^\times$. See Fig. 3. Because ${{\mathrm{conv}}}(C)$ is on one side of h, the intersection $h \cap {{\mathrm{conv}}}(C) = {{\mathrm{conv}}}(\overline{C})$ is a face of ${{\mathrm{conv}}}(C)$. Since h and ${{\mathrm{conv}}}(C)$ both contain the origin, the face ${{\mathrm{conv}}}(\overline{C})$ must contain the origin, too. Hence, $\overline{C}$ is ${\varvec{0}}$-embracing. $\square$

Lemma 2.3

Let $C \subset \mathbb {R}^d$ be a minimally ${\varvec{0}}$-embracing set. Then, the following holds:

• (i) C is affinely independent and all proper subsets of C are linearly independent.

• (ii) For all ${\varvec{c}}\in C$, the point $-{\varvec{c}}$ is ray-embraced by $C \setminus \{{\varvec{c}}\}$.

In particular, $\dim C = |C|-1$ and ${{\mathrm{pos}}}(C) = {{\mathrm{span}}}(C)$.

Proof

If C is affinely dependent, then by Theorem 1.1 there exists a proper subset that embraces the origin. Thus, C must be affinely independent. Hence, (i) is implied by Lemma 2.2. Write now C as ${\varvec{c}}_1,\dots ,{\varvec{c}}_n$ and let $\lambda _1,\dots ,\lambda _n \in \mathbb {R}_+$ be coefficients that sum to 1 such that ${\varvec{0}} = \sum _{i=1}^{m} \lambda _i {\varvec{c}}_i$. Then, $-\lambda _i {\varvec{c}}_i \in {{\mathrm{pos}}}(C)$ for all $i \in [n]$. Because $C \setminus \{{\varvec{c}}\}$ does not embrace the origin for any ${\varvec{c}}\in C$, we have $\lambda _i > 0$ for $i \in [n]$. This implies (ii). $\square$

Using the fact that all proper subsets of a minimally ${\varvec{0}}$-embracing set C are linearly independent, we show how to compute for each point in the positive span of C the coefficients of the positive combination.

Lemma 2.4

Let $C \subset \mathbb {R}^d$ be a minimally ${\varvec{0}}$-embracing set and let ${\varvec{q}}\in \mathrm{pos}(C)$ be a point. Then, we can compute the coefficients of a nontrivial positive combination of ${\varvec{q}}$ with the points in C in $\mathrm{O}({d^4})$ time.

Proof

Consider first the case that ${\varvec{q}}= {\varvec{0}}$. Let ${\varvec{c}}^\times \in C$ be an arbitrary point and denote with $\overline{C} = C \setminus \{{\varvec{c}}^\times \}$ the remaining points. By Lemma 2.3, $-{\varvec{c}}^\times$ is ray-embraced by $\overline{C}$. Thus, the linear system $A {\varvec{x}}= -{\varvec{c}}^\times$, where A is the matrix whose columns are the points from $\overline{C}$, has a solution. By Lemma 2.3 (i), the set $\overline{C}$ is linearly independent and hence this solution is unique. Thus, we can compute the coefficients $\psi _{{\varvec{c}}} \in \mathbb {R}$, ${\varvec{c}}\in \overline{C}$, such that $-{\varvec{c}}^\times = \sum _{{\varvec{c}}\in \overline{C}} \psi _{{\varvec{c}}} {\varvec{c}}$ in $\mathrm{O}({d^3})$ time with Gaussian elimination. Moreover, since the solution is unique, we must have $\psi _{{\varvec{c}}} \ge 0$ for all ${\varvec{c}}\in \overline{C}$. Set $\psi _{{\varvec{c}}^\times }$ to 1. Then, ${\varvec{0}} = \sum _{{\varvec{c}}\in C} \psi _{{\varvec{c}}} {\varvec{c}}$, all coefficients are nonnegative, and not all coefficients are zero.

Consider now the case that ${\varvec{q}}\ne {\varvec{0}}$. We iterate through all ${\varvec{c}}^\times \in C$ and solve the linear system $L_{{\varvec{c}}^\times }: A {\varvec{x}}= {\varvec{q}}$, where the columns of A are the points in $C \setminus \{{\varvec{c}}^\times \}$. Again by Lemma 2.3 (i), the columns of A are linearly independent and hence the solution ${\varvec{x}}_{{\varvec{c}}^\times }$ to $L_{{\varvec{c}}^\times }$ is unique, if it exists. If ${\varvec{x}}_{{\varvec{c}}^\times } \ge {\varvec{0}}$, we have found the desired coefficients. By Theorem 1.1, there exists a proper subset $C'$ of C that ray-embraces ${\varvec{q}}$ and thus there exists a point ${\varvec{c}}^\star \in C$ for which ${\varvec{x}}_{{\varvec{c}}^\star } \ge {\varvec{0}}$. Solving the linear system $L_{{\varvec{c}}^\times }$ takes $\mathrm{O}({d^3})$ time for each point ${\varvec{c}}^\times \in C$ with Gaussian elimination, and hence we need $\mathrm{O}({d^4})$ time in total until finding the ${\varvec{q}}$-embracing subset $C \setminus \{{\varvec{c}}^\star \}$ together with the coefficients of the positive combination. $\square$

We can now combine the previous results to show that given a ${\varvec{0}}$-embracing set, we can find a minimally ${\varvec{0}}$-embracing subset in polynomial time together with the coefficients of the convex combination of the origin.

Lemma 2.5

Let $C \subset \mathbb {R}^d$ be a ${\varvec{0}}$-embracing set of size n. Given the coefficients of the convex combination of ${\varvec{0}}$ with the points in C, we can find a minimally ${\varvec{0}}$-embracing subset $C' \subseteq C$ and the coefficients of the convex combination of ${\varvec{0}}$ with the points in $C'$ in $\mathrm{O}({n^2 + n d^3 + d^4})$ time.

Proof

First, we apply Lemma 2.1 to obtain an affinely independent subset $C'$ of C that embraces the origin. Then, we iteratively test for each point ${\varvec{c}}\in C'$ whether the set $C' \setminus \{{\varvec{c}}\}$ is linearly dependent. If so, we remove ${\varvec{c}}$ from $C'$. After iterating through all points, the resulting set still embraces the origin by Lemma 2.2 and moreover, since no proper subset is linearly dependent, it is minimally ${\varvec{0}}$-embracing.

The initial application of Lemma 2.1 needs $\mathrm{O}({n^2 + n d^3})$ time. Then, checking for one point ${\varvec{c}}\in C'$ whether $C' \setminus \{{\varvec{c}}\}$ is linearly dependent takes $\mathrm{O}({d^3})$ time with Gaussian elimination. Because $C'$ is affinely independent, we have $|C'|\le d+1$ and thus the claimed running time follows. $\square$

Fig. 4

An example of Lemma 2.6. The red points constitute the minimal ${\varvec{0}}$-embracing set C and the blue points constitute the set Q that embraces the origin when projected onto ${{\mathrm{span}}}(C)^\perp$. The point ${\varvec{c}}\in C$ is ${\varvec{0}}$-embracing equivalent to Q

Let now $Q \subset \mathbb {R}^d$ be a set and let $C \subset \mathbb {R}^d$ be a ${\varvec{0}}$-embracing set, as before. We say a subset $C'$ of C is ${\varvec{0}}$-embracing equivalent to Q with respect to C if $(C \setminus C') \cup Q$ embraces ${\varvec{0}}$. In the following, we show that if Q embraces the origin when orthogonally projected onto ${{\mathrm{span}}}(C)^\perp$, there is always at least one point in C that is ${\varvec{0}}$-embracing equivalent to Q. See Fig. 4.

Lemma 2.6

Let $C \subset \mathbb {R}^d$ be a ${\varvec{0}}$-embracing set and let Q be a set whose orthogonal projection $Q^\perp$ onto ${{\mathrm{span}}}(C)^\perp$ embraces ${\varvec{0}}$. Then, there exists a point ${\varvec{c}}\in C$ that is ${\varvec{0}}$-embracing equivalent to Q with respect to C. Furthermore, if both C and $Q^\perp$ are minimally ${\varvec{0}}$-embracing, we can compute ${\varvec{c}}$ together with the coefficients of the convex combination of ${\varvec{0}}$ with the points in $(C \setminus \{{\varvec{c}}\}) \cup Q$ in $\mathrm{O}({d^4})$ time.

Proof

We first prove that there is always a point in C that is ${\varvec{0}}$-embracing equivalent to Q. After that, we show how to find this point efficiently. We can assume without loss of generality that C is minimally ${\varvec{0}}$-embracing, since otherwise the statement holds trivially. Let now ${\varvec{q}}_1, \dots , {\varvec{q}}_m \in \mathbb {R}^d$ denote the points in Q and write each ${\varvec{q}}_i$, $i \in [m]$, as the sum of a vector ${\varvec{p}}_i \in {{\mathrm{span}}}(C)$ and a vector ${\varvec{p}}_i^\perp \in {{\mathrm{span}}}(C)^\perp$. Because Q projected onto ${{\mathrm{span}}}(C)^\perp$ is ${\varvec{0}}$-embracing, there are coefficients $\lambda _1,\dots ,\lambda _m \in \mathbb {R}_+$ that sum to 1 such that ${\varvec{0}} = \sum _{i=1}^{m} \lambda _i{\varvec{p}}_i^\perp$. Consider the convex combination ${\varvec{q}}= \sum _{i=1}^{m} \lambda _i {\varvec{q}}_i$ of the points in Q with the same coefficients. Since

$$\begin{aligned} {\varvec{q}}= \sum _{i=1}^{m} \lambda _i \big ({\varvec{p}}_i + {\varvec{p}}^\perp _i\big ) = \Big (\sum _{i=1}^{m} \lambda _i {\varvec{p}}_i \Big ) +\Big (\sum _{i=1}^{m} \lambda _i {\varvec{p}}^\perp _i\Big ) = \sum _{i=1}^{m} \lambda _i {\varvec{p}}_i, \end{aligned}$$

the point ${\varvec{q}}$ is contained in ${{\mathrm{span}}}(C)$. By Lemma 2.3, we have ${{\mathrm{pos}}}(C) = {{\mathrm{span}}}(C)$ and hence $-{\varvec{q}}$ is ray-embraced by C. Now, the cone version of Theorem 1.1 states that there is a linearly independent subset $C'$ of C that ray-embraces $-{\varvec{q}}$. Because $\dim C = |C|-1$ by Lemma 2.3, the set $C'$ must be a proper subset. Then, Q is ${\varvec{0}}$-embracing equivalent to all points in $C \setminus C' \ne \emptyset$.

Fig. 5

An example of Lemma 2.7. The set C consists of the vertices of the simplex, and the two representative points are with respect to the indicated partition

It remains to show how to find a point in $C \setminus C'$. Recall that we assume that both C and $Q^\perp$ are minimally ${\varvec{0}}$-embracing, where $Q^\perp$ is the orthogonal projection of Q onto ${{\mathrm{span}}}(C)^\perp$. Using the algorithm from Lemma 2.4, we compute the coefficients of the convex combination of the origin with the points in $Q^\perp$ and hence the point $-{\varvec{q}}$ in $\mathrm{O}({d^4})$ time. Applying Lemma 2.4 again, we can determine the coefficients of the positive combination of $-{\varvec{q}}$ with the points in C in $\mathrm{O}({d^4})$ time. Similar to the algorithm from Lemma 2.5, we try all $(|C|-1)$-subsets of C until we find the linearly independent subset of C that ray-embraces $-{\varvec{q}}$. Since the linear combination of $-{\varvec{q}}$ is unique, we thus obtain the minimally $(-{\varvec{q}})$-ray-embracing subset $C'$ of C in $\mathrm{O}({d^4})$ time. Then, we can choose any point in $C \setminus C'$ as ${\varvec{c}}$. Finally, since we know the coefficients of the convex combination of ${\varvec{q}}$ with the points in Q and since we can apply Lemma 2.4 to compute the coefficients of the positive combination of $-{\varvec{q}}$ with the points in $C'$, we can compute the coefficients of the convex combination of the origin with the points in $C' \cup Q$ by rescaling appropriately. The algorithm takes in total $\mathrm{O}({d^4})$ time, as claimed. $\square$

Lemma 2.6 by itself does not yet yield a nontrivial approximation algorithm. This is due to the weak guarantee that only a single point in C is ${\varvec{0}}$-embracing equivalent to Q. To amplify the number of points that can be replaced, we conclude this section by showing how to compute a set of representative points R for C. Each representative point stands for a specific subset of C such that if a point in R is ${\varvec{0}}$-embracing equivalent to a set Q with respect to R, then the corresponding subset of C is ${\varvec{0}}$-embracing equivalent to Q with respect to C. See Fig. 5.

Lemma 2.7

Let $C \subset \mathbb {R}^d$ be a minimally ${\varvec{0}}$-embracing set and let $C_1,\dots ,C_m$ be a partition of C into $m \ge 2$ sets with $|C_i|\ge 1$, for all $i \in [m]$. Then, we can compute in $\mathrm{O}({d^4})$ time a set of points $R= \{{\varvec{r}}_1,\dots ,{\varvec{r}}_m\}\subset \mathbb {R}^d$ with the following properties:

• (i) R is minimally ${\varvec{0}}$-embracing.

• (ii) Let $Q \subset \mathbb {R}^d$ be a set that is ${\varvec{0}}$-embracing equivalent to some point ${\varvec{r}}_j \in R$ with respect to R. Then, Q is ${\varvec{0}}$-embracing equivalent to $C_j$ with respect to C.

We call the points in R representative points for C with respect to the partition $C_1,\dots ,C_m$.

Proof

Since C is minimally ${\varvec{0}}$-embracing, we can write ${\varvec{0}}$ as a convex combination $\sum _{{\varvec{c}}\in C} \lambda _{\varvec{c}}{\varvec{c}}$ such that all $\lambda _{\varvec{c}}$ are strictly greater than 0 and sum to 1. With the algorithm from Lemma 2.4, we can compute these coefficients in $\mathrm{O}({d^4})$ time. For $i \in [m]$, set ${\varvec{r}}_i$ to $\sum _{{\varvec{c}}\in C_i} \lambda _{\varvec{c}}{\varvec{c}}$. Clearly, R is ${\varvec{0}}$-embracing. Moreover, for all $j \in [m]$, the set $\big \{{\varvec{r}}_i \,|\,i \in [m],\, i\ne j\big \}$ is not ${\varvec{0}}$-embracing since otherwise the set $\bigcup _{i=1,\, i\ne j}^m C_i$, a strict subset of C, is ${\varvec{0}}$-embracing, a contradiction to C being minimally ${\varvec{0}}$-embracing. Let now Q be a set that is ${\varvec{0}}$-embracing equivalent to some point ${\varvec{r}}_j \in R$ with respect to R. That is, the set $Q \cup (R \setminus \{{\varvec{r}}_j\})$ embraces the origin. Because ${\varvec{r}}_i \in \mathrm{pos}(C_i)$, for $i \in [m]$, then the set $Q \cup \big (\bigcup _{i=1,\, i\ne j}^m C_i\big )$ is ${\varvec{0}}$-embracing as well, and hence Q is ${\varvec{0}}$-embracing equivalent to $C_j$ with respect to C. $\square$

3 k-Colorful Choices

Lemmas 2.6 and 2.7 give rise to a simple approximation algorithm. Let $C_1,\dots ,C_m \subset \mathbb {R}^d$ be m color classes that each embrace the origin, and set $k=\max \big (d-m+2, \big \lceil \frac{d+1}{2}\big \rceil \big )$. Then, the following algorithm recursively computes a ${\varvec{0}}$-embracing k-colorful choice. First, we prune $C_1$ with Lemma 2.5 and partition it into two sets $C',\,C''$ of size at most $\lceil (d+1) / 2\rceil$. Using Lemma 2.7, we compute two representative points ${\varvec{r}}',\, {\varvec{r}}''$ for this partition of $C_1$. Then, we project the remaining $m-1$ color classes onto the $(d-1)$-dimensional space that is orthogonal to ${{\mathrm{span}}}({\varvec{r}}',{\varvec{r}}'')^\perp$, and we recursively compute a ${\varvec{0}}$-embracing k-colorful choice Q with respect to the projections of $C_2,\dots ,C_m$. By Lemmas 2.6 and 2.7, one of the two sets $C'$, $C''$, say $C'$, is ${\varvec{0}}$-embracing equivalent to Q with respect to $C_1$. Since Q is a k-colorful choice that does not contain points from $C_1$ and since $|C'|,|C''|\le k$, the set $C'' \cup Q$ is a ${\varvec{0}}$-embracing k-colorful choice. The recursion stops once only one color class is left. Then, we are in dimension $d-m+1$. Since $d-m+2 \le k$, pruning the single remaining color

class with Lemma 2.5 results already in a ${\varvec{0}}$-embracing k-colorful choice. For details, see Algorithm 3.1.

Theorem 3.2

Let $C_1, \ldots , C_m\subset \mathbb {R}^d$ be $m\le d$ color classes such that $C_i$ is a ${\varvec{0}}$-embracing set of size $\mathrm{O}({d})$, for $i \in [m]$. On input $C_1,\dots ,C_m$ and given the coefficients of the convex combination of the origin for each set $C_i$, Algorithm 3.1 computes a ${\varvec{0}}$-embracing $\max \big (d-m+2, \big \lceil \frac{d+1}{2}\big \rceil \big )$-colorful choice in $\mathrm{O}({d^5})$ time. In particular, for $m=\lfloor d / 2 \rfloor + 1$, the algorithm computes a $(\lceil d/2\rceil +1)$-colorful choice.

Proof

The correctness of Algorithm 3.1 is a direct consequence of Lemmas 2.6 and 2.7. It remains to analyze the running time. In each step of the recursion except for the last one, we prune two times a set of size $\mathrm{O}({d})$ with Lemma 2.5. This needs $\mathrm{O}({d^4})$ time. Furthermore, by Lemma 2.7, computing two representative points also takes $\mathrm{O}({d^4})$ time. Finally, given the set Q, determining which representative point is ${\varvec{0}}$-embracing equivalent to Q takes also $\mathrm{O}({d^4})$ by Lemma 2.6 and using the fact that the recursively computed solution is minimally embracing. Thus, we need $\mathrm{O}({d^4})$ time per step of the recursion and there are $\mathrm{O}({d})$ recursion steps in total. The total running time is $\mathrm{O}({d^5})$. $\square$

Although nontrivial, the fact that we can take in polynomial time half of the points from each color class to construct a ${\varvec{0}}$-embracing $(\left\lceil d/2\right\rceil +1)$-colorful choice may not be too surprising. In the remainder of this section, we present a generalization of Algorithm 3.1 that computes ${\varvec{0}}$-embracing $\lceil \varepsilon d\rceil$-colorful choices in polynomial time for any fixed $\varepsilon > 0$. The improved approximation guarantee is achieved by repeatedly replacing subsets of C with Lemmas 2.6 and 2.7 in each step of the recursion. To still ensure polynomial running time, we reduce the dimensionality by a constant fraction in each step of the recursion. Additionally, we slightly worsen the desired approximation guarantee in each level of the recursion, i.e., if the current recursion level is j and the dimensionality is $d'$, then we do not compute an $\lceil \varepsilon d'\rceil$-colorful choice, but a $\lceil (1-\varepsilon /2)^{-j/2} \varepsilon d'\rceil$-colorful choice. As we will see, this additional “slack” in the approximation guarantee limits the recursion depth to a constant depending only on $\varepsilon$.

In more detail, let $C_1,\dots ,C_{d+1}\subset \mathbb {R}^d$ be $d+1$ sets that each embrace the origin, and let $\varepsilon > 0$ be a parameter. We want to compute an $\lceil \varepsilon d\rceil$-colorful choice that embraces the origin. Set

$$\begin{aligned} d_j = \Big \lceil \Big (1-\frac{\varepsilon }{2}\Big )^j d \Big \rceil \quad \text { and } \quad k_j = \Big \lceil \varepsilon \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} d\Big \rceil , \end{aligned}$$

for $j \in \mathbb {N}$. The sequence $d_j$ controls the dimension reduction argument with Lemmas 2.6 and 2.7, i.e., in the jth recursion level, the dimensionality of the input will be $d_j$. The sequence $k_j$ defines the approximation guarantee in the jth recursion level. Note that $d_0 = d$ and $k_0 = \lceil \varepsilon d \rceil$. Assume now we are in recursion level j. That is, the input consists of $d_j+1$ color classes $C_1,\dots ,C_{d_j+1} \subset \mathbb {R}^{d_j}$ that each embrace the origin together with the coefficients of their convex combinations of the origin. We want to compute a ${\varvec{0}}$-embracing $k_j$-colorful choice. As in the previous algorithm, we begin by computing a minimal ${\varvec{0}}$-embracing subset C of $C_1$ with Lemma 2.5. If $k_j \ge d_j + 1$, then C is already a valid approximation. Otherwise, we iteratively transform C into a $k_j$-colorful choice. For this, we repeatedly replace subsets of C with points from $C_2 \cup \dots \cup C_{d_j + 1}$ until it contains at most $k_j$ points from each color. This is done as follows. Set $m = d_j - d_{j+1} + 1$. In the general situation, C contains points from several color classes, and we partition C into sets $D_1,\dots ,D_m$ by distributing the points from each color in C equally among these m sets. Then, we compute representative points ${\varvec{r}}_1,\dots ,{\varvec{r}}_m$ for this partition. Let $C^\star _1,\dots ,C^\star _{d_{j+1}+1} \in \bigl \{C_2,\dots ,C_{d_j+1}\bigr \}$ be $d_{j+1}+1$ color classes, where we discuss shortly how they are chosen. We recursively compute a $k_{j+1}$-colorful choice Q for $C^\star _1,\dots ,C^\star _{d_{j+1}+1}$ that embraces the origin when projected on $U = {{\mathrm{span}}}({\varvec{r}}_1,\dots ,{\varvec{r}}_m)^\perp$. Note that $\dim U = d_j-(m-1) = d_{j+1}$ and hence the dimensionality of the input in recursion level $j+1$ is $d_{j+1}$, as desired. Then, by Lemmas 2.6 and 2.7, at least one representative point ${\varvec{r}}_{i^\times }$ and hence at least one of the sets $D_{i^\times }$ is ${\varvec{0}}$-embracing equivalent to Q. We set C to $(C \setminus D_{i^\times }) \cup Q$ and prune it with Lemma 2.5. We repeat these steps until C is a $k_j$-colorful choice.

To ensure progress, m should be smaller than $k_j$ so that $D_{i^\times }$ is guaranteed to contain a point from each color that appears more than $k_j$ times in C. Furthermore, Q should not contain points with colors that appear “often” in C. We call a color class $C_i$ light with respect to C if $|C \cap C_i| \le k_j - k_{j+1}$, and heavy, otherwise. For the recursion, we use only light color classes. A $k_{j+1}$-colorful choice with light colors can be added safely to C without increasing any color over the threshold $k_j$. In particular, since we start with $C=C_1$ and use only light color classes, no other color class can ever occur more than $k_j$ times in C and hence we are finished once the number of points from $C_1$ is at most $k_j$. Please refer to Algorithm 3.3 for details.

The next lemma states that for $\varepsilon$ fixed, the number of necessary recursions before a trivial approximation with Lemma 2.5 suffices is constant.

Lemma 3.4

For any $\varepsilon = \Omega ({d^{-1/4}})$ there exists a $j = \Theta (\varepsilon ^{-1} \ln \varepsilon ^{-1})$ such that $k_j \ge d_j+1$.

Proof

Replacing $d_j$ with its definition, we obtain

$$\begin{aligned} d_j + 1 = \Big \lceil \Big (1-\frac{\varepsilon }{2}\Big )^j d \Big \rceil + 1 \le \Big (1-\frac{\varepsilon }{2}\Big )^j d + 2. \end{aligned}$$

(3)

Using $\ln \big (1- \frac{\varepsilon }{2}\big ) \ge -\varepsilon$ if $\varepsilon \le 1$, we have for $j \le \frac{1}{\varepsilon } \ln d$,

$$\begin{aligned} \Big (1-\frac{\varepsilon }{2}\Big )^j d \ge e^{-\varepsilon j}d \ge 1. \end{aligned}$$

(4)

Furthermore, using that $\ln \big (1-\frac{\varepsilon }{2}\big ) \le -\frac{\varepsilon }{2}$, we have for $j \ge \frac{4}{\varepsilon } \ln \frac{3}{\varepsilon }$

$$\begin{aligned} 3 \Big (1 - \frac{\varepsilon }{2}\Big )^{j/2} \le 3 e^{-\varepsilon j/4} \le \varepsilon . \end{aligned}$$

(5)

Combining (4) and (5) with (3), we get

$$\begin{aligned} d_j + 1 \le 3 \Big (1 - \frac{\varepsilon }{2}\Big )^j d \le \varepsilon \Big (1 - \frac{\varepsilon }{2}\Big )^{j/2} d \le \Big \lceil \varepsilon \Big (1 - \frac{\varepsilon }{2}\Big )^{j/2} d\Big \rceil = k_j. \end{aligned}$$

For $d = \Omega ({\varepsilon ^{-1/4}})$, there is a j with $\frac{4}{\varepsilon }\ln \frac{3}{\varepsilon } \le j \le \frac{1}{\varepsilon } \ln d$. The claim follows. $\square$

Next, we show that if the recursion depth is not too large, then we can always find enough light color classes.

Lemma 3.5

Let $j \in \mathbb {N}$ and let $C_1,\dots ,C_{d_j+1}\subset \mathbb {R}^{d_j}$ be $d_j+1$ color classes. Furthermore, let $C \subseteq \bigcup _{i=1}^{d_j+1} C_i$ be a set of size at most $d_j+1$. For all $j=\mathrm{O}({\varepsilon ^{-1} \ln (\varepsilon ^3 d)})$, there exist $d_{j+1}+1$ light color classes with respect to C.

Proof

We recall that a color class $C_i$, $i \in [d_j+1]$, is light with respect to C if $|C \cap C_i| \le k_j - k_{j+1}$. Then, the number of heavy color classes h is bounded by

$$\begin{aligned} h \le \Big \lceil \frac{d_j + 1}{k_j - k_{j+1}}\Big \rceil \le \frac{2 d_j}{k_j - k_{j+1}} + 1, \end{aligned}$$

(6)

since $d_j \ge 1$ for all $j \in \mathbb {N}$. We can bound the denominator as follows:

$$\begin{aligned} k_j - k_{j+1}= & {} \Big \lceil \varepsilon \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} d\Big \rceil - \Big \lceil \varepsilon \Big (1-\frac{\varepsilon }{2}\Big )^{(j+1)/2} d\Big \rceil \nonumber \\\ge & {} \varepsilon \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} d - \varepsilon \Big (1-\frac{\varepsilon }{2}\Big )^{(j+1)/2} d - 1 \nonumber \\= & {} \varepsilon \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} d \Big ( 1 - \sqrt{1-\frac{\varepsilon }{2}}\Big ) - 1 \ge \frac{\varepsilon ^2}{4} \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} d - 1, \end{aligned}$$

(7)

where we apply $1 - \sqrt{1 - \frac{\varepsilon }{2}} \ge \frac{\varepsilon }{4}$ in the last inequality. Using that $\ln \big (1-\frac{\varepsilon }{2}\big ) \ge -\varepsilon$ if $\varepsilon \le 1$, we have for $j \le \frac{2}{\varepsilon } \ln \frac{\varepsilon ^2 d}{8}$

$$\begin{aligned} 1 \le \frac{\varepsilon ^{2}}{8} e^{-\varepsilon j/2} d \le \frac{\varepsilon ^2}{8} \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} d \end{aligned}$$

(8)

and hence (7) can be simplified to

$$\begin{aligned} k_j - k_{j+1} \ge \frac{\varepsilon ^2}{8} \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} d. \end{aligned}$$

(9)

Plugging (9) into (6) and using (8), we obtain

$$\begin{aligned} h \le \frac{2 \big \lceil \big (1-\frac{\varepsilon }{2}\big )^j d\big \rceil }{\frac{\varepsilon ^2}{8} \big (1-\frac{\varepsilon }{2}\big )^{j/2} d} + 1 \le \frac{2 \big (1-\frac{\varepsilon }{2}\big )^j d}{\frac{\varepsilon ^2}{8} \big (1-\frac{\varepsilon }{2}\big )^{j/2} d} + 3 = \frac{16}{\varepsilon ^2} \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} + 3. \end{aligned}$$

Then, the number $\ell$ of light color classes is at least

$$\begin{aligned} \ell= & {} d_j + 1 - h \ge \Big \lceil \Big (1-\frac{\varepsilon }{2}\Big )^j d \Big \rceil - \frac{16}{\varepsilon ^2} \Big (1-\frac{\varepsilon }{2}\Big )^{j/2} - 2 \nonumber \\\ge & {} \Big (1-\frac{\varepsilon }{2}\Big )^j d \Big (1 - \frac{16}{\varepsilon ^2 \big (1-\frac{\varepsilon }{2}\big )^{j/2} d} - \frac{2}{\big (1-\frac{\varepsilon }{2}\big )^j d} \Big ). \end{aligned}$$

(10)

For $j \le \frac{2}{\varepsilon }\ln \frac{\varepsilon ^3 d}{128}$, using $\ln \big (1-\frac{\varepsilon }{2}\big ) \ge -\varepsilon$ if $\varepsilon \le 1$, we have

$$\begin{aligned} \frac{16}{\varepsilon ^2 \big (1-\frac{\varepsilon }{2}\big )^{j/2} d} + \frac{2}{\big (1-\frac{\varepsilon }{2}\big )^j d} \le \frac{16}{\varepsilon ^2 e^{-\varepsilon j/2} d} + \frac{2}{e^{-\varepsilon j/2} d} \le \frac{\varepsilon }{8} + \frac{\varepsilon }{8} \le \frac{\varepsilon }{4} \end{aligned}$$

and thus (10) implies

$$\begin{aligned} \ell \ge \Big (1-\frac{\varepsilon }{4}\Big )\Big (1-\frac{\varepsilon }{2}\Big )^j d. \end{aligned}$$

(11)

For $j \le \frac{2}{\varepsilon }\ln \frac{\varepsilon d}{2}$, using $\ln \big (1-\frac{\varepsilon }{2}\big ) \ge -\varepsilon$ if $\varepsilon \le 1$, we can bound

$$\begin{aligned} \frac{\varepsilon }{4} \Big (1-\frac{\varepsilon }{2}\Big )^j d \ge \frac{\varepsilon }{4} e^{-\varepsilon j/2} d \ge 2. \end{aligned}$$

(12)

Combining (12) with (11), we get

$$\begin{aligned} \ell\ge & {} \Big (1-\frac{\varepsilon }{2}\Big )^{j+1} d + \frac{\varepsilon }{4} \Big (1 - \frac{\varepsilon }{2}\Big )^j d \\\ge & {} \Big (1-\frac{\varepsilon }{2}\Big )^{j+1} d + 2 \ge \Big \lceil \Big (1-\frac{\varepsilon }{2}\Big )^{j+1} d \Big \rceil + 1 = d_{j+1} + 1. \end{aligned}$$

Thus, for $j = \mathrm{O}({\varepsilon ^{-1} \ln (\varepsilon ^3 d)})$, there are at least $d_{j+1} +1$ light color classes with respect to C. $\square$

Before we finally prove correctness, we show if the recursion depth j is not too large, then each set of the partition of C contains at least one point from $C_1$ until C is a $k_j$-colorful choice. This implies that each iteration of the while-loop decreases the amount of points from $C_1$ in C.

Lemma 3.6

For all $j = \mathrm{O}({\varepsilon ^{-1} \ln (\varepsilon d)})$, we have $m = d_j - d_{j+1} + 1 \le k_j + 1$.

Proof

First, we upper bound m as follows:

$$\begin{aligned} \begin{aligned} m = d_j - d_{j+1} + 1&= \Big \lceil \Big (1-\frac{\varepsilon }{2}\Big )^j d \Big \rceil - \Big \lceil \Big (1-\frac{\varepsilon }{2}\Big )^{j+1} d \Big \rceil + 1 \\&\le \Big (1-\frac{\varepsilon }{2}\Big )^j d - \Big (1-\frac{\varepsilon }{2}\Big )^{j+1} d + 2 = \frac{\varepsilon }{2} \Big (1-\frac{\varepsilon }{2}\Big )^j d + 2. \end{aligned} \end{aligned}$$

(13)

For $j \le \frac{2}{\varepsilon } \ln \frac{\varepsilon d}{2}$, with $\ln \big (1-\frac{\varepsilon }{2}\big ) \ge -\varepsilon$ if $\varepsilon \le 1$, we obtain $\frac{\varepsilon }{2} \big (1-\frac{\varepsilon }{2}\big )^j d \ge \frac{\varepsilon }{2} e^{-\varepsilon j/2}d \ge 1$. Using this in (13), we get

$$\begin{aligned} m \le \varepsilon \Big (1-\frac{\varepsilon }{2}\Big )^j d + 1 \le \Big \lceil \varepsilon \Big (1-\frac{\varepsilon }{2}\Big )^j d \Big \rceil + 1 = k_j + 1, \end{aligned}$$

as desired. $\square$

Theorem 3.7

Let $C_1, \ldots , C_{d+1}\subset \mathbb {R}^d$ be $d+1$ sets such that $C_i$ is a ${\varvec{0}}$-embracing set of size $\mathrm{O}({d})$, for $i \in [d+1]$, and let $\varepsilon = \Omega ({d^{-1/4}})$ be a parameter. On input 0, d, $\varepsilon$, $C_1,\dots ,C_{d+1}$, and given the coefficients of the convex combination of the origin with the points in $C_i$, for $i \in [d+1]$, Algorithm 3.3 computes a ${\varvec{0}}$-embracing $\lceil \varepsilon d\rceil$-colorful choice in $d^{\mathrm{O}({\varepsilon ^{-1} \ln \varepsilon ^{-1}})}$ time.

Proof

We begin by showing that if the algorithm enters the while loop in recursion level j, it is always possible to find $d_{j+1} + 1$ light color classes and that the projections of these color classes are ${\varvec{0}}$-embracing subsets of $\mathbb {R}^{d_{j+1}}$ (Line 9). In other words, we show that recursion is possible if C is not a $k_j$-colorful choice. Assume now the algorithm enters the while loop in recursion level j. Then, C is a minimally ${\varvec{0}}$-embracing subset of $C_1 \subset \mathbb {R}^{d_j}$ and has size at least $k_j+1$. In Line 6, we partition C into m sets $D_1,\dots ,D_m$ by distributing the points from each color class equally. By Lemma 3.6, we have $m\le k_j + 1$, for $j = \mathrm{O}({\varepsilon ^{-1} \ln (\varepsilon d)})$, and hence each set $D_i$ is nonempty. Thus, the algorithm from Lemma 2.7 can be applied in Line 7 to compute the representative points ${\varvec{r}}_1,\dots ,{\varvec{r}}_m$. Moreover $\dim {{\mathrm{span}}}({\varvec{r}}_1,\dots ,{\varvec{r}}_m) = m-1$ by Lemma 2.7 and Lemma 2.3. Thus, $\dim {{\mathrm{span}}}({\varvec{r}}_1,\dots ,{\varvec{r}}_m)^\perp = d - m + 1 = d_{j+1}$. Now, Lemma 3.5 guarantees that we can always find $d_{j+1}+1$ light color classes $C^\star _1,\dots ,C^\star _{d_{j+1}+1}$, if $j = \mathrm{O}({\varepsilon ^{-1} \ln \varepsilon ^3 d})$. Because each color class $C^\star _i$, $i \in [d_{j+1}+1]$, is ${\varvec{0}}$-embracing, so are their orthogonal projections onto ${{\mathrm{span}}}({\varvec{r}}_1,\dots ,{\varvec{r}}_k)^T$. Thus, recursion is possible if $j = \mathrm{O}({\varepsilon ^{-1} \ln \varepsilon ^3 d})$. By Lemma 3.4, the recursion depth is limited to $\Theta \big (\varepsilon ^{-1} \ln \varepsilon ^{-1}\big )$, since then pruning $C_1$ with Lemma 2.5 in Line 4 is already a ${\varvec{0}}$-embracing $k_j$-colorful choice. In this case, the while loop is never executed. We conclude that for $\varepsilon = \Omega ({d^{-1/4}})$, recursion is always possible as long as C is not a $k_j$-colorful choice.

Next, we prove that the algorithm computes in recursion level j a ${\varvec{0}}$-embracing $k_j$-colorful choice. As discussed above, the recursion terminates after $\mathrm{O}({\varepsilon ^{-1} \ln \varepsilon ^{-1}})$ steps when the set C from Line 4 is already a ${\varvec{0}}$-embracing $k_j$-colorful choice. If C is not already a valid approximation, the while loop is executed. In each iteration of the while loop, C is partitioned into m sets $D_1,\dots ,D_m$ by distributing the points from each color equally among the $D_i$. By Lemma 3.6, $m\le k_j + 1$ for $j = \mathrm{O}({\varepsilon ^{-1} \ln \varepsilon d})$ and hence each set $D_i$, $i \in [m]$, contains at least one point from $C_1$. Applying Lemmas 2.6 and 2.7, one of these sets, say $D_{i^\times }$, is replaced in C by a recursively computed $k_{j+1}$-colorful choice Q that is ${\varvec{0}}$-embracing when projected onto ${{\mathrm{span}}}({\varvec{r}}_1,\dots ,{\varvec{r}}_m)^\perp$. Since we use in the recursion only light color classes with respect to C, and since $C_1$ is not a light color class, each iteration of the while loop strictly decreases the number of points from $C_1$ in C. Moreover, because Q contains only points from light color classes and since it is a $k_{j+1}$-colorful choice, $(C \setminus D_{i^\times }) \cup Q$ contains at most $k_j$ points from the color classes $C_2,\dots ,C_{d_j+1}$. Thus, after $\mathrm{O}({d})$ iterations, C is a ${\varvec{0}}$-embracing $k_j$-colorful choice.

It remains to analyze the running time. The initial computation of C in Line 4 and each iteration of the while loop except for the recursive call takes $\mathrm{O}({d^4})$ time. Since the while loop is executed $\mathrm{O}({d})$ times and since the recursion depth is bounded by $\mathrm{O}({\varepsilon ^{-1} \ln \varepsilon ^{-1}})$, the total running time of Algorithm 3.3 is $d^{\mathrm{O}({\varepsilon ^{-1} \ln \varepsilon ^{-1}})}$. $\square$

3.1 Applications

As discussed in the introduction, the main motivation for k-colorful choices is their application in polynomial-time reductions to ColorfulCarathéodory. We begin by presenting the proofs whose interpretation as algorithms results in the polynomial reductions. Then, we give precise bounds on the quality of the obtained approximation algorithms for Centerpoint, Tverberg, and ColorfulKirchberger when having access to an algorithm that on input $d+1$ color classes $C_1,\dots ,C_{d+1}$, each ${\varvec{0}}$-embracing and of size at most $d+1$, computes a ${\varvec{0}}$-embracing k(d)-colorful choice in time W(d).

Theorem 3.8

(Centerpoint theorem [24, Thm. 1]) Let $P \subset \mathbb {R}^d$ be a point set. Then, there exists a point ${\varvec{q}}\in \mathbb {R}^d$ such that for any halfspace $h^-$ with ${\varvec{q}}\in h^-$, we have $|P \cap h^-| \ge \big \lceil \frac{|P|}{d+1}\big \rceil$. $\square$

Teng [28, Thm. 8.4] showed that given a point set $P \in \mathbb {R}^d$ and a candidate centerpoint ${\varvec{q}}\in \mathbb {R}^d$, it is coNP-complete to decide whether ${\varvec{q}}$ is a centerpoint of P, if d is part of the input. For $d=1$, a centerpoint is equivalent to a median of a set of numbers and hence can be computed in $\mathrm{O}({|P|})$ time [6]. Jadhav and Mukhopadhyay [9] showed that linear time is sufficient even in two dimensions. For $d\ge 3$ fixed, the best known algorithm is by Chan [7] who showed how to compute a point with maximum Tukey depth, a stronger notion than being a centerpoint, in expected time $\mathrm{O}({n^{d-1}})$.

Although it is in general coNP-complete to verify centerpoints, Tverberg partitions serve as polynomial-time checkable certificates for a subset of centerpoints. In recent years, this property has been exploited algorithmically to derive efficient approximation algorithms for centerpoints [20, 21]. The existence of Tverberg points is guaranteed by Tverberg’s theorem [29].

Theorem 3.9

(Tverberg’s theorem [29]) Let $P \subset \mathbb {R}^d$ be a point set of size n. Then, there always exists a Tverberg $\big \lceil \frac{|P|}{d+1}\big \rceil$-partition for P. Equivalently, let P be of size $(m-1)(d+1)+1$, with $m \in \mathbb {N}$. Then, there exists a Tverberg m-partition for P.

While Tverberg’s first proof is quite involved, several simplified subsequent proofs [25, 26, 30, 31] have been published. Here, we present Sarkaria’s proof [26] with further simplifications by Bárány and Onn [4] and Arocha et al.  [2]. The main tool is the next lemma that establishes a correspondence between the intersection of convex hulls of low-dimensional point sets and the embrace of the origin of certain high-dimensional point sets. It was extracted from Sarkaria’s proof by Arocha et al.  [2]. In the following, we denote with $\otimes$ the tensor product that maps two points ${\varvec{p}}\in \mathbb {R}^d$, ${\varvec{q}}\in \mathbb {R}^m$ to the point

$$\begin{aligned} {\varvec{p}}\otimes {\varvec{q}}= \begin{pmatrix} ({\varvec{q}})_1 {\varvec{p}}\\ ({\varvec{q}})_2 {\varvec{p}}\\ \vdots \\ ({\varvec{q}})_m {\varvec{p}}\end{pmatrix} \in \mathbb {R}^{dm}, \end{aligned}$$

where $({\varvec{q}})_i {\varvec{p}}$ denotes the vector ${\varvec{p}}$ scaled by the ith component of ${\varvec{q}}$, for $i \in [m]$. Then, $\otimes$ is bilinear, i.e., for all ${\varvec{p}}_1,{\varvec{p}}_2 \in \mathbb {R}^d$, ${\varvec{q}}\in \mathbb {R}^m$, and $\alpha _1,\alpha _2 \in \mathbb {R}$, we have

$$\begin{aligned} (\alpha _1 {\varvec{p}}_1 + \alpha _2 {\varvec{p}}_2) \otimes {\varvec{q}}= \alpha _1 ({\varvec{p}}_1 \otimes {\varvec{q}}) + \alpha _2 ({\varvec{p}}_2 \otimes {\varvec{q}}) \end{aligned}$$

and similarly, for all ${\varvec{p}}\in \mathbb {R}^d$, ${\varvec{q}}_1,{\varvec{q}}_2 \in \mathbb {R}^m$, and $\alpha _1,\alpha _2 \in \mathbb {R}$, we have

$$\begin{aligned} {\varvec{p}}\otimes (\alpha _1 {\varvec{q}}_1 + \alpha _2 {\varvec{q}}_2) = \alpha _1 ({\varvec{p}}\otimes {\varvec{q}}_1) + \alpha _2 ({\varvec{p}}\otimes {\varvec{q}}_2). \end{aligned}$$

Lemma 3.10

(Sarkaria’s Lemma [26], [2, Lem. 2]) Let $P_1,\dots ,P_m \subset \mathbb {R}^d$ be m point sets and let ${\varvec{q}}_1,\dots ,{\varvec{q}}_{m} \subset \mathbb {R}^{m-1}$ be m vectors with ${\varvec{q}}_i = {\varvec{e}}_i$ for $i \in [m-1]$ and ${\varvec{q}}_m = -{\varvec{1}}$. For $i \in [m]$, we define

$$\begin{aligned} {\widehat{P}}_i = \left\{ \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} \otimes {\varvec{q}}_i \big | {\varvec{p}}\in P_i \right\} \subset \mathbb {R}^{(d+1) (m-1)}. \end{aligned}$$

Then, the intersection of the convex hulls $\bigcap _{i=1}^m \text {conv}\big (P_{i}\big )$ is nonempty if and only if $\;\bigcup _{i=1}^m {\widehat{P}}_i$ embraces the origin.

Proof

Assume there is a point ${\varvec{p}}^\star \in \bigcap _{i=1}^m \text {conv}(P_{i})$. There exist coefficients $\lambda _{i,{\varvec{p}}} \in \mathbb {R}_+$ that sum to 1 such that ${\varvec{p}}^\star = \sum _{{\varvec{p}}\in P_i} \lambda _{i,{\varvec{p}}}{\varvec{p}}$. Consider the points ${\hat{{\varvec{p}}}}_i \in \text {conv}({\widehat{P}}_i)$, $i \in [m]$, that we obtain by using the same convex coefficients for the points in ${\widehat{P}}_i$, i.e., set

$$\begin{aligned} {\hat{{\varvec{p}}}}_{i} = \sum _{{\varvec{p}}\in P_i} \lambda _{i,{\varvec{p}}} \left( \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} \otimes {\varvec{q}}_i\right) \in \text {conv}({\widehat{P}}_i). \end{aligned}$$

We claim that $\sum _{i=1}^{m} {\hat{{\varvec{p}}}}_i = {\varvec{0}}$ and thus ${\varvec{0}} \in \text {conv}\big (\bigcup _{i=1}^{m} {\widehat{P}}_i\big )$. Indeed, we have

$$\begin{aligned} \sum _{i=1}^{m} {\hat{{\varvec{p}}}}_i= & {} \sum _{i=1}^{m} \sum _{{\varvec{p}}\in P_i} \lambda _{i,{\varvec{p}}} \left( \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} \otimes {\varvec{q}}_i \right) \\= & {} \sum _{i=1}^{m} \left( \sum _{{\varvec{p}}\in P_i} \lambda _{i,{\varvec{p}}} \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} \right) \otimes {\varvec{q}}_i = \sum _{i=1}^{m} \begin{pmatrix}{\varvec{p}}^\star \\ 1\end{pmatrix} \otimes {\varvec{q}}_i \\= & {} \begin{pmatrix}{\varvec{p}}^\star \\ 1\end{pmatrix} \otimes \Big ( \sum _{i=1}^{m} {\varvec{q}}_i \Big ) = \begin{pmatrix}{\varvec{p}}^\star \\ 1\end{pmatrix} \otimes {\varvec{0}} = {\varvec{0}}, \end{aligned}$$

using the bilinearity of $\otimes$.

Assume now that $\bigcup _{i=1}^m {\widehat{P}}_i$ embraces the origin. We want to show that $\bigcap _{i=1}^m \text {conv}(P_{i})$ is nonempty. Then, we can express the origin as a convex combination $\sum _{i=1}^{m} \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_i} \lambda _{i,{\hat{{\varvec{p}}}}} {\hat{{\varvec{p}}}}$ with $\lambda _{i,{\hat{{\varvec{p}}}}} \in \mathbb {R}_+$ for $i \in [m]$ and ${\hat{{\varvec{p}}}} \in {\widehat{P}}_i$, and $\sum _{i=1}^{m} \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_i} \lambda _{i,{\hat{{\varvec{p}}}}} = 1$. Hence, we have

$$\begin{aligned} {\varvec{0}} = \sum _{i=1}^{m} \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_i} \lambda _{i,{\hat{{\varvec{p}}}}} \left( \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} \otimes {\varvec{q}}_i \right) = \sum _{i=1}^{m} \left( \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_i} \lambda _{i,{\hat{{\varvec{p}}}}} \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} \right) \otimes {\varvec{q}}_i, \end{aligned}$$

again using the bilinearity of $\otimes$. By the choice of ${\varvec{q}}_1,\dots ,{\varvec{q}}_m$, there is (up to multiplication with a scalar) exactly one linear dependency: ${\varvec{0}} = \sum _{i=1}^{m} {\varvec{q}}_i$. Thus,

$$\begin{aligned} \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_1} \lambda _{1,{\hat{{\varvec{p}}}}} \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} = \dots = \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_m} \lambda _{m,{\hat{{\varvec{p}}}}} \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} = \begin{pmatrix}{\varvec{p}}^\star \\ c\end{pmatrix}, \end{aligned}$$

where ${\varvec{p}}^\star \in \mathbb {R}^d$ and $c \in \mathbb {R}$. In particular, the last equality implies that

$$\begin{aligned} \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_1} \lambda _{1,{\hat{{\varvec{p}}}}} = \dots = \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_m} \lambda _{m,{\hat{{\varvec{p}}}}} = c. \end{aligned}$$

Now, since for all $i \in [m]$ and ${\hat{{\varvec{p}}}} \in {\widehat{P}}_i$, the coefficient $\lambda _{i,{\hat{{\varvec{p}}}}}$ is nonnegative and since the sum $\sum _{i \in [m]} \sum _{{\hat{{\varvec{p}}}} \in {\widehat{P}}_i} \lambda _{i,{\hat{{\varvec{p}}}}}$ is 1, we must have $c = 1/m \in (0,1]$. Hence, the point $m {\varvec{p}}^\star$ is common to all convex hulls $\text {conv}(P_1),\dots ,\text {conv}(P_m)$. $\square$

Fig. 6

An example of Sarkaria’s lemma for $d=1$ and $m=2$. The set $P_1$ consists of the red points and the set $P_2$ consists of the blue points. Since the convex hulls of $P_1$ and $P_2$ intersect, the lifted points embrace the origin

Please refer to Fig. 6 for an example of Sarkaria’s lifting argument. Little work is now left to obtain Tverberg’s theorem from Lemma 3.10 and the colorful Carathéodory theorem.

Proof

of Theorem 3.9 Let $P =\{{\varvec{p}}_1,\dots ,{\varvec{p}}_n\} \subset \mathbb {R}^d$ be a point set of size $n=(d+1)(m-1)+1$ and let $P_1,\dots ,P_m$ denote m copies of P. For each set $P_j \subset \mathbb {R}^d$, $j \in [m]$, we construct a $((d+1) (m-1))$-dimensional set ${\widehat{P}}_j$ as in Lemma 3.10, i.e.,

$$\begin{aligned} {\widehat{P}}_j = \left\{ {\hat{{\varvec{p}}}}_{i,j} = \begin{pmatrix}{\varvec{p}}_i\\ 1\end{pmatrix} \otimes {\varvec{q}}_j \big | {\varvec{p}}_i \in P \right\} \subset \mathbb {R}^{(d+1) (m-1)} = \mathbb {R}^{n-1}. \end{aligned}$$

For $i \in [n]$, we denote with ${\widehat{C}}_i \subseteq \bigcup _{j=1}^m {\widehat{P}}_j$ the set of points $\{{\hat{{\varvec{p}}}}_{i,j} \,|\,j \in [m]\}$ that correspond to ${\varvec{p}}_i \in P$, and we color these points with color i. For $i \in [n]$, note that Lemma 3.10 applied to m copies of the singleton set $\{{\varvec{p}}_i\} \subseteq P$ guarantees that the color class ${\widehat{C}}_i \in \mathbb {R}^{n-1}$ embraces the origin. Hence, we have n color classes ${\widehat{C}}_1,\dots ,{\widehat{C}}_n$ that embrace the origin in $\mathbb {R}^{n-1}$. Now, by Theorem 1.2, there is a colorful choice ${\widehat{C}} = \{{\hat{{\varvec{c}}}}_1,\dots ,{\hat{{\varvec{c}}}}_n\} \subseteq \bigcup _{i=1}^n {\widehat{C}}_i$ with ${\hat{{\varvec{c}}}}_i \in {\widehat{C}}_i$ that embraces the origin, too. Because ${\widehat{C}}$ embraces the origin, Lemma 3.10 guarantees that the convex hulls of the sets $T_j = \{ {\varvec{p}}_i \in P \mid {\hat{{\varvec{p}}}}_{i,j} \in {\widehat{C}}\}$, $j \in [m]$, have a point in common. Moreover, since all points in $\bigcup _{j=1}^m {\widehat{P}}_j$ that correspond to the same point in P have the same color, each point ${\varvec{p}}_i \in P$ appears in exactly one set $T_j$, $j \in [m]$. Thus, $\mathcal {T} =\{T_1,\dots , T_m\}$ is a Tverberg m-partition of P. $\square$

Even less effort is required to obtain the colorful Kirchberger theorem from Lemma 3.10. Let $A, B \subset \mathbb {R}^d$ be two point sets. Kirchberger’s theorem [12] states that if for all subsets $C \subset A \cup B$ of size at most $d+2$, the sets $\text {conv}(A\cap C)$ and $\text {conv}(B \cap C)$ have an empty intersection, then $\text {conv}(A)$ and $\text {conv}(B)$ have an empty intersection. Arocha et al.  [2] presented a generalization based on the colorful Carathéodory theorem.³

Theorem 3.11

(Colorful Kirchberger theorem [2, special case of Thm. 3]) Let $C_1,\dots , C_n \subset \mathbb {R}^d$ be $n=(m-1)(d+1)+1$ pairwise disjoint color classes and let $\mathcal {T}_i = \{T_{i,1},\dots ,T_{i,m}\}$ denote a Tverberg m-partition for $C_i$, where $i \in [n]$. Then, there exists a colorful choice C, $|C|=n$, such that the family of sets

$$\begin{aligned} \mathcal {T}_{C} = \left\{ C \cap \Big ( \bigcup _{i=1}^n T_{i,j} \Big ) \big | j \in [m] \right\} \end{aligned}$$

is a Tverberg m-partition for C.

Proof

We lift each Tverberg partition to $\mathbb {R}^{n-1}$ as in Lemma 3.10: for $i \in [n]$ and $j \in [m]$, we denote with ${\widehat{T}}_{i,j}$ the set

$$\begin{aligned} {\widehat{T}}_{i,j} = \left\{ \begin{pmatrix}{\varvec{p}}\\ 1\end{pmatrix} \otimes {\varvec{q}}_j \big | {\varvec{p}}\in T_{i,j}\right\} \subset \mathbb {R}^{n-1}. \end{aligned}$$

By Lemma 3.10 and since each set $\mathcal {T}_i$, $i \in [n]$, is a Tverberg partition, the sets ${\widehat{C}}_i = \bigcup _{j=1}^m {\widehat{T}}_{i,j}$, $i \in [n]$, embrace the origin. We color the points in ${\widehat{C}}_i$ with color i. Since there are n color classes that embrace the origin in $n-1$ dimensions, Theorem 1.2 guarantees the existence of a colorful choice ${\widehat{C}}$ that embraces the origin. For $j \in [m]$, let ${\widehat{T}}_{j}={\widehat{C}} \cap \bigl ( \bigcup _{i=1}^n {\widehat{T}}_{i,j} \bigr )$ denote all points from a jth element in a Tverberg partition in ${\widehat{C}}C$. Since ${\widehat{C}}= \bigcup _{j=1}^m {\widehat{T}}_{j}$ embraces the origin, Lemma 3.10 implies that the convex hulls of the sets $T_j = \bigl \{ {\varvec{p}}\in \bigcup _{i=1}^n P_i \mid \left( {\begin{array}{c}{\varvec{p}}\\ 1\end{array}}\right) \otimes {\varvec{q}}_j \in {\widehat{T}}_j\bigr \}$ have a nonempty intersection. Further, since for $j \in [m]$, the set ${\widehat{T}}_{j}$ is a subset of $\bigcup _{i=1}^n {\widehat{T}}_{i,j}$, we have $T_j \subset \bigl ( \bigcup _{i=1}^n T_{i,j} \bigr )$. Moreover, since all points that correspond to the Tverberg partition $\mathcal {T}_i$, $i \in [n]$, have color i, exactly one of the sets $T_1,\dots ,T_m$ contains a point from $C_i$. The colorful choice C can be obtained by projecting ${\widehat{C}}$ down to $\mathbb {R}^d$. $\square$

We now give precise bounds on the quality and the running time of approximation algorithms obtained by combining algorithms for k-colorful choices with the presented reductions to ColorfulCarathéodory. Unfortunately, the approximation guarantee of Algorithm 3.3 is too weak to obtain a nontrivial approximation algorithm for Tverberg and therefore also for Centerpoint. On the positive side, it leads to a nontrivial approximation algorithm for ColorfulKirchberger.

In the following, let $\mathcal {A}$ be an algorithm that, when given $d+1$ color classes $C_1,\dots ,C_{d+1} \subset \mathbb {R}^d$, each embracing the origin and of size $\mathrm{O}({d})$, and for each $C_i$ the coefficients of the convex combination of the origin, outputs a ${\varvec{0}}$-embracing k(d)-colorful choice in W(d) time, where $k, W:\mathbb {N}\rightarrow \mathbb {N}$ are arbitrary but fixed functions.

Corollary 3.12

Let $P \subset \mathbb {R}^d$ be a point set of size n and let $\mathcal {A}$ be as above. Set

$$\begin{aligned} \widetilde{m} = \Big \lceil \frac{n}{(d+1)^2(k(n-1)-1)+d+1}\Big \rceil = \Omega \left( \frac{n}{d^2k(n-1)}\right) . \end{aligned}$$

Then, a Tverberg $\widetilde{m}$-partition $\mathcal {T}$ of P and a point ${\varvec{p}}\in \bigcap _{T \in \mathcal {T}} {{\mathrm{conv}}}(T)$ can be computed in $\mathrm{O}({(d^2 + m) n^2 + W(n-1)})$ time.

Proof

Set $m = \lceil n / (d+1)\rceil$. In the proof of Theorem 3.9, we lift m copies of P with Lemma 3.10 to $\mathbb {R}^{n-1}$. Lifting one point needs $\mathrm{O}({dm}) = \mathrm{O}({n})$ time and hence lifting all m copies takes $\mathrm{O}({mn^2})$ time. Then, each point ${\varvec{p}}_i \in \mathbb {R}^d$ from P corresponds to a color class $C_i = \big \{{\hat{{\varvec{p}}}}_{i,j} \,|\,j \in [m]\big \} \subset \mathbb {R}^{n-1}$ of size m and a ${\varvec{0}}$-embracing colorful choice of $C_1,\dots ,C_n$ corresponds to the Tverberg partition $\mathcal {T}=\{T_1,\dots ,T_m\}$ that we obtain by assigning ${\varvec{p}}_i \in P$ to $T_j$ if ${\hat{{\varvec{p}}}}_{i,j} \in C$. By construction of the color classes in the proof of Theorem 3.9, the barycenter of $C_i$ is the origin, for $i \in [n]$. Since we know then for each color class the coefficients of the convex combination of the origin, we can apply $\mathcal {A}$ to obtain a ${\varvec{0}}$-embracing $k(n-1)$-colorful choice $\widetilde{C} \subseteq \bigcup _{i=1}^n C_i$ together with the coefficients of the convex combination of the origin with the points in $\widetilde{C}$. Let $\widetilde{T}=\bigl \{\widetilde{T}_1,\dots ,\widetilde{T}_m\bigr \}$ be a family of subsets of P that we construct as before by assigning ${\varvec{p}}_i$ to $\widetilde{T}_j$ if ${\hat{{\varvec{p}}}}_{i,j} \in \widetilde{C}$. Here, $\widetilde{T}$ is a multiset, i.e., we allow $\widetilde{T}_i = \widetilde{T}_j$ for $i\ne j$. Since $\widetilde{C}$ embraces the origin, Lemma 3.10 guarantees that the intersection $\bigcap _{i=1}^m {{\mathrm{conv}}}(\widetilde{T}_i)$ is nonempty. Moreover, because we know the coefficients of the convex combination of the origin with the points in $\widetilde{C}$, we can compute in $\mathrm{O}({dn})$ time a point ${\varvec{p}}^\star \in \bigcap _{i=1}^m {{\mathrm{conv}}}(\widetilde{T}_i)$ together with the coefficients of the convex combination of ${\varvec{p}}^\star$ with the points in $\widetilde{T}_i$ for $i \in [m]$, as described in the proof of Lemma 3.10.

Now, we construct a Tverberg partition for P out of $\widetilde{\mathcal {T}}$ by a greedy strategy that iteratively removes sets from $\widetilde{\mathcal {T}}$. Let $\widetilde{T} \in \widetilde{\mathcal {T}}$ be some set and remove it from $\widetilde{\mathcal {T}}$. Since we know the coefficients of the convex combination of ${\varvec{p}}^\star$ with the points in $\widetilde{T}$, Lemma 2.1 can be applied to prune $\widetilde{T}$ to a ${\varvec{p}}^\star$-embracing set of size at most $d+1$ in $\mathrm{O}({d^3n + n^2})$ time. Then, for each point ${\varvec{p}}\in \widetilde{T}$, we remove the at most $k(n-1)-1$ other sets from $\widetilde{\mathcal {T}}$ that contain ${\varvec{p}}$. We continue with the next set in $\widetilde{\mathcal {T}}$ that has not yet been removed until $\widetilde{\mathcal {T}} = \emptyset$. Let $\mathcal {T}^\star \subseteq \widetilde{\mathcal {T}}$ be the family of sets that we obtain by this process. Clearly, $\mathcal {T}^\star$ is a Tverberg partition and because $\mathcal {T}^\star \subseteq \widetilde{\mathcal {T}}$, we have ${\varvec{p}}^\star \in \bigcap _{\widetilde{T} \in \mathcal {T}^\star } {{\mathrm{conv}}}(\widetilde{T})$. Moreover, for each set $\widetilde{T}_i \in \mathcal {T}^\star$, we remove at most $(d+1)(k(n-1)-1)$ other sets from $\widetilde{\mathcal {T}}$. Thus, the size of the Tverberg partition $\mathcal {T}^\star$ is at least

$$\begin{aligned} \Big |\mathcal {T}^\star \Big | \ge \Big \lceil \frac{m}{(d+1)(k(n-1)-1)+1}\Big \rceil \ge \Big \lceil \frac{n}{(d+1)^2(k(n-1)-1)+d+1}\Big \rceil . \end{aligned}$$

Constructing the ColorfulCarathéodory instance takes $\mathrm{O}({m n^2})$ time. Using $\mathcal {A}$, we need $W(n-1)$ time to compute a $k(n-1)$-colorful choice $\widetilde{C}$. Pruning every set of $\widetilde{\mathcal {T}}$ with Lemma 2.1 to at most $d+1$ points needs $\mathrm{O}({m (d^3 n + n^2)})=\mathrm{O}({(d^2 + m) n^2})$ time. Finally, constructing $\mathcal {T}^\star$ out of $\widetilde{\mathcal {T}}$ takes $\mathrm{O}({n^2})$ time with the naive algorithm. This results in the claimed running time of $\mathrm{O}({(d^2 + m) n^2 + W(n-1)})$. $\square$

Furthermore, we can use $\mathcal {A}$ to approximate ColorfulKirchberger.

Corollary 3.13

Let $\mathcal {A}$ be as above and let $C_1,\dots , C_n \subset \mathbb {R}^d$ be $n=(m-1)(d+1)+1$ pairwise disjoint color classes that are each of size n. Furthermore, for $i \in [n]$, let $\mathcal {T}_i = \{T_{i,1},\dots ,T_{i,m} \}$ denote a Tverberg m-partition for $C_i$. Then, given for each Tverberg partition $\mathcal {T}_i$, $i \in [n]$, a point ${\varvec{p}}_i \in \bigcap _{j=1}^m \text {conv}(T_{i,j})$, and for all $i \in [n]$ and $j \in [m]$, the coefficients of the convex combination of ${\varvec{p}}_i$ with the points in $T_{i,j}$, we can compute in $\mathrm{O}({n^3 + W(n-1)})$ time a $k(n-1)$-colorful choice $C\subseteq \bigcup _{i=1}^n C_i$ such that

$$\begin{aligned} \mathcal {T}_{C} = \left\{ C \cap \Big ( \bigcup _{i=1}^n T_{i,j} \Big ) \big | j \in [m] \right\} \end{aligned}$$

is a Tverberg m-partition for C.

Proof

In the proof of Theorem 3.11, we lift the points $\bigcup _{i=1}^n C_i$ to $\mathbb {R}^{n-1}$ so that the set of points ${\widehat{C}}_i$ that corresponds to the color class $C_i$ still embraces the origin, where $i \in [n]$. Moreover, if ${\widehat{C}}' \subseteq \bigcup _{i=1}^n {\widehat{C}}_i$ is a ${\varvec{0}}$-embracing colorful choice of the lifted points, then there is a corresponding colorful choice $C'$ with respect to $C_1,\dots ,C_n$ such that

$$\begin{aligned} \mathcal {T}_{C'} = \left\{ C' \cap \Big ( \bigcup _{i=1}^n T_{i,j} \Big ) \big | j \in [m] \right\} \end{aligned}$$

is a Tverberg m-partition for $C'$. Similarly, a ${\varvec{0}}$-embracing $k(n-1)$-colorful choice ${\widehat{C}}$ of the lifted color classes corresponds to a $k(n-1)$-colorful choice C with respect to $C_1,\dots ,C_n$ such that

$$\begin{aligned} \mathcal {T}_{C} = \left\{ C \cap \Big ( \bigcup _{i=1}^n T_{i,j} \Big ) \big | j \in [m] \right\} \end{aligned}$$

is a Tverberg m-partition for C.

Computing the tensor product $\left( {\begin{array}{c}{\varvec{p}}\\ 1\end{array}}\right) \otimes {\varvec{q}}$, where ${\varvec{p}}\in \mathbb {R}^{d}$ and ${\varvec{q}}\in \mathbb {R}^{m-1}$, needs $\mathrm{O}({dm}) = \mathrm{O}({n})$ time and hence lifting the point sets $C_1,\dots ,C_n \subset \mathbb {R}^d$ to $\mathbb {R}^{n-1}$ with Lemma 3.10 needs $\mathrm{O}({n^3})$ time in total. Since we know for each Tverberg partition $\mathcal {T}_i$, $i \in [n]$, a point ${\varvec{p}}_i \in \bigcap _{j=1}^m \text {conv}(T_{i,j})$ together with the coefficients of the convex combination of ${\varvec{p}}_i$ with the points in $T_{i,j}$ for $j \in [m]$, we can compute in $\mathrm{O}({n})$ time the coefficients of the convex combination of the origin with the points in ${\widehat{C}}_i$ as described in the proof of Lemma 3.10. Then, $\mathcal {A}$ can be applied to compute a ${\varvec{0}}$-embracing $k(n-1)$-colorful choice ${\widehat{C}}$ with respect to the lifted point sets in $W(n-1)$ time. Finally, constructing C and $\mathcal {T}_C$ out of ${\widehat{C}}$ needs $\mathrm{O}({n})$ time. Hence, the total time needed is $\mathrm{O}({n^3 + W(n-1)})$. $\square$

Now, given $d+1$ color classes $C_1,\dots ,C_{d+1} \subset \mathbb {R}^d$ that embrace the origin, we can compute with Algorithm 3.3 an $\lceil \varepsilon d\rceil$-colorful choice that embraces the origin in polynomial time. Combining this with Corollary 3.12, we obtain an algorithm that computes Tverberg partitions of size $\mathrm{O}({1})$ in polynomial time, a trivial result. However, combining Algorithm 3.3 with Corollary 3.13, we do obtain a nontrivial approximation algorithm for ColorfulKirchberger: given $n = (m-1)(d+1)+1$ color classes $C_1,\dots ,C_n$, each of size n, and for each color class a Tverberg m-partition $\mathcal {T}_i = \{T_{i,1},\dots ,T_{i,m} \}$ together with a point ${\varvec{p}}_i \in \bigcap _{j=1}^m \text {conv}(T_{i,j})$ and the coefficients of the convex combination of ${\varvec{p}}_i$ with the points in $T_{i,j}$, for all $j \in [m]$, we can compute in $n^{\mathrm{O}({\varepsilon ^{-1} \ln \varepsilon ^{-1}})}$ time an $\lceil \varepsilon n \rceil$-colorful choice C such that

$$\begin{aligned} \mathcal {T}_{C} = \left\{ C \cap \Big ( \bigcup _{i=1}^n T_{i,j} \Big ) \big | j \in [m] \right\} \end{aligned}$$

is a Tverberg m-partition for C, where $\varepsilon > 0$ is arbitrary but fixed.

4 Exact Algorithms for ColorfulCarathéodory

In contrast to the previous sections, we now focus on computing an exact solution for the convex version of ColorfulCarathéodory. Let $C_1,\dots ,C_{d+1} \subset \mathbb {Q}^d$ be $d+1$ sets that each embrace the origin, and assume all are of size at most $d+1$. The naive algorithm checks for all $\mathrm{O}({d^{d+1}})$ possible colorful choices whether they embrace the origin. This can be further improved by using the following result by Bárány.

Theorem 4.1

([3, Thm. 2.3]). Let $C_1,\dots ,C_{d} \subset \mathbb {R}^d$ be d sets that all embrace the origin and let ${\varvec{c}}\in \mathbb {R}^d$ be a point. Then, there exist d points ${\varvec{c}}_1 \in C_1,\dots ,{\varvec{c}}_d \in C_d$ such that the set $\{ {\varvec{c}}, {\varvec{c}}_1,\dots ,{\varvec{c}}_d \}$ embraces the origin. $\square$

In particular, Theorem 4.1 implies that every point ${\varvec{c}}\in \bigcup _{i=1}^{d+1} C_i$ participates in some ${\varvec{0}}$-embracing colorful choice and hence we can fix a point from one color class and check only all $\mathrm{O}({d^d})$ possibilities of extending it to a colorful choice.

We now consider two related settings that allow for further improvement. We begin with the simple case in which each color class consists of only two points (Sect. 4.1). Then, basic linear algebra suffices to compute a ${\varvec{0}}$-embracing colorful choice in polynomial-time. In Sect. 4.2, we show that many color classes help. Using an approach similar to the algorithm by Miller and Sheehy for approximating Tverberg partitions [20], we present a quasi-polynomial time algorithm that computes a ${\varvec{0}}$-embracing colorful choice when given $\Theta (d^2 \log d)$ color classes instead of only $d+1$.

4.1 A Simple Special Case

In the following, we assume that $|C_1| = \dots = |C_{d+1}| = 2$ and let ${\varvec{c}}_{i,1}, {\varvec{c}}_{i,2}$ denote the two points in $C_i$, for $i \in [d+1]$. Clearly, for all $i \in [d+1]$, the point $-{\varvec{c}}_{i,1}$ must be contained in the positive span of ${\varvec{c}}_{i,2}$. Furthermore, we assume without loss of generality that all points are different from the origin, as otherwise computing a ${\varvec{0}}$-embracing colorful choice is trivial. Then, the set $\big \{ {\varvec{c}}_{i,1} \,|\,i \in [d+1] \big \}$ is linearly dependent and hence there exist coefficients $\phi _1,\dots ,\phi _{d+1} \in \mathbb {R}$, not all 0, such that ${\varvec{0}} = \sum _{i=1}^{d+1} \phi _i {\varvec{c}}_{i,1}$. Now, since $-{\varvec{c}}_{i,1} \in \mathrm{pos}({\varvec{c}}_{i,2})$ for all $i \in [d+1]$, the set $C = \big \{ {\varvec{c}}_{i,1} \,|\,i \in [d+1],\, \phi _i \ge 0\big \} \cup \big \{ {\varvec{c}}_{i,2} \,|\,i \in [d+1],\, \phi _i < 0\big \}$ embraces the origin, and it is a colorful choice. Since the computation of the coefficients of the linear dependency can be carried out in $\mathrm{O}({d^3})$ time with Gaussian elimination, finding C takes $\mathrm{O}({d^3})$ time in total. The following theorem is now immediate.

Theorem 4.2

Let $C_1, \dots , C_{d+1}\subset \mathbb {R}^d$ be $d+1$ pairs of points that all embrace the origin. Then, a ${\varvec{0}}$-embracing colorful choice can be computed in $\mathrm{O}({d^3})$ time.

4.2 Many Colors

In the following, we assume that we are given $\Theta (d^2 \log d)$ instead of only $d+1$ color classes that all embrace the origin. The algorithm repeatedly combines k-colorful choices to one ${\varvec{0}}$-embracing $\lceil k/2\rceil$-colorful choice until a ${\varvec{0}}$-embracing 1-colorful choice is obtained. This approach is similar to the Miller–Sheehy approximation algorithm for Tverberg partitions [20], and it leads to an algorithm with total running time $d^{\mathrm{O}({\log d })}$.

Lemma 4.3

Let $C'_1,\dots ,C'_{d+1}\subset \mathbb {R}^d$ be ${\varvec{0}}$-embracing k-colorful choices of size $\mathrm{O}({d})$ such that each color appears in a unique k-colorful choice. Then, given the coefficients of the convex combination of the origin for each set $C'_i$, $i \in [d+1]$, a ${\varvec{0}}$-embracing $\lceil k/2\rceil$-colorful choice $C'$ can be computed in $\mathrm{O}({d^5})$ time.

Proof

First, we prune each k-colorful choice $C'_i$, $i \in [d+1]$, with Lemma 2.5 and then partition it into two sets $C'_{i,1}, C'_{i,2}$ by distributing the points from each color equally among both sets. Then, we apply the algorithm from Lemma 2.7 to obtain two representative points ${\varvec{r}}_{i,1}, {\varvec{r}}_{i,2}$ and set $R_i = \{{\varvec{r}}_{i,1},{\varvec{r}}_{i,2}\}$. Since the sets $R_1,\dots ,R_{d+1}$ each embrace the origin and consist of only two points, we can compute a 1-colorful choice R with respect to $R_1,\dots ,R_{d+1}$ with the algorithm from Theorem 4.2. Now, consider the set $C' = \big \{ C'_{i,j} \,|\,{\varvec{r}}_{i,j} \in R \big \}$. Since R is ${\varvec{0}}$-embracing, so is $C'$. Moreover, because a color j appears only in one of the k-colorful choices, say $C'_i$, and since each set of the partition $C'_{i,1}, C'_{i,2}$ contains at most $\lceil k/2 \rceil$ points with color j, the set $C'$ is a $\lceil k/2\rceil$-colorful choice.

Pruning each k-colorful choice with Lemma 2.5 and then computing the two representative points per partition takes $\mathrm{O}({d^5})$ time in total. This dominates the time needed for the computation of R and thus, we can compute $C'$ in $\mathrm{O}({d^5})$ time. $\square$

Note that Lemma 4.3 actually implies a second algorithm to compute $\lceil (d+1)/2 \rceil$-colorful choices that embrace the origin: let $C_1,\dots ,C_{d+1} \subset \mathbb {R}^d$ be ${\varvec{0}}$-embracing color classes and assume the sets have size $d+1$. Set $C'_i = C_i$ in Lemma 4.3, for $i \in [d+1]$. Then, $C'_i$ is trivially a $(d+1)$-colorful choice and hence the set $C'$ is a $\lceil (d+1)/2 \rceil$-colorful choice.

Now, we apply Lemma 4.3 repeatedly until we obtain a 1-colorful choice as follows. Let $C_1,\dots ,C_n \subset \mathbb {Q}^d$ be $n=\Theta (d^2\log d)$ color classes such that $C_i$ is ${\varvec{0}}$-embracing and has size $d + 1$, for $i \in [n]$. We create an array A of size $m=\Theta (\log d)$ that initially contains all n color classes in A[0]. Set $c_0 = d+1$ and for $i \in [k]$, set $c_i = \lceil c_{i-1}/2\rceil$. Throughout the algorithm, we maintain the invariant that the ith cell contains only ${\varvec{0}}$-embracing $c_i$-colorful choices and that each color appears in at most one set in all of A. Since $c_0 = d+1$, the invariant holds in the beginning. We repeatedly improve k-colorful choices with Lemma 4.3 as follows: let i be the maximum index of a cell in A that contains at least $d+1$ sets $C'_1,\dots ,C'_{d+1}$ and remove them from A[i]. By our invariant, these sets are ${\varvec{0}}$-embracing $c_i$-colorful choices. Applying Lemma 4.3, we can combine $C'_1,\dots ,C'_{d+1}$ to one $c_{i+1}$-colorful choice $C'$ that embraces the origin. We prune it with Lemma 2.5 and check whether it is a 1-colorful choice. If so, we have found a solution. Otherwise, we add it to $A[i+1]$. Furthermore, we check for colors that appeared in the removed sets $C'_1,\dots ,C'_{d+1}$ but not in $C'$ and add the corresponding color classes back to A[0]. The invariant is maintained since these colors only appeared in the removed sets. See Algorithm 4.5 for a detailed description of the algorithm.

We conclude this section by proving the correctness of Algorithm 4.5 and analyzing its running time.

Theorem 4.4

Let $C_1,\ldots ,C_{n} \subset \mathbb {R}^d$ be $n=\Theta (d^2 \log d)$ sets such that $C_i$ embraces the origin and $|C_i| = \mathrm{O}({d})$, for $i \in [n]$. Then, given the coefficients of the convex combination of the origin for each set $C_i$, $i \in [n]$, Algorithm 4.5 computes a ${\varvec{0}}$-embracing colorful choice in $d^{\mathrm{O}({\log d })}$ time.

Proof

Set $m = \lceil \log (d+1) \rceil +1$. We have already argued that the ith cell of the array A contains only ${\varvec{0}}$-embracing $c_i$-colorful choices. First, we observe that progress is always possible, i.e., that it is always possible to find a cell of A that contains at least $d+1$ sets: the array has $m = \Theta (\log d)$ levels and within each set in A, at most d colors appear. Thus, for $d^2 m + 1 = \Theta (d^2 \log d)$ colors, the pigeonhole principle guarantees a cell with at least $d+1$ sets.

We claim that a combination of $d+1$ sets in A[m] results in a ${\varvec{0}}$-embracing colorful choice. Since $c_i \le \frac{d+1}{2^i} + 2$, the sets in $A[m-1]$ are ${\varvec{0}}$-embracing 3-colorful choices, the sets in A[m] are 2-colorful choices and the combination of $d+1$ sets in A[m] gives a 1-colorful choice, as claimed.

Let T(i) denote the time to compute a set at level i. For this, we have to compute $d+1$ sets in level $i-1$. Since one application of Lemma 4.3 takes $\mathrm{O}({d^5})$ time, we have $T(i) = (d+1)T(i-1) + \mathrm{O}({d^5})$, for $i \ge 1$, and $T(0) = \mathrm{O}({1})$. This solves to $T(i) = d^{\mathrm{O}({i})}$. At the end, each level $i \ge 1$ of A contains at most $d+1$ sets, so the total running time is $\sum _{i = 1}^{m+1} (d+1)T(i) = \sum _{i = 1}^{m+1} d^{\mathrm{O}({i})} = d^{\text {O}(\log d)}$, as claimed. $\square$

5 The Complexity of a Related Problem

We can show that a related problem to ColorfulCarathéodory that is motivated by Bárány ’s original proof [3], the local search nearest colorful polytope problem (L-Ncp), is PLS-complete. Additionally, by adapting the PLS-completeness proof, we prove that finding a global optimum for Ncp (G-Ncp) is NP-hard. This answers a question by Bárány and Onn [4, p. 561]. We note that this question has been answered independently by Meunier and Sarrabezolles [18, Thm. 2]. In contrast to the previous sections, all algorithms in this section are analyzed in the Word-Ram with logarithmic costs. This models the number of steps on a Turing machine, as required by the definition of PLS.

5.1 The Complexity Class PLS

The complexity class polynomial local search (PLS) [1, 10, 19] captures search problems that can be solved by a local-improvement algorithm. Each improvement step can be carried out in polynomial time, but the total number of steps to a local optimum may be exponential. The existence of a local optimum is guaranteed, as the progress of the algorithm can be measured by a potential function that strictly decreases with each improvement step.

More formally, a problem in PLS is a relation $\mathcal {R}$ between a set of problem instances $\mathcal {I} \subseteq \{0,1\}^\star$ and a set of candidate solutions $\mathcal {S} \subseteq \{0,1\}^\star$ with the following properties:

• The set $\mathcal {I}$ is polynomial-time verifiable. Furthermore, there exists an algorithm that, given an instance $I \in \mathcal {I}$ and a candidate solution $s \in \mathcal {S}$, decides in time ${{\mathrm{poly}}}(|I|)$ whether s is valid for I. In the following, we denote with $\mathcal {S}_I \subseteq \mathcal {S}$ the set of valid candidate solutions for a given instance I.

• There exists a polynomial-time algorithm that on input $I \in \mathcal {I}$ returns a valid candidate solution $s_I \in \mathcal {S}_I$. We call $s_I$ the standard solution.

• There exists a polynomial-time algorithm that on input $I \in \mathcal {I}$ and $s \in \mathcal {S}_I$ returns a set $N_{I,s} \subseteq \mathcal {S}_I$ of valid candidate solutions for I. We call $N_{I,s}$ the neighborhood of s.

• There exists a polynomial-time algorithm that on input $I \in \mathcal {I}$ and $s \in \mathcal {S}_I$ returns a number $c_{I,s} \in \mathbb {Q}$. We call $c_{I,s}$ the cost of s.

We say a candidate solution $s \in \mathcal {S}$ is a local optimum for an instance $I \in \mathcal {I}$ if (i) $s \in \mathcal {S}_I$; and (ii) for all $s' \in N_{I,s}$, we have $c_{I,s} \le c_{I,s'}$ (minimization problem) or $c_{I,s} \ge c_{I,s'}$ (maximization problem). The relation $\mathcal {R}$ then consists of all pairs (I, s) such that s is a local optimum for I. This formulation implies a simple algorithm, the standard algorithm: begin with the standard solution, and repeatedly call the neighborhood-algorithm to improve the current solution until a local optimum is reached. Although each iteration takes polynomial time, the total number of iterations may be exponential, the time needed to cycle through all the exponentially many candidate solutions. There are straightforward examples where this happens. Moreover, there are PLS-problems for which it is PSPACE-complete to compute the local optimum found by the standard algorithm [1, Lem. 15].

Each problem instance I of a PLS-problem can be seen as a simple search problem on a directed graph $G_I=(V,E)$. The nodes of $G_I$ are the valid candidate solutions for I, and there is a directed edge from $u \in \mathcal {S}_I$ to $v \in \mathcal {S}_I$ if $v \in N_{I,u}$ and $c_{I,v} < c_{I,u}$ (minimization problem) or $c_{I,v} > c_{I,u}$ (maximization problem). Then, the set of local optima for I is precisely the set of sinks in $G_I$, i.e., the set of nodes with outdegree 0. Because the costs induce a topological order on the graph, at least one sink exists.

Since PLS contains relations and not languages, a different concept of reduction is necessary to define complete problems. We say a ${\small {\textsf {PLS}}}$ problem A is PLS -reducible (or just reducible) to a ${\small {\textsf {PLS}}}$ problem B if there exist two polynomial-time computable functions $f_{A \mapsto B}$ and $f_{B \mapsto A}$ with the following properties. Let $\mathcal {I}_{A}$ denote the set of instances of A and let $\mathcal {S}_{A}$ denote the set of candidate solutions of A. Define $\mathcal {I}_{B}$ and $\mathcal {S}_{B}$ similarly. The function $f_{A \mapsto B}:\mathcal {I}_{A} \rightarrow \mathcal {I}_{B}$ maps problem instances of A to problem instances of B. The function $f_{B \mapsto A}:\mathcal {I}_{A} \times \mathcal {S}_{B} \rightarrow \mathcal {S}_A$ maps candidate solutions of B to candidate solutions of A such that if $s_B \in \mathcal {S}_{B}$ is a candidate solution of B with $\big (f_{A\mapsto B}(I_A), s_B\big ) \in B$, then $\big (I_A, f_{B \mapsto A}(I_A, s_B)\big ) \in A$.⁴ The existence of these two functions implies that any polynomial-time algorithm for B yields a polynomial-time algorithm for A. We say a problem $A \in {\small {\textsf {PLS}}}$ is PLS -complete if all problems in PLS can be PLS-reduced to A. The canonical PLS-complete problem is FLIP [10, Thm. 1]: given a Boolean circuit of polynomial size with n inputs and m outputs, find an input-assignment such that the resulting output interpreted as a number in binary cannot be decreased by flipping one bit in the input. The set of PLS-complete problems includes, among various local search variants and heuristics for NP-complete problems, the Lin–Kernighan heuristic for the traveling salesman problem [22], computing stable configurations in Hopfield neural networks [27, Cor. 5.12], and computing pure Nash equilibria in congestion games [8, Thm. 3].

5.2 The Local Search Nearest Colorful Polytope Problem

Let $C_1,\dots ,C_{m} \subset \mathbb {Q}^d$ be m color classes that do not necessarily embrace the origin. For a given set $C' \subset \mathbb {Q}^d$, let $\delta (C') = \min \bigl \{ \Vert {\varvec{c}}\Vert _1 \mid {\varvec{c}}\in {{\mathrm{conv}}}(C') \bigr \}$ denote the minimum $\ell _1$-norm of a point in ${{\mathrm{conv}}}(C')$. In L-Ncp, we want to find a colorful choice C such that $\delta (C)$ cannot be decreased by swapping a single point with another point of the same color. In the language of PLS, L-Ncp is defined as follows.

Definition 5.1

L-Ncp

• Instances. The set of problem instances $\mathcal {I}$ consists of all tuples $(C_1,\dots ,C_m)$, where $d \in \mathbb {N}$ and for $i \in [m]$, we have $C_i \subset \mathbb {Q}^d$.

• Candidate solutions. The set of candidate solutions consists of all sets $C \subset \mathbb {Q}^d$, where $d \in \mathbb {N}$. For a fixed instance $I = (C_1,\dots ,C_m) \in \mathcal {I}$, we define the set of valid candidate solutions $\mathcal {S}_I$ of I to be the set of all colorful choices with respect to $C_1,\dots ,C_m$.

• Cost function. Let $s \in \mathcal {S}_I$ be a colorful choice. Then, the cost $c_{I,s}$ of s with respect to I is defined as $\delta (s)$. We want to minimize the costs.

• Neighborhood. Let $I \in \mathcal {I}$ be an instance and let $s \in \mathcal {S}_I$ be a valid candidate solution. Then, the set of neighbors $N_{I,s}$ of s consists of all colorful choices that can be obtained by swapping one point with another point of the same color in s.

We reduce the PLS-complete problem Max-2SAT/Flip  [27] to L-Ncp. In Max-2SAT/Flip, we are given a 2-CNF formula, i.e., a Boolean formula in conjunctive normal form in which each clause consists of at most 2 literals, and for each clause a weight. The task is to find an assignment such that the weighted sum of unsatisfied clauses cannot be decreased by flipping a single variable. More formally, Max-2SAT/Flip is defined as follows.

Definition 5.2

(Max-2SAT/Flip)

• Instances. The set of instances $\mathcal {I}'$ consists of all tuples $I = (n,K_1,\dots ,K_m)$ such that $n \in \mathbb {N}$ and for $i \in [n]$, the tuple $K_i$ has the form $(w_i, T_i, F_i)$, where $w_i \in \mathbb {Z}$ and $T_i, F_i \subseteq [n]$ with $|T_i \cup F_i| \le 2$ for all $i \in [n]$. Then, we identify with $K_i$ the clause ${\widehat{K}}_i = \bigl (\bigvee _{j \in T_j} x_j\bigr ) \vee \bigl (\bigvee _{j \in F_j} \overline{x}_j\bigr )$ with weight $w_i$, and we identify with I the 2-CNF formula ${\widehat{K}}_1 \wedge \dots \wedge {\widehat{K}}_m$ with variables $x_1,\dots ,x_n$.

• Candidate solutions. The set of candidate solutions $\mathcal {S}'$ contains all tuples $A=(v_1,\dots ,v_n)$, where $n \in \mathbb {N}$ and $v_i \in \{0,1\}$ for $i \in [n]$. Given an instance $I \in \mathcal {I}'$ in which n variables $x_1,\dots ,x_n$ appear, we define the set of valid candidate solutions $\mathcal {S}'_{I}$ for I as the set of all n-tuples from $\mathcal {S}'$. We interpret the ith entry of a tuple $A \in \mathcal {S}'_{I}$ as an assignment to $x_i$ and we denote it with $A(x_i)$.

• Cost function. Let $I \in \mathcal {I}'$ be an instance. Then, we define the cost $c'_{I,s}$ of a valid candidate solution $s \in \mathcal {S}'_I$ as the sum of the weights of all unsatisfied clauses. We want to minimize the cost.

• Neighborhood. Let $I \in \mathcal {I}'$ be an instance and $s \in \mathcal {S}'_I$ a tuple of size n. Then, the set of neighbors $N'_{I,s}$ of s consists of all tuples that can be obtained by replacing the ith entry $A(x_i)$ with $1-A(x_i)$, where $i \in [n]$.

The following theorem is due to Schäffer and Yannakakis.

Theorem 5.3

[27, Cor. 5.12] Max-2SAT/Flip is PLS-complete.

We continue with the reduction from Max-2SAT/Flip to L-Ncp.

Theorem 5.4

L-Ncp is PLS-complete.

Proof

Let $I'=(n,K_1,\dots ,K_d) \in \mathcal {I}'$ be an instance of Max-2SAT/Flip. We construct an instance $I \in \mathcal {I}$ of L-Ncp in which each colorful choice C encodes an assignment $A_C$ such that the cost $c_{I, C}$ of C equals the cost $c'_{I', A_C}$.

For each variable $x_i$, we introduce a color class $X_i = \{{\varvec{x}}_i, \overline{{\varvec{x}}}_i\}$ consisting of two points in $\mathbb {Q}^d$ that encode whether $x_i$ is set to 1 or 0. We assign the jth dimension to the jth clause and set

$$\begin{aligned} ({\varvec{x}}_i)_j = {\left\{ \begin{array}{ll} -n w_j, &{} \text {if } x_i = 1\text { satisfies }{\widehat{K}}_j, \text { and} \\ w_j, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

where $j \in [d]$. Similarly, we set

$$\begin{aligned} (\overline{{\varvec{x}}_i})_j = {\left\{ \begin{array}{ll} -n w_j, &{} \text {if } x_i = 0\text { satisfies }{\widehat{K}}_j\text {, and} \\ w_j, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

where $j \in [d]$. Then, a colorful choice C of $X_1, \dots , X_m$ corresponds to the assignment $A_C \in \mathcal {S}'_{I'}$ that sets $x_i$ to 1 if ${\varvec{x}}_i\in C$ and otherwise to 0. Conversely, an assignment $A \in \mathcal {S}'_{I'}$ can be interpreted directly as a colorful choice C of $X_1, \dots , X_m$.

In the following, we construct an instance of L-Ncp such that the convex hull of a colorful choice C contains the origin if projected onto the dimensions corresponding to clauses that are satisfied by $A_C$ (and hence do not contribute to the cost of C). Moreover, if projected onto the subspace corresponding to the unsatisfied clauses, $\delta (C)$ equals the total weight of unsatisfied clauses which then defines completely the cost of C.

We introduce additional helper color classes to decrease the distance to the origin in dimensions that correspond to satisfied clauses. In particular, we have for each clause ${\widehat{K}}_i$, $i \in [d]$, a color class $H_i = \{{\varvec{h}}_i\}$ consisting of a single point, where

$$\begin{aligned} ({\varvec{h}}_i)_j = {\left\{ \begin{array}{ll} (d+1) \big ((n+2) - \frac{d}{d+1}\big ) w_i, &{} \text {if } j = i,\text { and} \\ w_j, &{} \text { otherwise,} \end{array}\right. } \end{aligned}$$

where $j \in [d]$. The last helper color class $H_{d+1} = \{{\varvec{h}}_{d+1}\}$ again contains a single point, but now all coordinates are set to the clause weights, i.e.,

$$\begin{aligned} ({\varvec{h}}_{d+1})_j = w_j \quad \text { for } j \in [d]. \end{aligned}$$

See Fig. 7 for an example.

Fig. 7

Construction of the point sets corresponding to the Max-2SAT/Flip instance $\big (x_1 \vee \overline{x_2}\big ) \wedge \big (x_2 \vee x_3\big )$ with weights 3 and 6, respectively

Let now $I = (X_1,\ldots ,X_n, H_1, \ldots , H_{d+1}) \in \mathcal {I}$ denote the constructed L-Ncp instance. We continue with showing that the cost of a colorful choice equals the cost of the corresponding assignment by proving the following two inequalities.

• (i) for every colorful choice $C \in \mathcal {S}_I$, the cost are lower bounded by the cost of the corresponding assignment:

  $$\begin{aligned} c_{I,C} \ge c'_{I',A_C}. \end{aligned}$$

• (ii) for every colorful choice $C \in \mathcal {S}_I$, the cost are upper bounded by the cost of the corresponding assignment:

  $$\begin{aligned} c_{I,C} \le c'_{I',A_C}. \end{aligned}$$

Note that (i) and (ii) directly imply that L-Ncp is PLS-complete. To see this, consider a local optimum $s^\star \in \mathcal {S}_I$ of the L-Ncp instance I. By definition, the costs of all other colorful choices that can be obtained from $s^\star$ by swapping one point with another of the same color are greater or equal to $c_{I,s^\star }$. Then, the total weight of unsatisfied clauses by the corresponding assignment $A_{s^\star } \in \mathcal {S}'_{I'}$ cannot be decreased by flipping a variable. Thus, $A_{s^\star }$ is a local minimum of the Max-2SAT/Flip instance $I'$.

(i) Let $C \in \mathcal {S}_I$ be a colorful choice and assume some clause ${\widehat{K}}_j$ is not satisfied by the corresponding assignment $A_C \in \mathcal {S}'_{I'}$. By construction, the jth coordinate of each point ${\varvec{p}}$ in C is at least $w_j$. Thus, the jth coordinate of every convex combination of the points in C is at least $w_j$ and hence $c_{I,C} \ge c_{I',A_C}$.

(ii) Let $C \in \mathcal {S}_I$ be a colorful choice. In the following, we construct a convex combination of the points in C that results in a point ${\varvec{p}}$ whose $\ell _1$-norm is exactly the total weight of unsatisfied clauses in the corresponding assignment $A_C \in \mathcal {S}'_{I'}$ and thus $c_{I,C} \le c_{I',A_C}$. For $k=0,1,2$, let $S_k$ denote the set of clauses that are satisfied by exactly k literals with respect to the assignment $A_C$. As a first step towards constructing ${\varvec{p}}$, we show the existence of an intermediate point in the convex hull of the helper classes. $\square$

Lemma 5.5

There is a point ${\varvec{h}}\in {{\mathrm{conv}}}(H_1,\ldots ,H_{d+1})$ whose jth coordinate is $(n+2) w_j$, if $j\in S_2$, and $w_j$, otherwise.

Proof

Take ${\varvec{h}}= \sum \limits _{i\in S_2} \frac{1}{d+1} {\varvec{h}}_i + \big (1-\frac{|S_2|}{d+1}\big ) {\varvec{h}}_{d+1}$. Then, for $j\in S_0\cup S_1$, we have

$$\begin{aligned} ({\varvec{h}})_j&= \sum \limits _{i\in S_2} \frac{1}{d+1} ({\varvec{h}}_i)_j + \Big (1-\frac{|S_2|}{d+1}\Big ) ({\varvec{h}}_{d+1})_j \\&{\mathop {=}\limits ^{j\notin S_2}} \sum \limits _{i\in S_2} \frac{1}{d+1} w_j + \Big (1-\frac{|S_2|}{d+1}\Big ) w_j = w_j. \end{aligned}$$

And for $j \in S_2$, we have

$$\begin{aligned} ({\varvec{h}})_j&= \sum \limits _{i\in S_2} \frac{1}{d+1} ({\varvec{h}}_i)_j + \Big (1-\frac{|S_2|}{d+1}\Big ) ({\varvec{h}}_{d+1})_j \\&= \frac{1}{d+1} ({\varvec{h}}_j)_j + \sum \limits _{i\in S_2\setminus \{j\}} \frac{1}{d+1} ({\varvec{h}}_i)_j + \Big (1-\frac{|S_2|}{d+1}\Big ) ({\varvec{h}}_{d+1})_j \\&= \Big ((n+2) - \frac{d}{d+1}\Big ) w_j + \frac{d}{d+1} w_j = (n+2) w_j, \end{aligned}$$

as desired. $\square$

Let now ${\varvec{l}}_i$ be the point from $X_i$ in the colorful choice C and consider the point

$$\begin{aligned} {\varvec{p}}= \frac{1}{n+1} \Big (\sum _{i=1}^n {\varvec{l}}_i + {\varvec{h}}\Big ), \end{aligned}$$

where ${\varvec{h}}$ is the point from Lemma 5.5. We show that $({\varvec{p}})_j = w_j$ if $j\in S_0$, and otherwise $({\varvec{p}})_j = 0$. Let j be a clause index from $S_0$. Since $A_C$ does not satisfy ${\widehat{K}}_j$, the jth coordinate of the points ${\varvec{l}}_1,\ldots ,{\varvec{l}}_n$ is $w_j$. Also, $({\varvec{h}})_j = w_j$ by Lemma 5.5. Thus, $({\varvec{p}})_j = w_j$. Consider now some clause index $j\in S_1$ and let $b \in [2]$ be the index of the point ${\varvec{l}}_b$ that corresponds to the single literal that satisfies ${\widehat{K}}_j$. Then, we have

$$\begin{aligned} ({\varvec{p}})_j= & {} \sum _{i=1}^n \frac{1}{n+1} \,({\varvec{l}}_i)_j + \frac{1}{n+1}\, ({\varvec{h}})_j \\= & {} \frac{1}{n+1} \,({\varvec{l}}_b)_j + \sum _{i=1, i\ne b}^n \frac{1}{n+1}\, ({\varvec{l}}_i)_j + \frac{1}{n+1}\, ({\varvec{h}})_j\\&= \frac{-n}{n+1}\, w_j + \frac{n}{n+1}\, w_j = 0. \end{aligned}$$

Finally, consider some clause index $j\in S_2$ and let $b_1, b_2$ be the indices of the two literals that satisfy ${\widehat{K}}_j$. Then, we obtain

$$\begin{aligned} ({\varvec{p}})_j&= \sum \limits _{i=1}^n \frac{1}{n+1} \,({\varvec{l}}_i)_j + \frac{1}{n+1}\, ({\varvec{h}})_j \\&= \frac{1}{n+1}\, ({\varvec{l}}_{b_1})_j +\frac{1}{n+1} \,({\varvec{l}}_{b_2})_j + \sum \limits _{i=1, i\notin \{b_1, b_2\}}^n \frac{1}{n+1}\, ({\varvec{l}}_i)_j + \frac{1}{n+1}\, ({\varvec{h}})_j \\&= \frac{-2n}{n+1}\, w_j + \frac{n-2}{n+1}\, w_j + \frac{n+2}{n+1}\, w_j = 0, \end{aligned}$$

and thus $\Vert {\varvec{p}}\Vert _1 = c_{I',A_C}$, as claimed. $\square$

5.3 The Global Search Nearest Colorful Polytope Problem

In the global search variant G-Ncp of the nearest colorful polytope problem, we are looking for a colorful choice C such that $\delta (C)$ is minimum over all possible colorful choices. The proof of Theorem 5.4 can be adapted easily to reduce 3Sat to G-Ncp.

Theorem 5.6

G-Ncp is np-hard.

Proof

Given a set of clauses $K_1,\dots ,K_d$, we set the weight of each clause to 1 and construct the same point sets as in the PLS-reduction. Additionally, we introduce for each clause $K_j$ a new helper color class $H'_j = \{{\varvec{h}}'_j\}$, where

$$\begin{aligned} ({\varvec{h}}'_i)_j = {\left\{ \begin{array}{ll} (d+1) \big ((2n+3) - \frac{d}{d+1}\big ), &{} \text {if } i=j,\text { and} \\ 1, &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Let now C be a colorful choice and let $A_C$ be the corresponding assignment. As in the PLS-reduction, for $k = 0, \dots , 3$, let $S_k$ contain all clauses that are satisfied by exactly k literals in the assignment $A_C$. Then, the following point ${\varvec{h}}$ is contained in the convex hull of the helper points:

$$\begin{aligned} {\varvec{h}}= \sum \limits _{i\in S_2} \frac{{\varvec{h}}_i}{d+1} + \sum \limits _{j\in S_3} \frac{{\varvec{h}}'_{j}}{d+1} + \Big (1-\frac{|S_2|+|S_3|}{d+1}\Big ) {\varvec{h}}_{d+1}. \end{aligned}$$

As above, we see that $({\varvec{h}})_j = 1$, if $j \in S_0 \cup S_1$, $({\varvec{h}})_j = n+2$, if $j \in S_2$, and $({\varvec{h}})_j = 2n+3$, if $j \in S_3$. Indeed, for $j \in S_0 \cup S_1$, we have:

$$\begin{aligned} ({\varvec{h}})_j= & {} \sum \limits _{i\in S_2} \frac{1}{d+1}\, ({\varvec{h}}_i)_j + \sum \limits _{i\in S_3} \frac{1}{d+1}\, ({\varvec{h}}'_i)_j + \Big (1-\frac{|S_2|+|S_3|}{d+1}\Big ) ({\varvec{h}}_{d+1})_j \\&{\mathop {=}\limits ^{j\notin S_2 \cup S_3}}&\sum \limits _{i\in S_2 \cup S_3} \frac{1}{d+1} + \Big (1-\frac{|S_2| + |S_3|}{d+1}\Big ) = 1. \end{aligned}$$

For $j \in S_2$, we have

$$\begin{aligned} ({\varvec{h}})_j&= \sum \limits _{i\in S_2} \frac{1}{d+1} \,({\varvec{h}}_i)_j + \sum \limits _{i\in S_3} \frac{1}{d+1}\, ({\varvec{h}}'_i)_j + \Big (1-\frac{|S_2|+|S_3|}{d+1}\Big ) ({\varvec{h}}_{d+1})_j \\&= ({\varvec{h}}_j)_j + \sum \limits _{i\in S_2 \setminus j} \frac{1}{d+1} + \sum \limits _{i\in S_3} \frac{1}{d+1} + \Big (1-\frac{|S_2|+|S_3|}{d+1}\Big ) \\&= \Big ((n+2) - \frac{d}{d+1}\Big ) + \frac{d}{d+1} = n+2, \end{aligned}$$

and for $j \in S_3$,

$$\begin{aligned} ({\varvec{h}})_j&= \sum \limits _{i\in S_2} \frac{1}{d+1}\, ({\varvec{h}}_i)_j + \sum \limits _{i\in S_3} \frac{1}{d+1} \,({\varvec{h}}'_i)_j + \Big (1-\frac{|S_2|+|S_3|}{d+1}\Big ) ({\varvec{h}}_{d+1})_j \\&= ({\varvec{h}}'_j)_j + \sum \limits _{i\in S_2 } \frac{1}{d+1} + \sum \limits _{i\in S_3 \setminus j} \frac{1}{d+1} + \Big (1-\frac{|S_2|+|S_3|}{d+1}\Big ) \\&= \Big ((2n+3) - \frac{d}{d+1}\Big ) + \frac{d}{d+1} = 2n+3. \end{aligned}$$

As before, the convex combination ${\varvec{p}}= \sum _{i=1}^n \frac{1}{n+1} {\varvec{l}}_i + \frac{1}{n+1} {\varvec{h}}$ results in a point in the convex hull of C whose distance to the origin is the number of unsatisfied clauses, where ${\varvec{l}}_i$ denotes the point from $X_i$ in C. Indeed, if ${\widehat{K}}_j$ is not satisfied, then all j-components in the sum are 1, and $({\varvec{p}})_j = 1$. If $j \in S_1$, then, as discussed above

$$\begin{aligned} ({\varvec{p}})_j = \frac{-n}{n+1} + \frac{n-1}{n+1} + \frac{1}{n+1} = 0. \end{aligned}$$

If $j \in S_2$, then

$$\begin{aligned} ({\varvec{p}})_j = \frac{-2n}{n+1} +\frac{n-2}{n+1} + \frac{n+2}{n+1}= 0, \end{aligned}$$

and if $j \in S_3$, then

$$\begin{aligned} ({\varvec{p}})_j = \frac{-3n}{n+1} +\frac{n-3}{n+1} + \frac{2n+3}{n+1}= 0. \end{aligned}$$

Together with (i) from the proof of Theorem 5.4, 3Sat can be decided by knowing a global optimum $C^\star$ to the Ncp problem: if $\delta (C^\star ) = 0$, $A_{C^\star }$ is a satisfying assignment. If not, there exists no satisfying assignment at all. $\square$

As mentioned above, we can adapt the proof of Theorem 5.6 to answer a question by Bárány and Onn [4].

Corollary 5.7

Let $C_1,\dots ,C_m\subset \mathbb {Q}^d$ be an input for G-Ncp. Then, G-Ncp remains NP-hard even if $m=d+1$.

Proof

Let F be a 3Sat formula with d clauses and n variables. As in the proof of Theorem 5.6, we construct $n+2d+1 =: d'+1$ point sets in $\mathbb {Q}^d$ such that there is a colorful choice that embraces the origin if and only if F is satisfiable. Since $d' > d$, we can lift the point sets to $\mathbb {Q}^{d'}$ by appending 0-coordinates. Then, we have $d'+1$ point sets such that there is a colorful choice that embraces the origin if and only if F is satisfiable. $\square$

6 Conclusion

We conclude with several interesting open problems.

• The algorithm in Theorem 3.7 computes in polynomial time a ${\varvec{0}}$-embracing $\lceil \varepsilon d \rceil$-colorful choice for any fixed $\varepsilon > 0$. A more careful analysis shows that the algorithm needs only $c_\varepsilon$ color classes, where $c_\varepsilon >0$ is a constant depending only on $\varepsilon$. Hence, the algorithm does not use its complete input. Can this be used to further improve the approximation guarantee?

• Is it possible to compute a ${\varvec{0}}$-embracing $\mathrm{o}(d)$-colorful choice in polynomial time and in particular, is it possible to compute a ${\varvec{0}}$-embracing $\mathrm{O}(1)$-colorful choice in polynomial time?

• On the other hand, can it be shown that computing a ${\varvec{0}}$-embracing $\mathrm{O}(1)$-colorful choice is as hard as computing a ${\varvec{0}}$-embracing 1-colorful choice?

• In Sect. 4, we show that many color classes help to find a ${\varvec{0}}$-embracing 1-colorful choice. Can a ${\varvec{0}}$-embracing 1-colorful choice be computed in polynomial time if we have $\text {poly}(d)$ color classes?