Bounds on the Number of Connected Components for Tropical Prevarieties

Abstract

For a tropical prevariety in ${\mathbb {R}}^n$ given by a system of k tropical polynomials in n variables with degrees at most d, we prove that its number of the connected components is less than ${k+7n-1 \atopwithdelims ()3n} \cdot \frac{d^{3n}}{k+n+1}$. On a number of 0-dimensional connected components a better bound ${k \atopwithdelims ()n} \cdot \frac{d^n}{k-n+1}$ is obtained, which extends the Bezout bound due to B. Sturmfels from the case $k=n$ to an arbitrary $k\ge n$. Also we show that the latter bound is close to sharp, in particular, the number of connected components can depend on k.

1 Introduction

Let a tropical prevariety $V\subset \mathbb {R}^n$ (see e.g. [18]) be given by k tropical polynomials $f_1,\dots ,f_k$ in n variables with the (tropical) degrees at most d. The principal motivation of this paper is to bound the number c of connected components of V. Recall (see e.g. [18]) that V is a polyhedral complex. The main result (Corollary 9.3) states the bound

$$\begin{aligned} c\le {k+7n-1 \atopwithdelims ()3n} \cdot \frac{d^{3n}}{k+n+1}. \end{aligned}$$

(1)

For the number of isolated points of V (being its 0-dimensional connected components) we obtain (Theorem 7.2) a better bound

$$\begin{aligned} {k \atopwithdelims ()n} \cdot \frac{d^n}{k-n+1}. \end{aligned}$$

(2)

It can be treated as a generalization of the Bezout inequality on the number of stable solutions (see [18, 22] and Sect. 5 below) proved in the case $k=n$ to the case of overdetermined (i.e. $k>n$) tropical systems. Recall that $k\ge n$ in order V to have an isolated point since the local codimension at any point of V is less or equal to k [4,5,6], see also Theorem 3.8. Moreover, the tropical Bezout Theorem [18] states that the number of stable solutions (counted with multiplicities) of n tropical polynomials $f_1,\dots ,f_n$ with degrees $d_1,\dots ,d_n$ respectively, equals $d_1\cdots d_n$.

In Sect. 8 we show that bound (2) is close to sharp by an explicit construction of tropical systems.

The observed phenomenon of dependency of the number of connected components on k in (1) and in (2) occurs similarly for real semialgebraic sets (moreover, for the sum of Betti numbers which strengthens the bounds established by Oleinik-Petrovskii, Milnor, Thom) [2], while due to a different reason.

Note that in the case of an algebraic variety given by a polynomial system $g_1=\dots =g_k=0$ where the degrees of polynomials in n variables do not exceed d, the sum of the degrees of the irreducible components of the variety is bounded by $d^n$, i.e. the latter bound does not depend on k. This holds because the variety remains the same if one replaces $g_1,\dots ,g_k$ by $n+1$ generic linear combinations of $g_1,\dots ,g_k$ (see e.g. [7, 12]).

Our conjecture is that the sum of Betti numbers of a tropical prevariety V is bounded by (1). In Theorems 6.7 and 6.8 one can find somewhat weaker bounds on the sum of Betti numbers.

The important technical tool to study a system of tropical polynomials (see Sect. 4) is the star table (exploited in [13, 14]) consisting of the set of monomials from the given tropical system in which the minimum is attained at a given point $v\in V$ (here a monomial is treated as a classical linear function). In these terms we define a generalized vertex v of V when the star table is maximal under inclusion. We produce a description of generalized vertices in terms of the exponents vectors of the starred monomials (Theorem 4.11). Then we prove that any connected component of a tropical prevariety given by a system of tropical polynomials of fixed degrees with all finite coefficients contains a generalized vertex (Theorem 6.1).

In Sect. 5 we study stable points of a tropical prevariety given by n tropical polynomials, and provide a criterion to be a stable point again in terms of the exponent vectors of the starred monomials (Theorem 5.10). This implies that a generalized vertex of V is a stable point of a suitable multisubset of $\{f_1,\dots ,f_k\}$, consisting of n elements (Theorem 6.2). The established results provide a slightly better bound than (1) in case of finite coefficients (Corollary 6.4).

To get the bound (2) we prove in Sect. 7 that an isolated point of V is a stable point of an appropriate subset consisting of n elements among $\{f_1,\dots ,f_k\}$ (Theorem 7.1). We emphasize that here we consider a subset, rather than a multisubset as in Theorem 6.2, this explains the difference between bounds (1) and (2).

In Sect. 9 we show that adding n extra variables and 2n extra tropical polynomials to $\{f_1,\dots ,f_k\}$ we get a compact tropical prevariety being homotopy equivalent to V. Thus, the problem of bounding the number of connected components and moreover, the sum of Betti numbers of V reduces to a compact tropical prevariety. Also in Sect. 9 we discuss systems of tropical polynomials with coefficients allowed to include infinity which completes the proof of the bounds (1).

2 Tropical Semi-ring and Tropical Prevarieties

Definition 2.1

Semi-fields $\mathbb {R}$ and $\mathbb {R}_{\infty }=\mathbb {R}\cup \{\infty \}$ endowed with operations $\oplus := \min ,\, \otimes := +,\, \oslash :=-$ are called tropical semi-rings with or without infinity correspondingly.

We will denote tropical semi-rings with or without infinity as $\mathbb {K}$ and $\mathbb {K}_{\infty }$ correspondingly.

We also will use the notation for a tropical power: $x^{\otimes i}:= x\otimes \cdots \otimes x$.

In this paper we will study tropical polynomials and at first we have to define a tropical monomial:

Definition 2.2

A tropical monomial Q is defined as $Q=a\otimes x_1^{\otimes i_1}\otimes \cdots \otimes x_n^{\otimes i_n} = a+i_1\cdot x_1+\cdots +i_n\cdot x_n$, its tropical degree is $i_1+\cdots +i_n$.

Note 2.3

As for classic monomials we will often omit multiplication sign when it is clear whether we speak about the tropical multiplication or the classic one. In addition, we will omit a multiplier of 0 as it is the neutral element of tropical multiplication.

Now we can define a tropical polynomial:

Definition 2.4

Tropical polynomial f is defined as

$$\begin{aligned} f=\bigoplus _j \big (a_j\otimes x_1^{\otimes i_{j1}}\otimes \cdots \otimes x_n^{\otimes i_{jn}}\big )=\min _j \{Q_j\}, \end{aligned}$$

where the tropical monomial $Q_j:= a_j\otimes x_1^{\otimes i_{j1}}\otimes \cdots \otimes x_n^{\otimes i_{jn}}$. The tropical degree of f is the maximum of the tropical degrees of its monomials $Q_j$.

We say that $x=(x_1,\dots ,x_n)\in \mathbb {R}_{\infty }^n$ is a tropical zero of f if at the point x either the minimum $\min _j \{Q_j(x)\}$ is attained for at least two different values of j when $\min _j \{Q_j(x)\}$ is finite or $Q_j(x) = \infty$ for all j. If $x\in \mathbb {R}^n$ we say that the tropical zero is finite.

If all the monomials with the tropical degree at most d are present at f we say that f of the tropical degree d has all its coefficients finite.

Then we define a tropical hypersurface:

Definition 2.5

The set of the tropical zeros in $\mathbb {R}^n$ of a tropical polynomial is called a tropical hypersurface.

Definition 2.6

A tropical prevariety is the intersection of a finite number of tropical hypersurfaces.

3 Hahn Series and Tropical Varieties

To introduce tropical varieties it will be convenient to use a generalization of Puiseux series known as Hahn (or Hahn–Mal’cev–Neumann) series (see [16]).

Definition 3.1

The field of Hahn series $K[[T^\Gamma ]]$ in the indeterminate T over a field K and with a value (ordered) group $\Gamma$ is the set of formal expressions of the form $f = \sum \nolimits _{e \in \Gamma }{c_eT^e}$ with $c_e \in K$ such that the support $\{e \in \Gamma : c_e \ne 0\}$ of f is well-ordered. The sum and the product of $f = \sum \nolimits _{e \in \Gamma }{c_eT^e}$ and $g = \sum \nolimits _{e \in \Gamma }{d_eT^e}$ are given by $f + g = \sum \nolimits _{e \in \Gamma }{(c_e + d_e)T^e}$ and $fg = \sum \nolimits _{e \in \Gamma }{\sum \nolimits _{e^{\prime } + e^{\prime \prime } = e} {c_{e^{\prime }} d_{e^{\prime \prime }} T^e}}$ (the sum $\sum \nolimits _{e^{\prime } + e^{\prime \prime } = e}c_{e^{\prime }} d_{e^{\prime \prime }}$ is finite as a well-ordered set could not contain infinite decreasing sequence).

To define a tropical variety we have to introduce the operation of the tropicalization.

Definition 3.2

The tropicalization of $x^{\prime } \in K[[T^\Gamma ]]$ is a point $x \in \Gamma \cup \{\infty \}$ equal to the least power of T in $x^{\prime }$ if $x^{\prime }$ is not equal to zero, or $\infty$ otherwise.

We will denote the operation of the tropicalization by $\mathrm{trop}$.

The tropicalization V of a variety $V^{\prime }$ over the field of Hahn series $K[[T^\Gamma ]]$ consists of the closure in the euclidean topology of the set of points $x \in \Gamma ^n$

for which there is a point $x^{\prime }=(x^{\prime }_1, x^{\prime }_2, \ldots x^{\prime }_n) \in V^{\prime }$ with $x^{\prime }_1 \ldots x^{\prime }_n \ne 0$, such that $x=(\mathrm{trop}(x^{\prime }_1), \mathrm{trop}(x^{\prime }_2), \ldots \mathrm{trop}(x^{\prime }_n))$. The set V is referred to as a tropical variety.

While any tropical hypersurface is a tropicalization of a hypersurface over the field of Hahn series $\mathbb {C}[[T^{\mathbb {R}}]]$ (cf. [8]) some tropical prevarieties do not correspond to any varieties over $\mathbb {C}[[T^{\mathbb {R}}]]$. For example a tropical prevariety given by the linear system

$$\begin{aligned} A = {\left\{ \begin{array}{ll} 0 \oplus x \oplus y \oplus z,\\ 0 \oplus x \oplus 1y \oplus 1z \end{array}\right. } \end{aligned}$$

is not a tropical variety. However, any tropical variety is a tropical prevariety and moreover the following theorem holds (see [5, 18]):

Theorem 3.3

For any variety $V^{\prime }$ given by a polynomial system $A^{\prime }$ in Hahn series $\mathbb {C}[[T^{\mathbb {R}}]]^n$ its tropicalization V is a tropical prevariety in $\mathbb {R}^n$, and V coincides with the intersection of tropical hypersurfaces being the tropicalizations of all the polynomials from the ideal generated by $A'$. Moreover, V equals the tropical prevariety determined by the intersection of a finite number of the tropicalizations of hypersurfaces provided by polynomials from the ideal generated by $A'$ (such a finite subset is called a tropical basis of the ideal).

To study tropical prevarieties we will use some properties of Hahn series.

Theorem 3.4

[17] For any algebraically closed field K and ordered divisible group $\Gamma$ the field of Hahn series $K[[T^{\Gamma }]]$ is algebraically closed.

Thus (see e.g. [11, 20]) we can apply Bezout’s theorem to $\mathbb {C}[[T^{\mathbb {R}}]]$.

Definition 3.5

Let n projective hypersurfaces be given in $\mathbb {P}^{n}(\mathbb {C}[[T^{\mathbb {R}}]])$ by n homogeneous polynomials in $n + 1$ variables. A point x is a stable intersection point of these hypersurfaces with multiplicity e if under a generic small perturbation of the coefficients of the given polynomials the corresponding hypersurfaces will have exactly e intersection points in a small neighborhood of x.

Theorem 3.6

(Bezout’s theorem) Let n projective hypersurfaces be given in $\mathbb {P}^{n} (\mathbb {C}[[T^{\mathbb {R}}]])$ by n homogeneous polynomials in $n + 1$ variables, of degrees $d_1, d_2, \cdots , d_n$. Then the number of stable intersection points of these hypersurfaces is equal to $d_1 d_2 \cdots d_n$.

Another important property of the field of Hahn series $\mathbb {C}[[T^{\mathbb {R}}]]$ implied by the fact that it is algebraically closed is

Theorem 3.7

( Dimension of intersection [20]) Let a variety $V'$ be given by a polynomial system A in n variables over the field of Hahn series $\mathbb {C}[[T^{\mathbb {R}}]]$. Then if the system A consists of k polynomials the codimension of each irreducible component of $V'$ is less or equal to k.

This properties of Hahn series are important for studying tropical varieties and prevarieties due to the following theorem:

Theorem 3.8

[4,5,6] For any irreducible variety $V^{\prime }$ of dimension m over the field of Hahn series $\mathbb {C}[[T^{\mathbb {R}}]]$ the local dimension at any point x of its tropicalization V is equal to m.

Remark 3.9

While Theorem 3.8 was known for varieties over the field of Puiseux series, the proof can be literally extended to Hahn series.

4 Generalized Vertices

To study tropical prevarieties it will be convenient to use the following definition of a vertex:

Definition 4.1

By a vertex of a tropical prevariety we will mean a point for which one can not choose a direction in such a way that there is a neighborhood of the point where prevariety can be represented as a generalized open ended cylinder with axis parallel to the chosen direction (a generalized open ended cylinder is a product of an arbitrary set and a line interval).

In addition, we will need a generalization of this definition, and at first we give a definition of a star table of a tropical system similar to one introduced in [14]:

Definition 4.2

Let A be a tropical polynomial system of k polynomials in n variables with the tropical degree d, and a point $x\in \mathbb {R}^n$. We associate with A a table $A^{*x}$ of the size $k \times {{n + d - 1} \atopwithdelims ()d}$ with the rows corresponding to the polynomials and the columns corresponding to all the possible monomials of degrees at most d in n variables. We put $*$ to the entry (i, j) iff the j-th monomial treated as a (classical) linear function attains a minimal value among all the monomials at the point x in i-th polynomial and we leave all others entries empty (see Example 4.3).

Example 4.3

Consider a tropical system

$$\begin{aligned} A = {\left\{ \begin{array}{ll} 0 \oplus 1x \oplus y, \\ 0 \oplus -2x \oplus -2y \oplus -2x^{\otimes 2} \oplus -3xy \oplus -1y^{\otimes 2}. \end{array}\right. } \end{aligned}$$

At the point $(-1,0)$ this system is equal to

$$\begin{aligned} A = {\left\{ \begin{array}{ll} 0 \oplus 0 \oplus 0 \\ 0 \oplus -3 \oplus -2 \oplus -4 \oplus -4 \oplus -1, \end{array}\right. } \end{aligned}$$

so

$$\begin{aligned} A^{*(-1,0)} = \Bigg [{\begin{matrix} 0 &{} x &{} y &{} x^{\otimes 2} &{} xy &{} y^{\otimes 2} \\ \hline \\ *&{}*&{}*&{}&{}&{}\\ &{}&{}&{}*&{}*&{} \end{matrix}}\Bigg ]. \end{aligned}$$

At the point (1, 0) this system is equal to

$$\begin{aligned} A = {\left\{ \begin{array}{ll} 0 \oplus 2 \oplus 0 \\ 0 \oplus -1 \oplus -2 \oplus 0 \oplus -2 \oplus -1, \end{array}\right. } \end{aligned}$$

so

$$\begin{aligned} A^{*(1,0)} = \Bigg [{\begin{matrix} 0 &{} x &{} y &{} x^{\otimes 2} &{} xy &{} y^{\otimes 2} \\ \hline \\ *&{}&{}*&{}&{}&{}\\ &{}&{}*&{}&{}*&{} \end{matrix}}\Bigg ]. \end{aligned}$$

At the point $(-2,-1)$ this system is equal to

$$\begin{aligned} A = {\left\{ \begin{array}{ll} 0 \oplus -1 \oplus -1 \\ 0 \oplus -4 \oplus -3 \oplus -6 \oplus -6 \oplus -3, \end{array}\right. } \end{aligned}$$

so

$$\begin{aligned} A^{*(-2,-1)} = \Bigg [{\begin{matrix} 0 &{} x &{} y &{} x^{\otimes 2} &{} xy &{} y^{\otimes 2} \\ \hline \\ &{}*&{}*&{}&{}&{}\\ &{}&{}&{}*&{}*&{} \end{matrix}}\Bigg ]. \end{aligned}$$

Observe that for any point y in an appropriate neighborhood of x the star table $A^{*y}$ is contained in $A^{*x}$. Note that a point x satisfies A iff each row of the table $A^{*x}$ contains at least two stars. All the local properties of the tropical prevariety can be expressed in terms of this table (see the next theorem). In the next section we will show how to test stability of a solution of a tropical system using this table (Theorem 5.10), for another example see [14] where the star table is used to calculate the local dimension of a linear prevariety.

Theorem 4.4

Let a tropical prevariety V be given by a tropical system A, and $y,z{\in }V$. If $A^{*y} = A^{*z}$ then there is an $\varepsilon$, such that the $\varepsilon$-neighborhood of the point y of V is homeomorphic to the $\varepsilon$-neighborhood of the point z of V, moreover this homeomorphism is given by a (linear) shift of the coordinates which sends y to x.

Proof

Let d be the maximal (tropical) degree of the polynomials in A and $x = (x_1, x_2, \ldots , x_n)$ be a set of variables of these polynomials. Let’s denote by $\Delta _y$ and $\Delta _z$ the minimal differences between the values of the starred and non-starred monomials from the same polynomials at the point y and the point z correspondingly. Let $\Delta =\min (\Delta _y, \Delta _z)$. Denote $\varepsilon =\frac{\Delta }{3d}$.

Now we will prove that $\varepsilon$ fits the requirements of the theorem. Let’s make a change of variables $x'_i=x_i-y_i$ which corresponds to a shift of tropical prevariety in such a way that y is shifted to 0. The resulting tropical system we denote by B. Let’s denote the shifted prevariety by W. Due to our choice of $\varepsilon$ in the $\varepsilon$-neighborhood of 0 only the monomials which are starred at 0 can be starred (they are not greater than $0+d\varepsilon =\frac{\Delta }{3}$, while others are not lesser than $\Delta - d\varepsilon =\frac{2\Delta }{3}$), so while studying B in the $\varepsilon$-neighborhood of 0 we can w.l.o.g. assume that all non-starred monomials are infinite. In particular, the $\varepsilon$-neighborhood of 0 in W is determined just by the starred monomials. Moreover w.l.o.g. we can assume that all the coefficients in the starred monomials in B are equal to zero, otherwise we could tropically multiply the corresponding polynomials to change the coefficients to zero (see Example 4.5).

Now if we repeat the same operation replacing all the occurrences of y by z we will obtain the system which will be the same as B up to the assumptions we made in the end of the previous paragraph. So, the $\varepsilon$-neighborhood of z can be obtained from the $\varepsilon$-neighborhood of y by a shift (as both of them can be obtained by a shift from the $\varepsilon$-neighborhood of 0 of W). $\square$

Example 4.5

Consider a system

$$\begin{aligned} {\left\{ \begin{array}{ll} 2x^{\otimes 2} \oplus x \oplus 0. \end{array}\right. } \end{aligned}$$

Assume that we want to study the prevariety given by this system in the neighborhood of the point $x = -2$. First we make a change of the variable $x' = x + 2$:

$$\begin{aligned} {\left\{ \begin{array}{ll} -2x'^{\otimes 2} \oplus -2x' \oplus 0, \end{array}\right. } \end{aligned}$$

then tropically multiply the polynomial by 2:

$$\begin{aligned} {\left\{ \begin{array}{ll} x'^{\otimes 2} \oplus x' \oplus 2. \end{array}\right. } \end{aligned}$$

And in the $\frac{1}{3}$-neighborhood of 0 this system can be replaced by:

$$\begin{aligned} {\left\{ \begin{array}{ll} x'^{\otimes 2} \oplus x'. \end{array}\right. } \end{aligned}$$

Now we can give a definition of a generalized vertex:

Definition 4.6

A point x is a generalized vertex of a tropical polynomial system A iff x satisfies A and the star table $A^{*x}$ is strictly maximal with respect to inclusion, i.e. for any other point $y \ne x$ the star table $A^{*y}$ does not contain $A^{*x}$.

Example 4.7

The point $(-2, -1)$ is not a generalized vertex for a system A from Example 4.3 as $A^{*(-1,0)}$ is greater than $A^{*(-2,-1)}$ with respect to inclusion.

Theorem 4.8

A point x is a generalized vertex of a tropical polynomial system A iff there is no vector along which the directional derivative of every starred monomial in $A^{*x}$ in every polynomial is the same (the starred monomials from different polynomials can have different directional derivatives, see Example 4.9), i. e. there is no line that passes through the point x along which we can move while preserving star table the same in some neighborhood of x.

Proof

• (1) First we prove, that if there is a vector along which the directional derivative of every starred monomial in $A^{*x}$ in every polynomial is the same, then x is not a generalized vertex. It’s so because if we will move from point x in the direction of this vector there will be a neighborhood where we will preserve the star table (so initial star table was not strictly maximal).

• (2) Now we prove the converse: if x is not a generalized vertex then there is a vector along which the directional derivative of every starred monomial in $A^{*x}$ in every polynomial is the same. If x is not a generalized vertex, then there is a point y whose star table $A^{*y}$ contains $A^{*x}$. The directional derivative along the vector $x- y$ will be the same in each polynomial for all the points whose star table is contained in $A^{*x}$, because the difference between these monomials’ values in the same polynomial is the same (the monomials are equal both in the point x and in the point y).$\square$

Example 4.9

Consider the system A from Example 4.3. The point $(-2, -1)$ is not a generalized vertex, because we can choose a vector (1, 1), and the directional derivatives of all the starred monomials in the first polynomial along the euclidean normalization of this vector will be the same and equal to $\frac{1}{\sqrt{2}}$, while the directional derivatives of the starred monomials in the second polynomial along this vector will be the same and equal to $\sqrt{2}$.

The points (1, 0) and $(-1,0)$ are generalized vertices because we can not find a vector with the required property.

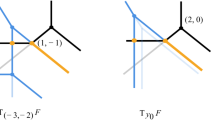
The corresponding prevariety is drawn in Fig. 1. The prevariety is depicted with the double lines, the first hypersurface is depicted with the dashed lines and the second one is depicted with the solid lines.

Fig. 1

Illustration for Example 4.9

Let’s define function $p_n$ which takes a tropical monomial in n variables $x_1,x_2,\cdots ,x_n$ as arguments and returns a vector in $\mathbb {R}^n$ in the following way: $p_n(cx_1^{\otimes a_1}x_2^{\otimes a_2} \ldots x_n^{\otimes a_n}) = (a_1, a_2, \ldots , a_n)$.

Let’s define function $v_n$ which takes two tropical monomials in n variables as arguments and returns a vector in $\mathbb {R}^n$ in the following way: $v_n(m_1, m_2) = p_n(m_2) - p_n(m_1)$.

Example 4.10

• $v_2(0, x_1) = (1, 0)$,

• $v_2(x_1^{\otimes 2}x_2, x_1x_2^{\otimes 2}) = (-1, 1)$,

• $v_3(0, 2x_1x_2x_3) = (1, 1, 1)$.

Now we can give a criterion of a point to be a generalized vertex in terms of the star table just of this point invoking also the function $v_n$.

Theorem 4.11

Assume that for a tropical polynomial system A of k polynomials in n variables with a solution at x we can choose 2n monomials $m_{i, j}, 1 \le i \le n, j=1,2$ with the following properties:

• one monomial can be chosen several times.

• the monomials $m_{i,1}$ and $m_{i,2}$ are marked with a star in $A^{*x}$ in the same line,

• the linear span of the vectors $v_n(m_{1,1}, m_{1,2}), v_n(m_{2,1},m_{2,2}), \ldots , v_n(m_{n,1}, m_{n,2})$ has the dimension equal to n.

Then x is a generalized vertex of this system, and conversely if x is a generalized vertex we can always choose 2n monomials in the described way.

Proof

• (1) First we prove the claim in one direction: if we can not choose 2n monomials with the required properties, then x is not a generalized vertex. If we could not choose 2n monomials with the required properties, then it would mean that the linear span of vectors $v_n(y, z)$ where y and z are arbitrary starred monomials from the same polynomial has the dimension (over all the polynomials) lesser than n. But if we choose a vector orthogonal to this linear span, the directional derivatives of any pair of starred monomials from the same polynomial along this vector will be the same (as the directional derivative of their difference will be equal to zero). And by Theorem 4.8 this means that x is not a generalized vertex.

• (2) Now we prove the converse: if x is not a generalized vertex then we can not choose 2n monomials with the required properties. By Theorem 4.8 we can choose a vector v along which all the directional derivatives of the starred monomials from the same polynomial will be the same (for all the polynomials from A). And this means that v is orthogonal to $v_n(y, z)$ for any monomials y and z starred in the same polynomial. But the latter contradicts to that the dimension of the linear span of the vectors $v_n(m_{1,1}, m_{1,2}), v_n(m_{2,1},m_{2,2}), \ldots , v_n(m_{n,1}, m_{n,2})$ equals n. $\square$

Generalized vertex is indeed a generalization of a vertex:

Theorem 4.12

If x is a vertex point of the prevariety V given by a tropical polynomial system A then x is a generalized vertex point of A.

Proof

Assume the contrary. Then by Theorem 4.8 we can choose a vector along which all the directional derivatives of the monomials starred in $A^{*x}$ will be the same. That means that if we choose a line passing through the point x and directed by this vector, then we can move along it in both directions while keeping the star table the same in some neighborhood of the point x. And by Theorem 4.4 in this neighborhood of the point x the prevariety V is a generalized open-ended cylinder. $\square$

However, the converse is not true:

Example 4.13

For the system of the tropical polynomials

$$\begin{aligned} {\left\{ \begin{array}{ll} 0 \oplus x \oplus y \oplus x^{\otimes 2}y \oplus xy^{\otimes 2}, \\ 0 \oplus x \oplus xy^{\otimes 2} \oplus x^{\otimes 4}y^{\otimes 3} \oplus x^{\otimes 4}y^{\otimes 5}, \\ 0 \oplus y \oplus yx^{\otimes 2} \oplus y^{\otimes 4}x^{\otimes 3} \oplus y^{\otimes 4}x^{\otimes 5}, \end{array}\right. } \end{aligned}$$

0 is a generalized vertex, but it is not a vertex [this prevariety is equal to the line directed by the vector $(-1,1)$].

5 Stability of Solutions Criteria

In this paper it will be convenient to use the following definition:

Definition 5.1

By the amplitude of a perturbation we will denote the maximal difference between the corresponding finite coefficients of the initial system and the perturbed one (the infinite coefficients are not perturbed).

In this section we always consider tropical system of n equations in n variables.

Following Sturmfels, and others [18] we will use the following definition of stability:

Definition 5.2

A point x is a stable point of a multiplicity s of a tropical polynomial system A of n equations in n variables if s is the maximal number of points (provided, there is a finite number of points) in a neighborhood of x of a tropical prevariety given by a sufficiently small perturbation of the system A.

Our results will be heavily based on the tropical Bezout’s equality, which states the following:

Theorem 5.3

(Tropical Bezout’s Equality [18]) Every n tropical polynomials with finite coefficients in n variables have D stable finite solutions counted with the multiplicities where D is the product of the degrees of the given polynomials.

Remark 5.4

For tropical polynomials not necessary with finite coefficients the sum of the multiplicities of the stable finite solutions does not exceed D [3, 21]. Moreover, in the latter papers the stronger bounds in terms of the Minkowski mixed volumes are provided.

As it was mentioned by Tabera [22] from this theorem the following property of stable points of a tropical prevariety can be obtained:

Theorem 5.5

Given n tropical hypersurfaces in n-dimensional space the stable points of the prevariety being their intersection form a well-defined set that varies continuously under perturbations of the given hypersurfaces.

In this section we will always consider systems with finite coefficients (see Sect. 2), unless we set some of the coefficients to infinity explicitly.

For the effective usage of Theorems 5.3 and 5.5 we have to introduce several simple criteria of stability. While proving theorems we will often w. l. o. g. study stability at point 0, and we will assume all the minimal coefficients (i. e. the coefficients of the starred monomials in $A^{*0}$) to be equal to 0 (this specific case can be obtained from the general case by the linear change of variables to shift the point under consideration to 0 and by the tropical multiplication of the equations by constants, see Example 4.5).

Theorem 5.6

Given a tropical polynomial system A with a solution in x, let us replace all the coefficients of the monomials which are starred in $A^{*x}$ by an arbitrary set of real numbers and the rest of the coefficients by the infinity (the resulting system denote by C). The point x is a stable solution of A iff for any set of the chosen real numbers the system C has a finite tropical solution.

Example 5.7

Consider a tropical system:

$$\begin{aligned} {\left\{ \begin{array}{ll} 0 \oplus 3x \oplus 0xy \oplus 0x^{\otimes 2}, \\ 3 \oplus 0x \oplus 0y^{\otimes 3}. \end{array}\right. } \end{aligned}$$

0 is a stable solution of this system as the system:

$$\begin{aligned} {\left\{ \begin{array}{ll} a_1 \oplus a_2xy \oplus a_3x^{\otimes 2}, \\ a_4x \oplus a_5y^{\otimes 3}, \end{array}\right. } \end{aligned}$$

has a finite solution for any reals $a_1, a_2, a_3, a_4, a_5$.

Proof

W. l. o. g. we can assume that x is zero and the coefficients of all the starred monomials in $A^{*0}$ are equal to 0.

Let d be the maximal tropical degree of the polynomials in the system A and let the smallest nonzero coefficient in A be equal to $\Delta$.

• (1) First we prove in one direction: if 0 is a stable point of A, then we can find a finite solution of C for any set of the coefficients taken as in the theorem. We will prove that for a fixed set of the coefficients there is a solution. W. l. o. g. we can assume that all the coefficients in C are positive (otherwise, we can tropically multiply the equations by a constant). Let the greatest (finite) coefficient in C be equal to M. As 0 is a stable solution of A we can choose $\delta$ with the following properties:

  • $0< \delta < \frac{\Delta }{4d}$,

  • for any perturbation of the coefficients of A with an amplitude less or equal to $\delta$ there will be a stable solution in the $\frac{\Delta }{4d}$-neighborhood of 0.

  Let’s consider a perturbation B of A with nonzero coefficients unchanged and zero coefficients replaced by the corresponding coefficients from C multiplied by $\frac{\delta }{M}$.

  By our choice of $\delta$ we can find a solution y of B in the $\frac{\Delta }{4d}$-neighborhood of 0. The non-starred monomials of A can not be minimal in this solution as they are too large. Indeed, as the coefficients change is not greater than $\delta$ and the solution coordinates are less than $\frac{\Delta }{4d}$ the value of any starred monomial of A after the perturbation in y is not greater than $\delta +d\frac{\Delta }{4d}<\frac{\Delta }{2}$, while the value of any non-starred monomial of A in y, after the perturbation is at least $\Delta -\delta -d\frac{\Delta }{4d}>\frac{\Delta }{2}$.

  If we classically multiply the solution and the coefficients of the equation from B by $\frac{M}{\delta }$, the point y will be a solution for the multiplied system, and if we change all the coefficients which were nonzero by the infinity, the solution still remains to be a solution as all the monomials we have changed were not minimal. So we have found a solution for C.

• (2) Now we prove the converse: if we can find a solution of a system C for any replacement of the coefficients then 0 is a stable point. We will prove that we can choose such a monotone function p that for any perturbation with an amplitude $\delta <\mathrm{{min}}\big (p^{-1}\big (\frac{\Delta }{4d}\big ),\frac{\Delta }{4d}\big )$ there is a solution in $p(\delta )$-neighborhood of 0. Let’s denote the perturbed system by E.

  Replace by the infinity all the monomials in E which are nonzero in the initial system A. By our assumption the resulting system will have a solution, hence an appropriate system L of linear equations and inequalities determined by the monomials of E has a real solution. Observe that L has integral coefficients at the variables and the constant part bounded by 2M, where M is the maximal coefficient of E. Therefore, the system L has a real solution with the absolute value bounded by $2M n! d^n$ due to the Cramer’s rule. So we can choose $p(\delta ) = 2\delta n! d^n$.

  This solution will be a solution of E, as its monomials corresponding to the non-starred monomials of A are too large to be minimal (as the coefficients change is not greater than $\delta$ and the solution coordinates are less than $p(\delta )$, the value of a monomial which was starred in $A^{*0}$ after the perturbation in the new solution point is at most $\delta +dp(\delta )<\frac{\Delta }{2}$ and the value of a non-starred monomial after the perturbation in the new solution point is at least $\Delta -\delta -dp(\delta )>\frac{\Delta }{2}$). For any small perturbation we have found a solution in a neighborhood of 0, so 0 is a stable point.$\square$

Using this theorem we can prove the following lemma:

Lemma 5.8

If x is a stable solution of a tropical system A, then for any tropical system F and a point y, if $F^{*y} = A^{*x}$, then y is a stable point of F.

Proof

W. l. o. g. we can assume that x and y are equal to 0, and that the coefficients of the monomials starred in $A^{*0}$ and $F^{*0}$ are equal to zero.

As 0 is a stable point of A, by Theorem 5.6 if we set all the coefficients in the monomials which are non-starred in $A^{*0}$ to the infinity and replace all the coefficients of the starred monomials by arbitrary real values the obtained system C will have a solution.

But the result of the replacement (the system C) is the same for systems A and F, so if in the system F we set all the coefficients in the monomials which are non-starred in $F^{*0}$ to the infinity and replace all the coefficients of the starred monomials by arbitrary real values the obtained system will have a solution. And by Theorem 5.6 this means that 0 is a stable solution of F. $\square$

This proposition can be strengthened to the following theorem:

Theorem 5.9

If x is a stable solution of a tropical system A, then for any tropical system F and point y, if $F^{*y}$ contains $A^{*x}$, then y is a stable point of F.

Proof

W. l. o. g. we can assume that x and y are equal to 0, and that the coefficients of the monomials starred in $A^{*0}$ and $F^{*0}$ are equal to zero.

Due to the Theorems 5.5 and 5.3 we can refer to a stable points movement under a parameter perturbation. We will prove that if we change one of the nonzero coefficients to zero (the resulting system we denote by G), still 0 remains a stable solution of G. The rest will immediately follow from Lemma 5.8. We will prove by contradiction. Let 0 be an unstable solution of G.

Let $\Delta$ be a minimal distance from 0 to stable solutions of G.

We can choose $\varepsilon > 0$ such that if we perturb G with an amplitude less than $\varepsilon$ then every stable solution will move by a distance less than $\Delta$. Now consider a perturbation of G with a new zero coefficient replaced by $\varepsilon$ and other coefficients unchanged. By Lemma 5.8 the perturbed system has 0 as a stable solution, but by the choice of $\varepsilon$ we get a contradiction as no stable solution could move to 0. $\square$

Now we can formulate the last criterion of stability we need (we will use functions $v_n$ defined in Sect. 4):

Theorem 5.10

Assume that for a tropical polynomial system A of n equations in n variables with a solution at x we can choose 2n monomials $m_{i, j}, 1 \le i \le n, j=1,2$ with the following properties:

• the monomials $m_{i,1}$ and $m_{i,2}$ are from i-th polynomial and they are starred in $A^{*x}$,

• the linear span of the vectors $v_n(m_{1,1}, m_{1,2}), v_n(m_{2,1},m_{2,2}), \ldots , v_n(m_{n,1}, m_{n,2})$ has the dimension equal to n.

Then x is a stable solution of system A, conversely if x is a stable solution we can always choose 2n monomials in the described way.

Proof

W. l. o. g. we can assume that x is equal to 0, and that the coefficients of the monomials starred in $A^{*0}$ are equal to zero.

• (1) First we will prove in one direction: if we could find monomials with the described properties, then 0 is a stable point. By Theorem 5.9 if we prove that 0 is a stable point of a system with all the coefficients of the monomials except $m_{i, j}, 1 \le i \le n, j=1,2$, replaced by say 1 (this system will have only 2 monomials with the zero coefficients in each equation), then 0 is a stable point of the system A. And by Theorem 5.6 0 is stable iff the system with the coefficients in the nonzero monomials replaced by the infinity will have a solution for any set of real coefficients replacing zeros. Now we can notice that a tropical polynomial system with two monomials in each polynomial is just a classical linear system (see Example 5.11) and the restriction on the monomials we imposed is just a criterion of this system to have rank n. So as required this system will have a solution for any set of coefficients.

• (2) Now we will prove the converse: if we could not find monomials with the described properties, then 0 is not a stable point. We will prove that we can replace all the nonzero coefficients by the infinity and the zero coefficients by arbitrary real numbers in such a way that the obtained system will have no solution and thus, by Theorem 5.6 0 is not a stable point.

  Let’s replace all the zero coefficients by arbitrary real numbers which are linearly independent over $\mathbb {Q}$ and the nonzero coefficients by the infinity. Consider a solution of this system. Let’s choose $f_{i, j}, j=1,2$ as the pairs of the starred monomials from i-th equation (if there are more than two starred monomials, we will choose just two arbitrary among them). The linear span of $v_n(f_{i,1}, f_{i,2}), 1 \le i \le n$ has the dimension lesser than n by the assumption, so the system of classical linear equations, expressing that $f_{i,1}=f_{i,2}, 1 \le i \le n$ will have the rank lesser than n. This system has rational coefficients of the variables, while free terms from its’ equations are linear independent over $\mathbb {Q}$, so it has no solutions, as otherwise a rational linear dependency between these constants could be found. So we come to a contradiction and this means that 0 is not a stable point. $\square$

Note that Theorems 4.11 and 5.10 entail that any stable solution is a generalized vertex.

Example 5.11

The tropical polynomial system:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1x_2 \oplus x_1^{\otimes 3}, \\ 6x_1^{\otimes 5} \oplus 4x_2^{\otimes 2}, \end{array}\right. } \end{aligned}$$

is equivalent to the classical linear system:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1 + x_2 = 3x_1, \\ 6 + 5x_1 = 4 + 2x_2. \end{array}\right. } \end{aligned}$$

The criterion from Theorem 5.10 of a point being a stable solution of a tropical system will be used further in our paper. In fact, this criterion can be tested in the polynomial time, by means of an algorithm which produces a maximal rank subset of an intersection of two matroids, see e.g. [1, 19], cf. also below the proof of Theorem 7.1.

6 Estimating the Number of Connected Components for Tropical Systems with Finite Coefficients

Using the theorems from Sect. 5 we can bound the number of connected components of a tropical prevariety.

As in the previous section we assume that all the coefficients in a tropical system are finite.

At first we will show that every connected component contains at least one generalized vertex.

Theorem 6.1

If a tropical prevariety V is given by a tropical polynomial system A with finite coefficients, then in any connected component of V there is at least one generalized vertex.

Proof

Consider a point x of V. If it is not a generalized vertex then by Theorem 4.8 there is a vector along which all the directional derivatives of starred monomials in each polynomial are the same. Let’s look at the star table while moving from the point x forward and backward along this vector. In some neighborhood of x the star table will not change, but at some point a new star has to appear (as the coefficients of A are finite all the monomials are present, so there will be at least one non-starred monomial whose derivative along the chosen vector differs from the derivatives of the starred monomials in the same polynomial, as there is no vector along which the derivatives of all the monomials are the same). Let’s choose this point as a new x. By this procedure we have increased the number of stars in $A^{*x}$. Now we can repeat the described process. But as there is a finite number of cells in the star table, we can’t repeat this process up to infinity, so at some step the chosen point x must be a generalized vertex. $\square$

To estimate the number of the generalized vertices we will prove the following theorem:

Theorem 6.2

For any generalized vertex x of a tropical polynomial system in n variables we can choose a multiset of n polynomials from this system in such a way that x is a stable solution for a tropical system given by the chosen polynomials (one polynomial can be chosen several times). Moreover, if there were $k \ge n$ polynomials in the initial system, then we can choose at least $k - n + 1$ different multisets of n polynomials with the described properties.

Proof

The existence of one multiset with the described properties immediately follows from Theorems 4.11 and 5.10.

The second part of the theorem can be proved in the following way: consider a multiset $\{p_1, p_2, \ldots , p_n\}$, of n polynomials with the described properties. As x is a stable point of these polynomials we can choose a set of monomials $m_{i,j}, 1\le i\le n, j=1,2$ as described in Theorem 5.10. Now we associate with each polynomial one vector: $a_i=v_n(m_{i,1},m_{i,2})$. By Theorem 5.10 these vectors form a basis in $\mathbb {R}^n$. Now we will prove that for any polynomial $p_{n+1}$ which is not present in the multiset $\{p_1,p_2,\ldots ,p_n\}$ we can choose a polynomial $p_i$ in such a way that x will be a stable point of the system given by the polynomials $\{p_1,p_2,\ldots ,p_{i-1},p_{i+1},\ldots ,p_n,p_{n+1}\}$. As x is a solution of $p_{n+1}$ there are at least two monomials which are starred in $p_{n+1}$ at the point x. Let’s denote them by $m_{n+1,1}$ and $m_{n+1,2}$ (if there are more than two starred monomials in $p_{n+1}$ at the point x we will choose an arbitrary pair of the starred monomials). As $\{a_1, a_2, \ldots , a_n\}$ is a basis, there should be a linear combination of this vectors which will be equal to $v_n(m_{n+1,1},m_{n+1,2})$, this means that $v_n(m_{n+1,1},m_{n+1,2})=ca_i+L(a_1,a_2,\ldots ,a_{i-1},a_{i+1},\ldots ,a_n)$ for some $c\ne 0$ and some $1 \le i \le n$, where L is a linear function. So $\{a_1,a_2,\ldots ,a_{i-1},a_{i+1},\cdots ,a_n,v_n(m_{n+1,1},m_{n+1,2})\}$ is a basis of $\mathbb {R}^n$, and by Theorem 5.10, this means that x is a stable point of the system of the polynomials $\{p_1,p_2,\ldots ,p_{i-1},p_{i+1},\ldots ,p_n,p_{n+1}\}$. As we can choose at least $k - n$ polynomials which are not included in the initial multiset, there are at least $k - n + 1$ multisets with the properties required in the theorem. $\square$

As a consequence from this theorem we can obtain a bound on the number of the generalized vertices:

Theorem 6.3

The number of the generalized vertices of a tropical prevariety in $\mathbb {R}^n$ given by k polynomials with the tropical degrees bounded by d and with finite coefficients is not greater than ${{k + n - 1} \atopwithdelims ()n} d^n$.

Proof

We can choose up to ${{k + n - 1} \atopwithdelims ()n}$ different multisets of equations and by Theorem 5.3 the system formed by any of these multisets has at most $d^n$ stable points. This implies the required bound. $\square$

By Theorem 6.1 we can obtain:

Corollary 6.4

The number of the connected components of a tropical prevariety in $\mathbb {R}^n$ given by k polynomials with the tropical degrees bounded by d and with finite coefficients is not greater than ${{k + n - 1} \atopwithdelims ()n} d^n$.

Remark 6.5

• (i) Theorem 6.3 holds for any tropical prevariety (allowing also infinite coefficients) due to Remark 5.4;

• (ii) Corollary 6.4 holds for any compact tropical prevariety (allowing also infinite coefficients) due to Theorem 4.12 because any compact connected component contains a vertex;

• (iii) The bounds in Theorem 6.3 and in Corollary 6.4 can be improved by ${{k + n - 1} \atopwithdelims ()n}\frac{d^n}{k - n + 1}$ when $k\ge n$ due to Theorem 6.2.

However, this bound is not sharp, and while it’s rather precise for considerably overdetermined system (in Theorem 8.1 we will show that for overdetermined systems a close bound can be achieved), for underdetermined systems a better bound can be proved:

Theorem 6.6

The number of the connected components of a tropical prevariety in $\mathbb {R}^n$ given by k polynomials with the tropical degrees bounded by d is not greater than ${{d + n} \atopwithdelims ()d}^{2k}$.

Proof

A tropical prevariety given by k tropical polynomials in n variables is a union of at most ${{d + n} \atopwithdelims ()d}^{2k}$ convex polyhedra, each of them given by a star table with exactly two stars in every row.

While this bound is not interesting for overdetermined system, for small k and d comparatively to n it can be much better than the bound from Corollary 6.4.

Now we can obtain a bound on the Betti numbers of a tropical prevariety. Recall that the discrete Morse’s theory states that the l-th Betti number of a compact tropical prevariety is bounded by the number of faces of the dimension l, see e. g. [9].

Theorem 6.7

For any $0\le l\le n$ the l-th Betti number of a compact tropical prevariety given by a system of k polynomials of maximal degree at most d in n variables does not exceed $\big ( {{k + n - 1} \atopwithdelims ()n} d^n\big )^{l+1}$.

Proof

This result follows from the fact that any l-dimensional face of a compact tropical prevariety contains at least $l + 1$ linearly independent vertices. In its turn, the number of vertices does not exceed ${{k + n - 1} \atopwithdelims ()n} d^n$ due to Theorems 6.3,  4.12, cf. Remark 6.5. $\square$

However, this result is far from sharp, for example for small d it can be improved by the bound on the number of faces for arrangements (an arrangement is a union of several hyperplanes, see e.g. [10])

Theorem 6.8

For any $0\le l\le n$ the l-th Betti number of a compact tropical prevariety given by a system of k polynomials of the maximal degree d in n variables does not exceed $(l+1)2^n \cdot {k {n+d \atopwithdelims ()n}^2 \atopwithdelims ()n}$

Proof

The number of l-dimensional faces in an arrangement can be estimated as $(l+1)2^n \cdot {m \atopwithdelims ()n}$ where n is the dimension and $m\ge 2n$ is the number of hyperplanes (see e.g. Buck’s formula in [10]). The set of the faces of a tropical prevariety is a subset of the faces of the arrangement of hyperplanes, where for every pair of monomials from the same polynomial we add a hyperplane where they are equal. Thus, we obtain the required bound (the number of monomials in each polynomial does not exceed ${n+d \atopwithdelims ()n}$).

$\square$

Remark 6.9

Observe that (unlike a tropical prevariety) a tropical variety can be compact only when it is finite.

7 Tropical Bezout Inequality for Overdetermined Systems

While the bound on the number of connected components obtained in Corollary 6.4 can be used as a bound on the number of isolated points, in this particular case it can be slightly improved.

Theorem 7.1

Given an overdetermined tropical polynomial system A of $k \ge n$ equations in n variables with an isolated solution at x we can always choose 2k monomials $m_{i,j}, 1 \le i \le k, 1 \le j \le 2$ with the following properties:

• monomials $m_{i,1}$ and $m_{i,2}$ are taken from i-th polynomial and starred in $A^{*x}$.

• the linear span of vectors $v_n(m_{1,1}, m_{1,2}), v_n(m_{2,1},m_{2,2}), \ldots , v_n(m_{k,1}, m_{k,2})$ has dimension equal to n.

Proof

Assume the contrary. W. l. o. g. we can assume that $x = 0$ (we can always shift a prevariety in such a way that it is).

Let $A=\{f_1,\dots ,f_k\}$. Consider a set P of all the vectors $v_n(m_1,m_2)\in \mathbb {R}^n$ where monomials $m_1,m_2$ are taken from $f_i$ for some $1\le i \le k$ being starred. W. l. o. g. one can assume that the coefficients at all the starred monomials vanish.

Introduce two matroids on P. The first matroid has the rank function $r_1$ equal the number of polynomials in A from which the monomials are picked. In other words, an independent set I consists of vectors of the form $v_n(m_{1,1}, m_{1,2}), v_n(m_{2,1},m_{2,2}), \ldots , v_n(m_{s,1}, m_{s,2})$ such that monomials $m_{j,1}, m_{j,2}$ are taken from $f_{i_j}$, and $i_1<\cdots <i_s$. Thus, $r_1(I)=s$. The second matroid has the rank function $r_2$ with respect to the usual linear independency.

Observe that the theorem claims that the intersection of these two matroids contains a subset with n elements (independent in both matroids).

Due to the Edmond’s theorem [19] the maximal cardinality of such subsets equals

$$\begin{aligned} \min _{U\subset P} \{r_1(U)+r_2(P\setminus U)\}. \end{aligned}$$

Hence, by the assumption, there exists $U\subset P$ for which $r_1(U)+r_2(P\setminus U) <n$. Denote $s:=r_1(U)$ and let U contain (a maximal independent set of) vectors $v_n(m_{j,1}, m_{j,2}),\, 1\le j\le s$, where $m_{j,1}, m_{j,2}$ being starred monomials in $f_{i_j}$ and $i_1<\cdots <i_s$. W. l. o. g. one can add to U all the vectors of this form from $f_{i_j},\, 1\le j\le s$.

Denote by $\mathcal {L}\subset \mathbb {R}^n$ the linear hull of all the vectors of the form $v_n(m_1,m_2)$ where $m_1,m_2$ being starred monomials from some polynomial $f_i$ with $i\not \in \{i_1,\dots ,i_s\}$. Then $r:=\dim \mathcal {L}= r_2(P \setminus U)<n-s$.

Choose a basis $v_n(m_{p_1},m_{q_1}),\dots ,v_n(m_{p_r},m_{q_r})$ in $\mathcal {L}$. Denote polynomials (binomials)

$$\begin{aligned} g_l:=m_{p_l}-m_{q_l}\in (\mathbb {C}[[T^{\mathbb {R}}]])[x_1,\dots ,x_n],\, 1\le l\le r. \end{aligned}$$

Clearly, $g_l(1,\dots ,1)=0,\, 1\le l\le r$.

Fix $1\le j\le s$ for the time being and let $f_{i_j}=\bigoplus _m c_m \bigotimes m$. Since 0 is a tropical zero of A, one can find among the coefficients at least two minima (recall that the minima equal zero). Pick one of these minima $c_{m_0}=0$. Consider a polynomial

$$\begin{aligned} h_j:=\sum _{m\ne m_0} T^{c_m}\cdot m - \Big (\sum _{m\ne m_0} T^{c_m}\Big )\cdot m_0 \in (\mathbb {C}[[T^{\mathbb {R}}]])[x_1,\dots ,x_n]. \end{aligned}$$

Then the tropicalization of $h_j$ coincides with $f_{i_j}$, and $h_j(1,\dots ,1)=0$.

Due to Theorems 3.7, 3.8 the tropicalization $V\subset \mathbb {R}^n$ of the variety in $(\mathbb {C}[[T^{\mathbb {R}}]]\setminus {0})^n$ given by $r+s$ polynomials $\{g_l,\, 1\le l\le r\}\cup \{h_j,\, 1\le j\le s\}$ has a local dimension at 0 greater or equal to $n-s-r\ge 1$. On the other hand, in an appropriate neighborhood of 0 V satisfies system A taking into the account that the vectors $v_n(m_{p_1},m_{q_1}),\dots ,v_n(m_{p_r},m_{q_r})$ constitute a basis in $\mathcal {L}$. This contradicts that 0 is an isolated zero of A. $\square$

The latter theorem leads to the desired bound on the number of 0-dimensional components of a tropical prevariety.

Theorem 7.2

The number of isolated solutions of an overdetermined tropical polynomial system of $k \ge n$ polynomials in n variables is not greater than $\frac{{k \atopwithdelims ()n}}{(k - n + 1)} D$, where D is the product of n greatest degrees of the given polynomials.

Proof

By Theorems 7.1 and 5.10 we can state that any isolated solution is a stable solution of some subsystem of the size n (by a suitable shift of variables we can always shift the solution to 0). There are less or equal than ${k \atopwithdelims ()n}$ subsystems and by Bezout’s equality (see Theorem 5.3 and Remark 5.4) each of them has at most D stable solutions. Moreover, each solution is counted at least $k - n + 1$ times (the reasoning is the same as in Theorem 6.2). $\square$

As we will show in the next section, this bound is close to sharp.

8 Lower Bounds on the Number of Isolated Tropical Solutions

In this section we will build an example, which shows that Theorem 7.2 in case of tropical polynomial systems is close to sharp. While we will omit some monomials (i.e. we will use infinite coefficients), an example like this can be built with finite coefficients only (replacing the infinite coefficients by sufficiently large real numbers).

Theorem 8.1

Given n one can build a series of tropical systems of $k(n-1), k \ge 3$ polynomials in $n \ge 2$ variables of degree $4d, d \ge 1$ in such a way that the number of isolated solutions of systems from this series is $2(k - 1)^{n - 1} d^n$.

Fig. 2

The hypersurface (the curve) $H_1$ given by the tropical polynomial $3 \oplus 1x_1 \oplus x_1x_2 \oplus 1x_2 \oplus x_1x_2^{\otimes 2} \oplus 2x_2^{\otimes 2}$ and its Newton’s polygon. $\alpha$ is equal to 2 and $\beta$ is equal to 3 in the picture

Proof

Consider a tropical polynomial system in 2 variables:

$$\begin{aligned} A= {\left\{ \begin{array}{ll} 3 \oplus 1x_1 \oplus x_1x_2 \oplus 1x_1 \oplus x_1x_2^{\otimes 2} \oplus 2x_2^{\otimes 2} \\ 3 \oplus 1x_1 \oplus 3x_1x_2 \oplus 4x_2 \oplus 6x_1x_2^{\otimes 2} \oplus 8x_2^{\otimes 2} \\ 3 \oplus 1x_1 \oplus 6x_1x_2 \oplus 7x_2 \oplus 12x_1x_2^{\otimes 2} \oplus 14x_2^{\otimes 2}\\ \cdots \\ 3 \oplus 1x_1 \oplus (3k - 3)x_1x_2 \oplus (3k -2)x_2 \oplus (6k - 6)x_1x_2^{\otimes 2} \oplus (6k - 4)x_2^{\otimes 2} \end{array}\right. } \end{aligned}$$

The graph of the hypersurface $H_1$ given by the first polynomial is depicted on Fig. 2. The prevariety (curve) $H_i$ of the i-th polynomial of A is obtained from $H_1$ by a vertical shift down by $3i-3$.

Therefore, the points ($\alpha$, $\beta - 3j$), $0 \le j \le k - 2$ are solutions of A.

Moreover, these points are isolated solutions since the prevariety of A consists of these points and of two vertical half-lines.

Now we construct a tropical system B in 2 variables consisting of k polynomials of degrees 4d for any $d \ge 1$. The Newton’s polygon of each of these polynomials is a square with the mesh 2d which is obtained from the $2 \times 2$ square depicted in Fig. 3 by replicating it $d^2$ times. The coefficients of these polynomials are chosen with suitable conditions imposed on the distances which follow. The curve of the first polynomial of B is depicted on Fig. 4. The curve consists of d horizontal layers of d hexagons each of a height and a width equal to 3 each obtained from the previous one by a vertical shift. We impose the condition that the first shift (which is equal $\delta - \kappa$) is greater than 3k. In a similar way the second shift $(\kappa - 3) - \nu$ is also greater than 3k and so on. The other polynomials are chosen in the way similar to system A: they give curves which are vertical shifts of the curve given by the first polynomial. The second curve is shifted down by 3, the third curve is shifted down by 6, $\ldots$, the k-th curve is shifted down by $3(k-1)$.

The solutions of B form d series of isolated points, each series consists of $2(k - 1)d$ points and of 2d half-lines. For each $0\le i\le d-1$ a series has the following isolated points: $(\gamma + 4i, \delta )$, $(\gamma + 4i + 1, \delta )$, $(\gamma + 4i, \delta - 3)$, $(\gamma + 4i + 1, \delta - 3)$, $\ldots$, $(\gamma + 4i, \delta - 3k + 3)$, $(\gamma + 4i + 1, \delta - 3k + 3)$; $(\gamma + 4i, (\kappa - 3) - 3)$, $(\gamma + 4i + 1, (\kappa - 3) - 3)$, $(\gamma + 4i, (\kappa - 3) - 6)$, $(\gamma + 4i + 1, (\kappa - 3) - 6)$, $\ldots$, $(\gamma + 4i, (\kappa - 3) - 3k + 3)$, $(\gamma + 4i + 1, (\kappa - 3) - 3k + 3)$; and so on.

Now consider a system $C_n$ in n variables which consists of $n-1$ copies of B such that in the l-th copy, $1\le l\le n-1$, the variable $x_2$ is replaced by $x_{l+1}$. The isolated solutions of the system $C_n$ form a n-dimensional lattice consisting of $2(k-1)^{n-1}d^n$ points (there are 2d series each with a fixed value of the coordinate $x_1$ containing $((k- 1)d)^{n-1}$ isolated points). $\square$

Fig. 3

Newton’s polygon used in Theorem 8.1

Fig. 4

Example for Theorem 8.1

Remark 8.2

The number of the solutions of the constructed system A in 2 variables consisting of k cubic tropical polynomials, is linear in k. In contrast, one can prove that a system in 2 variables consisting of an arbitrary number of quadratic tropical polynomials, has at most 72 solutions.

9 Compatification of Tropical Prevarieties

In this section we will show that for any tropical prevariety V we can build a compact tropical prevariety being homotopy equivalent to V. This technique can be used to reduce the problem of estimating the number of connected components of tropical prevarieties to the case of compact prevarieties.

We will use the following theorem:

Theorem 9.1

Given a tropical prevariety V we can find a constant s such that the intersection of V and a cube with the side equal to s and centered at the origin would be homotopy equivalent to V. In this theorem we allow the prevariety to be given by a system with infinite coefficients.

This theorem can be viewed as a simplification of Lemma 9 in [15], or it can be proved directly with the help of Cramer’s rule in the same way as it was used in Theorem 5.6.

Theorem 9.2

Consider a tropical prevariety V given by a tropical system A in n variables. We can add 2n extra variables and 4n extra polynomials which being added to the system A will form a system B that determines a compact tropical prevariety W being a homotopy equivalent to V.

Proof

Let 2s be a side of the cube from Theorem 9.1. For each variable $x_i$ we will add two variables: $u_i$ and $v_i$; and four tropical (linear) polynomials: $x_i \oplus u_i$, $x_i \oplus u_i \oplus s$, $v_i \oplus -s$ and $x_i \oplus v_i \oplus -s$. The first two polynomials will guarantee that $u_i = x_i \le s$, and the last two will guarantee that $x_i \ge v_i = -s$. Therefore, W is homeomorphic to $V\cap [-s,s]^n$. The prevariety W is compact and by Theorem 9.1 it is homotopy equivalent to V. While there are infinite coefficients in the added polynomials this is not an obstacle as one can replace all the infinite coefficients by $M + 2s^d$, where M is the maximal coefficient occurring in the polynomials from A and d is the maximal degree of the polynomials from A. No monomial with this coefficient $M + 2s^d$ could be minimal as the absolute values of all the variables are guaranteed to be less or equal than s. $\square$

The bound in Corollary 6.4 on the number of the connected components of a tropical prevariety is established for systems with finite coefficients because we used that a connected component contains a generalized vertex due to Theorem 6.1 [for compact prevarieties see Remark 6.5 (iii)]. However, Theorem 9.2 gives us the following generalizations to the case of arbitrary coefficients:

Corollary 9.3

The number of the connected components of a tropical prevariety given by k polynomials with the tropical degrees bounded by d and with allowed infinite coefficients is not greater than $\frac{d^{3n}}{k + n + 1} {{k + 7n - 1} \atopwithdelims ()3n}$.

The proof relies on Corollary 6.4 and on Remark 6.5 (iii).

Corollary 9.4

The l-th Betti number of a tropical prevariety does not exceed $\big ({{k+7n-1} \atopwithdelims ()3n}\cdot d^{3n}\big )^{l+1}.$

Follows from Theorem 6.7 and from Theorem 9.2.

Corollary 9.5

The l-th Betti number of a tropical prevariety does not exceed $(l+1)2^{3n}\cdot {{(k+4n)\cdot {3n+d \atopwithdelims ()3n}^2} \atopwithdelims ()3n}$

Follows from Theorem 6.8 and from Theorem 9.2.