A $t_k$ Inequality for Arrangements of Pseudolines

Abstract

Consider arrangements of n pseudolines in the real projective plane. Let $t_k$ denote the number of intersection points where exactly k pseudolines are incident. We present a new combinatorial inequality:

$$\begin{aligned} t_2+1.5t_3\ge 8+\sum _{k\ge 4}(2k-7.5)t_k, \end{aligned}$$

which holds if no more than $n-3$ pseudolines intersect at one point. It looks similar but is unrelated to the Hirzebruch inequality for arrangements of complex lines in the complex projective plane. Based on this linear inequality, we construct lower bounds for the number of regions via n and the maximal number of (pseudo)lines passing through one point.

1 Relations for $t_k$

By an arrangement of pseudolines we mean a finite collection of $n\ge 3$ smooth closed curves in the real projective plane $\mathbb {RP}^2$ such that

• Curves do not self-intersect;

• Curves intersect transversally at exactly one point;

• There is no point where all pseudolines of the arrangement are incident.

Let $t_k$, $2 \le k \le n-1$ denote the number of intersection points where exactly k pseudolines of the arrangement are incident. Each pseudoline of the arrangement is homotopically nontrivial and does not bound a disk in the plane $\mathbb {RP}^2$. Also, $t_n=0$.

Some known relations for values of $t_k$ are:

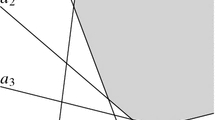
The Hirzebruch inequality holds for arrangements of complex lines in the complex projective plane; consequently, it also holds for arrangements of lines in the real projective plane. It is tight for several arrangements, e.g., for the real arrangements in Fig. 1 (in the right figure, three intersection points are at infinity). Tight examples of complex arrangements are presented in [8].

Fig. 1

$n=6,\,t_2=3,\,t_3=4;\quad n=9,\,t_2=6,\,t_3=4,t_4=3$

Some of these results were inspired and motivated by Sylvester’s conjecture ($t_2 \ge 1$) [14], the Dirac–Motzkin conjecture ($t_2 \ge [\frac{n}{2}]$) [3], and the orchard problem ($t_3 \le [n(n-3)/6]+1$, posed in [13]). One can find more problems related to values of $t_k$ in the reviews by Erdős and Purdy [5] and Nilakantan [11], and Grünbaum’s book [7].

2 Formulation of Main Results

2.1 Inequalities for $t_k$

Let us denote by $p_j$ the number of regions bounded by exactly j arcs of pseudolines.

Lemma 1

(Melchior [10]).

$$\begin{aligned} \sum _{k\ge 2} (3-k)t_k=3+\sum _{j\ge 3}(j-3)p_j. \end{aligned}$$

One may prove this using the Euler characteristic of the projective plane (see the next section for details). Since $p_j\ge 0$, we see that Melchior’s inequality follows from this.

Theorem 1

Suppose that $t_{n-1}=t_{n-2}=0$ for arrangements of n pseudolines. Then, we have

$$\begin{aligned}&\mathrm{{(a)}}\quad \,\,2t_2\le 1+ 3p_4+\sum _{j\ge 5}jp_j+\sum _{k\ge 3}(k-1.5)t_k;\\&\mathrm{{(b)}}\quad \quad \quad t_2+1.5t_3\ge 8+\sum _{k\ge 4}(2k-7.5)t_k. \end{aligned}$$

For convenience of reading, the proofs of Theorem 1(a), Lemma 1, and other lemmas are shifted to the next section. Now, we deduce Theorem 1(b) from Theorem 1(a) and Lemma 1. So, we have

$$\begin{aligned}&\sum _{k\ge 2}(9-3k)t_k=9+ 3p_4+\sum _{j\ge 5}(3j-9)p_j,\\&3p_4+\sum _{j\ge 5}jp_j\ge 2t_2-\sum _{k\ge 3}(k-1.5)t_k - 1, \end{aligned}$$

by Lemma 1 and Theorem 1(a), respectively. The inequalities

$$\begin{aligned}&\sum _{k\ge 2}(9-3k)t_k\ge 9+2t_2-\sum _{k\ge 3}(k-1.5)t_k - 1 \\&\quad \Longleftrightarrow t_2+1.5t_3 \ge 8+\sum _{k\ge 4}(2k-7.5)t_k \end{aligned}$$

follow from $3j-9\ge j$ for $j\ge 5$ and $p_j\ge 0$.

Remark 1

The inequalities of Theorem 1 are tight for and only for (up to combinatorial equivalence) the following arrangement of $n=7$ pseudolines [this will become clear after Lemma 4 and the proof of Theorem 1(a)]. Let each of the distinct points A and B have four incident pseudolines, with one of these pseudolines passing through both points. Then, $t_4=2$, $t_2=9$, and $t_3=t_k=0$ for $k\ge 5$. For other arrangements of pseudolines with $t_{n-1}=t_{n-2}=0$, we have

$$\begin{aligned} 2t_2\le 3p_4+\sum _{j\ge 5}jp_j+\sum _{k\ge 3}(k-1.5)t_k,\\ t_2+1.5t_3 \ge 9+\sum _{k\ge 4}(2k-7.5)t_k. \end{aligned}$$

Remark 2

The inequality in Theorem 1(b) looks similar to Hirzebruch’s inequality. However, neither of them follows from the other in the case of arrangements of real lines, when both inequalities hold.

2.2 Bounds for Number of Regions

Consider an arrangement of n pseudolines and denote by m, $m \le n-1$ the maximal number of pseudolines intersecting at one point. Let us associate with an arrangement a graph, drawn in the plane $\mathbb {RP}^2$. Vertices are intersection points, edges are arcs of pseudolines, and regions are connected components of the complement in the plane $\mathbb {RP}^2$ to the union of pseudolines. Let v, e, and f be the number of vertices, edges, and regions, respectively. The graph has no loops, because $t_n=0$. Now, we construct lower bounds for f, which depend on the numbers n and m. Since the characteristic of a real projective plane is 1, we obtain

$$\begin{aligned} v-e+f=1 \end{aligned}$$

by Euler’s formula. As

$$\begin{aligned} v=\sum _{k\ge 2} t_k,\quad \,e= \sum _{k\ge 2} kt_k \end{aligned}$$

and $t_k=0$ for $k>m$, then

$$\begin{aligned} f-1=\sum _{k=2}^{m}(k-1)t_k. \end{aligned}$$

The number of pairs of pseudolines is $\frac{n(n-1)}{2}$. Each pair of pseudolines intersects at exactly one point, and a point where k pseudolines are incident gives $\frac{k(k-1)}{2}$ such pairs. Thus, we have

$$\begin{aligned} n(n-1)=\sum _{k=2}^{m}k(k-1)t_k. \end{aligned}$$

Let us consider the general linear inequality

$$\begin{aligned} \sum _{k\ge 2}\alpha _kt_k\ge \alpha _0 \end{aligned}$$

(1)

for some real numbers $\alpha _0, \alpha _2, \alpha _3, \dots , \alpha _n$, possibly depending on n; For example, we may take Melchior’s or Hirzebruch’s inequality, or Theorem 1(b). Suppose that there exist coefficients $c_1=c_1(m,n)>0$ and $c_2=c_2(m,n)>0$ such that

$$\begin{aligned} c_1k(k-1)+c_2\alpha _k\le k-1 \end{aligned}$$

(2)

for all $2\le k \le m$. Let us multiply both sides of (2) by $t_k$ and sum up for $k=2, \dots , m$. Since $t_k\ge 0$, then

$$\begin{aligned}&c_1\sum _{k=2}^{m}k(k-1)t_k+c_2\sum _{k=2}^{m}\alpha _kt_k \le \sum _{k=2}^{m}(k-1)t_k \\&\quad \Longleftrightarrow c_1n(n-1)+c_2\sum _{k=2}^{m}\alpha _kt_k \le f-1. \end{aligned}$$

From the last inequality, inequality (1), and $c_2>0$, it follows that

$$\begin{aligned} f\ge c_1n(n-1)+c_2\alpha _0+1 \end{aligned}$$

(3)

for positive $c_1, c_2$, satisfying (2).

The lower bounds for f in the form (3) were firstly obtained by the author in [12]. This bound was applied to Melchior’s inequality to obtain a new proof of Martinov’s theorem [9], which determines all possible pairs (n, f). In contrast to [12], here we apply the prescribed construction to the inequalities of Hirzebruch and Theorem 1(b). Thus, we obtain the following bounds, which are stronger than in [12]:

Theorem 2

• (a) Suppose that $5 \le m<n-2$ for arrangements of lines in the real projective plane. Then, we have

  $$\begin{aligned} f\ge \frac{(3m-10)n^2+(m^2-6m+12)n}{m^2+3m-18}+1. \end{aligned}$$

• (b) Suppose that $12 \le m<n-2$ for arrangements of pseudolines in the real projective plane. Then, we have

  $$\begin{aligned} f\ge \frac{\big (3m-8.5\big )(n^2-n)+9m^2-21m+1}{m^2+3m-15}. \end{aligned}$$

3 Proofs of Theorems 1(a) and 2, and Auxiliary Lemmas

Let us recall that $t_n=0$ for arrangements of pseudolines. It follows that each arc of a pseudoline is incident to two different regions. Every pseudoline has at least two intersection points with other pseudolines of the arrangement. A region is bounded by arcs belonging to different pseudolines. Let us consider the graph associated with the arrangement. We call a vertex of the graph ordinary if it belongs to exactly two pseudolines (and, therefore, has degree 4 in the graph). An edge is called double ordinary if both of its endpoints are ordinary. We denote by $e_0$ the number of double ordinary edges. Let $e_1$ be the number of edges whose endpoints are both not ordinary. A region is called triangular if it is bounded by three edges; otherwise it is called nontriangular. Since $t_n=0$, we see that every nontriangular region is bounded by at least four edges. A region is called good if it is bounded by at least four edges and its boundary contains at least one ordinary vertex. Let $\gamma$ be an arbitrary good region, $e_0(\gamma )$ denote the number of double ordinary edges in the boundary of $\gamma$, $s(\gamma )$ denote the number of nonordinary vertices in the boundary of $\gamma$, and

Let

$$\begin{aligned} s=\sum _{\text {good}\,\gamma }s(\gamma ). \end{aligned}$$

We shall briefly say “a vertex belongs to the region” if the vertex belongs to the boundary of the region. A double ordinary edge is called perfect if it is incident to two good regions. In other words, both regions whose boundaries contain this edge are good. Let $e_p$ denote the number of perfect edges. A region is called excellent if it is bounded by four edges and all its vertices are ordinary (so, excellent regions are also good). We denote by $f_e$ the number of excellent regions. Let $\varphi$ denote the number of pairs $(\gamma ,\kappa )$ where $\gamma$ is an excellent region, $\kappa$ is a perfect edge, and $\kappa$ is incident to $\gamma$.

Let us denote by G the graph associated with the arrangement. For a nonordinary vertex V, let us delete all edges lying on pseudolines passing through V. The degrees of the vertices will change, and some vertices could disappear (which belong to at most one pseudoline, not passing through V). Let us denote by $G_{{V}}$ the obtained graph. Let us denote by $\gamma _{{V}}$ the region of the graph $G_{{V}}$ such that the vertex V belongs to the interior of $\gamma _{{V}}$.

For a nonordinary vertex $V \in G$, let us consider edges connecting V with nonordinary vertices of the graph G and good regions whose boundaries contain V; let q(V) denote the sum of the number of these edges and double the number of these regions. Suppose that V is connected with nonordinary vertices by $q_1$ edges and belongs to $q_2$ good regions, then $q(V)=q_1+2q_2$. Let q denote the sum of the numbers q(V) for all nonordinary vertices V of the graph G.

Proof of Lemma 1

The numbers of vertices v, edges e, and regions f can be found via $t_k$ and $p_j$ as follows:

$$\begin{aligned} v= & {} \sum _{k\ge 2}t_k, \qquad e=\sum _{k\ge 2}kt_k=0.5 \sum _{j\ge 3}jp_j, \\&f=1+\sum _{k\ge 2}(k-1)t_k=\sum _{j\ge 3}p_j. \end{aligned}$$

Let us substitute these equations into the Euler formula:

$$\begin{aligned} 3= & {} 3f-2e-e+3v=3\sum _{j\ge 3}p_j-\sum _{j\ge 3}jp_j-\sum _{k\ge 2}kt_k+3\sum _{k\ge 2}t_k\\= & {} \sum _{j\ge 3}(3-j)p_j+\sum _{k \ge 2}(3-k)t_k. \end{aligned}$$

$\square$

Lemma 2

• (a) Suppose that $t_{n-1}=0$, then every double ordinary edge is incident to at least one good region. Also,

  $$\begin{aligned} \sum _{\text {good}\,\gamma }e_0(\gamma )=e_0+e_p. \end{aligned}$$

• (b) Suppose that $t_{n-2}=t_{n-1}=0$, then every excellent region is incident to at least two perfect edges.

Proof

• (a) Let us assume the contrary, i.e., that there exists a double ordinary edge with endpoints A and B such that both regions incident to it are triangular. Let $l_1$ and $l_2$ be the pseudolines passing through one of the points A, B and not containing the edge AB. Let $l_1$ intersect $l_2$ at the point C. Then, both triangular regions which are incident to the edge AB contain C. Hence, $l_1$ could not have intersection points except A and C. As A is an ordinary point, it follows that C belongs to $n-1$ pseudolines, which contradicts $t_{n-1}=0$. So, every double ordinary edge is incident to at least one good region. Hence, there are $e_0-e_p$ double ordinary edges which are incident to exactly one good region, and $e_p$ double ordinary edges which are incident to two good regions.

• (b) Let us prove that each pair of opposite edges of an excellent region contains at least one perfect edge. Assume the contrary, i.e., that both edges AB and CD of an excellent region ABCD are not perfect, where A, B, C, D are vertices of G. Then, edges AB and CD are incident to triangular regions ABH and CDG. We denote by $l_1$ the pseudoline passing through points B and C. We denote by $l_2$ the pseudoline passing through points A and D. Then, the intersection point of $l_1$ and $l_2$ coincides with both points H and G. So $G=H$ and G belongs to $n-2$ pseudolines, all but two of which pass through points A, B and C, D. This is in contradiction with $t_{n-2}=0$. $\square$

Lemma 3

$$\begin{aligned} e_0=2t_2+e_1-\sum _{k\ge 3}kt_k. \end{aligned}$$

Proof

The graph contains $\sum _{k\ge 2}kt_k$ edges. There are $\sum _{k\ge 2}kt_k \ -e_0-e_1$ edges with one ordinary endpoint. Every ordinary vertex is an endpoint of four edges that have at least one ordinary endpoint. Thus, the total number of ordinary endpoints over all edges is

$$\begin{aligned} 4t_2=2e_0+\sum _{k\ge 2}kt_k \ - e_0-e_1. \end{aligned}$$

$\square$

Lemma 4

Suppose that $t_{n-1}=t_{n-2}=0$ and that there exist two points A, B such that each of the pseudolines in the arrangement contains at least one of them. Then, the statement of Theorem 1(a) holds:

$$\begin{aligned} 2t_2\le 1+ 3p_4+\sum _{j\ge 5}jp_j+\sum _{k\ge 3}(k-1.5)t_k. \end{aligned}$$

Proof

Let us denote by a and b the number of pseudolines passing through points A and B, respectively. We consider two cases.

In the first case, the arrangement does not contain a pseudoline passing through both points A and B. The inequalities $a\ge 3$ and $b \ge 3$ follow from $a+b=n$ and $t_{n-2}=0$. So, we have

$$\begin{aligned} t_2= & {} ab, \qquad \sum _{k\ge 3}(k-1.5)t_k=a+b-3, \\ p_4= & {} ab-a-b+3, \qquad p_j=0 \quad \text {for} \quad j\ge 5. \end{aligned}$$

In the second case, the arrangement contains a pseudoline passing through both of the points A and B. The inequalities $a\ge 4$ and $b \ge 4$ follow from $a+b=n+1$ and $t_{n-2}=0$. So, we have

$$\begin{aligned} t_2= & {} ab-a-b+1, \quad \sum _{k\ge 3} (k-1.5)t_k=a+b-3,\\ p_4= & {} ab-2a-2b+4, \qquad p_j=0 \quad \text {for} \quad j\ge 5. \end{aligned}$$

Now, it is easy to check that the required inequality holds in the first and second cases, for $a\ge 3, b \ge 3$ and $a\ge 4, b \ge 4$, respectively. $\square$

Lemma 5

Suppose that a good region $\gamma$ is bounded by j edges. Then,

$$\begin{aligned} s(\gamma )\le & {} j-1-e_0(\gamma )+\delta (\gamma ), \end{aligned}$$

(4)

$$\begin{aligned} s\le & {} \sum _{j\ge 4}(j-1)p_j+\sum _{\text {good}\ \gamma }(\delta (\gamma )-e_0(\gamma )). \end{aligned}$$

(5)

Proof

Let us consider three cases.

• (i) $e_0(\gamma )=0$. Then $s(\gamma )\le j-1$, because the boundary of $\gamma$ contains an ordinary point.

• (ii) $e_0(\gamma )=j$. Then $s(\gamma )=0$ and $\delta (\gamma )=1$.

• (iii) $0<e_0(\gamma )<j$. Let us consider the boundary of $\gamma$ consisting of j edges. Let the double ordinary edges in the boundary of $\gamma$ determine $z(\gamma )$ connected components in the boundary of $\gamma$, where the boundary is considered a separate topological space, homeomorphic to a circle. So, each connected component is a union of consecutive double ordinary edges. From $0<e_0(\gamma )<j$ it follows that $z(\gamma )\ge 1$ and that each connected component is homeomorphic to a segment. So, in each connected component, the number of vertices exceeds the number of edges by one. Hence, the boundary of $\gamma$ contains at least $e_0(\gamma )+z(\gamma )$ ordinary vertices. Since $z(\gamma )\ge 1$, then $s(\gamma )\le j-1-e_0(\gamma )$. Summing up (4) for all good regions $\gamma$, we get (5).

$\square$

Lemma 6

Suppose that $t_n=t_{n-1}=0$. Then,

$$\begin{aligned} s\le 3p_4-e_0+\sum _{j\ge 5}jp_j. \end{aligned}$$

Proof

There are $\sum _{\text {good} \ \gamma } \delta (\gamma )$ good regions, all vertices of which are ordinary. So,

$$\begin{aligned} \sum _{\text {good}\,\gamma }\delta (\gamma ) \le f_e+\sum _{j\ge 5}p_j. \end{aligned}$$

(6)

By Lemma 2(b), every excellent region is incident to at least two perfect edges, so $\varphi \ge 2f_e$. Every perfect edge is incident to at most two excellent regions, so $2e_p\ge \varphi$. Hence, $e_p\ge f_e$. The required inequality follows from Lemma 2(a) and inequalities (5), (6), and $e_p\ge f_e$. $\square$

Lemma 7

Suppose that there are no two points such that every pseudoline of the arrangement passes through at least one of them. Then, for every nonordinary vertex V, at least one of the following statements holds:

• (a) There are at least three edges of the graph G connecting V with the vertices of $\gamma _{{V}}$.

• (b) There are two edges of the graph G connecting V with the vertices of $\gamma _{{V}}$, and V is the vertex of a good region of the graph G.

• (c) V is the vertex of at least two good regions of the graph G.

Proof

The graph $G_{{V}}$ has at least two vertices for every vertex V. Each region of the graph $G_{{V}}$ is bounded by at least three edges of $G_{{V}}$ for every vertex V. Suppose that the vertex V is not connected by an edge of the graph G with some vertex U of the region $\gamma _{{V}}$. Then, U and V are vertices of some region $\gamma _{U,V} \subset \gamma _{{V}}$ of the graph G. The region $\gamma _{U,V}$ is bounded by at least four edges of the graph G. If $\gamma _{U,V}$ is not good, then all its vertices except V are vertices of the region $\gamma _{{V}}$, and so there are at least two edges of the graph G connecting V with the vertices of $\gamma _{{V}}$. If statement (a) is false for a vertex V, then one of the following cases holds:

• (1) V is connected by edges of the graph G with exactly two vertices of the region $\gamma _{V}$.

• (2) V is connected by edges of the graph G with at most one vertex of the region $\gamma _{V}$.

Case 1 Let these two vertices be $U_1$ and $U_2$.

Subcase 1.1 The points $U_1, U_2, V$ do not belong to one pseudoline of the arrangement. Let $W_1$ and $W_2$ be the intersection points of the boundary of $\gamma _{V}$ and the pseudolines passing through $V, U_1$ and $V, U_2$, respectively (so $W_1$ and $W_2$ are ordinary vertices of G). Then, on the part $U_1W_2W_1$ of the boundary of $\gamma _{V}$, there is at least one vertex U of $\gamma _{V}$ [otherwise we would have that the points $U_1, W_2, W_1$ belong to a pseudoline of the arrangement, intersecting the pseudoline $(U_1, V, W_1)$ at two points]. Then, U and V are vertices of some good region $\gamma _{U,V} \subset \gamma _{{V}}$ of the graph G, and we obtain statement (b).

Subcase 1.2 The points $U_1, U_2, V$ belong to one pseudoline of the arrangement. Points $U_1$ and $U_2$ divide the boundary of $\gamma _{V}$ into two open parts. Each part contains at least one vertex of $\gamma _{V}$ (disjoint from $U_1$ and $U_2$) and two ordinary vertices of graph G. So, in the graph G there are at least two good regions with vertex V and we obtain statements (b) and (c).

Case 2

Subcase 2.1 Suppose that the vertex V is connected by an edge of the graph G with a vertex U in the boundary of region $\gamma _{V}$. The pseudoline passing through points V and U divides the region $\gamma _{V}$ into two parts. Each of these parts contains at least one vertex of the region $\gamma _{V}$, disjoint from U. It follows that each part contains at least one good region for the graph G, so that V is a vertex of this good region.

Subcase 2.2 Suppose that V is not connected by an edge of the graph G with vertices in the boundary of region $\gamma _{V}$. Then, we may take a pseudoline of the arrangement passing through V and do the same as we did for a pseudoline passing through points V and U. So, in both subcases of case (2), we obtain statement (c). $\square$

Proof of Theorem 1, part (a)

Suppose there are two points such that each pseudoline of the arrangement passes through at least one of them, then we are done by Lemma 4. Thus, we may assume that there are no such points. By Lemma 7,

$$\begin{aligned} q(V)\ge 3 \quad \text {and} \quad q \ge 3\sum _{k\ge 3}t_k. \end{aligned}$$

Let us count q via edges and regions, then we have $q=2e_1+2s$. Hence,

$$\begin{aligned} e_1+s\ge 1.5\sum _{k\ge 3}t_k. \end{aligned}$$

(7)

From Lemmas 3 and 6 it follows that

$$\begin{aligned}&3p_4+\sum _{j\ge 5}jp_j-s \ge e_0=2t_2+e_1-\sum _{k\ge 3}kt_k\\&\quad \Longrightarrow 3p_4+\sum _{j\ge 5}jp_j +\sum _{k\ge 3}kt_k -2t_2\ge e_1+s. \end{aligned}$$

From the last inequality and inequality (7) it follows that

$$\begin{aligned}&3p_4+\sum _{j\ge 5}jp_j+\sum _{k\ge 3}kt_k - 2t_2 \ge 1.5 \sum _{k\ge 3}t_k \\&\quad \Longrightarrow 3p_4+\sum _{j\ge 5}jp_j+\sum _{k\ge 3}\big (k-1.5\big )t_k\ge 2t_2. \end{aligned}$$

$\square$

Proof of Theorem 2

(a) We use Hirzebruch’s inequality [8] as described in subsection “Bounds for Number of Regions” above. Hence, $m<n-2$ and we may present the inequality

$$\begin{aligned} t_2+0.75t_3\ge n+\sum _{k\ge 5}(2k-9)t_k \end{aligned}$$

in the form (1) with

$$\begin{aligned} \alpha _0=n,\quad \alpha _2=1, \quad \alpha _3=0.75, \quad \alpha _4=0, \quad \alpha _i=9-2i \quad \text {for}\quad i\ge 5. \end{aligned}$$

Let us take positive (for $m\ge 5$) numbers

$$\begin{aligned} c_1=\frac{3m-10}{m^2+3m-18}, \qquad c_2=\frac{m^2-3m+2}{m^2+3m-18}. \end{aligned}$$

The system (2) takes on the form

$$\begin{aligned}&1\ge 2c_1+c_2, \quad 2\ge 6c_1+0.75c_2, \quad 3\ge 12c_1, \\&\quad i-1\ge c_1i(i-1)-c_2(2i-9) \quad \text {for} \quad 5\le i \le m. \end{aligned}$$

Let us check these inequalities for $m\ge 5$ and for given $c_1, c_2$. The first three are obvious; to verify the last one for $5\le i \le m$, let us consider the quadratic polynomial

$$\begin{aligned} c_1i(i-1)-c_2(2i-9)-(i-1)=\frac{(i-m)(3mi-10(m+i)+24)}{(m-3)(m+6)} \le 0, \end{aligned}$$

because $3mi-10(m+i)+24>0$ for $m \ge 6$ and $i \ge 5$. So, we obtain (3) for given $c_1,c_2$, and hence the inequality of Theorem 2(a).

(b) Hence, $m<n-2$, then the inequality of Theorem 1(b) is valid and can be presented in the form (1) with

$$\begin{aligned} \alpha _0=8,\quad \alpha _2=1, \quad \alpha _3=1.5, \quad \alpha _k=7.5-2k \quad \text {for }\quad k\ge 4. \end{aligned}$$

Let us take positive (for $m\ge 12$) numbers

$$\begin{aligned} c_1=\frac{3m-8.5}{m^2+3m-15}, \qquad c_2=\frac{m^2-3m+2}{m^2+3m-15}. \end{aligned}$$

The system (2) takes on the form

$$\begin{aligned} 1\ge & {} 2c_1+c_2, \quad 2\ge 6c_1+1.5 c_2, \\&i-1\ge c_1i(i-1)-c_2(2i-7.5) \quad \text {for} \quad 4\le i \le m. \end{aligned}$$

Let us check these inequalities for $m\ge 12$ and for given $c_1, c_2$. The first two are obvious; to verify the last one for $4\le i \le m$, consider the quadratic polynomial

$$\begin{aligned}&c_1i(i-1)-c_2\big (2i-7.5\big )-(i-1)\\&\quad =\frac{(i-m)(3mi-8.5(m+i)+19.5)}{m^2+3m-15}\le 0, \end{aligned}$$

because $3mi-8.5(m+i)+19.5>0$ for $m \ge 12$ and $i \ge 4$. So, we obtain (3) for given $c_1,c_2$, and hence the inequality of Theorem 2(b). $\square$