Indecomposable Coverings with Homothetic Polygons

Abstract

We prove that for any convex polygon $S$ with at least four sides, or a concave one with no parallel sides, and any $m>0$, there is an $m$-fold covering of the plane with homothetic copies of $S$ that cannot be decomposed into two coverings.

1 Introduction

Let ${{\mathcal {C}}}=\{C_i\ |\ i\in I\}$ be a collection of planar sets. It is an m-fold covering if every point in the plane is contained in at least $m$ members of ${\mathcal {C}}$. A $1$-fold covering is simply called a covering.

A planar set $S$ is said to be cover-decomposable if there is a constant $m=m(S)$ such that every $m$-fold covering of the plane with translates of $S$ can be decomposed into two coverings. Pach [3] proposed the problem of determining all cover-decomposable sets in 1980. He conjectured that all planar convex sets are cover-decomposable. The conjecture has been verified, in several steps, for all convex polygons [9] (see also [4, 11]). However, very recently, Pálvölgyi proved that the unit disk is not cover-decomposable [8]. His result holds also for convex sets with smooth boundary.

The problem of determining cover-decomposable sets has been generalized in many directions, see [5] for a survey.

A homothetic transformation is the composition of a translation and a scaling. Keszegh and Pálvölgyi [1] proved that any $12$-fold covering of the plane with homothetic copies of a fixed triangle $T$ can be decomposed into two coverings. In this note we prove that, with a few possible exceptions, this result cannot be extended to other polygons.

Theorem 1

Let $S$ be a convex polygon with at least four sides, or a concave polygon with no parallel sides, and let $m>0$. There is an $m$-fold covering of the plane with homothetic copies of $S$ that cannot be decomposed into two coverings.

For convex polygons we can keep the sizes of the homothetic copies “almost equal.”

Theorem 2

Let $S$ be a convex polygon with at least four sides, and let $\varepsilon >0$ and $m>0$. There is a collection of homothetic copies of $S$, each of them with scaling factor between $1-\varepsilon$ and $1+\varepsilon$, which forms an $m$-fold covering of the plane that cannot be decomposed into two coverings.

Our method is based on the ideas of Pálvölgyi [7, 8].

2 Preparations

Most of the papers about cover-decomposability investigate the problem in its dual form.

Suppose that ${\mathcal {H}}=\{S_i\ |\ i\in I\}$ is collection of translates of $S$ that form an $m$-fold covering of the plane. For every $i\in I$, let $c_i$ be the center of gravity of $S_i$. Let ${\mathcal {H}}'=\{c_i\ |\ i\in I\}$ be the set of the centers. For any point $a$, let $-S(a)$ be a translate of $-S$ whose center of gravity is $a$. Then $a\in S_i$ if and only if $c_i\in -S(a)$. Therefore, the collection ${\mathcal {H}}$ can be decomposed into two coverings if and only if the points of the set ${\mathcal {H}}'$ can be colored with two colors such that every translate of $S$ contains points of both colors. This idea is originally due to Pach [4].

If we have homothetic copies, then the dual version of the problem is not equivalent to the original one. However, in this paper we give a tricky definition of the dual form.

Fix a coordinate system and let $o$ be the origin. If it does not lead to confusion, for any point $p$, we denote its position vector $\overrightarrow{op}$ also by $p$. For any $\alpha$ real, set $S$, and point $p$, let

$$\begin{aligned} \alpha \cdot S(p)=\{ \alpha \cdot x+p \ |\ x\in S\}. \end{aligned}$$

The Minkowski sum of any convex polygons $S$ and $T$ is defined as

$$\begin{aligned} S+T=\{ s+t \ |\ s\in S, t\in T\}. \end{aligned}$$

Let $S$ be a fixed convex polygon of at least four sides, $o\in S$. It is well known [10] that for any $\alpha , \beta \ge 0$

$$\begin{aligned} \alpha \cdot S+\beta \cdot S=(\alpha +\beta )\cdot S. \end{aligned}$$

As an easy consequence, we get the following statement.

Statement 1

Let $\alpha , \beta \ge 0$, $p, q\in {\mathbb {R}}^2$. $(\alpha +\beta )\cdot S(p)$ contains $q$ if and only if $\alpha \cdot S(p)$ and $-\beta \cdot S(q)$ intersect each other.

First, for every pair $(k, l)$, we will construct a collection of homothetic copies of $S$, ${\mathcal {X}}_{k,l}$ and a collection of translates of $-S$, ${\mathcal {Y}}_{k,l}$ with the property that for every red-blue coloring of the elements of ${\mathcal {X}}_{k,l}$, there is an element of ${\mathcal {Y}}_{k,l}$ which intersects exactly $k$ elements, all of which are red (resp. exactly $l$ elements, all of which are blue).

Then we “dualize” this construction, for $m=k=l$, as follows. Replace each element of ${\mathcal {X}}_{m,m}$ by a larger homothetic copy and let ${\mathcal {X}}'_{m,m}$ be the new collection. Replace each element of ${\mathcal {Y}}_{m,m}$ by a point and let ${\mathcal {Y}}'_{m,m}$ be the set of these points.

By Statement 1, ${\mathcal {X}}'_{m,m}$ and ${\mathcal {Y}}'_{m,m}$ have the following property.

For every red-blue coloring of the elements of ${\mathcal {X}}'_{m,m}$, there is an element (point) of ${\mathcal {Y}}'_{m,m}$ which is contained in exactly $m$ elements of ${\mathcal {X}}'_{m,m}$, all of which are of the same color.

So, for every $m$, ${\mathcal {X}}'_{m,m}$ forms a non-decomposable $m$-fold covering of the points in ${\mathcal {Y}}'_{m,m}$. Finally, we extend it to a non-decomposable $m$-fold covering of the whole plane.

3 Proof of Theorems 1 and 2

Let $S$ be a fixed convex polygon of at least four sides, $o\in S$. We say that $o$ is the center of $S$. We can assume that $S$ is contained in the unit disk of center $o$. By definition, $-S$ denotes the reflection of $S$ about the origin. Let $v_1, v_2, \ldots , v_{n}$ be the vertices of $-S$, ordered clockwise. Indices are understood mod $n$, that is, $v_{n+1}$ means $v_1$.

Definition 1

For every $i$, $1\le i\le n$, let $E^i$ denote the convex wedge whose apex is at the origin and its bounding halflines are the translates of $\overrightarrow{v_iv_{i-1}}$ and $\overrightarrow{v_iv_{i+1}}$. $E^i$ is called the wedge that belongs to vertex $v_i$ of $-S$.

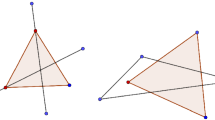
Choose a direction $d$ which is not parallel to the sides of $S$, and the two vertices $v_a$ and $v_b$, where $S$ can be touched by a line parallel to $d$, are not adjacent. Assume without loss of generality that $d$ is horizontal, and $v_a$ is the highest and $v_b$ is the lowest vertices of $S$. Let $Q$ be a quadrilateral created from $S$ by extending the sides at $v_a$ and $v_b$. Let $v_r$ and $v_l$ be the rightmost and the leftmost vertices of $Q$, respectively. See Fig. 1. We can assume without loss of generality that $v_l$ is not lower than $v_r$. Indeed, if $v_l$ is lower than $v_r$, then we can apply a reflection of $S$ about the $y$-axis. Let $\delta >0$ be a very small constant.

Fig. 1

$S, Q$ and the corresponding vertices

For every pair $(k,l)$, $k, l\ge 1$, we will construct a triple ${\mathcal {T}}_{k,l}=({\mathcal {X}}_{k,l}, {\mathcal {E}}^a_{k,l}, {\mathcal {E}}^b_{k,l})$, where ${\mathcal {X}}_{k,l}=\{\varepsilon _i\cdot S(p_i)\ |\ i\in I_{k,l}\}$, $\varepsilon _i>0$, a collection of homothetic copies of $S$, and ${\mathcal {E}}^a_{k,l}=\{E^a(q_j)\ |\ j\in J^a_{k,l}\}$, ${\mathcal {E}}^b_{k,l}=\{E^b(r_j)\ |\ j\in J^b_{k,l}\}$ are collections of translates of the wedges $E^a$ and $E^b$, respectively, for some $I_{k,l}, J^a_{k,l}, J^b_{k,l}$ index sets. ${\mathcal {T}}_{k,l}$ will have the following properties.

Property 1

For every red-blue coloring of the elements of ${\mathcal {X}}_{k,l}$, either there is an element of ${\mathcal {E}}^a_{k,l}$ which intersects exactly $k$ elements of ${\mathcal {X}}_{k,l}$, all of which are red, or there is an element of ${\mathcal {E}}^b_{k,l}$ which intersects exactly $l$ elements of ${\mathcal {X}}_{k,l}$, all of which are blue.

Property 2

There is a disk $D_{k,l}$ of radius $\delta$ which contains all apices of the wedges in ${\mathcal {E}}^a_{k,l}$ and ${\mathcal {E}}^b_{k,l}$, and all elements of ${\mathcal {X}}_{k,l}$.

First we define ${\mathcal {T}}_{k,1}$ and ${\mathcal {T}}_{1,l}$. For arbitrary $k$, let ${\mathcal {X}}_{k,1}$ be $k$ very small homothetic copies of $S$, very close to each other on a horizontal line. ${\mathcal {E}}^a_{k,1}$ contains one translate of the wedge $E^a$ that intersects all $k$ homothetic copies, and ${\mathcal {E}}^b_{k,1}$ contains $k$ translates of the wedge $E^b$, each intersecting exactly one of the $k$ homothetic copies, but each intersecting a different one. See Fig. 2. We define the triple ${\mathcal {T}}_{1,l}$ similarly for any $l$.

Fig. 2

The construction of ${\mathcal {T}}_{k,1}$

Suppose now that we have already defined ${\mathcal {T}}_{k,l-1}$ and ${\mathcal {T}}_{k-1,l}$. Take a translate of ${\mathcal {T}}_{k,l-1}$ so that the center of $D_{k,l-1}$ is $(0,0)$ and a translate of ${\mathcal {T}}_{k-1,l}$ so that the center of $D_{k-1,l}$ is $(1, 3\delta )$. Place a suitable homothetic copy $S'=\varepsilon \cdot S$ of $S$ between points $(0,0)$ and $(1, 3\delta )$ such that

• (i) $S'$ intersects all wedges in ${\mathcal {E}}^b_{k,l-1}$, and all wedges in ${\mathcal {E}}^a_{k-1,l}$,

• (ii) $S'$ does not intersect any of the wedges in ${\mathcal {E}}^a_{k,l-1}$, and any of the wedges in ${\mathcal {E}}^b_{k-1,l}$.

See Fig. 3. Let

$$\begin{aligned} {\mathcal {X}}_{k,l}= & {} {\mathcal {X}}_{k-1,l}\cup {\mathcal {X}}_{k,l-1}\cup \{S'\},\\ {\mathcal {E}}^a_{k,l}= & {} {\mathcal {E}}^a_{k-1,l}\cup {\mathcal {E}}^a_{k,l-1},\\ {\mathcal {E}}^b_{k,l}= & {} {\mathcal {E}}^b_{k-1,l}\cup {\mathcal {E}}^b_{k,l-1}. \end{aligned}$$

Apply a suitable scaling so that Property 2 is satisfied. We claim that Property 1 is also satisfied. Color the elements of ${\mathcal {X}}_{k,l}$ by red and blue. Suppose that $S'$ is red. In the subconfiguration that corresponds to ${\mathcal {T}}_{k-1,l}$, either there is a translate of $E^a$ that intersects exactly $k-1$ elements of ${\mathcal {X}}_{k-1,l}$, all of which are red, or there is a translate of $E^b$ that intersects exactly $l$ elements of ${\mathcal {X}}_{k-1,l}$, all of which are blue. In the first case, the corresponding translate of $E^a$ intersects exactly one more element of ${\mathcal {X}}_{k,l}$, $S'$, and it is red, so we are done. In the second case, the corresponding translate of $E^b$ does not intersect any other element of ${\mathcal {X}}_{k,l}$, so we are done again. We can argue the same way if $S'$ is colored blue. Consequently, Property 1 is satisfied.

Fig. 3

The induction step

To obtain a non-decomposable $m$-fold covering, consider ${\mathcal {T}}_{m,m}=({\mathcal {X}}_{m,m}, {\mathcal {E}}^a_{m,m}, {\mathcal {E}}^b_{m,m})$. ${\mathcal {X}}_{m,m}=\{\varepsilon _i\cdot S(p_i)\ |\ i\in I_{m,m}\}$, $\varepsilon _i>0$, a collection of homothetic copies.

Replace each element of ${\mathcal {E}}^a_{m,m}$ (resp. ${\mathcal {E}}^b_{m,m}$) by a translate of $-S$ such that its vertex $v_a$ (resp. $v_b$) moves to its apex. We obtain a collection of translates of $-S$, ${\mathcal {Y}}_{m,m}=\{-S(q_j)\ |\ j\in J_{m,m}\}$, with the property that for every red-blue coloring of the elements of ${\mathcal {X}}_{m,m}$, there is an element of ${\mathcal {Y}}_{m,m}$ which intersects exactly $m$ elements of ${\mathcal {X}}_{m,m}$, all of the same color.

Let ${\mathcal {X}}'_{m,m}=\{(1+\varepsilon _i)\cdot S(p_i)\ |\ i\in I_{m,m}\}$, a collection of homothetic copies of $S$, and let ${\mathcal {Y}}'_{m,m}=\{q_j\ |\ j\in J_{m,m}\}$, a collection of points. By Statement 1, for every red-blue coloring of the elements of ${\mathcal {X}}'_{m,m}$, there is an element (point) of ${\mathcal {Y}}'_{m,m}$ which is contained in exactly $m$ elements of ${\mathcal {X}}'_{m,m}$, all of the same color.

That is, ${\mathcal {X}}'_{m,m}$ forms a non-decomposable $m$-fold covering of the points in ${\mathcal {Y}}'_{m,m}$. Moreover, for any $\varepsilon >0$, if we choose $\delta$ small enough, then the scaling factor of each member of ${\mathcal {X}}'_{m,m}$ is between $1-\varepsilon$ and $1+\varepsilon$.

Now we extend ${\mathcal {X}}'_{m,m}$ to a non-decomposable $m$-fold covering of the whole plane as follows. We will add homothetic copies of $S$ to ${\mathcal {X}}'_{m,m}$ that do not contain any point in ${\mathcal {Y}}'_{m,m}$, but each point in the plane will be covered at least $m$ times. If we allow arbitrary small copies in the covering, then the extension is trivial since ${\mathcal {Y}}'_{m,m}$ is a finite point set. Just add all homothetic copies of $S$ that do not contain any point of ${\mathcal {Y}}'_{m,m}$.

If we want to keep the sizes almost equal, we have to be more careful. Points in ${\mathcal {Y}}'_{m,m}$ are of two types, type $a$ (resp. type $b$) is the set of those which come from a wedge in ${\mathcal {E}}^a_{m,m}$ (resp. ${\mathcal {E}}^b_{m,m}$). Observe that any two points of the same type determine a line which is almost horizontal. In fact, we can take two horizontal lines $\ell _a$ and $\ell _b$ at distance $\mathrm{Vert}(v_av_b)$ such that all points of type $a$ (resp. type $b$) are at distance at most $\delta$ from $\ell _a$ (resp. $\ell _b$). See Figs. 4 and 5.

Fig. 4

The points of type $a$ in ${\mathcal {X}}'_{m,m}$ are almost on the line $\ell _a$

Fig. 5

Extending the cover by translates of $(1-\varepsilon )S$

Add all translates of $(1-\varepsilon )S$ which avoid the points in ${\mathcal {Y}}'_{m,m}$. Now it is not hard to see that the resulting collection is an $m$-fold covering of the whole plane, and by the construction of ${\mathcal {X}}'_{m,m}$ and ${\mathcal {Y}}'_{m,m}$, it is not decomposable. This concludes the proof of Theorem 2 and also the proof of Theorem 1 in the special case when $S$ is convex.

Now suppose that $S$ is concave with no parallel sides and let $m>0$. Pálvölgyi [7] constructed a collection ${\mathcal {X}}'_{m,m}$ of translates of $S$ and a set ${\mathcal {Y}}'_{m,m}$ of points such that ${\mathcal {X}}'_{m,m}$ forms a non-decomposable $m$-fold covering of the points in ${\mathcal {Y}}'_{m,m}$. Add all homothetic copies of $S$ that do not contain any point of ${\mathcal {Y}}'_{m,m}$. The resulting collection is clearly an $m$-fold covering of the plane, and just like in the previous argument, it is not decomposable. This finishes the proof of Theorem 1.

Remark 1

The dual version of this problem is still open. Let $S$ be a polygon of at least four sides. Is there an $m=m(S)$ with the following property? Any point set ${\mathcal {P}}$ can be colored with two colors such that if a homothetic copy of $S$ contains at least $m$ points of ${\mathcal {P}}$, then it contains points of both colors. If $S$ is concave and has no parallel sides, then the answer is NO to this question, even if we use only translates instead of homothetic copies, by the result of Pálvölgyi [7].

On the other hand, if $S$ is convex and we use only translates, then the answer is YES, by Pálvölgyi and Tóth [9]. If we do not allow arbitrarily large and arbitrarily small homothetic copies, then the answer is still YES, and the proof in [9] works also in this case. But if we allow all homothetic copies, then the problem is unsolved. See [2] for related results.

Remark 2

We can define a hypergraph ${\mathcal {H}}_{k,l}$ to the pair $({\mathcal {X}}_{k,l}, {\mathcal {Y}}_{k,l})$ in a natural way: elements of ${\mathcal {X}}_{k,l}$ correspond to the vertices and elements of ${\mathcal {Y}}_{k,l}$ correspond to the hyperedges—a hyperedge contains a vertex if and only if the corresponding elements intersect each other. The same hypergraph was used by Pálvölgyi in [7, 8] to show that some concave polygons and the unit disk are not cover-decomposable.

Remark 3

It was shown in [6] that for every $m$, there exists an $m$-fold covering of the plane with axis-parallel rectangles that cannot be decomposed into two coverings. We can slightly strengthen this result.

Theorem 3

For any $m>0$, there is an $m$-fold covering of the plane with axis-parallel rectangles, each with unit horizontal side, that cannot be decomposed into two coverings.

The proof is almost identical to the proof of Theorem 1. The main difference is that in the induction step, instead of a very small copy of $S$, we add a very short vertical segment. We omit the details.

Remark 4

We believe that Theorem 2 can be extended to concave polygons with no parallel sides.