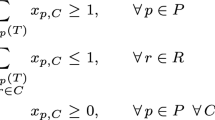Polynomial-time Combinatorial Algorithm for General Max–Min Fair Allocation

Abstract

In the general max–min fair allocation problem, there are m players and n indivisible resources, each player has his/her own utilities for the resources, and the goal is to find an assignment that maximizes the minimum total utility of resources assigned to a player. The problem finds many natural applications such as bandwidth distribution in telecom networks, processor allocation in computational grids, and even public-sector decision making. We introduce an over-estimation strategy to design approximation algorithms for this problem. When all utilities are positive, we obtain an approximation ratio of $\frac{c}{1-\epsilon }$, where c is the maximum ratio of the largest utility to the smallest utility of any resource. When some utilities are zero, we obtain an approximation ratio of $\bigl (1+3{\hat{c}}+O(\delta {\hat{c}}^2)\bigr )$, where ${\hat{c}}$ is the maximum ratio of the largest utility to the smallest positive utility of any resource.

1 Introduction

Fair resource allocation is an important concept that arises in a variety of real-world applications. One application is public-sector decision making; for instance, in health care, education and so on. Another example is bandwidth allocation in telecommunication networks. The objective is to treat all users as fairly as possible, while satisfying their demands. Such fairness problems appear in many practical scenarios, from the distribution of bandwidth allocation to grid/cloud computing to machine scheduling [2, 18, 19, 21]. Depending on the context, the resources may be divisible as in the bandwidth allocation, or indivisible as in the scheduling of jobs to machines.

In this paper, we consider the general max–min fair allocation problem. The input consists of a set P of m players and a set R of n indivisible resources. Each player $p \in P$ has his/her own non-negative utilities for the n resources, and we denote the utility of the resource r for p by $v_{p,r}$. In other words, each resource r has a set of non-negative utilities $\{v_{p,r}: p \in P \}$, one for each player. We assume that every $v_{p,r}$ is a rational number. For every subset S of resources, define the total utility of S for p to be $v_p(S) = \sum _{r \in S} v_{p,r}$. An allocation is a disjoint partition of R into $\{S_p: p \in P\}$ such that $S_p \subseteq R$ for all $p \in P$, and $S_p \cap S_q = \emptyset$ for any $p \not = q$. That is, p is assigned the resources in $S_p$. The max–min fair allocation problem is to find an allocation that maximizes $\min \{ v_p(S_p): p \in P\}$.

Throughout this paper, we follow the convention in previous studies that for any $\alpha \ge 1$, an $\alpha$-approximation algorithm or an approximation of $\alpha$ for the general max–min fair allocation problem means that the minimum total utility of a player is at least $1/\alpha$ times the optimum.

1.1 Prior Studies

The problem has received considerable attention in recent decades. A related problem is a classic scheduling problem that minimizes the maximum makespan of scheduling on unrelated parallel machines. The problem has the same input as the max–min fair allocation problem. The only difference between them is that the goal of the scheduling problem is to minimize the maximum load over all machines. Lenstra et al. [17] proposed a 2-approximation algorithm by rounding the relaxation of the assignment linear programming model (LP). However, Bezáková and Dani [7] proved that the assignment LP cannot guarantee the same performance for the general max–min allocation problem.

The machine covering problem is a special case of the general max–min fair allocation problem. The objective is to assign n jobs to m parallel identical machines so that the minimum machine load is maximized. Every job (resource) has the same positive utility for every machine (player), i.e., every $r \in R$ has a positive value $v_r$ such that $v_{p,r} = v_r > 0$ for all $p \in P$. Deuermeyer et al. [14] proved that the heuristic LPT algorithm returns a $\frac{4}{3}$-approximation allocation. Csirik et al. [12] improved the approximation ratio to $\frac{4m-2}{3m-1}$. Later, Woeginger [22] presented a polynomial time approximation scheme that gives an approximate ratio of $\frac{1}{1-\epsilon }$ for any fixed $\epsilon > 0$. There is a variant of the machine covering problem that specifies a speed $s_p$ for each machine p. So the processing time of a job r on a machine p is $v_{p,r} = v_r/s_p$. Azar et al. [5] proposed a polynomial time approximation scheme for this variant, achieving an approximation of $\frac{1}{1-\epsilon }$. The online machine covering problem was studied in [15, 16] for identical machines.

Table 1 Results on the max–min allocation problem

Bansal and Sviridenko [6] proposed a stronger LP relaxation, the configuration LP, for the general max–min fair allocation problem. They showed that the integrality gap of the configuration LP is $\Omega (\sqrt{m})$, where m is the number of players. Based on the configuration LP, Asadpour and Saberi [4] developed an approximation algorithm that achieves an approximation ratio of $O(\sqrt{m} \log ^3{m})$. Later, Saha and Srinivasan [20] reduced the approximation ratio to $O(\sqrt{m \log {m}})$. Chakrabarty et al. [8] developed a method to provide a trade-off between the approximation ratio and the running time: for all $\delta = \Omega (\log \log n/\log n)$, an approximation ratio of $O(m^\delta )$ can be obtained in $O(m^{1/\delta })$ time.

Bansal and Sviridenko [6] also defined the restricted max–min fair allocation problem. In the restricted case, each resource has the same utility $v_r$ for all players who are interested in it, that is, $v_{p,r} \in \{0, v_r\}$ for all $p \in P$. They proposed an $O\bigl (\frac{\log {\log m}}{\log {\log {\log m}}}\bigr )$-approximation algorithm by rounding the configuration LP. Later, Asadpour et al. [3] used the bipartite hypergraph matching technique to attack the restricted max–min fair allocation problem. They used local search to show that the integrality gap of the configuration LP is at most 4. However, it is not known whether the local search in [3] runs in polynomial time. Inspired by [3], Annamalai et al. [1] designed an approximation algorithm that enhances the local search with a greedy player strategy and a lazy update strategy. Their algorithm runs in polynomial time and achieves an approximation ratio of $12.325+\delta$ for any fixed $\delta \in (0,1)$. Cheng and Mao [9] adjusted the greedy strategy in a more flexible and aggressive way, and they successfully lowered the approximation ratio to $6+\delta$. Very recently, they introduced the limited blocking idea and improved the ratio to $4+\delta$ [10, 11]. This ratio was also obtained independently by Davies et al. [13]. Table 1 lists the related results.

1.2 Our Contribution

The major challenge for the general max–min fair allocation problem is that a resource may have different utilities for different players. Our key idea is to use a player-independent value to estimate the value of a particular set: for every resource $r \in R$, its over-estimated utility is $v_r^{max}=\textrm{max}\{v_{p,r}: p \in P \}$. Consider an instance where every utility in the set $\{v_{p,r}: p \in P, \, r \in R\}$ is positive. Such a problem setting is closely related to the machine covering problem. The main difference is that players are not identical and players have their own preferences for the resources. Using the player-independent over-estimation, we can transform this case to the machine covering problem. Then, we can apply the currently best algorithm proposed by [22] to obtain an allocation in which every player gets at least $(1-\epsilon )T^*_{oe}$ worth of resources, where $T^*_{oe}$ denotes the optimal solution for the transformed machine covering problem. Due to the over-estimation before the transformation, the allocation may be off by an additional factor of $c = \textrm{max}\bigl \{v_{p,r}/v_{q,r}: \, p,q \in P \, \wedge \, r \in R \bigr \}$. This gives our first result which is summarized in Theorem 1 below. Further discussions are provided in Sect. 2.

Theorem 1

For every fixed $\epsilon \in (0,1)$, there is a polynomial-time $\bigl (\frac{c}{1-\epsilon }\bigr )$-approximation algorithm for general max–min fair allocation problem, provided that every resource has a positive utility for every player.

Fig. 1

An illustration of (i) the restricted case, (ii) the general case and (iii) the over-estimation strategy

The problem becomes much more complicated when some resource has zero utility for some players. Our idea is to combine the over-estimation strategy with the algorithm of Cheng and Mao [11] for the restricted max–min fair allocation problem to obtain an approximation for the general case (as shown in Fig. 1). The over-estimation strategy allows us to use the maximum resource utilities in differentiating active and inactive resources. That is, active and inactive resources are defined differently from [11] (see Definition 1). This change requires us to adapt the proof of Lemma 2 in [11] to our new definitions. We also need to formulate and prove a new result, Lemma 3, in order to carry out the subsequent analysis of the approximation ratio in Lemma 4. At first sight, combining the over-estimation strategy with the algorithm in [11] seems to yield an approximation ratio of $(4+\delta ){\hat{c}}$, where ${\hat{c}} = \textrm{max}\bigl \{v_{p,r}/v_{q,r}: \, p, q \in P \, \wedge \, r \in R \, \wedge \, v_{q,r} > 0 \bigr \}$. Nevertheless, by a careful revision of the proof of Lemma 4 for our case, we obtain a better ratio of $1 + 3{\hat{c}} + O(\delta {\hat{c}}^2)$ for any fixed $\delta \in (0,1)$. Other than the above changes, we carry the rest of the algorithm in [11] for the restricted case over to the general case. The total utilities of a subset of resources assigned to a player is calculated using the actual utilities of those resources.

Theorem 2

For every fixed $\delta \in (0,1)$, there is a $(1+3{\hat{c}}+O(\delta {\hat{c}}^2))$-approximation algorithm that runs in polynomial time for the general max–min fair allocation problem.

Recall that the best known approximation ratio for the general max–min fair allocation problem is $O(\sqrt{m\log m})$ or $O(m^{\delta })$ [8, 20]. Given the difficulty of the problem, the approximation ratios in Theorems 1 and 2 are quite reasonable when c and ${\hat{c}}$ are small; for example, when the players rate the resources on a 5-point scale.

The remainder of this paper is organized as follows. In the next section, we consider the simpler case in which all utilities are positive. In Sect. 3, we propose an approximation algorithm for the case when some utilities may be zero. In Sect. 4, we analyze the performance and running time of this algorithm. We conclude with some open questions in Sect. 5.

2 Every Resource has a Positive Utility for Every Player

In this section, we consider the general max–min fair allocation problem in which all utilities are positive. This model is similar to the machine covering problem, but the major difference is that every player has his/her own preferences for the resources. There is a polynomial time approximation scheme for the machine covering problem, proposed by Woeginger [22], that achieves an approximation ratio of $1/(1-\epsilon )$.

Fr each resource $r \in R$, we use $v_r^\textrm{max}= \textrm{max}\{v_{p,r}: p \in P\}$ as the player-independent utility for r. Hence all players become identical. This transformed problem is exactly the machine covering problem which we denote by $H_{oe}$. Let H denote the original problem before the transformation. Let $T^*$ be the optimal target value for H, and let $T^*_{oe}$ be the optimal target value for $H_{oe}$. So $T^* \le T^*_{oe}$. Using the PTAS algorithm in [22], we can find an approximation allocation $\{S_p: p \in P\}$, where $\sum _{r \in S_p} v_r^\textrm{max}\ge (1-\epsilon )T^*_{oe}$ for every $p \in P$. When we consider the actual value $v_p(S_p)$, we have to allow for the over-estimation factor $c = \textrm{max}\{v_{p,r}/v_{q,r}: p,q \in P \, \wedge \, r \in R \}$.

The definition of c implies that $\sum _{r \in S_p} v_r^\textrm{max}\le c \cdot v_p(S_p)$, which further implies that $(1-\epsilon )T^*_{oe} \le \sum _{r \in S_p} v_r^\textrm{max}\le c \cdot v_p(S_p)$. That is, we guarantee that every player receives at least $(1-\epsilon )T^*_{oe}/c$ worth of resources. Since $T^*_{oe} \ge T^*$, the allocation is a $\bigl (\frac{c}{1-\epsilon }\bigr )$-approximation for the original problem H. This completes the discussion of Theorem 1.

3 Some Resources have Zero Utility for Some Players

At the high-level, we use binary search to identify largest value T such that we can find an allocation in which the resources assigned to every player have a total utility of at least $\lambda T$, where $\lambda$ is a value that will be proved to be at least $\bigl (1 + 3{\hat{c}} + O(\delta {\hat{c}}^2)\bigr )^{-1}$. The same binary process for $\lambda = (4+\delta )^{-1}$ is used in [11]. For each guess T, the desired allocation is computed using a local search. Depending on whether we succeed or not, we increase or decrease T correspondingly in order to zoom into the value $T^*$ of the optimal max–min allocation. The initial range for T for binary search is $(0,\frac{1}{m}\sum _{r \in R} v_r^{max})$. Since every $v^{\textrm{max}}_r$ is a rational number by assumption, the binary search will terminate in a polynomial number of probes.

In the rest of this section, we assume that $T = 1$, which can be enforced by scaling all resource utilities, and we describe how to find an allocation such that every player obtains resources with a total utility of at least $\lambda$.

3.1 Resources and Over-estimation

We call a resource r fat if $v_{p,r} \ge \lambda$ for all $p \in P$. Otherwise, there exists a player p such that $v_{p,r} < \lambda$, and we call r thin in this case. The input resources are thus divided into fat and thin resources; this is a generalization of the classification of fat and thin resources in the restricted case [11].

We introduce a new utility truncation that will simplify subsequent discussion and analysis. For every $r \in R$ and every $p \in P$, if $v_{p,r} > \lambda$, we reset $v_{p,r}:= \lambda$. This modification does not affect our goal of finding an allocation in which the resources assigned to every player have a total utility of at least $\lambda$. Note that $v_{p,r}$ is left unchanged if it is at most $\lambda$. Therefore, fat resources remain fat, and thin resources remain thin. Note that r still has zero utility for those players who are not interested in r, and different players may have different utilities for the same resource.

Since we have reset each $v_{p,r}$ so that it is at most $\lambda$, we have $v_r^\textrm{max}\le \lambda$. For any subset D of thin resources, let $v_\textrm{max}(D) = \sum _{r \in D} v_r^\textrm{max}$. For every player p, $v_p(D)$ still denotes $\sum _{r \in D} v_{p,r}$.

3.2 Fat Edges and Thin Edges

For better resource utilization, it suffices to assign a player p either a single fat resource (whose utilities are all equal to $\lambda$ after the above modification), or a subset D of thin resources such that $v_p(D) \ge \lambda$. We model the above possible assignment of resources to players using a bipartite graph G and a bipartite hypergraph H as in [11]. The vertices of G are the players and fat resources. For every player p and every fat resource $r_f$, G includes the edge $(p,r_f)$ which we call a fat edge. The vertices of H are the players and thin resources. For every subset D of thin resources and every player p, the hypergraph H includes the edge (p, D) if $v_p(D) \ge \lambda$, called a thin edge.

3.3 Overview of the Algorithm

We sketch the high-level ideas of the local search in [11]. We are interested in finding an allocation that corresponds to a maximum matching M in G and a subset ${\mathcal {E}}$ of hyperedges H such that every player is incident to an edge in M or ${\mathcal {E}}$, and no two edges in $M \cup {{\mathcal {E}}}$ share any resource.

To construct such an allocation, we start with an arbitrary maximum matching M of G and an empty matching ${\mathcal {E}}$ of H, process unmatched players one by one in an arbitrary order, and update M and ${\mathcal {E}}$ in order to match the next unmatched player. Once the algorithm matches a player, that player remains matched until the end of the algorithm. Also, although M may be updated, it is always some maximum matching of G. We call any intermediate $M \cup {{\mathcal {E}}}$ a partial allocation.

Let $G_M$ be a directed graph obtained by orienting the edges of G with respect to M of G as follows. If a fat edge $\{p,r_f\}$ belongs to the matching M, we orient $\{p,r_f\}$ from $r_f$ to p in $G_M$. Conversely, if $\{p,r_f\}$ does not belong to the matching M, we orient $\{p,r_f\}$ from p to $r_f$ in $G_M$.

Let $p_0$ be an arbitrary unmatched player with respect to the current partial allocation $M \cup {{\mathcal {E}}}$. We find a directed path $\pi$ from $p_0$ to a player $q_0$ in $G_M$. If $p_0 = q_0$, then $\pi$ is a trivial path. In this case, if $q_0$ is covered by a thin edge a that does not share any resource with the edges in $M \cup {\mathcal {E}}$, then we can update the partial allocation to be $M \cup ({{\mathcal {E}}} \cup \{a\})$ to match $p_0$. If $p_0 \not = q_0$, then $\pi$ is a non-trivial path. Note that $\pi$ has an even number of edges because both $p_0$ and $q_0$ are players. For $i \ge 0$, every $(2i+1)$-th edge in $\pi$ does not belong to M, but every $(2i+2)$-th edge in $\pi$ does. It is an alternating path in the matching terminology. The last edge in $\pi$ is a matching edge $(r_f,q_0)$ in M for some fat resource $r_f$. Suppose that $q_0$ is incident to a thin edge a that does not share any resource with any edge in $M \cup {\mathcal {E}}$. Then, we can update M to another maximum matching of G by flipping the edge in $\pi$. That is, delete every $(2i+2)$-th edge in $\pi$ from M and add every $(2i+1)$-th edge in $\pi$ to M. Denote this update of M by flipping $\pi$ as $M \oplus \pi$. Consequently, $p_0$ is now matched by M. Although $q_0$ is no longer matched by M, we can regain $q_0$ by including the thin edge a. In all, the updated partial allocation is $(M \oplus \pi ) \cup ({{\mathcal {E}}} \cup \{a\})$.

However, sometimes we cannot find a thin edge a that is incident to $q_0$ and shares no resource with the edges in $M \cup {\mathcal {E}}$. Let b be an edge in $M \cup {\mathcal {E}}$. If a and b share some resource, then a is blocked by b. That is, if we want to add a into ${\mathcal {E}}$, we must release the resources in b first. Thus, a is an addable edge and b is a blocking edge that forbids the addition of a. We will provide the formal definitions of addable and blocking edges shortly. To release the resources covered by b, we need to reconsider how to match the player covered by b. This defines a similar intermediate subproblem that needs to be solved first, namely, finding a thin edge that is incident to the player covered by b and shares no resource with the edges in $M \cup {{\mathcal {E}}}$. In general, the algorithm maintains a stack that consists of layers of addable and blocking edges; each layer correspond to some intermediate subproblems that need to be solved. Eventually, every blocking edge needs to be released in order that we can match $p_0$ in the end.

Annamalai et al. [1] introduced two ideas to enhance the above local search for the restricted max–min allocation problem. They are instrumental in obtaining a polynomial running time. First, when an unblocked addable edge is found, it is not used immediately to update the partial allocation. Instead, the algorithm waits until there are enough unblocked addable edges to reduce the number of blocking edges significantly. This ensures that the algorithm makes a substantial progress with each update of the partial allocation. This is called the lazy update strategy. Second, when the algorithm considers an addable edge (p, D), it requires $v_p(D)$ to be a constant factor larger than $\lambda$. As a result, (p, D) will induce more blocking edges, which will result in a geometric growth of the blocking edges in the layers from the bottom of the stack towards the top of the stack. This is called the greedy player strategy.

The greedy player strategy causes trouble sometimes, and a blocking edge may block too many addable edges. To this end, Cheng and Mao [11] introduced limited blocking which stops the resources in a blocking edge b from being picked in an addable edge if b shares too many resources with addable edges.

We provide more details of the algorithm in the remaining subsections.

3.4 Layers of Addable and Blocking Edges

For every thin edge e, we use $R_e$ to denote the resources covered by e. Given a set ${\mathcal {X}}$ of thin edges, we use $R({{\mathcal {X}}})$ to denote the set of resources covered by the edges in ${\mathcal {X}}$.

Let $\Sigma = (L_0,L_1,\ldots ,L_\ell )$ denote the current stack maintained by the algorithms, where each $L_i = ({{\mathcal {A}}}_i, {{\mathcal {B}}}_i)$ is a layer that consists of a set ${{\mathcal {A}}}_i$ of addable edges and a set ${{\mathcal {B}}}_i$ of blocking edges. That is, ${{\mathcal {B}}}_i = \{e \in {{\mathcal {E}}}: R_e \cap R({{\mathcal {A}}}_i) \not = \emptyset \}$. The layer $L_{i+1}$ is on top of the layer $L_i$. The layer $L_0 = ({{\mathcal {A}}}_0,{{\mathcal {B}}}_0)$ at the stack bottom is initialized to be $(\emptyset ,\{(p_0,\emptyset )\})$. It signifies that there is no addable edge initially, and replacing $(p_0,\emptyset )$ by some edge is equivalent to finding an edge that covers $p_0$ without causing any blocking. In general, when building a new layer $L_{\ell +1}$ in $\Sigma$, the algorithm starts with ${{\mathcal {A}}}_{\ell +1} = \emptyset$, ${{\mathcal {B}}}_{\ell +1} = \emptyset$, and addable and blocking edges will be added to ${{\mathcal {A}}}_{\ell +1}$ and ${{\mathcal {B}}}_{\ell +1}$.

We use ${{\mathcal {A}}}_{\le i}$ to denote ${{\mathcal {A}}}_0 \cup \ldots \cup {{\mathcal {A}}}_i$. Similarly, ${{\mathcal {B}}}_{\le i} = {{\mathcal {B}}}_0 \cup \ldots \cup {{\mathcal {B}}}_i$.

The current configuration of the algorithm can be specified by a tuple $(M,{{\mathcal {E}}},\Sigma ,\ell ,{{\mathcal {I}}})$, where $M \cup {{\mathcal {E}}}$ is the current partial allocation, $\Sigma$ is the current stack of layers, $\ell$ is the index of the highest layer, and ${\mathcal {I}}$ is a set of thin edges in H such that they cover the players of some edges in ${{\mathcal {B}}}_{\le \ell }$ and each edge in ${\mathcal {I}}$ does not share any resource with any edge in ${\mathcal {E}}$. Although the edges in ${\mathcal {I}}$ can be added to ${\mathcal {E}}$ immediately to release some blocking edges in ${{\mathcal {B}}}_{\le \ell }$, we do not do so right away in order to accumulate a larger ${\mathcal {I}}$ which will release more blocking edges in the future.

Definition 1

Let $(M,{{\mathcal {E}}},\Sigma ,\ell ,{{\mathcal {I}}})$ be the current configuration. A thin resource r can be active or inactive. It is inactive if at least one of the following three conditions is satisfied: (a) $r\in R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })$, (b) $r \in R({{\mathcal {A}}}_{\ell +1}\cup {\mathcal {I}})$, and (c) $r \in R_b$ for some $b \in {{\mathcal {B}}}_{\ell +1}$ and $v_\textrm{max}\bigl (R_b \cap R({{\mathcal {A}}}_{\ell +1})\bigr ) > \beta \lambda$, where $\beta$ is a positive parameter to be specified later. If none is satisfied, then r is active.

In Definition 1, condition (c) is a modification of the condition of $v\bigl (R_b \cap R({{\mathcal {A}}}_{\ell +1})\bigr ) > \beta \lambda$ in the definition of inactive resources in [11] in the restricted case. The switch to $v_\textrm{max}\bigl (R_b \cap R({{\mathcal {A}}}_{\ell +1})\bigr ) > \beta \lambda$ fits with our over-estimation strategy for the general case. The utilities of inactive resources are disregarded in judging whether a thin edge contributes enough total utility to be considered an addable edge. Avoiding inactive resources, especially those in condition (c), helps to improve the approximation ratio.

Let $A_i$, $B_i$, and I denote the sets of players covered by the edges in ${{\mathcal {A}}}_i$, ${{\mathcal {B}}}_i$, and ${\mathcal {I}}$, respectively. Let $A_{\le i} = A_0 \cup \ldots A_{i}$, and let $B_{\le i} = B_0 \cup \ldots \cup B_i$. Given two subsets of players S and T, we use $f_M[S,T]$ to denote the maximum number of node-disjoint paths from S to T in $G_M$. The alternating paths in $G_M$ from $B_{\le \ell }$ to I and other players are relevant. If we flip the alternating paths to I, we can release some blocking edges in ${{\mathcal {B}}}_{\le \ell }$ because they will be matched to fat resources instead. Also, if there is an alternating path from $B_{\le \ell }$ to a player p, then we can look for a thin edge that covers p to release a blocking edge.

Next, we define addable players, addable edges, and collapsible layers as in [11].

Definition 2

Let $(M,{{\mathcal {E}}},\Sigma ,\ell ,{{\mathcal {I}}})$ be the current configuration. We say that a player p is addable if $f_M[B_{\le \ell }, A_{\ell +1}\cup I \cup \{p\}] = f_M[B_{\le \ell },A_{\ell +1}\cup I]+1$.

Definition 3

Let $(M,{{\mathcal {E}}},\Sigma ,\ell ,{{\mathcal {I}}})$ be the current configuration. Given an addable player p, a thin edge (p, D) in H is addable if D is a set of active thin resources and $v_p(D) \ge \lambda$.

As mentioned before, the edges in ${\mathcal {I}}$ can be deployed any time to replace some blocking edges, but we only do so when we can release a significant number of blocking edges. When this is possible for a layer in $\Sigma$, we call that layer collapsible as defined below.

Definition 4

Let $(M,{{\mathcal {E}}},\Sigma ,\ell ,{{\mathcal {I}}})$ be the current configuration. Let $\mu \in (0,1)$be a parameter to be specified later. The layer $L_0$ in $\Sigma$ is collapsible if $f_M[B_0,I] = 1$ (note that $|B_0| = 1$), and for $i \in [1,\ell ]$, the layer $L_i$ is collapsible if $f_M[B_{\le i},I] - f_M[B_{\le i-1},I] > \mu |B_i|$.

3.5 The Local Search Step

We discuss how to match the next unmatched player $p_0$. Let $M \cup {{\mathcal {E}}}$ be the current partial allocation. Let $\Sigma = \bigl (L_0\bigr )$ be the initial stack. Let ${{\mathcal {I}}} = \emptyset$. We go into the Build phase to add a new layer to $\Sigma$. Afterwards, if some layer becomes collapsible, we go into the Collapse phase to prune $\Sigma$ and update the current partial allocation. Afterwards, we go back into the Build phase to add new layers to $\Sigma$ again. The above is repeated until $\Sigma$ becomes empty, which means that $p_0$ is matched eventually. We describe the Build and Collapse phases [11] in the following sections. (See an example in Fig. 2.)

Fig. 2

An illustration of the Build and Collapse phases. In (a), the local search attempts to match $p_0$, $L_0 = (\mathcal {A}_0,\mathcal {B}_0) = (\emptyset , \{(p_0,\emptyset )\})$, and $\mathcal {I} =\emptyset$. In (b), $L_1 = (\mathcal {A}_1,\mathcal {B}_1) = (\{a_1\},\{b_1,b_2\})$ and $\mathcal {I} = \emptyset$. In (c), $L_2 = (\mathcal {A}_2,\mathcal {B}_2) = (\{a_3\},\{b_3\})$, $\mathcal {I} = \{a_2'\}$, $L_1$ becomes collapsible, and the algorithm enters the Collapse phase. In (d), $L_2$ is removed, $b_1$ is removed from $\mathcal {B}_1$, and $\mathcal {I}$ becomes empty. The edge $a_1$ becomes unblocked, and the $\lambda$-minimal edge $a'_1$ is extracted from $a_1$ and added to $\mathcal {I}$. So $\mathcal {I}$ becomes $\{a_1'\}$, $L_0$ becomes collapsible, and the algorithm remains in the Collapse phase. In (e), $p_0$ is matched by $a_1'$, i.e., the local search suceeds to match $p_0$

3.5.1 Build Phase

We start with ${{\mathcal {A}}}_{\ell +1} = {{\mathcal {B}}}_{\ell +1} = \emptyset$. We grow ${{\mathcal {A}}}_{\ell +1}$ and ${{\mathcal {B}}}_{\ell +1}$ as long as we can find some appropriate thin edge (p, D) in H that falls into one of the two cases below:

• Suppose that there is an unblocked addable thin edge (p, D). That is, $R(D) \cap R({{\mathcal {E}}}) = \emptyset$. It is natural to add such an edge to ${\mathcal {I}}$, but for better resource utilization, there is no need to use the whole D if $v_p(D)$ is way larger than $\lambda$. We greedily extract a $\lambda$-minimal thin edge $(p,D')$ from (p, D): (i) $D'$ is a subset of D such that $v_p(D') \ge \lambda$, and (ii) $v_p(D'') < \lambda$ for all subset $D'' \subset D'$. We add $(p,D')$ to ${\mathcal {I}}$.

• Assume that all addable thin edges are blocked. Suppose that there is a blocked addable thin edge (p, D) that is $(1+\gamma )\lambda$-minimal for an appropriate $\gamma \in (0,1)$ that will be specified later. That is, $v_p(D) \ge (1+\gamma )\lambda$ and for all $D' \subset D$, $v_p(D') < (1+\gamma )\lambda$. This is in accordance with the greedy player strategy. Let E be the subset of thin edges in ${\mathcal {E}}$ that block (p, D), i.e., $E = \{ e \in {{\mathcal {E}}}: R_e \cap R(D) \not = \emptyset \}$. Add (p, D) to ${{\mathcal {A}}}_{\ell +1}$ and update ${{\mathcal {B}}}_{\ell +1}:= {{\mathcal {B}}}_{\ell +1} \cup E$.

Our definitions of $\lambda$-minimal and $(1+\gamma )\lambda$-minimal thin edges are player-dependent, in contrast to their player-independent counterparts in the restricted max–min case [11].

If no more edge can be added to ${{\mathcal {I}}}$, or ${{\mathcal {A}}}_{\ell +1}$ and ${{\mathcal {B}}}_{\ell +1}$, then we push $({{\mathcal {A}}}_{\ell +1},{{\mathcal {B}}}_{\ell +1})$ onto $\Sigma$ and increment $\ell$. If some layer becomes collapsible, we go into the Collapse phase; otherwise, we repeat the Build phase to construct another new layer.

3.5.2 Collapse Phase

Let $L_k$ be the lowest collapsible layer in $\Sigma$. We are going to prune ${{\mathcal {B}}}_k$ which will make all layers above $L_k$ invalid. Correspondingly, some of the unblocked addable edges in ${\mathcal {I}}$ also become invalid because they are generated using blocking edges in ${{\mathcal {B}}}_i$ for $i \in [k+1,\ell ]$. So a key step is to decompose ${{\mathcal {I}}}$ into a disjoint partition $\bigcup _{i=0}^\ell {{\mathcal {I}}}_i$ such that, among the $f_M[B_{\le \ell },I]$ paths in $G_M$ from $B_{\le \ell }$ to I, there are exactly $|I_i|$ paths from $B_i$ to $I_i$ for $i \in [0,\ell ]$, where $I_i$ denotes the set of players covered by ${{\mathcal {I}}}_i$.

We remove $L_i$ for $i \ge k+1$ from $\Sigma$, and we also remove ${{\mathcal {I}}}_i$ for $i \ge k+1$. We change M by flipping the alternating paths from $B_k$ to $I_k$. The sources of these paths form a subset of $B_k$, which are covered by a subset ${{\mathcal {B}}}^*_k \subseteq {{\mathcal {B}}}_k$. The flipping of the alternating paths from $B_k$ to $I_k$ has the effect of replacing ${{\mathcal {B}}}^*_k$ by ${{\mathcal {I}}}_k$ in ${\mathcal {E}}$.

If $k = 0$, it means that the next unmatched player $p_0$ is now matched and the local search has succeeded. Otherwise, some of the addable edges in ${{\mathcal {A}}}_k$ may no longer be blocked due to the removal of ${{\mathcal {B}}}^*_k$ from ${\mathcal {E}}$. We reset ${{\mathcal {I}}}:= {{\mathcal {I}}}_{\le k-1}$. For each edge $(p,D) \in {{\mathcal {A}}}_k$ that becomes unblocked, we delete (p, D) from ${{\mathcal {A}}}_k$, and if $f_M[B_{\le k-1}, I \cup \{p\}] = f_M[B_{\le k-1},I] + 1$,¹ then we extract a $\lambda$-minimal thin edge $(p,D')$ from (p, D) and add $(p,D')$ to ${{\mathcal {I}}}$. After pruning ${{\mathcal {A}}}_k$, we reset $\ell := k$.

We repeat the above as long as some layer in $\Sigma$ is collapsible. When this is no longer the case and $p_0$ is not matched yet, we go back to the Build phase.

4 Analysis

For any $\delta \in (0,1)$, we show that we can set $\gamma = \Theta (\delta )$, $\beta = \gamma ^2$, and $\mu = \gamma ^3$ so that the local search runs in polynomial time, and if the target value 1 is feasible, the local search returns an allocation that achieves a value of $\lambda = 1/(1+3{\hat{c}}+O(\delta {\hat{c}}^2))$ or more. Recall that ${\hat{c}} = \textrm{max}\{v_{p,r}/v_{q,r}: \, p,q \in P \, \wedge \, r \in R \, \wedge \, v_{q,r} > 0\}$.

The key is to show that the stack $\Sigma$ has logarithmic depth for these choices of $\gamma$, $\beta$ and $\mu$. The numbers of blocking edges $|{{\mathcal {B}}}_i|$ for $i \in [0,\ell ]$ induce a signature vector that increases lexicographically as the local search proceeds. Therefore, if $\Sigma$ has logarithmic depth, the local search must terminate in polynomial time before we run out of all possible signature vectors (see the proof of Lemma 6). To show that $\Sigma$ has logarithmic depth, we are to prove that the number of blocking edges increases geometrically from one layer to the next as we go up $\Sigma$.

We extract Lemma 1 below from [11].

Lemma 1

(Lemma 12 in [11]) For $i \in [0,\ell ]$, let $z_i = |{{\mathcal {A}}}_i|$ right after the creation of the layer $L_i$. Whenever no layer is collapsible, $|{{\mathcal {A}}}_{i+1}| \ge z_{i+1} - \mu |{{\mathcal {B}}}_{\le i}|$ for $i \in [0,\ell -1]$.

The next result is the same as Lemma 14 in [11], but its proof is changed in order to accommodate our new definition of active and inactive resources.

Lemma 2

For $i \in [0,\ell ]$, $|{{\mathcal {A}}}_i| < \bigl (1+\frac{\beta }{\gamma }\bigr )|{{\mathcal {B}}}_i|$.

Proof

First, we claim that for every blocking edge $b \in \mathcal {B}_i$, there is an edge $a \in \mathcal {A}_i$ such that $v_{max}\bigl (R(b) \cap R(\mathcal {A}_i {\setminus } \{a\})\bigr )\le \beta \lambda$. Take a blocking edge $b \in \mathcal {B}_i$. Let a be the last edge added to $\mathcal {A}_i$ in the chronological order that is blocked by b. Let $\tilde{\mathcal {A}}_i$ be the subset of edges in $\mathcal {A}_i$ that were added to $\mathcal {A}_i$ before a. Some resource in b must be active at the time when a was added to $\mathcal {A}_i$ in order that b blocks a. For this to happen, Definition 1 implies that $v_{max}\bigl (R_b \cap R(\tilde{\mathcal {A}}_i)\bigr ) \le \beta \lambda$. Moreover, the edges added to $\mathcal {A}_i$ after a do not share any resource with b because they are not blocked by b. As a result, $v_{max}\bigl (R(b) \cap R(\mathcal {A}_i {\setminus } \{a\})\bigr )\le \beta \lambda$, establishing our claim.

By our claim, for every $b \in \mathcal {B}_i$, there is an edge $a_b \in \mathcal {A}_i$ such that $v_{max}\bigl (R_b \cap R(\mathcal {A}_i {\setminus } \{a_b\})\bigr ) \le \beta \lambda$. Define $\mathcal {A}'_i = \{a_b: b \in \mathcal {B}_i\}$. Note that $|\mathcal {A}_i'| \le |\mathcal {B}_i|$. Define $\mathcal {A}''_i = \mathcal {A}_i {\setminus } \mathcal {A}_i'$. For every edge $b \in \mathcal {B}_i$, we have $v_{max}\bigl (R_b \cap R(\mathcal {A}_i'')\bigr ) \le v_{max}\bigl (R_b \cap R(\mathcal {A}_i {\setminus } \{a_b\})\bigr ) \le \beta \lambda$. Summing over all edges in $\mathcal {B}_i$, we obtain

$$\begin{aligned} v_{max}\bigl (R(\mathcal {B}_i) \cap R(\mathcal {A}_i'')\bigr ) \le \beta \lambda |\mathcal {B}_i|. \end{aligned}$$

(1)

Since the edges in $\mathcal {A}''_i$ are blocked, for every edge $a \in \mathcal {A}_i''$, more than $\gamma \lambda$ worth of resources in $R_a$ must be shared by edges in $\mathcal {B}_i$. Notice that these are the actual utilities of the resources in $R_a$ with respect to the players of the blocking edges in $\mathcal {B}_i$. By the over-estimation strategy, the over-estimated utilities of these resources in $R_a$ cannot be smaller. As a result, $v_{max}\big (R(\mathcal {B}_i) \cap R_a\bigr ) > \gamma \lambda$. Moreover, every resource in $R(\mathcal {B}_i) \cap R_a$ is occupied by a distinct edge in $\mathcal {B}_i$ because the edges in $\mathcal {B}_i$ are matching edges. Therefore, summing over all edges in $\mathcal {A}''_i$ gives

$$\begin{aligned} v_{max}\bigl (R(\mathcal {B}_i) \cap R(\mathcal {A}_i'')\bigr ) > \gamma \lambda |\mathcal {A}_i''|. \end{aligned}$$

(2)

We conclude from (1) and (2) that $\beta \gamma |\mathcal {B}_i| \ge v_{max}\bigl (R(\mathcal {B}_i) \cap R(\mathcal {A}''_i)\bigr ) > \gamma \lambda |\mathcal {A}_i''|$, which implies that $|\mathcal {A}_i''| < \beta |\mathcal {B}_i|/\gamma$. As a result, $|\mathcal {A}_i| = |\mathcal {A}'_i| + |\mathcal {A}_i''| < |\mathcal {B}_i| + \beta |\mathcal {B}_i|/\gamma = (1+\beta /\gamma )|\mathcal {B}_i|$. $\square$

The analogous version of Lemma 3 below in [11] gives the inequality $|{{\mathcal {B}}}'_i| < \frac{(2+\gamma )}{\beta } |{{\mathcal {A}}}_i|$ in the restricted max–min case. We prove that a similar bound with the extra over-estimation factor ${\hat{c}}$ holds for the general max–min case.

Lemma 3

Let ${{\mathcal {B}}}'_i$ be the subset of ${{\mathcal {B}}}_i$ such that all resources in ${{\mathcal {B}}}'_i$ are inactive, i.e., ${{\mathcal {B}}}'_i = \bigl \{b \in {{\mathcal {B}}}_i \mid v_{max}\bigl (R_b \cap R({{\mathcal {A}}}_i)\bigr ) > \beta \lambda \bigr \}$. Then, $|{{\mathcal {B}}}'_i| < \frac{(2+\gamma ){\hat{c}}}{\beta } |{{\mathcal {A}}}_i|$.

Proof

Summing over the edges in ${{\mathcal {B}}}'_i$ gives $v_{max}\bigl (R({{\mathcal {B}}}'_i) \cap R({{\mathcal {A}}}_i)\bigr ) > \beta \lambda |{{\mathcal {B}}}'_i|$.

Every edge $(p,D) \in {{\mathcal {A}}}_i$ is $(1+\gamma )\lambda$-minimal by definition, so $v_p(D) \le (2+\gamma )\lambda$. Summing over the edges in ${{\mathcal {A}}}_i$ gives $\sum _{(p,D)\in {{\mathcal {A}}}_i} v_p(D) \le (2+\gamma )\lambda |{{\mathcal {A}}}_i|$. The definition of ${\hat{c}}$ implies that $v_r^\textrm{max}\le {\hat{c}}\,v_{p,r}$, which implies that $v_{max}(R({{\mathcal {A}}}_i)) \le \sum _{(p,D)\in {{\mathcal {A}}}_i} {\hat{c}} \, v_p(D)\le (2+\gamma )\lambda {\hat{c}}\,|{{\mathcal {A}}}_i|$.

Combining the inequalities above gives $\beta \lambda |{{\mathcal {B}}}'_i| < v_{max}(R({{\mathcal {B}}}'_i) \cap R({{\mathcal {A}}}_i)) \le v_{max}(R({{\mathcal {A}}}_i)) \le (2+\gamma )\lambda {\hat{c}}\, |{{\mathcal {A}}}_i|$, which implies that $|{{\mathcal {B}}}'_i| < \frac{(2+\gamma ){\hat{c}}}{\beta } |{{\mathcal {A}}}_i|$. $\square$

Lemma 3 is instrumental in proving Lemma 4 below which is the key to showing a geometric growth in the numbers of blocking edges. Its proof explains why we need to set $\lambda$ to be $\bigl (1 + 3{\hat{c}} + O(\delta {\hat{c}}^2)\bigr )^{-1}$. We give the proof in the appendix; it is a careful adaptation of an analogous result in [11].

Lemma 4

Suppose that the target value 1 is feasible for the general max–min allocation problem. Suppose that $\lambda = \bigl (1 + 3{\hat{c}} + O(\delta {\hat{c}}^2)\bigr )^{-1}$. Then, immediately after the construction of a new layer $L_{\ell +1}$, if no layer is collapsible, then $|{{\mathcal {A}}}_{\ell +1}| > 2\mu |{{\mathcal {B}}}_{\le \ell }|$.

We show how to use Lemma 4 to obtain the geometric growth.

Lemma 5

If no layer is collapsible, then $\bigl |{{\mathcal {B}}}_{i+1}\bigr | > \frac{\gamma ^3}{1+\gamma }\bigl |{{\mathcal {B}}}_{\le i}\bigr |$. Hence, $\bigl |{{\mathcal {B}}}_{\le i+1}\bigr | > \bigl (1 + \frac{\gamma ^3}{1+\gamma }\bigl |{{\mathcal {B}}}_{\le i}\bigr |\bigr )$.

Proof

Let $(L_0,L_1,\ldots ,L_\ell )$ be the current stack $\Sigma$. Take any $i \in [0,\ell -1]$. Since the most recent construction of $L_{i+1}$, $L_{i+1}$ and any layer below it is not collapsible. If not, $L_{i+1}$ would be deleted, which means that there would be another construction of it after the most recent construction, a contradiction. Therefore, Lemma 4 implies that $z_{i+1} > 2\mu |{{\mathcal {B}}}_{\le i}|$, where $z_{i+1}$ is the value of $|{{\mathcal {A}}}_{i+1}|$ right after the construction of $L_{i+1}$. By Lemma 1, $|{{\mathcal {A}}}_{i+1}| \ge z_{i+1} - \mu |{{\mathcal {B}}}_{\le i}|$. Substituting $z_{i+1} > 2\mu |{{\mathcal {B}}}_{\le i}|$ into this inequality gives $|{{\mathcal {A}}}_{i+1}| > 2\mu |{{\mathcal {B}}}_{\le i}| - \mu |{{\mathcal {B}}}_{\le i}| = \mu |{{\mathcal {B}}}_{\le i}|$. Lemma 2 implies that $|{{\mathcal {B}}}_{i+1}|> \frac{\gamma }{\gamma + \beta } |{{\mathcal {A}}}_{i+1}| > \frac{\gamma \mu }{\gamma +\beta }|{{\mathcal {B}}}_{\le i}|$. Plugging in $\beta = \gamma ^2$ and $\mu = \gamma ^3$ gives $|{{\mathcal {B}}}_{i+1}| > \gamma ^3|{{\mathcal {B}}}_{\le i}|/(1+\gamma )$. $\square$

The next result shows that a polynomial running time follows from Lemma 5.

Lemma 6

Suppose that the target value 1 is feasible for the general max–min allocation problem. Then, the local search matches a player in $poly(m,n)\cdot m^{poly(1/\delta )}$ time.

Proof

The proof follows the argument in [1]. Let $h = \gamma ^3/(1+\gamma )$. Define the signature vector $(s_1,s_2,...,s_\ell ,\infty )$, where $s_i = \bigl \lfloor \log _{1/(1-\mu )} \bigl (|{{\mathcal {B}}}_i|h^{-i-1}\bigr )\bigr \rfloor$.

By Lemma 5, $|{{\mathcal {B}}}_\ell | \ge h|{{\mathcal {B}}}_{\le \ell -1}| \ge h|{{\mathcal {B}}}_{\ell -1}|$. So $\infty > s_\ell \ge s_{\ell -1}$, which means that the coordinates of the signature vector are non-decreasing.

When a (lowest) layer $L_t$ is collapsed in the Collapse phase, we update ${{\mathcal {B}}}_t$ to ${{\mathcal {B}}}'_t$ where $(1-\mu )|{{\mathcal {B}}}_t| > |{{\mathcal {B}}}'_t|$. By definition, the signature vector is updated to $(s_1,s_2,...,s'_t)$ where $s'_t \le s_t - 1$. So the signature vector decreases lexicographically. By Lemma 5, the number of layers in $\Sigma$ is at most $\log _{1+h}m$, where m is the number of players. One can verify that the sum of coordinates in every signature vector is at most $U^2$ where $U = \log m \cdot O(\frac{1}{\mu h}\log \frac{1}{h})$. Every signature vector corresponds to a distinct partition of an integer that is no more than $U^2$.

By counting the distinct partitions of integers that are no more than $U^2$, we get the upper bound of $m^{O(\frac{1}{\mu h}\log \frac{1}{h})}$ on the number of signature vectors. Since $\gamma = \Theta (\delta )$, $\mu = \gamma ^3$, and $h = \gamma ^3/(1+\gamma )$, this upper bound is $m^{ poly (1/\delta )}$. This also bounds the number of calls on Build and Collapse. It is not difficult to make the construction of a layer and the collapse of a layer run in $poly (m,n)$ time. $\square$

We have not discussed how to handle the case that the target value 1 is infeasible for the general max–min allocation problem. In this case, the local search must fail at some point. From the previous proofs, we know that as long as the conclusion of Lemma 4 holds immediately after the construction of a new layer $L_{\ell + 1}$, that is, if no layer is collapsible, then $|{{\mathcal {A}}}_{\ell +1}| > 2\mu |{{\mathcal {B}}}_{\le \ell }|$, the local search must succeed and finish in polynomial time. As a result, we must encounter a situation that no layer is collapsible and yet $|{{\mathcal {A}}}_{\ell +1}| \le 2\mu |{{\mathcal {B}}}_{\le \ell }|$ for the first time during the local search. This situation can be checked explicitly. It means that the guessed target value is too high. So we abort the local search and continue with the binary search probe for the next guess of the target value. Since the conclusion of Lemma 4 has held so far, the running time up to the point of abortion is polynomial. This completes the proof of Theorem 2.

5 Conclusion

We provide two solutions for the general max–min fair allocation problem. If every resource has a positive utility for every player, the problem can be transformed to the machine covering problem using our over-estimation strategy. By using an existing polynomial time approximation scheme for the machine covering problem, we obtain a $\bigl (\frac{c}{1-\epsilon }\bigr )$-approximation algorithm that runs in polynomial time, where $\epsilon$ is any constant in the range (0, 1) and $c = \textrm{max}\{v_{p,r}/v_{q,r}: \, p, q \in P \, \wedge \, r \in R \}$. If some resource has zero utility for some players, we show how to combine the over-estimation strategy with the approximation algorithm in [10] for the restricted max–min allocation problem to obtain an approximation ratio of $1+3{\hat{c}}+O(\delta {\hat{c}}^2)$ for any $\delta \in (0,1)$ in polynomial time, where ${\hat{c}} = \textrm{max}\{v_{p,r}/v_{q,r}: \, p,q \in P \, \wedge \, r \in R \, \wedge \, v_{q,r} > 0\}$. We conclude with two research questions. The first question is whether the approximation ratios presented here can be improved further. Despite its theoretical guarantee, the local search step is still quite challenging to implement. So the second question is whether there is a simpler algorithm that can also achieve a good approximation ratio in polynomial time.

Appendix A: Proof of Lemma 4

We give a proof by contradiction. Suppose to the contrary that $z_{\ell +1}=|{{\mathcal {A}}}_{\ell +1}| < 2\mu |{{\mathcal {B}}}_{\le \ell }|$.

For every $p \in P$, a configuration C for p is a subset of resources (fat or thin) such that p is interested in the resources in C and $v_p(C) \ge 1$. Let ${{\mathcal {C}}}_p(1)$ denote the set of all such configurations for p. The LP relaxation below is the configuration LP for the general max–min allocation problem.

Primal                     Min   0

$$\begin{aligned}\begin{array}{rlrclll} \mathbf{s.t.} &{}&{} \displaystyle \sum _{C\in {{{\mathcal {C}}}_p(1)}}x_{p,C} &{} \ge &{} 1 , &{}~~~~&{} \forall p \in P, \\ &{}&{} \displaystyle \sum _{p\in P}\sum _{r\in C}x_{p,C}&{} \le &{} 1, &{} &{} \forall r\in R, \\ &{}&{} x_{p,C} &{} \ge &{} 0, &{} &{} \forall p \in P, \,\, \forall C \in {{\mathcal {C}}}_p(1). \\ \end{array} \end{aligned}$$

Dual                     Max $\displaystyle \quad \sum _{p \in P}y_p - \sum _{r \in R}z_r$

$$\begin{aligned}\begin{array}{rlrclll} \mathbf{s.t.} &{}&{} \displaystyle y_p &{} \le &{} \displaystyle \sum _{r \in C}z_r, &{} ~~~~ &{} \forall p \in P, \,\, \forall C\in {{\mathcal {C}}}_p(1) \\ &{}&{} y_p &{} \ge &{} 0, &{} &{} \forall p \in P, \\ &{}&{} z_r &{} \ge &{} 0, &{} &{} \forall r \in R. \\ \end{array} \end{aligned}$$

We will define a solution for the dual of configuration LP and show that it is feasible and gives a positive objective function value. We can then scale up this feasible dual solution arbitrarily, which gives an arbitrarily large objective function value. Therefore, the dual of the configuration LP is unbounded, which implies the contradiction that the configuration LP is infeasible. Our proof is largely the same as the counterpart of Lemma 4 in [10, 11], but adaptions to our setting is needed in defining the dual solution and in proving that the objective function value is positive.

To define the dual solution, we need to classify certain subsets of players and resources. Consider the moment right after the completion of the construction of the layer $L_{\ell +1}$.

Let $\Pi$ be a maximum set of node-disjoint paths in $G_M$ from $B_{\le \ell }$ to $A_{\ell +1} \cup I$. Let $src (\Pi )$ denote the set of sources of the paths in $\Pi$. It is possible that the sets $B_{\le \ell }$ and $A_{\ell +1} \cup I$ share some common player, in which case $\Pi$ may contain a path that consists of a single node. We call such a path a trivial path. Other paths in $\Pi$ are non-trivial paths. Let $\Pi ^+$ be the set of non-trivial paths in $\Pi$, i.e., paths with at least one edge. Let $src ({\Pi ^+})$ denote the set of sources of the paths in $\Pi ^+$. The non-trivial paths in $\Pi$ are alternating, that is, for $i \ge 0$, every $(2i+2)$-th edge belongs to M and every $(2i+1)$-th edge does not.

If we flip the alternating paths in $\Pi$, M is updated to another maximum matching of G. Let $M \oplus \Pi$ denote the resulting maximum matching. Note that flipping a trivial path in $\Pi$ does not change anything. The players in $src ({\Pi ^+})$ are not matched in M, but they are now matched in $M \oplus \Pi$, which means that there are directed edges in $G_{M \oplus \Pi }$ from fat resources to the players in $src (\Pi ^+)$. So players in $src (\Pi ^+)$ have in-degree exactly one in $G_{M\oplus \Pi }$.

Let ${P^+}$ be the set of players that can be reached in $G_{M \oplus \Pi }$ from $B_{\le \ell }{\setminus } src (\Pi )$. Let ${R^+_f}$ be the set of fat resources that can be reached in $G_{M \oplus \Pi }$ from $B_{\le \ell }{\setminus } src (\Pi )$. Let ${R^+_t}$ be the set of inactive thin resources. We can now define the desired dual solution $(\{y_p^*\}_{p \in P},\{z_r^*\}_{r \in R})$ as follows:

$$\begin{aligned} y_p^*={\left\{ \begin{array}{ll} \ 1-(1+\gamma )\lambda &{} \text {if }p \in P^+,\\ \ 0 &{} \text {otherwise}. \end{array}\right. } \\ z_r^*={\left\{ \begin{array}{ll} \ 1-(1+\gamma )\lambda &{} \text {if }r \in R^+_f,\\ \ v_r^{\textrm{max}} &{} \text {if } r \in R^+_t,\\ \ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

We will need the following properties of $G_{M\oplus \Pi }$.

Proposition 1

In $G_{M\oplus \Pi }$, the players in $B_{\le \ell } {\setminus } src (\Pi )$ have zero in-degrees, and the fat resources in $R_f^+$ have out-degrees exactly one.

Proof

The players in $B_{\le \ell }$ are matched by thin edges in ${\mathcal {E}}$, so they are not matched by M to fat resources. Hence, players in $B_{\le \ell }$ have in-degree zero in $G_M$. After flipping the paths in $\Pi$, among the players in $B_{\le \ell }$, only those in $src (\Pi )$ may now be matched to fat resources in $M \oplus \Pi$, and therefore, players in $B_{\le \ell } {\setminus } src (\Pi )$ are still unmatched in $M \oplus \Pi$. So players in $B_{\le \ell } {\setminus } src (\Pi )$ have zero in-degrees.

By the definition of $R_f^+$, for every resource $r \in R_f^+$, there is a path to r in $G_{M \oplus \Pi }$ from a player in $B_{\le \ell } \setminus src (\Pi )$. If r is not matched in $M \oplus \Pi$, we can flip this path to increase the matching size, contradicting the fact that $M\oplus \Pi$ is a maximum matching. So r is matched in $M\oplus \Pi$, implying that its out-degree in $G_{M\oplus \Pi }$ is exactly one. $\square$

Note that the rest of the proof considers the moment right after completing the construction of $L_{\ell +1}$, and there is no more $(1+\gamma )\lambda$-minimal addable edge that can be discovered.

1.1 A.1 Feasibility

We first prove that the dual solution is feasible, which requires us to show that $y_p^* \le \sum _{r \in C} z_r^*$, $\forall p \in P$, $\forall C \in {{\mathcal {C}}}_i(1)$. The feasibility constraint is trivially satisfied if $p\notin P^+$ because $y_p^* = 0$ in this case and $z_r^* \ge 0$ for all $r \in R$. Take any $p \in P^+$. So $y_p^* = 1 - (1+\gamma )\lambda$ by definition. As $p \in P^+$, there is a path $\pi$ from $B_{\le \ell } {\setminus } src (\Pi )$ to p in $G_{M \oplus \Pi }$. We prove that $\sum _{r \in C} z_r^* \ge 1-(1+\gamma )\lambda$ for all $C \in {{\mathcal {C}}}_p(1)$.

Case 1: C contains a fat resource $r_f$. Since $r_f$ belongs to a configuration for p, p desires r, which means that $G_{M\oplus \Pi }$ contains either the directed edge $(p,r_f)$ or the directed edge $(r_f,p)$. We show that $r_f \in R_f^+$ below. It immediately follows that $z_{r_f}^* = 1 - (1+\gamma )\lambda$, so $\sum _{r \in C} z_r^* \ge z_{r_f}^* = 1 - (1+\gamma )\lambda$.

If $G_{M\oplus \Pi }$ contains the edge $(p,r_f)$, then $r_f \in R_f^+$ because we can follow the path $\pi$ to p and then the edge $(p,r_f)$ to $r_f$. Suppose that $G_{M\oplus \Pi }$ contains the edge $(r_f,p)$. By the property of matching, p has in-degree at most one in $G_{M\oplus \Pi }$, so $(r_f,p)$ is the only edge entering p. It follows that the path $\pi$ reaches $r_f$ first before p, so the prefix of $\pi$ up to $r_f$ certifies that $r_f \in R_f^+$.

Case 2: C contains only thin resources. We consider the moment after completing the construction of $L_{\ell +1}$. Recall that $\Pi$ is a maximum set of node-disjoint paths in $G_M$ from $B_{\le \ell }$ to $A_{\ell +1} \cup I$. The existence of the path $\pi$ in $G_{M \oplus \Pi }$ to p means that there are more than $|\Pi |$ node-disjoint paths in $G_M$ from $B_{\le \ell }$ to $A_{\ell +1} \cup I \cup \{p\}$. Therefore, p is an addable player according to Definition 2. However, we cannot find any $(1+\gamma )\lambda$-minimal addable edge for p upon the completion of $L_{\ell +1}$. Since $C \in {{\mathcal {C}}}_p(1)$, we have $v_p(C) \ge 1$. Therefore, the total utility of active resources in C for p must be less than $(1+\gamma )\lambda$, which means that the total utility of inactive resources in C for p is greater than $1 - (1+\gamma )\lambda$. Since $R_t^+$ is the set of inactive thin resources, we have $\sum _{r \in C} z_r^* \ge \sum _{r \in C \cap R_t^+} z_r^* = \sum _{r \in C \cap R_t^+} v_r^\textrm{max}\ge \sum _{r \cap C \cap R_t^+} v_{p,r} > 1-(1+\gamma )\lambda$.

1.2 A.2 Positive Objective Function Value

By definition, $y_p^* = 0$ if $p \notin P^+$, and $z_r^* = 0$ if $r \notin R_f^+ \cup R_t^+$. So we only need to prove that $\sum _{p \in P^+} y_p^* - \sum _{r \in R_f^+} z_r^* - \sum _{r \in R_t^+} z_r^* > 0$.

First we consider the value of $\sum _{p\in P^+}y_p^* - \sum _{r\in R_f^+} z_r^*$. By definition, $y_p^* = z_r^* = 1-(1+\gamma )\lambda$ for all $p\in P^+$ and $r \in R_f^+$. Then

$$\begin{aligned} \sum _{p \in P^+}y_p^* - \sum _{r\in R_f^+} z_r^* = \Bigl (1-(1+\gamma )\lambda \Bigr )\left( |P^+|-|R_f^+|\right) . \end{aligned}$$

Take any $r \in R_f^+$. By Proposition 1, there is an edge $(r_f,p)$ in $G_{M \oplus \Pi }$ for some player p, i.e., p is matched to $r_f$ in $M\oplus \Pi$. There is a path from $B_{\le \ell } {\setminus } src (\Pi )$ to $r_f$ by the definition of $R_f^+$, which implies that there is a path from $B_{\le \ell } {\setminus } src (\Pi )$ to p. Hence, $p \in P^+$. We can thus charge every $r_f \in R_f^+$ to a player in $P^+$ such that, by the property of matching, no player in $P^+$ is charged more than once. As discussed previously, every player in $B_{\le \ell } {\setminus } src (\Pi )$ is not matched in $M\oplus \Pi$, so players in $B_{\le \ell } \setminus src (\Pi )$ are not charged. Moreover, every player in $B_{\le \ell } {\setminus } src (\Pi )$ belongs to $P^+$ because there is a trivial path from every such player to himself/herself. As a result,

$$\begin{aligned} |P^+|-|R_f^+| \ge |B_{\le \ell }\setminus src (\Pi )|. \end{aligned}$$

Since $\Pi$ is a maximum set of node-disjoint paths in $G_M$ from $B_{\le \ell }$ to $A_{\ell +1} \cup I$, we have $| src (\Pi )| = |\Pi | \le |A_{\ell +1}| + |I|$. Therefore,

$$\begin{aligned} |P^+|-|R_f^+| \ge |B_{\le \ell }\setminus src (\Pi ) | \ge |{{\mathcal {B}}}_{\le \ell }|-|{{\mathcal {A}}}_{\ell +1}|-|{{\mathcal {I}}}|. \end{aligned}$$

We conclude that

$$\begin{aligned} \sum _{p_i \in P^+}y_i^* - \sum _{r_j\in R_f^+} z_j^*= & {} \Bigl (1-(1+\gamma )\lambda \Bigr )\left( |P^+|-|R_f^+|\right) \nonumber \\\ge & {} \Bigl (1-(1+\gamma )\lambda \Bigr ) \Bigl (|{{\mathcal {B}}}_{\le \ell }|-|{{\mathcal {A}}}_{\ell +1}|-|{{\mathcal {I}}}|\Bigr ). \end{aligned}$$

(A.1)

It remains to analyze $\sum _{r \in R_t^+} z_r^*$. Every resource $r \in R_t^*$ is inactive. By definition, the inactive resources appear in three disjoint subsets of thin edges: (i) ${{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell }$, (ii) ${{\mathcal {A}}}_{\ell +1} \cup {{\mathcal {I}}}$, and (iii) ${{\mathcal {B}}}'_{\ell +1} = \bigl \{b \in {{\mathcal {B}}}_{\ell +1}: v_\textrm{max}\bigl (R_b \cap R({{\mathcal {A}}}_{\ell +1}) \bigr )> \beta \lambda \bigr \}$. It follows that

$$\begin{aligned} \sum _{r\in R_t^+} z_r^*= & {} \sum _{r \in R_t^+} v_r^{\textrm{max}} \\= & {} v_{\textrm{max}}\bigl (R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })\bigr ) + v_{\textrm{max}}\bigl (R({{\mathcal {A}}}_{\ell +1}\cup {{\mathcal {I}}})\bigr ) + v_{\textrm{max}}\bigl (R({{\mathcal {B}}}'_{\ell +1})\bigr ). \end{aligned}$$

We first consider $v_{\textrm{max}}\bigl (R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })\bigr )$. Every edge (p, D) in ${{\mathcal {A}}}_{\le \ell }$ is a blocked addable edge. So $v_p\bigl (D {\setminus } R({{\mathcal {B}}}_{\le \ell })\bigr ) < \lambda$. Every edge in ${{\mathcal {B}}}_{\le \ell }$ is $\lambda$-minimal. Thus, we can use the over-estimate strategy to bound $v_\textrm{max}\bigl (R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })\bigr )$:

$$\begin{aligned} v_{\textrm{max}}(R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })){} & {} \le \sum _{(p,D)\in {{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell }} {\hat{c}} \cdot v_p(D) \nonumber \\ [.5em]\le & {} {\hat{c}} \cdot \lambda |{{\mathcal {A}}}_{\le \ell }| + {\hat{c}} \cdot 2\lambda |{{\mathcal {B}}}_{\le \ell }| \nonumber \\{} & {} \mathop {<}\limits ^{\textrm{Lemma}~2} \left( 3+\frac{\beta }{\gamma }\right) {\hat{c}}\cdot \lambda |{{\mathcal {B}}}_{\le \ell }|. \end{aligned}$$

(A.2)

We analyze $v_\textrm{max}\bigl (R({{\mathcal {A}}}_{\ell +1}\cup {\mathcal {I}})\bigr )$ next. Every edge in ${{\mathcal {A}}}_{\ell +1}$ is $(1+\gamma )\lambda$-minimal, and every edge in ${\mathcal {I}}$ is $\lambda$-minimal. Therefore,

$$\begin{aligned} v_{\textrm{max}}\bigl (R({{\mathcal {A}}}_{\ell +1}\cup {\mathcal {I}})\bigr )\le & {} \sum _{(p,D)\in {{\mathcal {A}}}_{\ell +1}\cup {{\mathcal {I}}}} {\hat{c}} \cdot v_p(D) \nonumber \\\le & {} (2+\gamma ) {\hat{c}} \cdot \lambda |{{\mathcal {A}}}_{\ell +1}| + 2{\hat{c}} \cdot \lambda |{\mathcal {I}}|. \end{aligned}$$

(A.3)

Lastly, consider $v_{\textrm{max}}\bigl (R({{\mathcal {B}}}'_{\ell +1})\bigr )$. Edges in ${{\mathcal {B}}}'_{\ell +1}$ are $\lambda$-minimal. Therefore,

$$\begin{aligned} v_{\textrm{max}}\bigl (R({{\mathcal {B}}}'_{\ell +1})\bigr ){} & {} \le \sum _{(p,D)\in {{\mathcal {B}}}'_{\ell +1}} {\hat{c}} \cdot v_p(D) \nonumber \\{} & {} \le 2{\hat{c}} \cdot \lambda |{{\mathcal {B}}}'_{\ell +1}| \nonumber \\{} & {} \mathop {<}\limits ^{\textrm{Lemma} ~3} \left( \frac{4+2\gamma }{\beta }\right) {\hat{c}}^2 \cdot \lambda |{{\mathcal {A}}}_{\ell +1}|. \end{aligned}$$

(A.4)

Summing (A.2), (A.3)) and (A.4) gives

$$\begin{aligned} \sum _{r\in R_t^+} z_r^* < \left( 3+\frac{\beta }{\gamma }\right) {\hat{c}}\lambda |{{\mathcal {B}}}_{\le \ell }| + \left( (2+\gamma ){\hat{c}} + \left( \frac{4+2\gamma }{\beta }\right) {\hat{c}}^2\right) \lambda |{{\mathcal {A}}}_{\ell +1}| + 2{\hat{c}}\lambda |{\mathcal {I}}|.\nonumber \\ \end{aligned}$$

(A.5)

Combining (A.1) and (A.5) gives

$$\begin{aligned}{} & {} \sum _{p\in P^+}y_p^* - \sum _{r\in R_f^+} z_r^* - \sum _{r\in R_t^+} z_r^* \nonumber \\{} & {} \quad > \left( 1 - (1 + \gamma )\lambda - \left( 3 + \frac{\beta }{\gamma }\right) {\hat{c}}\lambda \right) |{{\mathcal {B}}}_{\le \ell }| \nonumber \\{} & {} \qquad - \left( 1 - (1+\gamma )\lambda + (2+\gamma ){\hat{c}}\lambda + \left( \frac{4+2\gamma }{\beta }\right) {\hat{c}}^2\lambda \right) |{{\mathcal {A}}}_{\ell +1}| \nonumber \\{} & {} \qquad - \bigl (1 - (1+\gamma )\lambda + 2{\hat{c}}\lambda \bigr )|{{\mathcal {I}}}|. \end{aligned}$$

(A.6)

We claim that $|{{\mathcal {I}}}| \le \mu |{{\mathcal {B}}}_{\le \ell }|$ because no layer is collapsible. If $|{{\mathcal {I}}}| > \mu |{{\mathcal {B}}}_{\le \ell }|$, there would be some ${{\mathcal {I}}}_i$ in the disjoint partition $\bigcup _{i=1}^\ell {{\mathcal {I}}}_i$ of ${\mathcal {I}}$ such that $|{{\mathcal {I}}}_i| > \mu |{{\mathcal {B}}}_i|$. Note that $|{{\mathcal {I}}}_i| = |I_i|$ because $I_i$ consists of the destinations of node-disjoint paths from ${{\mathcal {B}}}_i$ to ${{\mathcal {I}}}_i$. Also, $|{{\mathcal {B}}}_i| = |B_i|$ because edges in ${{\mathcal {B}}}_i$ belong to a matching of the hypergraph H, so no two edges in ${{\mathcal {B}}}_i$ are incident to the same player. By definition, $f_M[B_{\le i},I] - f_M[B_{\le i-1},I] = |I_i| > \mu |B_i|$. But then the layer $L_i$ is collapsible according to Definition 4, a contradiction to the assumption that no layer is collapsible. This proves our claim.

We have assumed to the contrary of Lemma 4 that $|{{\mathcal {A}}}_{\ell +1}| \le 2\mu |{{\mathcal {B}}}_{\le \ell }|$.

Plugging $\beta = \gamma ^2$, $\mu = \gamma ^3$, and the two inequalities above into (A.6) gives

$$\begin{aligned}{} & {} \sum _{p \in P^+}y_i^* - \sum _{r\in R_f^+} z_r^* - \sum _{r\in R_t^+} z_r^* \\{} & {} \quad > \bigl (1-3\gamma ^3\bigr ) |{{\mathcal {B}}}_{\le \ell }| - \bigl (1 + \gamma - 3\gamma ^3 - 3\gamma ^4\bigr )\lambda |{{\mathcal {B}}}_{\le \ell }| - \bigl (3+\gamma + 6\gamma ^3 + 2\gamma ^4){\hat{c}}\lambda |{{\mathcal {B}}}_{\le \ell }| \\{} & {} \qquad - \bigl (8\gamma +4\gamma ^2){\hat{c}}^2\lambda |{{\mathcal {B}}}_{\le \ell }|. \end{aligned}$$

One can set $\gamma = \Theta (\delta )$ so that

$$\begin{aligned}{} & {} \frac{1-3\gamma ^3}{(1+\gamma -3\gamma ^3-3\gamma ^4)+(3+\gamma +6\gamma ^3+2\gamma ^4){\hat{c}}+(8\gamma +4\gamma ^2){\hat{c}}^2} \\{} & {} \quad > \frac{1}{1+3{\hat{c}}+O(\delta {\hat{c}}^2)} \\{} & {} \quad = \lambda , \end{aligned}$$

which implies that the objective function value is positive.