Convex-Straight-Skeleton Voronoi Diagrams for Segments and Convex Polygons

Abstract

In this paper, we study the convex-straight-skeleton Voronoi diagrams of line segments and convex polygons. We explore the combinatorial complexity of these diagrams, and provide efficient algorithms for computing compact representations of them.

1 Introduction

Voronoi diagrams are well studied in a variety of fields, primarily computational geometry, but including as well biology, astrophysics, robot motion planning, medical diagnosis, and many others (see, e.g., [3, 5]). Given a collection of disjoint geometric objects, such as points, segments, or polygons, which are called sites, the Voronoi diagram is a subdivision of the plane into cells, such that all the points in the same cell have the same nearest site according to some distance function.

There are many different types of metrics that can be used to determine the nearest site (see, e.g., [5, 16, 22, 25]), depending on the application. In this paper, we focus on a distance function (which is not even a metric), which is based on offsets of a convex polygon. Conceptually, this distance function is measured by locally translating the edges of an underlying convex polygon by some amount (keeping them parallel to their original versions), either inward or outward. Such offset distance functions are motivated by applications to problems in three-dimensional modeling and folding (see, e.g., [1, 7, 8]), and are related to a structure known as the straight skeleton [2, 10, 13]. Throughout this paper, we refer to such functions as convex-straight-skeleton distance functions.

In this paper, we focus on Voronoi diagrams of line segments and convex polygons. We study the combinatorial complexity of the convex-straight-skeleton Voronoi diagrams (CSSVD), and provide efficient algorithms for computing compact representations (in which Voronoi edges, which are polygonal chains, are represented implicitly) of these diagrams.

1.1 Related work

Using the Euclidean metric, the combinatorial complexity of the Voronoi diagram is O(n), where the sites are n points [12] or n disjoint line segments [4, 21]. These diagrams can be constructed in $O(n\log n)$ time, which is worst-case optimal. For a set of n disjoint convex polygonal sites, each of complexity k, the Voronoi Diagram under the Euclidean metric has combinatorial complexity O(kn) [14, 17, 25].

McAllister et al. [18] introduced the concept of a compact representation of a Voronoi diagram of convex polygonal sites, with distance defined either by the standard Euclidean metric or by scaling a convex polygon. (The latter metric is related to, but nevertheless different from the convex-straight-skeleton distance function studied in this paper.) They represent chains of piecewise-algebraic curves as single segments, and show that their compact representation can be used to quickly answer nearest-site queries. Given a compact representation of a Voronoi diagram, one can compute the original diagram in time proportional to its combinatorial complexity. They show that such a compact Voronoi diagram can be stored in O(n) space, where n is the number of sites, irrespective of the complexities of the sites. They provide an algorithm, whose running time is $O(n(\log n+\log k)\log m+m)$, for constructing such a compact Voronoi diagram of n convex polygons, each of size k, using a scaled distance function based on a convex m-gon. Cheong et al. [11] showed that under the Euclidean metric, the farthest-site compact Voronoi diagram of n convex polygons, each of complexity k, also has combinatorial complexity O(n), and it can be computed in $O(n\log ^3 n)$ time.

The combinatorial complexity of the convex-straight-skeleton Voronoi diagram of a set of n points is shown [7] to be O(nm), where m is the combinatorial complexity of the underlying convex polygon defining the convex-straight-skeleton distance. Furthermore, it is shown [ibid.] that compact representations of such diagrams can be computed in $O(n(\log n+\log ^2 m)+m)$ time.

1.2 Our Contributions

In this paper, we generalize the definition of the convex-straight-skeleton distance function, $D_{{\mathcal {P}}}(z,\sigma )$, to be from a point z to an object $\sigma$ (either a line segment or a convex polygon, rather than just another point), where ${{\mathcal {P}}}$ is, as before, an m-sided convex polygon. Next, we study the properties and complexities of both nearest- and farthest-site convex-straight-skeleton Voronoi diagrams of disjoint line segments and convex polygons.

We show that the combinatorial complexity of the nearest-site convex-straight-skeleton Voronoi diagram (NSCSSVD) of n disjoint line segments is O(nm), which is asymptotically the same as that of the nearest-site Voronoi diagram of n point sites. Next, we prove that the combinatorial complexity of the nearest-site Voronoi diagram of n polygonal sites, each having at most k sides, is $O(n(m+k))$. Then, we show that the farthest-site Voronoi diagrams for both line segments and convex polygons are tree-like structures (in the sense that the diagram does not contain any finite cells), and that they have the same combinatorial complexity as their nearest-site counterparts.

Finally, we show that one can compute a compact representation of NSCSSVD of n line segments in $O(n(\log n+\log ^2m)+m^2)$ time, and a similar structure for n convex polygon sites, each of complexity at most k, in $O(n(\log n+\log k \log ^2m)+m^2)$ time.

Our algorithms are based on new insights into the geometry of convex-straight-skeleton distance functions with respect to line segment and convex polygon, which allow us to show how to compute efficiently a number of geometric primitives for these types of sites. For instance, we present an $O(\log m)$-time algorithm for computing the distance $D_{{\mathcal {P}}}(z, s)$ between a point z and a line segment s, using the offset distance defined by a convex m-gon ${{\mathcal {P}}}$. We also present an $O(\log ^2m )$-time algorithm for computing another elementary query, ${\textit{vertex}}(s_1,s_2,s_3)$: Given three line segments $s_1$, $s_2$, and $s_3$, find the point that is equidistant from the three segments. Our data structures for answering both types of queries require $O(m^2)$ preprocessing time. For convex polygon sites, we show that the elementary query operation $D_{{\mathcal {P}}}(z,q)$ can be answered in $O(\log k\log m)$ time, where z is a point and q is a convex polygon with at most k sides. We also show that the primitive ${\textit{vertex}}(q_1,q_2,q_3)$, which returns the point equidistant from three sites, runs in $O(\log k \log ^2 m)$ time, where $q_i$ ($i \in \{1,2,3\}$) is a convex polygon with at most k sides. Both operations use data structures requiring $O(m^2)$ preprocessing time.

1.3 Organization

The paper is organized as follows. First, we give some relevant definitions and preliminaries in Sect. 2. In Sect. 3, we introduce some properties and definitions of the distance function $D_{{{\mathcal {P}}}}$. Then, the combinatorial complexity of NSCSSVD of line segments and convex polygons is studied in Sect. 4. We introduce necessary primitive tools for computing NSCSSVD in Sect. 5. We illustrate the computation of the compact representation of NSCSSVD in Sect. 6. Finally, the farthest-site convex-straight-skeleton Voronoi diagram (FSCSSVD) is studied in Sect. 7. We end in Sect. 8 with some concluding remarks.

2 Preliminaries

Let us borrow a few definitions from an earlier paper [7]. Given a convex polygon ${{\mathcal {P}}}$, described as the intersection of m closed half-planes $\{H_i\}$, an offset copy of ${{\mathcal {P}}}$ (offset by $\varepsilon$), denoted by $O_{{{\mathcal {P}}},\varepsilon }$, is defined as the intersection of the closed half-planes $\{H_i(\varepsilon )\}$, where ${H_i(\varepsilon )}$ is the half-plane parallel to $H_i$ with bounding line translated by $\varepsilon$ in a direction orthogonal to the line. Depending on whether the value of $\varepsilon$ is positive or negative, the translation is done, respectively, outward or inward of ${{\mathcal {P}}}$; see Fig. 1a. Let $\varepsilon _0 < 0$ be the value for which $O_{{{\mathcal {P}}},\varepsilon _0}$ degenerates into a single point c (or a line segment s). We say that $r=|\varepsilon _0|$ is the radius of ${{\mathcal {P}}}$, and the point c (or any point on s) is the center of ${{\mathcal {P}}}$.

Fig. 1

a Offsets of a convex polygon ${{\mathcal {P}}}$, drawn along its straight skeleton (which is identical to the medial axis of ${{\mathcal {P}}}$); b Offsets of the convex polygon $(-{{\mathcal {P}}})$ along the straight skeleton of ${{\mathcal {P}}}$

Using the above concept, the convex-straight-skeleton distance function $D_{{\mathcal {P}}}$ from one point to another point, and to a general object, is defined as follows.

Definition 1

(Point-to-point distance [7]) Let $z_1$ and $z_2$ be two points in ${\mathbb {R}}^2$, and $O_{{{\mathcal {P}}},\varepsilon }$ be an offset of ${{\mathcal {P}}}$, such that $z_2$ lies on the boundary of the translated copy of $O_{{{\mathcal {P}}},\varepsilon }$ centered at $z_1$. The convex-straight-skeleton distance from $z_1$ to $z_2$ is defined as $D_{{\mathcal {P}}}(z_1,z_2) = \frac{\varepsilon +|\varepsilon _0|}{|\varepsilon _0|} = \frac{\varepsilon }{|\varepsilon _0|}+1$.

Note that this distance function is not a metric since it is not symmetric. On the other hand, observe that $D_{{\mathcal {P}}}(z_1,z_2)=D_{-{{\mathcal {P}}}}(z_2,z_1)$, where $(-{{\mathcal {P}}})=\{-z|z\in {{\mathcal {P}}}\}$ is a “flipped” copy of ${{\mathcal {P}}}$; see Fig. 1b. This fact is widely used to compute the Voronoi diagram of point sites [7].

Definition 2

(Point-to-object distance) Let z and $\sigma$ be a point and an object, respectively, in ${\mathbb {R}}^2$. The convex-straight-skeleton distance from z to $\sigma$ is defined as $D_{{\mathcal {P}}}(z,\sigma )=\min _{z' \in \sigma }D_{{\mathcal {P}}}(z,z')$.

Let us generalize our distance function to an object-to-point distance as follows.

Definition 3

(Object-to-point distance) Let $\sigma$ and z be an object and a point, respectively, in ${\mathbb {R}}^2$. The convex-straight-skeleton distance from $\sigma$ to z is defined as $D_{{\mathcal {P}}}(\sigma ,z)=\min _{z' \in \sigma }D_{{\mathcal {P}}}(z',z)$.

The following lemma is crucial for our analysis.

Lemma 1

$D_{{\mathcal {P}}}(z,\sigma )=D_{-{{\mathcal {P}}}}(\sigma ,z)$.

Proof

Let $z_1$ be a point in $\sigma$, such that $D_{{\mathcal {P}}}(z,z_1) = D_{{\mathcal {P}}}(z,\sigma )$. Since $D_{{\mathcal {P}}}(z,z_1) = D_{-{{\mathcal {P}}}}(z_1,z)$, and $D_{-{{\mathcal {P}}}}(\sigma ,z) = \min _{z'\in \sigma }D_{-{{\mathcal {P}}}}(z',z)$ by Definition 3, we have that $D_{-{{\mathcal {P}}}}(\sigma ,z)\le D_{{\mathcal {P}}}(z,\sigma )$.

Similarly, let $z_2$ be a point in $\sigma$, such that $D_{-{{\mathcal {P}}}}(z_2,z) = D_{-{{\mathcal {P}}}}(\sigma ,z)$. Since $D_{-{{\mathcal {P}}}}(z_2,z) = D_{{\mathcal {P}}}(z,z_2)$, and $D_{{\mathcal {P}}}(z,\sigma ) = \min _{z'\in \sigma }D_{{\mathcal {P}}}(z,z')$ by Definition 2, we have that $D_{{\mathcal {P}}}(z,\sigma )\le D_{-{{\mathcal {P}}}}(\sigma ,z)$. The claim follows.$\square$

2.1 Basic Properties of $D_{{\mathcal {P}}}$

The following properties hold for the generalized distance function $D_{{\mathcal {P}}}$.

Property 1

[7, §3.1, Prop. 1] The distance function $D_{{\mathcal {P}}}$ induces a Euclidean topology in the plane. In other words, each small neighborhood of a point contains an $L_2$-neighborhood of it, and vice versa.

Property 2

[7, §3.1, Prop. 2] The distance between every pair of points is invariant under translation.

Property 3

[7, Thm. 6] The distance function $D_{{\mathcal {P}}}$ is complete, and for each pair of points $z_1,z_3\in {\mathbb {R}}^2$, there exists a point $z_2 \notin \{z_1,z_3\}$ such that $D_{{\mathcal {P}}}(z_1,z_2) + D_{{\mathcal {P}}}(z_2,z_3) = D_{{\mathcal {P}}}(z_1,z_3)$.

Property 4

[7, Thm. 7] For each pair of points $z_1,z_2\in {\mathbb {R}}^2$, there exists a point $z_3 \ne z_2$, such that $D_{{\mathcal {P}}}(z_1,z_2) + D_{{\mathcal {P}}}(z_2,z_3) = D_{{\mathcal {P}}}(z_1,z_3)$.

It is also easy to observe the following property of $D_{{\mathcal {P}}}$.

Observation 1

Let z be a point and $\sigma$ be a convex object. Then, the function $D_{{\mathcal {P}}}(z,\sigma )$ increases monotonically when z moves along any ray originating at a point on the boundary of $\sigma$ and never crossing it again.

2.2 The Convex-Straight-Skeleton Voronoi Diagram (CSSVD)

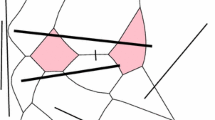
Under the convex-straight-skeleton distance function, the bisector of two points (as defined originally in Ref. [7]) can be 2-dimensional instead of 1-dimensional in degenerate situations. (Figure 2 illustrates this phenomenon. Since the edge of the underlying polygon ${{\mathcal {P}}}$, that is facing the two segments, is parallel to $\ell$, the line joining the two near endpoints of the segments, the offset versions of ${{\mathcal {P}}}$ can slide along $\ell$ without affecting the offset distance. Hence, the bisector has a nonzero area.) This makes the Voronoi diagram of points unnecessarily complicated. To make it simple, as is also done by Klein and Woods [16], we redefine the bisector and Voronoi diagram with respect to the offset distance function $D_{{\mathcal {P}}}$ as follows.

Fig. 2

a Three different positions of the offset polygons from where both line segments are equidistant; b The bisector of two line segments according to the definition used in [7]; and c The bisector according to our definition

Let z be a point, and $\Sigma =\{\sigma _i\}$ a set of objects in the plane. In order to avoid 2-dimensional bisectors between two objects in $\Sigma$, we define the index of the objects as the “tie breaker” for the relation ‘$\prec$’ between distances from z to the objects. That is, $D_{{\mathcal {P}}}(z,\sigma _i) \prec D_{{\mathcal {P}}}(z,\sigma _j)$ if $D_{{\mathcal {P}}}(z,\sigma _i) < D_{{\mathcal {P}}}(z,\sigma _j)$, or, in case $D_{{\mathcal {P}}}(z,\sigma _i) = D_{{\mathcal {P}}}(z,\sigma _j)$, if $i<j$.¹ Note that the relation ‘$\prec$’ does not allow distance equality if $i \ne j$. Therefore, the definition below uses the closure of portions of the plane in order to have proper boundaries between the regions of the diagram.

Definition 4

(Nearest-Site Convex-Straight-Skeleton Voronoi Diagram) Let $\Sigma =\{\sigma _1,\sigma _2,\ldots ,\sigma _n\}$ be a set of sites in ${\mathbb {R}}^2$. For a pair of sites $\sigma _i,\sigma _j \in \Sigma$, the region of $\sigma _i$ with respect to $\sigma _j$ is $NV_{{\mathcal {P}}}^{\sigma _j}(\sigma _i) = \{z\in {\mathbb {R}}^2|D_{{\mathcal {P}}}(z,\sigma _i)\prec D_{{\mathcal {P}}}(z,\sigma _j)\}.$ The bisecting curve $B_{{\mathcal {P}}}(\sigma _i,\sigma _j)$ is defined as $\overline{NV_{{\mathcal {P}}}^{\sigma _j}(\sigma _i)}\cap \overline{NV_{{\mathcal {P}}}^{\sigma _i}(\sigma _j)}$, where ${\overline{X}}$ is the closure of X. The region of a site $\sigma _i$ in the convex-straight-skeleton Voronoi diagram of $\Sigma$ is

$$\begin{aligned} \hbox {NV}_{{\mathcal {P}}}(\sigma _i) = \{z\in {\mathbb {R}}^2\,|\,D_{{\mathcal {P}}}(z,\sigma _i) \prec D_{{\mathcal {P}}}(z,\sigma _j) \quad \forall j\ne i\}. \end{aligned}$$

The nearest-site convex-straight-skeleton Voronoi diagram is the union of the boundaries of the regions

$$\begin{aligned} \hbox {NV}_{{\mathcal {P}}}(\Sigma )=\bigcup _{i\ne j}\left( \overline{NV_{{\mathcal {P}}}(\sigma _i)} \cap \overline{NV_{{\mathcal {P}}}(\sigma _j)}\right) . \end{aligned}$$

In other words, the diagram $\hbox {NV}_{{\mathcal {P}}}(\Sigma )$ is a partition of the plane, such that if a point $p\in {\mathbb {R}}^2$ has more than one closest site, then it belongs to the region of the site with the smallest index. The bisectors between regions are defined by taking the closures of the open regions. The farthest-site convex-straight-skeleton Voronoi diagram, $\hbox {FV}_{{\mathcal {P}}}(\Sigma )$, is defined analogously.

3 $D_{{\mathcal {P}}}$ and the Straight Skeleton of $(-\varvec{{{\mathcal {P}}}})$

3.1 Points

The medial axis of a polygon ${{\mathcal {P}}}$ is defined as the set of points inside ${{\mathcal {P}}}$ that have more than one closest point among the points of $\partial P$. A strong relationship was observed [7] between the continuous change of $O_{{{\mathcal {P}}},\varepsilon }$ (as a function of $\varepsilon$) and the medial axis of ${{\mathcal {P}}}$. It is well-known that the straight skeleton and the medial axis identify for convex polygons. Outside ${{\mathcal {P}}}$, we simply extend this structure by the bisectors of the external angles of ${{\mathcal {P}}}$. It was noticed that if we vary continuously the value of $\varepsilon$, then the vertices of $O_{{{\mathcal {P}}},\varepsilon }$ slide along the edges of the medial axis of ${{\mathcal {P}}}$. This observation was used for computing efficiently the convex-straight-skeleton distance in the plane. In fact, for our purposes, we need the straight skeleton of $(-{{\mathcal {P}}})$.

Lemma 2

[7, Thm. 10] Allowing O(m) time for preprocessing the polygon $(-{{\mathcal {P}}}),$ the distance $D_{{\mathcal {P}}}(z_1,z_2)$ can be computed in $O(\log m)$ time, where $z_1$ and $z_2$ are two points in ${\mathbb {R}}^2.$

3.2 Line Segments

Let $(-{{\mathcal {P}}})^s$ be the convex polygon obtained by taking the union of translated copies of $(-{{\mathcal {P}}})$ centered at all points belonging to the line segment s. The Split-and-Extruded (SaE) $\varepsilon$-offset copy of $(-{{\mathcal {P}}})^s$, denoted by ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$, is defined to be the convex polygon obtained by taking the union of translated copies of $O_{-{{\mathcal {P}}},\varepsilon }$ centered at all points in s. Note that $(-{{\mathcal {P}}})^s$ (resp., ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$) is the convex-hull of two translated copies of $(-{{\mathcal {P}}})$ (resp., $O_{-{{\mathcal {P}}},\varepsilon }$) centered at the two endpoints of s. Note also that for $\varepsilon _0 = -r$, where r is the radius of $(-{{\mathcal {P}}})$, we have that ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon _0}$ degenerates to s. We refer to s as the center of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$, for $\varepsilon \ge \varepsilon _0$. Furthermore, note that even in the worst case, the complexity of $(-{{\mathcal {P}}})^s$ is not twice the complexity of ${{\mathcal {P}}}$, but at most $|{{\mathcal {P}}}|+2$. (The complexity of $(-{{\mathcal {P}}})^s$ can be smaller than $|{{\mathcal {P}}}|+2$ in the degenerate case in which a common tangent supports an edge of ${{\mathcal {P}}}$.) If we fix the center of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$ at s and increase the value of $\varepsilon$ continuously (starting from $\varepsilon _0$), then the moving vertices of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$ in $(-{{\mathcal {P}}})^s$ (as $\varepsilon$ varies) define the extruded medial axis of $(-{{\mathcal {P}}})^s$. In other words, if we change the value of $\varepsilon$ continuously, the vertices of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$ slide along the edges of the extruded medial axis (see Fig. 3a). Finally, note that the extruded medial axis of $(-{{\mathcal {P}}})^s$ may be different from the medial axis of $(-{{\mathcal {P}}})^s$ (see Fig. 3a, b for a comparison).

Fig. 3

a A convex polygon $(-{{\mathcal {P}}})^s$ (colored in red), and ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$ for different values of $\varepsilon$; the extruded medial axis of $(-{{\mathcal {P}}})^s$ is colored in blue; and b The medial axis of $(-{{\mathcal {P}}})^s$ (colored in blue) (Color figure online)

Let us define the following distance function.

Definition 5

($D_{(-{{\mathcal {P}}})^s}(s,z)$) Let z and s be a point and a line segment, respectively, in ${\mathbb {R}}^2$, and let ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$ be an SaE offset copy of $(-{{\mathcal {P}}})^s$ (centered at s), such that ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$ contains z on its boundary. The offset distance from s to z (with respect to ${{\mathcal {P}}}$) is defined as $D_{(-{{\mathcal {P}}})^s}(s,z)= \frac{\varepsilon +|\varepsilon _0|}{|\varepsilon _0|}=\frac{\varepsilon }{|\varepsilon _0|}+1$.

Lemma 3

$D_{-{{\mathcal {P}}}}(s,z)=D_{(-{{\mathcal {P}}})^s}(s,z)$.

Proof

Let $z_1$ be a point in s, such that $D_{-{{{\mathcal {P}}}}}(s,z) = D_{-{{{\mathcal {P}}}}}(z_1,z)$. Let $O_{(-{{\mathcal {P}}}),\varepsilon }$ be the offset copy of $(-{{\mathcal {P}}})$, centered at $z_1$, that contains z on its boundary. Since $O_{(-{{\mathcal {P}}})^s,\varepsilon }$ is the union of translated offset copies $O_{-{{\mathcal {P}}},\varepsilon }$, centered at all points $z' \in s$, it follows that $O_{(-{{\mathcal {P}}})^s,\varepsilon }$ contains z. According to Definition 5, we have that $D_{(-{{\mathcal {P}}})^s}(s,z) \le \frac{\varepsilon }{|\varepsilon _0|}+1$. Note that according to Definition 1, we also have that $D_{-{{\mathcal {P}}}}(z_1,z) = \frac{\varepsilon }{|\varepsilon _0|}+1$. Combining these two assertions, we conclude that $D_{(-{{\mathcal {P}}})^s}(s,z)\le D_{-{{\mathcal {P}}}}(s,z)$.

Conversely, let $O_{(-{{\mathcal {P}}})^s,\varepsilon }$ be the smallest offset copy that contains z on its boundary, so that $D_{(-{{\mathcal {P}}})^s}(s,z) = \frac{\varepsilon }{|\varepsilon _0|}+1$. Since $O_{(-{{\mathcal {P}}})^s,\varepsilon }$ is the union of translated offset copies of $O_{(-{{\mathcal {P}}}),\varepsilon }$, centered at all points $z' \in s$, it follows that there exists a point $z_2\in s$, such that the offset copy $O_{(-{{\mathcal {P}}}),\varepsilon }$, centered at $z_2$, contains z on its boundary. According to Definition 1, we have that $D_{-{{\mathcal {P}}}}(z_2,z) = \frac{\varepsilon }{|\varepsilon _0|}+1$. On the other hand, according to Definition 3, we have that $D_{-{{\mathcal {P}}}}(s,z)\le D_{-{{\mathcal {P}}}}(z_2,z)$. We conclude that $D_{-{{\mathcal {P}}}}(s,z) \le D_{(-{{\mathcal {P}}})^s}(s,z)$. The claim follows. $\square$

Combining Lemmata 1 and 3, we conclude the following.

Lemma 4

$D_{{{\mathcal {P}}}}(z,s)=D_{(-{{\mathcal {P}}})^s}(s,z)$. $\square$

We now illustrate the properties of the extruded medial axis of $(-{{\mathcal {P}}})^s$. Fix some value of $\varepsilon$. Place two translated copies $T_{1,\varepsilon }$ and $T_{2,\varepsilon }$ of the offset polygon $O_{-{{\mathcal {P}}},\varepsilon }$, centered at the two endpoints $z_1$ and $z_2$ of the line segment s (see Fig. 3a). Let $u_{1}^\varepsilon$ and $u_{2}^\varepsilon$ be the two vertices of the upper common tangent² of $T_{1,\varepsilon }$ and $T_{2,\varepsilon }$. Observe that $u_{1}^\varepsilon$ and $u_{2}^\varepsilon$ are the same vertex of the original offset polygon $O_{-{{\mathcal {P}}},\varepsilon }$. Similarly, let $\ell _{1}^\varepsilon$ and $\ell _{2}^\varepsilon$ be the two vertices of the lower common tangent of $T_{1,\varepsilon }$ and $T_{2,\varepsilon }$. Note that if we vary continuously the value of $\varepsilon$, then both $u_{i}^\varepsilon$ and $\ell _{i}^\varepsilon$ move continuously along the medial axis of $T_{i,\varepsilon }$, $i\in \{1,2\}$, and the upper and lower common tangents also move but always stay parallel to s. Thus, the extruded medial axis of $(-{{\mathcal {P}}})^s$ is a subset of the union of the medial axes of $T_{1,\varepsilon }$ and $T_{2,\varepsilon }$. Specifically, the portion of the medial axis of $T_{i,\varepsilon }$, that lies between $u_{i}^\varepsilon$ and $\ell _{i}^\varepsilon$ and whose end vertices are in the convex hull of $T_{1,\varepsilon }$ and $T_{2,\varepsilon }$, belongs to the extruded medial axis of $(-{{\mathcal {P}}})^s$. We refer to this part of the medial axis of $T_{i,\varepsilon }$ as the ith medial region of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$. We define the parallel region as the part of the polygon ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$ that does not have dominating edges from the medial region. (See Fig. 8 for an illustration of these terms.) Note that the parallel region is empty if and only if the line segment s is a point. In this case, the extruded medial axis of $(-{{\mathcal {P}}})^s$ is identical to the medial axis of $(-{{\mathcal {P}}})^s$.

3.3 Convex Polygons

We now generalize the tools described above from line segments to convex polygons. Let q be a convex polygon with k sides, and denote its boundary by $\partial q$. Let $(-{{\mathcal {P}}})^q$ be the convex polygon that is the union of the translated copies of $(-{{\mathcal {P}}})$ centered at all points $z \in q$. Similarly to Sect. 3.2, define the Split-and-Extruded (SaE) offset copy of $(-{{\mathcal {P}}})^q$, denoted by ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$, as the convex polygon obtained by uniting the translated copies of $O_{-{{\mathcal {P}}},\varepsilon }$ centered at all points $z \in q$. Note that $(-{{\mathcal {P}}})^q$ (resp., ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$) is the convex hull of k translated copies of $(-{{\mathcal {P}}})$ (resp., $O_{-{{\mathcal {P}}},\varepsilon }$) centered at the vertices of q. Also note that when $\varepsilon$ takes the value $\varepsilon _0$, the inverse of the radius of $(-{{\mathcal {P}}})$, we have that ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon _0}$ degenerates into the polygon q. We refer to the (entire) polygon q as the center of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$, for $\varepsilon \ge \varepsilon _0$. Obviously, the complexity of $(-{{\mathcal {P}}})^q$ is at most $|(-{{\mathcal {P}}})^q| = |{{\mathcal {P}}}|+k$ because each side of $(-{{\mathcal {P}}})$ can appear at most once along the boundary of $(-{{\mathcal {P}}})^q$, and there are exactly k common tangents. If we fix the center at q and increase the value of $\varepsilon$ continuously (starting from $\varepsilon _0$), then the moving vertices of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$ in $(-{{\mathcal {P}}})^q$ (as $\varepsilon$ varies) define the extruded medial axis of $(-{{\mathcal {P}}})^q$ (see Fig. 9).

We define the following distance function.

Definition 6

($D_{(-{{\mathcal {P}}})^q}(q,z)$) Let z and q be a point and a convex polygon, respectively, in ${\mathbb {R}}^2$, and let ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$ be an SaE offset copy of $(-{{\mathcal {P}}})^q$ (centered at q), such that ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$ contains z on its boundary. The offset distance from q to z (with respect to ${{\mathcal {P}}}$) is defined as $D_{(-{{\mathcal {P}}})^q}(q,z) = \frac{\varepsilon +|\varepsilon _0|}{|\varepsilon _0|}=\frac{\varepsilon }{|\varepsilon _0|}+1$.

Lemma 5

$D_{-{{\mathcal {P}}}}(q,z)=D_{(-{{\mathcal {P}}})^q}(q,z)$.

Proof

The proof of this lemma is similar to the proof of Lemma 3. $\square$

Combining Lemmata 1 and 5, we conclude the following.

Lemma 6

$D_{{{\mathcal {P}}}}(z,q)=D_{(-{{\mathcal {P}}})^q}(q,z)$. $\square$

Let us illustrate the properties of the extruded medial axis of $(-{{\mathcal {P}}})^q$. Fix some value of $\varepsilon$. Place k translated copies $T_{i,\varepsilon }$, $i \in \{1,\ldots , k\}$, of the offset polygon $O_{-{{\mathcal {P}}},\varepsilon }$ centered at the k vertices $\{z_i\}$, $i \in \{1,\ldots , k\}$, of the polygon q (see Fig. 9a). Here, $T_{i-1,\varepsilon }$, $T_{i,\varepsilon }$, and $T_{i+1,\varepsilon }$ are three clockwise consecutive copies of $O_{-{{\mathcal {P}}},\varepsilon }$. Let $t_i$ be the outer common tangent of $T_{i,\varepsilon }$ and $T_{i+1,\varepsilon }$, where indices are taken modulo k. Let $u_{i,2}^\varepsilon$ (resp., $u_{i,1}^\varepsilon$) and $u_{{(i+1)},1}^\varepsilon$ (resp., $u_{{(i-1)},2}^\varepsilon$) be the two vertices of the outer tangent of the convex hull joining $T_{i,\varepsilon }$ and $T_{i+1,\varepsilon }$ (resp. $T_{i-1,\varepsilon }$). Observe that the pair $u_{i,2}^\varepsilon$ and $u_{{(i+1)},1}^\varepsilon$ (as well as the pair $u_{i,1}^\varepsilon$ and $u_{{(i-1)},2}^\varepsilon$) represent the same vertex of the original offset polygon $O_{-{{\mathcal {P}}},\varepsilon }$. Note that if we vary continuously the value of $\varepsilon$, then all vertices $u_{i,j}^\varepsilon$ move continuously along the medial axis of $T_{i,\varepsilon }$, $i\in \{1,2,\ldots , k\}$, $j\in \{1,2\}$, and all k outer tangents also move parallel to themselves. Thus, the extruded medial axis of $(-{{\mathcal {P}}})^q$ is a subset of the union of the medial axes of $T_{i,\varepsilon }$, $i\in \{1,2,\ldots , k\}$ (see Fig. 9b). Specifically, the portion of the medial axis of $T_{i,\varepsilon }$, that lies between $u_{i,1}^\varepsilon$ and $u_{i,2}^\varepsilon$ and whose end vertices appear as vertices in ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$, belongs to the extruded medial axis of $(-{{\mathcal {P}}})^q$. As with the segment case in Sect. 3.2, we refer to this part of the medial axis of $T_{i,\varepsilon }$ as the ith medial region of $(-{{\mathcal {P}}})^q$. We define the ith parallel region as the part of the polygon ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$ that does not have dominating edges from the medial region and that lies between $T_{i,\varepsilon }$ and $T_{i+1,\varepsilon }$. (See Fig. 9b for an illustration of these terms.) Like with sites that are line segments, the case in which copies of ${{\mathcal {P}}}$, centered at vertices of q, have a non-empty intersection, is insignificant. This is because the parallel regions never vanish. Actually, they disappear only if an edge of q has length 0, but we naturally assume that this never happens.

4 Combinatorial Complexity

4.1 Abstract Voronoi Diagram

We extend the abstract-Voronoi-diagram paradigm of Klein and Wood [16, Thm. 4.1] to the case of a set of objects, for which the following version of Property 4 is satisfied:

Property 5

For every pair of object $\sigma$ and a point z in ${\mathbb {R}}^2$, there exists a point $z' \ne z$, such that $D_{{\mathcal {P}}}(\sigma ,z) + D_{{\mathcal {P}}}(z,z') = D_{{\mathcal {P}}}(\sigma ,z')$.

Lemma 7

Property 5holds for objects that are either line segments or convex polygons.

Fig. 4

Different cases of the position of z (in the proof of Lemma 7)

Proof

Consider the SaE $\varepsilon$-offset copy of $(-{{\mathcal {P}}})^{\sigma }$ and its extruded medial axis. Depending on the position of z, we can find a point $z' \ne z$ which satisfies the required property.

• The point z lies in a parallel region (see Fig. 4a). Let $B_i$ be one of the two boundaries defining the parallel region, and $q^*$ be the projection of z on $\sigma$, parallel to $B_i$. Any point $z'$ away from z along this direction of projection satisfies the property: Indeed, $D_{{\mathcal {P}}}(\sigma ,z) + D_{{\mathcal {P}}}(z,z') = D_{{\mathcal {P}}}(\sigma ,z')$ since $q^*$ is the point of object $\sigma$ that is $D_{{{\mathcal {P}}}}$-closest to both z and $z'$.

• The point z lies in the ith medial region, where $i \in \{1,2\}$ if $\sigma$ is a line segment, and $i \in \{1,2,\ldots ,k\}$ if $\sigma$ is a k-sided polygon (see Fig. 4b, c). In this case, the extreme point $z_i$ of the object $\sigma$ is the $D_{{{\mathcal {P}}}}$-closest point to z. Consider the partition imposed by the extruded medial axis. In this partition, let C be the cell containing z. If the line segment $z_i z$ is completely contained in cell C (see Fig. 4b), then any point $z'$ on the extension of $z_i z$ contained in C satisfies the equality $D_{{\mathcal {P}}}(\sigma ,z) + D_{{\mathcal {P}}}(z,z') = D_{{\mathcal {P}}}(\sigma ,z')$. Otherwise, if $z_i z$ is not completely contained in C (see Fig. 4c), we can find a point $x_i$ in an infinitesimal extension of the line segment $z_i z$ (beyond z) in the same cell C, such that $D_{{\mathcal {P}}}(\sigma ,z) + D_{{\mathcal {P}}}(z,x_i) < D_{{\mathcal {P}}}(\sigma ,x_i)$, i.e., $D_{{\mathcal {P}}}(\sigma ,x_i) - D_{{\mathcal {P}}}(z,x_i) > D_{{\mathcal {P}}}(\sigma ,z)$. In the same cell C, we can also find a point $x_j$ which is closer to $z_i$ than z (according to $D_{{\mathcal {P}}}$). For this point, we have that $D_{{\mathcal {P}}}(\sigma ,z) + D_{{\mathcal {P}}}(z,x_j) > D_{{\mathcal {P}}}(\sigma ,x_j)$, i.e., $D_{{\mathcal {P}}}(\sigma ,x_j) - D_{{\mathcal {P}}}(z,x_j) < D_{{\mathcal {P}}}(\sigma ,z)$. Now, define a function $g(x) = D_{{\mathcal {P}}}(\sigma ,x) - D_{{\mathcal {P}}}(z,x)$. Since $D_{{\mathcal {P}}}$ is continuous along any path from $x_i$ to $x_j$, the function g(x) is also continuous along any such path. Choose a path from $x_i$ to $x_j$ that is completely contained in C and does not pass through z. Finally, according to the mean-value theorem, we can find a point $z'$ along this path, for which we have that $g(x) = D_{{\mathcal {P}}}(\sigma ,z)$.

• The point z lies on a path of the extruded medial axis (see Fig. 4d). in this case, it is easy to verify that any point $z'$ on that path of the extruded medial axis beyond z satisfies the required property.$\square$

We now give a few definitions, following the terminology of Ref. [16].

Definition 7

(${D_{{{\mathcal {P}}}}}$ -straight directed path) A directed path $\pi (\overrightarrow{zz'})$ is called a $D_{{\mathcal {P}}}$-straight directed path if for each triple of points $z_1,z_2,z_3$, which are consecutive along $\overrightarrow{zz'}$, we have that $D_{{\mathcal {P}}}(z_1,z_2) + D_{{\mathcal {P}}}(z_2,z_3) = D_{{\mathcal {P}}}(z_1,z_3)$.

Note that a $D_{{\mathcal {P}}}$-straight directed path $\pi (\overrightarrow{zz'})$ is the minimum $D_{{\mathcal {P}}}$-length path among all curves connecting z to $z'$, i.e., it is a $D_{{\mathcal {P}}}$-shortest path. In addition, since $D_{{\mathcal {P}}}(z,z') = D_{-{{\mathcal {P}}}}(z',z)$, the reverse directed path $\pi (\overrightarrow{z'z})$ is a $D_{(-{{\mathcal {P}}})}$-straight directed path of the same length.

Definition 8

(${D_{{\mathcal {P}}}}$-starshaped region) A set R is called a $D_{{\mathcal {P}}}$-starshaped region with respect to a site $\sigma$ if for each point $z \in R$, every $D_{{\mathcal {P}}}$-straight directed path $\overrightarrow{zz'}$, where $z' \in \sigma$ is such that $D_{{\mathcal {P}}}(z,z') = D_{{\mathcal {P}}}(z,\sigma )$, is entirely contained in R.

Note that if R is a $D_{{\mathcal {P}}}$-starshaped region with respect to a site $\sigma$, then R is a connected region.

Theorem 1

If the underlying distance function, applied to some set of objects, has Properties 1, 3, and 5, then all regions in the respective Voronoi diagram are simply connected.

Proof

Consider the Voronoi region $\hbox {NV}_{{\mathcal {P}}}(\sigma )$ of some site $\sigma$. First, we prove that $\hbox {NV}_{{\mathcal {P}}}(\sigma )$ is $D_{{\mathcal {P}}}$-starshaped with respect to $\sigma$, using Properties 1 and 3. Let z be a point in $\hbox {NV}_{{\mathcal {P}}}(\sigma )$ and $z' \in \sigma$ satisfying $D_{{\mathcal {P}}}(z,z')=D_{{\mathcal {P}}}(z,\sigma )$. Due to Property 3, the existence of a $D_{{\mathcal {P}}}$-straight directed path $\overrightarrow{zz'}$ between z and $z'$ is guaranteed [16, 20, 24]. For proving the starshapedness of $\hbox {NV}_{{\mathcal {P}}}(\sigma )$, assume for contradiction that $\overrightarrow{zz'}$ is not entirely contained by this region. Hence, there exists a point $z^*$ along the path $\overrightarrow{zz'}$ that is closer to some other site $\sigma '$, i.e., $D_{{\mathcal {P}}}(z^*,\sigma ') \prec D_{{\mathcal {P}}}(z^*,\sigma ) = D_{{\mathcal {P}}}(z^*,z')$. Therefore, $D_{{\mathcal {P}}}(z,z^*) + D_{{\mathcal {P}}}(z^*,\sigma ') \prec D_{{\mathcal {P}}}(z,z^*) + D_{{\mathcal {P}}}(z^*,z') = D_{{\mathcal {P}}}(z,z') = D_{{\mathcal {P}}}(z,\sigma ).$ This implies that $D_{{\mathcal {P}}}(z,\sigma ') \prec D_{{\mathcal {P}}}(z,\sigma )$, which is a contradiction since z is inside $\hbox {NV}_{{\mathcal {P}}}(\sigma )$. Thus, $\hbox {NV}_{{\mathcal {P}}}(\sigma )$ is a $D_{{\mathcal {P}}}$-starshaped region.

Next, using Property 5, we prove that each region $\hbox {NV}_{{\mathcal {P}}}(\sigma )$ is simply connected. Consider any simple closed curve ${{\mathcal {C}}}$ in $\hbox {NV}_{{\mathcal {P}}}(\sigma )$. Proving that the region $I({{\mathcal {C}}})$ encircled by ${{\mathcal {C}}}$ is entirely contained by $\hbox {NV}_{{\mathcal {P}}}(\sigma )$ suffices for proving the claim. We prove this by showing that any point $z \in I(C)$ is contained by $\hbox {NV}_{{\mathcal {P}}}(\sigma )$. Let $z' \in \sigma$ be a point which satisfies $D_{-{{\mathcal {P}}}}(z',z) = D_{-{{\mathcal {P}}}}(\sigma ,z)$. Now, due to Property 3, the $D_{(-{{\mathcal {P}}})}$-straight directed path $\overrightarrow{z'z}$ exists, and due to Property 5, this $D_{(-{{\mathcal {P}}})}$-straight directed path, originally from $z'$ to z, can be prolonged to a $D_{(-{{\mathcal {P}}})}$-straight directed halfpath (infinite on one side) $\ell$. Being unbounded in the sense that it must go to infinity (since it is based on a distance function), $\ell$ cannot wind forever within a finite region, and therefore it must intersect ${{\mathcal {C}}}$ at some point $z'' \in \hbox {NV}_{{\mathcal {P}}}(\sigma )$. Now, we have that $D_{-{{\mathcal {P}}}}(z', z'') = D_{-{{\mathcal {P}}}}(\sigma , z'')$. As a result, due to Lemma 1, we have that $D_{{\mathcal {P}}}(z'',z') = D_{{\mathcal {P}}}(z'',\sigma )$.

Since the path $\ell _{z'z''}$ is a $D_{(-{{\mathcal {P}}})}$-straight directed path, the inverse directed path $\ell _{z''z'}$ is a $D_{{\mathcal {P}}}$-straight directed path as well. Since $\hbox {NV}_{{\mathcal {P}}}(\sigma )$ is a $D_{{\mathcal {P}}}$-starshaped region and $\ell _{z''z'}$ is a $D_{{\mathcal {P}}}$-straight directed path with $D_{{\mathcal {P}}}(z'',z') = D_{{\mathcal {P}}}(z'',\sigma )$, the path $\ell _{z''z'}$ is entirely contained by $\hbox {NV}_{{\mathcal {P}}}(\sigma )$. Therefore, z is also contained by $\hbox {NV}_{{\mathcal {P}}}(\sigma )$, which is exactly what we needed to show. Hence, $\hbox {NV}_{{\mathcal {P}}}(\sigma )$ is a simply-connected region. $\square$

4.2 Line Segments

Let ${\mathscr {S}}=\{s_1,s_2,\ldots , s_n\}$ be a set of n line segments in ${\mathbb {R}}^2$. First, we study the combinatorial complexity of the nearest-site Voronoi diagram $\hbox {NV}_{{\mathcal {P}}}({\mathscr {S}})$ with respect to $D_{{\mathcal {P}}}$, where ${{\mathcal {P}}}$ is an m-sided convex polygon.

Lemma 7 tells us that Property 5 is satisfied for a set of line segments. Therefore, as a direct consequence of Theorem 1, we have the following.

Corollary 1

Every Voronoi region $\hbox {NV}_{{\mathcal {P}}}(s_i)$ in $\hbox {NV}_{{\mathcal {P}}}({\mathscr {S}})$ is simply connected.

Let $s_1,s_2$ be two line segments in the plane, and $B_{{\mathcal {P}}}(s_1,s_2)$ be the bisector of $s_1$ and $s_2$ with respect to the convex-straight-skeleton distance function $D_{{\mathcal {P}}}$. In the sequel, we will use the term polycurve to denote a curve, all of whose basic pieces are described by low-degree geometric polynomials.

Lemma 8

• (i) Let $s_1,s_2$ be two line segments in the plane. The bisecting curve $B_{{\mathcal {P}}}(s_1,s_2)$ is a polycurve with O(m) arcs and line segments.

• (ii) Two different bisecting curves intersect O(m) times.

As part of the proof, we will need the following definition, which is useful by its own for understanding the offsetting process.

Definition 9

(Skeleton order) Let ${{\mathcal {P}}}$ be a convex polygon. The (clockwise) skeleton order of ${{\mathcal {P}}}$ is a total (cyclic) order on the vertices of the straight skeleton of ${{\mathcal {P}}}$, obtained by combining all the partial orders on these vertices imposed by offset versions of ${{\mathcal {P}}}$, and all ordered triples $(v_1,v_2,v_3)$ implied by pairs of vertices $v_1,v_3$ collapsing into a vertex $v_2$ by offsetting ${{\mathcal {P}}}$ inward.

It is easy to verify that the skeleton order of any convex polygon is unique. For example, the skeleton order of the polygon shown in Fig. 1a is $(v_1,v_8,v_2,v_3,v_9,v_4,v_5,v_7,v_6)$.

Fig. 5

Status configurations at position t. a For line segments: Vertices x and y of ${{\mathcal {P}}}$, and the endpoints b and d of segments $s_1$ and $s_2$, respectively; and b For convex polygons: vertices x and y of ${{\mathcal {P}}}$, and the endpoints b and g of polygons $p_1$ and $p_2$, respectively

Proof

• (i) Let us sweep a point t along the bisector $B_{{\mathcal {P}}}(s_1,s_2)$ from end to end, and characterize every position of t by (a) the elements (vertices or sides) of the current offset of ${{\mathcal {P}}}$ (which now touches simultaneously $s_1$ and $s_2$) that touch the two segments; and (b) the location of the touching points on the two segments (either one of the endpoints, or a point internal to the segment, in which case we also distinguish between the two sides of the segment). We call this characterization the status of the bisector at t; see Fig. 5a for an illustration. During this sweep, a new basic piece of the bisector is manifested by a change in the status. In between such changes, the piece of the bisector is described by a low-degree geometric polynomial. Bounding from above the complexity of the bisector boils down to setting an upper bound on the total number of such changes in the status. There are two crucial issues to observe.

  • First, when t is swept along $B_{{\mathcal {P}}}(s_1,s_2)$, the offset-distance from $B_{{\mathcal {P}}}(s_1,s_2)$ to $s_1$ (or $s_2$) first decreases monotonically until a minimum point (or an interval of the same minimum value, in the degenerate case of two parallel segments whose mutual orthogonal projection is non-empty), and then it increases monotonically. Indeed, the minimum occurs where the smallest possible offset of ${{\mathcal {P}}}$ touches simultaneously the two segments. In the degenerate case, in which the two segments are parallel and an offset version of ${{\mathcal {P}}}$ touches simultaneously the interiors of the two segments, the minimum offset occurs in a continuous section of $B_{{\mathcal {P}}}(s_1,s_2)$, whose endpoints correspond to two translated copies of the same offset version of ${{\mathcal {P}}}$ that touch an endpoint of one of the segments. All other cases are nondegenerate, and exhibit a single minimum in which an offset version of ${{\mathcal {P}}}$ touches either an endpoint of one segment and an internal point of the other segment, or endpoints of the two segments. In either case, going further away (to either side) along the bisector allows ${{\mathcal {P}}}$ to open up, and, hence, the offset to increase. The above discussion implies that while sliding t along $B_{{\mathcal {P}}}(s_1,s_2)$, the polygon ${{\mathcal {P}}}$ first shrinks continuously (a process in which sides only “disappear”) and then expands (the opposite process in which sides only “appear”). During this process, the touching vertex moves cyclically around the skeleton order of ${{\mathcal {P}}}$. Hence, the status can change O(m) times due to which element of $O_{{{\mathcal {P}}},\varepsilon }$ touches each segment. Merging two lists, each of complexity O(m), results in a list of the same complexity. The fact that $O_{{{\mathcal {P}}},\varepsilon }$ first shrinks and then expands does not change this upper bound—it only implies that some elements of ${{\mathcal {P}}}$ are skipped without contributing to these changes.

  • Second, the touching point on each segment also rotates about it. For example, in Fig. 5a, when the offset polygon sweeps in the marked direction, it first touches the lower side of $s_2$, and later its upper side. This means that each segment contributes an additional constant number of changes to the status.

  In conclusion, the total number of changes of the status during the sweep is O(m), and, hence, the complexity of the bisector $B_{{\mathcal {P}}}(s_1,s_2)$ is O(m) as well.

• (ii) The proof of this item uses the same idea as the proof of the previous item, with only some additional bookkeeping. Let $B_{{\mathcal {P}}}(s_1,s_2)$ and $B_{{\mathcal {P}}}(s_3,s_4)$ be the two respective bisectors of two pairs of segments $s_1,s_2$ and $s_3,s_4$. It is easy to verify that each bisector can be divided into at most 7 pieces, each of which is classified by the same features (endpoint or a side) of the corresponding segments. (See Fig. 6 for an illustration of this fact.) Therefore, there are at most 49 pairs of such portions, one of each bisector, that we need to consider. (In reality, intersections of the two bisectors can occur between much less than these 49 portions of bisections, but this does not change the asymptotic count.) Let us then ignore the constant factor of 49, and focus on a single pair of portions, one of each bisector, in which the involved features of the segments (endpoints or sides) remain unchanged. As in the proof of the previous item, note that in each such portion of a bisector, the touching vertex of the offset polygon, $O_{{{\mathcal {P}}},\varepsilon }$, moves cyclically along the skeleton order of ${{\mathcal {P}}}$. This time, we have four moving touching points: Two points along the boundary of the offset polygon touching simultaneously $s_1$ and $s_2$, and two other points along the boundary of the offset polygon touching simultaneously $s_3$ and $s_4$. Again, the measure that we seek is the number of changes of the configurations, this time of two bisectors instead of one. This process resembles a merge of four ordered lists, each one of complexity O(m): The complexity of the merged list is O(m) as well. Between two successive changes of the combined configuration (of the two bisectors), we have two basic pieces (described by trigonometric polynomials). Such a pair of pieces can intersect at most some constant amount of times. The total count of intersections is, therefore, O(m). $\square$

Fig. 6

A symbolic drawing of the (at most) seven different parts of a bisector $B_{{\mathcal {P}}}(s_1,s_2)$. Each part is defined by a pair of features (one of each segment), either the interior of a segment ($s_i$) or a segment endpoint ($p_i$ or $q_i$). The distinction between the two sides of a segment is done by the notation $s_i$ and $\hat{s_i}$. Similarly, the two ways to arrive at a segment endpoint are distinguished by $p_i$ and $\hat{p_i}$ (or $q_i$ and $\hat{q_i}$)

Fig. 7

In this orientation, in order to squeeze into the small gap between $s_1$ and $s_2$, polygon ${{\mathcal {P}}}$ needs to be offset inward significantly. Therefore, while sliding the center of ${{\mathcal {P}}}$ along the bisector from bottom-right to top-left, the feature which touches $s_1$ will be (in order) $v_1$, then $v_7$, $v_8$, and $v_9$. Note that when ${{\mathcal {P}}}$ shrinks, some of its edges disappear. For example, $v_7$ will appear when $v_1$ and $v_2$ will be united

Remark

It is easy to construct examples in which (i) the complexity of a single bisector, or (ii) the number of intersections of two bisectors, is $\varTheta (m)$. For (i), simply put two segments perpendicular to each other, such that two of their endpoints are almost touching, and design the underlying polygon ${{\mathcal {P}}}$ so that while it sweeps along the bisector from an initial small size (near the almost-touching segment endpoints) further away, almost all vertices of ${{\mathcal {P}}}$ “appear” and become the feature touching one of the segments. See Fig. 7 for a demonstration. For (ii), design ${{\mathcal {P}}}$ and fix the four segments so as to have $\varTheta (m)$ intersections between the two extreme portions of the bisectors, in which the features of the segments, which control the bisectors, are an endpoint of each segment. Such a construction is identical to the case of two point sites, for which it is already known [7, Thm. 3(c)] that one can obtain $\varTheta (m)$ intersections between two different bisectors.

Theorem 2

[16, Thm. 2.5] Assume that a distance function $D_{{\mathcal {P}}}$ induces the Euclidean topology in the plane. Furthermore, assume that each bisector of two sites consists of disjoint simple curves, and curves belonging to different bisectors can intersect only finitely often within each bounded area. Finally, assume that all possible Voronoi regions are connected sets. Then, $\hbox {NV}_{{\mathcal {P}}}({\mathscr {S}}),$ where ${\mathscr {S}}$ is a set of n sites, has n faces and O(n) edges and vertices. $\square$

Property 1, Corollary 1, and Lemma 8(i) ensure that all the premises of Theorem 2 are satisfied. As a corollary to the theorem above, and due to Lemma 8(ii), we have the following.

Theorem 3

The combinatorial complexity of the Voronoi diagram $\hbox {NV}_{{\mathcal {P}}}({\mathscr {S}}),$ where ${\mathscr {S}}$ is a set of n line segments and ${{\mathcal {P}}}$ is a convex m -gon, is O(nm). $\square$

Remark

The bound O(nm) on the complexity of the diagram is attainable. For example, put n line segments aligned horizontally and well spaced, so that most of the bisector of every pair of consecutive segments is present in the diagram, for a total complexity of $\varOmega (nm)$. Hence, the complexity of the diagram is $\varTheta (nm)$ in the worst case.

4.3 Convex Polygons

We can easily extend the discussion from line segments to convex polygons. Let ${\mathscr {Q}}=\{p_1,p_2,\ldots ,p_n\}$ be a set of n convex polygonal sites, each having at most k sides, and let $\hbox {NV}_{{\mathcal {P}}}({\mathscr {Q}})$ be the nearest-site Voronoi diagram of these sites with respect to the convex-straight-skeleton distance function $D_{{\mathcal {P}}}$, where ${{\mathcal {P}}}$ is an m-sided convex polygon.

As in the segments case, Lemma 7 tells us that Property 5 is satisfied for convex polygonal objects. Therefore, as a consequence of Theorem 1, we have the following.

Corollary 2

Every Voronoi region $\hbox {NV}_{{\mathcal {P}}}(p_i)$ in the nearest-site Voronoi diagram $\hbox {NV}_{{\mathcal {P}}}({\mathscr {Q}})$ is simply-connected. $\square$

In the same manner, the following generalizes Lemma 8 to deal with polygonal sites.

Lemma 9

• (i) The bisecting curve $B_{{\mathcal {P}}}(p_1,p_2)$ of a pair of convex polygons $p_1,p_2,$ each having at most k sides, is a polycurve with $O(m+k)$ arcs and segments.

• (ii) Any two such bisecting curves intersect $O(m+k)$ times.

The proof of the lemma above is identical to that of Lemma 8 with the following refinements (see Fig. 5b).

• 1. The offset of ${{\mathcal {P}}}$ can touch any of the k corners and k sides of each of the sites.

• 2. When sweeping the point t along the bisector, the touching points on the two sites move sequentially along their boundaries without turning back, therefore, decomposing the bisector according to the touching points contributes at most 4k additional pieces.

• 3. Except that, the proofs of the two parts of the lemma are identical. Therefore, the complexity O(m) is replaced by $O(m+k)$.

In the polygonal-site case, similarly to the argument in the proof of Theorem 3, we have that Property 1, Corollary 2, and Lemma 9 also ensure that all the premises of Theorem 2 are satisfied, and due to Lemma 9(ii), we have the following.

Theorem 4

For a set ${\mathscr {Q}}$ of n convex polygons, each having at most k sides, the combinatorial complexity of the Voronoi diagram $\hbox {NV}_{{\mathcal {P}}}({\mathscr {Q}})$ is $O(n(m+k)),$ where m is the number of sides of ${{\mathcal {P}}}$. $\square$

5 Algorithmic Tools

5.1 Line Segments

Our current goal is to preprocess the underlying polygon and to compute a data structure which will enable us to answer efficiently distance queries, that is, to compute $D_{{\mathcal {P}}}(z,s)$ for a point z and a line segment s in ${\mathbb {R}}^2$.

Let us now show how to compute efficiently the point-to-segment distance, $D_{{\mathcal {P}}}(z,s)$, from a point z to a line segment s in ${\mathbb {R}}^2$. From Lemma 4, we know that this operation is equivalent to computing $D_{(-{{\mathcal {P}}})^s}(s,z)$. We show below that, provided that the extruded medial axis of ${(-{{\mathcal {P}}})^s}$ is computed in a preprocessing step, the distance $D_{(-{{\mathcal {P}}})^s}(s,z)$ can be computed in the same running time as in Lemma 2. Note that $D_{{\mathcal {P}}}(z,s)$ is a primitive operation for the computation of the compact Voronoi diagram (a term which will be explained in Sect. 6). Thus, simply preprocessing the extruded medial axis of ${(-{{\mathcal {P}}})^s}$ for every segment $s \in {\mathscr {S}}$ would result in increased preprocessing space (i.e., O(nm) space in total). However, we prove that even with preprocessing only the medial axis of $(-{{\mathcal {P}}})$, we can compute the point-to-segment distance $D_{{\mathcal {P}}}(z,s)$ with the same query time as that of computing a point-to-point distance $D_{{\mathcal {P}}}(z,z')$, $z,z'\in {\mathbb {R}}^2$.

Let $z_1$ and $z_2$ be the two endpoints of a line segment s. For a point z that lies in the ith medial region, $i\in \{1,2\}$, note that $D_{{\mathcal {P}}}(z,s)$ can be calculated by simply computing $D_{{\mathcal {P}}}(z,z_i)$. For a point z which lies in the parallel region of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$, let $z'$ be the projection of z on the boundary between the medial region of $T_{i,\varepsilon }$, $i\in \{1,2\}$, and the parallel region. (Note that one can equally choose $i=1$ or $i=2$ since the two boundaries are identical.) Then, $D_{{\mathcal {P}}}(z,s)$ can be calculated by simply computing $D_{{\mathcal {P}}}(z',z_i)$.

Fig. 8

The extruded medial axis of $(-{{\mathcal {P}}})^s$: The medial regions and the parallel region are colored with seagreen and light blue, respectively (Color figure online)

Lemma 10

Let z and s be a point and a line segment, respectively. Allowing $O(m^2)$ time and space for preprocessing the m -gon $(-{{\mathcal {P}}}),$ the distance $D_{{\mathcal {P}}}(z,s)$ can be computed in $O(\log m)$ time. Within this amount of time, a point $q^* \in s,$ satisfying $D_{{\mathcal {P}}}(z,q^*) = D_{{\mathcal {P}}}(z,s),$ can be reported.

Proof

We keep two copies, $T_1$ and $T_2$, of the processed medial axis of $(-{{\mathcal {P}}})$ as required by Lemma 2. In addition, we preprocess $(-{{\mathcal {P}}})$, such that both traversing and binary searching are possible along every vertex-to-center path of $(-{{\mathcal {P}}})$. Since there are m vertices, there are m such paths. By simply storing each path as a sorted list, we need a total of $O(m^2)$ space and time for preprocessing this data structure.

To answer the query $D_{{\mathcal {P}}}(z,s)$, we proceed as follows.

• Step 1 Compute the upper and lower common tangents of the two translated copies $T_1$ and $T_2$, centered at $z_1$ and $z_2$, respectively, where $z_1$ and $z_2$ are the endpoints of the line segment s. Let $u_i$ and $\ell _i$ be the points in which the upper and lower common tangents $T_i$, $i\in \{1,2\}$, touch the two polygons.

• Step 2 (2.1) If z lies in the ith medial region, then set the value of $D_{{\mathcal {P}}}(z,s)$ by invoking $D_{{\mathcal {P}}}(z,z_i)$, and return the point $q^*$. (2.2) Otherwise (if z is in the parallel region), invoke a ray-shooting query on the boundary $B_i$ between the medial region of $T_i$ and the parallel region of ${(-{{\mathcal {P}}})^s}$ in order to find $z'$, the projection of z on $B_i$ (see Fig. 8). Set the value of $D_{{\mathcal {P}}}(z,s)$ by invoking $D_{{\mathcal {P}}}(z',z_i)$. Then, find and return the point $q^*$ by translating the point $z_i$ by $|z z'|$ along s, where $|z z'|$ is the Euclidean distance between z and $z'$.

Step 1 takes $O(\log m)$ time, assuming that $(-{{\mathcal {P}}})$ is available as a cyclic list of vertices. Step 2.1 can be performed in $O(\log m)$ time, as in Lemma 2. Since $B_i$ is a path from a vertex to the center along the medial of $(-{{\mathcal {P}}})$, we can perform a binary search and find $z'$ in $O(\log m)$ time. Hence, Step 2.2 takes $O(\log m)$ time as well. In total, the query time complexity is $O(\log m)$. This completes the proof. $\square$

Another primitive operation computes the Voronoi vertex $v^*$, around which the Voronoi cells for sites $s_1,s_2,s_3$, with respect to the polygon-offset distance $D_{{\mathcal {P}}}$, occur in a counter-clockwise order. Applying the tentative prune-and-search paradigm [15], we can find $v^*$ in the same manner as in Ref. [7]. The only difference is that here, three different polygons $(-{{\mathcal {P}}})^{s_1}$, $(-{{\mathcal {P}}})^{s_2}$, and $(-{{\mathcal {P}}})^{s_3}$ are involved in the computation instead of three identical copies of $(-{{\mathcal {P}}})$. However, this does not affect the performance of the general paradigm. Thus, we have the following:

Lemma 11

Given three line segments $s_1,s_2,s_3$ and a convex m -gon ${{\mathcal {P}}}$ in the plane, the Voronoi vertex $v^*,$ where the Voronoi cells for sites $s_1,s_2,s_3,$ with respect to the polygon-offset distance $D_{{\mathcal {P}}},$ occur in counter-clockwise order, can be computed in $O(\log ^2 m)$ time (allowing $O(m^2)$ time for preprocessing ${{\mathcal {P}}}).$ $\square$

5.2 Convex Polygonal Sites

Let q be a convex polygon with k vertices $\{z_i\}$, for $i\in \{1,2,\ldots ,k\}$, and z be any point in ${\mathbb {R}}^2$. First, we show how to compute the distance $D_{{\mathcal {P}}}(z,q)$ efficiently. Similarly to the line-segment case, for a point z that lies in the ith medial region, for $i\in \{1,2, \ldots ,k\}$, note that $D_{{\mathcal {P}}}(z,q)$ can be calculated by simply computing $D_{{\mathcal {P}}}(z,z_i)$. For a point z which lies in the ith parallel region of ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$, let $z'$ be the projection of z on the boundary between the ith medial region and the ith parallel region. (As in the segment case, one can equally project z onto this boundary or onto the boundary between the ith parallel region and the $(i+1)$st medial region.) Then, $D_{{\mathcal {P}}}(z,q)$ can be calculated by simply computing $D_{{\mathcal {P}}}(z',z_i)$.

Fig. 9

a $(-{{\mathcal {P}}})^q$: the polygon q is colored gray. Translated copies of $(-{{\mathcal {P}}})$, centered at the vertices of q, are shown with dotted lines. The extruded medial axis of $(-{{\mathcal {P}}})^q$ is marked with blue. b The medial regions and parallel regions are colored light green and light blue, respectively (Color figure online)

Lemma 12

Let z and q be a point and a convex polygon of (at most) k sides, respectively. Allowing $O(m^2)$ time and space for preprocessing the m -gon $(-{{\mathcal {P}}}),$ the distance $D_{{\mathcal {P}}}(z,q)$ can be computed in $O(\log k \log m)$ time. Within this amount of time, a point $q^* \in \partial q,$ satisfying $D_{{\mathcal {P}}}(z,q^*) = D_{{\mathcal {P}}}(z,q),$ can be reported.

Proof

We keep three copies $T_j$, $j\in \{-1,0,1\}$ of the processed medial axis of $(-{{\mathcal {P}}})$ as required by Lemma 2. In addition, we preprocess $(-{{\mathcal {P}}})$, such that both traversing and binary searching are possible along every vertex-to-center path of $(-{{\mathcal {P}}})$. Since there are m vertices, there are m such paths. By simply storing each path as a sorted list, we need a total of $O(m^2)$ space and time for preprocessing this data structure.

In order to answer a query $D_{{\mathcal {P}}}(z,q)$, we perform a binary search along the cyclic list of vertices of q. At each step of the search, we pick $z_i$, the ith vertex of q, and decide whether either (i) z is in the medial region; (ii) z is in the parallel region of the corresponding translated copy of $(-{{\mathcal {P}}})$; or (iii) z is to the left or to the right of $z_i$ in the cyclic order of vertices of q.

To decide whether z is in the medial region or in the parallel region of the corresponding translated copy of $(-{{\mathcal {P}}})$, centered at the ith vertex, we proceed as follows.

• Step 1 Let $z_i$ be the ith vertex of q. Place three copies $T_j$ of the processed medial axis of $(-{{\mathcal {P}}})$, $j\in \{-1,0,1\}$, at the $(i{-}1)$st, ith, and $(i{+}1)$st vertices of q.

• Step 2 Find the outer common tangents of $T_{-1}, T_0$ and of $T_0, T_1$. This will allow us to detect the medial region and parallel region of $T_0$ with respect to q.

• Step 3 (3.1) If z is in the medial region of $T_0$, then set the value of $D_{{\mathcal {P}}}(z,q)$ by invoking $D_{{\mathcal {P}}}(z,z_i)$, and return the point $q^*$.

  (3.2) Otherwise, if z is in the parallel region (see Fig. 9b), invoke a ray-shooting query on the common boundary $B_i$ between the medial region and the parallel region of $T_{i}$ in order to find $z'$, the projection of z on $B_i$. Set the value of $D_{{\mathcal {P}}}(z,q)$ by computing $D_{{\mathcal {P}}}(z',z_i)$. Then, find and return the point $q^*$ by translating the point $z_i$ by $d(z,z')$ along the ith edge of q, where $d(z,z')$ is the Euclidean distance between z and $z'$.

  (3.3) Otherwise, determine whether z lies to the left or to the right of $z_i$ in the cyclic list of vertices of q, and continue accordingly the binary search.

Step 1 takes constant time. Step 2 takes $O(\log m)$ time, assuming that $(-{{\mathcal {P}}})$ is available as a cyclic list of vertices. Step 3.1 can be performed in $O(\log m)$ time, as in Lemma 2. Since $B_i$ is a path from a vertex to the center along the medial of $(-{{\mathcal {P}}})$, we can perform a binary search and find $z'$ in $O(\log m)$ time. Hence, Step 3.2 takes $O(\log m)$ time as well. Step 3.3 takes constant time. Thus, each step of the binary search requires $O(\log m)$ time. In total, the query time complexity is $O(\log k \log m)$. This completes the proof. $\square$

Another primitive operation computes the Voronoi vertex $v^*$, around which the Voronoi cells for polygonal sites $q_1,q_2,q_3$, with respect to the polygon-offset distance $D_{{\mathcal {P}}}$, occur in a counter-clockwise order. As in the line-segments case, by applying the tentative prune-and-search paradigm [15], we can find $v^*$ in the same manner as in Ref. [7]. The main difference is that here, three different polygons $(-{{\mathcal {P}}})^{q_1}$, $(-{{\mathcal {P}}})^{q_2}$, and $(-{{\mathcal {P}}})^{q_3}$ are involved in the computation instead of three identical copies of $(-{{\mathcal {P}}})$. However, this does not affect the performance of the general paradigm. Nevertheless, each $O(\log m)$-time distance evaluation function is replaced by an $O(\log k \log m)$-time operation for evaluating $D_{{\mathcal {P}}}(z,q)$ (by Lemma 12). Thus, we have the following:

Lemma 13

Given three polygons $p_1,p_2,p_3,$ each having at most k sides, and a convex m -gon ${{\mathcal {P}}}$ in the plane, the Voronoi vertex $v^*,$ where the Voronoi cells for sites $p_1,p_2,p_3,$ with respect to the polygon-offset distance $D_{{\mathcal {P}}},$ occur in counter-clockwise order, can be computed in $O(\log k \log ^2 m)$ time (allowing $O(m^2)$ time for preprocessing ${{\mathcal {P}}}).$ $\square$

6 Compact Voronoi Diagram

As mentioned earlier, McAllister et al. [18] presented an algorithm for computing a compact representation of the nearest-site Voronoi diagram of a set of convex polygonal sites with respect to a convex (scaling) distance function. Here, we show how to adapt their method to obtain the compact representation of $\hbox {NV}_{{\mathcal {P}}}({\mathscr {Q}})$, where ${\mathscr {Q}}$ is a set of n convex polygonal sites, each having at most k sides, and ${{\mathcal {P}}}$ is an m-sided convex polygon.

For any point z and a polygonal site q, spoke(z, q) is defined as the line segment $\overline{z,z^*}$ with $z^*\in q$, such that $D_{{\mathcal {P}}}(z,z^*) = \min \limits _{z'\in q} D_{{\mathcal {P}}}(z,z')$. Here, $z^*$ is referred to as the attachment point of the spoke. Note that spoke(z, q) can be computed in $O(\log k \log m)$ time (with $O(m^2)$ preprocessing time), where the polygon q has complexity k (by Lemma 12).

For three sites $q_1,q_2,q_3$, ${\textit{vertex}}(q_1,q_2,q_3)$ is defined as the point v equidistant from $q_1,q_2,q_3$ with respect to the convex polygon-offset distance function $D_{{\mathcal {P}}}$. By Lemma 13, we know that ${\textit{vertex}}(q_1,q_2,q_3)$ can be computed in $O(\log k\log ^2 m)$ time (with $O(m^2)$ preprocessing time).

The compact Voronoi diagram is a simplified version of the full Voronoi diagram. In this diagram, we maintain a set of spokes from the Voronoi vertices around the site, and each polygonal site q is replaced by its core, where a core is the convex hull of the attachment points that lie on the boundary of q (see Ref. [18, Fig. 4]). As a result, we obtain a compact representation whose combinatorial complexity is O(n), which is much smaller than $O(n(m+k))$, the combinatorial complexity of the full diagram $\hbox {NV}_{{\mathcal {P}}}({\mathscr {Q}})$.

Note that each cell of this compact diagram is actually composed of portions of two cells of the full Voronoi diagram. Thus, we can answer point-location queries as follows. Given a point z, we can obtain the cell in the compact diagram, and the two corresponding candidate sites $q_i$ and $q_j$, in $O(\log n)$ time. Then, by spending additional $O(\log k \log m)$ time for comparing between $D_{{\mathcal {P}}}(z,q_i)$ and $D_{{\mathcal {P}}}(z,q_j)$, we can determine the identity of the cell of the full Voronoi diagram in which z is located.

As observed earlier [7, §4], the geometric properties of the compact Voronoi diagram are preserved when we use a convex polygon-offset distance function instead of a convex distance function. Hence, we can apply Theorem 3.10 of Ref. [18], which states that the compact representation of the Voronoi diagram can be computed in $O(n(\log n +T_v))$ time, where $T_v$ is the time needed for performing primitive operations like spoke(z, q) and $vertex(q_1,q_2,q_3)$. By Lemmata 12 and 13, we know that $T_v = O(\log k\log ^2 m)$ for convex polygonal sites. Thus, we can compute in $O(n(\log n + \log k \log ^2 m)+m^2)$ time a compact representation for $\hbox {NV}_{{\mathcal {P}}}({\mathscr {Q}})$, where ${\mathscr {Q}}$ is a set of n disjoint convex polygonal sites, each having at most k sides. Thus, we have the following.

Theorem 5

Let ${{\mathcal {P}}}$ be a convex m -gon. For a set ${\mathscr {Q}}$ of n convex polygonal sites, each having at most k sides, a compact representation of $\hbox {NV}_{{\mathcal {P}}}({\mathscr {Q}})$ can be computed in expected $O(n(\log n + \log k \log ^2 m)+m^2)$ time. $\square$

Following the same arguments as in the proof of Theorem 5, we also obtain the following.

Theorem 6

For a set ${\mathscr {S}}$ of n line segments, a compact representation of $\hbox {NV}_{{\mathcal {P}}}({\mathscr {S}})$ can be computed in $O(n(\log n + \log ^2 m)+m^2)$ time, where m is the complexity of a convex m -gon ${{\mathcal {P}}}$. $\square$

7 Farthest-Site Voronoi Diagrams

We are given a set ${\mathscr {S}}=\{\sigma _1,\sigma _2,\ldots ,\sigma _n\}$ of n sites (line segments or convex polygons) in ${\mathbb {R}}^2$. In this section, following the framework of Mehlhorn et al. [19] (and generalizing the approach of Barequet et al. [7, §5]), we obtain the combinatorial complexity of the farthest-site Voronoi diagram of ${\mathscr {S}}$ with respect to the distance function $D_{{\mathcal {P}}}$, where ${{\mathcal {P}}}$ is a convex polygon with m sides.

Let $\sigma _i$, $\sigma _j$ be a pair of sites in ${\mathscr {S}}$. As in Sect. 2, we define $\hbox {NV}_{{\mathcal {P}}}^{\sigma _j}(\sigma _i)$ to contain all the points in the plane that are closer to $\sigma _i$ than to $\sigma _j$ with respect to $D_{{\mathcal {P}}}$. Let us also define the dominant set $M(\sigma _i,\sigma _j)$ to be the region of $\hbox {NV}_{{\mathcal {P}}}^{\sigma _j}(\sigma _i)$ except the bisecting curve $\partial M(\sigma _i,\sigma _j) = B_{{\mathcal {P}}}(\sigma _i,\sigma _j)$.

Consider the family $M=\{M(\sigma _i,\sigma _j)|1 \le i \ne j \le n \}$. The family M is called a dominance system if for all $\sigma _i,\sigma _j\in S$, the following properties are satisfied:

• 1. $M(\sigma _i,\sigma _j)$ is open and non-empty;

• 2. $M(\sigma _i,\sigma _j)\cap M(\sigma _j,\sigma _i)=\emptyset$ and $\partial M(\sigma _i,\sigma _j) = \partial M(\sigma _j,\sigma _i)$; and

• 3. $\partial M(\sigma _i,\sigma _j)$ is homeomorphic to the open interval (0, 1).

Similarly to the argument given in Ref. [7, Thm. 16], we can prove the following.

Lemma 14

The family M is a dominance system.

Proof

We argue why the properties of a dominance system are satisfied.

• 1. $M(\sigma _i,\sigma _j)$ is open and non-empty because it is precisely one of the two portions of the plane bounded by the infinite Jordan curve $B_{{\mathcal {P}}}(\sigma _i,\sigma _j)$.

• 2. Centering ${{\mathcal {P}}}$ at any point $r\in {\mathbb {R}}^2$, if we “pump” ${{\mathcal {P}}}$ up, then either it hits $\sigma _i$ first, or $\sigma _j$ first, or hits simultaneously $\sigma _i$ and $\sigma _j$. In the first case, $r \in M(\sigma _i,\sigma _j)$; in the second case, $r \in M(\sigma _j,\sigma _i)$; and in the third case, $r \in M(\sigma _i,\sigma _j)$ or $r \in M(\sigma _j,\sigma _i)$, depending on whether $i<j$ or $j<i$. Hence, $M(\sigma _i,\sigma _j) \cap M(\sigma _j,\sigma _i)=\emptyset$. On the other hand, $\partial M(\sigma _i,\sigma _j)= B_{{\mathcal {P}}}(\sigma _i,\sigma _j) = \overline{\hbox {NV}_{{\mathcal {P}}}^{\sigma _j}(\sigma _i)} \cap \overline{\hbox {NV}_{{\mathcal {P}}}^{\sigma _i}(\sigma _j)}=B_{{\mathcal {P}}}(\sigma _j,\sigma _i) = \partial M(\sigma _j,\sigma _i)$.

• 3. $\partial M(\sigma _i,\sigma _j)$ is homeomorphic to the open interval (0, 1) since $B_{{\mathcal {P}}}(\sigma _i,\sigma _j)$ is a polycurve [see Lemma 9(i)].$\square$

A dominance system is admissible if it also satisfies the following properties.

• 4. Any two bisecting curves intersect finitely-many times.

• 5. For all non-empty subsets $S'$ of S, and for every re-ordering of indices in S,

  • (a) The (nearest neighbor) Voronoi cell of every site $\sigma _i \in S'$ (with respect to $S'$) is connected and it has a non-empty interior; and

  • (b) The union of all the (nearest neighbor) Voronoi cells of all sites $\sigma _i \in S'$ (with respect to $S'$) is the entire plane.

A dominance system which satisfies only Properties 4 and 5(b) is called semi-admissible.

It is easy to verify from Corollary 2 and Lemmata 9(ii) and 14 that the family M is admissible. Thus, we have the following.

Theorem 7

The family M is admissible. $\square$

The fact that M is semi-admissible suffices for our purposes. Consider now the family $M^*$, the “dual” of M, in which the dominance relation and the ordering of the sites are reversed. We have the following theorem.

Theorem 8

[19, Lemma 1] If M is semi-admissible, then $M^*$ is semi-admissible too. Moreover, the farthest site Voronoi diagram that corresponds to $M^*$ is identical to the nearest site Voronoi diagram that corresponds to M. $\square$

As a consequence, we obtain the following.

Theorem 9

Let ${{\mathcal {P}}}$ be a convex polygon with m sides.

• (i) For a set of n line segments, the combinatorial complexity of the farthest-site Voronoi diagram (with respect to $D_{{\mathcal {P}}})$ is O(nm);

• (ii) For a set of n convex polygons, each having at most k sides, the combinatorial complexity of the farthest-site Voronoi diagram (with respect to $D_{{\mathcal {P}}})$ is $O(n(m+k))$. $\square$

Since the farthest-site Voronoi diagram can be defined as a dominance system, we can adopt the framework of Ref. [19]. Thus, the farthest site Voronoi diagram is a tree, and we can compute it by using a randomized algorithm in expected $O(n\log n T_v+ m)$ time, where $T_v$ is the time needed for computing a primitive function that computes the diagram of five sites. With $O(m^2)$ preprocessing time, this primitive takes $O(\log ^2 m)$ time for line-segment sites, and $O(\log k+ \log ^2m)$ time for polygonal sites, each having at most k sides (applying the same technique of Lemmata 11 and 13, respectively). Thus, the diagram $\hbox {FV}_{{\mathcal {P}}}({\mathscr {S}})$ can be computed in expected $O(n\log n \log ^2 m + m^2)$ time, where ${\mathscr {S}}$ is a set of n disjoint line segments, and $\hbox {FV}_{{\mathcal {P}}}({\mathscr {Q}})$ can be computed in expected $O(n\log n(\log k+ \log ^2m) + m^2)$ time, where ${\mathscr {Q}}$ is a set of n disjoint convex polygons, each having at most k sides.

For computing the diagram in a deterministic manner, we can apply the three-dimensional plane-sweep approach of Rappaport [23]. In this method, we have polyhedral cones emanating from each site, and the plane sweep detects their intersections and produces the corresponding Voronoi vertices. For a line-segment site s, the base of the polyhedral cone is the convex polygon $(-{{\mathcal {P}}})^s$. Considering the plane $H_{\varepsilon }$ at height $\varepsilon$, the intersection of $H_{\varepsilon }$ with the polyhedral cone is an SaE $\varepsilon$-offset copy of $(-{{\mathcal {P}}})^s$, denoted by ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^s,\varepsilon }$. Since, with a preprocessing time of $O(m^2)$, we can find the intersection of any three such SaE $\varepsilon$-offset copies in $O(\log ^2 m)$ time (by Lemma 11), and the total number of events (i.e., vertices of the diagram) is O(n), we can enumerate all the vertices of $\hbox {FV}_{{\mathcal {P}}}({\mathscr {S}})$ in $O(n(\log ^2m + \log n) +m^2)$ time. (Note that $O(\log n)$ time is needed for each queue operation.) One can store $\hbox {FV}_{{\mathcal {P}}}({\mathscr {S}})$ compactly by representing each bisecting curve by a list of the relative positions of their respective sites.

Similarly, for a convex polygonal site q, the base of the polyhedral cone is the convex polygon $(-{{\mathcal {P}}})^q$, and the intersection of $H_{\varepsilon }$ with the polyhedral cone is an SaE $\varepsilon$-offset copy of $(-{{\mathcal {P}}})^q$, denoted by ${{\mathcal {O}}}_{(-{{\mathcal {P}}})^q,\varepsilon }$. We can compute a compact representation of $\hbox {FV}_{{\mathcal {P}}}({\mathscr {Q}})$ in $O(n(\log k\log ^2m + \log n) +m^2)$ time.

8 Conclusion

We discuss the structural complexity and algorithms for computing the nearest- and farthest-site Voronoi diagram of line segments or convex polygons under the convex polygon-offset distance function. It would be challenging to reduce the time needed to compute the diagrams by improving the query times of elementary operations. Another interesting direction for future research is the investigation of higher-order Voronoi diagram in a similar setting.